Поверхности (линии) уровня
Пусть в трехмерном пространстве имеется область D, в которой задана функция
.
В этом случае говорят, что в области Dзадано скалярное поле.
Если, например, функция обозначает температуру в точке, то говорят, что задано скалярное поле температур; если областьDзаполнена жидкостью или газом иобозначает давление, то имеется скалярное поле давлений и т. д.
Рассмотрим точки области D,
в которых функцияимеет постоянное значение :
:
.
Совокупность этих точек образует
некоторую поверхность. Если возьмем
другое значение  ,
то получим другую поверхность. Эти
поверхности называются поверхностями
уровня.
,
то получим другую поверхность. Эти
поверхности называются поверхностями
уровня.
Пример. Пусть задано скалярное поле
.
Здесь поверхностями уровня будут поверхности
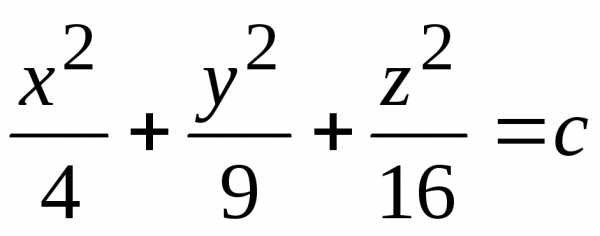 ,
,
т. е. эллипсоиды с полуосями 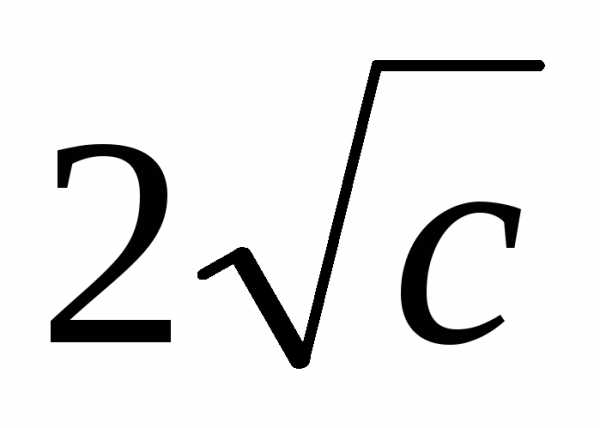 ,
, ,
,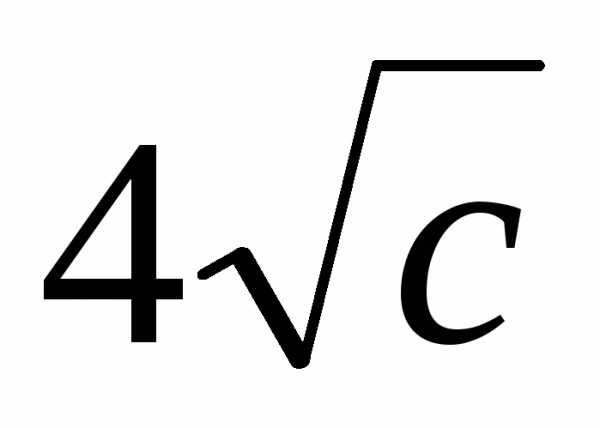 .
.
Если функция  есть функция двух переменных
есть функция двух переменных и
и :
:
,
то «поверхностями» уровня будут линии
на плоскости  :
:
,
которые называются линиями уровня.
Если значения 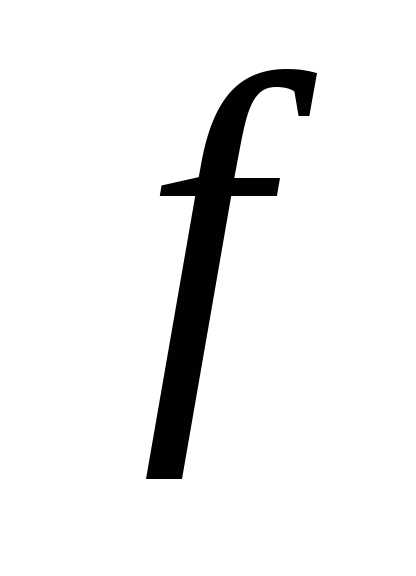
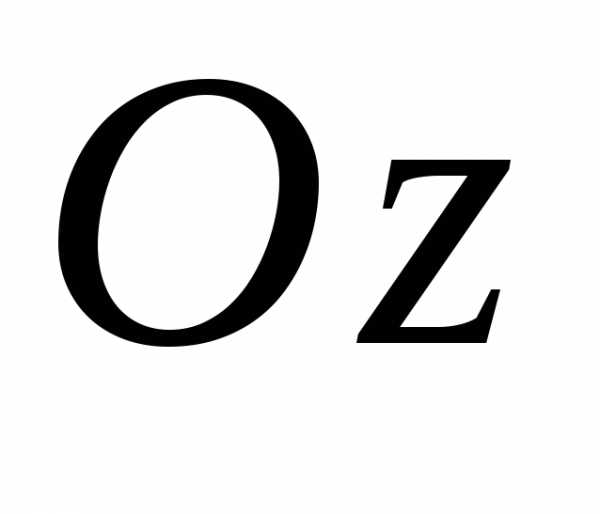 ,
то линиями уровня на плоскости
,
то линиями уровня на плоскости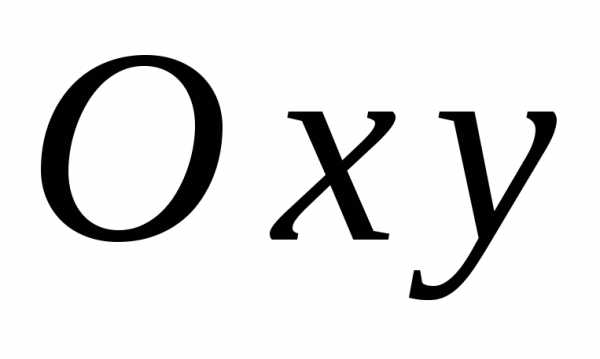 будут проекции линий, которые
получаются в пересечении поверхностис плоскостями
будут проекции линий, которые
получаются в пересечении поверхностис плоскостями .
Зная линии уровня, легко исследовать
характер поверхности.
.
Зная линии уровня, легко исследовать
характер поверхности. 
Пример. Определить линии уровня функции.
Решение.Линиями уровня будут линии
с уравнениями.
Это окружности радиуса .
В частности, при
.
В частности, при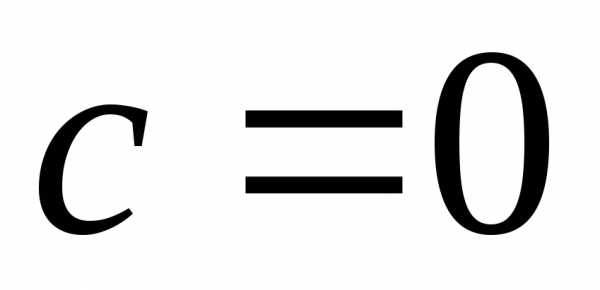 получаем окружность
получаем окружность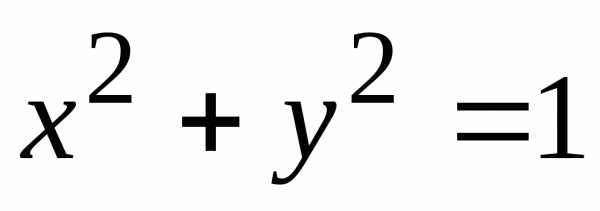 .
График данной функции, а также получаемые
линии уровня изображены на рисунке.
.
График данной функции, а также получаемые
линии уровня изображены на рисунке.
Предел функции нескольких переменных
Определение.Число А называется
пределом функциипри,
т.е. в точке,
если для любого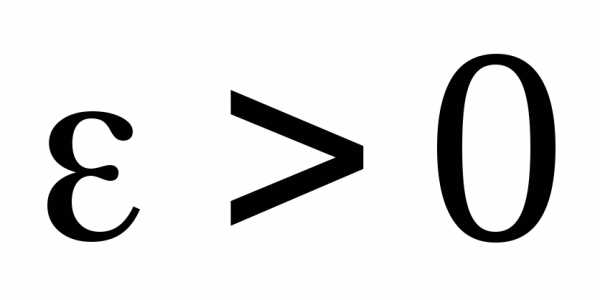 существует
существует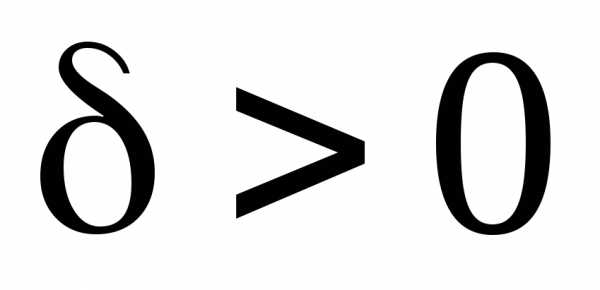 ,
такое, что при всех
,
такое, что при всех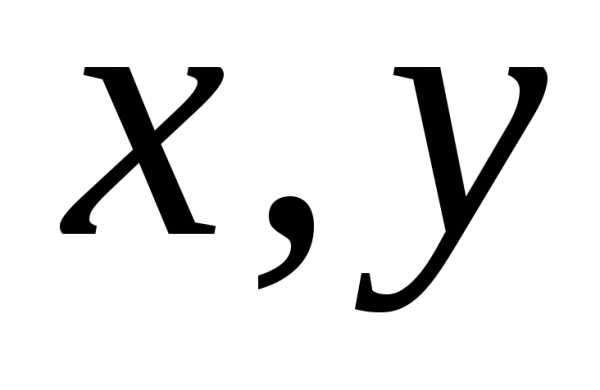 ,
удовлетворяющих условиям
,
удовлетворяющих условиям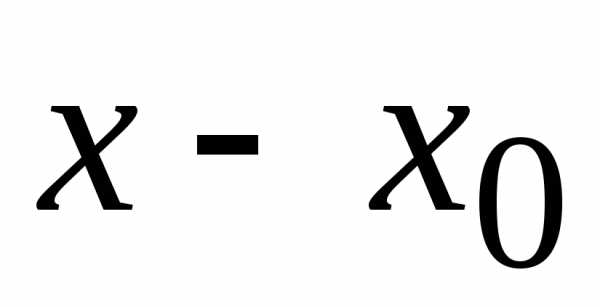
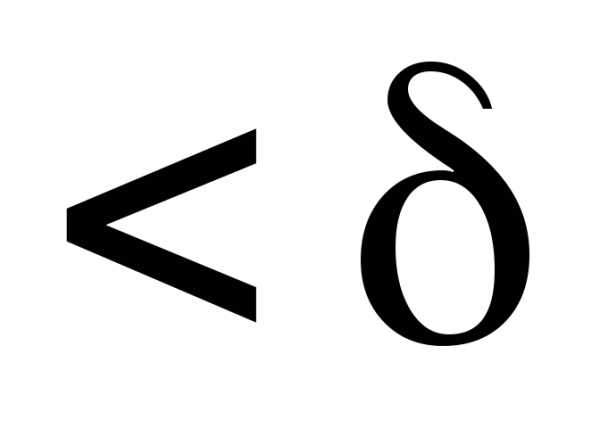 и
и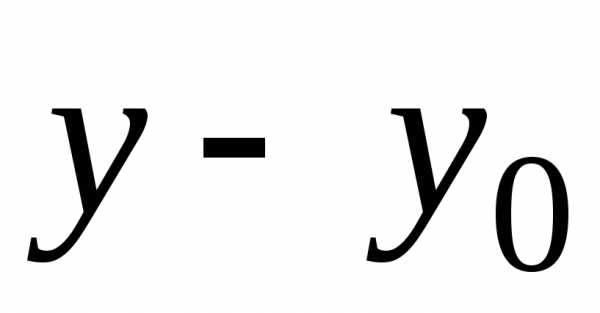
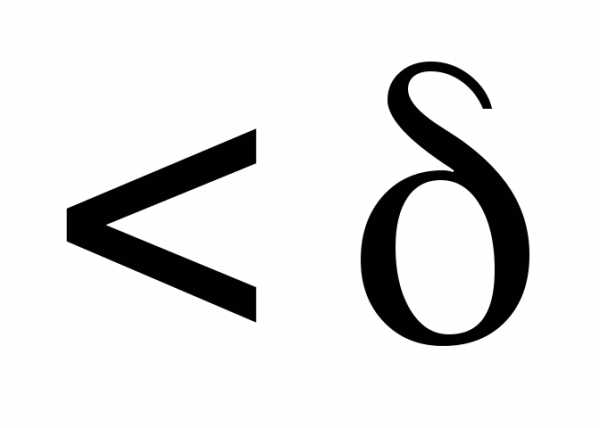 ,
выполняется неравенство
,
выполняется неравенство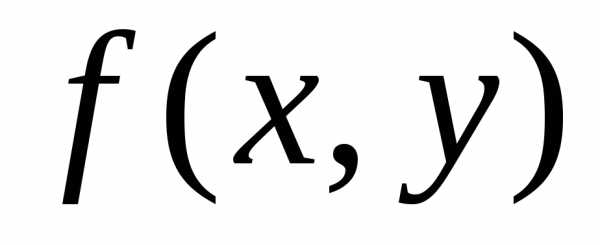 — А
— А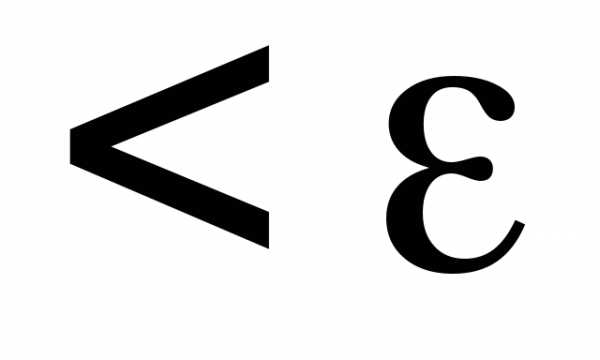 .
.
Данное определение в символьном виде можно записать так:
Для обозначения предела функции в точкеиспользуют и другую форму записи:
.Замечание. При определении предела функциив точкеполагают, что функция может быть и не определена в самой точке.
Пример.Доказать, пользуясь
определением предела по Коши, что 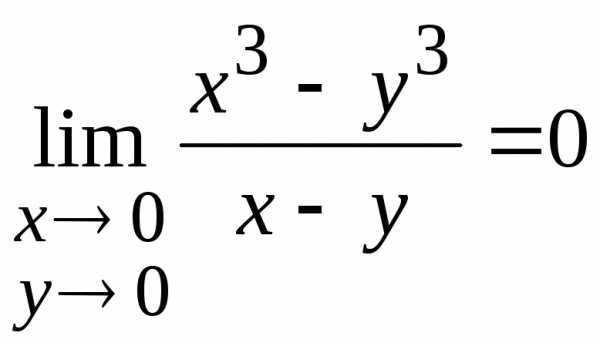 .
.
Решение.Область определения данной
функцииD.
Выберем произвольное число и найдем
и найдем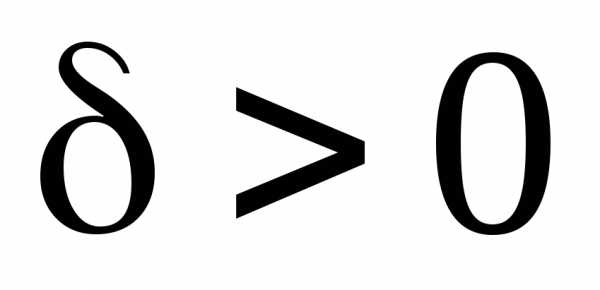 ,
такое, что для любой точки
,
такое, что для любой точки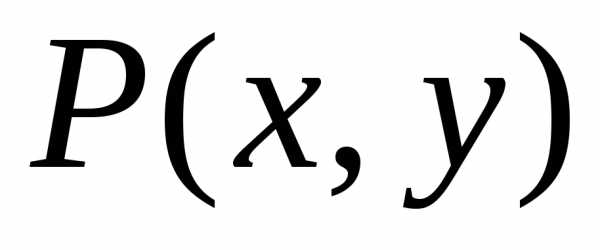 ,
для которой справедливо
,
для которой справедливо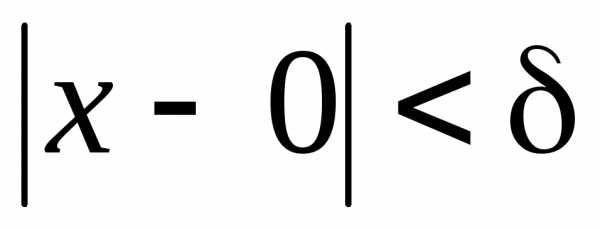 ,
,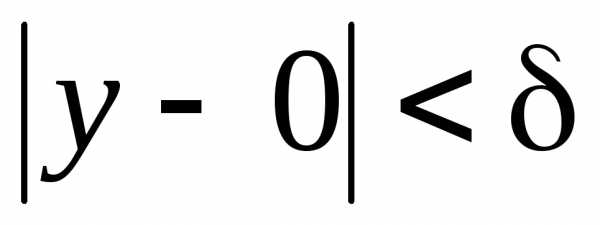 выполняется неравенство.
Так как для любой точки
выполняется неравенство.
Так как для любой точки D
D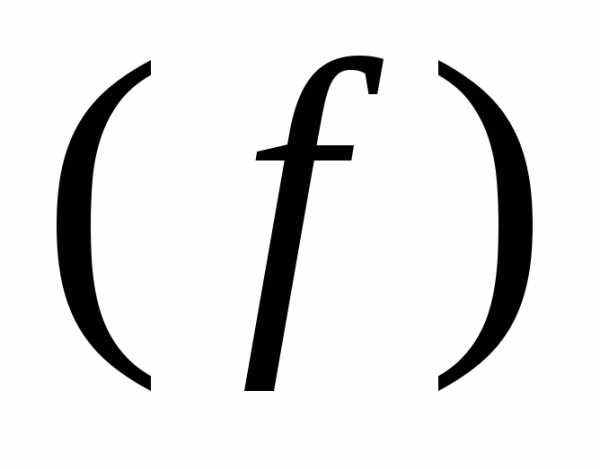 справедливо соотношение
справедливо соотношение
,
то
Оценим 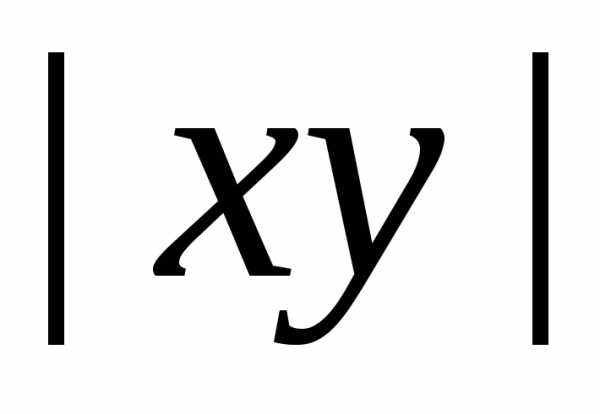 :
:
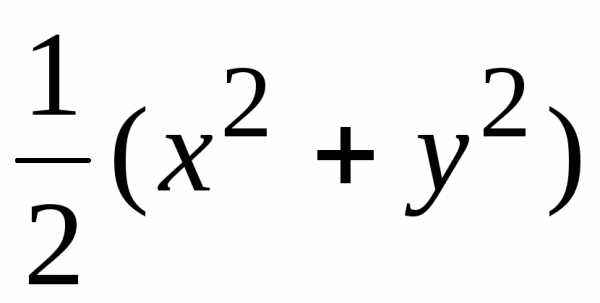 .
.
Таким образом,
,
где 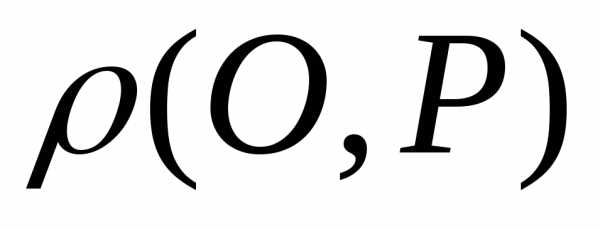 — расстояние от точки
— расстояние от точки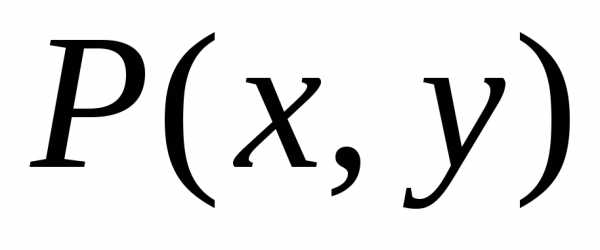 до точки
до точки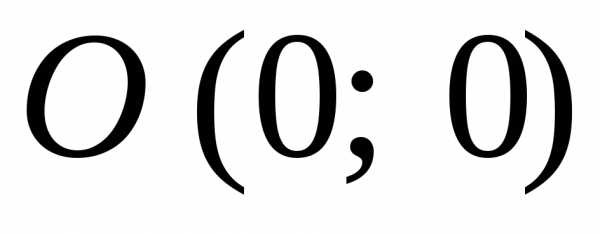 .
.
Следовательно, для любого 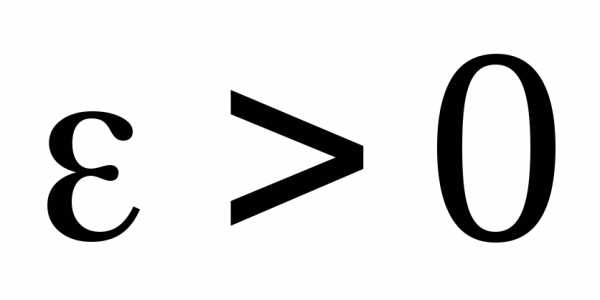 мы нашли число
мы нашли число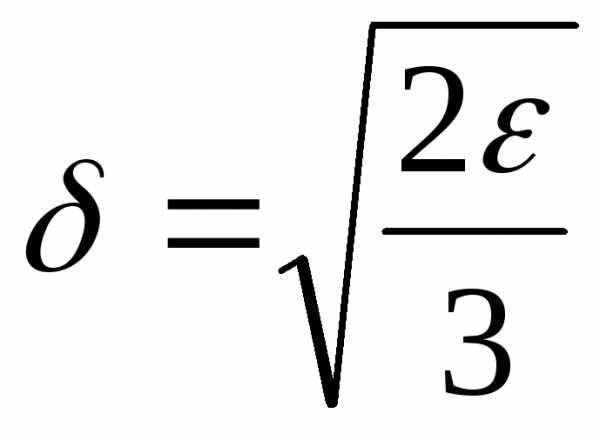 ,
такое, что для любой точки
,
такое, что для любой точки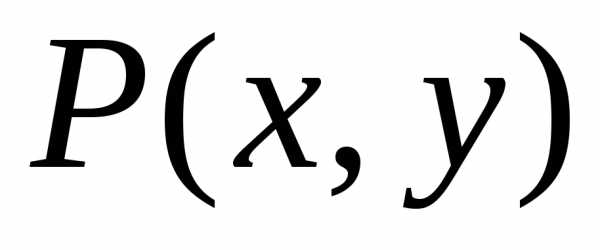 ,
принадлежащей
,
принадлежащей -окрестности
точки
-окрестности
точки ,
т.е. при
,
т.е. при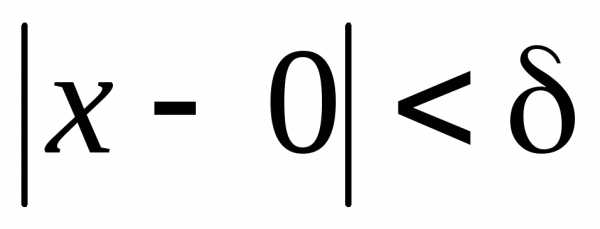 ,
,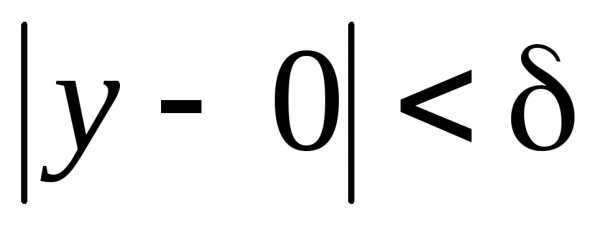 будет выполняться неравенство
будет выполняться неравенство
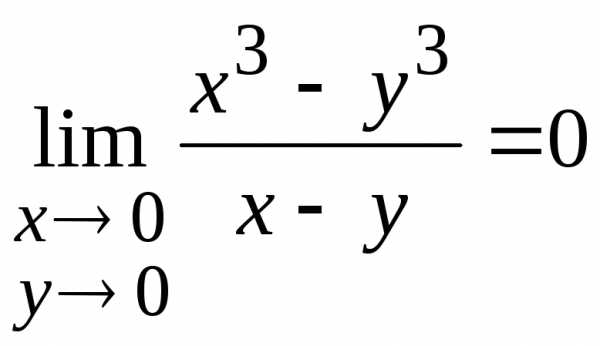 .
.
Что и требовалось доказать.
Приведенные выше определения предела
функции двух переменных без труда
обобщаются на случай функций трех и
более переменных. Обобщим, например,
определение предела по Коши на случай
функции 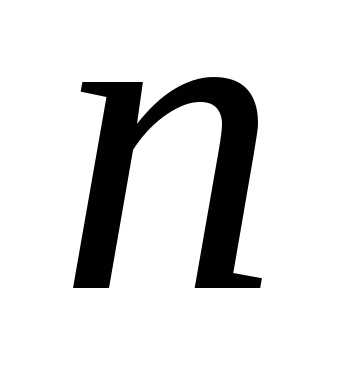 независимых переменных.
независимых переменных.
Определение.Число А называется
пределом функциипри,т.е.
в точке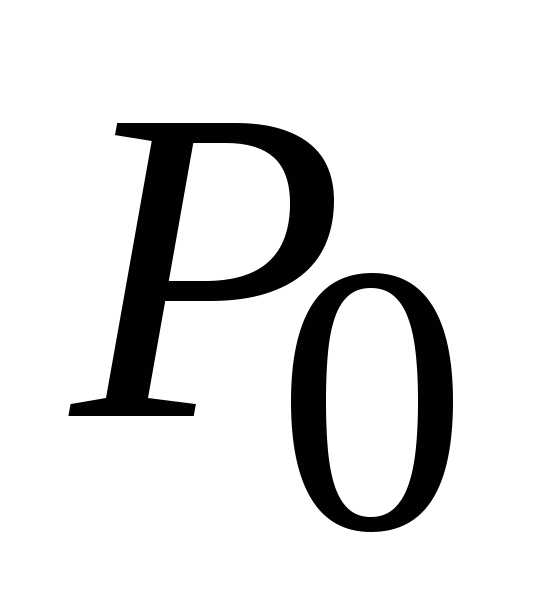 ,
если для любого
,
если для любого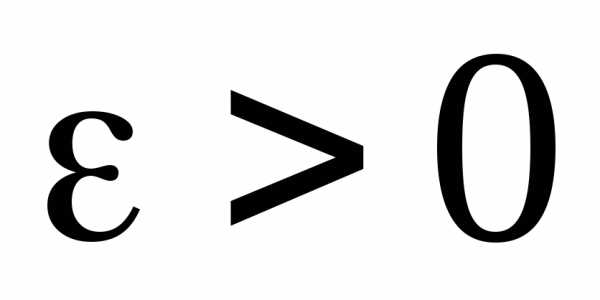 существует
существует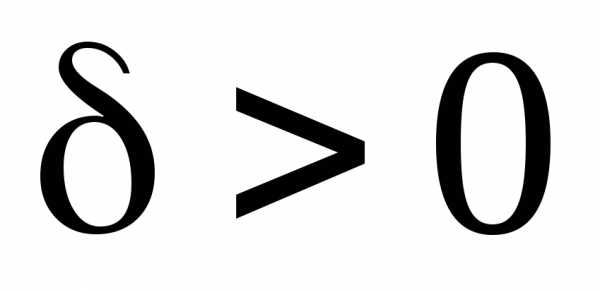 ,
такое, что при всех
, удовлетворяющих условиям
,
такое, что при всех
, удовлетворяющих условиям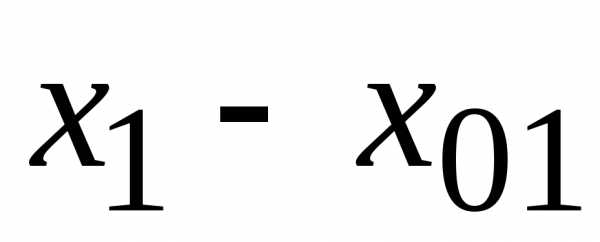
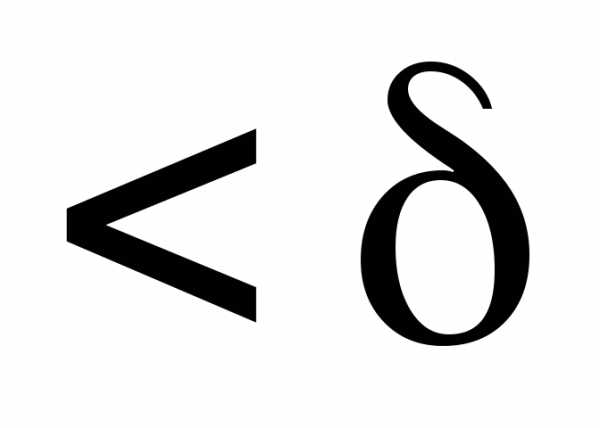 ,
,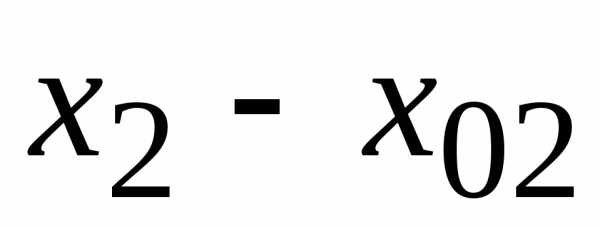
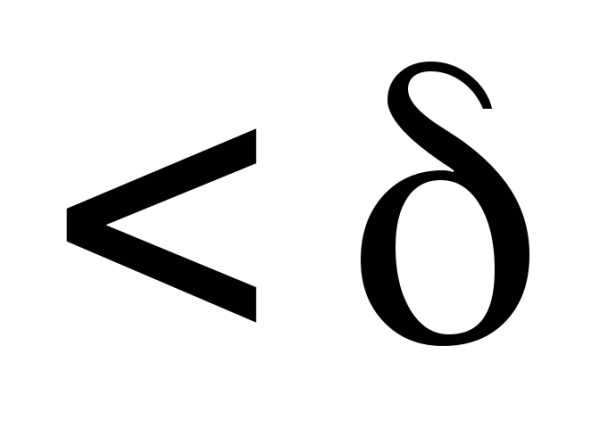
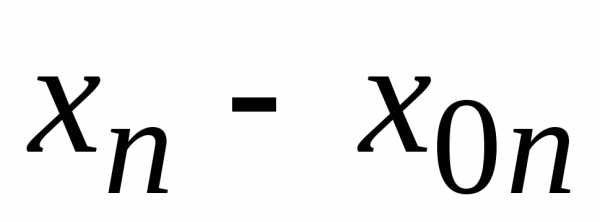
 ,
выполняется неравенство— А
,
выполняется неравенство— А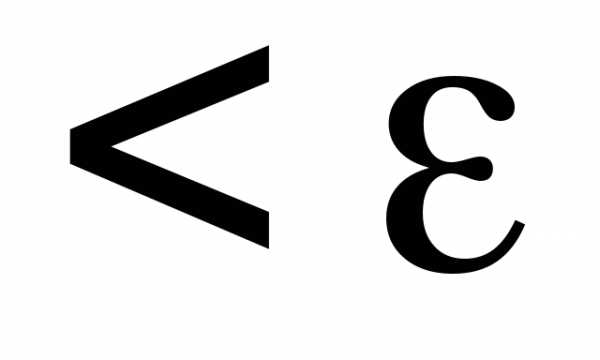 .
. Пользуясь понятием предела функции,
можно дать определение бесконечно малой
функции при  (),
вывести основные свойства бесконечно
малых функций, сравнить бесконечно
малые функции, доказать теорему о том,
что разность между функцией, имеющей
предел, и ее пределом есть бесконечно
малая функция, сформулировать основные
теоремы об арифметических операциях
над пределами. Все эти теоремы для случая
(),
вывести основные свойства бесконечно
малых функций, сравнить бесконечно
малые функции, доказать теорему о том,
что разность между функцией, имеющей
предел, и ее пределом есть бесконечно
малая функция, сформулировать основные
теоремы об арифметических операциях
над пределами. Все эти теоремы для случая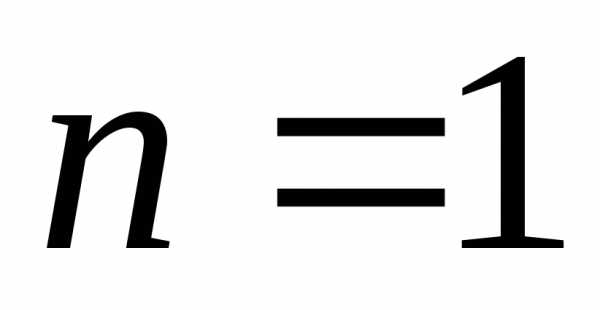 были рассмотрены при изучении функций
одной переменной.
были рассмотрены при изучении функций
одной переменной.
studfiles.net
Линия уровня — это… Что такое Линия уровня?
линия уровня — линия равного уровня Геометрическое место точек пространства, для которых значения исследуемой функции одинаковы. Это определение можно записать так: {x ? En | F (x) = const}. Такая запись означает, что для некоторых xi, принадлежащих… … Справочник технического переводчика
линия уровня — izohipsa statusas T sritis Standartizacija ir metrologija apibrėžtis Vienodo aukščio kreivė. atitikmenys: angl. curve of equal altitude; isohypse; level curve vok. Höhengleiche, f; Isohypse, f; Niveaulinie, f rus. изогипса, f; линия равной высоты … Penkiakalbis aiškinamasis metrologijos terminų žodynas
линия уровня — izohipsa statusas T sritis fizika atitikmenys: angl. curve of equal altitude; isohypse; level curve vok. Höhengleiche, f; Isohypse, f; Niveaulinie, f rus. изогипса, f; линия равной высоты, f; линия уровня, f pranc. courbe de niveau, f; courbe… … Fizikos terminų žodynas
линия уровня приведенных зазоров модифицированных поверхностей зубьев конической передачи
линия уровня моря — — [http://slovarionline.ru/anglo russkiy slovar neftegazovoy promyishlennosti/] Тематики нефтегазовая промышленность EN sea level line … Справочник технического переводчика
Линия уровня приведенных зазоров модифицированных поверхностей зубьев конической передачи — 154. Линия уровня приведенных зазоров модифицированных поверхностей зубьев конической передачи Линия уровня приведенных зазоров зубьев Источник: ГОСТ 19325 73: Передачи зубчатые конические. Термины, определения и обозначения … Словарь-справочник терминов нормативно-технической документации
Линия — Участок двух , трех или четырехпроводной электрической сети Источник: ФЕРп 2001: Приложения (редакция 2009 г.). Приложения. Федеральные единичные расценки на пусконаладочные работы … Словарь-справочник терминов нормативно-технической документации
Линия — В Викисловаре есть статья «линия» Линия (от лат. linea «льняная нить, шнур; линия») протяжённый и тонкий п … Википедия
линия равной высоты — izohipsa statusas T sritis Standartizacija ir metrologija apibrėžtis Vienodo aukščio kreivė. atitikmenys: angl. curve of equal altitude; isohypse; level curve vok. Höhengleiche, f; Isohypse, f; Niveaulinie, f rus. изогипса, f; линия равной высоты … Penkiakalbis aiškinamasis metrologijos terminų žodynas
линия равной высоты — izohipsa statusas T sritis fizika atitikmenys: angl. curve of equal altitude; isohypse; level curve vok. Höhengleiche, f; Isohypse, f; Niveaulinie, f rus. изогипса, f; линия равной высоты, f; линия уровня, f pranc. courbe de niveau, f; courbe… … Fizikos terminų žodynas
economic_mathematics.academic.ru
Линии уровня Википедия
 Построение изогипсы
Построение изогипсыИзоли́ния, или линия уровня (функции) (от др.-греч. ισος — «равный») — условное обозначение на карте, чертеже, схеме или графике, представляющее собой линию, в каждой точке которой измеряемая величина сохраняет одинаковое значение. Изолинии — способ представления скалярной функции от двух переменных на плоскости.
Виды изолиний
Метеорологические изотермы среднегодовой температуры в Европе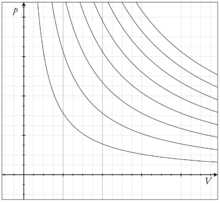 Графики изотермических процессов в идеальном газе
Графики изотермических процессов в идеальном газе- Изоанемона — линия одинаковых среднегодовых скоростей ветра.
- Изобаза — линия на карте, соединяющая точки с равной амплитудой и направлением неотектонических движений.
- Изобара — изолиния одинакового давления:
- Изобата — линия на карте, или плане, соединяющая точки одинаковых глубин водоёма (озера, моря).
- Изогалина — линия на географической карте, соединяющая точки с одинаковой солёностью воды.
- Изогиета — изолиния одинакового выпадения атмосферных осадков.
- Изогипса (горизонталь) — изолиния одинаковых высот (обычно для отображения рельефа на топографической карте).
- Изогона — изолиния ориентации каких-либо физических величин.
- Изодинама (от изо … и греч. dynamis — сила) — изолиния полной напряжённости земного магнитного поля или её составляющих (горизонтальной, вертикальной и др.) на магнитных картах.
- Изотерма — изолиния одинаковых температур:
- Изокванта — изолиния одинакового объёма производства продукта в зависимости от факторов производства.
- Изокоста — линия, демонстрирующая комбинации факторов производства, которые можно купить за одинаковую общую сумму денег.
- Изопахита — изолиния одинаковых мощностей пласта горных пород.
- Изотаха — изолиния одинаковых скоростей ветра (на карте максимальных ветров).
- Изохора — изолиния одинаковых объёмов.
Бергштрих
Бергштрих — чёрточка, проведённая перпендикулярно изолинии и указывающая свободным концом направление уменьшения обозначаемой изолиниями величины (для изогипс и изобат — в каком направлении склон снижается). Изначально бергштрих использовали при изображении рельефа местности горизонталями, для более лёгкого определения направления скатов[1].
См. также
Примечания
Ссылки
wikiredia.ru
Начертательная геометрия
8.4. Линии уровня плоскости
Прямые, лежащие в данной плоскости и параллельные одной из плоскостей проекций, называются линиями уровня плоскости.
Прямая, лежащая в данной плоскости и параллельная горизонтальной плоскости проекций П1, называется горизонталью плоскости (рис. 69). Все горизонтали плоскости параллельны между собой, поскольку каждая из них может быть получена как линия пересечения данной плоскости общего положения и горизонтальной плоскости уровня.
Рис. 69. Горизонтали плоскости:Рассмотрим построение горизонтали плоскости общего положения α(ABC) (рис. 70, а).
Рис. 70. Линии уровня плоскости: а – горизонталь плоскости α(ABC):б – фронталь плоскости β(a∥b) :Фронтальная проекция любой горизонтали всегда перпендикулярна линиям связи, поэтому построение горизонтали начинается с построения ее фронтальной проекции h2 ⊥(A1A2) . Поскольку горизонталь лежит в плоскости, она пересекается с прямой (AB) в точке 1, а с прямой (BC) – в точке 2. Горизонтальные проекции точек 1 и 2 однозначно определят положение горизонтальной проекции горизонтали h1(11-21).
Фронталь плоскости β(a||b) строится аналогично, но построение фронтали начинается с построения ее горизонтальной проекции (рис. 70, б). Все фронтали плоскости также параллельны между собой, поскольку каждая из них может быть получена как линия пересечения данной плоскости общего положения и фронтальной плоскости уровня.
Таким образом, любую плоскость общего положения можно представить как совокупность параллельных линий уровня – горизонталей, фронталей или профильных прямых. Иными словами, плоскость общего положения, заданную любым способом, можно также задать параллельными линиями уровня или пересекающимися горизонталью и фронталью. Такой способ задания плоскостей наиболее удобен для решения ряда метрических задач.
cdot-nntu.ru
Линии уровня в плоскости общего положения
Линиями уровня плоскости называются прямые, параллельные плоскостям проекций и лежащие в данной плоскости. В практике наиболее часто применяются горизонтали и фронтали плоскости. Горизонталью данной плоскости называется прямая, лежащая в этой плоскости и параллельная горизонтальной плоскости проекций П1.
На рис. 108, а такой прямой является горизонталь h||П1. Она параллельна горизонтали l, являющейся горизонтальным следом плоскости kXl. Установив эту параллельность, мы легко построим проекции горизонтали h, зная, что у параллельных прямых параллельны их одноименные проекции: h1||l1 и h2||l2 (или оси x12). Установленное свойство формулируется так: горизонтальная проекция горизонтали данной плоскости параллельна горизонтальной проекции горизонтального следа этой плоскости, а ее фронтальная проекция параллельна оси проекций. Горизонталь на двух плоскостях проекций имеет один фронтальный след N. На комплексном чертеже (рис. 108, б) фронтальная проекция V2 следа горизонтали N будет находиться на фронтальной проекции k2 фронтального следа плоскости, а горизонтальная проекция — на горизонтальной проекции k1 этого следа.
n
n
TBegin—>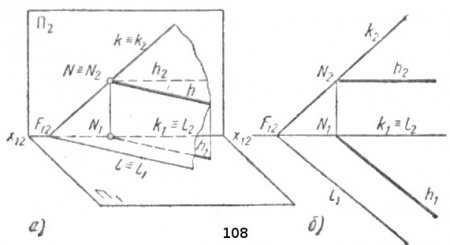 TEnd—>
TEnd—>
n
n
Фронталью данной плоскости называется прямая, лежащая в этой плоскости и параллельная фронтальной плоскости проекций П2 (рис. 109, а).
Фронталь f параллельнафронта-льному следу k плоскости; из этого следует, что f2||k2 и f1||k1 (или оси х12), т. е. фронтальная проекция фронтали данной плоскости параллельна фронтальной проекции фронтального следа этой плоскости, а ее горизонтальная проекция параллельна оси проекций. На комплексном чертеже проекции фронтали f удобно строить, используя проекции М1 и М2 горизонтального следа фронтали М (рис. 109, б). Через проекции точки М проводим k2 и оси х12 прямые f2 и fx, соответственно параллельные k2 и оси x12.
n
n
TBegin—>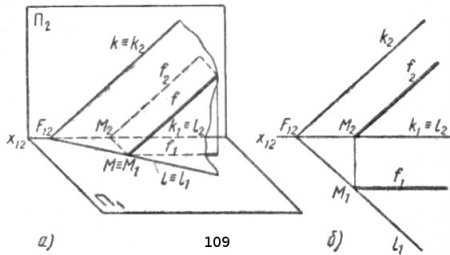 TEnd—>
TEnd—>
n
n
Выведенные свойства проекций горизонтали и фронтали легко использовать при построении этих прямых, принадлежащих плоскостям, заданным плоским отсеком.
Пусть требуется построить горизонталь плоскости треугольника АBС (рис. 110, а). Зная, что фронтальная проекция горизонтали всегда перпендикулярна вертикальным линиям связи (горизонтальна), проводим фронтальную проекцию горизонтали в любом месте фронтальной проекции A2В2С2 треугольника. Линия фпг пересечет стороны треугольника в точках D2 и E2. Чтобы точка D принадлежала прямой АВ, необходимо, чтобы ее горизонтальная проекция D1 принадлежала горизонтальной проекции А1В1 стороны треугольника; проводим из точки D2 вертикальную линию связи и в точке пересечения прямых находим точку D1. Рассуждая таким же образом, находим точку Е1 на горизонтальной проекции В1С1Х. Полученные при этом точки D1 и Е1 соединяем; линия D1Е1 — горизонтальная проекция горизонтали (сокращенно — гпг).
Линия D2E2 — фпг. Построение можно было несколько упростить, проведя фронтальную проекцию горизонтали не в произвольном месте, а через точку А2; в этом случае нужно было бы построить только одну новую точку Е.
n
n
TBegin—>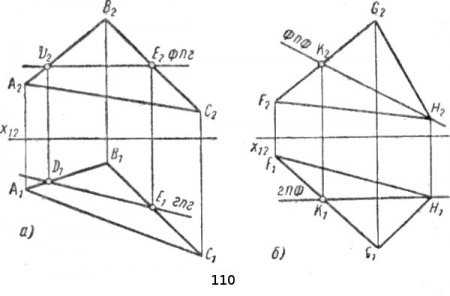 TEnd—>
TEnd—>
n
n
Аналогично строится фронталь плоскости общего положения (рис. 110 б). Построение начинаем с проведения горизонтальной проекции фронтали (гпф), поскольку известно ее горизонтальное направление. Эту прямую для упрощения проводим через точку Н1; прямая пересекает проекцию F1G1 стороны FG треугольника в точке К1. С помощью вертикальной линии связи находим фронтальную проекцию К2 на фронтальной проекции F1G1, Проводим фронтальную проекцию K2H2 фронтали КН (фпф).
Горизонтали и фронтали плоскостей общего положения, заданных плоскими отсеками, часто используются при решении различных задач начертательной геометрии.
polynsky.com.kg
Линия уровня — Энциклопедия по экономике
Множество допустимых значений вектора на рис. 1.8. На этом рисунке также изображены линии уровня критерия U( x). [c.51]Здесь p — параметр, не меньший размерности пространства критериев г, BI,. .., ег — положительные малые параметры. Чтобы представить себе смысл функции полезности (3.12), рассмотрим ее линии уровня (кривые безразличия) в пространстве критериев / при заданном значении / (рис. 6.6). [c.303]
Линии уровня этой функции в пространстве критериев / при заданной цели / приведены на рис. 6.6, а. Поскольку из-за малости величин EJ (/ = 1,. .., г) правое слагаемое практически не влияет на вид диний уровня, то получаем обычную функцию полезности [c.303]
Теперь рассмотрим случай р > г. Изучим структуру линий уровня функции (3.12) в том случае, когда не выполняется условие / /. Пусть min(/j — fj) достигается при / = /о. Так как ус- [c.304]
Линии уровня дйя этого случая приведены на рис. 6.6, в. В промежуточном случае, как можно проверить, линии уровня имеют вид, изображенный на рис. 6.6, б. [c.304]
Однако экономически содержательная интерпретация может быть наиболее убедительно продемонстрирована на плоскости ( 1(0, 0, поверхности безразличия в виде кривых функции полезности. Более подробное изображение этой плоскости представлено на рис. 11.4, который помогает прояснить логику геометрического способа построения кривых безразличия. [c.234]
Если провести на рис. 2.2 и 2.3 горизонтальную прямую, соответствующую достигнутому на молотовых линиях уровню приведенных затрат для коленчатого вала 10,9 р./шт. и для балки 10,4 р./шт., то экономически оправданными будут только те значения q и г 3, которые лежат ниже достигнутого уровня. [c.55]
Не только доходности достигли ключевой целевой области, но также и несколько циклов, наблюдаемых за эти годы проектировали, что облигации провели достаточно времени, падая в цене (повышаясь в доходности). С тестированием трендовой линией уровня 1981, это было хорошее место для изменения тренда. Когда доходность, коротко проколола эту восемнадцати-с-лишним-летнюю трендовую линию и не смогла пойти выше, прозвенел звонок (для агрессивных трейдеров) с сигналом покупать облигации. (Одна из стратегий, используемых агрессивными трейдерами заключается в противоположной торговле, когда рынок оказывается не в состоянии производить «ожидаемое» поведение. Прорыв восемнадцатилетней трендовой линии должен был привести к большой распродаже. Когда это не произошло, были сделаны покупки.) [c.200]
Нижние две линии Фибоначчи, построенные на медвежьем тренде, явились неплохими уровнями сопротивления для будущего рынка, а верхняя линия — уровнем поддержки после быстрого ее пробития. [c.134]
На рисунке 11 приведены линии уровня целевой функции цен- [c.71]
| Рис. 12. Линии уровня суммарного действия в зависимости |  |
Различные виды функций й(/о,/, А) в разной степени отвечают этим требованиям. Чтобы выбрать способ расширения и обосновать существование Л, важно разобраться в том, как изменяется максимальное значение функции /о при переходе от одной линии уровня функции / к другой. [c.338]
| Рис. 9.7. Линии уровня целевой функции, функции / (о) и функции достижимости (б) для задачи, изображенной на рис. 9.4 |  |
| Рис. 9.8. Случай совпадения условного и безусловного максимумов (а) — линии уровня целевой функции и ограничения (б) — характер функции достижимости |  |
Представление о функции может дать и метод линий уровня. Геометрическое место точек плоскости, в которых функция z — /(ж, у) принимает постоянное значение, называется линией уровня. Это линия пересечения поверхности z — /(ж, у) плоскостью z = С и ортогонально спроектированная на плоскость Оху. Сделав несколько таких сечений плоскостями z = С, [c.280]
Сечения плоскостями z = 1, Линии уровня окружности z — 2, z — 3 радиуса 1, /2, /3 [c.281]
| Рис. 14.2. Линии уровня функции z = х1 + у1 |  |
Линии уровня функции z = х2 + у2 — концентрические окружности [c.345]
Параллельный способ строения учетных регистров предусматривает размещение записей в процессе их регистрации по дебету и кредиту на одной линии (уровне), хотя сам регистр по строению может быть представлен в форме односторонней таблицы, двусторонней или мнографной (штафельной). Применение соответствующей формы регистрации связано прежде всего с содержанием хозяйственной операции. [c.327]
Линия тренда — это прямая линия. Линия поддержки соединяет локальные минимумы, линия сопротивления — локальные максимумы. С линиями (уровнями) поддержки и сопротивления в горизонтальном коридоре цен в фазе Инь мы уже познакомились в параграфе 1.3. Здесь же мы рассмотрим их более подробно. Сторонники теханализа считают, что существующая тенденция должна проявлять себя внутри линий тренда. Эти линии, таким образом, служат чем-то вроде рельсов, по которым катится локомотив рынка. Если, скажем, происходит пробой линии, то это важный сигнал к смене тенденции. Например, если пробивается линия поддержки на восходящем тренде, то это веский аргумент в пользу того, что восходящий тренд сменится либо горизонтальной, либо нисходящей тенденцией (см. рис. 51) [116] [c.137]Линия l(q) уровня q —f(L,K) производственной функции Q = f(L,K) называется изоквантой. Иными словами, линия уровня q — это множество точек, в которых объем производства постоянен и равен q. Различные наборы (v v и (wj, w затрачиваемых (используемых) ресурсов, принадлежащие одной и той же изо-кванте l(q), дают один и тот же объем выпуска q. Как и в случае с кривыми безразличия, углу наклона изокванты соответствует предельная норма технической замены одного ресурса другим. [c.175]
БАЗИСНОЕ РЕШЕНИЕ (опорный план) [basi solution] — термин линейного программирования, одно из допустимых решений, находящихся в вершинах области допустимых решений, либо (если линия уровня параллельна одному из отрезков границы области) Б.р. — весь этот отрезок (см. рис. Л.2 к ст. «Линейное программирование»). Оно является решением системы линейных ограничений, которое нельзя представить в виде линейной комбинации никаких других решений. [c.26]
КРИВЫЕ БЕЗРАЗЛИЧИЯ [indifferen e urves] — геометрическое место точек пространства товаров, характеризующихся состоянием безразличия с точки зрения равной полезности для потребителя. Она является линией уровня для функции полезности этого потребителя. С другой стороны, это графическая иллюстрация взаимозаменяемости товаров. Применение К.б. — метод теоретического анализа спроса и потребления (а также некоторых других экономических явлений). [c.162]
Остается найти ту из них, которая даст наибольшую прибыль, т.е. максимум целевой функции. Выбрав произвольно прямую с1х1 + с2х2 = П с произвольной константой П и обозначив ее ММ, находим на чертеже все точки (варианты планов), где прибыль одинакова при любом сочетании х, и х2 (см. Линия уровня). Перемещая эту линию параллельно ее исходному положению, найдем точку, которая в наибольшей мере удалена от начала координат, однако не вышла за пределы области допустимых значений. (Перемещая линию уровня еще дальше, уже выходим из нее и, следовательно, нарушаем ограничения задачи.) Точка М0 и будет искомым оптимальным планом. Она находится в одной из вершин многоугольника. Мо- [c.171]
ЛИНИЯ УРОВНЯ [ ontour line] (или линия равного уровня) — геометрическое место точек пространства аргументов, для которых значения исследуемой функции одинаковы. Это определение можно записать так [c.174]
Поясним причины недифференцируемости функции достижимости в случае вырожденного решения. Причина заключается в том, что вырожденному решению соответствует изолированная точка а на плоскости х. На рис. 9.7, а показано расположение линий уровня, соответствующих задаче, изображенной на рис. 9.4. При замене равенства /1 = 0 на /1 = С поверхность Д перестанет касаться с плоскостью, соответствующей значению С . Если точка касания а при сколь угодно малом изменении С исчезнет, то произойдет скачок функции достижимости в сторону ее уменьшения (рис. 9.7, б). [c.340]
Градиент совпадает с нормалью к линии уровня /(ж, у) = = onst в точке MQ. [c.294]
Переход к производственным функциям с семейством монотонных линий уровня f (k, I) — onst, имеющих горизонтальные и вертикальные асимптоты и конечные пределы вида lim / (k, 10) = F (/0) и lim f (k0t. [c.46]
I) = G (k0), не позволяет отразить в производственной функции внешние связи и связи между факторами и показателями их эффективности. Представляется, что производственные функции у = f (k, I) с линиями уровня f (k, I) = onst, задаваемыми немонотонными кривыми k — k (I), дают возможность более полного учета связей между факторами и внешних связей. [c.46]
Заметим также, что при использовании производственных функций с монотонными линиями уровня у = onst оценка параметров на основе имеющейся статистики неизбежно приводит к экстраполяции свойств производственной функции, присущих ограниченной области изменения ее аргументов, на более широкую область. Между тем для анализа и прогноза темпов экономического развития при качественно новых соотношениях для его факторов выход в эту, не просканированную практически область может стать принципиально необходимым. В таком случае от производственной функции придется требовать правильного отражения соче- [c.46]
economy-ru.info
Начертательная геометрия
4.1.1. Линии уровня
Прямые линии, параллельные какой-либо плоскости проекций, называются линиями уровня.
Горизонталь h – прямая, параллельная горизонтальной плоскости проекций h∥, П 1(рис. 12, 13).
Рис. 12. Горизонталь
Рис. 13. Комплексный чертеж горизонтали
Поскольку высоты всех точек горизонтали равны между собой: h2 ⊥A2A2 или h2∥x12 .
Любой отрезок горизонтали проецируется на П1 в натуральную величину: [A1B1]=[AB] .
Угол наклона h к П2 также проецируется на П1 в натуральную величину: ∠α1=∠α=∠h, П2.
Фронталь f – прямая, параллельная фронтальной плоскости проекций f∥, П 2 (рис. 14, 15).
Рис. 14. Фронталь
Рис. 15. Комплексный чертеж фронтали
Поскольку глубина всех точек фронтали одинакова: f1 ⊥ C1C2
Отрезки фронтали и угол наклона к П1 проецируются на П1 в натуральную величину: [C2D2] =[CD]; ∠β1=∠β=∠f, П1.
Профильная прямая p – прямая, параллельная профильной плоскости проекций p∥, П 3 (рис. 16, 17).
Рис. 16. Профильная прямая
Рис. 17. Комплексный чертеж профильной прямой
Поскольку широта всех точек профильной прямой одинакова: p2 ⊥ E2E1 .
Отрезки профильной прямой и углы наклона к П1 и П2 проецируются на П3 в натуральную величину: [E3F3] =[EF]; ∠τ3=∠τ=∠р, П1∠φ3=∠φ=∠р, П2.
cdot-nntu.ru
