Что такое значение функции в алгебре – Значение функции это

Содержание

Функции: понятие функция и аргумент, функциональная зависимость

Если две переменные величины находятся между собой в такой зависимости, что каждому значению одной переменной соответствует строго определённое значение другой, то первая величина называется аргументом, а вторая его функцией.

Функция – это зависимая переменная величина. Аргумент – это независимая переменная. Зависимость функции от аргумента называется функциональной зависимостью.

Если нужно указать на тот факт, что y функция от x, не акцентируя внимания на то, в какой именно зависимости находится функция от аргумента, то пишут просто:

y = f(x)

где f (начальная буква слова function – функция) заменяет слово функция, y – это функция, а x – аргумент.

Иногда чтобы показать, что y зависит от x пишут просто:

y(x)

Обратите внимание, что вместо y и x могут использоваться любые другие буквы.

Значение y, соответствующее заданному значению x называют значением функции. Все значения, которые принимает аргумент, образуют область определения функции. Все значения, которые принимает зависимая переменная, образуют множество значений функции. Для функции f приняты следующие обозначения:

D(f) – область определения функции
(множество значений аргумента)

E(f) – множество значений функции

f(x₀) – значение функции в точке x₀

Пример. Возьмём формулу нахождения расстояния по скорости и времени:

S = vt

где S – это расстояние, v – скорость, а t – время. Если взять скорость равную 50 км/ч, то каждому неотрицательному значению

t будет соответствовать строго определённое значение S:

t (ч)	1	1,5	2	2,5	3
S (км)	50	75	100	125	150

Следовательно, S является функцией от t – S(t), область определения функции – D(S) &ges; 0, так как время не может быть отрицательным, но при этом можно не затратить времени вообще если не двигаться, в этом случае t = 0. Значение этой функции в точке t₀ можно обозначить в виде S(t₀), то есть записать таблицу со значениями в таком виде:

S(1) = 50, S(1,5) = 75, S(2) = 100, S(2,5) = 125, S(3) = 150

naobumium.info

Что такое алгебра?! Функция и аргумент в алгебре.

В данной статье разберемся, что такое алгебра. Узнаем о таких понятиях, как функция и аргумент в алгебре и дадим простые и понятные определения.

Один из разделов математики это алгебра, которая подразумевает выполнение различных операций с числами, так как сложение, умножение и т.д. Можно сказать, что алгебра это нечто вроде расширения арифметики до более высокого уровня. Понять, что такое алгебра и откуда она взялась, помогут исторические факты. Первые предпосылки алгебры появились в разных уголках мира, людям нужна была алгебра для того, чтобы решить определенные уравнения. Например, в Древней Греции впервые об уравнениях заговорил Диофант, это был 2-3 век нашей эры.

В Китае примерно 2 тысячи лет до нашей времени уже было умение решать квадратные уравнения и уравнения первой степени. Также некоторые предпосылки алгебры встречались у индийского народа и жителей арабских стран. Согласно историческому прошлому, также отличилось издание «Алгебра» аль-Хваризми, которое стало популярным в 12-ом веке благо переводу на латинском языке. Человечество нуждалось в проведение расчетов, так появилась алгебра. Что такое алгебра для вас и нужна или нет, каждый решает сам. Потребность в алгебре появилась, как необходимость решать однотипные задачи. В школе алгебра всегда была и остается обязательным предметом.

Когда начинают учить алгебру в школе?

Разделение математики на несколько областях определило для алгебры решение определенных уравнений, под названием алгебраические уравнения. Что такое алгебра как предмет можно узнать только в 7-ом классе. Именно тогда вместе привычной математики появляется два отдельных предмета: алгебра и геометрия. Изучение начинается с простых понятий, также как и в случае других учебных процессов, все строится от простого материала к сложному.

7 класс оптимальное время для того, чтобы узнать, что такое алгебра. Вместо обычных операций с числами осуществляется переход на переменные. Так проще понять общие законы арифметики, научиться работать с неизвестными и функциями. Алгебру можно разделить на 5 отдельных категорий:

— общая алгебра

— элементарная алгебра

— линейная алгебра

— универсальная алгебра

— алгебраическая комбинаторика.

Школьная программа подразумевает изучение исключительно элементарной категории. Элементарная алгебра занимается изучением операций с вещественными числами. Перемененные и постоянные обозначены в алгебре символами в виде букв. С их помощью происходит преображение уравнений и математических выражений на основе четких правил.

Функция в алгебре

Понимание алгебры как предмет требует знание определенных элементов, так как функция, аргумент и определение. Что такое функция в алгебре и чем она определена? Функция является одним из основных понятий и определяет зависимость между переменными с неодинаковой величиной.

Что такое функция?:

Функция в алгебре представляет собой сопоставимость между двумя множествами. Согласно этому каждый элемент множества соответствует по одному единственному элементу другого множества.

Функция задается различным образом:

— таблицей

— графиками

— согласно словесной формулировке (описание словами)

— аналитическим образом (используя формулу).

Школьная алгебра всецело сосредоточена над изучением числовых функций. Функция и аргумент указаны в виде чисел. Пример: y=f(x), где

x перемена независимого типа, а y функция наоборот зависимая. У функции есть еще такие параметры как: область определения (D) и область значения (E). Первый параметр представляет собой совокупность значений для переменной «х», в то время как второй обозначает множество значений для «у».

Аргумент в алгебре

Что такое аргумент в алгебре? Это не что иное, как перемена х, от которой зависит у, то есть функция. Аргумент функции в алгебре это независимая перемена с помощью которой определяется значение функции.

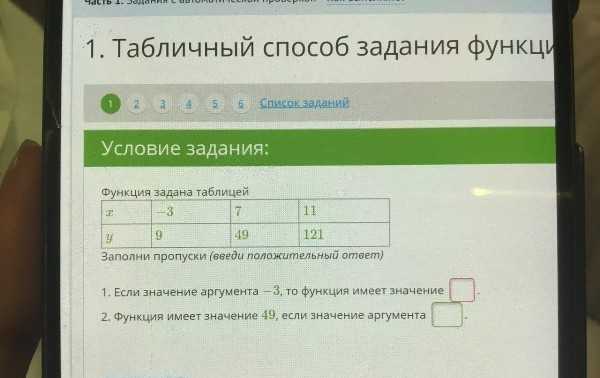
Значение аргумента можно определить по значению функции. Для определения аргумента по функции y=f(x), надо заменить y заданным значением. Остается только решить уравнение относительно x для того, чтобы значение стало известным. Существует возможность определения данного параметра и по графику функции.

Определение алгебры и ее практическая польза

Определение, что такое алгебра, позволяет понять какая от нее практическая польза. Только понимая область деятельности этой части математики, появляется стремление ее изучать. Благодаря алгебре, можно шагать на более высокий уровень познания математики. Алгебра это та простая ступень, которая позволяет делать прогресс в процессе изучения современной математики. Благодаря ней, появилась возможность взглянуть иначе на множества.

Постепенно элементарные значения алгебры перешли в более сложные понятия. Так появилась универсальная алгебра, которая стала основой для развития топологии. Алгебра это ступень, которая позволяет ступать дальше, и без нее не быть некоторым явлений прогресса. Знания некоторых людей, может завершиться на элементарных основ дисциплины, но в определенных областях глубокое изучение обязательно.

Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:

reshit.ru

Значение функции

Область значений функции

Область значений (или множество значений) функции — множество, состоящее из всех значений, которые принимает функция[1][2][3].

Определение

Пусть на множестве X {\displaystyle X} задана функция f {\displaystyle f} , которая отображает множество X {\displaystyle X} в Y {\displaystyle Y} , то есть: f : X → Y {\displaystyle f:X\to Y} . Тогда областью (или множеством) значений функции f {\displaystyle f} называется совокупность всех её значений, которая является подмножеством множества Y {\displaystyle Y} и обозначается f ( X ) {\displaystyle f(X)} :

f ( X ) = y ∈ Y {\displaystyle f(X)=\y\in Y} .

Множество значений функции f {\displaystyle f} обозначается также символами E ( f ) {\displaystyle E(f)} , R ( f ) {\displaystyle R(f)} или r a n f {\displaystyle \mathrm {ran} \,f} (от англ.

range).

Терминология

В некоторых источниках различаются понятия области значений и множества значений функции. При этом областью значений функции называют её кодомен, то есть множество Y {\displaystyle Y} в обозначении функции f : X → Y {\displaystyle f:X\to Y} [4], сохраняя термин множество значений для обозначения совокупности всех значений функции f {\displaystyle f} .

Множество значений f ( X ) {\displaystyle f(X)} называется также образом множества X {\displaystyle X} при отображении f {\displaystyle f} .

Иногда множество значений функции называют множеством всех значений или областью изменения функции[3].

ru.wikipedia.org⁫>

Понятие и свойства функции. Область определения и область значения

Основные данные о работе

Версия шаблона	2.1
ЦДОР
Вид работы	Творческое эссе
Название дисциплины	Математика (курс 13)
Тема	Понятие и свойства функции. Область определения и область значения.
Фамилия
Имя
Отчество
№ контракта

Содержание

Понятие и свойства функции. Область определения и область значения……………3

Список использованных интернет-ресурсов……………………………………………9

Основная часть

Понятие и свойства функции. Область определения и область значения

1.Фукция и её свойства.

Функция (отображение, оператор, преобразование) — это математическое понятие, отражающее связь между элементами множеств. Так же можно сказать, что функция — это «закон», по которому каждому элементу одного множества (называемому областью определения) ставится в соответствие некоторый элемент другого множества (называемого областью значений).

Математическое понятие функции выражает интуитивное представление о том, как одна величина полностью определяет значение другой величины. Так значение переменной однозначно определяет значение выражения, а значение месяца однозначно определяет значение следующего за ним месяца, а также любому человеку можно сопоставить другого человека — его отца. Аналогично, некоторый задуманный заранее алгоритм по варьируемым входным данным выдаёт определённые выходные данные.

Термин «функция» (в некотором более узком смысле) был впервые использован Лейбницем в 1692 год. В свою очередь, Иоганн Бернулли в письме к Лейбницу употребил этот термин в смысле, более близком к современному.

Первоначально, понятие функции было неотличимо от понятия аналитического представления. Впоследствии появилось определение функции, которое дал Эйлер в 1751 год, затем — Лакруа в 1806 год — уже практически в современном виде. Наконец, общее определение функции (в современной форме, но для числовых функций) было дано Лобачевским в 1834 году и Дирихле в 1837 году.

К концу XIX века понятие функции переросло рамки числовых систем. Первыми это сделали векторные функции, вскоре Фреге ввёл логические функции (1879), а после появления теории множеств Дедекинд (1887) и Пеано (1911) сформулировали современное универсальное определение.

Часто под термином «функция» понимается числовая функция; то есть функция, которая ставит одни числа в соответствие другим. Эти функции удобно представляются на рисунках в виде графиков.

Функция – это одно из основных математических и общенаучных понятий. Оно сыграло и поныне играет большую роль в познании реального мира.

Функция — это зависимость переменной у от переменной х, если каждому значению х соответствует единственное значение у.

Переменная х – это независимая переменная или аргумент.

Переменная у – это зависимая переменная.

Значение функции – это значение у, соответствующее заданному значению х.

Область определения функции – это все значения, которые принимает независимая переменная.

Область значений функции (множество значений)- это все значения, которые принимает функция.

Функция является четной — если для любого х из области определения функции выполняется равенство f(х)=f(-х)

Функция является нечетной — если для любого х из области определения функции выполняется равенство f(-х)=-f(х)

Возрастающая функция — если для любых х1 и х2, таких, что х1< х2, выполняется неравенство f(х1)

Убывающая функция — если для любых х1 и х2, таких, что х1< х2, выполняется неравенство f(х1)>f(х2)

2. Способы задания функции.

Чтобы задат

zna4enie.ru

Как найти значение функции 🚩 значение функции это 🚩 Математика

27 декабря 2018

Автор КакПросто!

Под понятием функции в математике понимают связь между элементами множеств. Если говорить более точно, это «закон», по которому каждому элементу одного множества (называемому областью определения) ставится в соответствие некоторый элемент другого множества (называемого областью значений).

Статьи по теме:

Вам понадобится

Знания в области алгебры и математического анализа.

Инструкция

Значения функции это некая область, значения из которой может принимать функция. Например область значения функции f(x)=|x| от 0 до бесконечности. Чтобы найти значение функции в конкретной точке необходимо подставить вместо аргумента функции его числовой эквивалент, полученное число и будет значением функции. Пусть дана функция f(x)=|x| — 10 + 4x. Найдем значение функции в точке x=-2. Подставим вместо x число -2: f(-2)=|-2| — 10 + 4*(-2) = 2 — 10 — 8 = -16. То есть значение функции в точке -2 равно -16.

Обратите внимание

Прежде чем искать значение функции в точке — убедитесь, что она входит в область определения функции.

Полезный совет

Аналогичным способом можно найти значение функции нескольких аргументов. Отличие в том, что вместо одного числа необходимо будет подставить несколько — по числу аргументов функции.

Совет полезен?

Распечатать

Как найти значение функции

Статьи по теме:

Не получили ответ на свой вопрос?
Спросите нашего эксперта:

www.kakprosto.ru

Значение функции. Поясните Значение функции это есть значения У (игрек) Так?

Значение зависимой переменной называют значениями функции

линейная функция — y=kx+b

Наибольшее и наименьшее значение формулы

у — это значение функции, или можно назвать результат функции, или ответ функции

touch.otvet.mail.ru