Применение производной для нахождения наибольшего и наименьшего значений непрерывной функции на промежутке
Тема: Производная
Урок: Применение производной для отыскания наибольшего и наименьшего значений непрерывной функции на промежутке
На этом занятии рассмотрим более простую задачу, а именно, будет задан промежуток, будет задана непрерывная функция на этом промежутке. Надо узнать наибольшее и наименьшее значение заданной функции на заданном промежутке.
№ 32.1 (б). Дано: , . Нарисуем график функции (см. рис.1).
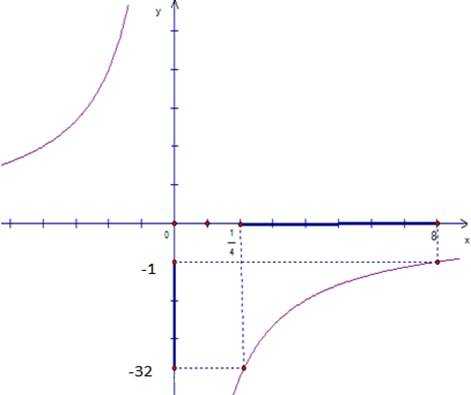
Рис. 1. График функции .
Известно, что эта функция возрастает на промежутке , значит, она возрастает и на отрезке . А значит, если найти значение функции в точках и , то будут известны пределы изменения данной функции, ее самое большое и самое маленькое значение.
Когда аргумент возрастает от до 8, функция возрастает от до .
Ответ: ; .
№ 32.2 (а) Дано: Найти наибольшее и наименьшее значения функции на заданном промежутке.
Построим график этой функции (см. рис.2).
Если аргумент меняется на промежутке , то функция возрастает от -2 до 2. Если аргумент возрастает от , то функция убывает от 2 до 0.
Рис. 2. График функции .
Найдем производную .
, . Если , то и это значение принадлежит заданному отрезку . Если , то . Легко проверить, если принимает другие значения, соответствующие стационарные точки выходят за пределы заданного отрезка. Сравним значения функции на концах отрезка и в отобранных точках, в которых производная равна нулю. Найдем
;
;
.
Ответ: ;.
Итак, ответ получен. Производную в данном случае можно использовать, можно не использовать, применить свойства функции, которые были изучены ранее. Так бывает не всегда, иногда применение производной – это единственный метод, который позволяет решать подобные задачи.
№ 32.10 (а)
Дано: , . Найти наибольшее и наименьшее значение функции на данном отрезке.
Если в предыдущем случае можно было обойтись без производной – мы знали, как себя ведет функция, то в данном случае функция довольно сложная. Поэтому, ту методику, которую мы упомянули на предыдущей задаче, применим в полном объеме.
1. Найдем производную . Найдем критические точки , отсюда , — критические точки. Из них выбираем те, которые принадлежат данному отрезку: . Сравним значение функции в точках , , . Для этого найдем
;
;
.
Проиллюстрируем результат на рисунке (см. рис.3).
Рис. 3. Пределы изменения значений функции
Видим, что если аргумент меняется от 0 до 2, функция изменяется в пределах от -3 до 4. Функция меняется не монотонно: она либо возрастает, либо убывает.
Ответ: ;.
Итак, на трех примерах была продемонстрирована общая методика нахождения наибольшего и наименьшего значения функции на промежутке, в данном случае – на отрезке.
Алгоритм решения задачи на нахождение наибольшего и наименьшего значений функции:
1. Найти производную функции.
2. Найти критические точки функции и отобрать те точки, которые находятся на заданном отрезке.
3. Найти значения функции на концах отрезка и в отобранных точках.
4. Сравнить эти значения, и выбрать наибольшее и наименьшее.
Рассмотрим еще один пример.
Найти наибольшее и наименьшее значение функции , .
Ранее был рассмотрен график этой функции (см. рис.4).

Рис. 4. График функции .
На промежутке область значения этой функции . Точка — точка максимума. При — функция возрастает, при – функция убывает. Из чертежа видно, что , — не существует.
Итак, на уроке рассмотрели задачу о наибольшем и наименьшем значении функции, когда заданным промежутком является отрезок; сформулировали алгоритм решения подобных задач.
Список рекомендованной литературы
1. Алгебра и начала анализа, 10 класс (в двух частях). Учебник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. –М.: Мнемозина, 2009.
2. Алгебра и начала анализа, 10 класс (в двух частях). Задачник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. –М.: Мнемозина, 2007.
3. Виленкин Н.Я., Ивашев-Мусатов О.С., Шварцбурд С.И. Алгебра и математический анализ для 10 класса (учебное пособие для учащихся школ и классов с углубленным изучением математики).-М.: Просвещение, 1996.
4. Галицкий М.Л., Мошкович М.М., Шварцбурд С.И. Углубленное изучение алгебры и математического анализа.-М.: Просвещение, 1997.
5. Сборник задач по математике для поступающих во ВТУЗы (под ред. М.И.Сканави).-М.:Высшая школа, 1992.
6. Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебраический тренажер.-К.: А.С.К., 1997.
7. ЗвавичЛ.И., Шляпочник Л.Я., Чинкина
interneturok.ru
13. Схема нахождения наибольшего и наименьшего значений функции на отрезке. (Пример из т.Р.II, задача №13)
Пусть функция y=f(x)непрерывна на отрезке. Как известно, такая функция достигает своих наибольшего и наименьшего значений. Эти значения функция может принять либо во внутренней точкеx0отрезка, либо на границе отрезка, т. е. приx0=a илиx0=b. Еслиx0, то точкуx0следует искать среди критических точек данной функции.
Правило нахождения наибольшего и наименьшего значений функции на отрезке :
Найти критические точки функции на интервале ;
Вычислить значения функции в найденных критических точках;
Вычислить значения функции на концах отрезка, т. е. в точках x=a иx=b;
Среди всех вычисленных значений функции выбрать наибольшее и наименьшее.
Замечания: 1. Если функция y=f(x)на отрезкеимеет лишь одну критическую точку и она является точкой максимума (минимума), то в этой точке функция принимает наибольшее (наименьшее) значение.
2. Если функция y=f(x)на отрезкене имеет критических точек, то это означает, что на нем функция монотонно возрастает или убывает. Следовательно, свое наибольшее значение функция принимает на одном конце отрезка, а наименьшее – на другом.
Пример нахождения наибольшего и наименьшего значений функции на отрезке – задача №13 из тип. Расчета II (Вариант 6).
Найти наибольшее и наименьшее значения функции на отрезке.
Находим критические точки. Для этого находим производную от данной функции, приравниваем её к нулю и находим корни полученного уравнения:
x1=0, x2=2
x1, x2.
Вычисляем значение функции в найденной критической точке: .
Вычисляем значение функции на концах отрезка: ,
Ответ: yнаиб=-2приx=1,yнаим=3приx=2.
14. Понятия периодической, четной, нечетной, монотонной, ограниченной функций. Графики элементарных функций. Привести примеры.
Функция y=f(x), определенная на множествеD, называетсяпериодической на этом множестве, если существует такое число, что при каждомзначениеи. При этом числоназываетсяпериодом функции. Если- период функции, то ее периодами будут также числа, гдеТак например, дляпериодами будут числаОсновной период (наименьший положительный) – это период. Вообще обычно за основной период берут наименьшее положительное число, удовлетворяющее равенству.
Функция y=f(x), определенная на множествеD, называетсячетной, есливыполняются условияи. Функцияy=f(x), определенная на множествеD, называетсянечетной, есливыполняются условияи. График четной функции симметричен относительно оси, а нечетной – относительно начала координат. Например,,,- четные функции;,- нечетные функции.
Пусть функция y=f(x)определена на множествеDи пусть. Если для любых значенийx1, x2аргументов из неравенстваx1 x2вытекает неравенство:, то функция называетсявозрастающей
Функция y=f(x), определенная на множествеD, называетсяограниченнойна этом множестве, если существует такое число, что для всехвыполняется неравенство(короткая запись:, называется ограниченной на, если). Отсюда следует, что график ограниченной функции лежит между прямыми.
Функция, задаваемая одной формулой, составленной из основных элементарных функций и постоянных с помощью конечного числа арифметических операций (сложения, вычитания, умножения, деления) и операций взятия от функции, называется элементарной функцией.
Графики элементарных функций:
Показательнаяфункция.
Степеннаяфункция.
Логарифмическаяфункция.
Тригонометрические функции.
Обратные тригонометрические функции.
Примерами элементарных функций могут служить функции:;;.
studfiles.net
Схема нахождения наибольшего и наименьшего значения функции
Раздаточный материал
Схема нахождения наибольшего и наименьшего значения функции, непрерывной на отрезке
Этапы
Пример для функции
у = на отрезке 
1. Найти область определения функции.
D( у) =
2. Найти производную 
 .
.
3. Найти на данном отрезке критические точки, т. е. точки, в которых  = 0 или не существует.
= 0 или не существует.
D ( ) = R.
) = R.
 = 0
= 0
4. Вычислить значения функции в критических точках и на концах отрезка.
у( ) =
у( ) =
у( ) =
5. Из вычисленных значений выбрать наименьшее и наибольшее.
max у(x) = у( ) =
min у(x) = у( ) =
__________________________________________________________________________________
Отыскание наибольшего и наименьшего значения непрерывной
функции на промежутке.
Случай незамкнутого промежутка.
Непрерывная функция на незамкнутом промежутке может иметь и может не иметь уmax., уmin.
Простейшие случаи:
Если непрерывная функция у = f (х) имеет в промежутке только одну точку экстремума х0 и если х0 – точка максимума, то f (х0) = уmax.
Если непрерывная функция у = f (х) имеет в промежутке только одну точку экстремума х0 и если х0 – точка минимума, то f (х0) = уmin.
infourok.ru
Задача на нахождение наименьшего значения функции
Решим задачу:
Окружность с центром в точке (4;1) касается параболы . Найдите абсциссу точки касания.
Построим чертеж к нашей задаче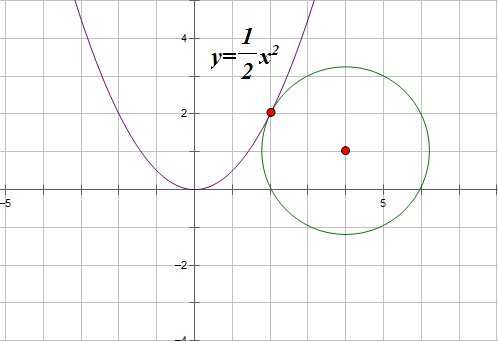
Точки, лежащие на параболе, имеют координаты .
Для нас важно, что расстояние от центра окружности до точки касания меньше, чем расстояние от центра окружности до любой другой точки параболы: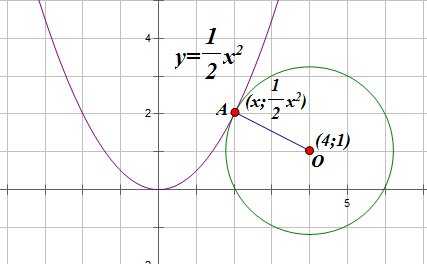
Итак, найдем, при каком значении длина отрезка принимает наименьшее значение.
Зависимость длины отрезка от выражается следующей формулой:
Найдем, при каком значении функция принимает наименьшее значение.
Так как функция является возрастающей, следовательно, меньшему значению значению аргумента соответствует меньшее значение функции. То есть функция принимает наименьшее значение в той же точке, что и подкоренное выражение, то есть функция .
Найдем, в какой точке функция принимает наименьшее значение.
Найдем производную:
Найдем нули производной:
Выясним знаки производной. При производная положительна:
Мы получили, что — точка минимума функции, то есть при длина отрезка минимальна, и абсцисса точки касания равна 2.
Ответ: 2
И.В. Фельдман, репетитор по математике.
ege-ok.ru
8. Нахождения наибольшего и наименьшего значений непрерывной функции на отрезке
Алгоритм нахождения наибольшего и наименьшего значений непрерывной функции на отрезке:
1)
Найти все критические точки функции,
принадлежащие отрезку 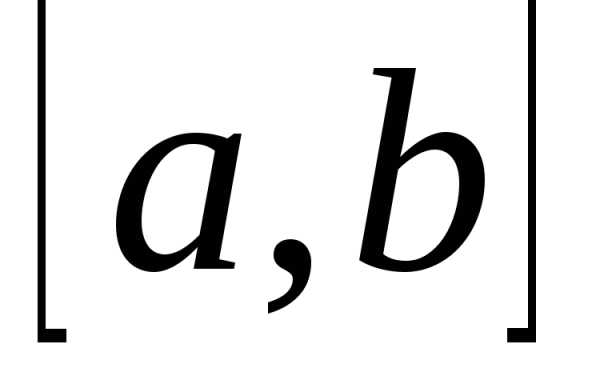 ;
;
2) Вычислить значения функции в этих точках и на концах отрезка;
3) Из полученных значений выбрать наибольшее и наименьшее.
Пример
8.1. Найти
наибольшее и наименьшее значения функции
на отрезке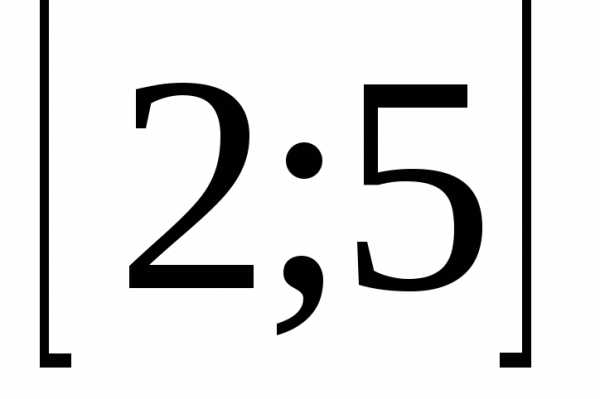 .
.
Решение. 1) Найдем критические точки функции.
, 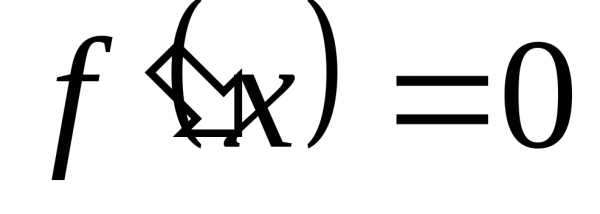
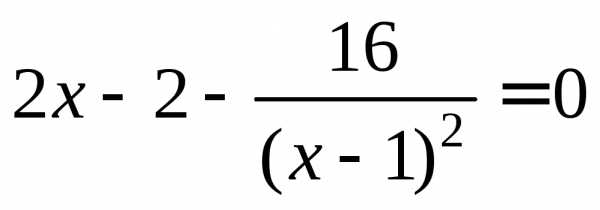
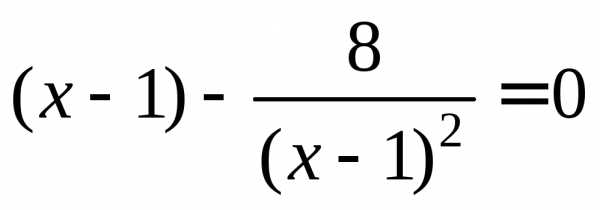
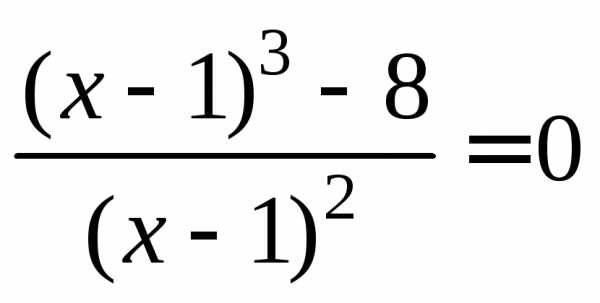 .
.
На
отрезке 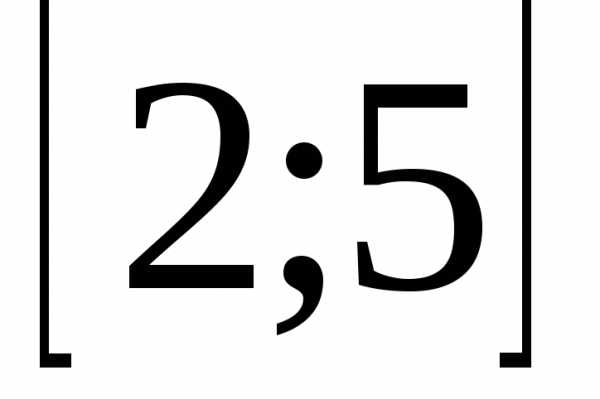 знаменатель не обращается в нуль.
Следовательно, дробь равна нулю тогда
и только тогда, когда числитель равен
нулю:
знаменатель не обращается в нуль.
Следовательно, дробь равна нулю тогда
и только тогда, когда числитель равен
нулю:
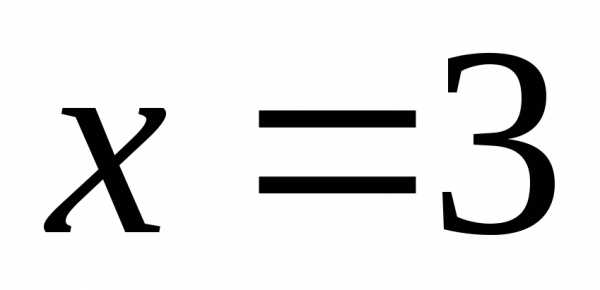 .
.
Значит, 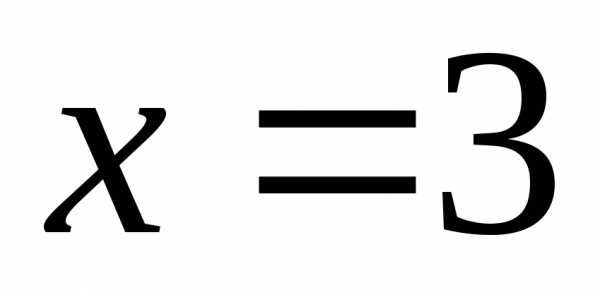 – критическая точка функции. Она
принадлежит данному отрезку.
– критическая точка функции. Она
принадлежит данному отрезку.
Найдем значение функции в критической точке:
.
2) Найдем значения функции на концах отрезка:
, .
3) Из полученных значений выбираем наибольшее и наименьшее:
, .
9. Задачи на отыскание наибольших и наименьших значений величин
При решении задач на вычисление наименьших и наибольших значений величин надо прежде всего определить, для какой величины в задаче требуется найти наименьшее или наибольшее значение. Эта величина и будет исследуемой функцией. Затем одну из величин, от изменения которых зависит применение функции, следует взять за независимую переменную и выразить через неё функцию. При этом нужно в качестве независимой переменной выбрать ту величину, через которую исследуемая функция выражается проще всего. После этого решается задача на нахождение наименьшего и наибольшего значения полученной функции в некотором промежутке изменения независимой переменной, которое обычно устанавливается из самого существа задачи.
Пример
9.1. Найти
высоту конуса наибольшего объёма,
который можно вписать в шар радиуса  .
.
Р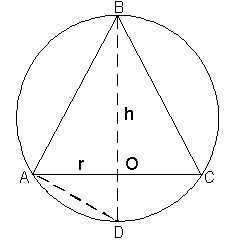 ешение. Обозначив радиус основания, высоту и
объём конуса соответственно
ешение. Обозначив радиус основания, высоту и
объём конуса соответственно 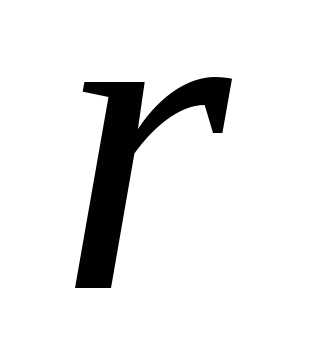 ,
,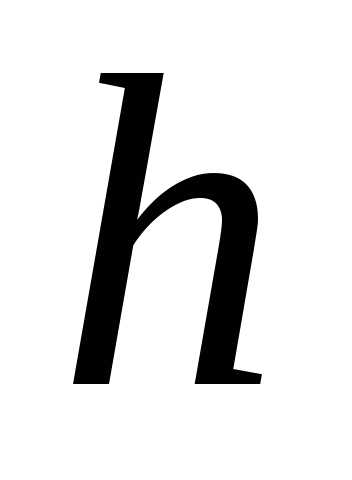 и
и ,
запишем
,
запишем .
Это равенство выражает зависимость от
двух переменных
.
Это равенство выражает зависимость от
двух переменных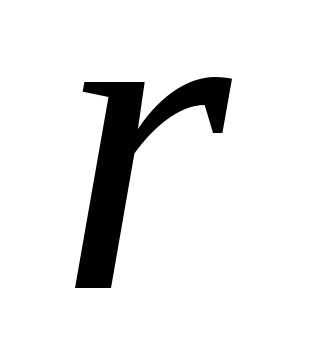 и
и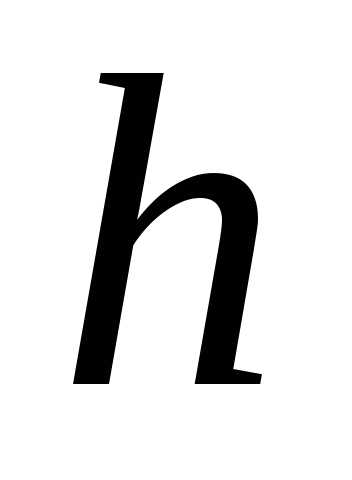 ;
исключим одну из этих величин, а именно
;
исключим одну из этих величин, а именно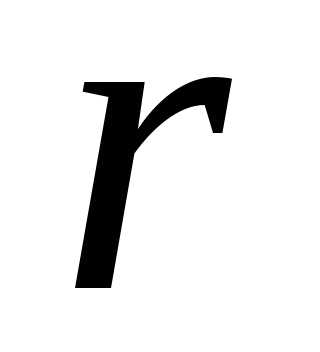 .
Для этого из прямоугольного треугольника
.
Для этого из прямоугольного треугольника выводим (по теореме о квадрате
перпендикуляра, опущенного из вершины
прямого угла на гипотенузу):
выводим (по теореме о квадрате
перпендикуляра, опущенного из вершины
прямого угла на гипотенузу):
Рисунок 6 – Иллюстрация к примеру 9.1.
или .
Подставив
значение 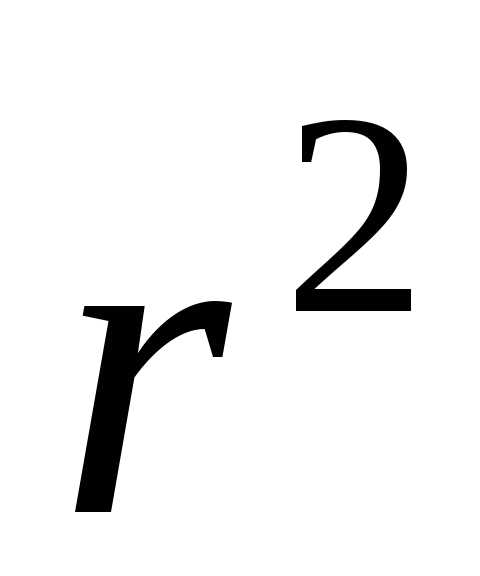 в формулу
объёма конуса, получим:
в формулу
объёма конуса, получим:
.
Мы видим, что объём  конуса, вписанного в шар радиуса
конуса, вписанного в шар радиуса ,есть
функция от высоты этого конуса
,есть
функция от высоты этого конуса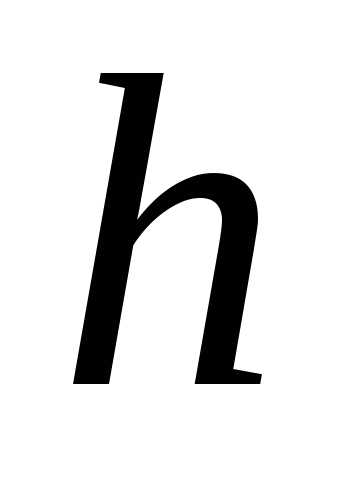 .
Найти высоту при которой вписанный
конус имеет большой объём, это значит
найти такое
.
Найти высоту при которой вписанный
конус имеет большой объём, это значит
найти такое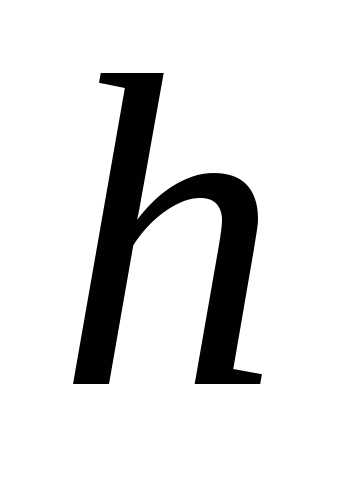 ,
при котором функция
,
при котором функция имеет максимум. Ищем максимум функции:
имеет максимум. Ищем максимум функции:
1) ,
2) 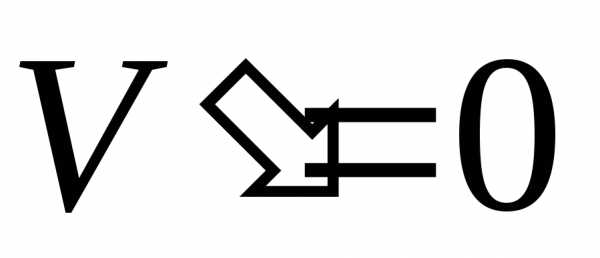 ,
,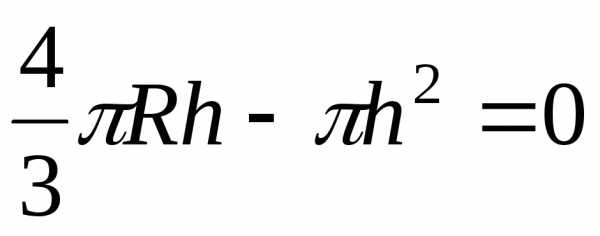 ,
,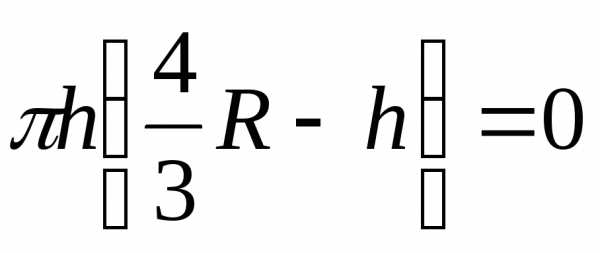 ,
откуда
,
откуда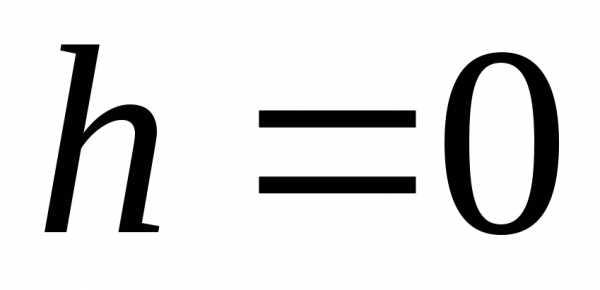 или
или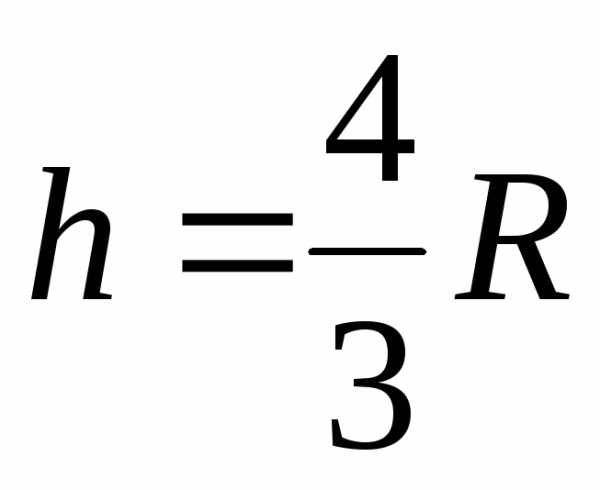 ,
,
3) .
Подставив вместо 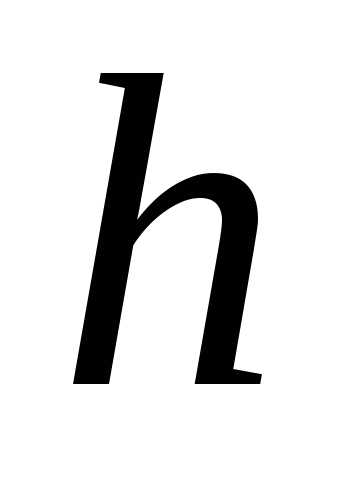 сначала
сначала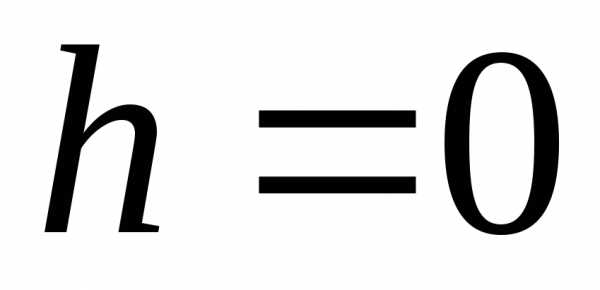 ,
а потом
,
а потом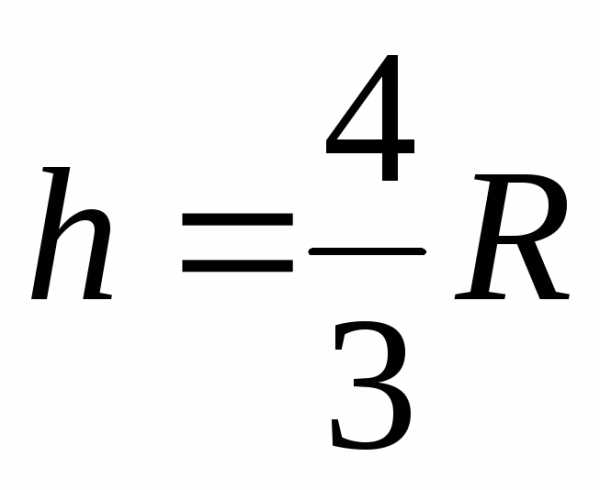 ,
получим:
,
получим:
В первом случае
имеем минимум ( при
при 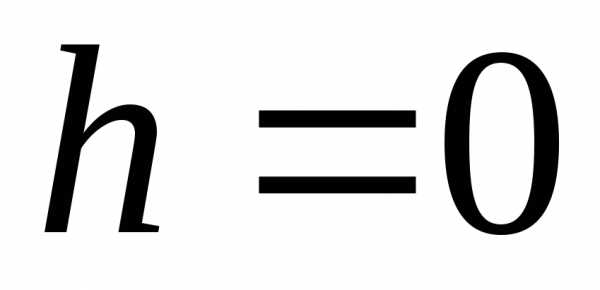 ),
во втором искомый максимум (так как
),
во втором искомый максимум (так как при
при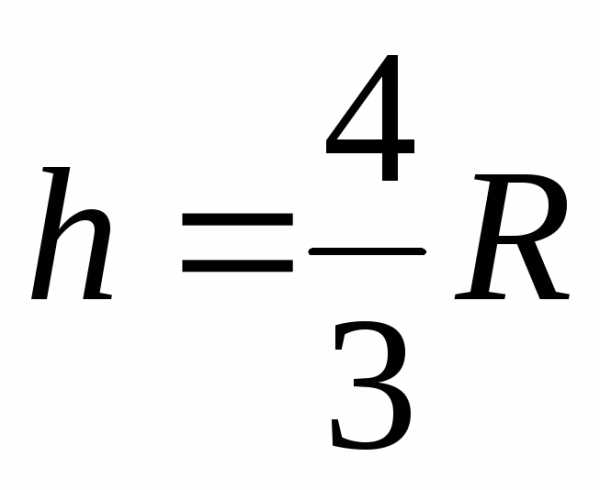 ).
).
Следовательно,
при 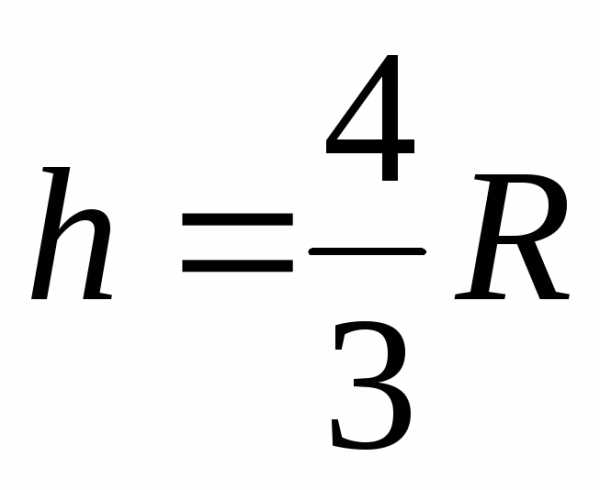 конус, вписанный в шар радиуса
конус, вписанный в шар радиуса , имеет
наибольший объём.
, имеет
наибольший объём.
Пример 9.2. Требуется огородить проволочной сеткой длиной 60 м прямоугольный участок, прилегающий к стене дома (рис. 7). Каковы должны быть длина и ширина участка, чтобы он имел наибольшую площадь?
Решение. Пусть ширина участка 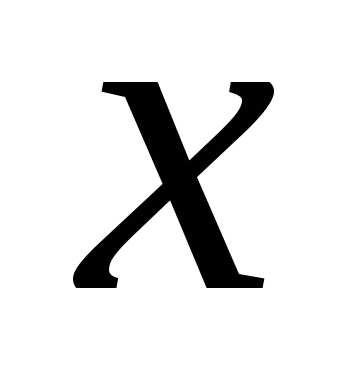 м,
а площадь
м,
а площадь  м2,
тогда:
м2,
тогда:
Рисунок 7 – Иллюстрация к пр. 9.2.
.
Значения 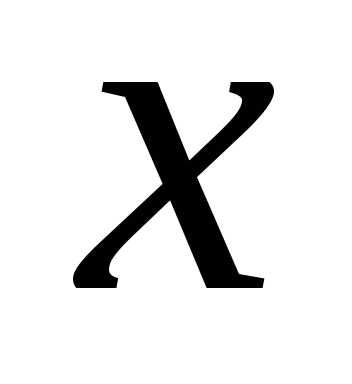 и
и не могут быть отрицательными, поэтому
множитель ,
а
.
не могут быть отрицательными, поэтому
множитель ,
а
.
Площадь  есть функция
есть функция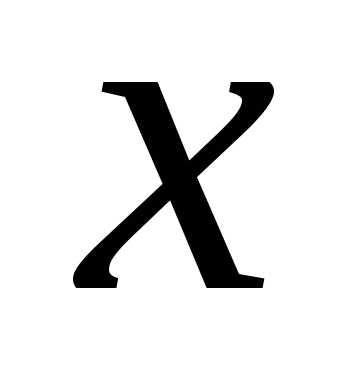 ,
определим промежутки ее возрастания и
убывания:
,
определим промежутки ее возрастания и
убывания:
. 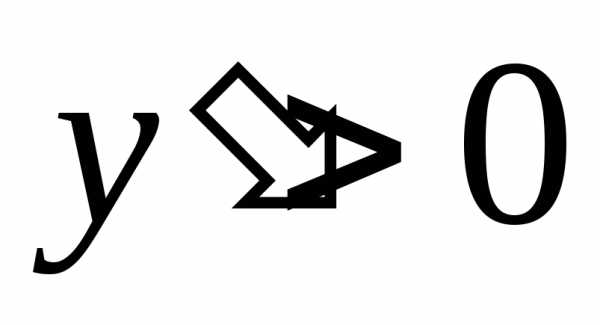 ,
и функция возрастает, когда
,
и функция возрастает, когда 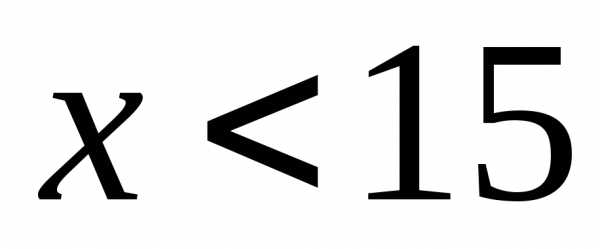 ;
; 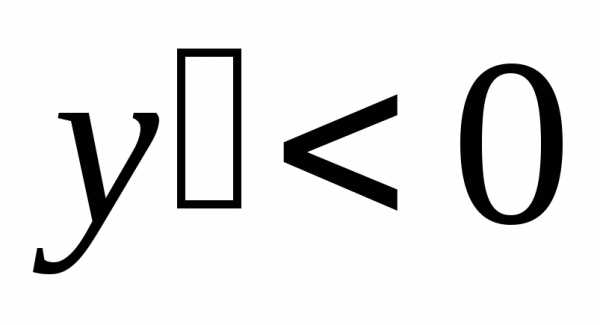 ,
и функция убывает, когда
,
и функция убывает, когда 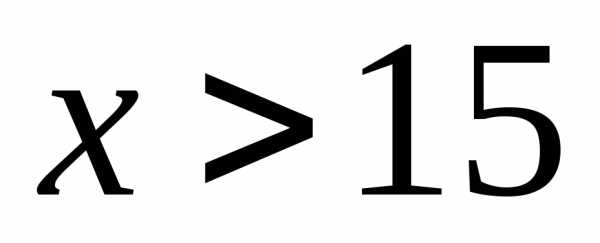 .
Следовательно, точка
.
Следовательно, точка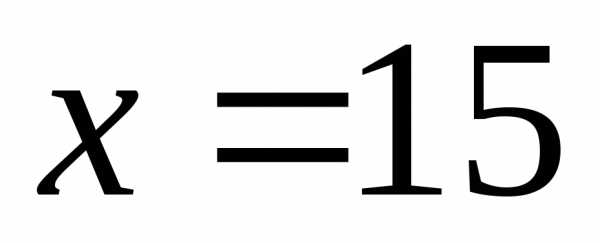 является точкой максимума. Так как это
единственная точка, принадлежащая
интервалу,
то в точке
является точкой максимума. Так как это
единственная точка, принадлежащая
интервалу,
то в точке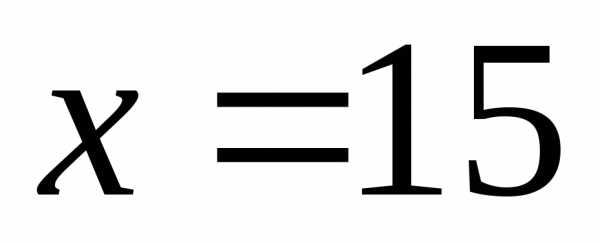 функция имеет наибольшее значение.
функция имеет наибольшее значение.
Следовательно,
площадь участка наибольшая (максимум),
если ширина 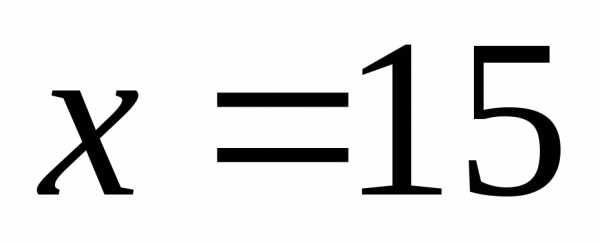 м, а
длина м.
м, а
длина м.
Пример 9.3. Каковы должны быть размеры прямоугольной комнаты, площадь которой 36 м2, чтобы периметр ее был наименьший?
Решение.
Пусть длина равна 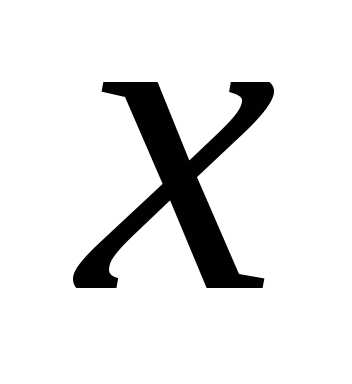 м, тогда
ширина прямоугольника
м, тогда
ширина прямоугольника 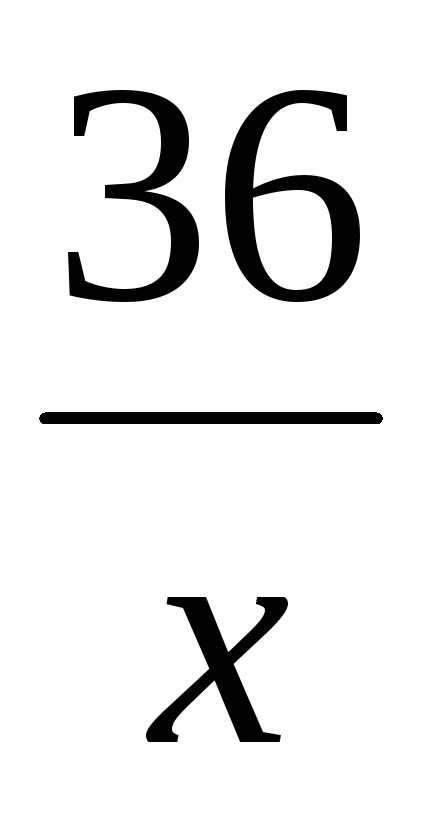 м, а периметр:
м, а периметр:
.
Периметр  есть функция
длины
есть функция
длины 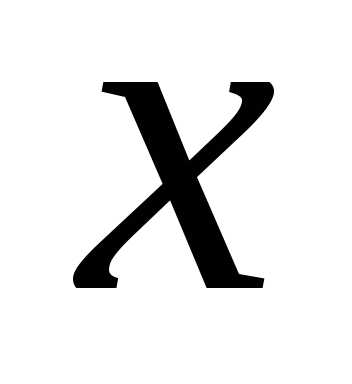 ,
определенная для всех положительных
значений
,
определенная для всех положительных
значений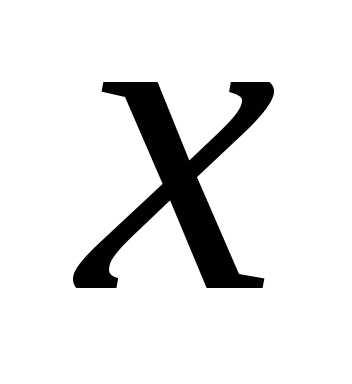 :.
:.
Определим промежутки ее возрастания и убывания:
.
Знак
производной определяется знаком разности 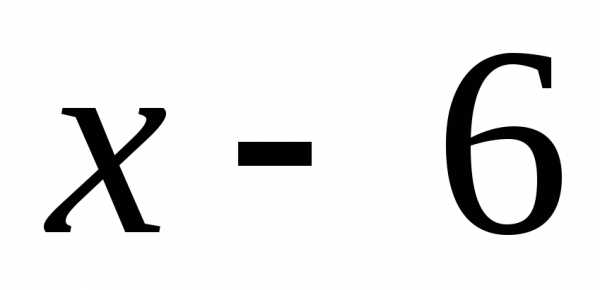 .
В промежутке
.
В промежутке
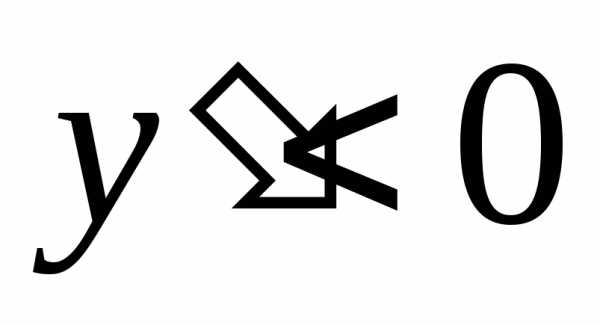 ,
а в промежутке
,
а в промежутке  .
.
Следовательно,
точка 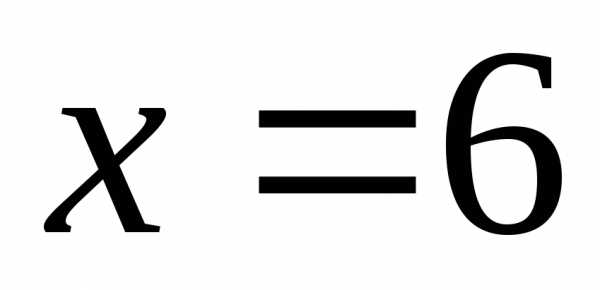 является точкой минимума. Так как это
единственная точка, принадлежащая
интервалу:,
то в точке
является точкой минимума. Так как это
единственная точка, принадлежащая
интервалу:,
то в точке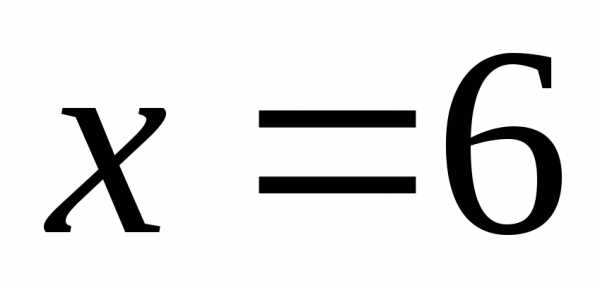 функция
имеет наименьшее значение.
функция
имеет наименьшее значение.
Следовательно,
периметр прямоугольника имеет наименьшее
значение (минимум), если длина его 6 м и
ширина 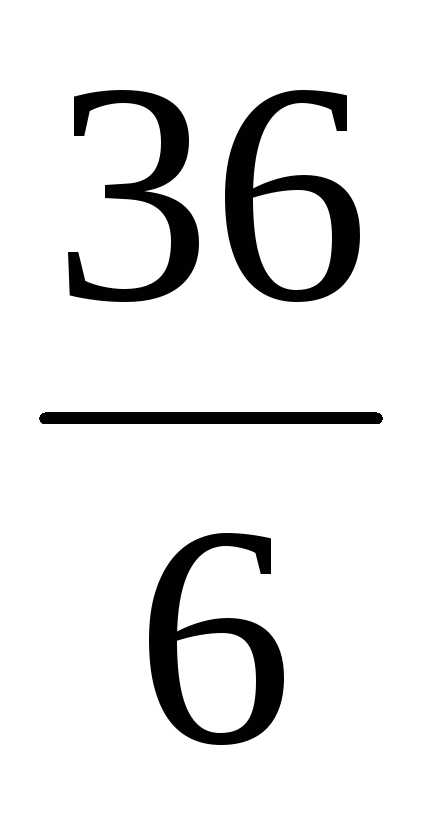 м = 6 м, т. е.
когда он квадрат.
м = 6 м, т. е.
когда он квадрат.
studfiles.net
