метод фогеля
Транспортная задача.
Стоимость доставки единицы груза из каждого пункта отправления в соответствующие пункты назначения задана матрицей тарифов
1 | 2 | 3 | 4 | 5 | Запасы | |
1 | 12 | 13 | 4 | 14 | 8 | |
2 | 9 | 8 | 11 | 16 | 7 | 165 |
3 | 14 | 8 | 12 | 6 | 7 | 200 |
4 | 5 | 7 | 12 | 6 | 9 | 385 |
5 | 15 | 12 | 5 | 13 | 11 | 300 |
Потребности | 145 | 155 | 182 | 193 | 520 |
Проверим необходимое и достаточное условие разрешимости задачи.
∑a = 145 + 165 + 200 + 385 + 300 = 1195
∑b = 145 + 155 + 182 + 193 + 520 = 1195
Условие баланса соблюдается. Запасы равны потребностям. Следовательно, модель транспортной задачи является закрытой.
1 | 2 | 3 | 4 | 5 | Запасы | |
1 | 12 | 13 | 4 | 14 | 8 | 145 |
2 | 9 | 8 | 11 | 16 | 7 | 165 |
3 | 14 | 8 | 12 | 6 | 7 | 200 |
4 | 5 | 7 | 12 | 6 | 9 | 385 |
5 | 15 | 12 | 5 | 13 | 11 | 300 |
Потребности | 145 | 155 | 182 | 193 | 520 |
Этап I. Поиск первого опорного плана.
Находим разности по строкам.
Для строки N=1 первый минимальный элемент min11 = 4, второй минимальный элемент min21 = 8. Их разность равна d = min21 — min11 = 4.
Для строки N=2 первый минимальный элемент min12 = 7, второй минимальный элемент min22 = 8. Их разность равна d = min22 — min12 = 1.
Для строки N=3 первый минимальный элемент min13 = 6, второй минимальный элемент min23 = 7. Их разность равна d = min23 — min13 = 1.Для строки N=4 первый минимальный элемент min14 = 5, второй минимальный элемент min24 = 6. Их разность равна d = min24 — min14 = 1.
Для строки N=5 первый минимальный элемент min15 = 5, второй минимальный элемент min25 = 11. Их разность равна d = min25 — min15 = 6.
Находим разности по столбцам.
Для
столбца N=1 первый минимальный элемент
min11 = 5. второй минимальный элемент min21 9. Их разность d = min21 — min1
Для столбца N=2 первый минимальный элемент min12 = 7. второй минимальный элемент min22 8. Их разность d = min22 — min12 = 1.
Для столбца N=3 первый минимальный элемент min13 = 4. второй минимальный элемент min23 5. Их разность d = min23 — min13 = 1.
Для столбца N=4 первый минимальный элемент min14 = 6. второй минимальный элемент min24 6. Их разность d = min24 — min14 = 0.
Для столбца N=5 первый минимальный элемент min15 = 7. второй минимальный элемент min25 7. Их разность d = min25 — min15 = 0.
Вычислив все разности, видим, что наибольшая из них соответствует строке (5). В этой строке минимальный тариф записан в клетке, находящейся на пересечении строки (5) и столбца (3).
1 | 2 | 3 | 4 | 5 | Запасы | Разности по строкам | |
1 | 12 | 13 | 4 | 14 | 8 | 145 | 4 |
2 | 9 | 8 | 11 | 16 | 7 | 165 | 1 |
3 | 14 | 8 | 12 | 6 | 7 | 200 | 1 |
4 | 5 | 7 | 12 | 6 | 9 | 385 | 1 |
5 | 15 | 12 | 5 | 13 | 11 | 300 | 6 |
Потребности | 145 | 155 | 182 | 193 | 520 | 0 | 0 |
Разности по столбцам | 4 | 1 | 1 | 0 | 0 | 0 |
Искомый элемент равен 5
Для этого элемента запасы равны 300, потребности 182. Поскольку минимальным является 182, то вычитаем его.
x53 = min(300,182) = 182.
0 | 0 | x | 0 | 0 | 0 |
0 | 0 | x | x | 0 | 0 |
0 | 0 | x | x | 0 | 0 |
0 | 0 | x | x | 0 | 0 |
0 | 0 | 0 | x | 0 | 300 — 182 = 118 |
0 | x | 182 — 182 = 0 | x | x | x |
Находим разности по строкам.
Для строки N=1 первый минимальный элемент min11 = 8, второй минимальный элемент min21 = 12. Их разность равна d = min21 — min11 = 4.
Для строки N=2 первый минимальный элемент min12 = 7, второй минимальный элемент min22 = 8. Их разность равна d = min22 — min12 = 1.
Для строки N=3 первый минимальный элемент min13 = 6, второй минимальный элемент min23 = 7. Их разность равна d = min23 — min13 = 1.
Для строки N=4 первый минимальный элемент min14 = 5, второй минимальный элемент min24 = 6. Их разность равна d = min24 — min14 = 1.
Для строки N=5 первый минимальный элемент min15 = 11, второй минимальный элемент min25 = 12. Их разность равна d = min25 — min15 = 1.
Находим разности по столбцам.
Для столбца N=1 первый минимальный элемент min11 = 5. второй минимальный элемент min21 9. Их разность d = min21 — min11 = 4.
Для столбца N=2 первый минимальный элемент min12 = 7. второй минимальный элемент min22 8. Их разность d = min22 — min12 = 1.
Для столбца N=4 первый минимальный элемент min14 = 6. второй минимальный элемент min24 6. Их разность d = min24 — min14 = 0.
Для столбца N=5 первый минимальный элемент min15 = 7. второй минимальный элемент min25 7. Их разность d = min25 — min15 = 0.
Вычислив все разности, видим, что наибольшая из них соответствует строке (1). В этой строке минимальный тариф записан в клетке, находящейся на пересечении строки (1) и столбца (5).
1 | 2 | 3 | 4 | 5 | Запасы | Разности по строкам | |
1 | 12 | 13 | 4 | 14 | 8 | 145 | 4 |
2 | 9 | 8 | 11 | 16 | 7 | 165 | 1 |
3 | 14 | 8 | 12 | 6 | 7 | 200 | 1 |
4 | 5 | 7 | 12 | 6 | 9 | 385 | 1 |
5 | 15 | 12 | 5 | 13 | 11 | 118 | 1 |
Потребности | 145 | 155 | 0 | 193 | 520 | 0 | 0 |
Разности по столбцам | 4 | 1 | — | 0 | 0 | 0 |
Искомый элемент равен 8
Для этого элемента запасы равны 145, потребности 520. Поскольку минимальным является 145, то вычитаем его.
x15 = min(145,520) = 145.
x | x | 0 | x | 0 | 145 — 145 = 0 |
0 | x | x | x | x | x |
0 | 0 | 0 | 0 | 0 | x |
0 | 0 | 0 | 0 | 0 | x |
0 | 0 | 0 | 0 | 0 | x |
0 | 0 | 0 | 0 | 520 — 145 = 375 | x |
Находим разности по строкам.
Для строки N=2 первый минимальный элемент min12 = 7, второй минимальный элемент min22 = 8. Их разность равна d = min22 — min12 = 1.
Для строки N=3 первый минимальный элемент min13 = 6, второй минимальный элемент min23 = 7. Их разность равна d = min23 — min13 = 1.
Для строки N=4 первый минимальный элемент min14 = 5, второй минимальный элемент min24 = 6. Их разность равна d = min24 — min14 = 1.
Для строки N=5 первый минимальный элемент min15 = 11, второй минимальный элемент min25 = 12. Их разность равна d = min25 — min15 = 1.
Находим разности по столбцам.
Для столбца N=1 первый минимальный элемент min11 = 5. второй минимальный элемент min21 9. Их разность d = min21 — min11 = 4.
Для столбца N=2 первый минимальный элемент min12 = 7. второй минимальный элемент min22 8. Их разность d = min22 — min12 = 1.
Для столбца N=4 первый минимальный элемент min14 = 6. второй минимальный элемент min24 6. Их разность d = min24 — min14 = 0.
Для столбца N=5 первый минимальный элемент min15 = 7. второй минимальный элемент min25 7. Их разность d = min25 — min15 = 0.
Вычислив все разности, видим, что наибольшая из них соответствует столбцу (1). В этом столбце минимальный тариф записан в клетке, находящейся на пересечении строки (4) и столбца (1).
1 | 2 | 3 | 4 | 5 | Запасы | Разности по строкам | |
1 | 12 | 13 | 4 | 14 | 8 | 0 | — |
2 | 9 | 8 | 11 | 16 | 7 | 165 | 1 |
3 | 14 | 8 | 12 | 6 | 7 | 200 | 1 |
4 | 5 | 7 | 12 | 6 | 9 | 385 | 1 |
5 | 15 | 12 | 5 | 13 | 11 | 118 | 1 |
Потребности | 145 | 155 | 0 | 193 | 375 | 0 | 0 |
Разности по столбцам | 4 | 1 | — | 0 | 0 | 0 |
Искомый элемент равен 5
Для этого элемента запасы равны 385, потребности 145. Поскольку минимальным является 145, то вычитаем его.
x41 = min(385,145) = 145.
0 | 0 | 0 | 0 | 0 | 0 |
x | x | 0 | 0 | 0 | 0 |
x | x | 0 | 0 | 0 | 0 |
0 | x | 0 | 0 | 0 | 385 — 145 = 240 |
x | x | x | x | x | x |
145 — 145 = 0 | x | 0 | 0 | 0 | 0 |
Находим разности по строкам.
Для строки N=2 первый минимальный элемент min12 = 7, второй минимальный элемент min22 = 8. Их разность равна d = min22 — min12 = 1.
Для строки N=3 первый минимальный элемент min13 = 6, второй минимальный элемент min23 = 7. Их разность равна d = min23 — min13 = 1.
Для строки N=4 первый минимальный элемент min14 = 6, второй минимальный элемент min24 = 7. Их разность равна d = min24 — min14 = 1.
Для строки N=5 первый минимальный элемент min15 = 11, второй минимальный элемент min25 = 12. Их разность равна d = min25 — min15 = 1.
Находим разности по столбцам.
Для столбца N=2 первый минимальный элемент min12 = 7. второй минимальный элемент min22 8. Их разность d = min22 — min12 = 1.
Для столбца N=4 первый минимальный элемент min14 = 6. второй минимальный элемент min24 6. Их разность d = min24 — min14 = 0.
Для столбца N=5 первый минимальный элемент min15 = 7. второй минимальный элемент min25 7. Их разность d = min25 — min15 = 0.
Вычислив все разности, видим, что наибольшая из них соответствует строке (5). В этой строке минимальный тариф записан в клетке, находящейся на пересечении строки (5) и столбца (5).
1 | 2 | 3 | 4 | 5 | Запасы | Разности по строкам | |
1 | 12 | 13 | 4 | 14 | 8 | 0 | — |
2 | 9 | 8 | 11 | 16 | 7 | 165 | 1 |
3 | 14 | 8 | 12 | 6 | 7 | 200 | 1 |
4 | 5 | 7 | 12 | 6 | 9 | 240 | 1 |
5 | 15 | 12 | 5 | 13 | 11 | 118 | 1 |
Потребности | 0 | 155 | 0 | 193 | 375 | 0 | 0 |
Разности по столбцам | — | 1 | — | 0 | 0 | 0 |
Искомый элемент равен 11
Для этого элемента запасы равны 118, потребности 375. Поскольку минимальным является 118, то вычитаем его.
x55 = min(118,375) = 118.
0 | 0 | 0 | 0 | 0 | 0 |
0 | 0 | 0 | 0 | 0 | x |
0 | 0 | 0 | 0 | 0 | x |
0 | 0 | 0 | 0 | 0 | x |
0 | x | 0 | x | 0 | 118 — 118 = 0 |
0 | x | x | x | 375 — 118 = 257 | x |
Находим разности по строкам.
Для строки N=2 первый минимальный элемент min12 = 7, второй минимальный элемент min22 = 8. Их разность равна d = min22 — min12 = 1.
Для строки N=3 первый минимальный элемент min13 = 6, второй минимальный элемент min23 = 7. Их разность равна d = min23 — min13 = 1.
Для строки N=4 первый минимальный элемент min14 = 6, второй минимальный элемент min24 = 7. Их разность равна d = min24 — min14 = 1.
Находим разности по столбцам.
Для столбца N=2 первый минимальный элемент min12 = 7. второй минимальный элемент min22 8. Их разность d = min22 — min12 = 1.
Для столбца N=4 первый минимальный элемент min14 = 6. второй минимальный элемент min24 6. Их разность d = min24 — min14 = 0.
Для столбца N=5 первый минимальный элемент min15 = 7. второй минимальный элемент min25 7. Их разность d = min25 — min15 = 0.
studfiles.net
Транспортная задача: метод аппроксимации Фогеля
Среди четырех, чаще всего применяющихся на практике, методов формирования опорного плана в транспортной задаче самый необычный – метод аппроксимации Фогеля. Последовательность действий при его использовании совершенно иная, чем при заполнении транспортной таблицы методом «Северо-Западного угла» или методом «Минимального элемента». На первый взгляд аппроксимация Фогеля сложнее, но это ложное впечатление. Метод простой и позволяет получить опорный план более приближенный к оптимальному решению, чем в случае применения других методов (за исключением разве что метода «Двойного предпочтения»).
Сущность аппроксимации Фогеля в нахождении разности (по модулю) между парой минимальных тарифов в каждой строке и столбце. Затем строка или столбец с наибольшей разностью заполняются в направлении от клетки с минимальным тарифом к клетке с максимальным. Подробнее далее.
ФОРМИРОВАНИЕ ОПОРНОГО ПЛАНА МЕТОДОМ АППРОКСИМАЦИИ ФОГЕЛЯ
Первым делом добавляем к транспортной таблице дополнительные строку и столбец. Далее находим для каждой строки и каждого столбца абсолютные разности (по модулю, т.е. без знака) между двумя минимальными тарифами. Если в строке/столбце две клетки с одинаковыми и минимальными значениями тарифов, то берем именно их. Тогда разность будет равна 0.
Найденные разности выписываем в добавочный столбец и добавочную строку.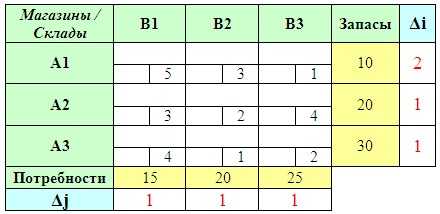
Среди вычисленных разностей (и по строкам, и по столбцам!) выбираем наибольшую.
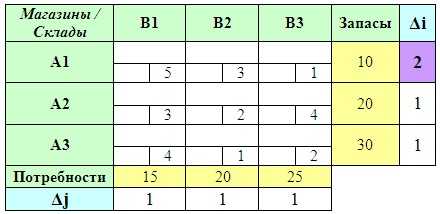
Затем в строке (или столбце), которой соответствует максимальная разность, ищем клетку с минимальным тарифом. Заполняем ее.
Если клеток с минимальным тарифом несколько, то заполняем ту из них, которой соответствует наибольшая разность.
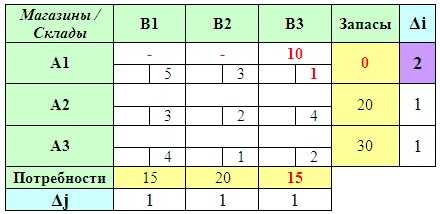
Затем повторяем все вышеописанные действия снова, только уже не учитывая заполненные клетки. И так до тех пор, пока не будет полностью найден опорный план.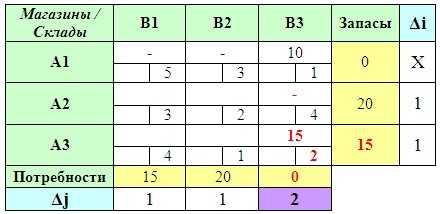
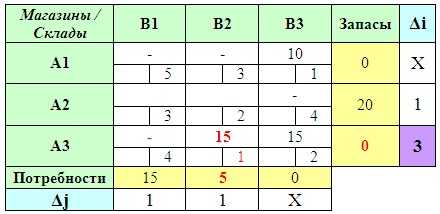
Оставшиеся ячейки транспортной матрицы уже и так очевидно каким образом следует заполнить:
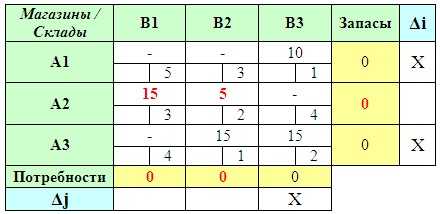
В результате мы получаем опорный план:
Зачастую опорный план, полученный аппроксимацией Фогеля, оказывается либо сразу оптимальным (как в этом примере), либо очень близким к оптимальному. Но именно часто, а не всегда!
ИСТОЧНИКИ И ССЫЛКИ
Викиучебник. Аппроксимация Фогеля. — http://ru.wikibooks.org/wiki/Аппроксимация_Фогеля
Галяутдинов Р.Р.
© Копирование материала допустимо только при указании прямой гиперссылки на источник: Галяутдинов Р.Р.
galyautdinov.ru
3. Метод аппроксимации Фогеля
Основным недостатком метода минимального элемента является неучет будущих тарифов: в первых шагах алгоритма тарифы минимальны, на заключительных шагах возможно использование перевозок с высокими тарифами, тем самым, опорный план будетотличаться от оптимального, хотя и не так сильно, какв методе северо-западного угла.
Метод аппроксимации Фогеля лишен выше указанных недостатков, однако довольно сложен для исполнения по сравнению двумя предыдущими методами.
Алгоритм метода Фогеля состоит в следующем:
На каждой итерации вычисляют по всем столбцам и строкам разность между двумя записанными в них минимальными тарифами,
Среди указанных разностей выбирают максимальную.
В строке (или столбце) с выбранной разностью определяют минимальный тариф и заполняют ее, полностью удовлетворяя потребности или полностью исчерпав запасы.
Если минимальный тариф одинаков для нескольких клеток данной строки (столбца), то для заполнения выбирают ту клетку, которая расположена в столбце (строке), соответствующим (ей) наибольшей разности между двумя минимальными тарифами, находящимися в данном (ей) столбце (строке).
Строка с израсходованным запасом или столбец с удовлетворенной потребностью исключаются из рассмотрения, и в соответствующей разности ставится прочерк.
Рассмотрим процесс составления опорного плана по методу Фогеля. На первом шаге разности между двумя соседними минимальными тарифами равны для строк (2-1=1. 5-4=1, 3-2=1), для столбцов (7-4=3, 5-2=3, 3-1=2, 6-2=4). Максимальная разность имеет место для четвертого столбца (4). Заполняем клетку А1B4, удовлетворив всю потребность четвертого предприятия, в результате чего у первого поставщика останется 50 единиц сырья, а четвертый столбец исключается из дальнейшего рассмотрения (вместо разностей ставится прочерк).
На втором шаге итерации вычислим разности между соседними минимальными тарифами оставшихся клеток для строк (7-1=6, 5-4=1, 3-2=1) и для столбцов (7-4=3, 5-2=3, 3-1=2). Максимальная разность будет для первой строки (6). Заполняем клетку А1B3, исчерпав оставшееся сырье первого поставщика, при этом третьему потребителю нужно еще 190-50=140 единиц сырья. В итоге из рассмотрения исключаем первую строку.
На следующем этапе разности равны для строк (5-4=1, 3-2=1) и для столбцов (9-4=5, 5-2=3, 9-3=6). Максимальная разность у третьего столбца (6). Заполняем клетку А3B3, полностью удовлетворив потребности третьего предприятия, в результате чего у третьего производителя останется 170-140=30 единиц сырья. Из дальнейшего рассмотрения исключаем третий столбец.
Далее разности равны для строк (5-4=1, 9-2=7) и для столбцов (9-4=5, 5-2=3). Разность максимальной будет для третьей строки. Следовательно, заполняем клетку А3B2, исключив из последующих шагов третью строку.
На последнем шаге остается только одна разность для второй строки (5-4=1). Поэтому заполняем оставшиеся клетки данной строки в порядке возрастания тарифов, сначала клетку А2B1, затем А2B2.
В результате опорный план будет задаваться следующей матрицей: , при этом общая стоимость перевозок составит: Q=1*50+2*110+4*120+5*20+2*30+3*140=1330 условных единиц.
Сравнение трех методов нахождения опорного плана позволяет сделать вывод, что план, самый близкий к оптимальному, дает метод аппроксимации Фогеля.
studfiles.net
Приближенный метод Фогеля
Как правило, этот метод дает лучший результат, чем МНС. Метод дает оптимальное, либо близкое к оптимальному решение.
Алгоритм
Шаг 1. Вычислитьштрафдля каждого столбца и для каждой строки. Для этого в каждой строке (столбце) отыскивается элемент с минимальной стоимостью и ближайший к нему по стоимости элемент. Разность этих стоимостей и естьштраф.
1 | 2 | 3 | 4 | Штраф за не вывоз | ||
1 | 10 | 0 | 20 | 11 | 15 | 10 |
2 | 12 | 7 | 9 | 20 | 25 | 2 |
3 | 0 | 14 | 16 | 18 | 5 | 14 |
5 | 15 | 15 | 10 | |||
10 | 7 | 7 | 7 | Штраф за недопоставку |
Шаг 2. Отметить строку или столбец с самым большим штрафом. Если таких несколько, выбрать среди них любую строку или любой столбец.
Шаг 3. В отмеченной строке (или столбце) выбрать переменную с самой низкой стоимостью и придать ей максимально возможное значение. Скорректировать объем производства и спрос и вычеркнуть строку или столбец, соответствующий выполненному ограничению.
Примечание. Если ограничение выполняется одновременно по строке и столбцу, то вычеркнуть либо строку, либо столбец. Оставшемуся столбцу придать нулевой спрос (нулевой объем производства).
Строка (или столбец) с нулевым объемом производства (или спроса) хотя и не вычеркивается, но в дальнейших вычислениях не участвует!!!
Шаг 4. Если остается не вычеркнутой только одна строка (столбец) с положительным объемом производства (или один столбец с положительным объемом спроса), базисные переменные вычисляютсяметодом наименьшей стоимости. При этом в задачу включаются не вычеркнутые строки (с нулевыми объемами производства) и не вычеркнутые столбцы (с нулевыми объемами спроса).Конец.
В противном случае выполняется шаг 1.
Пример.
Табл. 1
1 | 2 | 3 | 4 | |||
1 | 10 | 0 | 20 | 11 | 15 | 10 |
2 | 12 | 7 | 9 | 20 | 25 | 2 |
3 | 0 5 | 14 | 16 | 18 | 5 0 | 14 |
5 | 15 | 15 | 10 | |||
10 | 7 | 7 | 7 |
Табл. 2
1 | 2 | 3 | 4 | |||
1 | 10 | 0 15 | 20 | 11 | 15 0 | 11 |
2 | 12 | 7 | 9 | 20 | 25 | 2 |
3 | 0 5 | 14 | 16 | 18 | 0 | Не участв. |
5 | 15 | 15 | 10 | |||
7 | 11 | 9 |
Табл. 3 (осталась не вычеркнутой одна строка). МНС
1 | 2 | 3 | 4 | |||
1 | 10 | 0 15 | 20 | 11 | 0 | Не участв. |
2 | 12 | 7 | 9 15 | 20 | 25 10 | |
3 | 0 5 | 14 | 16 | 18 | 0 | Не участв. |
5 | 15 | 15 | 10 | |||
Табл. 4
1 | 2 | 3 | 4 | |||
1 | 10 | 0 15 | 20 | 11 0 | 0 | |
2 | 12 | 7 | 9 15 | 20 10 | 10 | |
3 | 0 5 | 14 | 16 | 18 0 | 0 | |
5 | 15 | 15 | 10 |
Z=335!
studfiles.net
Аппроксимация Фогеля — Викиучебник
Материал из Викиучебника — открытых книг для открытого мира
При определении опорного плана транспортной задачи методом аппроксимации Фогеля на каждой итерации по всем столбцам и по всем строкам находят разность между двумя записанными в них минимальными тарифами. Эти разности записывают в специально отведенных для этого строке и столбце в таблице условий задачи. Среди указанных разностей выбирают максимальную. В строке (или в столбце), которой данная разность соответствует, определяют минимальный тариф. Клетку, в которой он записан, заполняют на данной итерации. Если минимальный тариф одинаков для нескольких клеток данной строки (столбца), то для заполнения выбирают ту клетку, которая расположена в столбце (строке), соответствующем наибольшей разности между двумя минимальными тарифами, находящимися в данном столбце (строке).
Используя метод аппроксимации Фогеля, найти опорный план транспортной задачи, исходные данные которой приведены в таблице (опорный план этой задачи ранее был найден методом минимального элемента).
| Пункты отправления | Пункты назначения | Запасы | |||
| B1 | B2 | B3 | B4 | ||
| A1 | 7 | 8 | 1 | 2 | 160 |
| A2 | 4 | 5 | 9 | 8 | 140 |
| A3 | 9 | 2 | 3 | 6 | 170 |
| Потребности | 120 | 50 | 190 | 110 | 470 |
Для каждой строки и столбца таблицы условий найдем разности между двумя минимальными тарифами, записанными в данной строке или столбце, и поместим их в соответствующем дополнительном столбце или дополнительной строке таблица ниже.
| Пункты отправления | Пункты назначения | Запасы | Разности по строкам | ||||||||
| B1 | B2 | B3 | B4 | ||||||||
| A1 | 7 | 8 | 1 | 2 | 160 | 1 | 6 | — | — | — | — |
| A2 | 4 | 5 | 9 | 8 | 140 | 1 | 1 | 1 | 1 | 1 | 0 |
| A3 | 9 | 2 | 3 | 6 | 170 | 1 | 1 | 1 | 7 | — | — |
| Потребности | 120 | 50 | 190 | 110 | 470 | ||||||
| Разности по столбцам | 3 | 3 | 2 | 4 | |||||||
| 3 | 3 | 2 | — | ||||||||
| 5 | 3 | 6 | — | ||||||||
| 5 | 3 | — | — | ||||||||
| 0 | 0 | — | — | ||||||||
| — | 0 | — | — | ||||||||
Так, в строке А2 минимальный тариф равен 4, а следующий за ним равен 5, разность между ними 5-4=1. Точно так же разность между минимальными элементами в столбце В4 равна 6-2=4. Вычислив все эти разности, видим, что наибольшая из них соответствует столбцу В4. В этом столбце минимальный тариф записан в клетке, находящейся на пересечении строки А1 и столбца В4. Таким образом, эту клетку следует заполнить. Заполнив ее, тем самым мы удовлетворим потребности пункта В4. Поэтому исключим из рассмотрения столбец В4 и будем считать запасы пункта А1 равными 160—110=50 ед. После этого определим следующую клетку для заполнения. Снова найдем разности между оставшимися двумя минимальными тарифами в каждой из строк и столбцов и запишем их во втором дополнительном столбце и во второй дополнительной строке таб
ru.wikibooks.org
Метод Фогеля — Энциклопедия по экономике
Рассмотрим три метода нахождения начального решения транспортной задачи метод «северо-западного» угла, метод минимального элемента и метод Фогеля. [c.340]В методе Фогеля используются штрафы, взимаемые за неудачный выбор маршрута. Рассчитанные на шаге 2 разности между двумя уровнями затрат на перевозку являются штрафами за неверно выбранный маршрут перевозки. [c.342]
Метод Фогеля — наиболее трудоемкий, однако начальный план перевозок, построенный с его использованием, обычно бывает близок к оптимальному плану, а в некоторых случаях является оптимальным планом. [c.342]
Решим транспортную задачу методом Фогеля. В каждой строке и столбце матрицы кратчайших расстояний найдем два наименьших элемента и определим абсолютную разность между ними. Например, для первой строки, относящейся к первому пункту погрузки, значения наименьших элементов равны 10 км, таким образом, разность равна нулю. Затем выбираем наибольшую величину разности в строке разностей и в клетку с минимальным элементом заносим максимально возможную загрузку, учитывая при этом ресурсы поставщика и спрос потребителя. При наличии двух одинаковых наибольших разностей загрузку записывают в клетку, имеющую наименьший элемент (табл. 10.24). Если окажется, что спрос потребителя полностью удовлетворен или ресурс поставщика полностью исчерпан, то данная строка или столбец из дальнейшего рассмотрения исключается. [c.348]
Найти методом Фогеля план перевозок в задачах 8.40-8.43 [c.305]Опорный план является допустимым решением ТЗ и используется в качестве начального базисного решения при нахождении оптимального решения методом потенциалов. Существует три метода нахождения опорных планов метод северо-западного угла, метод минимального элемента и метод Фогеля. «Качество» опорных планов, полученных этими методами, различается в общем случае метод Фогеля дает наилучшее решение (зачастую оптимальное), а метод северо-западного угла — наихудшее. [c.70]
На каждом шаге метода Фогеля для каждой i-й строки вычисляются штрафы d как разность между двумя наименьшими тарифами строки. Таким [c.71]
На первом шаге нахождения опорного плана методом Фогеля возникает ситуация равенства значений максимальных штрафов транспортной матрицы (см. табл. 5.3) [c.75]
Т.к. d2i > d32 то выбираем на первом шаге для заполнения клетку (2,1). Опорный план Хф, найденный методом Фогеля [c.75]
Шаг 1. Получение начального плана перевозок по методу «северо-западного» угла, минимального элемента, Фогеля или любым другим методом. [c.343]
Первым этапом этого алгоритма является начальное распределение (составление начального плана перевозок). Для этого имеется ряд методов северо-западного угла, наименьших стоимостей, аппроксимаций Фогеля и др. Второй этап — построение системы потенциалов на основе равенства (25.33), а третий — проверка начального плана на оптимальность, причем в случае его неоптимальности переходят к четвертому этапу, содержание которого заключается в реализации так называемых циклов перераспределения плана прикрепления потребителей к поставщикам, после чего переходят опять к третьему этапу. Совокупность процедур четвертого и третьего этапов образует одну итерацию, и эти итерации повторяются, пока план перевозок не окажется оптимальным по критерию (25.29) [c.526]
Существует много частных способов (например, способ Фогеля, методы потенциалов, дифференциальных рент, способ Лебедева — Тихомирова, венгерский метод и др.), а также универсальных методов (например, алгоритм симплекс-метода) решения задач линейного программирования с такого рода условиями. Представляет интерес, как сам результат вычисления, так и его интерпретация. [c.246]
Для решения транспортной задачи — метод аппроксимации Фогеля, являющийся способом составления первого допустимого плана. Полученное распределение, особенно при небольшой размерности задачи, является оптимальным или достаточно близким к нему. [c.347]
Первый вариант — отсутствие складов. В этом случае решается классическая транспортная задача закрепления п потребителей за т поставщиками. Расстояние между объектами определяется как корень квадратный из суммы квадратов разностей их координат, см. формулу (11.9). Для распределения объемов перевозок используется ускоренный алгоритм Фогеля с последующим поиском оптимального варианта — минимума транспортной работы методом потенциалов. [c.398]
Как известно, метод потенциалов позволяет за конечное число шагов найти оптимальный план, следовательно, желательно, чтобы первый опорный план был ближе к оптимальному. Способ получения опорного плана, предложенный американским ученым У. Фогелем, позволяет найти практически оптимальный план. Найденный план или совпадение с оптимальным, или незначительно от него отличается. [c.286]
Однако, указав на возможность применения линейного программирования, Р. Фогель использует в работе другой, более простой, хотя, быть может, и менее точный метод. Вычисление общественного сбережения ведется по формуле [c.291]
Интересно отметить, что у Р. Фогеля были достаточно правдоподобные данные о закупках пшеницы двумя районами. Проведя для этих районов изложенные выше вычисления, Р. Фогель получил показатели, очень близкие к имеющимся, что говорит о неплохой точности предложенного метода. [c.292]
Более легкая из этих проблем — обработка количественных данных — почти всегда решается с помощью математической техники. При этом, как видно у Р. Фогеля, эффективными могут оказаться даже самые простые методы вычисление процентных отношений, средних, индексов и т. д. Вместе с тем в зависимости от поставленной задачи исследователям приходится обращаться и к более сложным математическим построениям. Чаще всего при этом используется регрессионный анализ, позволяющий измерять взаимосвязи между самыми различными явлениями и процессами, выраженными количественно. Так, в книге П. Мак- [c.310]
Другой интересный математический метод— линейное программирование, предложенное Р. Фогелем для вычисления межобластного общественного сбережения . [c.311]
В начале 1968 г, Э. Фогель-младший, который в то время был вице-президентом по сбыту, фирмы Anheuser-Bus h, предложил группе исследователей заняться решением проблем, связанных с рекламой, и обратить особое даимание на качество рекламных сообщений. Группа начала свою работу с изучения организаций, занимающихся. оценкой рекламных сообщений О каждой из них был собран большой объем информации, на основе которой было отобрано несколько организаций для более тщательного анализа. Затем исследователи посетили каждую такую организацию и ознакомились с методами ее работы. В результате одному из рекламных агентств, методы работы которого группа считала наиболее правильными, было сделано следующее предложение исследователи проводят экспериментальную проверку оценок агентством рекламных сообщений, и если результаты окажутся благоприятными, то агентство может использовать их по своему усмотрению в противном случае в печать не поступает никакой информации о проведенном исследовании. Предложение было принято. [c.185]
Норт (Nort) Дуглас (р. 1920), американский экономист, один из основателей направления институционализма (см. Институциональный подход) в экономике. Лауреат Нобелевской премии по экономике 1993 г. Формула награждения «за работы в области новой экономической истории» (совместно с Р. Фогелем). Образование (включая докторскую степень) получил в Калифорнийском университете (Беркли). Профессор Вашингтонского университета в Сиетле и университета Вашингтона в Сент-Луисе. Исследовал вопросы экономического роста и роль в нем государственных и иных институтов, является ведущим исследователем т.н. клиометрии — исторической науки, использующей методы математико-статистического анализа и математического моделирования. [c.446]
Лит. Ч а р н с А., Купер В. и ХендерсонА., Введение в линейное программирование, [пер. с англ.], М., I960 Г е р ч у к Я., Проблемы оптимального планирования (Линейное программирование), М., 1961 Ю д и н Д. Б., Г о л ь т т е и н Е. Г., Задачи и методы линейного программировании, М., 1961 Рейнфельд Н., Фогель У., Математическое программирование, [пер. с англ.], М., 1960. . Я. П. Герчук. [c.23]
Норт Д. (р. 1920) — американский экономист, один из основателей институционализма в экономике. Лауреат Нобелевской премии по экономике 1993 г. за работы в области новой экономической истории (совместно с Р. Фогелем). Исследовал вопросы экономического роста и роль в нем государственных и иных институтов. Является ведущим исследователем так называемой клиометрии — исторической науки, использующей методы математико-статистического анализа и математического моделирования. [c.47]
В середине 50-х и начале 60-х годов нашего века в американской экономической истории сформировалось новое направление, которое сейчас называется новой экономической историей , или эконометрической историей . Объекты исследований представителей нового направления не отличаются от традиционных тем экономической истории. В обоих случаях главный интерес сосредоточен на изучении экономического развития. Отход же от прошлого, который и позволил новой экономической истории выделиться в самостоятельное направление, заключается в использовании иных, не применявшихся ранее методов исследования. Такими отличительными методическими чертами, по мнению одного из ведущих представителей эконометриче-ского направления, Роберта Фогеля, являются 1) статистическая ориентированность новой экономической истории , 2) приложение экономической теории к изучению экономической истории и 3) попытка дать все объяснения прошлого экономического развития в форме обоснованных гипотетических дедуктивных моделей х. [c.283]
Чтобы исключить это завышение-, Р. Фогель предлагает другой метод вычисления общественного сбережения для внутриобластного случая. Без железных дорог из-за высокой цены фургонных перевозок ведение товар ного сельского хозяйства продолжалось бы только на землях, лежащих не дальше некоторого расстояния от водных путей. Определение этого расстояния выявит зоны, в которых сохранилось бы производство продуктов на продажу. А зная эти зоны, можно было бы разбить вычисление общественного сбережения на две части 1) вычислить разницу между ценой перевозок продуктов с ферм, лежащих внутри зон товарного производства , на рынки, которая действительно была в 1890 г., и ценой перевозки тех же объемов тех же товаров между теми же пунктами, но в случае отсутствия железных дорог (фактически это оценка а для зон товарного производства) 2) определить потерю в национальном доходе, вызванную сокращением товарного сельскохозяйственного производства. Сумма этих двух чисел и даст новую оценку общественного сбережения . [c.298]
Количественный подход к решению различных проблем в настоящее время довольно широко практикуется во многих разделах американской исторической науки. Как видно из приведенного сообщения, в экономической истории этот подход проявился в форме новой экономической истории . Несомненно, использование числовой информации, применение ЭВМ и математических методов для ее обработки — все это способно оказать существенную помощь в исторических исследованиях. Однако, какой бы совершенной ни была используемая методика, ее эффективность и полезность определяются прежде всего теми методологическими концепциями, которыми руководствуется исследователь. Работы американских историков строятся на традиционной для историографии США буржуазной методологии. Именно в этом следует видеть главную причину ряда выводов, полученных на основе применения количественного аппарата некоторыми представителями новой, экономической истории . Мы имеем в виду, например, работы Дж. Мейера и А. Конрада, Я- Ясубы, С. Энгер-мана, Р. Фогеля 20, в которых количественный анализ [c.318]
economy-ru.info
