| «В этом уроке Вы познакомитесь с основными элементами рисунка: точкой, линией и пятном. Вы узнаете об их видах и использовании. Эти элементы являются средствами, при помощи которых можно создать любой рисунок как в иллюзии пространства на плоскости, так и в реальном пространстве. Затем мы познакомимся с другими, «производными» по отношению к упомянутым, элементами рисунка. Итогом нашей встречи станет рассмотрение различных способов рисования. ОТ ТОЧКИ К ФИГУРЕ В ПРОСТРАНСТВЕ Что такое точка Евклид (ок. 365-300 до н. э.) утверждал, что существует неделимая, не имеющая размеров математическая, геометрически воображаемая точка. Портрет Евклида (рис. 1) состоит из похожих, маленьких нарисованных точек с меньшей или большей степенью их концентрации (насыщенности). Практическое задание 1 Нарисуйте контуром, состоящим из точек, произвольную форму, например, человеческую фигуру. Если мы при помощи карандаша зарисуем точками формат прямоугольника (рис. 4), то получим разновидность растра, который издалека выглядит как серая плоскость. Присмотревшись, мы заметим, что эти точки незначительно отлича¬ются друг от друга и располагаются неравномерно. На распечатке подобного рисунка, созданного в компьютерной программе, могли бы получиться идентич¬ные точки, расположенные на одинаковых расстояниях друг от друга. Практическое задание 2 При помощи произвольного инструмента зарисуйте точками формат небольшого квадрата, стараясь соблюдать одинаковую их светлоту, величину, а также одинаковые расстояния между ними. На втором рисунке такого же формата попытайтесь изменить одну из этих характеристик (валёр, размер или расположение). Практическое задание 3 Выполните подобный «frottage» в виде точек. Используйте её как основу (фон) для изображения объекта. Часть полученной фроттажной «графики» сотрите ластиком так, чтобы появившееся белое пятно напоминало определенную форму — к примеру, чашку, дерево, фигуру человека. Практическое задание 4 Выполните в подобной технике (тушью или капиллярной ручкой) рисунок любой другой несложной фигуры. Сами выберите вариант светотеневой моделировки формы объекта — с большей или меньшей концентрацией точек. Объемность в рисунке точками можно по¬лучить при помощи их дифференциации (различия, контраста) по размеру, светло¬те, форме, расположению и т.д. Практическое задание 5 Выберите любую иллюстрацию, наложите на нее прозрачную кальку и перерисуйте изображение двумя способами: первый раз — используя точки одного вида, а второй -дифференцированные (по своему усмотрению). Силуэт — это ограниченное пятно, обозначающее упрощенную форму, очертание предмета. Рисунок объекта мы можем также начать с контура, а затем нарисовать точки на объекте, основании и фоне. Рисунки, помещенные ниже, показывают последовательность такого процесса. Так, на рис. 9а изображен конус, нарисо¬ванный контуром на квадратном формате, разделенном линией на основание и фон. Затем с помощью точек изображаются собственная и падающая тени, а также вертикальная и горизонтальная поверхности фона (рис. 9 б). На последнем рисунке (9е) контурные линии убираются и остаются только теневые фрагменты на фоне редких точек. Обратите внимание на то, что линия контура оказывает более сильное визуальное воздействие, чем деликатно выполненная тень. На рисунке 10а этот же конус нарисован с использованием уже другого художественного приема — таким образом, что образуемые при помощи точек тень и свет (белизна бумажного листа) воздействуют на нас сильнее, чем контур. Следующие рисунки фигур — шара (б) и куба (в) — выполнены по тому же принципу. В них применяется слабый контур и более активно проработанная светотень. От точки к фигуре Оказывается, что любые формы, имеющиеся в натуре, можно получить, исходя из фиксации точки на плоскости — при помощи ее увеличения, изменения или придания объемности. Теперь рассмотрим, в чем именно состоит увеличение точки. Если к точке (рис. 14а) мы прибавим эту же точку, повторенную многократно и расположенную без разрыва одна за другой, то получим сначала короткий отрезок (14 б), а потом — линию (в). Изменяя направление развития точки, мы можем вместо прямой линии получить кривую (г). Если мы последовательно увеличим количество правильных точек, то получим линию с правильными краями, если увеличим неправильные точки — получим рваную линию (д).
Осуществляя ряд постепенных, начинающихся с точки преобразований, мы в результате можем получить различные плоские или объемные элементы. Затем, если мы размоем плоскую фигуру или силуэт, то получим пятно (рис. 17). Накладывая друг на друга в определенной композиционной последовательности такие разные элементы, мы сможем получать разнообразные, художественно более выразительные и сложные формы. Точка — исходное понятие геометрии, не имеющее измерения. Линия — это последовательно расположенная в одном направлении группа точек, не имеющая разрывов. Пятно — это группа точек с нечеткими границами (очертаниями). Растр — это изображение простого рисовального или графического знака, многократно повторяемого в определенной последовательности. Плоская фигура — это ограниченное формой пятно. Элементы рисунка можно наносить разными инструментами (карандашом, углем, кистью, пером, фломастером, и т. д.) с использованием различных материалов и техник (черная тушь, нанесенная пером; белая гуашь, наложенная кистью или поролоновой губкой на разную основу — бумагу, кальку, картон, стекло и т. д.). Таблица, приведенная ниже, представляет основные звенья в цепочке элементов рисунка, полученных из точки в результате ее развития (преобразования), а рядом — их объемные эквиваленты. Элемент рисунка-Его объемный эквивалент точка-объемная точка Предыдущие примеры, демонстрирующие увеличение, произвольное изменение или придание объемности точке, являющейся изображением (записью) на плоскости воображаемой математической точки, наглядно убеждают в том, что из неё можно получить все объемные элементы и формы, включая трехмерные фигуры. Очевидно, что более развитые элементы рисунка, находящиеся в цепочке на удаленных местах, можно получить из элементов, расположенных ближе к ее начальному звену — точке. К примеру, фигуру человека можно нарисовать точками, контуром, пятном, силуэтом и т. д. Перед тем, как мы рассмотрим более подробно некоторые примеры плоских и объемных элементов, встречающихся в натуре, запомним для себя простой, но важный вывод: все изображения на рисунке возникают из точки, линии, пятна и их взаимных комбинаций. ЧТО ТАКОЕ ЛИНИЯ Линия в натуральной перспективе Надеюсь, Вы хорошо усвоили, что натуральная сходящаяся перспектива подра¬зумевает воображаемые линии, сходящиеся в воображаемой точке схода, лежащей на линии горизонта. На рисунках из предыдущего урока, иллюстрирующих сходящуюся перспективу, нанесенных там линий в действительности не существует. Следует отличать видение линии в натуре от видения линии в рисунке. Мы уже говорили о том, что в природе нет линий, которыми были бы обведены какие-то формы, а значит, в натуре не существует контура — линии, очерчивающей форму. В то же время на рисунке мы можем увидеть следующие линии: самостоятельную, контурную или тонирующую (светотеневую). Самостоятельная линия Линии этого вида встречается очень часто. Они наиболее произвольны по своему характеру, направленности и не отображают конкретной формы. Такие линии выступают в рисунке «сами по себе», то есть как самостоятельный изобразительный элемент. Посмотрите на рисунок 19, который выполнен семилетней Евой. Здесь основой для изображаемой фигуры (моей!) являются, собственно, разновидности этого вида линии. Она будет еще часто появляться в иллюстрациях этого выпуска, а в каких именно — постарайтесь определить сами. Контурная линия и «воздействие» контура Еще раз посмотрите на рисунок Евы, которая на уровне незамысловатого детского воображения изобразила очертание фигуры. Аналогичным образом она нарисовала тучки, цветок и два других неизвестных растения. В её рисунке присутствуют контурные и самостоятельные линии. В ушах, чем-то напоминающих воздушные шарики, тоже есть замкнутые контуры. Помните мою фотографию, напечатанную в первом уроке? Сравните с ней рисунок. Очень удачный получился у ребенка портрет, неправда ли? Тонирующая линия — это, другими словами, светотеневая линия. Она применяется там, где, согласно нашему воображению или видению объектов в натуре, мы хотим на рисунке ввести тень. Мы можем наносить эти линии так, как это показано на рис. 27, где партию света играет естественная белизна бумажного листа. Штриховка — это один из наиболее распространенных приемов тонирования в рисунке или графике с помощью как идентичных параллельных, так и (или) пересекающихся линий. Нарисуйте контуром простой предмет, расположенный на горизонтальной плоскости. Затем, используя приемы разнообразной штриховки, постарайтесь выразить его форму с собственной падающей тенью и условной передачей фона и основания. Думаю, что иллюстрация рисунка Леонардо да Винчи поможет Вам правильно выполнить задание. Линия (черта) возникает из последовательного сочетания многих точек. В рисунке ее получают путем передвижения рисовального инструмента, оставляющего след на поверхности формата. Зарисовка всей плоскости формата линией Зарисовка квадратного формата мелким растром (сеткой из тонкой линии одного вида, то есть без каких-либо контрастов) привела к появлению своего рода серого пятна, плоскости в одинаковом валёре (рисунок 35а выполнен в компьютерной графике). Следующий рисунок более дифференцированный, поскольку вертикальные, под линейку нарисованные линии различаются между собой по светлоте и толщине, воздействуя при этом более сильно в той части, где они темнее и насыщеннее (356). На рис. 38 показана градация прямой вертикальной линии в шести стадиях: от темной широкой — до светлой тонкой (рис. 38а). Близлежащие линии между собой не контрастируют, зато если мы сравним крайние линии, то контраст между ними очевиден. Из прямой геометрической линии можно также получить линию иного вида, например, зигзагообразную, как на иллюстрации 39; где контраст наглядно виден уже между каждой линией. Для одного и того же вида линии возможны варианты преобразования, которые представлены на следующих рисунках. Рисунок 41а демонстрирует отдельную волнистую линию -промежуточную между биологической и геометрической, многократно повторенную с одинаковым промежутком в формате квадрата. Рисунок выглядит как изображение волнистой выпуклой или вогнутой плоскости. Если мы сделаем линии более толстыми, а также увеличим расстояния между ними, то получим такой набор линий, как на рис. 416, а если будем утолщать их и дальше — такой, как на рис. 41 в. В последнем рисунке введены контрасты за счет чередования тонкой и толстой линий, взятых из рис. 41а и 41в и изменения их наклона. Практическое задание 7 В иллюстрации рисунка Леонардо да Винчи, на который я уже дважды ссылался, попытайтесь найти линии, аналогичные представленным на рисунках 42.
Перекрывающее наложение линий Нанесение линий с перекрытием, то есть, таким образом, когда одна заслоняет другую, также часто используется в рисунках. В зависимости от степени контраста линий между собой, их размера и расположения, возникает определенный оптический эффект. |
tyblako.livejournal.com
Как создаются 3D рисунки. — Как это сделано, как это работает, как это устроено
В этом посте я расскажу о принципах создания 3d-рисунков на асфальте и не только на нем. Под словом асфальт подразумевается горизонтальная плоскость по которой мы ходим каждый день, это может быть и бетон и деревянная основа, стекло и даже песок, да-да сейчас есть и такое- 3d рисунок на песке. Так уж повелось, что у нас его стали называть «на асфальте», видимо потому, что в детстве мы говорили: «Рисунок мелом на асфальте», хотя зачастую рисовали их больше на бетоне, возможно что слово бетон не звучит. За рубежом в буквальном переводе- 3d уличная живопись на англ. 3d street painting.
Многие из вас, кто сейчас читает эту статью уже знакомы с таким видом уличного искусства по фотографиям, которые находили в интернете или даже может кто из вас видел 3d-рисунки вживую, а может даже и пытался создать собственноручно и наверняка большинство задавалось вопросом, а как же уличные художники добиваются 3d-эффекта?
Уверен, что часть из вас уже сейчас воскликнула: «Тю, да что тут секретного!?…Это же элементарная проекция изображения на плоскость!» И будут правы. Я бы уточнил, что это проекция + перспектива, хотя конечно же понятие проекции не может быть разделено от перспективы, это взаимодействующие понятия.

Так с чего же начинается работа над 3d-рисунком? А работа начинается как и у всех художников, с определения сюжета и разработки эскиза, который зависит от размеров площадки на котором будет выполняться рисунок. Вы спросите каким образом сюжет зависит от размеров площадки?

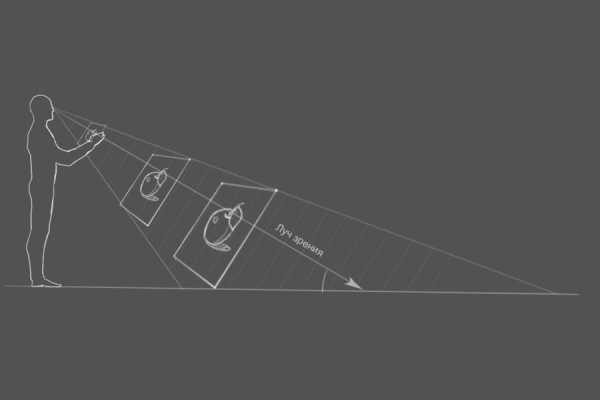
Для этого нужно понимать, что рисунок на асфальте это проекция на плоскость, которая находится к нам под углом и имеет свое перспективное сокращение и если вы решили изобразить объект, который больше человеческого роста, предположим взрослого медведя нападающего на человека, которым будет являться фотографируемый, то такой рисунок у нас растянется на многие метры, это при условии, что высота в точке осмотра, с которой человек смотрит на рисунок, равна среднему росту человека. Поэтому иногда художники могут используют комбинацию из плоскости под ногами и стенкой, а то и двумя стенками при которой задействуються три и четыре плоскости (пол, потолок и две стенки)- угловая часть комнаты.

На этом изображении вы можете видеть как изменяются размеры изображения во время проецирования на плоскость лучом зрения. И чем острее будет угол луча зрения к плоскости асфальта, тем более вытянутым у нас будет рисунок.
Да знали это все и без тебя, давай дальше!
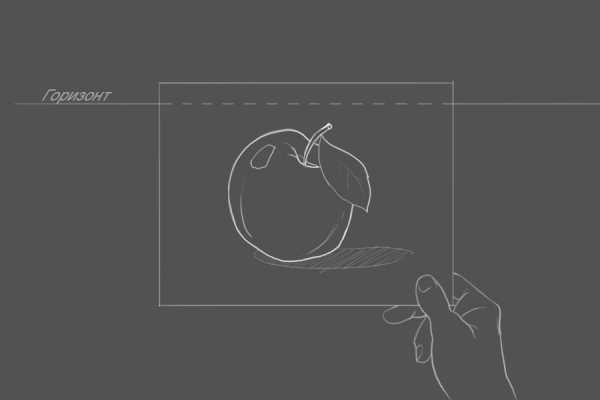
После того как вы определились с эскизом, вам нужно его перенести на плоскость в нашем случае асфальт. Как же это сделать?
Часть из вас уже воскликнула, да с помощью проектора! Да, отвечу я, можно и с помощью проектора, но есть одно маленькое условие, рисунок вам нужно выполнить в течении одного светового дня, как это может происходить предположим на фестивале, при котором процесс использования проектора становиться невозможным- проецируемое изображение попросту не видно при ярком свете. Итак как!?…
Для этого буду по чуть-чуть вводить вас в курс предмета перспектива и способом построения геометрических предметов в пространстве- метод архитектора. Почему геометрических? Потому что для начала нам нужно будет построить сетку в пространстве. Этот метод знаком в большей степени художникам и архитекторам соответствующих учебных заведений, хотя кто-то сталкивался с основами в предмете черчение.
Из точки осмотра 3d рисунок должен выглядеть точно так, как у вас на эскизе.
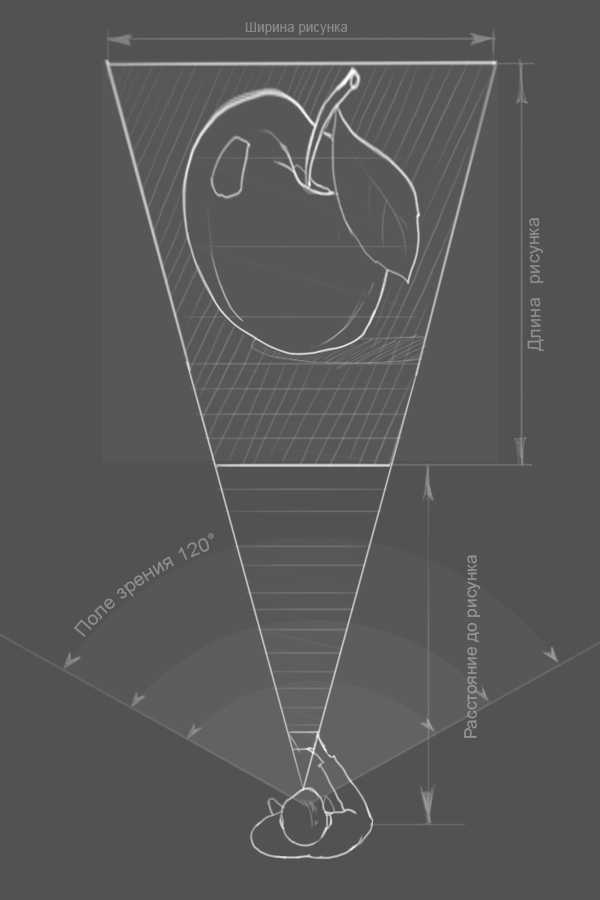
В то же время на асфальте рисунок яблока будет выглядеть следующим образом (вид сверху). Видно как деформируется рисунок на плоскости, поэтому на 3d-рисунок или как его еще могут называть анаморфный рисунок, не путать с аморфным!:) нужно смотреть только с одной точки.
На схеме показано поле зрения у человека это прбл. 120°.
Точка осмотра для зрителя обозначается таким знаком (который использую я) или любым дуругим, дающий понять человеку, что находиться и снимать нужно именно здесь и именно в этом направлении. Так что искать для качественной фотографии нужно именно такой знак.

Пару фоток для понимания насколько рисунок меняется в размерах.
На этом фото 3d-рисунок на асфальте, через объектив камеры с назначенной точки осмотра.

А вот как рисунок трансформируется (вид с обратной стороны)
Нарисованный канализационный люк, который выглядит с точки осмотра (там где стоит штатив) круглым лежащим блином, ширина которого больше длины почти в два раза, на самом деле имеет форму вытянутого в длину овала, который имеет противоположные величины- длина больше чем ширина.

Пример использования двух плоскостей для 3d-рисунка

Как выглядит деформация такого рисунка с другой точки просмотра.

Для начала нужно задать размер прямоугольной площадки, которая будет захватывать ваш рисунок на асфальте и определить перспективный масштаб, а именно масштаб длины и ширины. Для этого на листе бумаги нужно наметить горизонт и провести линию H, параллельную горизонту, эта линия является краем картинной плоскости на нашем чертеже до которой мы еще дойдем, на асфальте же эта линия является краем прямоугольной сетки, которая будет разбита на квадраты размером 50×50 см.
Размер этот задается художником произвольно, в зависимости от сложности изображения, по принципу чем больше деталей, тем меньше квадраты- для более точного определения положения линий в рисунке.
Все мы помним про то, что горизонт проходит на уровне глаз человека, при условии если луч зрения человека смотрящего на эту фигуру находиться на одной высоте, т.е грубо говоря если эти фигуры одинакового роста. И разумеется если кто-то выше или ниже, линия горизонта у нас меняеться.
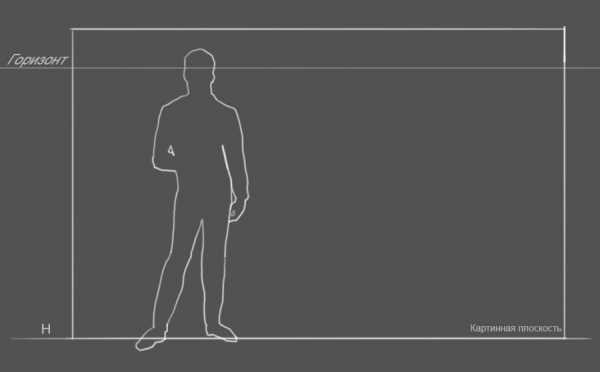
Таким образом зная рост человека (возьмем средний рост 170 см) мы можем задать метраж на картинной плоскости, т.е на линии H.
Далее проводим осевую линию, которая находится под углом 90° к краю картинной плоскости, в даном случае к линии H.
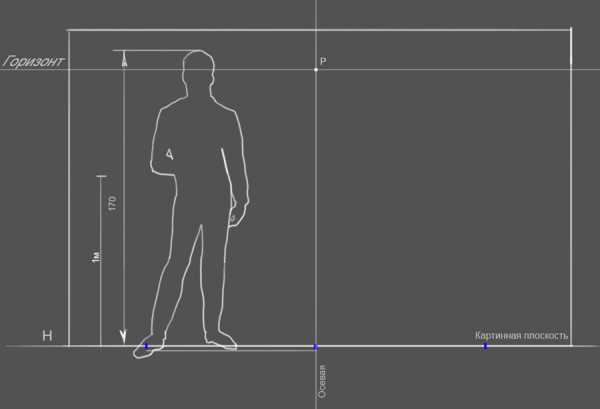
Для удобства я разбиваю метровые отрезки по полам и соединяю с точкой P на горизонте, получив таким образом точку схода P и масштаб длины отрезков, которые у нас равны 50 см.
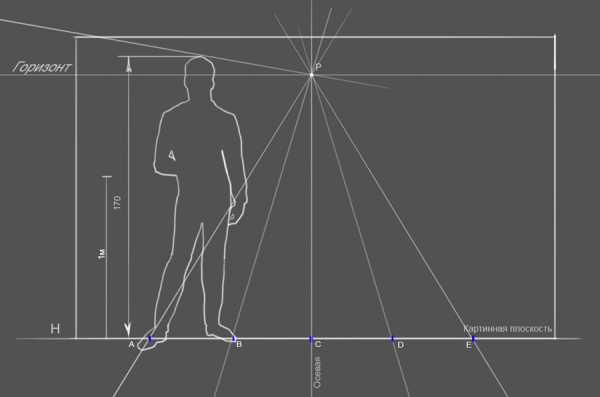
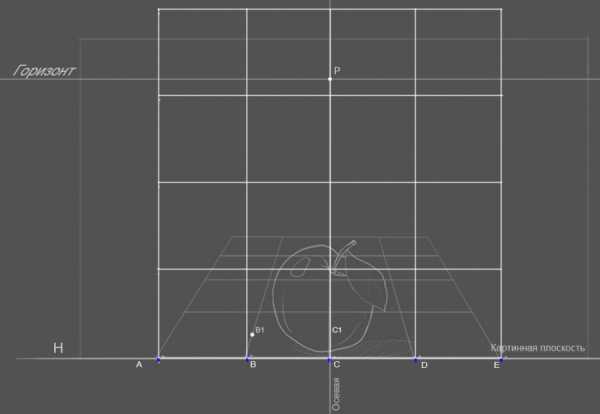
Теперь основное, нам нужно определить масштаб ширины или можно еще сказать масштаб глубины отрезка длинной 50см. Проще говоря нам нужно определить насколько визуально у нас будет сокращаться сетка в перспективе, положенная на асфальт. Рекомендую изначально запастись форматом бумаги для чертежа побольше.
Задаем расстояние до основной точки осмотра (с которой публика будет фотографировать 3d рисунок) т.е до края вашего рисунка (вернее сказать до края вашей будущей сетки на асфальте) Я задаю 2 метра, художник произвольно задает дистанцию, которая ему необходима, но не думаю что ее имеет смысл делать меньше 1.5 метра.
На осевой линии нашего чертежа, от края картинной плоскости, чем является линия H, откладываем расстояние 2 метра в итоге получая отрезок CN. Сама эта точка N для дальнейшего построения чертежа не играет роль.
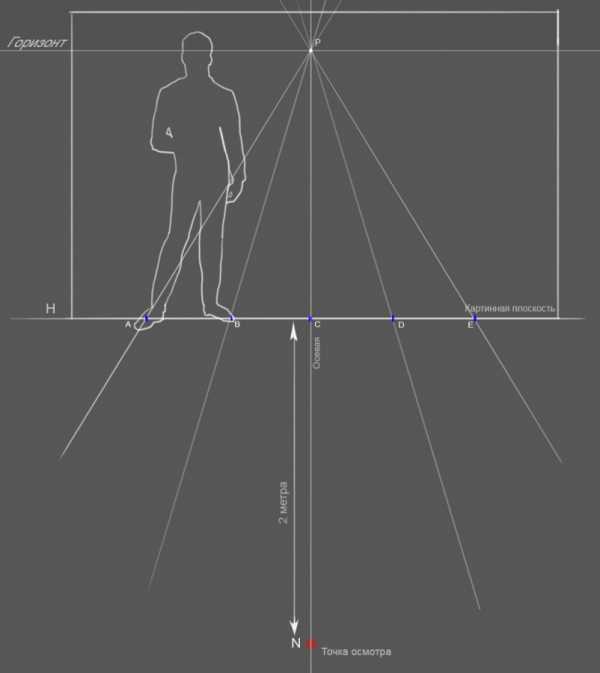
Далее нам нужно получить дистанционную точку D1 на горизонте, из которой луч будет пересекать картинную плоскость под углом в 45° , в точке C, это поможет нам определить вершину квадрата. Для этого задаем расстояние в два раза больше высоты фигуры человека, поскольку фигура является объектом от которого мы и ведем измерение. Почему в 2 раза от картинной плоскости? Причина в устройстве человеческого глаза, угол захвата по ширине у нас больше чем по высоте. Для более-менее нормального, не искаженного восприятия, нам нужно находиться на растоянии от объекта в два раза превышающего его высоту)
Таким образом получаем точку Q (на площадке она нам не понадобиться). От основной точки схода P отложим (можно с помощью циркуля) отрезок равный PQ на линии горизонта, таким образом получив точку D1 и D2, чаще всего она у вас будет выходить за лист бумаги, поэтому отрезок PQ делится на 2 для получения точки D½ и на четыре для точки D¼. Проведя луч через точки D1,C мы получаем прямую, которая пресекает плоскость картины под углом в 45° в перспективе.
Полученная точка B1 отрезка BP является вершиной квадрата, отрезок B,B1 -стороной длинною 50см в перспективе.
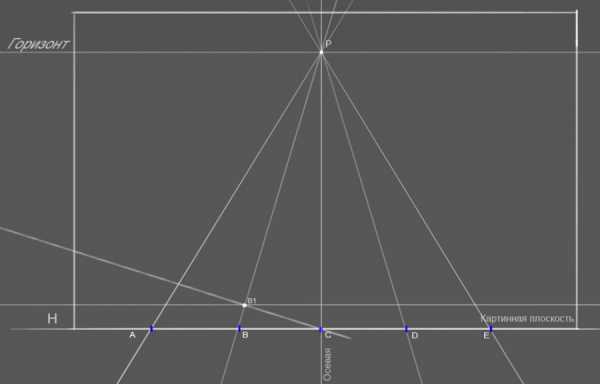
Как я говорил выше, дистанционная точка D1 выходит за лист бумаги, для удобства отрезок D1,P делится на четыре части и получаем точку D¼
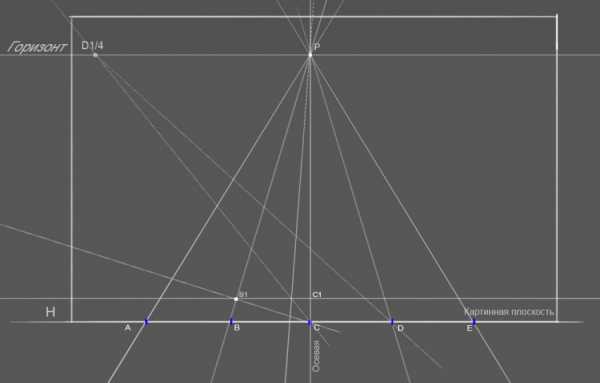
Используя дистанционную точку D¼ учитывайте, что в данном случае лучи пересекают сторону квадрата B1,C1 под другим уже углом (это в прбл. 75° ) к картинной плоскости. И для нахождения точки пересечения, отрезок BC делится на четыре равные части как и любой другой отрезок на линии картинной плоскости, из точки пересечения проводиться прямая в точку схода P , из D¼ в С- точка перечечения и будет определять сторону B1,C1 как это и делает луч проведенный из D1 в С.
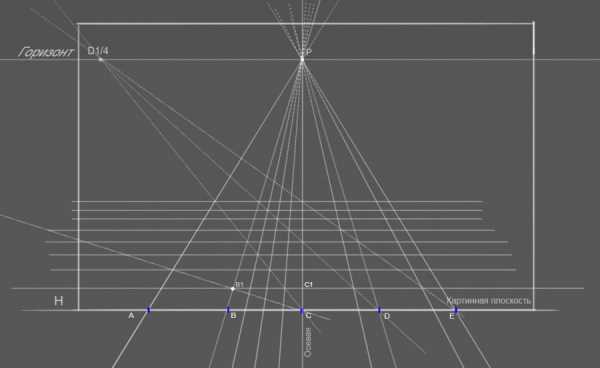
Таким хитрым способом на пересечениях лучей из дистанционной точки с лучами сокращений AP, BP, CP, DP, EP мы получаем сетку размером 2 на 2 метра в перспективном сокращении с размером квадратных секций 50х50 см. Вуаля!
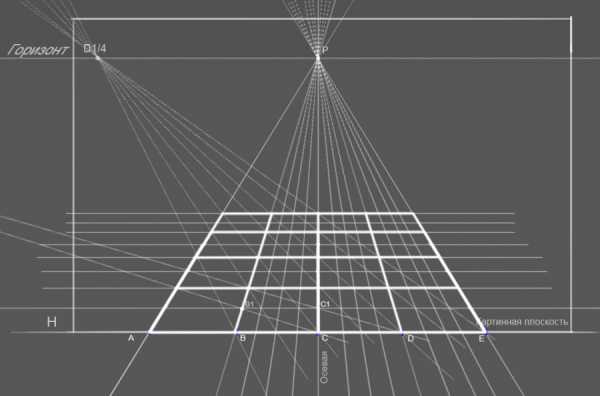
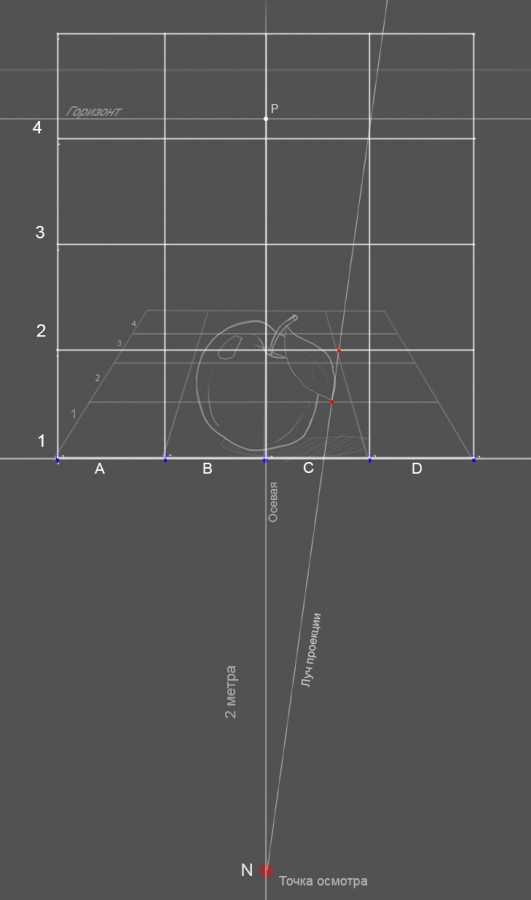
Высота фигуры человека на картинке и высота смотрящего, находящегося в точке осмотра -170 см., расстояние до точки осмотра-2 метра.
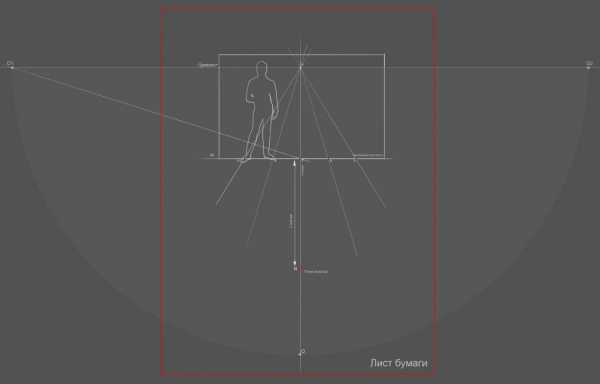
Как вы можете видеть на фото ниже, поместив наш эскиз яблока на полученую сетку, 3d-рисунок с точки осмотра на площадке должен выглядеть точно так же, как и на эскизе, т.е без искажений и деформаций.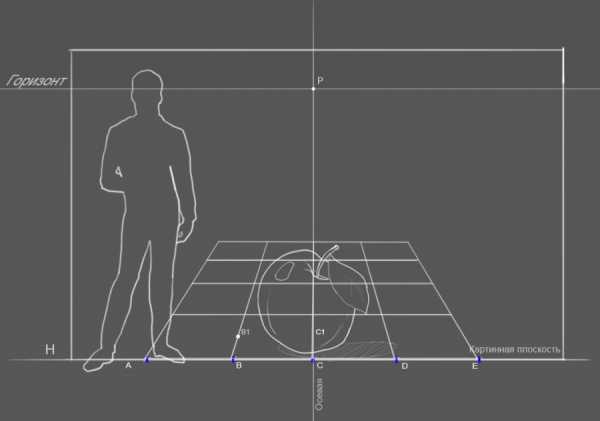
Теперь нам нужно начертить сетку без искажений, это наш проекционный эскиз, с которым мы и будем работать на площадке и переносить изображение на асфальт.
Строится наша сетка на крае картинной плоскости, которым является у нас прямая H, сетка будет параллельна картинной плоскости и перпендикулярна плоскости основания, т.е «асфальту». Размер квадратов сетки все тот же-50 см, на чертеже конечно же он у вас в выбранном вами масштабе.
Далее следите за руками… Нумеруем для удобства квадраты. Проводим луч, я назвал его «луч проекции», из точки осмотра N, в точку любого пересечения нашего рисунка с сеткой, которая лежит у нас в перспективе, я выбрал край листика яблока- он находится на линии нашей сетки в перспективе (основание квадрата С2). Пересекая нашу обычную сетку, которая параллельна нам, луч проекции отбивает точку, которая и является краем нашего листика яблока.
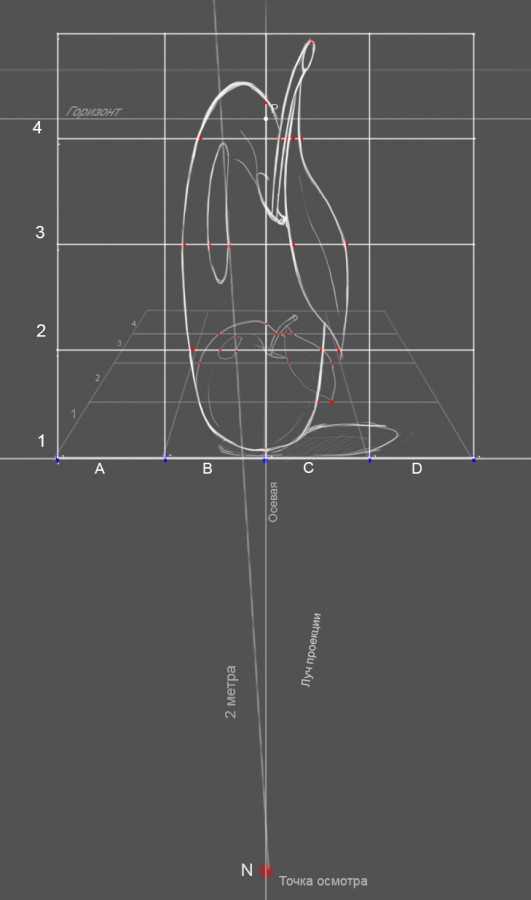
Таким хитрым способом мы находим все точки пересечения на нашей сетке. Точки которые попадают на осевую линию, находятся методом пропорционального расчета.
Для достижения более точного результата построения деталей и линий 3d-рисунка, сетка задается меньшим шагом клетки.
Соединяем все точки плавной линией, как это было в детском садике когда-то …
3d-рисунок в проекционном эскизе готов!
Как видно из полученного результата эскиз у нас получился деформированным. Теперь осталось его перенести на асфальт в натуре, где вы уже расчертили сетку сидите и ждете.
По такому же принципу изображение выстраивается на стенах и потолках. Тут и сказочки конец.
И не забывайте, что 3d-рисунок это в первую очередь рисунок, который требует навыков рисования,владения цветом и композиции, в противном случае работа может получиться не эффектной.
Несмотря на то, что 3d рисунок называется рисунком, он может быть выполнен и краской, где по логике вещей его правильнее было бы называть 3d-живописью на асфальте, но так случилось, что называть у нас его стали рисунком, напомню за рубежом чаще всего называют 3d уличная живопись- 3d street painting, хотя иногда можно встретить термин 3d drawings как у нас.

Взят у maksiov в Секрет создания 3D рисунка. Часть1 и Секрет создания 3D рисунка Часть2
Если у вас есть производство или сервис, о котором вы хотите рассказать нашим читателям, пишите на [email protected] Лера Волкова ([email protected]) и Саша Кукса ([email protected]) и мы сделаем самый лучший репортаж, который увидят не только читатели сообщества, но и сайта http://bigpicture.ru/.
Подписывайтесь также на наши группы в фейсбуке, вконтакте, одноклассниках и в гугл+плюс, где будут выкладываться самое интересное из сообщества, плюс материалы, которых нет здесь и видео о том, как устроены вещи в нашем мире.
Жми на иконку и подписывайся!
kak-eto-sdelano.livejournal.com
Положение плоскости картины — Урок 3.3
Держите лист прозрачного пластика или кусок стекла вертикально перед глазами. Вы видите предмет или местность перед собой через прозрачную поверхность. Если вы нарисуете на стекле эту сцену так, как вы ее видите, у вас получится рисунок в перспективе. Прозрачную поверхность в данном случае можно считать чем-то вроде листа рисовальной бумаги или холста на мольберте. В данном случае поверхность, что бы она собой ни представляла, называют плоскостью картины. Поразмыслим о рисунке в перспективе, изображенном на плоскости картины.
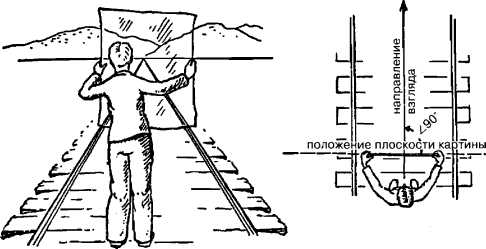
Плоскость картины стоит прямо (перпендикулярно) между художником и объектом, который он рисует. Кроме того, плоскость картины размещается прямо поперек той линии (направления), в котором смотрит художник (под прямым углом к ней). Схема справа от рисунка объясняет это расположение.
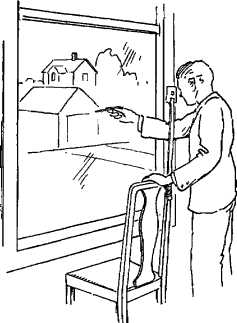
Рисование в перспективе на плоскости картины можно понять, если встать перед окном и при помощи тонкого маркера нарисовать на стекле контуры здания, которое вы видите за окном. При этом маркер должен точно проследить эти линии так, как вы видите их.
Чтобы помочь зафиксировать точку зрения, можно взять листок бумаги с отверстием в нем и поместить его на расстоянии длины руки от окна. Смотрите в это отверстие и рисуйте так, как если бы окно представляло собой поверхность бумаги. Просто обрисуйте на стекле линии зданий и ландшафта так, как вы видите их сквозь окно. В результате у вас получится рисунок в перспективе.
Предположим, что мы вынем из рамы стекло, на которое нанесен этот рисунок, и положим его на стол. На столе оно будет выглядеть, как любой другой рисунок в перспективе, нарисованный, к примеру, на бумаге.
Как можно нарисовать такой рисунок, не обводя его для начала н
risovatlegko.ru
Плоскость и пятно- Уроки ИЗО
Цель: установить равновесие между изобразительной плоскостью и изображением.
Нужно напомнить, что восприятие любого предмета (пятна) человеком должно идти по следующей системе:
- расположение предмета в пространстве;
- величина расстояния между предметами;
- степень яркости предмета.
Материал: кисть, черная и белая гуашь, белый картон, черная и серая бумага.
Упражнение по композиции в рисунке № 1.
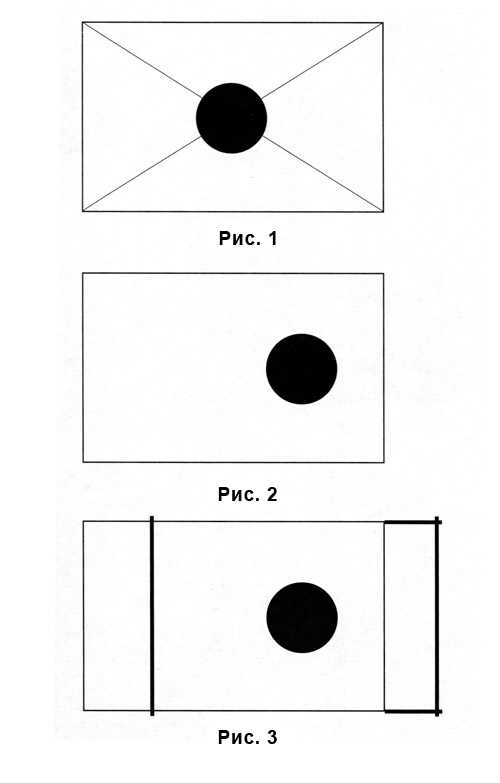
Вырежьте из белого картона прямоугольник или квадрат размерами не менее 15 см по меньшей стороне и круги из черной или серой бумаги диаметром 5-6 см. Найдите с помощью диагоналей центр плоскости и положите черный круг (рис. 1). В этом положении круг будет иметь самое устойчивое положение.
Теперь сдвиньте круг вправо до того момента, когда глаз станет воспринимать его стремящимся выскочить за пределы плоскости (рис. 2).
Образовавшееся расстояние между кругом и краем плоскости как бы нуждается в дополнительном пространстве.
Возьмите лист бумаги, зафиксируйте это положение и добавьте справа формат фона до того момента, когда это чувство необходимости дополнительного пространства исчезнет, очертите формат четко (рис. 3).
Двигая круг, можно заметить, что он не просто занимает определенное место на плоскости, но кажется в некоторых точках плоскости каким-то нетерпеливым, неустойчивым. Возникает внутренняя невидимая линия, по которой круг стремится к движению в каком-то определенном направлении. Появляется это ощущение оттого, что круг начинает взаимодействовать с окружающей его плоскостью (рис. 4).
Упражнение по композиции в рисунке № 2.
Передвигайте круг в различных направлениях по отношению к плоскости, каждый раз внимательно наблюдая за ним и фиксируя в себе вызванные чувства. Можно заметить, что в одних случаях круг будет казаться более устойчивым, в других — вызывать нити натяжения в определенных направлениях, в третьих — неопределенное состояние, в четвертых — колеблющееся.
Фиксируйте на бумаге те положения круга, когда он кажется более устойчивым.
Упражнение по композиции в рисунке № 3.
Перемещая круг по диагоналям плоскости, наблюдайте, когда появится неприятное чувство. Оно возникнет при неопределенном положении круга. Глаз не может решить, в каком направлении происходит давление на круг со стороны границ плоскости. Если возникает неприятное чувство, сдвиньте круг по диагонали к центру и сделайте рисунок.
После проведения таких, казалось бы, очень простых упражнений глаз начинает настраиваться на определенный режим восприятия плоскости и пятна.
Итак, в центре плоскости все силы натяжения находятся в состоянии равновесия. Самое спокойное состояние круга — центральное (рис. 5).
Второе спокойное состояние круга находим, перемещая его по диагоналям. Остановится «спокойный круг», не дойдя до угла плоскости на расстояние примерно своего радиуса.
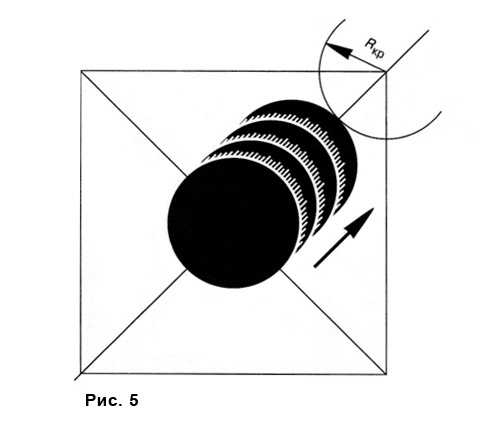
Упражнение по композиции в рисунке № 4
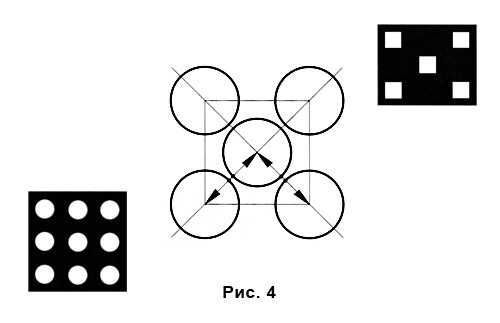
Возьмите два одинаковых черных круга и плоскость. Перемещая круги по плоскости и относительно друг к другу, можно заметить, что возникает эффект взаимодействия не только между кругом и плоскостью, но и между кругами.
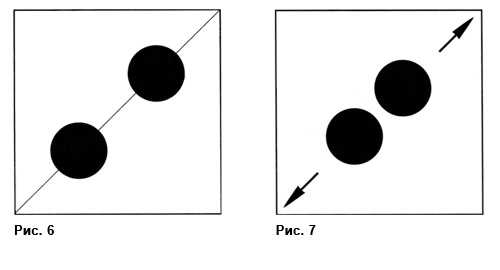
Если два круга рядом, они притягиваются и выглядят как одно целое пятно. Передвигая два круга по плоскости, добейтесь стабильного состояния при восприятии кругов и плоскости как единого (рис. 6).
Круги являются симметричной парой, но в целом композиция не уравновешена, так как глаз не может остановиться у какого-либо края плоскости, а свободные углы плоскости давят и вытягивают группу в «узкую нитку».
Если круги очень близко расположены, они будут «отталкиваться» друг от друга (рис. 7).
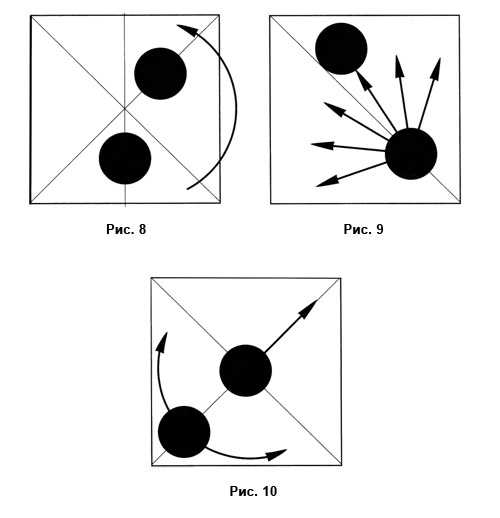
Поставьте один круг по вертикальной оси ниже геометрического центра, а второй водите по радиусу, добиваясь баланса между группой и белым полем (рис. 8).
Поставьте один круг по диагонали плоскости, а второй двигайте по направлению луча, исходящего из центра первого круга, в различных направлениях (рис. 9).
Положите один круг строго в центре, а второй — по диагонали. Затем сдвиньте круги на такое расстояние и в том направлении, чтобы они замкнули оставшееся белое поле (рис. 10).
Упражнение по композиции в рисунке № 5
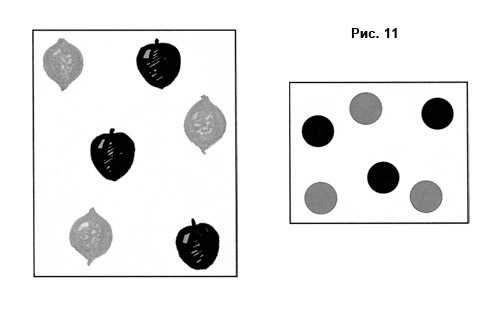
Положите на плоскость три черных и три серых круга. Добейтесь равновесия между белым полем и пятнами так, чтобы одноцветные пятна стремились друг к другу.
Лучшее расположение появляется тогда, когда круги одного цвета образуют треугольник. Черные круги будут стремиться к сближению и отталкиваться от серых (рис. 11, 12).

Упражнение по композиции в рисунке № 6
Возьмите восемь одинаковых кругов и расположите их группами (3+3+2) так, чтобы различные по расположению группы уравновешивали белое или черное поле (рис. 13).

Упражнение по композиции в рисунке № 7 (для самостоятельной работы).
Положите в любом месте плоскости черный круг, сдвинув его от центра, а затем несколькими кругами замкните белое поле, придав определенное направление всей композиции.
Авторы: Жабинский В. И., Винтова А. В.
urokizo.ru
Построение геометрических фигур по точкам на координатной плоскости
Данная программа позволит Вам построить практически любой многоугольник. Все что Вам надо сделать, это ввести количество точек, которые Вы хотите соединить, затем ввести их координаты и программа построит Вашу геометрическую фигуру на координатной плоскости.
Сейчас Вам нужно выбрать количество точек, которое Вы хотите соединить. Помните, что фигура должна быть замкнута, тоесть ломаная должна начинаться и заканчиваться одной и той же точкой. Суммарное количество точек будет на 1 больше количества вершин многоугольника.
Также, при помощи нашей программы, можно просто строить фигуры, делать чертежи к задачам. Для этого надо указать, что Вы хотите убрать координатные оси и не хотите около каждой точки писать ее координаты. Для таких рисунков Вам понадобится размеченая плоскость, для узнавания точек, которые вы хотите соединить.
Ниже Вы можете посмотреть примеры использования программы!
Сколько точек Вы хотите соединить?
Примеры использования программы
1) Изображение схемотичного рисунка к задаче. Подобный рисунок был нужен, когда на нашем форуме просили решить задачу — тема на форуме.
Рисунок к данной задаче.
Для того, чтобы наисовать такую схему нужно отменить координатные оси и отменить писание координат точек.
2) Рисунок к задаче, построение фигуры по точкам. Наример построение высоты в треугольнике.
Рисунок к данной задаче.
Программа имеет много применений, только надо включить фантазию!
Если после использования данного онлайн калькулятора (Построение геометрических фигур по точкам) у Вас возникли какие-то вопросы по работе сервиса или вопросы образовательного характера, то Вы всегда можете задать их на нашем форуме.
Вы поняли, как решать? Нет?
Помощь с решением
Добавить комментарий
www.webmath.ru
Начертательная геометрия. Теория.
Краткий курс начертательной геометрии
Лекции предназначены для студентов инженерно–технических специальностей
Введение
Тема 1. Проецирование точки
Тема 2. Проецирование прямой
Тема 3. Положение прямой относительно плоскостей проекций. Следы прямой
Тема 4. Плоскость. Способы задания плоскостей
Тема 5. Положение плоскости. Следы плоскости
Тема 6. Взаимное положение прямой и плоскости
Тема 7. Взаимное положение плоскостей
Тема 8. Плоскопараллельное перемещение. Вращение. Замена плоскостей проекций
Начертательная геометрия входит в состав учебной дисциплины федерального значения, название которой в зависимости от специальности: «Начертательная геометрия и инженерная графика», «Инженерная и машинная графика» или просто «Инженерная графика». Инженерная графика – это единственная дисциплина целью, которой является непосредственно обучение студентов работе с различной по виду и содержанию графической информацией, основам графического представления информации, методам графического моделирования геометрических объектов, правилам разработки и оформления конструкторской документации, графических моделей явлений и процессов.
Тема 1. Проецирование точки
Если информацию о расстоянии точки относительно плоскости проекции дать не
с помощью числовой отметки, а с помощью второй проекции точки, построенной
на второй плоскости проекций, то чертеж называют двухкартинным или комплексным.
Основные принципы построения таких чертежей изложены Г. Монжем.
Изложенный Монжем метод — метод ортогонального проецирования, причем берутся
две проекции на две взаимно перпендикулярные плоскости проекций, — обеспечивая
выразительность, точность и удобоизмеримость изображений предметов на
плоскости, был и остается основным методом составления технических чертежей
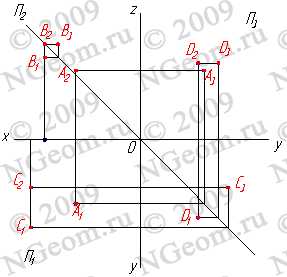
Рисунок 1.1 Точка в системе трех плоскостей проекций
Модель трех плоскостей проекций показана на рисунке 1.1. Третья плоскость, перпендикулярная и П1, и П2, обозначается буквой П3 и называется профильной. Проекции точек на эту плоскость обозначаются заглавными буквами или цифрами с индексом 3. Плоскости проекций, попарно пересекаясь, определяют три оси 0x, 0y и 0z, которые можно рассматривать как систему декартовых координат в пространстве с началом в точке 0. Три плоскости проекций делят пространство на восемь трехгранных углов — октантов. Как и прежде, будем считать, что зритель, рассматривающий предмет, находится в первом октанте. Для получения эпюра точки в системе трех плоскостей проекций плоскости П1 и П3 вращают до совмещения с плоскостью П2. При обозначении осей на эпюре отрицательные полуоси обычно не указывают. Если существенно только само изображение предмета, а не его положение относительно плоскостей проекций, то оси на эпюре не показывают. Координатами называют числа, которые ставят в соответствие точке для определения ее положения в пространстве или на поверхности. В трехмерном пространстве положение точки устанавливают с помощью прямоугольных декартовых координат x , y и z (абсцисса, ордината и аппликата).
К началу страницы
Тема 2. Проецирование прямой
Для определения положения прямой в пространстве существуют следующие методы: 1.Двумя точками ( А и В ). Рассмотрим две точки в пространстве А и В (рис. 2.1). Через эти точки можно провести прямую линию получим отрезок [AB]. Для того чтобы найти проекции этого отрезка на плоскости проекций необходимо найти проекции точек А и В и соединить их прямой. Каждая из проекций отрезка на плоскости проекций меньше самого отрезка: [A1B1]<[AB]; [A2B2]<[AB]; [A3B3]<[AB].
Рисунок 2.1 Определение положения прямой по двум точкам
2. Двумя плоскостями (a; b). Этот способ задания определяется тем что две непараллельные плоскости пересекаются в пространстве по прямой линии (этот способ подробно рассматривается в курсе элементарной геометрии).
3. Точкой и углами наклона к плоскостям проекций. Зная координаты точки принадлежащей прямой и углы наклона ее к плоскостям проекций можно найти положение прямой в пространстве.
К началу страницы
Тема 3. Положение прямой относительно плоскостей проекций. Следы прямой
В зависимости от положения прямой по отношению к плоскостям проекций она может занимать как общее, так и частные положения. 1. Прямая не параллельная ни одной плоскости проекций называется прямой общего положения (рис.3.1).
Рисунок 3.1 Прямая общего положения
2. Прямые параллельные плоскостям проекций, занимают частное положение в пространстве и называются прямыми уровня. В зависимости от того, какой плоскости проекций параллельна заданная прямая, различают:
2.1. Прямые параллельные горизонтальной плоскости проекций называются горизонтальными или горизонталями (рис.3.2).
Рисунок 3.2 Горизонтальная прямая
2.2. Прямые параллельные фронтальной плоскости проекций называются фронтальными или фронталями(рис.3.3).
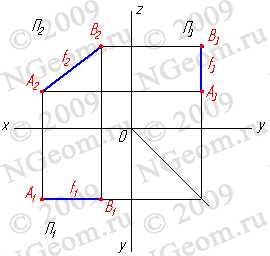
Рисунок 3.3 Фронтальная прямая
2.3. Прямые параллельные профильной плоскости проекций называются профильными (рис. 3.4).
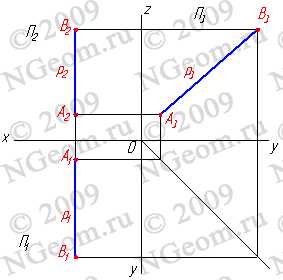
Рисунок 3.4 Профильная прямая
3. Прямые, перпендикулярные плоскостям проекций, называются проецирующими. Прямая перпендикулярная одной плоскости проекций, параллельна двум другим. В зависимости от того, какой плоскости проекций перпендикулярна исследуемая прямая, различают:
3.1. Фронтально-проецирующая прямая — АВ (рис. 3.5).
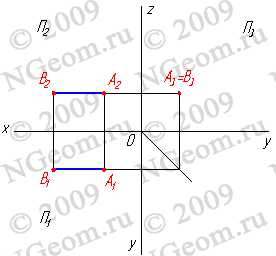
Рисунок 3.5 Фронтально-проецирующая прямая
3.2. Профильно проецирующая прямая — АВ (рис.3.6).
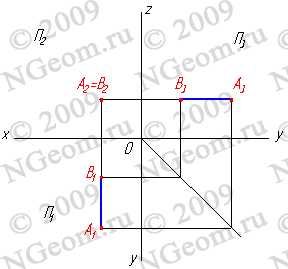
Рисунок 3.6 Профильно-проецирующая прямая
3.3. Горизонтально-проецирующая прямая — АВ (рис.3.7).
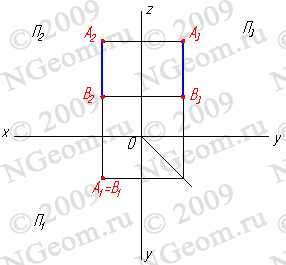
Рисунок 3.7 Горизонтально-проецирующая прямая
К началу страницы
Тема 4. Плоскость. Способы задания плоскостей
Плоскость – одно из основных понятий геометрии. При систематическом изложении геометрии понятие плоскость обычно принимается за одно из исходных понятий, которое лишь косвенным образом определяется аксиомами геометрии. Некоторые характеристические свойства плоскости: 1. Плоскость есть поверхность, содержащая полностью каждую прямую, соединяющую любые ее точки; 2. Плоскость есть множество точек, равноотстоящих от двух заданных точек.
Способы графического задания плоскостей Положение плоскости в пространстве можно определить:
1. Тремя точками, не лежащими на одной прямой линии (рис.4.1).
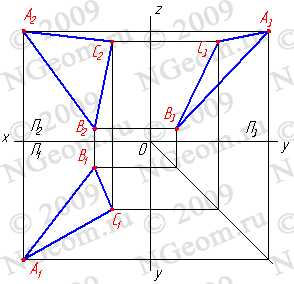
Рисунок 4.1 Плоскость заданная тремя точками, не лежащими на одной прямой
2. Прямой линией и точкой, не принадлежащей этой прямой (рис.4.2).
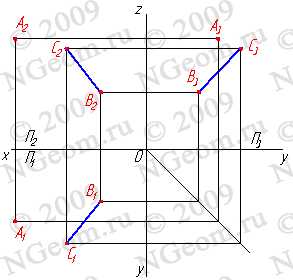
Рисунок 4.2 Плоскость заданная прямой линией и точкой, не принадлежащей этой линии
3. Двумя пересекающимися прямыми (рис.4.3).
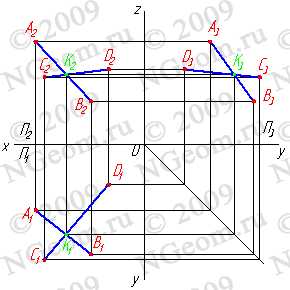
Рисунок 4.3 Плоскость заданная двумя пересекающимися прямыми линиями
4. Двумя параллельными прямыми (рис.4.4).
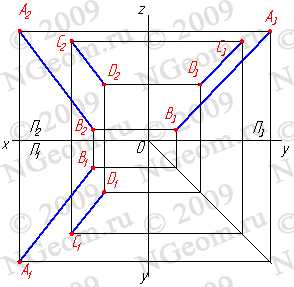
Рисунок 4.4 Плоскость заданная двумя параллельными прямыми линиями
Тема 5. Положение плоскости. Следы плоскости
К началу страницы
Различное положение плоскости относительно плоскостей проекций
В зависимости от положения плоскости по отношению к плоскостям проекций она может занимать как общее, так и частные положения.
1. Плоскость не перпендикулярная ни одной плоскости проекций называется плоскостью общего положения. Такая плоскость пересекает все плоскости проекций (имеет три следа: — горизонтальный S1; — фронтальный S2; — профильный S3). Следы плоскости общего положения пересекаются попарно на осях в точках ax,ay,az. Эти точки называются точками схода следов, их можно рассматривать как вершины трехгранных углов, образованных данной плоскостью с двумя из трех плоскостей проекций. Каждый из следов плоскости совпадает со своей одноименной проекцией, а две другие разноименные проекции лежат на осях (рис.5.1).
2. Плоскости перпендикулярные плоскостям проекций – занимают частное положение в пространстве и называются проецирующими. В зависимости от того, какой плоскости проекций перпендикулярна заданная плоскость, различают:
2.1. Плоскость, перпендикулярная горизонтальной плоскости проекций ( S^П1) , называется горизонтально-проецирующей плоскостью. Горизонтальная проекция такой плоскости представляет собой прямую линию, которая одновременно является её горизонтальным следом. Горизонтальные проекции всех точек любых фигур в этой плоскости совпадают с горизонтальным следом (рис.5.2).
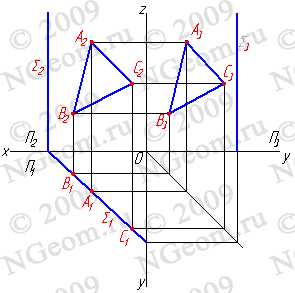
Рисунок 5.2 Горизонтально-проецирующая плоскость
2.2. Плоскость, перпендикулярная фронтальной плоскости проекций ( S^П2) — фронтально-проецирующая плоскость. Фронтальной проекцией плоскости S является прямая линия, совпадающая со следом S2 (рис.5.3).
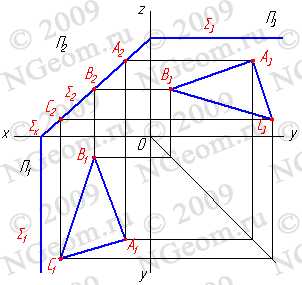
Рисунок 5.3 Фронтально-проецирующая плоскость
2.3. Плоскость, перпендикулярная профильной плоскости ( S^П3) — профильно-проецирующая плоскость. Частным случаем такой плоскости является биссекторная плоскость (рис.5.4).
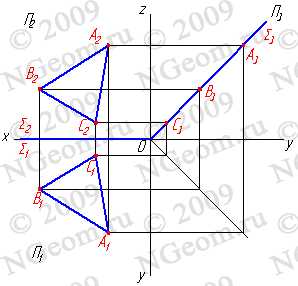
Рисунок 5.4 Профильно-проецирующая плоскость
3. Плоскости параллельные плоскостям проекций – занимают частное положение в пространстве и называются плоскостями уровня. В зависимости от того, какой плоскости параллельны исследуемая плоскость, различают:
3.1. Горизонтальная плоскость — плоскость параллельная горизонтальной плоскости проекций ( S//П1) — (S^П2, S^П3). Любая фигура в этой плоскости проецируется на плоскость П1 без искажения, а на плоскости П2 и П3 в прямые — следы плоскости S2 и S3 (рис.5.5).
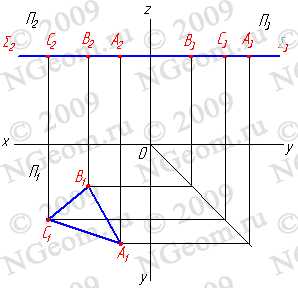
Рисунок 5.5 Горизонтальная плоскость
3.2. Фронтальная плоскость — плоскость параллельная фронтальной плоскости проекций (S//П2), (S^П1, S^П3). Любая фигура в этой плоскости проецируется на плоскость П2 без искажения, а на плоскости П1 и П3 в прямые — следы плоскости S1 и S3 (рис.5.6).
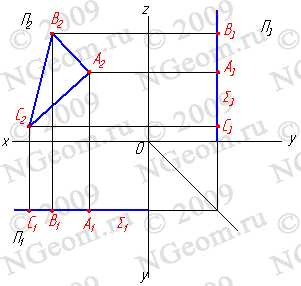
Рисунок 5.6 Фронтальная плоскость
3.3. Профильная плоскость — плоскость параллельная профильной плоскости проекций (S//П3), (S^П1, S^П2). Любая фигура в этой плоскости проецируется на плоскость П3 без искажения, а на плоскости П1 и П2 в прямые — следы плоскости S1 и S2 (рис.5.7).
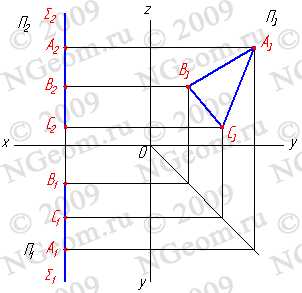
Рисунок 5.7 Профильная плоскость
Следом плоскости называется линия пересечения плоскости с плоскостями проекций. В зависимости от того с какой из плоскостей проекций пересекается данная, различают: горизонтальный, фронтальный и профильный следы плоскости.
Каждый след плоскости является прямой линией, для построения которых необходимо знать две точки, либо одну точку и направление прямой( как для построения любой прямой). На рисунке 5.8 показано нахождение следов плоскости S (АВС). Фронтальный след плоскости S2, построен, как прямая соединяющая две точки 12 и 22, являющиеся фронтальными следами соответствующих прямых, принадлежащих плоскости S. Горизонтальный следS1 – прямая, проходящая через горизонтальный след прямой АВ и Sx. Профильный следS3 – прямая соединяющая точки (Sy и Sz) пересечения горизонтального и фронтального следов с осями.

Рисунок 5.8 Построение следов плоскости
К началу страницы
Тема 6. Взаимное положение прямой и плоскости, точки и плоскости
Определение взаимного положения прямой и плоскости — позиционная задача, для решения которой применяется метод вспомогательных секущих плоскостей. Сущность метода заключается в следующем: через прямую проведем вспомогательную секущую плоскость Q и установим относительное положение двух прямых a и b, последняя из которых является линией пересечения вспомогательной секущей плоскости Q и данной плоскости T(рис.6.1).
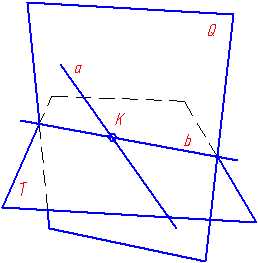
Рисунок 6.1 Метод вспомогательных секущих плоскостей
Каждому из трех возможных случаев относительного расположения этих прямых соответствует аналогичный случай взаимного расположения прямой и плоскости. Так, если обе прямые совпадают, то прямая а лежит в плоскости T, параллельность прямых укажет на параллельность прямой и плоскости и, наконец, пересечение прямых соответствует случаю когда прямая а пересекает плоскость T. Таким образом возможны три случая относительного расположения прямой и плоскости: Прямая принадлежит плоскости; Прямая параллельна плоскости; Прямая пересекает плоскость, частный случай – прямая перпендикулярна плоскости. Рассмотрим каждый случай.
Аксиома 1. Прямая принадлежит плоскости, если две её точки принадлежат той же плоскости (рис.6.2).
Задача. Дана плоскость (n,k) и одна проекция прямой m2. Требуется найти недостающие проекции прямой m если известно, что она принадлежит плоскости, заданной пересекающимися прямыми n и k. Проекция прямой m2 пересекает прямые n и k в точках В2 и С2, для нахождения недостающих проекций прямой необходимо найти недостающие проекции точек В и С как точек лежащих на прямых соответственно n и k. Таким образом точки В и С принадлежат плоскости заданной пересекающимися прямыми n и k, а прямая m проходит через эти точки, значит согласно аксиоме прямая принадлежит этой плоскости.
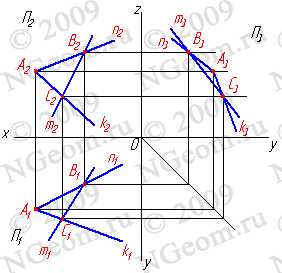
Рисунок 6.2 Прямая и плоскость имеют две общие точки
Аксиома 2. Прямая принадлежит плоскости, если имеет с плоскостью одну общую точку и параллельна какой-либо прямой расположенной в этой плоскости (рис.6.3).
Задача. Через точку В провести прямую m если известно, что она принадлежит плоскости заданной пересекающимися прямыми n и k. Пусть В принадлежит прямой n лежащей в плоскости заданной пересекающимися прямыми n и k. Через проекцию В2 проведем проекцию прямой m2 параллельно прямой k2, для нахождения недостающих проекций прямой необходимо построить проекцию точки В1, как точки лежащей на проекции прямой n1 и через неё провести проекцию прямой m1 параллельно проекции k1. Таким образом точки В принадлежат плоскости заданной пересекающимися прямыми n и k, а прямая m проходит через эту точку и параллельна прямой k, значит согласно аксиоме прямая принадлежит этой плоскости.
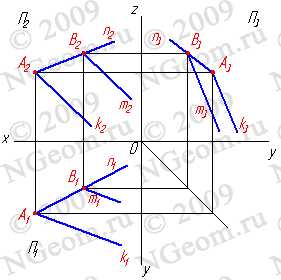
Рисунок 6.3 Прямая имеет с плоскостью одну общую точку и параллельна прямой расположенной в этой плоскости
Среди прямых линий, принадлежащих плоскости, особое место занимают прямые, занимающие частное положение в пространстве:
1. Горизонтали h — прямые, лежащие в данной плоскости и параллельные горизонтальной плоскости проекций (h//П1)(рис.6.4).
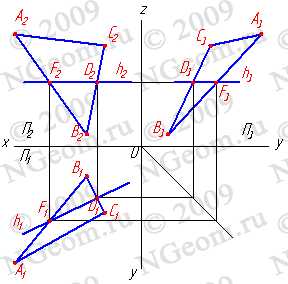
Рисунок 6.4 Горизонталь
2. Фронтали f — прямые, расположенные в плоскости и параллельные фронтальной плоскости проекций (f//П2)(рис.6.5).
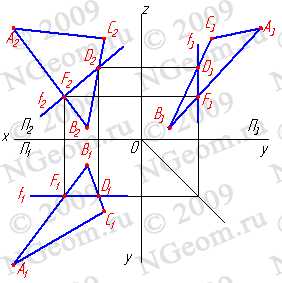
Рисунок 6.5 Фронталь
3. Профильные прямые р — прямые, которые находятся в данной плоскости и параллельны профильной плоскости проекций (р//П3) (рис.6.6). Следует заметить, что следы плоскости можно отнести тоже к главным линиям. Горизонтальный след — это горизонталь плоскости, фронтальный — фронталь и профильный — профильная линия плоскости.
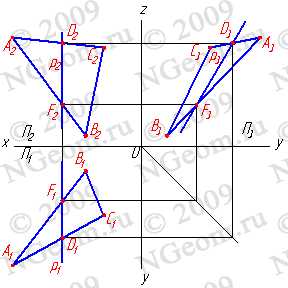
Рисунок 6.6 Профильная прямая
4. Линия наибольшего ската и её горизонтальная проекция образуют линейный угол j , которым измеряется двугранный угол, составленный данной плоскостью и горизонтальной плоскостью проекций (рис.6.7). Очевидно, что если прямая не имеет двух общих точек с плоскостью, то она или параллельна плоскости, или пересекает ее.
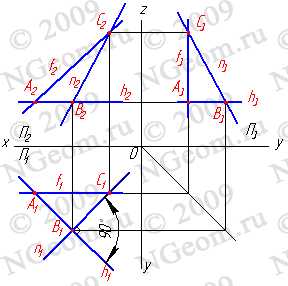
Рисунок 6.7 Линия наибольшего ската
Возможны два варианта взаимного расположения точки и плоскости: либо точка принадлежит плоскости, либо нет. Если точка принадлежит плоскости то из трех проекций, определяющих положение точки в пространстве, произвольно задать можно только одну. Рассмотрим пример (рис.6.8): Построение проекции точки А принадлежащей плоскости общего положения заданной двумя параллельными прямыми a(a//b).
Задача. Дано: плоскость T(а,в) и проекция точки А2. Требуется построить проекцию А1 если известно, что точка А лежит в плоскости в,а. Через точку А2 проведем проекцию прямой m2, пересекающую проекции прямых a2 и b2 в точках С2 и В2. Построив проекции точек С1 и В1, определяющие положение m1, находим горизонтальную проекцию точки А.
Рисунок 6.8. Точка, принадлежащая плоскости
К началу страницы
Тема 7. Взаимное положение плоскостей
Две плоскости в пространстве могут быть либо взаимно параллельны, в частном случае совпадая друг с другом, либо пересекаться. Взаимно перпендикулярные плоскости представляют собой частный случай пересекающихся плоскостей.
1. Параллельные плоскости. Плоскости параллельны, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости. Это определение хорошо иллюстрируется задачей, через точку В провести плоскость параллельную плоскости, заданной двумя пересекающимися прямыми ab (рис.7.1). Задача. Дано: плоскость общего положения, заданную двумя пересекающимися прямыми ab и точка В. Требуется через точку В провести плоскость, параллельную плоскости ab и задать её двумя пересекающимися прямыми c и d. Согласно определения если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости то эти плоскости параллельны между собой. Для того чтобы провести на эпюре параллельные прямые необходимо воспользоваться свойством параллельного проецирования — проекции параллельных прямых — параллельны между собой d||a, с||b; d1||a1,с1||b1; d2||a2 ,с2||b2; d3||a3,с3||b3.
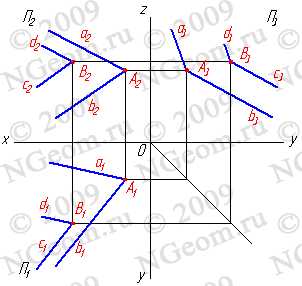
Рисунок 7.1. Параллельные плоскости
2. Пересекающиеся плоскости, частный случай – взаимно перпендикулярные плоскости. Линия пересечения двух плоскостей является прямая, для построения которой достаточно определить две её точки, общие обеим плоскостям, либо одну точку и направление линии пересечения плоскостей. Рассмотрим построение линии пересечения двух плоскостей, когда одна из них проецирующая (рис.7.2).
Задача. Дано: плоскость общего положения задана треугольником АВС, а вторая плоскость — горизонтально проецирующая T. Требуется построить линию пересечения плоскостей. Решение задачи заключается в нахождении двух точек общих для данных плоскостей, через которые можно провести прямую линию. Плоскость, заданная треугольником АВС можно представить, как прямые линии (АВ), (АС), (ВС). Точка пересечения прямой (АВ) с плоскостью T — точка D, прямой (AС) -F. Отрезок [DF] определяет линию пересечения плоскостей. Так как T — горизонтально проецирующая плоскость, то проекция D1F1 совпадает со следом плоскости T1, таким образом остается только построить недостающие проекции [DF] на П2 и П3.
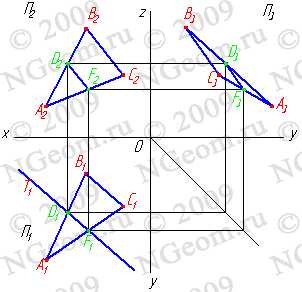
Рисунок 7.2. Пересечение плоскости общего положения с горизонтально проецирующей плоскостью
Перейдем к общему случаю. Пусть в пространстве заданы две плоскости общего положения a(m,n) и b (ABC) (рис.7.3).
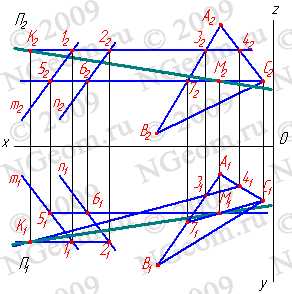
Рисунок 7.3. Пересечение плоскостей общего положения
Рассмотрим последовательность построения линии пересечения плоскостей a(m//n) и b(АВС). По аналогии с предыдущей задачей для нахождения линии пересечения данных плоскостей проведем вспомогательные секущие плоскости g и d. Найдем линии пересечения этих плоскостей с рассматриваемыми плоскостями. Плоскость g пересекает плоскость a по прямой (12), а плоскость b — по прямой (34). Точка К — точка пересечения этих прямых одновременно принадлежит трем плоскостям a, b и g, являясь таким образом точкой принадлежащей линии пересечения плоскостей a и b. Плоскость d пересекает плоскости a и b по прямым (56) и (7C) соответственно, точка их пересечения М расположена одновременно в трех плоскостях a, b, d и принадлежит прямой линии пересечения плоскостей a и b. Таким образом найдены две точки принадлежащие линии пересечения плоскостей a и b — прямая (КМ).
Некоторого упрощения при построении линии пересечения плоскостей можно достичь, если вспомогательные секущие плоскости проводить через прямые, задающие плоскость.
Взаимно перпендикулярные плоскости. Из стереометрии известно, что две плоскости взаимно перпендикулярны, если одна из них проходит через перпендикуляр к другой. Через точку А можно провести множество плоскостей перпендикулярных данной плоскости a(f,h). Эти плоскости образуют в пространстве пучок плоскостей, осью которого является перпендикуляр опущенный из точки А на плоскость a . Для того чтобы из точки А провести плоскость перпендикулярную плоскости заданной двумя пересекающимися прямыми hf необходимо из точки А провести прямую n перпендикулярную плоскости hf (горизонтальная проекция n перпендикулярна горизонтальной проекции горизонтали h, фронтальная проекция n перпендикулярна фронтальной проекции фронтали f). Любая плоскость проходящая через прямую n будет перпендикулярна плоскости hf, поэтому для задания плоскости через точки А проводим произвольную прямую m. Плоскость заданная двумя пересекающимися прямыми mn будет перпендикулярна плоскости hf (рис.7.4).
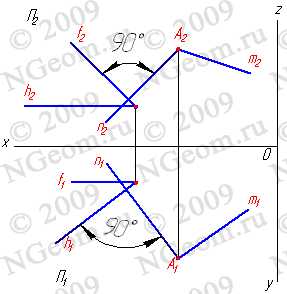
Рисунок 7.4. Взаимно перпендикулярные плоскости
К началу страницы
Тема 8. Плоскопараллельное перемещение. Вращение. Замена плоскостей проекций
Изменение взаимного положения проецируемого объекта и плоскостей проекций методом плоскопараллельного перемещения осуществляется путем изменения положения геометрического объекта так, чтобы траектория движения её точек находилась в параллельных плоскостях. Плоскости носители траекторий перемещения точек параллельны какой-либо плоскости проекций (рис. 8.1). Траектория произвольная линия. При параллельном переносе геометрического объекта относительно плоскостей проекций, проекция фигуры хотя и меняет свое положение, но остается конгруэнтной проекции фигуры в ее исходном положении.
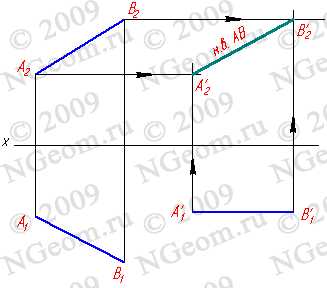
Рисунок 8.1 Определение натуральной величины отрезка методом плоскопараллельного перемещения
Свойства плоскопараллельного перемещения:
1. При всяком перемещении точек в плоскости параллельной плоскости П1, её фронтальная проекция перемещается по прямой линии, параллельной оси х.
2. В случае произвольного перемещения точки в плоскости параллельной П2, её горизонтальная проекция перемещается по прямой параллельной оси х.
Плоскости носитель траекторий перемещения точек параллельны плоскости проекций. Траектория — дуга окружности, центр которой находится на оси перпендикулярной плоскости проекций. Для определения натуральной величины отрезка прямой общего положения АВ (рис. 8.2), выберем ось вращения (i) перпендикулярную горизонтальной плоскости проекций и проходящую через В1. Повернем отрезок так, чтобы он стал параллелен фронтальной плоскости проекций (горизонтальная проекция отрезка параллельна оси x). При этом точка А1 переместиться в А’1, а точка В не изменит своего положения. Положение точки А’2 находится на пересечении фронтальной проекции траектории перемещения точки А (прямая линия параллельная оси x) и линии связи проведенной из А’1. Полученная проекция В2 А’2 определяет натуральную величину самого отрезка.
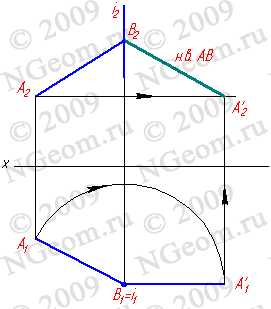
Рисунок 8.2 Определение натуральной величины отрезка методом вращения вокруг оси перпендикулярной горизонтальной плоскости проекций
Рассмотрим этот способ на примере определения угла между пересекающимися прямыми (рис.8.3). Рассмотрим две проекции пересекающихся прямых а и в которые пересекаются в точке К. Для то чтобы определить натуральную величину угла между этими прямыми необходимо произвести преобразование ортогональных проекций так, чтобы прямые стали параллельны плоскости проекций. Воспользуемся способом вращения вокруг линии уровня — горизонтали. Проведем произвольно фронтальную проекцию горизонтали h3 параллельно оси Ох, которая пересекает прямые в точках 12 и 22 . Определив проекции 11 и 11, построим горизонтальную проекцию горизонтали h2 . Траектория движения всех точек при вращении вокруг горизонтали — окружность, которая проецируется на плоскость П1 в виде прямой линии перпендикулярной горизонтальной проекции горизонтали.
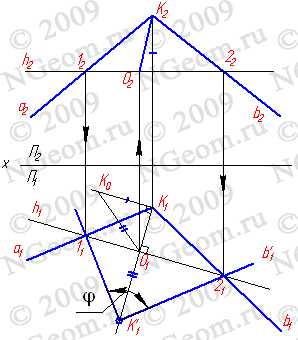
Рисунок 8.3 Определение угла между пересекающимися прямыми, вращением вокруг оси параллельной горизонтальной плоскости проекций
Таким образом, траектория движения точки К1 определена прямой К1О1, точка О -центр окружности — траектории движения точки К. Чтобы найти радиус этой окружности найдем методом треугольника натуральную величину отрезка КО .Продолжим прямую К1О1 так чтобы |О1К’1|=|КО| . Точка К’1 соответствует точке К , когда прямые а и в лежат в плоскости параллельной П1 и проведенной через горизонталь — ось вращения. С учетом этого через точку К’1 и точки 11 и 21 проведем прямые, которые лежат теперь в плоскости параллельной П1, а следовательно и угол фи — натуральная величина угла между прямыми а и в.
Изменение взаимного положения проецируемой фигуры и плоскостей проекций методом перемены плоскостей проекций, достигается путем замены плоскостей П1 и П2 новыми плоскостями П4 (рис. 8.4). Новые плоскости выбираются перпендикулярно старым. Некоторые преобразования проекций требуют двойной замены плоскостей проекций (рис. 8.5). Последовательный переход от одной системы плоскостей проекций другой необходимо осуществлять, выполняя следующее правило: расстояние от новой проекции точки до новой оси должно равняться расстоянию от заменяемой проекции точки до заменяемой оси.
Задача 1: Определить натуральную величину отрезка АВ прямой общего положений (рис. 8.4). Из свойства параллельного проецирования известно, что отрезок проецируется на плоскость в натуральную величину, если он параллелен этой плоскости. Выберем новую плоскость проекций П4, параллельно отрезку АВ и перпендикулярно плоскости П1. Введением новой плоскости, переходим из системы плоскостей П1П2 в систему П1П4 , причем в новой системе плоскостей проекция отрезка А4В4 будет натуральной величиной отрезка АВ.
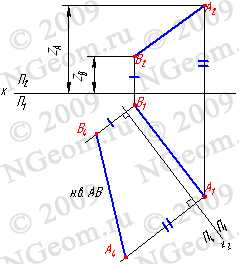
Рисунок 8.4. Определение натуральной величины отрезка прямой методом замены плоскостей проекций
Задача 2: Определить расстояние от точки C до прямой общего положения, заданной отрезком АВ (рис. 8.5).
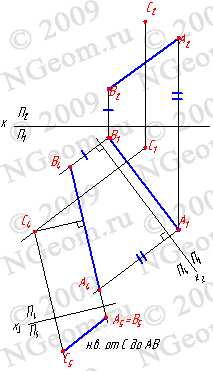
Рисунок 8.5. Определение натуральной величины отрезка прямой методом замены плоскостей проекций
К началу страницы
www.ngeom.ru
Глава 7. Прямые и плоскости в пространстве.
В планиметрии (курс геометрии в 7 — 9 классах) изучаются свойства геометрических фигур на плоскости. Теперь Вы начинаете знакомиться с элементами стереометрии (от греческих слов стереос – «объёмный, пространственный» и метрео – «измерять, рассматривать») – разделом геометрии, в котором изучаются свойства геометрических фигур (тел) в пространстве.
§ 1. Изображение пространственных фигур на плоскости.
Основными фигурами в пространстве являются точка, прямая и плоскость. Для обозначения точек будем использовать прописные (заглавные) буквы латинского алфавита: А, В, С,…, прямые будем обозначать малыми («строчными») буквами латинского алфавита: a,b,c… или двумя большими латинскими буквами АВ, СD,…, соответствующие двум точкам прямой. (Иногда ставят скобки (АВ) – прямая, проходящая через точку A и точку B). Плоскости обычно обозначают греческими буквами α, β, γ, … или тремя буквами АВС, (АВС) – плоскость, определяемая тремя точками А,В и С, не лежащими на одной прямой. Изображают плоскости в виде параллелограмма (плоскость α) или некоторой области (плоскость β).
α | β |
Как правило, изображением пространственной фигуры на плоскости служит её проекция на ту или иную плоскость. Выбирают то изображение, которое создаёт правильное представление о форме фигуры и наиболее удобно для её исследования.
При параллельном проектировании (именно такое проектирование используют в общеобразовательных курсах стереометрии) сохраняются отношение параллельности и отношение «лежать между»; сохранение последнего отношения означает, что при изображении сохраняется пропорциональность отрезков.
Из свойств параллельного проектирования следуют основные правила изображения пространственных фигур на плоскости:
– параллельные отрезки изображаются параллельными отрезками;
– отрезки, не являющиеся параллельными, изображаются не параллельными;
– сохраняется отношение «лежать между», т.е. если на оригинале точка делила ребро куба пополам, то и изображение данной точки будет серединой изображения данного ребра;
– углы и длины при изображении не сохраняются.
Из вышеперечисленного следует, что:
– параллелограмм (в том числе квадрат, ромб, прямоугольник) изображается произвольным параллелограммом;
– трапеция изображается трапецией;
– треугольник (остроугольный, тупоугольный, прямоугольный, равнобедренный, равносторонний) изображается произвольным треугольником;
– окружность изображается эллипсом.
При этом невидимые части (линии) фигур изображаются пунктирными (штриховыми) линиями.
Некоторые фигуры хорошо Вам известны: пирамида, прямоугольный параллелепипед, куб, шар, цилиндр, конус.
Вот некоторые изображения:
Треугольная пирамида (тетраэдр — слово образовано из двух греческих слов: тетра – четыре, эдрос – грань, то есть четырехгранник). | М В А С |
Прямоугольный параллелепипед ABCDA1B1C1D1 | В1 С1 А1 D1 В С А D |
R
Цилиндр R – радиус цилиндра l – образующая цилиндра | l |
Конус R – радиус конуса l – образующая конуса | l R |
Вопросы и задачи |
Изобразите пятиугольную призму и покажите, как её можно составить из треугольных призм.
Изобразите прямую треугольную призму, на верхнее основание которой поставлена наклонная призма с таким же основанием так, что основания совпадают.
Изобразите четырехугольную призму, не являющуюся параллелепипедом.
Верно ли утверждение, что понятия «правильная четырехугольная призма» и «куб» совпадают?
Изобразите какой-нибудь многогранник, составленный из прямоугольного параллелепипеда и треугольной призмы.
а) На рисунке изображен куб ABCDA1B1C1D1, его пересечения с плоскостью, проходящей через точки A,D1 и C (с плоскостью AD1C) и отдельно пересечение плоскости AD1C и граней AA1D1D, CC1D1D и ABCD. Проанализируйте этот чертёж.
B1 C1 D1 А1 В С D А | А А1 D1 D D | D1 C1 С | D С В А |
б) Изобразите куб ABCDA1B1C1D1 и пересечение его с плоскостью, проходящей через точки A, B1 и C. (сечение куба плоскостью A B1C).
Изобразите треугольную призму ABCA1B1C1 и её сечение плоскостью A1BC (пересечение призмы этой плоскостью).
Может ли сечение куба быть треугольником? четырехугольником? семиугольником?
Можете ли вы определить, глядя на изображение тетраэдра, правильный ли тетраэдр изображён?
Изобразите треугольную и четырехугольную призмы и объясните, как их можно сложить из тетраэдров.
Существуют ли тетраэдры, у которых:
а) все грани – остроугольные треугольники;
б) три грани – прямоугольные треугольники, а одна – остроугольный;
в) три грани – тупоугольные треугольники, а одна – остроугольный?
Если да, объясните почему (как бы вы стали изготовлять их модели)
Внутрь тетраэдра помещена треугольная призма так, что вершины её верхнего основания лежат на боковых рёбрах тетраэдра, одна из вершин нижнего основания лежит на медиане нижнего основания тетраэдра, а стороны её основания параллельны сторонам основания тетраэдра. Нарисуйте эту конструкцию.
Изобразите правильный тетраэдр SABC и перпендикуляр, опущенный из вершины A на сторону BC.
Покажите, пользуясь чертежом или моделью, как можно сложить из тетраэдров пирамиду:
а) четырёхугольную;
б) пятиугольную.
Все рёбра правильной четырёхугольной пирамиды равны друг другу. Что вы можете сказать о её гранях и углах граней?
Объясните, пользуясь моделью куба, как разбить куб на правильные четырехугольные пирамиды.
На какое минимальное число пирамид можно разбить треугольную призму?
Прямоугольный параллелепипед расположен внутри правильной четырёхугольной пирамиды так, что вершины его верхнего основания лежат на боковых рёбрах пирамиды, а вершины нижнего основания – в плоскости основания пирамиды. Нарисуйте эту конструкцию.
Дан тетраэдр SABC, M — середина ребра BC. Изобразите этот тетраэдр и то, что получится при пересечении его с плоскостью, проходящей через точки S, A, M (сечение тетраэдра плоскостью SAM).
Дан тетраэдр SABC, M — середина SC, N — середина ребра SA, K — середина ребра SB. Изобразите этот тетраэдр и то, что получится при пересечении его с плоскостью, проходящей через точки M, N, K(сечение тетраэдра плоскостью MNK).
Через середины трёх рёбер правильного тетраэдра, идущих из одной вершины, проводят плоскость. Четырьмя такими плоскостями от исходного тетраэдра отсекают меньшие тетраэдры. Нарисуйте оставшийся многогранник. Знаком ли он вам?
Может ли сечение тетраэдра быть пятиугольником?
Нарисуйте сечение четырёхугольной пирамиды, которое является:
а) треугольником;
б) четырёхугольником.
Рассматриваются два многогранника с одинаковым числом вершин: призма и пирамида. Может ли это число быть четным? нечётным? У какого из этих многогранников больше граней, рёбер?
Приведите пример фигуры, которую нельзя отнести ни к многогранникам, ни к телам вращения.
Назовите все возможные случаи взаимного расположения сферы и прямой; сферы и плоскости. Сделайте рисунки.
Тетраэдр расположен так, что три его вершины лежат на сфере, а четвёртая – в центре сферы. Сделайте рисунок.
Треугольная призма расположена так, что все её вершины лежат на сфере. Сделайте рисунок.
Сколько общих точек может иметь прямая и поверхность цилиндра? Сделайте рисунки.
Цилиндр и шар расположены так, что основания цилиндра являются сечениями шара. Сделайте рисунок.
Сколько общих точек может иметь конус и прямая?
Четырехугольная пирамида и конус расположены так, что их вершины совпадают, а все вершины основания пирамиды лежат на окружности основания конуса. Сделайте рисунок.
Четырехугольная пирамида и конус расположены так, что их вершины совпадают, а окружность основания конуса вписана в основание пирамиды. Сделайте рисунок.
Конус и шар расположены так, что основание конуса является каким-то сечением шара, а вершина конуса лежит на сфере. Сделайте рисунок.
Треугольник ABC с тупым углом при вершине B вращается вокруг прямой AC. Нарисуйте получающуюся фигуру.
Треугольник ABC с тупым углом при вершине B вращается вокруг прямой AB. Нарисуйте получающуюся фигуру.
Прямоугольная трапеция ABCD вращается вокруг прямой, содержащей сторону AB, являющейся высотой трапеции. Нарисуйте получающуюся фигуру. Объясните, как будет выглядеть развертка.
studfiles.net
