Физические основы механики
Закон всемирного тяготения позволяет установить масштабы расстояний и масс в Солнечной системе.
Радиус Земли можно найти с помощью геометрических измерений на ее поверхности. Первым это сделал Эратосфен (276–194 г. до н.э.), нашедший для радиуса Земли величину R3 = 6 311 км. Эратосфен ошибся всего на 1 %: современное измерения для среднего радиуса Земли дают следующий результат: R3 = 6 371,03 км. В действительности Земля не является шаром, более точная модель «фигуры Земли» такая: сплюснутый эллипсоид вращения со средним экваториальным радиусом (большая полуось эллипсоида) км и полярным радиусом (меньшая ось эллипсоида) км. Эксцентриситет этого эллипсоида вращения весьма невелик , поэтому в большинстве задач Землю, с вполне достаточной точностью, можно считать шаром.
Схема опыта Эратосфена показана на рис. 5.6. В полдень в день летнего солнцестояния в городе Сиен (ныне Асуан) Солнце находилось в зените, и предметы не отбрасывали тени. В тот же день и в то же время в городе Александрия, находившемся в 5 000 стадиях от Сиена Солнце отклонялось от зенита примерно на 7°. Это составляет примерно 1/50 полного круга (360°), откуда получается, что окружность Земли равна 250 000 стадий.
В тот же день и в то же время в городе Александрия, находившемся в 5 000 стадиях от Сиена Солнце отклонялось от зенита примерно на 7°. Это составляет примерно 1/50 полного круга (360°), откуда получается, что окружность Земли равна 250 000 стадий.
Зная длину меридиана, можно узнать каким «стадием» пользовался Эратосфен, поскольку в древности в ходу были следующие стадии:
• вавилонский = 194 м
• греческий = 178 м
o аттический = 177,6 м
o олимпийский = 192,27 м
• египетский = 172,5 м
o стадий системы фараонов = 209,4 м
• птолемеевский и римский = 185 м
• стадий (гхальва) ассиро-халдейско-персидской системы = 230,4 м
Рис. 5.6. Опыт Эратосфена по определению радиуса Земли
Как найти массу Земли? Каждое тело массой притягивается к ней с силой
где — масса Земли, а — расстояние от тела до центра Земли. С другой стороны, отношение силы к массе — это ускорение свободного падения (вращением Земли пренебрегаем):
Отсюда следует, что не зависит от массы и размеров тела и определяется исключительно параметрами Земли и расстоянием до нее. Вблизи поверхности Земли
Вблизи поверхности Земли
и = 9,81 м/с2. Находим отсюда массу Земли:
Ближайшим к Земле небесным телом является Луна. Определим расстояние до Луны. Мы знаем, что период обращения Луны вокруг Земли равен = 27,32 сут = 27,32·86 400 = 2,36·106 с. Центростремительное ускорение Луны
должно быть равно ускорению свободного падения на орбите Луны при = . Приравнивая и , находим:
Скорость Луны на орбите равна
Легко определить угловой диаметр Луны: большой палец, толщина которого примерно равна 1 см, закрывает при вытянутой руке (то есть на расстоянии примерно 1 м) ее диск. Отсюда
Более точные измерения дают для углового диаметра
Отсюда радиус Луны будет
Зная расстояние от Земли до Луны, с помощью геометрии можно определить расстояние от Земли до Солнца. Когда Луна находится в первой четверти, направления от нее в сторону Земли и в сторону Солнца составляют прямой угол (рис.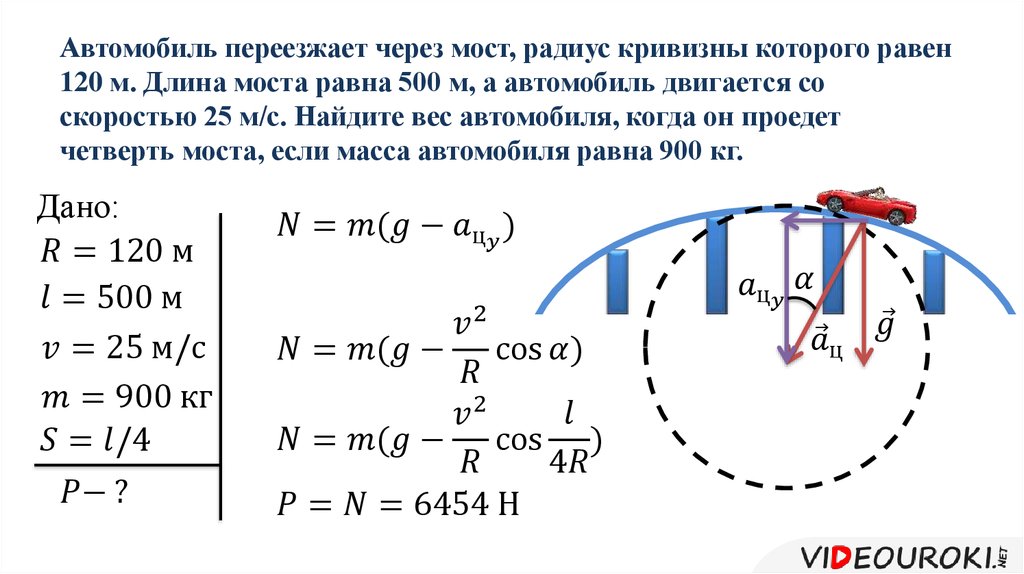 5.7).
5.7).
Рис. 5.7. Геометрический метод определения расстояния от Земли до Солнца
Если в этот момент на Земле измерить угол между направлениями на Луну и Солнце, то расстояние до Солнца определится как
Угол оказывается близким к прямому: = 89°51′. Поэтому удобнее будет пользоваться дополнительным углом = /2 – β = 9′ = 0,15° = 0,0026 рад. Тогда расстояние до Солнца будет равно
Это расстояние называется астрономической единицей (А или a.e., выше оно обозначено ). Более точно, A = 1,496·1011 м.
Зная период обращения Земли вокруг Солнца = 1 год = 365,25 сут = 3,156·107 с, находим скорость Земли на орбите:
Наконец, мы определим параметры Солнца. Видимый с Земли угловой диаметр Солнца примерно таков же, как и у Луны: φ = 32′ = 0,533° = 9,31·10–3 рад. Отсюда находим радиус Солнца:
Массу Солнца получаем из закона всемирного тяготения: центростремительное ускорение Земли на орбите
должно быть равно ускорению свободного падения Земли на Солнце
Приравнивая и , получаем:
В этом выражении мы видим знакомую по третьему закону Кеплера комбинацию: отношение куба расстояния от планеты до Солнца к квадрату периода обращения. У всех планет это отношение одинаково, так как они вращаются вокруг одной и той же звезды.
У всех планет это отношение одинаково, так как они вращаются вокруг одной и той же звезды.
Орбитальную скорость Земли можно также записать в виде
Это выражение справедливо для любой планеты при соответствующем изменении радиуса орбиты .
Приведенные оценки показывают, как много можно узнать о мире, наблюдая его из удобного кресла и … понимая законы природы.
Дополнительная информация
http://www.plib.ru/library/book/14978.html — Сивухин Д.В. Общий курс физики, том 1, Механика Изд. Наука 1979 г. — стр. 41–42 (§ 4, задача 4): о скорости движения тени Луны по поверхности Земли во время полного солнечного затмения.
http://school-collection.edu.ru/catalog/res/e6609a18-088c-4979-83f0-faeeeef9faa1/?sort=order&from=ffb3b711-8f44-408c-aea4-a29842431067&&rubric_id%5B%5D=110200&rubric_id%5B%5D=110201 — Соросовский образовательный журнал, 1998 г., № 2 — анимация «Вращение Земли вокруг Солнца. День, ночь, времена года, фазы Луны».
http://www. somit.ru/fisika7_1.html — анимация, демонстрирующая причину смены дня и ночи на Земле и движение Луны.
somit.ru/fisika7_1.html — анимация, демонстрирующая причину смены дня и ночи на Земле и движение Луны.
Физики решили загадку радиуса протона для электрон-протонного рассеяния
Физика
Сложность 8.8
W. Xiong et al / Nature, 2019
Физики применили метод интерполяции с помощью непрерывной дроби к данным двух экспериментов по упругому рассеянию электронов на протонах, из которых следовали различные значения зарядового радиуса протона. В результате для обоих опытов они смогли получить близкие по величине значения радиуса, разрешив таким образом имевшееся противоречие. Работа опубликована в
Работа опубликована в
Среднеквадратичный зарядовый радиус протона — это фундаментальная физическая константа, которая в недавнем прошлом оказалась в центре внимания физиков по всему миру. Эта величина характеризует степень неточечности протона безотносительно к деталям распределения заряда внутри него. До 2010 года было всего два типа экспериментов, которые могли определить ее с достаточной точностью: спектроскопия атома водорода и упругое рассеяние электронов на протонах — и оба они давали примерно одно и то же значение, близкое к 0,88 фемтометрам.
Однако в 2010 году были опубликованы первые эксперименты по спектроскопии мюонного водорода, в которых радиус протона оказался равен 0,84 фемтометрам. Обнаруженное расхождение получило название «загадка радиуса протона» и заставило многие группы повторять и перепроверять старые эксперименты. Подробнее об этой загадке вы можете прочитать в нашем материале «Щель в доспехах».
Со временем стали появляться результаты перепроверок экспериментов обоих типов, и в ряде случаев перепроверка давала меньшее значение.
Результаты измерения радиуса протона, полученные в разных экспериментах. Желтым цветом показан радиус, переизвлеченный авторами из двух предыдущих работ.
Z.-F. Cui et al / Physical Review Letters, 2021
Поделиться
В русле этой идеи группа физиков из Германии, Италии и Китая при участии Крэйга Робертса (Craig Roberts) из Нанкинского университета, решила пересмотреть результаты недавних экспериментов по электрон-протонному рассеянию, проведенных в лаборатории имени Джефферсона коллаборацией PRad (об этом мы также писали), в которых значение радиуса протона получилось равным 0,831(19) фемтометров, и более старых экспериментов, проведенных коллаборацией A1 в Майнце, в которых оно оказалось равным 0,879(8) фемтометров.
Слабым местом при извлечении информации о размере протона из данных об упругих рассеяниях электрона на протонах стало то, что в случае, если передаваемый импульс от одной частицы к другой оказывается очень мал, мы не можем точно знать детали такого взаимодействия. В частности, при извлечении радиуса протона ключевую роль играет электрический формфактор, а точнее, его производная в точке нулевого квадрата передаваемого импульса. К сожалению, его точный вид нам неизвестен, а расчет в рамках квантовой хромодинамики пока не достижим, поэтому физикам приходится опираться на разнообразные феноменологические модели.
Авторы новой работы вместо использования подгоночных функций применили метод, развитый ранее Шлессингером. Метод подходит для решения задач, в которых необходима модельно-независимая экстра- или интерполяция. Его суть заключается в построении аналитической функции на базе исходных данных с помощью непрерывной дроби. Важно, что при этом такая интерполяция способна уловить как локальные, так и глобальные особенности поведения функции, что оказалось достаточно для вычисления производной от формфактора в точке с нулевым импульсом.
Важно, что при этом такая интерполяция способна уловить как локальные, так и глобальные особенности поведения функции, что оказалось достаточно для вычисления производной от формфактора в точке с нулевым импульсом.
Для учета статистических ошибок физики повторяли эту процедуру с тысячей разных наборов данных, которые генерировались путем замены каждой точки в исходном наборе на случайное значение, лежащее в пределах исходной дисперсии. Применяя такой подход к данным PRad, авторы получили значение радиуса протона, равное 0,838(5) фемтометров. Похожим образом они пересчитали радиус протона для эксперимента группы A1, и он составил 0,856(14) фемтометров. Комбинация этих двух значений дала итоговую величину радиуса по экспериментам с электрон-протонным рассеянием, равную 0,847(8) фемтометров, что находится в хорошем согласии с результатами спектроскопии мюонного водорода.
Исследование рассеяний частиц на разнообразных мишенях играет важную роль в фундаментальной физике. Так, мы уже писали про то, как упругое рассеяние ограничило отклонения нейтрино от Стандартной модели.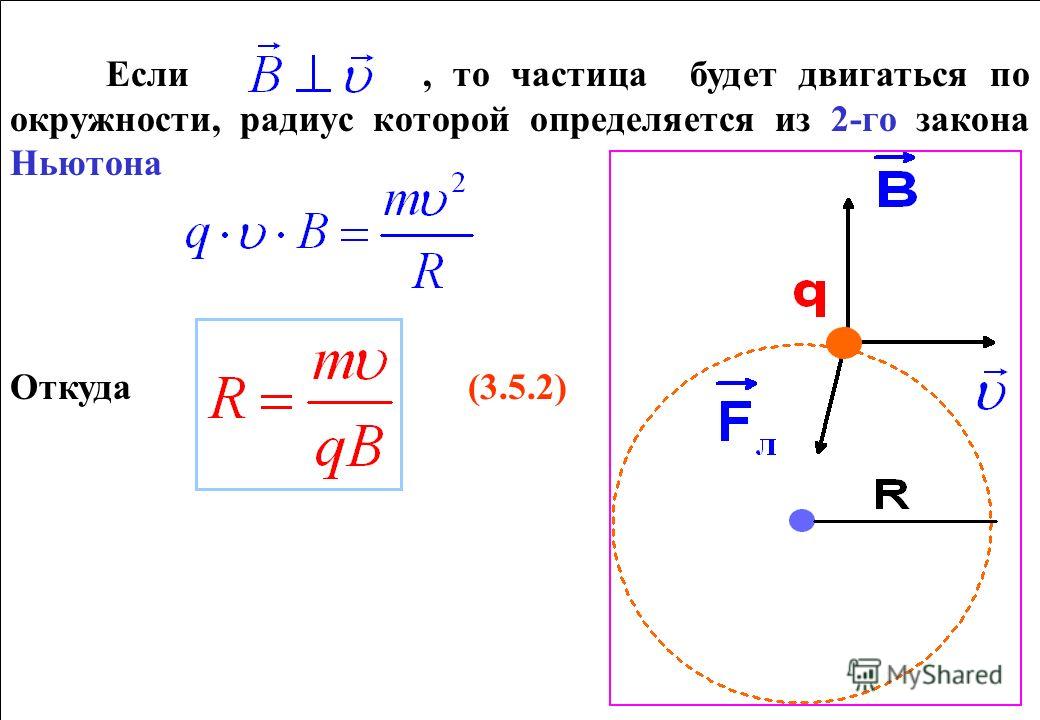
Марат Хамадеев
Урок 4. равномерное движение точки по окружности — Физика — 10 класс
Физика, 10 класс
Урок 04.Равномерное движение точки по окружности
Перечень вопросов, рассматриваемых на уроке:
- Равномерное движение точки по окружности и его характеристики.
- Центростремительное ускорение.
Глоссарий по теме
Криволинейное движение – это движение по дугам окружностей разных радиусов.
Ускорение – это векторная величина, равная отношению изменения скорости к промежутку времени, в течение которого это изменение произошло, при ∆t → 0
Равномерное движение точки по окружности — движение точки с постоянной по модулю скоростью (ν = const) по траектории, представляющей собой окружность.
Ключевые слова
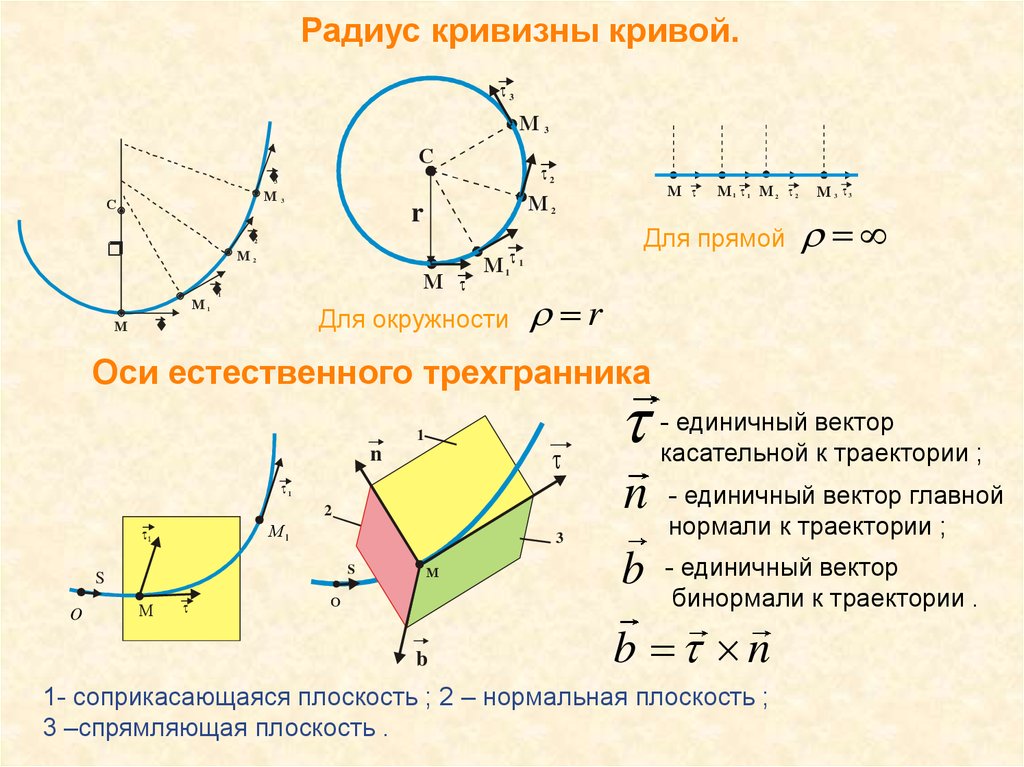
Криволинейное движение; движение по окружности; скорость; радиус кривизны; изменение скорости; центростремительное ускорение.
Основная и дополнительная литература по теме урока:
Мякишев Г. Я., Буховцев Б.Б., Сотский Н.Н. Физика.10 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2016. С.55-56
Я., Буховцев Б.Б., Сотский Н.Н. Физика.10 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2016. С.55-56
Марон Е.А., Марон А.Е. Сборник качественных задач по физике. М., Просвещение, 2006
Рымкевич А.П. Сборник задач по физике. 10-11 класс.-М.:Дрофа,2009.-С.20-22
Открытые электронные ресурсы:
http://kvant.mccme.ru/1986/11/kinematika_vrashchatelnogo_dvi.htm
Теоретический материал для самостоятельного изучения
1. Мы уже знакомы с равноускоренным движением. Как же меняются скорость и ускорение при криволинейном движении? Сегодня рассмотрим равномерное движение по окружности, узнаем, что такое центростремительное ускорение.
Если траектория движения тела прямая линия, то движение прямолинейное; если траектория кривая линия – криволинейное движение. Напомним, что траектория – это линия, вдоль которой двигалось тело.
При изучении равноускоренного движения мы заметили, что в некоторых случаях тело движется по прямой, например свободное падение тел, а в некоторых по кривой – тело, брошенное под углом к горизонту.
Рассмотрим движение тела, брошенного под углом к горизонту. Траекторией является парабола.
Возьмем разные точки на линии и нарисуем векторы скорости . Вектор скорости направлен по касательной, а ускорение свободного падения направлен вниз.
Векторы и не лежат на одной прямой, угол между ними не равен нулю.
Это естественно, так как, если ускорение образует угол со скоростью, то изменение скорости направлено не так, как скорость. Это приводит к изменению направления скорости. Изменение скорости направлено как ускорение. Скорость через некоторый промежуток времени образует некоторый угол с Итак, сформулируем первый вывод: если угол между векторами скорости и ускорения не равен нулю, то движение будет криволинейным.
2.Может ли быть движение одновременно равномерным и криволинейным? Да, например, движение по окружности.
Равномерное движение точки по окружности — это движение точки с постоянной по модулю скоростью (v = const) по траектории, представляющей собой окружность. Но, скорость – это векторная величина, а для векторной величины одинаково важны и модуль, и направление. Т.к. при движении по окружности скорость всегда направлена по касательной к траектории движения, то по направлению она изменяется. Если есть изменение скорости (точнее её направления), значит, есть ускорение
Но, скорость – это векторная величина, а для векторной величины одинаково важны и модуль, и направление. Т.к. при движении по окружности скорость всегда направлена по касательной к траектории движения, то по направлению она изменяется. Если есть изменение скорости (точнее её направления), значит, есть ускорение
Сформулируем второй важный вывод: любое криволинейное движение является движением с ускорением, потому что меняется направление вектора скорости.
Решим задачу: найдем ускорение тела, равномерно движущегося по окружности.
Рассмотрим равномерное движение тела по окружности с центром в точке О. В какой-то момент времени, скорость тела в точке А была.
Модули скоростей равны:
но вектора скоростей не равны.
Поэтому построим вектор для тела, движущегося по окружности. Перенесем вектор в начало вектораи найдем разность векторов.
направлен в сторону.
Вспомним, что векторнаправлен по касательной, а касательная перпендикулярна радиусу окружности. Проведем радиусы к обеим точкам и обозначим угол между ними через ?.
Проведем радиусы к обеим точкам и обозначим угол между ними через ?.
Что можно сказать об угле между векторами ? Он равен малому углу, как углы с взаимно перпендикулярными сторонами.
Рассмотрим равнобедренный треугольник со сторонами , . Углы у основания равны.
Если угол φ стремится к нулю, то углы у основания совпадут и станут равными 900
Вектор будет перпендикулярен вектору в пределе, а значит вектор ускорения тоже перпендикулярен т.е направлен по радиусу к центру окружности. Поэтому часто его называют центростремительным ускорением
Теперь следующая задача: как найти модуль вектора ускорения. Давайте рассмотрим два треугольника: треугольник, образованный векторами и треугольник, образованный радиусами и хордой. У этих треугольников углы при вершинах равны, они равнобедренные. Треугольники подобны и, следовательно, выполняются соотношения подобия.
Промежуток времени мал, поэтому очень мал и угол при вершине, в пределе он стремится к нулю. Тогда можно сказать, что длина хорды s равна длине дуги АВ при
Тогда можно сказать, что длина хорды s равна длине дуги АВ при
Длина дуги АВ это путь, пройденный точкой от А до В,
тогда запишем:
Умножим наи получим:
В левой части мы получили отношение изменения скорости за некоторый промежуток времени к этому промежутку времени т.е. ускорение:
Равномерное движение точки по окружности является движением с переменным ускорением и переменной скоростью. Модули скорости и ускорения остаются постоянными
- Криволинейное движение — это движение по дугам окружностей разных радиусов.
А если меняется радиус, то меняется и центростремительное ускорение. Чем меньше радиус, тем больше ускорение при одинаковой скорости.
Всегда при равномерном криволинейном движении вектор ускорения перпендикулярен вектору скорости, поэтому центростремительное ускорение иногда называют нормальным ускорением, от слова нормаль, т.е. перпендикуляр.
Основные выводы:
— движение криволинейное, так как траекторией является окружность;
— движение равномерное, так как модуль скорости не меняется;
— вектор скорости направлен по касательной к окружности;
-вектор ускорения направлен к центру окружности;
— модуль центростремительного ускорения равен:
Примеры и разбор решения заданий
1.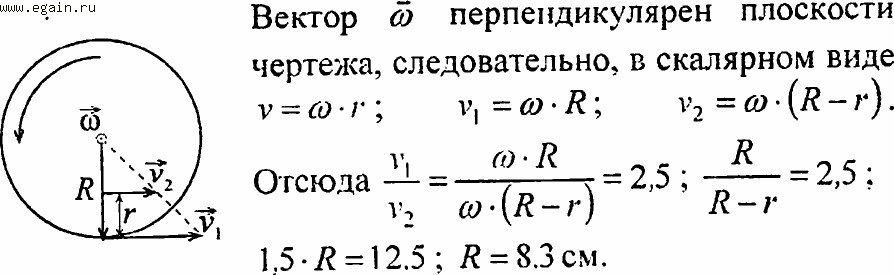 Велосипедист движется по закруглению дороги радиусом 50 м со скоростью 36 км/ч. С каким ускорением он проходит закругление?
Велосипедист движется по закруглению дороги радиусом 50 м со скоростью 36 км/ч. С каким ускорением он проходит закругление?
При движении по окружности линейная скорость и центростремительное ускорение связаны соотношением
где R = 50 м; υ= км/ч = 10 м/с.
Тогда ac = (10 м/с)2 / 50 м = 2 м/с2.
Ответ: 2 м/с2
2. Две материальные точки движутся по окружностям радиусами R1 = 10 см и R2 = 30 см с одинаковыми скоростями 0,20 м/с. Во сколько раз отличаются их центростремительные ускорения?
Дано:
R1 =10см = 0,10 м
R2 = 30см = 0,30 м
Найти —
Задано два объекта:
1) материальная точка, которая движется по окружности R1;
2) материальная точка, которая движется по окружности R2.
При движении по окружности центростремительное ускорение и линейная скорость связаны соотношением
Для тела 1 уравнение (1) примет вид:
для тела 2:
Тогда
Центростремительное ускорение тела (2) меньше ускорения тела (1) в 3 раза.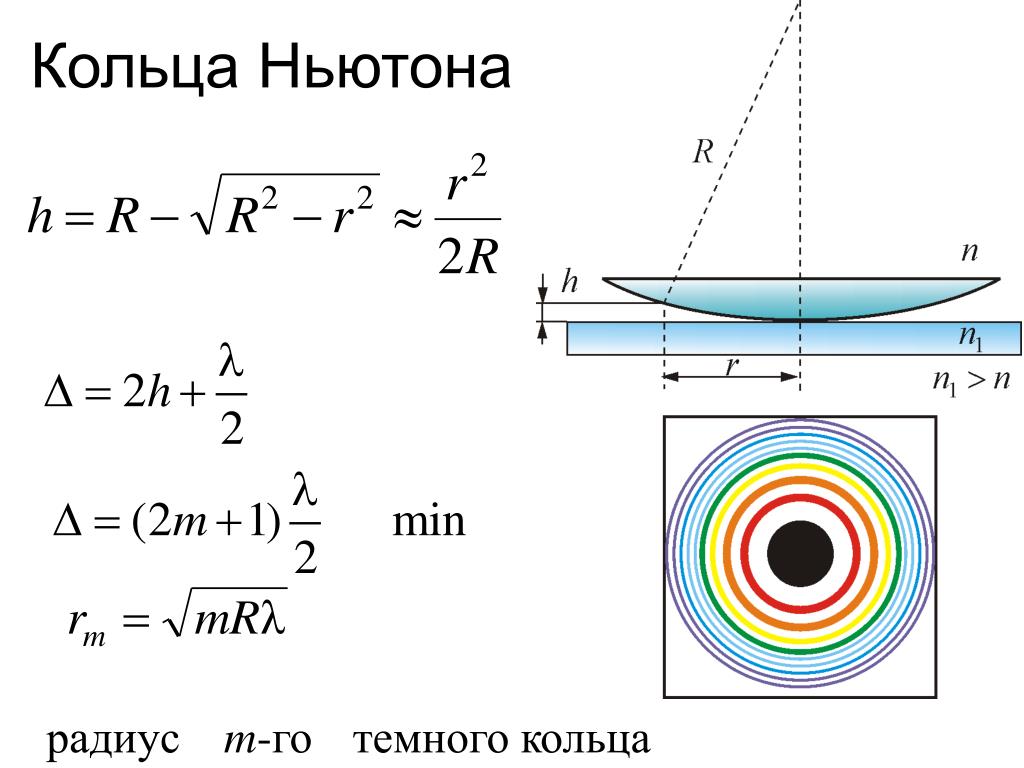
Физика микромира
Во введении рассматриваются основные составляющие новой физики, возникшей на рубеже XIX и XX столетий:- Теория относительности, изменившая существующие в классической физике представления о пространстве и времени.
- Квантовая теория, изменившая представление о структуре материи. Явление радиоактивности, открытие электрона, сложная структура атома, протон-нейтронная структура атомного ядра, открытие фундаментальных частиц и взаимодействий привели к современному представлению об окружающем мире.
- Открытия в области физики частиц, коренным образом повлиявшие на понимание процессов, происходящих во Вселенной.
- 1.1. Масштабы явлений в физике
- 1.2. Упругое рассеяние α-частиц. Формула Резерфорда
- 1.3. Сечение реакции
- 1.4. Размер ядра
- 1.5. Радиоактивность
- 1.6. Преобразования Лоренца
- 1.7. Эффект Доплера
- 1.
 8.
Системы отсчета
8.
Системы отсчета - 1.9. Основные формулы релятивистской физики
- 1.10. Система единиц Гаусса
- 1.11. Энергия и порог реакции
- 1.12. Энергии частиц в двухчастичном распаде
- Задачи
1.1. Масштабы явлений в физике
Диапазон временных интервалов во Вселенной | |
| Возраст Вселенной | 13.8 млрд. лет |
| Возраст Солнца | 4.6 млрд. лет |
| Возраст Земли | 4.5 млрд. лет |
| Появление жизни на Земле | ~3.5 млрд. лет |
| Время прохождения светом расстояния Солнце–Земля | ~5·102 с |
| Время прохождения светом расстояния 1 метр | 3·10–9 с |
| Время прохождения светом расстояния, равного радиусу атома | ~10–19 с |
| Время прохождения светом расстояния, равного радиусу атомного ядра | ~10–24 с |
Диапазон расстояний во Вселенной | |
| Видимая граница Вселенной | ~1010 св. лет лет |
| Ближайшая галактика (Магеллановы облака) | 163 000 св. лет |
| Диаметр галактики Млечный путь | 100 000 св. лет |
| Ближайшая звезда Проксима Центавра | |
| Расстояние Земля–Солнце (астрономические единицы) | 1.5·1013 см |
| Радиус Солнца | 6.9·1010 см |
| Радиус Земли | 6.4·108 см |
| Радиус Луны | 1.7·108 см |
| Радиус атома водорода | ~0.5·10–8 см |
| Радиус атомного ядра водорода | ~0.8·10–13 см |
| Размеры лептонов, кварков | <10–17 см |
| 1 световой
год (расстояние, которое проходит свет за 1 год) | ~9.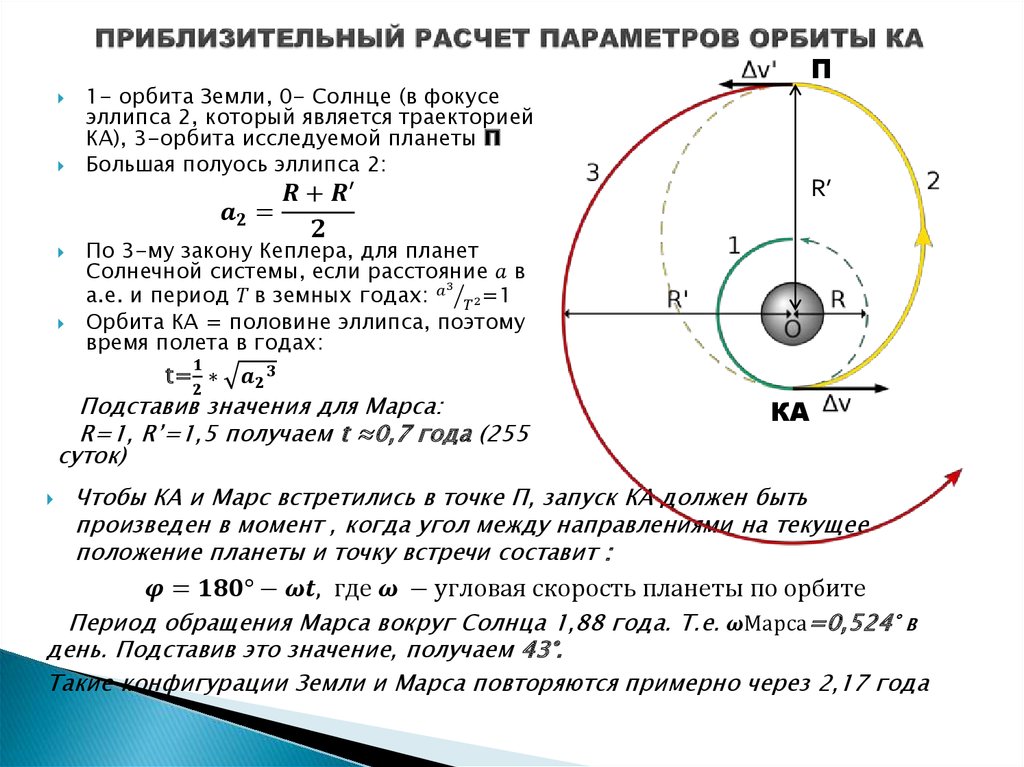 5·1017 см 5·1017 см |
| 1 парсек | 3.1·1018 см = = 3.26 светового года |
Диапазон масс во Вселенной | |
| Масса видимого вещества во Вселенной | ~1056 г |
| Масса видимого вещества нашей галактики Млечный путь | ~1012 масс Солнца |
| Масса Солнца | 1.99·1033 г |
| Масса Земли | 5.98·1027 г |
| Масса Луны | 7.35·1025 г |
| Масса 1 куб. м свинца | 1.135·107 г |
Масса 1 куб. | 1.204·103 г |
Масса атома свинца | 3.45·10−22 г |
| Масса протона | 1.67·10–24 г |
| Масса электрона | 9.11·10–28 г |
1.2. Упругое рассеяние α-частиц. Формула Резерфорда
Классическая
физика основана на ряде блестящих экспериментов, среди которых особое место
занимают эксперименты
Г. Кавендиша и
Ш. Кулона. С помощью крутильных весов ими
были установлены законы гравитационного и электрического взаимодействий
макроскопических тел. Однако метод эксперимента, который использовался
Кавендишем и Кулоном, не может использоваться в микрофизике из-за малых размеров
исследуемых объектов.
Новый метод изучения микроскопических систем, был предложен
Э. Резерфордом.
Он первым разработал и применил метод исследования с помощью рассеяния пробной
«частицы-снаряда» на исследуемом объекте. В своем первом эксперименте Резерфорд
использовал рассеяние α-частиц на
атомах для того, чтобы изучить атомную структуру. Выяснив, что вероятность
рассеяния α-частиц на атоме, как
функция угла рассеяния θ, подчиняется
формуле Резерфорда для рассеяния ее на точечном кулоновском центре
В своем первом эксперименте Резерфорд
использовал рассеяние α-частиц на
атомах для того, чтобы изучить атомную структуру. Выяснив, что вероятность
рассеяния α-частиц на атоме, как
функция угла рассеяния θ, подчиняется
формуле Резерфорда для рассеяния ее на точечном кулоновском центре
| вероятность рассеяния ~ , | (1.1) |
где Zα, Zя – заряды (в единицах элементарного заряда) α-частицы и ядра-мишени, Т – кинетическая энергия α-частицы, он установил, что в атоме имеется ядро размером менее 5·10–12 см, сосредотачивающее в себе почти всю массу атома.
| Рис. 1.1 Рассеяние α-частицы на
ядре мишени с зарядом Zя.
Угол рассеяния θ
зависит от прицельного параметра b: tg(θ/2) = ZαZяe2/(2bT). 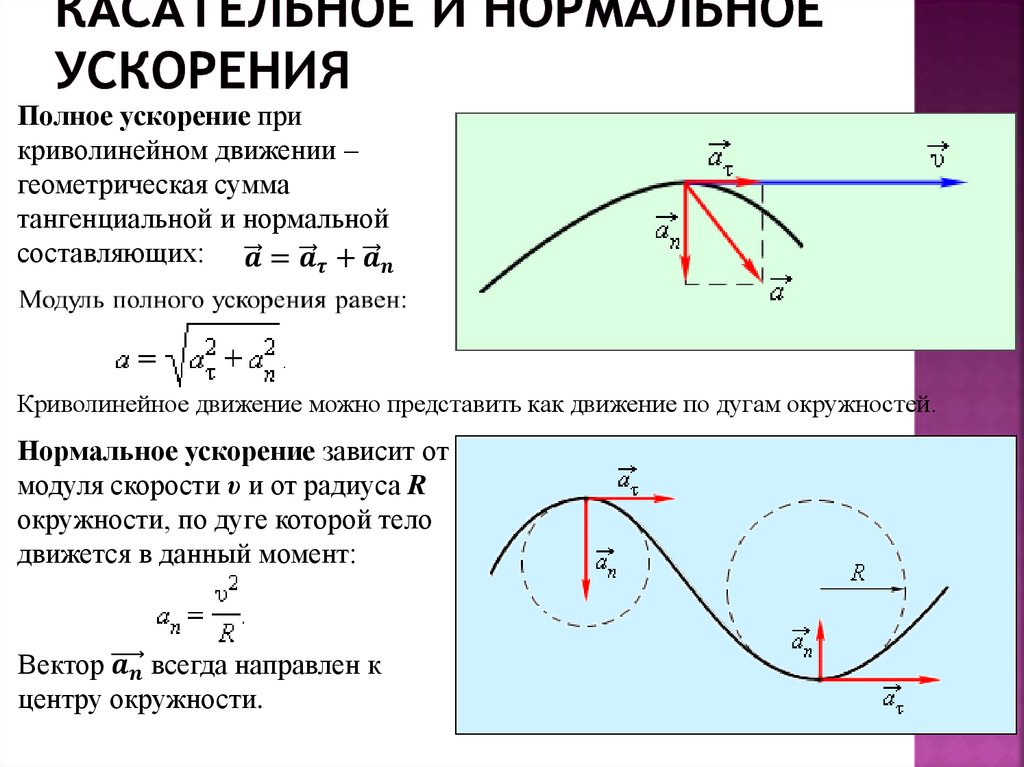 |
| Атом состоит из ядра и
связанных с ним электронов. Атомное ядро состоит из
нуклонов: Z протонов и N нейтронов. Массовое число А = Z
+ N соответствует суммарному числу протонов и нейтронов. В нейтральном атоме число электронов равно числу протонов Z. |
1.3. Сечение реакции
Для характеристики вероятности процессов в микромире пользуются понятиями полного эффективного сечения σ
и дифференциального эффективного сечения dσ/dΩ.
Дифференциальное сечение используется для описания вероятности процесса
взаимодействия частиц. Если мишень содержит NМ ядер и вся находится в
пучке падающих частиц плотностью
j (j —
число частиц, падающих в единицу времени на единицу поперечной площади мишени),
то число dN(0)/dΩ частиц, рассеиваемых мишенью в единицу времени на угол
θ в пределах телесного угла
dΩ, определяется соотношением:
(1. 2) 2) |
Полное число частиц, рассеиваемых мишенью в единицу времени под всеми углами, определяется соотношением
| (1.3) |
σ − полное эффективное сечение, NМ = nSd − характеристика мишени (n − число ядер мишени в единице объёма, S − облучаемая поперечная площадь мишени, d − толщина мишени в направлении падающего пучка частиц). Полное сечение измеряется в барнах (1 барн = 10–24см2).
1.4. Размер ядра
Наиболее распространенный метод исследования атомных ядер – это рассеяние на ядрах различных частиц и ядер, ускоренных до высоких энергий. Точные данные по размерам атомных ядер были получены из экспериментов по рассеянию электронов. Радиусы ядер R растут с увеличением массового числа А и хорошо описываются соотношением
R ≈ 1. 3·10-13·A1/3 см
= 1.3·A1/3 Фм. 3·10-13·A1/3 см
= 1.3·A1/3 Фм. | (1.4) |
Численный коэффициент в (1.4) зависит от методики определения радиуса ядра и меняется в пределах 1.1÷1.4. Здесь и далее будет использоваться значение 1.3.
1.5. Радиоактивность
Радиоактивность – свойство атомных ядер самопроизвольно (спонтанно) изменять свой состав (заряд Z, массовое число A) в результате испускания частиц или ядерных фрагментов. К явлению радиоактивности относится также испускание атомным ядром гамма-квантов, но при этом ни заряд Z, ни массовое число A не изменяются.
Основные виды
радиоактивных распадов:
из атомного ядра испускается α-частица – ядро атома 4He. из атомного ядра испускаются электрон e– и антинейтрино e, один из нейтронов ядра превращается в протон.  из атомного ядра испускаются позитрон e+ и нейтрино νe, один из протонов ядра превращается в нейтрон. в результате взаимодействия между протоном и электроном атомной оболочки из ядра испускается нейтрино, один из протонов ядра превращается в нейтрон из возбужденного атомного ядра испускается один или несколько гамма-квантов. |
Рис. 1.2. Зависимость активности от времени (слева). Данная
зависимость в логарифмическом масштабе отображается прямой, тангенс
угла наклона которой равен постоянной распада λ. Справа приведена
кривая активации (наведенной радиоактивности) в зависимости от
времени. Рост числа радиоактивных ядер практически прекращается при
достижении активации насыщения за время t ≈ 5T1/2
Процесс радиоактивного распада, как и все процессы в микромире, – это случайный
(статистический) процесс. Атомные ядра одного сорта распадаются за разное
время. Однако среднее время жизни τ ядер, вычисленное по наблюдению большого числа распадов, оказывается не
зависящим от способа получения этих ядер и от внешних условий. Среднее время
жизни τ
ядра характеризует скорость их распада. Постоянная распада λ:
Атомные ядра одного сорта распадаются за разное
время. Однако среднее время жизни τ ядер, вычисленное по наблюдению большого числа распадов, оказывается не
зависящим от способа получения этих ядер и от внешних условий. Среднее время
жизни τ
ядра характеризует скорость их распада. Постоянная распада λ:
| λ = 1/τ. | (1.5) |
Физический
смысл
λ
– это вероятность распада радиоактивного ядра в единицу времени.
Закон радиоактивного распада показывает, как со временем
изменяется в среднем число радиоактивных ядер в образце. Если в момент времени
t имеется большое число N
радиоактивных ядер, то к моменту t + dt
распад испытают в среднем λNdt
ядер. Поэтому изменение их числа dN определяется соотношением
| dN = -λNdt | (1. 6) 6) |
Знак минус означает, что общее число радиоактивных ядер (частиц) уменьшается в процессе распада. Интегрируя соотношение (1.6), получим закон радиоактивного распада:
| N = N0e—λt, | (1.7) |
где
N0 − число радиоактивных ядер в начальный момент
t = 0. Закон радиоактивного распада
относится к статистическим средним и справедлив лишь при достаточно большом
числе распадающихся ядер.
Среднее время жизни τ
ядра вычисляется по формуле
| . | (1.8) |
Часто для характеристики скорости радиоактивного распада атомных ядер используют
величину, называемую периодом полураспада –
T1/2. Период полураспада – это время, за которое число радиоактивных ядер уменьшается
вдвое:
N0/2 = N0,
откуда
Период полураспада – это время, за которое число радиоактивных ядер уменьшается
вдвое:
N0/2 = N0,
откуда
| T1/2 = ln2/λ ≈ 0.693/λ = 0.693τ. | (1.9) |
Активность образца А – число распадов в единицу времени, является производной от N по времени, взятой с обратным знаком:
| A = -dN/dt = λN. | (1.10) |
Активность образца уменьшается со временем по тому же экспоненциальному закону, что и число нестабильных ядер. Активность измеряют в беккерелях или в кюри.
1 Бк (беккерель) = 1 распад в секунду, |
Энергия распадающейся системы в соответствии с принципом неопределенностей Гейзенберга, не может быть точно определена. Всякое распадающееся состояние, имеющее среднее время жизни τ, описывается волновой функцией ψ(t), квадрат модуля которой убывает со временем по экспоненциальному закону радиоактивного распада
|ψ(t)|2 = |ψ(0)|2e-t/τ.
Ядро в любом состоянии с τ ≠ ∞
имеет энергетическую неопределённость ΔE
≈ Г,
которая связана с τ
соотношением неопределённостей Г·τ ≈ ћ , где Г –
ширина уровня на половине высоты.
Подавляющее число частиц также являются нестабильными и распадаются по тем
же законам радиоактивного распада, как и атомные ядра. Традиционно
радиоактивность атомных ядер описывают, используя период полураспада
T1/2, а распады частиц описывают, использую среднее
время жизни τ
1.
 6. Преобразования Лоренца
6. Преобразования ЛоренцаОсновные положения специальной теории относительности изучались в разделе «Механика» общего курса физики. Здесь лишь напомним основные соотношения релятивистской физики.
| Принцип относительности
– все законы природы должны быть
одинаковыми для всех наблюдателей, двигающихся друг
относительно друга с постоянной скоростью. Специальная теория относительности была построена на двух постулатах, сформулированных Эйнштейном в 1905 году: 1. Законы физики одинаковы во всех инерциальных системах отсчета. 2. Скорость света в вакууме равна постоянной величине с независимо от скорости движения источника. |
| Рис.  1.3. Штрихованная система S’
движется относительно системы S
со скоростью вдоль оси z. 1.3. Штрихованная система S’
движется относительно системы S
со скоростью вдоль оси z. |
Рассмотрим материальную точку с массой покоя m. Ее координаты в инерциальной системе отсчета S определяются как (t,) = (t,x,y,z), а скорость v = ||. Координаты той же точки в другой инерциальной системе отсчета S’ (t’,x’,y’,z’), движущейся относительно S вдоль оси z с постоянной скоростью , связаны с координатами в системе S преобразованиями Лоренца. В случае, если координатные оси систем z и z’ сонаправлены с вектором и в начальный момент времени t = t’ = 0 начала координат обеих систем совпадали, то преобразования Лоренца даются выражениями:
| x’ = x, y’ = y, z’ = γ(z − βct), ct’ = γ(ct − βz), | (1.11) |
где
β = v/c (0 < β < 1), а γ = 1/(1 – β2)1/2 – лоренц-фактор.
Скорость частицы ‘ в системе S’ связана со скоростью в системе S соотношением:
| (1.12) |
Обратные преобразования Лоренца получаются взаимной заменой координат ri → ri‘, vi → vi‘ и учетом изменения направления скорости v → -v:
| x = x’, y = y’, z = γ(z’ + βct’), ct = γ(ct’ + βz’) | (1.13) |
При малых скоростях преобразования Лоренца совпадают с выражениями для нерелятивистских преобразований Галилея:
Преобразования Лоренца | Преобразования Галилея |
x’ = x, y’ = y | x’ = x, y’ = y |
z’ = γ(z − vt) | z’ = z – vt |
ct’ = γ(ct − βz) | t’ = t |
Относительность пространственных расстояний (Сокращение Лоренца-Фитцджеральда):
| ℓ’ = ℓ/γ | (1. 14) 14) |
Относительность промежутков времени между событиями (релятивистское замедление времени):
| Δt’ = γΔt. | (1.15) |
Относительность одновременности событий. Если в системе S для событий A и B tA = tB и xA ≠ xB, то в системе S’
| t’A = t’B + γv/c2 (xB − xA). | (1.16) |
В общем случае преобразования Лоренца записываются в
терминах
4-векторов a = (a0,)
= (a0,a1,a2,a3). При относительном
движении систем S и S’, как на рис. 1.2, 4-вектор a преобразуется следующим образом:
| a’0 = γ(a0 − βa3), a’1 = a1, a’2 = a2, a’3 = γ(a3 − βa0), | (1.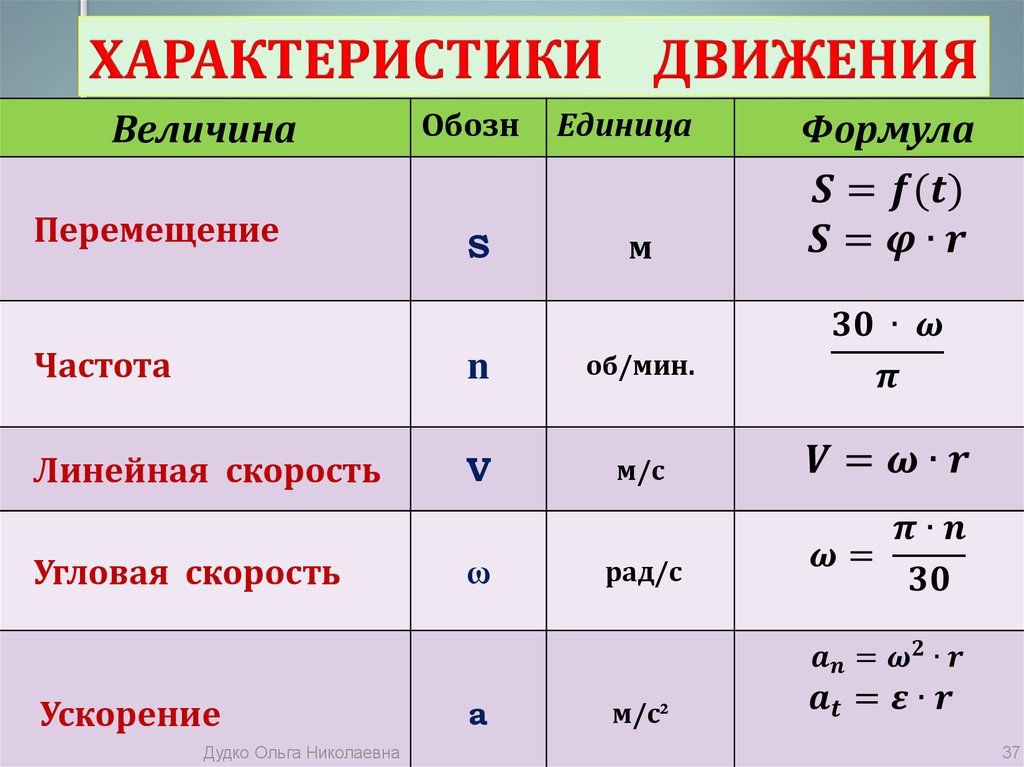 17) 17) |
| Скалярное произведение двух
4-векторов a и b
в 4-мерном пространстве времени определяется как: и является инвариантом, т.е. сохраняется во всех инерциальных системах отсчета. |
Таким образом, квадрат 4-вектора также является инвариантом. Например, квадрат 4-вектора координаты
| (X)2 = (ct,)2 = c2t2 − ()2 = τ2 | (1.18) |
определяет «собственное» время частицы (т.е. время в ее системе отсчета).
4-вектор скорости
u = γ(c,)
вводится таким образом, чтобы (u)2 = c2. 4-импульс, определяется как произведение массы на скорость
P = mu = mγ(c,)
= (E/c,). | (1.19) |
Так как u2 = c2, то (P)2 = m2c2 = (E/c)2 − ()2, или
| E2 = p2c2 + m2c4. | (1.20) |
Следовательно,
| E = γmc2, = γm, = c2/E. | (1.21) |
Преобразования Лоренца для 4-импульса (1.17):
E’/c = γ(E/c − βpz),
p’x = px, p’y = py,
p’z = γ(p’z − βE/c).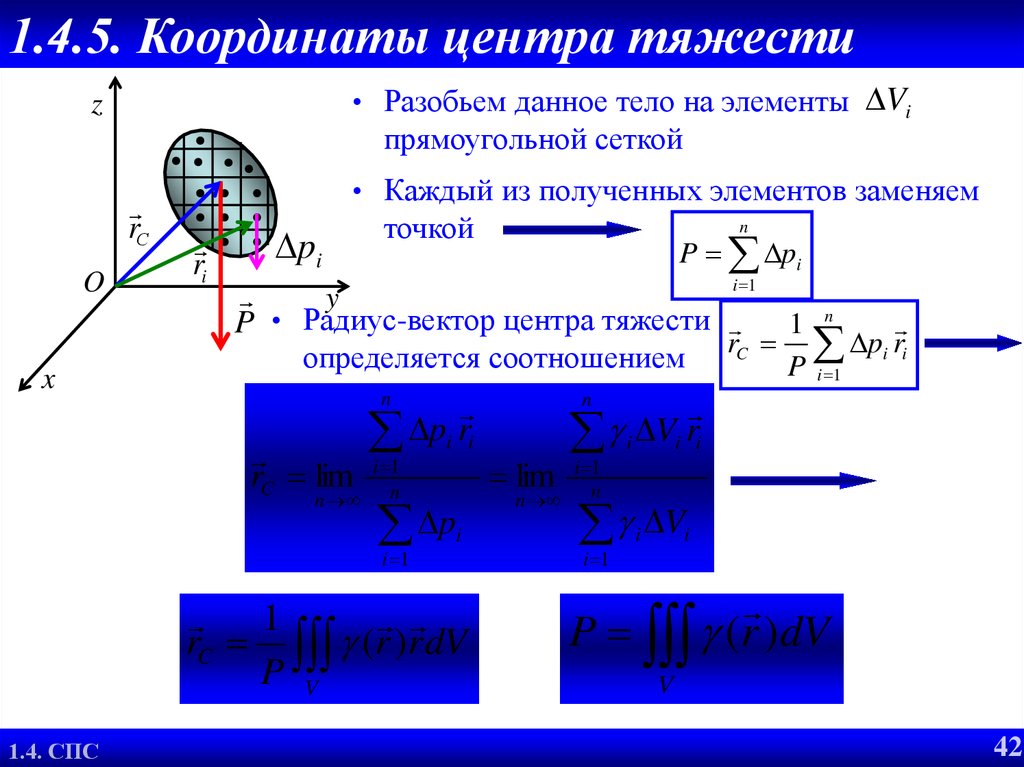 | (1.22) |
Скалярное произведение 4-импульсов является инвариантом по определению. Вместо произведения 4-импульсов двух частиц, например P1P2, обычно используют квадрат инвариантной массы двух частиц (s-инвариант):
| (1.23) |
или квадрат переданного импульса (t-инвариант)
1.7. Эффект Доплера
Если в системе S (рис. 1.2) в направлении оси z испущен фотон энергии E0 = p0c, то его энергия E, длина волны λ и частота ν в системе отсчета S’ (наблюдатель удаляется от источника света) составит
E = γ(E0 − βp0c) = γE0(1 − β),
(1. 24) 24) |
Параметр смещения z в этом случае z = (λ − λ0)/λ0 = (ν0 − )/ν > 0, что соответствует красному смещению λ > λ0, ν < ν0. Если скорость системы S’ направлена в противоположную сторону (наблюдатель приближается к источнику света), то знаки изменяются на противоположные:
| (1.25) |
В данном случае наблюдается синее смещение: λ < λ0. Поскольку в
общем случае преобразование Лоренца записывается как E = γ(E0 − ()/c2, то, в отличие от
классической физики, в релятивистском случае наблюдается поперечный эффект
Доплера: v/v0 = γ.
Из формул, соответствующих синему смещению, можно получить
классическую формулировку эффекта Доплера, используя разложение в ряд:
Тогда для относительного изменения частоты излучения: Δν/ν0 = β = v/c, что соответствует классической формулировке эффекта Доплера (без учета среды):
ν = ν0(1 + ν/νзвук).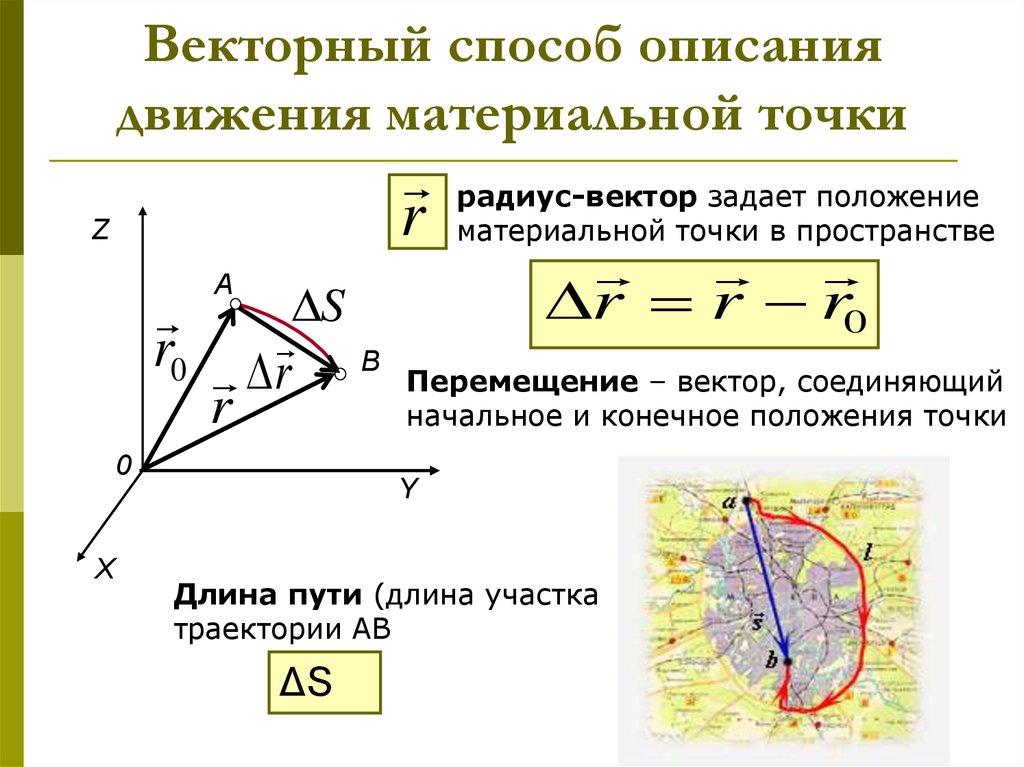
1.8. Системы отсчета
Рассмотрим двухчастичный процесс a + b → c + d. 4-х импульсы
сталкивающихся частиц
Pa = (Ea/c,a) и Pb = (Eb/c,b) соответственно.
При описании взаимодействий частиц и атомных ядер, как и в
классической физике, обычно используются две системы отсчета: система покоя
мишени и система центра инерции (рис. 1.4).
Рис. 1.4. Определение некоторых систем отсчета
1. Система покоя мишени – система, в которой частица b (мишень) покоится, pb = 0, Eb = mbc2. Обычно под лабораторной системой (ЛС) отсчета подразумевается система покоя мишени. В данной системе s-инвариант:
| (1.26) |
Энергия налетающей частицы, выраженная через s-инвариант:
(1. 27) 27) |
2. Система центра инерции (СЦИ) – система, в которой *a = *b = 0. Величины в СЦИ в дальнейшем будут отмечаться звездочкой. В СЦИ . s-инвариант в СЦИ:
| (1.28) |
В экспериментах физики высоких энергий часто используется система встречных пучков – система, в которой частицы равной массы и равных по абсолютной величине импульсов сталкиваются под углом π − θ. При θ = 0 система встречных пучков совпадает с СЦИ.
1.9. Основные формулы релятивистской физики
Универсальность законов сохранения приводит к необходимости установить для релятивистской кинематики такие уравнения, которые удовлетворяли бы к законам сохранения энергии и импульса и были инвариантны относительно преобразований Лоренца:
- E = (m2c4 + p2c2)1/2 = γmc2 = mc2 + T,
E – полная энергия частицы, m – масса частицы,
с – скорость света в вакууме,
= γm – релятивистский импульс частицы,
β = v/c, γ = (1 – β2)-1/2 – Лоренц-фактор, – скорость частицы,
T = mc2(γ – 1) – релятивистская кинетическая энергия частицы.
- p2c2 = T(2mc2 + T).
- τ = γτ0 – релятивистское замедление времени,
τ0 – время жизни частицы в состоянии покоя,
τ – времени жизни частицы, движущейся со скоростью . - l = l0/γ,
- E2 – p2c2 = inv = m2c4,
E – полная энергия частицы или системы частиц,
p – импульс частицы или суммарный импульс системы частиц. - Энергия налетающих частиц Е в ускорителе с неподвижной мишенью,
эквивалентном коллайдеру с пучками частиц массы m и энергии E*:
(1.29) - Порог реакции. Если на неподвижной мишени b
под действием налетающих частиц a происходит реакция a + b → c + d +… и
энергия реакции (изменение суммарной массы частиц) Q = (∑mi – ∑mf)c2 < 0, то минимальная кинетическая энергия
частицы а, необходимая для осуществления такой реакции
(1.  30)
30)
1.10. Система единиц Гаусса
| Время | 1 с |
| Энергия, масса E = mc2 | 1 эВ (электрон-Вольт) = 1.6·10-19 эрг
= = 1.6·10-19 Дж. 1эВ = 10-3 кэВ = 10-6 МэВ = 10-9 ГэВ = = 10-12 ТэВ |
| Энергия покоя электрона протона нейтрона | 0.511 МэВ 938.3 МэВ 939.6 МэВ |
| Длина | 1 Фм (ферми, фемтометр) = 10-13 см 1 Å (ангстрем) = 10-8 см |
| Скорость света в вакууме | с = 3·1010 см/с |
| Заряд электрона | e = 4.8·10-10 ед. СГС |
| Приведенная постоянная Планка Константы | ћ = h/2π = 6.58·10-22 Мэв·с |
| ћс = 197 МэВ·Фм; α = e2/ћс = 1/137 |
При решении задач будет использоваться система единиц Гаусса,
в которой основными единицами являются сантиметр, грамм и секунда. В данной
системе диэлектрическая и магнитная проницаемости являются безразмерными
величинами, причём для вакуума они приняты равными единице. В качестве единицы
измерения энергии используется внесистемная единица 1 эВ (электрон-Вольт) –
энергия, приобретаемая электроном при прохождении потенциала в 1 Вольт.
В данной
системе диэлектрическая и магнитная проницаемости являются безразмерными
величинами, причём для вакуума они приняты равными единице. В качестве единицы
измерения энергии используется внесистемная единица 1 эВ (электрон-Вольт) –
энергия, приобретаемая электроном при прохождении потенциала в 1 Вольт.
1.11. Энергия и порог реакции
Частица массы ma налетает на покоящуюся частицу массы mb. В результате реакции в конечном состоянии образуется n частиц с массами m’1,…m’n Определить энергию и порог реакции.Обозначим суммарную массу взаимодействующих частиц ma + mb = ∑mi (индекс i соответствует начальному состоянию (initial)), суммарную массу образовавшихся частиц m’1 + m’2 +… m’n = ∑mf (индекс f обозначает конечное состояние (final)). Энергия реакции Q соответствует изменению суммарной массы частиц:
Q = (∑mi − ∑mf )c2. | (1.31) |
Пороговая энергия реакции – это дополнительная кинетическая энергия,
необходимая для осуществления эндотермической реакции (Q < 0). Данное значение
энергии соответствует предельному случаю, когда продукты реакции образуются с
нулевыми импульсами в СЦИ и s-инвариант в конечном состоянии равен квадрату
суммы масс конечных продуктов:
.
В начальном состоянии в СЦИ
.
Следовательно, необходимая суммарная энергия сталкивающихся частиц должна быть
.
Пороговая кинетическая энергия в СЦИ:
В лабораторной системе отсчета частица-мишень покоится: |b| = 0, Eb = mbc2. Соответственно, s-инвариант в лабораторной системе в начальном состоянии равен:
Приравнивая s в начальном и конечном состояниях, получаем:
(1. 32) 32) |
| (1.33) |
Раскладывая разность квадратов и выделяя Q, получим (1.31):
| (1.34) |
Значение пороговой энергии реакции в лабораторной системе всегда больше соответствующего значения в системе центра инерции. Их разность определяет ту часть энергии, которая идет на движение центра инерции в лабораторной системе.
1.12. Энергии частиц в двухчастичном распаде
Получим выражение для энергий и импульсов продуктов распада C → A + B через массы частиц в релятивистском случае в СЦИ.СЦИ связана с распадающейся частицей С, ее энергия в данной системе EС = mСc2, продукты распада разлетаются под углом 180°.
 Законы сохранения энергии и импульса:
Законы сохранения энергии и импульса:Учитывая, что (pc)2 = E2 − (mc2)2 и подставляя выражение EB через EA во второе уравнение, получим:
E2A − (mAc2)2 = (mСc2 − EA)2 − (mBc2)2.
Отсюда для частицы A:
| (1.35) |
Выражения для частицы B получаются перестановкой соответствующих индексов.
Полезно выписать выражения для энергий продуктов распада в
некоторых частных случаях:
а) распад на частицы равной массы mA = mB.
(1.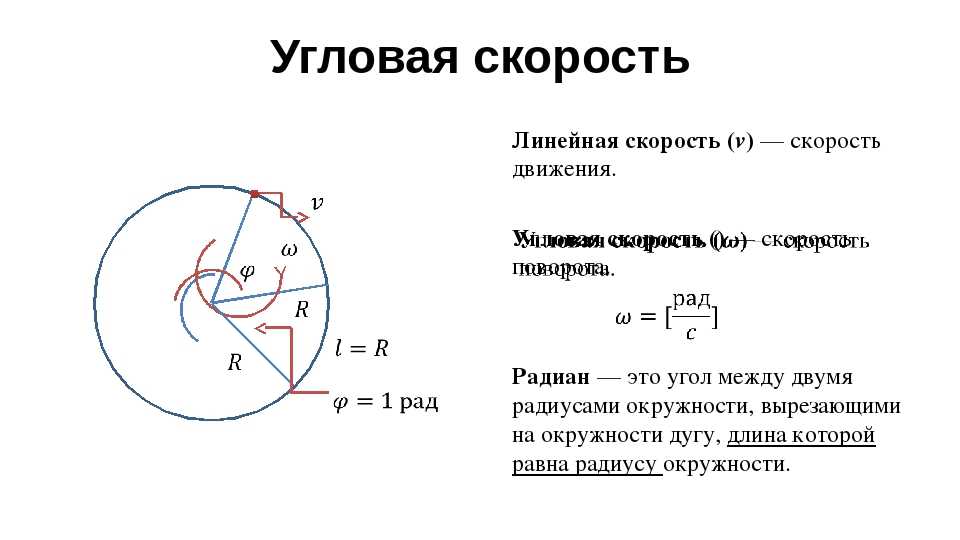 36) 36) |
б) образование безмассовой частицы mA = 0.
| (1.37) |
в) нерелятивистский случай: Q << mCc2, mC ≈ mA + mB
| (1.38) |
Задачи
1.1. Альфа-частица (Zα = 2) с кинетической энергией T = 5 МэВ испытывает лобовое столкновение с ядром золота (Zя = 79). Рассчитать расстояние максимального сближения α-частицы с ядром золота.
1.2. Протон с кинетической энергией Т = 2 МэВ налетает на неподвижное
ядро 197Au. Определить дифференциальное сечение рассеяния dσ/dΩ на
угол θ = 60° .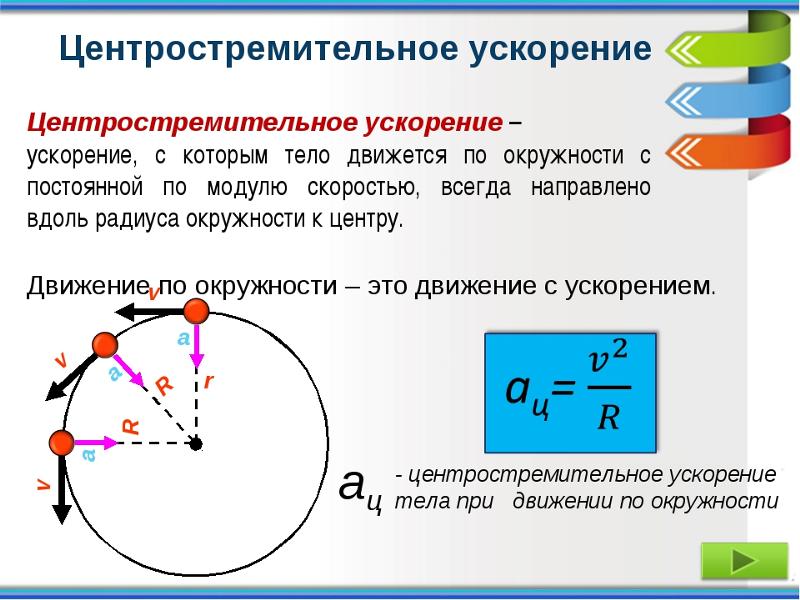 Как изменится величина дифференциального сечения рассеяния, если
в качестве рассеивающего ядра выбрать 27Al?
Как изменится величина дифференциального сечения рассеяния, если
в качестве рассеивающего ядра выбрать 27Al?
1.3. Частица массы ma налетает на покоящуюся частицу массы mb. В результате реакции в конечном состоянии образуется n частиц с массами m’1,…m’n. Определить энергию и порог реакции.
Обозначим суммарную массу взаимодействующих частиц
ma + mb = ∑imi (индекс i соответствует начальному состоянию (initial)), суммарную массу образовавшихся
частиц
m’1 + m’2 + …+ m’n = ∑f mf (индекс f обозначает конечное состояние (final)). Энергия реакции Q
соответствует изменению суммарной массы частиц:
Q = (∑imi − ∑fmf )c2. | (1.31) |
Пороговая энергия реакции – это дополнительная
кинетическая энергия, необходимая для осуществления эндотермической реакции (Q <
0). Данное значение энергии соответствует предельному случаю, когда продукты
реакции в СЦИ образуются с нулевыми импульсами и s-инвариант в конечном
состоянии равен квадрату суммы масс конечных продуктов:
s = (∑f Pf )/c2 = (∑fmf ). В начальном состоянии в СЦИ s = (∑i P*i )/c2 = (E*a + E*b)2/c4. Следовательно,
необходимая суммарная энергия сталкивающихся частиц должна быть
E*a + E*b = ∑fmf c2.
Пороговая кинетическая энергия в СЦИ:
T*a +T*b = ∑fmf c2 − ∑imic2 = |Q|.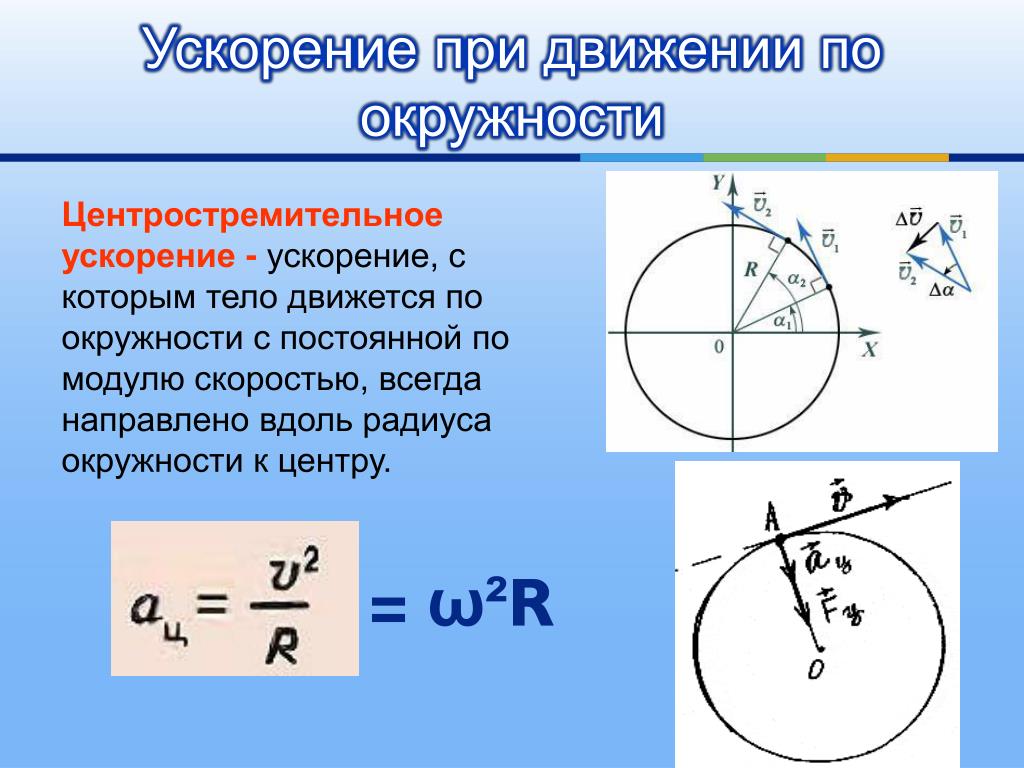
В лабораторной системе отсчета частица-мишень покоится: |b| = 0, Eb = mbc2. Соответственно, s-инвариант в лабораторной системе в начальном состоянии равен:
s = (Pa + Pb)/c2 = (Ea/c2 + Eb/c2) − (a/c − b/c)2 = ma2 + mb2 − 2Eamb/c2.
Приравнивая s в начальном и конечном состояниях, получаем:
| (1.32) |
| (1.33) |
Раскладывая разность квадратов и выделяя Q, получим (1.30):
(1. 30) 30) |
Значение пороговой энергии реакции в лабораторной системе всегда больше соответствующего значения в системе центра инерции. Их разность определяет ту часть энергии, которая идет на движение центра инерции в лабораторной системе.
1.4. Получим выражение для энергий и импульсов продуктов распада C → A +
B через массы частиц в релятивистском случае в СЦИ.
СЦИ связана с распадающейся частицей С, ее энергия в данной
системе EС = mСc2, продукты распада разлетаются
под углом 180°. Законы сохранения энергии и импульса:
Учитывая, что (pc)2 = E2 − (mc2)2 и подставляя выражение EB через EA во второе уравнение, получим:
E2A − (mAc2)2 = (mСc2 − EA)2 − (mBc2)2.
Отсюда для частицы A:
| (1.35) |
Выражения для частицы B получаются перестановкой соответствующих индексов.
Полезно выписать выражения для энергий продуктов распада в
некоторых частных случаях:
а) распад на частицы равной массы mA = mB.
| (1.36) |
б) образование безмассовой частицы mA = 0.
| (1.37) |
в) нерелятивистский случай: Q << mCc2, mC ≈ mA + mB
(1. 38) 38) |
1.5. Рассчитать кинетические энергии α-частицы и ядра 222Rn,
образующихся при распаде
226Ra → 222Rn + α.
(mRn = 206764.10 МэВ, mRa = 210496.35 МэВ, mα =
3727.38 МэВ.)
Ответ: Qα = 4.87 МэВ,
Tα = 4.78 МэВ,
TRn = 0.086 МэВ
1.6. Рассчитать дифференциальное сечение рассеяния α-частицы с
кинетической энергией 10 МэВ
1) на ядре кальция 40Ca на угол 60°,
2) на ядре меди 63Cu на угол 90°,
3) на ядре молибдена 96Mo на угол 120°,
4) на ядре серебра 79Ag на угол 180°.
Ответ: 1) 0.33 барн/стер, 2) 0.17 б/стер, 3) 0.16 б/стер, 4) 0.11 б/стер
1.7. Рассчитать отношение сечений рассеяния α-частиц с кинетической
энергиями 10 МэВ на ядре 197Au под углами 6° и 180°.
Ответ: W = 13.3·104
1.8. Рассчитать расстояния максимального сближения R
1) α-частицы с кинетической энергией 5 МэВ с ядром 197Au и 7Li,
2) α-частицы с кинетической энергией 10 МэВ с ядром 40Ca,
3) протона с кинетической энергией 7 МэВ с ядром 197Au,
4) α-частицы с кинетической энергией 5 МэВ с ядром 208Pb.
Ответ: 1) R = 1.7
Фм, 2) R = 5.8
Фм, 3) R = 16.2
Фм, 4) R = 47.2
Фм
1.9.Пучок α-частиц с энергией Tα = 5 МэВ
падает перпендикулярно на фольгу из серебра толщиной 1 мг/см2.
α-частицы, рассеянные под углом 60°, регистрируются детектором площадью 1 см2,
расположенном на расстоянии 20 см от мишени. Какая доля от полного числа
рассеянных α-частиц ΔN/N будет зарегистрирована детектором?
Ответ: ∆N(60º)/N = 4·10–10
1.10. В ходе эксперимента медная фольга (Z = 29,
Mmol = 63.55 г/моль) толщиной 2 мг/см2 облучается пучком
α-частиц с с кинетической энергией Тα = 5 МэВ
и интенсивностью 105 частиц в секунду. Сколько α-частиц в минуту ∆N
будет регистрировать детектор площадью 1 см2, расположенный на
расстоянии 10 см от мишени под следующими углами к направлению падающего пучка:
1) 30°, 2) 90°, 3) 120°?
Ответ: 1) ∆N(30º) ≈ 44 част. ,
2) ∆N(90º) ≈ 0.8 част.,
3) ∆N(120º) ≈ 0.4 част.
,
2) ∆N(90º) ≈ 0.8 част.,
3) ∆N(120º) ≈ 0.4 част.
1.11. Почему из экспериментов по упругому рассеянию α-частиц следовало, что в атоме расположено положительно заряженное атомное ядро размером < 5·10–12 см? Почему полученные результаты нельзя было объяснить на основании модели Томсона?
1.12. Во сколько раз число распадов ядер радиоактивного изотопа йода 131I в течение первых суток больше числа распадов в течение вторых суток? Период полураспада изотопа T1/2(131I) = 193 часа.
1.13. Пучок π–-мезонов движется со скоростью v = 0.9c.
Среднее время жизни π–-мезонов составляет τ = 2.6·10–8 с.
Какое расстояние в среднем они пройдут до своего распада?
Ответ: Lπ = 16
м
1.14. На каком расстоянии интенсивность пучка мюонов с кинетической
энергией T = 0.5 ГэВ, движущихся в вакууме, уменьшается до половины
первоначального значения?
mμ = 105. 66 МэВ, τμ = 2.197·10-6 сек.
66 МэВ, τμ = 2.197·10-6 сек.
Ответ: L = 2.6
км
1.15. Полная энергия электрона составляет 2.5 МэВ. Определите его импульс
и скорость в лабораторной системе отсчета.
Ответ: p = 2.45 МэВ/c,
v = 0.989c
1.16. Электрон и протон ускоряются разностью потенциалов 107 В.
Рассчитайте фактор γ, скорость, импульс и полную энергию каждой частицы.
Ответ: 1) E ≈ pc = 10.5 МэВ, γ = 20.57, v = 0.999c; 2) E = 948.27 МэВ, pc = 137.35 МэВ, γ = 1.01, v = 0.147c
1.17. Какую энергию надо затратить, чтобы электрон достиг скорости
а) 0.5 c, б) 0.9 c, в) 0.99 c.
Какая энергия необходима, чтобы протон достиг тех же скоростей?
Ответ: а) Te = 0.08 МэВ,
Tp = 145.2 МэВ;
б)
Te = 0.66 МэВ,
Tp = 1.2 ГэВ;
в) Te = 3.11 МэВ,
Tp = 5.7
ГэВ.
1.18. Какую энергию надо затратить, чтобы увеличить скорость протона а) от 0. 20 c
до 0.21 c,
20 c
до 0.21 c,
б) от 0.80 c до 0.81 c, в) от 0.90 c до 0.91 c, г) от 0.98 c до 0.99 c.
Ответ: а) Tp = 2.05 МэВ,
б) Tp = 36.2
МэВ, в) Tp = 110.5
МэВ, г) Tp = 1 936
МэВ
1.19. Полная энергия частицы в два раза больше ее энергии покоя. Рассчитайте отношение v/c для этой частицы и определите ее импульс.
1.20. Определите массу частицы если известно, что ее импульс равен
500 МэВ/c,
а энергия – 1746 МэВ.
1.21. Рассчитайте скорость уменьшения массы Солнца, если известно, что плотность лучистой энергии Солнца на Земле в среднем равна 1.37·103 Вт/м2.
1.22. Энергия связи электрона в атоме водорода составляет 13.6 эВ. Насколько масса атома водорода меньше суммы масс электрона и протона?
1.23. Энергия связи дейтрона (система, состоящая из протона и нейтрона) составляет 2.224 МэВ. Насколько масса ядра дейтрона меньше суммы масс составляющих его нуклонов?
1. 24. Энергия, выделяющаяся при делении одного ядра 235U,
составляет ~200 МэВ. Какое количество массы ядра урана превращается в энергию?
24. Энергия, выделяющаяся при делении одного ядра 235U,
составляет ~200 МэВ. Какое количество массы ядра урана превращается в энергию?
1.25. Какой должна быть относительная скорость двух наблюдателей,
чтобы измеряемые ими интервалы времени различались на 5 %?
Ответ: υ =
0.33с
1.26. На какое время разойдутся показания часов земного наблюдателя и
наблюдателя на спутнике Земли с периодом обращения 90 мин через 5 лет?
Ответ: ∆t
= 0.05
с
1.27. Используя разложение в ряд, получите следующие формулы для
приближенного вычисления релятивистских поправок в случае
v << c:
;
;
.
1.28. Исходя из релятивистского соотношения между энергией и импульсом, покажите, что в нерелятивистском пределе выполняется соотношение для кинетической энергии T = mv2/2.
1.29. Длина волны, излучаемая атомом водорода, составляет λ0 = 6560 Å. Измерение длины волны этого же излучения из удаляющейся галактики
составляет λ1 = 14580 Å.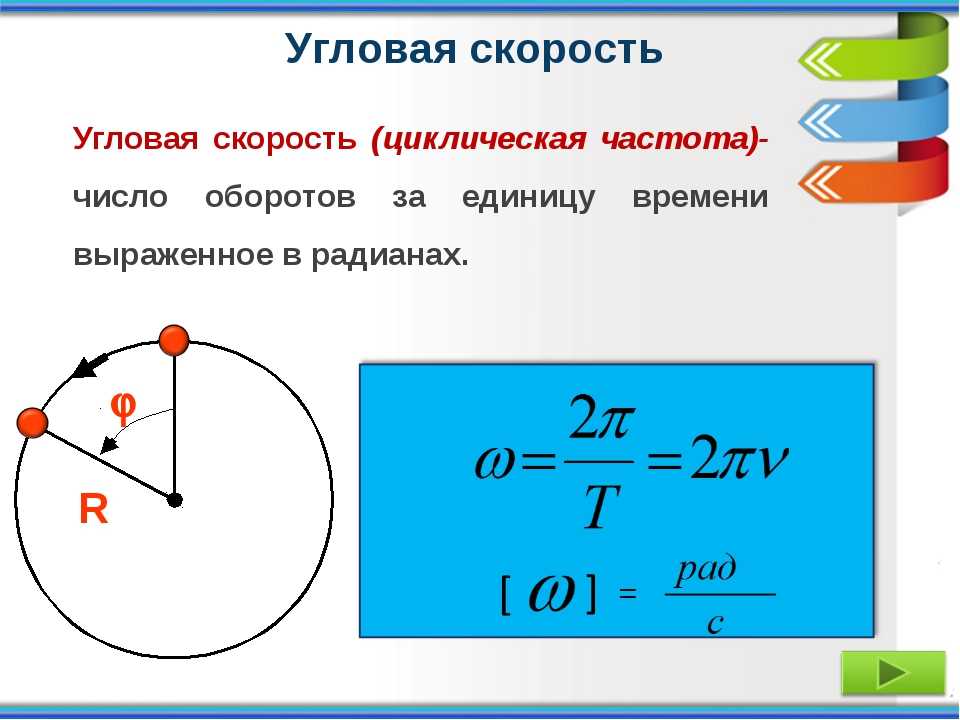 Определите скорость, с которой галактика
удаляется от Земли.
Определите скорость, с которой галактика
удаляется от Земли.
Ответ: υ = 2·108 м/с
1.30. Галактика удаляется от земного наблюдателя со скоростью 1.9·107 м/с.
Определите относительную величину красного смещения (λ1 − λ0)/λ0 для света этой галактики.
Ответ: z = 0.065 ≈ β
1.31. Измерение гравитационного потенциала ∆φ при удалении на бесконечность с расстояния R от центра сферического не вращающегося тела массы M составляет При этом величина красного смещения света определяется соотношением . Оцените величину красного смещения линии водорода в гравитационном поле Солнца. Оцените величину синего смещения этой линии в гравитационном поле Земли.
1.32. Видимый свет от близкой звезды смещен в фиолетовую часть спектра
на 5 %. С какой лучевой скоростью движется звезда?
Ответ: β
= 0.05c, v
= 1.5·107 м/с
1.33. С какой скоростью должен двигаться автомобиль, чтобы красный
свет светофора выглядел зеленым? Сравните результат с космическими скоростями.
1.34. Определить порог реакции α + α → 7Li + p. Определить долю кинетической энергии налетающей частицы,
идущую на движение центра инерции. mα = 3727.38 МэВ, mp =
938.27 МэВ,
mLi = 6533.83 МэВ.
1.35. Рассчитать порог реакции 14N + α → 17O + p в двух случаях:
- налетающей частицей является ядро азота 14N,
- налетающей частицей является α-частица.
Объяснить полученный результат.
1.36. 1) В коллайдере LHC энергия пучков протонов составляет E*p = 7 ТэВ.
Определите энергию столкновения √s в
системе центра инерции. Какая энергия протонного пучка Ep потребовалась
бы для достижения данной энергии в ускорителе с неподвижной мишенью? Сравните
результат с энергией протонов космических лучей.
2) В условии задачи 1) рассмотрите столкновение пучков электронов и позитронов с
энергиями
E*e = 500 ГэВ
(проект ILC).
3) В условии задачи 1) рассмотрите столкновение пучков
протонов с энергиями E*p = 1 ТэВ
(коллайдер TEVATRON).
4) В условии задачи 1) рассмотрите столкновение пучков электронов с энергиями E*e = 100 ГэВ
(коллайдер LEP)
Ответ: 1) Ep = 108 ГэВ, 2)
Ee = 109 ГэВ, 3)
Ep = 2·106 ГэВ, 4)
Ee = 4·107 ГэВ
26.10.2016
Все главные формулы по физике — Физика — Теория, тесты, формулы и задачи
Оглавление:
- Кинематика
- Динамика
- Статика
- Гидростатика
- Импульс
- Работа, мощность, энергия
- Молекулярная физика
- Термодинамика
- Электростатика
- Электрический ток
- Магнетизм
- Колебания
- Оптика
- Атомная и ядерная физика
- Основы специальной теории относительности (СТО)
- Равномерное движение по окружности
- Расширенная PDF версия документа «Все главные формулы по школьной физике»
Кинематика
К оглавлению. ..
..
Путь при равномерном движении:
Перемещение S (расстояние по прямой между начальной и конечной точкой движения) обычно находится из геометрических соображений. Координата при равномерном прямолинейном движении изменяется по закону (аналогичные уравнения получаются для остальных координатных осей):
Средняя скорость пути:
Средняя скорость перемещения:
Определение ускорения при равноускоренном движении:
Выразив из формулы выше конечную скорость, получаем более распространённый вид предыдущей формулы, которая теперь выражает зависимость скорости от времени при равноускоренном движении:
Средняя скорость при равноускоренном движении:
Перемещение при равноускоренном прямолинейном движении может быть рассчитано по нескольким формулам:
Координата при равноускоренном движении изменяется по закону:
Проекция скорости при равноускоренном движении изменяется по такому закону:
Скорость, с которой упадет тело падающее с высоты h без начальной скорости:
Время падения тела с высоты h без начальной скорости:
Максимальная высота на которую поднимется тело, брошенное вертикально вверх с начальной скоростью v0, время подъема этого тела на максимальную высоту, и полное время полета (до возвращения в исходную точку):
Формула для тормозного пути тела:
Время падения тела при горизонтальном броске с высоты H может быть найдено по формуле:
Дальность полета тела при горизонтальном броске с высоты H:
Полная скорость в произвольный момент времени при горизонтальном броске, и угол наклона скорости к горизонту:
Максимальная высота подъема при броске под углом к горизонту (относительно начального уровня):
Время подъема до максимальной высоты при броске под углом к горизонту:
Дальность полета и полное время полета тела брошенного под углом к горизонту (при условии, что полет заканчивается на той же высоте с которой начался, т. е. тело бросали, например, с земли на землю):
е. тело бросали, например, с земли на землю):
Определение периода вращения при равномерном движении по окружности:
Определение частоты вращения при равномерном движении по окружности:
Связь периода и частоты:
Линейная скорость при равномерном движении по окружности может быть найдена по формулам:
Угловая скорость вращения при равномерном движении по окружности:
Связь линейной и скорости и угловой скорости выражается формулой:
Связь угла поворота и пути при равномерном движении по окружности радиусом R (фактически, это просто формула для длины дуги из геометрии):
Центростремительное ускорение находится по одной из формул:
Динамика
К оглавлению…
Второй закон Ньютона:
Здесь: F — равнодействующая сила, которая равна сумме всех сил действующих на тело:
Второй закон Ньютона в проекциях на оси (именно такая форма записи чаще всего и применяется на практике):
Третий закон Ньютона (сила действия равна силе противодействия):
Сила упругости:
Общий коэффициент жесткости параллельно соединённых пружин:
Общий коэффициент жесткости последовательно соединённых пружин:
Сила трения скольжения (или максимальное значение силы трения покоя):
Закон всемирного тяготения:
Если рассмотреть тело на поверхности планеты и ввести следующее обозначение:
Где: g — ускорение свободного падения на поверхности данной планеты, то получим следующую формулу для силы тяжести:
Ускорение свободного падения на некоторой высоте от поверхности планеты выражается формулой:
Скорость спутника на круговой орбите:
Первая космическая скорость:
Закон Кеплера для периодов обращения двух тел вращающихся вокруг одного притягивающего центра:
Статика
К оглавлению. ..
..
Момент силы определяется с помощью следующей формулы:
Условие при котором тело не будет вращаться:
Координата центра тяжести системы тел (аналогичные уравнения для остальных осей):
Гидростатика
К оглавлению…
Определение давления задаётся следующей формулой:
Давление, которое создает столб жидкости находится по формуле:
Но часто нужно учитывать еще и атмосферное давление, тогда формула для общего давления на некоторой глубине h в жидкости приобретает вид:
Идеальный гидравлический пресс:
Любой гидравлический пресс:
КПД для неидеального гидравлического пресса:
Сила Архимеда (выталкивающая сила, V — объем погруженной части тела):
Импульс
К оглавлению…
Импульс тела находится по следующей формуле:
Изменение импульса тела или системы тел (обратите внимание, что разность конечного и начального импульсов векторная):
Общий импульс системы тел (важно то, что сумма векторная):
Второй закон Ньютона в импульсной форме может быть записан в виде следующей формулы:
Закон сохранения импульса. Как следует из предыдущей формулы, в случае если на систему тел не действует внешних сил, либо действие внешних сил скомпенсировано (равнодействующая сила равна нолю), то изменение импульса равно нолю, что означает, что общий импульс системы сохраняется:
Как следует из предыдущей формулы, в случае если на систему тел не действует внешних сил, либо действие внешних сил скомпенсировано (равнодействующая сила равна нолю), то изменение импульса равно нолю, что означает, что общий импульс системы сохраняется:
Если внешние силы не действуют только вдоль одной из осей, то сохраняется проекция импульса на данную ось, например:
Работа, мощность, энергия
К оглавлению…
Механическая работа рассчитывается по следующей формуле:
Самая общая формула для мощности (если мощность переменная, то по следующей формуле рассчитывается средняя мощность):
Мгновенная механическая мощность:
Коэффициент полезного действия (КПД) может быть рассчитан и через мощности и через работы:
Формула для кинетической энергии:
Потенциальная энергия тела поднятого на высоту:
Потенциальная энергия растянутой (или сжатой) пружины:
Полная механическая энергия:
Связь полной механической энергии тела или системы тел и работы внешних сил:
Закон сохранения механической энергии (далее – ЗСЭ). Как следует из предыдущей формулы, если внешние силы не совершают работы над телом (или системой тел), то его (их) общая полная механическая энергия остается постоянной, при этом энергия может перетекать из одного вида в другой (из кинетической в потенциальную или наоборот):
Как следует из предыдущей формулы, если внешние силы не совершают работы над телом (или системой тел), то его (их) общая полная механическая энергия остается постоянной, при этом энергия может перетекать из одного вида в другой (из кинетической в потенциальную или наоборот):
Молекулярная физика
К оглавлению…
Химическое количество вещества находится по одной из формул:
Масса одной молекулы вещества может быть найдена по следующей формуле:
Связь массы, плотности и объёма:
Основное уравнение молекулярно-кинетической теории (МКТ) идеального газа:
Определение концентрации задаётся следующей формулой:
Для средней квадратичной скорости молекул имеется две формулы:
Средняя кинетическая энергия поступательного движения одной молекулы:
Постоянная Больцмана, постоянная Авогадро и универсальная газовая постоянная связаны следующим образом:
Следствия из основного уравнения МКТ:
Уравнение состояния идеального газа (уравнение Клапейрона-Менделеева):
Газовые законы. Закон Бойля-Мариотта:
Закон Бойля-Мариотта:
Закон Гей-Люссака:
Закон Шарля:
Универсальный газовый закон (Клапейрона):
Давление смеси газов (закон Дальтона):
Тепловое расширение тел. Тепловое расширение газов описывается законом Гей-Люссака. Тепловое расширение жидкостей подчиняется следующему закону:
Для расширения твердых тел применяются три формулы, описывающие изменение линейных размеров, площади и объема тела:
Термодинамика
К оглавлению…
Количество теплоты (энергии) необходимое для нагревания некоторого тела (или количество теплоты выделяющееся при остывании тела) рассчитывается по формуле:
Теплоемкость (С — большое) тела может быть рассчитана через удельную теплоёмкость (c — маленькое) вещества и массу тела по следующей формуле:
Тогда формула для количества теплоты необходимой для нагревания тела, либо выделившейся при остывании тела может быть переписана следующим образом:
Фазовые превращения. При парообразовании поглощается, а при конденсации выделяется количество теплоты равное:
При парообразовании поглощается, а при конденсации выделяется количество теплоты равное:
При плавлении поглощается, а при кристаллизации выделяется количество теплоты равное:
При сгорании топлива выделяется количество теплоты равное:
Уравнение теплового баланса (ЗСЭ). Для замкнутой системы тел выполняется следующее (сумма отданных теплот равна сумме полученных):
Если все теплоты записывать с учетом знака, где «+» соответствует получению энергии телом, а «–» выделению, то данное уравнение можно записать в виде:
Работа идеального газа:
Если же давление газа меняется, то работу газа считают, как площадь фигуры под графиком в p–V координатах. Внутренняя энергия идеального одноатомного газа:
Изменение внутренней энергии рассчитывается по формуле:
Первый закон (первое начало) термодинамики (ЗСЭ):
Для различных изопроцессов можно выписать формулы по которым могут быть рассчитаны полученная теплота Q, изменение внутренней энергии ΔU и работа газа A. Изохорный процесс (V = const):
Изохорный процесс (V = const):
Изобарный процесс (p = const):
Изотермический процесс (T = const):
Адиабатный процесс (Q = 0):
КПД тепловой машины может быть рассчитан по формуле:
Где: Q1 – количество теплоты полученное рабочим телом за один цикл от нагревателя, Q2 – количество теплоты переданное рабочим телом за один цикл холодильнику. Работа совершенная тепловой машиной за один цикл:
Наибольший КПД при заданных температурах нагревателя T1 и холодильника T2, достигается если тепловая машина работает по циклу Карно. Этот КПД цикла Карно равен:
Абсолютная влажность рассчитывается как плотность водяных паров (из уравнения Клапейрона-Менделеева выражается отношение массы к объему и получается следующая формула):
Относительная влажность воздуха может быть рассчитана по следующим формулам:
Потенциальная энергия поверхности жидкости площадью S:
Сила поверхностного натяжения, действующая на участок границы жидкости длиной L:
Высота столба жидкости в капилляре:
При полном смачивании θ = 0°, cos θ = 1. В этом случае высота столба жидкости в капилляре станет равной:
В этом случае высота столба жидкости в капилляре станет равной:
При полном несмачивании θ = 180°, cos θ = –1 и, следовательно, h < 0. Уровень несмачивающей жидкости в капилляре опускается ниже уровня жидкости в сосуде, в которую опущен капилляр.
Электростатика
К оглавлению…
Электрический заряд может быть найден по формуле:
Линейная плотность заряда:
Поверхностная плотность заряда:
Объёмная плотность заряда:
Закон Кулона (сила электростатического взаимодействия двух электрических зарядов):
Где: k — некоторый постоянный электростатический коэффициент, который определяется следующим образом:
Напряжённость электрического поля находится по формуле (хотя чаще эту формулу используют для нахождения силы действующей на заряд в данном электрическом поле):
Принцип суперпозиции для электрических полей (результирующее электрическое поле равно векторной сумме электрических полей составляющих его):
Напряженность электрического поля, которую создает заряд Q на расстоянии r от своего центра:
Напряженность электрического поля, которую создает заряженная плоскость:
Потенциальная энергия взаимодействия двух электрических зарядов выражается формулой:
Электрическое напряжение это просто разность потенциалов, т. е. определение электрического напряжения может быть задано формулой:
е. определение электрического напряжения может быть задано формулой:
В однородном электрическом поле существует связь между напряженностью поля и напряжением:
Работа электрического поля может быть вычислена как разность начальной и конечной потенциальной энергии системы зарядов:
Работа электрического поля в общем случае может быть вычислена также и по одной из формул:
В однородном поле при перемещении заряда вдоль его силовых линий работа поля может быть также рассчитана по следующей формуле:
Определение потенциала задаётся выражением:
Потенциал, который создает точечный заряд или заряженная сфера:
Принцип суперпозиции для электрического потенциала (результирующий потенциал равен скалярной сумме потенциалов полей составляющих итоговое поле):
Для диэлектрической проницаемости вещества верно следующее:
Определение электрической ёмкости задаётся формулой:
Ёмкость плоского конденсатора:
Заряд конденсатора:
Напряжённость электрического поля внутри плоского конденсатора:
Сила притяжения пластин плоского конденсатора:
Энергия конденсатора (вообще говоря, это энергия электрического поля внутри конденсатора):
Объёмная плотность энергии электрического поля:
Электрический ток
К оглавлению. ..
..
Сила тока может быть найдена с помощью формулы:
Плотность тока:
Сопротивление проводника:
Зависимость сопротивления проводника от температуры задаётся следующей формулой:
Закон Ома (выражает зависимость силы тока от электрического напряжения и сопротивления):
Закономерности последовательного соединения:
Закономерности параллельного соединения:
Электродвижущая сила источника тока (ЭДС) определяется с помощью следующей формулы:
Закон Ома для полной цепи:
Падение напряжения во внешней цепи при этом равно (его еще называют напряжением на клеммах источника):
Сила тока короткого замыкания:
Работа электрического тока (закон Джоуля-Ленца). Работа А электрического тока протекающего по проводнику обладающему сопротивлением преобразуется в теплоту Q выделяющуюся на проводнике:
Мощность электрического тока:
Энергобаланс замкнутой цепи
Полезная мощность или мощность, выделяемая во внешней цепи:
Максимально возможная полезная мощность источника достигается, если R = r и равна:
Если при подключении к одному и тому же источнику тока разных сопротивлений R1 и R2 на них выделяются равные мощности то внутреннее сопротивление этого источника тока может быть найдено по формуле:
Мощность потерь или мощность внутри источника тока:
Полная мощность, развиваемая источником тока:
КПД источника тока:
Электролиз
Масса m вещества, выделившегося на электроде, прямо пропорциональна заряду Q, прошедшему через электролит:
Величину k называют электрохимическим эквивалентом. Он может быть рассчитан по формуле:
Он может быть рассчитан по формуле:
Где: n – валентность вещества, NA – постоянная Авогадро, M – молярная масса вещества, е – элементарный заряд. Иногда также вводят следующее обозначение для постоянной Фарадея:
Магнетизм
К оглавлению…
Сила Ампера, действующая на проводник с током помещённый в однородное магнитное поле, рассчитывается по формуле:
Момент сил действующих на рамку с током:
Сила Лоренца, действующая на заряженную частицу движущуюся в однородном магнитном поле, рассчитывается по формуле:
Радиус траектории полета заряженной частицы в магнитном поле:
Модуль индукции B магнитного поля прямолинейного проводника с током I на расстоянии R от него выражается соотношением:
Индукция поля в центре витка с током радиусом R:
Внутри соленоида длиной l и с количеством витков N создается однородное магнитное поле с индукцией:
Магнитная проницаемость вещества выражается следующим образом:
Магнитным потоком Φ через площадь S контура называют величину заданную формулой:
ЭДС индукции рассчитывается по формуле:
При движении проводника длиной l в магнитном поле B со скоростью v также возникает ЭДС индукции (проводник движется в направлении перпендикулярном самому себе):
Максимальное значение ЭДС индукции в контуре состоящем из N витков, площадью S, вращающемся с угловой скоростью ω в магнитном поле с индукцией В:
Индуктивность катушки:
Где: n — концентрация витков на единицу длины катушки:
Связь индуктивности катушки, силы тока протекающего через неё и собственного магнитного потока пронизывающего её, задаётся формулой:
ЭДС самоиндукции возникающая в катушке:
Энергия катушки (вообще говоря, это энергия магнитного поля внутри катушки):
Объемная плотность энергии магнитного поля:
Колебания
К оглавлению. ..
..
Уравнение описывающее физические системы способные совершать гармонические колебания с циклической частотой ω0:
Решение предыдущего уравнения является уравнением движения для гармонических колебаний и имеет вид:
Период колебаний вычисляется по формуле:
Частота колебаний:
Циклическая частота колебаний:
Зависимость скорости от времени при гармонических механических колебаниях выражается следующей формулой:
Максимальное значение скорости при гармонических механических колебаниях:
Зависимость ускорения от времени при гармонических механических колебаниях:
Максимальное значение ускорения при механических гармонических колебаниях:
Циклическая частота колебаний математического маятника рассчитывается по формуле:
Период колебаний математического маятника:
Циклическая частота колебаний пружинного маятника:
Период колебаний пружинного маятника:
Максимальное значение кинетической энергии при механических гармонических колебаниях задаётся формулой:
Максимальное значение потенциальной энергии при механических гармонических колебаниях пружинного маятника:
Взаимосвязь энергетических характеристик механического колебательного процесса:
Энергетические характеристики и их взаимосвязь при колебаниях в электрическом контуре:
Период гармонических колебаний в электрическом колебательном контуре определяется по формуле:
Циклическая частота колебаний в электрическом колебательном контуре:
Зависимость заряда на конденсаторе от времени при колебаниях в электрическом контуре описывается законом:
Зависимость электрического тока протекающего через катушку индуктивности от времени при колебаниях в электрическом контуре:
Зависимость напряжения на конденсаторе от времени при колебаниях в электрическом контуре:
Максимальное значение силы тока при гармонических колебаниях в электрическом контуре может быть рассчитано по формуле:
Максимальное значение напряжения на конденсаторе при гармонических колебаниях в электрическом контуре:
Переменный ток характеризуется действующими значениями силы тока и напряжения, которые связаны с амплитудными значениями соответствующих величин следующим образом. Действующее значение силы тока:
Действующее значение силы тока:
Действующее значение напряжения:
Мощность в цепи переменного тока:
Трансформатор
Если напряжение на входе в трансформатор равно U1, а на выходе U2, при этом число витков в первичной обмотке равно n1, а во вторичной n2, то выполняется следующее соотношение:
Коэффициент трансформации вычисляется по формуле:
Если трансформатор идеальный, то выполняется следующее соотношение (мощности на входе и выходе равны):
В неидеальном трансформаторе вводится понятие КПД:
Волны
Длина волны может быть рассчитана по формуле:
Разность фаз колебаний двух точек волны, расстояние между которыми l:
Скорость электромагнитной волны (в т.ч. света) в некоторой среде:
Скорость электромагнитной волны (в т.ч. света) в вакууме постоянна и равна с = 3∙108 м/с, она также может быть вычислена по формуле:
Скорости электромагнитной волны (в т. ч. света) в среде и в вакууме также связаны между собой формулой:
ч. света) в среде и в вакууме также связаны между собой формулой:
При этом показатель преломления некоторого вещества можно рассчитать используя формулу:
Оптика
К оглавлению…
Оптическая длина пути определяется формулой:
Оптическая разность хода двух лучей:
Условие интерференционного максимума:
Условие интерференционного минимума:
Формула дифракционной решетки:
Закон преломления света на границе двух прозрачных сред:
Постоянную величину n21 называют относительным показателем преломления второй среды относительно первой. Если n1 > n2, то возможно явление полного внутреннего отражения, при этом:
Формула тонкой линзы:
Линейным увеличением линзы Γ называют отношение линейных размеров изображения и предмета:
Атомная и ядерная физика
К оглавлению. ..
..
Энергия кванта электромагнитной волны (в т.ч. света) или, другими словами, энергия фотона вычисляется по формуле:
Импульс фотона:
Формула Эйнштейна для внешнего фотоэффекта (ЗСЭ):
Максимальная кинетическая энергия вылетающих электронов при фотоэффекте может быть выражена через величину задерживающего напряжение Uз и элементарный заряд е:
Существует граничная частота или длинна волны света (называемая красной границей фотоэффекта) такая, что свет с меньшей частотой или большей длиной волны не может вызвать фотоэффект. Эти значения связаны с величиной работы выхода следующим соотношением:
Второй постулат Бора или правило частот (ЗСЭ):
В атоме водорода выполняются следующие соотношения, связывающие радиус траектории вращающегося вокруг ядра электрона, его скорость и энергию на первой орбите с аналогичными характеристиками на остальных орбитах:
На любой орбите в атоме водорода кинетическая (К) и потенциальная (П) энергии электрона связаны с полной энергией (Е) следующими формулами:
Общее число нуклонов в ядре равно сумме числа протонов и нейтронов:
Дефект массы:
Энергия связи ядра выраженная в единицах СИ:
Энергия связи ядра выраженная в МэВ (где масса берется в атомных единицах):
Формула альфа-распада:
Формула бета-распада:
Закон радиоактивного распада:
Ядерные реакции
Для произвольной ядерной реакции описывающейся формулой вида:
Выполняются следующие условия:
Энергетический выход такой ядерной реакции при этом равен:
Основы специальной теории относительности (СТО)
К оглавлению. ..
..
Релятивистское сокращение длины:
Релятивистское удлинение времени события:
Релятивистский закон сложения скоростей. Если два тела движутся навстречу друг другу, то их скорость сближения:
Релятивистский закон сложения скоростей. Если же тела движутся в одном направлении, то их относительная скорость:
Энергия покоя тела:
Любое изменение энергии тела означает изменение массы тела и наоборот:
Полная энергия тела:
Полная энергия тела Е пропорциональна релятивистской массе и зависит от скорости движущегося тела, в этом смысле важны следующие соотношения:
Релятивистское увеличение массы:
Кинетическая энергия тела, движущегося с релятивистской скоростью:
Между полной энергией тела, энергией покоя и импульсом существует зависимость:
Равномерное движение по окружности
К оглавлению…
В качестве дополнения, в таблице ниже приводим всевозможные взаимосвязи между характеристиками тела равномерно вращающегося по окружности (T – период, N – количество оборотов, v – частота, R – радиус окружности, ω – угловая скорость, φ – угол поворота (в радианах), υ – линейная скорость тела, an – центростремительное ускорение, L – длина дуги окружности, t – время):
Расширенная PDF версия документа «Все главные формулы по школьной физике»:
К оглавлению. ..
..
Все формулы по физике — intmag24.ru
Все основные формулы по школьной физике, которые помогут для подготовке к ЕГЭ, а также для решения задач в 7, 8, 9, 10 и 11 классах. Все формулы структурированы, что позволит из запомнить гораздо быстрее.
| Равномерное движение | |
| S= U∙t, U= S/t, t=S/U | Уравнение движения при равномерном движении? где U-скорость, t-время, S-расстояние |
| x=x0+U0t | Координата при равномерном прямолинейном движении |
| Равномерное движение по окружности | |
| T=t/N, T=1/v, Т=2π/ω T=2πR/U, T=2π ∙√(R/a) | T – период N – количество оборотов |
| v=1/T, v=ω/2π, v=U/2πR, v=1/2π ∙√(a/R), v=N/t, v=L/t | v – частота R – радиус окружности |
| ω=2π/Т, ω=2πv, ω=φ/t ω=U/R, ω=√(a/R) | ω – угловая скорость t – время |
| υ=2πR/Т, υ=2πvR, U=ωR U=√(a/R), U=L/t | U – линейная скорость тела |
a=υ2/R, a=ω2R, a=Uω | a – центростремительное ускорение |
| L=φR | L – длина дуги окружности (φ – угол поворота (в радианах)) |
| Равноускоренное движение | |
| X=X0+υ0∙t+(a∙t2)/2 | Уравнение прямолинейного равноускоренного движения |
| S=U0t+a∙t2/2 S= (υ2-υ02) /2а S= (υ+υ0) ∙t /2 = Uср∙t | Расстояние при равноускоренном движении |
| υ=υ0+a∙t | Rонечная скорость тела при равноускоренном движении |
| a=(υ-υ 0)/t | Ускорение |
| U=√(2gh) tпадения=√(2h/g) S=U∙√(2h/g) | — Падение тела с высоты — Горизонтальный бросок (h-высота падения, g – ускорение свободного падения 9,8м/с2, t-время падения, S-расстояние) |
| hmax=U02/2g | Максимальная высота на которую поднимется тело, брошенное вертикально вверх с начальной скоростью U0 |
| tподъема=U0/g | Время подъема тела на максимальную высоту |
| tполета=2U0/g | Полное время полета (до возвращения в исходную точку) |
| Sторм=U02/2a | Тормозной путь тела двигавшегося до начала торможения со скоростью U0 , а затем тормозившего с ускорением а |
| U = √(U02+(gt)2) tgβ = Uy/Ux = gt/U0 | Полная скорость в произвольный момент времени при горизонтальном броске, и угол наклона скорости к горизонту |
| hmax=(U0∙sinα)2/2g tподъема=(U0∙sinα)/g | Бросок с земли на землю под углом к горизонту равным α. Время подъема до высшей точки и Время подъема до высшей точки имаксимальная высота |
Sx=Ux∙tполета | Полное время и дальность полета при броске под углом к горизонту |
| Импульс | |
p=mυ | Импульс тела |
Ft=∆p | Импульс силы |
F=∆p/∆t | Второй закон Ньютона в импульсной форме |
pk=pn | Закон сохранения импульса: в случае если на систему тел не действует внешних сил, либо действие внешних сил скомпенсировано (равнодействующая сила равна нолю), то изменение импульса равно нолю, что означает, что общий импульс системы сохраняется |
| Энергия | |
A=F∙S∙cosα | Механическая работа (F – сила, S – путь, – угол между направлением движения и силой) |
P=A/t=F∙υ | Мощность (если мощность переменная, то рассчитывается средняя мощность) |
Eп=mgh | Потенциальная энергия тела, поднятого над землей |
Eп=kx2/2 | Потенциальная энергия упруго деформированного тела |
η=Aп/Аз | Коэффициент полезного действия |
Ek=mυ2/2 | Кинетическая энергия тела |
| Молекулярная физика | |
ρ=m/V | Плотность (ρ – его плотность, m – масса вещества, V – объем) |
ν=N/ Na = m/M | Количество вещества (N – число частиц вещества, содержащееся в массе вещества m, Na – число Авогадро, m0 – масса одной молекулы вещества, M – молярная масса) |
М=m/ν | Молярная масса |
m0=m/N=M/Na | Масса одной молекулы вещества |
P=nkT=1/3nm0υ2 | Основное уравнение молекулярно-кинетической теории идеального газа (p – давление газа, n = N/V – концентрация его молекул, m0 – масса одной молекулы, Uкв – средняя квадратичная скорость) |
Uкв=√(3kT/m0), Uкв=√(3RT/M) | Cредняя квадратичная скорость |
Ek=3/2∙kT | Средняя кинетическая энергия поступательного движения одной молекулы (k – постоянная Больцмана, T – абсолютная температура) |
kNa=R | Связь универсальной газовой постоянной и постоянной Авогадро |
PV=m/M∙RT | Уравнение состояния идеального газа (уравнение Клапейрона-Менделеева) |
PV=const (m=const и T= const) | Газовые законы. Закон Бойля-Мариотта (изотермический процесс) Закон Бойля-Мариотта (изотермический процесс) |
V/T=const (m=const и p= const) | Газовые законы. Закон Гей-Люссака (изобарный процесс) |
P/T =const (m=const и V= const) | Газовые законы. Закон Шарля (изохорный процесс) |
PV/T=const (m=const ) | Газовые законы. Универсальный газовый закон (Клапейрона) |
V=Vo(1+λt) | Тепловое расширение газов описывается законом Гей-Люссака. (V – объем жидкости при 0 °С, V – при температуре t , λ – коэффициент объемного расширения жидкости) |
l=lo(1+αt) | Изменение линейных размеров, площади и объема тела (lo, So , Vo – соответственно длина, площадь поверхности и объем тела при 0 °С, α – коэффициент линейного расширения тела) |
| Динамика | |
Первый закон Ньютона | Существуют такие системы отсчёта, называемые инерциальными, относительно которых материальные точки, когда на них не действуют никакие силы (или действуют силы взаимно уравновешенные), находятся в состоянии покоя или равномерного прямолинейного движения |
F=ma | Второй закон Ньютона (F – сила, m – масса, а – ускорение). |
F1-2 = — F2-1 | Третий закон Ньютона (сила действия равна силе противодействия) |
Fупр = kx | Сила упругости (k – жесткость пружины, х – величина растяжения (или сжатия) пружины, оно равно разности между конечной и начальной длиной деформируемой пружины) |
Fy=-kx | Закон Гука |
Fтр.скольжения=Fтр.макс = μТ | Сила трения скольжения ( μ– коэффициент трения, N – сила реакции опоры.) |
F=mg | Сила тяжести — Закон Всемирного тяготения (G – гравитационная постоянная, F – сила с которой притягивается тело массой m к телу или планете массой M, r – расстояние между центрами этих тел) |
gh = GM/(Rn+h)2 = | Ускорение свободного падения на некоторой высоте от поверхности планеты (h – высота над поверхностью планеты) |
U = √(GM/(Rn+h)) | Скорость спутника на круговой орбите радиусом r = Rn + h |
U=√(gRn) | Первая космическая скорость (скорость движения спутника по орбите вблизи поверхности планеты) |
T12/T22 = R13/R23 | Закон Кеплера для периодов обращение T1 и T2 двух тел, вращающихся вокруг одного притягивающего центра на расстояниях R1 и R2 соответственно |
Р=m(g+a) | Вес тела, движущегося с ускорением а↑ |
| Термодинамика | |
Q=cm(T2-T1) | Количество теплоты (энергии) необходимое на нагревания некоторого тела (C-теплоемкость, c-удельная теплоемкость, m- масса, t- температура) |
Q=λm | Количество теплоты при плавлении (λ – удельная теплота плавления, m – масса расплавившегося тела или кристаллизовавшейся жидкости) |
Q=rm | Количество теплоты при парообразовании (r – удельная теплота парообразования, m – масса испарившейся жидкости или конденсировавшегося пара) |
Q=qm | Количество теплоты при сгорании топлива (q – удельная теплота сгорания топлива, m – масса сгоревшего топлива) |
A=P∙ΔV = m/M∙ R∙ΔT, p = const | Работа идеального газа |
U=3/2∙M/µ∙RT | Внутренняя энергия идеального одноатомного газа |
ΔU=A+Q | Первый закон (начало) термодинамики (ЗСЭ) (Q – теплота полученная (отданная) газом) |
η= (Q1 — Q2)/ Q1 | КПД тепловых двигателей |
η= (Т1 — Т2)/ Т1 | КПД идеальных двигателей (цикл Карно) |
ρ=pM/RT | Абсолютная влажность (ρ — абсолютная влажность, р – парциальное давление водяного пара, М – молярная масса, R – универсальная газовая постоянная, Т – абсолютная температура) |
φ=ρ/ρ0∙100% | Относительная влажность (ρ — абсолютная влажность, ρ0 -количество водяного пара, которое необходимо для насыщения 1 м3 воздуха при данной температуре) (P — давление водяного пара, Pо — давление насыщенного пара при данной температуре) |
Ep = σS | Поверхностное натяжение (σ – коэффициент поверхностного натяжения данной жидкости) |
Fн= σL | Сила поверхностного натяжения, действующая на участок границы жидкости длиной L |
| Статика и Гидростатика | |
M=F∙ℓ | Момент силы (F – сила, ℓ – плечо силы, т. е. кратчайшее расстояние между точкой опоры, относительно которой происходит вращение и линией действия силы) е. кратчайшее расстояние между точкой опоры, относительно которой происходит вращение и линией действия силы) |
Р=F/S | Давление (F – сила, S – площадь на которую распределено действие силы) |
P=ρ∙g∙h | Давление на глубине жидкости (p0 – атмосферное давление, ρ – плотность жидкости, g – ускорение свободного падения, h – высота столба жидкости) |
Fa=ρж∙g∙V | Закон (сила) Архимеда (V – объем погруженной части тела, который иногда также называют объемом вытесненной жидкости) |
| Электростатика | |
q = Ne | Электрический заряд (N – количество элементарных зарядов, е – элементарный заряд) |
λ=q/L, σ=q/S, ρ=q/V | Линейная, поверхностная и объемная плотность заряда |
F=k∙q1∙q2/R2 | Закон Кулона (сила электростатического взаимодействия двух зарядов величиной q1 и q2, находящихся на расстоянии r друг от друга в веществе с диэлектрической проницаемостью ε): |
E=1/(4πεε0) | Напряженность электрического поля, которую создает заряд Q на расстоянии r от своего центра |
E= σ/(2εε0) | Напряженность электрического поля, которую создает заряженная плоскость |
ε=E0/E | Диэлектрическая проницаемость |
E=F/q | Напряженность электрического поля |
E=k∙q/R2 | Напряженность электрического поля точечного заряда |
E=2πkσ | Напряженность электрического поля бесконечной плоскости |
W= k∙q1q2/R = k∙q1q2/εr | Потенциальная энергия взаимодействия двух электрических зарядов |
U=Ed, Δφ=E∙ Δl | Cвязь между напряженностью поля и напряжением |
A=qU, U=A/q | Работа электрического поля, Напряжение |
A= qEd, U=E∙d | Работа электрического поля в однородном поле при перемещении заряда вдоль его силовых линий, Напряжение для однородного электрического поля |
φ=W/q | Потенциал |
φ=k∙q/R | Потенциал точечного заряда |
C=q/U | Электроемкость |
C=S∙ε∙ε0/d | Электроемкость плоского конденсатора |
q=CU | Заряд конденсатора |
E = U/d = σ/εε0 | Напряженность поля внутри конденсатора |
F=qE/2 | Сила притяжения пластин конденсатора |
W=qU/2=q²/2С=CU²/2 | Энергия заряженного конденсатора |
| Электрический ток | |
I=q/t | Сила тока (q – заряд, протекший через некоторое поперечное сечение проводника за время t) |
R=ρ∙ℓ/S | Сопротивление проводника (l – длина проводника, S – площадь его поперечного сечения, ρ – удельное сопротивление материала проводника) |
R=R0(1+αt) | Сопротивление проводника |
I=U/R | Закон Ома для участка цепи (U – электрическое напряжение) |
I1=I2=I, U1+U2=U, R1+R2=R | Законы последовательного соединения |
U1=U2=U, I1+I2=I, 1/R1+1/R2=1/R | Законы параллельного соединения |
ε=Aст/q | Электродвижущая сила источника тока, ЭДС (Aст – работа сторонних сил по перемещению заряда q) |
I=ε/(R+r) | Закон Ома для полной цепи |
I=ε/r | Сила тока короткого замыкания (R=0) |
Q=A=I2Rt | Работа электрического тока (закон Джоуля-Ленца). Работа А электрического тока, протекающего по проводнику, обладающему сопротивлением преобразуется в теплоту Q выделяющуюся на проводнике Работа А электрического тока, протекающего по проводнику, обладающему сопротивлением преобразуется в теплоту Q выделяющуюся на проводнике |
P=IU=U2/R=I2R | Мощность электрического тока |
m = kQ = kIt | Электролиз. Масса m вещества, выделившегося на электроде, прямо пропорциональна заряду Q, прошедшему через электролит |
| Магнетизм | |
Fa=IBℓsinα | Сила Ампера (В – индукция магнитного поля, I – сила тока в проводнике, l – его длина, α – угол между направлением силы тока (т.е. самим проводником) и вектором индукции магнитного поля) |
M = NBIS∙sinα | Момент сил, действующих на рамку с током (N – количество витков, S – площадь рамки, α – угол между нормалью к рамке и вектором магнитной индукции) |
Fл=Bqυ∙sinα | Сила Лоренца (q – электрический заряд частицы, υ – её скорость, α – угол между направлением движения частицы и вектором индукции магнитного поля) |
R=mU/qB | Радиус траектории полета заряженной частицы в магнитном поле |
B=Fmax/ℓ∙I | Вектор магнитной индукции |
Ф=BSсos α Ф=LI | Магнитный поток Φ через площадь S |
Ei=ΔФ/Δt | Закон электромагнитной индукции |
Ei=Вℓυsinα | ЭДС индукции при движении проводника |
Esi=-L∙ΔI/Δt | ЭДС самоиндукции |
Wм=LI2/2 | Энергия магнитного поля катушки |
| Колебания | |
a+ω02x=0 | Уравнение описывает физические системы способные совершать гармонические колебания с циклической частотой ω0 |
x = A cos (ωt + φ0) | Уравнением движения для гармонических колебаний (x– координата тела в некоторый момент времени t, A – амплитуда колебаний, ω – циклическая частота колебаний, φ0 –начальная фаза колебаний). |
Х=Хmax∙cos ωt | Уравнение гармонических колебаний |
T=t/N, v=N/t=1/T | Связь некоторых характеристик колебательного процесса (T – период, N – количество полных колебаний, v – частота колебаний, ω – циклическая частота) |
υ = x'(t) = –Aω sin (ωt + φ0) | Скорость тела при колебательном движении |
υm = ωA | Максимальное (амплитудное) значение скорости |
a = υ'(t) = x»(t) | Ускорение тела при колебательном движении |
am = Aω2 | Максимальное (амплитудное) значение ускорения |
ω0=√(g/ℓ) | Циклическая частота и период колебаний математического маятника (l – длина маятника, g – ускорение свободного падения) |
ω0=√(k/m) | Циклическая частота и период колебаний пружинного маятника (m – масса груза, k – коэффициент жесткости пружины маятника) |
W=CU2/2+LI2/2 | Электрический контур |
T=2π ∙√LC | Период колебаний кол. контура и циклическая частота контура и циклическая частота |
Iд=I0/√2, Iд=Imax/√2 | Переменный ток характеризуется действующими значениями силы тока и напряжения, которые связаны с амплитудными значениями соответствующих величин; Действующее значение силы тока и напряжения |
P=UдIд =Iд2R=Uд2/R | Мощность в цепи переменного тока |
U1/U2=n1/n2 | Трансформатор: если напряжение на входе в трансформатор равно U1, а на выходе U2, при этом число витков в первичной обмотке равно n1, а во вторичной n2 |
λ= υТ=υ/v | Волны. Длина волны (υ – скорость распространения волны, T – период, v – частота) |
XL=ωL=2πLν | Индуктивное сопротивление |
Xc=1/ωC | Емкостное сопротивление |
Z=√(Xc-XL)2+R2 | Полное сопротивление |
| Оптика | |
Lопт=Ln | Оптическая длина пути (L – геометрическая длина траектории, по которой «идет» луч света, n – показатель преломление среды, в которой это происходит) |
x=mλL/d | Интерференционная схема Юнга (L – расстояние между экраном и плоскостью в которой расположены две щели, d – расстояние между этими щелями, λ – длина волны света, которым освещаются щели).  |
d∙sin φ=k λ | Формула дифракционной решетки (d – период решетки, или расстояние между соседними штрихами, φ – угол под которым наблюдается очередной дифракционный максимум, k – номер (порядок) максимума, λ – длина волны света, падающего на дифракционную решетку) |
n21=n2/n1= υ 1/ υ 2 | Закон преломления света на границе двух прозрачных сред (α – угол падения, β – угол преломления, n1 – показатель преломления первой среды, из которой падает луч, n2 – показатель преломления второй среды, в которую проникает луч) |
n21=sinα/sinβ | Показатель преломления |
1/F=1/d + 1/f | Формула линзы (d – расстояние от линзы до предмета, f – расстояние от линзы до изображения, F – фокусное расстояние, D – оптическая сила линзы) |
D=1/F | Оптическая сила линзы |
Δd=kλ, Δd=(2k+1)λ/2 | max интерференции, min интерференции |
| Атомная и ядерная физика | |
E=hv=hc/λ | Энергия кванта света, т. е. фотона (h – постоянная Планка, λ – длина волны света, v – частота света) е. фотона (h – постоянная Планка, λ – длина волны света, v – частота света) |
P=mc=h/ λ=Е/с | Импульс фотона |
hν=Aвых+(mU2/2)max | Формула Эйнштейна для внешнего фотоэффекта (ЗСЭ) (Авых – работа выхода, слагаемое в скобках –максимальная кинетическая энергия вылетающих электронов, v – частота падающего света) |
(mU2/2)max=еUз | Максимальная кинетическая энергия вылетающих электронов |
νк = Aвых/h | Красная граница фотоэффекта |
hνnm = |En – Em| | Второй постулат Бора (правило частот). При переходе атома из одного стационарного состояния с энергией En в другое стационарное состояние с энергией Em излучается или поглощается квант, энергия которого равна разности энергий стационарных состояний |
N=N0∙2—t/T | Закон радиоактивного распада |
ECB=(Zmp+Nmn-Mя)∙c2 | Энергия связи атомных ядер |
| Основы СТО | |
ℓ=ℓ0∙√1-υ2/c2 | Релятивистское сокращение длины. Длина тела, движущегося со скоростью V в инерциальной системе отсчета уменьшается в направлении движения до длины Длина тела, движущегося со скоростью V в инерциальной системе отсчета уменьшается в направлении движения до длины |
t=t1/√(1-υ2/c2) | Релятивистское удлинение времени события. Время, за которое происходит некоторое событие в движущейся системе отсчета с точки зрения наблюдателя из неподвижной системы отсчета |
υ=(υ1+υ2)/1+ υ1∙υ2/c2 | Релятивистский закон сложения скоростей |
Е = mс2 | Связь энергии и массы тела. Наименьшей энергией Е0 тело обладает в инерциальной системе отсчета относительно которой оно покоится и называется собственной энергией тела (энергия покоя тела) |
Наборы задач по круговому движению и гравитации
Наборы задач || Обзор физики || Устаревший набор задач
У нас есть 18 готовых наборов задач по теме Круговое движение и Гравитация. Эти наборы задач сосредоточены на использовании законов движения Ньютона и всемирного тяготения для математического анализа ситуаций, связанных с круговым движением или движением спутника.
Эти наборы задач сосредоточены на использовании законов движения Ньютона и всемирного тяготения для математического анализа ситуаций, связанных с круговым движением или движением спутника.
Щелкните ссылку, чтобы открыть набор задач.
Набор задач CG1: Линейная скорость
Используйте уравнение v = 2•π•R/T для определения скорости, радиуса или периода. Включает 4 задачи.
Набор задач CG2: Центростремительное ускорение 1
Используйте уравнения кругового движения, чтобы связать линейную скорость или центростремительное ускорение с радиусом окружности и периодом. Включает 7 задач.
Набор задач CG3: Центростремительное ускорение 2
Используйте уравнения кругового движения, чтобы связать линейную скорость или центростремительное ускорение со скоростью вращения. Включает 7 задач.
Набор задач CG4: Центростремительная сила
Используйте уравнения кругового движения, чтобы связать линейную скорость или центростремительное ускорение с центростремительной силой. Включает 5 задач.
Включает 5 задач.
Набор задач CG5: Круговое движение и анализ силы 1
Используйте уравнения кругового движения, анализ силы и второй закон Ньютона для анализа ситуаций с объектами, движущимися по вертикальным окружностям. Большинство проблем включают в себя строительные леса. Включает 7 задач.
Набор задач CG6: круговое движение и анализ силы 2
Используйте уравнения кругового движения, анализ силы и второй закон Ньютона для анализа ситуаций с объектами, движущимися по горизонтальным кругам. Включает 5 задач.
Набор задач CG7: Круговое движение и анализ силы 3
Используйте уравнения кругового движения, анализ силы и второй закон Ньютона для анализа ситуаций с объектами, движущимися по кругу. Включает 7 задач.
Набор задач CG8: круговое движение и анализ силы 4
Используйте уравнения кругового движения, анализ силы и второй закон Ньютона для анализа ситуаций с объектами, движущимися по кругу. Включает 7 задач.
Включает 7 задач.
Набор задач CG9: Гравитационная сила 1
Используйте закон всемирного тяготения Ньютона для расчета силы притяжения между двумя объектами с известной массой и расстоянием между ними. Включает 7 задач.
Набор задач CG10: Гравитационная сила 2
Используйте закон всемирного тяготения Ньютона для расчета силы притяжения между двумя объектами с известной массой и расстоянием между ними. Включает 5 задач.
Набор задач CG11: Гравитационная сила 3
Используйте закон всемирного тяготения Ньютона как инструмент пропорционального рассуждения и как инструмент решения проблем для некоторых сложных сценариев. Включает 4 задачи.
Набор задач CG12: Напряженность гравитационного поля
Используйте уравнение для напряженности гравитационного поля, чтобы вычислить значение g при различных условиях. Включает 6 задач.
Включает 6 задач.
Набор задач CG13: Орбитальная скорость
Используйте уравнение для орбитальной скорости, чтобы связать радиус орбиты, период обращения и массу центрального тела. Включает 8 задач.
Набор задач CG14: Орбитальное ускорение
Соотнесите орбитальный период и орбитальный радиус с орбитальным ускорением. Включает 6 задач.
Набор задач CG15: Математика движения спутников
Используйте уравнения орбитального движения, чтобы связать радиус орбиты, орбитальную скорость, период обращения и массу центрального тела. Включает 4 задачи.
Набор задач CG16: Третий закон Кеплера 1
Используйте третий закон Кеплера для анализа данных периода-орбитального радиуса, чтобы определить неизвестный период или радиус орбиты. Включает 4 задачи.
Включает 4 задачи.
Набор задач CG17: Третий закон Кеплера 2
Используйте третий закон Кеплера, чтобы связать период обращения, радиус обращения и массу центрального тела. Включает 7 задач.
Набор задач CG18: Третий закон Кеплера 1
Объедините третий закон Кеплера с навыками пропорционального рассуждения, чтобы определить неизвестный период или радиус орбиты. Включает 5 задач.
Математика кругового движения
Есть три математические величины, которые будут представлять для нас наибольший интерес при анализе движения объектов по кругу. Этими тремя величинами являются скорость, ускорение и сила. Скорость объекта, движущегося по окружности, определяется следующим уравнением.
Ускорение объекта, движущегося по кругу, можно определить с помощью любого из двух следующих уравнений.
Уравнение справа (выше) получено из уравнения слева заменой выражения для скорости.
Суммарная сила ( F net ), действующая на объект, движущийся по кругу, направлена внутрь. Хотя на объект может действовать более одной силы, векторная сумма всех их должна составлять результирующую силу. В общем, внутренняя сила больше, чем внешняя сила (если она есть), так что внешняя сила уравновешивается, а неуравновешенная сила направлена в центр круга. Суммарная сила связана с ускорением объекта (как всегда) и, таким образом, определяется следующими тремя уравнениями:0005
Уравнения в середине (вверху) и справа (вверху) получаются из уравнения слева заменой выражений для ускорения.
Этот набор уравнений кругового движения можно использовать двумя способами:
- как «рецепт» для решения алгебраических задач для решения неизвестной величины.
- как руководство к размышлению о том, как изменение одной величины повлияет на другую величину.

Эти два способа показаны ниже.
Уравнение выражает математическую связь между величинами, присутствующими в этом уравнении. Например, уравнение для второго закона Ньютона определяет, как ускорение связано с результирующей силой и массой объекта.
Связь, выраженная уравнением, заключается в том, что ускорение объекта прямо пропорционально действующей на него чистой силе. Другими словами, чем больше значение чистой силы, тем больше будет значение ускорения. По мере увеличения чистой силы ускорение увеличивается. На самом деле, если бы результирующая сила увеличилась в 2 раза, уравнение предсказало бы, что ускорение увеличилось бы в 2 раза. Точно так же, если бы результирующая сила уменьшилась в 2 раза, уравнение предсказало бы, что ускорение ускорение уменьшилось бы в 2,9 раза.0005
Уравнение второго закона Ньютона также раскрывает связь между ускорением и массой. Согласно уравнению, ускорение объекта обратно пропорционально массе объекта. Другими словами, чем больше значение массы, тем меньше значение ускорения. С увеличением массы ускорение уменьшается. На самом деле, если бы масса увеличилась в 2 раза, уравнение предсказало бы, что ускорение уменьшится в 2 раза. Точно так же, если бы масса уменьшилась в 2 раза, уравнение предсказало бы, что ускорение уменьшится. увеличить в 2,9 раза0005
Согласно уравнению, ускорение объекта обратно пропорционально массе объекта. Другими словами, чем больше значение массы, тем меньше значение ускорения. С увеличением массы ускорение уменьшается. На самом деле, если бы масса увеличилась в 2 раза, уравнение предсказало бы, что ускорение уменьшится в 2 раза. Точно так же, если бы масса уменьшилась в 2 раза, уравнение предсказало бы, что ускорение уменьшится. увеличить в 2,9 раза0005
Как упоминалось ранее, уравнения позволяют делать прогнозы о влиянии изменения одной величины на другую величину. Поскольку уравнение второго закона Ньютона показывает три величины, каждая из которых возведена в первую степень, предсказательная способность уравнения довольно проста. Предсказательная способность уравнения усложняется, когда одна из величин, входящих в уравнение, возводится в степень. Например, рассмотрим следующее уравнение, связывающее результирующую силу ( F net ) к скорости ( v ) объекта, движущегося в равномерном круговом движении.
Это уравнение показывает, что чистая сила, необходимая для движения объекта по кругу, прямо пропорциональна квадрату скорости объекта. Для постоянной массы и радиуса сеть F пропорциональна скорости 2 .
Коэффициент, на который изменяется результирующая сила, равен квадрату коэффициента, на который изменяется скорость. Следовательно, если скорость объекта удваивается, чистая сила, необходимая для кругового движения этого объекта, увеличивается в четыре раза. А если скорость объекта уменьшится вдвое (уменьшится в 2 раза), необходимая результирующая сила уменьшится в 4 раза.0005
Приведенные выше математические уравнения для движения объектов по окружности можно использовать для решения задач о движении по окружности, в которых необходимо определить неизвестную величину. Процесс решения задачи о круговом движении очень похож на любую другую задачу на уроках физики. Этот процесс включает в себя внимательное прочтение задачи, идентификацию известной и требуемой информации в переменной форме, выбор соответствующих уравнений, подстановку известных значений в уравнение и, наконец, алгебраические манипуляции с уравнением для определения отвечать. Рассмотрим применение этого процесса к следующим двум задачам о круговом движении.
Процесс решения задачи о круговом движении очень похож на любую другую задачу на уроках физики. Этот процесс включает в себя внимательное прочтение задачи, идентификацию известной и требуемой информации в переменной форме, выбор соответствующих уравнений, подстановку известных значений в уравнение и, наконец, алгебраические манипуляции с уравнением для определения отвечать. Рассмотрим применение этого процесса к следующим двум задачам о круговом движении.
Автомобиль массой 900 кг, движущийся со скоростью 10 м/с, совершает поворот по окружности радиусом 25,0 м. Определить ускорение и результирующую силу, действующую на автомобиль. |
Решение этой задачи начинается с идентификации известной и запрашиваемой информации.
Известная информация: м = 900 кг | Запрашиваемая информация: а = ???? |
Для определения ускорения автомобиля используйте уравнение a = v 2 / R. Решение выглядит следующим образом:
Решение выглядит следующим образом:
а = (10,0 м/с) 2 / (25,0 м)
а = (100 м 2 /с 2 ) / (25,0 м)
а = 4 м/с 2
Чтобы определить результирующую силу, действующую на автомобиль, используйте уравнение F net = m•a. Решение заключается в следующем.
F нетто = (900 кг) • (4 м/с 2 )
F нетто = 3600 Н
Полузащитник весом 95 кг делает разворот на футбольном поле. Полузащитник прокладывает путь, который представляет собой часть круга радиусом 12 метров. Полузащитник делает четверть оборота по кругу за 2,1 секунды. |
Решение этой задачи начинается с идентификации известной и запрашиваемой информации.
Известная информация: м = 95,0 кг | Запрашиваемая информация: v = ???? |
Чтобы определить скорость полузащитника, используйте уравнение v = d / t, где d — одна четвертая длины окружности, а время — 2,1 с. Решение следующее:
v = (0,25 • 2 • пи • R) / t
v = (0,25 • 2 • 3,14 • 12,0 м) / (2,1 с)
v = 8,97 м/с
Для определения ускорения полузащитника воспользуемся уравнением a = v 2 /R. Решение будет следующим:
Решение будет следующим:
а = (8,97 м/с) 2 / (12,0 м)
а = (80,5 м 2 /с 2 ) / (12,0 м)
а = 6,71 м/с 2
Чтобы определить результирующую силу, действующую на полузащитника, используйте уравнение F нетто = м•а. Решение заключается в следующем.
F нетто = (95,0 кг)*(6,71 м/с 2 )
F нетто = 637 Н
В уроке 2 этого модуля принципы кругового движения и приведенные выше математические уравнения будут объединены для объяснения и анализа различных реальных сценариев движения, включая аттракционы в парке развлечений и круговые движения в легкой атлетике.
Мы хотели бы предложить…
Иногда недостаточно просто прочитать об этом. Вы должны взаимодействовать с ним! И это именно то, что вы делаете, когда используете один из интерактивов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием либо нашего интерактивного равномерного кругового движения, либо нашего моделирования горизонтального круга. Вы можете найти их в разделе Physics Interactives на нашем сайте. Интерактивное приложение «Равномерное круговое движение» позволяет учащимся в интерактивном режиме исследовать взаимосвязь между скоростью, ускорением и силой для объекта, движущегося по кругу. Наше моделирование горизонтального круга моделирует движение трех разных объектов, движущихся по горизонтальному кругу, при этом анализируя влияние, которое изменения переменной могут оказать на движение.
Вы должны взаимодействовать с ним! И это именно то, что вы делаете, когда используете один из интерактивов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием либо нашего интерактивного равномерного кругового движения, либо нашего моделирования горизонтального круга. Вы можете найти их в разделе Physics Interactives на нашем сайте. Интерактивное приложение «Равномерное круговое движение» позволяет учащимся в интерактивном режиме исследовать взаимосвязь между скоростью, ускорением и силой для объекта, движущегося по кругу. Наше моделирование горизонтального круга моделирует движение трех разных объектов, движущихся по горизонтальному кругу, при этом анализируя влияние, которое изменения переменной могут оказать на движение.
Посетите: Интерактивное равномерное круговое движение || Моделирование горизонтального круга
1. Анна Литикал тренируется дома с демонстрацией центростремительной силы. Она наполняет ведро водой, привязывает его к прочной веревке и раскручивает по кругу. Анна крутит ведро, когда оно наполовину наполнено водой и когда оно на четверть. В каком случае требуется большее усилие, чтобы вращать ведро по кругу? Объясните, используя уравнение как «руководство к мышлению».
Она наполняет ведро водой, привязывает его к прочной веревке и раскручивает по кругу. Анна крутит ведро, когда оно наполовину наполнено водой и когда оно на четверть. В каком случае требуется большее усилие, чтобы вращать ведро по кругу? Объясните, используя уравнение как «руководство к мышлению».
2. Линкольн Континенталь и Юго делают поворот. Lincoln в четыре раза массивнее Yugo. Если они совершают поворот с одинаковой скоростью, то как соотносятся центростремительные силы, действующие на два автомобиля? Объяснять.
3. Cajun Cliffhanger в Great America – это аттракцион, в котором участники выстраиваются вдоль периметра цилиндра и вращаются по кругу с высокой скоростью. Когда цилиндр начинает вращаться очень быстро, пол убирается из-под ног гонщиков. Как влияет удвоение скорости на центростремительную силу? Объяснять.
4. Определить центростремительную силу, действующую на ребенка массой 40 кг, который делает 10 оборотов вокруг скалодрома за 29,3 секунды. Радиус ствола составляет 2,90 метра.
Определить центростремительную силу, действующую на ребенка массой 40 кг, который делает 10 оборотов вокруг скалодрома за 29,3 секунды. Радиус ствола составляет 2,90 метра.
Перейти к следующему уроку:
6.3 Центростремительная сила | University Physics Volume 1
Цели обучения
К концу раздела вы сможете:
- Объясните уравнение для центростремительного ускорения
- Применить второй закон Ньютона для получения уравнения центростремительной силы
- Использовать концепции кругового движения при решении задач, связанных с законами движения Ньютона
В книге «Движение в двух и трех измерениях» мы рассмотрели основные понятия кругового движения. Объект, совершающий круговое движение, например один из гоночных автомобилей, показанных в начале этой главы, должен ускоряться, потому что он меняет направление своей скорости. Мы доказали, что это центральное ускорение, называемое 9{2}. [/latex]
[/latex]
Угловая скорость показывает скорость, с которой объект вращается по кривой, в рад/с. Это ускорение действует по радиусу криволинейной траектории и поэтому также называется радиальным ускорением.
Ускорение должно создаваться силой. Любая сила или комбинация сил может вызвать центростремительное или радиальное ускорение. Вот лишь несколько примеров: натяжение веревки на тросовом шаре, сила земного притяжения на Луне, трение между роликовыми коньками и полом катка, сила наклона проезжей части, действующая на автомобиль, и силы на трубе вращающейся центрифуги. . Любая результирующая сила, вызывающая равномерное круговое движение, называется центростремительная сила . Направление центростремительной силы совпадает с направлением центростремительного ускорения к центру кривизны. Согласно второму закону движения Ньютона, результирующая сила равна массе, умноженной на ускорение: [латекс] {F}_{\text{net}}=ma. [/latex] Для равномерного кругового движения ускорение равно центростремительному ускорению: . [латекс] a={a}_{\text{c}}. [/latex] Таким образом, величина центростремительной силы [латекс] {F}_{\text{c}} [/латекс] равна 9{2}}{{F}_{\text{c}}}. [/latex]
[латекс] a={a}_{\text{c}}. [/latex] Таким образом, величина центростремительной силы [латекс] {F}_{\text{c}} [/латекс] равна 9{2}}{{F}_{\text{c}}}. [/latex]
Это означает, что для данной массы и скорости большая центростремительная сила вызывает малый радиус кривизны, то есть крутую кривую, как на (рис.).
Рисунок 6.20 Сила трения дополняет центростремительную силу и численно равна ей. Центростремительная сила перпендикулярна скорости и вызывает равномерное круговое движение. Чем больше [латекс] {F}_{\text{c}}, [/латекс], тем меньше радиус кривизны r и тем острее кривая. Вторая кривая имеет такое же значение v, но чем больше [латекс] {F}_{\text{c}} [/латекс], тем меньше r’.
Пример
Какой коэффициент трения необходим автомобилям на плоской кривой?
(a) Рассчитайте центростремительную силу, действующую на автомобиль массой 900,0 кг, который движется по кривой радиусом 500,0 м со скоростью 25,00 м/с. (b) Предполагая, что кривая не имеет наклона, найдите минимальный статический коэффициент трения между шинами и дорогой, причем статическое трение является причиной, удерживающей автомобиль от проскальзывания ((Рисунок)).
Рисунок 6.21 Этот автомобиль на ровном месте удаляется и поворачивает влево. Центростремительная сила, заставляющая автомобиль поворачивать по круговой траектории, возникает из-за трения между шинами и дорогой. Необходим минимальный коэффициент трения, иначе автомобиль будет двигаться по кривой с большим радиусом и сойдет с проезжей части. 9{2}}{(500.0\,\text{m})}=1125\,\text{N}\text{.} [/latex]
(Поскольку коэффициенты трения являются приблизительными, ответ дается только двумя цифрами. )
)
Значение
Коэффициент трения, показанный на (Рисунок)(b), намного меньше, чем обычно наблюдается между шинами и дорогами. Автомобиль все еще преодолевает кривую, если коэффициент больше 0,13, потому что статическое трение — это реактивная сила, способная принимать значение меньше, но не больше, чем [латекс] {\ mu } _ {\ text {s}} Н. [/latex] Более высокий коэффициент также позволит автомобилю проходить поворот на более высокой скорости, но если коэффициент трения меньше, безопасная скорость будет меньше 25 м/с. Обратите внимание, что масса отменяется, а это означает, что в этом примере не имеет значения, насколько сильно загружена машина для преодоления поворота. Масса компенсируется, потому что предполагается, что трение пропорционально нормальной силе, которая, в свою очередь, пропорциональна массе. Если бы поверхность дороги была наклонной, нормальная сила была бы меньше, как обсуждается далее.
Проверьте правильность понимания
Автомобиль, движущийся со скоростью 96,8 км/ч, движется по кривой окружности радиусом 182,9 м по ровной проселочной дороге. Каким должен быть минимальный коэффициент трения покоя, чтобы автомобиль не скользил?
Каким должен быть минимальный коэффициент трения покоя, чтобы автомобиль не скользил?
Показать решение
Кривые с виражами
Теперь рассмотрим кривых с виражами , где наклон дороги помогает вам преодолевать кривую ((Рисунок)). Чем больше угол [латекс]\тета[/латекс], тем быстрее вы сможете взять кривую. Например, гоночные трассы для велосипедов и автомобилей часто имеют крутые повороты. В «идеально наклонной кривой» угол [латекс]\тета[/латекс] таков, что вы можете двигаться по кривой на определенной скорости без помощи трения между шинами и дорогой. Мы выведем выражение для [латекс] \тета [/латекс] для идеально изогнутой кривой и рассмотрим пример, связанный с ним.
Рисунок 6.22 Автомобиль на этой кривой с наклоном удаляется и поворачивает влево.
Для идеального крена чистая внешняя сила равна горизонтальной центростремительной силе при отсутствии трения. Составляющие нормальной силы Н в горизонтальном и вертикальном направлениях должны быть равны центростремительной силе и весу автомобиля соответственно. {2}\text{/}r. [/latex] Поскольку это решающая сила, и она горизонтальна, мы используем систему координат с вертикальной и горизонтальной осями. Только нормальная сила имеет горизонтальную составляющую, поэтому она должна равняться центростремительной силе, то есть 9{2}}{р}. [/latex]
{2}\text{/}r. [/latex] Поскольку это решающая сила, и она горизонтальна, мы используем систему координат с вертикальной и горизонтальной осями. Только нормальная сила имеет горизонтальную составляющую, поэтому она должна равняться центростремительной силе, то есть 9{2}}{р}. [/latex]
Поскольку автомобиль не отрывается от поверхности дороги, результирующая вертикальная сила должна быть равна нулю, а это означает, что вертикальные составляющие двух внешних сил должны быть равны по величине и противоположны по направлению. Из (рис.) мы видим, что вертикальная составляющая нормальной силы равна [латекс] Н\,\текст{cos}\,\theta , [/латекс], а единственная другая вертикальная сила – это вес автомобиля. Они должны быть равны по величине; таким образом,
[латекс] N\,\text{cos}\,\theta = мг. [/латекс] 9{2}}{рг}). [/latex]
Это выражение можно понять, если рассмотреть, как [латекс] \тета [/латекс] зависит от v и r . Большой [латекс]\тета[/латекс] получается для большого v и маленького р. То есть дороги должны иметь крутой уклон для высоких скоростей и крутых поворотов. Трение помогает, потому что оно позволяет вам проходить кривую с большей или меньшей скоростью, чем если бы кривая была без трения. Обратите внимание, что [латекс]\тета[/латекс] не зависит от массы транспортного средства.
То есть дороги должны иметь крутой уклон для высоких скоростей и крутых поворотов. Трение помогает, потому что оно позволяет вам проходить кривую с большей или меньшей скоростью, чем если бы кривая была без трения. Обратите внимание, что [латекс]\тета[/латекс] не зависит от массы транспортного средства.
Пример
Какова идеальная скорость для крутого крутого поворота?
Кривые на некоторых тестовых трассах и гоночных трассах, таких как Daytona International Speedway во Флориде, очень крутые. Этот крен с помощью трения шин и очень стабильной конфигурации автомобиля позволяет проходить повороты на очень высокой скорости. Чтобы проиллюстрировать это, рассчитайте скорость, с которой следует двигаться по кривой радиусом 100,0 м с уклоном [latex] 31,0\text{°} [/latex], если бы на дороге не было трения. 9{2})(0,609)}=24,4\,\text{м/с}\text{.} [/latex]
Значимость
Это примерно 165 км/ч, что соответствует очень крутому склону и довольно резкий изгиб. Трение в шинах позволяет автомобилю проходить поворот на значительно более высоких скоростях.
Трение в шинах позволяет автомобилю проходить поворот на значительно более высоких скоростях.
Самолеты также совершают повороты по крену. Подъемная сила из-за силы воздуха, действующей на крыло, действует под прямым углом к крылу. Когда самолет кренится, пилот получает большую подъемную силу, чем необходимо для горизонтального полета. Вертикальная составляющая подъемной силы уравновешивает вес самолета, а горизонтальная составляющая ускоряет его. Угол крена, показанный на (Рисунке), определяется как [латекс] \тета [/латекс]. Мы анализируем силы так же, как рассматривали случай, когда автомобиль огибает кривую с креном.
Рисунок 6.23 В повороте с креном горизонтальная составляющая подъемной силы выходит из равновесия и ускоряет самолет. Нормальная составляющая подъемной силы уравновешивает вес самолета. Угол крена задается как [латекс] \тета [/латекс]. Сравните векторную диаграмму с представленной на (Рисунок).
Вместе с божьей коровкой исследуйте вращательное движение. Вращайте карусель, чтобы изменить ее угол или выбрать постоянную угловую скорость или угловое ускорение. Узнайте, как круговое движение связано с ошибкой xy — положение, скорость и ускорение с использованием векторов или графиков.
Вращайте карусель, чтобы изменить ее угол или выбрать постоянную угловую скорость или угловое ускорение. Узнайте, как круговое движение связано с ошибкой xy — положение, скорость и ускорение с использованием векторов или графиков.
Круговое движение требует силы, так называемой центростремительной силы, которая направлена к оси вращения. Эта упрощенная модель карусели демонстрирует эту силу.
Силы инерции и неинерциальные (ускоренные) системы отсчета: сила Кориолиса
Что имеют в виду взлет реактивного самолета, поворот на автомобиле, катание на карусели и круговое движение тропического циклона? общий? Каждая проявляет силы инерции — силы, которые просто кажутся возникающими из-за движения, потому что система отсчета наблюдателя ускоряется или вращается. Большинство людей согласятся, что при взлете в реактивном самолете вас как будто вдавливают обратно в сиденье, когда самолет ускоряется на взлетно-посадочной полосе. Однако физик сказал бы, что вы склонны оставаться неподвижными, в то время как сиденье толкает вас вперед. Еще более распространенный опыт возникает, когда вы делаете крутой поворот на своей машине, скажем, вправо ((Рисунок)). Вы чувствуете, как будто вас отбрасывает (то есть принудительно ) влево относительно автомобиля. Опять же, физик сказал бы, что вы едете по прямой (вспомните первый закон Ньютона), но машина движется вправо, а не то, что вы испытываете силу слева.
Еще более распространенный опыт возникает, когда вы делаете крутой поворот на своей машине, скажем, вправо ((Рисунок)). Вы чувствуете, как будто вас отбрасывает (то есть принудительно ) влево относительно автомобиля. Опять же, физик сказал бы, что вы едете по прямой (вспомните первый закон Ньютона), но машина движется вправо, а не то, что вы испытываете силу слева.
Рис. 6.24 (a) Водитель автомобиля чувствует себя вынужденным сместиться влево относительно автомобиля при повороте направо. Это сила инерции, возникающая из-за использования автомобиля в качестве системы отсчета. б) В земной системе отсчета водитель движется прямолинейно, подчиняясь первому закону Ньютона, а машина движется вправо. Слева на водителя относительно Земли силы нет. Вместо этого справа на автомобиль действует сила, заставляющая его поворачиваться.
Мы можем согласовать эти точки зрения, изучив используемые системы отсчета. Давайте сосредоточимся на людях в машине. Пассажиры инстинктивно используют автомобиль в качестве системы отсчета, тогда как физик может использовать Землю. Физик может сделать такой выбор, потому что Земля представляет собой почти инерциальную систему отсчета, в которой все силы имеют идентифицируемое физическое происхождение. В такой системе отсчета законы движения Ньютона принимают форму, данную в законах движения Ньютона. Машина неинерциальная система отсчета , потому что она ускоряется в сторону. Сила слева, воспринимаемая пассажирами автомобиля, представляет собой инерционную силу , не имеющую физического происхождения (она обусловлена исключительно инерцией пассажира, а не какой-либо физической причиной, такой как напряжение, трение или гравитация). Автомобиль, как и водитель, фактически ускоряется вправо. Эта сила инерции называется силой инерции, потому что она не имеет физического происхождения, такого как гравитация.
Пассажиры инстинктивно используют автомобиль в качестве системы отсчета, тогда как физик может использовать Землю. Физик может сделать такой выбор, потому что Земля представляет собой почти инерциальную систему отсчета, в которой все силы имеют идентифицируемое физическое происхождение. В такой системе отсчета законы движения Ньютона принимают форму, данную в законах движения Ньютона. Машина неинерциальная система отсчета , потому что она ускоряется в сторону. Сила слева, воспринимаемая пассажирами автомобиля, представляет собой инерционную силу , не имеющую физического происхождения (она обусловлена исключительно инерцией пассажира, а не какой-либо физической причиной, такой как напряжение, трение или гравитация). Автомобиль, как и водитель, фактически ускоряется вправо. Эта сила инерции называется силой инерции, потому что она не имеет физического происхождения, такого как гравитация.
Физик выберет любую систему отсчета, наиболее удобную для анализируемой ситуации. Для физика не проблема включить силы инерции и второй закон Ньютона, как обычно, если это удобнее, например, на карусели или на вращающейся планете. Неинерциальные (ускоренные) системы отсчета используются, когда это полезно. При обсуждении движения астронавта в космическом корабле, летящего со скоростями, близкими к скорости света, необходимо учитывать различные системы отсчета, как вы оцените при изучении специальной теории относительности.
Для физика не проблема включить силы инерции и второй закон Ньютона, как обычно, если это удобнее, например, на карусели или на вращающейся планете. Неинерциальные (ускоренные) системы отсчета используются, когда это полезно. При обсуждении движения астронавта в космическом корабле, летящего со скоростями, близкими к скорости света, необходимо учитывать различные системы отсчета, как вы оцените при изучении специальной теории относительности.
А теперь давайте мысленно прокатимся на карусели, а именно на быстро вращающейся игровой карусели ((Рисунок)). Вы принимаете карусель за систему отсчета, потому что вращаетесь вместе. При вращении в этой неинерциальной системе отсчета вы чувствуете силу инерции, которая стремится сбить вас с толку; это часто называют центробежной силой (не путать с центростремительной силой). Центробежная сила является широко используемым термином, но на самом деле его не существует. Вы должны крепко держаться, чтобы противодействовать своей инерции (которую люди часто называют центробежной силой). В земной системе отсчета нет силы, пытающейся сбросить вас; подчеркнем, что центробежная сила — фикция. Вы должны цепляться за то, чтобы заставить себя двигаться по кругу, потому что иначе вы пойдете по прямой, сразу же с карусели, в соответствии с первым законом Ньютона. Но сила, которую вы прикладываете, действует по направлению к центру круга.
В земной системе отсчета нет силы, пытающейся сбросить вас; подчеркнем, что центробежная сила — фикция. Вы должны цепляться за то, чтобы заставить себя двигаться по кругу, потому что иначе вы пойдете по прямой, сразу же с карусели, в соответствии с первым законом Ньютона. Но сила, которую вы прикладываете, действует по направлению к центру круга.
Рисунок 6.25 (a) Всадник на карусели чувствует, как будто его сбрасывают. Эту силу инерции иногда ошибочно называют центробежной силой, пытаясь объяснить движение всадника во вращающейся системе отсчета. б) В инерциальной системе отсчета и по законам Ньютона его увлекает инерция (у незаштрихованного всадника [латекс] {F}_{\text{net}}=0 [/латекс] и головы по прямой). Сила [латекс] {F} _ {\ text {центростремительная}} [/латекс] необходима, чтобы вызвать круговой путь.
Этот инерционный эффект, уносящий вас от центра вращения, если нет центростремительной силы, вызывающей круговое движение, хорошо используется в центрифугах ((Рисунок)). Как упоминалось ранее в этой главе, центрифуга очень быстро вращает образец. Если смотреть со стороны вращающейся системы отсчета, сила инерции выбрасывает частицы наружу, ускоряя их осаждение. Чем больше угловая скорость, тем больше центробежная сила. Но на самом деле происходит то, что инерция частиц несет их вдоль линии, касательной к окружности, в то время как пробирка движется по круговой траектории под действием центростремительной силы.
Как упоминалось ранее в этой главе, центрифуга очень быстро вращает образец. Если смотреть со стороны вращающейся системы отсчета, сила инерции выбрасывает частицы наружу, ускоряя их осаждение. Чем больше угловая скорость, тем больше центробежная сила. Но на самом деле происходит то, что инерция частиц несет их вдоль линии, касательной к окружности, в то время как пробирка движется по круговой траектории под действием центростремительной силы.
Рисунок 6.26 Центрифуги используют инерцию для выполнения своей задачи. Частицы в жидком осадке оседают, потому что их инерция уносит их от центра вращения. Большая угловая скорость центрифуги ускоряет седиментацию. В конечном итоге частицы вступают в контакт со стенками пробирки, которые затем создают центростремительную силу, необходимую для их движения по окружности постоянного радиуса.
Давайте теперь рассмотрим, что происходит, если что-то движется во вращающейся системе отсчета. Например, что, если вы сдвинете мяч прямо от центра карусели, как показано на (рис. )? Мяч движется по прямой относительно Земли (при условии пренебрежимо малого трения) и по кривой вправо на поверхности карусели. Человек, стоящий рядом с каруселью, видит, как мяч движется прямо, а карусель вращается под ним. В системе отсчета карусели мы объясняем кажущуюся кривую вправо с помощью силы инерции, называемой 9.0011 Сила Кориолиса , которая заставляет мяч искривляться вправо. Любой человек в этой системе отсчета может использовать силу Кориолиса, чтобы объяснить, почему объекты следуют кривым траекториям, и позволяет нам применять законы Ньютона в неинерциальных системах отсчета.
)? Мяч движется по прямой относительно Земли (при условии пренебрежимо малого трения) и по кривой вправо на поверхности карусели. Человек, стоящий рядом с каруселью, видит, как мяч движется прямо, а карусель вращается под ним. В системе отсчета карусели мы объясняем кажущуюся кривую вправо с помощью силы инерции, называемой 9.0011 Сила Кориолиса , которая заставляет мяч искривляться вправо. Любой человек в этой системе отсчета может использовать силу Кориолиса, чтобы объяснить, почему объекты следуют кривым траекториям, и позволяет нам применять законы Ньютона в неинерциальных системах отсчета.
Рисунок 6.27 Глядя вниз на вращение карусели против часовой стрелки, мы видим, что мяч, скользящий прямо к краю, следует по кривой вправо. Человек двигает мяч к точке B, начиная с точки A. Обе точки поворачиваются к заштрихованным позициям (A’ и B’), показанным во времени, когда мяч следует по кривой траектории во вращающейся системе отсчета и по прямой траектории в системе Земли. .
.
До сих пор мы считали Землю инерциальной системой отсчета, практически не беспокоясь о последствиях ее вращения. Однако такие эффекты существуют, например, при вращении погодных систем. Большинство последствий вращения Земли можно качественно понять по аналогии с каруселью. Если смотреть сверху на Северный полюс, Земля вращается против часовой стрелки, как и карусель на (рис.). Как и на карусели, любое движение в Северном полушарии Земли вызывает действие силы Кориолиса вправо. Как раз обратное происходит в Южном полушарии; там сила слева. Поскольку угловая скорость Земли невелика, сила Кориолиса обычно незначительна, но для крупномасштабных движений, таких как ветры, она оказывает существенное влияние.
Сила Кориолиса заставляет ураганы в северном полушарии вращаться против часовой стрелки, тогда как тропические циклоны в южном полушарии вращаются по часовой стрелке. (Термины ураган, тайфун и тропический шторм являются региональными названиями циклонов, представляющих собой штормовые системы, характеризующиеся центрами низкого давления, сильными ветрами и проливными дождями. ) (Рисунок) помогает показать, как происходят эти вращения. Воздух течет к любой области низкого давления, а тропические циклоны имеют особенно низкое давление. Таким образом, ветры направляются к центру тропического циклона или к погодной системе низкого давления на поверхности. В Северном полушарии эти внутренние ветры отклоняются вправо, как показано на рисунке, создавая циркуляцию против часовой стрелки на поверхности для зон низкого давления любого типа. Низкое давление у поверхности связано с восходящим воздухом, что также приводит к охлаждению и образованию облаков, что делает модели низкого давления хорошо видимыми из космоса. И наоборот, циркуляция ветра вокруг зон высокого давления в Южном полушарии происходит по часовой стрелке, но она менее заметна, поскольку высокое давление связано с опусканием воздуха, что приводит к чистому небу.
) (Рисунок) помогает показать, как происходят эти вращения. Воздух течет к любой области низкого давления, а тропические циклоны имеют особенно низкое давление. Таким образом, ветры направляются к центру тропического циклона или к погодной системе низкого давления на поверхности. В Северном полушарии эти внутренние ветры отклоняются вправо, как показано на рисунке, создавая циркуляцию против часовой стрелки на поверхности для зон низкого давления любого типа. Низкое давление у поверхности связано с восходящим воздухом, что также приводит к охлаждению и образованию облаков, что делает модели низкого давления хорошо видимыми из космоса. И наоборот, циркуляция ветра вокруг зон высокого давления в Южном полушарии происходит по часовой стрелке, но она менее заметна, поскольку высокое давление связано с опусканием воздуха, что приводит к чистому небу.
Рис. 6.28 (a) Вращение этого урагана в северном полушарии против часовой стрелки является основным следствием действия силы Кориолиса. (b) Без силы Кориолиса воздух попадал бы прямо в зону низкого давления, например, в тропических циклонах. (c) Сила Кориолиса отклоняет ветры вправо, вызывая вращение против часовой стрелки. (d) Ветер, идущий от зоны высокого давления, также отклоняется вправо, создавая вращение по часовой стрелке. (e) Противоположное направление вращения создается силой Кориолиса в Южном полушарии, что приводит к тропическим циклонам. (кредит a и кредит e: модификации работы НАСА)
(b) Без силы Кориолиса воздух попадал бы прямо в зону низкого давления, например, в тропических циклонах. (c) Сила Кориолиса отклоняет ветры вправо, вызывая вращение против часовой стрелки. (d) Ветер, идущий от зоны высокого давления, также отклоняется вправо, создавая вращение по часовой стрелке. (e) Противоположное направление вращения создается силой Кориолиса в Южном полушарии, что приводит к тропическим циклонам. (кредит a и кредит e: модификации работы НАСА)
Вращение тропических циклонов и движение шарика на карусели можно с таким же успехом объяснить инерцией и вращением системы под ними. Когда используются неинерциальные системы отсчета, необходимо изобрести силы инерции, такие как сила Кориолиса, чтобы объяснить кривую траекторию. Не существует идентифицируемого физического источника этих сил инерции. В инерциальной системе отсчета инерция объясняет траекторию, и ни одна сила не имеет идентифицируемого источника. Любая точка зрения позволяет нам описывать природу, но точка зрения в инерциальной системе отсчета является самой простой в том смысле, что все силы имеют происхождение и объяснения.
Резюме
Концептуальные вопросы
Если вы хотите уменьшить напряжение (которое связано с центростремительной силой) на высокоскоростных шинах, вы бы использовали шины большого или малого диаметра? Объяснять.
Дайте определение центростремительной силе. Может ли любой тип силы (например, напряжение, сила тяжести, трение и т. д.) быть центростремительной силой? Может ли любая комбинация сил быть центростремительной силой?
Показать решение
Если центростремительная сила направлена к центру, почему вы чувствуете, что вас «отбрасывает» от центра, когда автомобиль движется по кривой? Объяснять.
Гонщики обычно срезают углы, как показано ниже (Путь 2). Объясните, как это позволяет выполнять кривую с наибольшей скоростью.
Показать решение
Во многих парках развлечений есть аттракционы с вертикальными петлями, как показано ниже. В целях безопасности вагоны крепятся к рельсам таким образом, что они не могут упасть. Если автомобиль перевернется с нужной скоростью, центростремительная сила будет обеспечена только гравитацией. Какая другая сила действует и каково ее направление, если:
Если автомобиль перевернется с нужной скоростью, центростремительная сила будет обеспечена только гравитацией. Какая другая сила действует и каково ее направление, если:
(a) Автомобиль выходит из-под контроля на скорости, превышающей эту?
(b) Автомобиль переезжает через верх на скорости ниже этой?
Что приводит к удалению воды с одежды в центробежной сушилке?
Показать решение
Когда фигурист образует круг, какая сила отвечает за его поворот? Используйте диаграмму свободного тела в своем ответе.
Предположим, ребенок едет на карусели на расстоянии примерно посередине между ее центром и краем. У нее есть коробка для завтрака, покоящаяся на вощеной бумаге, так что между ней и каруселью очень мало трения. По какому пути, показанному ниже, пойдет коробка для завтрака, когда она отпустит ее? Ланч-бокс оставляет след в пыли на карусели. Эта тропа прямая, изогнутая влево или изогнутая вправо? Поясните свой ответ.
Показать решение
Чувствуете ли вы, что вас бросает в обе стороны, когда вы преодолеваете поворот, который идеально подходит для скорости вашего автомобиля? Как направлена сила, действующая на вас со стороны автокресла?
Предположим, что масса движется по круговой траектории на столе без трения, как показано ниже. В земной системе отсчета нет центробежной силы, оттягивающей массу от центра вращения, но есть сила, натягивающая веревку, прикрепляющую массу к гвоздю. Используя понятия, связанные с центростремительной силой и третьим законом Ньютона, объясните, какая сила растягивает струну, определяя ее физическое происхождение.
Показать решение
При смыве унитаза или сливе воды из раковины вода (и другой материал) начинает вращаться вокруг слива по пути вниз. Предполагая отсутствие начального вращения и поток, первоначально направленный прямо к стоку, объясните, чем вызвано вращение и какое направление оно имеет в Северном полушарии. (Обратите внимание, что это небольшой эффект, и в большинстве туалетов вращение вызвано направленными струями воды.) Изменится ли направление вращения, если вода будет нагнетаться в канализацию?
(Обратите внимание, что это небольшой эффект, и в большинстве туалетов вращение вызвано направленными струями воды.) Изменится ли направление вращения, если вода будет нагнетаться в канализацию?
Автомобиль поворачивает и натыкается на лед с очень низким коэффициентом кинетической фантастики. Автомобиль соскальзывает с дороги. Опишите путь автомобиля при выезде с дороги.
Показать решение
В одном из аттракционов в парке аттракционов участники входят в большую вертикальную бочку и встают у стены на ее горизонтальном полу. Ствол раскручивается, и пол падает. Всадники чувствуют, как будто они прижаты к стене силой, похожей на силу гравитации. Это сила инерции, ощущаемая и используемая гонщиками для объяснения событий во вращающейся системе отсчета ствола. Объясните в инерциальной системе отсчета (Земля почти один), что прижимает всадников к стене, и определите все силы, действующие на них. 9{2} [/латекс]. С кем вы согласны и почему?
Показать решение
Невращающаяся система отсчета, расположенная в центре Солнца, является почти инерциальной. Почему это не совсем инерциальная система отсчета?
Почему это не совсем инерциальная система отсчета?
Задачи
(a) Ребенок массой 22,0 кг катается на карусели на игровой площадке, которая вращается со скоростью 40,0 об/мин. Какая центростремительная сила действует, если он находится на расстоянии 1,25 м от его центра? б) Какая центростремительная сила действует, если карусель вращается со скоростью 3,00 об/мин и находится на расстоянии 8,00 м от ее центра? в) Сравните каждую силу с ее весом.
Показать решение
Рассчитайте центростремительную силу на конце лопасти ветровой турбины радиусом 100 м, вращающейся со скоростью 0,5 об/с. Предположим, что масса равна 4 кг.
Каков идеальный угол крена для плавного поворота радиусом 1,20 км на шоссе с ограничением скорости 105 км/ч (около 65 миль/ч) при условии, что все едут с ограничением?
Показать решение
Какова идеальная скорость для прохождения кривой радиусом 100,0 м с виражом под углом [latex] 20,0\text{°} [/latex]?
(a) Каков радиус бобслейного поворота с креном [латекс] 75,0\text{°} [/латекс] и скоростью 30,0 м/с при идеальном крене? б) Рассчитайте центростремительное ускорение. в) Вам кажется, что это ускорение велико?
в) Вам кажется, что это ускорение велико?
Показать решение
Частью езды на велосипеде является наклон под правильным углом при выполнении поворота, как показано ниже. Чтобы быть устойчивым, сила, действующая на землю, должна быть на линии, проходящей через центр тяжести. Силу, действующую на велосипедное колесо, можно разделить на две перпендикулярные составляющие: трение, параллельное дороге (которое должно обеспечивать центростремительную силу) и вертикальную нормальную силу (которая должна равняться весу системы). (a) Покажите, что [латекс] \тета [/латекс] (в соответствии с приведенным определением) связан со скоростью 9{2}\текст{/}рг). [/latex] (b) Рассчитайте [latex] \theta [/latex] для поворота со скоростью 12,0 м/с и радиусом 30,0 м (как в гонке).
Если автомобиль движется по виражу со скоростью ниже идеальной, необходимо трение, чтобы предотвратить скольжение внутрь поворота (проблема на обледенелых горных дорогах). (a) Рассчитайте идеальную скорость для прохождения кривой радиусом 100,0 м с уклоном [latex] 15,0\text{°} [/latex]. б) Каков минимальный коэффициент трения, необходимый для того, чтобы испуганный водитель мог пройти ту же кривую на скорости 20,0 км/ч?
(a) Рассчитайте идеальную скорость для прохождения кривой радиусом 100,0 м с уклоном [latex] 15,0\text{°} [/latex]. б) Каков минимальный коэффициент трения, необходимый для того, чтобы испуганный водитель мог пройти ту же кривую на скорости 20,0 км/ч?
Показать решение
Современные американские горки имеют вертикальные петли, как показано здесь. Радиус кривизны вверху меньше, чем по бокам, поэтому центростремительное ускорение вниз вверху будет больше, чем ускорение свободного падения, и пассажиры будут плотно прижаты к своим сиденьям. а) Какова скорость американских горок в верхней части петли, если радиус кривизны равен 15,0 м, а ускорение автомобиля вниз равно 1,50 г 9{3}\,\text{кг} [/латекс].
Ребенок массой 40,0 кг находится в вагоне американских горок, который движется по петле радиусом 7,00 м. В точке А скорость автомобиля 10,0 м/с, а в точке В скорость 10,5 м/с. Предположим, что ребенок не держится и не пристегнут ремнем безопасности. а) С какой силой автокресло действует на ребенка в точке А? б) Какова сила воздействия автокресла на ребенка в точке В? в) Какая минимальная скорость необходима, чтобы удержать ребенка на своем месте в точке А?
а) С какой силой автокресло действует на ребенка в точке А? б) Какова сила воздействия автокресла на ребенка в точке В? в) Какая минимальная скорость необходима, чтобы удержать ребенка на своем месте в точке А?
Автомобиль огибает кривую радиусом 65 м без обвала. Если коэффициент трения покоя между дорогой и автомобилем равен 0,70, какова максимальная скорость, с которой автомобиль проходит кривую без проскальзывания?
Показать решение
Автомобильная дорога с уклоном предназначена для движения транспорта со скоростью 90,0 км/ч. Радиус кривой 310 м. Какой угол наклона шоссе?
Глоссарий
- изогнутая кривая
- поворот на дороге с наклоном, который помогает транспортному средству преодолевать поворот
- центростремительная сила
- любая результирующая сила, вызывающая равномерное круговое движение
- Сила Кориолиса
- сила инерции, вызывающая кажущееся отклонение движущихся объектов, если смотреть на них во вращающейся системе отсчета
- идеальный банкинг
- наклон кривой на дороге, когда угол наклона позволяет транспортному средству преодолевать кривую на определенной скорости без помощи трения между шинами и дорогой; чистая внешняя сила, действующая на транспортное средство, равна горизонтальной центростремительной силе при отсутствии трения
- сила инерции
- сила, не имеющая физического происхождения
- неинерциальная система отсчета
- ускоренная система отсчета
6.
 2 Равномерное движение по окружности — физика
2 Равномерное движение по окружности — физикаРаздел Цели обучения
К концу этого раздела вы сможете делать следующее:
- Описывать центростремительное ускорение и связывать его с линейным ускорением
- Опишите центростремительную силу и свяжите ее с линейной силой
- Решение задач на центростремительное ускорение и центростремительную силу
Поддержка учителей
Поддержка учителей
Цели обучения в этом разделе помогут вашим учащимся освоить следующие стандарты:
- (4) Научные концепции. Учащийся знает и применяет законы, управляющие движением, в различных ситуациях. Ожидается, что студент:
- (C) анализировать и описывать ускоренное движение в двух измерениях, используя уравнения, включая примеры снарядов и окружностей.
- (D) рассчитать действие сил на объекты, включая закон инерции, связь между силой и ускорением и природу пар сил между объектами.

Кроме того, в Руководстве по физике для средней школы рассматривается содержание этого раздела лабораторной работы под названием «Круговое и вращательное движение», а также следующие стандарты:
- (4) Научные концепции. Учащийся знает и применяет законы, управляющие движением, в различных ситуациях. Ожидается, что студент:
- (C) анализировать и описывать ускоренное движение в двух измерениях, используя уравнения, включая примеры снарядов и окружностей.
Основные термины раздела
| центробежная сила | центростремительное ускорение | центростремительная сила | равномерное круговое движение |
Центростремительное ускорение
Поддержка учителей
Поддержка учителей
[BL][OL] Проверить равномерное круговое движение. Попросите учащихся привести примеры кругового движения. Просмотрите линейное ускорение.
Попросите учащихся привести примеры кругового движения. Просмотрите линейное ускорение.
В предыдущем разделе мы определили круговое движение. Простейшим случаем кругового движения является равномерное круговое движение, когда объект движется по круговому пути с постоянной скоростью . Обратите внимание, что, в отличие от скорости, линейная скорость объекта в круговом движении постоянно меняется, потому что он всегда меняет направление. Из кинематики мы знаем, что ускорение есть изменение скорости либо по величине, либо по направлению, либо по тому и другому. Следовательно, объект, совершающий равномерное круговое движение, всегда ускоряется, даже если величина его скорости постоянна.
Вы сами испытываете это ускорение каждый раз, когда едете в машине, когда она поворачивает за угол. Если вы держите руль неподвижно во время поворота и двигаетесь с постоянной скоростью, вы выполняете равномерное круговое движение. Что вы заметите, так это ощущение скольжения (или отбрасывания, в зависимости от скорости) от центра поворота. Это не реальная сила, действующая на вас — это происходит только потому, что ваше тело хочет продолжать движение по прямой линии (согласно первому закону Ньютона), в то время как автомобиль сворачивает с этой прямолинейной траектории. Внутри машины создается впечатление, что вас выталкивает из центра поворота. Эта фиктивная сила известна как центробежная сила. Чем круче кривая и чем больше ваша скорость, тем заметнее становится этот эффект.
Это не реальная сила, действующая на вас — это происходит только потому, что ваше тело хочет продолжать движение по прямой линии (согласно первому закону Ньютона), в то время как автомобиль сворачивает с этой прямолинейной траектории. Внутри машины создается впечатление, что вас выталкивает из центра поворота. Эта фиктивная сила известна как центробежная сила. Чем круче кривая и чем больше ваша скорость, тем заметнее становится этот эффект.
Поддержка учителей
Поддержка учителей
[BL][OL][AL] Продемонстрируйте круговое движение, привязав груз к веревке и вращая ее. Спросите учащихся, что произойдет, если вы внезапно перережете веревку? В каком направлении будет двигаться объект? Почему? Что это говорит о направлении ускорения? Попросите учащихся привести примеры случаев, когда они столкнулись с центростремительным ускорением.
На рис. 6.7 показан объект, движущийся по круговой траектории с постоянной скоростью. Направление мгновенной тангенциальной скорости показано в двух точках вдоль траектории. Ускорение направлено в сторону изменения скорости; в этом случае он указывает примерно на центр вращения. (Центр вращения находится в центре кругового пути). Если представить, что ΔsΔs становится все меньше и меньше, то ускорение будет равно точно к центру вращения, но этот случай сложно нарисовать. Мы называем ускорение объекта, движущегося в равномерном круговом движении, центростремительным ускорением a c , потому что центростремительное означает поиск центра .
Направление мгновенной тангенциальной скорости показано в двух точках вдоль траектории. Ускорение направлено в сторону изменения скорости; в этом случае он указывает примерно на центр вращения. (Центр вращения находится в центре кругового пути). Если представить, что ΔsΔs становится все меньше и меньше, то ускорение будет равно точно к центру вращения, но этот случай сложно нарисовать. Мы называем ускорение объекта, движущегося в равномерном круговом движении, центростремительным ускорением a c , потому что центростремительное означает поиск центра .
Рисунок
6.7
Показаны направления скорости объекта в двух разных точках, и видно, что изменение скорости ΔvΔv указывает примерно на центр кривизны (см. маленькую вставку). Для чрезвычайно малого значения ΔsΔs ΔvΔv указывает точно на центр круга (но это трудно нарисовать). Поскольку ac=Δv/Δtac=Δv/Δt, ускорение также направлено к центру, поэтому а в называется центростремительным ускорением.
Поддержка учителей
Поддержка учителей
См. рис. 6.7. На рисунке изображен объект, движущийся по круговой траектории с постоянной скоростью и направлением мгновенной скорости двух точек по траектории. Ускорение направлено в сторону изменения скорости и указывает на центр вращения. Это строго верно только тогда, когда ΔsΔs стремится к нулю.
Теперь, когда мы знаем, что направление центростремительного ускорения направлено к центру вращения, давайте обсудим величину центростремительного ускорения. Для объекта, движущегося со скоростью v по круговой траектории с радиусом r , модуль центростремительного ускорения равен
ac=v2r.ac=v2r.
Центростремительное ускорение больше на высоких скоростях и в крутых поворотах (меньший радиус), как вы, возможно, заметили, управляя автомобилем, потому что автомобиль фактически толкает вас к центру поворота. Но немного удивительно, что a c пропорционально квадрату скорости. Это означает, например, что ускорение в четыре раза больше при движении по кривой на скорости 100 км/ч, чем на скорости 50 км/ч.
Но немного удивительно, что a c пропорционально квадрату скорости. Это означает, например, что ускорение в четыре раза больше при движении по кривой на скорости 100 км/ч, чем на скорости 50 км/ч.
Мы также можем выразить a c через величину угловой скорости. Подставляя v=rωv=rω в приведенное выше уравнение, мы получаем ac=(rω)2r=rω2ac=(rω)2r=rω2 . Следовательно, величина центростремительного ускорения через величину угловой скорости равна
ac=rω2.ac=rω2.
6,9
Советы для успеха
Уравнение, выраженное в форме a c = rω 2 , полезно для решения задач, где вы знаете угловую скорость, а не тангенциальную скорость.
Виртуальная физика
Божья коровка в 2D
В этой симуляции вы экспериментируете с положением, скоростью и ускорением божьей коровки в круговом и эллиптическом движении. Переключите тип движения с линейного на круговой и наблюдайте за векторами скорости и ускорения. Затем попробуйте эллиптическое движение и обратите внимание, как векторы скорости и ускорения отличаются от векторов кругового движения.
Переключите тип движения с линейного на круговой и наблюдайте за векторами скорости и ускорения. Затем попробуйте эллиптическое движение и обратите внимание, как векторы скорости и ускорения отличаются от векторов кругового движения.
Проверка захвата
Каков угол между ускорением и скоростью при равномерном круговом движении? Какое ускорение испытывает тело при равномерном движении по окружности?
- Угол между ускорением и скоростью равен 0°, и тело испытывает линейное ускорение.
- Угол между ускорением и скоростью равен 0°, и тело испытывает центростремительное ускорение.
- Угол между ускорением и скоростью равен 90°, и тело испытывает линейное ускорение.
- Угол между ускорением и скоростью равен 90°, и тело испытывает центростремительное ускорение.
Центростремительная сила
Поддержка учителей
Поддержка учителей
[BL][OL][AL] Используя ту же демонстрацию, что и раньше, попросите учащихся предсказать отношения между величинами угловой скорости, центростремительного ускорения, массы и центростремительной силы. Предложите учащимся поэкспериментировать, используя веревки разной длины и разного веса.
Предложите учащимся поэкспериментировать, используя веревки разной длины и разного веса.
Поскольку объект, совершающий равномерное круговое движение, испытывает постоянное ускорение (за счет изменения направления), из второго закона Ньютона мы знаем, что на объект должна действовать постоянная результирующая внешняя сила.
Любая сила или комбинация сил может вызвать центростремительное ускорение. Всего несколько примеров: натяжение веревки на шаре, сила земного притяжения на Луне, трение между дорогой и шинами автомобиля при движении по кривой или нормальная сила американских горок. след на тележке во время петли.
Любая результирующая сила, вызывающая равномерное круговое движение, называется центростремительной силой. Центростремительная сила направлена к центру вращения, как и центростремительное ускорение. Согласно второму закону движения Ньютона, результирующая сила вызывает ускорение массы в соответствии с F нетто = м a . Для равномерного кругового движения ускорение равно центростремительному ускорению: a = a c . Следовательно, величина центростремительной силы F c равна Fc=macFc=mac .
Для равномерного кругового движения ускорение равно центростремительному ускорению: a = a c . Следовательно, величина центростремительной силы F c равна Fc=macFc=mac .
Используя две разные формы уравнения для величины центростремительного ускорения, ac=v2/rac=v2/r и ac=rω2ac=rω2, мы получаем два выражения, включающие величину центростремительной силы Ф с . Первое выражение в терминах тангенциальной скорости, второе в терминах угловой скорости: Fc=mv2rFc=mv2r и Fc=mrω2Fc=mrω2.
Обе формы уравнения зависят от массы, скорости и радиуса кругового пути. Вы можете использовать любое более удобное выражение для центростремительной силы. Второй закон Ньютона также гласит, что объект будет ускоряться в том же направлении, что и результирующая сила. По определению центростремительная сила направлена к центру вращения, поэтому объект также будет ускоряться по направлению к центру. Прямая линия, проведенная от кругового пути к центру круга, всегда будет перпендикулярна тангенциальной скорости. Обратите внимание, что если вы решите первое выражение для р , получается
Прямая линия, проведенная от кругового пути к центру круга, всегда будет перпендикулярна тангенциальной скорости. Обратите внимание, что если вы решите первое выражение для р , получается
r=mv2Fc.r=mv2Fc.
Из этого выражения мы видим, что при данной массе и скорости большая центростремительная сила вызывает малый радиус кривизны, то есть крутую кривую.
Рисунок
6,8
На этом рисунке сила трения ф служит центростремительной силой F c . Центростремительная сила перпендикулярна тангенциальной скорости и вызывает равномерное круговое движение. Чем больше центростремительная сила F c , тем меньше радиус кривизны r и тем острее кривая. Нижняя кривая имеет ту же скорость v , но большая центростремительная сила F c создает меньший радиус r′r′ .
Смотреть физику
Центростремительная сила и интуиция ускорения
В этом видео показано, почему центростремительная сила создает центростремительное ускорение и равномерное круговое движение. Он также охватывает разницу между скоростью и скоростью и показывает примеры равномерного кругового движения.
Поддержка учителей
Поддержка учителей
Предупреждение о заблуждении
Некоторые учащиеся могут путать центростремительную силу и центробежную силу. Центробежная сила — это не реальная сила, а результат ускоряющейся системы отсчета, такой как вращающаяся машина или вращающаяся Земля. Центробежная сила относится к вымышленному центру , убегающему от силы .
Представьте, что вы раскачиваете йойо по вертикали по часовой стрелке перед собой, перпендикулярно направлению взгляда. Если струна порвется, как только йо-йо достигнет крайнего нижнего положения, ближайшего к полу. Что будет с йойо после того, как порвется струна?
Если струна порвется, как только йо-йо достигнет крайнего нижнего положения, ближайшего к полу. Что будет с йойо после того, как порвется струна?
Йо-йо полетит внутрь в направлении действия центростремительной силы.
Йо-йо будет лететь наружу в направлении действия центростремительной силы.
Йо-йо полетит влево в направлении тангенциальной скорости.
Йо-йо полетит вправо в направлении тангенциальной скорости.
Решение задач центростремительного ускорения и центростремительной силы
Чтобы получить представление о типичных величинах центростремительного ускорения, мы проведем лабораторную работу, оценив центростремительное ускорение теннисной ракетки, а затем в нашем первом рабочем примере сравним центростремительное ускорение автомобиля, совершающего поворот, с ускорением свободного падения. Для второго рабочего примера мы рассчитаем силу, необходимую для поворота автомобиля по кривой.
Для второго рабочего примера мы рассчитаем силу, необходимую для поворота автомобиля по кривой.
Снап Лаборатория
Оценка центростремительного ускорения
В этом упражнении вы измерите замах клюшки для гольфа или теннисной ракетки, чтобы оценить центростремительное ускорение конца клюшки или ракетки. Вы можете сделать это в замедленном темпе. Напомним, что уравнение для центростремительного ускорения имеет вид ac=v2rac=v2r или ac=rω2ac=rω2.
- Одна теннисная ракетка или клюшка для гольфа
- Один таймер
- Одна линейка или рулетка
Процедура
- Работа с партнером. Стойте на безопасном расстоянии от партнера, когда он или она размахивает клюшкой для гольфа или теннисной ракеткой.
- Опишите движение качелей — это равномерное круговое движение? Почему или почему нет?
- Постарайтесь, чтобы качание было как можно ближе к равномерному круговому движению.
 Какие коррективы должен был внести ваш партнер?
Какие коррективы должен был внести ваш партнер? - Измерьте радиус кривизны. Что вы измеряли физически?
- Используя таймер, найдите либо линейную, либо угловую скорость, в зависимости от того, какое уравнение вы решите использовать.
- Каково приблизительное центростремительное ускорение на основе этих измерений? Как вы думаете, насколько они точны? Почему? Как вы и ваш партнер можете сделать эти измерения более точными?
Поддержка учителей
Поддержка учителей
Замах клюшки для гольфа или ракетки можно сделать очень близким к равномерному круговому движению. Для этого человек должен был бы перемещать его с постоянной скоростью, не сгибая руки. Длина руки плюс длина клюшки или ракетки – это радиус кривизны. Точность измерений угловой скорости и углового ускорения будет зависеть от разрешающей способности используемого таймера и ошибки человеческого наблюдения. Замах клюшки для гольфа или ракетки можно сделать очень близким к равномерному круговому движению. Для этого человек должен был бы перемещать его с постоянной скоростью, не сгибая руки. Длина руки плюс длина клюшки или ракетки – это радиус кривизны. Точность измерений угловой скорости и углового ускорения будет зависеть от разрешающей способности используемого таймера и ошибки человеческого наблюдения.
Для этого человек должен был бы перемещать его с постоянной скоростью, не сгибая руки. Длина руки плюс длина клюшки или ракетки – это радиус кривизны. Точность измерений угловой скорости и углового ускорения будет зависеть от разрешающей способности используемого таймера и ошибки человеческого наблюдения.
Проверка захвата
Было ли полезнее использовать уравнение ac=v2rac=v2r или ac=rω2ac=rω2 в этом упражнении? Почему?
- Должно быть проще использовать ac=rω2ac=rω2, потому что измерение угловой скорости путем наблюдения было бы проще.
- Должно быть проще использовать ac=v2rac=v2r, поскольку было бы проще измерить тангенциальную скорость посредством наблюдения.
- Должно быть проще использовать ac=rω2ac=rω2, потому что измерение угловой скорости путем наблюдения будет затруднено.
- Должно быть проще использовать ac=v2rac=v2r, потому что измерение тангенциальной скорости путем наблюдения будет затруднено.

Рабочий пример
Сравнение центростремительного ускорения автомобиля, огибающего кривую, с ускорением под действием силы тяжести
Автомобиль следует по кривой радиусом 500 м со скоростью 25,0 м/с (около 90 км/ч). Чему равно центростремительное ускорение автомобиля? Сравните центростремительное ускорение для этой довольно плавной кривой, снятой на скорости шоссе, с ускорением под действием силы тяжести ( г ).
Стратегия
Поскольку дана линейная, а не угловая скорость, наиболее удобно использовать выражение ac=v2rac=v2r для нахождения величины центростремительного ускорения.
Решение
Ввод данных значений v = 25,0 м/с и r = 500 м в выражение для a c дает
ac=v2r=(25,20 м/с) м/с2.ac=v2r=(25,0 м/с)2500 м=1,25 м/с2.
Обсуждение
Чтобы сравнить это с ускорением свободного падения ( г = 9,80 м/с 2 ), возьмем отношение ac/g=(1,25 м/с2)/(9,80 м/с2)=0,128ac/ g=(1,25 м/с2)/(9,80 м/с2)=0,128 . Следовательно, ac=0,128gac=0,128g, что означает, что центростремительное ускорение составляет примерно одну десятую ускорения свободного падения.
Следовательно, ac=0,128gac=0,128g, что означает, что центростремительное ускорение составляет примерно одну десятую ускорения свободного падения.
Рабочий пример
Сила трения на автомобильных шинах, огибающих кривую
- Рассчитайте центростремительную силу, действующую на автомобиль массой 900 кг, который движется по кривой радиусом 600 м на горизонтальной поверхности со скоростью 25,0 м/с.
- Статическое трение предотвращает скольжение автомобиля. Найдите величину силы трения между шинами и дорогой, которая позволяет автомобилю пройти поворот, не соскальзывая по прямой.
Стратегия и решение для (а)
Мы знаем, что Fc=mv2rFc=mv2r . Следовательно,
Fc=mv2r=(900кг)(25,0м/с)2600м=938Н.Fc=mv2r=(900кг)(25,0м/с)2600м=938Н.
Стратегия и решение для (б)
На изображении выше показаны силы, действующие на автомобиль при движении по кривой. На этой диаграмме автомобиль въезжает на страницу, как показано, и поворачивает налево. Трение действует влево, ускоряя автомобиль к центру кривой. Поскольку трение является единственной горизонтальной силой, действующей на автомобиль, в данном случае оно обеспечивает всю центростремительную силу. Следовательно, сила трения является центростремительной силой в этой ситуации и направлена к центру кривой.
На этой диаграмме автомобиль въезжает на страницу, как показано, и поворачивает налево. Трение действует влево, ускоряя автомобиль к центру кривой. Поскольку трение является единственной горизонтальной силой, действующей на автомобиль, в данном случае оно обеспечивает всю центростремительную силу. Следовательно, сила трения является центростремительной силой в этой ситуации и направлена к центру кривой.
f=Fc=938Nf=Fc=938N
Обсуждение
Так как мы нашли силу трения в части (b), мы могли также найти коэффициент трения, так как f=µsN=µsmgf=µsN=µsmg .
Практические задачи
9.
Какое центростремительное ускорение испытывают пассажиры автомобиля, движущегося со скоростью 12 м/с по кривой радиусом 2,0 м?
3 м/с 2
6 м/с 2
36 м/с 2
72 м/с 2
10.
Рассчитайте центростремительное ускорение объекта, следующего по пути с радиусом кривизны 0,2 м и с угловой скоростью 5 рад/с.
- 1 м/с
- 5 м/с
- 1 м/с 2
- 5 м/с 2
Проверьте свое понимание
11.
Что такое равномерное круговое движение?
Равномерное круговое движение — это когда объект ускоряется по круговой траектории с постоянно увеличивающейся скоростью.
Равномерное круговое движение — это когда объект движется по круговой траектории с переменным ускорением.
Равномерное круговое движение — это когда объект движется по круговой траектории с постоянной скоростью.

Равномерное круговое движение — это когда объект движется по круговой траектории с переменной скоростью.
12.
Что такое центростремительное ускорение?
- Ускорение объекта, движущегося по круговой траектории и направленного радиально к центру круговой орбиты
- Ускорение объекта, движущегося по круговой траектории и направленного по касательной по круговой траектории
- Ускорение объекта, движущегося по прямолинейному пути и направленного в направлении движения объекта
- Ускорение объекта, движущегося по прямолинейному пути и направленного в сторону, противоположную движению объекта
13.
Есть ли результирующая сила, действующая на объект при равномерном круговом движении?
Да, объект ускоряется, поэтому на него должна действовать результирующая сила.

Да потому что разгона нет.
Нет, потому что есть ускорение.
Нет, потому что нет ускорения.
14.
Приведите два примера сил, которые могут вызвать центростремительное ускорение.
- Сила притяжения Земли на Луну и нормальная сила
- Сила земного притяжения на Луне и натяжение веревки на орбитальном шаре
- Нормальная сила и сила трения, действующие на движущийся автомобиль
- Нормальная сила и натяжение веревки на шаре
Поддержка учителей
Поддержка учителей
Используйте вопросы «Проверьте свое понимание», чтобы оценить, справляются ли учащиеся с целями обучения этого раздела. Если учащиеся борются с определенной задачей, формирующее оценивание поможет определить, какая цель вызывает проблему, и направит учащихся к соответствующему содержанию.
Если учащиеся борются с определенной задачей, формирующее оценивание поможет определить, какая цель вызывает проблему, и направит учащихся к соответствующему содержанию.
6.3: Равномерное круговое движение — Physics LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 19400
- Howard Martin пересмотрено Аланом Нг
- University of Wisconsin-Madison
Как мы видели в главе 4, «равномерное круговое движение» определяется как движение по окружности с постоянной скоростью. Сейчас самое время вернуться к разделу 4.4, посвященному кинематике движения по окружности. В частности, для равномерного кругового движения объекта по окружности радиуса \(R\) следует вспомнить, что: 92/р\).
В частности, следует помнить, что даже если скорость постоянна, вектор ускорения всегда отличен от нуля при равномерном круговом движении, потому что скорость меняет направление 92/р\). Поскольку ускорение направлено к центру окружности, мы иногда называем его «радиальным» ускорением (параллельным радиусу), \(a_R\), или «центростремительным» ускорением (направленным к центру), \(a_c \).
Рассмотрим объект, совершающий равномерное круговое движение в горизонтальной плоскости на поверхности без трения, как показано на рисунке \(\PageIndex{1}\).
Рисунок \(\PageIndex{1}\): Объект, совершающий равномерное круговое движение по поверхности без трения, вид сверху. Единственный способ для объекта совершить равномерное круговое движение, как показано, — это если результирующая сила, действующая на объект, направлена к центру круга. Один из способов получить силу, направленную к центру круга, — это прикрепить веревку между центром круга и объектом, как показано на рисунке \(\PageIndex{1}\). Если струна натянута, сила натяжения всегда будет направлена к центру окружности. Таким образом, силы, действующие на объект, равны:
Один из способов получить силу, направленную к центру круга, — это прикрепить веревку между центром круга и объектом, как показано на рисунке \(\PageIndex{1}\). Если струна натянута, сила натяжения всегда будет направлена к центру окружности. Таким образом, силы, действующие на объект, равны:
- \(\vec F_g\), его вес с величиной \(мг\).
- \(\vec N\), нормальная сила, действующая на поверхность.
- \(\vec T\), сила натяжения струны.
Силы изображены на диаграмме свободного тела, показанной на рисунке \(\PageIndex{2}\) (вид сбоку), где мы также нарисовали вектор ускорения. Обратите внимание, что эта диаграмма свободного тела «действительна» только в определенный момент времени, поскольку вектор ускорения постоянно меняет направление и не всегда будет выровнен с осью \(x\).
Рисунок \(\PageIndex{2}\) совершает равномерное круговое движение. Запись компонентов \(x\) и \(y\) второго закона Ньютона: \[\begin{aligned} \sum F_x &= T = ma_R\\ \sum F_y &= N — F_g =0\end {aligned}\] Компонент \(y\) просто говорит нам, что нормальная сила должна иметь ту же величину, что и вес, потому что объект не ускоряется в вертикальном направлении. 2}{R}\\\end{aligned} \] Таким образом, мы находим, что натяжение нити увеличивается пропорционально квадрату скорости и уменьшается пропорционально радиусу окружности.
2}{R}\\\end{aligned} \] Таким образом, мы находим, что натяжение нити увеличивается пропорционально квадрату скорости и уменьшается пропорционально радиусу окружности.
Упражнение \(\PageIndex{1}\)
Рисунок \(\PageIndex{3}\): Возможные траектории (выделены красным), по которым будет следовать блок в случае разрыва строки.Объект совершает равномерное круговое движение в горизонтальной плоскости, когда внезапно обрывается нить, соединяющая объект с центром вращения. По какому пути пойдет блок после разрыва нити?
- А
- Б
- С
- Д
- Ответить
Пример \(\PageIndex{1}\)
Рисунок \(\PageIndex{4}\): Автомобиль движется по кривой, которую можно аппроксимировать дугой окружности радиусом \(R\). Автомобиль движется по кривой, которую можно аппроксимировать дугой окружности радиуса \(R\), как показано на рисунке \(\PageIndex{4}\). Коэффициент статического трения между шинами автомобиля и дорогой равен \(µ_{s}\). С какой максимальной скоростью автомобиль может пройти поворот без заноса?
Коэффициент статического трения между шинами автомобиля и дорогой равен \(µ_{s}\). С какой максимальной скоростью автомобиль может пройти поворот без заноса?
Решение :
Если автомобиль движется с постоянной скоростью по кругу, то сумма сил, действующих на автомобиль, должна быть направлена к центру круга. Единственная сила, действующая на автомобиль, которая может быть направлена к центру круга, — это сила трения между шинами и дорогой. Если бы дорога была идеально гладкой (представьте себе вождение в условиях гололеда), было бы невозможно объехать поворот, поскольку не было бы силы трения. Силы на автомобиль:
- \(\vec F_g\), его вес с величиной \(мг\).
- \(\vec N\), нормальная сила, действующая вверх со стороны дороги.
- \(\vec f_s\), сила трения покоя между шинами и дорогой. Это статическое трение, потому что поверхность шины не двигается относительно поверхности дороги, если автомобиль не буксует.
 2 &\ leq \ mu_s g R \\ \ поэтому v &\ leq \ sqrt {\ mu_s g R} \ end {align} \ ] Таким образом, если скорость меньше \(\sqrt{\mu_s g R}\), автомобиль не будет скользить и величина силы трения покоя, приводящая к ускорению по направлению к центру окружности, будет быть меньше или равно его максимально возможному значению.
2 &\ leq \ mu_s g R \\ \ поэтому v &\ leq \ sqrt {\ mu_s g R} \ end {align} \ ] Таким образом, если скорость меньше \(\sqrt{\mu_s g R}\), автомобиль не будет скользить и величина силы трения покоя, приводящая к ускорению по направлению к центру окружности, будет быть меньше или равно его максимально возможному значению.Обсуждение:
Модель максимальной скорости, с которой автомобиль может двигаться по кривой, имеет смысл, потому что:
- Размерность \(\sqrt{\mu_s g R}\) — это скорость.
- Скорость тем больше, чем больше радиус кривой (можно двигаться быстрее по более широкой кривой без заноса).
- Скорость тем больше, чем больше коэффициент трения (чем больше сила трения, тем больше может поддерживаться радиальное ускорение).
Пример \(\PageIndex{2}\)
Рисунок \(\PageIndex{6}\): Шарик, прикрепленный к веревке, совершает круговое движение в вертикальной плоскости.Шарик, прикрепленный к невесомой нити, совершает круговое движение по окружности радиусом \(R\), лежащей в вертикальной плоскости, как показано на рисунке \(\PageIndex{6}\).
 Может ли скорость мяча быть постоянной? Какова минимальная скорость мяча в верхней части круга, если он в состоянии сделать это вокруг круга?
Может ли скорость мяча быть постоянной? Какова минимальная скорость мяча в верхней части круга, если он в состоянии сделать это вокруг круга?Решение :
Силы, действующие на шар:
- \(\vec F_g\), его вес с величиной \(мг\).
- \(\vec T\), сила натяжения струны.
На рисунке \(\PageIndex{7}\) показана диаграмма свободного тела для сил, действующих на мяч в трех разных точках вдоль траектории окружности.
Рисунок \(\PageIndex{7}\): Шарик, прикрепленный к нити, совершает круговое движение в вертикальной плоскости.Для того чтобы мяч двигался по кругу, на мяче должна быть по крайней мере составляющая чистой силы, которая всегда направлена к центру круга. В нижней половине окружности (позиции 1 и 2) только натяжение может иметь составляющую, направленную к центру окружности.
Рассмотрим, в частности, положение, отмеченное цифрой 2, когда струна горизонтальна и натяжение равно \(\vec T_2\).
 Диаграмма свободного тела на рисунке \(\PageIndex{7}\) также показывает векторную сумму веса и напряжения в положении 2 (красная стрелка, обозначенная \(\sum \vec F\)), которая указывает вниз и к слева. Таким образом, очевидно, что вектор ускорения не может быть направлен к центру окружности, и ускорение будет иметь компоненты, которые являются как тангенциальными (\(a_T\)) к окружности, так и радиальными (\(a_R\)), как показано вектором \(\vec a_2\) на рисунке \(\PageIndex{7}\).
Диаграмма свободного тела на рисунке \(\PageIndex{7}\) также показывает векторную сумму веса и напряжения в положении 2 (красная стрелка, обозначенная \(\sum \vec F\)), которая указывает вниз и к слева. Таким образом, очевидно, что вектор ускорения не может быть направлен к центру окружности, и ускорение будет иметь компоненты, которые являются как тангенциальными (\(a_T\)) к окружности, так и радиальными (\(a_R\)), как показано вектором \(\vec a_2\) на рисунке \(\PageIndex{7}\).Радиальная составляющая ускорения изменит направление вектора скорости так, что мяч останется на окружности, а тангенциальная составляющая уменьшит величину вектора скорости. Таким образом, согласно нашей модели, мяч не может двигаться по окружности с постоянной скоростью, а скорость должна уменьшаться по мере перехода от положения 2 к положению 3, как бы ни тянули за нитку (вы можете убедиться в этом сами). это путем рисования диаграммы свободного тела в любой точке между точками 2 и 3).
Минимальная скорость мяча в верхней части круга определяется условием, что натяжение нити равно нулю только в верхней части траектории (позиция 3).
 2}{R}\\ \поэтому v_{min}&=\sqrt{\frac{gR}{m}}\end{aligned}\] — это минимальная скорость в верхней части траектории, при которой мяч может двигаться по кругу. Натяжение нити будет меняться по мере того, как мяч будет двигаться по кругу, и будет самым высоким в нижней части траектории, поскольку натяжение должно быть больше силы тяжести, чтобы результирующая сила в нижней части траектории была направлена вверх (к центр круга).
2}{R}\\ \поэтому v_{min}&=\sqrt{\frac{gR}{m}}\end{aligned}\] — это минимальная скорость в верхней части траектории, при которой мяч может двигаться по кругу. Натяжение нити будет меняться по мере того, как мяч будет двигаться по кругу, и будет самым высоким в нижней части траектории, поскольку натяжение должно быть больше силы тяжести, чтобы результирующая сила в нижней части траектории была направлена вверх (к центр круга).Обсуждение:
Модель минимальной скорости мяча в верхней части круга имеет смысл, потому что:
- \(\sqrt{\frac{gR}{m}}\) имеет размерность скорость.
- Минимальная скорость больше, если окружность имеет больший радиус (попробуйте это с грузом, прикрепленным к концу нити).
- Минимальная скорость тем больше, чем больше масса (опять же, попробуйте дома!).
Упражнение \(\PageIndex{2}\)
Рассмотрим мяч, прикрепленный к веревке, который вращается по вертикальному кругу (например, изображенному на рисунке \(\PageIndex{6}\)).
 Если вы укоротите нить, как изменится минимальная угловая скорость (измеренная в верхней части траектории), необходимая для того, чтобы мяч совершил движение по кругу?
Если вы укоротите нить, как изменится минимальная угловая скорость (измеренная в верхней части траектории), необходимая для того, чтобы мяч совершил движение по кругу?- Уменьшится
- Он останется прежним
- Это увеличит
- Ответить
Кривые с наклоном
Как мы видели в примере 6.3.1 , существует максимальная скорость, с которой автомобиль может пройти поворот, прежде чем он начнет скользить. Вы, наверное, заметили, что дороги, особенно автомагистрали, имеют крен там, где есть повороты. Гоночные трассы для автомобилей, которые движутся по овалу (скучный вид автомобильных гонок), также имеют виражи. Как мы увидим, это позволяет увеличить скорость транспортных средств при движении по кривой; или, скорее, делает повороты безопаснее, чем скорость, с которой транспортные средства бы салазки повыше. В примере 6.3.1 мы видели, что именно сила статического трения между шинами автомобиля и дорогой обеспечивала единственную силу с составляющей, направленной к центру круга.
 Идея использования кривой с наклоном состоит в том, чтобы изменить направление нормальной силы между дорогой и автомобильными шинами так, чтобы она тоже имела составляющую, направленную к центру круга.
Идея использования кривой с наклоном состоит в том, чтобы изменить направление нормальной силы между дорогой и автомобильными шинами так, чтобы она тоже имела составляющую, направленную к центру круга.Рассмотрим автомобиль, изображенный на рисунке \(\PageIndex{8}\), который, если смотреть сзади, совершает левый поворот по кривой, наклоненной под углом \(\theta\) к горизонтали и поддающейся моделированию как дуга из окружности радиуса \(R\).
Рисунок \(\PageIndex{8}\): Автомобиль, въезжающий на страницу и объезжающий вираж, поворачивает влево (центр круга находится слева).Силы, воздействующие на автомобиль, такие же, как и в Пример 6.3.1 , за исключением того, что они направлены в разные стороны. Силы равны:
- \(\vec F_g\), его вес с величиной \(мг\).
- \(\vec N\), нормальная сила, действующая на дорогу перпендикулярно поверхности дороги.
- \(\vec f_s\), сила трения покоя между шинами и дорогой. Это статическое трение, потому что поверхность шины не двигается относительно поверхности дороги, если автомобиль не буксует.
 Сила трения покоя имеет величину не более \(f_s\leq\mu_sN\) и перпендикулярна нормальной силе. Сила может быть направлена либо вверх, либо вниз, , в зависимости от других сил, действующих на автомобиль .
Сила трения покоя имеет величину не более \(f_s\leq\mu_sN\) и перпендикулярна нормальной силе. Сила может быть направлена либо вверх, либо вниз, , в зависимости от других сил, действующих на автомобиль .
Диаграмма свободного тела для сил, действующих на автомобиль, показана на рис. 6.3.9., а также ускорение (которое находится в радиальном направлении, к центру круга) и наш выбор системы координат (выбор \(x\) параллельно ускорению). Направление силы трения покоя неизвестно априори и зависит от скорости автомобиля:
- Если скорость автомобиля равна нулю, сила трения покоя направлена вверх. При нулевой скорости радиальное ускорение равно нулю, и поэтому сумма сил должна быть равна нулю. Препятствующим движению автомобиля будет скольжение по кривой с наклоном (точно так же, как блок на наклонной поверхности).
- Если скорость автомобиля очень велика, сила трения покоя направлена вниз, так как препятствующее движению автомобиля движение будет скользить вверх по берегу.
 Естественным движением автомобиля является прямолинейное движение (первый закон Ньютона). Если компоненты нормальной силы и силы трения покоя, направленные к центру круга, слишком малы, чтобы позволить машине повернуться, то машина будет скользить вверх по берегу (таким образом, препятствующее движение будет движением вверх по берегу, а сила трения покоя направлена вниз).
Естественным движением автомобиля является прямолинейное движение (первый закон Ньютона). Если компоненты нормальной силы и силы трения покоя, направленные к центру круга, слишком малы, чтобы позволить машине повернуться, то машина будет скользить вверх по берегу (таким образом, препятствующее движение будет движением вверх по берегу, а сила трения покоя направлена вниз).
Таким образом, существует «идеальная скорость» при в котором сила трения покоя точно равна нулю, а составляющая \(х\) нормальной силы отвечает за радиальное ускорение. На более высоких скоростях сила трения покоя направлена вниз и увеличивается по величине, чтобы удерживать ускорение автомобиля по направлению к центру круга. При некоторой максимальной скорости сила трения достигнет своего максимального значения и больше не сможет удерживать ускорение автомобиля, направленное к центру круга.
 На скоростях ниже идеальной сила трения направлена вверх, чтобы предотвратить скольжение автомобиля по берегу. Если коэффициент статического трения слишком низкий, возможно, что на низких скоростях автомобиль начнет скользить по берегу (поэтому будет минимальная скорость, ниже которой автомобиль начнет скользить вниз). 92}{gR}\\ \therefore v_{ideal} &=\sqrt{gR\tan\theta}\end{aligned}\] При этой скорости сила трения покоя равна нулю. На практике можно использовать это уравнение, чтобы определить, какой угол крена использовать при проектировании дороги, чтобы идеальная скорость была около ограничения скорости или средней скорости движения. Мы оставляем в качестве упражнения определение максимальной скорости, с которой автомобиль может двигаться по кривой, прежде чем выскользнуть из нее.
На скоростях ниже идеальной сила трения направлена вверх, чтобы предотвратить скольжение автомобиля по берегу. Если коэффициент статического трения слишком низкий, возможно, что на низких скоростях автомобиль начнет скользить по берегу (поэтому будет минимальная скорость, ниже которой автомобиль начнет скользить вниз). 92}{gR}\\ \therefore v_{ideal} &=\sqrt{gR\tan\theta}\end{aligned}\] При этой скорости сила трения покоя равна нулю. На практике можно использовать это уравнение, чтобы определить, какой угол крена использовать при проектировании дороги, чтобы идеальная скорость была около ограничения скорости или средней скорости движения. Мы оставляем в качестве упражнения определение максимальной скорости, с которой автомобиль может двигаться по кривой, прежде чем выскользнуть из нее.Силы инерции при круговом движении
Когда вы сидите в машине, которая движется по кривой, вы почувствуете, что вас толкает наружу, в сторону от центра круга, по которому движется машина.
 Это происходит из-за вашей инерции (Первый закон Ньютона), и ваше тело двигалось бы по прямой линии, если бы машина не оказывала на вас суммарной силы по направлению к центру круга. Вы не столько ощущаете силу, толкающую вас наружу, сколько эффект от автомобильного кресла, толкающего вас внутрь; если бы вы прислонились к стороне автомобиля, которая находится снаружи кривой, вы бы почувствовали, как сторона автомобиля толкает вас внутрь к центру кривой, даже если «чувствуется», что вы толкаете наружу против поворота. сторона автомобиля.
Это происходит из-за вашей инерции (Первый закон Ньютона), и ваше тело двигалось бы по прямой линии, если бы машина не оказывала на вас суммарной силы по направлению к центру круга. Вы не столько ощущаете силу, толкающую вас наружу, сколько эффект от автомобильного кресла, толкающего вас внутрь; если бы вы прислонились к стороне автомобиля, которая находится снаружи кривой, вы бы почувствовали, как сторона автомобиля толкает вас внутрь к центру кривой, даже если «чувствуется», что вы толкаете наружу против поворота. сторона автомобиля.Если мы смоделируем ваше движение, глядя на вас с земли, мы включим силу трения между автомобильным сиденьем (или боковой частью автомобиля, или обоими) и вами, которая указывает на центр круга, так что сумма сил, действующих на вас, направлена к центру круга. Мы также можем смоделировать ваше движение по неинерциальной раме автомобиля. Как вы помните, поскольку это неинерциальная система отсчета, нам нужно включить дополнительную инерционную силу, \(\vec F_I\), которая указывает направление, противоположное ускорению автомобиля, с величиной \(F_I=ma_R\ ) (если чистое ускорение автомобиля равно \(a_R\)).
 2}{R} &= 0\end{ выровнены}\] что, конечно, математически точно эквивалентно. Сила инерции не является реальной силой в том смысле, что на нее ничто не действует. Это вступает в игру только потому, что мы пытаемся использовать законы Ньютона в неинерциальной системе отсчета. Тем не менее, он обеспечивает хорошую модель для описания ощущения, которое мы испытываем, когда автомобиль выталкивает наружу, когда машина проходит поворот. Иногда люди называют эту силу «центробежной» силой, что означает «сила, направленная от центра». Однако вы должны помнить, что это не реальная сила, действующая на объект, а результат моделирования движения в неинерциальной системе отсчета.
2}{R} &= 0\end{ выровнены}\] что, конечно, математически точно эквивалентно. Сила инерции не является реальной силой в том смысле, что на нее ничто не действует. Это вступает в игру только потому, что мы пытаемся использовать законы Ньютона в неинерциальной системе отсчета. Тем не менее, он обеспечивает хорошую модель для описания ощущения, которое мы испытываем, когда автомобиль выталкивает наружу, когда машина проходит поворот. Иногда люди называют эту силу «центробежной» силой, что означает «сила, направленная от центра». Однако вы должны помнить, что это не реальная сила, действующая на объект, а результат моделирования движения в неинерциальной системе отсчета.Упражнение \(\PageIndex{3}\)
Джейми едет на своем трехколесном велосипеде вокруг круглого пруда. Джейми чувствует центробежную силу с величиной \(F_I\). Если Джейми будет крутить педали в два раза быстрее, какой будет величина центробежной силы, которую он будет испытывать?
- \(\sqrt{2}F_I\)
- \(\frac{1}{2}F_I\)
- \(2F_I\)
- \(4F_I\)
- Ответить
Сноски
1.
 Сумма сил часто называется «чистой силой», действующей на объект, а в конкретном случае равномерного кругового движения эту результирующую силу иногда называют «центростремительной силой», однако это не сила. сама по себе, и это всегда сумма сил, направленных к центру круга.
Сумма сил часто называется «чистой силой», действующей на объект, а в конкретном случае равномерного кругового движения эту результирующую силу иногда называют «центростремительной силой», однако это не сила. сама по себе, и это всегда сумма сил, направленных к центру круга.Эта страница под названием 6.3: Равномерное круговое движение распространяется под лицензией CC BY-SA, автором, ремиксом и/или куратором выступил Ховард Мартин, редактируемый Аланом Нг.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- Райан Мартин и др.
- Лицензия
- CC BY-SA
- Показать оглавление
- нет
- Теги

Калькулятор центростремительной силы
Автор Wojciech Sas, кандидат наук
Отзыв Стивена Вудинга
Последнее обновление: 06 августа 2021 г.
Содержание:- Что такое центростремительная сила? Уравнение центростремительной силы
- Единицы измерения центростремительной силы
- Центростремительная и центробежная силы. В чем разница между центростремительным и центробежным?
- Как найти центростремительную силу с помощью калькулятора центростремительной силы?
- Центростремительная сила и принцип сохранения энергии
- Часто задаваемые вопросы
Добро пожаловать в калькулятор центростремительной силы. Этот простой в использовании инструмент поможет вам найти ответы на самые распространенные и интригующие вопросы о центростремительной силе . Задумывались ли вы когда-нибудь:
- Что такое центростремительная сила?
- Как рассчитать центростремительную силу?
- Как найти центростремительную силу, действующую на тело, движущееся по окружности?
- Центростремительная сила и центробежная сила — в чем разница?
Если да, то это правильное место для начала! Давайте вместе прочитаем статью, чтобы узнать об определении центростремительной силы и единицах измерения центростремительной силы.
 Вы также можете найти пару примеров центростремительной силы для самостоятельного расчета .
Вы также можете найти пару примеров центростремительной силы для самостоятельного расчета .Что такое центростремительная сила? Уравнение центростремительной силы
Книжное определение центростремительной силы говорит нам, что это сила, действующая на любой объект, который движется по криволинейной траектории. Направление силы всегда параллельно радиусу кривизны
r.Обычно мы имеем дело с примерами центростремительной силы, когда говорим о круговом движении . Это самый простой тип нелинейного движения. В этом случае радиус кривизны, естественно, равен радиусу окружности.
Формулу центростремительной силы можно записать так:
F = m * v² / r,где:
-
F— центростремительная сила; -
m– масса объекта; -
v— его скорость; и -
r– радиус кривизны (окружности).
Согласно второму закону Ньютона,
a = v² / r— это формула центростремительного ускорения.Взгляните на диаграмму центростремительной силы, чтобы понять, что такое определение центростремительной силы:
Мы также можем переписать уравнение центростремительной силы, заменив скорость угловой скоростью
ω:F = m * ω² * r.Единицы измерения центростремительной силы
Поскольку центростремительная сила — это сила, она имеет точно такие же единицы измерения, как и другие силы в физике . Итак, , что такое единица центростремительной силы?
- Единицей центростремительной силы в системе СИ является Ньютон,
N ; - Британской единицей центростремительной силы является фунтал,
pdl; - Английской инженерной единицей центростремительной силы является фунт-сила,
lbf; - Единицей центростремительной силы в СГС является дина,
dy.
Однако вам не нужно беспокоиться о преобразовании единиц силы при использовании нашего калькулятора центростремительной силы. Вы можете изменить их автоматически одним щелчком мыши!
Аналогично, единицей центростремительного ускорения является
м/с².Центростремительная и центробежная сила. В чем разница между центростремительным и центробежным?
На первый взгляд может показаться, что между центростремительной и центробежной силой нет никакой разницы, так как формула центробежной силы точно такая же, как уравнение для центростремительной :
F = m * v² / r.Решающим фактором, который помогает нам различить эти два числа с помощью , является система отсчета . Представьте круговое движение, например, ребенок на карусели:
В инерциальной системе отсчета (родитель наблюдает за ребенком на расстоянии), присутствует только одна сила, изменяющая направление движения — центростремительная сила;
В неинерциальной системе отсчета (точка зрения ребенка), существуют две соответствующие силы одинаковых величин, которые уравновешивают друг друга .
 Еще раз, есть центростремительная сила, действующая к центру вращения. Вторая — центробежная сила — представитель силы инерции.
Еще раз, есть центростремительная сила, действующая к центру вращения. Вторая — центробежная сила — представитель силы инерции.
Как видите, центростремительная сила присутствует в обеих системах отсчета, а центробежная проявляется только в неинерциальной.
Не всегда очевидно, имеем ли мы дело с инерциальной или неинерциальной системой отсчета. Как отличить их? Давайте посмотрим на две диаграммы со сравнением центростремительной и центробежной силы:
Как найти центростремительную силу с помощью калькулятора центростремительной силы?
Имея в виду теорию, давайте попробуем решить несколько примеров центростремительной силы.
Как рассчитать центростремительную силу, действующую на автомобиль, движущийся по круговой трассе? Масса автомобиля
2 т, скорость45 км/ч, радиус пути10 м:- Прежде чем приступить к вычислениям, переведем массу в килограммы и поменяем единицы измерения скорости с
км/чнам/с.
2 т = 2000 кг,45 км/ч = 12,5 м/с; - Примените уравнение центростремительной силы,
F = m * v² / r = 2000 * (12,5)² / 10 = 31 250 Н; - Мы также можем записать решение, используя экспоненциальную запись,
F = 3,125*10⁴ Нили с соответствующим суффиксом,F = 31,25 кН.
- Прежде чем приступить к вычислениям, переведем массу в килограммы и поменяем единицы измерения скорости с
Найдем скорость объекта, который движется по окружности радиусом
r = 5 футов, когда центростремительная сила равна3,6 пдл. Его масса2 фунта:- Измените формулу центростремительной силы, чтобы получить квадрат скорости. Для этого умножьте обе части уравнения на
rи разделите наm; -
v² = F * r / m = 3,6 * 5 / 2 = 9; - Извлеките квадратный корень из предыдущего результата, чтобы получить скорость,
v = √9 = 3 фут/с; - Мы также можем переписать результат с другой единицей измерения.
 Скорость равна
Скорость равна 0,914 м/спосле округления до трех значащих цифр.
- Измените формулу центростремительной силы, чтобы получить квадрат скорости. Для этого умножьте обе части уравнения на
Всякий раз, когда вы заблудились или просто хотите проверить результаты, не стесняйтесь использовать наш калькулятор центростремительной силы. Выполняется точно так же, как и в этих примерах центростремительной силы, так что вы можете вычислить любую из переменных уравнения центростремительной силы !
Центростремительная сила и принцип сохранения энергии
Мы также можем переписать определение центростремительной силы так, чтобы направление силы всегда перпендикулярно движению .
Теперь вспомним определение произведения:
W = F · s.Если угол между перемещением
sи силойFравен90°, то работа равна нулю, и, следовательно, никакая дополнительная энергия не поступает и не выходит из системы . Каковы последствия?
Каковы последствия?Если на объект действует только центростремительная сила, полная энергия системы сохраняется . Одними из самых известных примеров такого рода являются планетные системы. Вот почему планеты веками обращаются вокруг Солнца по стабильным орбитам.
Часто задаваемые вопросы
Как рассчитать центростремительную силу?
Чтобы рассчитать центростремительную силу для тела, движущегося в круговом движении , необходимо:
- Найти квадрат его линейной скорости ,
v². - Умножить это значение по его массе ,
м. - Разделить всего на радиус окружности ,
r.
В чем разница между центростремительной и центробежной силой?
Центростремительная сила заставляет объект двигаться по криволинейной траектории, и она указывает на центр вращения .
 Центробежная сила — это кажущаяся сила , ощущаемая телом, движущимся по криволинейной траектории, и она точек вне кривизны .
Центробежная сила — это кажущаяся сила , ощущаемая телом, движущимся по криволинейной траектории, и она точек вне кривизны .Как центростремительная сила влияет на круговое движение?
Центростремительная сила перпендикулярна скорости и меняет свое направление, не меняя своей величины . Если это единственная сила, действующая на объект, это приводит к равномерному круговому движению .
Что вызывает центростремительную силу?
В зависимости от ситуации в качестве центростремительной силы могут выступать разные силы:
- Гравитационная сила — для Луны или спутников, вращающихся вокруг Земли;
- Трение — для автомобиля или конькобежца, совершающего поворот;
- Натяжение — для шарика на резьбе;
- Контактная сила — для человека на американских горках или в самолете.

Какая сила вызывает центростремительное движение Земли?
Гравитационное притяжение вызывает центростремительное движение Земли. Земля движется вокруг Солнца из-за гравитационной силы, притягивающей эти два тела. Центростремительная сила указывает на Солнце, которое изменяет направление скорости Земли и приводит к эллиптическому движению .
Какая связь между центростремительной силой и массой?
Центростремительная сила пропорциональна массе . Удвоение массы удваивает центростремительную силу. Точно так же деление массы на коэффициент десять уменьшает центростремительную силу в десять раз.
Почему для кругового движения необходима центростремительная сила?
Чтобы двигаться по кругу, нам нужно приложить центростремительную силу, которая изменяет направление скорости . В противном случае, согласно первому закону Ньютона, объект двигался бы прямолинейно с постоянной скоростью, если бы не было результирующей силы .


 8.
Системы отсчета
8.
Системы отсчета 7·1010 Бк.
7·1010 Бк.
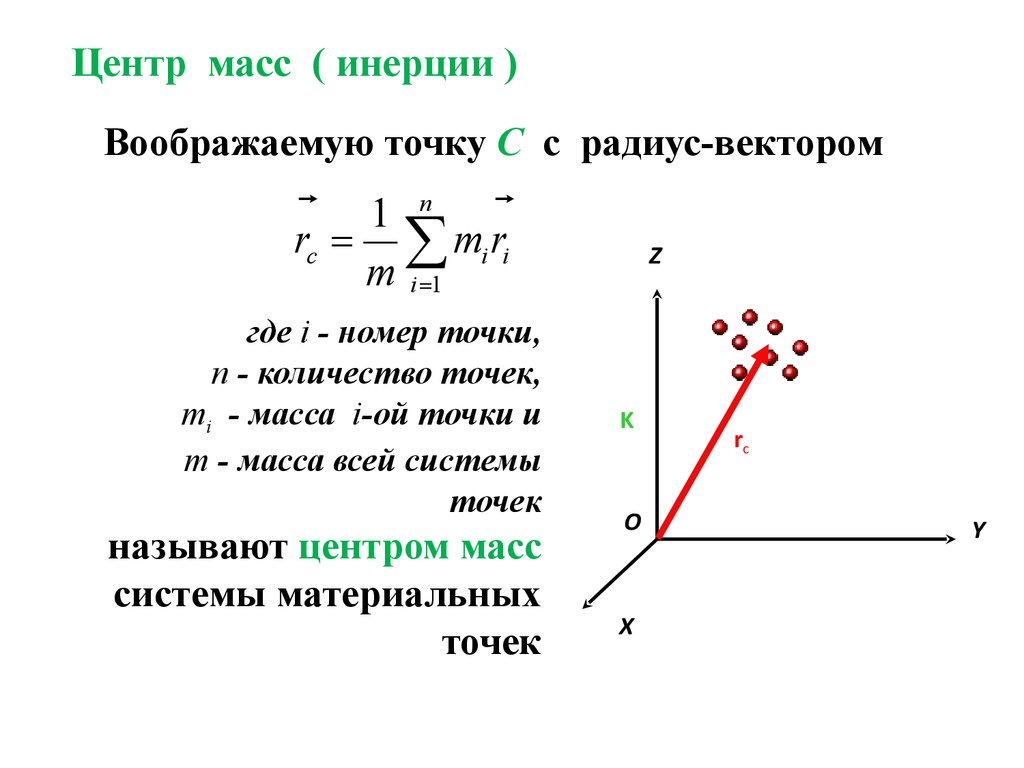 30)
30)