Как решать методом замены переменных систему уравнений: 503 Service Temporarily Unavailable

Презентация «СИСТЕМЫ УРАВНЕНИЙ С ДВУМЯ ПЕРЕМЕННЫМИ»

Материал опубликовала

#11 класс #Алгебра #Учебно-методические материалы #Презентация #Учитель-предметник #Школьное образование

СИСТЕМЫ УРАВНЕНИЙ С ДВУМЯ ПЕРЕМЕННЫМИ Методы решения МБОУ «Гимназия № 94» Московского района г. Казани Учитель Владимирова Р.В.

Решением системы уравнений с двумя переменными называется пара значений переменных (x;y), обращающая каждое уравнение системы в верное равенство. Решением системы уравнений с двумя переменными называется пара значений переменных (x;y), обращающая каждое уравнение системы в верное равенство. Решить систему уравнений – значит найти все её решения или доказать, что решений нет.

Системы уравнений Графический способ Аналитический способ Метод подстановки Метод сложения Метод замены пере менной

Метод подстановки Выразить из какого-нибудь уравнения системы одну переменную через другую.

Подставить в другое уравнение системы вместо этой переменной полученное выражение. Решить получившееся уравнение с одной переменной. Найти соответствующее значение второй переменной.

Умножьте почленно уравнения системы, подбирая множители так, чтобы коэффициенты при одной из переменных стали противоположными числами. Умножьте почленно уравнения системы, подбирая множители так, чтобы коэффициенты при одной из переменных стали противоположными числами. Сложите почленно левые и правые части уравнений системы. Решите получившееся уравнение с одной переменной. Найдите соответствующее значение второй переменной. Метод сложения

Построить график функции, заданной первым уравнением системы. Построить график функции, заданной первым уравнением системы. Построить график функции, заданной вторым уравнением системы. Определить координаты точек пересечения графиков функций. Графический метод

Замени одно или два выражения в уравнениях системы новыми переменными так, чтобы вновь полученные уравнения стали более простыми. Замени одно или два выражения в уравнениях системы новыми переменными так, чтобы вновь полученные уравнения стали более простыми. Реши полученную систему уравнений методом, наиболее подходящим для этой системы уравнений. Сделай обратную замену, для того, чтобы найти значения первоначальных переменных. Запиши ответ в виде пар значений (x,y), которые были найдены на третьем шаге. Введение новой переменной

Задание 1 a) x²=-y²-3xy-1, б) x²+y²+3xy =-1, в) x²+y²+3xy =-1, x+2y= 0; 2y=-x; x=-2y. x²+y²+3xy =-1, x+2y= 0; Какой из учеников применил метод подстановки наиболее рационально? Метод подстановки

x²-2y² =14, x²+2y²= 18; 2x² =32, + x² =16, x =4; Можно ли записывать ответ? Метод сложения Задание 2

у х 0 На рисунке изображена парабола и три прямые. Укажите систему уравнений, которая не имеет решений. Задание 3 Графический метод

Сколько решений имеет система уравнений? 3 -8 y x У = x2 – 8 У =3х-3 Задание 4 Графический метод НАЙДИ ОШИБКУ!

у х 0 1 1 Такой системы нет 4 3 -4 -4 Пользуясь рисунком, укажите систему уравнений, Решением которой является пара Графический метод Задание 5

у х 0 1 1 Ответ: ( ; ) 1 1 1 Используя графики функций решите уравнение Задание 6 Графический метод НАЙДИ ОШИБКУ!

1 2 3 Решить систему уравнений

Введение новой переменной Пример 1 Замена Ответ:(1;27), (27;1).

Решим систему уравнений Решим систему уравнений Из второго уравнения системы находим 2х-у=1, откуда у=2х-1. Подставляя вместо у в первое уравнение выражение 2х-1 получим , откуда . Обозначим , получим квадратное уравнение . Находим корни этого уравнения: . Уравнение замены решений не имеет. Корнем уравнения является число х=2. Соответствующее значение у=3. Ответ:(2;3). Системы показательных уравнений Пример 2

Решим систему уравнений Решим систему уравнений Первое уравнение системы равносильно уравнению у-х=2, а второе – уравнению , причём х>0 и у>0. Подставляя у=х+2 в уравнение , получим х(х+2)=48, откуда ,т.е. х= -8 или х=6.Но так как х>0, то х=6 и тогда у=8. Итак, данная система уравнений имеет одно решение: х=6, у=8. Ответ: (6;8). Системы логарифмических уравнений Пример 3

Системы тригонометрических уравнений http://ege. sdamgia.ru/test?theme=203

1. 2. 1. 2. 3. 4. 5. 6. Системы показательных уравнений

1. 2. 1. 2. 3. 4. 5. 6. Системы логарифмических уравнений

1. 2. 1. 2. 3. 4. 5. 6. Метод подстановки

1. 2. 1. 2. 3. 4. 5. 6. Метод сложения

1. 2. 1. 2. 3. 4. 5. 6. Графический метод

5.3 Метод замены переменной.

Алгоритм решения:

1. Берем некоторое выражение за новую переменную t.

2. Заменяем dx по формуле: .

3. Подставляем в изначальное выражение.

4. Делаем обратную замену.

Советы:

1. Берите «средние» функции – не простые и не сложные (Пример: (kx+m) – простая функция, — сложная, — средняя).

2. Старайтесь брать за t так, чтобы в итоге все оставшиеся после замены выражения с х сократились с .

3. Ничего страшного если взяли за t не то выражение, возьмите другое.

Примеры:

11.9 .

Решение:

1. t=arctg(x)

3. .

11.15

Решение:

3. .

11.27

Решение:

3. .

5.4 Определенный интеграл.

Определенный интеграл высчитывается точно также как и неопределенный, но в конце мы подставляем значения пределов интегрирования по четвертому свойству интегралов.

Пример:

11.54 =.

5.5 Двойные интегралы.

Двойной интеграл имеет вид: , где D – пределы интегрирования по х и по у.

Чтобы решить данный интеграл необходимо взять поочередно определенный интеграл по одной переменной, а затем по другой. При этом стоит учитывать, что если пределы интегрирования заданы константами, то нет разницы, какой интеграл сначала брать: по х или по у, но если один из пределов задан через переменную, то необходимо сначала взять интеграл с переменной в пределах интегрирования.

Примеры:

18.1

Решение:

Запишем в виде:

Т.е. мы взяли сначала интеграл по х с пределами интегрирования по х, а затем по у с пределами интегрирования у.

18.2

Этот пример осложнен тем, что один из пределов интегрирования выражается через переменную. Возьмем сначала интеграл по у (т.к. его предел интегрирования выражается через х), а затем по х:

18.12

Решение:

=

P.S. Заметьте, что когда мы берем интеграл от -6х по у, мы получаем -6ху, т.к. считаем, что в этом случае х – константа (что аналогично взятию производной от функции нескольких переменных)

Глава VI. Точки экстремума функции нескольких переменных.

6.1 Локальный экстремум функции.

Для того чтобы найти точки минимума/максимума функции необходимо выполнить два условия:

1. Необходимое условие. Находим все возможные критические точки.

Для этого необходимо приравнять каждую производную функции по всем переменным к нулю, а затем решить систему.

2. Достаточное условие. Находим точки минимума и максимума.

Теперь необходимо работать с матрицой Гессе:

Во-первых, необходимо найти все вторые производные матрицы и заполнить таблицу.

Во-вторых, если у нас >0 либо <0 в некой критической точке, то перед нами точка минимума, а если знаки чередуются (например, ), то максимума. В ином случае – точки экстремума нет.

.

P.S. соответственно, если у нас функция не от 3х переменных, а от двух, то матрица Гессе будет 2х2 и не будет вообще.

Пример:

16.1.

1) . Как видно у нас всего одна критическая точка.

2) 8 max.

Ответ: (1;2) – точка максимума.

16.17.

2. .

Определим сначала точку : — max.

Теперь точку : — не является экстремумом.

Ответ: (-1;-3;-2) – max.

6.2 Локальный условный экстремум.

Отличается локальный условный экстремум, лишь некоторыми нововведениями:

Примеры:

Решение:

1. Выразим х через у и подставим в z:

Теперь найдем критические точки, взяв производную и приравняв ее к 0.

.

2. Можно решать через матрицу Гессе, а можно вспомнить школьный курс:

Отсюда видно, что в точке у=1,5 – максимум.

Ответ: — max.

17.24. Найдите наибольшее и наименьшее значения функции в области, ограниченной осями координат и прямой .

Решение:

Эта задача отличается тем, что мы ищем максимальное и минимальное значение z, а не только точки максимума минимума, это значит, что нужно смотреть чему z равняется на границах.

1. Найдем точки экстремума: и найдем значение z в этой точке:

2. Сделаем чертеж области:

И найдем значения z в указанных точках:

3. Найдем критические точки на прямых, ограничивающих область:

Ось ОХ: на оси х , значит на этой прямой , а значит: .

Ось ОУ: на оси у х=0, значит на этой прямой , а значит:

Прямая : .

4. Выбираем минимальное и максимальное значение z.

Ответ: .

Метод замены переменной — Энциклопедия по экономике

В соответствии с изложенным была сформирована модель оптимизации топливного производства НПЗ. Размеры модели характеризуются следующими данными число ограничений — 211, число основных переменных — 272, число дополнительных переменных — 211. В сформированной модели 44 установки представлены векторами с переменными коэффициентами выпуска и затрат. Об эффективности предлагаемого подхода с точки зрения размерности моделей можно судить на основании сравнения с эквивалентной моделью, сформированной с помощью обычных методов (например, метод замены переменных). Такая модель имела бы размерность 938 ограничений и 1153 переменных.  [c.102]
Определение нелинейной корреляционной зависимости. Одним из способов нахождения зависимости является метод замены переменной. Этот метод довольно часто используется при решении различных математических задач. Он заключается в том, что независимый фактор заменяется некоторой функцией этого фактора, которая переводит нелинейную зависимость в разряд линейных.  [c.57]

Метод замены переменной  [c.210]

Метод замены переменной (или метод подстановки) основан на следующей теореме.  [c.210]

Метод замены переменной 211  [c.211]

При вычислении этого интеграла был использован метод интегрирования по частям и метод замены переменной. Приближенно вычислено лишь последнее слагаемое (а именно, число 0,025). Таким образом, потребление энергии за год составляет (Ьио + + 0,5 a b + 0,025 а с) единиц мощности. А  [c.275]

Метод замены переменной. Вводят новую переменную с помощью соотношения x —

[c.151]

Общий недостаток методов исключения тенденции заключается в том, что эти методы предполагают некоторую модификацию модели (6.1) вследствие либо замены переменных, либо добавления в эту модель фактора времени. Однако большая часть соотношений, постулируемых экономической теорией, верификацией которых занимается эконометрика, сформулирована в терминах уровней временных рядов, а не их последовательных разностей или отклонений от трендов и предполагает измерение взаимосвязи переменных без включения в модель каких-либо дополнительных факторов (например, переменной времени).  [c.282]

Рассмотренная задача в отдельных частных случаях решается иным методом — путем замены переменных /Х/ [c.47]

К наиболее важным методам интегрирования относятся методы непосредственного интегрирования, замены переменной, интегрирования по частям.  [c.210]

Замена переменных в неопределенном интеграле. Метод интегрирования интегралов.  [c.14]

После создания модели, переменным задаются количественные значения. Это позволяет объективно сравнить и описать каждую переменную и отношения между ними. Ключевой характеристикой науки управления является замена словесных рассуждений и описательного анализа моделями, символами и количественными значениями. Вероятно, самый крупный толчок к применению количественных методов в управлении дало развитие компьютеров. Компьютер позволил исследователям операций конструировать математические модели возрастающей сложности, которые наиболее близко приближаются к реальности и, следовательно, являются более точными.  [c.71]

Рассмотрим некоторые особенности применения данного метода при разработке ассортиментного плана в ситуации падения спроса на один из выпускаемых видов продукции. Предположим, предприятие производит три вида продукции А, В и С. Спрос на продукцию А и В стабилен. Продукция С перестала пользоваться спросом. У предприятия есть возможность заменить ее продукцией D, изготавливаемой на том же оборудовании, что и продукция С, но с меньшими переменными затратами. Однако продажная цена изделия D ниже, чем изделия С, на 4 ДЕ. Требуется определить, позволит ли такая замена сохранить выручку от реализации на базисном уровне в объеме 280 тыс. ДЕ и не приведет ли это к потере прибыли. Постоянные затраты при обоих вариантах составляют 80 тыс. ДЕ (табл. 6.3).  [c.212]

Возможности применения моделей с переменными технологическими коэффициентами при решении задач планирования и управления комплексами непрерывного действия освещены также в работах [21—25]. В частности, в [22] рассматривается нелинейная задача статической оптимизации непрерывного производства. Предлагаются кусочно-линейная аппроксимация переменных коэффициентов и замена исходной нелинейной задачи некоторой приближенной задачей, для решения которой могут быть использованы методы линейного программирования.  [c.16]

Результаты свидетельствуют о целесообразности построения модели по отдельным частным совокупностям. Ввиду разной зависимости уровня квалификации рабочих от уровня занятости ручным трудом по заводам с традиционной и прогрессивной технологиями производства уравнение регрессии по совокупности в целом не позволило выявить наличие связи. Не улучшился результат модели и с введением фиктивной переменной, ибо этот метод предполагает равенство коэффициентов регрессии при х по частным совокупностям и возможность их замены общим коэффициентом регрессии Ь.  [c.149]

При проведении такой замены оборудования необходимо осуществлять технико-экономическую оценку целесообразности этих мероприятий. Варианты совершенствования состава оборудования могут быть весьма разнообразными, что требует создания соответствующих им методов проведения технико-экономического обоснования. Рассмотрим следующие методы сбалансирования экономических переменных для наиболее типичных случаев изменения состава оборудования, затрат и цены.  [c.111]

Свое наименование С. м. л. п. получил из математич. понятия симплекс , обозначающего простейший выпуклый многогранник в пространстве с числом измерений, равным п (напр., при п=2 симплекс представлен многогранником на плоскости, при га=3 — тетраэдром и т. д.). Связь С. м. л. п. с математич. понятием симплекса заключается в том, что этот метод основан на замене перебора множества возможных значений переменных, геометрически представимых как точки такого многогранника, перебором одних только угловых точек, лежащих на границах соответствующего симплекса, в к-рых только и могут находиться отыскиваемые в рассматриваемых задачах экстремальные значения переменных. Такая замена дает огромную экономию в расчетах, что, собственно, и выводит задачи линейного программирования в число решаемых задач.  [c.21]

Наиболее распространен следующий метод снижения цены исполнения опциона старый опцион аннулируется и вместо него выпускается новый с более низкой ценой исполнения. Аннулирование опциона (или выкуп его за наличные) и немедленная замена другим с более низкой ценой исполнения повлекут за собой его отражение в бухгалтерском учете как переменной выплаты. Кроме того, считается, что цена исполнения снижена, если выпуск нового опциона с более низкой ценой для тех же самых менеджеров имел место не более чем за 6 месяцев до или в течение в месяцев после аннулирования предыдущего опциона. Поэтому многие компании, аннулируя старые опционы с завышенной ценой исполнения, обязуются предоставить их владельцам новые опционы с более выгодными условиями через «шесть месяцев и один день» (так называемые опционы «шесть, плюс один»).  [c.374]

В каждой модели ее переменные задаются количественными значениями, что позволяет объективно сравнивать что было до и стало после оказания управленческих воздействий. В этом отношении именно количественным методам, позволяющим поставить управленческий процесс на рельсы математики, принадлежит ведущая роль в формировании самой науки управления. Последнее обстоятельство наглядно доказывает, что управление все более становится наукой и лишь в определенной мере остается искусством в исполнении руководителя. Ибо «ключевой характеристикой науки управления является замена словесных рассуждений и описательного анализа моделями, символами и количественными значениями» [32, с. 71].  [c.13]

Обсудить процесс «очищения» данных и методы, используемые для работы с пропущенными ответами замена их нейтральными значениями, использование вмененных ответов, исключение наблюдения и попарное исключение переменных.  [c.519]

Замена пропущенного условным (вменение Для определения условного значения или вычисления подходящих ответов на вопросы можно использовать структуру ответов респондентов по другим вопросам. На основе имеющихся данных исследователь пытается определить, какие ответы дал бы конкретный респондент, если бы он ответил на все вопросы. Это можно сделать статистически, на основе собранных данных, определив взаимосвязи между пропущенной переменной и другими переменными. Так, показатель частоты использования товара можно связать с размером семей респондентов, предоставивших информацию по этим показателям. Затем пропущенные данные по использованию товара можно вычислить, воспользовавшись показателем размера семьи респондента. Однако следует помнить, что этот метод очень трудоемок и нередко серьезно искажает данные. Чтобы избежать этого, для вычисления условных значений по пропущенным ответам разработаны сложные статистические процедуры, о чем рассказывается в следующем примере.  [c.531]

В ряде случаев метод замены переменных приводят к значительному увеличении размера задачи. Например, в достаточно типичной задаче размером 200 х 200 при двух варьируемых параметрах и одном уравнении их баланса в каждом столбце линеаризация описанным выю методом приводит к задаче линейного программирования размере t 200×400, в то время как при замене переменных размер возрастает до 1200 х 600.  [c.47]

Замена переменной интегрирования является одним из самых эффек тивных приемов сведения неопределенного интеграла к табчинному Такой прием называется методом подстановки или методом замены переменной. Он основан на следующей теореме.  [c.130]

Подобная замена переменных, позволяющая линеаризовать систему ограничений, используется в двушаговом методе решения задачи теории контрактов [15, 93]. 30  [c.30]

Методы Тагути (термин методы Тагути появился в США, сам же Тагути называет свою концепцию инжиниринг качества ) представляют собой один из принципиально новых подходов к решению вопросов качества. Главное в философии Тагути — это повышение качества с одновременным снижением расходов. Согласно Тагути, экономический фактор (стоимость) и качество анализируются совместно. Оба фактора связаны общей характеристикой, называемой функцией потерь. Методология Тагути опирается на признание фактора неравноценности значений показателя внутри допуска. Функция потерь качества является параболой с вершиной (потери равны нулю) в точке наилучшего значения (номинала), при удалении от номинала потери возрастают и на границе поля достигают своего максимального значения — потери от замены изделия. При анализе рассматриваются потери как со стороны потребителя, так и со стороны производителя. Методы Тагути позволяют проектировать изделия и процессы, нечувствительные к влиянию так называемых шумов , т. е. переменных факторов, вызывающих разброс значений параметров, которые трудно, невозможно или дорого изменить. С экономической точки зрения любые, даже самые малые шумы уменьшают прибыль, поскольку при этом растут производственные издержки и затраты на гарантийное обслуживание. Такую устойчивость принято называть робастностью (от англ, robust — крепкий, устойчивый). Тагути акцентирует внимание на  [c.124]

Помимо того что проводники стратегии обязаны лично находиться на переднем плане борьбы за новые нормы поведения и разъяснять причины новых подходов, они должны убедить всех заинтересованных лиц, что речь не идет лишь о косметических изменениях . Разговоры и планы следует подкрепить содержательными мерами и реальными действиями. Эти действия должны внушать доверие, быть заметными и недвусмысленно указывать на серьезность намерений руководства в отношении новых стратегических инициатив и связанных с ними культурных перемен. Для этого существует несколько способов. Один из них — достижение некоторых быстрых успехов, которые указывали бы на преимущества новой стратегии и культуры и тем самым поддерживали перемены. Однако немедленные результаты обычно не столь важны, как наличие воли и терпения для формирования надежной, квалифицированной команды, психологически приверженной реализации стратегии. Самыми верными признаками того, что руководство намеренно насадить новую культуру, являются замена менеджеров, действующих в традициях старой культуры, менеджерами новой формации изменение сложившихся политики и методов работы, которые препятствуют новым инициативам осуществление крупных шагов в области реорганизации с целью приведения структуры в более полное соответсвтвие со стратегией непосредственная увязка материальных стимулов с новыми показателями стратегической результативности перераспределение сметы в пользу проектов и программ в рамках новой стратегии. Кроме того, главные проводники стратегии обязаны подавать личный пример. Например, если стратегия компании предполагает достижения наименьших удельных затрат в отрасли, старшие менеджеры должны  [c.390]

Мы предпочитаем оценки коэффициентов регрессии у г, которые эффективны и для которых можно проверить значимость. Оценки эффективны, если они являются наилучшими линейными несмещенными оценками (НЛНО). Термин наилучшие относится к свойству минимальности дисперсии. Оценки обобщенного МНК, будут такими оценками (НЛНО), но они требуют знания ковариационной матрицы ошибок наблюдений (2г и 2 в (2.8) и (2.17) в дополнении 2). К сожалению, нам ковариационная матрица неизвестна. Мы можем оценить элементы этой матрицы. (Ее диагональные элементы, т. е. дисперсии, оцениваются величинами sfr, обобщенный МНК для системы уравнений также требует оценивания ковариаций эти ковариации не оценивались в данном эксперименте, но они оценивались в дополнительном эксперименте.) Замена ковариационной матрицы в обобщенном методе ковариационной матрицей оценок позволяет получить несмещенные оценки 7о-> но эти оценки не лучше оценок (НЛНО). Мы не знаем, имеют ли они еще и меньшую дисперсию, чем обычные МНК-оценки (сравните с литературой)9. Мы знаем, что МНК-оценки обладают преимуществом простоты вычислений, поскольку при ортогональной матрице независимых переменных не нужна обратная матрица. Обращение матрицы с помощью ЭВМ может приводить к значительным ошибкам  [c.300]

Другой важный вид замены полного внутрирыночного теста, который проводит исследовательская компания, — это тест, контролирующий телевизионные сигналы, получаемые телевизорами. Компания разделяет семьи на равноценные группы. Затем посылает рекламу одной из групп семей и собирает точные данные о покупках всех семей. Так как реклама в этом случае является единственной изменяемой переменной, метод позволяет однозначно проследить связь причины и следствия. Данные, собранные таким способом, известны, как данные из одного источника, потому что информация о показе рекламы и покупках действительно исходит из одного источника, ввввввввввввввввввввввв Данные из одного источника дают ис-  [c. 651]

Исчисление III — Замена переменных

Показать мобильное уведомление Показать все примечания Скрыть все примечания

Мобильное уведомление

Похоже, вы находитесь на устройстве с «узкой» шириной экрана ( т.е. вы, вероятно, на мобильном телефоне). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.

Раздел 4-8. Замена переменных{{\,d}}{{f\left( u \right)\,du}}\hspace{0,25in}{\mbox{где}}u = g\left( x \right)\]

В сущности, это взятие интеграла в терминах \(x\) и преобразование его в термины \(u\). Мы хотим сделать что-то подобное для двойных и тройных интегралов. На самом деле мы уже сделали это в определенной степени, когда преобразовали двойные интегралы в полярные координаты и когда мы преобразовали тройные интегралы в цилиндрические или сферические координаты. Основное отличие состоит в том, что мы на самом деле не вдавались в детали происхождения формул. Если вы помните, в каждом из этих случаев мы отмечали, что в конце концов обосновываем формулы для \(dA\) и \(dV\). Сейчас самое время сделать это оправдание.

Хотя часто причиной изменения переменных является получение интеграла, который мы можем сделать с новыми переменными, другой причиной изменения переменных является преобразование региона в более удобный для работы регион. Когда мы преобразовывали полярные, цилиндрические или сферические координаты, мы не беспокоились об этом изменении, поскольку было достаточно легко определить новые пределы на основе заданной области. Однако это не всегда так. Итак, прежде чем мы перейдем к изменению переменных с помощью нескольких интегралов, нам сначала нужно увидеть, как область может измениться при замене переменных. 92} & = 4\конец{выравнивание*}\]

Итак, мы начали с эллипса и после преобразования получили диск радиуса 2.

b \(R\) — область, ограниченная \(y = — x + 4\), \(y = x + 1\) и \(\displaystyle y = \frac{x}{3} — \frac {4}{3}\) и преобразование \(\displaystyle x = \frac{1}{2}\left( {u + v} \right)\), \(\displaystyle y = \frac{1 }{2}\left( {u — v} \right)\). Показать решение

Как и в первой части, нам нужно будет подставить преобразование в уравнение, но в этом случае нам нужно будет сделать это три раза, по одному разу для каждого уравнения. Прежде чем мы это сделаем, давайте нарисуем граф региона и посмотрим, что у нас получилось.

Итак, у нас есть треугольник. Теперь займемся трансформацией. Мы применим преобразование к каждому краю треугольника и посмотрим, что получится.

Сначала сделаем \(y = — x + 4\). Подключение к трансформации дает,

\[\begin{align*}\frac{1}{2}\left( {u — v} \right) & = — \frac{1}{2}\left( {u + v} \right) + 4\\ u — v & = — u — v + 8\\ 2u & = 8\\ u & = 4\end{align*}\]

Первая граница очень хорошо преобразуется в гораздо более простое уравнение.

Теперь давайте посмотрим на \(y = x + 1\),

\[\begin{align*}\frac{1}{2}\left( {u — v} \right) & = \frac{1}{2}\left( {u + v} \right) + 1 \\ u — v & = u + v + 2\\ — 2v & = 2\\ v & = — 1\end{align*}\]

Опять же, гораздо более приятное уравнение, чем то, с которого мы начали.

Наконец, давайте преобразуем \(y = \frac{x}{3} — \frac{4}{3}\).

\[\begin{align*}\frac{1}{2}\left( {u — v} \right) & = \frac{1}{3}\left({\frac{1}{2}\ left( {u + v} \right)} \right) — \frac{4}{3}\\ 3u — 3v & = u + v — 8\\ 4v & = 2u + 8\\ v & = \frac {u}{2} + 2\end{выравнивание*}\]

Итак, мы снова получили несколько более простое уравнение, хотя и не такое красивое, как первые два.

Давайте взглянем на новый регион, который мы получаем при преобразовании.

Мы по-прежнему получаем треугольник, но гораздо более красивый.

Обратите внимание, что мы не всегда можем ожидать преобразования области определенного типа (например, треугольника) в область того же типа. Вполне возможно, что треугольник преобразуется в область, в которой каждое из краев изогнуто и никоим образом не напоминает треугольник.

Обратите внимание, что в каждом из приведенных выше примеров мы брали двумерную область, по которой было бы несколько сложно интегрировать, и преобразовывали ее в область, по которой интегрировать было бы намного лучше. Как мы отметили в начале этого набора примеров, это часто является одним из моментов трансформации. В дополнение к преобразованию подынтегрального выражения во что-то более простое, оно часто также преобразует область в область, с которой гораздо легче иметь дело.

Прежде чем перейти к следующей теме, давайте обратимся к другому моменту. Иногда нам также потребуется знать диапазон \(u\) и/или \(v\) для каждого из новых уравнений, которые мы получаем в результате преобразования. Нам это не нужно для двух приведенных выше примеров, и это не то, что нам часто понадобится. Однако иногда это может помочь в определении нового региона.

Итак, давайте рассмотрим быстрый пример, чтобы увидеть, как мы это делаем.

Пример 2. Для области, ограниченной \(y = — x + 4\), \(y = x + 1\) и \(y = \frac{x}{3} — \frac{4}{3} \) и преобразования \(x = \frac{1}{2}\left( {u + v} \right)\), \(y = \frac{1}{2}\left( {u — v } \right)\) определяют диапазоны \(u\) и \(v\) для каждого из новых уравнений преобразования.

Показать решение

Хорошо, мы уже знаем, как выглядит новая область и каковы новые уравнения из предыдущего примера. Итак, вот краткий обзор преобразования каждого из исходных уравнений.

\[\begin{align*} & y = — x + 4& \Rightarrow & \hspace{0.25in}u = 4\\ & y = x + 1& \Rightarrow & \hspace{0.25in}v = — 1\\ & y = \frac{x}{3} — \frac{4}{3}& \Rightarrow & \hspace{0.25in}v = \frac{u}{2} + 2\end{align*}\]

Вот новый регион, который мы получаем при трансформации.

Обратите внимание, что в этом случае мы можем определить диапазон \(u\) и \(v\) для каждого уравнения из схемы выше. Однако в тех случаях, когда нам действительно могут понадобиться диапазоны, это обычно не вариант, поскольку нам часто нужны диапазоны для \(u\) и/или \(v\), чтобы получить точный эскиз новой области.

Итак, давайте приступим к решению задачи.

Начнем с уравнения \(u = 4\). Во-первых, здесь нам не нужен «диапазон» \(u\), так как уравнение ясно показывает, что у нас есть единственное значение \(u\), а именно \(u = 4\). Итак, давайте определим диапазон \(v\), который мы должны получить.

Давайте начнем с преобразования \(x\) и подставим известное значение \(u\) для этого уравнения. Это дает,

\[x = \frac{1}{2}\left( {u + v} \right) = \frac{1}{2}\left( {4 + v} \right)\]

Теперь мы знаем, что диапазон значений \(x\) для исходного уравнения \(y = — x + 4\) равен \(\frac{3}{2} \le x \le 4 \). Мы также знаем сверху, что такое \(x\) с точки зрения \(v\), так что подставьте это в этот диапазон и проделайте небольшую манипуляцию следующим образом:

\[\begin{array}{c}\displaystyle \frac{3}{2} \le x \le 4\\\displaystyle \frac{3}{2} \le \frac{1}{2}\left ( {4 + v} \right) \le 4\\ 3 \le 4 + v \le 8\\ — 1 \le v \le 4\end{массив}\]

Итак, диапазон значений \(v\) для \(u = 4\) должен быть равен \( — 1 \le v \le 4\), что прекрасно соответствует тому, что мы ожидаем от графика новый регион.

Обратите внимание, что мы могли бы так же легко использовать преобразование \(y\) и диапазон \(y\) для исходного уравнения и получить тот же результат.

Хорошо, давайте теперь перейдем к \(v = — 1\), и мы не будем вдаваться в подробности этой части.

Во-первых, для этого нам не нужен диапазон \(v\), потому что у нас явно есть только одно значение \(v\). Итак, чтобы получить диапазон \(u\), давайте снова начнем с преобразования \(x\), подставим в него \(v = — 1\), а затем воспользуемся диапазоном \(x\) из исходное уравнение, \(y = x + 1\).

Вот эта работа.

\[\begin{array}{c}\displaystyle — \frac{7}{2} \le x \le \frac{3}{2}\\ \displaystyle — \frac{7}{2} \le \ frac{1}{2}\left( {u — 1} \right) \le \frac{3}{2}\\ — 7 \le u — 1 \le 3\\ — 6 \le u \le 4 \конец{массив}\]

Итак, диапазон \(u\) для \(v = — 1\) равен \( — 6 \le u \le 4\), что, опять же, совпадает с тем, что мы видим на графике. Также обратите внимание, что мы снова могли бы использовать диапазоны \(y\) для выполнения этой работы.

Наконец, давайте найдем диапазон \(u\) и \(v\) для \(v = \frac{u}{2} + 2\). На этот раз давайте воспользуемся преобразованием \(y\), чтобы можно было сказать, что мы использовали его в одном из них. Итак, мы начнем с диапазона \(y\) для исходного уравнения, \(y = \frac{x}{3} — \frac{4}{3}\), подставьте \ (y\) преобразование, а затем подставьте его для \(v\). Выполнение этого дает,

\[\begin{array}{c} \displaystyle — \frac{5}{2} \le y \le 0\\ \displaystyle — \frac{5}{2} \le \frac{1}{2} \left( {u — \left( {\frac{u}{2} + 2} \right)} \right) \le 0\\ \displaystyle — 5 \le \frac{u}{2} — 2 \ le 0\\ \displaystyle — 3 \le \frac{u}{2} \le 2\\ — 6 \le u \le 4\end{массив}\]

Итак, мы снова получаем диапазон \(u\), который мы ожидаем получить из графика. Как только мы получим их, соответствующий диапазон \(v\) можно найти из самого уравнения следующим образом:

\[\begin{array}{c} \displaystyle — 6 \le u \le 4\\ — 3 \le \frac{u}{2} \le 2\\ \displaystyle — 1 \le \frac{u} {2} + 2 \le 4\\ — 1 \le v \le 4\end{массив}\]

По сути, начнем с диапазона \(u\) и «построим» уравнение для стороны, и мы получим диапазон \(v\) для этой стороны.

Итак, теперь мы знаем, как получить диапазоны \(u\) и/или \(v\) для новых уравнений при преобразовании. Тем не менее, это не то, что делается ужасно часто, но это полезный навык на случай, если он где-то возникнет.

Теперь, когда мы рассмотрели несколько примеров преобразования областей, нам нужно теперь поговорить о том, как мы на самом деле делаем замену переменных в интеграле. Начнем с двойных интегралов. Для замены переменных в двойном интеграле нам понадобится Якобиан преобразования. Вот определение якобиана.

Определение

Якобиан преобразования \(x = g\left( {u,v} \right)\), \(y = h\left( {u,v} \right)\) равен

\[\frac{{\partial \left( {x,y} \right)}}{{\partial \left({u,v} \right)}} = \left| {\ begin {array} {* {20} {c}} {\ displaystyle \ frac {{\ partial x}} {{\ partial u}}} & { \ displaystyle \ frac {{\ partial x}} {{ \ partial v}}} \\ { \ displaystyle \ frac {{\ partial y}} {{\ partial u}}} & \ displaystyle {\ frac {{ \ partial y}} {{\ partial v}}} \ конец{массив}} \справа|\]

Якобиан определяется как определитель матрицы 2×2, если вы не знакомы с этим, ничего страшного. Вот как вычислить определитель.

\[\слева| {\ begin {array} {* {20} {c}} a & b \\ c & d \ end {array}} \ right | = объявление — до н.э.\]

Следовательно, другая формула для определителя:

\[\frac{{\partial \left( {x,y} \right)}}{{\partial \left({u,v} \right)}} = \left| {\ begin {массив} {* {20} {c}} {\ Displaystyle \ гидроразрыва {{\ парциальное х}} {{\ парциальное и}}} & \ Displaystyle {\ гидроразрыва {{\ парциальное х}} {{ \partial v}}}\\{ \displaystyle \frac{{\partial y}}{{\partial u}}}&{ \displaystyle \frac{{\partial y}}{{\partial v}}}\ конец {массив}} \right| = \frac{{\partial x}}{{\partial u}}\frac{{\partial y}}{{\partial v}} — \displaystyle \frac{{\partial x}}{{\partial v }} \ frac {{\ парциальное у}} {{\ парциальное и}} \]

Теперь, когда у нас есть якобиан, мы можем дать формулу замены переменных для двойного интеграла.

Замена переменных для двойного интеграла

Предположим, что мы хотим проинтегрировать \(f\left( {x,y} \right)\) по области \(R\). При преобразовании \(x = g\left( {u,v} \right)\), \(y = h\left( {u,v} \right)\) область становится \(S\) и интеграл становится,

\[\iint\limits_{R}{{f\left( {x,y} \right)\,dA}} = \iint\limits_{S}{{f\left( {g\left( {u, v} \right),h\left( {u,v} \right)} \right)\left| {\ frac {{\ partial \ left ({x, y} \ right)}} {{\ partial \ left ({u, v} \ right)}}} \ right | \, d \ overline {A}} }\]

Обратите внимание, что мы используем \(d\overline{A}\) в интеграле \(u\)/\(v\) выше, чтобы обозначить, что он будет выражен в терминах \(du\) и \(dv\) ) после преобразования в два одиночных интеграла вместо \(dx\) и \(dy\), которые мы привыкли использовать для \(dA\). Это только обозначение, и мы обычно просто используем \(dA\) для обоих и просто помним, что «новое» \(dA\) выражается в терминах \(du\) и \(dv\).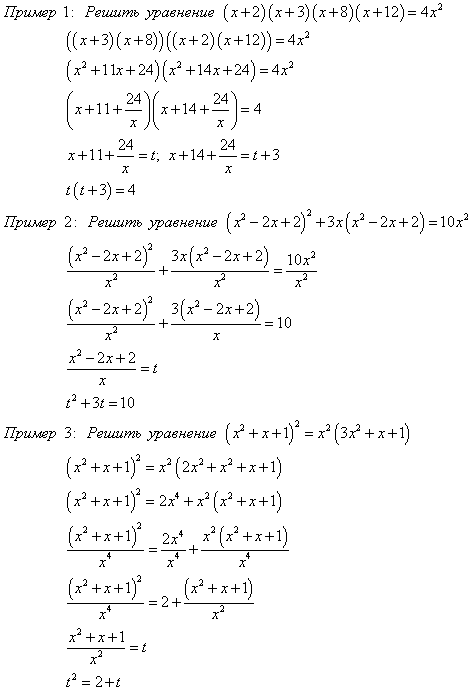

Также обратите внимание, что мы берем абсолютное значение якобиана.

Если мы посмотрим только на дифференциалы в приведенной выше формуле, мы также можем сказать, что

\[дА = \влево| {\ frac {{\ partial \ left ({x, y} \ right)}} {{\ partial \ left ({u, v} \ right)}}} \ right | \, d \ overline {A} \ ]

Пример 3. Покажите, что при переходе к полярным координатам имеем \(dA = r\,dr\,d\theta \)

Показать решение

Итак, что мы здесь делаем, так это оправдываем формулу, которую мы использовали, когда интегрировали по полярным координатам. Все, что нам нужно сделать, это использовать приведенную выше формулу для \(dA\).

Преобразование здесь стандартные формулы преобразования,

\ [x = r \ cos \ theta \ hspace {0,25 дюйма} \ hspace {0,25 дюйма} y = r \ sin \ theta \]

Якобиан для этого преобразования:

\[\begin{align*}\frac{{\partial \left({x,y} \right)}}{{\partial \left({r,\theta} \right)}} & = \left| {\ begin {array} {* {20} {c}} {\ displaystyle \ frac {{\ partial x}} {{\ partial r}}} & {\ displaystyle \ frac {{\ partial x}} {{ \ partial \ theta }}} \\\ displaystyle {\ frac {{\ partial y}} {{\ partial r}}} & \ displaystyle {\ frac {{\ partial y}} {{\ partial \ theta}} }\end{массив}} \right|\\ & = \left| {\ begin {array} {* {20} {c}} {\ cos \ theta} & { — r \ sin \ theta} \\ {\ sin \ theta} & {r \ cos \ theta} \ end {array }} \right|\\ & = r{\cos ^2}\theta — \left( { — r{{\sin}^2}\theta} \right)\\ & = r\left( {{{ \cos}^2}\theta + {{\sin}^2}\theta} \right)\\ & = r\end{align*}\]

Получаем,

\[дА = \влево| {\ гидроразрыва {{\ парциальное \ влево ({х, у} \ справа)}} {{\ парциальное \ влево ( {г, \ тета} \ вправо)}}} \ вправо | \, др \, д \ тета = \ влево | r \right|dr\,d\theta = r\,dr\,d\theta \]

Итак, формула, которую мы использовали в разделе о полярных интегралах, была правильной.

Теперь давайте посчитаем пару интегралов.

Пример 4. Вычислите \(\displaystyle \iint\limits_{R}{{x + y\,dA}}\), где \(R\) — трапециевидная область с вершинами, заданными \(\left( {0,0} \right)\), \(\left( {5,0} \right)\), \(\displaystyle \left( {\frac{5}{2},\frac{5}{2}} \right )\) и \(\displaystyle \left( {\frac{5}{2}, — \frac{5}{2}} \right)\) с помощью преобразования \(x = 2u + 3v\) и \ (у = 2и — 3у\).

Показать решение

Сначала нарисуем область \(R\) и найдем уравнения для каждой из сторон.

Каждое из уравнений было найдено с использованием того факта, что мы знаем две точки на каждой линии (, т.е. две вершины, образующие ребро).

Хотя мы могли бы вычислить этот интеграл в терминах \(x\) и \(y\), он включал бы два интеграла, что потребовало бы некоторой работы.

Используем трансформацию и посмотрим, что у нас получится. Мы сделаем это, вставив преобразование в каждое из приведенных выше уравнений.

Начнем процесс с \(y = x\).

\[\begin{align*}2u — 3v & = 2u + 3v\\ 6v & = 0\\ v & = 0\end{align*}\]

Преобразование \(y = — x\) аналогично.

\[\begin{align*}2u — 3v & = — \left( {2u + 3v} \right)\\ 4u & = 0\\ u & = 0\end{align*}\]

Далее мы преобразуем \(y = — x + 5\).

\[\begin{align*}2u — 3v & = — \left( {2u + 3v} \right) + 5\\ 4u & = 5\\ u & = \frac{5}{4}\end{align *}\]

Наконец, преобразуем \(y = x — 5\).

\[\begin{align*}2u — 3v & = 2u + 3v — 5\\ — 6v & = — 5\\ v & = \frac{5}{6}\end{align*}\]

Область \(S\) представляет собой прямоугольник, стороны которого равны \(u = 0\), \(v = 0\), \(u = \frac{5}{4}\) и \ (v = \frac{5}{6}\), поэтому диапазоны \(u\) и \(v\) равны

\[0 \le u \le \frac{5}{4}\hspace{0,25 дюйма}\hspace{0,25 дюйма}0 \le v \le \frac{5}{6}\]

Далее нам нужен якобиан. {\ frac {5} {6}} \\ & = \frac{{125}}{4}\end{align*}\] 92} \le 2\) и с помощью преобразования \(x = \sqrt 2 \,u — \sqrt {\frac{2}{3}} \,v\), \(y = \sqrt 2 \,u + \ sqrt {\ frac {2} {3}} \, v \).

Показать решение

Прежде чем мы приступим к этой проблеме. Давайте сделаем быстрый график границы области \(R\). Мы утверждали, что это эллипс, но явно не в «стандартной» форме. Вот граница \(R\).

Итак, это эллипс, только тот, который расположен под углом, а не симметричен относительно осей \(x\) и \(y\), как мы привыкли иметь дело. 92}} \справа)\]

в терминах \(u\) и \(v\), поэтому нам не придется переделывать эту работу, когда придет время вычислять интеграл.

Наконец, нам нужно найти якобиан.

\[\frac{{\partial \left( {x,y} \right)}}{{\partial \left({u,v} \right)}} = \left| {\ begin {array} {* {20} {c}} {\ sqrt 2} & { — \ sqrt {\ frac {2} {3}}} \\ {\ sqrt 2} & {\ sqrt {\ frac {2}{3}} }\end{массив}} \right| = \ frac {2} {{\ sqrt 3}} + \ frac {2} {{\ sqrt 3}} = \ frac {4} {{\ sqrt 3}} \] 9{{2\pi}}{{\frac{1}{4}\,d\theta}}\\ & = \frac{{4\pi}}{{\sqrt 3}}\end{align*} \]

Давайте теперь кратко рассмотрим тройные интегралы. В этом случае мы снова начнем с области \(R\) и воспользуемся преобразованием \(x = g\left( {u,v,w} \right)\), \(y = h\left( {u ,v,w} \right)\) и \(z = k\left( {u,v,w} \right)\) для преобразования области в новую область \(S\). Чтобы вычислить интеграл, нам понадобится якобиан, как и в случае с двойными интегралами. Вот определение якобиана для такого преобразования.

\[\frac{{\partial \left( {x,y,z} \right)}}{{\partial \left({u,v,w} \right)}} = \left| {\ begin {массив} {* {20} {c}} {\ Displaystyle \ гидроразрыва {{\ парциальное х}} {{\ парциальное и}}} & \ displaystyle {\ гидроразрыва {{\ парциальное х}} {{ \ partial v}}} & \ displaystyle {\ frac {{\ partial x}} {{\ partial w}}} \\ \ displaystyle {\ frac {{\ partial y}} {{\ partial u}}} & \displaystyle {\frac{{\partial y}}{{\partial v}}}& \displaystyle {\frac{{\partial y}}{{\partial w}}}\\ \displaystyle{\frac{{ \ partial z}} {{\ partial u}}} & \ displaystyle {\ frac {{\ partial z}} {{\ partial v}}} & \ displaystyle {\ frac {{\ partial z}} {{\ частичное w}}}\end{массив}} \right|\]

В этом случае якобиан определяется через определитель матрицы 3×3. Мы видели, как их оценивать, когда рассматривали перекрестные произведения еще в Calculus II. Если вам нужно освежить знания о том, как их вычислять, вам следует вернуться и просмотреть этот раздел.

Интеграл этого преобразования равен

\[\iiint\limits_{R}{{f\left( {x,y,z} \right)\,dV}} = \iiint\limits_{S}{{f\left( {g\left( { u,v,w} \right),h\left( {u,v,w} \right),k\left( {u,v,w} \right)} \right)\left| {\ frac {{\ partial \ left ({x, y, z} \ right)}} {{\ partial \ left ({u, v, w} \ right)}}} \ right | \, d \ overline {В}}}\]

Как и в случае с двойными интегралами, мы использовали \(d\overline{V}\) в интеграле \(u\)/\(v\)/\(w\) выше, чтобы напомнить себе, что нам нужно будет использовать \( du\), \(dv\) и \(dw\) при переходе к одиночным интегралам. Опять же, это просто обозначение и обычно пишется просто \(dV\).

Мы можем посмотреть только на дифференциалы и отметить, что у нас должно быть

\[dV = \влево| {\ frac {{\ partial \ left ({x, y, z} \ right)}} {{\ partial \ left ({u, v, w} \ right)}}} \ right | \, d \ overline {В}\] 92}\sin \varphi \,d\rho \,d\theta \,d\varphi \) при использовании сферических координат. 2}\sin \varphi \end{align* }\] 92}\sin\varphi\,d\rho\,d\theta\,d\varphi\]

Напомним, что мы ограничили \(\varphi \) диапазоном \(0 \le \varphi \le \pi \) для сферических координат, и поэтому мы знаем, что \(\sin \varphi \ge 0\), и поэтому мы не нужны абсолютные значения баров на синусе.

Мы предоставим вам проверить формулу \(dV\) для цилиндрических координат, если хотите. Формулу проверить гораздо проще.

Решение систем уравнений: какой метод использовать?

Системы уравнений — это несколько уравнений, имеющих общее решение. Учащиеся сталкиваются с этими системами уравнений, когда есть несколько «неизвестных» или переменных, которые им еще не заданы. Когда это происходит, цель учащихся состоит в том, чтобы использовать данную информацию в уравнениях для решения всех переменных.

 

Для решения систем уравнений учащимся полезно иметь общее представление о простых алгебраических уравнениях, переменных и графических линейных уравнениях.

 

Как решить систему уравнений?

 

Для решения систем уравнений используются три метода: построение графика, замена и исключение.

 

Чтобы решить систему с помощью графика, вы просто рисуете заданные уравнения и находите точки, в которых они все пересекаются. Координата этой точки даст вам значения переменных, которые вы решаете. Это наиболее эффективно, когда уравнения уже записаны в форме пересечения наклона.

 

Следующий метод — подстановка. Подстановку лучше всего использовать, когда одно из уравнений выражает одну из переменных, например y=2x+4, но уравнениями всегда можно манипулировать. Первым шагом в этом методе является решение одного из уравнений для одной переменной. Как только выражение для переменной найдено, замените или вставьте выражение в другое уравнение, где исходная переменная должна была найти числовое значение следующей переменной. Последним шагом является замена найденного числового значения на соответствующую переменную в исходном уравнении.

 

Третий метод — исключение. Исключение — это сложение уравнений вместе, чтобы создать уравнение только с одной переменной. Это можно сделать только в том случае, когда коэффициенты одной переменной в обоих уравнениях противоположны и будут компенсировать друг друга после сложения. Исключение лучше всего использовать, когда это уже происходит в уравнениях, но уравнения также можно манипулировать для создания общих коэффициентов путем умножения или деления уравнений на определенное число. Следующим шагом будет использование уравнения, которое мы создали, чтобы найти значение переменной, а затем подставить это значение обратно в исходное уравнение, чтобы найти оставшуюся переменную.

 

Вот пример задачи, в которой необходимо решить систему уравнений:

 

Логан ответил на 0,8 вопросов по математике больше, чем вопросов по испанскому, и на 5 вопросов по английскому языку больше, чем по испанскому. Если Логан ответил в общей сложности на 33 вопроса, на сколько математических вопросов ответил Логан?

 

Как решить эту проблему?

 

Первым шагом является создание уравнений из задачи со словами. Для этого мы должны присвоить переменные каждой неизвестной части задачи. Переменные x, y и z будут представлять количество математических, испанских и английских вопросов, на которые Логан ответил соответственно.

 

Поскольку Логан ответил в 0,8 раза на большее количество математических вопросов, чем на испанский, уравнение, представляющее это, будет 0,8y=x. Второе уравнение будет выглядеть так: z=y+5, чтобы представить, как Логан ответил на пять английских вопросов больше, чем испанских. Окончательное уравнение будет x+y+z=33, чтобы показать, как Логан ответил в общей сложности на 33 вопроса.

 

Оглядываясь назад на исходный вопрос, цель этой задачи — найти, на сколько математических вопросов ответил Логан. Поскольку первое уравнение, которое мы нашли, было 0,8y=x, мы видим, что нам нужна только переменная y, чтобы найти значение x или количество математических вопросов, на которые были даны ответы. Поскольку два уравнения уже решены с двумя переменными, 0,8y=x и z=y+5, подстановка будет наиболее эффективным методом. Чтобы использовать этот метод, мы заменим этими уравнениями переменные x и y третьего уравнения, что даст нам (0,8y)+y+(y+5)=33.

 

Следующим шагом будет решение этого уравнения для переменной y путем объединения одинаковых членов: 2,8y=28, что даст нам y=10 или 10 ответов на испанские вопросы. Теперь, когда мы нашли значение переменной y, мы можем снова подставить его в уравнение 0,8y=x, чтобы найти значение x. Заменив y его значением 10, мы получим 0,8(10)=x, что даст нам значение 8 для x.

 

Какой ответ?

Логан ответил на 8 математических вопросов.

 

Какие понятия мы использовали?

 

Чтобы решить эту примерную задачу, мы использовали несколько различных математических концепций. Первым, что мы использовали, было то, как писать уравнения из текстовых задач. Благодаря нашему пониманию проблемы мы смогли присвоить каждому неизвестному аспекту проблемы переменную, а затем создать уравнения, основанные на их отношениях в проблеме, которые мы затем распознали как систему уравнений.

 

Вторая концепция, которую мы использовали, — это решение системы. Уравнения не были записаны в форме пересечения наклона, поэтому построение графиков было бы неэффективным методом. Противоположные друг другу переменные отсутствовали, поэтому мы также исключили метод исключения. Признав подстановку лучшим методом, мы смогли эффективно использовать наши математические навыки для решения неизвестных переменных в системе уравнений.

 

 

Если это то, что вы хотите для своего ребенка — Начать просто!

Позвоните сейчас (303) 502-8345 и узнайте больше!

 

Каковы математические способности вашего ребенка?

И вы, и ваш ребенок можете принять участие в наших интерактивных викторинах, чтобы узнать, как много вы помните! На каком они этапе обучения?

Раздел 2.2 Вопрос 1 – Часто задаваемые вопросы по математике

Существуют две основные стратегии решения системы двух линейных уравнений и двух переменных. В каждой стратегии одна из переменных исключается, что позволяет нам найти оставшуюся переменную. Эти две стратегии называются методом замещения и методом исключения.

Хотя метод подстановки можно использовать для решения системы с любым количеством переменных и любым количеством уравнений, мы будем использовать метод подстановки для систем двух уравнений с двумя неизвестными. Метод исключения также можно использовать для решения систем уравнений с двумя переменными. Кроме того, метод исключения можно легко масштабировать для решения систем уравнений с более чем двумя переменными.

Метод подстановки

1. Найдите одну из переменных в одном из уравнений. Если трудно решить для переменной, метод исключения может лучше подходить для решения системы.
2. В другом уравнении замените переменную, которую вы нашли на шаге 1, эквивалентным выражением. После того, как вы заменили переменную в другом уравнении, в этом уравнении должна быть только одна переменная.
3. Решите уравнение, содержащее только одну переменную для этой переменной.
4. Чтобы найти значение другой переменной, подставьте значение, полученное на шаге 3, в уравнение из шага 1.

Пример 1    Найти решение системы

Решите систему линейных уравнений

методом подстановки.

Решение Используя первое уравнение, найдите x . Добавьте 2 y к обеим сторонам, чтобы получить x = 2 y – 5. Замените x на 2 y – 5 во втором уравнении и найдите y :

4 9 значение 9 x находится путем подстановки y = 2 в уравнение x = 2 y – 5. Это дает x = -1. Решение системы ( x, y ) = (-1, 2).

Мы можем проверить решение, подставив его в исходную систему:

Поскольку упорядоченная пара делает оба уравнения верными, мы нашли решение системы.

---

В примере 6 раздела 2. 1 мы нашли точку пересечения системы уравнений

Напомним, что первое уравнение описывает общую стоимость Y для работы на молочной ферме с коровами Q . Второе уравнение описывает общий доход Y для молочной фермы с Q коров. Когда общий доход и общие затраты равны, бизнес находится в точке безубыточности. Эту точку можно найти графически, найдя точку пересечения на графиках общих затрат и общих доходов. Эту же точку можно найти алгебраически, используя метод подстановки. Эта стратегия идеальна для этой системы, поскольку одно (в данном случае два) уравнения в системе имеет форму пересечения наклона и решается для переменной.

Пример 2    Точка безубыточности молочной промышленности

Решите систему уравнений

с помощью метода подстановки.

Решение Поскольку каждое уравнение решается относительно переменной Y , мы можем заменить эту переменную в первом уравнении эквивалентным выражением из второго уравнения:

Чтобы решить для Q:

Соответствующее значение для Y равно Y ≈ 3547(104,68) ≈ 371 299,96. Это говорит нам о том, что безубыточное количество составляет 104,68 коров, а выручка и затраты составляют около 371 299,96 долларов.

---

Если найти переменную непросто, можно использовать метод исключения, чтобы исключить переменную из системы двух уравнений. Метод исключения основан на концепции эквивалентных систем уравнений. Две системы уравнений эквивалентны, если они имеют одно и то же решение. Систему уравнений можно преобразовать в эквивалентную систему уравнений с помощью преобразований уравнений.

Систему уравнений можно преобразовать в эквивалентную систему уравнений,

1. поменяв местами любые два уравнения;
2. умножение каждого члена уравнения на ненулевое число;
3. замена любого уравнения в системе суммой одного из уравнений, умноженного на ненулевое число, и другого уравнения, умноженного на ненулевое число.

Используя эти три преобразования, мы можем преобразовать заданную систему в более простую систему, решение которой легко найти. Эти преобразования могут быть применены к системе уравнений с двумя или более чем двумя переменными.

Метод исключения

1. Запишите каждое уравнение системы с переменными в левой части и константами в правой части уравнения.
2. Переставьте члены в левой части уравнения так, чтобы переменные шли в одном и том же порядке в каждом уравнении. Напишите термины так, чтобы каждый термин с определенной переменной был выровнен по вертикали с терминами, содержащими ту же переменную.
3. Умножьте первое уравнение на обратную величину коэффициента первого члена (старшего коэффициента). После этого преобразования коэффициент первой переменной в первом уравнении должен быть равен 1,9.0028
4. Удалите первую переменную из всех уравнений, кроме первого уравнения, используя преобразования уравнений.
5. Умножьте второе уравнение на обратную величину старшего коэффициента. После этого преобразования старший коэффициент второго уравнения должен быть равен 1.
6. Исключите переменную, соответствующую старшему коэффициенту, из всех остальных уравнений, кроме второго уравнения.
7. Продолжайте этот процесс для каждого уравнения и ведущего коэффициента.
8. Решите каждое уравнение для ведущей переменной, чтобы получить решение системы уравнений.

Пример 3    Найти решение системы

Решить систему линейных уравнений

методом исключения.

Решение Эта система уже имеет переменные в левой части уравнений и константы в правой части уравнения. Термины выровнены таким образом, что каждая переменная в левой части отображается под терминами с той же переменной.

Чтобы сделать коэффициент x в первом уравнении равным 1, умножьте первое уравнение на обратную величину 5 или ¹ / ₅

Если мы заменим первое уравнение этим множителем первого уравнения, мы получаем эквивалентную систему уравнений

Теперь, когда старший коэффициент в первом уравнении равен 1, исключим x из второго уравнения. Для этого замените второе уравнение на -2, умноженное на первое уравнение, добавленное ко второму уравнению:

Замените второе уравнение этой суммой, чтобы получить эквивалентную систему уравнений,

Старший коэффициент второго уравнения равен –  ²⁴ / ₅ . Чтобы изменить старший коэффициент на 1, умножьте второе уравнение на –  ⁵ / ₂₄  :

Поместите это уравнение вместо второго уравнения, чтобы получить эквивалентную систему уравнений,

Чтобы завершить задачу , нам нужно исключить y в первом уравнении. Умножьте второе уравнение на – ² / ₅ и добавьте его к первому уравнению:

Замените первое уравнение этой суммой, чтобы получить эквивалентную систему уравнений,

Поскольку эта система эквивалентна исходная система уравнений, решение исходной системы уравнений: ( х , у ) = ( ⁶ / ₅ , – ⁵ / ₂ ).

---

Пример 4    Найти решение системы

Решить систему линейных уравнений

методом исключения.

Решение Эта система из трех уравнений имеет три переменные, и каждое уравнение не имеет всех трех переменных. Однако это не меняет стратегии, представленной ранее. Прежде чем мы сможем преобразовать уравнения, чтобы исключить переменные, нам нужно переместить все переменные члены в левую часть уравнений, а константы — в правую часть уравнений. Вычтите из обеих частей третьего уравнения и выровняйте переменные, чтобы получить систему

Обратите внимание на вертикальное расположение каждой переменной. Если переменная отсутствует, мы просто вставляем пробел, чтобы убедиться, что все переменные расположены правильно.

Старший коэффициент в первом уравнении равен 1, поэтому нам нужно исключить x из всех остальных уравнений.

Чтобы исключить x из третьего уравнения, умножьте первое уравнение на 3 и прибавьте к третьему уравнению:

Замените третье уравнение в системе уравнений этой суммой,

Умножьте второе уравнение на обратную величину его старшего коэффициента, ¹ / ₂ :

Поместите это уравнение вместо второго уравнения, чтобы получить эквивалентную систему уравнений,

исключить y из первого и третьего уравнений,

Замена этих новых уравнений в системе уравнений дает эквивалентную систему,

Старший коэффициент третьего уравнения изменяется на 1 путем умножения третье уравнение на ¹ / ₅ ,

Замените третье уравнение на это новое уравнение, чтобы дать

, чтобы закончить преобразования, мы должны исключить Z из первого и второго уравнения:

Замена этих новых уравнений в системе оставляет нас с

Поскольку эта система эквивалентна исходной системе, решение ( x, y, z ) = (-1, 0, 2).

---

Кривая спроса и предложения для молочных продуктов может быть записана в виде системы уравнений

В этой системе уравнений первое уравнение соответствует функции спроса. Эта строка связывает цену P с количеством молока Q , требуемым потребителями по этой цене. Второе уравнение, функция предложения, связывает количество молока Q , которое поставщики готовы поставить по цене P . Эта система эквивалентна системе

, которую мы нашли для молочных ферм в главе 1.0011

Найдите точку равновесия, решив систему уравнений

методом исключения.

Решение Чтобы решить систему, нам нужно использовать преобразования уравнений, чтобы изменить старший коэффициент первого уравнения. Умножая первое уравнение на ¹ / ₁₀₀ , старший коэффициент становится равным 1:

. Замените первое уравнение в системе новым уравнением, чтобы получить эквивалентную систему уравнений:

Теперь мы должны исключить P из второго уравнения. *$ представляет собой прямоугольник, что упрощает интегрирование. См. апплет на карте полярных координат прямоугольника, чтобы визуализировать это преобразование из прямоугольника в диск. 92. \конец{выравнивание*} Частные производные преобразования $\cvarf(r,\theta)=(r \cos\theta, r \sin \theta)$ равны \начать{выравнивать*} \pdiff{\cvarfc_1}{r}(r,\theta) & = \pdiff{}{r}(r \cos\theta)= \cos\theta\\ \pdiff{\cvarfc_2}{r}(r,\theta) & = \pdiff{}{r}(r \sin\theta) =\sin \theta\\ \pdiff{\cvarfc_1}{\theta}(r,\theta) & = \pdiff{}{\theta}(r \cos\theta)= -r\sin\theta\\ \pdiff{\cvarfc_2}{\theta}(r,\theta) & = \pdiff{}{\theta}(r \sin\theta) =r \cos\theta. \конец{выравнивание*} Собирая их вместе, матрица частных производных замены переменных в полярных координатах имеет вид \начать{выравнивать*} \jacm{\cvarf}(r,\theta) &= \left( \begin{массив}{cc} \cos\тета и \sin\тета\\ -r\sin\theta & r\cos\theta \конец{массив} \Правильно) \конец{выравнивание*} который имеет определитель \начать{выравнивать*} \det \jacm{\cvarf}(r,\theta) &= r \cos^2\theta — (-r) \sin^2\theta = r(\cos^2\тета + \sin^2\тета) = r. 4}{2}. \конец{выравнивание*}

Преимущество преобразования переменных в полярные координаты заключается в том, что вам нужно вычислить коэффициент расширения области только один раз. При любой замене переменных на полярные координаты коэффициент расширения площади всегда будет равен $r$. Вы можете просто запомнить, что $dA=dx\,dy = r\,dr\,d\theta$. Однако важно помнить, откуда появился этот $r$, особенно если вам нужно вычислить какое-либо общее изменение переменных, как в следующих примерах.

Если вы не верите в эту формулу, мы можем мотивировать результат следующим образом. Разделите диск на сетку, соответствующую разделению $r$ полярных координат на интервалы длины $\Delta r$ и разбивая $\theta$ полярных координат на интервалы длины $\Delta\theta$, так же, как мы делали это для вводная страница. А один «изогнутый прямоугольник» с углом $\cvarf(r,\theta)$ изображен ниже.

Пусть $\Delta A$ — площадь «изогнутого прямоугольника». Вы можете видеть, что площадь зависит от радиуса $r$, так как ее ширина примерно $r\Delta\theta$ и его высота примерно равна $\Delta r$. Следовательно площадь $\Delta A$ приблизительно равна $r \Delta r \Delta \theta$. В этом наброске показана причина, по которой $dA$ становится $r\,dr\,d\theta$, когда перевод переменных в полярные координаты. Вы также можете изучить апплет о районе преобразование карты полярных координат, чтобы увидеть, как увеличивается площадь расширения с радиусом $r$.

Пример 2

Вычислить интеграл $\iint_D (3x-2y)dA$ по параллелограмму $D$, ограниченному прямыми $y=\frac{3}{2}x — 4$, $y=\frac {3}{2}x+2$, $y=-2x+1$ и $y=-2x+3$. Используйте линейную замену переменных $$(x,y)=\cvarf(\cvarfv,\cvarsv)=(\cvarfv+2\cvarsv, -2\cvarfv+3\cvarsv).$$

Решение : Поскольку замена переменных является линейной, мы знаем, что она отображает параллелограммы в параллелограммы. Если преобразовать уравнения для параллельных прямых через переменные $\cvarfv$ и $\cvarsv$, то снова получим уравнения для параллельных прямых.

Перепишите уравнения границ параллелограмма в виде \begin{выравнивание*}3x -2y&=8\\ 3x-2y&=-4\\ 2х+у&=1\\ 2х+у&=3. *$ равны $7\cvarfv = 8$, $7\cvarfv=-4$, $7\cvarsv=1$ и $7\cvarsv=3$. Кроме того, подынтегральная функция равна просто $7\cvarfv$. 9*$ равно $0 \le \cvarfv \le 1$, $1 \le \cvarsv \le 2$.

Наша замена переменных, выраженная в уравнении \eqref{thechangevar}, дает $\cvarfv$ и $\cvarsv$ через $x$ и $y$. В нашем формула замены переменных, нам нужно чтобы $x$ и $y$ были выражены через $\cvarfv$ и $\cvarsv$ с использованием некоторых функция $(x,y)=\cvarf(\cvarfv,\cvarsv)$. Таким образом, один из способов решения этой проблемы состоит в том, чтобы решить уравнение \eqref{thechangevar} для $x$ и $y$, чтобы определить функция $\cvarf$. Тогда мы могли бы вычислить \начать{выравнивать*} \pdiff{(x,y)}{(\cvarfv,\cvarsv)} = \det \jacm{\cvarf}(\cvarfv,\cvarsv), \конец{выравнивание*} что нам и нужно для формулы замены переменных.

В этом примере мы будем использовать другой метод, который пропускает этот шаг. Мы оставит $\cvarfv$ и $\cvarsv$, выраженные через $x$ и $y$ (как в уравнение \eqref{thechangevar}) и вычислить $\displaystyle \pdiff{(\cvarfv,\cvarsv)}{(x,y)}$ вместо $\displaystyle\pdiff{(x,y)}{(\cvarfv,\cvarsv)}$. Поскольку мы знаем, что \начать{выравнивать*} \pdiff{(x,y)}{(\cvarfv,\cvarsv)} = \frac{1}{\displaystyle \pdiff{(\cvarfv,\cvarsv)}{(x,y)}}, \конец{выравнивание*} мы можем легко получить правильный коэффициент для нашей замены переменных формула.

Чтобы вычислить $\displaystyle \pdiff{(\cvarfv,\cvarsv)}{(x,y)}$, мы просматриваем $\cvarfv$ и $\cvarsv$ как функции от $x$ и $y$: $\cvarfv(x,y)$ и $\cvarsv(x,y)$. Частичное производные от $\cvarfv$ и $\cvarsv$ по $x$ и $y$ равны \начать{выравнивать*} \pdiff{\cvarfv}{x} = -1, \qquad \pdiff{\cvarfv}{y} = 1, \qquad \pdiff{\cvarsv}{x} = y, \qquad \text{и} \qquad \pdiff{\cvarsv}{y} = x. \конец{выравнивание*} Мы вычисляем \начать{выравнивать*} \pdiff{(\cvarfv,\cvarsv)}{(x,y)} &= \det \left( \begin{массив}{cc} \displaystyle \pdiff{\cvarfv}{x} & \displaystyle \pdiff{\cvarfv}{y}\\ \displaystyle \pdiff{\cvarsv}{x} & \displaystyle \pdiff{\cvarsv}{y} \конец{массив} \Правильно)\\ &= \pdiff{\cvarfv}{x} \pdiff{\cvarsv}{y} — \pdiff{\cvarfv}{y}\pdiff{\cvarsv}{x}\\ &= -х -у, \конец{выравнивание*} чтобы \начать{выравнивать*} \pdiff{(x,y)}{(\cvarfv,\cvarsv)} = \frac{1}{-x -y}. \конец{выравнивание*} Коэффициент, который нам нужен для нашей формулы замены переменных, тогда \начать{выравнивать*} \left|\pdiff{(x,y)}{(\cvarfv,\cvarsv)}\right| = \ гидроразрыва {1} {х + у} \конец{выравнивание*} так как $x$ и $y$ положительны в нашей области определения. 92}\справа) \конец{выравнивание*}

Другой пример

Вы можете ознакомиться с другим примером, где трансформация функции изменения переменных иллюстрируется интерактивной графикой.

15.7 Изменение переменных

Одним из наиболее полезных методов вычисления интегралов является замена, оба «$u$-подстановка» и тригонометрический подстановка, при которой мы меняем переменную на нечто большее удобный. Как мы видели, иногда переходя от прямоугольного координаты в другую систему координат полезно, и это тоже изменяет переменные. Это, конечно, более сложное изменение, так как вместо замены одной переменной на другую мы меняем всю набор переменных, но, как оказалось, он действительно очень похож на виды замены переменных, которые мы уже знаем как замену. 92и}\,ду $$ не одинаковы; ясно, что правая часть больше. Один из способов понять, проблема заключается в том, чтобы отметить, что если обе области аппроксимированы используя, скажем, десять подынтервалов, чтобы аппроксимирующие прямоугольники на справа шире, чем их аналоги слева, как указано. В на рисунке ширина прямоугольника слева $\Delta x=0.1$, от 0,7$ до 0,8$. Прямоугольник справа расположен между соответствующими значениями $\arcsin(0.7)$ и $\arcsin(0.8)$, поэтому что $\Delta u=\arcsin(0.8)-\arcsin(0.7)$. К чтобы ширина совпадала, а площади, следовательно, были одинаковыми, мы можем умножить $\Delta u$ на поправочный коэффициент; в этом случае поправочный коэффициент приблизительно равен $\cos u=\cos(\arcsin(0.7))$, что мы вычисляем, когда конвертируем $dx$ в $\cos u\,du$. 9{y_1} f(x,y)\,dy\,dx$$ использовать новые переменные $u$ и $v$. В случае с одной переменной как правило, есть только одна причина изменить переменную: сделать функцию «лучше», так что мы можем найти первообразную. В двух переменный случай, есть вторая потенциальная причина: двумерный область, по которой надо интегрироваться, как-то неприятно, и мы хотите, чтобы регион с точки зрения $u$ и $v$ был лучше — чтобы прямоугольник, например. В идеале, конечно, новая функция и новый регион будет не хуже оригиналов, и хотя бы один из они будут лучше; это не всегда срабатывает. 92}\;r\,dr\,d\theta={\pi\over3}.$$ Но давайте вместо этого подойдем к этому как к проблеме замены, начиная где $x=r\cos\theta$, $y=r\sin\theta$. Эта пара уравнений описывает функцию из пространства «$r$-$\theta$» в «пространство $x$-$y$», и поскольку он включает в себя знакомые понятия, его не так уж сложно понять. понять, что он делает. На рис. 15.7.2 мы геометрически немного показали, как это функция ведет себя. Четыре точки, обозначенные a – d в плоскости $r$-$\theta$ соответствуют трем точкам в плоскости $x$-$y$; точки и и б оба перейти в начало координат, потому что $r=0$. Горизонтальная стрелка в В плоскости $r$-$\theta$ $r=1$ везде, а $\theta$ изменяется от 0 до $\pi$, поэтому соответствующие точки $x=r\cos\theta$, $y=r\sin\theta$ начинаются с $(1,0)$ и следуют за единицей круг против часовой стрелки. Наконец, вертикальная стрелка имеет $\theta=\pi/4$ и $r$ находятся в диапазоне от 0 до 1, так что это соответствует прямому стрелка в плоскости $x$-$y$. Экстраполируя эти несколько примеров, нетрудно заметить, что каждая вертикальная линия в плоскости $r$-$\theta$ преобразуется в прямую, проходящую через начало координат в плоскости $x$-$y$, и каждая горизонтальная линия в плоскости $r$-$\theta$ преобразуется в окружность с центром в начале координат в $x$-$y$ самолет. Поскольку нас интересует интегрирование по полудиску в плоскости $x$-$y$ будем интегрировать по прямоугольнику $[0,\pi]\times[0,1]$ в плоскости $r$-$\theta$, потому что теперь мы видим что точки в этом прямоугольнике направляются точно в верхнюю половину диск на $x=r\cos\theta$ и $y=r\sin\theta$. 92\тета} = r.& (15.7.1)\кр }$$ Последняя и самая трудная задача — выяснить, что заменяет $дх\,ди$. (Конечно, мы на самом деле знаем ответ, потому что мы находимся в эффект преобразования в полярные координаты. Чего мы действительно хотим, так это последовательность шагов, которые приведут к правильному ответу, но это также сработает для других замен, которые не так знакомы. 1 r (?) \,dr\,d\theta.& (15.7.2)\кр }$$ Чего нам не хватает, так это правильного количества, чтобы заменить «?» чтобы мы получили правильный ответ. Разумеется, этот интеграл также результат приближения, в котором мы складываем объемы ящиков это $\Delta r\times\Delta \theta\times\hbox{height}$; проблема заключается в том, что высота, которая даст нам правильный ответ, не просто $р$. Или, другими словами, мы можем думать о правильной высоте как $r$, но площадь основания $\Delta r\Delta\theta$ неверна. высота $r$ получается из уравнения 15.7.1, которое то есть она точно такая же, как и соответствующая высота в $x$-$y$ версия интеграла. Проблема в том, что площадь основание $\Delta x\times \Delta y$ не совпадает с площадью основания $\Delta r\times\Delta\theta$. Мы можем думать о «?» в интеграле как о поправочный коэффициент, необходимый для того, чтобы $?\,dr\,d\theta$ = $dx\,dy$.

Итак, давайте подумаем, что это за маленькая база $\Delta r\times\Delta\theta$ соответствует. Мы знаем, что каждый бит горизонтальная линия в плоскости $r$-$\theta$ соответствует биту дуга окружности в плоскости $x$-$y$, и каждый бит вертикальной линии в плоскости $r$-$\theta$ соответствует немного «радиальная линия» в плоскости $x$-$y$. На рисунке 15.7.3 мы показываем типичный прямоугольник в плоскость $r$-$\theta$ и соответствующая ей область в плоскости $x$-$y$.

Система координат $\theta r$ и система координат $xy$ связаны соотношениями $x=r\cos\theta$ и $y=r\sin\theta$. Маленький прямоугольник в плоскости $\theta r$ соответствует при отображении четырехсторонняя фигура в плоскости $xy$. Большой прямоугольник на плоскости $\theta r$ равен $[0,\pi]\times[0,1]$ и соответствует полуокружности в плоскости $xy$.

Перетащите синяя точка в плоскости $\theta r$ для перемещения прямоугольника; перетащите зеленый точка, чтобы изменить размер прямоугольника.

Рисунок 15.7.3. Соответствующие области.

В этом случае область в плоскости $x$-$y$ составляет примерно прямоугольник с размерами $\Delta r\times r\Delta\theta$, но в вообще углы углов не будут прямыми углами, поэтому область будет обычно (почти) параллелограмм. Нам нужно вычислить площадь этот параллелограмм. Мы знаем изящный способ сделать это: вычислить длину определенного перекрестного произведения (раздел 12.4). Если мы сможем определить подходящие два вектора, мы почти закончили.

К счастью, мы действительно делали это раньше. Стороны области в плоскости $x$-$y$ образуются путем временной фиксации либо $r$, либо $\theta$ и позволяя другой переменной изменяться в пределах небольшого интервала. На рис. 15.7.4, например, правый верхний край области формируется фиксированием $\theta=2\pi/3$ и выделением $r$ от 0,5$ до 0,75$. Другими словами, у нас есть векторная функция ${\bf v}(r)=\langle r\cos\theta_0, r\sin\theta_0, 0\rangle$, и мы интересует ограниченный набор значений для $r$. Тангенс вектора этому пути задается производной ${\bf v}'(r)=\langle \cos\theta_0, \sin\theta_0, 0\rangle$ и небольшой касательный вектор, с длиной, приблизительно равной стороне области, равно $\langle \cos\theta_0, \sin\theta_0, 0\rangle\,dr$. Аналогично, если мы исправим $r=r_0=0.5$, получаем векторную функцию ${\bf w}(\theta)=\langle r_0\cos\theta, r_0\sin\theta, 0\rangle$ с производной ${\bf w}'(\theta)=\langle -r_0\sin\theta, r_0\cos\theta, 0\rangle$ и малый касательный вектор $\langle -r_0\sin\theta_0, r_0\cos\theta_0, 0\rangle\,d\theta$, когда $\theta=\theta_0$ (в углу мы сфокусироваться на). Эти векторы показаны на рисунок 15.7.4, с фактическим область, очерченная пунктирной границей. Конечно, поскольку оба $\Delta r$ и $\Delta\theta$ довольно велики, параллелограмм не является особенно хорошее приближение к истинной площади. 92\theta_0\rangle\,d\theta\,dr\cr &=\langle 0,0,-r_0\rangle\,d\theta\,dr.\cr }$$ Длина этого вектора равна $r_0\,dr\,d\theta$. Так что в целом для любые значения $r$ и $\theta$, площадь в плоскости $x$-$y$ соответствующий маленькому прямоугольнику, привязанному к $(\theta,r)$ в Плоскость $r$-$\theta$ приблизительно равна $r\,dr\,d\theta$. Другими словами, «$r$» заменяет «?» в уравнении 15.7.2.

В общем случае подстановка начинается с уравнений $x=f(u,v)$ и $y=g(u,v)$. Опять же, будет просто преобразовать функцию быть интегрированным. Преобразование пределов потребует, как указано выше, понимание того, как функции $f$ и $g$ преобразуют плоскость $u$-$v$ в плоскость $x$-$y$. Наконец, малые векторы, которые мы нужно приблизить площадь будет $\langle f_u,g_u,0\rangle\,du$ и $\langle f_v,g_v,0\rangle\,dv$. Их векторное произведение равно $\langle 0,0,f_ug_v-g_uf_v\rangle\,du\,dv$ с длиной $|f_ug_v-g_uf_v|\,du\,dv$. Количество $|f_ug_v-g_uf_v|$ обычно обозначенный $ $ \ влево | {\ парциальное (х, у) \ над \ парциальное (и, v)} \ вправо | = | f_ug_v-g_uf_v | $ $ и назвал Якобиан . Обратите внимание, что это абсолютное значение определителя два на два. $$\left|\matrix{f_u&g_u\cr f_v&g_v\cr}\right|,$$ что может быть легче запомнить. (Как ни странно, матрица, определитель матрицы, а абсолютное значение определителя все они называются якобианами различными авторами.)

Потому что нужно беспокоиться о двух вещах, а именно о форме функция и область интегрирования, превращения в два (или больше) переменные довольно сложно обнаружить. 92=2$

Существует аналогичная формула замены переменных для тройных интегралов, хотя это немного сложнее получить. Предположим, мы используем три функции подстановки: $x=f(u,v,w)$, $y=g(u,v,w)$ и $z=h(u,v,w)$. Теперь определитель Якоби $$ {\ парциальное (х, у, г) \ над \ парциальное (и, v, ш)} = \left|\matrix{f_u&g_u&h_u\cr f_v&g_v&h_v\cr f_w&g_w&h_w\cr}\right|. $$ Затем интеграл преобразуется аналогичным образом: $$ \int\!\int\!\int_R F(x,y,z) \, dV = \int\!\int\!\int_S F(f(u,v,w),g(u,v,w),h(u,v,w)) \ влево | {\ парциальное (х, у, г) \ над \ парциальное (и, v, ш)} \ вправо | \,ду\,дв\,дв, $$ где, конечно, область $S$ в пространстве $uvw$ соответствует область $R$ в пространстве $xyz$. 92} = 1,$$ с помощью преобразования $x=au$, $y=bv$ и $z=cw$. (отвечать)

Как использовать Гауссоанскую ликвидацию для решения систем уравнений

: Ян Куанг и Эллин Казе и

Обновлен: 07-08-2021

Из книги: Pre-Calcus для Dummies

1. Предварительное исчисление для чайников

Исследуйте книгу Купить на Amazon

Метод исключения Гаусса, вероятно, является лучшим методом решения систем уравнений, если у вас нет графического калькулятора или компьютерной программы, которая могла бы вам помочь.

Цель исключения Гаусса состоит в том, чтобы сделать левый верхний угловой элемент равным 1, использовать элементарные операции со строками, чтобы получить 0 во всех позициях под этой первой 1, получить 1 для ведущих коэффициентов в каждой строке по диагонали от левого верхнего угла к нижнему. -правый угол и получить 0 под всеми ведущими коэффициентами. По сути, вы исключаете все переменные в последней строке, кроме одной, все переменные, кроме двух, в уравнении выше этой, и так далее, и так далее до верхнего уравнения, в котором есть все переменные. Затем вы можете использовать обратную подстановку для решения одной переменной за раз, подставляя известные вам значения в уравнения снизу вверх.

Вы выполняете это исключение, исключая x (или любую другую переменную, стоящую первой) во всех уравнениях, кроме первого. Затем исключите вторую переменную во всех уравнениях, кроме первых двух. Этот процесс продолжается, удаляя еще одну переменную в строке, пока в последней строке не останется только одна переменная. Затем решите для этой переменной.

Вы можете выполнить три операции над матрицами, чтобы исключить переменные в системе линейных уравнений:

• Любую строку можно умножить на константу (кроме нуля).

  умножает третью строку на -2, чтобы получить новую третью строку.

• Вы можете поменять местами любые две строки.

  меняет местами первую и вторую строки.

• Можно сложить две строки вместе.

  добавляет первую и вторую строки и записывает их во вторую строку.

Вы даже можете выполнить более одной операции. Вы можете умножить строку на константу, а затем добавить ее к другой строке, чтобы изменить эту строку. Например, вы можете умножить первую строку на 3, а затем добавить это ко второй строке, чтобы создать новую вторую строку:

Рассмотрим следующую расширенную матрицу:

Теперь взглянем на цели исключения Гаусса, чтобы выполнить следующие шаги для решения этой матрицы:

1. Выполните первую цель: получить 1 в верхнем левом углу.

   У вас уже есть это!

2. Выполните вторую цель: получить 0 под единицей в первом столбце.

   Здесь необходимо использовать комбинацию двух матричных операций. Вот что вы должны спросить: «Что мне нужно добавить во вторую строку, чтобы 2 превратились в 0?» Ответ -2.

   Этот шаг можно выполнить, умножив первую строку на –2 и добавив полученную строку ко второй строке. Другими словами, вы выполняете операцию

   , который создает эту новую строку:

   1. .

      (–2 –4 –6 : 14) + (2 –3 –5 : 9) = (0 –7 –11: 23)

   Теперь у вас есть эта матрица:

3. В третьей строке поставить 0 под 1.

   Для выполнения этого шага необходима операция

   После этого расчета у вас должна получиться следующая матрица:

4. Получить 1 во второй строке, во втором столбце.

   Чтобы выполнить этот шаг, вам нужно умножить на константу; другими словами, умножьте вторую строку на соответствующую обратную величину:

   .

   Этот расчет дает новую вторую строку:

5. Получите 0 под единицей, которую вы создали во второй строке.

   Вернуться к старой доброй комбинированной операции для третьего ряда:

   Вот еще вариант матрицы:

6. Получите еще 1, на этот раз в третьей строке, в третьем столбце.

   Умножьте третью строку на обратную величину коэффициента, чтобы получить 1:

   Вы завершили главную диагональ после математических вычислений:

Теперь у вас есть матрица в форме эшелона строк, которая дает вам решения при использовании обратной замены (последняя строка подразумевает, что 0 x + 0 y + 1 z = 4, или z = –4 ). Однако, если вы хотите знать, как преобразовать эту матрицу в сокращенную эшелонированную форму строк, чтобы найти решения, выполните следующие действия:

1. Получить 0 во второй строке, в третьем столбце.

   Умножение третьей строки на константу –11/7 и последующее сложение второй и третьей строк

   дает вам следующую матрицу:

2. Получить 0 в первой строке третьего столбца.

   No related posts.