Делимые факториалы / Хабр
Недавно я был совершенно сбит с толку этим твитом «Библиотеки Ферма»:
«Вот что получится, если в факториале не умножать, а делить.»
Когда я увидел его, мне пришлось бросить свои дела, схватить блокнот и проверить формулу. Результат в черновом виде казался логичным. Так как мультипликативная версия при увеличении стремится к бесконечности, то «делительная» версия должна стремиться к нулю. И ведёт себя именно так; полиномиальная функция растёт медленнее, чем степенная функция для достаточно больших :
Но почему результат деления принимает именно вид ? Откуда берётся ?
Чтобы ответить на этот вопрос, мне пришлось разбередить старую травму, связанную с изучением деления дробей, но я справился с болью. Двигаясь по формуле из твита слева направо, мы сначала получаем . Затем, поделив эту величину на , получаем
Чтобы прийти к показанному в твите результату , мы просто умножим числитель и знаменатель на .
(Хотя на мой вкус, выражение более понятно.)
Я официально признанный фанат факториалов. Оставьте при себе свои последовательности Фибоначчи; вот моя любимая функция. Каждый раз, когда я изучаю новый язык программирования, моим первым упражнением становится написание нескольких процедур для вычисления факториалов. За многие годы я придумал несколько вариаций этой темы, например, замену в определении на (что даёт нам треугольные числа). Но кажется, что раньше я никогда не задумывался о замене на . Получается странно. Так как умножение коммутативно и ассоциативно, мы можем определить просто как произведение всех целых чисел от до , не беспокоясь о порядке операций. Но при делении порядок игнорировать не получится. В общем случае, и .
В твите «Библиотеки Ферма» делители поставлены в порядке по убыванию: . Очевиднее всего будет заменить это на порядок по возрастанию: . Что произойдёт, если мы зададим факториал деления как ? Ещё один возврат к школьному алгоритму деления дробей даёт нам простой ответ:
Другими словами, когда мы многократно выполняем деление, выполняя подсчёт от до , окончательный результат будет равен величине, обратной .
(Мне хотелось бы поставить в конце этого предложения восклицательный знак, но увы!) Если вы ищете канонический ответ на вопрос «Что мы получим при делении вместо умножения в ?», то я бы заявил, что — лучший кандидат, чем . Почему бы нам не принять симметрию между и обратной ему величиной?
Разумеется, есть множество других способов размещения n целочисленных значений во множестве . Но сколько именно? Как оказалось, ровно ! Поэтому, может показаться, что есть уникальных способов задания делительной функции . Однако, изучение ответов двух показанных выше перестановок даёт нам понять, что здесь работает более простой паттерн. Какой бы элемент последовательности не появился первым, он оказывается в числителе большой дроби, а знаменателем оказывается произведение всех других элементов. Поэтому в итоге остаётся всего различных результатов (если предположить, что мы всегда выполняем операции деления строго слева направо). Для любого целочисленного в интервале от до , поставив в начало очереди, мы создаём делительное , равное , поделённому на все другие коэффициенты.
И таким образом мы решили небольшую загадку о том, как в этом твите превратилось в .
Стоит заметить, что все эти функции сходятся к нулю при стремлении к бесконечности. С асимптотической точки зрения, идентичны.
Та-да! Миссия выполнена. Задача решена. Дело сделано. Теперь мы знаем всё, что нам нужно, о делительных факториалах, верно?
Ну, возможно, есть ещё один вопрос. Что скажет компьютер? Если взять наш любимый алгоритм факториала, и сделать то, что предлагается в твите, заменив все вхождения оператора (или *) на /, то что случится? Какие из вариантов делительного выдаст нам программа?
Вот мой любимый алгоритм для вычисления факториалов в виде программы на Julia:
function mul!(n)
if n == 1
return 1
else
return n * mul!(n - 1)
end
end
Этот алгоритм познакомил целые поколения нердов с концепцией рекурсии.
Вы можете спросить, что произойдёт, если будет равным нулю или отрицательным. Спросить вы можете, но лучше не надо. Для наших текущих целей .
Начав с любого положительного , последовательность рекурсивных вызовов рано или поздно опустится к .
Функцию можно записать более лаконично с помощью однострочного стиля определений Julia:
mul!(n) = n == 1 ? 1 : n * mul!(n - 1)
Правая часть оператора присваивания — это условное выражение, или тернарный оператор, имеющий вид a ? b : c. Здесь a — булево условие теста, которое должно вернуть значение или true, или false. Если a равно true, то вычисляется выражение b, а результат становится значением всего выражения. В противном случае вычисляется c.
Просто чтобы убедиться, что я сделал всё верно, вот первые 10 факториалов, вычисленных этой программой:
[mul!(n) for n in 1:10]
10-element Array{Int64,1}:
1
2
6
24
120
720
5040
40320
362880
3628800
Теперь давайте изменим это определение и преобразуем единственное вхождение * в /, оставив всё остальное неизменным (за исключением названия функции).
div!(n) = n == 1 ? 1 : n / div!(n - 1)
И вот что вернёт программа, если мы запустим её для значений от до :
[div!(n) for n in 1:20]
20-element Array{Real,1}:
1
2.0
1.5
2.6666666666666665
1.875
3.2
2.1875
3.657142857142857
2.4609375
4.063492063492063
2.70703125
4.432900432900433
2.9326171875
4.773892773892774
3.14208984375
5.
092152292152292
3.338470458984375
5.391690662278897
3.523941040039063
5.675463855030418
Что? Это точно не походит на схождение к нулю, как и на или . На самом деле значения так не выглядят, потому что и не собираются сходиться. Судя по показанному ниже графику, последовательность состоит из двух перемежающихся компонентов, каждый из которых, похоже, медленно растёт в сторону бесконечности, а также отклоняется от другого.
Разбираясь с тем, что же мы здесь наблюдаем, полезно будет изменить тип выходных данных функции div!. Вместо использования оператора деления /, который возвращает значение как число с плавающей запятой, мы можем заменить его оператором //, возвращающим точное рациональное значение, округлённое до младшего члена.
div!(n) = n == 1 ? 1 : n // div!(n - 1)
Вот последовательность значений для n в интервале 1:20:
20-element Array{Real,1}:
1
2//1
3//2
8//3
15//8
16//5
35//16
128//35
315//128
256//63
693//256
1024//231
3003//1024
2048//429
6435//2048
32768//6435
109395//32768
65536//12155
230945//65536
262144//46189
В списке полно любопытных паттернов.
Это двойная спираль, в которой чётные и нечётные числа зигзагами перемещаются в комплементарных нитях. Чётные числа не просто чётные, все они являются степенями . Кроме того, они появляются в парах — сначала в числителе, затем в знаменателе — и их последовательность неубывающая. Но существуют пробелы; присутствуют не все степени . Нечётная нить выглядит ещё более сложной, в числах появляются и исчезают разные небольшие простые коэффициенты. (Простые числа
Этот результат удивил меня. Я ожидал увидеть гораздо более смирную последовательность, наподобие тех, которые я вычислял на бумаге. Все эти изломанные скачки вверх и вниз не имели никакого смысла. Как не имел смысла и общий тренд к неограниченному росту соотношения. Как мы можем постоянно делить, получая при этом всё бОльшие и бОльшие числа?
На этом этапе можете приостановить чтение и попытаться придумать собственную теорию о том, откуда взялись эти зигзагообразные числа.
Если вам нужна подсказка, то у вас она есть, и очень сильная, почти спойлер: поищите последовательность числителей или последовательность знаменателей в «Онлайн-энциклопедии целочисленных последовательностей».
Вот ещё одна подсказка. Небольшое изменение в программе div! полностью преобразует выходные данные. Просто изменим последнее выражение, заменив n // div!(n - 1) на div!(n - 1) // n.
div!(n) = n == 1 ? 1 : div!(n - 1) // n
Теперь результаты выглядят вот так:
10-element Array{Real,1}:
1
1//2
1//6
1//24
1//120
1//720
1//5040
1//40320
1//362880
1//3628800
Это обратная функция факториала, которую мы уже видели, ряд значений, сгенерированные при обходе слева направо по возрастающей последовательности делителей .
Неудивительно, что изменение последнего выражения в процедуре менят результат. В конце концов, мы знаем, что деление не коммутативно и не ассоциативно. Но сложно понять, почему последовательность сгенерированных исходной программой значений даёт такую странную зигзагообразную форму. Какой механизм порождает такие парные степени двойки и попеременные нечётные и чётные значения?
Я обнаружил, что объяснить происходящее в зигзагообразной последовательности проще на итеративной версии процедуры, а не на рекурсивной. (Это заявление может показаться досадным тем, кто считает рекурсивные определения более простыми, но так уж получилось.) Вот как выглядит программа:
function div!_iter(n)
q = 1
for i in 1:n
q = i // q
end
return q
end
Я заявляю, что эта процедура с циклом по функционалу идентична рекурсивной функции, в том смысле, что если div!(n) и div!_iter(n) возвращают результат для какого-то положительного целого n, то он всегда будет одинаковым.
Вот моё доказательство:
[div!(n) for n in 1:20] [div!_iter(n) for n in 1:20]
1 1//1
2//1 2//1
3//2 3//2
8//3 8//3
15//8 15//8
16//5 16//5
35//16 35//16
128//35 128//35
315//128 315//128
256//63 256//63
693//256 693//256
1024//231 1024//231
3003//1024 3003//1024
2048//429 2048//429
6435//2048 6435//2048
32768//6435 32768//6435
109395//32768 109395//32768
65536//12155 65536//12155
230945//65536 230945//65536
262144//46189 262144//46189
Чтобы понять процесс, порождающий эти числа, рассмотрим последовательные значения переменных и при каждом выполнении цикла.
Изначально и равны ; поэтому после первого прохода цикла выражение q = i // q даёт значение . Затем , а , то есть новое значение равно . При третьей итерации , а , что даёт нам . Если это всё ещё сбивает вас с толку, то представьте как . Важным наблюдением здесь является то, что при каждом обходе цикла получает обратное значение, становясь .
Если развернуть эти операции и посмотреть на умножения и деления, входящие в каждый элемент ряда, то возникает паттерн:
В общем виде:
Функции для нечётного и для чётного имеют собственное название! Они называются двойными факториалами, и записываются как .
Ужасная терминология, правда? Лучше бы их назвали «полуфакториалами». И если бы я этого не знал, то прочитал бы как «факториал факториала».
Двойной факториал n определяется как произведение n и всех меньших положительных целых чисел той же чётности. Таким образом, наша любопытная последовательность зигзагообразных значений — это просто .
В статье 2012 года Генри У. Гулда и Джослин Куэнтенс (увы, находящаяся за paywall) исследуются применения двойных факториалов. Они встречаются гораздо чаще, чем можно подумать. В середине 17-го века Джон Валлис вывел следующее тождество:
Ещё более странный ряд с участием куба значений двойных факториалов суммируется в . Его обнаружил не кто иной, как Сриниваса Рамануджан.
Гулд и Киэнтенс также рассматривали эквивалент двойного факториала для биномиальных коэффициентов. Стандартный биномиальный коэффициент определяется как:
Двойная версия выглядит так:
Заметьте, что наши зигзагообразные числа соответствуют этому описанию, а потому могут считаться биномиальными коэффициентами двойных факториалов. Говоря конкретнее, они являются такими числами:
Обычный бином не очень интересен; он просто равен .
Но двойная версия , как мы видели, танцует более оживлённый танец. И в отличие от обычного бинома она не всегда бывает целочисленной. (Единственные целые значения — это и .)
Взгляд на зигзагообразные числа как на частное двойных факториалов объясняет довольно многие их свойства, начиная с попеременных чётных и нечётных значений. Также мы можем увидеть, почему все чётные числа в последовательности являются степенями 2. Рассмотрим пример с . Числитель этой дроби — это , получающий от множитель . Но знаменатель равен . Тройки сверху и снизу сокращаются, оставляя нам . Такие сокращения происходят в каждом из случаев. Каждый раз, когда в последовательности чётных чисел появляется нечётный множитель , он обязательно имеет вид , но к этому времени само уже должно появиться в последовательности нечётных чисел.
Является ли последовательность зигзагообразных чисел разумным ответом на вопрос: «Что произойдёт, если мы будем делить, а не умножать в ?» Или генерирующая их компьютерная программа просто оказалась ошибочным алгоритмом? По моему личному мнению, — более интуитивный ответ, зато — более интересный.
Более того, само существование зигзагообразной последовательности расширяет наши горизонты. Как сказано выше, если вы настаиваете, что алгоритм деления всегда должен по порядку проходить по списку числителей , на каждом шаге деля число слева на число справа, то имеется всего возможных результатов, и все они выглядят очень похожими. Но зигзагообразное решение обеспечивает намного более широкие возможности. Мы можем сформулировать задачу следующим образом: возьмём множество числителей , выберем его подмножество и обратим все элементы этого подмножества; теперь перемножим все числители, как обратные, так и прямые. Если обращённое подмножество пусто, то результатом будет обычный факториал . Если все числители превратились в обратные им значения, то мы получаем обратный . А если обращён каждый второй числитель, начиная с , то результатом будет элемент зигзагообразной последовательности.
Это только некоторые из множества возможных вариантов; в сумме здесь есть подмножеств из элементов.
Например, можно брать обратные значения каждого числа, являющегося простым или степенью простого числа . При малых результаты скачут, но постоянно остаются меньше, чем :
Однако если бы я продолжил этот график для бОльших , он бы взлетел в стратосферу. Степени простых чисел становятся очень разреженными на числовой прямой.
Теперь я задам вопрос. Мы видели вариации факториалов, приближающиеся к нулю при стремлении к бесконечности, например . Мы видели другие вариации, растущие при увеличении безгранично, в том числе сам и зигзагообразные числа. Существуют ли какие-то разновидности процесса факториалов, сходящиеся к какой-то конечной границе, не являющейся нулём?
В первую очередь мне пришёл в голову такой алгоритм:
function greedy_balance(n)
q = 1
while n > 0
q = q > 1 ? q /= n : q *= n
n -= 1
end
return q
end
Мы циклически перебираем целые значения от вниз до , вычисляя в процессе текущее произведение/частное .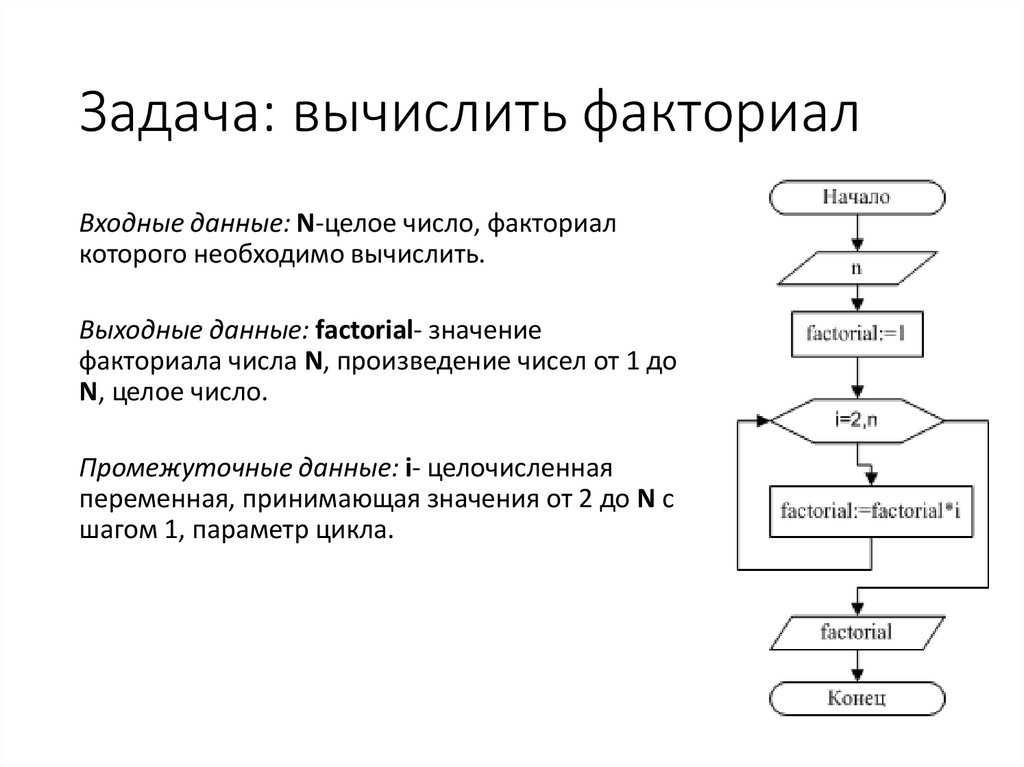
На каждом шаге, если текущее значение больше , мы делим его на следующий числитель, в противном случае, выполняем умножение. Эта схема реализует своего рода управление обратной связью или поведение поиска цели. Если становится слишком большим, мы уменьшаем его; если слишком маленьким, мы увеличиваем его. Я предположил, что при стремлении к бесконечности, будет сходиться к постоянно сужающемуся интервалу значений рядом с .
Но эксперимент подкинул мне ещё один сюрприз:
Такая пилообразная волна — не совсем то, чего я ожидал. Любопытно, что кривая не симметрична около ; отклонения сверху имеют бОльшую амплитуду, чем снизу. Но это искажение больше визуальное, чем математическое. Так как является частным, расстояние от до такое же, как расстояние от до , но в линейном масштабе таким не выглядит. Исправить это можно, составив логарифмический график частного:
Теперь график симметричен, или хотя бы приблизительно таков, и центрирован относительно значения , которое является логарифмом .
Но остаётся более серьёзная тайна. Пилообразная волна очень регулярна и имеет период , при этом не показывает признаков сжатия по направлению к ожидаемому ограничивающему значению . Численные значения предполагают, что при стремлении к бесконечности пики кривой сходятся к значению чуть выше , а минимумы приближаются к значению чуть ниже . (Соответствующие логарифмы по основанию примерно равны ). Мне не удалось разобраться, почему так происходит. Возможно, кто-то сможем объяснить.
Неудача с этим жадным алгоритмом не означает, что мы не сможем делительный факториал, сходящийся к .
Если мы будем работать с логарифмами числителей, то эта процедура становится случаем хорошо известной вычислительной задачи под названием «задача разбиения множества чисел». Нам даётся множество вещественных чисел, и мы должны разделить их на два множества, сумма которых равна, или как можно ближе к равенству. Это подтверждённо сложная задача, но её также называют (PDF) «простейшей сложной задачей».
Для любого мы можем обнаружить, что при использовании обратных значений какого-то другого подмножества числителей даёт нам лучшее приближение к . Для малых мы можем решить эту задачу способом перебора: просто рассмотреть все подмножеств и выбрать самое лучшее.
Я вычислил оптимальные разбиения вплоть до , когда выбирать нужно из миллиарда вариантов.
Очевидно, что график становится всё более плоским. Можно использовать тот же метод для принудительного схождения к любому другому значению в интервале от до .
И таким образом мы получаем ещё один ответ на вопрос, заданный твитом и начавший наше путешествие. Что произойдёт, если мы будем делить, а не умножать в ? Всё, что нам угодно.
| ГОСТы, СНиПы Карта сайта TehTab.ru Поиск по сайту TehTab.ru | Навигация по справочнику TehTab.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Нашли ошибку? Есть дополнения? Напишите нам об этом, указав ссылку на страницу. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
TehTab.ru Реклама, сотрудничество: [email protected] | Обращаем ваше внимание на то, что данный интернет-сайт носит исключительно информационный характер. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Все риски за использование информаци с сайта посетители берут на себя. Проект TehTab.ru является некоммерческим, не поддерживается никакими политическими партиями и иностранными организациями. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ru: главная страница / / Техническая информация/ / Математический справочник/ / Таблицы численных значений. (Таблица квадратов, кубов, синусов ….) + Таблицы Брадиса / / Точная и приблизительная таблицы факториалов (1-255)
ru:Калькулятор факториалов онлайн (n!)
Число:
Факториал:
Онлайн-калькулятор факториала помогает вычислить факториал (n!) Заданного положительного числа n. Кроме того, вы можете складывать, вычитать, умножать и делить факториал двух чисел с помощью калькулятора для поиска факториалов.
Здесь для вас у нас есть факторное определение, как его вычислить, и некоторые важные материалы, которые могут лучше всего подойти для вас!
Содержание
- Что такое факториал?
- Формула для вычисления факториала
- Почему невозможно иметь отрицательный факторный фактор?
- Факториал нуля (0!) — это особый случай:
- Часто задаваемые вопросы (FAQ):
- Как рассчитать факториал в Excel?
- При чем здесь символ! иметь в виду?
- Сколько N факториалов умножить на n факториалов?
- Как мне ответить на этот вопрос? (к + 1)! + (k + 1) !?
- Заключительные слова:
- Таблица факториалов до 30
В математике функция факториала (!) Называется произведением каждого положительного числа от 1 до n.
Например: если n = 5, то 5! это n! = 1 * 2 * 3 * 4 * 5 = 120. Если n = 7, то 7! равно 1 * 2 * 3 * 4 * 5 * 6 * 7 = 5040.
Что ж, вы также можете найти количество возможных комбинаций из большого набора данных с помощью онлайн-калькулятора комбинаций.
И, если вы хотите определить количество возможных подмножеств из разных порядков, то калькулятор перестановок — лучший способ!
Данная формула поможет рассчитать факториал:
n!=n×(n−1)×(n−2)×…….×1
Где, n — это желаемое число, для которого вы хотите произвести расчеты.
Кроме того, вы можете просто добавить положительное число в онлайн-калькулятор факториалов и позволить ему просто факторизовать в течение нескольких секунд.
Рассмотрим этот бесплатный калькулятор разложения на простые множители, который помогает вычислять простые множители любого числа, создавать список всех простых чисел вплоть до любого числа.
Почему невозможно иметь отрицательный факторный фактор?Факториальная формула ясно показывает, что она может применяться только к положительным числам, которые обязывают нас не опускаться ниже. 1. Поскольку он дает количество способов перестановки объекта, вы не можете иметь объект меньше нуля(0).
Прежде всего, имейте в виду, что 0! равно одному (0!=1). Это похоже на ошибку, но это факт, поэтому это особый случай. Теперь углубимся в эту логику:
Проблема, которая возникла, когда мы собирались вычислить факториал 0 в том, что:
0! = 0!×(0−1)!
Мы знаем, что факториал п определяется только тогда, когда п>0, вот где и происходит путаница. Срок(0−1)!дает неопределенные результаты в математике и не имеет такого же значения, как при делении на ноль. Проблема не в том, что вы не можете его вычислить, а просто в том, что в этом нет никакого смысла. Если мы поместим значение0! к 1, мы можем получить ожидаемые значения для п!. Наш калькулятор факториалов определяет факториал нуля и других положительных целых чисел.
Часто задаваемые вопросы (FAQ):Как рассчитать факториал в Excel?Используйте функцию=FАCТ, чтобы вычислить факториал данного числа.
Это математическое выражение, обозначенное восклицательным знаком «! также упоминается для факториальной функции». Вы должны умножить все числа, которые существуют между числами, чтобы вычислить факториал числа.
Сколько N факториалов умножить на n факториалов?Поскольку формула n(n−1)! означает n раз (n−1)!. Итак, чем меньше множитель, тем больше факториал N.
Как мне ответить на этот вопрос? (к + 1)! + (k + 1) !?Вы можете ответить на этот вопрос, умножив (k+1)! к 2.
Заключительные слова:Факториал числа может быть полезен в статистике для определения перестановки и комбинации чисел. Кроме того, когда дело доходит до исчисления, он определяет ряд Тейлора, биномиальную теорему для симметризации операций и производной n-й функции и многое другое. Просто вы можете использовать этот онлайн-калькулятор факториала, который помогает студентам, а также профессионалам вычислять факториал чисел.
Таблица факториалов до 30
| n | n! |
|---|---|
| 1 | 1 |
| 2 | 2 |
| 3 | 6 |
| 4 | 24 |
| 5 | 120 |
| 6 | 720 |
| 7 | 5040 |
| 8 | 40320 |
| 9 | 362880 |
| 10 | 3628800 |
| 11 | 39916800 |
| 12 | 479001600 |
| 13 | 6227020800 |
| 14 | 87178291200 |
| 15 | 1307674368000 |
| 16 | 20922789888000 |
| 17 | 355687428096000 |
| 18 | 6402373705728000 |
| 19 | 121645100408832000 |
| 20 | 2432902008176640000 |
| 21 | 51090942171709440000 |
| 22 | 1124000727777607680000 |
| 23 | 25852016738884976640000 |
| 24 | 620448401733239439360000 |
| 25 | 15511210043330985984000000 |
| 26 | 403291461126605635584000000 |
| 27 | 10888869450418352160768000000 |
| 28 | 304888344611713860501504000000 |
| 29 | 8841761993739701954543616000000 |
| 30 | 265252859812191058636308480000000 |
Факториал на алгоритмическом языке — Altarena.
ru — технологии и ответы на вопросыСодержание
- Алгоритмы быстрого вычисления факториала
- Пятничный JS: единственно верный способ вычисления факториала
- Введение
- Начнём издалека
- Что-то это напоминает
- Скрещиваем ежа с ужом
- Заключение
- Факториал на алгоритмическом языке
- Наивный алгоритм
- Готовые работы на аналогичную тему
- Алгоритм вычисления деревом
- Алгоритм вычисления факторизацией
- Самый быстрый факториал
- 8 ответов 8
- Типы со знаком (signed)
- Типы без знака (unsigned)
- 64-разрядные типы
- Сколькими способами можно записать факториал на Scheme?
- Видео
Алгоритмы быстрого вычисления факториала
Понятие факториала известно всем. Это функция, вычисляющая произведение последовательных натуральных чисел от 1 до N включительно: N! = 1 * 2 * 3 *… * N. Факториал — быстрорастущая функция, уже для небольших значений N значение N! имеет много значащих цифр.
Попробуем реализовать эту функцию на языке программирования. Очевидно, нам понадобиться язык, поддерживающий длинную арифметику. Я воспользуюсь C#, но с таким же успехом можно взять Java или Python.
Итак, простейшая реализация (назовем ее наивной) получается прямо из определения факториала:
На моей машине эта реализация работает примерно 1,6 секунд для N=50 000.
Далее рассмотрим алгоритмы, которые работают намного быстрее наивной реализации.
Алгоритм вычисления деревом
Первый алгоритм основан на том соображении, что длинные числа примерно одинаковой длины умножать эффективнее, чем длинное число умножать на короткое (как в наивной реализации). То есть нам нужно добиться, чтобы при вычислении факториала множители постоянно были примерно одинаковой длины.
Пусть нам нужно найти произведение последовательных чисел от L до R, обозначим его как P(L, R). Разделим интервал от L до R пополам и посчитаем P(L, R) как P(L, M) * P(M + 1, R), где M находится посередине между L и R, M = (L + R) / 2.
Заметим, что множители будут примерно одинаковой длины. Аналогично разобьем P(L, M) и P(M + 1, R). Будем производить эту операцию, пока в каждом интервале останется не более двух множителей. Очевидно, что P(L, R) = L, если L и R равны, и P(L, R) = L * R, если L и R отличаются на единицу. Чтобы найти N! нужно посчитать P(2, N).
Посмотрим, как будет работать наш алгоритм для N=10, найдем P(2, 10):
P(2, 10)
P(2, 6) * P(7, 10)
( P(2, 4) * P(5, 6) ) * ( P(7, 8) * P(9, 10) )
( (P(2, 3) * P(4) ) * P(5, 6) ) * ( P(7, 8) * P(9, 10) )
( ( (2 * 3) * (4) ) * (5 * 6) ) * ( (7 * 8) * (9 * 10) )
( ( 6 * 4 ) * 30 ) * ( 56 * 90 )
( 24 * 30 ) * ( 5 040 )
720 * 5 040
3 628 800
Получается своеобразное дерево, где множители находятся в узлах, а результат получается в корне
Реализуем описанный алгоритм:
Для N=50 000 факториал вычисляется за 0,9 секунд, что почти вдвое быстрее, чем в наивной реализации.
Алгоритм вычисления факторизацией
Для наглядности посчитаем, сколько раз двойка содержится в 10! Двойку дает каждый второй множитель (2, 4, 6, 8 и 10), всего таких множителей 10 / 2 = 5.
Каждый четвертый дает четверку (2 2 ), всего таких множителей 10 / 4 = 2 (4 и 8). Каждый восьмой дает восьмерку (2 3 ), такой множитель всего один 10 / 8 = 1 (8). Шестнадцать (2 4 ) и более уже не дает ни один множитель, значит, подсчет можно завершать. Суммируя, получим, что показатель степени при двойке в разложении 10! на простые множители будет равен 10 / 2 + 10 / 4 + 10 / 8 = 5 + 2 + 1 = 8.
Если действовать таким же образом, можно найти показатели при 3, 5 и 7 в разложении 10!, после чего остается только вычислить значение произведения:
10! = 2 8 * 3 4 * 5 2 * 7 1 = 3 628 800
Осталось найти простые числа от 2 до N, для этого можно использовать решето Эратосфена:
Эта реализация также тратит примерно 0,9 секунд на вычисление 50 000!
Как справедливо отметил pomme скорость вычисления факториала на 98% зависит от скорости умножения. Попробуем протестировать наши алгоритмы, реализовав их на C++ с использованием библиотеки GMP. Результаты тестирования приведены ниже, по ним получается что алгоритм умножения в C# имеет довольно странную асимптотику, поэтому оптимизация дает относительно небольшой выигрыш в C# и огромный в C++ с GMP.
Однако этому вопросу вероятно стоит посвятить отдельную статью.
Все алгоритмы тестировались для N равном 1 000, 2 000, 5 000, 10 000, 20 000, 50 000 и 100 000 десятью итерациями. В таблице указано среднее значение времени работы в миллисекундах.
График с линейной шкалой
График с логарифмической шкалой
Идеи и алгоритмы из комментариев
Хабражители предложили немало интересных идей и алгоритмов в ответ на мою статью, здесь я оставлю ссылки на лучшие из них
Исходные коды реализованных алгоритмов приведены под спойлерами
Источник
Пятничный JS: единственно верный способ вычисления факториала
Введение
Вычисление факториала — одна из традиционных программистских задач для собеседований. Если вдруг кто забыл, факториал натурального числа N обозначается как N! и равняется произведению всех натуральных чисел от единицы до N включительно. Например, . Казалось бы, что тут сложного? Однако есть свои нюансы.
Например, сравним два самых распространённых способа вычисления факториала.
Многие скажут, что первый способ лучше, но это не так. Во-первых, циклы уже не в тренде, сейчас модно функциональное программирование. Во-вторых, чем больше людей используют второй способ, тем быстрее в основных джаваскриптовых движках появится оптимизация хвостовой рекурсии.
В любом случае, оба эти способа слишком примитивны, чтобы по ним судить о знаниях кандидата. А вот опытный разработчик на React.js уже может написать что-то в этом роде:
Согласитесь, выглядит гораздо солиднее. Впрочем, невооружённым глазом видно, что это всего лишь вариант рекурсивного вычисления. Сходство станет ещё сильнее, если переписать Factorial как функциональный компонент. И, разумеется, я не стал бы писать этот хабрапост, если бы не был готов предложить нечто принципиально новое.
Начнём издалека
Какую из возможностей Javascript недолюбливают и недооценивают сильнее всего? Недолюбливают настолько, что про неё даже придумали специальную поговорку? Конечно же, это eval. Можно сказать, что eval — это тёмная сторона Силы.
А как мы помним из фильмов Джорджа Лукаса, нет ничего более крутого и впечатляющего, чем тёмная сторона Силы, поэтому давайте попробуем ей овладеть.
Можно было бы запихнуть в строку какой-нибудь из методов, приведённых в начале поста, а затем передать эту строку в eval, но в этом не было бы новизны. Поставим задачу таким образом, чтобы сделать этот хак невозможным. Пусть у нас есть такой вот каркас:
— и мы хотим, внеся изменения лишь в литерал строки f, сделать так, чтобы функция factorial взаправду вычисляла факториал. Вот задача, достойная истинного ситха.
Что-то это напоминает
Нам нужен код, который возвращает код, который возвращает код… Если забыть про конечную задачу — вычисление факториала, то есть одна хорошо известная штука, которая нам подойдёт. Эта штука называется квайн — программа, которая выводит свой собственный текст.
Про квайны на Хабре написано уже немало, потому я напомню лишь основные принципы квайностроительства.
Чтобы сделать простейший квайн, нам нужно:
В строке o.s содержится весь остальной код, а также специальные подстановочные последовательности, начинающиеся с подчёркивания. Страшное выражение внутри console.log заменяет каждую подстановочную последовательность на соответствующее свойство объекта o, что обеспечивает выполнение пунктов 2 и 3 хитрого плана по созданию квайна.
Здесь меня могут поправить: товарищ, это не простейший квайн, а монстр какой-то. Простейший квайн на js выглядит так:
Это правда, но не совсем. Такой квайн считается «читерским», поскольку он из тела функции получает доступ к её же тексту. Это почти то же самое, что прочитать с жёсткого диска файл с исходным кодом программы. Моветон, одним словом.
Скрещиваем ежа с ужом
Как же сделать так, чтобы наш квази-квайн модифицировал сам себя, а в результате превратился в одно-единственное число? Давайте забудем пока про вычисление факториала и постараемся просто написать строку, которая «схлопывается» через определённое количество eval’ов.
Для этого нам понадобится:
Обратите внимание на отсутствие return внутри строки: в нём нет необходимости, eval возвращает значение последнего выражения. Запустив этот код в консоли, можно c благоговением наблюдать, как с каждой итерацией цикла значение n уменьшается на 1. Если кто-то скажет, что для такого эффекта достаточно:
— то у него нет чувства прекрасного.
После этого подготовительного этапа уже совсем нетрудно написать итоговую версию вычисления факториала. Просто добавляется ещё одна переменная и чуть усложняется строчка с изменением.
Теперь вы можете смело идти на собеседование.
Заключение
С живым кодом можно поиграться здесь. Как и в прошлой статье из рубрики «Пятничный JS» напоминаю: если вы сделаете что-нибудь подобное на продакшене, то попадёте в ад. С другой стороны, если вы сделаете это на собеседовании, то вам не дадут возможности сделать это на продакшене, и вы не попадёте в ад. Так что делайте это на собеседовании. Спасибо за внимание.
Источник
Факториал на алгоритмическом языке
Алгоритмы для вычисления факториала — это алгоритм определения произведения всех натуральных чисел, начиная от единицы и до заданного числа включительно.
Под термином факториал числа понимается функция, которая вычисляет произведение последовательности натуральных чисел от единицы до N включительно: N! = 1 • 2 • 3 • … • N. Факториал является очень быстро увеличивающейся функцией, поскольку даже при относительно малых по величине N, значение его факториала будет уже многоразрядным. Рассмотрим некоторые алгоритмы, позволяющие вычислить факториал числа.
Наивный алгоритм
Этот алгоритм является самой простой реализацией, так как просто выполняет действия, заложенные в определении факториала:
Готовые работы на аналогичную тему
Рисунок 1. Наивный алгоритм. Автор24 — интернет-биржа студенческих работ
Эта программа выполняется за интервал времени менее двух секунд для N до пятидесяти тысяч.
Но есть и более продвинутые алгоритмы и один из них рассмотрим далее.
Алгоритм вычисления деревом
Этот алгоритм базируется на таком положении, что операция умножения с числами большой и примерно одинаковой разрядности будет эффективнее умножения большого числа на маленькое. Исходя из этого, необходимо обеспечить при определении факториала примерно равный размер сомножителей на постоянной основе. Пускай требуется вычислить произведение последовательности чисел от L до R. Введём обозначение этого произведения как Р (L, R). Поделим промежуток между L и R на два и вычислим Р (L, R) как P(L, M) • P(M + 1, R), здесь M является серединой чисел L и R, то есть M = (L + R) / 2. Следует отметить, что сомножители получаются примерно одинаковыми. Затем по аналогии разбиваем далее P(L, M) и P(M + 1, R). Эту процедуру необходимо выполнять до тех пор, пока каждый интервал не будет иметь больше двух сомножителей. Понятно, что Р (L, R) = L, когда L и R равны, и P(L, R) = L • R, если L и R имеют единичное отличи.
Для того, чтобы вычислить N!, требуется определить Р(2, N). Рассмотрим действие этого алгоритма для N=10, определим Р (2, 10):
( P(2, 4) • P(5, 6) ) • ( P(7, 8) • P(9, 10) )
( (P(2, 3) • P(4) ) • P(5, 6) ) • ( P(7, 8) • P(9, 10) )
( ( (2 • 3) • (4) ) • (5 • 6) ) • ( (7 • 8) • (9 • 10) )
( ( 6 • 4 ) • 30 ) • ( 56 • 90 )
В итоге мы получили подобие дерева, у которого сомножители расположены в узлах, а результирующее значение находится в корневой системе.
Рисунок 2. Дерево. Автор24 — интернет-биржа студенческих работ
Программная реализация этого алгоритма приведена ниже:
Рисунок 3. Программа. Автор24 — интернет-биржа студенческих работ
По этой программе для числа пятьдесят тысяч вычисление факториала длится менее секунды, что в два раза быстрее предыдущего алгоритма.
Алгоритм вычисления факторизацией
Далее с возрастанием степени будет такая же картина. В финале имеем следующую формулу для показателя степени простого сомножителя К:
$N / K+ N / K^2 + N / K^3 + N / K^4 +…$
Для примера определим, сколько раз двойка в различных степенях входит в факториал десяти.
32:
Поэтому начиная с 34 все результаты fac(uint32_t) будут равны нулю.
64-разрядные типы
Таким образом, использование таблицы факториалов из 66 элементов покроет всех типы до 64 разрядов:
Вот есть интересная статейка. Там предлагают считать факториал за O(loglogn*M(nlogn)) (где M(n) — время перемножения двух n-значных чисел). Быстрее вряд ли получится.
Также гляньте вот эту статью — там считают факториал по простому модулю.
Есть интересные материалы по этому поводу. Во-первых, есть калькулятор факториалов на JavaScript. Он мгновенно вычисляет факториалы чисел до 9.999.999.999
Там же есть материалы по алгоритмам факториалов: http://www.luschny.de/math/factorial/FastFactorialFunctions.htm. Я думаю, тут действительно хорошие алгоритмы 😉
На этом же сайте описывается некий метод, который, как я понял использовался в калькуляторах HP. Некий RPN-калькулятор.
Думаю, что самый быстрый алгоритм вычисления факториала определяется структурой вычислительных средств.
Например, формула Стирлинга допускает представление вида
n!
Ну я такой вариант сочинил.
Вопрос очень быстро решается при помощи гугла, ответ взят с сайта algolist.manual.ru:
Вот приближение десятичного логарифма факториала:
Целая часть этого покажет количество знаков числа-1, а с мантиссой можно работать.
Можно вычислять факториал как eln(n!), и это будет быстрее, чем прямое умножение. Но это не будет точное значение для больших значений n, где есть реальный выигрыш в скорости.
Тем не менее, часто(например, в вычислении биномиальных коэффициентов) нам нужен не сам факториал, а некое значение, получающееся в результате деления громадного факториала на другие числа того же порядка, и в результате получается небольшое число.
В этом случае имеет смысл оперировать именно с логарифмом факториала, который вычисляется (как видно, например, из исходника выше) гораздо проще и быстрее. Деление и умножение будут заменены разностью и суммой логарифмов.
Если нужны реально эффективные вычисления, то такой путь при контроле точности вычислений, безусловно, предпочтительнее.
Источник
Сколькими способами можно записать факториал на Scheme?
Рассмотрим некоторые возможные способы записи вычисления факториала. Заодно получится своеобразная ода языку программирования Scheme. Думаю, этот замечательный язык того вполне заслуживает.
У меня получилось 10 вариантов записи определений функций, которые можно свести к 3 основным способам вычисления: традиционному линейно-рекурсивному вычислительному процессу, итерации, генерации последовательности чисел с последующей сверткой умножением. Предлагаю рассмотреть эти варианты подробнее. Попутно мы рассмотрим: оптимизацию хвостовой рекурсии, функции высших порядков и метапрограммирование, отложенные вычисления, бесконечные списки, мемоизацию, способ создать статическую переменную в Scheme и гигиенические макросы.
Для экспериментов был использован старый добрый диалект Scheme R5RS и популярный принцип изобразительного искусства «минимум средств — максимум впечатлений».
Все примеры на Scheme были подготовлены в среде DrRacket 6.2 в режиме R5RS. Замеры времени выполнения были выполнены в Guile 2.0 в среде ОС OpenSUSE Leap 15.
Для начала можно взять рекурсивное определение факториала и просто переписать формулу на Scheme:
Получилось определение функции (в терминах Scheme — процедуры, хотя по-сути она является функцией) для вычисления факториала, которое можно увидеть в бесчисленном множестве руководств по программированию, начиная с бессмертной книги Х. Абельсона и Д. Сассмана «Структура и интерпретация компьютерных программ».
Читать и понимать этот код можно так: факториал есть если , иначе — . Таким образом, этот код соответствует рекурсивному определению факториала, принятому в математике. Единственное, мы не проверяем принадлежность неотрицательным числам.
Будучи рекурсивным, код выше содержит очевидное ограничение на величину : на стеке будут накапливаться данные рекурсивных вызовов, пока не достигнет 0. Это может вызвать переполнение стека при больших .
Как можно снять это ограничение? Надо оптимизировать хвостовую рекурсию: переписать код таким образом, чтобы рекурсивный вызов стал хвостовым (т.е. последним в процедуре). Это позволит интерпретатору Scheme выполнить оптимизацию — заменить рекурсивное вычисление итеративным.
Если воспользоваться рекомендациями авторов упомянутой выше книги, можно получить следующее:
Этот код является расхожим примером, и, начиная с книги «Структура и интерпретация компьютерных программ», именно на нем обычно объясняют оптимизацию хвостовой рекурсии.
Scheme славится своим удобством для символьных вычислений в силу «единства кода и данных» (так иногда говорят о языках семейства Лисп). Используем эту особенность: сформируем выражение для вычисления факториала числа , а затем его вычислим:
Scheme поддерживает отложенные вычисления. Haskell, который испытал значительное влияние Scheme, использует ленивую модель вычислений, т.е. не вычисляет значение выражения до тех пор, пока результат этих вычислений не будет востребован.
Это позволяет иметь в программах такие своеобразные структуры данных, как бесконечные списки. Если из них брать только часть, необходимую для дальнейших вычислений, программа не будет зацикливаться:
На Haskell получение из бесконечного списка можно записать так:
Используя пару форм Scheme delay / force попробуем сделать нечто подобное. Ключевое слово delay создает обещание вычислить значение выражения. Ключевое слово force распоряжается осуществить эти вычисления, полученное значение вычисляется и запоминается. При повторном обращении новых вычислений не производится, а возвращается значение, вычисленное ранее.
Конструктор ленивой пары lazy-cons реализован в виде макроса. Это сделано для того, чтобы избежать вычисления значения второго элемента пары при ее создании.
Идея состоит в том, чтобы создать бесконечный список значений, а потом взять из него то, которое нужно. Для этого определим ленивую версию процедуры для получения элемента по индексу:
Здесь n! и n+1 — имена переменных.
В Scheme, по-сравнению с другими языками, существует очень немного символов, которые нельзя использовать в идентификаторах.
Обратите внимание, что генератор бесконечного списка generate-factorials не содержит выхода из рекурсии. Тем не менее, он не будет зацикливаться, так как при его вызове будет вычисляться только голова списка, хвост же будет представлен обещанием вычислить значение.
Теперь можно определить как получение -го элемента списка факториалов:
Это работает. При этом, если в одной сессии интерпретатора вычислять факториалы различных чисел, то вычисления будут происходить быстрее, чем в строгих версиях, ведь часть значений в ленивом списке будет уже вычислена.
Кстати, для повышения производительности можно применить запоминание уже вычисленных значений — мемоизацию. Будем хранить вычисленные значения в ассоциативном списке, в котором ключами будут числа, а значениями — их факториалы. При вызове, просмотрим список на предмет уже вычисленных значений. Если значение присутствует в списке, будем возвращать это сохраненное значение.
Если значение в списке отсутствует, будем вычислять его, помещать в список, и только потом возвращать. Чтобы этот список всегда находился при вызываемой функции, а не в глобальном окружении, разместим его в статической переменной:
является принятым в Scheme способом создать процедуру со статической переменной. Принцип такого объявления удобно пояснить на более коротком примере — процедуре, возвращающей число своих вызовов:
В одной сессии интерпретатора первый вызов (count) вернет 1, второй — 2, третий — 3 и т.д. Как это работает?
Без синтаксического сахара определение count выглядит так:
Данная реализация также обещает прирост производительности при неоднократном вычислении факториалов различных чисел в одной сессии интерпретатора.
Разумеется, здесь также возможна оптимизация хвостовой рекурсии:
Конструкция do — достаточно универсальная, и именно поэтому — не слишком удобочитаемая. Не лучше ли организовать свой собственный цикл в императивном стиле? В этом помогут макросы:
Благодаря оптимизации хвостовой рекурсии интерпретатором, получим цикл, к каким мы привыкли в императивных языках программирования.
Благодаря оптимизации хвостовой рекурсии, стек расти не будет.
Определение факториала с использованием for :
Отсюда, шаблоном синтаксического правила будет сформирован следующий код:
Возможен еще один вариант, внешне похожий на императивный цикл for — со встроенной процедурой for-each :
Велик и могуч язык Scheme! А что с производительностью?
Для замеров производительности воспользуемся GNU Guile — в этой среде можно замерить время вычисления выражения наиболее просто.
Guile работает следующим образом: компилирует исходный текст программы в байт-код, который затем выполняется виртуальной машиной. Это — только одна из реализаций и один из нескольких возможных способов выполнения программы на Scheme, существуют и другие: Racket (использует JIT-компиляцию), Chicken Scheme (использует «честную» интерпретацию или компиляцию в подмножество C) и т.д. Очевидно, что и ограничения, и производительность программ в этих средах могут несколько отличаться.
Замеры будем производить при некотором значении .
Каким должно быть это ? Таким, с каким наибольшим смогут «справиться» предложенные варианты. С настройками Guile 2.0 по-умолчанию, на ПК с Intel Core i5 и 4 Гб ОЗУ, меня получилось следующее:
| Процедура | Проблема |
|---|---|
| factorial-classic | переполнение стека при 10\,000$» data-tex=»inline»> |
| factorial-classic-tco | нет ( ) |
| factorial-fold | переполнение стека при 10\,000$» data-tex=»inline»> |
| factorial-eval | переполнение стека при 8\,000$» data-tex=»inline»> |
| factorial-lazy | при использует раздел подкачки и зависает |
| factorial-memoized | переполнение стека при 10000$» data-tex=»inline»> только при первом запуске |
| factorial-memoized-tco | при 1\,000$» data-tex=»inline»> использует раздел подкачки и зависает |
| factorial-do | нет ( ) |
| factorial-for | нет ( ) |
| factorial-for-each | нет ( ) |
Отсюда, тесты производительности выполнялись при .
Результаты представлены в таблице ниже, где — время выполнения, — время работы сборщика мусора в секундах.
Для всех процедур, кроме ленивых и мемоизованных, указаны наименьшие значения времени выполнения и соответствующее ему время работы сборщика мусора, полученные по итогам трех запусков при .
Для мемоизованных и ленивых процедур указано время выполнения первого вызова, далее — меньшее из трех вызовов.
| Процедура | , с | , с | Примечания |
|---|---|---|---|
| factorial-classic | 0,051 | 0,034 | |
| factorial-classic-tco | 0,055 | 0,041 | |
| factorial-fold | 0,065 | 0,059 | |
| factorial-eval | 0,070 | 0,040 | |
| factorial-lazy | 0,076 | 0,036 | первый вызов |
| factorial-lazy | 0,009 | — | последующие вызовы |
| factorial-memoized | 0,077 | 0,041 | первый вызов |
| factorial-memoized | 0,002 | — | последующие вызовы |
| factorial-memoized-tco | 0,077 | 0,041 | первый вызов |
| factorial-memoized-tco | 0,002 | — | последующие вызовы |
| factorial-do | 0,052 | 0,025 | |
| factorial-for | 0,059 | 0,044 | |
| factorial-for-each | 0,066 | 0,042 |
У нас есть 4 варианта, которые могут работать с большими .
При они имеют следующие времена вычисления и сборки мусора:
| Процедура | , с | , с |
|---|---|---|
| factorial-classic-tco | 8,468 | 6,628 |
| factorial-do | 8,470 | 6,632 |
| factorial-for | 8,440 | 6,601 |
| factorial-for-each | 9,998 | 7,985 |
Можно видеть, что при не слишком больших наиболее быстрым и, одновременно, самым коротким и оказывается первый. Этот же вариант наиболее полно соответствует математическому определению факториала. Вариант с оптимизацией хвостовой рекурсии ему не сильно уступает в производительности. Оба этих варианта являются идиоматическими, рекомендованными авторами языка. Вывод во многом очевиден: если не оговорено иное, подход, являющийся для языка «типовым», является предпочтительным, по-крайней мере, для первой реализации алгоритма или метода.
В то же время, язык Scheme позволил написать нам много вариантов реализации вычисления факториала, используя при этом весьма ограниченный набор примитивов (то самое «минимум средств — максимум впечатлений»).
Поэтому, несмотря на почтенный возраст и не слишком широкую распространенность, этот язык всё ещё можно рекомендовать для исследовательского программирования: похоже, на нем можно реализовать всё что угодно и каким угодно (и каким удобно) способом.
Источник
Видео
Алгоритм нахождения факториала (Factorial algorithm)
Факториал
Java урок — 9.2 Рекурсия. Задача нахождения факториала числа n
Что такое факториал | Математика
Комбинаторика: перестановка, размещение и сочетание | Математика | TutorOnline
Рекурсия. Факториал числа c++ рекурсивно. Рекурсия факториал. Рекурсивный алгоритм факториал. #44
Факториал
Пошаговое объяснение программы для вычисления факториала
Факториал
Блок-схема циклического алгоритма. Вычисление n!
Калькулятор Факториалов — как посчитать факториал
Этот бесплатный онлайн-факториал калькулятор поможет вам посчитать факториал для заданных n чисел. Кроме того, калькулятор факториалов вычисляет факториал, а также выполняет следующие арифметические операции с факториалом двух чисел:
- Дополнение.
- Вычитание.
- Умножение.
- Дивизия.
Полностью прочтите этот важный и полезный контент, мы дадим определение, формулу, как посчитать факториал вручную и различные другие полезные термины, связанные с нашей темой.
Читать дальше!
что такое факториал формула?Формула, используемая в этом онлайн факториал калькулятор, следующая:
п! = n × (n – 1) × (n – 2) × ……. × 1
Куда,
n – желаемое число, для которого вы хотите произвести расчеты.
Рассмотрим этот бесплатный калькулятор разложения на простые множители, который помогает вычислять простые множители любого числа, создавать список всех простых чисел вплоть до любого числа.
Почему нельзя иметь отрицательный факторный фактор?Формула ясно показывает, что она может применяться только к положительным числам, которые ограничивают нас не опускаться ниже 1. Поскольку она дает количество способов перестановки объекта, у вас не может быть объекта меньше нуля (0).
Прежде всего, имейте в виду, что 0! равно единице (0! = 1). Это похоже на ошибку, но это факт, поэтому это особый случай. Теперь мы углубимся в эту логику:
Когда мы собирались вычислить факториал 0, возникла проблема:
0! = 0! * (0-1)!
Мы знаем, что факториал n определяется только тогда, когда n> 0, поэтому у нас есть проблема. Срок (0-1)! дает неопределенные результаты в математике и не имеет такого же значения, как при делении на ноль. Проблема не в том, что мы не можем его вычислить; проблема в том, что это не имеет никакого значения. Если поставить значение 0! равным 1, мы можем получить ожидаемые значения для n !. Наш факториал калькулятор также определяет факториал нуля и других положительных целых чисел.
Как использовать этот факторный калькулятор:Вычисление факториалов становится очень простым с этим бесплатным калькулятор факториалов, который определяет точные результаты заданных чисел.
Читать дальше!
Чтобы вычислить простой факториал (найдите n!):Чтобы найти n !, просто выполните следующие действия:
Входы:
• Прежде всего, введите номер, для которого вы хотите показать результат, в предназначенное для этого поле.
• Затем нажмите кнопку «Рассчитать».
Выходы:
После ввода в поле калькулятор показывает:
• Факториал числа.
• Пошаговые (расчеты).
Чтобы вычислить арифметические операции:Чтобы выполнять арифметические операции с факториалом заданных чисел, просто придерживайтесь следующих пунктов:
Входы:
• Прежде всего, введите первое число.
• Совсем рядом, плагин второй номер.
• Наконец, нажмите кнопку «Рассчитать».
Выходы:
Калькулятор показывает:
• Факториал обоих чисел.
• Арифметическая операция над факториалом двух чисел в соответствии с выбранной опцией.
• Пошаговые расчеты.
[Как рассчитать факторный] числа (шаг за шагом):* Формула *, используемая для вычисления между числами, следующая:
п! = n × (n – 1) × (n – 2) × ……. × 1
Куда,
n – номер.
Давайте приведем примеры для каждого метода, чтобы четко понять концепцию с полными пошаговыми вычислениями.
Найти!Приведем пример:
Например:
посчитать факториал 8?
Решение:
Здесь n = 8
Шаг 1:
8! = 8 × (8−1) × (8−2) × (8−3) × (8−4) × (8−5) × (8−6) × (8−7)
Шаг 2:
8! = 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1
Шаг 3:
8! = 40320
Чтобы найти (n! + M!):В качестве дополнения у нас есть пример:
Например:
Сложить факториал 3 и 4?
Решение:
Здесь n = 3
м = 4
Шаг 1:
Найдите n! = 3
3! = 3 × (3−1) × (3−2)
3! = 3 × 2 × 1
3! = 6
Шаг 2:
Найдите m! = 4
4! = 4 × (4−1) × (4−2) × (4−3)
4! = 4 × 3 × 2 × 1
4! = 24
Шаг 3:
п! + м! = 6 + 24
п! + м! = 30
Найти (n! – m!):Для вычитания у нас есть пример:
Например:
Вычтем факториал 5 и 3?
Решение:
Здесь n = 5
м = 3
Шаг 1:
Найдите n! = 5
5! = 5 × (5−1) × (5−2) × (5−3) × (5−4)
5! = 5 × 4 × 3 × 2 × 1
5! = 120
Шаг 2:
Найдите m! = 3
3! = 3 × (3−1) × (3−2)
3! = 3 × 2 × 1
3! = 6
Шаг 3:
п! – м! = 120 – 6
п! – м! = 114
Чтобы найти (n! X m!):Для умножения у нас есть пример:
Например:
Умножить факториал 7 и 4?
Решение:
Здесь n = 7
м = 4
Шаг 1:
Найдите n! = 7
7! = 7 × (7−1) × (7−2) × (7−3) × (7−4) × (7−5) × (7−6)
7! = 7 × 6 × 5 × 4 × 3 × 2 × 1
7! = 5040
Шаг 2:
Найдите m! = 4
4! = 4 × (4−1) × (4−2) × (4−3)
4! = 4 × 3 × 2 × 1
4! = 24
Шаг 3:
п! × м! = 5040 × 24
п! × м! = 120960
Найти (n! / M!):Для деления у нас есть пример:
Например:
Разделить факториал 5 и 6?
Решение:
Здесь n = 5
м = 6
Шаг 1:
Найдите n! = 5
5! = 5 × (5−1) × (5−2) × (5−3) × (5−4)
5! = 5 × 4 × 3 × 2 × 1
5! = 120
Шаг 2:
Найдите m! = 6
6! = 6 × (6−1) × (6−2) × (6−3) × (6−4) × (6−5)
6! = 6 × 5 × 4 × 3 × 2 × 1
6! = 720
Шаг 3:
п! / м! = 120/720
п! / м! = 0,16666
Вы можете использовать наш калькулятор факториалов, чтобы проверить все примеры, в которых все (вычисления) выполнялись согласно факториальной формуле , и точно определить быстрые результаты.
Что такое факториал?
Его можно определить как «число, которое является произведением всех положительных целых чисел, меньших или равных числу n». Он представлен восклицательным знаком (!). Проще говоря, это функция, которая умножает число на каждое число под ним.
Как рассчитать факториал?Это число, которое определяется умножением его «минус один», затем «минус два» и так далее до 1. Оно обозначается как n !.
Как рассчитать факториал в Excel?Excel использует функцию = ФАКТ, чтобы вычислить факториал данного числа.
Что значит символ! подлый?Это математическое выражение, помеченное восклицательным знаком «!». Вы должны умножить все числа, которые существуют между числами, чтобы посчитать факториал числа.
Сколько N факториалов умножить на n факториалов?Поскольку формула n (n-1)! означает n раз (n-1) !.
Итак, чем меньше фактор большего факториала N.
Вы можете ответить на этот вопрос, умножив (k + 1)! пользователем 2.
Заключительные слова:Факториал числа может быть полезен в статистике для определения перестановки и комбинации чисел. Кроме того, когда дело доходит до исчисления, он определяет ряд Тейлора, биномиальную теорему для симметризации операций и производной n-й функции и многое другое. Просто вы можете использовать этот онлайн калькулятор факториалов , который помогает студентам, а также профессионалам вычислять факториал чисел.
Other Languages: Factorial Calculator, Faktöriyel Hesaplama, Silnia Kalkulator, Fakultät Rechner, Kalkulator Faktorial, 階乗 計算, 팩토리얼 계산기, Faktoriál Kalkulačka, Calculadora Fatorial, Calcul Factoriel, Fattoriale Di Un Numero
Формула вычисления факториала числа
Определение факториала и числа перестановок
Пусть имеется $n$ различных объектов.
Будем переставлять их всеми возможными способами (число и состав объектов остается неизменными, меняется только их порядок). Получившиеся комбинации называются перестановками, а их число равно
$$P_n=n!=1cdot 2cdot 3 cdot . cdot (n-1) cdot n$$
Символ $n!$ называется факториалом и обозначает произведение всех целых чисел от $1$ до $n$. По определению, считают, что $0!=1, 1!=1$. Факториал растет невероятно быстро (недаром он обозначается восклицательным знаком!), например, $$10!=3628800,$$ а $$50!=30414093201713378043612608166064768844377641568960512000000000000.$$ Как найти факториал? Умножать вручную, использовать функцию ФАКТР() в Excel или, если устанете умножать самостоятельно, используйте калькулятор ниже.
Пример всех перестановок из $n=3$ объектов (различных фигур) – на картинке справа. Согласно формуле ниже, их должно быть ровно $P_3=3!=1cdot 2cdot 3 =6$, так и получается (вам не напоминает картинка табло игральных автоматов?:)).
Общая формула, которая позволяет найти число перестановок из $n$ элементов, имеет вид (она же – формула для факториала числа $n$):
$$P_n=n!=1cdot 2cdot 3 cdot . cdot (n-1) cdot n.$$
Найти число перестановок из n элементов
Чтобы вычислить число перестановок $P_n$ онлайн, используйте калькулятор ниже.
Видеоролик о перестановках и Excel
Не все понятно? Посмотрите наш видеообзор для формулы перестановок: как использовать Excel для нахождения факториала и числа перестановок, как решать типовые задачи и использовать онлайн-калькулятор.
Расчетный файл из видео можно бесплатно скачать
Полезные ссылки
Поиск решенных задач
Решебник по комбинаторике и теории вероятностей:
- Как найти факториал числа
- Как найти n в арифметической прогрессии
- Как найти наибольшее из чисел
Чтобы найти факториал числа, необходимо вычислить произведение всех чисел, в промежутке от 1 до заданного числа. k = (n + k -1)!/(n – 1)!
Праймориал числа равен произведению простых чисел меньше самого числа и обозначается #, например:
12# = 2*3*5*7*11, очевидно, что 13# = 11# = 12#.
Суперфакториал равен произведению факториалов чисел на интервале от 1 до исходного числа, т.е.:
sf(n) = 1!*2!*3*…(n – 1)!*n!, например, sf(3) = 1!*2!*3! = 1*1*2*1*2*3 = 12.
Факториал натурального числа n – произведение первых по счету, n натуральных чисел от 1 до n включительно, обозначается n!
n! = 1 • 2 • 3 • 4 • 5 • . • n
Факториа́л числа – это число, умноженное на «себя минус один», затем на «себя минус два» и так далее, до единицы.
n! = n • (n – 1) • (n – 2) • . • 1
Для приближённого вычисления факториала и гамма-функции используется формула Стирлинга . Названа в честь Джеймса Стирлинга и Абрахама де Муавра, последний считается автором формулы
Вычисление факториала числа (n!) по формуле в Стирлинга. Этот калькулятор может быть использован для вычисления значений n больше 100.
Расчет факториала по формуле Джеймса Стирлинга
Приближенное значение не ограничено по колличеству n
Расчет факториала от 0 до 100
Точное значение, ограниченное по колличеству n
Формула Джеймса Стирлинга для расчета факториала
n! ≈ √(2π) × n (n+1/2) × e -n
Примеры значений для разных n:
1! = 1
2! = 2 × 1 = 2
3! = 3 × 2 × 1 = 6
4! = 4 × 3 × 2 × 1 = 24
5! = 5 × 4 × 3 × 2 × 1 = 120
Не стоит забывать
По общепринятой договоренности 0! = 1 (факториал нуля равен единице). Этот факт важен, к примеру, для вычисления биномиальных коэффициентов.
Полезный факт
Факториал числа, функцию от натурального аргумента можно продолжить на все действительные числа с помощью т.н. Гамма-функции (важно отметить, что для этого требуется определенный математический аппарат). В таком случае, мы сможем посчитать факториал любого действительного числа. Например, факториал (или, Гамма-функция, что математически правильнее) числа Пи. π! приблизительно равен 2.28803779534 . Факториал числа Эйлера, другого трансцендентного числа, Γ(e)
1.567468255 (упрощенно, факториал числа e ).
алгебраическое предварительное исчисление — Упрощение дроби с факториалами: $\frac{(3(n+1))!}{(3n)!}$
спросил
Изменено 5 лет, 7 месяцев назад
Просмотрено 3к раз
$\begingroup$
Я пытался решить лимит: 9{3n}}}$$
Используя корневой критерий пределов (который справедлив в данном случае, поскольку $b_n$ монотонно возрастает):
$$L= \lim_{n \to \infty} \frac{ a_n}{b_n} = \lim_{n \to \infty} \frac{a_{n+1}-a_n}{b_{n+1}-b_n}$$
Теперь я понимаю, что использование формулы Стерлинга сделает все проще, но мой первый подход заключался в упрощении факториала после применения критерия, о котором я упоминал ранее. Итак, после нескольких неудачных попыток я посмотрел на Mathematica, и там было сказано, что $\frac{(3(n+1))!}{(3n)!}$ (это одна из дробей, которую нужно упростить) равно $3(n+1)(3n+1)(3n+2)$. Поскольку я не могу добраться туда сам, я хочу знать, как бы вы это сделали. 93
\end{align}$$
как и ожидалось!
Используемые инструменты: суммы Римана и непрерывность экспоненциальной функции.
$\endgroup$
$\begingroup$
$$ (3(n+1))! \neq 3 \cdot 2 \cdot 3 \cdot 3 \cdot 3 \cdot 4 \cdots 3 \cdot (n+1) $$ Чтобы было понятно, в чем проблема, запишем правую часть в скобках: $ $ (3 \cdot 2) \cdot (3 \cdot 3) \cdot (3 \cdot 4) \cdots (3 \cdot (n+1)) $$ Это просто умножение всех положительных кратных 3 меньше, чем $ 3 (n+1) $ вместе; факториал определяется как умножение все целых положительных чисел меньше $ 3(n+1) $. Таким образом, правильное расширение: \begin{align*}
(3(n+1))! &= 2 \cdot 3 \cdot 4 \cdot 5 \cdot 6 \cdots (3n-2) \cdot (3n-1) \cdot 3n \cdot (3n+1) \cdot (3n+2) \cdot 3( п+1) \\
(3н)! &= 2 \cdot 3 \cdot 4 \cdot 5 \cdot 6 \cdots (3n-2) \cdot (3n-1) \cdot 3n
\конец{выравнивание*}
у которых явно есть частное, которое Mathematica дала вам.
$\endgroup$
1
$\begingroup$ 9а $.
$\endgroup$
4
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
. 92 \cdot 7 &= n! \\
\end{array}$$Я действительно не видел, чтобы это мне помогало.
Затем я попробовал $6 \cdot 6 \cdot 6 \cdot 6 \cdot 25 \cdot 16 \cdot 7$, но $25$ имеет только $5$ в качестве двойного коэффициента.
Есть идеи?
- факториал
$\endgroup$
2
$\begingroup$
У нас есть
$$3!\cdot 5!\cdot 7!=(1\cdot 2\cdot 3)\cdot (1 \cdot 2\cdot 3\cdot 4\cdot 5)\cdot 1\cdot 2 \cdot 3\cdot 4\cdot 5\cdot 6\cdot 7,$$
и объединение некоторых из них дает
$$1\cdot 2\cdot 3\cdot 4\cdot 5\cdot 6\cdot 7\cdot \underbrace{(2\cdot 4)}_8\cdot \underbrace{(3 \cdot 3)}_9\cdot \underbrace{(2\cdot 5)}_{10}=10!$$
$\endgroup$
0
$\begingroup$
Если формула верна, это может быть только $8!$, $9!$ или $10!$, потому что $11!$ и выше имеют коэффициент $11$. $8!$ не обладает достаточной силой $3$, а $9!$ не имеет достаточно большой степени $5$, поэтому, если формула верна, она должна быть равна $10!$.
$\endgroup$
6
$\begingroup$
У вас уже есть несколько умных ответов; здесь менее умный подход. Ты хочешь $$ 3!\cdot5!\cdot7!=n!=7!\cdot8\cdot9\cdots\cdot n, $$ Итак, отмена 7! и вычислив $3!\cdot 5!=6\cdot120=720$, вы хотите $$ 720=8\cdot9\cdots\cdot п. $$ Теперь начните делить обе части на 8, затем на 9.и т.д., пока не получите ответ. Деление на 8 дает вам $90=9\cdots n$, а затем вы либо уже видите ответ, либо делите обе части на 9, чтобы получить результат.
$\endgroup$
2
$\begingroup$
$$\begin{выравнивание}
3! \cdot 5! \cdot 7! &= 6 \cdot 120 \cdot 7! \\
&= 6 \cdot 15 \cdot 8! \\
&= 2 \cdot 5 \cdot 9! \\
&= 10 \cdot 9! \\
&= 10!
\end{выравнивание}$$ 92 \cdot 5\cdot 4)$$
Это хорошее начало, но теперь нам нужно 8. Мы получаем 8, используя наши 4 и коэффициент 2 из одной из наших 6. Это дает: $$2\cdot3\cdot4\cdot5\cdot6\cdot7\cdot8\cdot(3\cdot6\cdot5)$$
Мы можем получить 9, используя наши 3 и коэффициент 3 из оставшихся 6. Что осталось: $$2\cdot3\cdot4\cdot5\cdot6\cdot7\cdot8\cdot9\cdot(2\cdot5)=10!$$
Как насчет этого?
$\endgroup$
$\begingroup$
Обратите внимание, $\color{red}{3}$, $\color{red}{5}$, $\color{red}{7}$ — простые числа (нельзя разложить на множители), тогда факториалы можно последовательно уменьшить следующим образом: $$3!5!7!=(3\cdot 2!)\cdot (5\cdot 4!)\cdot (7\cdot 6!)$$ $$=\color{red}{3}\cdot \color{red}{5}\cdot \color{red}{7}\cdot (2!)\cdot (4!)\cdot (6!)$ $ $$=\color{red}{3}\cdot \color{red}{5}\cdot \color{red}{7}\cdot (2\cdot 1)\cdot (4\cdot 3!)\cdot (6\cdot 5!)$$ $$=1\cdot 2\cdot \color{red}{3}\cdot4\cdot \color{red}{5}\cdot 6\cdot \color{red}{7}\cdot (3!)\cdot (5!)$$
$$=1\cdot 2\cdot 3\cdot4\cdot 5\cdot 6\cdot 7\cdot (3\cdot 2\cdot1 )\cdot (5\cdot 4\cdot 3\cdot 2\cdot 1) $$ $$=1\cdot 2\cdot 3\cdot4\cdot 5\cdot 6\cdot 7\cdot ((2\cdot 4)\cdot(3\cdot 3) \cdot(2\cdot 5))$$ $$=1\cdot 2\cdot 3\cdot4\cdot 5\cdot 6\cdot 7 \cdot8\cdot9\cdot 10$$$$=10!=n!$$ $$\цвет{красный}{n=10}$$
$\endgroup$
$\begingroup$
Можно (и, возможно, нужно) быть даже менее умным, чем предлагает Андреас. Просто вычислите 3! 5! 7! (получив 3628800), а затем с помощью грубой силы найдите число, факториал которого равен этому числу. Например, очевидно, что число больше 7!, так что начните с 8! и работайте вверх. 8! = 40320, слишком мало. 9! = 362880, слишком мало. 10! = 3628800, в самый раз — и готово.
Если бы число было намного больше, требуя поиска в большем диапазоне возможных n , вы могли бы искать менее безмозглым способом. Например, найдите один n , который слишком мал, и один, который слишком велик, затем несколько раз попробуйте один в середине и уменьшите размер диапазона вдвое.
Обратите внимание, что это не требует ни ума, ни удачи, и не имеет ничего общего с факториалами!
$\endgroup$
2
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя адрес электронной почты и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
последовательностей и рядов.
Нужна помощь в понимании формулы факториала $n!=n(n-1)(n-2)\cdots(3)(2)(1)$спросил
Изменено 8 лет, 10 месяцев назад
Просмотрено 6к раз
$\begingroup$
Заголовок гласит следующее:
Если $n$ такое целое число, что $n \ge 0$, то факториал $n$ определяется как
$$n!=n(n-1)(n- 2)\cdots(3)(2)(1)$$
, если $n \ge 1$ по определению.
Меня просто смущает $(3)(2)(1)$ в формуле, и если $n!$ действительно просто (например): $5! = (5)(4)(3)(2)(1)$, тогда почему бы этому просто не закончиться, когда он достигает $(n-4)$, если $n$ равно 5?
Я пытаюсь понять это, поскольку последовательность и серия требуют отмены факториалов при определенных тестах. {n}i=1\cdot2\cdot3\cdots\cdot(n-1)\cdot n.
$$
К нотации «$\cdots$» нужно немного привыкнуть; в основном это означает «и так далее» или «продолжая таким образом». Это говорит о том, что действует закономерность, и эта закономерность продолжается очевидным образом. Первые несколько терминов используются для установления шаблона, а последние термины описывают, где шаблон заканчивается.
$\endgroup$
1
$\begingroup$
Финал (1) просто для полноты. Окончание на n-(n-1) не имеет значения.
Факториал определяется как произведение первых N строго положительных целых чисел до N.
$\endgroup$
$\begingroup$
По сути тот же ответ, что и другие, но немного другой взгляд на него.
$n!$ определен только для неотрицательных целых чисел и $n! = 1$, если $n=0$ или $n = 1$, $n! = n \cdot (n-1)!$ в противном случае.
Например, $5!$
$$ $$\begin{выравнивание} 5! & = 5 \ умножить на 4! \\ & = 5 х 4 х 3! \\ & = 5 х 4 х 3 х 2! \\ & = 5 х 4 х 3 х 2 х 1! \\ & = 5 \× 4 \× 3 \× 2 \× 1 \\ & = 120 \end{выравнивание}$$ $$
$\endgroup$
$\begingroup$
Я думаю, что проблема ОП здесь может быть связана с тем, как в математике используется обозначение «$\dots$», чтобы указать последовательность (в данном случае последовательность умножаемых факторов) путем перечисления первых нескольких терминов и ( если последовательность конечна) последние несколько членов, предоставляя читателю возможность мысленно заполнить остальные (при условии, что желаемая закономерность будет ясна). Когда это обозначение используется для последовательности, которая может быть довольно длинной (для больших $n$ в случае $n!$), но также может быть и довольно короткой (для малых $n$), результатом будет то, что явно указанное первым несколько терминов и последние несколько терминов могут, в случае коротких последовательностей, быть больше , чем предполагалось на самом деле. Правило для понимания этой системы обозначений состоит в том, чтобы вычислить образец и затем интерпретировать его, даже в случае коротких последовательностей, как начало и конец, как указано, но между ними, следуя образцу , а не , обязательно включая все термины, которые были написано, чтобы показать образец.
Таким образом, в случае $n(n-1)(n-2)\cdots3\cdot2\cdot1$ шаблон «начинается с $n$ и идет обратный отсчет (уменьшая множитель на 1 на каждом шаге) пока не достигнешь 1». Для любого $n\leq5$ это будет включать меньше терминов, чем написано. Например, если взять то, что написано буквально для $n=4$, то получится $4\cdot3\cdot2\cdots3\cdot2\cdot1$, но правильная интерпретация не повторяет $3$ и $2$. Когда $n=2$, буквальное чтение еще хуже, так как множитель $(n-2)$ тогда равен $0$, но предполагаемое значение по-прежнему «начинается с $n$ и продолжается до $1$», так что вы получить $2\cdot 1$ (не $2\cdot1\cdot0\cdots3\cdot2\cdot1$). 9{н} к. $$
$\endgroup$
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.Что такое факториал n и как он обозначается? Что такое факториал 100?
Что такое факториал n и как он обозначается?
В математике факториал представляет собой произведение всех натуральных чисел, меньших или равных данному положительному целому числу, и обозначается этим целым числом и восклицательным знаком. Таким образом, факториал n записывается как n !, то есть
n ! = 1 × 2 × 3 × … × ( n −2) × ( n −1) × n .
Обозначение факториала:
Факториал n представлен несколькими символами.
- Обычно факториал n обозначается целым числом n и восклицательным знаком, то есть символом
п !
- Факториал n также может обозначаться символом
Читается как факториал n или n факториал.
- Во многих книгах иногда обозначается символом Γ( n +1), где
Γ( n +1) = n !
Читается как гамма n +1.
- В некоторых книгах, особенно в Германии, факториал n обозначается символом ∏ n (здесь ∏ — греческая буква, которую можно рассматривать как обозначение произведения).
Отсюда окончательно получаем следующую формулу для факториала n :
∏ n = Γ( n +1) = n ! = |_ n = n × ( n −1) × ( n −2)× . . . ×3×2×1.
Определение факториала:
Проще говоря, произведение первых n натуральных чисел (т. по н !. Другими словами, факториал неотрицательного целого числа n является произведением всех положительных целых чисел, меньших или равных n . Обозначается н !.
То есть, говоря математическим языком, факториал n , или, n факториал для всех натуральных чисел n определяется следующим образом:
« n ! ! = n · ( n −1) · ( n −2) · … · 3 · 2 · 1
А,
0! = 1».
Например,
5! = 5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1 = 120.
Формула множителя:
Если n — натуральное число, большее или равное 1, то
п ! = n × ( n −1) × ( n −2) × … × 3×2×1 .
Если n = 0, то n ! = 0! = 1 , по соглашению.
Примеры факториала
n :Факториалы первых 11 натуральных чисел следующие:
- Значение факториала 0, или 0 факториала, или 0! есть,
0! = 1
- Значение факториала 1, или 1 факториал, или 1! есть,
1! = 1
- Значение факториала 2, или 2 факториала, или 2! есть,
2! = 2 ⋅ 1 = 2
- Значение факториала 3, или 3 факториала, или 3! есть,
3! = 3 ⋅ 2 ⋅ 1 = 6
- Значение факториала 4, или 4 факториала, или 4! есть,
4! = 4 ⋅ 3 ⋅ 2 ⋅ 1 = 24
- Значение факториала 5, или 5 факториала, или 5! есть,
5! = 5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1 = 120
- Значение факториала 6, или 6 факториала, или 6! есть,
6! = 6 ⋅ 5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1 = 720
- Значение факториала 7, или 7 факториала, или 7! есть,
7! = 7 ⋅ 6 ⋅ 5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1 = 5 040
- Значение факториала 8, или 8 факториала, или 8! есть,
8! = 8 ⋅ 7 ⋅ 6 ⋅ 5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1 = 40 320
- Значение факториала 9, или 9 факториала, или 9! есть,
9! = 9 ⋅ 8 ⋅ 7 ⋅ 6 ⋅ 5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1 = 3,62,880
- Значение факториала 10, или 10 факториала, или 10! есть,
10! = 10 ⋅ 9 ⋅ 8 ⋅ 7 ⋅ 6 ⋅ 5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1 = 36,28,800
- Значение факториала 11, или 11 факториала, или 11! есть,
11! = 11 ⋅ 10 ⋅ 9 ⋅ 8 ⋅ 7 ⋅ 6 ⋅ 5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1 = 3,99,16,800
и так далее.
Что такое факториал 100:
Значение факториала 100 или 100 факториала рассчитывается по его определению следующим образом:
100! = 100 ⋅ 99 ⋅ 98 ⋅ … ⋅ 3 ⋅ 2 ⋅ 1
= 93326215444394415268169923885626670049682643881621468592963895175999322999156689146397615999322299156689463976155999322н9н
Приблизительное значение 100! равно 9,3326215443944e+157.
В числе 100! количество нулей в конце равно 24.
В числе 100! количество цифр равно 158.
Свойства факториала:
- n ! = n · ( n −1) · ( n −2) · … · 3 · 2 · 1
- 0! = 1! = 1
- n ! = н · ( н −1)! = n · ( n −1) · ( n −2)!
- n ! / р ! = n · ( n −1) … ( r +1)
- Факториалы отрицательных чисел и дробей не определены.
- Определение функции факториала можно распространить на неотрицательные аргументы с помощью гамма-функции, где
Γ( n +1) = n !
Почему факториал важен в математике:
Вообще факториалу уделялось много внимания на протяжении всей истории математики, что совершенно справедливо. Факториальная функция, вероятно, является одной из самых известных функций в математике, особенно в комбинаторике, алгебре и математическом анализе.
Факториал важен в математике, потому что он представляет количество способов, которыми мы можем упорядочить вещи. Например, рассмотрим книжную полку с 12 журналами. Как вы думаете, сколькими различными способами вы могли бы их расположить? Правильный ответ на этот вопрос — 12! а мы знаем что 12! = 47
00, значит, существует 47
00 способов расположить 12 журналов.
Как видно из приведенного выше примера, факториальная функция растет очень быстро! На самом деле, он растет со сверхэкспоненциальной скоростью. То есть она растет быстрее, чем в геометрической прогрессии.
(Источник – Различные книги из библиотеки колледжа)
Теги: что такое 100 факториал, что такое факториал сотни, n факториал, формула n факториала, что такое n факториал
Факториал: простое определение, примеры & Распределение
Распределение вероятностей >
Содержание:
- Что такое факториал?
- Что такое факториальное распределение?
См. также: Superfactorial: Определение (Sloane, Pickover’s)
Посмотрите видео с определением и тем, как вычислять факториалы.
Факториалы! Примеры и упрощение
Посмотрите это видео на YouTube.
Видео не видно? Кликните сюда.
Факториалы (!) — произведения всех целых чисел от 1 до n. Другими словами, возьмите число и умножьте его на 1.
Например:
- Если n равно 3, то 3! 3 х 2 х 1 = 6.
- Если n равно 5, то 5! 5 х 4 х 3 х 2 х 1 = 120,
Это сокращенный способ записи чисел. Например, вместо 47
00 можно написать 12! вместо этого (что составляет 12 х 11 х 10 х 9 х 8 х 7 х 6 х 5 х 4 х 3 х 2 х 1).
Для чего используется факториал в статистике?
В алгебре вы наверняка сталкивались с уродливыми факториалами вроде (x – 10!)/(x + 9!). Не волнуйся; Вы не увидите ничего из этого в своем начальном классе статистики. Фу! только раз вы увидите их для задач перестановки и комбинации.
Уравнения выглядят так:
И это то, что вы можете ввести в свой калькулятор (или Google!).
Статья по теме (с сайта CalculusHowTo.com): Почему нулевой факториал равен единице?
Факторное распределение происходит, когда набор переменных является независимым событием. Другими словами, переменные вообще не взаимодействуют; Учитывая два события x и y, вероятность x не изменится, если вы умножите y. Следовательно, вероятность x при условии, что произошло y — P(x|y) — будет такой же, как P(x).
Факторное распределение можно записать разными способами (Hinton, 2013; Olshausen, 2004):
- p(x,y) = p(x)p(y)
- р(х,у,г) = р(х)р(у)р(г)
- р(х 1 , х 2 , х 3 , х 4 ) = р(х 1 ) Р(х 2 ) р(х 9 х 9 3 )
В случае вектора вероятности смысл точно такой же. То есть вектор вероятности из факторного распределения является произведением вероятностей отдельных элементов вектора.
Вы могли заметить отсутствие символа факториала (!) в любом из определений. Это потому, что распределение названо потому, что последовательные частоты являются факторными величинами, а не сами термины являются факториалами.
Определение факторного распределения
Для факторного распределения P(x,y) = P(x)P(y). Мы можем обобщить это для более чем двух переменных (Olshausen, 2004) и написать:
P(x 1 , x 2 ,…,x n ) = P(x 1 ) · P(x 2 · …· P(x n ).
Это выражение также можно записать более кратко:
P(x 1 , x 2 ,…x n )= Π i P(x i )
Примеры факторного распределения
, ситуации, лучше всего представленные сложными, неразрешимыми распределениями вероятностей, аппроксимируются факторными распределениями, чтобы воспользоваться этой простотой манипулирования.0005
Одним из примеров часто встречающегося факторного распределения является p-обобщенное нормальное распределение , представленное уравнением
Я не буду здесь вдаваться в смысл этой формулы; если вы хотите углубиться, не стесняйтесь читать об этом здесь. Но обратите внимание, что когда p = 2, это в точности нормальное распределение. Таким образом, нормальное распределение также является факториальным.
Гамма-функция (иногда называемая Гамма-функцией Эйлера ) связано с факториалами следующей формулой:
Γ(n) = (x – 1)!.
Другими словами, гамма-функция равна факториальной функции . Однако, хотя функция факториала определена только для неотрицательных целых чисел, гамма может работать как с дробями, так и с комплексными числами.
Многомерная гамма-функция (MGF) является расширением гамма-функции для нескольких переменных. В то время как гамма-функция может обрабатывать только один вход («x»), многомерная версия может обрабатывать многие. Обычно определяется как:
Ссылки
Абрамовиц, М. и Стегун, И. А. (ред.). «Гамма (факториальная) функция» и «Неполная гамма-функция». §6.1 и 6.5 в Справочнике по математическим функциям с формулами, графиками и математическими таблицами, 9-е издание. Нью-Йорк: Довер, стр. 255-258 и 260-263, 1972.
Grötschel, M. et al. (ред.) (2013). Онлайн-оптимизация крупномасштабных систем. Springer Science & Business Media.
Хинтон, Г. (2013). Лекция 1: Введение в машинное обучение и графические модели. Получено 28 декабря 2017 г. с: https://www.cs.toronto.edu/~hinton/csc2535/notes/lec1new.pdf
Джордан, И. и др. (2001). Графические модели: основы нейронных вычислений. Массачусетский технологический институт Пресс.
Ольсхаузен, Б. (2004). Учебник вероятности. Получено 27 декабря 2017 г. с:
Получено с http://redwood.berkeley.edu/bruno/npb163/probability.pdf
Sinz, F. (2008). Характеристика p-обобщенного нормального распределения. Получено 27 декабря 2017 г. с http://www.orga.cvss.cc/media/publications/SinzGerwinnBethge_2008.pdf от 27 декабря 2017 г.
ЦИФРОВАТЬ ЭТО КАК:
Стефани Глен . «Факториал: простое определение, примеры и распространение» От StatisticsHowTo.com : Элементарная статистика для всех нас! https://www.statisticshowto.com/factorial-distribution/
————————————————— ————————-
Нужна помощь с домашним заданием или контрольным вопросом? С Chegg Study вы можете получить пошаговые ответы на свои вопросы от эксперта в данной области. Ваши первые 30 минут с репетитором Chegg бесплатны!
Комментарии? Нужно опубликовать исправление? Пожалуйста, Свяжитесь с нами .
Учебное пособие по Прологу — 2.2
Учебное пособие по Прологу — 2.2Два определения предиката, вычисляющие факториальную функцию, находятся в файле 2_2.pl, который читатель может просмотреть, щелкнув ссылку «Код» внизу этой страницы. Первый из этих определений:
факториал (0,1). факториал(N,F):- N>0, N1 это N-1, факториал(N1,F1), F равно N * F1.
Эта программа состоит из двух пунктов . Первое предложение — это единичное предложение, не имеющее тела.
Второе правило, потому что у него есть корпус . Тело второго предложения находится на
правая часть ‘:-‘, которая может быть прочитана как «если». Тело состоит из литералов, разделенных
запятыми ‘,’ каждая из которых может быть прочитана как «и». Глава предложения — это целое
пункт, если пункт является раздельным пунктом, в противном случае заголовок пункта является частью, появляющейся
слева от двоеточия в ‘:-‘. Декларативное прочтение первого (единичного) предложения говорит о том, что
факториал 0 равен 1», а второе предложение объявляет, что «факториал N равен F, если N>0 и
N1 равно N-1, а факториал N1 равен F1, а F равен N*F1″.
Цель Пролога вычислить факториал числа 3 отвечает значением W, целевая переменная:
?-факториал(3,W). Вт=6
Рассмотрим следующее дерево предложений, построенное для литерала ‘factorial(3,W)’. Как объяснялось в предыдущем разделе, дерево предложений не содержит свободных переменных. но вместо этого имеет экземпляры (значения) переменных. Каждое ответвление под узлом определяется предложение в исходной программе с использованием соответствующих экземпляров переменных; узел определяется некоторым экземпляром заголовка предложения и литералов тела предложения определить дочерние элементы узла в дереве предложений.
Рис. 2.2
Все арифметические листья верны по оценке (в предполагаемой интерпретации), и
самая нижняя ссылка в дереве соответствует самому первому пункту программы для факториала. Это первое предложение может быть написано
факториал(0,1) :- истина.
и, на самом деле, ?- true — это цель Пролога, которая всегда достигает успеха (true — это , встроенное в ). Ради для краткости мы не рисовали «настоящие» листья под истинными арифметическими литералами.
Дерево пунктов программы предоставляет , означающее программы для цели в корне дерева. То есть факториал(3,6) является следствием программы на Прологе, потому что существует дерево предложений с корнем в факториале (3,6), все листья которого истинны. Буквальный ‘factorial(5,2)’, с другой стороны, не является следствием программы, потому что нет дерево предложений, укорененное в факториале (5,2) и имеющее все истинные листья. Таким образом, значение программа для буквального «факториала (5,2)» заключается в том, что оно ложно. Фактически,
?-факториал(3,6). да ?-факториал(5,2). нет
как и ожидалось. Деревья предложений — это так называемые И-деревья , так как для того, чтобы корень был
Следствие программы, каждое из ее поддеревьев также должно иметь корни в литералах, которые
сами последствия программы. Мы еще поговорим о деревьях предложений.
потом. Мы указали, что деревья предложений обеспечивают смысл или семантику для программ.
Мы увидим другой подход к семантике программ в главе 6. Деревья предложений
обеспечить интуитивный, а также правильный подход к семантике программы.
Нам нужно будет различать деревья предложений программы и так называемые деревья вывода Пролога. Деревья предложений являются «статическими» и могут быть построены для программы и цели независимо от особый процессуальный механизм достижения цели. Грубо говоря, деревья предложений соответствуют декларативному чтению программы.
Деревья вывода , с другой стороны, учитывают механизм связывания переменных Пролога и
порядок рассмотрения подцелей. Деревья вывода обсуждаются в разделе 3. 1 (но
см. анимацию ниже).
Трассировка выполнения Пролога также показывает, как связаны переменные, чтобы удовлетворять цели. В следующем примере показано, как включается типичный трассировщик Prolog. и выкл.
?- след. % Отладчик сначала будет ползти, показывая все (трассировка). да [след] ?-факториал(3,Х). (1) 0 Вызов: factorial(3,_8140) ? (1) 1 Головка [2]: factorial(3,_8140) ? (2) 1 вызов (встроенный): 3>0 ? (2) 1 Готово (встроено): 3>0 ? (3) 1 вызов (встроенный): _8256 3-1? (3) 1 Готово (встроено): 2 равно 3-1 ? (4) 1 Вызов: factorial(2, _8270) ? ... (1) 0 Выход: факториал(3,6) ? Х=6 [след] ?- нерас. % Отладчик выключен да
Анимированное дерево ниже дает еще один взгляд на дерево вывода для Пролога. цель ‘факториал(3,X)’. Чтобы запустить (или перезапустить) анимацию, просто нажмите на значок Кнопка «Шаг».
Название этого раздела относится к двум определениям факториала.