Galina7v71
Всего 3 ответа.
Как посчитать 1000 в минус одной третьей степени?
Хочу-задать Вопрос3А Интернет тебе на что?
http://www.algebraclass.ru/otricatelnaya-stepen/
http://www.algebraclass.ru/drobnaya-stepen/
Почему ты не можешь сам найти ссылку, а заставляешь это делать посторонних людей?
1000 в степени 1/3 – это кубический КОРЕНЬ из 1000. То есть, 10.
А отрицательная степень – это обратное число. То есть, 1/10.Дмитрий Низяев2
Всего 6 ответов.
X+12=2x-6 как решить подробно?
Nadija K.61) Для начала сделаем так, чтобы переменная оказалась с одной стороны. Для этого можно вычесть x из обеих частей уравнения
x + 12 = 2x – 6 | -x
12 = x – 6
2) Затем оставим переменную “в одиночестве”, для этого можно прибавить к обеи частям 6:
12 = x – 6 | + 6
18 = x
3) Всё, мы разделили переменную и постоянные значения. 0 постулируется равным единице. Допускаю, что там (в теории), все же, возможны и альтернативные мнения (равен нулю / значение не определено). В любом случае, для прикладных задач это не играет роли (см. “во-вторых”) и лично мне, например, ни разу не интересно. Можно формально определить и так, и сяк и наперекосяк, но реально придется смотреть предел, а не “сколько будет точный ноль в степени точный ноль”.
0 постулируется равным единице. Допускаю, что там (в теории), все же, возможны и альтернативные мнения (равен нулю / значение не определено). В любом случае, для прикладных задач это не играет роли (см. “во-вторых”) и лично мне, например, ни разу не интересно. Можно формально определить и так, и сяк и наперекосяк, но реально придется смотреть предел, а не “сколько будет точный ноль в степени точный ноль”.
Nekto V-Palto51
Всего 8 ответов.
Вам также может понравиться
Как умножить на 10 в минус 3 степени
Отрицательная степень
В учебниках по математике можно встретить такое определение:
«Степенью n числа а является произведение множителей величиной а n раз подряд»
Например, a n — степень, где:
- a — основание степени,
- n — показатель степени.

Читается такое выражение как a в степени n.
Если говорить проще, то степень, а точнее показатель степени (n), говорит нам о том, сколько раз следует умножить данное число (основание степени) само на себя.
А значит, если у нас есть задачка, где спрашивают, как возвести число в степень, например, число 2 в третью степень, то она решается довольно просто:
2 3 = 2 · 2 · 2, где:
- 2 — основание степени,
- 3 — показатель степени.
Онлайн-курсы по математике за 7 класс помогут закрепить новые знания на практике с талантливым преподавателем.
Степень с отрицательным показателем
Число в минусовой степени равно дроби, числителем которой является единица, а знаменателем данное число с положительным показателем:
К примеру, 4 в минус 2 степени — это 1/4 2 , 2 в минус 3 степени — это 1/2 3 , 3 в минус 1 степени — это 1/3, 10 в минус первой степени — это 1/10 или 0,1.
Степени с отрицательным показателям помогают компактно записывать крайне малые или постоянно уменьшающиеся величины. Например, одну миллиардную долю (0, 000 000 001) можно записать как 10 в минус 9 степени (10 -9 ). В школьной программе такие величины — редкость: чаще всего используют 10 в минус 1 степени или 2 в минус 1 степени.
Например, одну миллиардную долю (0, 000 000 001) можно записать как 10 в минус 9 степени (10 -9 ). В школьной программе такие величины — редкость: чаще всего используют 10 в минус 1 степени или 2 в минус 1 степени.
Чтобы разобраться, как возводить число в отрицательную степень, вспомним правило деления степеней с одинаковыми основаниями.
Деление степеней с одинаковыми основаниями, но разными показателями осуществляется по следующей формуле: показатели отнимаются, а основание остается неизменным.
Поэтому если степень делимого будет меньше степени делителя, то в результате получится число с отрицательной степенью:
a 3 : a 6 =a 3 — 6 = a -3
Если записать деление в виде дроби, то при сокращении в числителе останется 1, а в знаменателе число будет иметь положительную степень:
Действия с отрицательными степенями
Умножение отрицательных степеней
При умножении отрицательных степеней с одинаковыми основаниями показатели степеней складываются, так же как и при умножении положительных степеней:
a m · a n = a m + n
Деление отрицательных степеней
При делении отрицательных степеней с одинаковыми основаниями из показателя степени делимого вычитается показатель делителя, так же как и при делении положительных степеней:
Возведение дроби в отрицательную степень
Чтобы возвести дробь в отрицательную степень, надо возвести в эту степень отдельно числитель и знаменатель:
Возведение произведения в отрицательную степень
Чтобы возвести произведение в отрицательную степень, необходимо возвести в эту степень каждый множитель произведения отдельно:
Калькулятор степеней
Предлагаем попробовать наш калькулятор степеней, который поможет возвести в степень онлайн любое число.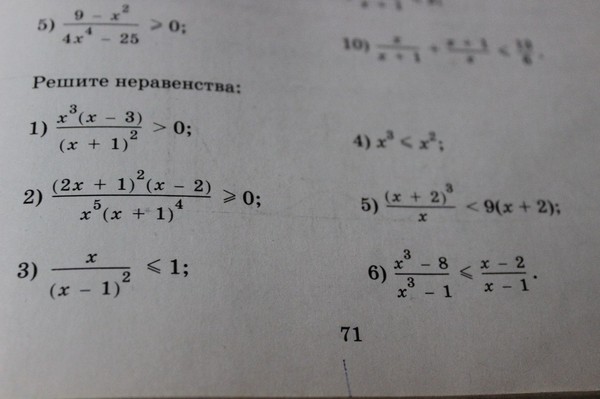
Использовать калькулятор очень просто — введите число, которое вы хотите возвести в степень, а затем число — степень и нажмите на кнопку «Посчитать».
Примечательно то, что наш онлайн калькулятор степеней может возвести в степень как положительную, так и отрицательную. А для извлечения корней на сайте есть другой калькулятор.
Как возвести число в степень.
Давайте рассмотрим процесс возведения в степень на примере. Пусть нам необходимо возвести число 5 в 3-ю степень. На языке математики 5 — это основание, а 3 — показатель (или просто степень). И записать это можно кратко в таком виде:
Возведение в степень
А чтобы найти значение, нам будет необходимо число 5 умножить на себя 3 раза, т. е.
5 3 = 5 x 5 x 5 = 125
Соответственно, если мы хотим найти значение числа 7 в 5 степени, мы должны число 7 умножить на себя 5 раз, т. е. 7 x 7 x 7 x 7 x 7. Другое дело когда требуется возвести число в отрицательную степень.
Как возводить в отрицательную степень.

При возведении в отрицательную степень необходимо использовать простое правило:
как возводить в отрицательную степень
Все очень просто — при возведении в отрицательную степень мы должны поделить единицу на основание в степени без знака минус — т. е. в положительной степени. Таким образом, чтобы найти значение
2 -3
Отрицательная степень
Прежде чем перейти к изучению определения «отрицательная степень» рекомендуем повторно прочитать урок «Степень» и «Свойства степеней».
Необходимо уверенно понимать, что такое положительная степень числа и уверенно использовать её свойства в решении примеров.
Как возвести число в отрицательную степень
Запомните!
Чтобы возвести число в отрицательную степень нужно:
- «перевернуть» число. Записать его в виде дроби с единицой наверху (в числителе) и с исходным числом в степени внизу;
- заменить отрицательную степень на положительную ;
- возвести число в положительную степень.

Общая формула возведения в отрицательную степень выглядит следующим образом.
a −n =
,где a ≠ 0, n ∈ z ( n принадлежит целым числам).
Примеры возведения в отрицательную степень.
- 6 −2 =
=
- (−3) −3 =
1 (−3) 3 =
= −
- 0,2 −2 =
1 0,2 2 =
1 0,04
Запомните!
Любое число в нулевой степени — единица.
Примеры возведения в нулевую степень.
- (
) 0 = 1
- (−5) 0 = 1
Как найти
10 в минус 1 степениВ уроке 8 класса «Стандартный вид числа» мы уже сталкивались с записью:
Теперь, зная определение отрицательной степени, давайте разберемся, почему « 10 » в минус первой степени равно « 0,1 ».
Возведем « 10 −1 » по правилам отрицательной степени. Перевернем « 10 » и запишем её в виде дроби «
» и заменим отрицательную степень « −1 » на
положительную степень « 1 ».
10 −1 =
| 1 |
| 10 1 |
Возведем « 10 » в « 1 » степень. Помним, что любое число в первой степени равно самому числу.
10 −1 =
| 1 |
| 10 1 |
=
Теперь по определению десятичной дроби запишем обыкновенную дробь в виде десятичной.
10 −1 =
| 1 |
| 10 1 |
=
= 0,1
По такому же принципу можно найти « 10 » в минус второй, третьей и т.д.
Запомните!
Для упрощения перевода « 10 » в минус первую, вторую и т.д степени, нужно запомнить правило:
«Количество нулей после запятой равно положительному значению степени минус один ».
Проверим правило выше для « 10 −2 ».
Т.к. у нас степень « −2 », значит, будет всего один ноль (положительное значение степени « 2 − 1 = 1 ». Сразу после запятой ставим один ноль и за ним « 1 ».
Рассмотрим « 10 −1 ».
Т.к. у нас степень « −1 », значит, нулей после запятой не будет (положительное значение степени « 1 − 1 = 0 ». Сразу после запятой ставим « 1 ».
Сразу после запятой ставим « 1 ».
То же самое правило работает и для « 10 −12 ». При переводе в десятичную дробь будет « 12 − 1 = 11 » нулей и « 1 » в конце.
Как возвести в отрицательную степень дробь
Запомните!
Чтобы возвести дробь в отрицательную степень нужно:
- «перевернуть» дробь;
- заменить отрицательную степень на положительную ;
- возвести дробь в положительную степень.
Пример. Требуется возвести в отрицательную степень дробь.
Перевернем дробь «
» и заменим отрицательную степень « −3 » на положительную « 3 ».
(
) −3 = (
) 3
Возведем дробь в положительную степень по правилу возведения дроби в положительную степень. Т.е. возведем и числитель « 3 », и знаменатель « 10 » в третью степень.
(
) −3 = (
) 3 =
| 3 3 |
| 10 3 |
=
| 27 |
| 1000 |
Для более грамотного ответа запишем полученный результат в виде десятичной дроби.
(
) −3 = (
) 3 =
| 3 3 |
| 10 3 |
=
| 27 |
| 1000 |
= 0,027
Как возвести отрицательное число в отрицательную степень
Как и при возведении отрицательного числа в положительную степень, в первую очередь необходимо определить конечный знак результата возведения в степень. Вспомним основные правила еще раз.
Запомните!
Отрицательное число, возведённое в чётную степень, — число положительное .
Отрицательное число, возведённое в нечётную степень, — число отрицательное .
Перевернем число « −5 » и заменим отрицательную степень « −2 »
на положительную « 2 ».
(−5) −2 = (−
) 2 =
Так как степень « 2 » — четная , значит, результат возведения в степень будет положительный . Поэтому убираем знак минуса при раскрытии скобок.
Далее откроем скобки и возведем во вторую степень и числитель « 1 »,
и знаменатель « 5 ».
(−5) −2 = (−
) 2 =
| 1 2 |
| 5 2 |
=
Как возвести отрицательную дробь в отрицательную степень
Конечный знак результата возведения в степень отрицательной дроби определяется по тем же правилам, что и для целого отрицательного числа.
Запомните!
Отрицательная дробь, возведённая в чётную степень, — дробь положительная .
Отрицательная дробь, возведённая в нечётную степень, — дробь отрицательная .
Разберемся на примере. Задание: возвести отрицательную дробь « (−
) » в « −3 » степень.
По правилу возведения дроби в отрицательную степень перевернем дробь и заменим отрицательную степень « −3 » на положительную « 3 ».
(−
) −3 = (−
) 3 =
Теперь определим конечный знак результата возведения в « 3 » степень.
Степень « 3 » — нечетная , значит, по правилу возведения отрицательного числа в степень дробь останется отрицательной .
Нам остается только раскрыть скобки и возвести в степень и числитель « 3 », и знаменатель « 2 » в третью степень.
(−
) −3 = (−
) 3 = −
| 3 3 |
| 2 3 |
= −
Для окончательного ответа выделим целую часть из дроби.
(−
) −3 = (−
) 3 = −
| 3 3 |
| 2 3 |
= −
= − 3
Рассмотрим другой пример возведения отрицательной дроби в отрицательную степень.
Правило возведения отрицательного числа в степень гласит: если степень четная , значит, результат возведения будет положительным .
(−
) −2 = (−
) 2 =
| 11 2 |
| 9 2 |
=
| 121 |
| 81 |
= 1
Свойства отрицательной степени
Все свойства степени, которые используются для положительной степени, точно также применяются и для отрицательной степени.
В этом уроке мы не будем повторно подробно разбирать каждое свойство степени, но еще раз приведем основные формулы свойств степени и покажем примеры их использования.
признаки, профилактика и коррекция близорукости третьей степени
Содержание статьи:- Общие сведения
- Симптомы миопии высокой степени
- Чем опасна близорукость третьей степени?
- Особенности диагностирования
- Близорукость высокой степени – что делать?
- Контактные линзы при миопии третьей степени
Такой дефект зрения, как миопия (близорукость), имеет 3 степени – слабую, среднюю и высокую. Труднее всего обстоят дела с миопией высокой степени – при ней аномалия рефракции составляет -6 и более диоптрий. Человеку с таким диагнозом сложнее взаимодействовать с окружающим миром – он видит четко лишь те предметы, которые находятся непосредственно перед ним на расстоянии не более 15 см! Как возникает миопия высокой степени, по каким симптомам ее можно распознать и как скорректировать?
Общие сведения о близорукости
Близорукость – офтальмологическое заболевание, при котором человек видит вблизи лучше, чем вдаль. Например, он не испытывает проблем при чтении книги или использования телефона, но удаленные объекты так же хорошо рассмотреть не может – возникает расплывчатость, силуэты теряют четкость. Чем выше степень миопии, тем сильнее размытость предметов.
Например, он не испытывает проблем при чтении книги или использования телефона, но удаленные объекты так же хорошо рассмотреть не может – возникает расплывчатость, силуэты теряют четкость. Чем выше степень миопии, тем сильнее размытость предметов.
Близорукость бывает врожденной и приобретенной. По статистике, врожденная миопия чаще всего диагностируется детям до 6 лет. Это связано с наследственным характером заболевания
Из-за чего близорукость может прогрессировать?
- Избыточные нагрузки на глаза у детей раннего возраста.
- Регулярное несоблюдение основных советов по профилактике зрения. Например, работа при плохом освещении, продолжительное взаимодействие с гаджетами (планшетами, телефонами, компьютерами).
- Другие факторы. К примеру, малоподвижный образ жизни, недостаточное время на улице в светлое время суток, и прочие.
- Для близорукости высокой степени характерно увеличение глазного яблока по сравнению со здоровым глазом на 2 мм и более.
 Удлинение оси глаза на 1 мм в среднем приводит к прогрессированию миопии на 3 диоптрии и значительному ухудшению зрения.
Удлинение оси глаза на 1 мм в среднем приводит к прогрессированию миопии на 3 диоптрии и значительному ухудшению зрения.
Симптомы миопии высокой степени у детей и взрослых
В отличие от близорукости слабой степени, которая может протекать бессимптомно, миопия высокой степени имеет выраженную симптоматику. Ее можно заподозрить даже у малышей, которые еще не могут рассказать родителям о нарушении визуального восприятия мира. Например, ребенок активно не следит за игрушками, у него нет реакции на взрослых при визуальном контакте (она появляется только в том случае, если взрослый заговорил).
Если не диагностировать высокую степень близорукости вовремя у ребенка дошкольного возраста и не предпринимать мер по ее сдерживанию, то есть высокий риск необратимого ухудшения зрения в будущем на фоне прогрессирования миопии до сверхвысоких значений (вплоть до -30,0)
Как миопия высокой степени проявляется у взрослых?
- Зрение очень снижено. Человек на расстоянии вытянутой руки может видеть только крупные предметы.

- Ощущение усталости и дискомфорта в глазах. Могут возникать жжение и боль из-за перенапряжения.
- Головные боли. Неприятные ощущения локализованы в области лба, переносицы или висков.
- Заболевание часто сочетается с другими дефектами зрения. Например, с астигматизмом или с амблиопией.
Чем опасна миопия высокой степени?
Чем выше степень миопии, тем выше риск ее осложнения вплоть до слепоты. Растяжение оболочек удлиненного глазного яблока приводит к их истончению. Обмен веществ в растянутых тканях глазного яблока нарушается. На уязвимых тонких участках сетчатки могут появляться очаги дистрофии и разрывы.
Близорукость высокой степени также создает благоприятные предпосылки для формирования таких заболеваний глаз как глаукома и катаракта. Эти “возрастные” заболевания глаз встречаются у пациентов с миопией в более раннем возрасте.
Также существует вероятность отслойки сетчатки на фоне миопии. Отслойка сетчатки может проявляться дефектом периферического зрения с последующим формированием «темной шторки», за границы которой ничего не видно. Возможные последствия – слепота, если ничего не предпринимать.
Отслойка сетчатки может проявляться дефектом периферического зрения с последующим формированием «темной шторки», за границы которой ничего не видно. Возможные последствия – слепота, если ничего не предпринимать.
В зоне риска по отслойке сетчатки беременные женщины с миопией высокой степени и изменениями на глазном дне.
Диагностика миопии высокой степени
В большинстве случаев близорукость высокой степени диагностируется тем, кто уже страдал миопией на протяжении нескольких лет или больше.
Важно! Миопия высокой степени не возникает из ниоткуда. Это, как правило, последствие непринятия мер по стабилизации миопии и отсутствие ее коррекции на ранних стадиях.
Полную диагностику осуществляет врач-офтальмолог или оптометрист в оптике. В нее включены:
- Клинический осмотр. Врач оценивает внешний вид глаз, состояние век, реакцию зрачков.
- Визометрия – обследование с использованием таблиц для контроля остроты зрения.

- Авторефрактометрия – диагностическая автоматизированная процедура для предварительного уточнения преломляющих свойств глаза (рефракции).
- Тонометрия. Врач измеряет ВГД (внутриглазное давление).
- Биомикроскопия. Исследование оптических сред и тканей глаза с помощью щелевой лампы. На щелевой лампе с помощью высокодиоптрийных асферических линз или линзы Гольдмана врач также может провести осмотр глазного дна с предварительной инстилляцией специальных глазных капель.
Возможны и иные методики для осмотра глазного дна по решению врача.
Все упомянутые процедуры помогают врачу поставить диагноз миопии, определить ее степень и наличие осложнений, дать рекомендации по методам коррекции и стабилизации состояния.
Только врач-офтальмолог или оптометрист определяют параметры рецепта на очки и контактные линзы. Рецепты на линзы и очки могут отличаться, и практически всегда отличаются при миопии высокой степени.
Мониторинг параметров зрения показан всем, у кого есть нарушения зрения.
Близорукость высокой степени – что делать?
Вылечить близорукость нельзя. Лечение близорукости подразумевает коррекцию зрения и принятие мер по замедлению прогрессирования. Методы стабилизации миопии можно комбинировать и менять при необходимости по решению врача. При высокой скорости прогрессирования и/или миопии высокой степени по решению врача может быть назначено хирургическое вмешательство с целью стабилизации миопии.
Также лечащий врач может назначить:
- Прием препаратов. Они предназначены для усиления микроциркуляции и восстановления кровоснабжения глазного яблока. Это могут быть ноотропы, мидриатические препараты, различные витаминно-минеральные комплексы.
- ЛФК (лечебная физкультура). Задача глазной гимнастики – возвращение ослабленной мышечной системе глаза тонуса и его поддержка. Комплекс упражнений подбирается специалистом строго индивидуально.

- Гигиена зрения. К примеру, ежедневные дозированные нагрузки, период отдыха для глаз (особенно если работа пациента связана с компьютером).
- Очки – самый простой и доступный способ восстановить зрение, но они уступают современным линзам в практичности и удобстве. Например, очки искажают периферическое зрение, размер и форму предметов, запотевают, могут разбиться или потеряться в самый неподходящий момент. И если пациент со слабой степенью близорукости сможет беспрепятственно передвигаться и без очков, то при тяжелой степени ориентация в пространстве существенно затруднена. Кроме того, в очках тяжело вести активный образ жизни, особенно детям, которые нередко еще и подвергаются насмешкам со стороны одноклассников.
Внимание! Под лечением подразумевают в первую очередь торможение прогрессирования заболевания. Чаще всего терапия направлена на замедление прогрессирования заболевания с целью предупреждения осложнений.
Контактные линзы при миопии высокой степени
Контактные линзы можно использовать людям с любой степенью близорукости. Они не ограничивают угол обзора и не запотевают в любую погоду, не выпадают из глаз и не могут их травмировать, в них можно полноценно заниматься спортом.
Самые распространенные – мягкие контактные линзы (МКЛ). В отличие от жестких, они пропускают больше кислорода, комфортны в ношении, к ним легко адаптироваться даже детям. При их изготовлении используют гидрогелевые и силикон-гидрогелевые материалы. Линзы имеют широкий диапазон оптической силы. Даже с рефракцией глаза — 20 диоптрий человеку можно подобрать оптимальные МКЛ. Некоторые линзы особых дизайнов исправляют все несовершенства зрения. Например, если миопии сопутствует астигматизм, рекомендованы торические линзы.
Миопия высокой степени значительно сказывается на зрении. Отсутствие своевременных мер стабилизации и коррекции опасно осложнениями и возможной слепотой в зрелом возрасте. Чтобы предупредить возможные негативные последствия и восстановить четкость зрения, следует обратиться к врачу-офтальмологу.
Чтобы предупредить возможные негативные последствия и восстановить четкость зрения, следует обратиться к врачу-офтальмологу.
Ничто в этой статье не должно быть истолковано как медицинский совет или заменять рекомендации медицинского работника. По конкретным вопросам обращайтесь к своему офтальмологу.
Фото: Shutterstock
Близорукость (миопия) – что это, степени, причины, симптомы, лечение и профилактика
Миопия — что это такое? Попросту — близорукость, распространенный дефект зрения, при котором человек плохо видит то, что находится на сравнительно большом расстоянии от него.
Запишись на бесплатную проверку зрения
Основная причина возникновения такого дефекта — глазное яблоко, которое увеличено в длину. Из-за этого оптическая система глаза преломляет световые лучи так, что они фокусируются не на сетчатке, а перед ней. Соответственно, близорукий человек на дальних и средних дистанциях (в зависимости от степени миопии) видит объекты не четко, а размыто.
Реже встречается рефракционная миопия. Этот дефект вызван тем, что оптический аппарат глаза чересчур сильно преломляет световые лучи и они, опять же, сходятся в фокус перед сетчаткой, а не на ней.
Близорукость порой называют наиболее серьезным заболеванием XXI века. По разным оценкам, к 2020 году от нее уже страдают от 1,8 до 2,5 млрд человек. В 2016 году каждый четвертый россиянин имел близорукость, а среди студентов этот показатель был еще выше.
Поэтому специалисты рекомендуют посещать офтальмолога хотя бы раз в год — своевременно выявленное нарушение проще контролировать, а шансы замедлить прогрессирование миопии становятся выше.
Из этой статьи вы узнаете о причинах и методах лечения миопии.
Содержание
- Причины развития близорукости
- Виды близорукости
- Симптомы близорукости
- Лечение близорукости
Почему возникает миопия у взрослых и детей
Ученые до сих пор не могут однозначно назвать причину возникновения миопии. Есть распространенное мнение, что близорукость — это следствие того, что человек слишком много времени проводит перед телевизором или компьютером. Действительно, интенсивная зрительная нагрузка, работа и чтение в условиях слабого освещения, длительное использование смартфона или компьютера ухудшают состояние глаз. Но есть множество других факторов, из-за которых возникает и развивается это заболевание.
Есть распространенное мнение, что близорукость — это следствие того, что человек слишком много времени проводит перед телевизором или компьютером. Действительно, интенсивная зрительная нагрузка, работа и чтение в условиях слабого освещения, длительное использование смартфона или компьютера ухудшают состояние глаз. Но есть множество других факторов, из-за которых возникает и развивается это заболевание.
Наследственность является одной из возможных причин возникновения миопии
Первый из них — наследственность. Но здесь нужно понимать, что наследуется не сама миопия, а только предрасположенность к ней. Если от близорукости страдали оба родителя, то вероятность того, что она возникнет и у детей, стремится к 50%. Если же близоруким был только один родитель, возможность того, что миопия будет и у ребенка, составит примерно 20%.
В большинстве случаев признаки близорукости у детей могут встречаться в возрасте 7-12 лет, но стоит внимательно следить за зрением ребенка, так как проблемы могут возникнуть и у малышей. Причем у девочек симптомы миопии проявляются немного раньше, чем у мальчиков. Это, скорее всего, связано с изменениями в организме, которые происходят в период полового созревания.
Причем у девочек симптомы миопии проявляются немного раньше, чем у мальчиков. Это, скорее всего, связано с изменениями в организме, которые происходят в период полового созревания.
Другие факторы, оказывающие влияние на возникновение и развитие близорукости, — это:
- неправильное питание;
- ослабление организма, вызванное переутомлением и серьезными болезнями, такими, как корь, скарлатина, туберкулез, а также нарушениями опорно-двигательного аппарата;
- травмы.
Существует и врожденная близорукость. Она вызвана нарушениями нормального развития глазного яблока, произошедшими, когда ребенок еще находился в материнской утробе. Они, в свою очередь, могут быть связаны с недоношенностью, гипоксией (кислородным голоданием) и различными заболеваниями матери, особенно в первые месяцы беременности.
Виды близорукости
По степени тяжести специалисты выделяют три основных типа миопии:
- слабая — менее 3 диоптрий;
- средняя — от 3 до 6 диоптрий;
- высокая — свыше 6 диоптрий.

По клиническому течению выделяют два вида близорукости: непрогрессирующий и прогрессирующий.
Непрогрессирующая миопия – проблема, которая, как правило, решается с помощью очков или контактных линз. В данном случае дополнительное лечение не понадобится.
Прогрессирующая миопия – более серьезное заболевание, признаком которого считается ухудшение зрения минимум на одну диоптрию в год. С ней нередко сталкиваются школьники, у которых значительно увеличивается зрительная нагрузка. В одних случаях такая миопия может перестать прогрессировать, когда прекращается рост организма. В других случаях зрение продолжает ухудшаться, а итогом становятся слепота и инвалидность.
Прогрессирующая миопия накладывает на человека множество ограничений. Ему противопоказаны борьба и бокс, прыжки в длину и высоту, а также многие другие виды спорта. Нежелателен также подъем тяжести, а это уже может сказываться и на повседневной жизни.
Чем выше степень близорукости, тем больше вероятность возникновения различных осложнений. Диспропорция глазного яблока ведет к растяжению его оболочек, они истончаются, при этом растягиваются проходящие по ним сосуды, и из-за этого ухудшается кровоток, возникают проблемы с обменом веществ. На истонченных участках могут возникнуть разрывы — их вызывает не только поднятие тяжестей или повышенная зрительная нагрузка, но и психоэмоциональный стресс.
Без своевременной коррекции зрение может продолжить ухудшаться
Дальше становится только хуже. Отслаивается сетчатка, причем отслаивание прогрессирует: сначала пропадает часть периферического зрения, затем возникает ощущение «черной шторки», через которую ничего не видно, и она увеличивается до тех пор, пока человек не теряет зрение полностью.
Как правило, это не сопровождается болевыми ощущениями, поэтому близорукий человек не всегда может своевременно отреагировать на резкое ухудшение зрения.
Основные симптомы близорукости
Основной симптом миопии – это ухудшение зрения. Это можно заметить и со стороны, например, так часто замечают признаки расстройства зрения у ребенка. Он:
- щурится, жмурится, рассматривая предметы или пытаясь читать;
- подносит книгу как можно ближе к глазам;
- при работе за компьютером или просмотре телевизора, наоборот, старается приблизить глаза к экрану.
Как и при любом другом заболевании, в случае подозрения на миопию нужно как можно быстрее обратиться к врачу. Специалист проведет необходимые исследования, определит степень серьезности проблемы и предложит оптимальные варианты коррекции зрения и лечения близорукости.
Запишись на бесплатную проверку зрения
Современные медицинские технологии позволяют диагностировать миопию с помощью вспомогательного оборудования. Специалисты применяют, например:
- автоматическую рефрактометрию — этот метод позволяет определить место нахождения оптического фокуса относительно сетчатки глаза;
- эхобиометрию — ультразвуковое исследование длины глазного яблока;
- оптическую когерентную томографию (ОКТ) – используется для оценки состояния структур глазного дна и дает возможность выявить осложнения миопии.

Есть и другие методы, предполагающие использование современного высокоточного оборудования.
Лечение миопии
Современная медицина позволяет эффективно выполнять коррекцию и лечение миопии различных степеней. Есть несколько распространенных методов как вылечить близорукость. Это:
- ношение очков и контактных линз — их должен подбирать специалист;
- различные технологии лазерной коррекции (фоторефрактивная кератоэктомия, лазерный кератомилез) — оптическая поверхность роговицы корректируется с применением лазера, за счет чего фокус изображения переносится на сетчатку;
- склеропластика — укрепление глазного яблока, которое не улучшает зрение, но позволяет остановить его дальнейшее ухудшение, чтобы миопия не прогрессировала;
- ортокератология или ОК-терапия, — использование жестких газопроницаемых контактных линз во время сна, метод позволяет перестроить эпителий роговицы и повысить остроту зрения.

Современная медицина предлагает различные способы коррекции и лечения миопии
Эффективность любой из перечисленных выше методик зависит как от уровня профессиональной подготовки специалиста и качества оборудования, которое находится в его распоряжении, так и от того, на каком этапе диагностирована болезнь и как быстро удалось начать ее лечение. Помните! Профилактика миопии не менее важна, чем её своевременное обнаружение.
Возведение в степень
Квадратный корень: math.sqrt () и cmath.sqrt
math модуль содержит math.sqrt() -функции , который может вычислить квадратный корень из любого числа (которые могут быть преобразованы в float ) , и результат всегда будет float :
import math
math.sqrt(9) # 3.0
math.sqrt(11.11) # 3.3331666624997918
math.sqrt(Decimal('6.25')) # 2.5
math.sqrt() функция вызывает ValueError , если результат будет complex :
math.sqrt(-10)
ValueError: ошибка математического домена
math.sqrt(x) быстрее , чем math.pow(x, 0.5) или x ** 0.5 , но точность результатов является то же самое. cmath модуль очень похож на math модуля, за исключением того , что можно вычислить комплексные числа , и все его результаты в виде + би исключением. Он может также использовать .sqrt() :
import cmath cmath.sqrt(4) # 2+0j cmath.sqrt(-4) # 2j
Что с j ? j является эквивалентом квадратного корня из -1. Все числа можно записать в виде a + bi или в этом случае a + bj. реальная часть числа , как 2 в 2+0j.Так как она не имеет мнимую часть, b равно 0. b представляет собой часть мнимой части числа , как 2 — в 2j.Поскольку нет никакой реальной части в этом, 2j также можно записать в виде 0 + 2j .
Экспонирование с использованием встроенных функций: ** и pow ()
Возведение может быть использован с помощью встроенного pow -функции или ** оператора:
2 ** 3 # 8 pow(2, 3) # 8
Для большинства (все в Python 2. x) арифметических операций тип результата будет типом более широкого операнда. Это не верно для ** ; следующие случаи являются исключениями из этого правила:
x) арифметических операций тип результата будет типом более широкого операнда. Это не верно для ** ; следующие случаи являются исключениями из этого правила:
Основание: int , показатель: int < 0 :
2 ** -3 # Out: 0.125 (result is a float)
Это также верно для Python 3.x.
Перед Python 2.2.0, это поднял ValueError .
Основание: int < 0 или float < 0 , показатель: float != int
(-2) ** (0.5) # also (-2.) ** (0.5)# Out: 0.125 (result is a float) Out: (8.659560562354934e-17+1.4142135623730951j) (result is complex)
operator модуль содержит две функции, которые эквивалентны ** -оператора:
import operator operator.pow(4, 2) # 16 operator.__pow__(4, 3) # 64
или можно напрямую вызвать __pow__ метод:
val1, val2 = 4, 2 val1.__pow__(val2) # 16 val2.__rpow__(val1) # 16 # in-place power operation isn't supported by immutable classes like int, float, complex: # val1.__ipow__(val2)
Экспонирование с использованием математического модуля: math.pow()
math модуль содержит другой math.pow() функцию. Разница в встроено pow() -функции или ** оператора является то , что результат всегда float :
import math math.pow(2, 2) # 4.0 math.pow(-2., 2) # 4.0
Что исключает вычисления со сложными входами:
math.pow(2, 2+0j)
Ошибка типа: невозможно преобразовать сложное в плавающее
и вычисления, которые привели бы к сложным результатам:
math.pow(-2, 0.5)
ValueError: ошибка математического домена
Экспоненциальная функция: math.exp () и cmath.exp ()
Как math и cmath модуль содержит число Эйлера: е и использовать его с встроено pow() -функции или ** -оператором работает в основном как math.exp() :
import math math.e ** 2 # 7.3890560989306495 math.------------
Магические методы и возведение в степень: построение, математика и математика
Предположим, у вас есть класс, который хранит чисто целочисленные значения:
class Integer(object):
def __init__(self, value):
self.value = int(value) # Cast to an integer
def __repr__(self):
return '{cls}({val})'.format(cls=self.__class__.__name__,
val=self.value)
def __pow__(self, other, modulo=None):
if modulo is None:
print('Using __pow__')
return self.__class__(self.value ** other)
else:
print('Using __pow__ with modulo')
return self.__class__(pow(self.value, other, modulo))
def __float__(self):
print('Using __float__')
return float(self.value)
def __complex__(self):
print('Using __complex__')
return complex(self.value, 0)
Использование встроенной pow функции или ** оператор всегда вызывает __pow__ :
Integer(2) ** 2 # Integer(4) # Prints: Using __pow__ Integer(2) ** 2.5 # Integer(5) # Prints: Using __pow__ pow(Integer(2), 0.5) # Integer(1) # Prints: Using __pow__ operator.pow(Integer(2), 3) # Integer(8) # Prints: Using __pow__ operator.__pow__(Integer(3), 3) # Integer(27) # Prints: Using __pow__
Второй аргумент __pow__() метод может подаваться только с помощью builtin- pow() или путем непосредственного вызова метода:
pow(Integer(2), 3, 4) # Integer(0) # Prints: Using __pow__ with modulo Integer(2).__pow__(3, 4) # Integer(0) # Prints: Using __pow__ with modulo
В то время как math -функции всегда преобразовать его в float и использовать флоат-вычисления:
import math math.pow(Integer(2), 0.5) # 1.4142135623730951 # Prints: Using __float__
cmath -функции попытаться преобразовать его в complex , но может также Откат к float , если нет явного преобразования в complex :
import cmath cmath.exp(Integer(2)) # (7.38905609893065+0j) # Prints: Using __complex__ del Integer.__complex__ # Deleting __complex__ method - instances cannot be cast to complex cmath.exp(Integer(2)) # (7.38905609893065+0j) # Prints: Using __float__
Ни math , ни cmath будет работать , если также __float__() -метод отсутствует:
del Integer.__float__ # Deleting __complex__ method math.sqrt(Integer(2)) # also cmath.exp(Integer(2))
Ошибка типа: требуется плавающее число
Модульное возведение в степень: pow() с 3 аргументами
Обеспечение pow() с аргументами 3 pow(a, b, c) оценивает модульного возведения в степень а б мод C:
pow(3, 4, 17) # 13 # equivalent unoptimized expression: 3 ** 4 % 17 # 13 # steps: 3 ** 4 # 81 81 % 17 # 13
Для встроенных типов использование модульного возведения в степень возможно только в том случае, если:
- Первый аргумент является
int - Второй аргумент является
int >= 0 - Третий аргумент является
int != 0
Эти ограничения также присутствуют в Python 3.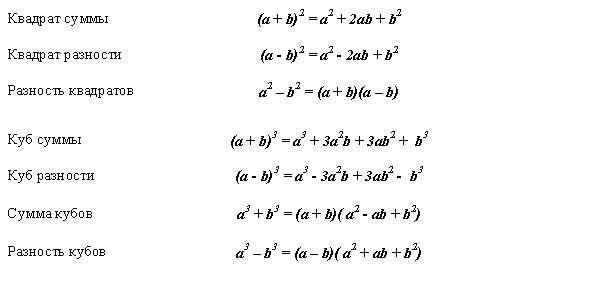 x
x
Например, можно использовать 3-аргумент форму pow определить модульную обратную функцию:
def modular_inverse(x, p):
"""Find a such as a·x ≡ 1 (mod p), assuming p is prime."""
return pow(x, p-2, p)
[modular_inverse(x, 13) for x in range(1,13)]
# Out: [1, 7, 9, 10, 8, 11, 2, 5, 3, 4, 6, 12]
Корни: n-корень с дробными показателями
В то время как math.sqrt функция предусмотрена для конкретного случая квадратных корней, это часто бывает удобно использовать оператор возведения в степень ( ** ) с дробными показателями для выполнения п-корневые операции, как кубические корни.
Обратное возведение в степень является возведением в степень по взаимности экспоненты. Таким образом, если вы можете кубизировать число, указав его в показателе степени 3, вы можете найти корень куба в числе, указав его в показателе 1/3.
>>> x = 3 >>> y = x ** 3 >>> y 27 >>> z = y ** (1.0 / 3) >>> z 3.0 >>> z == x True
Вычисление больших целочисленных корней
Несмотря на то, что Python изначально поддерживает большие целые числа, получение n-го корня очень больших чисел может привести к сбою в Python.
x = 2 ** 100 cube = x ** 3 root = cube ** (1.0 / 3)
OverflowError: long int слишком велико для преобразования в float
При работе с такими большими целыми числами вам нужно будет использовать пользовательскую функцию для вычисления n-го корня числа.
def nth_root(x, n):
# Start with some reasonable bounds around the nth root.
upper_bound = 1
while upper_bound ** n <= x:
upper_bound *= 2
lower_bound = upper_bound // 2
# Keep searching for a better result as long as the bounds make sense.
while lower_bound < upper_bound:
mid = (lower_bound + upper_bound) // 2
mid_nth = mid ** n
if lower_bound < mid and mid_nth < x:
lower_bound = mid
elif upper_bound > mid and mid_nth > x:
upper_bound = mid
else:
# Found perfect nth root. return mid
return mid + 1
x = 2 ** 100
cube = x ** 3
root = nth_root(cube, 3)
x == root
# True
return mid
return mid + 1
x = 2 ** 100
cube = x ** 3
root = nth_root(cube, 3)
x == root
# TrueСколько будет 0 в степени? — IronSet
Plan
- 1 Сколько будет 0 в степени?
- 2 Сколько будет 0 в третьей степени?
- 3 Сколько будет 5 2 степени?
- 4 Сколько будет 5 в 8 степени?
- 5 Как в калькуляторе возвести число в степень?
- 6 Как определить степень многочлена?
- 7 Сколько будет 10 в 8 степени?
- 8 Сколько будет 10 в 2 степени?
- 9 Что значит в минус второй степени?
- 10 Сколько будет 3 в минус второй степени?
- 11 Сколько будет 10 в минус шестой степени?
- 12 Сколько будет 10 в 12 степени?
Сколько будет 0 в степени?
Известно, что абсолютно любое число в нулевой степени равно единице. Почему 0 в степени 0 равно 1? Доказать это просто, при умножении степеней с одинаковым основанием их показатели складываются, а при делении – вычитаются.
Сколько будет 0 в третьей степени?
0 в 3 степени равен нулю….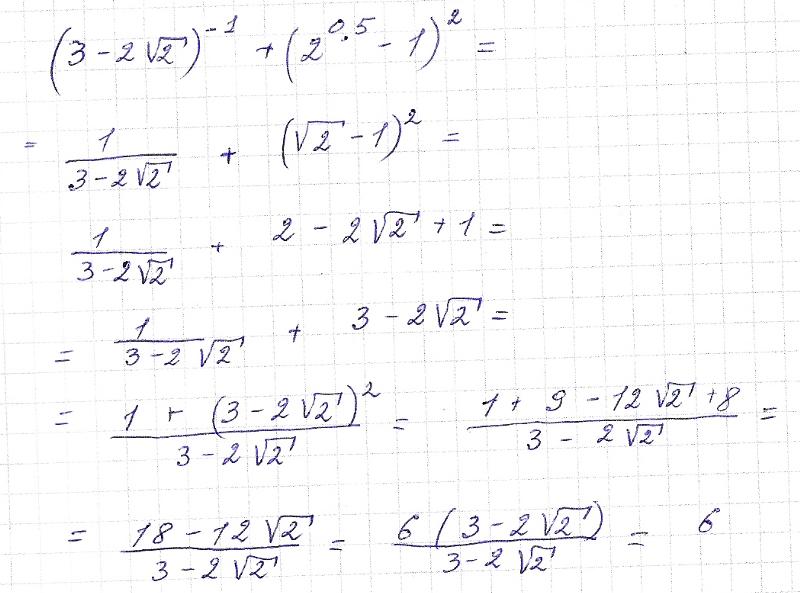 3=(6*6)*6=36*6=216….
3=(6*6)*6=36*6=216….
Как правильно считать степени?
Чтобы вычислить значение степени, нужно выполнить действие умножения, то есть перемножить основания степени указанное число раз. На умении быстро умножать и основано само понятие степени с натуральным показателем. Приведем примеры. Условие: возведите – 2 в степень 4 ….
Как в калькуляторе возвести число в степень?
Введите число, которое нужно возвести в степень. После ввода числа щелкните по кнопке с символом xʸ. Затем введите показатель степени и кликните по «равно». Калькулятор произведет необходимые вычисления и отобразит результат….
Как определить степень многочлена?
Итак, чтобы найти степень многочлена:
- Можно привести многочлен к стандартному виду.
- Найти степень всех входящих в него одночленов — членов многочлена.
- Выбрать наибольшую из этих степеней.
Сколько будет 6 в 9 степени?
Шесть в девятой степени равно Быстро вычислить любое число в любой степени можно с помощью калькулятора возведения в степень. 2 степени….
2 степени….
Сколько будет 10 в минус 2 степени?
Ответ: 0,01….
Сколько будет два в кубе?
Таблица кубов
| 0 | 5 | |
|---|---|---|
| 1 | 1000 | 3375 |
| 2 | 8000 | 15625 |
| 3 | 27000 | 42875 |
| 4 | 64000 | 91125 |
Что значит в минус второй степени?
Отрицательное число, возведённое в нечётную степень, — число отрицательное. Пример. на положительную «2». Так как степень «2» — четная, значит, результат возведения в степень будет положительный.
Сколько будет 3 в минус второй степени?
3 в минус 2 степени +4 в минус 1 степени= Ответы: это будет одна третья во.
Сколько будет 4 в минус второй степени?
Степень с отрицательным показателем К примеру, 4 в минус 2 степени — это 1/42, 2 в минус 3 степени — это 1/23, 3 в минус 1 степени — это 1/3, 10 в минус первой степени — это 1/10 (0,1)….
Сколько будет 10 в минус 12 степени?
Приставки для дольных единиц
| Десятичный множитель | Приставка | Обозначение |
|---|---|---|
| русская | русское | |
| 10−9 | нано | н |
| 10−12 | пико | п |
| 10−15 | фемто | ф |
Сколько будет 10 в минус шестой степени?
10 в 6 степени = 1000000 10 в минус 9 степени = 0, 6 * 10 в 18 степени = 6 и ещё 18 нулей.
Сколько будет 10 в 12 степени?
Именные названия степеней тысячи
| Название | Значение | |
|---|---|---|
| Русское | Латинское | Короткая шкала |
| триллион (трлн) | trillion | 1012 |
| триллиард | trilliard | — |
| квадриллион | quadrillion | 1015 |
Как считать в задачах по физике степени?
Первый множитель — первая значащая цифра, затем запятая и остальные цифры (в нашем примере это «3», «запятая», «75»). Показатель степени равен позиции после запятой, на которой стоит первая отличная от нуля цифра (в нашем примере это вторая позиция, поскольку именно там стоит первая ненулевая цифра «3»).
Показатель степени равен позиции после запятой, на которой стоит первая отличная от нуля цифра (в нашем примере это вторая позиция, поскольку именно там стоит первая ненулевая цифра «3»).
Основные плюсы и минусы экспонентов
NegativeSci. Not’nEng. Not’nFractional
Purplemath
Что такое экспоненты?
Показатели, также называемые степенями или порядками, являются сокращением для многократного умножения одного и того же самого на себя. Например, сокращение для умножения трех копий числа 5 показано справа от знака «равно» в (5)(5)(5) = 5 3 . «Показатель степени», равный 3 в этом примере, означает, сколько раз значение умножается. То, на что умножается число 5 в этом примере, называется «базой».
Содержание продолжается ниже
MathHelp.com
Экспоненты: Основные правила: Правило произведения
Этот процесс использования экспонент называется «возведением в степень», где экспонента — это «степень». Выражение 5 3 произносится как «пять в третьей степени», «пять в третьей степени» или «пять в третьей степени».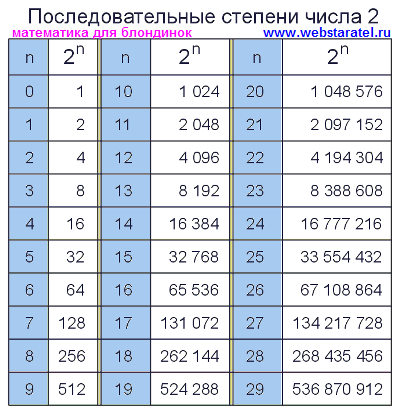
Есть две специально названные степени: «во второй степени» обычно произносится как «квадрат», а «в третьей степени» обычно произносится как «куб». Итак 5 3 обычно произносится как «пять в кубе».
Когда мы имеем дело с числами, мы обычно просто упрощаем; мы бы предпочли иметь дело с 27, чем с 3 3 . Но с переменными нам нужны показатели степени, потому что мы скорее будем иметь дело с x 6 , чем с xxxxxx .
Каковы правила упрощения с показателями?
Правила упрощения с показателями следующие:
- ( x м ) ( x n ) = x м + n
- ( x м ) n = x м × n
- ( x м )/( x n ) = x м — n
Итак, что означают эти правила? Далее я проиллюстрирую каждое правило, чтобы вы могли понять, как и почему они работают. Как только вы поймете «почему», обычно довольно легко запомнить «как».
Как только вы поймете «почему», обычно довольно легко запомнить «как».
Упростить (
x 3 )( x 4 ).
Чтобы упростить это, я могу думать о том, что означают эти показатели степени. «К третьему» означает «умножение трех копий», а «к четвертому» означает «умножение четырех копий». Используя этот факт, я могу «расширить» два фактора, а затем вернуться к упрощенной форме.
Сначала расширяю:
( x 3 ) ( x 4 ) = ( xxx ) ( xxxx )
Теперь я могу удалить круглые круг и составить все факторы:
(9 xx )( xxxx ) = xxxxxxx
Подсчитав, я вижу, что это семь копий переменной. «Умножение семи копий» означает «в седьмой степени», поэтому это можно переформулировать как:
xxxxxxx = x 7
Собирая все это вместе, шаги следующие:
( x 3 ) ( x 4 ) = ( XXX ) ( XXXX )
= = = ) ( xxxx )
= xx ) ( xxxx )
=
= xx ) ( xxxx ).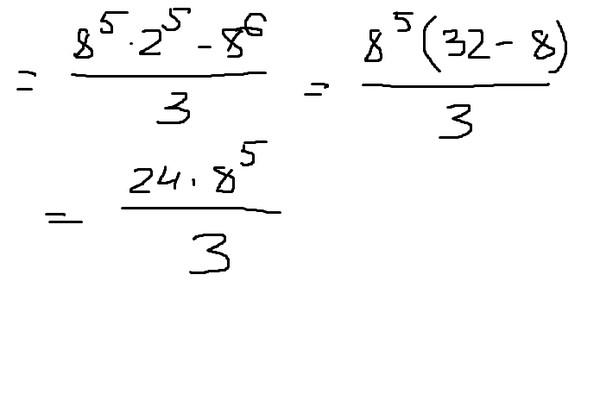 xxxxxxx
xxxxxxx
= x 7
Then the simplified form of ( x 3 )( x 4 ) is:
x 7
Note that х 7 также равно x (3+4) . Это демонстрирует первое основное правило экспоненты:
Всякий раз, когда вы умножаете два члена с одним и тем же основанием, вы можете упростить, добавляя экспоненты: ( m + n )
Однако обратите внимание, что мы НЕ МОЖЕМ упростить ( x 4 )( y 3 ) путем сложения показателей степени, потому что основания разные: ( x 4 ) ( Y 3 ) = xxxxyyy = ( x 4 ) ( Y 3 ). Ничего не совмещает.
Теперь, когда я знаю правило (а именно, что я могу добавлять способности к одной и той же базе), я могу начать с перемещения баз, чтобы получить все одинаковые базы рядом друг с другом:
( a 5 б 3 ) ( а б 7 ) = ( а 5 ) ( A ) ( B 3 ) ( B 7 )
Теперь я хочу добавить силы на A ‘S и B ‘. Однако второй и , похоже, не обладает силой. Что мне делать с этим фактором?
Однако второй и , похоже, не обладает силой. Что мне делать с этим фактором?
Все, что не имеет явной силы, в техническом смысле «возводится в степень 1». Все, что в степени 1, является просто самим собой, поскольку оно «умножает одну копию» самого себя. Таким образом, приведенное выше выражение можно переписать как:
( A 5 ) ( A ) ( B 3 ) ( B 7 ) = ( A 5 ) ( A 1 ) (9 5 ) ( A 1 ) (9 5 ) ( A 1 ) (9 5 ). b 3 ) ( B 7 )
Теперь я могу комбинировать:
( A 5 ) ( A 1 ) ( B 3 ) ( B. 7 ) = а 5+1 б 3+7 = A 6 B 10
Собрав все это вместе, моя работа в руках будет выглядеть следующим образом:
( A 5 B 3 ) ( A b 7 ) = ( a 5 a 1 ) ( b 3 b 7 ) =
a 6 b 10
В следующем примере есть две силы, причем одна сила в некотором смысле находится «внутри» другой.
Упростить (
x 2 ) 4
Для упрощения я могу начать с размышлений о том, что означают показатели степени. «До четвертого» снаружи означает, что я умножаю четыре копии любого основания, которое находится внутри круглых скобок. В этом случае основание четвертой степени равно х 2 . Умножение четырех копий этого основания дает мне:
( x 2 ) 4 = ( x 2 ) ( x 2 ) ( x 2 ) ( x 2 )
). в приведенном выше расширении «умножение двух копий» переменной. This expands as:( x 2 )( x 2 )( x 2 )( x 2 ) = ( xx )( xx )( хх )( XX )
Удаление скобков, I GET:
( XX ) ( XX ) ( XX ) ( XX ) = xxxxxxx 3 . переменная. «Умножение восемь экземпляров» означает «для восьмой мощности», так что это означает:
переменная. «Умножение восемь экземпляров» означает «для восьмой мощности», так что это означает:
XXXXXXX = x 8
Сделать все вместе:
( x 2 ) 4 101010101010101011 ( x 2 ) 4 1010101010101011 ( x 2 )01010101010101010101. ( x 2 )( x 2 )( x 2 )( x 2 )
= ( xx )( xx )( xx )( XX )
= XXXXXXXX
= x 8
Обратите внимание, что ( x 2 ) 4 = x 8 , и это 4 = x 8 , и это 40010 = x 90, и это 4 = x 9 , и это демонстрирует второе правило экспоненты:
Всякий раз, когда у вас есть выражение экспоненты, которое само возводится в степень, вы можете упростить, умножив внешнюю степень на внутреннюю степень:
( x m ) n = x m n
Если у вас есть произведение внутри круглых скобок и мощность в скобках, то мощность передается каждому элементу внутри. For instance:
For instance:
( xy 2 ) 3 = ( xy 2 )( xy 2 )( xy 2 )
= ( xxx )( г 2 г 2 y 2 )
= ( xxx )( yyyyyy )
= x 3 y 6
= ( x ) 3 ( y 2 ) 3
Другой пример:
Примечание. Это правило НЕ работает, если в скобках указана сумма или разность. Экспоненты, в отличие от умножения, НЕ «распределяют» над сложением.
Например, учитывая (3 + 4) 2 , НЕ поддавайтесь искушению сказать: « Эй, это равно 3 2 + 4 2 = 9 + 16 = 25 », потому что это неправильно. На самом деле, (3 + 4) 2 = (7) 2 = 49, а не 25.
Если сомневаетесь, запишите выражение в соответствии с определением мощности. Например, учитывая ( x − 2) 2 , не пытайтесь сделать это в уме. Вместо этого напишите это; «квадрат» означает «умножение двух копий», поэтому:
Например, учитывая ( x − 2) 2 , не пытайтесь сделать это в уме. Вместо этого напишите это; «квадрат» означает «умножение двух копий», поэтому:
( x — 2) 2 = ( x — 2) ( x — 2)
= x ( x — 2) — 2 ( x — 2)
= хх — 2 х — 2 х + 4
= х 2 — 4 х + 4,
. пытаются все делать в уме, вместо того, чтобы показывать свои работы. Делайте все аккуратно, и вероятность того, что вы совершите эту ошибку, снизится.
Упрощение (
a 2 b 3 c ) 4
Теперь, когда я знаю правило о силах на силах, я могу применить 4 к каждому из внутренних факторов. (Мне нужно помнить, что число c в скобках, не имеющее явной силы над ним, следует рассматривать как возведенное «в степень 1». )
)
( A 2 ) 4 ( B 3 ) 4 ( C 1 ) 4
= ( A 2 × 4 ) ( A 2 × 4 ) ( A 2 × 4 ) ( A 2 × 4 ) ( A 2 × 40010) ( A 2 × 40010). B 3 × 4 ) ( C 1 × 4 )
= A 8 B 12 C 4
- 0 9003 / и 2
Чтобы упростить это, я сначала расширю числитель и знаменатель.
( AAAAA )/( AA )
Очевидно, две копии фактора A дублируются, так что я могу отменить их:
( AA )/(10003
( AA )/(10003
( AA )/(10003
( AA )/(10003
( AA )/(10003
( AA )/(10003
(Помните, что, когда «все» сокращается, остается понятный, но обычно игнорируемый множитель 1, который остается. ) окончательный ответ:
) окончательный ответ:
aaa = a 3
Note that ( a 5 )/( a 2 ) = a 5−2 = a 3 , и что 5 − 2 = 3. Это иллюстрирует правило третьей степени:
Всякий раз, когда у вас есть одно и то же основание в числителе и знаменателе дроби, вы можете упростить, вычитая степени:
( x м ) / ( x n ) = x m − n
(Да, это правило может привести к отрицательным показателям степени. На следующей странице вы узнаете, как с ними работать.)
Есть еще одно правило. которые могут или не могут быть рассмотрены в вашем классе на данном этапе:
Все, что в нулевой степени равно 1 (до тех пор, пока «что угодно» само по себе не является нулем).
Это правило объясняется на следующей странице. Однако на практике это правило означает, что некоторые упражнения могут быть намного проще, чем могут показаться на первый взгляд:
Кого волнует то, что заключено в квадратные скобки? Уж точно нет, потому что нулевая мощность снаружи означает, что значение всего этого всего равно 1. Ха!
Ха!
[(3 x 4 y 7 z 12 ) 5 (−5 x 9 y 3 z 4 ) 2 ] 0 = 1
Кстати, как только ваш класс перейдет «в нулевую степень», вы должны ожидать упражнение, подобное приведенному выше, на следующем тесте. Это обычный вопрос с подвохом, созданный для того, чтобы вы потратили впустую много своего ограниченного времени, но он работает только в том случае, если вы не обращаете внимания.
Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в упрощении выражений с показателями степени. Попробуйте введенное упражнение или введите свое собственное упражнение. Затем нажмите кнопку, чтобы сравнить свой ответ с ответом Mathway. (Или пропустите виджет и продолжите урок, или просмотрите множество рабочих примеров здесь.)
Пожалуйста, примите куки-файлы настроек, чтобы включить этот виджет.
Щелкните здесь, чтобы перейти непосредственно на сайт Mathway, если вы хотите проверить их программное обеспечение или получить дополнительную информацию.
URL: https://www.purplemath.com/modules/exponent.htm
Страница 2Страница 3Страница 4Страница 5
Полный курс алгебры
Навыки
в
А Л Г Е Б Р А
Содержание | Дом
13
Степени числа
Значение показателя степени
Отрицательное основание
Секция 2
Три правила показателей степени
, ЕСЛИ ВСЕ МНОЖИТЕЛИ РАВНЫ — 2 · 2 · 2 · 2, — мы называем произведение степенью этого числа (Урок 1).
Чтобы увидеть ответ, наведите указатель мыши на цветную область.
: Чтобы снова закрыть ответ, нажмите «Обновить» («Reload»).
Сначала решай задачу сам!
Задача 1. Какое число равно
?а) третья степень числа 2? 2 · 2 · 2 = 8
б) четвертая степень числа 3? = 81
c) пятая степень числа 10? = 100 000
d) первая степень числа 8? = 8
Теперь вместо того, чтобы записывать третью степень числа 2 как 2 · 2 · 2, мы пишем 2 только один раз и ставим показатель степени: 2 3 . 2 — повторяющееся умноженное число — называется основанием.
2 — повторяющееся умноженное число — называется основанием.
Показатель степени указывает, сколько раз нужно повторить основание как множитель.
Учащийся должен следить за тем, чтобы не спутать 3 и , что означает 3 умножить на на , с на 3 , что означает на на .
| 3 и | = | + + , |
| а 3 | = | · · . |
Задача 2. Что означает каждый символ?
| а) | x 5 = x x x x x | б) | 5 3 = 5 · 5 · 5 | в) | 5 · 3 = 3 + 3 + 3 + 3 + 3. |
| г) | (5 a ) 3 = 5 · 5 · 5 | д) | 5 a 3 = 5 a a a |
В части d) в скобках указано, что основание равно 5 a . В части e) только и являются базовыми. Показатель степени не применяется к 5.
В части e) только и являются базовыми. Показатель степени не применяется к 5.
Задача 3. 3 4 = 81,
а) Какое число называется основанием? 3
б) Какое число является степенью? 81 это мощность из 3.
c) Какое число является показателем степени?
4. Это указывает на мощность, а именно 4-ю.
Задача 4. Запишите значение этих символов.
а) а 2 а 3 = ·
б) ( аб ) 3 = аб · аб · аб
C) ( A 2 ) 3 = A 2 · A 2 · A · A · A · A .
Задача 5. Запишите значение этих символов.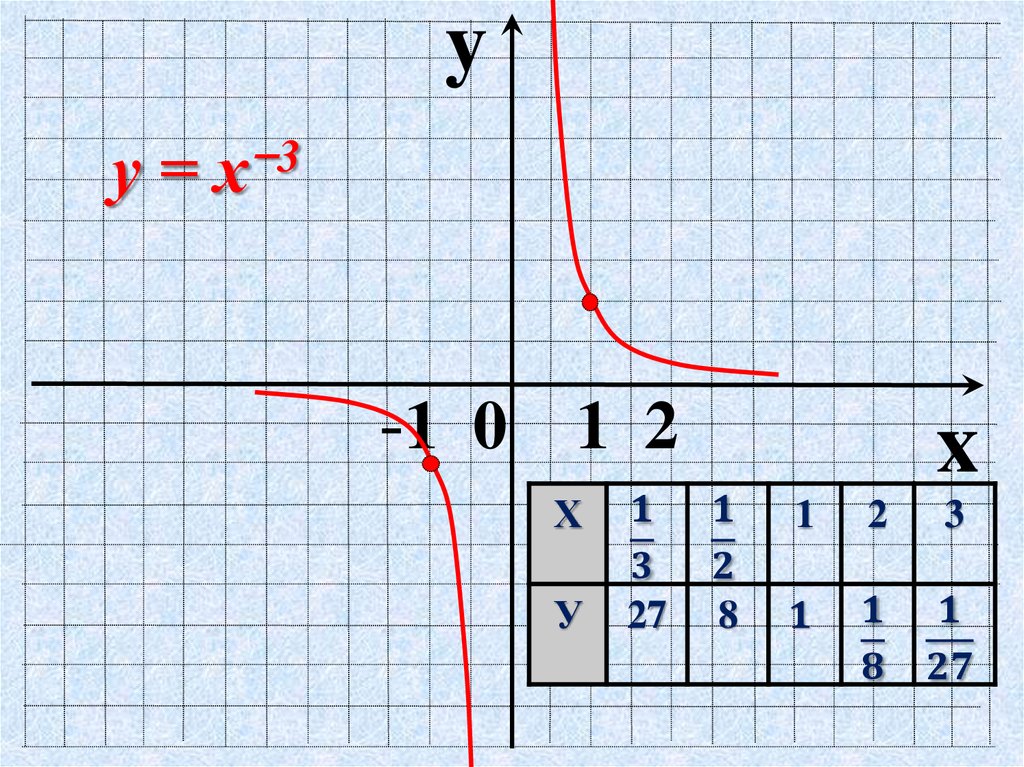 В каждом из них что является основой?
В каждом из них что является основой?
а) 4 = . База .
| б) | − а 4 | = | − а а а а . База снова . Это минус из a 4 . Знак минус всегда означает отрицательное значение следующего за ним числа. −5 является минусом 5. И − a 4 является минусом a 4 . |
c) (− a ) 4 = (− a )(− a )(− a )(− a ). Здесь база равна (− a ).
Задача 6. Оценить.
а) 2 4 = 16.
б) −2 4 =
−16. Это минус от 2 4 . Основание равно 2. См.
Задача 5b) выше.
− a = (−1) a , для любого числа a . (Урок 5.) Следовательно −2 4 = (−1)2 4 . И поэтому согласно порядку операций (Урок 1) это (−1)16 = −16.
(Урок 5.) Следовательно −2 4 = (−1)2 4 . И поэтому согласно порядку операций (Урок 1) это (−1)16 = −16.
в) (−2) 4 =
+16, согласно Правилу знаков (Урок 4).
В скобках указано, что основание равно −2. См. задачу 5c).
Пример 1. Отрицательное основание.
(−2) 3 = (−2)(−2)(−2) = −8,
снова в соответствии с Правилом знаков. Принимая во внимание, что
(−2) 4 = +16.
Если основание отрицательное, а показатель степени равен , нечетное , то произведение равно отрицательный. Но когда основание отрицательное, а показатель степени равен даже , тогда произведение равно положительный.
Задача 7. Оценить.
| а) | (−1) 2 = 1 | б) | (−1) 3 = −1 | в) | (−1) 4 = 1 | г) | (−1) 5 = −1 | |||
| д) | (−1) 100 = 1 | е) | (−1) 253 = −1 | г) | (−2) 4 = 16 | ч) | (−2) 5 = −32 | |||
Задача 8. Перепишите, используя показатели степени.
Перепишите, используя показатели степени.
| а) | xxxxxx = x 6 | б) | xxyyyy = x 2 y 4 | |
| в) | xyxxyx = x 4 y 2 | г) | xyxyxy = x 3 y 3 | |
Задача 9. Перепишите, используя показатели степени.
| а) | ( x + 1)( x + 1) = ( x + 1) 2 | б) | ( х — 1)( х — 1)( х — 1) = ( x − 1) 3 | |
| в) | ( x + 1)( x — 1)( x + 1)( x — 1) = ( x + 1) 2 ( x | |||
Раздел 2.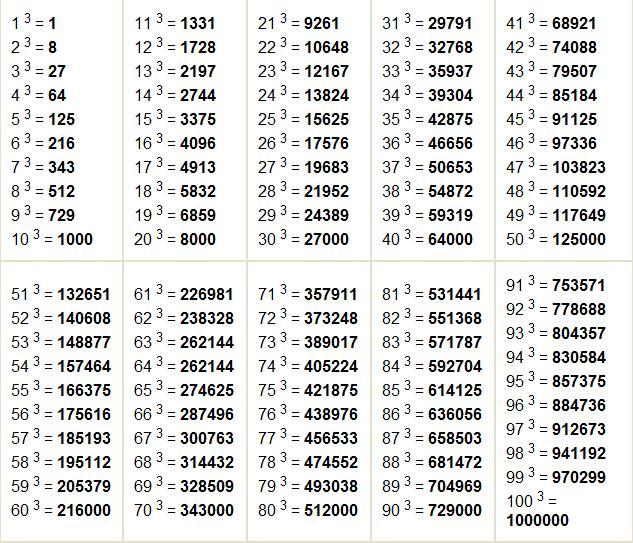 Три правила показателей степени
Три правила показателей степени
Содержание | Дом
Пожалуйста, сделайте пожертвование, чтобы TheMathPage оставался онлайн.
Даже 1 доллар поможет.
Copyright © 2021 Лоуренс Спектор
Вопросы или комментарии?
Электронная почта: [email protected]
Инволюция и силы, вторая, третья, четвертая степени
Когда количество умножается на само , произведение называется степенью .
Таким образом, 2 × 2 = 4, квадрат или вторая степень числа 2.
2×2×2 = 8, куб или третья степень.
2×2×2×2 = 16, четвертая степень.
Итак, 10×10 = 100, вторая степень числа 10.
10×10×10 = 1000, третья степень.
10×10×10×10 = 10000 в четвертой степени.
И a×a = aa, вторая степень a
a×a×a = aaa, третья степень
а×а×а×а = аааа, четвертая степень.
Сама первоначальная величина, хотя и не произведенная путем умножения, подобно проистекающим из нее силам, тем не менее называется первой степенью . Его также называют базовым .
Его также называют базовым .
Поскольку неудобно, особенно в случае больших мощностей, записывать все буквы или множители, из которых состоят мощности, обычно используется сокращенный метод записи. Основание пишется только один раз, а затем цифра или буква помещается справа и немного приподнята, чтобы показать, сколько раз основание равно 9.0962 используется как коэффициент для производства энергии. Это число или буква называется показателем степени или показателем степени . Таким образом, 2 ставится вместо а×а или аа, потому что а дважды повторяется как множитель для получения мощности аа. А 3 означает ааа; ибо здесь и повторяют трижды как множитель.
Показатель первой степени равен 1; но это обычно опускается. Таким образом, 1 совпадает с a.
Показатель степени не следует путать с коэффициентами . Коэффициент показывает, как часто количество принимается за часть целого. Экспонента показывает, как часто количество принимается как фактор в продукте.
Экспонента показывает, как часто количество принимается как фактор в продукте.
Таким образом, 4а = а + а + а + а. Но 4 = а×а×а×а
Схема записи в экспонентах имеет то особое преимущество, что позволяет нам выразить 90 962 неизвестных 90 963-степеней.
Для этой цели показатель степени равен 9.0962 буква , вместо числовой цифры. При решении задачи может встретиться величина, о которой мы знаем, что она равна некоторой степени другой величины. Но может быть еще не установлено, квадрат ли это, куб или какая-то высшая сила.
Таким образом, в выражении a x показатель степени x означает, что a возводится в в некоторой степени , хотя он не определяет в какой степени . Таким образом, b m и d n являются степенями b и d; и читаются как m-я степень b и n-я степень d. Когда значение показателя степени найдено, номер обычно заменяется буквой. Таким образом, если m = 3, то b m = b 3 ; но если m = 5, то b m = b 5 .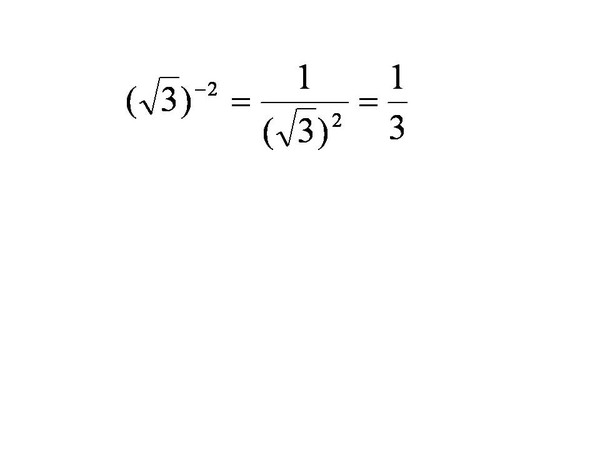
Метод выражения степеней в показателях также имеет большое преимущество в случае составных величин.
Таким образом, (a + b + d) 3 равно (a + b + d)×(a + b + d)×(a + b + d), то есть кубу числа (o+6+d).
a 3 + 3a 2 b + 3a 2 d + 3ab 2 + 6abd + 3ad 2 + б 3 + д 3 .
Если мы возьмем ряд степеней, индексы которых увеличиваются или уменьшаются на 1, мы обнаружим, что сами степени увеличиваются на общего множителя или уменьшаются на общего делителя ; и что этот множитель или делитель есть первоначальная величина, из которой возводятся силы.
Таким образом, в ряду ааааа, аааа, ааа, аа, а;
или 5 , 4 , 3 , 2 , 1 ;
индексы, отсчитываемые справа налево, равны 1, 2, 3, 4, 5; и общая разница между ними есть единица. Если мы начнем с 90 962 правых 90 963 и 90 962, умножив 90 963 на а, мы получим несколько степеней последовательно, справа налево.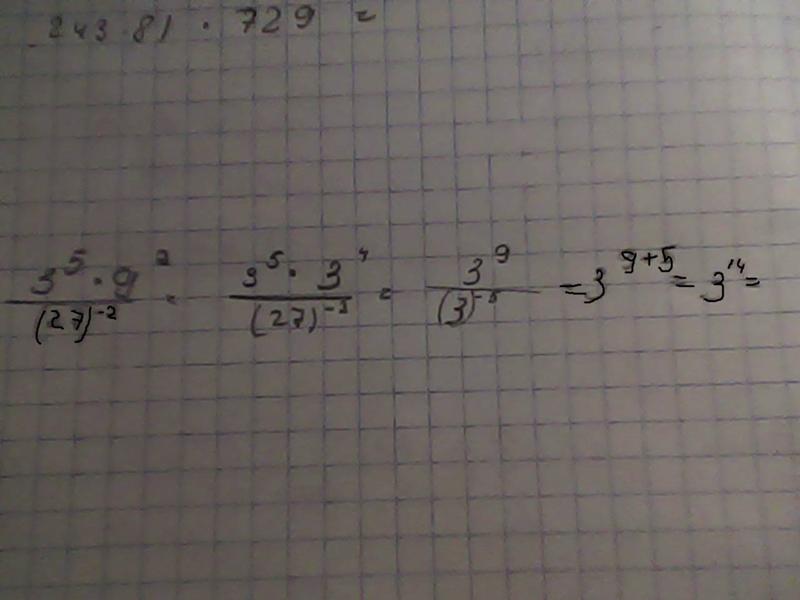
Таким образом, второй член a×a = a 2 . И a 3 ×a = a 4
a 2 ×a = a 3 третий член. а 4 × а = а 5 .
Если мы начнем с осталось , а разделить на a,
У нас есть 5 :a = a 4
И 3 :a = a 2 .
а 4 :а = а 3
а 2 :а = а 1
Но это деление может быть продолжено еще дальше; и тогда мы получим новый набор величин.
Таким образом, $a:a = \frac{a}{a} = 1$.
$\frac{1}{a}:a = \frac{1}{aa}$
$1:a = \frac{1}{a}$ $\frac{1}{aa}:a = \frac{1}{aaa}$
9{-4}$.
А чтобы индексы представляли собой полный ряд с 1 для общей разности, член $\frac{a}{a}$ или 1, который считается отсутствием степени, записывается как 0 .
Силы как прямые, так и взаимные* tnen,
Вместо аааа, ааа, аа, а, $\frac{a}{a}$, $\frac{1}{a}$, $\frac{1}{aa}$, $\frac{1} {ааа}$, $\frac{1}{аааа}$.
Будет 4 , 3 , 2 , 1 , 0 , -1 , -2 , -3 , -4 .
Или +4 , +3 , +2 , +1 , 0 , -1 , -1 9090, 0
И взятые сами по себе индексы будут,
+4, +3, +2, +1, 0, -1, -2, -3, -4.
Основание степени может быть выражено более чем одной буквой.
Таким образом, aa×aa, или (aa) 2 — это вторая степень числа aa.
И аа×аа×аа, или (аа) 3 — третья степень числа аа.
Следовательно, определенная мощность одной величины может быть другой мощностью другой величины. Таким образом, 4 — это вторая степень числа а и четвертая степень числа а.
Все степени 1 одинаковы. Для 1×1 или 1×1×1. все еще 1.
Инволюция — это нахождение любой степени количества путем умножения его на себя. Причина следующего общего правила очевидна из природы сил.
Умножьте количество на себя, пока оно не будет принято за множитель, столько раз, сколько единиц в той степени, в которую количество должно быть возведено.
Это правило охватывает все случаи, которые могут иметь место в инволюции. Но уместно будет дать объяснение того, как оно применяется к частным случаям.
Одна буква возводится в степень повторением ее столько раз, сколько ее показатель степени.
Четвертая степень числа а равна 4 или аааа.
Шестая степень y равна y 6 или yyyyyy.
N-я степень x равна x n или xxx….. n повторений.
Способ привлечения количества, состоящего из нескольких факторов, зависит от того принципа, что мощность произведения нескольких факторов равна произведению их мощностей.
Таким образом, (ау) 2 = а 2 у 2 Для (ау) 2 = ау×ау.
Но ай×ай = айай = аайй = а 2 y 2 .
So (bmx) 3 = bmx×bmx×bmx = bbbmmmxxx = b 3 m 3 x 3 .
Таким образом, находя мощность продукта, мы можем либо поднять все сразу; или мы можем поднять каждый из факторов отдельно, а затем умножить их несколько сил друг на друга.
Бывший. 1. 4-я степень dhy равна (dhy) 4 или d 4 h 4 y 4 .
2. Третья степень числа 4b равна (4b) 3 , или 4 3 b 3 , или 64b 3 .
3. N-я степень числа 6ad равна (6ad) n или 6 n a n d n .
4. Трехмерная степень 3m×2y равна (3m×2y) 3 или 27m 3 × 8y 3 .
Составное количество, состоящее из десятков, соединенных + и -, возводится в действительное произведение нескольких его частей. Таким образом,
(a + b) 1 = a + b, первая степень.(a + b) 2 = a 2 + 2ab + b 2 , вторая степень (a + b).

(a + b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3 , третья степень.
(а + б) 4 = а 4 + 4а 3 б + 6а 2 б 2 + 4аб 3 + б 4 -я степень.
2. Квадрат a — b, это 2 — 2ab + b 2 .
3. Куб а + 1 равен 3 + 3а 2 + 3а + 1.
4. Квадрат a + b + h равен a 2 + 2ab + 2ah + b 2 + 2bh + h 2
5. Требуемый куб a + 2d + 3
6. Требуется 4-я степень b + 2.
7. Требуется 5-я степень x + 1.
8. Требуется 6-я степень числа 1 — b.
Квадраты бинома и остатка 9Величины 0963 встречаются в алгебраических процессах так часто, что важно их освоить.
Если мы умножим a + h на себя, а также a — h,
Имеем (a + h)(a + h) = a 2 + 2ah + h 2
И (a — h)(a — h) = a 2 — 2ah + h 2 .
Здесь будет видно, что в каждом случае первый и последний члены являются квадратами a и h; и что средний член равен удвоенному произведению a на h. Следовательно, квадраты биномиальных и остаточных величин, не умножая каждый из членов в отдельности, могут быть найдены по следующему предложению.
Квадрат двучлена, оба члена которого положительны, равен квадрату первого члена + удвоенному произведению двух членов + квадрату последнего члена.
А квадрат остаточного количества равен квадрату первого слагаемого, — удвоенному произведению двух слагаемых + квадрату последнего слагаемого.
Пример. 1. Квадрат 2a + b равен 4a 2 + 4ab + b 2 .
2. Квадрат ab + cd равен 9.0009 2 б 2 + 2abcd + в 2 г 2 .
3. Квадрат 3d — h равен 9d 2 + 6dh + h 2 .
4. Квадрат a — 1 равен 2 — 2a + 1.
О методе нахождения высших степеней биномов см. в одном из следующих разделов.
в одном из следующих разделов.
Для многих целей будет достаточно выразить степени составных величин с помощью показателей степени без фактического умножения.
Таким образом, квадрат a + b равен (a + b) 2 .
N-я степень числа bc + 8 + x равна (bc + 8 + x) n
В случаях такого рода винкулум должен быть нарисован по всем терминам, из которых состоит составная величина.
Но если основание состоит из нескольких 90 962 множителей 90 963 , то винкулум, употребляемый для выражения мощности, может либо распространяться на все целое; или могут быть применены к каждому из факторов отдельно, как это может потребовать удобство.
Таким образом, квадрат (a + b)(c + d) равен либо [(a + b)×(c + d)] 2 , либо (a + b) 2 × (c + d) 2 .
Ибо первое из этих выражений есть квадрат произведения двух множителей, а последнее — произведение их квадратов. Но одно из них равно другому.
Куб a×(b + d) равен [a×(b + d)] 3 или a 3 × (b + d) 3 .
Когда величина, степень которой была выражена переменной и показателем степени, впоследствии возводят к фактическому умножению слагаемых, говорят, что оно равно расширенный .
Что касается знака, который должен стоять перед величинами, возведенными в , важно заметить, что когда основание положительно, все его положительные степени также положительны; но когда основание отрицательно, нечетных степеней отрицательны, а четных степеней положительны.
2-я степень -а равна +а 2
3-я степень -а равна -а 3
4-я степень равна +а 4
5-я степень равна -а 5 .
215. Следовательно, любая нечетная степень имеет тот же знак, что и ее основание. Но степень даже положительна, независимо от того, положительна ли ее основа или отрицательна.
Таким образом, +a×+a = +a 2
И -a×-a = +a 2
Величина, которая уже является степенью, возводится путем умножения ее показателя в показатель степени, в которую она должна быть возведена.
Для a 2 = aa: и куб aa равен aa×aa×aa = aaaaaa = a 6 ; что является 6-й степенью а, но 3-й степенью 2 .
2. Четвертая степень числа 3 b 2 , равна a 3×4 b 2×4 = a 12 b 8
3. 3-я степень числа 4 2 x равна 64a 6 x 3 .
4. Пятая степень числа (a + b) 2 равна (a + b) 10 .
5. N-я степень числа 3 равна 3n
.6. N-я степень (x — y) m , равна (x — y) mn
7.(а 3 × b 3 ) 2 = а 6 × b 6
8. (а 3 б 2 ч 4 ) 3 = а 9 б 6 ч 12
217. Правило равно применимо и к степеням, показатели которых отрицательные . 9{-6}$
9{-6}$
2. Четвертая степень числа 2 b -3 равна 8 b -12 или 8 /b 12 .
3. Квадрат b 3 x -1 , равен b 6 x -2 .
4. N-я степень ax -m равна x -mn , или 1/x.
Если знак перед в степени равен -, то он должен быть заменен на + всякий раз, когда показатель степени становится четным числом.
Пример: квадрат -a 3 равен +a 6 . Квадрат -а 3 равен -а 3 .-а 3 , что согласно правилам знаков при умножении равно +а 6 .
2. Но куб -a 3 равен -a 9 . For-a 3 .-a 3 .-a 3 = -a 9 .
3. N-я степень -a 3 равна ±a 3n .
Здесь мощность будет положительной или отрицательной, в зависимости от того, является ли число, которое представляет n, четным или нечетным. 92}$
92}$
2. 2d, 3d и n-я степени числа 1/a равны 1/a 2 , 1/a 3 и 1/a n .
Примеров двучленов , в которых одним из слагаемых является дробь.
1. Найдите квадрат x + 1/2 и x — 1/2, как в 210.
(х + 1/2) 2 = х 2 + 2.х.(1/2) + 1/2 2 = х 2 + х + 1/4
(х — 1/2) 2 = х 2 — 2.х.(1/2) + 1/2 2 = х 2 — х + 1/4
2. Квадрат а + 2/3 равен 2 + 4а/3 + 4/9.
3. Квадрат x + b/2 = x 2 + bx + b 2 /4.
4 Квадрат x — b/m, равен x 2 — 2bx/m + b 2 /m 2 .
Показано, что дробный коэффициент можно перевести из числителя в знаменатель дроби или из знаменателя в числитель. Возвращаясь к схеме обозначения обратных степеней, можно увидеть, что любой множитель также может быть перенесен, если изменить знак его показателя степени .
1 Таким образом, в дроби ax -2 /y мы можем перенести x из числителя в знаменатель.
Для оси -2 /y = (a/y).x -2 = (a/y).(1/x 2 = a/yx 2 .
2. В дроби a/by 3 можно перенести y из знаменателя в числитель.
Для a/by 2 = (a/b).(1/y 3 ) = (a/b).y -3 = ау -3 /б.
Таким же образом мы можем перенести множитель с положительным показателем в числителе или с отрицательным показателем в знаменателе.
1. Таким образом, ах 3 /b = a/bx -3 . Для x 3 является обратной величиной x -3 , то есть x 3 = 1/x -3 .
Следовательно, знаменатель любой дроби может быть полностью удален или числитель может быть уменьшен до единицы без изменения значения выражения. 93-8
Научное обозначение | Учебник для начинающих
Некоторые люди сильно сопротивляются использованию научного обозначения The format contains a decimal fraction multiplied by ten raised to a power»> * . Почти каждый раз, когда я провожу вводное занятие по естествознанию, у меня есть один или два ученика с сильными математическими способностями, которые настаивают на том, чтобы выполнять все свои расчеты в стандартной системе счисления. Это неизменно приводит к ошибкам, которые приводят к потере баллов на экзаменах и домашнем задании.
Чтобы разобраться в научных обозначениях, требуется немного усилий, но после того, как вы их выучите, это станет эффективным способом сэкономить время и избежать ошибок при работе с очень большими и маленькими числами. Это особенно полезно при использовании калькуляторов или компьютеров для прикладной работы. Гораздо проще избежать ошибок при написании 4,6х10 -14 по сравнению с записью 0.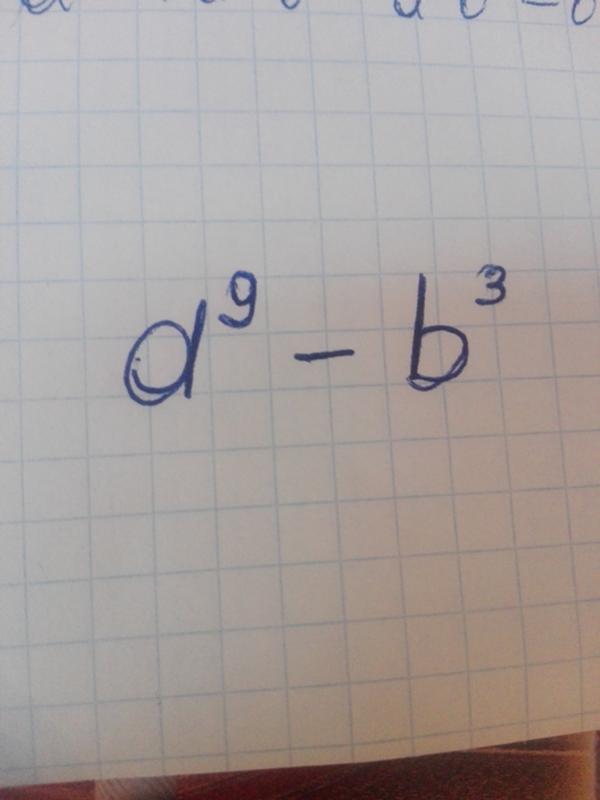 000000000000046.
000000000000046.
Преобразование числа из стандартной записи в экспоненциальную включает перемещение десятичного знака до тех пор, пока слева от десятичной дроби не останется одна цифра, а затем умножение этого значения на десять, возведенное в ту же степень, что и число перемещенных разрядов. 300, записанное в экспоненциальном представлении, равно 3×10 2 ; говорил как «Трижды десять к двум». Десять, возведенные в степень двойки, указывают на то, что для преобразования значения обратно в стандартную запись десятичная запятая должна переместиться на два разряда. Знак показателя Negative exponents indicate that a number should be multiplied by one over itself which is the same as dividing.»> * зависит от направления движения десятичной дроби.
Переместите ползунок, чтобы сравнить значения в стандартной и экспоненциальной записи
Все значения, записанные в экспоненциальном представлении, имеют одинаковую структуру: само число, за которым следует символ умножения, затем число 10, возведенное в степень.
Число называется коэффициентом. Степень 10, в которую возводят, называется показателем степени. Коэффициент может быть любым действительным числом. Показатель степени должен быть целым числом, хотя он может быть и отрицательным.
Части структуры обозначений имеют имена
Положительная экспонента означает, что число больше единицы, а десятичная дробь перемещается вправо для преобразования научной записи в стандартную. 3,0 x 10 2 становится 300.
Отрицательная экспонента означает, что число меньше единицы, а десятичная дробь перемещается влево для преобразования научной записи в стандартную. 3,0 x 10 -2 становится 0,03.
3,0 x 10 -2 становится 0,03.
Перемещение десятичной дроби на то же количество разрядов, что и 10, работает, потому что перемещение десятичной дроби на одно место эквивалентно делению или умножению числа на 10:
- Шаг 1 — разделить 300 на 10: 300 ÷ 10 = 30
- Шаг 2 — результат шага 1 снова разделите на 10: 30 x 10 1 ÷ 10 = 3
Поскольку нам пришлось два раза разделить на 10, чтобы получить от 300 до 3, показатель степени научной записи равен 2. Это показывает, что исходное число можно воссоздать, умножив 3 на 10 два раза.
Следовательно, 3,0 x 10 2 , 3,0 x 10 x 10 и 300 представляют одно и то же значение.
Один и тот же шаблон работает независимо от размера числа. 2 300 000 000 000 можно записать как 2,3 x 10 12 , который говорит, что это 2,3, умноженное на 10 12 раз.
Паттерн работает и для больших чисел
Значения, которые меньше единицы, работают одинаково. Разница в том, что преобразование из стандартной записи в экспоненциальную предполагает умножение на 10, а не деление. Умножение на 10 сдвигает десятичную дробь вправо. Чтобы записать число 0,0003 в экспоненциальном представлении, 0,0003 многократно умножается на 10, пока первое ненулевое число (в данном случае 3) не окажется слева от десятичного знака:
Разница в том, что преобразование из стандартной записи в экспоненциальную предполагает умножение на 10, а не деление. Умножение на 10 сдвигает десятичную дробь вправо. Чтобы записать число 0,0003 в экспоненциальном представлении, 0,0003 многократно умножается на 10, пока первое ненулевое число (в данном случае 3) не окажется слева от десятичного знака:
- Шаг 1 — умножить на 10: 0,0003 x 10 = 0,003
- Шаг 2 — снова умножьте на 10: 0,003 x 10-1 x 10 = 0,03
- Шаг 3 — снова умножьте на 10: 0,03 x 10-2 x 10 = 0,3
- Шаг 4 — снова умножьте на 10: 0,3 x 10-3 x 10 = 3
Это преобразование заняло 4 шага, поэтому число умножается на 10, возведенное в минус числа, поэтому шаги указывают, что для возврата к исходному числу требуется деление на 10 4 раза. Показатель степени отрицательный, потому что исходное число меньше единицы.
В дополнение к упрощению выражения больших и малых чисел экспоненциальное представление упрощает сравнение значений. Запись двух значений в виде:
Запись двух значений в виде:
0,000000035 и 0,0000000098
затрудняет с первого взгляда понять, какой из них больше, при написании их как
3,5 x 10 -8 и 9,8 x 10 -9
становится намного яснее, что первый больше.
Наиболее распространенный способ записи значений в экспоненциальном представлении — это структура x10exponent. С появлением компьютеров и калькуляторов буква Е заменила «х10», так что 3200 можно записать как 3200, 3,2Е3 или 3,2х109.0009 3 .
Попробуйте решить задачи на научную нотацию, чтобы проверить свое понимание понятий, охватываемых этой иллюстрацией.
Связанный контент:
- Практические задачи
Знаки степени (символы математической экспоненты на клавиатуре)
Степени или экспоненты — это математические текстовые символы (мы поговорим об их значении позже), которые люди писали в тексте со времен, когда была разработана кодировка ASCII. И вы можете набирать их прямо с клавиатуры. Я покажу вам, как это сделать, используя различные методы в зависимости от вашей операционной системы и вкусов.
И вы можете набирать их прямо с клавиатуры. Я покажу вам, как это сделать, используя различные методы в зависимости от вашей операционной системы и вкусов.
| Полномочия | ⁰ | ¹ | ² | ³ |
|---|---|---|---|---|
| ⁴ | ⁵ | ⁶ | ⁷ | |
| ⁸ | ⁹ | ⁺ | ⁻ | |
| ⁼ | ⁽ | ⁾ | ⁿ |
Текстовые символы
Сила математики степеней
Возведение в степень — это математическая операция, записываемая как 9.0962 bⁿ , включающий два числа: основание b и показатель степени (или индекс, или степень) n . Когда n — целое положительное число, возведение в степень соответствует повторному умножению; другими словами, это произведение числа b , умноженного само на себя n раз.
Показатель степени обычно отображается в виде надстрочного индекса справа от основания. Возведение в степень bⁿ можно прочитать как: b возведено в n-е в степени, b в степени n или b в степени n , наиболее кратко как b в n . Некоторые показатели степени имеют собственное произношение: например, b² обычно читается как b в квадрате, а b³ как b в кубе.
Возведение в степень bⁿ можно прочитать как: b возведено в n-е в степени, b в степени n или b в степени n , наиболее кратко как b в n . Некоторые показатели степени имеют собственное произношение: например, b² обычно читается как b в квадрате, а b³ как b в кубе.
Степень bⁿ может быть определена также, когда n является отрицательным целым числом, для ненулевого b . Нет естественного расширения для всех реальных b и n существуют, но когда основание b является положительным действительным числом, bⁿ может быть определено для всех действительных и даже комплексных показателей степени n с помощью экспоненциальной функции e x .
Также эти символы индекса используются в химии для обозначения химических элементов (например, ²⁴⁰ᶠPu, ⁵⁸ᵐCo).
Как вводить символы мощности
Выберите свою систему, чтобы узнать.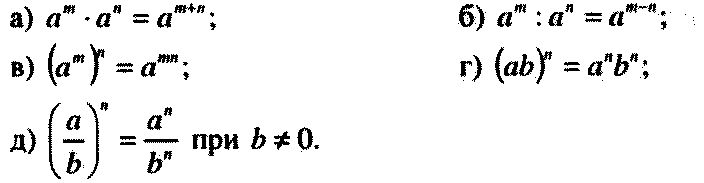
Окна
С клавиатуры
Альтернативные коды
Техника быстрого доступа, которая работает на настольных компьютерах и большинстве ноутбуков под управлением MS Windows. Вы нажимаете Alt и, удерживая его, набираете код на цифровой клавиатуре, пока она включена. Пожалуйста, прочитайте руководство, если вы используете ноутбук. С помощью этого метода вы можете ввести много часто используемых символов.
| Альтернативный код | Символ |
|---|---|
| 0176 | ° |
| 0185 | ¹ |
| 0178 | ² |
| 0179 | ³ |
Состояния переключения
Настройте раскладку клавиатуры в Windows, чтобы вы могли вводить все дополнительные символы так же просто, как и любой другой текст.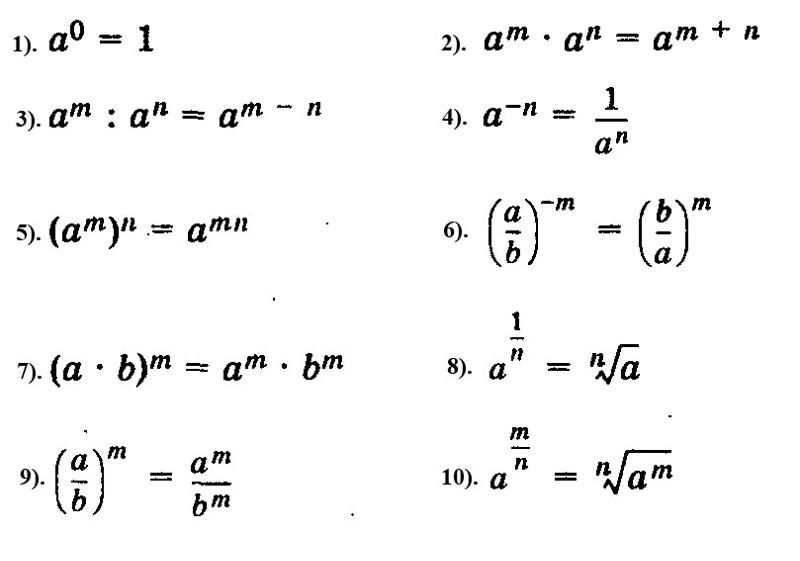 Настройка занимает около 5-10 минут, но вы будете печатать как босс.
С помощью этой техники вы можете назначить на клавиатуру символы бесконечности и любые другие текстовые символы.
Настройка занимает около 5-10 минут, но вы будете печатать как босс.
С помощью этой техники вы можете назначить на клавиатуру символы бесконечности и любые другие текстовые символы.
Карта символов
CharMap позволяет вам просматривать и использовать все символы и символы, доступные во всех шрифтах (некоторые примеры шрифтов: «Arial», «Times New Roman», «Webdings»), установленных на вашем компьютере. Вы можете вводить знаки силы, используя его.
Мак
Emoji на iOS (iPhone, iPad и iPod touch)
Текстовые символы с клавиатурой Emoji iPhone 📲Простой и красивый способ узнать, как добавить виртуальную клавиатуру для символов Emoji, видимых в виде маленьких картинок. Сама клавиатура предустановлена на вашем устройстве iOS, поэтому вам не нужно ничего скачивать или покупать.
Палитра символов
Палитра символов позволяет просматривать и использовать все символы и символы, включая знаки силы, доступные во всех шрифтах (некоторые примеры шрифтов: «Arial», «Times New Roman», «Webdings»), установленных на вашем компьютере.
линукс
С клавиатуры
| Шестнадцатеричный код Юникода | Символ | Шестнадцатеричный код Юникода | Символ | Шестнадцатеричный код Юникода | Символ |
| 2070 | ⁰ | 00B9 | ¹ | 00B2 | ² |
| 00B3 | ³ | 2074 | ⁴ | 2075 | ⁴ |
| 2076 | ⁶ | 2077 | ⁷ | 2078 | ⁸ |
| 2079 | ⁹ | 207А | ⁺ | 207Б | ⁻ |
| 207с | ⁼ | 207Д | ⁽ | 207Э | ⁾ |
| 207F | ⁿ | 1D2C | ᴬ | 1D2D | ᴭ |
| 1D2F | ᴮ | 1D2F | ᴯ | 1Д30 | ᴰ |
| 1Д31 | ᴱ | 1Д32 | ᴲ | 1Д33 | ᴳ |
| 1Д34 | ᴴ | 1Д35 | ᴵ | 1Д36 | ᴶ |
| 1Д37 | ᴷ | 1Д38 | ᴸ | 1Д39 | ᴹ |
| 1D3A | ᴺ | 1D3B | ᴻ | 1D3C | ᴼ |
| 1D3D | ᴽ | 1D3E | ᴾ | 1D3F | ᴿ |
| 1Д40 | ᵀ | 1Д41 | ᵁ | 1Д42 | ᵂ |
| 1Д43 | ᵃ | 1Д44 | ᵄ | 1Д45 | ᵅ |
| 1Д46 | ᵆ | 1Д47 | ᵇ | 1Д48 | ᵈ |
| 1Д49 | ᵉ | 1D4A | ᵊ | 1D4B | ᵋ |
| 1D4C | ᵌ | 1D4D | ᵍ | 1D4E | ᵎ |
| 1D4F | ᵏ | 1Д50 | ᵐ | 1Д51 | ᵑ |
| 1Д52 | ᵒ | 1Д53 | ᵓ | 1Д54 | ᵔ |
| 1Д55 | ᵕ | 1Д56 | ᵖ | 1Д57 | ᵗ |
| 1Д58 | ᵘ | 1Д59 | ᵙ | 1Д5Б | ᵛ |
На самом деле существует 3 разных способа ввода символов в Linux с помощью клавиатуры.


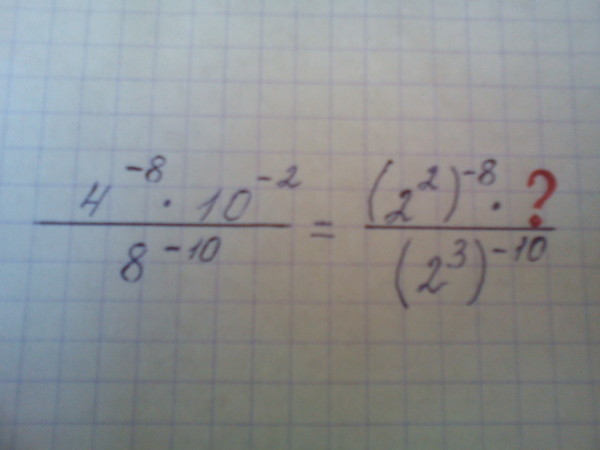
 Удлинение оси глаза на 1 мм в среднем приводит к прогрессированию миопии на 3 диоптрии и значительному ухудшению зрения.
Удлинение оси глаза на 1 мм в среднем приводит к прогрессированию миопии на 3 диоптрии и значительному ухудшению зрения.


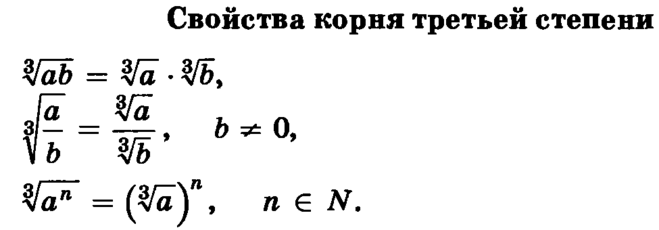


 sqrt(-10)
sqrt(-10)
 __ipow__(val2)
__ipow__(val2)  ------------
------------  5 # Integer(5)
# Prints: Using __pow__
pow(Integer(2), 0.5) # Integer(1)
# Prints: Using __pow__
operator.pow(Integer(2), 3) # Integer(8)
# Prints: Using __pow__
operator.__pow__(Integer(3), 3) # Integer(27)
# Prints: Using __pow__
5 # Integer(5)
# Prints: Using __pow__
pow(Integer(2), 0.5) # Integer(1)
# Prints: Using __pow__
operator.pow(Integer(2), 3) # Integer(8)
# Prints: Using __pow__
operator.__pow__(Integer(3), 3) # Integer(27)
# Prints: Using __pow__
 exp(Integer(2)) # (7.38905609893065+0j)
# Prints: Using __complex__
del Integer.__complex__ # Deleting __complex__ method - instances cannot be cast to complex
cmath.exp(Integer(2)) # (7.38905609893065+0j)
# Prints: Using __float__
exp(Integer(2)) # (7.38905609893065+0j)
# Prints: Using __complex__
del Integer.__complex__ # Deleting __complex__ method - instances cannot be cast to complex
cmath.exp(Integer(2)) # (7.38905609893065+0j)
# Prints: Using __float__  0
>>> z == x
True
0
>>> z == x
True  return mid
return mid + 1
x = 2 ** 100
cube = x ** 3
root = nth_root(cube, 3)
x == root
# True
return mid
return mid + 1
x = 2 ** 100
cube = x ** 3
root = nth_root(cube, 3)
x == root
# True