Площадь поверхности цилиндра – формула полной и боковой площади поверхности
4.6
Средняя оценка: 4.6
Всего получено оценок: 9358.
Обновлено 11 Января, 2021
4.6
Средняя оценка: 4.6
Всего получено оценок: 9358.
Обновлено 11 Января, 2021
Цилиндр представляет собой геометрическое тело, ограниченное двумя параллельными плоскостями и цилиндрической поверхностью. В статье поговорим о том, как найти площадь поверхности цилиндра и, применив формулу, решим для примера несколько задач.
Материал подготовлен совместно с учителем высшей категории Харитоненко Натальей Владимировной.
Опыт работы учителем математики — более 33 лет.
У цилиндра есть три поверхности: вершина, основание, и боковая поверхность.
Основаниями цилиндра (их два: верхние и нижнее) являются окружности, их легко определить.
Известно, что площадь окружности равна πr2. Поэтому, формула площади двух окружностей (двух оснований цилиндра) будет иметь вид πr2 + πr2 = 2πr
Боковая поверхность цилиндра
Третья, боковая поверхность цилиндра, является изогнутой стенкой цилиндра. Для того чтобы лучше представить эту поверхность попробуем преобразовать её, чтобы получить узнаваемую форму. Представьте себе, что цилиндр, это обычная консервная банка, у которой нет верхней крышки и дна. Сделаем вертикальный надрез на боковой стенке от вершины до основания банки (Шаг 1 на рисунке) и попробуем максимально раскрыть (выпрямить) полученную фигуру (Шаг 2).
После полного раскрытия полученной банки мы увидим уже знакомую фигуру (Шаг 3), это прямоугольник. Площадь прямоугольника вычислить легко. Но перед этим вернемся на мгновение к первоначальному цилиндру. Верхнее основание исходного цилиндра является окружностью, а мы знаем, что длина окружности вычисляется по формуле: L = 2πr. На рисунке она отмечена красным цветом.
Когда боковая стенка цилиндра полностью раскрыта, мы видим, что длина окружности становится длиной полученного прямоугольника.
Формула площади боковой поверхности цилиндра
Sбок. = 2πrh
r – радиус цилиндра, h – высота цилиндра
Площадь полной поверхности цилиндра
Наконец, если мы сложим площадь всех трёх поверхностей, мы получим формулу площади полной поверхности цилиндра. Площадь полной поверхности цилиндра равна площадь верхнего основания цилиндра + площадь нижнего основания цилиндра + площадь боковой поверхности цилиндра или S = πr2 + πr2 + 2πrh = 2πr2 + 2πrh. Иногда это выражение записывается идентичной формулой 2πr (r + h).
Формула площади полной поверхности цилиндра
r – радиус цилиндра, h – высота цилиндра
Примеры расчета площади поверхности цилиндра
Для понимания приведенных формул, попробуем посчитать площадь поверхности цилиндра на примерах.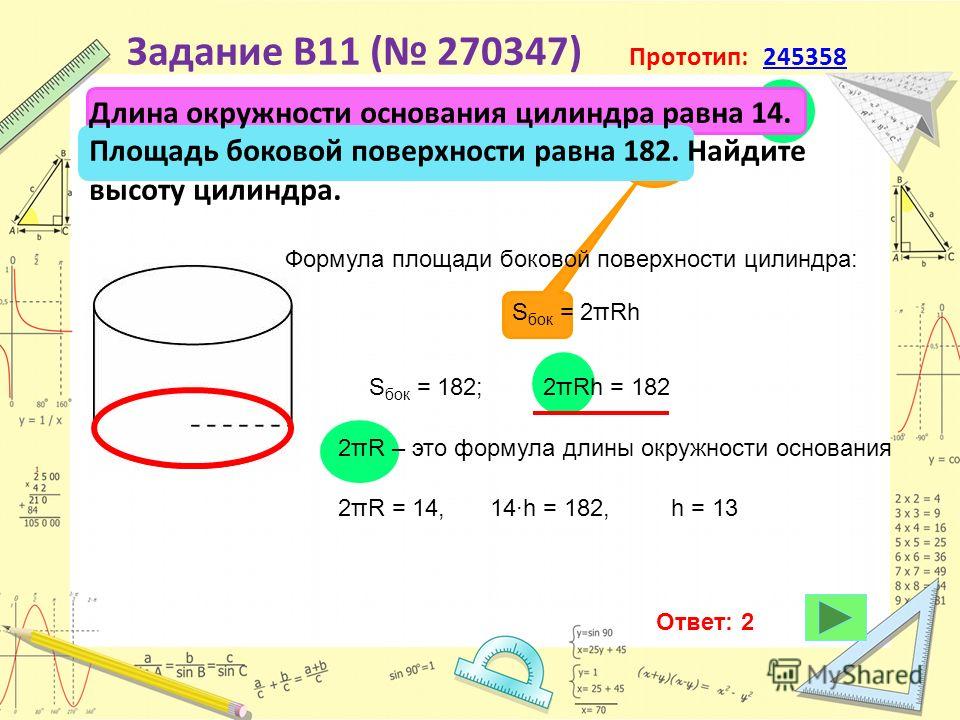
1. Радиус основания цилиндра равен 2, высота равна 3. Определите площадь боковой поверхности цилиндра.
Площадь боковой поверхности рассчитывается по формуле: Sбок. = 2πrh
Sбок. = 2 * 3,14 * 2 * 3
Sбок. = 6,28 * 6
Sбок. = 37,68
Площадь боковой поверхности цилиндра равна 37,68.
2. Как найти площадь поверхности цилиндра, если высота равна 4, а радиус 6?
Площадь полной поверхности рассчитывается по формуле: S = 2πr2 + 2πrh
S = 2 * 3,14 * 62 + 2 * 3,14 * 6 * 4
S = 2 * 3,14 * 36 + 2 * 3,14 * 24
S = 226,08 + 150,72
S = 376,8
Площадь поверхности цилиндра равна 376,8.
3. Площадь боковой поверхности прямого кругового цилиндра равна 24π, а диаметр основания — 3. Найдите высоту цилиндра.
Из формулы расчета площади боковой поверхности цилиндра Sбок.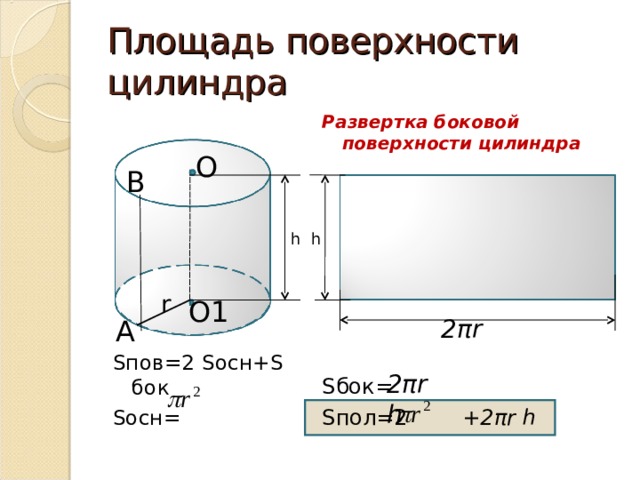 = 2πrh следует, что высота равна:
= 2πrh следует, что высота равна:
h = Sбок./2πr
Значение радиуса получаем из формулы: d = 2r
h = 24π / (2π * 0,5d)
h = 24π / (2π * 0,5 * 3)
h = 12 / 1,5
h = 8
Высота цилиндра равна 8.
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Dark Spyro
5/5
Татьяна Матвиенко
5/5
Юрий Евдокимов
5/5
Михаил Чепурной
5/5
Дмитрий Новиков
5/5
Дилноза Саипова
4/5
Darya Simonova
5/5
Тамара Иванова
5/5
Татьяна Немчинова
5/5
Рамиль Сагиров
5/5
Оценка статьи
4.6
Средняя оценка: 4.6
Всего получено оценок: 9358.
А какая ваша оценка?
Площадь цилиндра формула онлайн калькулятор.
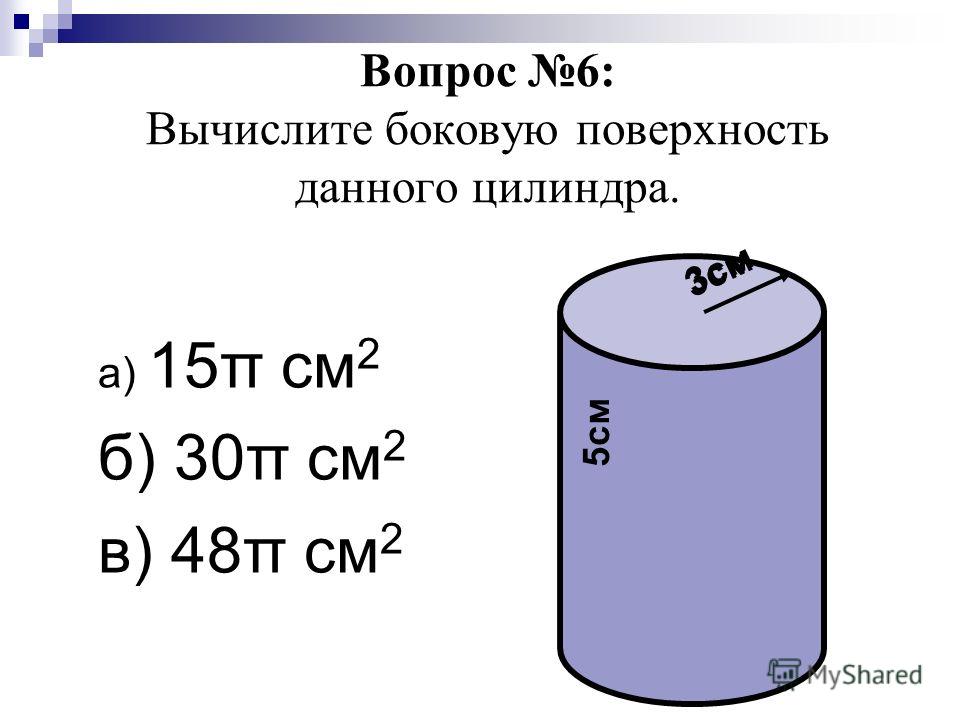 Примеры того, как вычислить площадь цилиндра
Примеры того, как вычислить площадь цилиндраПлощадь поверхности цилиндра. В этой статье мы рассмотрим задания связанные с площадью поверхности . На блоге уже рассмотрены задания с таким телом вращения как конус. Цилиндр тоже относится к телам вращения. Что требуется и нужно знать о площади поверхности цилиндра? Давайте посмотрим на развёртку цилиндра:
Верхнее и нижнее основание это два равных круга:
Боковая поверхность это прямоугольник. При чём одна сторона этого прямоугольника равна высоте цилиндра, а другая длине окружности основания. Напомню, что длина окружности равна:
Итак, формула поверхности цилиндра:
*Учить эту формулу не нужно! Достаточно знать формулы площади круга и длины его окружности, тогда вы всегда сможете записать указанную формулу. Важно её понимание! Рассмотрим задачи:
Длина окружности основания цилиндра равна 3. Площадь боковой поверхности равна 6. Найдите высоту и площадь поверхности цилиндра (считайте, что число Пи равно 3,14 и результат округлите до десятых).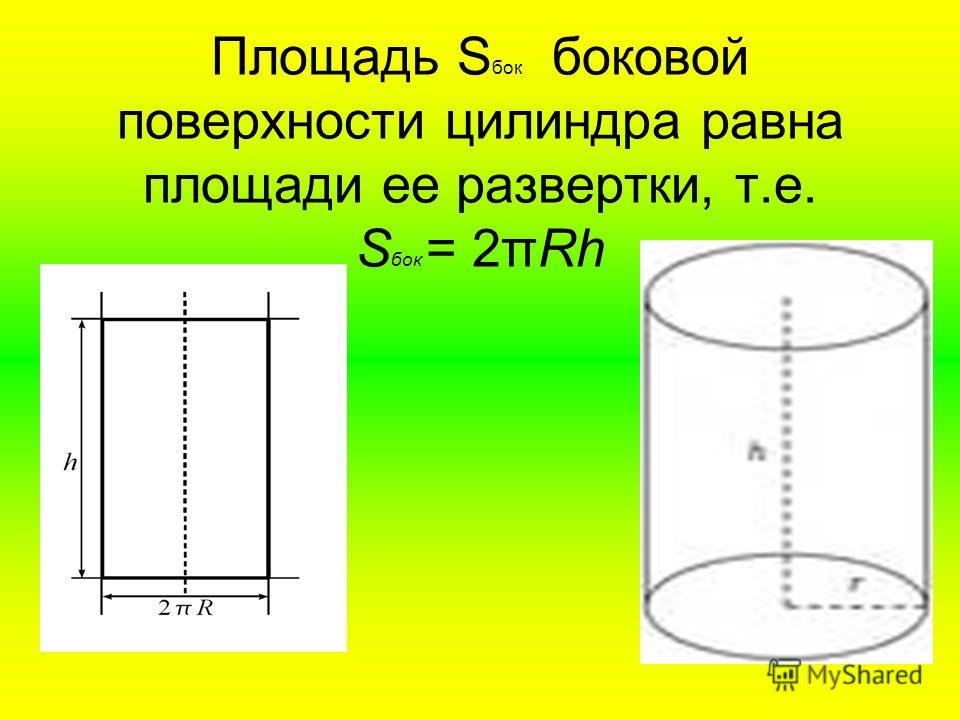
Площадь полной поверхности цилиндра:
Даны длина окружности основания и площадь боковой поверхности цилиндра. То есть, нам дана площадь прямоугольника и одна его сторона, требуется найти другую сторону (это есть высота цилиндра):
Требуется радиус и тогда мы сможем найти указанную площадь.
Длина окружности основания равна трём, тогда запишем:
Таким образом
Округляем до десятых, получаем 7,4.
Ответ: h = 2; S = 7,4
Площадь боковой поверхности цилиндра равна 72Пи, а диаметр основания — 9. Найдите высоту цилиндра.
Значит
Ответ: 8
Площадь боковой поверхности цилиндра равна 64Пи, а высота — 8 . Найдите диаметр основания.
Площадь боковой поверхности цилиндра находится по формуле:
Диаметр равен двум радиусам, значит:
Ответ: 8
27058. Радиус основания цилиндра равен 2, высота равна 3. Найдите площадь боковой поверхности цилиндра, деленную на Пи.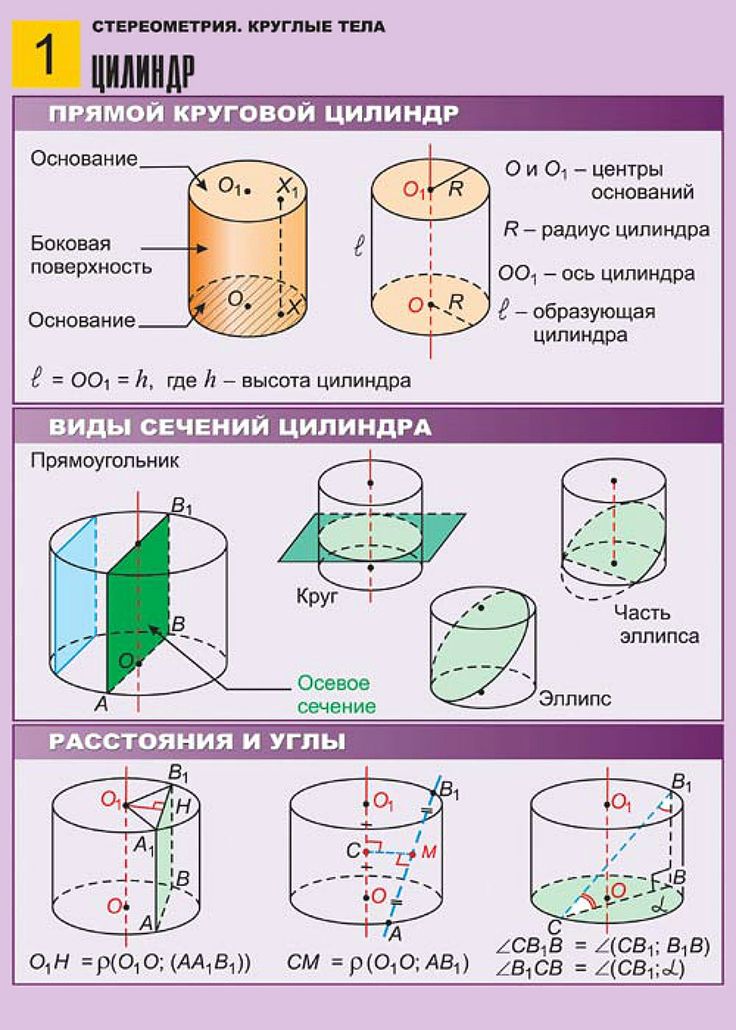
27133. Длина окружности основания цилиндра равна 3, высота равна 2. Найдите площадь боковой поверхности цилиндра.
Рассмотрим цилиндр вращения радиуса R и высоты h (рис. 383). В основание этого цилиндра впишем правильный многоугольник (на рис. 383 — шестиугольник) и с его помощью построим правильную призму, вписанную в цилиндр. Таким же путем можно описывать вокруг цилиндра правильные призмы с произвольно большим числом боковых граней.
За площадь боковой поверхности цилиндра принимается по определению предел, к которому стремятся площади боковых поверхностей вписанных и описанных вокруг него правильных призм по мере неограниченного удвоения (или вообще увеличения) числа их боковых граней.
То, что такой предел существует, мы сейчас и докажем. Если возьмем вписанную правильную призму, построенную на правильном -угольнике, как на основании, то для ее боковой поверхности будем иметь выражение , где — периметр правильного -угольника, вписанного в круг основания цилиндра.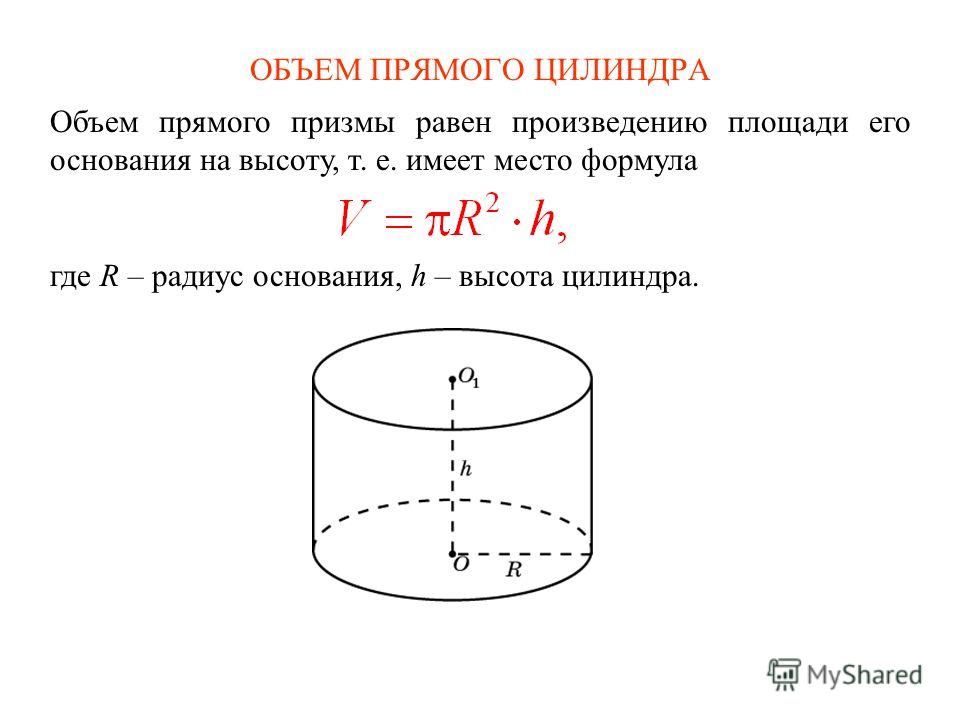 При . Точно такое же вычисление для описанной призмы дает тот же самый результат. Итак, площадь боковой поверхности цилиндра вращения выражается формулой
При . Точно такое же вычисление для описанной призмы дает тот же самый результат. Итак, площадь боковой поверхности цилиндра вращения выражается формулой
Боковая поверхность цилиндра равна произведению длины образующей на периметр (т. е. длину окружности) основания.
Задача 1. Отрезок, соединяющий диаметрально противоположные точки А и В верхнего и нижно оснований цилиндра (рис. 384), равен 10 см и наклонен к плоскости основания под углом в 60°. Найти площадь боковой поверхности цилиндра.
Решение. Проведем через отрезок Л Всечение плоскостью, перпендикулярной к основанию цилиндра. Из треугольника имеем
откуда находим для боковой поверхности цилиндра
Задача 2. Треугольник ABC, вершины А и В которого суть концы диаметра нижнего основания цилиндра, а вершина С-конец перпендикулярного к нему диаметра верхнего основания, равносторонний со стороной а,
Найти площади боковой и полной поверхностей цилиндра. Решение. Радиус основания цилиндра равен Высота треугольника ABC (рис.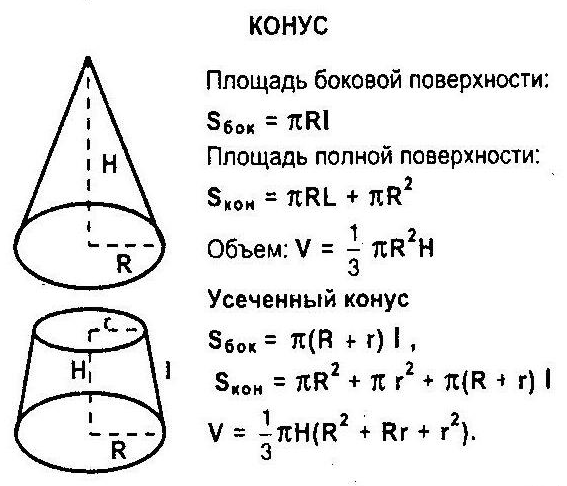 385) равна а образующая цилиндра вычисляется как
385) равна а образующая цилиндра вычисляется как
Отсюда боковая поверхность цилиндра получается равной
а полная поверхность (равная сумме площади боковой поверхности и площади двух оснований цилиндра) равнаУпражнения
1. Диагонали боковых граней прямоугольного параллелепипеда наклонены к плоскости основания под углами, соответственно равными . Найти угол наклона к той же плоскости диагонали параллелепипеда.
2. В прямом параллелепипеде острый угол основания равен а, а одна из сторон основания равна а. Сечение, проведенное через эту сторону и противоположное ребро верхнего основания, имеет площадь Q, и плоскость его наклонена к плоскости основания под углом . Найти объем и полную поверхность параллелепипеда.
3. Основанием наклонной треугольной призмы служит равнобедренный прямоугольный треугольник, а проекция одного из боковых ребер на плоскость основания совпадает с медианой m одного из катетов треугольника. Найти угол наклона боковых ребер к плоскости основания, если объем призмы равен V.
4. В правильной шестиугольной призме через сторону основания проведены два сечения: 1) содержащее противоположную сторону верхнего основания, 2) содержащее центр верхнего основания. При какой высоте призмы угол между плоскостями сечений имеет наибольшую величину и чему он равен в этом случае?
Название науки «геометрия» переводится как «измерение земли». Зародилась стараниями самых первых древних землеустроителей. А было так: во время разливов священного Нила потоки воды иногда смывали границы участков земледельцев, а новые границы могли не совпасть со старыми. Налоги же крестьянами уплачивались в казну фараона пропорционально величине земельного надела. Измерением площадей пашни в новых границах после разлива занимались специальные люди. Именно в результате их деятельности и возникла новая наука, получившая развитие в Древней Греции. Там она и название получила, и приобрела практически современный вид. В дальнейшем термин стал интернациональным названием науки о плоских и объёмных фигурах.
Планиметрия — раздел геометрии, занимающийся изучением плоских фигур. Другим разделом науки является стереометрия, которая рассматривает свойства пространственных (объёмных) фигур. К таким фигурам относится и описываемая в этой статье — цилиндр.
Примеров присутствия предметов цилиндрической формы в повседневной жизни предостаточно. Цилиндрическую (гораздо реже — коническую) форму имеют почти все детали вращения — валы, втулки, шейки, оси и т.д. Цилиндр широко используется и в строительстве: башни, опорные, декоративные колонны. А кроме того посуда, некоторые виды упаковки, трубы всевозможных диаметров. И наконец — знаменитые шляпы, ставшие надолго символом мужской элегантности. Список можно продолжать бесконечно.
Определение цилиндра как геометрической фигуры
Цилиндром (круговым цилиндром) принято называть фигуру, состоящую из двух кругов, которые при желании совмещаются с помощью параллельного переноса. Именно эти круги и являются основаниями цилиндра. А вот линии (прямые отрезки), связывающие соответствующие точки, получили название «образующие».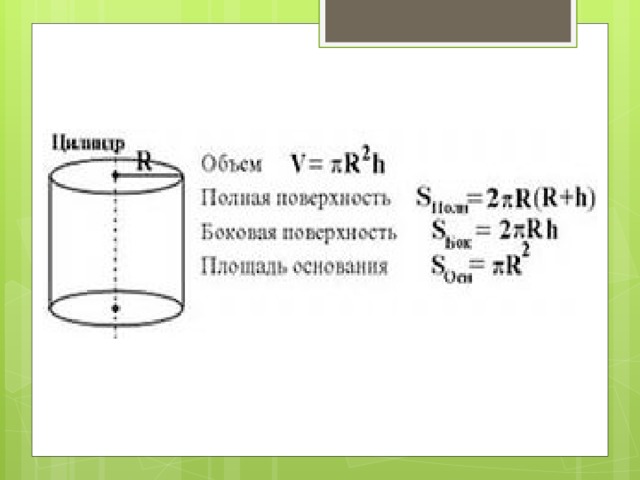
Важно, что основания цилиндра всегда равны (если это условие не выполняется, то перед нами — усечённый конус, что-либо другое, но только не цилиндр) и находятся в параллельных плоскостях. Отрезки же, соединяющие соответствующие точки на кругах, параллельны и равны.
Совокупность бесконечного множества образующих — не что иное, как боковая поверхность цилиндра — один из элементов данной геометрической фигуры. Другая её важная составляющая — рассмотренные выше круги. Называются они основаниями.
Виды цилиндров
Самый простой и распространённый вид цилиндра — круговой. Его образуют два правильных круга, выступающих в роли оснований. Но вместо них могут быть и другие фигуры.
Основания цилиндров могут образовывать (кроме кругов) эллипсы, другие замкнутые фигуры. Но цилиндр может иметь не обязательно замкнутую форму. Например основанием цилиндра может служить парабола, гипербола, другая открытая функция. Такой цилиндр будет открытым или развернутым.
По углу наклона образующих к основаниям цилиндры могут быть прямыми или наклонными. У прямого цилиндра образующие строго перпендикулярны плоскости основания. Если данный угол отличается от 90°, цилиндр — наклонный.
У прямого цилиндра образующие строго перпендикулярны плоскости основания. Если данный угол отличается от 90°, цилиндр — наклонный.
Что такое поверхность вращения
Прямой круговой цилиндр, без сомнения — самая распространённая поверхность вращения, используемая в технике. Иногда по техническим показаниям применяется коническая, шарообразная, некоторые другие типы поверхностей, но 99% всех вращающихся валов, осей и т.д. выполнены именно в форме цилиндров. Для того чтобы лучше уяснить, что такое поверхность вращения, можно рассмотреть, как же образован сам цилиндр.
Допустим, имеется некая прямая a , расположенная вертикально. ABCD — прямоугольник, одна из сторон которого (отрезок АВ) лежит на прямой a . Если вращать прямоугольник вокруг прямой, как это показано на рисунке, объём, который он займёт, вращаясь, и будет нашим телом вращения — прямым круговым цилиндром с высотой H = AB = DC и радиусом R = AD = BC.
В данном случае, в результате вращения фигуры — прямоугольника — получается цилиндр.
Площадь поверхности цилиндра
Для того чтобы вычислить площадь поверхности обычного прямого кругового цилиндра, необходимо подсчитать площади оснований и боковой поверхности.
Вначале рассмотрим, как вычисляют площадь боковой поверхности. Это произведение длины окружности на высоту цилиндра. Длина окружности, в свою очередь, равняется удвоенному произведению универсального числа П на радиус окружности.
Площадь круга, как известно, равняется произведению П на квадрат радиуса. Итак, сложив формулы для площади определения боковой поверхности с удвоенным выражением площади основания (их ведь два) и произведя нехитрые алгебраические преобразования, получаем окончательное выражение для определения площади поверхности цилиндра.
Определение объёма фигуры
Объем цилиндра определяется по стандартной схеме: площадь поверхности основания умножается на высоту.
Таким образом, конечная формула выглядит следующим образом: искомое определяется как произведение высоты тела на универсальное число П и на квадрат радиуса основания.
Полученная формула, надо сказать, применима для решения самых неожиданных задач. Точно так же, как объем цилиндра, определяется, например, объём электропроводки. Это бывает необходимо для вычисления массы проводов.
Отличия в формуле только в том, что вместо радиуса одного цилиндра стоит делённый надвое диаметр жилы проводки и в выражении появляется число жил в проводе N . Также вместо высоты используется длина провода. Таким образом рассчитывается объем «цилиндра» не одного, а по числу проводков в оплётке.
Такие расчёты часто требуются на практике. Ведь значительная часть ёмкостей для воды изготовлена в форме трубы. И вычислить объем цилиндра часто бывает нужно даже в домашнем хозяйстве.
Однако, как уже говорилось, форма цилиндра может быть разной. И в некоторых случаях требуется рассчитать, чему равен объем цилиндра наклонного.
Отличие в том, что площадь поверхности основания умножают не на длину образующей, как в случае с прямым цилиндром, а на расстояние между плоскостями — перпендикулярный отрезок, построенный между ними.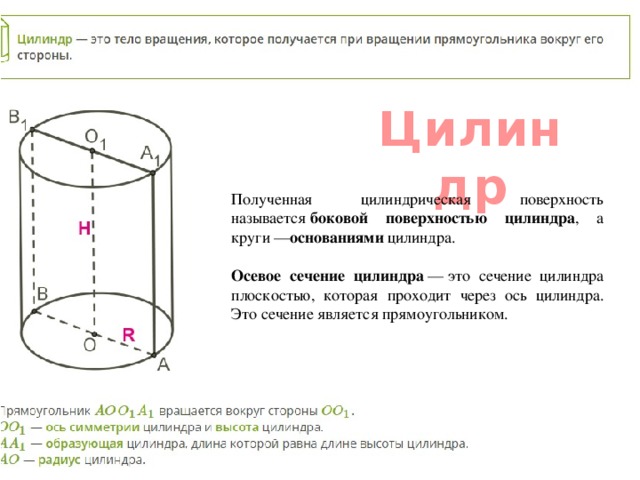
Как видно из рисунка, такой отрезок равен произведению длины образующей на синус угла наклона образующей к плоскости.
Как построить развёртку цилиндра
В некоторых случаях требуется выкроить развёртку цилиндра. На приведённом рисунке показаны правила, по которым строится заготовка для изготовления цилиндра с заданными высотой и диаметром.
Следует учитывать, что рисунок приведен без учёта швов.
Отличия скошенного цилиндра
Представим себе некий прямой цилиндр, ограниченный с одной стороны плоскостью, перпендикулярной образующим. А вот плоскость, ограничивающая цилиндр с другой стороны, не перпендикулярна образующим и не параллельна первой плоскости.
На рисунке представлен скошенный цилиндр. Плоскость а под неким углом, отличным от 90° к образующим, пересекает фигуру.
Такая геометрическая форма чаще встречается на практике в виде соединений трубопроводов (колена). Но бывают даже здания, построенные в виде скошенного цилиндра.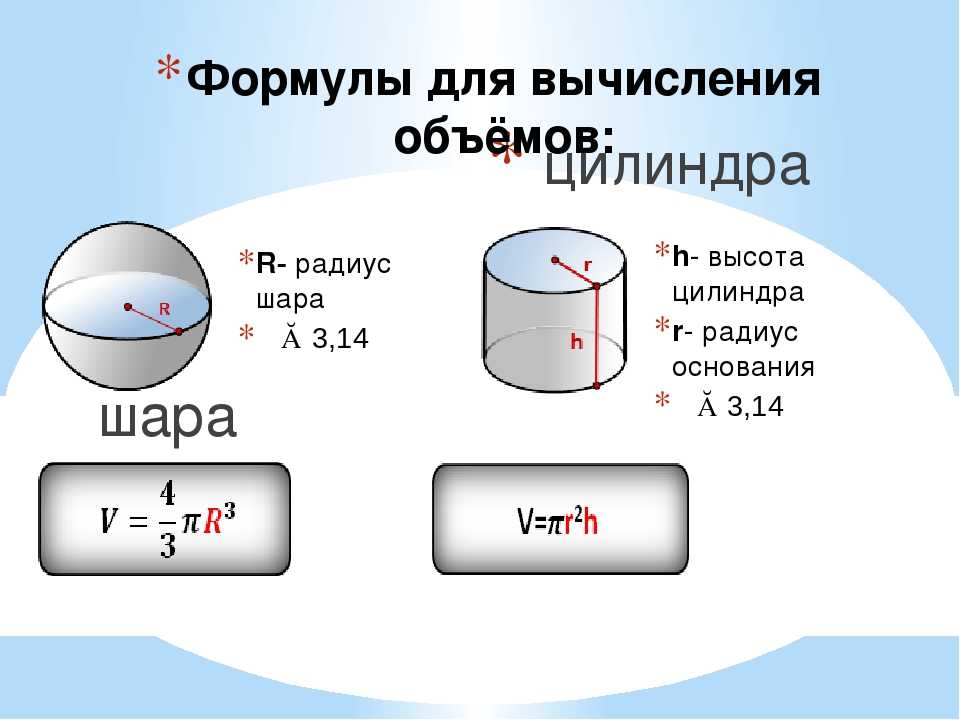
Геометрические характеристики скошенного цилиндра
Наклон одной из плоскостей скошенного цилиндра слегка изменяет порядок расчёта как площади поверхности такой фигуры, так и ее объёма.
Цилиндр (происходит из греческого языка, от слов «каток», «валик») — это геометрическое тело, которое ограничено снаружи поверхностью, называющейся цилиндрической, и двумя плоскостями. Данные плоскости пересекают поверхность фигуры и являются параллельными друг другу.
Цилиндрическая поверхность — это поверхность, которая получена прямой линии в пространстве. Эти движения таковы, что выделенная точка этой прямой линии совершает движение вдоль кривой плоского типа. Такая прямая линия называется образующей, а кривая линия — направляющей.
Цилиндр состоит из пары оснований и боковой цилиндрической поверхности. Цилиндры бывают нескольких видов:
1. Круговой, прямой цилиндр. У такого цилиндра основания и направляющая перпендикулярны образующей линии, и имеется
2. Наклонный цилиндр. У него угол между образующей линией и основанием не является прямым.
Наклонный цилиндр. У него угол между образующей линией и основанием не является прямым.
3. Цилиндр иной формы. Гиперболический, эллиптический, параболический и другие.
Площадь цилиндра, а также площадь полной поверхности любого цилиндра находится с помощью сложения площадей оснований этой фигуры и площади боковой поверхности.
Формула, по которой вычисляется полная площадь цилиндра для кругового, прямого цилиндра:
Sp = 2п Rh + 2п R2 = 2п R (h+R).
Площадь боковой поверхности ищется чуть сложнее, чем площадь цилиндра целиком, она вычисляется путем умножения длины образующей линии на периметр сечения, образованного плоскостью, которая перпендикулярна образующей линии.
Данная цилиндра для кругового, прямого цилиндра узнается по развертке этого объекта.
Развертка — это прямоугольник, который имеет высоту h и длину P, которая приравнивается периметру основания.
Отсюда следует, что боковая площадь цилиндра является равной площади развертки и может быть вычислена по данной формуле:
Если взять круговой, прямой цилиндр, то для него:
P = 2п R, а Sb = 2п Rh.
Если цилиндр наклонный, то площадь боковой поверхности должна быть равна произведению длины его образующей линии и периметра сечения, которое перпендикулярно данной образующей линии.
К сожалению, не существует простой формулы для выражения площади боковой поверхности наклонного цилиндра через его высоту и параметры его основания.
Чтобы вычислить цилиндра, необходимо знать несколько фактов. Если сечение своей плоскостью пересекает основания, то такое сечение всегда является прямоугольником. Но эти прямоугольники будут разными, в зависимости от положения сечения. Одна из сторон осевого сечения фигуры, которое перпендикулярно основаниям, равна высоте, а другая — диаметру основания цилиндра. А площадь такого сечения, соответственно, приравнивается произведению одной стороны прямоугольника на другую, перпендикулярную первой, или произведению высоты данной фигуры на диаметр его основания.
Если сечение будет перпендикулярно основаниям фигуры, но не будет проходить через ось вращения, то площадь этого сечения будет равна произведению высоты этого цилиндра и определенной хорды.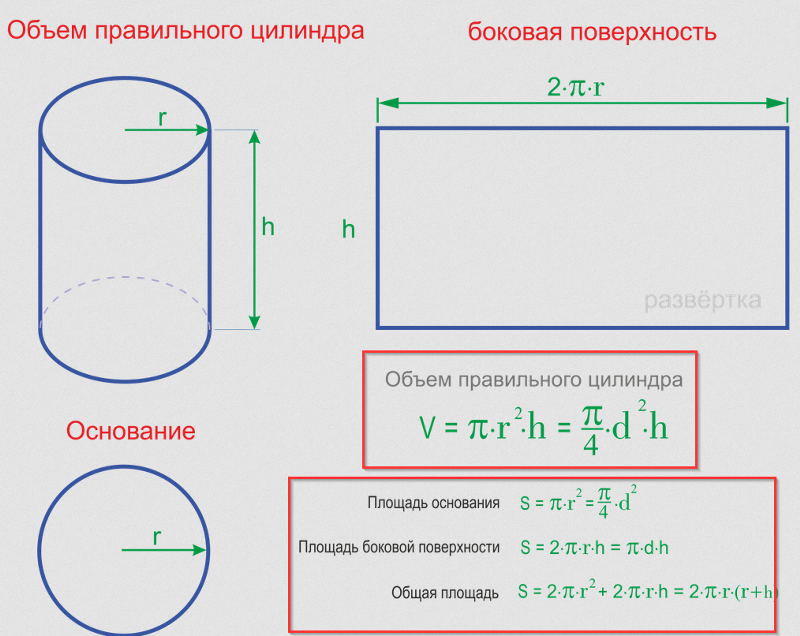 Чтобы получить хорду, нужно построить окружность у основания цилиндра, провести радиус и отложить на нем расстояние, на котором находится сечение. А от этой точки нужно провести перпендикуляры к радиусу от пересечения с окружностью. Точки пересечения соединяются с центром. А основание треугольника — это искомая которой ищется по звучит так: «Сумма квадратов двух катетов равна гипотенузе, возведенной в квадрат»:
Чтобы получить хорду, нужно построить окружность у основания цилиндра, провести радиус и отложить на нем расстояние, на котором находится сечение. А от этой точки нужно провести перпендикуляры к радиусу от пересечения с окружностью. Точки пересечения соединяются с центром. А основание треугольника — это искомая которой ищется по звучит так: «Сумма квадратов двух катетов равна гипотенузе, возведенной в квадрат»:
С2 = А2 + В2.
Если сечение не затрагивает основания цилиндра, а сам цилиндр круговой и прямой, то площадь этого сечения находится как площадь окружности.
Площадь окружности равна:
S окр. = 2п R2.
Чтобы найти R, нужно ее длину C разделить на 2п:
R = C \ 2п, где п — число пи, математическая постоянная, вычисленная для работы с данными окружности и равная 3,14.
При изучении стереометрии одной из главных тем становится «Цилиндр». Площадь боковой поверхности считается если не главной, то немаловажной формулой при решении геометрических задач. Однако важно помнить и определения, которые помогут сориентироваться в примерах и при доказательстве различных теорем.
Однако важно помнить и определения, которые помогут сориентироваться в примерах и при доказательстве различных теорем.
Понятие цилиндра
Вначале нужно рассмотреть несколько определений. Только после их изучения можно приступать к рассмотрению вопроса о формуле площади боковой поверхности цилиндра. На основе этой записи можно вычислить и иные выражения.
- Под цилиндрической поверхностью понимают плоскость, описываемую образующей, движущейся и остающейся параллельной заданному направлению, скользящей по имеющейся кривой.
- Имеется и второе определение: цилиндрическую поверхность образуют множество параллельных прямых, пересекающих заданную кривую.
- Образующей называют условно высоту цилиндра. При ее перемещении вокруг оси, проходящей через центр основания, получается обозначенное геометрическое тело.
- Под осью подразумевают прямую, проходящую через оба основания фигуры.
- Цилиндром называется стереометрическое тело, ограниченное пересекающимися боковой поверхностью и 2 параллельными плоскостями.

Существуют разновидности данной объемной фигуры:
- Под круговым подразумевают цилиндр, направляющая которого — это окружность. Его главными составляющими считаются радиус основания и образующая. Последняя равна высоте фигуры.
- Существует прямой цилиндр. Свое название он получил благодаря перпендикулярности образующей к основаниям фигуры.
- Третий вид — скошенный цилиндр. В учебниках можно встретить и другое его название «круговой цилиндр со скошенным основанием». Данную фигуру определяет радиус основания, минимальная и максимальная высоты.
- Под равносторонним цилиндром понимают тело, имеющее равные между собой высоту и диаметр круглой плоскости.
Условные обозначения
Традиционно основные «компоненты» цилиндра принято называть следующим образом:
- Радиус основания — R (он же заменяет аналогичную величину стереометрической фигуры).
- Образующая — L.
- Высота — H.
- Площадь основания — S осн (иначе говоря, необходимо найти указанный параметр круга).

- Высоты скошенного цилиндра — h 1 ,h 2 (минимальная и максимальная).
- Площадь боковой поверхности — S бок (если ее развернуть, то получится своего рода прямоугольник).
- Объем стереометрической фигуры — V.
- Площадь полной поверхности — S.
«Компоненты» стереометрической фигуры
Когда изучается цилиндр, площадь боковой поверхности играет немаловажную роль. Связано это с тем, что данная формула входит в несколько других, более сложных. Поэтому необходимо быть хорошо подкованным в теории.
Основными составляющими фигуры являются:
- Боковая поверхность. Как известно, она получается благодаря движению образующей по заданной кривой.
- Полная поверхность включает в себя имеющиеся основания и боковую плоскость.
- Сечением цилиндра, как правило, выступает прямоугольник, расположенный параллельно оси фигуры. Иначе его называют плоскостью. Оказывается, длина и ширина по совместительству являются составляющими других фигур.
 Так, условно длинами сечения являются образующие. Ширина — параллельные хорды стереометрической фигуры.
Так, условно длинами сечения являются образующие. Ширина — параллельные хорды стереометрической фигуры. - Под осевым сечением подразумевают расположение плоскости через центр тела.
- И наконец, завершающее определение. Касательной называют плоскость, проходящую через образующую цилиндра и находящуюся под прямым углом к осевому сечению. При этом должно выполниться одно условие. Указанная образующая должна входить в плоскость осевого сечения.
Основные формулы для работы с цилиндром
Для того чтобы ответить на вопрос, как найти площадь поверхности цилиндра, необходимо изучить основные «компоненты» стереометрической фигуры и формулы их нахождения.
Данные формулы отличаются тем, что вначале даются выражения для скошенного цилиндра, а затем — для прямого.
Примеры с разобранным решением
Необходимо узнать площадь боковой поверхности цилиндра. Дана диагональ сечения AC = 8 см (причем оно является осевым). При соприкосновении с образующей получается
Решение. Поскольку известны величины диагонали и угла, то в таком случае:
Поскольку известны величины диагонали и угла, то в таком случае:
- CD = AC*cos 30°.
Комментарий. Треугольник ACD, в конкретном примере, прямоугольный. Это означает, что частное от деления CD и AC = косинусу имеющегося угла. Значение тригонометрических функций можно найти в специальной таблице.
Аналогично, можно найти и значение AD:
- AD = AC*sin 30°
Теперь необходимо вычислить по следующей формулировке нужный результат: площадь боковой поверхности цилиндра равна удвоенному результату перемножения «пи», радиуса фигуры и ее высоты. Следует воспользоваться и другой формулой: площадью основания цилиндра. Она равняется результату перемножения «пи» на квадрат радиуса. И наконец, последняя формула: общая площадь поверхности. Она равна сумме предыдущих двух площадей.
Даны цилиндры. Их объем = 128*п см³. У какого из цилиндров наименьшая полная поверхность?
Решение. Для начала нужно воспользоваться формулами нахождения объема фигуры и ее высоты.
Поскольку площадь полной поверхности цилиндра известна из теории, необходимо применить ее формулу.
Если рассматривать полученную формулу в качестве функции площади цилиндра, то минимальный «показатель» будет достигнут в точке экстремума. Для получения последнего значения необходимо воспользоваться дифференцированием.
Формулы можно посмотреть в специальной таблице по нахождению производных. В дальнейшем найденный результат приравнивается к нулю и находится решение уравнения.
Ответ: S min будет достигнута при h = 1/32 см, R = 64 см.
Дана стереометрическая фигура — цилиндр и сечение. Последнее проведено таким образом, что располагается параллельно оси стереометрического тела. У цилиндра следующие параметры: ВК = 17 см, h = 15 см, R = 5 см. Необходимо найти расстояние между сечением и осью.
Поскольку под сечением цилиндра понимается ВСКМ, т. е. прямоугольник, то его сторона ВМ = h. Необходимо рассмотреть ВМК. Треугольник является прямоугольным.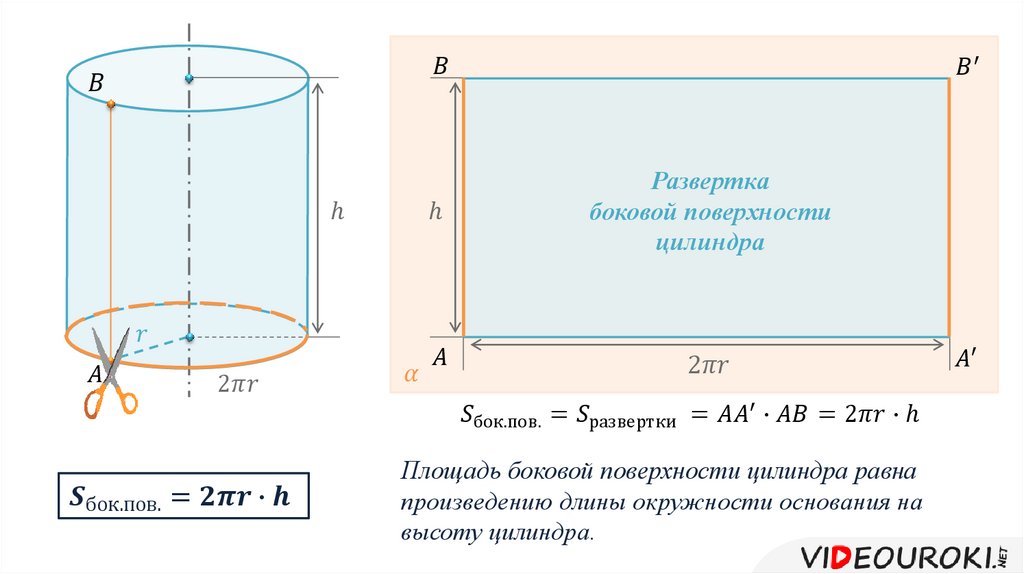 Исходя из этого утверждения, можно вывести верное предположение, что МК = ВС.
Исходя из этого утверждения, можно вывести верное предположение, что МК = ВС.
ВК² = ВМ² + МК²
МК² = ВК² — ВМ²
МК² = 17² — 15²
Отсюда можно сделать вывод, что МК = ВС = 8 см.
Следующий шаг — проведение сечения через основание фигуры. Необходимо рассмотреть получившуюся плоскость.
AD — диаметр стереометрической фигуры. Он параллелен сечению, упомянутому в условии задачи.
BC — прямая, расположенная на плоскости имеющегося прямоугольника.
ABCD — трапеция. В конкретном случае она считается равнобедренной, поскольку вокруг нее описана окружность.
Если найти высоту полученной трапеции, то можно получить ответ, поставленный в начале задачи. А именно: нахождение расстояния между осью и проведенным сечением.
Для этого необходимо найти величины AD и ОС.
Ответ: сечение располагается 3 см от оси.
Задачи на закрепление материала
Дан цилиндр. Площадь боковой поверхности используется в дальнейшем решении. Известны другие параметры. Площадь основания — Q, площадь осевого сечения — М. Необходимо найти S. Иными словами, полную площадь цилиндра.
Площадь основания — Q, площадь осевого сечения — М. Необходимо найти S. Иными словами, полную площадь цилиндра.
Дан цилиндр. Площадь боковой поверхности необходимо найти в одном из шагов решения задачи. Известно, что высота = 4 см, радиус = 2 см. Необходимо найти полную площадь стереометрической фигуры.
Цилиндр площадь боковой поверхности и объем. Тела и поверхности вращения
Цилиндр представляет собой геометрическое тело, ограниченное двумя параллельными плоскостями и цилиндрической поверхностью. В статье поговорим о том, как найти площадь цилиндра и, применив формулу, решим для примера несколько задач.
У цилиндра есть три поверхности: вершина, основание, и боковая поверхность.
Вершина и основание цилиндра являются окружностями, их легко определить.
Известно, что площадь окружности равна πr 2 . Поэтому, формула площади двух окружностей (вершины и основания цилиндра) будет иметь вид πr 2 + πr 2 = 2πr 2 .
Третья, боковая поверхность цилиндра, является изогнутой стенкой цилиндра. Для того чтобы лучше представить эту поверхность попробуем преобразовать её, чтобы получить узнаваемую форму. Представьте себе, что цилиндр, это обычная консервная банка, у которой нет верхней крышки и дна. Сделаем вертикальный надрез на боковой стенке от вершины до основания банки (Шаг 1 на рисунке) и попробуем максимально раскрыть (выпрямить) полученную фигуру (Шаг 2).
Для того чтобы лучше представить эту поверхность попробуем преобразовать её, чтобы получить узнаваемую форму. Представьте себе, что цилиндр, это обычная консервная банка, у которой нет верхней крышки и дна. Сделаем вертикальный надрез на боковой стенке от вершины до основания банки (Шаг 1 на рисунке) и попробуем максимально раскрыть (выпрямить) полученную фигуру (Шаг 2).
После полного раскрытия полученной банки мы увидим уже знакомую фигуру (Шаг 3), это прямоугольник. Площадь прямоугольника вычислить легко. Но перед этим вернемся на мгновение к первоначальному цилиндру. Вершина исходного цилиндра является окружностью, а мы знаем, что длина окружности вычисляется по формуле: L = 2πr. На рисунке она отмечена красным цветом.
Когда боковая стенка цилиндра полностью раскрыта, мы видим, что длина окружности становится длиной полученного прямоугольника. Сторонами этого прямоугольника будут длина окружности(L = 2πr) и высота цилиндра(h). Площадь прямоугольника равна произведению его сторон – S = длина х ширина = L x h = 2πr x h = 2πrh. В результате мы получили формулу для расчета площади боковой поверхности цилиндра.
В результате мы получили формулу для расчета площади боковой поверхности цилиндра.
Формула площади боковой поверхности цилиндра
S бок. = 2πrh
Площадь полной поверхности цилиндра
Наконец, если мы сложим площадь всех трёх поверхностей, мы получим формулу площади полной поверхности цилиндра. Площади поверхности цилиндра равна площадь вершины цилиндра + площадь основания цилиндра + площадь боковой поверхности цилиндра или S = πr 2 + πr 2 + 2πrh = 2πr 2 + 2πrh. Иногда это выражение записывается идентичной формулой 2πr (r + h).
Формула площади полной поверхности цилиндра
S = 2πr 2 + 2πrh = 2πr(r + h)
r – радиус цилиндра, h – высота цилиндра
Примеры расчета площади поверхности цилиндра
Для понимания приведенных формул попробуем посчитать площадь поверхности цилиндра на примерах.
1. Радиус основания цилиндра равен 2, высота равна 3. Определите площадь боковой поверхности цилиндра.
Площадь полной поверхности рассчитывается по формуле: S бок. = 2πrh
= 2πrh
S бок. = 2 * 3,14 * 2 * 3
S бок. = 6,28 * 6
S бок. = 37,68
Площадь боковой поверхности цилиндра равна 37,68.
2. Как найти площадь поверхности цилиндра, если высота равна 4, а радиус 6?
Площадь полной поверхности рассчитывается по формуле: S = 2πr 2 + 2πrh
S = 2 * 3,14 * 6 2 + 2 * 3,14 * 6 * 4
S = 2 * 3,14 * 36 + 2 * 3,14 * 24
\[{\Large{\text{Цилиндр}}}\]
Рассмотрим окружность \(C\)
с центром \(O\)
радиуса \(R\)
на плоскости \(\alpha\)
. Через каждую точку окружности \(C\)
проведем прямую перпендикулярно плоскости \(\alpha\)
. Поверхность, образованная этими прямыми, называется цилиндрической поверхностью .
Сами прямые называются образующими данной поверхности.
Проведем теперь через некоторую точку некоторой образующей плоскость \(\beta\parallel \alpha\)
. Множество точек, по которым образующие пересекут плоскость \(\beta\)
, образует окружность \(C»\)
, равную окружности \(C\)
.
Часть пространства, ограниченная двумя кругами \(K\)
и \(K»\)
с границами \(C\)
и \(C»\)
соответственно, а также частью цилиндрической поверхности, заключенной между плоскостями \(\alpha\)
и \(\beta\)
, называется цилиндром .
Круги \(K\) и \(K»\) называются основаниями цилиндра; отрезки образующих, заключенных между плоскостями, – образующими цилиндра; часть цилиндрической поверхности, образованная ими, — боковой поверхностью цилиндра. Отрезок, соединяющий центры оснований цилиндра равен образующей цилиндра и равен высоте цилиндра (\(l=h\) ).
Теорема
Площадь боковой поверхности цилиндра равна \
где \(R\) – радиус основания цилиндра, \(h\) – высота (образующая).
Теорема
Площадь полной поверхности цилиндра равна сумме площади боковой поверхности и площадей обоих оснований \
Теорема
Объем цилиндра вычисляется по формуле \
\[{\Large{\text{Конус}}}\]
Рассмотрим плоскость \(\alpha\)
и на ней окружность \(C\)
с центром \(O\)
и радиусом \(R\)
. Через точку \(O\)
проведем прямую, перпендикулярную плоскости \(\alpha\)
. Отметим на этой прямой некоторую точку \(P\)
. Поверхность, образованная всеми прямыми, проходящими через точку \(P\)
и каждую точку окружности \(C\)
, называется конической поверхностью , а эти прямые – образующими конической поверхности. Часть пространства, ограниченная кругом с границей \(C\)
и отрезками образующих, заключенными между точкой \(P\)
и точкой на окружности, называется конусом . Отрезки \(PA\)
, где \(A\in \text{окр. }
C\)
, называются образующими конуса ; точка \(P\)
– вершина конуса; круг с границей \(C\)
– основание конуса; отрезок \(PO\)
– высота конуса.
Часть пространства, ограниченная кругом с границей \(C\)
и отрезками образующих, заключенными между точкой \(P\)
и точкой на окружности, называется конусом . Отрезки \(PA\)
, где \(A\in \text{окр. }
C\)
, называются образующими конуса ; точка \(P\)
– вершина конуса; круг с границей \(C\)
– основание конуса; отрезок \(PO\)
– высота конуса.
Замечание
Заметим, что у конуса высота и образующая не равны друг другу, как было в случае с цилиндром.
Теорема
Площадь боковой поверхности конуса равна \
где \(R\) – радиус основания конуса, \(l\) – образующая.
Теорема
Площадь полной поверхности конуса равна сумме площади боковой поверхности и площадей основания \
Теорема
Объем конуса вычисляется по формуле \
Замечание
Заметим, что цилиндр в каком-то смысле является призмой, только в основании находится не многоугольник (как у призмы), а круг.
Формула объема цилиндра такая же, как и формула объема призмы: произведение площади основания на высоту.
Аналогично конус в каком-то смысле является пирамидой. Поэтому формула объема конуса такая же, как и у пирамиды: треть площади основания на высоту.
\[{\Large{\text{Сфера и шар}}}\]
Рассмотрим множество точек пространства, равноудаленных от некоторой точки \(O\)
на расстояние \(R\)
. Это множество называется сферой с центром в точке \(O\)
радиуса \(R\)
.
Отрезок, соединяющий две точки сферы и проходящий через ее центр называется диаметром сферы.
Сфера вместе со своей внутренностью называется шаром .
Теорема
Площадь сферы вычисляется по формуле \
Теорема
Объем шара вычисляется по формуле \
Определение
Шаровой сегмент – это часть шара, отсекаемая от него некоторой плоскостью.
Пусть плоскость пересекла шар по кругу \(K\)
с центром в точке \(Q\)
. Соединим точки \(O\)
(центр шара) и \(Q\)
и продлим этот отрезок до пересечения со сферой – получим радиус \(OP\)
. Тогда отрезок \(QP\)
называется высотой сегмента.
Теорема
Пусть \(R\) – радиус шара, \(h\) – высота сегмента, то объем шарового сегмента равен \
Определение
Шаровой слой – это часть шара, заключенная между двумя параллельными плоскостями, пересекающими этот шар. Круги, по которым плоскости пересекают шар, называются основаниями шарового слоя, отрезок, соединяющий центры оснований – высотой шарового слоя.
Две оставшиеся части шара являются в этом случае шаровыми сегментами.
Объем шарового слоя равен разности объема шара и объемов шаровых сегментов с высотами \(AP\) и \(BT\) .
Название науки «геометрия» переводится как «измерение земли». Зародилась стараниями самых первых древних землеустроителей. А было так: во время разливов священного Нила потоки воды иногда смывали границы участков земледельцев, а новые границы могли не совпасть со старыми. Налоги же крестьянами уплачивались в казну фараона пропорционально величине земельного надела. Измерением площадей пашни в новых границах после разлива занимались специальные люди.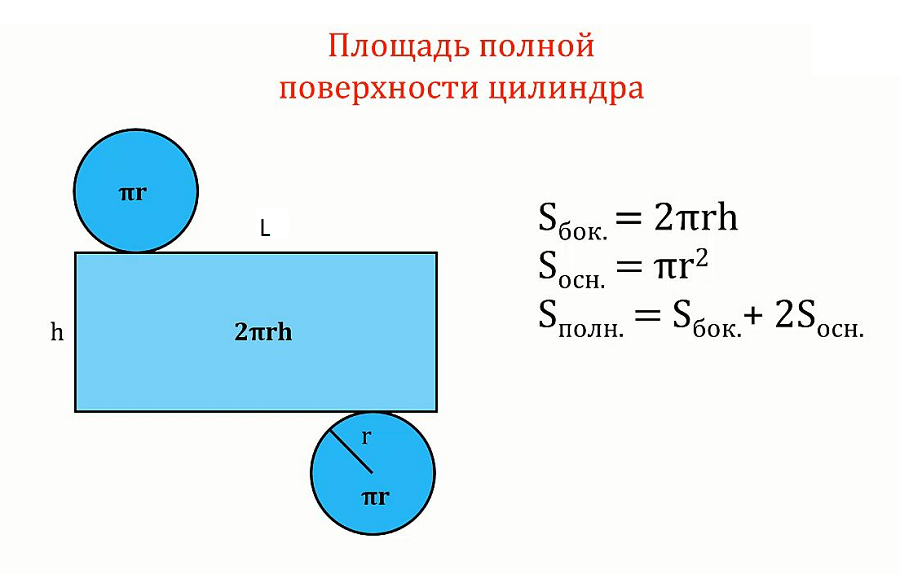 Именно в результате их деятельности и возникла новая наука, получившая развитие в Древней Греции. Там она и название получила, и приобрела практически современный вид. В дальнейшем термин стал интернациональным названием науки о плоских и объёмных фигурах.
Именно в результате их деятельности и возникла новая наука, получившая развитие в Древней Греции. Там она и название получила, и приобрела практически современный вид. В дальнейшем термин стал интернациональным названием науки о плоских и объёмных фигурах.
Планиметрия — раздел геометрии, занимающийся изучением плоских фигур. Другим разделом науки является стереометрия, которая рассматривает свойства пространственных (объёмных) фигур. К таким фигурам относится и описываемая в этой статье — цилиндр.
Примеров присутствия предметов цилиндрической формы в повседневной жизни предостаточно. Цилиндрическую (гораздо реже — коническую) форму имеют почти все детали вращения — валы, втулки, шейки, оси и т.д. Цилиндр широко используется и в строительстве: башни, опорные, декоративные колонны. А кроме того посуда, некоторые виды упаковки, трубы всевозможных диаметров. И наконец — знаменитые шляпы, ставшие надолго символом мужской элегантности. Список можно продолжать бесконечно.
Определение цилиндра как геометрической фигуры
Цилиндром (круговым цилиндром) принято называть фигуру, состоящую из двух кругов, которые при желании совмещаются с помощью параллельного переноса. Именно эти круги и являются основаниями цилиндра. А вот линии (прямые отрезки), связывающие соответствующие точки, получили название «образующие».
Именно эти круги и являются основаниями цилиндра. А вот линии (прямые отрезки), связывающие соответствующие точки, получили название «образующие».
Важно, что основания цилиндра всегда равны (если это условие не выполняется, то перед нами — усечённый конус, что-либо другое, но только не цилиндр) и находятся в параллельных плоскостях. Отрезки же, соединяющие соответствующие точки на кругах, параллельны и равны.
Совокупность бесконечного множества образующих — не что иное, как боковая поверхность цилиндра — один из элементов данной геометрической фигуры. Другая её важная составляющая — рассмотренные выше круги. Называются они основаниями.
Виды цилиндров
Самый простой и распространённый вид цилиндра — круговой. Его образуют два правильных круга, выступающих в роли оснований. Но вместо них могут быть и другие фигуры.
Основания цилиндров могут образовывать (кроме кругов) эллипсы, другие замкнутые фигуры. Но цилиндр может иметь не обязательно замкнутую форму. Например основанием цилиндра может служить парабола, гипербола, другая открытая функция. Такой цилиндр будет открытым или развернутым.
Например основанием цилиндра может служить парабола, гипербола, другая открытая функция. Такой цилиндр будет открытым или развернутым.
По углу наклона образующих к основаниям цилиндры могут быть прямыми или наклонными. У прямого цилиндра образующие строго перпендикулярны плоскости основания. Если данный угол отличается от 90°, цилиндр — наклонный.
Что такое поверхность вращения
Прямой круговой цилиндр, без сомнения — самая распространённая поверхность вращения, используемая в технике. Иногда по техническим показаниям применяется коническая, шарообразная, некоторые другие типы поверхностей, но 99% всех вращающихся валов, осей и т.д. выполнены именно в форме цилиндров. Для того чтобы лучше уяснить, что такое поверхность вращения, можно рассмотреть, как же образован сам цилиндр.
Допустим, имеется некая прямая a , расположенная вертикально. ABCD — прямоугольник, одна из сторон которого (отрезок АВ) лежит на прямой a . Если вращать прямоугольник вокруг прямой, как это показано на рисунке, объём, который он займёт, вращаясь, и будет нашим телом вращения — прямым круговым цилиндром с высотой H = AB = DC и радиусом R = AD = BC.
В данном случае, в результате вращения фигуры — прямоугольника — получается цилиндр. Вращая треугольник, можно получить конус, вращая полукруг — шар и т.д.
Площадь поверхности цилиндра
Для того чтобы вычислить площадь поверхности обычного прямого кругового цилиндра, необходимо подсчитать площади оснований и боковой поверхности.
Вначале рассмотрим, как вычисляют площадь боковой поверхности. Это произведение длины окружности на высоту цилиндра. Длина окружности, в свою очередь, равняется удвоенному произведению универсального числа П на радиус окружности.
Площадь круга, как известно, равняется произведению П на квадрат радиуса. Итак, сложив формулы для площади определения боковой поверхности с удвоенным выражением площади основания (их ведь два) и произведя нехитрые алгебраические преобразования, получаем окончательное выражение для определения площади поверхности цилиндра.
Определение объёма фигуры
Объем цилиндра определяется по стандартной схеме: площадь поверхности основания умножается на высоту.
Таким образом, конечная формула выглядит следующим образом: искомое определяется как произведение высоты тела на универсальное число П и на квадрат радиуса основания.
Полученная формула, надо сказать, применима для решения самых неожиданных задач. Точно так же, как объем цилиндра, определяется, например, объём электропроводки. Это бывает необходимо для вычисления массы проводов.
Отличия в формуле только в том, что вместо радиуса одного цилиндра стоит делённый надвое диаметр жилы проводки и в выражении появляется число жил в проводе N . Также вместо высоты используется длина провода. Таким образом рассчитывается объем «цилиндра» не одного, а по числу проводков в оплётке.
Такие расчёты часто требуются на практике. Ведь значительная часть ёмкостей для воды изготовлена в форме трубы. И вычислить объем цилиндра часто бывает нужно даже в домашнем хозяйстве.
Однако, как уже говорилось, форма цилиндра может быть разной. И в некоторых случаях требуется рассчитать, чему равен объем цилиндра наклонного.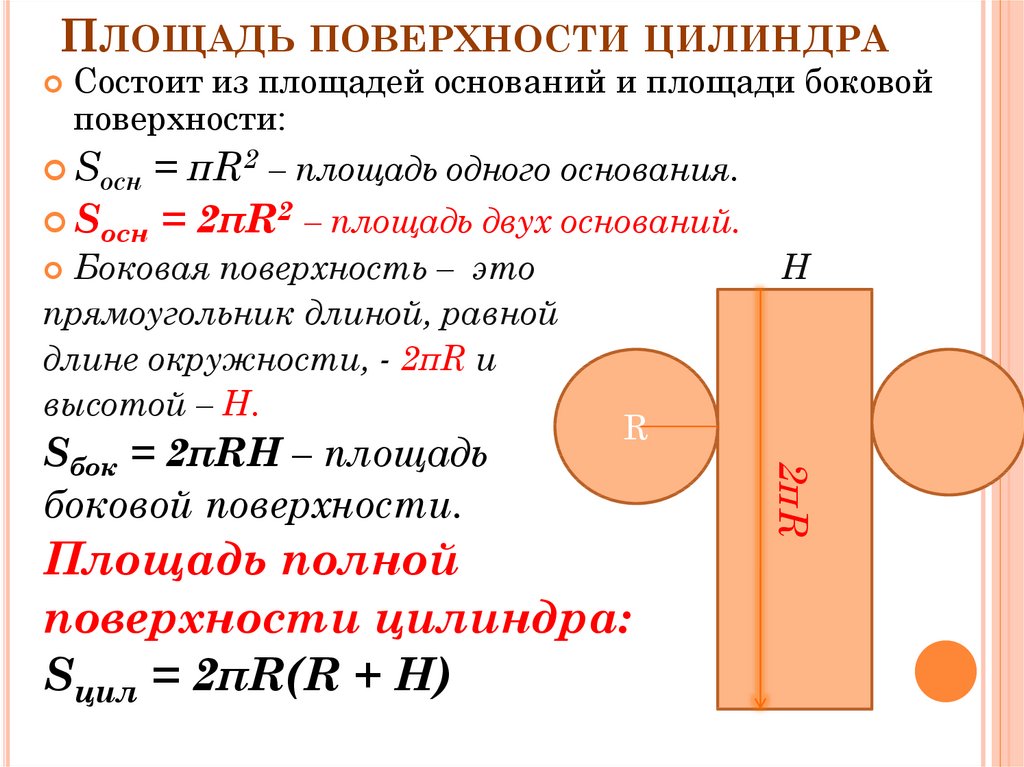
Отличие в том, что площадь поверхности основания умножают не на длину образующей, как в случае с прямым цилиндром, а на расстояние между плоскостями — перпендикулярный отрезок, построенный между ними.
Как видно из рисунка, такой отрезок равен произведению длины образующей на синус угла наклона образующей к плоскости.
Как построить развёртку цилиндра
В некоторых случаях требуется выкроить развёртку цилиндра. На приведённом рисунке показаны правила, по которым строится заготовка для изготовления цилиндра с заданными высотой и диаметром.
Следует учитывать, что рисунок приведен без учёта швов.
Отличия скошенного цилиндра
Представим себе некий прямой цилиндр, ограниченный с одной стороны плоскостью, перпендикулярной образующим. А вот плоскость, ограничивающая цилиндр с другой стороны, не перпендикулярна образующим и не параллельна первой плоскости.
На рисунке представлен скошенный цилиндр. Плоскость а под неким углом, отличным от 90° к образующим, пересекает фигуру.
Такая геометрическая форма чаще встречается на практике в виде соединений трубопроводов (колена). Но бывают даже здания, построенные в виде скошенного цилиндра.
Геометрические характеристики скошенного цилиндра
Наклон одной из плоскостей скошенного цилиндра слегка изменяет порядок расчёта как площади поверхности такой фигуры, так и ее объёма.
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.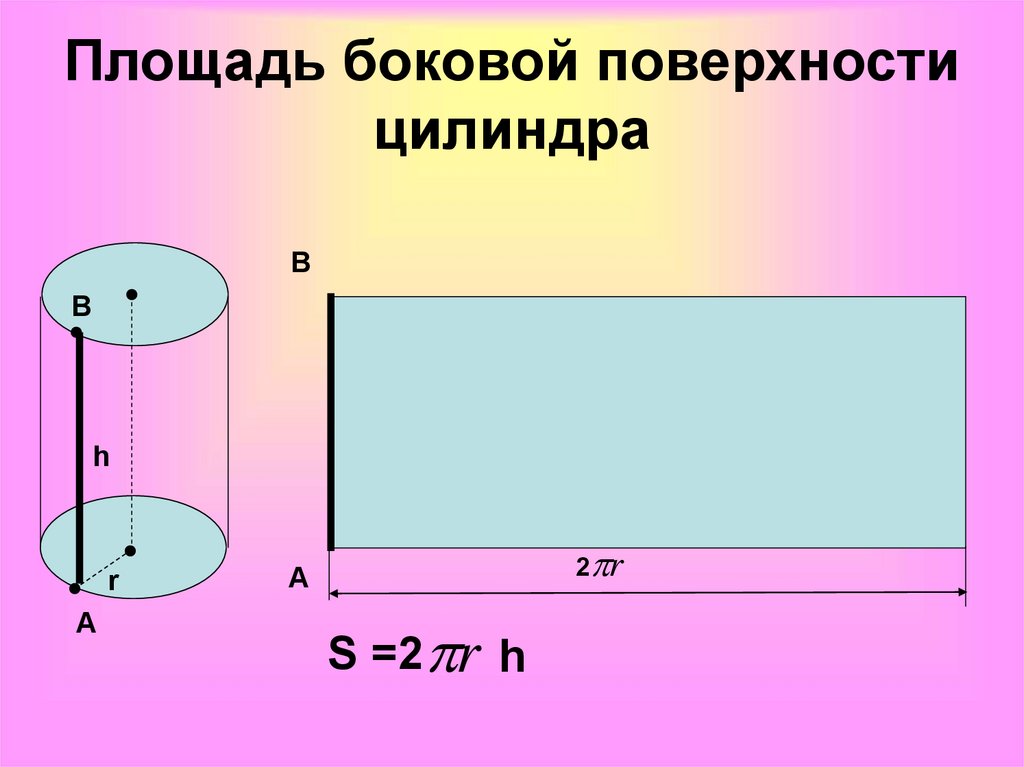
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.

Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.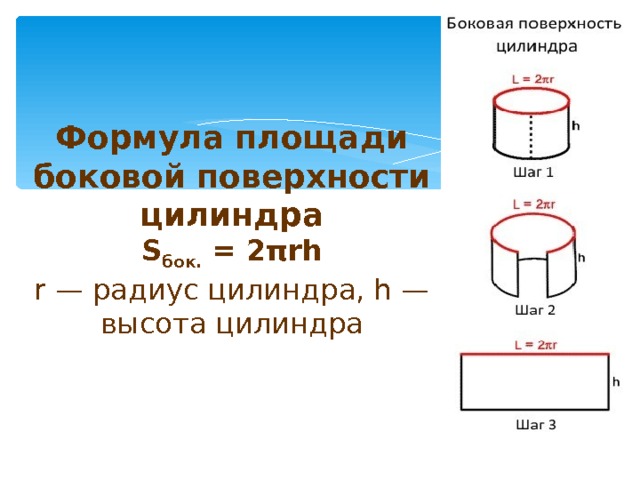
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
Применяйте формулы объема и площади поверхности цилиндра, конуса и шара. Все они есть в нашей таблице. Учите наизусть. Отсюда начинается знание стереометрии.
1. Объем конуса равен 16.Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.
Очевидно, что объем меньшего конуса в 8 раз меньше объема большого и равен двум.
Для решения некоторых задач полезны начальные знания стереометрии. Например — что такое правильная пирамида или прямая призма. Полезно помнить, что у цилиндра, конуса и шара есть еще общее название — тела вращения.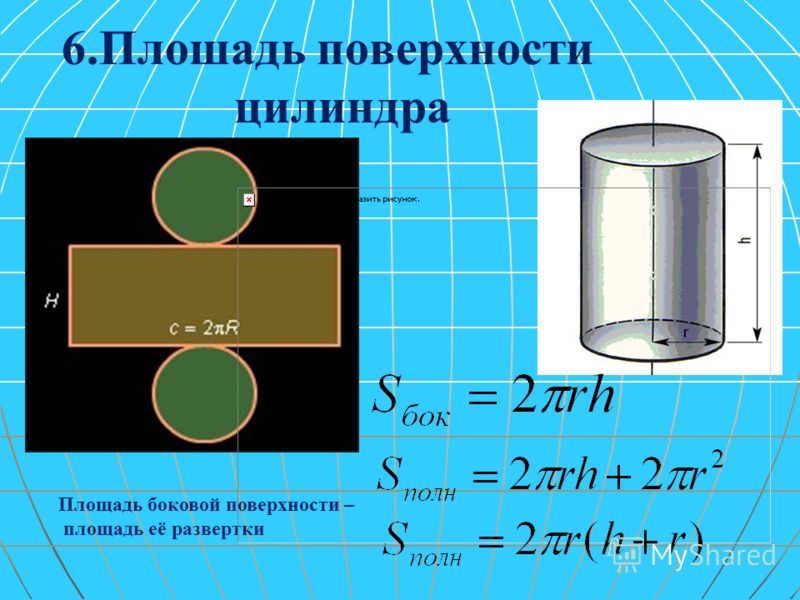 Что сферой называется поверхность шара. А, например, фраза «образующая конуса наклонена к плоскости основания под углом 30 градусов предполагает, что вы знаете, что такое угол между прямой и плоскостью. Вам также может пригодиться теорема Пифагора и простые формулы площадей фигур.
Что сферой называется поверхность шара. А, например, фраза «образующая конуса наклонена к плоскости основания под углом 30 градусов предполагает, что вы знаете, что такое угол между прямой и плоскостью. Вам также может пригодиться теорема Пифагора и простые формулы площадей фигур.
Иногда неплохо нарисовать вид сверху. Или, как в этой задаче, — снизу.
2. Во сколько раз объем конуса, описанного около правильной четырехугольной пирамиды, больше объема конуса, вписанного в эту пирамиду?
Всё просто — рисуем вид снизу. Видим, что радиус большего круга в раз больше, чем радиус меньшего. Высоты у обоих конусов одинаковы. Следовательно, объем большего конуса будет в 2 раза больше.
Упражнения для самостоятельной работы.
1.Измерение прямоугольного параллелепипеда 15, 50 и 36 м. Найти ребро равновеликого ему куба.
2.В правильной 4-угольной пирамиде высота 3 см, боковое ребро 5 см. Найти объем пирамиды.
3.Осевое сечение цилиндра – прямоугольник со сторонами 8 дм и 12 дм.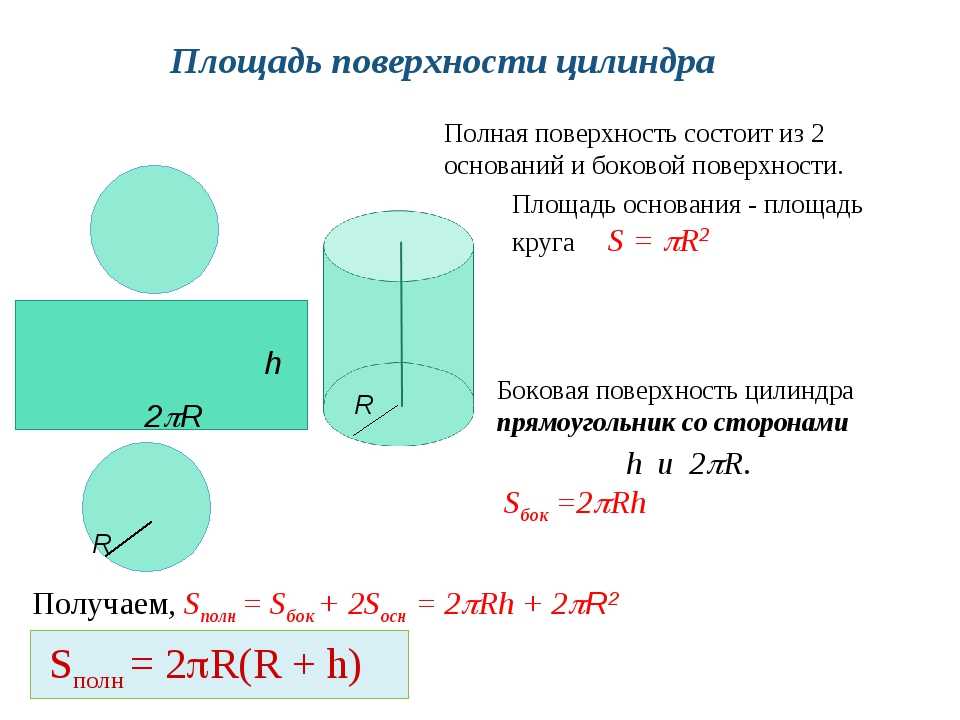 Найти объем цилиндра.
Найти объем цилиндра.
4.Образующая конуса наклонена к плоскости основания под углом 30°, радиус основания равен 3 дм. Найти объем конуса.
5.Радиус шара равен 4 м. Найти объем шарового сегмента высотой, равной 3 м.
Список литературы
Геометрия, 10-11: Учеб. для общеобразовательных учреждений/ Л.С. Атанасян, В.Ф. Бутузов, С. Б. Кадомцев и др.-Москва: Просвещение, 2009 год
2. Ершова А.П., Голобородько В.В., Ершова А.С. Самостоятельные и контрольные работы по геометрии для 10 класса.- 4-е издание, испр. и доп.- М.:Илекса, 2007,- 175 с.
3. Геометрия. 10-11 классы: тесты для текущего и обобщающего контроля/авт.сост.Г.И.Ковалёва, Н.И.Мазурова.- Волгоград: Учитель, 2009, 187 стр.
4. Виртуальная школа Кирилла и Мефодия. Репетитор по математике. Москва. 2007 год
5. Учебное электронное издание. Математика 5- 11 класссы. Практикум. Под редакцией Дубровского В.Н., 2004.
ПРАКТИЧЕСКАЯ РАБОТА № 16
«Использование координат и векторов при решении математических задач»
Цель урока:
1) Обобщить теоретические знания по теме: «Использование координат и векторов при решении математических задач».
2) Рассмотреть алгоритмы решений заданий теме «Использование координат и векторов при решении математических задач», решить задачи.
3) Формировать потребность к самопознанию, самоконтролю, достижению поставленных целей.
Теоретический материал
Похожая информация:
- F. Новый максимум цен сопровождается увеличением объема, аналогично точке А. Продолжайте удерживать позицию на повышение
Чему равна площадь боковой поверхности цилиндра формула. Как найти площадь цилиндра
Тела вращения, изучаемые в школе, — это цилиндр, конус и шар.
Если в задаче на ЕГЭ по математике вам надо посчитать объем конуса или площадь сферы — считайте, что повезло.
Применяйте формулы объема и площади поверхности цилиндра, конуса и шара. Все они есть в нашей таблице. Учите наизусть. Отсюда начинается знание стереометрии.
Иногда неплохо нарисовать вид сверху. Или, как в этой задаче, — снизу.
2. Во сколько раз объем конуса, описанного около правильной четырехугольной пирамиды, больше объема конуса, вписанного в эту пирамиду?
Всё просто — рисуем вид снизу. Видим, что радиус большего круга в раз больше, чем радиус меньшего. Высоты у обоих конусов одинаковы. Следовательно, объем большего конуса будет в раза больше.
Видим, что радиус большего круга в раз больше, чем радиус меньшего. Высоты у обоих конусов одинаковы. Следовательно, объем большего конуса будет в раза больше.
Еще один важный момент. Помним, что в задачах части В вариантов ЕГЭ по математике ответ записывается в виде целого числа или конечной десятичной дроби. Поэтому никаких или у вас в ответе в части В быть не должно. Подставлять приближенное значение числа тоже не нужно! Оно обязательно должно сократиться!. Именно для этого в некоторых задачах задание формулируется, например, так: «Найдите площадь боковой поверхности цилиндра, деленную на ».
А где же еще применяются формулы объема и площади поверхности тел вращения? Конечно же, в задаче С2 (16). Мы тоже расскажем о ней.
Рассмотрим цилиндр вращения радиуса R и высоты h (рис. 383). В основание этого цилиндра впишем правильный многоугольник (на рис. 383 — шестиугольник) и с его помощью построим правильную призму, вписанную в цилиндр. Таким же путем можно описывать вокруг цилиндра правильные призмы с произвольно большим числом боковых граней.
За площадь боковой поверхности цилиндра принимается по определению предел, к которому стремятся площади боковых поверхностей вписанных и описанных вокруг него правильных призм по мере неограниченного удвоения (или вообще увеличения) числа их боковых граней.
То, что такой предел существует, мы сейчас и докажем. Если возьмем вписанную правильную призму, построенную на правильном -угольнике, как на основании, то для ее боковой поверхности будем иметь выражение , где — периметр правильного -угольника, вписанного в круг основания цилиндра. При . Точно такое же вычисление для описанной призмы дает тот же самый результат. Итак, площадь боковой поверхности цилиндра вращения выражается формулой
Боковая поверхность цилиндра равна произведению длины образующей на периметр (т. е. длину окружности) основания.
Задача 1. Отрезок, соединяющий диаметрально противоположные точки А и В верхнего и нижно оснований цилиндра (рис. 384), равен 10 см и наклонен к плоскости основания под углом в 60°. Найти площадь боковой поверхности цилиндра.
Найти площадь боковой поверхности цилиндра.
Решение. Проведем через отрезок Л Всечение плоскостью, перпендикулярной к основанию цилиндра. Из треугольника имеем
откуда находим для боковой поверхности цилиндра
Задача 2. Треугольник ABC, вершины А и В которого суть концы диаметра нижнего основания цилиндра, а вершина С-конец перпендикулярного к нему диаметра верхнего основания, равносторонний со стороной а,
Найти площади боковой и полной поверхностей цилиндра. Решение. Радиус основания цилиндра равен Высота треугольника ABC (рис. 385) равна а образующая цилиндра вычисляется как
Отсюда боковая поверхность цилиндра получается равной
а полная поверхность (равная сумме площади боковой поверхности и площади двух оснований цилиндра) равна
Упражнения
1. Диагонали боковых граней прямоугольного параллелепипеда наклонены к плоскости основания под углами, соответственно равными . Найти угол наклона к той же плоскости диагонали параллелепипеда.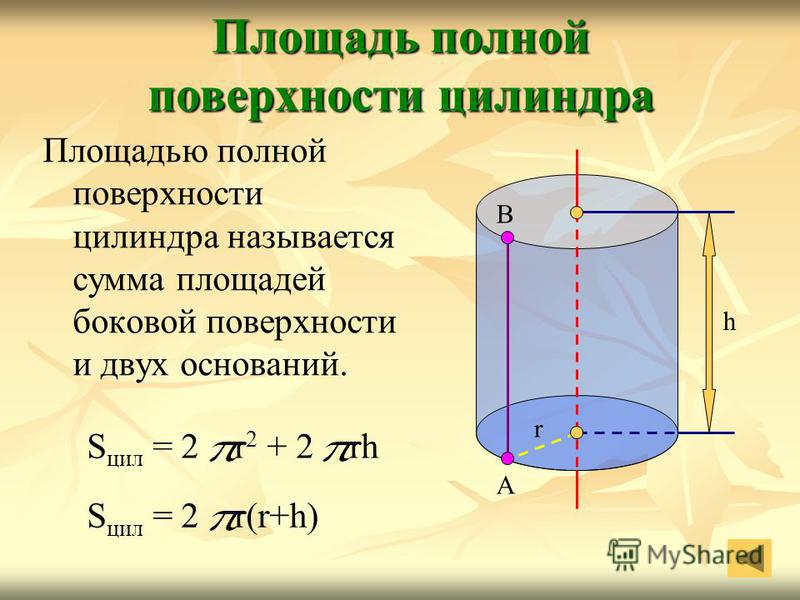
2. В прямом параллелепипеде острый угол основания равен а, а одна из сторон основания равна а. Сечение, проведенное через эту сторону и противоположное ребро верхнего основания, имеет площадь Q, и плоскость его наклонена к плоскости основания под углом . Найти объем и полную поверхность параллелепипеда.
3. Основанием наклонной треугольной призмы служит равнобедренный прямоугольный треугольник, а проекция одного из боковых ребер на плоскость основания совпадает с медианой m одного из катетов треугольника. Найти угол наклона боковых ребер к плоскости основания, если объем призмы равен V.
4. В правильной шестиугольной призме через сторону основания проведены два сечения: 1) содержащее противоположную сторону верхнего основания, 2) содержащее центр верхнего основания. При какой высоте призмы угол между плоскостями сечений имеет наибольшую величину и чему он равен в этом случае?
Представляет собой геометрическое тело, ограниченное двумя параллельными плоскостями и цилиндрической поверхностью.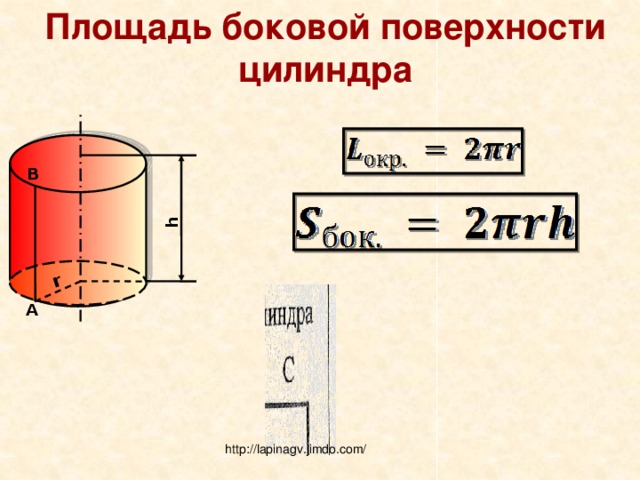
Цилиндр состоит из боковой поверхности и двух оснований. Формула площади поверхности цилиндра включает в себя отдельный расчет площади оснований и боковой поверхности. Так как основания в цилиндре равны, то полная его площадь будет рассчитываться по формуле:
Пример расчета площади цилиндра мы рассмотрим после того, как узнаем все необходимые формулы. Для начала нам понадобится формула площади основания цилиндра. Так как основанием цилиндра является круг, то нам потребуется применить :
Мы помним, что в этих расчетах используется постоянное число Π = 3,1415926, которое рассчитано как соотношение длины окружности к ее диаметру. Это число является математической константой. Пример расчета площади основания цилиндра мы также рассмотрим чуть позже.
Площадь боковой поверхности цилиндра
Формула площади боковой поверхности цилиндра представляет собой произведение длины основания на его высоту:
А теперь рассмотрим задачу, в которой нам потребуется рассчитать полную площадь цилиндра. В заданной фигуре высота h
= 4 см, r
= 2 см. Найдем полную площадь цилиндра.
В заданной фигуре высота h
= 4 см, r
= 2 см. Найдем полную площадь цилиндра.
Для начала рассчитаем площадь оснований:
Теперь рассмотрим пример расчета площади боковой поверхности цилиндра. В развернутом виде она представляет прямоугольник. Его площадь рассчитывается по приведенной выше формуле. Подставим в нее все данные:
Полная площадь круга представляет собой сумму двойной площади основания и боковой:
Таким образом, используя формулы площади оснований и боковой поверхности фигуры, мы смогли найти полную площадь поверхности цилиндра.
Осевое сечение цилиндра представляет собой прямоугольник, в котором стороны равны высоте и диаметру цилиндра.
Формула площади осевого сечения цилиндра выводится из формулы расчета :
Цилиндр представляет собой геометрическое тело, ограниченное двумя параллельными плоскостями и цилиндрической поверхностью. В статье поговорим о том, как найти площадь цилиндра и, применив формулу, решим для примера несколько задач.
У цилиндра есть три поверхности: вершина, основание, и боковая поверхность.
Вершина и основание цилиндра являются окружностями, их легко определить.
Известно, что площадь окружности равна πr 2 . Поэтому, формула площади двух окружностей (вершины и основания цилиндра) будет иметь вид πr 2 + πr 2 = 2πr 2 .
Третья, боковая поверхность цилиндра, является изогнутой стенкой цилиндра. Для того чтобы лучше представить эту поверхность попробуем преобразовать её, чтобы получить узнаваемую форму. Представьте себе, что цилиндр, это обычная консервная банка, у которой нет верхней крышки и дна. Сделаем вертикальный надрез на боковой стенке от вершины до основания банки (Шаг 1 на рисунке) и попробуем максимально раскрыть (выпрямить) полученную фигуру (Шаг 2).
После полного раскрытия полученной банки мы увидим уже знакомую фигуру (Шаг 3), это прямоугольник. Площадь прямоугольника вычислить легко. Но перед этим вернемся на мгновение к первоначальному цилиндру. Вершина исходного цилиндра является окружностью, а мы знаем, что длина окружности вычисляется по формуле: L = 2πr.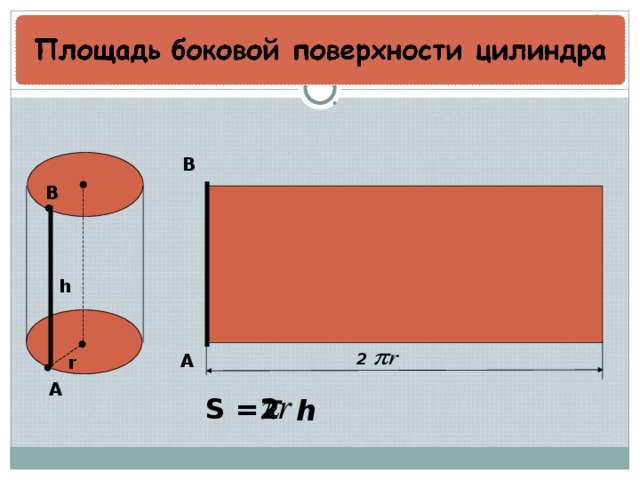 На рисунке она отмечена красным цветом.
На рисунке она отмечена красным цветом.
Когда боковая стенка цилиндра полностью раскрыта, мы видим, что длина окружности становится длиной полученного прямоугольника. Сторонами этого прямоугольника будут длина окружности(L = 2πr) и высота цилиндра(h). Площадь прямоугольника равна произведению его сторон – S = длина х ширина = L x h = 2πr x h = 2πrh. В результате мы получили формулу для расчета площади боковой поверхности цилиндра.
Формула площади боковой поверхности цилиндра
S бок. = 2πrh
Площадь полной поверхности цилиндра
Наконец, если мы сложим площадь всех трёх поверхностей, мы получим формулу площади полной поверхности цилиндра. Площади поверхности цилиндра равна площадь вершины цилиндра + площадь основания цилиндра + площадь боковой поверхности цилиндра или S = πr 2 + πr 2 + 2πrh = 2πr 2 + 2πrh. Иногда это выражение записывается идентичной формулой 2πr (r + h).
Формула площади полной поверхности цилиндра
S = 2πr 2 + 2πrh = 2πr(r + h)
r – радиус цилиндра, h – высота цилиндра
Примеры расчета площади поверхности цилиндра
Для понимания приведенных формул попробуем посчитать площадь поверхности цилиндра на примерах.
1. Радиус основания цилиндра равен 2, высота равна 3. Определите площадь боковой поверхности цилиндра.
Площадь полной поверхности рассчитывается по формуле: S бок. = 2πrh
S бок. = 2 * 3,14 * 2 * 3
S бок. = 6,28 * 6
S бок. = 37,68
Площадь боковой поверхности цилиндра равна 37,68.
2. Как найти площадь поверхности цилиндра, если высота равна 4, а радиус 6?
Площадь полной поверхности рассчитывается по формуле: S = 2πr 2 + 2πrh
S = 2 * 3,14 * 6 2 + 2 * 3,14 * 6 * 4
S = 2 * 3,14 * 36 + 2 * 3,14 * 24
Площадь поверхности цилиндра. В этой статье мы рассмотрим задания связанные с площадью поверхности . На блоге уже рассмотрены задания с таким телом вращения как конус. Цилиндр тоже относится к телам вращения. Что требуется и нужно знать о площади поверхности цилиндра? Давайте посмотрим на развёртку цилиндра:
Верхнее и нижнее основание это два равных круга:
Боковая поверхность это прямоугольник. При чём одна сторона этого прямоугольника равна высоте цилиндра, а другая длине окружности основания. Напомню, что длина окружности равна:
При чём одна сторона этого прямоугольника равна высоте цилиндра, а другая длине окружности основания. Напомню, что длина окружности равна:
Итак, формула поверхности цилиндра:
*Учить эту формулу не нужно! Достаточно знать формулы площади круга и длины его окружности, тогда вы всегда сможете записать указанную формулу. Важно её понимание! Рассмотрим задачи:
Длина окружности основания цилиндра равна 3. Площадь боковой поверхности равна 6. Найдите высоту и площадь поверхности цилиндра (считайте, что число Пи равно 3,14 и результат округлите до десятых).
Площадь полной поверхности цилиндра:
Даны длина окружности основания и площадь боковой поверхности цилиндра. То есть, нам дана площадь прямоугольника и одна его сторона, требуется найти другую сторону (это есть высота цилиндра):
Требуется радиус и тогда мы сможем найти указанную площадь.
Длина окружности основания равна трём, тогда запишем:
Таким образом
Округляем до десятых, получаем 7,4.
Ответ: h = 2; S = 7,4
Площадь боковой поверхности цилиндра равна 72Пи, а диаметр основания — 9. Найдите высоту цилиндра.
Значит
Ответ: 8
Площадь боковой поверхности цилиндра равна 64Пи, а высота — 8 . Найдите диаметр основания.
Площадь боковой поверхности цилиндра находится по формуле:
Диаметр равен двум радиусам, значит:
Ответ: 8
27058. Радиус основания цилиндра равен 2, высота равна 3. Найдите площадь боковой поверхности цилиндра, деленную на Пи.
27133. Длина окружности основания цилиндра равна 3, высота равна 2. Найдите площадь боковой поверхности цилиндра.
Площадь поверхности цилиндра
Примечание. В данном уроке изложены задачи по геометрии о площади поверхности цилиндра. Если Вам необходимо решить задачу по геометрии, которой здесь нет — пишите об этом в форуме. Почти наверняка курс будет дополнен.
Решение.
Формула нахождения объема цилиндра
V = πr2 h
Поскольку объем цилиндра нам известен, то
πr2 h = 128π
откуда
r2 h = 128
h = 128 / r2
Площадь полной поверхности цилиндра равна площади его оснований и площади боковой поверхности. Таким образом, формула площади поверхности цилиндра будет выглядеть следующим образом:
S = 2πr2 + 2πrh
где
πr2 — площадь основания цилиндра (площадь круга)
2πr — длина окружности основания
Подставим значение высоты цилиндра в полученную формулу
S = 2πr2 + 2πrh
S = 2πr2 + 2πr * 128 / r2
S = 2πr2 + 256π / r
Если представить полученную формулу как функцию площади заданного в задаче цилиндра, то минимальная площадь цилиндра будет достигнута в точке экстремума данной функции. Для нахождения экстремума дифференцируем полученную функцию.
Для нахождения экстремума дифференцируем полученную функцию.
f(r) = 2πr2 + 256π / r
Формулы дифференцирования можно посмотреть в таблице производных. Получим:
f ‘(r) = 4πr — 256π / r2
Поскольку в точке экстремума производная функции равна нулю, приравняем f ‘(r) к нулю и решим уравнение.
4πr — 256π / r2 = 0
получим
4πr ( 1 — 64/r3 ) = 0
откуда
4πr = 0 или 1 — 64/r3 = 0
первый найденный корень уравнения r = 0 отбрасываем,
1 — 64/r3 = 0
r3 = 64
r = 4
Откуда
h = 128 / 16
h = 8
Ответ: минимальная площадь цилиндра будет достигнута при h = 8 см, r =4 см
Задача
Площадь основания цилиндра равна Q, а площадь осевого сечения М. Чему равна полная поверхность цилиндра? Чему равна полная поверхность цилиндра?
|
Площа основи циліндра дорівнює Q, а площа осьового перерізу М. Чому дорівнює повна поверхня циліндра? |
Решение. Рiшення.
|
Найдем площадь осевого сечения цилиндра. S = 2HR По условию задачи 2HR = M откуда 2R = M / H Площадь каждого основания цилиндра Площадь полной поверхности цилиндра равна сумме площадей оснований и площади боковой поверхности. |
Знайдемо площу осьового перетину циліндра. S = 2HR По умові завдання 2HR = M звідки 2R = M / H Площа кожної основи циліндра Площа повної поверхні циліндра дорівнює сумі площ підстав і площі бічної поверхні. |
Ответ: Sп = 2Q + πМ
0
Диагональ цилиндра | Описание курса | Конус
Как посчитать площадь цилиндра? — Авто-ремонт
Площадь боковой поверхности цилиндра равна произведению высоты цилиндра на длину окружности основания. где R — радиус окружности основания, h — высота цилиндра. Полная площадь поверхности цилиндра равна сумме боковой поверхности цилиндра и двойной площади основания цилиндра.
где R — радиус окружности основания, h — высота цилиндра. Полная площадь поверхности цилиндра равна сумме боковой поверхности цилиндра и двойной площади основания цилиндра.
Как посчитать площадь цилиндра формула?
Площадь полной поверхности цилиндра равна площадь верхнего основания цилиндра + площадь нижнего основания цилиндра + площадь боковой поверхности цилиндра или S = πr2 + πr2 + 2πrh = 2πr2 + 2πrh. Иногда это выражение записывается идентичной формулой 2πr (r + h).
Как найти площадь цилиндра онлайн?
Полная площадь цилиндра рассчитывается по следующим формулам:
- Если нам известен радиус: S=2πR(h+R)
- Если нам известен диаметр: S=πD(h+D/2)
Как посчитать площадь круглой поверхности?
Полная площадь поверхности круглого цилиндра равна сумме площадей боковой поверхности круглого цилиндра и удвоенной площади основания. Основание круглого цилиндра есть круг и его площадь вычисляется по формуле площади круга: 2.
2.…
Расшифровать формулу просто:
- V – объем цилиндра;
- π – 3,14;
- R – радиус цилиндра;
- D – диаметр.
Как определить диаметр цилиндра?
Для измерения диаметра цилиндра прибор помещается внутрь отверстия так, чтобы его стержень находился перпендикулярно продольной оси изделия. Нужное положение достигается с помощью легких покачиваний. Если стрелка отклоняется влево от нуля, то диаметр исследуемого отверстия больше размера образца.
Как найти площадь емкости?
V=S*L — расчет объема цилиндра, где S — площадь поперечного сечения цилиндра, L — длина цилиндрической части. Площадь поперечного сечения емкости в форме цилиндра рассчитывается по формуле: S=3,14*d*d/4 — площадь круга с диаметром d.
Как узнать сколько литров в круглом баке?
V=S*L – формула расчета объема бака цилиндрической формы, где: L — длина тела. S — площадь поперечного сечения резервуара.
Как посчитать объем цилиндра онлайн?
Формулы для расчета объема цилиндра:
1) Объем цилиндра равен произведению площади основания на высоту. 2) Объем цилиндра равен произведению числа пи (3.1415) на квадрат радиуса основания на высоту.
2) Объем цилиндра равен произведению числа пи (3.1415) на квадрат радиуса основания на высоту.
Как найти площадь круга?
Формула вычисления площади круга
- S = π * r2, где r — это радиус, π — это константа, которая выражает отношение длины окружности к диаметру, она всегда равна 3,14.
- S = d2 : 4 * π, где d — это диаметр.
- S = L2 : 4 * π, где L — это длина окружности.
23.07.2020
Как посчитать наружную площадь цилиндра?
Площадь боковой поверхности цилиндра равна произведению высоты цилиндра на длину окружности основания. где R — радиус окружности основания, h — высота цилиндра. Полная площадь поверхности цилиндра равна сумме боковой поверхности цилиндра и двойной площади основания цилиндра.
Какие элементы цилиндра нужно знать для вычисления площади полной поверхности цилиндра?
Чтобы найти площадь поверхности цилиндра необходимо знать радиус его основания и высоту. Очень важно понимать, что существует две поверхности — боковая и полная. 2*H, где R – радиус основания цилиндра, H – искомая высота.
2*H, где R – радиус основания цилиндра, H – искомая высота.
Как найти объем по диаметру и высоте?
Формула вычисления объема цилиндра
- Через площадь основания и высоту
- V = S ⋅ H.
- Через радиус основания и высоту
- V = π ⋅ R2 ⋅ H.
- Примечание: в расчетах значение числа π округляется до 3,14.
- Через диаметр основания и высоту
- V = π ⋅ (d/2)2 ⋅ H.
- Задание 1.
Как найти высоту цилиндра зная только радиус?
— Если известен объем и высота цилиндра, можно найти его радиус, как корень квадратный из объема деленного на произведение числа пи на высоту цилиндра:
- R = √V / πh. где V — объем цилиндра, h — высота. …
- S (п. п.) …
- S (б.п.) = hP = 2πrh. …
- r = S (б.п.) / 2πh. …
- 2S (осн.) = πr 2. …
- r = √S (осн.) / π
- S (п. п.)
10.03.2020
Как определить объем по диаметру и высоте?
S = Пи х R² х h. В этой формуле необходимо площадь основания умножить на высоту. Для того чтобы найти площадь основания нужно знать радиус. Или диаметр.
Для того чтобы найти площадь основания нужно знать радиус. Или диаметр.
Площадь поверхности цилиндра. Калькулятор
Автор Dominik Czernia, кандидат наук
Отзыв от Bogna Szyk
Последнее обновление: 13 апреля 2022 г.
Содержание:- Как найти площадь поверхности цилиндра?
- Какова площадь поверхности цилиндра?
- Примеры расчетов
- Часто задаваемые вопросы
Этот калькулятор площади поверхности цилиндра представляет собой удобный инструмент, который быстро находит все три типа площадей поверхности:
- Площадь базовой поверхности цилиндра;
- Площадь боковой поверхности цилиндра; и
- Общая площадь поверхности цилиндра.
Цилиндр представляет собой трехмерное твердое тело, состоящее из двух конгруэнтных поверхностей ( оснований ) и одной боковой поверхности . Хотя цилиндры могут иметь множество различных форм, термин цилиндр обычно означает правый круговой цилиндр . Наш калькулятор площади поверхности цилиндра предназначен для этого типа цилиндров. Цилиндр прямое , когда одно из его оснований лежит точно над другим основанием, и косое , если нет. Стоит отметить, что основанием цилиндра может быть любая плоская замкнутая поверхность, например, круглый цилиндр имеет круглое основание, а прямоугольный цилиндр имеет прямоугольное основание.
Наш калькулятор площади поверхности цилиндра предназначен для этого типа цилиндров. Цилиндр прямое , когда одно из его оснований лежит точно над другим основанием, и косое , если нет. Стоит отметить, что основанием цилиндра может быть любая плоская замкнутая поверхность, например, круглый цилиндр имеет круглое основание, а прямоугольный цилиндр имеет прямоугольное основание.
Продолжайте читать, если хотите узнать, что такое площадь поверхности цилиндра и как найти площадь поверхности цилиндра. Вы также можете рассчитать другие параметры цилиндра — просто воспользуйтесь нашим калькулятором правильных цилиндров!
Как найти площадь поверхности цилиндра?
Чтобы оценить площадь поверхности цилиндра, вам нужно представить его как сеть . Это как если бы вы открыли цилиндр, как картонную коробку, а затем расплющили его. Использовать ваше воображение! И что вы получите? Ответ заключается в том, что правильный круговой цилиндр состоит из двух кругов и одного прямоугольника, как вы можете видеть на рисунке ниже.
Следовательно, площадь основания цилиндра равна удвоенной площади круга радиусом r , а площадь боковой поверхности цилиндра равна площади прямоугольника. Первая сторона этого прямоугольника — высота цилиндра h , а вторая — длина окружности основания 2 * π * r .
Какова площадь поверхности цилиндра?
Теперь, когда мы знаем, как найти площадь поверхности цилиндра, давайте выведем соответствующие формулы для площади поверхности прямоугольного цилиндра. Чтобы вычислить площадь базовой поверхности, вам нужно вычислить площадь круга с радиусом р . Но помните, что у каждого цилиндра два основания! Таким образом, нужно умножить на два:
base_area = 2 * π * r²
Оценка площади боковой поверхности еще проще. Поскольку площадь прямоугольника является произведением его сторон, мы можем написать, что:
lateral_area = (2 * π * r) * h ,
, где
-
2 * π * r— длина окружности. базового круга,
базового круга, -
hвысота цилиндра.
Наконец, формула общей площади поверхности цилиндра представляет собой просто сумму площади основания и площади боковой поверхности :
общая_площадь = базовая_площадь + боковая_площадь ,
или общая_площадь = 2 * π * r² + (2 * π * r) * h ,
или общая_площадь = 2 * π * r * (r + h) .
С нашим калькулятором площади поверхности цилиндра вы можете выполнять все расчеты в различных единицах измерения. Если вы хотите узнать больше о преобразовании единиц площади, ознакомьтесь с нашим конвертером площади прямо сейчас!
В расширенном режиме этого калькулятора вы также можете рассчитать объем цилиндра. Интересен тот факт, что каждый цилиндр с одинаковой высотой и площадью основания имеет одинаковый объем . Неважно, прямой это цилиндр или косой.
Примеры расчетов
Давайте решим несколько примеров задач с вычислением площади поверхности цилиндра.
- Вопрос : Какова площадь поверхности цилиндра с радиусом основания r = 2 см и высотой h = 3 см?
- Ответ : Площадь основания равна 25,133 см², площадь боковой поверхности равна 37,7 см², а общая площадь поверхности равна 62,83 см².
- Вопрос : Какова площадь поверхности цилиндра с диаметром основания d = 10 см и высотой h = 5 см?
- Ответ: Во-первых, вам нужно разделить диаметр на два, чтобы оценить радиус окружности r = d/2 = 5 см. Затем введите его вместе с высотой в пустые поля нашего калькулятора. В этой задаче площадь поверхности основания равна 157,08 см², площадь боковой поверхности равна 157,08 см², а площадь полной поверхности равна 314,16 см².
- Вопрос : Какова высота цилиндра с общей площадью поверхности 200 см² и радиусом r = 2 см?
- Ответ : Вы можете использовать наш калькулятор площади поверхности цилиндра и в этом случае! Просто введите вышеуказанные значения, и вы узнаете, что высота равна 13,915 см.

Часто задаваемые вопросы
Как найти площадь боковой поверхности цилиндра?
Чтобы найти площадь боковой поверхности цилиндра радиусом r и высоту h , выполните следующие действия:
- Рассчитайте периметр круглого основания, используя
C = 2πr. - Умножьте это значение на высоту цилиндра, чтобы получить площадь его боковой поверхности,
Aₗ = 2πrh. - Проверьте свои результаты, используя калькулятор площади поверхности цилиндра!
Как найти радиус по площади поверхности цилиндра?
Чтобы найти Radius , R , цилиндра из его площади поверхности A , вы также должны знать высоту цилиндра , H :
- Заместитель . уравнения цилиндра,
A = 2πr² + 2πrh.
- Сложите всех членов этого уравнения в одну сторону, чтобы получить
2πr² + 2πrh - A = 0. Обратите внимание, что это квадратное уравнение относительноr. - Решите это уравнение, используя квадратную формулу, чтобы получить
r = (-2πh ± √(4π²h² + 8πA))/4π.
Возьмите только положительный корень этого квадратного уравнения, так как радиус должен быть положительным.
Сколько поверхностей у цилиндра?
Цилиндр имеет три поверхности . К ним относятся две основные круглые поверхности и одна боковая (или изогнутая) поверхность .
Как рассчитать площадь поверхности полого цилиндра?
для вычисления площади поверхности из Полого цилиндра с внутренним радиусом , Rᵢ , Внешний радиус , Rₒ и Height , H 666, и Height , H 666666 и HEISH , H 666666666 гг.
- Рассчитайте площадь поверхности колец сверху и снизу по формуле
Aᵣ = 2π(rₒ² - rᵢ²). - Определить площадь боковой поверхности наружной цилиндрической поверхности по формуле
Аₒ = 2πrₒh. - Найдите площадь боковой поверхности внутренней цилиндрической поверхности по формуле
Aᵢ = 2πrᵢh. - Добавьте всех этих площадей, чтобы найти общую площадь поверхности полого цилиндра, чтобы получить
A = 2π((rₒ² - rᵢ²) + rₒh + rᵢh).
Доминик Черня, кандидат наук
Радиус основания (r)
Высота (h)
Площадь поверхности
Боковая
Посмотреть 20 похожих калькуляторов 3d геометрии 📦
Площадь полусферыКубКуб Рассчитать: найти v, a, d… Еще 17
Площадь поверхности цилиндра — Формула, Примеры
Площадь поверхности цилиндра можно определить как общее пространство, занимаемое плоскими поверхностями оснований цилиндра и его криволинейной поверхности. Общая площадь поверхности цилиндра состоит из двух компонентов: площади криволинейной поверхности и двух площадей плоской поверхности.
Общая площадь поверхности цилиндра состоит из двух компонентов: площади криволинейной поверхности и двух площадей плоской поверхности.
Давайте узнаем больше о том, что такое площадь поверхности цилиндра и как рассчитать общую площадь поверхности и площадь боковой поверхности цилиндра.
| 1. | Что такое площадь поверхности цилиндра? |
| 2. | Формула площади поверхности цилиндра |
| 3. | Изогнутая поверхность цилиндра |
| 4. | Общая площадь поверхности цилиндра |
| 5. | Как рассчитать площадь поверхности цилиндра? |
| 6. | Часто задаваемые вопросы о площади поверхности цилиндра |
Какова площадь поверхности цилиндра?
Площадь поверхности цилиндра может быть определена как площадь, занимаемая плоской поверхностью основания цилиндра и криволинейной поверхностью цилиндра. Общая площадь поверхности цилиндра включает площадь двух оснований цилиндра, имеющих форму круга, и площадь криволинейной поверхности. Площадь поверхности выражается в квадратных единицах, таких как квадратные сантиметры, квадратные дюймы, квадратные футы и так далее. Цилиндр — это трехмерный твердый объект, состоящий из двух круглых оснований, соединенных изогнутой гранью. Обратите внимание на приведенный ниже рисунок, на котором показаны различные части цилиндра, используемые для определения площади поверхности цилиндра.
Общая площадь поверхности цилиндра включает площадь двух оснований цилиндра, имеющих форму круга, и площадь криволинейной поверхности. Площадь поверхности выражается в квадратных единицах, таких как квадратные сантиметры, квадратные дюймы, квадратные футы и так далее. Цилиндр — это трехмерный твердый объект, состоящий из двух круглых оснований, соединенных изогнутой гранью. Обратите внимание на приведенный ниже рисунок, на котором показаны различные части цилиндра, используемые для определения площади поверхности цилиндра.
Формула площади поверхности цилиндра
Формула площади поверхности цилиндра используется для определения площади поверхности, занимаемой основаниями цилиндра и криволинейной поверхностью цилиндра. Поскольку цилиндр имеет криволинейную поверхность, мы можем выразить площадь его криволинейной поверхности, а также общую площадь поверхности. Это означает, что цилиндр имеет два типа площадей поверхности — общую площадь поверхности (TSA) и площадь криволинейной поверхности (TSA).
Площадь криволинейной поверхности цилиндра
Площадь криволинейной поверхности цилиндра – это площадь поверхности, покрытая только его криволинейной поверхностью. Если радиус основания цилиндра равен «r», а высота цилиндра равна «h», площадь криволинейной поверхности цилиндра рассчитывается по следующей формуле:
Площадь криволинейной поверхности цилиндра Формула
Криволинейная поверхность площадь цилиндра = 2πrh
, где
- r = радиус цилиндра
- h = высота цилиндра
- π = 22/7 или 3,14
Пример: Найдите площадь криволинейной поверхности цилиндра радиусом 7 см и высотой 14 см.
Решение: Площадь криволинейной поверхности цилиндра можно рассчитать по формуле CSA = 2πrh. После подстановки значения r = 7, h = 14 получаем: CSA = 2πrh = 2 × 3,14 × 7 × 14 = 615,8 см 2
Общая площадь поверхности цилиндра
Общая площадь поверхности цилиндра получается путем сложения площади двух оснований и площади криволинейной поверхности. Таким образом, формула для общей площади поверхности цилиндра имеет следующий вид:
Таким образом, формула для общей площади поверхности цилиндра имеет следующий вид:
Общая площадь поверхности цилиндра = Площадь двух оснований + Площадь криволинейной поверхности. Поскольку основания цилиндра имеют круглую форму, их общая площадь будет πr 2 + πr 2 . Мы уже знаем, что площадь криволинейной поверхности цилиндра равна 2πrh.
Общая площадь поверхности цилиндра ⇒ (πr 2 + πr 2 ) + 2πrh
⇒ 2πr 2 + 2πrh
Общая площадь поверхности цилиндра = 2πr (r + h)
.
Пример: Найдите общую площадь поверхности (TSA) цилиндра радиусом 5 см и высотой 8 см.
Решение: Общая площадь поверхности (TSA) цилиндра может быть рассчитана по формуле TSA = 2πr(r + h). После подстановки значений r = 5, h = 8 получаем: TSA = 2πr(r + h) = 2πr(r + h) = 2 × 3,14 × 5(5 + 8) = 615,8 см 2
Вывод формулы площади поверхности цилиндра
Площадь любой формы – это занимаемое ею пространство. Цилиндр имеет 2 плоские поверхности, которые представляют собой круги, и изогнутую поверхность, которая открывается в виде прямоугольника. Рассмотрим приведенный ниже цилиндр, высота которого равна «h», а радиус — «r». Давайте откроем цилиндр в 2-мерной форме и поймем это.
Цилиндр имеет 2 плоские поверхности, которые представляют собой круги, и изогнутую поверхность, которая открывается в виде прямоугольника. Рассмотрим приведенный ниже цилиндр, высота которого равна «h», а радиус — «r». Давайте откроем цилиндр в 2-мерной форме и поймем это.
Обратите внимание на приведенный выше рисунок, на котором площадь изогнутой поверхности раскрывается в виде прямоугольника, а два основания представляют собой круги.
- Теперь площадь двух кругов равна (πr 2 + πr 2 ), радиус основания которых равен r.
- В прямоугольнике одна сторона равна высоте цилиндра h , а длина этого прямоугольника равна длине окружности, то есть 2πr.
- Таким образом, площадь этого прямоугольника (l × b) равна 2πr × h = 2πrh, что также является площадью криволинейной поверхности цилиндра.
- Следовательно, общая площадь поверхности цилиндра = 2πr 2 + 2πrh = 2πr(r + h)
Как рассчитать площадь поверхности цилиндра?
Площадь поверхности цилиндра равна площади поверхности, занимаемой основаниями цилиндра и криволинейной поверхностью цилиндра. Используя приведенные ниже шаги, давайте найдем общую площадь поверхности цилиндра, имеющего радиус 7 единиц и высоту 9 единиц.
Используя приведенные ниже шаги, давайте найдем общую площадь поверхности цилиндра, имеющего радиус 7 единиц и высоту 9 единиц.
- Шаг 1: Обратите внимание на радиус ‘r’ и высоту ‘h’ цилиндра. Убедитесь, что оба имеют одинаковые единицы измерения. Здесь r = 7, h = 9
- Шаг 2: В данном вопросе нам нужно найти общую площадь поверхности цилиндра, поэтому мы будем использовать формулу для полной площади поверхности цилиндра, общая площадь поверхности = 2πr(r + h)
- Шаг 3: Подставьте данные значения и дайте ответ в квадратных единицах. После подстановки значений в формулу получаем общую площадь поверхности = 2πr(r + h) ⇒ 2π × 7(7 + 9) ⇒ 2π × 112 ⇒ 2 × 3,14 × 112 ⇒ 703,6 квадратных единиц.
☛ Связанные статьи
- Площадь поверхности куба
- Площадь поверхности прямоугольного параллелепипеда
- Площадь поверхности призмы
- Площадь поверхности конуса
- Площадь поверхности сферы
- Разница между площадью и площадью поверхности
Примеры площади поверхности цилиндра
Пример 1: Радиус цилиндра 5 дюймов, высота цилиндра 15 дюймов.
 Найдите площадь поверхности цилиндра. (Возьмите значение пи как 3,14)
Найдите площадь поверхности цилиндра. (Возьмите значение пи как 3,14)Решение:
Радиус, r = 5 в
Высота цилиндра, h = 15 дюймовПлощадь поверхности цилиндра: A = 2πr(r+h)
= 2π × 5 × (5 + 15)
= 2π × 5 × 20= 2 × 3,14 × 5 × 20
= 628Следовательно, площадь поверхности цилиндра равна 628 квадратных дюймов.
Пример 2: Самуил имеет цилиндр с площадью поверхности 1728π квадратных единиц. Найдите высоту цилиндра, если радиус основания окружности равен 24 единицам.
Решение:
Площадь поверхности цилиндра, A = 1728π; радиус (r) = 24; ч = ?
Подставим данные значения в формулу, чтобы найти высоту цилиндра.А = 2πr(r + h)
1728π = 2π × 24 × (24 + ч)
⇒ 1728/48 = (24 + ч)
⇒ 36 = (24 + ч)
⇒ h = 12Следовательно, высота цилиндра равна 12 единицам.
Пример 3: Укажите истинное или ложное значение.

а.) Общая площадь поверхности цилиндра получается путем сложения площади двух оснований и площади криволинейной поверхности.
б.) Полная площадь поверхности цилиндра рассчитывается по формуле Общая площадь поверхности = 2πrh
Решение:
а.) Полная площадь поверхности цилиндра получается прибавлением площади два основания и площадь криволинейной поверхности.
b.) Неверно, общая площадь поверхности цилиндра рассчитывается по формуле Общая площадь поверхности = 2πr(r + h)
перейти к слайдуперейти к слайдуперейти к слайду
Как ваш ребенок может освоить математические понятия?
Мастерство математики приходит с практикой и пониманием «почему» за «что». Почувствуйте разницу Cuemath.
Записаться на бесплатный пробный урок
Практические вопросы по площади поверхности цилиндра
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о площади поверхности цилиндра
Что такое площадь поверхности цилиндра?
Площадь поверхности цилиндра определяется как общая площадь или область, покрытая поверхностью формы. Поскольку цилиндр имеет 2 плоские поверхности и 1 изогнутую поверхность, общая площадь поверхности включает площадь плоских поверхностей и площадь криволинейной поверхности. Площадь поверхности цилиндра выражается в квадратных единицах, например, м 2 , дюймы 2 , см 2 , ярды 2 и т. д.
Поскольку цилиндр имеет 2 плоские поверхности и 1 изогнутую поверхность, общая площадь поверхности включает площадь плоских поверхностей и площадь криволинейной поверхности. Площадь поверхности цилиндра выражается в квадратных единицах, например, м 2 , дюймы 2 , см 2 , ярды 2 и т. д.
Как найти площадь поверхности цилиндра?
Площадь поверхности цилиндра можно найти, используя шаги, указанные ниже:
- Шаг 1: Запишите радиус основания ‘r’ и высоту ‘h’ цилиндра. Убедитесь, что единицы измерения совпадают.
- Шаг 2: Примените соответствующую формулу, чтобы найти площадь поверхности цилиндра, заданного как,
Площадь криволинейной поверхности цилиндра = 2πrh
Общая площадь поверхности цилиндра = 2πr(h + r) - Шаг 3: Подставьте данные значения и выразите ответ в квадратных единицах.
Какова формула общей площади поверхности цилиндра?
Формула для расчета общей площади поверхности цилиндра выражается следующим образом: общая площадь поверхности цилиндра = 2πr(r + h). Эта общая площадь поверхности включает площадь двух оснований (2πr 2 ) и площадь изогнутой поверхности (2πrh). Здесь «r» — радиус, а «h» — высота цилиндра.
Эта общая площадь поверхности включает площадь двух оснований (2πr 2 ) и площадь изогнутой поверхности (2πrh). Здесь «r» — радиус, а «h» — высота цилиндра.
☛Также проверьте:
- Формулы площади поверхности
- Формулы измерения
Как найти площадь поверхности цилиндра с открытым верхом?
Площадь поверхности цилиндра с открытым верхом можно рассчитать, найдя площадь одного основания и криволинейной поверхности. Таким образом, площадь цилиндра без верха можно выразить как площадь поверхности цилиндра с открытым верхом = πr(r + 2h), где r — радиус, а h — высота цилиндра. Следует отметить, что мы взяли площадь одного основания, потому что у цилиндра нет вершины.
По какой формуле найти площадь основания цилиндра?
Основание цилиндра имеет форму круга. Таким образом, формула для нахождения площади основания цилиндра выражается как πr 2 , где r — радиус основания цилиндра. Если требуется площадь обоих оснований, то она будет равна πr 2 + πr 2 = 2πr 2
Как рассчитать площадь поверхности цилиндра с помощью калькулятора?
Площадь поверхности цилиндра можно легко определить с помощью «калькулятора площади поверхности цилиндра». Это самый быстрый метод, с помощью которого мы можем оценить площадь поверхности в течение нескольких секунд. Чтобы использовать его, нам нужно ввести значение определенных параметров на экране калькулятора, таких как радиус и высота цилиндра. Воспользуйтесь онлайн-калькулятором площади поверхности цилиндра Cuemath и получите ответы одним щелчком мыши. Ознакомьтесь с рабочими листами площади поверхности цилиндров для большей практики.
Это самый быстрый метод, с помощью которого мы можем оценить площадь поверхности в течение нескольких секунд. Чтобы использовать его, нам нужно ввести значение определенных параметров на экране калькулятора, таких как радиус и высота цилиндра. Воспользуйтесь онлайн-калькулятором площади поверхности цилиндра Cuemath и получите ответы одним щелчком мыши. Ознакомьтесь с рабочими листами площади поверхности цилиндров для большей практики.
Как найти площадь криволинейной поверхности цилиндра?
Площадь криволинейной поверхности цилиндра рассчитывается по формуле площадь криволинейной поверхности цилиндра = 2πrh, где r — радиус, а h — высота цилиндра.
Как найти площадь поверхности цилиндра с диаметром и высотой?
Если диаметр и высота цилиндра известны, мы можем найти площадь поверхности цилиндра, используя ту же формулу. Мы можем получить радиус цилиндра, используя диаметр, поскольку диаметр = 2 × радиус. После нахождения радиуса мы можем использовать формулу Общая площадь поверхности цилиндра = 2πr(r + h)
Какой будет площадь криволинейной поверхности цилиндра с радиусом 7 м и высотой 10 м?
Площадь криволинейной поверхности цилиндра можно рассчитать по формуле Площадь криволинейной поверхности цилиндра = 2πrh; где r = радиус цилиндра и h = высота цилиндра. После подстановки значений в формулу где r = 7, h = 10, получаем, Площадь криволинейной поверхности цилиндра = 2πrh = 2 × 3,14 × 7 × 10 = 439,6 м 2
После подстановки значений в формулу где r = 7, h = 10, получаем, Площадь криволинейной поверхности цилиндра = 2πrh = 2 × 3,14 × 7 × 10 = 439,6 м 2
Площадь поверхности цилиндра
Вы сталкивайтесь с цилиндрами в повседневных делах, например, когда вы пьете газировку, открываете металлическую банку с едой или шлепаете своих друзей цилиндрической лапшой для бассейна. Цилиндр математически представляет собой трехмерный объект, пару конгруэнтных окружностей, разделенных изогнутой поверхностью.
Содержание
- Определение цилиндра
- Площадь поверхности цилиндра
- Площадь поверхности цилиндра Формула
- Площадь боковой поверхности цилиндра
- Формула площади боковой поверхности
- Как найти площадь поверхности цилиндра
Определение цилиндра
Цилиндр имеет две грани, две криволинейные кромки, где изогнутая стенка встречается с конечными кругами, и криволинейную поверхность, проходящую между двумя круговыми концами.
Цилиндр представляет собой трехмерное тело, имеющее высоту (h), ширину (w) или диаметр (D) и длину (l). Поскольку он трехмерный, он имеет площади поверхности , а не просто площадь (площадь обычно ассоциируется только с двумерными формами, такими как круг или прямоугольник).
Цилиндры обычно имеют стороны, перпендикулярные их концам, что делает их правильными цилиндрами . Цилиндры тоже могут быть наклонными. Два их круглых конца могут не совпадать, поэтому стена или изогнутая поверхность наклоняются, как 9.0022 косой цилиндр знаменитой Пизанской башни.
Площадь поверхности цилиндра
Когда мы говорим о площади поверхности цилиндра, мы имеем в виду две площади поверхности: площадь боковой поверхности и общую площадь поверхности . Общая площадь поверхности обычно упоминается как площадь поверхности.
Если вас попросили найти площадь поверхности цилиндра, то вы хотите найти площади двух концов и криволинейной поверхности.
Убедитесь, что вы понимаете связь между радиусом, диаметром и π, поскольку все они играют роль в определении площади поверхности правильного цилиндра.
Диаметр и радиус цилиндра определяются двумя окружностями, которые обычно считаются основаниями или верхом и низом цилиндра, хотя математических причин для того, чтобы цилиндр стоял, не существует. Подумайте о цистернах в поезде; они представляют собой цилиндры «по бокам», их основания с обоих концов.
Все, что вы делаете при расчете площади поверхности, это измеряете площадь двух окружностей, высоту h цилиндра и связываете их с помощью числа π.
Площадь поверхности цилиндра Формула
Формула площади поверхности цилиндра:
A = 2πrh + 2πr2
оба конца, h — высота, а π — иррациональное число, которое мы упрощаем и сокращаем до 3,141595 или даже короче, до 3,14.
Формула площади на самом деле является формулой для криволинейной поверхности (то есть части 2πrh), добавленной к площади обоих концов (то есть части 2πr2). Если вы видите фразу «площадь основания цилиндра», автор имеет в виду верхний и нижний концы, а не изогнутую поверхность между ними.
Если вы видите фразу «площадь основания цилиндра», автор имеет в виду верхний и нижний концы, а не изогнутую поверхность между ними.
Площадь всегда будет выражаться в квадратных единицах исходя из линейных единиц в задаче, так как любые две линейные меры, умноженные друг на друга, дают квадратные единицы.
Площадь боковой поверхности цилиндра
Как упоминалось выше, существует также площадь боковой поверхности объекта. Боковая поверхность объекта определяется как площадь всех сторон объекта, исключая площадь его основания и вершины. Для цилиндра площадь боковой поверхности представляет собой изогнутую поверхность, соединяющую основание и вершину.
Формула площади боковой поверхности
Формула для расчета площади боковой поверхности аналогична приведенной выше формуле площади поверхности, но поскольку мы не учитываем верх или основание, мы должны удалить эту часть формулы. Формула площади боковой поверхности:
L. S.A = 2πrh
S.A = 2πrh
Как найти площадь поверхности цилиндра
Вот цилиндр из сердцевины рулона бумажных полотенец:
[чертеж картонной трубки диаметром 1,7 дюйма и длиной 11 дюймов ]
Представьте, что мы храним внутри что-то прекрасное, например, персонализированные палочки для еды или вырезанные вручную шампуры для шашлыка. Нам нужно закрыть оба конца. Зная, что картонная трубка имеет ширину 1,7 дюйма и длину 11 дюймов, если бы мы закрыли концы, какова была бы площадь ее поверхности?
Здесь у нас не было радиуса r; нам сказали диаметр, но вспоминая соотношение между частями окружностей, мы помним:
Диаметр(D) = 2 × Радиус(r)
1,7 = 2r
85 = r
Поставим значения r и h в формулу, используя 3,14 для π:
a = 2πrh+2πr2
a = 2π*0,85*11+2π*0,852
A = (6,283185*9,352)+(6,283185*0,72252)
A = 63,28733373333185*0,72252)
A = 63,2873373333333333333338392185*0,72252)
,A = 63,2873337928792185*0,72252)
,A = 63,287 3833792185*0,72252)
928379287928185*0,72252).
На тубу для бумажных полотенец уходит чуть больше 0,4 квадратных фута картона!
Вот обычная банка из-под газировки. Приблизительно, сколько алюминия, по вашим оценкам, необходимо для его изготовления?
[вставьте мультяшный рисунок с этикетками 4,83 дюйма в высоту, 2,60 дюйма в диаметре в самом широком месте тела]
Правда, газировка может немного вдавиться с обоих концов, но нам просто нужна оценка. Во-первых, нам нужен радиус, поэтому мы берем половину диаметра банки:
2r = D
2r = 2,60
r = 1,30
Давайте вспомним нашу формулу и подставим то, что мы знаем:
a = 2πrh+2πr2
a = (2π*1,30*4,83)+(2π*1,32)
A = (6,283185*6,2792)+(6,283185*1,692)
A = 50,070702
, что это более трети квадратного фута переработанного алюминия в каждой банке. Теперь вы понимаете, почему важна переработка алюминия — всего три банки расходуют квадратный фут металла!
Next Lesson:
Площадь поверхности пирамиды
Площадь поверхности цилиндра – объяснение и примеры
Прежде чем мы перейдем к теме площади поверхности цилиндра, давайте рассмотрим цилиндр. В геометрии цилиндр — это трехмерная фигура с двумя круглыми основаниями, параллельными друг другу, и криволинейной поверхностью.
В геометрии цилиндр — это трехмерная фигура с двумя круглыми основаниями, параллельными друг другу, и криволинейной поверхностью.
Как найти площадь поверхности цилиндра?
Площадь поверхности цилиндра представляет собой сумму двух параллельных и конгруэнтных круглых граней и площади криволинейной поверхности.
В этой статье будет обсуждаться, как найти общую площадь поверхности и площадь боковой поверхности цилиндра .
Чтобы вычислить площадь поверхности цилиндра , вам нужно найти площадь основания (B) и площадь криволинейной поверхности (CSA). Следовательно, площадь поверхности или общая поверхность цилиндра равна сумме площади основания, умноженной на два, и площади криволинейной поверхности.
Криволинейная поверхность цилиндра равна прямоугольнику, длина которого 2 πr , а ширина h.
Где r = радиус круглой поверхности и h = высота цилиндра.
Площадь криволинейной поверхности = Площадь прямоугольника =l x w = πdh
Площадь основания, B = Площадь круга = πr 2
Площадь цилиндра формула40
40 Формула для общей площади поверхности цилиндра имеет следующий вид:
Общая площадь поверхности цилиндра = 2πr 2 + 2πrh
TSA = 2πr 2 + 2πrh
90 площадь верхней и нижней круговых граней, а 2πrh — площадь криволинейной поверхности.
Взяв 2πr в качестве общего множителя из RHS, мы получим;
ВСП = 2πr (h + r) ……………………………………. ( Площадь поверхности цилиндра формула )
Давайте решим примеры задач на площадь поверхности цилиндра.
Пример 1
Найдите общую площадь поверхности цилиндра, радиус которого 5 см, а высота 7 см.
Раствор
По формуле
TSA = 2πr (h + r)
= 2 x 3,14 x 5 (7 + 5)
= 31,4 x 12
= 376,8 см 2
Пример 2
Найдите радиус цилиндра. футов, а высота 3 фута.
футов, а высота 3 фута.
Решение
Дано:
TSA = 2136,56 квадратных футов
Высота, H = 3 фута
Но, TSA = 2πr (H + R)
2136,56 = 2 x 3.14 x R (3 + R)
2136,56 = 2 x 3.14 x R (3 + R)
2136,56 = 2 x 3.14 x R (3 + R)
2136,56 = 2 x 3.14 x R (3 + R)
2136,56 = 6,28r (3 + r)
по распределительным свойствам умножения на RHS, мы имеем
2136,56 = 18,84R + 6,28R 2
Разделите каждый термин на 6,28
340,22 = 3R + R 2
R 2
R 2
9000 2
9000 2
9000 2 9000 2 9000 2 9000 2
9000 2 9000 2
9000 2 9000 290,22 = 3R + R 2 9000 2
340,22 = 3R + R 2 9000 2
9000 290,22. 3r – 340,22 = 0 ……… ( квадратное уравнение )
Решая уравнение по квадратной формуле, получаем,
r = 17
Следовательно, радиус цилиндра равен 17 футам.
Пример 3
Стоимость покраски цилиндрической емкости $0,04 за см 2 . Найдите стоимость покраски 20 контейнеров радиусом 50 см и высотой 80 см.
Найдите стоимость покраски 20 контейнеров радиусом 50 см и высотой 80 см.
Решение
Рассчитайте общую площадь поверхности 20 контейнеров.
TSA = 2πr (H + R)
= 2 x 3,14 x 50 (80 + 50)
= 314 x 130
= 40820 см 2
Общая площадь 20 контейнеров = 40 820 см
2 x 20
=816 400 см 2
Стоимость покраски = 816 400 см 2 x 0,04 доллара США за см 2
= 32 656 долларов США.
Следовательно, стоимость покраски 20 контейнеров составляет 32 656 долларов.
Пример 4
Найдите высоту цилиндра, если его общая площадь поверхности составляет 2552 в 2 , а радиус составляет 14 дюймов
Раствор
Дано:
TSA = 2552 в
Дано:
TSA = 2552 в
Дано:
TSA = 2552 в
. 2
Радиус, r = 14 дюймов
Но, TSA = 2πr (h + r)
2552 = 2 x 3,14 x 14 (14 + h)
2552 = 87,92(14 + h)
Разделите обе части на 87,90, чтобы получить
26
6 29 14 + h
Вычесть по 14 с обеих сторон.
h = 15
Следовательно, высота цилиндра равна 15 дюймам.
Площадь боковой поверхности цилиндра
Как указывалось ранее, площадь криволинейной поверхности цилиндра называется боковой поверхностью область. Простыми словами, площадь боковой поверхности цилиндра — это площадь поверхности цилиндра без учета площади основания и дна (круговой поверхности).
Формула дает площадь боковой поверхности цилиндра;
LSA = 2πrh
Пример 5
Найдите площадь поверхности цилиндра диаметром 56 см и высотой 20 см.
Решение
Дано:
Диаметр = 56 см, отсюда радиус, r = 56/2 = 28 см
Высота, h = 20 см 2 х 3,14 х 28 х 20
= 3516,8 см 2 .
Таким образом, площадь боковой поверхности цилиндра равна 3516,8 см 2 .
Пример 6
Площадь боковой поверхности цилиндра составляет 144 фута 2 . Найдите высоту цилиндра, если радиус цилиндра равен 7 м.
Найдите высоту цилиндра, если радиус цилиндра равен 7 м.
Решение
Дано;
LSA = 144 фута 2
Радиус, r = 7 футов
144 = 2 x 3,14 x 7 x h
144 = 43,96 ч
Разделить на 43,96 с обеих сторон.
3,28 = H
Таким образом, высота цилиндра составляет 3,28 фута
Площадь боковой поверхности цилиндра
✖radius является радиальной линией с фокусировкой на любую пункт до любого пункта до любого пункта до любого пункта до любого пункта. кривой.ⓘ Радиус [r] | A.U. of LengthAlnAngstromArpentAstronomical UnitAttometerBarleycornBillion Light YearBohr RadiusCable (International)Cable (UK)Cable (US)CaliberCentimeterChainCubit (Greek)Cubit (UK)DecameterDecimeterEarth-Moon DistanceEarth’s Distance from SunEarth’s Equatorial RadiusEarth’s Polar RadiusElectron Radius (Classical)EllExameterFamnFathomFemtometerFermiFinger (Cloth)FingerbreadthFootFoot (US Survey)FurlongGigameterHandHandbreadthHectometerInchKenKilometerKiloparsecKiloyardLeagueLeague (Statute)Light YearLinkLong CubitLong ReedMegameterMegaparsecMeterMicroinchMicrometerMicronMilMileMile (Roman)Mile (US Survey)MillimeterMillion Light YearNail (Cloth)NanometerNautical League (int)Nautical League UKNautical Mile (International)Nautical Mile (UK)ParsecPerchPetameterPicaPicometerPlanck LengthPointPoleQuarterReedRodRoman ActusRopeRussian ArchinSpan (Cloth)Sun’s RadiusTerameterTwipVara CastellanaVara ConuqueraVara De TareaYardYoctometerYottameterZeptometerZettameter | +10% -10% | |
✖Высота — это расстояние между самой низкой и самой высокой точками человека/фигуры/объекта, стоящего прямо. | +10% -10% |
✖Площадь боковой поверхности объекта – это площадь всех сторон объекта, за исключением площади его основания и верхней части. | AcreAcre (US Survey)AreArpentBarnCarreauCircular InchCircular MilCuerdaDecareDunamElectron Cross SectionHectareHomesteadMile (Roman)²Mile (Statute)²MuPingPlazaPyongRoodSabinSectionSquare AngstromSquare CentimeterSquare ChainSquare DecameterSquare DecimeterSquare FootSquare Foot (US Survey)Square HectometerSquare InchSquare KilometerSquare MeterSquare MicrometerSquare MilSquare MileSquare Mile (US Survey)Square MillimeterSquare NanometerSquare PerchSquare PoleSquare RodSquare Rod ( Исследование США) Square YardStremmaTownshipVaras Castellanas CuadVaras Conuqueras Cuad | ⎘ Копировать |
👎
Формула
Перезагрузить
👍
Площадь боковой поверхности цилиндрического раствора
ШАГ 0: Сводка предварительного расчета
ШАГ 1: Преобразование входных данных в базовые единицы
Радиус: 10 метров —> 10 метров Преобразование не требуется
Высота: 12 метров —> 12 метров Преобразование не требуется
ШАГ 2: Вычисление формулы
ШАГ 3: Преобразование результата в единицу измерения
753,98223686155 Квадратный метр —> Преобразование не требуется
< 4 Калькуляторы круглых цилиндровПлощадь боковой поверхности цилиндра Формула
Площадь боковой поверхности = 2*pi*радиус*высота
SA Боковой = 2*pi*r*h
Как рассчитать площадь боковой поверхности цилиндра?
Калькулятор площади боковой поверхности цилиндра использует . Площадь боковой поверхности = 2*pi*радиус*высота для расчета площади боковой поверхности. Площадь боковой поверхности цилиндра можно определить как площадь поверхности всех сторон цилиндра, исключая его база и верх. Площадь боковой поверхности обозначается цифрой 9.1224 SA Боковой символ.
Площадь боковой поверхности = 2*pi*радиус*высота для расчета площади боковой поверхности. Площадь боковой поверхности цилиндра можно определить как площадь поверхности всех сторон цилиндра, исключая его база и верх. Площадь боковой поверхности обозначается цифрой 9.1224 SA Боковой символ.
Как рассчитать площадь боковой поверхности цилиндра с помощью этого онлайн-калькулятора? Чтобы использовать этот онлайн-калькулятор для площади боковой поверхности цилиндра, введите радиус (r) и высоту (h) и нажмите кнопку расчета. Вот как можно объяснить расчет площади боковой поверхности цилиндра с заданными входными значениями -> 753,9822 = 2*pi*10*12 .
Часто задаваемые вопросы
Что такое площадь боковой поверхности цилиндра?
Площадь боковой поверхности цилиндра может быть определена как площадь поверхности всех сторон цилиндра, за исключением его основания и верхней части, и представлена как SA Боковая = 2*pi*r*h или Боковая поверхность Площадь = 2*пи*радиус*высота . Радиус — это радиальная линия от фокуса до любой точки кривой, а высота — это расстояние между самой низкой и самой высокой точками человека/фигуры/объекта, стоящего вертикально.
Радиус — это радиальная линия от фокуса до любой точки кривой, а высота — это расстояние между самой низкой и самой высокой точками человека/фигуры/объекта, стоящего вертикально.
Как рассчитать площадь боковой поверхности цилиндра?
Площадь боковой поверхности цилиндра может быть определена как площадь поверхности всех сторон цилиндра, за исключением его основания и верхней части, рассчитывается по формуле Площадь боковой поверхности = 2*pi*Радиус*Высота . Чтобы рассчитать площадь боковой поверхности цилиндра, вам нужны радиус (r) и высота (h) . С помощью нашего инструмента вам нужно ввести соответствующее значение радиуса и высоты и нажать кнопку расчета. Вы также можете выбрать единицы измерения (если есть) для ввода (ов) и вывода.
Поделиться
Скопировано!
Определение, формула, вывод и пример
Площадь поверхности цилиндра определяется как площадь, занимаемая плоской поверхностью оснований цилиндра и криволинейной поверхностью цилиндра. Общая площадь поверхности цилиндра включает площадь двух круглых оснований цилиндра, а также площадь криволинейной поверхности. Подробное объяснение и вывод формулы площади поверхности цилиндра вместе с примерами см. в статье ниже 9.0003
Общая площадь поверхности цилиндра включает площадь двух круглых оснований цилиндра, а также площадь криволинейной поверхности. Подробное объяснение и вывод формулы площади поверхности цилиндра вместе с примерами см. в статье ниже 9.0003
Цилиндр представляет собой трехмерную структуру, образованную двумя параллельными круглыми основаниями, соединенными криволинейной поверхностью. Центры круглых оснований перекрывают друг друга, образуя правильный цилиндр. Ось — это отрезок, соединяющий два центра и представляющий высоту цилиндра. Вид сверху цилиндра напоминает круг, а вид сбоку – прямоугольник. Цилиндр, в отличие от конуса, куба или параллелепипеда, не имеет вершин из-за его изогнутой формы и отсутствия прямых линий. На его лице два концентрических круга.
Формулы площади поверхности цилиндра
Формула площади поверхности цилиндра используется для расчета площади поверхности, занимаемой основаниями цилиндра и криволинейной поверхностью. Поскольку цилиндр имеет криволинейную поверхность, мы можем выразить как площадь его криволинейной поверхности, так и общую площадь поверхности. Цилиндр имеет два типа площадей поверхности: общую площадь поверхности и площадь криволинейной поверхности. Мы обсудим их обоих один за другим.
Поскольку цилиндр имеет криволинейную поверхность, мы можем выразить как площадь его криволинейной поверхности, так и общую площадь поверхности. Цилиндр имеет два типа площадей поверхности: общую площадь поверхности и площадь криволинейной поверхности. Мы обсудим их обоих один за другим.
Изогнутая поверхность цилиндра заключена между двумя параллельными круглыми основаниями. Она также известна как площадь боковой поверхности. Формула заключается в следующем:
Площадь изогнутой поверхности = 2πrh
Где,
R = радиус цилиндра
H = высота цилиндра
Пример. цилиндра радиусом 7 см и высотой 44 см.
Решение:
Общая площадь поверхности цилиндраИмеем, r = 7 см и h = 44 см
Площадь криволинейной поверхности цилиндра = 2πrh ) (5) (2)
= 1936 см 2
Общая площадь поверхности цилиндра равна сумме площади его изогнутой поверхности и площади двух его круглых оснований. Он рассчитывается путем суммирования площадей двух оснований и криволинейной поверхности. В результате формула для полной площади поверхности цилиндра выглядит следующим образом:
Он рассчитывается путем суммирования площадей двух оснований и криволинейной поверхности. В результате формула для полной площади поверхности цилиндра выглядит следующим образом:
Общая площадь поверхности цилиндра = 2πr 2 + 2πrh = 2πr (r + h)
, где
R = радиус цилиндра
H = высота из цилиндров
H = высота Cylinder
H = высота Cylinder
H = высота из цилиндров
H . Пример: Рассчитайте общую площадь поверхности цилиндра радиусом 7 см и высотой 10 см.
Решение:
Вывод формулы для площади поверхности цилиндраИмеем r = 7 и h = 10.
Общая площадь поверхности = 2πr 2 + 2πrh
= 2 (22/7) (7) 2 + 2 (22/7) (7) (10)
= 2 (22)(7) + 2 (22) (10)
= 308 + 440
= 748 кв. см
Рассмотрим цилиндр, радиус которого равен r, а высота равна h.
Цилиндр разделен на три части: одно круглое основание, одна прямоугольная область и еще одно круглое основание.
Прямоугольная площадь имеет длину 2πr и ширину h. Итак, район А 1 = 2πrh, что также является площадью криволинейной поверхности цилиндра.
Площадь круглого основания с радиусом r определяется выражением πr 2 . Итак, площадь двух таких оснований равна A 2 = (πr 2 + πr 2 ) = 2πr 2 .
Теперь общая площадь поверхности цилиндра равна сумме двух вышеуказанных площадей.
A = A 1 + A 2
= 2πr 2 + 2πrh
= 2πr(r + h)
Отсюда выводится формула площади поверхности цилиндра.
Как найти площадь поверхности цилиндра?
Площадь поверхности цилиндра – это площадь, занимаемая основаниями цилиндра, и площадь криволинейной поверхности цилиндра. Используйте приведенные ниже шаги, чтобы найти общую площадь поверхности цилиндра, имеющего радиус 14 см и высоту 10 см.
Шаг 1: Отметьте радиус «r» и высоту «h» цилиндра. Помните, что оба имеют одинаковые единицы измерения. Здесь, учитывая r = 14 см, h = 10 см
Шаг 2: Здесь мы должны найти общую площадь поверхности цилиндра, формула для общей площади поверхности цилиндра = 2πr(r + h)
Шаг 3: Подставьте указанные значения в приведенные выше формулы и найдите ответ в квадратных единицах. Замените значения в формуле, которую мы получаем,
9
Общая площадь поверхности = 2πr (r + h)
= 2π × 14 (14 + 10)
= 2π × 336
= 2 × 3,14 × 336
= 2110,08 квадрат См
= 2110,08 кв. Решенные примеры на площади поверхности цилиндраПример 1: Найдите площадь криволинейной поверхности цилиндра радиусом 3 см и высотой 7 см.
Решение:
Имеем r = 3 и h = 7.
Площадь криволинейной поверхности цилиндра = 2πrh 22) (3)
= 132 см 2
Пример 2: Найти радиус цилиндра с криволинейной поверхностью площадью 220 кв.
см и высотой 7 см.
Решение:
Имеем, A = 220 и h = 7.
Площадь кривизны цилиндра = 2πrh
220 = 2 (22/7) (r) (7) /44
r = 5 см
Пример 3: Найдите общую площадь поверхности цилиндра радиусом 21 см и высотой 42 см.
Решение:
Имеем r = 21 и h = 42.
Общая площадь поверхности = 2πr 2 + 2πrh
= 2 (212/7) (22/7) (21) (42)
= 2 (22) (3) (21) + 2 (22) (3) (42)
= 2772 + 5544
= 8316 кв. см
Пример 4. Найдите общую поверхность цилиндр при площади криволинейной поверхности 176 кв. см и высоте 21 см.
Решение:
Имеем A = 176 и h = 21.
Площадь кривизны цилиндра = 2πrh
176 = 2 (22/7) (r) 2 (22) (r) (3)
r = 176/132
r = 1,33 см
Общая площадь поверхности = 2πr 2 + 2πrh
= 2 (3,14) (1,33) (1,33) + 176
= 11,10 + 176
= 187,1 кв.
цилиндра, если сумма его высоты и радиуса равна 7 см, так что общая площадь поверхности равна 440 кв. см.
Решение:
Имеем (r + h) = 7 и A = 440.
Общая площадь поверхности = 2πr(r + h)
440 = 2 (22/7) (r) (7)
2 (22) (r) = 440
44r = 440
r = 10 см
Пример 6. Найдите площадь криволинейной поверхности цилиндра, если его общая площадь поверхности составляет 528 кв. см, а радиус равен 7. см.
Решение:
Имеем A = 528 и r = 7 см.
Общая площадь поверхности = 2πr(r + h)
528 = 2 (22/7) (7) (7 + h)
2 (22) (7 + h) = 528
7 + h = 12
h = 5 см
Площадь кривизны цилиндра = 2πrh
= 2 (22/7) (7) (5)
= 2 (22) (5)
= 220 кв. см
Часто задаваемые вопросы о площади поверхности цилиндра цилиндр?
Ответ:
Цилиндр представляет собой трехмерную форму, имеющую два параллельных друг другу круглых основания, соединенных криволинейной поверхностью.
Вопрос 2: Как найти площадь поверхности цилиндра?
Ответ:
Чтобы найти площадь поверхности цилиндра, мы найдем площадь криволинейной поверхности и площадь круглых оснований цилиндра. Теперь сложите все площади, чтобы получить общую площадь поверхности.
Вопрос 3: Напишите формулу нахождения площади цилиндра.
Ответ :
Формула для нахождения площади цилиндра:
Общая площадь поверхности = 2πr (h + r) кв. единица
Площадь криволинейной поверхности = 2πrh кв. единица
где,
r радиус и
h высота цилиндраВопрос 4: Напишите формулу объема цилиндра.
Ответ:
Формула для нахождения объема цилиндра: πr 2 ч кубических единиц.
Вопрос 5: Как найти площадь поверхности цилиндра с открытым верхом?
Ответ:
Площадь поверхности цилиндра с открытым верхом можно рассчитать, найдя площадь нижнего круглого основания и криволинейной поверхности цилиндра, а затем сложив оба результата.



 Так, условно длинами сечения являются образующие. Ширина — параллельные хорды стереометрической фигуры.
Так, условно длинами сечения являются образующие. Ширина — параллельные хорды стереометрической фигуры.