Наименьшее общее кратное числа 2. Как найти наименьшее общее кратное, нок для двух и более чисел
Как найти наименьшее общее кратное?
Как найти НОК
Вот видео, в котором вам будет предложено два способа нахождения наименьшего общего кратного (НОК).
 1 = 4457 = 560.
1 = 4457 = 560.НОК(16, 20, 28) = 560.
Таким образом, в итоге расчета получилось число 560. Оно является наименьшим общим кратным, то есть делится на каждое из трх чисел без остатка.
Наименьшее общее кратное число — это такая цифра, которая разделится на несколько предложенных чисел без остатка. Для того, чтобы такую цифру высчитать, надо взять каждое число и разложить его на простые множители. Те цифры, которые совпадают, убираем. Оставляет всех по одной, перемножаем их между собой по очереди и получаем искомое — наименьшее общее кратное.
НОК, или наименьшее общее кратное , — это наименьшее натуральное число двух и более чисел, которое делится на каждое из данных чисел без остатка.
Вот пример того, как найти наименьшее общее кратное 30 и 42.
- Первым делом нужно разложить данные числа на простые множители.
Для 30 — это 2 х 3 х 5.
Для 42 — это 2 х 3 х 7. Так как 2 и 3 имеются в разложении числа 30, то вычеркиваем их.

- Выписываем множители, которые входят в разложение числа 30. Это 2 х 3 х 5 .
- Теперь нужно домножить их на недостающий множитель, который имеем при разложении 42,а это 7. Получаем 2 х 3 х 5 х 7.
- Находим, чему равно 2 х 3 х 5 х 7 и получаем 210.
В итоге получаем, что НОК чисел 30 и 42 равен 210.
Чтобы найти наименьшее общее кратное , нужно выполнить последовательно несколько простых действий. Рассмотрим это на примере двух чисел: 8 и 12
Нужно найти каждый множитель каждого из двух чисел, у которых находим наименьшее общее кратное, а потом перемножить друг на друга множители, которые совпали у первого и второго числа. Результатом произведения будет искомое кратное.
Например у нас есть числа 3 и 5 и нам надо найти НОК(наименьшее общее кратное). Нам надо умножать и тройку и пятрку на все числа начиная с 1 2 3 … и т д пока мы не увидим одинаковое число и там и там.
Множим тройку и получаем: 3, 6, 9, 12, 15
Множим пятрку и получаем: 5, 10, 15
Метод разложения на простые множители — самый классический для нахождения наименьшего общего кратного (НОК) для нескольких чисел. Наглядно и просто продемонстрирован этот метод в следующем видеоролике:
Складывать, умножать, делить, приводить к общему знаменателю и другие арифметические действия очень увлекательное занятие, особенно восхищают примеры, занимающие целый лист.
Итак найти общее кратное для двух чисел, которое будет являться самым маленьким числом на которое делятся два числа. Хочу заметить, что не обязательно в дальнейшем прибегать к формулам, чтобы найти искомое, если можешь считать в уме (а это можно натренировать), то цифры сами всплывают в голове и потом дроби щелкаются как орешки.
Для начала усвоим, что можно умножить два числа друг на друга, а потом эту цифру уменьшать и делить поочередно на данные два числа, так мы найдем наименьшее кратное.
Например, два числа 15 и 6. Умножаем и получаем 90. Это явно больше число. Причем 15 делится на 3 и 6 делится на 3, значит 90 тоже делим на 3. Получаем 30. Пробуем 30 разделить 15 равно 2. И 30 делим 6 равно 5. Так как 2 это предел, то получается, что наименьшее кратное для чисел 15 и 6 будет 30.
С цифрами побольше будет немного трудней. но если знать, какие цифры дают нулевой остаток при делении или умножении, то трудностей, в принципе, больших нет.
- Разлагаем оба числа на простые множители: 8=2*2*2 и 12=3*2*2
- Сокращаем одинаковые множители у одного из чисел. В нашем случае совпадают 2*2, сократим их для числа 12, тогда у 12 останется один множитель: 3.
- Находим произведение всех оставшихся множителей: 2*2*2*3=24
Проверяя, убеждаемся, что 24 делится и на 8 и на 12, причем это наименьшее натуральное число, которое делится на каждое из этих чисел. Вот мы и нашли наименьшее общее кратное .
Попробую объяснить на примере цифр 6 и 8. Наименьшее общее кратное — это число, которое можно разделить на эти числа(в нашем случае 6 и 8) и остатка не будет.
Наименьшее общее кратное — это число, которое можно разделить на эти числа(в нашем случае 6 и 8) и остатка не будет.
Итак, начинаем умножать сначала 6 на 1, 2, 3 и т. д и 8 на 1, 2, 3 и т. д.
Наибольшее натуральное число, на которое делятся без остатка числа a и b, называют наибольшим общим делителем этих чисел. Обозначают НОД(a, b).
Рассмотрим нахождения НОД на примере двух натуральных чисел 18 и 60:
60 = 2 × 2 × 3 × 5
18 = 2 × 3 × 3
60 = 2 × 2 × 3 × 5
Разложим числа на простые множители:
324 = 2 × 2 × 3 × 3 × 3 × 3
111 = 3 × 37
432 = 2 × 2 × 2 × 2 × 3 × 3 × 3
Вычеркнуть из первого числа, множители которых нету во втором и третьем числе, получим:
2 × 2 × 2 × 2 × 3 × 3 × 3 = 3
В результате НОД(324
, 111 , 432 )=3Нахождение НОД с помощью алгоритма Евклида
Второй способ нахождения наибольшего общего делителя с помощью алгоритма Евклида . Алгоритм Евклида является наиболее эффективным способом нахождения НОД , используя его нужно постоянно находить остаток от деления чисел и применять рекуррентную формулу .
Алгоритм Евклида является наиболее эффективным способом нахождения НОД , используя его нужно постоянно находить остаток от деления чисел и применять рекуррентную формулу .
Рекуррентная формула для НОД, НОД(a, b)=НОД(b, a mod b) , где a mod b — остаток от деления a на b.
Алгоритм Евклида
Пример Найти наибольший общий делитель чисел
7920 и 594Найдем НОД(7920 , 594 ) с помощью алгоритма Евклида, вычислять остаток от деления будем с помощью калькулятора.
- 7920 mod 594 = 7920 — 13 × 594 = 198
- 594 mod 198 = 594 — 3 × 198 = 0
В результате получаем НОД(7920 , 594 ) = 198
Наименьшее общее кратное
Для того, чтобы находить общий знаменатель при сложении и вычитании дробей с разными знаменателями необходимо знать и уметь рассчитывать наименьшее общее кратное (НОК).
Кратное числу « a » — это число, которое само делится на число « a » без остатка.
Числа кратные 8 (то есть, эти числа разделятся на 8 без остатка): это числа 16, 24, 32 …
Кратные 9: 18, 27, 36, 45 …
Чисел, кратных данному числу a бесконечно много, в отличии от делителей этого же числа. Делителей — конечное количество.
Общим кратным двух натуральных чисел называется число, которое делится на оба эти числа нацело .
Наименьшим общим кратным (НОК) двух и более натуральных чисел называется наименьшее натуральное число, которое само делится нацело на каждое из этих чисел.
Как найти НОК
НОК можно найти и записать двумя способами.
Первый способ нахождения НОК
Данный способ обычно применяется для небольших чисел.
- Выписываем в строчку кратные для каждого из чисел, пока не найдётся кратное, одинаковое для обоих чисел.
- Кратное числа « a » обозначаем большой буквой «К».
Пример. Найти НОК 6 и 8 .
Найти НОК 6 и 8 .
Второй способ нахождения НОК
Этот способ удобно использовать, чтобы найти НОК для трёх и более чисел.
Количество одинаковых множителей в разложениях чисел может быть разное.
НОК (24, 60) = 2 · 2 · 3 · 5 · 2
Ответ: НОК (24, 60) = 120
Оформить нахождение наименьшего общего кратного (НОК) можно также следующим образом. Найдём НОК (12, 16, 24) .
24 = 2 · 2 · 2 · 3
Как видим из разложения чисел, все множители 12 вошли в разложение 24 (самого бóльшего из чисел), поэтому в НОК добавляем только одну 2 из разложения числа 16 .
НОК (12, 16, 24) = 2 · 2 · 2 · 3 · 2 = 48
Ответ: НОК (12, 16, 24) = 48
Особые случаи нахождения НОК

Например, НОК (60, 15) = 60
Так как взаимно простые числа не имеют общих простых делителей, то их наименьшее общее кратное равно произведению этих чисел.
На нашем сайте вы также можете с помощью специального калькулятора найти наименьшее общее кратное онлайн, чтобы проверить свои вычисления.
Если натуральное число делится только на 1 и на само себя, то оно называется простым.
Любое натуральное число всегда делится на 1 и на само себя.
Число 2 — наименьшее простое число. Это единственное чётное простое число, остальные простые числа — нечётные.
Простых чисел много, и первое среди них — число 2 . Однако нет последнего простого числа. В разделе «Для учёбы» вы можете скачать таблицу простых чисел до 997 .
Но многие натуральные числа делятся нацело ещё и на другие натуральные числа.
- число 12 делится на 1 , на 2 , на 3 , на 4 , на 6 , на 12 ;
- число 36 делится на 1 , на 2 , на 3 , на 4 , на 6 , на 12 , на 18 , на 36 .
- разложить делители чисел на простые множители;
Числа, на которые число делится нацело (для 12 это 1, 2, 3, 4, 6 и 12) называются делителями числа.
Делитель натурального числа a — это такое натуральное число, которое делит данное число « a » без остатка.
Натуральное число, которое имеет более двух делителей называется составным.
Обратите внимание, что числа 12 и 36 имеют общие делители. Это числа: 1, 2, 3, 4, 6, 12 . Наибольший из делителей этих чисел — 12 .
Общий делитель двух данных чисел « a » и « b » — это число, на которое делятся без остатка оба данных числа « a » и « b ».
Наибольший общий делитель (НОД) двух данных чисел « a » и « b » — это наибольшее число, на которое оба числа « a » и « b » делятся без остатка.
Кратко наибольший общий делитель чисел « a » и « b » записывают так :
Пример: НОД (12; 36) = 12 .
Делители чисел в записи решения обозначают большой буквой «Д».
Числа 7 и 9 имеют только один общий делитель — число 1 . Такие числа называют взаимно простыми числами .
Взаимно простые числа — это натуральные числа, которые имеют только один общий делитель — число 1 .
Как найти наибольший общий делитель
Чтобы найти НОД двух или более натуральных чисел нужно:
Вычисления удобно записывать с помощью вертикальной черты. Слева от черты сначала записываем делимое, справа — делитель. Далее в левом столбце записываем значения частных.
Поясним сразу на примере. Разложим на простые множители числа 28 и 64 .
- Подчёркиваем одинаковые простые множители в обоих числах.
28 = 2 · 2 · 7
64 = 2 · 2 · 2 · 2 · 2 · 2
Находим произведение одинаковых простых множителей и записать ответ;
НОД (28; 64) = 2 · 2 = 4
Ответ: НОД (28; 64) = 4
Оформить нахождение НОД можно двумя способами: в столбик (как делали выше) или «в строчку».
Первый способ записи НОД
Найти НОД 48 и 36 .
НОД (48; 36) = 2 · 2 · 3 = 12
Второй способ записи НОД
Теперь запишем решение поиска НОД в строчку. Найти НОД 10 и 15 .
На нашем информационном сайте вы также можете с помощью программы помощника найти наибольший общий делитель онлайн, чтобы проверить свои вычисления.
Нахождение наименьшего общего кратного, способы, примеры нахождения НОК.
Представленный ниже материал является логическим продолжением теории из статьи под заголовком НОК — наименьшее общее кратное, определение, примеры, связь между НОК и НОД. Здесь мы поговорим про нахождение наименьшего общего кратного (НОК) , и особое внимание уделим решению примеров. Сначала покажем, как вычисляется НОК двух чисел через НОД этих чисел. Дальше рассмотрим нахождение наименьшего общего кратного с помощью разложения чисел на простые множители. После этого остановимся на нахождении НОК трех и большего количества чисел, а также уделим внимание вычислению НОК отрицательных чисел.
Навигация по странице.
Вычисление наименьшего общего кратного (НОК) через НОД
Один из способов нахождения наименьшего общего кратного основан на связи между НОК и НОД. Существующая связь между НОК и НОД позволяет вычислять наименьшее общее кратное двух целых положительных чисел через известный наибольший общий делитель. Соответствующая формула имеет вид НОК(a, b)=a·b:НОД(a, b) . Рассмотрим примеры нахождения НОК по приведенной формуле.
Существующая связь между НОК и НОД позволяет вычислять наименьшее общее кратное двух целых положительных чисел через известный наибольший общий делитель. Соответствующая формула имеет вид НОК(a, b)=a·b:НОД(a, b) . Рассмотрим примеры нахождения НОК по приведенной формуле.
Найдите наименьшее общее кратное двух чисел 126 и 70 .
В этом примере a=126 , b=70 . Воспользуемся связью НОК с НОД, выражающуюся формулой НОК(a, b)=a·b:НОД(a, b) . То есть, сначала нам предстоит найти наибольший общий делитель чисел 70 и 126 , после чего мы сможем вычислить НОК этих чисел по записанной формуле.
Найдем НОД(126, 70) , используя алгоритм Евклида: 126=70·1+56 , 70=56·1+14 , 56=14·4 , следовательно, НОД(126, 70)=14 .
Теперь находим требуемое наименьшее общее кратное: НОК(126, 70)=126·70:НОД(126, 70)= 126·70:14=630 .
Чему равно НОК(68, 34) ?
Так как 68 делится нацело на 34 , то НОД(68, 34)=34 . Теперь вычисляем наименьшее общее кратное: НОК(68, 34)=68·34:НОД(68, 34)= 68·34:34=68 .
Заметим, что предыдущий пример подходит под следующее правило нахождения НОК для целых положительные чисел a и b: если число a делится на b , то наименьшее общее кратное этих чисел равно a .
Нахождение НОК с помощью разложения чисел на простые множители
Другой способ нахождения наименьшего общего кратного базируется на разложении чисел на простые множители. Если составить произведение из всех простых множителей данных чисел, после чего из этого произведения исключить все общие простые множители, присутствующие в разложениях данных чисел, то полученное произведение будет равно наименьшему общему кратному данных чисел .
Озвученное правило нахождения НОК следует из равенства НОК(a, b)=a·b:НОД(a, b) . Действительно, произведение чисел a и b равно произведению всех множителей, участвующих в разложениях чисел a и b . В свою очередь НОД(a, b) равен произведению всех простых множителей, одновременно присутствующих в разложениях чисел a и b (о чем написано в разделе нахождение НОД с помощью разложения чисел на простые множители).
Приведем пример. Пусть мы знаем, что 75=3·5·5 и 210=2·3·5·7 . Составим произведение из всех множителей данных разложений: 2·3·3·5·5·5·7 . Теперь из этого произведения исключим все множители, присутствующие и в разложении числа 75 и в разложении числа 210 (такими множителями являются 3 и 5), тогда произведение примет вид 2·3·5·5·7 . Значение этого произведения равно наименьшему общему кратному чисел 75 и 210 , то есть, НОК(75, 210)= 2·3·5·5·7=1 050 .
Разложив числа 441 и 700 на простые множители, найдите наименьшее общее кратное этих чисел.
Разложим числа 441 и 700 на простые множители:
Получаем 441=3·3·7·7 и 700=2·2·5·5·7 .
Теперь составим произведение из всех множителей, участвующих в разложениях данных чисел: 2·2·3·3·5·5·7·7·7 . Исключим из этого произведения все множители, одновременно присутствующие в обоих разложениях (такой множитель только один – это число 7): 2·2·3·3·5·5·7·7 . Таким образом, НОК(441, 700)=2·2·3·3·5·5·7·7=44 100 .
НОК(441, 700)= 44 100 .
Правило нахождения НОК с использованием разложения чисел на простые множители можно сформулировать немного иначе. Если ко множителям из разложения числа a добавить недостающие множители из разложения числа b , то значение полученного произведения будет равно наименьшему общему кратному чисел a и b .
Для примера возьмем все те же числа 75 и 210 , их разложения на простые множители таковы: 75=3·5·5 и 210=2·3·5·7 . Ко множителям 3 , 5 и 5 из разложения числа 75 добавляем недостающие множители 2 и 7 из разложения числа 210 , получаем произведение 2·3·5·5·7 , значение которого равно НОК(75, 210) .
Найдите наименьшее общее кратное чисел 84 и 648 .
Получаем сначала разложения чисел 84 и 648 на простые множители. Они имеют вид 84=2·2·3·7 и 648=2·2·2·3·3·3·3 . К множителям 2 , 2 , 3 и 7 из разложения числа 84 добавляем недостающие множители 2 , 3 , 3 и 3 из разложения числа 648 , получаем произведение 2·2·2·3·3·3·3·7 , которое равно 4 536 . Таким образом, искомое наименьшее общее кратное чисел 84 и 648 равно 4 536 .
Нахождение НОК трех и большего количества чисел
Наименьшее общее кратное трех и большего количества чисел может быть найдено через последовательное нахождение НОК двух чисел. Напомним соответствующую теорему, дающую способ нахождения НОК трех и большего количества чисел.
Пусть даны целые положительные числа a 1 , a 2 , …, a k , наименьшее общее кратное m k этих чисел находится при последовательном вычислении m 2 =НОК(a 1 , a 2) , m 3 =НОК(m 2 , a 3) , …, m k =НОК(m k−1 , a k) .
Рассмотрим применение этой теоремы на примере нахождения наименьшего общего кратного четырех чисел.
Найдите НОК четырех чисел 140 , 9 , 54 и 250 .
Сначала находим m 2 =НОК(a 1 , a 2)=НОК(140, 9) . Для этого по алгоритму Евклида определяем НОД(140, 9) , имеем 140=9·15+5 , 9=5·1+4 , 5=4·1+1 , 4=1·4 , следовательно, НОД(140, 9)=1 , откуда НОК(140, 9)=140·9:НОД(140, 9)= 140·9:1=1 260 . То есть, m 2 =1 260 .
Теперь находим m 3 =НОК(m 2 , a 3)=НОК(1 260, 54) . Вычислим его через НОД(1 260, 54) , который также определим по алгоритму Евклида: 1 260=54·23+18 , 54=18·3 .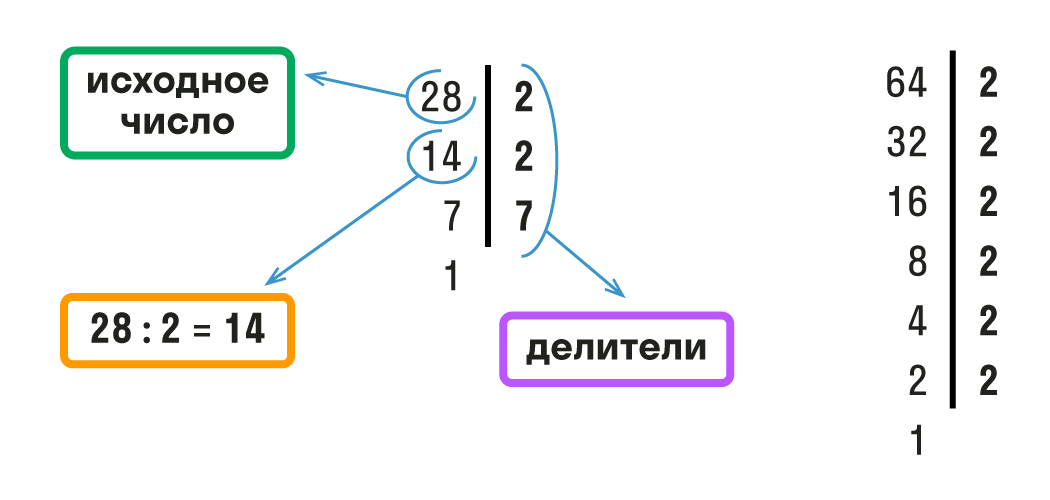 Тогда НОД(1 260, 54)=18 , откуда НОК(1 260, 54)= 1 260·54:НОД(1 260, 54)= 1 260·54:18=3 780 . То есть, m 3 =3 780 .
Тогда НОД(1 260, 54)=18 , откуда НОК(1 260, 54)= 1 260·54:НОД(1 260, 54)= 1 260·54:18=3 780 . То есть, m 3 =3 780 .
Осталось найти m 4 =НОК(m 3 , a 4)=НОК(3 780, 250) . Для этого находим НОД(3 780, 250) по алгоритму Евклида: 3 780=250·15+30 , 250=30·8+10 , 30=10·3 . Следовательно, НОД(3 780, 250)=10 , откуда НОК(3 780, 250)= 3 780·250:НОД(3 780, 250)= 3 780·250:10=94 500 . То есть, m 4 =94 500 .
Таким образом, наименьшее общее кратное исходных четырех чисел равно 94 500 .
НОК(140, 9, 54, 250)=94 500 .
Во многих случаях наименьшее общее кратное трех и большего количества чисел удобно находить с использованием разложений данных чисел на простые множители. При этом следует придерживаться следующего правила. Наименьшее общее кратное нескольких чисел равно произведению, которое составляется так: ко всем множителям из разложения первого числа добавляются недостающие множители из разложения второго числа, к полученным множителям добавляются недостающие множители из разложения третьего числа и так далее
.
Рассмотрим пример нахождения наименьшего общего кратного с использованием разложения чисел на простые множители.
Найдите наименьшее общее кратное пяти чисел 84 , 6 , 48 , 7 , 143 .
Сначала получаем разложения данных чисел на простые множители: 84=2·2·3·7 , 6=2·3 , 48=2·2·2·2·3 , 7 (7 – простое число, оно совпадает со своим разложением на простые множители) и 143=11·13 .
Для нахождения НОК данных чисел к множителям первого числа 84 (ими являются 2 , 2 , 3 и 7) нужно добавить недостающие множители из разложения второго числа 6 . Разложение числа 6 не содержит недостающих множителей, так как и 2 и 3 уже присутствуют в разложении первого числа 84 . Дальше к множителям 2 , 2 , 3 и 7 добавляем недостающие множители 2 и 2 из разложения третьего числа 48 , получаем набор множителей 2 , 2 , 2 , 2 , 3 и 7 . К этому набору на следующем шаге не придется добавлять множителей, так как 7 уже содержится в нем. Наконец, к множителям 2 , 2 , 2 , 2 , 3 и 7 добавляем недостающие множители 11 и 13 из разложения числа 143 . Получаем произведение 2·2·2·2·3·7·11·13 , которое равно 48 048 .
Получаем произведение 2·2·2·2·3·7·11·13 , которое равно 48 048 .
Следовательно, НОК(84, 6, 48, 7, 143)=48 048 .
НОК(84, 6, 48, 7, 143)=48 048 .
Нахождение наименьшего общего кратного отрицательных чисел
Иногда встречаются задания, в которых требуется найти наименьшее общее кратное чисел, среди которых одно, несколько или все числа являются отрицательными. В этих случаях все отрицательные числа нужно заменить противоположными им числами, после чего находить НОК положительных чисел. В этом и состоит способ нахождения НОК отрицательных чисел. Например, НОК(54, −34)=НОК(54, 34) , а НОК(−622, −46, −54, −888)= НОК(622, 46, 54, 888) .
Мы можем так поступать, потому что множество кратных числа a совпадает со множеством кратных числа −a (a и −a – противоположные числа). Действительно, пусть b – какое-то кратное числа a , тогда b делится на a , и понятие делимости утверждает существование такого целого числа q , что b=a·q . Но будет справедливо и равенство b=(−a)·(−q) , которое в силу того же понятия делимости означает, что b делится на −a , то есть, b есть кратное числа −a . Справедливо и обратное утверждение: если b – какое-то кратное числа −a , то b является кратным и числа a .
Справедливо и обратное утверждение: если b – какое-то кратное числа −a , то b является кратным и числа a .
Найдите наименьшее общее кратное отрицательных чисел −145 и −45 .
Заменим отрицательные числа −145 и −45 на противоположные им числа 145 и 45 . Имеем НОК(−145, −45)=НОК(145, 45) . Определив НОД(145, 45)=5 (например, по алгоритму Евклида), вычисляем НОК(145, 45)=145·45:НОД(145, 45)= 145·45:5=1 305 . Таким образом, наименьшее общее кратное отрицательных целых чисел −145 и −45 равно 1 305 .
www.cleverstudents.ru
Продолжаем изучать деление. В данном уроке мы рассмотрим такие понятия, как НОД и НОК .
НОД — это наибольший общий делитель.
НОК — это наименьшее общее кратное.
Тема довольно скучная, но разобраться в ней нужно обязательно. Не понимая этой темы, не получится эффективно работать с дробями, которые являются настоящей преградой в математике.
Наибольший общий делитель
Определение. Наибольшим общим делителем чисел a и b a и b делятся без остатка.
Чтобы хорошо понять это определение, подставим вместо переменных a и b любые два числа, например, вместо переменной a подставим число 12, а вместо переменной b число 9. Теперь попробуем прочитать это определение:
Наибольшим общим делителем чисел 12 и 9 называется наибольшее число, на которое 12 и 9 делятся без остатка.
Из определения понятно, что речь идёт об общем делителе чисел 12 и 9, причем этот делитель является наибольшим из всех существующих делителей. Этот наибольший общий делитель (НОД) нужно найти.
Для нахождения наибольшего общего делителя двух чисел, используется три способа. Первый способ довольно трудоёмкий, но зато позволяет хорошо понять суть темы и прочувствовать весь ее смысл.
Второй и третий способы довольны просты и дают возможность быстро найти НОД. Мы с вами рассмотрим все три способа. А какой применять на практике — выбирать вам.
Первый способ заключается в поиске всех возможных делителей двух чисел и в выборе наибольшего из них. Рассмотрим этот способ на следующем примере: найти наибольший общий делитель чисел 12 и 9 .
Рассмотрим этот способ на следующем примере: найти наибольший общий делитель чисел 12 и 9 .
Сначала найдём все возможные делители числа 12. Для этого разделим 12 на все делители в диапазоне от 1 до 12. Если делитель позволит разделить 12 без остатка, то мы будем выделять его синим цветом и в скобках делать соответствующее пояснение.
12: 1 = 12
(12 разделилось на 1 без остатка, значит 1 является делителем числа 12)
12: 2 = 6
(12 разделилось на 2 без остатка, значит 2 является делителем числа 12)
12: 3 = 4
(12 разделилось на 3 без остатка, значит 3 является делителем числа 12)
12: 4 = 3
(12 разделилось на 4 без остатка, значит 4 является делителем числа 12)
12: 5 = 2 (2 в остатке)
(12 не разделилось на 5 без остатка, значит 5 не является делителем числа 12)
12: 6 = 2
(12 разделилось на 6 без остатка, значит 6 является делителем числа 12)
12: 7 = 1 (5 в остатке)
(12 не разделилось на 7 без остатка, значит 7 не является делителем числа 12)
12: 8 = 1 (4 в остатке)
(12 не разделилось на 8 без остатка, значит 8 не является делителем числа 12)
12: 9 = 1 (3 в остатке)
(12 не разделилось на 9 без остатка, значит 9 не является делителем числа 12)
12: 10 = 1 (2 в остатке)
(12 не разделилось на 10 без остатка, значит 10 не является делителем числа 12)
12: 11 = 1 (1 в остатке)
(12 не разделилось на 11 без остатка, значит 11 не является делителем числа 12)
12: 12 = 1
(12 разделилось на 12 без остатка, значит 12 является делителем числа 12)
Теперь найдём делители числа 9. Для этого проверим все делители от 1 до 9
Для этого проверим все делители от 1 до 9
9: 1 = 9
(9 разделилось на 1 без остатка, значит 1 является делителем числа 9)
9: 2 = 4 (1 в остатке)
(9 не разделилось на 2 без остатка, значит 2 не является делителем числа 9)
9: 3 = 3
(9 разделилось на 3 без остатка, значит 3 является делителем числа 9)
9: 4 = 2 (1 в остатке)
(9 не разделилось на 4 без остатка, значит 4 не является делителем числа 9)
9: 5 = 1 (4 в остатке)
(9 не разделилось на 5 без остатка, значит 5 не является делителем числа 9)
9: 6 = 1 (3 в остатке)
(9 не разделилось на 6 без остатка, значит 6 не является делителем числа 9)
9: 7 = 1 (2 в остатке)
(9 не разделилось на 7 без остатка, значит 7 не является делителем числа 9)
9: 8 = 1 (1 в остатке)
(9 не разделилось на 8 без остатка, значит 8 не является делителем числа 9)
9: 9 = 1
(9 разделилось на 9 без остатка, значит 9 является делителем числа 9)
Теперь выпишем делители обоих чисел. Числа выделенные синим цветом и являются делителями. Их и выпишем:
Числа выделенные синим цветом и являются делителями. Их и выпишем:
Выписав делители, можно сразу определить, какой является наибольшим и общим.
Согласно определению, наибольшим общим делителем чисел 12 и 9, является число, на которое 12 и 9 делятся без остатка. Наибольшим и общим делителем чисел 12 и 9 является число 3
И число 12 и число 9 делятся на 3 без остатка:
Значит НОД (12 и 9) = 3
Второй способ нахождения НОД
Теперь рассмотрим второй способ нахождения наибольшего общего делителя. Суть данного способа заключается в том, чтобы разложить оба числа на простые множители и перемножить общие из них.
Пример 1 . Найти НОД чисел 24 и 18
Сначала разложим оба числа на простые множители:
Теперь перемножим их общие множители. Чтобы не запутаться, общие множители можно подчеркнуть.
Смотрим на разложение числа 24. Первый его множитель это 2. Ищем такой же множитель в разложении числа 18 и видим, что он там тоже есть. Подчеркиваем обе двойки:
Подчеркиваем обе двойки:
Снова смотрим на разложение числа 24. Второй его множитель тоже 2. Ищем такой же множитель в разложении числа 18 и видим, что его там второй раз уже нет. Тогда ничего не подчёркиваем.
Следующая двойка в разложении числа 24 также отсутствует в разложении числа 18.
Переходим к последнему множителю в разложении числа 24. Это множитель 3. Ищем такой же множитель в разложении числа 18 и видим, что там он тоже есть. Подчеркиваем обе тройки:
Итак, общими множителями чисел 24 и 18 являются множители 2 и 3. Чтобы получить НОД, эти множители необходимо перемножить:
Значит НОД (24 и 18) = 6
Третий способ нахождения НОД
Теперь рассмотрим третий способ нахождения наибольшего общего делителя. Суть данного способа заключается в том, что числа подлежащие поиску наибольшего общего делителя раскладывают на простые множители. Затем из разложения первого числа вычеркивают множители, которые не входят в разложение второго числа. Оставшиеся числа в первом разложении перемножают и получают НОД.
Оставшиеся числа в первом разложении перемножают и получают НОД.
Например, найдём НОД для чисел 28 и 16 этим способом. В первую очередь, раскладываем эти числа на простые множители:
Получили два разложения: и
Теперь из разложения первого числа вычеркнем множители, которые не входят в разложение второго числа. В разложение второго числа не входит семерка. Её и вычеркнем из первого разложения:
Теперь перемножаем оставшиеся множители и получаем НОД:
Число 4 является наибольшим общим делителем чисел 28 и 16. Оба этих числа делятся на 4 без остатка:
Пример 2. Найти НОД чисел 100 и 40
Раскладываем на множители число 100
Раскладываем на множители число 40
Получили два разложения:
Теперь из разложения первого числа вычеркнем множители, которые не входят в разложение второго числа. В разложение второго числа не входит одна пятерка (там только одна пятёрка). Её и вычеркнем из первого разложения
Перемножим оставшиеся числа:
Получили ответ 20.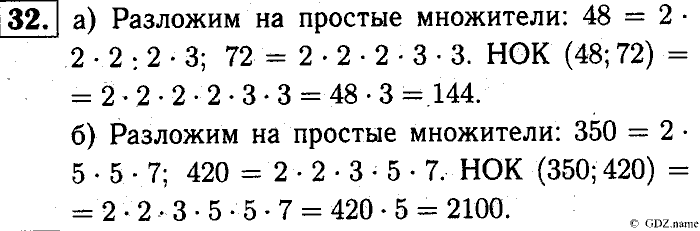 Значит число 20 является наибольшим общим делителем чисел 100 и 40. Эти два числа делятся на 20 без остатка:
Значит число 20 является наибольшим общим делителем чисел 100 и 40. Эти два числа делятся на 20 без остатка:
НОД (100 и 40) = 20.
Пример 3. Найти НОД чисел 72 и 128
Раскладываем на множители число 72
Раскладываем на множители число 128
2 × 2 × 2 × 2 × 2 × 2 × 2
Теперь из разложения первого числа вычеркнем множители, которые не входят в разложение второго числа. В разложение второго числа не входят две тройки (там их вообще нет). Их и вычеркнем из первого разложения:
Получили ответ 8. Значит число 8 является наибольшим общим делителем чисел 72 и 128. Эти два числа делятся на 8 без остатка:
НОД (72 и 128) = 8
Нахождение НОД для нескольких чисел
Наибольший общий делитель можно находить и для нескольких чисел, а не только для двух. Для этого числа, подлежащие поиску наибольшего общего делителя, раскладывают на простые множители, затем находят произведение общих простых множителей этих чисел.
Например, найдём НОД для чисел 18, 24 и 36
Разложим на множители число 18
Разложим на множители число 24
Разложим на множители число 36
Получили три разложения:
Теперь выделим и подчеркнём общие множители в этих числах. Общие множители должны входить во все три числа:
Общие множители должны входить во все три числа:
Мы видим, что общие множители для чисел 18, 24 и 36 это множители 2 и 3. Перемножив эти множители, мы получим НОД, который ищем:
Получили ответ 6. Значит число 6 является наибольшим общим делителем чисел 18, 24 и 36. Эти три числа делятся на 6 без остатка:
НОД (18, 24 и 36) = 6
Пример 2. Найти НОД для чисел 12, 24, 36 и 42
Разложим на простые множители каждое число. Затем найдём произведение общих множителей этих чисел.
Разложим на множители число 12
Разложим на множители число 42
Получили четыре разложения:
Теперь выделим и подчеркнём общие множители в этих числах. Общие множители должны входить во все четыре числа:
Мы видим, что общие множители для чисел 12, 24, 36, и 42 это множители 2 и 3. Перемножив эти множители, мы получим НОД, который ищем:
Получили ответ 6. Значит число 6 является наибольшим общим делителем чисел 12, 24, 36 и 42. Эти числа делятся на 6 без остатка:
НОД (12, 24 , 36 и 42) = 6
Из предыдущего урока мы знаем, что если какое-то число без остатка разделилось на другое, его называют кратным этого числа.
Оказывается, кратное может быть общим у нескольких чисел. И сейчас нас будет интересовать кратное двух чисел, при этом оно должно быть максимально маленьким.
Определение. Наименьшее общее кратное (НОК) чисел a и b — a и b a и число b .
Определение содержит две переменные a и b . Давайте подставим вместо этих переменных любые два числа. Например, вместо переменной a подставим число 9, а вместо переменной b подставим число 12. Теперь попробуем прочитать определение:
Наименьшее общее кратное (НОК) чисел 9 и 12 — это наименьшее число, которое кратно 9 и 12 . Другими словами, это такое маленькое число, которое делится без остатка на число 9 и на число 12 .
Из определения понятно, что НОК это наименьшее число, которое делится без остатка на 9 и на 12. Этот НОК требуется найти.
Для нахождения наименьшего общего кратного (НОК) можно пользоваться двумя способами. Первый способ заключается в том, что можно выписать первые кратные двух чисел, а затем выбрать среди этих кратных такое число, которое будет общим для обоих чисел и маленьким. Давайте применим этот способ.
Первый способ заключается в том, что можно выписать первые кратные двух чисел, а затем выбрать среди этих кратных такое число, которое будет общим для обоих чисел и маленьким. Давайте применим этот способ.
В первую очередь, найдем первые кратные для числа 9. Чтобы найти кратные для 9, нужно эту девятку поочерёдно умножить на числа от 1 до 9. Получаемые ответы будут кратными для числа 9. Итак, начнём. Кратные будем выделять красным цветом:
Теперь находим кратные для числа 12. Для этого, поочерёдно умножаем 12 на все числа 1 до 12.
Рассмотрим решение следующей задачи. Шаг мальчика составляет 75 см, а шаг девочки 60 см. Необходимо найти наименьшее расстояние, на котором они оба сделают по целому числу шагов.
Решение. Весь путь который пройдут ребята, должен делиться без остатка на 60 и на 70, так как они должны сделать каждый целое число шагов. Другими словами, в ответе должно быть число, кратное как 75 так и 60.
Сначала будем выписывать все кратные числа, для числа 75. Получаем:
Получаем:
- 75, 150, 225, 300, 375, 450, 525, 600, 675, … .
Теперь выпишем числа, которые будут кратны 60. Получаем:
- 60, 120, 180, 240, 300, 360, 420, 480, 540, 600, 660, … .
Теперь находим числа которые есть в обоих рядах.
- Общими кратными чисел будут числа, 300, 600, и т.д.
Самое наименьшее из них, это число 300. Оно в данном случае будет называться наименьшим общим кратным чисел 75 и 60.
Возвращаясь к условию задачи, наименьшее расстояние, на котором ребята сделают целое число шагов будет 300 см. Мальчик пройдет этот путь за 4 шага, а девочке потребуется сделать 5 шагов.
Определение наименьшего общего кратного
- Наименьшим общим кратным двух натуральных чисел a и b называется наименьшее натуральное число, которое кратно как a, так и b.
Для того, чтобы найти наименьшее общее кратное двух чисел, не обязательно выписывть подряд все кратные для этих чисел.
Можно воспользоваться следующим методом.
Как найти наименьшее общее кратное
Сначала необходимо разложить данные числа на простые множители.
- 60 = 2*2*3*5,
- 75=3*5*5.
Теперь выпишем все множители которые есть в разложении первого числа (2,2,3,5) и добавим к нему все недостающие множители из разложения второго числа (5).
Получим в итоге ряд простых чисел: 2,2,3,5,5. Произведение этих чисел и будет наименьшим общим сомножителем для данных чисел. 2*2*3*5*5 = 300.
Общая схема нахождения наименьшего общего кратного
- 1. Разложить числа на простые множители.
- 2. Выписать простые множители которые входят в состав одного из них.
- 3. Добавить к этим множителям все те, которые есть в разложении остальных, но нет в выбранном.
- 4. Найти произведение всех выписанных сомножителей.
Данный способ универсален. С его помощью можно найти наименьшее общее кратное любого количества натуральных чисел.
Онлайн калькулятор позволяет быстро находить наибольший общий делитель и наименьшее общее кратное как для двух, так и для любого другого количества чисел.
Калькулятор для нахождения НОД и НОК
Найти НОД и НОК
Найдено НОД и НОК: 6433
Как пользоваться калькулятором
- Введите числа в поле для ввода
- В случае ввода некорректных символов поле для ввода будет подсвечено красным
- нажмите кнопку «Найти НОД и НОК»
Как вводить числа
- Числа вводятся через пробел, точку или запятую
- Длина вводимых чисел не ограничена , так что найти НОД и НОК длинных чисел не составит никакого труда
Что такое НОД и НОК?
Наибольший общий делитель нескольких чисел – это наибольшее натуральное целое число, на которое все исходные числа делятся без остатка. Наибольший общий делитель сокращённо записывается как НОД .
Наименьшее общее кратное нескольких чисел – это наименьшее число, которое делится на каждое из исходных чисел без остатка. Наименьшее общее кратное сокращённо записывается как НОК .
Как проверить, что число делится на другое число без остатка?
Чтобы узнать, делится ли одно число на другое без остатка, можно воспользоваться некоторыми свойствами делимости чисел. Тогда, комбинируя их, можно проверять делимость на некоторые их них и их комбинации.
Тогда, комбинируя их, можно проверять делимость на некоторые их них и их комбинации.
Некоторые признаки делимости чисел
1. Признак делимости числа на 2
Чтобы определить, делится ли число на два (является ли оно чётным), достаточно посмотреть на последнююю цифру этого числа: если она равна 0, 2, 4, 6 или 8, то число чётно, а значит делится на 2.
Пример: определить, делится ли на 2 число 34938 .
Решение: смотрим на последнюю цифру: 8 — значит число делится на два.
2. Признак делимости числа на 3
Число делится на 3 тогда, когда сумма его цифр делится на три. Таким образом, чтобы определить, делится ли число на 3, нужно посчитать сумму цифр и проверить, делится ли она на 3. Даже если сумма цифр получилась очень большой, можно повторить этот же процесс вновь.
Пример: определить, делится ли число 34938 на 3.
Решение: считаем сумму цифр: 3+4+9+3+8 = 27. 27 делится на 3, а значит и число делится на три.
3. Признак делимости числа на 5
Число делится на 5 тогда, когда его последняя цифра равна нулю или пяти.
Пример: определить, делится ли число 34938 на 5.
Решение: смотрим на последнюю цифру: 8 — значит число НЕ делится на пять.
4. Признак делимости числа на 9
Этот признак очень похож на признак делимости на тройку: число делится на 9 тогда, когда сумма его цифр делится на 9.
Пример: определить, делится ли число 34938 на 9.
Решение: считаем сумму цифр: 3+4+9+3+8 = 27. 27 делится на 9, а значит и число делится на девять.
Как найти НОД и НОК двух чисел
Как найти НОД двух чисел
Наиболее простым способом вычисления наибольшего общего делителя двух чисел является поиск всех возможных делителей этих чисел и выбор наибольшего из них.
Рассмотрим этот способ на примере нахождения НОД(28, 36) :
- Раскладываем оба числа на множители: 28 = 1·2·2·7 , 36 = 1·2·2·3·3
- Находим общие множители, то есть те, которые есть у обоих чисел: 1, 2 и 2.

- Вычисляем произведение этих множителей: 1·2·2 = 4 — это и есть наибольший общий делитель чисел 28 и 36.
Как найти НОК двух чисел
Наиболее распространены два способа нахождения наименьшего кратного двух чисел. Первый способ заключается в том, что можно выписать первые кратные двух чисел, а затем выбрать среди них такое число, которое будет общим для обоих чисел и при этом наименьшем. А второй заключается в нахождении НОД этих чисел. Рассмотрим только его.
Для вычисления НОК нужно вычислить произведение исходных чисел и затем разделить его на предварительно найденный НОД. Найдём НОК для тех же чисел 28 и 36:
- Находим произведение чисел 28 и 36: 28·36 = 1008
- НОД(28, 36), как уже известно, равен 4
- НОК(28, 36) = 1008 / 4 = 252 .
Нахождение НОД и НОК для нескольких чисел
Наибольший общий делитель можно находить и для нескольких чисел, а не только для двух. Для этого числа, подлежащие поиску наибольшего общего делителя, раскладывают на простые множители, затем находят произведение общих простых множителей этих чисел.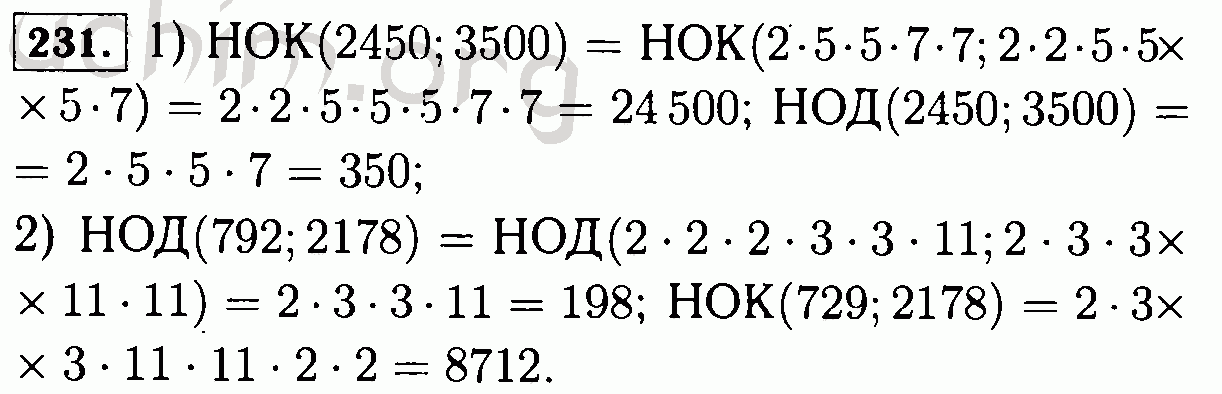 Также для нахождение НОД нескольких чисел можно воспользоваться следующим соотношением: НОД(a, b, c) = НОД(НОД(a, b), c) .
Также для нахождение НОД нескольких чисел можно воспользоваться следующим соотношением: НОД(a, b, c) = НОД(НОД(a, b), c) .
Аналогичное соотношение действует и для наименьшего общего кратного чисел: НОК(a, b, c) = НОК(НОК(a, b), c)
Пример: найти НОД и НОК для чисел 12, 32 и 36.
- Cперва разложим числа на множители: 12 = 1·2·2·3 , 32 = 1·2·2·2·2·2 , 36 = 1·2·2·3·3 .
- Найдём обшие множители: 1, 2 и 2 .
- Их произведение даст НОД: 1·2·2 = 4
- Найдём теперь НОК: для этого найдём сначала НОК(12, 32): 12·32 / 4 = 96 .
- Чтобы найти НОК всех трёх чисел, нужно найти НОД(96, 36): 96 = 1·2·2·2·2·2·3 , 36 = 1·2·2·3·3 , НОД = 1·2·2·3 = 12 .
- НОК(12, 32, 36) = 96·36 / 12 = 288 .
Представленный ниже материал является логическим продолжением теории из статьи под заголовком НОК — наименьшее общее кратное, определение, примеры, связь между НОК и НОД . Здесь мы поговорим про нахождение наименьшего общего кратного (НОК) , и особое внимание уделим решению примеров. Сначала покажем, как вычисляется НОК двух чисел через НОД этих чисел. Дальше рассмотрим нахождение наименьшего общего кратного с помощью разложения чисел на простые множители. После этого остановимся на нахождении НОК трех и большего количества чисел, а также уделим внимание вычислению НОК отрицательных чисел.
Сначала покажем, как вычисляется НОК двух чисел через НОД этих чисел. Дальше рассмотрим нахождение наименьшего общего кратного с помощью разложения чисел на простые множители. После этого остановимся на нахождении НОК трех и большего количества чисел, а также уделим внимание вычислению НОК отрицательных чисел.
Навигация по странице.
Вычисление наименьшего общего кратного (НОК) через НОД
Один из способов нахождения наименьшего общего кратного основан на связи между НОК и НОД . Существующая связь между НОК и НОД позволяет вычислять наименьшее общее кратное двух целых положительных чисел через известный наибольший общий делитель. Соответствующая формула имеет вид НОК(a, b)=a·b:НОД(a, b) . Рассмотрим примеры нахождения НОК по приведенной формуле.
Пример.
Найдите наименьшее общее кратное двух чисел 126 и 70 .
Решение.
В этом примере a=126
, b=70
. Воспользуемся связью НОК с НОД, выражающуюся формулой НОК(a, b)=a·b:НОД(a, b)
. То есть, сначала нам предстоит найти наибольший общий делитель чисел 70
и 126
, после чего мы сможем вычислить НОК этих чисел по записанной формуле.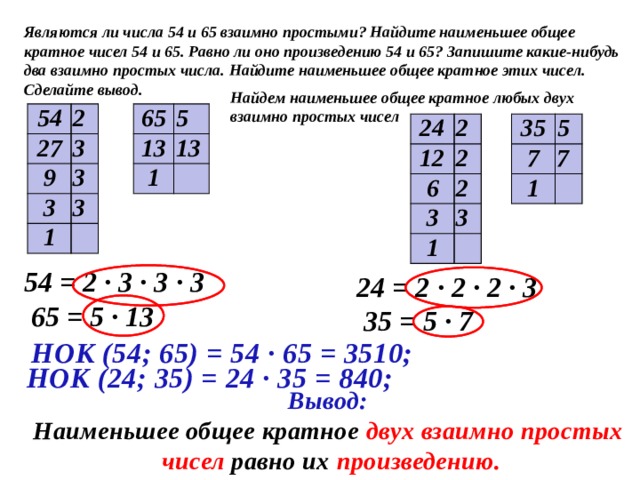
Найдем НОД(126, 70) , используя алгоритм Евклида: 126=70·1+56 , 70=56·1+14 , 56=14·4 , следовательно, НОД(126, 70)=14 .
Теперь находим требуемое наименьшее общее кратное: НОК(126, 70)=126·70:НОД(126, 70)= 126·70:14=630 .
Ответ:
НОК(126, 70)=630 .
Пример.
Чему равно НОК(68, 34) ?
Решение.
Так как 68 делится нацело на 34 , то НОД(68, 34)=34 . Теперь вычисляем наименьшее общее кратное: НОК(68, 34)=68·34:НОД(68, 34)= 68·34:34=68 .
Ответ:
НОК(68, 34)=68 .
Заметим, что предыдущий пример подходит под следующее правило нахождения НОК для целых положительные чисел a и b : если число a делится на b , то наименьшее общее кратное этих чисел равно a .
Нахождение НОК с помощью разложения чисел на простые множители
Другой способ нахождения наименьшего общего кратного базируется на разложении чисел на простые множители . Если составить произведение из всех простых множителей данных чисел, после чего из этого произведения исключить все общие простые множители, присутствующие в разложениях данных чисел, то полученное произведение будет равно наименьшему общему кратному данных чисел
.
Озвученное правило нахождения НОК следует из равенства НОК(a, b)=a·b:НОД(a, b) . Действительно, произведение чисел a и b равно произведению всех множителей, участвующих в разложениях чисел a и b . В свою очередь НОД(a, b) равен произведению всех простых множителей, одновременно присутствующих в разложениях чисел a и b (о чем написано в разделе нахождение НОД с помощью разложения чисел на простые множители).
Приведем пример. Пусть мы знаем, что 75=3·5·5 и 210=2·3·5·7 . Составим произведение из всех множителей данных разложений: 2·3·3·5·5·5·7 . Теперь из этого произведения исключим все множители, присутствующие и в разложении числа 75 и в разложении числа 210 (такими множителями являются 3 и 5 ), тогда произведение примет вид 2·3·5·5·7 . Значение этого произведения равно наименьшему общему кратному чисел 75 и 210 , то есть, НОК(75, 210)= 2·3·5·5·7=1 050 .
Пример.
Разложив числа 441
и 700
на простые множители, найдите наименьшее общее кратное этих чисел.
Решение.
Разложим числа 441 и 700 на простые множители:
Получаем 441=3·3·7·7 и 700=2·2·5·5·7 .
Теперь составим произведение из всех множителей, участвующих в разложениях данных чисел: 2·2·3·3·5·5·7·7·7 . Исключим из этого произведения все множители, одновременно присутствующие в обоих разложениях (такой множитель только один – это число 7 ): 2·2·3·3·5·5·7·7 . Таким образом, НОК(441, 700)=2·2·3·3·5·5·7·7=44 100 .
Ответ:
НОК(441, 700)= 44 100 .
Правило нахождения НОК с использованием разложения чисел на простые множители можно сформулировать немного иначе. Если ко множителям из разложения числа a добавить недостающие множители из разложения числа b , то значение полученного произведения будет равно наименьшему общему кратному чисел a и b .
Для примера возьмем все те же числа 75
и 210
, их разложения на простые множители таковы: 75=3·5·5
и 210=2·3·5·7
. Ко множителям 3
, 5
и 5
из разложения числа 75
добавляем недостающие множители 2
и 7
из разложения числа 210
, получаем произведение 2·3·5·5·7
, значение которого равно НОК(75, 210)
.
Пример.
Найдите наименьшее общее кратное чисел 84 и 648 .
Решение.
Получаем сначала разложения чисел 84 и 648 на простые множители. Они имеют вид 84=2·2·3·7 и 648=2·2·2·3·3·3·3 . К множителям 2 , 2 , 3 и 7 из разложения числа 84 добавляем недостающие множители 2 , 3 , 3 и 3 из разложения числа 648 , получаем произведение 2·2·2·3·3·3·3·7 , которое равно 4 536 . Таким образом, искомое наименьшее общее кратное чисел 84 и 648 равно 4 536 .
Ответ:
НОК(84, 648)=4 536 .
Нахождение НОК трех и большего количества чисел
Наименьшее общее кратное трех и большего количества чисел может быть найдено через последовательное нахождение НОК двух чисел. Напомним соответствующую теорему, дающую способ нахождения НОК трех и большего количества чисел.
Теорема.
Пусть даны целые положительные числа a 1 , a 2 , …, a k
, наименьшее общее кратное m k
этих чисел находится при последовательном вычислении m 2 =НОК(a 1 , a 2)
, m 3 =НОК(m 2 , a 3)
, …, m k =НОК(m k−1 , a k)
.
Рассмотрим применение этой теоремы на примере нахождения наименьшего общего кратного четырех чисел.
Пример.
Найдите НОК четырех чисел 140 , 9 , 54 и 250 .
Решение.
В этом примере a 1 =140 , a 2 =9 , a 3 =54 , a 4 =250 .
Сначала находим m 2 =НОК(a 1 , a 2)=НОК(140, 9) . Для этого по алгоритму Евклида определяем НОД(140, 9) , имеем 140=9·15+5 , 9=5·1+4 , 5=4·1+1 , 4=1·4 , следовательно, НОД(140, 9)=1 , откуда НОК(140, 9)=140·9:НОД(140, 9)= 140·9:1=1 260 . То есть, m 2 =1 260 .
Теперь находим m 3 =НОК(m 2 , a 3)=НОК(1 260, 54) . Вычислим его через НОД(1 260, 54) , который также определим по алгоритму Евклида: 1 260=54·23+18 , 54=18·3 . Тогда НОД(1 260, 54)=18 , откуда НОК(1 260, 54)= 1 260·54:НОД(1 260, 54)= 1 260·54:18=3 780 . То есть, m 3 =3 780 .
Осталось найти m 4 =НОК(m 3 , a 4)=НОК(3 780, 250)
. Для этого находим НОД(3 780, 250)
по алгоритму Евклида: 3 780=250·15+30
, 250=30·8+10
, 30=10·3
. Следовательно, НОД(3 780, 250)=10
, откуда НОК(3 780, 250)=
3 780·250:НОД(3 780, 250)=
3 780·250:10=94 500
.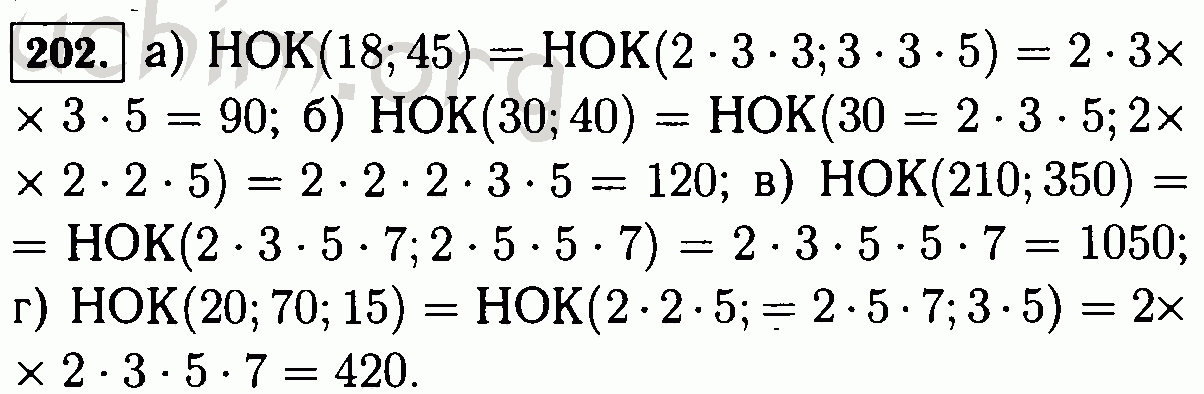 То есть, m 4 =94 500
.
То есть, m 4 =94 500
.
Таким образом, наименьшее общее кратное исходных четырех чисел равно 94 500 .
Ответ:
НОК(140, 9, 54, 250)=94 500 .
Во многих случаях наименьшее общее кратное трех и большего количества чисел удобно находить с использованием разложений данных чисел на простые множители. При этом следует придерживаться следующего правила. Наименьшее общее кратное нескольких чисел равно произведению, которое составляется так: ко всем множителям из разложения первого числа добавляются недостающие множители из разложения второго числа, к полученным множителям добавляются недостающие множители из разложения третьего числа и так далее .
Рассмотрим пример нахождения наименьшего общего кратного с использованием разложения чисел на простые множители.
Пример.
Найдите наименьшее общее кратное пяти чисел 84 , 6 , 48 , 7 , 143 .
Решение.
Сначала получаем разложения данных чисел на простые множители: 84=2·2·3·7
, 6=2·3
, 48=2·2·2·2·3
, 7
(7
– простое число , оно совпадает со своим разложением на простые множители) и 143=11·13
.
Для нахождения НОК данных чисел к множителям первого числа 84 (ими являются 2 , 2 , 3 и 7 ) нужно добавить недостающие множители из разложения второго числа 6 . Разложение числа 6 не содержит недостающих множителей, так как и 2 и 3 уже присутствуют в разложении первого числа 84 . Дальше к множителям 2 , 2 , 3 и 7 добавляем недостающие множители 2 и 2 из разложения третьего числа 48 , получаем набор множителей 2 , 2 , 2 , 2 , 3 и 7 . К этому набору на следующем шаге не придется добавлять множителей, так как 7 уже содержится в нем. Наконец, к множителям 2 , 2 , 2 , 2 , 3 и 7 добавляем недостающие множители 11 и 13 из разложения числа 143 . Получаем произведение 2·2·2·2·3·7·11·13 , которое равно 48 048 .
Презентация по математике на тему Наименьшее общее кратное (1 урок). (5 класс) доклад, проект
48 см
40 см
?
?
НОД чисел 48 и 40 — длина стороны квадрата
Проверка домашнего задания:
Лист картона имеет форму прямоугольника, длина которого 48 см, а ширина 40 см. Этот лист надо разрезать без отходов на равные квадраты. Какие наибольшие квадраты можно получить из этого листа? Сколько таких квадратов получится?
Этот лист надо разрезать без отходов на равные квадраты. Какие наибольшие квадраты можно получить из этого листа? Сколько таких квадратов получится?
НОД (48, 40) = 8,
значит, квадраты будут со стороной 8 см.
48 ∙ 40 = 1920 (см2) – площадь прямоугольника.
8 ∙ 8 = 64 (см²) — площадь квадрата,
1920 : 64 = 30 (квадратов)
Ответ: квадраты со стороной 8 см; 30 квадратов.
Слово «крат» — старинное русское слово (XI век), означающее «раз». Слова «многократно» означает «много раз».
Понятием кратного пользуются в жизненной практике при установлении вида года. Через каждые три обыкновенных года, в каждом из которых по 365 дней (в феврале 28 дней), бывает четвертый год, так называемый високосный, в котором 366 дней (в феврале 29 дней).
Если число, которым выражается указанный год, есть число, кратное 4, то указанный год високосный, а если не кратно 4, то год обыкновенный. Так, 2008 год — високосный, так как 2008 кратно 4, 2007 — не високосный, так как 2007 не кратно 4.
Историческая минутка.
Сколько кратных может иметь натуральное число?
Есть ли среди них наибольшее?
Наименьшее?
Сколько кратных может быть у нескольких чисел?
Могут ли среди них быть общие кратные? Наибольшие? Наименьшие?
Предположите тему урока.
Дайте определение кратному числа. Назовите несколько кратных числу 12, числу 60, числу р.
К 12: 12, 24, 36, 48, 60, 72…
К 60: 60,120,180,240, 300,360…
К р: р, 2р, 3р, 4р, 5р…
Наименьшее
общее кратное.
От одной пристани до другой ходят два катера. Начинают работу одновременно в 8 ч утра. Первый катер на рейс туда и обратно тратит 2 часа, а второй – 3 часа. Через какое наименьшее время оба катера окажутся на первой пристани и сколько рейсов за это время сделает каждый катер?
Задача.
— кратные 2
— кратные 3
: 2, 4, 6, 8, 10, 12, 14, 16, 18…
: 3, 6, 9, 12, 15, 18, 21…
Наименьшее общее кратное:
6
Через 6 часов после начала работы два катера
одновременно окажутся на первой пристани
1
2
6 : 2 = 3 (рейса)
— 1 катер
3
6 : 3 = 2 (рейса)
— 2 катер
Определение.
Наименьшим общим кратным натуральных чисел а и b называют наименьшее натуральное число, делящееся на каждое из чисел а и b.
Обозначение: НОК (2, 3) = 6.
1 способ удобен тогда, когда данные натуральные числа небольшие!
2 способ.
Алгоритм нахождения НОК:
Найдите наименьшее общее кратное чисел: 75 и 60.
75 = 3 ∙ 5∙ 5
60 = 2∙ 2∙ 3 ∙ 5
НОК (75, 60) = 3 ∙ 5 ∙ 5∙ 2∙ 2 = 75∙ 2 ∙ 2 = 300.
1. Разложить все числа на простые множители.
2. Написать разложение одного из чисел (лучше наибольшего).
3. Дополнить данное разложение теми множителями из разложения других чисел, которые не вошли в написанное разложение.
Задача. Шаг Володи 75 см, а шаг Кати 60 см. На каком наименьшем расстоянии они сделают по целому числу шагов?
1)НОК (а, b) = 2 ∙ 2 ∙ 5 ∙ 5 ∙ 11 ∙ 3 = 3300;
2) НОК (а, b) = 2 ∙ 2 ∙ 5 ∙ 5 ∙ 7 = 700
Так как b делится на а, то НОК будет само число b;
Найдите наименьшее общее кратное чисел:
396 и 180;
НОК (396, 180) = 2 ∙ 2 ∙ 3 ∙ 3 ∙ 11 ∙ 5 = 1980;
396 = 2 ∙ 2 ∙ 3 ∙ 3 · 11; 180 = 2 ∙ 2 ∙ 3 ∙ 3 · 5
168, 231 и 60.
Найдите наименьшее общее кратное чисел:
НОК (168, 231, 60) = 2 ∙ 2 ∙ 2 ∙ 3 · 7 · 11 ∙ 5 = 9240
168 = 2 ∙ 2 ∙ 2 ∙ 3 · 7; 231 = 3 · 7 ∙ 11; 60 = 2 ∙ 2 ∙ 3 ∙ 5
НОК (35, 12) =
?
35
12
= 5 · 7
= 2 · 2 · 3
НОК (35, 12) =
12 · 35
= 420
НОК (45,180) =
?
45
180
= 3 · 3 · 5
= 2 · 2 · 3 · 3 · 5
НОК (45,180) =
180
НОК (72, 99) =
?
72
99
= 2 · 2 · 2 · 3 · 3
= 3 · 3 · 11
НОК (72, 99) =
99 · 2 · 2 · 2
= 792
НОК (210,350) =
?
210
350
= 2 · 3 · 5 · 7
= 2 · 5 · 5 · 7
НОК (210,350) =
= 1050
350 · 3
Разложим числа 35 и 40 на простые множители.
35=5∙7, 40=2∙2∙2∙5 или 40=23∙5
Берем разложение большего числа 40 и дополняем его недостающими множителями.
НОК(35, 40)=23∙5∙7=40∙7=280.
НОК(35, 40)=280
Найти НОК(35, 40).
Раскладываем числа 45 и 54 на простые множители.
45=32∙5, 54=2∙33.
Берем разложение числа 54 и умножаем на недостающие множители из разложения числа 45, т. е. на число 5.
НОК(45, 54)=2∙33∙5=54∙5=270.
Ответ: НОК(45,54)=270.
Найти НОК(45, 54).
Разложим числа 75, 120 и 150 на простые множители.
75=3∙52, 120=23∙3∙5, 150=2∙3∙52
Возьмем разложение большего числа 150 и дополним его двумя «двойками», так как в разложении числа 120 имеется три «двойки», а в разложении числа 150 – только одна.
НОК(75, 120, 150) =
=2∙3∙52∙2∙2=150∙4=600.
Ответ: НОК(75, 120, 150)=600.
Найти НОК(75, 120, 150).
Физкультминутка
Раз, два, три, четыре, пять!
Все мы умеем считать,
Отдыхать умеем тоже.
Руки за спину положим,
Голову поднимем выше
И легко-легко подышим.
Подтянитесь на носочках столько раз
Сколько пальцев на руках у вас!
№ 682 (а, д, в),№ 683 а,в,д, № 687 (1столбик)
Работа по учебнику
Рабочая тетрадь
Был ли он для вас познавательным?
— Что нового вы узнали?
— Что удалось?
— Над чем надо ещё поработать?
— Как вы оцениваете свою работу сегодня на уроке?
Рефлексия
Домашнее задание:
П.3.6. читать,
О.У. № 682 б,г,е, 683 б,г,е, 687(2 столбик)
П. У. В портовом городе начинаются три туристских теплоходных рейса, первый из которых длится 15 суток, второй 20 суток и третий 12 суток. Вернувшись в порт, теплоходы в этот же день снова отправляются в рейс. Сегодня из порта вышли теплоходы по всем трем маршрутам. Через сколько суток они впервые снова вместе уйдут в плавание?
У. В портовом городе начинаются три туристских теплоходных рейса, первый из которых длится 15 суток, второй 20 суток и третий 12 суток. Вернувшись в порт, теплоходы в этот же день снова отправляются в рейс. Сегодня из порта вышли теплоходы по всем трем маршрутам. Через сколько суток они впервые снова вместе уйдут в плавание?
Наибольший общий делитель и наименьшее общее кратное
Открытый урок
Учителя математики : Ситниковой О.В.
по теме : «НОД и НОК чисел»
Учебник Г.В.Дорофеев , Л.Г.Петерсон «Математика , 5»
Тип урока: комбинированный .
Цели: формировать умение находить НОД и НОК чисел разными способами; находить значение выражений, содержащих степени; повторить и закрепить признаки делимости; простые и составные числа .
Образовательные цели: отработка навыков нахождения НОД и НОК чисел разными способами и выбор наиболее удобного способа; применение полученных знаний для решения задач .
Развивающие цели: развивать познавательный интерес к предмету; наблюдательность, внимание; формировать потребность приобретения знаний .
Воспитательные цели: воспитывать у учащихся культуру труда, взаимоуважение, стремление хорошо учиться.
Задачи: 1) обобщить и систематизировать знания учащихся по теме: «НОД и НОК чисел.»;
2) коррекция мыслительных процессов на основе выполненных упражнений;
3) развивать внимание, память, речь, интерес к математике.
Оборудование: компьютер, проектор, экран, доска, раздаточный материал.
Ход урока .
Организационный момент .
Здравствуйте, ребята! Садитесь.
Давайте вспомним, чем мы занимались на предыдущих уроках?
(Мы находили НОД и НОК чисел разными способами и решали задачи )
Постановка задачи: Сегодня мы с вами обобщим все полученные знания по данной теме.
Откройте тетради, запишите число, классная работа, тема: «НОД и НОК чисел».
2. Устная работа .
И прежде чем начать решать, давайте вспомним некоторые правила.
Что называется наибольшим общим делителем чисел a и b?
( Наибольшим общим делителем чисел a и b — называется наибольшее натуральное число , которое делит числа a и b без остатка .)
Как найти НОД чисел? (1. разложить на простые множители ; 2. выписать общие множители; 3. перемножить их .)
А если нет общих множителей, чему равен НОД этих чисел?
( 1 ) Как называются эти числа ? ( взаимно – простыми )
Приведите пример взаимно-простых чисел
Что называется наименьшим общим кратным чисел a и b?
( Наименьшим общим делителем чисел a и b — называется наименьшее натуральное число, которое делиться на a и b без остатка. )
)
Как найти НОК чисел ?
( 1. разложить на простые множители; 2. выписать множители первого числа; 3. добавить недостающие множители из второго числа; 4. найти произведение получившихся множителей )
Мы говорили, что число нужно разложить на простые множители, а какие числа называются простыми? ( простыми называются числа, которые имеют только два делителя : 1 и само число )
Приведите примеры . 3 , 5 , 7 , 11 , 13 , 17 , 19 , 23 , 29 и т.д.
Какие числа называются составными? ( составными называются числа имеющие более двух делителей )
Приведите примеры . 9 , 25 , 100 и т.д.
А 1 – какое это число? ( ни простое, ни составное ) Почему?
3. Выполнение упражнений.
А теперь перейдем к выполнению упражнений.
( задание записано на доске )
№ 1. Найдите НОД и НОК чисел 8 и 12 методом перебора.
Найдите НОД и НОК чисел 8 и 12 методом перебора.
Решение: выпишем делители меньшего числа. Почему меньшего?
Д (8) = 1, 2, 4, 8 проверим являются ли эти числа делителями числа 12 ; проверяем с наибольших делителей .
12 не делится на 8 ; 12 делиться на 4
НОД ( 8 ; 12 ) = 4
Выпишем кратные большего числа. Почему большего ?
К (12) = 12 , 24 , 36 , 48 , 60 , … Проверим являются ли эти числа кратными 8. Начнем с наименьшего кратного .
12 не делиться на 8 ; 24 делиться на 8
НОК(8;12) = 24
Чему равно произведение НОД и НОК этих чисел ? 4 · 24 = 96
А чему равно произведение чисел a и b ? 8 · 12 = 96
Какой сделаем вывод : НОД(a ; b)·НОК(a ; b) = a · b .
№ 2. Найдите НОД и НОК чисел 252 и 264 методом разложения на простые множители .
Решение :
2 52 2 264 2 Признак делимости на 2 .
126 2 132 2 Признак делимости на 3.
63 3 66 2
21 3 33 3
7 7 11 11
1 1
252 = 2²·3²·7 264= 2³·3·11
НОД(252 ; 264) = 2²·3 = 12 С какими показателями мы берем степени ? с наименьшими .
НОК(252;264) = 2³·3²·7·11= 5544 С какими показателями мы берем степени ? с наибольшими .
4. Выполнение упражнений с самопроверкой по эталону .
Задание: Найдите НОД и НОК чисел наиболее удобным способом :
а) 12 и 40 ; б) 9 и 40 ; в) 12 и 72 .
На задание дается 5 мин?
Каким способом удобнее решать каждое упражнение?
Разбор по слайду .
а) Удобнее решать методом разложения на простые множители
12 = 2·2·3 ; 40 = 2·2·2·5
НОД(12;40)=2·2=4 ; НОК(12;40) = 2·2·2·3·5 = 120
б) есть ли общие делители у чисел 9 и 40 ? ( есть , 1.)
Как называются эти числа? ( взаимно простые .)
Чему равен НОД этих чисел? ( НОД(9;40) = 1)
Чему равен НОК этих чисел? ( НОК(9;40) = 9· 40=360.)
в) Что вы можете сказать о числах 12 и 72 ? ( 72 делиться на 12 ) Какое правило мы знаем? ( если одно число делится на другое , то НОД = наименьшему числу , а НОК — наибольшему )
НОД(12;72) = 12 ; НОК(12;72) = 72
Сверьте данные, которые у вас получились , с эталоном на вашем столе .
5 . Выполнение упражнения.
Задание: Выбрать истиные высказывания:
НОД ( 13, 39 ) = 39
16 – кратное 3
НОК ( 9,18) = 18
5 – кратное числа 6
7 – делитель числа 14
НОД (2; 15) = 1
Каждое число имеет делитель 1
НОК (2;3) = 6
Из предложенных верных ответов составить наибольшее натуральное число, кратное числу 5.
Ответ: верные 3,5,6,7,8. Наибольшее натуральное число, кратное 5 —
87635.
6. Физкультминутка
Поднимите руки класс – это «раз»
Повернулась голова – это «два»
Руки вниз, вперёд смотри – это «три»
Руки в стороны пошире развернули на «четыре»
Ссилой их к плечам прижать – это «пять»
Всем ребятам надо сесть – это «шесть»
7. Решение задач .
Где мы уже используем наши знания НОДа и НОКа чисел?
При решении задач .
У учащихся на столе раздаточный материал с задачами.
Задача № 1
Ребята получили на новогодней елке одинаковые подарки . Во всех подарках вместе было 123 апельсина и 82 яблока. Сколько ребят присутствовало на елке? Сколько апельсинов и сколько яблок получил каждый?
( необходимо найти НОД чисел 123 и 82
123 = 3· 41 ; 82= 2· 41 НОД(123 ; 82) = 41
Ответ : 41 ребят, по 3 апельсина и 2 яблока . )
)
Ребята, скоро новый год. Вы все хотели бы получить к празднику хорошие
подарки ?
А для того чтобы получить хорошие подарки, вы должны порадовать Деда Мороза и родителей своими знаниями и отличными оценками.
Задача №2
Из речного порта одновременно 1 мая 1999 года вышли два теплохода . Продолжительность рейса одного из них – 15 суток, а продолжительность рейса второго – 24 суток. Через сколько дней теплоходы снова одновременно отправятся в рейс? Сколько рейсов за это время сделает первый теплоход? А сколько второй?
Необходимо найти НОК чисел 15 и 24.
1) 15 = 3·5 ; 24 = 2· 2· 2· 3
НОК(15;24) = 2·2·2·3·5=120
2)120 : 15 = 8 (р) первый;
3)120 : 24=5(р) второй
Ответ : через 120 дней , первый сделает 8 рейсов , а второй – 5 рейсов .
Задача №3.
Расшифруйте название птицы, которая видит все, что происходит вокруг нее, даже не поворачивая головы.
Для этого найдите наименьшее общее кратное каждой пары чисел , затем впишите букву , соответствующую этому числу , в таблицу .
1) НОК(3,12) = 12 л 5) НОК(9;15) = 45 н
2) НОК(4;5;8)= ___40 е 6) НОК(12;10)= 60 п
3) НОК(8;12)= 24 в 7) НОК(9;6) = 18 ь
4) НОК(16;12)= 48 д 8) НОК(10;20)= 20 ш
Свободный столбик в таблице заполните, учитывая данные:
НОК(25;4) = 100 а
24 | 12 | 18 | 48 | 20 | 45 | 40 | 60 | |
в | а | л | ь | д | ш | н | е | п |
8. Самостоятельная работа.
Самостоятельная работа.
А теперь давайте проверим ваши знания с помощью самостоятельной работы. Возьмите на столе карточку и все записи делаем в ней.
Вариант 1. Вариант 2 .
Найдите НОД и НОК чисел наиболее удобным способом .
а) 12 и 18 ; а) 10 и 15 ;
б) 13 и 39 ; б) 19 и 57 ;
в) 11 и 15 ; в) 7 и 12 .
Решение :
Вариант1.
а) 12 =2·2·3 ; 18=2·3·3 ; НОД=6 НОК=36
б) т.к. 3 9 делится на 13 НОД = 13 НОК=39
в) 11 и 15 взаимно простые НОД=1 , НОК = 11 ·15 = 165
Вариант 2.
а) 10 = 2·5 ; 15 = 3·5 НОД =5 , НОК =30
б) т.к. 57 делится на 19 НОД=19 , НОК=57
в) 7 и 12 взаимно простые НОД = 1 , НОК=7·12=84
9. Подведение итогов урока.
Подведение итогов урока.
Сегодня мы повторили почти все правила по теме «Наибольший общий делитель и наименьшее общее кратное» и готовы написать контрольную работу. Надеюсь, вы с ней справитесь хорошо .
За урок получили оценки :
10. Домашнее задание .
Откройте дневники и запишите домашнее задание.
Повторить правила, выполнить № 801, № 802, № 803, № 807.
11. Заполнение карточки рефлексии .
А теперь заполните карточки рефлексии.
Карточка для этапа рефлексии.
Тема | Знаю | Умею |
Нахождение НОД методом перебора | ||
Нахождение НОК методом перебора | ||
Разложение на простые множители | ||
Нахождение НОД методом разложения на простые множители | ||
Нахождение НОК методом разложения на простые множители |
Карточка для этапа рефлексии.
Тема | Знаю | Умею |
Нахождение НОД методом перебора | ||
Нахождение НОК методом перебора | ||
Разложение на простые множители | ||
Нахождение НОД методом разложения на простые множители | ||
Нахождение НОК методом разложения на простые множители |
Карточка для этапа рефлексии.
Тема | Знаю | Умею |
Нахождение НОД методом перебора | ||
Нахождение НОК методом перебора | ||
Разложение на простые множители | ||
Нахождение НОД методом разложения на простые множители | ||
Нахождение НОК методом разложения на простые множители |
Карточка для этапа рефлексии.
Тема | Знаю | Умею |
Нахождение НОД методом перебора | ||
Нахождение НОК методом перебора | ||
Разложение на простые множители | ||
Нахождение НОД методом разложения на простые множители | ||
Нахождение НОК методом разложения на простые множители |
Эталон для самопроверки .
а) НОД(12 ;40)
1 2 2 40 2 1) Разложить числа на простые
6 2 20 2 множители.
3 3 10 2 2) Воспользоваться признаками
1 5 5 делимости на 2 , на 3 и на 5 .
1
12 = 2 · 2 · 3 ; 40 = 2 · 2 · 2 · 5
2 · 2 3) Выписать произведение
общих множителей.
НОД(12;40) = 4 4) Вычислить выписанное
произведение.
НОК (12;40)
2 · 2 · 3 · 2 · 5 5) Выписать множители
одного из чисел.
6) Домножить на недостающие
множители из разложения другого .
НОК(12;40)=120 7) Найти полученное
произведение.
б) Числа 9 и 40 взаимно простые .
НОД(9;40) = 1.
Чтобы найти их НОК надо их перемножить .
НОК(9;40 )= 9 · 40 = 360.
в) Так как 72 делиться на 12 , то
НОД(12;72)=12 ; НОК(12;72) = 72 .
Задача № 1.
Р ебята получили на новогодней ёлке одинаковые подарки. Во всех подарках вместе было 123 апельсина и 82 яблока. Сколько ребят присутствовало на ёлке ? Сколько апельсинов и сколько яблок получил каждый ?
Задача № 2.
Из речного порта одновременно 1 мая 2011 года вышли два теплохода. Продолжительность рейса одного из них – 15 суток , а продолжительность рейса второго – 24 суток. Через сколько дней теплоходы снова одновременно отправятся в рейс ? Сколько рейсов за это время сделает первый теплоход ? А сколько второй ?
Через сколько дней теплоходы снова одновременно отправятся в рейс ? Сколько рейсов за это время сделает первый теплоход ? А сколько второй ?
Самостоятельная работа
учени__ 5 А класса
______________________
Фамилия , Имя .
Вариант 1 .
Найдите НОД и НОК чисел наиболее удобным способом :
а) 12 и 18
Решение :
Ответ: НОД(12;18) = _____, НОК(12;18) = ____.
б) 13 и 39
Решение :
Ответ :НОД(13 ; 39) = _____, НОК(13;39) = ______ .
в) 11 и 15
Решение :
Ответ : НОД(11;15) = ____, НОК(11 ; 15) = _____ .
Оценка :
Самостоятельная работа
учени__ 5 А класса
______________________
Фамилия , Имя .
Вариант 2 .
Найдите НОД и НОК чисел наиболее удобным способом :
а) 10 и 15
Решение :
Ответ: НОД(10;15) = _____, НОК(10;15) = ____.
б) 19 и 57
Решение :
Ответ :НОД(19 ; 57) = _____, НОК(19;57) = ______ .
в) 7 и 12
Решение :
Ответ : НОД(7;12) = ____, НОК(7 ; 12) = _____ .
Оценка :
Задача №3.
Расшифруйте название птицы, которая видит все, что происходит вокруг нее, даже не поворачивая головы.
Для этого найдите наименьшее общее кратное каждой пары чисел , затем впишите букву , соответствующую этому числу , в таблицу.
1) НОК(3,12) = л 5) НОК(9;15) = н
2) НОК(4;5;8)= ___ е 6) НОК(12;10)= п
3) НОК(8;12)= в 7) НОК(9;6) = ь
4) НОК(16;12)= д 8) НОК(10;20)= ш
Свободный столбик в таблице заполните, учитывая данные:
НОК(25;4) = а
24 | 12 | 18 | 48 | 20 | 45 | 40 | 60 | |
315 | 96 | 90 | 1014 | 78 | 270 | 800 | 54 | 1200 | 150 | |
к | н | д | р | л | а | е | т | п | о | с |
Простая физика — EASY-PHYSIC
Задачи эти предлагались репетиторам на сертификации по математике портала «Профи. ру». Задачи не очень сложные, их уровень вполне соответствует 19 задаче ЕГЭ, но интересные.
ру». Задачи не очень сложные, их уровень вполне соответствует 19 задаче ЕГЭ, но интересные.
Задача 1.
Чему равно наименьшее восьмизначное число, дающее при делении на 297 остаток 289, при делении на 61 остаток 53, при делении на 21 остаток 13, при делении на 45 остаток 37, при делении на 826 остаток 818?
Решение: обозначим искомое число . Тогда
Глядя на это выражение, становится понятно, что решение затянется… Но можно заметить, что указанное выше выражение можно записать и так:
Тогда становится понятно, что нужно найти наименьшее общее кратное чисел 297, 61, 21, 45 и 826.
61 – простое число. Следовательно,
Ответ: .
Задача 2.
Дату 9 октября 1963 года можно записать тремя числами: 9.10.63, которые оказались расположены в порядке неубывания. Во все дни, когда соответствующие три числа располагались в порядке неубывания, на металлообрабатывающем заводе проводились заседания. Чему равно количество дней, которые были посвящены заседаниям, если завод работал с 24 января 1957 года по 6 декабря 2004 года, а даты открытия и закрытия также учитываются?
Чему равно количество дней, которые были посвящены заседаниям, если завод работал с 24 января 1957 года по 6 декабря 2004 года, а даты открытия и закрытия также учитываются?
Начинаем считать. В 57 году было проведено заседаний: 2 в феврале, 3 в марте, 4 в апреле и так далее, 12 в декабре. Итого (сумма прогрессии):
Итак, всего 77 заседаний – так как в январе завод еще не был открыт.
С 58 по 99 год, таким образом, проводилось по 78 заседаний – еще одно в январе.
В 2000 году заседаний не было. В 2001 – только 1, 1 января.
В 2002 – три, одно в январе и 2 в феврале.
В 2003 – 6 (в январе, феврале и марте), в 2004 – 10 (в январе, феврале, марте и апреле).
Осталось сложить:
Ответ: 3373.
Задача 3.
Число 1447243 написали 45 раз подряд, при этом получилось 315-значное число. Из этого числа требуется вычеркнуть 3 цифры. Сколькими способами это можно сделать, если полученное 312-значное число должно делиться на 6?
Так как число 6 делится на два и на три, то полученное 312-значное число обязано быть четным. Поэтому последнюю тройку надо вычеркивать. Далее, так как число 1447243 написали 45 раз подряд, то даже без последней тройки оно делится на 3. Поэтому две вычеркнутые нами цифры в сумме обязаны делиться на три. Это 7 и 2 или 2 и 4, или 1 и 2 – никакие две другие в сумме не дадут кратную трем сумму. При этом последнюю в записи 312-значного числа 4 тоже можно вычеркнуть, но нельзя вычеркнуть сразу и 2 и 4, идущие последними. Имеем 135 четверок, 45 семерок, 45 единиц и 45 двоек – двойку вычеркнуть обязательно. Поэтому у нас 45 способов это сделать. После этого у нас 45 способов вычеркнуть 7 – итого 2025 способов. Также 45 способов вычеркнуть 1 – это еще 2025 способов.Если вместе с двойкой вычеркиваем четверку — то у нас 134 способа – последнюю нельзя. Итого 6030 способов. Всего 10080 способов.
Поэтому последнюю тройку надо вычеркивать. Далее, так как число 1447243 написали 45 раз подряд, то даже без последней тройки оно делится на 3. Поэтому две вычеркнутые нами цифры в сумме обязаны делиться на три. Это 7 и 2 или 2 и 4, или 1 и 2 – никакие две другие в сумме не дадут кратную трем сумму. При этом последнюю в записи 312-значного числа 4 тоже можно вычеркнуть, но нельзя вычеркнуть сразу и 2 и 4, идущие последними. Имеем 135 четверок, 45 семерок, 45 единиц и 45 двоек – двойку вычеркнуть обязательно. Поэтому у нас 45 способов это сделать. После этого у нас 45 способов вычеркнуть 7 – итого 2025 способов. Также 45 способов вычеркнуть 1 – это еще 2025 способов.Если вместе с двойкой вычеркиваем четверку — то у нас 134 способа – последнюю нельзя. Итого 6030 способов. Всего 10080 способов.
Ответ: 10080.
Задача 4.
Чему равно наибольшее количество цифр, стертых в 1740-значном числе , если сумма оставшихся цифр равна 1808?
Заметим, что часть 8633 составляет «период» данного числа. Эта часть состоит из 4 цифр, следовательно, в числе она повторяется раз. Сумма цифр этой части равна 20, следовательно, общая сумма всех цифр числа равна . Раз осталась сумма 1808 – следовательно, сумма вычеркнутых равна . Так как требуется вычеркнуть наибольшее количество цифр, то будем вычеркивать сначала все тройки. Сумма всех троек в числе равна . Теперь, если вычеркнуть все шестерки – это дает еще 2610. Остается вычеркнуть еще какое-то количество восьмерок. Определим, сколько:
Эта часть состоит из 4 цифр, следовательно, в числе она повторяется раз. Сумма цифр этой части равна 20, следовательно, общая сумма всех цифр числа равна . Раз осталась сумма 1808 – следовательно, сумма вычеркнутых равна . Так как требуется вычеркнуть наибольшее количество цифр, то будем вычеркивать сначала все тройки. Сумма всех троек в числе равна . Теперь, если вычеркнуть все шестерки – это дает еще 2610. Остается вычеркнуть еще какое-то количество восьмерок. Определим, сколько:
Итого, мы вычеркнули 870 троек, 435 шестерок и 209 восьмерок – всего 1514 цифр.
Задача 5.
Число 5081500199 написали 37 раз подряд, при этом получилось 370-значное число. Из этого 370-значного числа требуется вычеркнуть 5 цифр. Чему равно количество способов, которыми это можно сделать, если полученное после вычеркивания 365-значное число должно делиться на 30?
Так как 30 делится на 5, на 2 и на 3, то придется обязательно вычеркивать три последние цифры – 199. Остается вычеркнуть еще 2. Сумма цифр числа 5081500199 – 38 — не делится на три, число 37 – также. Поэтому надо вычеркивать такие цифры, чтобы добиться делимости на три. После вычеркивания последних трех цифр (199) мы также не добились того, чтобы число делилось на три.
Остается вычеркнуть еще 2. Сумма цифр числа 5081500199 – 38 — не делится на три, число 37 – также. Поэтому надо вычеркивать такие цифры, чтобы добиться делимости на три. После вычеркивания последних трех цифр (199) мы также не добились того, чтобы число делилось на три.
Сумма цифр числа после вычеркивания 199 составляет 1387.
Чтобы добиться делимости на три, нужно вычеркивать либо две пятерки (1377 делится на 3), либо 1 и 0 (1386), либо 8 и 5 (1374) – эти суммы «заберут» лишнюю единицу, и число будет делиться на три. При вычеркивании ноля может быть вычеркнут и последний – это не изменит четности и делимости на 5. Итак, считаем. У нас 74 пятерки, то есть первую можно вычеркнуть 74 способами. Вторую – уже 73. Следовательно, способов вычеркнуть две пятерки — . Вторая пара: единицу можем выбрать 73 способами (одна зачеркнута в самом начале), 0 – 111 способами. Следовательно, вторую пару можно выбрать способами.
Способов выбрать восьмерку – 37, пятерку – 74. Поэтому эта пара даст способов. Итого способа.
Итого способа.
Ответ: 16243 способа.
1 2 3 4 5 6 7 8 9 … 53 Bog’liq
1 2 3 4 5 6 7 8 9 … 53 Ma’lumotlar bazasi mualliflik huquqi bilan himoyalangan ©hozir.org 2022 | Bosh sahifa |
2.
 10: Факторизация простых чисел и наименьшее общее кратное (часть 2)
10: Факторизация простых чисел и наименьшее общее кратное (часть 2)- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 5963
- OpenStax
- OpenStax
Нахождение наименьшего общего кратного (НОК) двух чисел
Одной из причин, по которой мы рассматриваем кратные и простые числа, является использование этих методов для нахождения наименьшего общего кратного двух чисел. Это будет полезно, когда мы будем складывать и вычитать дроби с разными знаменателями.
Метод перечисления кратных
Общее кратное двух чисел — это число, кратное обоим числам. Предположим, мы хотим найти общие кратные 10 и 25. Мы можем перечислить первые несколько кратных каждого числа. Затем мы ищем кратные, общие для обоих списков — это общие кратные.
Мы можем перечислить первые несколько кратных каждого числа. Затем мы ищем кратные, общие для обоих списков — это общие кратные.
\[\begin{split} 10 & \двоеточие \; 10, 20, 30, 40, \textbf{50}, 60, 70, 80, 90, \textbf{100}, 110, \ldots \\ 25 & \двоеточие \; 25, \textbf{50}, 75, \textbf{100}, 125, \ldots \end{split} \nonumber \]
Мы видим, что \(50\) и \(100\) присутствуют в обоих списках. Они являются общими кратными \(10\) и \(25\). Мы бы нашли больше общих кратных, если бы продолжили список кратных для каждого.
Наименьшее число, кратное двум числам, называется наименьшим общим кратным (ЛЦМ). Таким образом, наименьший НОК из \(10\) и \(25\) равен \(50\).
КАК: НАЙТИ НАИМЕНЬШЕЕ ОБЩЕЕ КРАСТНОЕ (НОК) ДВУХ ЧИСЕЛ, ПЕРЕЧИСЛЯЯ КРАСТНЫЕ
Шаг 1. Перечислите первые несколько кратных каждого числа.
Шаг 2. Найдите кратные, общие для обоих списков. Если в списках нет общих кратных, выпишите дополнительные кратные для каждого числа.
Шаг 3. Найдите наименьшее число, общее для обоих списков.
Шаг 4. Этот номер — LCM.
Пример \(\PageIndex{5}\): lcm
Найдите LCM для \(15\) и \(20\), перечислив кратные.
Решение
Перечислите первые несколько кратных \(15\) и \(20\). Найдите первое общее кратное.
\[\begin{split}15 & \двоеточие \; 15, 30, 45, \textbf{60}, 75, 90, 105, 120 \\ 20 & \двоеточие\; 20, 40, \textbf{60}, 80, 100, 120, 140, 160 \end{split} \nonumber\]
Наименьшее число в обоих списках равно \(60\), поэтому \(60\ ) является наименьшим общим кратным \(15\) и \(20\). Обратите внимание, что \(120\) также присутствует в обоих списках. Это общее кратное, но не наименьшее общее кратное.
Упражнение \(\PageIndex{9}\)
Найдите наименьшее общее кратное (НОК) данных чисел: \(9\) и \(12\)
- Ответ
\(36\)
Упражнение \(\PageIndex{10}\)
Найдите наименьшее общее кратное (НОК) данных чисел: \(18\) и \(24\)
- Ответ
\(72\)
Метод простых множителей
Другой способ найти наименьшее общее кратное двух чисел — использовать их простые множители. Мы будем использовать этот метод, чтобы найти LCM \(12\) и \(18\).
Мы будем использовать этот метод, чтобы найти LCM \(12\) и \(18\).
Начнем с нахождения разложения каждого числа на простые множители.
\[12 = 2 \cdot 2 \cdot 3 \qquad \qquad 18 = 2 \cdot 3 \cdot 3 \nonumber\]
Затем мы записываем каждое число как произведение простых чисел, по возможности сопоставляя простые числа по вертикали.
\[\begin{split} 12 & = 2 \cdot 2 \cdot 3 \\ 18 & = 2 \cdot \quad \; 3 \cdot 3 \end{split} \nonumber \]
Теперь выведем простые числа в каждом столбце. LCM является продуктом этих факторов.
Обратите внимание, что простые множители \(12\) и простые множители \(18\) включены в LCM. При сопоставлении общих простых чисел каждый общий простой множитель используется только один раз. Это гарантирует, что \(36\) является наименьшим общим кратным.
КАК: НАЙТИ МОК, ИСПОЛЬЗУЯ МЕТОД ПРОСТЫХ МНОЖИТЕЛЕЙ
Шаг 1. Найдите разложение каждого числа на простые множители.
Шаг 2. Запишите каждое число как произведение простых чисел, по возможности сопоставляя простые числа по вертикали.
Шаг 3. Сократите простые числа в каждом столбце.
Шаг 4. Перемножьте коэффициенты, чтобы получить LCM.
Пример \(\PageIndex{6}\): lcm
Найдите НОК для \(15\) и \(18\), используя метод простых множителей.
Решение
| Запишите каждое число как произведение простых чисел. | \(15 = 3 \cdot 5 \qquad \qquad 18 = 2 \cdot 3 \cdot 3\) |
| Запишите каждое число как произведение простых чисел, по возможности сопоставляя простые числа по вертикали. | \(\begin{split} 15 & = \quad \; 3 \cdot \qquad 5 \\ 18 & = 2 \cdot 3 \cdot 3 \end{split}\) |
| Сократите простые числа в каждом столбце. | |
| Умножьте множители, чтобы получить LCM. | НОК = 2 • 3 • 3 • 5 LCM 15 и 18 равен 90. |
Упражнение \(\PageIndex{11}\)
Найдите НОК с помощью метода простых множителей: \(15\) и \(20\)
- Ответить
\(60\)
Упражнение \(\PageIndex{12}\)
Найдите НОК с помощью метода простых множителей: \(15\) и \(35\)
- Ответ
\(105\)
Пример \(\PageIndex{7}\): lcm
Найдите LCM для \(50\) и \(100\), используя метод простых множителей.
Решение
| Напишите простую факторизацию каждого числа. | \(50 = 2 \cdot 5 \cdot 5 \qquad 100 = 2 \cdot 2 \cdot 5 \cdot 5\) |
| Запишите каждое число как произведение простых чисел, по возможности сопоставляя простые числа по вертикали. | \(\begin{split} 50 & = \quad \; 2 \cdot 5 \cdot 5 \\ 100 & = 2 \cdot 2 \cdot 5 \cdot 5 \end{split}\) |
| Сократите простые числа в каждом столбце. | |
| Умножьте множители, чтобы получить LCM. | НОК = 2 • 2 • 5 • 5 НОК 50 и 100 равен 100. |
Упражнение \(\PageIndex{13}\)
Найдите НОК с помощью метода простых множителей: \(55, 88\)
- Ответ
\(440\)
Упражнение \(\PageIndex{14}\)
Найдите НОК с помощью метода простых множителей: \(60, 72\)
- Ответ
\(360\)
Доступ к дополнительным онлайн-ресурсам
- Пример 1: простая факторизация
- Пример 2: простая факторизация
- Пример 3: простая факторизация
- Пример 1: простая факторизация с использованием деления с накоплением
- Пример 2: простая факторизация с использованием деления с накоплением
- Наименьшее общее кратное
- Пример.
 Определение наименьшего общего кратного с использованием списка кратных
Определение наименьшего общего кратного с использованием списка кратных - Пример. Определение наименьшего общего кратного с помощью простой факторизации
Ключевые понятия
- Найдите разложение составного числа на простые множители с помощью метода дерева.
- Найдите любую пару множителей заданного числа и используйте эти числа для создания двух ветвей.
- Если множитель простой, эта ветвь завершена. Обведите штрих.
- Если множитель не является простым, запишите его как произведение пары множителей и продолжите процесс.
- Запишите составное число как произведение всех обведенных простых чисел.
- Найдите простую факторизацию составного числа с помощью лестничного метода.
- Разделите число на наименьшее простое число.
- Продолжайте делить на это простое число, пока оно не перестанет делиться равномерно.

- Деление на следующее простое число до тех пор, пока оно не перестанет делиться равномерно.
- Продолжайте, пока частное не станет простым.
- Запишите составное число как произведение всех простых чисел на сторонах и на вершине лестницы.
- Найдите LCM, перечислив кратные.
- Список первых нескольких кратных каждого числа.
- Найдите кратные, общие для обоих списков. Если в списках нет общих кратных, выпишите дополнительные кратные для каждого числа.
- Найдите наименьшее число, общее для обоих списков.
- Это номер LCM.
- Найдите LCM, используя метод простых множителей.
- Найдите простую факторизацию каждого числа.
- Запишите каждое число как произведение простых чисел, по возможности сопоставляя простые числа по вертикали.
- Уменьшите количество простых чисел в каждом столбце.

- Умножьте множители, чтобы получить LCM.
Глоссарий
- наименьшее общее кратное
Наименьшее число, кратное двум числам, называется наименьшим общим кратным (НОК).
- простая факторизация
Простая факторизация числа — это произведение простых чисел, равное числу.
Практика ведет к совершенству
Найдите разложение составного числа на простые множители
В следующих упражнениях найдите разложение каждого числа на простые множители, используя метод дерева факторов.
- 86
- 78
- 132
- 455
- 693
- 420
- 115
- 225
- 2475
- 1560
В следующих упражнениях найдите простую факторизацию каждого числа с помощью лестничного метода.
- 56
- 72
- 168
- 252
- 391
- 400
- 432
- 627
- 2160
- 2520
В следующих упражнениях найдите разложение каждого числа на простые множители любым методом.
- 150
- 180
- 525
- 444
- 36
- 50
- 350
- 144
Найдите наименьшее общее кратное (НОК) двух чисел
В следующих упражнениях найдите наименьшее общее кратное (НОК), перечислив кратные.
- 8, 12
- 4, 3
- 6, 15
- 12, 16
- 30, 40
- 20, 30
- 60, 75
- 44, 55
В следующих упражнениях найдите наименьшее общее кратное (НОК), используя метод простых множителей.
- 8, 12
- 12, 16
- 24, 30
- 28, 40
- 70, 84
- 84, 90
В следующих упражнениях найдите наименьшее общее кратное (НОК) любым методом.
- 6, 21
- 9, 15
- 24, 30
- 32, 40
Математика на каждый день
- Покупка продуктов Хот-доги продаются упаковками по десять штук, а булочки для хот-догов продаются упаковками по восемь штук.
 Какое наименьшее количество хот-догов и булочек можно купить, если вы хотите иметь одинаковое количество хот-догов и булочек? (Подсказка: это LCM!)
Какое наименьшее количество хот-догов и булочек можно купить, если вы хотите иметь одинаковое количество хот-догов и булочек? (Подсказка: это LCM!) - Покупка продуктов Бумажные тарелки продаются в упаковках по 12 штук, а чашки для вечеринок — в упаковках по 8 штук. Какое наименьшее количество тарелок и чашек вы можете купить, если хотите, чтобы их было одинаковое количество? (Подсказка: это LCM!)
Письменные упражнения
- Вы предпочитаете находить разложение составного числа на простые множители с помощью метода факторного дерева или метода лестницы? Почему?
- Вы предпочитаете находить LCM, перечисляя кратные или используя метод простых множителей? Почему?
Самопроверка
(a) После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство в выполнении целей этого раздела.
(b) В целом, после просмотра контрольного списка, как вы думаете, хорошо ли вы подготовились к следующей главе? Почему или почему нет?
Авторы и ссылки
- Линн Маречек (Колледж Санта-Ана) и МэриЭнн Энтони-Смит (ранее работавшая в Колледже Санта-Ана).
 Этот контент создан OpenStax и распространяется по лицензии Creative Commons Attribution License 4.0.
Этот контент создан OpenStax и распространяется по лицензии Creative Commons Attribution License 4.0.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- ОпенСтакс
- Версия лицензии
- 4,0
- Показать страницу TOC
- нет
- Теги
Наименьшее общее кратное
Дом
Узнать
Смысл числа
- Экспонента
- Римские цифры
- Правила делимости
- Факторы
- Факториал
- ЛКМ
- ГКФ
- Модульная арифметика
- Научные обозначения
Наименьшее общее кратное — это наименьшее натуральное число, которое делится по обоим заданным числам.
Примечание:
- Если a или b равно 0, LCM считается равным нулю. Обозначается LCM.
- НОК относительных простых чисел является произведением этих чисел.
Наименьшее общее кратное (НОК) группы чисел — это наименьшее число, кратное всем числам. Например, НОК 16 и 20 равен 80; 80 — это наименьшее число, которое одновременно кратно 16 и кратно 20. Вы можете найти НОК двух или более чисел различными способами.
Это идеальный метод для больших чисел. Этот метод факторизует оба числа до простых чисел, которые умножаются, чтобы создать это число как продукт.
Например: — Допустим, вы ищете наименьшее общее кратное 20 и 42. Вот как вы их разложите: 20 = 2 x 2 x 5 и 42 = 2 x 3 x 7
Если число встречается только в одном числе, то оно имеет одно вхождение. Вот список большинства вхождений каждого простого числа из предыдущего примера 2 → 2 раза 3 → 1 раз 5 → 1 раз 7 → 1 раз
Вот список большинства вхождений каждого простого числа из предыдущего примера 2 → 2 раза 3 → 1 раз 5 → 1 раз 7 → 1 раз
Так как 2 встречается дважды, вам придется умножить его дважды. Вот что вам нужно сделать, чтобы найти LCM: 2 х 2 х 3 х 5 х 7 = 420.
Simple Example
Example 1:
Example 2:
Example 3:
Example 4:
Example 5:
Example 6:
Example 7:
Запишите числа в верхней части таблицы общих факторов (как показано в примере). Оставьте небольшое пространство слева от цифр и как можно больше места под цифрами. Допустим, мы работаем с числами 18, 12 и 30. Просто запишите каждое число в отдельной строке вверху сетки.
Запишите наименьший общий простой множитель чисел в пространстве слева. Просто обратите внимание на наименьший простой множитель (например, 2, 3 или 5).
что вы можете вытащить из всех чисел. Они все ровные, так что вы можете вытащить 2.
Просто обратите внимание на наименьший простой множитель (например, 2, 3 или 5).
что вы можете вытащить из всех чисел. Они все ровные, так что вы можете вытащить 2.
Разделите каждое исходное число на общий простой множитель. Запишите частное под каждым числом. Вот как это сделать:
18/2 = 9, поэтому напишите 9до 18 лет.
12/2 = 6, поэтому запишите 6 под 12.
30/2 = 15, поэтому запишите 15 под 30.
Повторяйте процесс извлечения и деления на наименьший простой множитель до тех пор, пока не перестанут существовать общие множители. Просто повторите процесс из предыдущих шагов, используя на этот раз числа 9, 6 и 15.
Вытяните 3 из этих чисел. 3 — наименьший простой делитель или наименьшее простое число, которое делится без остатка на оба числа. Найдите наименьшее общее кратное двух чисел
Разделите все три числа на 3 и запишите результат под этими числами. Найдите наименьшее общее кратное двух чисел
Найдите наименьшее общее кратное двух чисел
9/3 = 3, поэтому напишите 3 под 9; 6/3 = 2, поэтому напишите 2 под 6; 15/3 = 5, поэтому напишите 5 под 15.
Если два числа по-прежнему имеют общий простой делитель, то продолжайте процесс до тех пор, пока ни одна пара нижних чисел не будет иметь общего делителя. В этом конкретном примере все готово.
Например, если нижние три числа 2, 39 и 122, разделите 2 и 122 на 2, оставив новую нижнюю строку как 1, 39 и 61.
Умножьте все числа первого столбца, содержащие общие простые множители, на числа внизу всех остальных столбцов. Это ЛКМ. В этом примере произведение столбца общего множителя равно 6 (2 x 3). Умножьте 6 на цифры внизу другой столбики: 6 х 3 х 2 х 5 = 180.
LCM 18, 12 и 30 равен 180.
Простой пример
Две небольшие емкости вмещают соответственно 250 и 550 литров воды. Находить
минимальная вместимость цистерны, которая может вместить воду из обеих емкостей
при использовании точное количество раз.
Находить
минимальная вместимость цистерны, которая может вместить воду из обеих емкостей
при использовании точное количество раз.
2750
Объяснение :
Нам требовался танкер, который имеет минимальную вместимость, чтобы удерживать воду из обоих водоемов.
контейнеры точное количество раз.
Минимальная вместимость такого танкера LCM 250 и 550.
Можно найти и методом деления.
Теперь перемножьте все делители, чтобы получить НОК заданных чисел.
Таким образом, НОК = 2 × 5 × 5 × 5 × 11 = 2750
МОК 250 и 550 равно 2750.
Следовательно, минимальная вместимость такой цистерны 2750 литров.
Первый контейнер заполнит танкер в 11 раз, а второй в 5 раз.
Что нужно помнить
Краткие советы
- НОК из более чем двух целых чисел – это наименьшее целое число, которое делится на каждое из них.
- Общие кратные – это числа, содержащиеся в списках каждого заданного числа.
Подумай
- Для двух простых чисел a, b; может ли LCM быть больше их продукта или меньше чем их продукт или похожий на их продукт?
- Может ли LCM когда-либо быть равным одному из чисел, заданных из 2 чисел x < y? Если да, поясните сценарий?
Базовые математические ссылки
- Дополнение
- Вычитание
- Умножение
- Подразделение
- Целые числа
- Натуральные числа
- Четное нечетное
Спираль
Станьте участником сегодня!
Зарегистрируйтесь (это бесплатно)Вы член? Войти!
Войдите в свой аккаунтЧасть A: Модели для кратных и множителей (75 минут)
В этой части: модель диаграммы Венна
Числа 24 и 36 имеют некоторые общие черты, в том числе много общих их. Например, 2, 3 и 6 являются общими факторами. Наибольшее такое число называется «наибольшим общим множителем». В этом случае наибольший общий делитель 24 и 36 равен 12. Никакое число больше 12 не является делителем каждого из этих чисел. См. примечание 2 ниже.
Например, 2, 3 и 6 являются общими факторами. Наибольшее такое число называется «наибольшим общим множителем». В этом случае наибольший общий делитель 24 и 36 равен 12. Никакое число больше 12 не является делителем каждого из этих чисел. См. примечание 2 ниже.
Еще одна характерная черта, которую могут иметь общие числа, — это общее кратное — третье число, которое делится без остатка и на 24, и на 36. Наименьшее такое число называется «наименьшим общим кратным». В этом случае наименьшее общее кратное равно 72. Никакое число меньше 72 не делится без остатка на каждое число.
Один из способов исследовать общие делители и кратные двух чисел — использовать диаграмму Венна:
Круг слева содержит все простые делители (т. ) числа 24, а круг справа содержит все простые делители числа 36. (Число 1 не считается простым, потому что оно имеет только один делитель.)
Числа, содержащиеся в пересечении, это те множители, которые есть в обоих числах; т. е. их общие факторы. Это означает, что двойки и 3 на пересечении, как по отдельности, так и перемноженные вместе (2 • 2, 2 • 3 и 2 • 2 • 3 — или 2, 3, 4, 6 и 12), — все это общие множители. .
Это означает, что двойки и 3 на пересечении, как по отдельности, так и перемноженные вместе (2 • 2, 2 • 3 и 2 • 2 • 3 — или 2, 3, 4, 6 и 12), — все это общие множители. .
Обратите внимание, что наибольший из этих делителей равен 12. Наибольший общий делитель (НОД) 24 и 36 равен 2 • 2 • 3, или 12, произведению всех чисел в перекрытии.
Поскольку круг слева содержит все множители числа 24, каждое число, кратное 24, должно содержать все эти множители. Точно так же, поскольку круг справа содержит все множители числа 36, каждое число, кратное 36, должно содержать все эти множители.
Чтобы быть кратным обоим числам, число должно содержать все множители обоих чисел. Наименьшее число для этого — 2 • 2 • 2 • 3 • 3, или 72, произведение всех множителей в кружках. Таким образом, наименьшее общее кратное (НОК) чисел 24 и 36 равно 72.
См. примечание 3 ниже.
Задача A1
Используйте диаграмму Венна для определения GCF и LCM для чисел 18 и 30.
В этой части: Нахождение простых делителей
Числа, которые мы рассмотрели до сих пор, было довольно просто разложить на множители. Теперь давайте рассмотрим общий метод нахождения простых множителей. См. примечание 4 ниже.
Один из способов — нарисовать дерево факторов. Для этого напишите число — например, 24 — и нарисуйте под ним перевернутую букву V. Эта буква V представляет собой две «ветви» дерева факторов. Задумайте пару чисел с произведением 24; например, 4 и 6. Проверьте, является ли одно из этих чисел простым. В этом случае ответ — нет.
Под каждым числом, не являющимся простым, нарисуйте еще одну букву V и найдите два множителя для каждого из этих чисел. В этом случае мы найдем множители 2 и 2 для 4, а 2 и 3 для 6. Теперь у нас есть четыре множителя, 2, 2, 2 и 3, все из которых являются простыми числами. Это простая факторизация числа 24.
В математике нам нравится делать вещи с помощью согласованных алгоритмов. Таким образом, вместо того, чтобы просто выбирать два множителя, было бы неплохо сделать процесс более последовательным, сначала найдя наименьший простой множитель и его партнера, а затем повторив этот процесс на партнере (поскольку первое число гарантированно будет простым). Например, вы можете разложить на множители все возможные двойки, затем все тройки, затем 5, 7 и так далее, пока число не будет полностью разложено на множители. Вот как выглядят схемы для чисел 24 и 36:
Например, вы можете разложить на множители все возможные двойки, затем все тройки, затем 5, 7 и так далее, пока число не будет полностью разложено на множители. Вот как выглядят схемы для чисел 24 и 36:
Задача A2
Важен ли порядок умножения числа? Всегда ли продукт уникален этим номером? Чтобы ответить на эти вопросы, используйте факторное дерево, чтобы найти простую факторизацию числа 60 следующими способами:
a. Начните с вынесения на множитель 2 с.
б. Сделайте еще одну диаграмму, но на этот раз начните с разложения на множители десятков.
в. Нарисуйте третью диаграмму, но на этот раз начните с разложения на множители 6.
д. Что общего и что отличается в ваших результатах?
Когда вы делите число на множители, независимо от того, с чего вы начинаете, вы всегда получаете один и тот же набор множителей; единственная разница может заключаться в порядке их появления. Это явление называется фундаментальной теоремой арифметики, которая утверждает, что любое целое число (кроме 0 и 1) можно разложить на множители в произведение простых чисел и что это произведение уникально, за исключением порядка множителей. Это еще одна причина, по которой 1 нельзя считать простым — иначе этот и любой другой результат, основанный на нем, развалится.
Это еще одна причина, по которой 1 нельзя считать простым — иначе этот и любой другой результат, основанный на нем, развалится.
Например, мы можем разложить 6 на множители бесконечным числом способов:
… и так далее, для любого количества единиц, которое мы хотим использовать.
Задача A3
Нарисуйте дерево множителей, чтобы найти делители чисел 231 и 195. Деталь: Модель района
Модель района делает процесс нахождения GCF и LCM визуальным. См. примечание 5 ниже.
Наибольший общий множитель
Если мы представим числа 24 и 36 как размеры прямоугольника, то отсюда следует, что любой общий множитель может быть размером квадрата, который замостил бы этот прямоугольник целиком.
Например, квадрат 1 на 1 замостил бы прямоугольник 24 на 36 без пробелов и перекрытий. То же самое и с квадратом 2 на 2 или 3 на 3. Обратите внимание, что все эти числа являются общими делителями 24 и 36.
Чтобы определить GCF, мы хотим найти размеры наибольшего квадрата, который мог бы замостить весь прямоугольник без пробелов или перекрытий. Вот один быстрый метод.
Вот один быстрый метод.
Начните с прямоугольника 36 на 24:
Самая большая квадратная плитка, которая помещается внутри этого прямоугольника и находится заподлицо с одной стороной, имеет размер 24 на 24. Подойдет только одна плитка такого размера:
Самая большая квадратная плитка, которая помещается внутри оставшегося прямоугольника и находится заподлицо с одной стороной, имеет размеры 12 на 12. Две плитки такого размера подойдут. Исходный прямоугольник теперь полностью заполнен:
Наименьшее общее кратное
Обратите внимание, что квадрат 24 на 24 также может быть заполнен плитками 12 на 12, поэтому 12 на 12 — это самая большая плитка, которая может заполнить исходный прямоугольник 24 на 36; следовательно, 12 — это GCF 24 и 36.
И наоборот, если мы подумаем о 24 и 36 как о размерах прямоугольника, из которого можно замостить квадрат, то отсюда следует, что любое общее кратное может быть размерами квадрата, который можно замостить этим прямоугольником.
Например, поскольку 24 • 36 = 864, квадрат размером 864 на 864 можно замостить прямоугольником 24 на 36. НОК 24 и 36 будут размерами наименьшего квадрата, который можно замостить прямоугольником 24 на 36.
Вот быстрый метод определения LCM.
Начните с прямоугольника 24 на 36. Ваша цель состоит в том, чтобы сделать квадрат, замощенный прямоугольниками следующих размеров:
Так как ширина (24) меньше высоты (36), добавьте столбец плиток справа от прямоугольника (в данном случае одну плитку) . Получится прямоугольник 48 на 36:
Ширина (48) теперь больше высоты (36), поэтому добавьте ряд плиток под существующим прямоугольником (в данном случае две плитки). Получится прямоугольник 48 на 72:
Ширина (48) теперь меньше высоты (72), поэтому добавьте еще один столбец (две плитки) справа от существующих прямоугольников. Размеры теперь 72 на 72 — и вы сделали квадрат!
Используйте следующее интерактивное задание, чтобы ответить на Задание A5. Квадрат 72 на 72 — это наименьший квадрат, который можно замостить прямоугольником 24 на 36. Следовательно, НОК 24 и 36 равен 72.
Квадрат 72 на 72 — это наименьший квадрат, который можно замостить прямоугольником 24 на 36. Следовательно, НОК 24 и 36 равен 72.
Для неинтерактивной версии этого задания используйте миллиметровую бумагу при рисовании квадратов и прямоугольников, которые вы хотите изобразить, чтобы убедиться, что размеры фигур точны.
Задача A5
Используйте площадную модель, чтобы найти GCF и LCM следующего:
а. 30 и 42
б. 18 и 30
Видеосегмент
В этом видеосегменте Бен и Дуг используют модель площади, чтобы найти GCF для двух чисел, следуя аналогии с мозаикой прямоугольника с самым большим квадратом, который они могут уместить. Посмотрите этот отрывок после того, как решите задачу A5.
Обратите внимание, что учителя пропустили один шаг и не использовали квадрат размером 12 на 12, чтобы замостить прямоугольник 12 на 30. Подумайте, почему выполнение всех шагов гарантирует, что результатом будет наибольший общий фактор, а не просто любой общий фактор.
Вы можете найти этот фрагмент на видео сеанса примерно через 6 минут и 4 секунды после логотипа Annenberg Media.
Задача A6
Не могли бы вы объяснить своими словами, почему работает площадная модель?
Видеосегмент
Здесь Бен и Дуг используют модель площади, чтобы найти НОК для двух чисел, следуя аналогии с поиском самого большого квадрата, который можно замостить прямоугольником, размеры которого равны двум исходным числам. Обратите внимание на связь, которую они устанавливают между площадной моделью и диаграммами Венна.
Вы можете найти этот фрагмент на видео сеанса примерно через 8 минут и 32 секунды после логотипа Annenberg Media.
Наименьшее общее кратное – определение, факты и примеры
ЧТО ТАКОЕ L.C.M?
Л.К.М. означает наименьшее общее кратное.
L.C.M — наименьшее целое число, кратное двум или более числам.
Давайте разберемся с наименьшим общим кратным.
Что такое кратность?
Мы получаем кратность числа, когда умножаем число на другие числа. Как умножение на 1, 2, 3, 4 и т. д. (не на ноль, поскольку умножение любого числа на ноль дает ноль)
Примеры:
Число, кратное 5, равно 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60….
Число, кратное 6, равно 6, 12, 18, 24, 30, 36, 42, 48, 54, 60….
Что такое общее кратное?
Давайте посмотрим на числа, кратные 5 и 6
Число, кратное 5, равно 5, 10, 15, 20, 25, 30 , 35, 40, 45, 50, 55, 60 ….
Число, кратное 6, равно 6, 12, 18, 24, 30 , 36, 42, 48, 54, 60 ….
Каковы общие кратные чисел 5 и 6?
Поскольку 30 и 60 входят в таблицу 5 и 6.
Итак, общие кратные 5 и 6: 30 и 60
Какое наименьшее общее кратное?
Общие кратные чисел 5 и 6 равны 30 и 60
И наименьшее кратное среди них равно 30.
Итак, наименьшее общее кратное чисел 5 и 6 равно 30.
Итак, L. C.M можно определить как наименьшее или наименьшее из общих кратных. НЦМ двух чисел a и b можно представить как НЦМ(a,b).
C.M можно определить как наименьшее или наименьшее из общих кратных. НЦМ двух чисел a и b можно представить как НЦМ(a,b).
ПРИМЕЧАНИЕ : В компьютерных науках L.C.M чисел помогает создавать закодированные сообщения с использованием криптографии.
ФОРМУЛА ДЛЯ ВЫЧИСЛЕНИЯ L.C.M
Если a и b — два заданных целых числа. Формула для нахождения L.C.M для a и b задается следующим образом:
L.C.M(a,b) = a × b / G.C.F(a,b)
Где GCD (a,b) означает наибольший общий делитель или наибольший общий делитель а и б.
Формула L.C.M для дробей
Формула для нахождения L.C.M дробей:
Л.К.М. = L.C.M числителя/H.C. F знаменателя
ЧТО ТАКОЕ G.C.F. или ХКФ?
Наибольший общий делитель, который точно делит заданный набор чисел, известен как наибольший общий делитель (HCF). HCF также известен как G.C.F или G.C.D (Greatest Common Factor or Greatest Common Divisor)
ОТНОШЕНИЕ МЕЖДУ LCM и HCF
LCM и H. C.F — два важных метода нахождения множителей и множителей в математике.
C.F — два важных метода нахождения множителей и множителей в математике.
L.C.M означает наименьшее общее кратное и используется для нахождения наименьшего возможного общего кратного двух или более чисел, тогда как HCF означает наивысший общий множитель — это метод нахождения максимально возможного общего множителя среди чисел.
Формула L.C.M и G.C.F. приведен ниже:
НЦМ(a,b) = a × b / G.C.F(a,b)
G.C.F(a,b) = a × b / НЦМ(a,b)
два числа.
КАКОВЫ СПОСОБЫ ПОЛУЧЕНИЯ L.C.M?
Мы можем найти НОК тремя способами:
- Чтобы найти кратные заданным числам .
Первый способ найти НОК чисел — составить список кратных каждого числа.
В этом методе запишите несколько кратных заданному числу.
Затем выделите общие кратные данных чисел.
Затем выберите из них наименьшее общее кратное.
Это будет L.C.M заданных чисел.
Возьмем, к примеру, числа 9, 12 и 18.
Кратные 9 равны 9, 18, 27, 36 , 45, 54, 63, 72 ,81, 90. …
…
Кратные 12 равны 12, 24, 36 , 48, 60, 72 , 84,96 …
Клажу 18 — 18, 36 , 54, 72 , 90, 84,108, 126…
. и 72.
Наименьшее общее кратное равно 36.
Итак, L.C.M(9, 12, 18) = 36
2. Чтобы найти L.C.M, используя метод простой факторизации:
Второй метод нахождения НОК заданных чисел — факторизация простых чисел.
В этом методе мы сначала должны найти множители данных чисел, а затем мы должны соединить общие простые множители, чтобы получить L.C.M.
Возьмем в качестве примера 12, 15 и 20
12 = 2 x 2 x 3
15 = 3 x 5
20 = 2 x 2 x 5
Теперь запишите простые множители всех трех чисел вместе ,
12 х 15 х 20 = 2 х 2 х 3 х 3 х 5 х 2 х 2 х 5
= 2 x 2 x 2 x 2 x 3 x 3 5 x 5
Теперь соедините общие простые множители, и мы получим НОК.
Следовательно, имеется четыре двойки, две тройки и две пятерки.
Итак, L.C.M. = 2 x 2 x 3 x 5 = 60
3. Чтобы узнать НВМ с помощью метода деления:
Второй метод нахождения НВМ заданных чисел – это метод деления.
Ниже приведены шаги для нахождения НОК методом деления:
Во-первых, этот метод состоит из группировки путем разделения чисел с правой стороны запятыми, а с левой стороны мы помещаем простые числа, которые делят любое из чисел на правая сторона.
Разделите все ряды чисел на наименьшее простое число, которое делится без остатка хотя бы на одно из чисел
Продолжайте делить ряд чисел на простые числа, и мы остановимся только тогда, если мы не получим результаты как 1 в полной строке.
Теперь L.C.M чисел будет равен произведению всех простых чисел, полученных методом деления
Возьмем в качестве примера 6 и 8
2/ 6,8
2/ 3,4
2/ 3,2
3/ 3,1
1/ 1,1
Итак, L.C.M – это произведение простых чисел в первом столбце.
Итак, НЦМ = 2 x 2 x 2 x 3 = 24
СВОЙСТВА НЦМ
1. Ассоциативное свойство :
Ассоциативное свойство :
НЦМ трех чисел ассоциативен.
НЦМ (a,b,c) = НЦМ (НЦМ (a,b),c) = НЦМ(a,НЦМ (b,c))
2. Перестановочное свойство:
числа коммутативны.
НЦМ (a, b) = НЦМ (b, a)
3. Распределительное свойство :
НЦМ чисел является распределительным.
НЦМ(da, db, dc) = d НЦМ(a, b, c)
Где d — любая константа.
Кратные 8 – Как найти кратные числа 8
Кратные числа – это числа, которые делят число полностью без остатка. Множители — это произведение заданного числа на целое число. Например, мы можем сказать, что числа, кратные 8, — это числа, полученные произведением 8 на натуральные числа, такие как 1, 2, 3, 4 и т. д. Некоторые числа, кратные 8, — это 8, 16, 24, 32, 40, 48 и т. д. Невозможно перечислить все числа, кратные 8, поскольку существует бесконечное количество натуральных чисел. В этой статье давайте изучим все кратные 8 и как определить кратные 8.
Что такое число, кратное 8?
К кратным 8 относятся все числа, полученные в результате умножения 8 на другое целое или целое число. Любое число, которое может быть представлено в виде 8n , где n считается целым числом, кратным 8
Говорят, что целое число «n» кратно целому числу «m», если существует целое число «k», такое что n = m x k.
Итак, чтобы узнать число, кратное 8, нужно подставить m = 8 в уравнение.
Следовательно, n = 8 x k получается.
То есть, кратные 8 — это все те числа, которые можно записать как 8, умноженное на некоторое целое число. Например:
n = 8 x 1, тогда 8 кратно 8.
n = 8 x (- 3), тогда -24 кратно 8. кратные 8, мы должны быть знакомы с таблицей умножения 8. Кратные 8 будут произведением 8 на любое натуральное число, т.е. 8n, где n — любое натуральное число.
Finding the Common Multiples of 8, We Can Write it as:
Writing the numbers from 8 to 0 in the following manner:
8 | 6 | 4 | 2 | 0 |
8 | 6 | 4 | 2 | 0 |
Now, for the ten’s digit in each column in Row 1 will be written from 0 to 4 as:
08 | 16 | 24 | 32 | 40 |
8 | 6 | 4 | 2 | 0 |
Similarly, we will write for the ten’s digit from 4 to 8 in Row 2 as:
08 | 16 | 24 | 32 | 40 |
48 | 56 | 64 | 72 | 80 |
So, we get the first 10 multiples of 8 as:
08
16
24
32
40
48
56
64
72
80
Similarly, the next 10 кратных 8:
8 x 11 = 88
8 x 12 = 96
8 x 13 = 104
8 x 14 = 112
8 x 15 = 120
8 x 16 = 128
. 8 х 17 = 136
8 х 17 = 136
8 х 18 = 144
8 х 19= 152
8 x 20 = 160
Однако у нас есть простой трюк, чтобы записать первые 20 кратных 8, а именно:
Напишите числа 8, 6, 4, 2, 0, написав 4 два times in the following manner:
8 | 6 | 4 | 2 | 0 | 8 | 6 | 4 | 2 | 0 |
8 | 6 | 4 | 2 | 0 | 8 | 6 | 4 | 2 | 0 |
, но цифры. Следующие номера.0034
Следующие номера.0034
08 | 16 | 24 | 32 | 40 |
48 | 56 | 64 | 72 | 80 |
Теперь от 8 до 16, написав 12 два раза следующим образом:
88
96
104
112
120
128
136
144
152
160
Теперь, соединяя эти два прямоугольника, мы получаем первые 20 кратных 8:
08 | 16 | 24 | 32 | 40 | 88 | 96 | 104 | 112 | 120 |
48 | 56 | 64 | 72 | 80 | 128 | 136 | 144 | 152 | 160 |
From here, we concluded that the first multiple of 8 is 8 itself, второе — это просто его двойное число, т. е. 16, а третье — это просто три умножения на 8, т. е. 8 x 3 = 24. Теперь, если я попрошу вас заполнить столбец для определения n-го кратного, давайте начнем эта игра:
е. 16, а третье — это просто три умножения на 8, т. е. 8 x 3 = 24. Теперь, если я попрошу вас заполнить столбец для определения n-го кратного, давайте начнем эта игра:
1. 8, 24,____,56 ,_____,______,_________, 112
Здесь будем нумеровать от первого номера до последнего, включая пробелы:
1 — 8
2 — 24
3- пробел
4 — 56
5 — пробел
6 — пробел7 — пробел
8 — 112
Мы можем наблюдать закономерность, поскольку первое кратное равно 8 x 1 = 8, второе — это третье кратное, т. е. 8 x 3 = 24, за которым следует пробел, а затем 8 х 7 = 56. Отсюда делаем вывод, что узор как:
1-й, 3-й, 5-й, 7-й, 91-е, 11-е и 13-е число, кратное 8, где каждое кратное отличается на 2. Таким образом, наш шаблон для пустого столбца выглядит следующим образом:
1. Третий пробел
8 x 5 = 40
2. Пятый пробел
Пятый пробел
8 х 9 = 72
3. Шестой пробел
8 х 11 = 88
4. Седьмой пробел
8 х 13 = 104
Таким образом, получается: 8, 24, 40, 56 88, 104.
В этой игре вам снова предлагается заполнить пропущенные места:
___, ___, 80, 72, 64, ___
В этом шаблоне можно увидеть таблицу умножения на 8 в порядке убывания, в которой последний член будет равен 8 x 7 = 56, а остальные члены будут следующими:
1-й пробел = 8 x 12 = 96 и 2-й пробел = 8 x 11 = 88
Итак, сформировавшаяся последовательность 96, 88, 8, 72, 64, 56
Возьмем другой пример: вы это определите?
1. 24
2. 34
3. 56
4. 40
Начнем с опций. Если мы посмотрим на 24, то это третье число, кратное 8, т. е. 8 x 3 = 24.
Второй вариант не кратен 8, тогда 56 — это 7-е число, кратное 8. Наконец, 40 — это 5-е число. кратно 8, потому что 8 х 5 = 40. Итак, вариант 4 — правильный ответ.
Наконец, 40 — это 5-е число. кратно 8, потому что 8 х 5 = 40. Итак, вариант 4 — правильный ответ.
Список чисел, кратных 8
Число, кратное 8, может быть бесконечным. Вот список первых 20 кратных 8.
Кратных 8
Multiplication of 8 With An Integer | Multiples 0f 8 | |||
8 x 1 = | 8 | |||
8 x 2 = | 16 | |||
8 x 3 = | 24 | |||
8 x 4 = | 32 | |||
8 x 5 = | 40 | |||
8 x 6 = | 48 | |||
8 x 7 = | 56 | |||
8 x 8 = | 64 | |||
8 x 9 = | 72 | |||
8 x10= | 80 | |||
8 x 11= | 88 | |||
8 x 12= | 96 | |||
8 x 13= | 104 | |||
8 x 14= | 112 | |||
8 x 15= | 120 | |||
8 x 16= | 128 | |||
8 x 17 = | 136 | |||
8 x 18= | 144 | |||
8 x 19= | 152 | |||
8 x 20= | 160 | |||
Multiples of 8 by Division
Поскольку мы знаем, что операции умножения и деления обратны друг другу, кратное любому числу можно найти даже с помощью операции деления.
Предположим, нам нужно проверить, является ли число 120 кратным 8 или нет.
120/8 = 15, так как 120 полностью делится на 8, мы можем сказать, что 120 кратно 8.
Что такое обыкновенное кратное?
Обыкновенные кратные определяются как общие кратные числа из набора из двух или более чисел. Разберемся на приведенном примере.
Например, 3 и 9:
Некоторые числа, кратные 3, равны 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39
Некоторые числа, кратные 9, равны 9 , 18, 27, 36, 45, 54, 63, 72, 81,90, 99, 108, 117
Общие числа 3 и 9 являются кратными 9, 18, 27, 36
Решенные примеры
Запишите 5 кратных следующих
1. 6
Решение: 6, 18, 36, 48, 04.
2. 13
Решение: 13, 36, 39, 52, 65.
Время викторины
Запишите любые три числа, кратные следующим числам.
1. 15
2. 20
3. 17
4. 23
Интересные факты
Каждое число имеет бесконечное число кратных.
Каждое число кратно самому себе.
Каждое кратное данному числу больше или равно данному числу.
Ноль кратен каждому числу.
Первое кратное любого заданного числа есть само число.
Актуальность изучения кратных в математике
Множественные числа играют важную роль в математике и в нашей жизни. Она лежит в основе всех математических расчетов. Что-то такое простое, как посещение салона каждый 5-й день недели, потребует знания множителей. Бизнесмены используют мультипликаторы для количественной оценки роста и возможностей бизнеса. Они также используют мультипликаторы, чтобы сравнить, как обстоят дела у других компаний-конкурентов. Множественные числа необходимо понимать на базовом уровне в школе, чтобы все учащиеся могли хорошо считать и укреплять свои основы. Изучение того, как выполнять простые вычисления сейчас, поможет им в дальнейшем понять сложные.
Изучение того, как выполнять простые вычисления сейчас, поможет им в дальнейшем понять сложные.
ее ближний круг показывает «неправильное разнообразие» – почему эволюция верна автор колонок, но бывший редактор книжного обозрения газеты. На этом сайте были выделены три ее колонки: «Крайне левые и крайне правые согласны в одном: женщины не в счет», «Пределы жизненного опыта» и «Она написала роман-антиутопию. То, что произошло дальше, было довольно антиутопично». Как вы можете понять из заголовков, Пол настроен против пробуждения или, по крайней мере, «неортодоксален», что, вероятно, вызывает у нее неприятный запах среди других сотрудников NYT. Но я уверен, что ей все равно: она работает в газете с 2013 года, и ее работа обеспечена.
На этой неделе у нас есть еще одна колонка Пола, противоречащая тенденциям Нью-Йорк Таймс. Нажмите, чтобы прочитать.
Как и Пол, я не «политически согласен с [Лиз] Трасс по большинству вопросов». Новый премьер-министр — тори, и я думаю, что большинство ее взглядов ужасны. Но что я подчеркиваю сегодня, так это то, что освещение нового кабинета Трусса, который настолько этнически «разнообразен», насколько можно надеяться, недостаточно хорош для левых. Это потому, что это «неправильное разнообразие», поскольку «разнообразные» члены ближайшего окружения Трасса, хотя среди них нет белых мужчин, все же являются консерваторами. И это вызвало недовольство прессы (Пол не упоминает о недовольстве ее собственной газеты, которое я привожу ниже). Из столбца:
Но что я подчеркиваю сегодня, так это то, что освещение нового кабинета Трусса, который настолько этнически «разнообразен», насколько можно надеяться, недостаточно хорош для левых. Это потому, что это «неправильное разнообразие», поскольку «разнообразные» члены ближайшего окружения Трасса, хотя среди них нет белых мужчин, все же являются консерваторами. И это вызвало недовольство прессы (Пол не упоминает о недовольстве ее собственной газеты, которое я привожу ниже). Из столбца:
Но даже среди всей этой помпы одна новость из Великобритании привлекла на удивление мало внимания. Лиз Трусс, новый премьер-министр от консерваторов, объявила о своем кабинете, и впервые ни один член внутреннего круга — так называемых высших государственных должностей — не является белым человеком.
Министр внутренних дел Суэлла Браверман — дочь кенийских и маврикийских иммигрантов. Мать министра иностранных дел Джеймса Клеверли эмигрировала из Сьерра-Леоне. Новый канцлер казначейства Кваси Квартенг родился в семье выходцев из Ганы.
Можно было бы написать колонку, в которой говорилось бы: «Трусс назначает разнообразный кабинет», но это не продало бы газеты, как и «Трусс назначает консервативный кабинет». Нет, прессе пришлось настаивать на том, что разнообразие было неправильным видом разнообразия:
Левые зааплодировали? Были ли осанны в прогрессивном Твиттере, провозглашающие это расовое, этническое и гендерное разнообразие шагом вперед для общества?
Не совсем так.
Вместо этого изменение было надлежащим образом передано, часто с оговорками. «Кабинет Лиз Трасс: разнообразный, но догматичный», — отмечает The Guardian. Новую команду критиковали как элиту, продукт таких школ, как Итон, Кембридж и Сорбонна. Эти люди не из рабочего класса, указывали другие. Они недостаточно поддерживают права тех, кто ищет убежища в Великобритании, или политику, направленную на борьбу с изменением климата.
Возможно, зная, с какой стороны ее хлеб намазан маслом, Пол не упоминает колонку ее собственной газеты, опубликованную десятью днями ранее:
И эта колонка не так уж отличается от той, что была в Guardian . Цитата из Castle and Landler:
Цитата из Castle and Landler:
Тем не менее, ближайшее окружение г-жи Трасс, хотя и прогрессивное по своему этническому составу, также имеет твердую идеологическую подоплеку, что, по мнению критиков, делает маловероятным проведение политики, более дружелюбной по отношению к британскому меньшинству или к беженцам, прибывающим на берега страны.
В самом деле, некоторые утверждают, что разнообразие членов кабинета министров дает г-же Трасс прикрытие для реализации еще более радикальных подходов, таких как план отправки некоторых лиц, ищущих убежища, в Руанду — политика, которая теперь находится в ведении Суэллы Браверман, нового министра внутренних дел, чей отец приехал в Великобританию из Кении в 1968 году.
«Есть различие, которое не имеет значения, и изменение, которое не приводит к изменению», — сказал Кехинде Эндрюс, профессор изучения чернокожих в Бирмингемском городском университете, приведя в качестве примера иммиграционную политику консерваторов и план Руанды.
И кабинет также подвергся критике за то, что был виновен в МЕРИТОКРАТИИ, страшном слове на букву М, которое становится все более уничижительным, потому что оно часто противоречит разнообразию. Здесь у нас есть разнообразный кабинет, выбранный по качеству — меритократический кабинет, но — это тоже неправильная меритократия.
Пол:
«Это меритократический прогресс для людей, которые преуспели в образовании, юриспруденции и бизнесе», — сказал CNN Сандер Катвала, директор British Future, аналитического центра, который занимается вопросами иммиграции, интеграции и национальной идентичности. «Это не прогресс с точки зрения социального класса».
Это интересная критика. «Меритократический», используемый здесь в уничижительном смысле, означает, что он основан на способностях и достижениях, полученных благодаря сочетанию таланта и упорного труда. Традиционно заслуги служили основным фактором при найме, но сегодня некоторые люди считают сами системы, присуждающие заслуги, сфальсифицированными, особенно в отношении меньшинств.
В попытке исправить этот дисбаланс и диверсифицировать рабочую силу, особенно для руководящих должностей, стало обычной практикой при найме — в деловых и некоммерческих сферах, а также в правительстве — сделать расовое или этническое разнообразие более важным фактором.
Беда в том, что для многих одних и тех же людей этническое и расовое разнообразие имеет значение только в сочетании с определенной точкой зрения. Еще до того, как был завершен кабинет Трусса, один из членов лейбористской оппозиции написал в Твиттере: «Ожидается, что ее кабинет будет разнообразным, но он будет самым правым на памяти живущих, поддерживая политическую повестку дня, которая будет нападать на права трудящихся. особенно меньшинства».
Другой представитель лейбористов написал: «Недостаточно быть чернокожим политиком или политиком из числа этнических меньшинств в этой стране или членом кабинета министров. Дело не в репрезентации. На самом деле это символизм».
Подразумевается, что есть только один способ достоверно представить свою расу, этническую принадлежность или пол — иначе вы будете фальшивкой или пешкой. Это справедливо?
Это риторический вопрос, конечно. В науке можно попасть в беду из-за поощрения найма или профессионального продвижения на основе заслуг, потому что, как всем известно, это иногда противоречит «справедливости». Если вы напишете статью о том, что ученых надо ценить по их заслугам, а не по их идеологии, как это сделала моя подруга Анна Крылова в The Journal of Physical Chemistry Letters , вы получаете тонну возражений. Отпор — это, конечно, нормально (это свобода слова), но что поразило Анну и меня, так это упорное и повсеместное утверждение, что меритократия — это фальшивка — просто еще одна тактика, которую сторонники превосходства белой расы используют для подавления меньшинств. (Вот почему, конечно же, американские колледжи направо и налево отменяют стандартизированные тесты и оценки. )2122 Конечно, Трасс назначит консервативный кабинет, и, судя по реакции, это был качественный кабинет. Но это был кабинет консерваторов. Я бы предпочел, чтобы было больше либералов, но серьезно, чего можно ожидать от премьер-министра-консерватора?
)2122 Конечно, Трасс назначит консервативный кабинет, и, судя по реакции, это был качественный кабинет. Но это был кабинет консерваторов. Я бы предпочел, чтобы было больше либералов, но серьезно, чего можно ожидать от премьер-министра-консерватора?
Помимо неоправданного принижения меритократии, другой момент заключается в том, что как в Великобритании, так и в США вы не можете ожидать, что кто-то будет придерживаться определенного набора взглядов из-за их этнической принадлежности, цвета кожи или «расы». Надо, конечно, но не всегда так получается. В Америке многие умные чернокожие являются «неортодоксами», включая Джона Маквортера, Гленна Лури, Уилфреда Райли и Коулмана Хьюза. Поскольку они не согласны с такими, как Ибрам Кенди или Та Нехиси Коутс, их считают предателями «черного дела» или даже «черными, ненавидящими себя». Но дело в том, что все эти мужчины говорили вдумчивые и умные вещи — они просто не согласны с другими людьми с похожей пигментацией.
Когда мы поймем, что нужно оценивать аргументы по их достоинству, а не по тому, кто их выдвигает? Это элементарно и является продолжением знаменитого (и высмеиваемого) заявления доктора Кинга о том, что нельзя судить людей по расе.
Кроме того, игнорирование разнообразия мнений среди членов группы может иметь последствия — политические. Пол отмечает это:
Черные избиратели и избиратели из других этнических меньшинств в Великобритании также не всегда являются левыми. В 2019 году они отдали 20% голосов за консерваторов..
Подобное разнообразие политических мнений среди меньшинств существует и в Соединенных Штатах, и это сбивает с толку левых. Все большее число латиноамериканцев баллотируются и голосуют за кандидатов-республиканцев. Дональд Трамп получил больше голосов от этнических меньшинств в 2020 году, чем в 2016 году. Во второй раз поддержка Трампа чернокожими мужчинами увеличилась на шесть процентных пунктов. И это было 92 122 после 92 123 убийства Джорджа Флойда, события, которое, как предполагается, воодушевило многих левых избирателей из числа меньшинств.
В своей дальновидной книге 1991 года «Размышления о ребенке позитивного действия» профессор права Стивен Картер осудил многие предположения о разнообразии, зарождавшиеся в то время, в том числе представление о том, что расовые или этнические меньшинства должны мыслить как группа, а не как личности.
Он оплакивал «идею о том, что чернокожие, получившие власть или влияние, несут особую ответственность за формулирование предполагаемых взглядов других чернокожих — по сути, думать, действовать и говорить определенным образом, Черный путь — и что есть что-то особенное в чернокожих, которые настаивают на том, чтобы делать что-то еще».
Прошло три десятилетия с тех пор, как книга Картера была опубликована, и это прискорбное предположение только набирает популярность. Как он отметил тогда: «В прежние времена такие настроения могли быть отмечены как откровенно расистские. Однако теперь они стали почти евангелием для людей, которые хотят продемонстрировать свою приверженность равенству».
Предположение о том, что ваша этническая принадлежность дает вам особое право говорить о расе и что вы должны продвигать этнически «правильную» точку зрения, также может огорчить университеты. На самом деле уже есть, ибо «учебные» отделы выкачивают идеологически однородные продукты, которые продолжают продвигать только одну точку зрения и имеют тенденцию душить несогласных. И они уходят в другие «учебные» отделы, увековечивая удушающее единообразие мысли (и леденя речь оппонентов).
И они уходят в другие «учебные» отделы, увековечивая удушающее единообразие мысли (и леденя речь оппонентов).
Я закончу аналогичным заявлением, сделанным конгрессменом от штата Массачусетс и «прогрессивным отрядом» Аянной Прессли во время встречи в 2019 году. Как сообщал The Hill : не нужно «больше черных лиц, которые не хотят быть черными голосами» во время либеральной конференции Netroots Nation в субботу, комментарий, который прозвучал, когда расовая политика угрожает разделить партию.
The Washington Post сообщает, что Прессли заявила, что не заинтересована в том, чтобы поставить «стул к старому столу».
«Пришло время встряхнуть этот стол. … Нам больше не нужны коричневые лица, которые не хотят быть коричневым голосом», — как сообщается, сказал Прессли во время мероприятия. «Нам больше не нужны черные лица, которые не хотят быть черным голосом».
Одной из причин создания групп этнически разнообразными является обеспечение разнообразия точек зрения, столкновение которых может привести к чему-то вроде истины или, по крайней мере, к согласию.

 1 = 4457 = 560.
1 = 4457 = 560.
