Физики предложили новый метод решения задачи трёх тел / Хабр
Израильские учёные из Института физики им. Рака при Еврейском университете предложили новый способ упрощения задачи трёх тел, позволяющий точно оценить вероятность покидания системы любым из этих тел. Работа опубликована в журнале Celestial Mechanics and Dynamical Astronomy.
Задача трёх тел подразумевает описание поведения небесных тел в трёхмерном пространстве, взаимно притягивающихся друг к другу. Ею впервые заинтересовался Исаак Ньютон, пытавшийся в XVII веке описать движения планет Солнечной системы. Он попробовал вывести формулу, описывающую движение Луны вокруг Земли с учётом того, что Земля движется вокруг Солнца. Однако оказалось, что это одна из тех задач, которую легко сформулировать и трудно решить.
Проблемой в разное время занимались такие величайшие математики, как Эйлер, Лагранж, Якоби и Пуанкаре. Анри Пуанкаре в XIX веке обнаружил, что поведение системы отличается крайней чувствительностью к начальным условиям – первоначальным положениям и скоростям тел.
Появление вычислительных мощностей в XX веке позволило подступиться к этой задаче при помощи численного моделирования. Оказалось, что при неких достаточно общих допущениях в системе трёх тел хаотичные периоды движения сменяются периодическими, пока, наконец, она не распадается на пару тел, вращающихся относительно центра их масс, и третье тело, удаляющееся от них.
Из-за хаотичного поведения системы нельзя было рассчитывать на то, что компьютеры выдадут точные и долгосрочные прогнозы поведения такой системы. Однако в 1976 году появилась идея о возможности статистического решения этой задачи, предсказывающего вероятность убегания одного из тел.
Даже такая задача оказалась настолько сложной, что её удалось решить только 45 лет спустя. Доктор Николас Стоун из Еврейского университета со своими коллегами использовали новый метод расчётов, и впервые получили замкнутое математическое выражение для статистического решения задачи.
Предыдущие методы опирались на т.н. фазовое пространство – набор всех положений и скоростей частиц, составляющих систему. К примеру, фазовое пространство единственной частицы, которая может двигаться по отрезку длиной метр со скоростями не более двух метров в секунду, будет представлять собой прямоугольник с шириной в 1 м и длиной в 4 м/с – поскольку скорость может иметь как положительный, так и отрицательный знак.
Обычно физики имеют дело с объёмом фазового пространства, или, сокращённо, с фазовым объёмом. Например, вероятность найти частицу в левой половине отрезка связывается с объёмом левой половины прямоугольника в фазовом пространстве, составляющим половину объёма всего прямоугольника.
Поскольку три тела не ограничены в пространстве, а сила гравитации действует на любом расстоянии, объём фазового пространства в этой задаче бесконечен, и, следовательно, вероятности тоже бесконечны. Поэтому все предыдущие методы принимали некий объём пространства за «область сильного взаимодействия», игнорируя всё остальное.
В новой работе предлагается изучать «поток фазового объёма». Если мы представим себе ёмкость с газом, в стенке которой есть пара отверстий, то вероятность того, что конкретная молекула вылетит через одно из них, будет пропорциональной потоку газа через каждое из отверстий.
Поток конечен даже в бесконечном пространстве, поэтому новый подход одновременно избегает бесконечных вероятностей и не прибегает к искусственному ограничению объёма. В итоге теория позволяет предсказать вероятность убегания любого из тел. По словам профессора Кола, одного из авторов работы, миллионы компьютерных симуляций показывают, что предсказания теории очень хорошо соответствуют численным компьютерным симуляциям.
Ожидается, что исследование повлияет как на решение различных задач астрофизики, так и на понимание целого класса проблем механики.
Абстрактная математика помогает физике
Иногда на первый взгляд совершенно абстрактные математические теории помогают физикам-теоретикам понять, как устроен наш мир.
В год окончания Первой мировой войны двое немецких математиков геттингенской выучки опубликовали работы, имеющие огромное значение для теоретической физики. Одна из самых блестящих алгебраистов XX века Эмми Нётер представила доказательства двух знаменитых ныне теорем, связывающих законы сохранения различных величин (энергии, импульса, углового момента, заряда и т. д.) с симметриями уравнений, описывающих физическую систему.
Эти теоремы стали мощным и универсальным средством выявления подобных законов в ньютоновской и релятивистской механиках, в теории тяготения, электродинамике, квантовой теории поля и физике элементарных частиц.
Статья Германа Вейля «Гравитация и электричество», опубликованная не в Геттингене, а в Берлине, известна гораздо меньше. Между тем она и ее продолжение, вышедшее годом позже, положили начало чрезвычайно эффективному подходу к конструированию теорий микромира, который сформировался уже во второй половине XX века. С его помощью была создана объединенная теория трех фундаментальных взаимодействий, сильного, слабого и электромагнитного, которую назвали Стандартной моделью.
РЕКЛАМА – ПРОДОЛЖЕНИЕ НИЖЕ
От сил к потенциалам
Как обычно и бывает, у Вейля имелись предшественники. В начале XIX века работы нескольких математиков, прежде всего Гаусса и Пуассона, преобразовали математический аппарат ньютоновской теории тяготения. В новой интерпретации она предстала как силовое поле, пронизывающее Вселенную. Это поле стали описывать гравитационным потенциалом — скалярной функцией, зависящей от пространственных координат, но не от времени. При этом сила тяготения в любой точке полностью определяется тем, насколько резко изменяется вблизи нее этот потенциал (то есть его градиентом).
Это нововведение обогатило математический аппарат небесной механики и других разделов физики, где приходится иметь дело с тяготением, но ввело в описание гравитации некую неопределенность. В законе Ньютона фигурируют силы тяготения, которые можно измерять непосредственно, и определяются они однозначно (в выбранной системе единиц).
А вот значения гравитационного потенциала можно изменить на любую постоянную величину — градиент останется тем же. В те времена это выглядело тривиальным следствием математического формализма, не имеющим отношения к реальной физике.
В калибровочных теориях существует очень обширная симметрия, которая неодинаково проявляет себя в разных точках пространства и времени. Поэтому при математическом описании симметрий такого типа появляются параметры, которые зависят от пространственно-временных координат. И вот оказывается, что существование калибровочных симметрий накладывает весьма сильные ограничения на свойства объектов, которые эти теории описывают.
«Для примера возьмем квантовую электродинамику, — объясняет академик Валерий Рубаков. – Электромагнитные взаимодействия переносят частицы с единичным спином – фотоны. Спин фотона может быть ориентирован только в двух направлениях, вдоль или против его движения. В первом случае мы говорим о правой поляризации, во втором — о левой. Но если строить теорию фотонов чисто формально, ни о чем не задумываясь, появятся еще две поляризации с нулевыми проекциями спина на направление движения.
Если такое допустить, теория рассыпется, потеряет самосогласованность. А в теории с правильно подобранной калибровочной симметрией эта проблема не возникает, лишние поляризации оттуда уходят. Аналогичная ситуация имеет место и в теории глюонного поля, переносящего сильные взаимодействия, и в теории слабого взаимодействия, переносящего промежуточные векторные бозоны. Все эти частицы имеют единичный спин, и у всех возникают неприемлемые состояния, которые не исчезают сами по себе, однако изгоняются калибровочной симметрией».
Столетием позже таким же образом переписали классическую электродинамику. В первоначальной форме она была представлена уравнениями Максвелла, куда входят измеряемые на опыте напряженности электрического и магнитного поля. Эти уравнения тоже удобно выразить через потенциал, только более сложный, чем у ньютоновской гравитации (помимо скалярной части, в него входит вектор, определяющий величину магнитного поля).
Уравнения электродинамики в такой записи выглядят очень элегантно и естественно встраиваются в пространство-время специальной теории относительности.
Однако они становятся неоднозначными, поскольку одному и тому же полю могут соответствовать разные потенциалы. Например, к векторному потенциалу можно добавить любой постоянный вектор, а к скалярному — любое число.
Более того, эти добавки могут меняться и в пространстве, и во времени, лишь бы они были правильно связаны друг с другом, так что произвол в выборе электромагнитных потенциалов существенно больше, чем в случае ньютоновской гравитации. Физики и математики начала прошлого века прекрасно видели эту неоднозначность, но, как и предшественники, не придавали ей особого значения.
Калибровочные преобразования
Это свойство электромагнитных потенциалов имеет глубокий физический смысл. Их взаимные изменения компенсируют друг друга точно таким образом, чтобы сохранить в прежнем виде уравнения Максвелла. Неоднозначность выбора фактически отражает неразрывную связь между электричеством и магнетизмом.
Преобразования потенциалов, не меняющих уравнений электромагнитного поля, называют калибровочными (этот термин тоже восходит к статьям Вейля) — как говорят физики, эти уравнения инвариантны относительно калибровочных преобразований.
В квантовой электродинамике такая инвариантность, в соответствии с теоремой Нётер, влечет за собой закон сохранения электрического заряда. Таким образом, калибровочная инвариантность, несмотря на свой вроде бы формальный характер, открывает возможность заключений, имеющих прямой физический смысл!
И не только в отношении электромагнетизма. Принцип эквивалентности, на котором базируется общая теория относительности (ОТО), утверждает, что поле тяготения вызывает такие же физические эффекты, как и ускорение. Если недалеко от звездолета с работающим двигателем поместить тяготеющие массы, то в принципе можно полностью скомпенсировать импульсы двигателя и создать в кабине зону невесомости. Такая компенсация ускорений посредством переменного гравитационного потенциала аналогична взаимной компенсации изменений потенциалов электромагнитного поля. Это наводит на мысль, что уравнения ОТО должны подчиняться какому-то аналогу калибровочных преобразований.
Такие рассуждения сейчас кажутся вполне естественными, но сто лет назад до них никто не додумался.
Калибровочная инвариантность — и как идея, и как термин — пришла в теоретическую физику иным путем. Чтобы понять, как это произошло, обратимся к работам Вейля.
Мир переменных масштабов
Вейль записал уравнения гравитационного поля в пространстве с иной геометрией, чем та, которой воспользовался Эйнштейн. В итоге к ним добавились формулы, в которых Вейль увидел основные черты уравнений Максвелла. Этим путем он получил математическую конструкцию, которую счел единой теорией электричества и тяготения.
Уравнения ОТО записываются в римановом пространстве, искривленном четырехмерном пространстве-времени с однозначной метрикой. В отличие от «плоского» евклидового пространства, где при перенесении произвольного вектора вдоль замкнутой кривой по возвращении в исходную точку он окажется в прежней позиции, в римановом пространстве такой перенос закончится поворотом вектора на ненулевой угол, который будет мерой кривизны пространства в этой точке. С другой стороны, длина вектора после переноса остается той же самой — в этом и состоит однозначность метрики.
От этого ограничения и отказался Вейль. Он предположил, что уравнения тяготения не должны зависеть от масштабов, применяемых для измерения длины. В обыденной жизни можно с равным успехом пользоваться метрами, футами, аршинами и вершками. Численные значения длины любого отрезка зависят от единицы измерения, но отношения между ними строго сохраняются.
Нечто подобное происходит и в геометрии Вейля, только масштабная единица непрерывно изменяется от точки к точке. Вслед за ней изменяются и длины, но отношения этих длин для любой пары векторов с общим началом остаются неизменными. Операцию смены масштабов Вейль назвал перекалибровкой. Она сохраняет уравнения гравитационного поля — это и есть калибровочная инвариантность в своей ранней исторической ипостаси.
В теоретической физике инвариантность к определенным преобразованиям приводит к появлению специальных свойств. К примеру, ньютоновское уравнение движения инвариантно к трансляции (смещению на некоторое расстояние в пространстве), что приводит к закону сохранения импульса.
Калибровочные преобразования на первый взгляд кажутся абстрактными, но они приводят к существованию различных калибровочных полей, связанных с математическим понятием групп симметрии. В группе U(1) только один фазовый угол, в Стандартной модели ему соответствует один бозон (электромагнитного взаимодействия – фотон), группа SU(2) имеет три фазовых угла (в СМ – три бозона слабого взаимодействия), SU(3) – восемь фазовых углов (восемь бозонов сильного взаимодействия — глюонов).
Но причем здесь электричество? В ОТО длины векторов сохраняются, поэтому сравнить их не представляет проблемы. А вот Вейлю пришлось ввести математические правила, позволяющие выяснить, имеют ли два вектора в соседних точках одинаковую длину (хотя сама длина при этом не определена!).
Эти правила он интерпретировал как уравнения Максвелла для электромагнитных потенциалов. Изменение длины вектора определяется именно этими потенциалами (подобно тому, как изменение его ориентации задается кривизной пространства, которая проявляется через гравитацию).
Вейль отправил рукопись своей статьи Эйнштейну и попросил рекомендовать ее к публикации. Эйнштейн так и сделал, но отметил, что если теория Вейля верна, то частоты оптических спектров должны зависеть от истории излучающих атомов, а это явно противоречит эксперименту. Были выдвинуты и другие возражения, поставившие крест на вейлевском объединении электричества и гравитации. Изумительная по красоте модель оказалась физически несостоятельной.
Однако гравитация, с которой все начиналось, в Стандартную модель не входит. По словам академика Рубакова, гравитация имеет свою специфику: «При квантовании поля тяготения возникают гравитоны. Это тоже бозоны, но уже не векторные — их спин равен не единице, а двойке. Однако теория гравитации опять-таки подчиняется калибровочной симметрии. Гравитон, подобно фотону, имеет лишь две поляризации, в то время как число математически возможных поляризаций у частицы со спином 2 равно пяти. Калибровочная симметрия гравитационного поля позволяет убрать лишние поляризации и тем самым сделать теорию непротиворечивой. Эту симметрию фактически нашел еще Эйнштейн, хотя в ОТО нет никаких гравитонов. Но там имеется симметрия пространства-времени относительно всех гладких преобразований координат, а это и есть калибровочная симметрия.
Впрочем, калибровочные теории очень сильны, но все же не всемогущи. Сегодняшние теории элементарных частиц очень сложно объединить с гравитацией, и в этом их очевидная слабость. Все попытки создать квантовую теорию тяготения пока не увенчались успехом. Так что наши нынешние калибровочные модели — это, конечно, еще не вся правда. Я думаю, что для объединенного описания всех четырех фундаментальных взаимодействий придется изобрести новую теорию с еще более широкой калибровочной симметрией. Многие возлагают надежду на теории суперструн, но скорее всего, понадобится что-то еще шире. Но я не сомневаюсь, что в основе этой будущей теории окажутся какие-то калибровочные симметрии. Некоторые ее черты просматриваются уже сейчас, но когда она появится и какую примет форму, я предсказывать не берусь».
Однако позднее стало ясно, что идея калибровочной инвариантности глубока и конструктивна, а Вейль ошибся лишь в ее конкретном приложении. В 1920-е годы это поняли несколько физиков, в том числе Фриц Лондон — впоследствии один из авторов первой квантовой теории сверхпроводимости. В 1927 году он предложил новую интерпретацию теории Вейля, сделавшую ее частью квантовой физики.
Вся сила в фазе
Вот как выглядит идея Лондона в современном выражении. Квантовые объекты описываются комплексной (в математическом смысле) волновой функцией. Измерить ее экспериментально (как и электромагнитные потенциалы!) невозможно. Опытным путем можно выявить лишь вероятности значений физических величин, которые определяются квадратом модуля этой волновой функции. Поэтому ее можно умножить на любое комплексное число с единичным модулем — вероятность от этого не изменится. Если записать такое число в виде экспоненты с чисто мнимым показателем, то операция его умножения на волновую функцию приведет к изменению ее фазы.
Если на квантовую частицу не действуют никакие силы, изменение фазы не повлечет за собой значимых последствий. Движение заряженной частицы в электромагнитном поле в нерелятивистском случае описывается уравнением Шредингера, которое при умножении на фазовый множитель изменяет свой вид и становится неинвариантным. Это препятствие можно обойти, если одновременно изменить электромагнитные потенциалы с помощью того самого классического преобразования, которое после работ Вейля называется калибровочным. Если записать показатель экспоненты в виде произведения мнимой единицы на заряд частицы и скалярную функцию времени и координат, то эта функция как раз и будет задавать требуемое калибровочное преобразование потенциалов. Оно точно компенсирует те дополнительные члены в уравнении Шредингера, которые появляются после изменения фазы волновой функции.
В чем физический смысл этой вроде бы чисто абстрактной математики? Состояния частицы, чьи волновые функции различаются лишь фазовыми множителями, с точки зрения эксперимента эквивалентны.
Если частица заряжена и, следовательно, подчиняется действию электромагнитного поля, возможность произвольной смены фазового множителя обеспечивается соответствующим изменением электромагнитных потенциалов. Инвариантность уравнения движения частицы относительно выбора фазы волновой функции автоматически приводит к калибровочной инвариантности полевых уравнений.
Если записать уравнение Шредингера для заряженной частицы без каких-либо электромагнитных потенциалов, найти его решение в виде волновой функции и умножить ее на фазовый множитель, в уравнении появятся добавочные члены. Следовательно, оно должно содержать какие-то компоненты, которые своими изменениями скомпенсируют эти добавки. В качестве таких компонент как раз и выступают электромагнитные потенциалы. Получается, что если волновые функции, различающиеся на произвольный фазовый множитель, описывают одно и то же состояние заряженной квантовой частицы, то должны существовать и электромагнитные поля, которые подчиняются уравнениям Максвелла.
Таким образом, мы пришли к удивительному результату — фазовая инвариантность порождает электромагнетизм! Этого еще нет у Лондона, хотя логика его рассуждений подводит к такому выводу. Впервые его четко сформулировал Вейль в статье «Электрон и гравитация», опубликованной в 1929 году (хотя он использовал не уравнение Шредингера, а дираковское уравнение для релятивистского электрона). Умножение волновой функции на фазовый множитель у Вейля предстает как новое калибровочное преобразование, тесно связанное с преобразованием электромагнитных потенциалов.
Инструмент предсказаний
Идеи Вейля настолько привлекли Вольфганга Паули, что в 1933 году он пересказал их в статье «Волновая механика». В середине 1940-х годов ее прочел молодой китайский физик Янг Чжэньнин, которого очень заинтересовало доказательство связи между фазовой инвариантностью и сохранением электрического заряда. В 1953—1954 годах в Брукхейвенской национальной лаборатории Чжэньнин и аспирант Роберт Миллс применили эти идеи для анализа ядерных сил.
Их совместная статья «Сохранение изотопического спина и обобщенная калибровочная инвариантность» сыграла огромную роль в развитии теоретической физики.
Янг и Миллс первыми показали, что на основе калибровочной симметрии можно предсказывать существование ранее неизвестных физических полей и, как следствие, еще не открытых частиц (Паули пришел к сходным выводам за год до Янга и Миллса, однако воздержался от их публикации). В 1960—1970-е годы этот росток дал обильный урожай в виде Стандартной модели элементарных частиц.
«Все фундаментальные взаимодействия, за исключением гравитации, переносятся векторными частицами, — говорит профессор МГУ и главный научный сотрудник Института ядерных исследований РАН, автор монографии о калибровочных полях академик Валерий Рубаков, — так уж устроен мир. А при таком раскладе просто необходимо пользоваться калибровочными симметриями, иначе получаются сплошные патологии. Физики шли к пониманию этих вещей очень разными путями. Калибровочная природа электромагнетизма известна еще со времен Вейля, больше 80 лет.
Объединенная калибровочная теория слабых и электромагнитных взаимодействий была развита Стивеном Вайнбергом и Абдусом Саламом во второй половине 1960-х годов и окончательно доработана лишь в начале 1970-х. А потом настала очередь и внутриядерных сил. Как раз тогда экспериментаторы показали, что на очень малых дистанциях взаимодействие между кварками не растет, а слабеет. Это явление назвали асимптотической свободой, и поначалу оно не находило разумного объяснения. Однако трое физиков-теоретиков — Дэвид Гросс, Фрэнк Вильчек и Дэвид Политцер — вскоре показали, что в калибровочных моделях глюонных полей асимптотическая свобода возникает естественным образом. Отсюда было недалеко до объединения теорий электрослабых и сильных взаимодействий в единую теоретическую конструкцию, которую назвали Стандартной моделью».
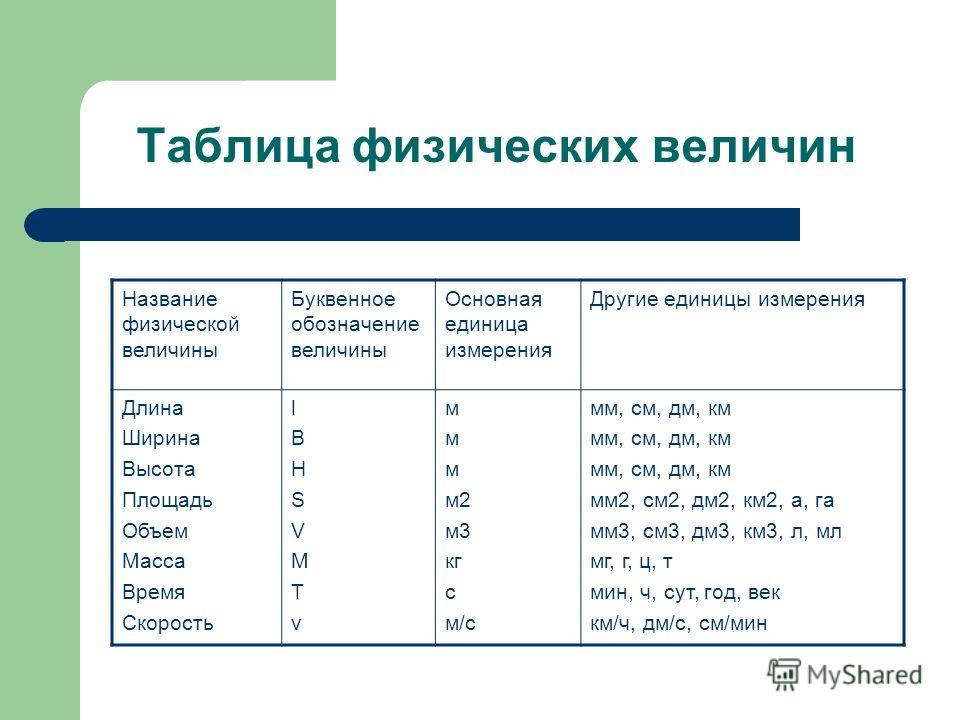
Символы физики — список физических символов и названий
В физике существует большое количество физических величин, которые мы учитываем при выполнении вычислений.
Чтобы сделать их более удобными для пользователей, а также более простыми в использовании и запоминании, мы часто используем обозначения/символы для представления этих физических величин. Эти обозначения/символы, которые мы используем для представления физических величин при решении связанных с ними задач или для других целей, являются символами.
В физике все обозначается английским/греческим алфавитом, например, скорость света, длина волны, скорость и так далее.
Предположим, женщина едет на своей машине со скоростью 30 км/ч и добирается до родного города за 2 часа, а если она едет со скоростью 50 км/ч, то добирается за 1,5 часа. Итак, если нам нужно представить эти единицы в виде символов, как мы можем это сделать?
В этой статье вы найдете самые популярные физические символы, а также те, которые мы обычно используем в физике, с их названиями, типом величин и соответствующими единицами измерения в табличном формате.
Примеры физических символов
Кроме того, символы, используемые для физических величин, сильно различаются.
Иногда символ может быть первой буквой физических величин, которые они представляют, например «d», что означает расстояние. В других случаях они могут быть совершенно не связаны с названием физических величин, например, c символизирует скорость света. Они также могут быть в виде греческих символов, таких как λ, что означает длину волны.
Ниже приведен подробный список наиболее часто используемых символов в физике с их единицами СИ. Обратите внимание, что один и тот же символ может относиться к нескольким величинам.
Symbols for Physical Quantities Related to Space and Time
Symbols | Quantity/ Coefficients | S.I. Unit | Physical Quantity (Scalar/Vector) | ||||
R | Радиус, радиус Curvature | Meter | . | Вектор | |||
d | Расстояние | Метр | |||||
θ | Агловое смещение, | Radian | 2923232323232323232323232323232323232323232323232323. величина и направление, но не является векторной величиной. | ||||
x, y, z | Декартовы координаты | Unitless | Scalar | ||||
î, ĵ, k̂ | Cartesian unit vectors | Unitless | Vector | ||||
r, θ, φ | Сферические координаты | метра/Radian | Вектор | ||||
R̂, θ̂, φ̂ | Spherical Vectors 9000 | . | Unitless | Vector | |||
r, θ, z | Cylindrical coordinates | Metre/Radian | Scalar | ||||
r̂, θ̂, ẑ | Цилиндрические векторы | БЕЗСПОЛЬЗОВАНИЕ | Вектор | ||||
N̂ | Нормальный вектор 0030 | Unitless | Vector | ||||
t̂ | Tangential unit vector | Unitless | Vector | ||||
h | Height, Depth | Метр | Скаляр | ||||
л, л | Длина | ||||||
t | Time | Second | Scalar | ||||
D (= 2 r) | Diameter | Metre | Scalar | ||||
C | Окружность | МЕТР | Скалер | ||||
| 9002 0002 A | Area | Square Metre | Functions as both scalar and vector (like Area vector in a magnetic flux formula) | ||||
V | Volume | Cubic Метр (M3) | Скаляр | ||||
τ | Постоянная времени | секунда (S) | Скалар | (S) | 003 | ||
T | Periodic time | Second (s) | Scalar | ||||
f | Frequency | 1/second or (1/s | Scalar | ||||
ω | Угловая частота | RAD/S | Scalar | 0479 Ниже приведены некоторые символы, часто используемые в физике, с их названиями, типом величин и соответствующими единицами СИ в табличном формате. Physics Symbols Related to Mechanics
Физические символы, относящиеся к гидромеханике
Symbols Related to Solid Mechanics
Physical Quantities Related to Thermal Physics
Physical Symbol Related to Wave and Optics
Physics Symbols Related к электричеству и магнетизму
Символы, используемые в современной физике
Из приведенного выше текста по физике для обозначения величин мы понимаем, что в физике мы используем различные символы или обозначения. Также было интересно увидеть, что некоторые физические символы очень близки (например, «d» для расстояния), а некоторые не связаны (например, «c» для скорости света или «λ» для длины волны). Кроме того, мы заметили, что конкретный символ связан с более чем одной величиной. общая теория относительности — Объемная форма в терминах символа Леви-Чивитыспросил Изменено 2 года, 3 месяца назад Просмотрено 936 раз $\begingroup$ Сейчас я читаю книгу Шона Кэрролла по общей теории относительности, и в какой-то момент он пишет: 9{\ му_п},
\end{уравнение}
поскольку и произведение клина, и символ Леви-Чивиты полностью антисимметричны. Как мне это заметить? Я изо всех сил пытаюсь понять, как тот факт, что оба объекта полностью антисимметричны, подразумевает приведенное выше уравнение. Означает ли это, что любой полностью антосимметричный тензор может быть записан как сокращение над символом Леви-Чивиты (надеюсь, это правильная терминология; поправьте меня, если я ошибаюсь)?
$\begingroup$ Полностью антисимметричный символ размерности $n$ с индексами $n$ имеет только одну независимую компоненту. Например. если $\rho_{a_1…a_n}$ — вполне антисимметричный символ, то $$\rho_{a_1…a_n}=\rho_{12…n}\tilde{\epsilon}_{a_1. ..a_n},$$, где $\tilde\epsilon$ — символ Леви-Чивиты. Это связано с тем, что в размерностях $n$ антисимметричный символ индексов $k$ имеет компоненты $\left(\begin{matrix}n \\ k\end{matrix}\right)$, а $\left(\begin{matrix }n \\ n\end{matrix}\right)=1$. |
0003
m/s
м2/с
Номер
0027
0.0.30030
K
27 SI
C)
I Unit
Обозначения упрощают представление величин.
