Что такое минуты и секунды в геометрии: Что такое градус,минута,секунда? — ответ на Uchi.ru

Градус (геометрия) | это… Что такое Градус (геометрия)?

У этого термина существуют и другие значения, см. Градус.

Градус, минута, секунда — общепринятые единицы измерения плоских углов. Также эти величины используются в картографии для определения координат произвольной точки земной поверхности.

Содержание 1 Градус 2 Минуты и секунды 3 Угловая секунда 3.1 Использование 3.2 Дольные единицы 4 Примечания 5 Литература 6 См. также

Градус

Градус (от лат. gradus — деление шкалы, шаг, ступень) обозначается °. Один оборот равен 360°. В прямом угле, таким образом, 90°, в развёрнутом — 180°.

Деление окружности на 360° придумали аккадцы (вавилоняне).

• 1° = радиан ≈ 0,017453293 радиан
• 1° = оборота ≈ 0,002777 оборота
• 1° = градов ≈ 1,111111 градов

Минуты и секунды

По аналогии с делением часа как интервала времени градус делят на 60 минут (от лат.

 minutus — маленький, мелкий; обозначается знаком ′), а минуту — на 60 секунд (от лат. secunda divisio — второе деление; обозначается знаком ″). Корни такого деления лежат в Древнем Вавилоне, где использовалась шестидесятеричная система счисления.

• 1′ = ≈ 2,9088821·10⁻⁴ радиан.
• 1″ = ≈ 4,8481368·10⁻⁶ радиан.

Угловая секунда

Одна угловая секунда примерно соответствует углу, под которым виден футбольный мяч с расстояния около 45 километров.

Углова́я секу́нда (англ. arcsecond, arc second, as, second of arc; синонимы: дуговая секунда, секунда дуги^[1]) — внесистемная астрономическая единица измерения малых углов, тождественная секунде плоского угла^[2].

Использование

Угловая секунда (обозначается ″) используется в астрономии при измерении плоских углов в градусных мерах. При измерении углов в часовых мерах (в частности, для определения прямого восхождения) используется единица измерения «секунда» (обозначается ^с). Соотношение между этими величинами определяется формулой 1^c = 15″.^[3]

Иногда угловую секунду (и производные от неё дольные единицы) ошибочно называют арксекундой^[1][4], что является простой транслитерацией с англ. arcsecond.

Дольные единицы

По аналогии с международной системой единиц (СИ), наряду с угловой секундой применяются и её дольные единицы измерения: миллисекунды (англ. 

milliarcseconds, mas), микросекунды (англ. microarcseconds, µas) и пикосекунды (англ. picoarcseconds, pas). Они не входят в СИ (СИ рекомендует миллирадианы и микрорадианы), но допускаются к применению^[2]. Однако, согласно ГОСТ 8.417-2002, наименование и обозначения единиц плоского угла (градус, минута, секунда) не допускается применять с приставками^[5], в связи с чем такие дольные величины должны приводиться либо к единицам СИ (миллирадианам и т. п.), либо к угловым секундам, либо обозначаться исходными единицами (mas, µas и pas соответственно).

Связь различных угловых единиц измерения

единица	величина	обозначение	аббревиатура	радиан (прибл.)
градус	1/360 окружности	°	deg	17,4532925 mrad
минута	1/60 градуса	′	arcmin, amin, , MOA	290,8882087 µrad
секунда	1/60 минуты	″	arcsec	4,8481368 µrad
миллисекунда	1/1000 секунды		mas	4,8481368 nrad
микросекунда	1 × 10−6 секунды		μas	4,8481368 prad

Дольные единицы могут использоваться для обозначения собственного движения звёзд и галактик, годичного параллакса и углового диаметра звёзд^[6].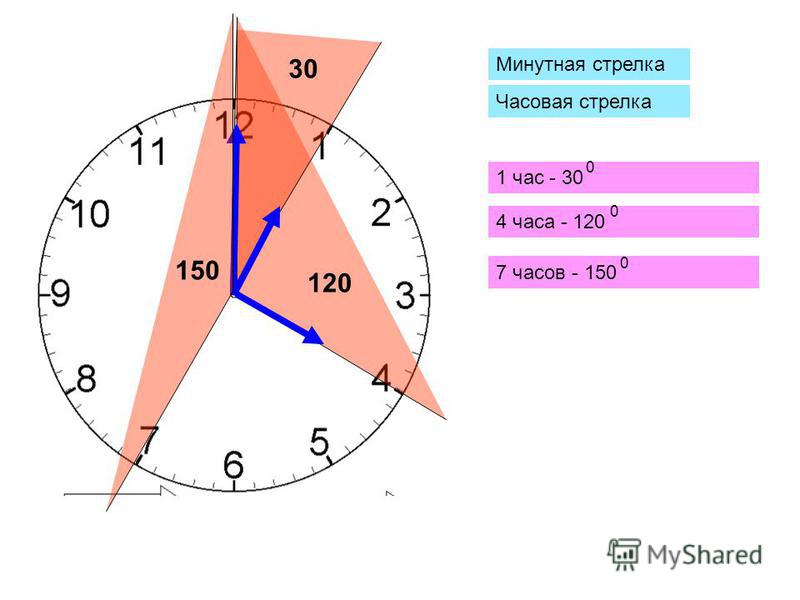

Для наблюдения астрономических объектов под такими сверхмалыми углами астрономы прибегают к методу интерферометрии, при котором сигналы, принимаемые несколькими разнесёнными радиотелескопами, комбинируются в процессе апертурного синтеза. Так, используя методику интерферометрии со сверхдлинной базой, астрономы получили возможность измерить собственное движение галактики Треугольника.

[источник не указан 168 дней]

В видимом свете существенно труднее достичь миллисекундного разрешения. Тем не менее, спутник Hipparcos справился с этой задачей в процессе астрометрических измерений, по результатам которых были составлены наиболее точные (по состоянию на 1997 год) каталоги звёзд Tycho (TYC) и Hipparcos (HIP)^[7][8].

Примечания

1. ↑ ^{1 2} Англо-русско-английский астрономический словарь. Astronet. Архивировано из первоисточника 23 августа 2011. Проверено 23 декабря 2007.
2. ↑ ^{1 2} Non-SI units accepted for use with the International System of Units  (англ.). SI brochure (8th ed.). Bureau International des Poids et Mesures. — Описание СИ на сайте Международного бюро мер и весов. Архивировано из первоисточника 23 августа 2011. Проверено 23 декабря 2007.
3. ↑ Справочник. Некоторые внесистемные единицы. ASTROLAB. Архивировано из первоисточника 23 августа 2011. Проверено 23 декабря 2007.
4. ↑ Glossary entry for English term «arcsecond»  (англ.). Справочник по услугам профессионального перевода, предоставляемым независимыми переводчиками и бюро перевода. ProZ.com. Архивировано из первоисточника 23 августа 2011. Проверено 23 декабря 2007.
5. ↑ ГОСТ 8.417-2002. Единицы величин. Введён в действие с 1 сентября 2003 г. // Информационная система по оборудованию «Прибор.
   Инфо» : справочник. — 2003.
6. ↑ Источник: статья Minute of arc в en-wiki.
7. ↑ Гурьянов С. Почему звезды называются именно так?. проект «Астрогалактика» (29 октября 2005 года). Архивировано из первоисточника 23 августа 2011. Проверено 26 декабря 2007.
8. ↑ Цветков А. С. Общие сведения о проекте Hipparcos // Руководство по практической работе с каталогом Hipparcos. — СПб.: АИ СПбГУ.

Литература

• Гельфанд И. М., Львовский С. М., Тоом А. Л. Малые углы // Тригонометрия. — М.: МЦНМО, 2002. — 199 с. — ISBN 5-94057-050-X

См. также

• Град, минута, секунда
• Оборот
• Радиан

Градус (геометрия) | это… Что такое Градус (геометрия)?

У этого термина существуют и другие значения, см. Градус.

Градус, минута, секунда — общепринятые единицы измерения плоских углов. Также эти величины используются в картографии для определения координат произвольной точки земной поверхности.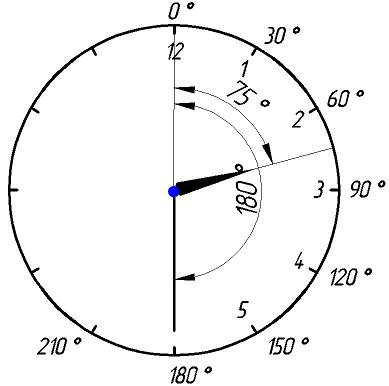

Содержание 1 Градус 2 Минуты и секунды 3 Угловая секунда 3.1 Использование 3.2 Дольные единицы 4 Примечания 5 Литература 6 См. также

Градус

Градус (от лат. gradus — деление шкалы, шаг, ступень) обозначается °. Один оборот равен 360°. В прямом угле, таким образом, 90°, в развёрнутом — 180°.

Деление окружности на 360° придумали аккадцы (вавилоняне).

• 1° = радиан ≈ 0,017453293 радиан
• 1° = оборота ≈ 0,002777 оборота
• 1° = градов ≈ 1,111111 градов

Минуты и секунды

По аналогии с делением часа как интервала времени градус делят на 60 минут (от лат. minutus — маленький, мелкий; обозначается знаком ′), а минуту — на 60 секунд (от лат. 

secunda divisio — второе деление; обозначается знаком ″). Корни такого деления лежат в Древнем Вавилоне, где использовалась шестидесятеричная система счисления.

• 1′ = ≈ 2,9088821·10⁻⁴ радиан.
• 1″ = ≈ 4,8481368·10⁻⁶ радиан.

Угловая секунда

Одна угловая секунда примерно соответствует углу, под которым виден футбольный мяч с расстояния около 45 километров.

Углова́я секу́нда (англ. arcsecond, arc second, as, second of arc; синонимы: дуговая секунда, секунда дуги^[1]) — внесистемная астрономическая единица измерения малых углов, тождественная секунде плоского угла^[2].

Использование

Угловая секунда (обозначается ″) используется в астрономии при измерении плоских углов в градусных мерах. При измерении углов в часовых мерах (в частности, для определения прямого восхождения) используется единица измерения «секунда» (обозначается ^с). Соотношение между этими величинами определяется формулой 1^c = 15″.^[3]

Иногда угловую секунду (и производные от неё дольные единицы) ошибочно называют арксекундой^[1][4], что является простой транслитерацией с англ.  arcsecond.

Дольные единицы

По аналогии с международной системой единиц (СИ), наряду с угловой секундой применяются и её дольные единицы измерения: миллисекунды (англ. 

milliarcseconds, mas), микросекунды (англ. microarcseconds, µas) и пикосекунды (англ. picoarcseconds, pas). Они не входят в СИ (СИ рекомендует миллирадианы и микрорадианы), но допускаются к применению^[2]. Однако, согласно ГОСТ 8.417-2002, наименование и обозначения единиц плоского угла (градус, минута, секунда) не допускается применять с приставками^[5], в связи с чем такие дольные величины должны приводиться либо к единицам СИ (миллирадианам и т. п.), либо к угловым секундам, либо обозначаться исходными единицами (mas, µas и pas соответственно).

Связь различных угловых единиц измерения

единица	величина	обозначение	аббревиатура	радиан (прибл. )
градус	1/360 окружности	°	deg	17,4532925 mrad
минута	1/60 градуса	′	arcmin, amin, , MOA	290,8882087 µrad
секунда	1/60 минуты	″	arcsec	4,8481368 µrad
миллисекунда	1/1000 секунды		mas	4,8481368 nrad
микросекунда	1 × 10−6 секунды		μas	4,8481368 prad

Дольные единицы могут использоваться для обозначения собственного движения звёзд и галактик, годичного параллакса и углового диаметра звёзд^[6].

Для наблюдения астрономических объектов под такими сверхмалыми углами астрономы прибегают к методу интерферометрии, при котором сигналы, принимаемые несколькими разнесёнными радиотелескопами, комбинируются в процессе апертурного синтеза.

Так, используя методику интерферометрии со сверхдлинной базой, астрономы получили возможность измерить собственное движение галактики Треугольника.^{[источник не указан 168 дней]}

В видимом свете существенно труднее достичь миллисекундного разрешения. Тем не менее, спутник Hipparcos справился с этой задачей в процессе астрометрических измерений, по результатам которых были составлены наиболее точные (по состоянию на 1997 год) каталоги звёзд Tycho (TYC) и Hipparcos (HIP)^[7][8].

Примечания

1. ↑ ^{1 2} Англо-русско-английский астрономический словарь. Astronet. Архивировано из первоисточника 23 августа 2011. Проверено 23 декабря 2007.
2. ↑ ^{1 2} Non-SI units accepted for use with the International System of Units  (англ.). SI brochure (8th ed.). Bureau International des Poids et Mesures. — Описание СИ на сайте Международного бюро мер и весов. Архивировано из первоисточника 23 августа 2011. Проверено 23 декабря 2007.
3. ↑ Справочник. Некоторые внесистемные единицы. ASTROLAB. Архивировано из первоисточника 23 августа 2011. Проверено 23 декабря 2007.
4. ↑ Glossary entry for English term «arcsecond»  (англ.). Справочник по услугам профессионального перевода, предоставляемым независимыми переводчиками и бюро перевода. ProZ.com. Архивировано из первоисточника 23 августа 2011. Проверено 23 декабря 2007.
5. ↑ ГОСТ 8.417-2002. Единицы величин. Введён в действие с 1 сентября 2003 г. // Информационная система по оборудованию «Прибор.Инфо» : справочник. — 2003.
6. ↑ Источник: статья Minute of arc в en-wiki.
7. ↑ Гурьянов С. Почему звезды называются именно так?. проект «Астрогалактика» (29 октября 2005 года). Архивировано из первоисточника 23 августа 2011. Проверено 26 декабря 2007.
8. ↑ Цветков А. С. Общие сведения о проекте Hipparcos // Руководство по практической работе с каталогом Hipparcos. — СПб.: АИ СПбГУ.

Литература

• Гельфанд И. М., Львовский С. М., Тоом А. Л. Малые углы // Тригонометрия. — М.: МЦНМО, 2002. — 199 с. — ISBN 5-94057-050-X

См. также

• Град, минута, секунда
• Оборот
• Радиан

десятичных градусов в градусы, минуты и секунды — Grasshopper

FordEarl 21 июня 2019 г., 14:25

1

Здравствуйте, сообщество GH,

Я надеюсь, что сообщество сможет помочь и подсказать направление. Я хотел бы добиться этого без каких-либо других плагинов, используя стандартные математические функции GH, чтобы я мог видеть, что происходит.

У меня есть круг, разделенный на 196 точек, и я хотел бы:

A) пометить каждую точку эталоном от 0 до 195 (уже сделано)
B) пометить каждую опорную точку (0-195) другим тегом, показывающим десятичную степень, измеренную от 0-1, 0-2, 0-3 и так далее до 0-195 по часовой стрелке — можно ли быстро сделать это вместо того, чтобы каждый раз изолировать две точки, как я пытался в определении?
C) пометьте каждую контрольную точку (0-195) соответствующим градусом, минутой и секундой.

гол.JPG1224×769 38,2 КБ

До сих пор я измерил десятичный угол между точками 0 и 1, который составляет 1,836733 градуса.

Вопрос 1: Можно ли разделить десятичное число «1,836733» на две части? Одна часть будет целым числом, в данном случае «1», а вторая часть будет дробным числом, в данном случае «0,836733».

Отсюда я могу рассчитать «минуты», умножив дробное число (0,836733) на 60.
В результате получится «50,203956» минут.

Затем я снова разделил бы число на целое число и дробный остаток от «0,203956», чтобы найти секунды, умножив «0,2039». 56 на 60.

Я хотел бы, чтобы вся эта информация выше (десятичные градусы, градусы, минуты и секунды) была привязана к соответствующей точке.

заранее спасибо за любую помощь.

градусов минут секунд.гх (12,6 КБ)

jeremy5 (Джереми) 21 июня 2019 г., 15:37

2

Вот один из способов разделить число:

image.png1112×238 31,2 КБ

С уважением
Джереми

1 Нравится

(Джереми) 21 июня 2019 г., 15:50

3

Или другой:

image. png1133×244 31,4 КБ

2 лайка

HS_Kim 21 июня 2019 г., 16:21

4

Используя метод, предложенный Джереми, остальная часть (угол маркировки) не составит труда.

Canvas%20at%2000%3B54%3B471466×681 133 КБ

градусы минуты second_re.gh (21,8 КБ)

2 лайка

Джозеф_Остер 21 июня 2019 г., 16:57

5

Поскольку это круг, зачем измерять Vec2Pt углов? Вы знаете, что каждый угол будет одинаковым (360/количество точек). Вот так:

Преобразование этих дробных градусов в минуты и секунды — простая математика… Дополнение однозначных чисел начальным нулем и отображение тегов в радиальном порядке — дополнительная работа. Наверное, это можно упростить.

DMS_2019Jun21a.gh (20,5 КБ) (устарело)

DMS_2019Jun21a.png1366×625 104 КБ

P.S. Лучше избегать запуска данных через текстовые панели. Подключите их, чтобы их можно было удалить, не влияя на результаты.

П.П.С. Возьми два, это был беспорядок. Даже не посмотрел на вывод, который был явно неправильным. Дох!

Итак, я взял пару битов из @HS_Kim (спасибо за Range и символы DMS в форматировании) и реализовал эти инструкции дословно, отсюда:
https://www.rapidtables.com/convert/number/градусы-в-градусы-минуты-секунды.html

Один градус (°) равен 60 минутам (’) и равен 3600 секундам («):

1° = 60’ = 3600 дюймов

Целые градусы (d) равны целой части десятичных градусов (dd):

д = целое число (дд)

Минуты (m) равны целой части десятичных градусов (dd) минус целое число градусов (d), умноженное на 60:

м = целое число ((дд — д) × 60)

Секунды (s) равны десятичным градусам (dd) минус целое число градусов (d) минус минуты (m), деленное на 60, умноженное на 3600:

с = (дд — д — м/60) × 3600

Результат намного лучше:

DMS_2019JUN21B.