Деление на ноль. Увлекательная математика. Методы решения пределов. Неопределённости.Порядок роста функции. Метод замены Раскрытие неопределённостей вида «ноль умножить на бесконечность»
Число 0 можно представить, как некую границу, отделяющую мир реальных чисел от мнимых или отрицательных. Благодаря двусмысленному положению, многие операции с этой числовой величиной не подчиняются математической логике. Невозможность деления на нуль — яркий тому пример. А разрешенные арифметические действия с нулем могут быть выполнены с помощью общепринятых определений.
История нуля
Ноль является точкой отсчета во всех стандартных системах исчисления. Европейцы стали использовать это число сравнительно недавно, но мудрецы Древней Индии пользовались нулем за тысячу лет до того, как пустое число стало регулярно использоваться европейскими математиками. Ещё раньше индийцев ноль являлся обязательной величиной в числовой системе майя. Этот американский народ использовал двенадцатеричную систему исчисления, а нулем у них начинался первый день каждого месяца.
Интересно, что у майя знак, обозначающий «ноль», полностью совпадал со знаком, определяющим «бесконечность». Таким образом, древние майя делали вывод о тождественности и непознаваемости этих величин.
Математические действия с нулем
Стандартные математические операции с нулем можно свести к нескольким правилам.
Сложение: если к произвольному числу добавить ноль, то оно не изменит своего значения (0+x=x).
Вычитание: при вычитании нуля из любого числа значение вычитаемого остается неизменным (x-0=x).
Умножение: любое число, умноженное на 0, дает в произведении 0 (a*0=0).
Деление: ноль можно разделить на любое число, не равное нулю. При этом значение такой дроби будет 0. А деление на ноль запрещено.
Возведение в степень. Это действие можно выполнить с любым числом. Произвольное число, возведенное в нулевую степень, даст 1 (x 0 =1).
Ноль в любой степени равен 0 (0 а =0).
При этом сразу возникает противоречие: выражение 0 0 не имеет смысла.
Парадоксы математики
О том, что деление на ноль невозможно, многие знают со школьной скамьи. Но объяснить причину такого запрета почему-то не получается. В самом деле, почему формула деления на ноль не существует, а вот другие действия с этим числом вполне разумны и возможны? Ответ на этот вопрос дают математики.
Все дело в том, что привычные арифметические действия, которые школьники изучают в начальных классах, на самом деле далеко не так равноправны, как нам кажется. Все простые операции с числами могут быть сведены к двум: сложению и умножению. Эти действия составляют суть самого понятия числа, а остальные операции строятся на использовании этих двух.
Сложение и умножение
Возьмем стандартный пример на вычитание: 10-2=8. В школе его рассматривают просто: если от десяти предметов отнять два, останется восемь. Но математики смотрят на эту операцию совсем по-другому. Ведь такой операции, как вычитание, для них не существует. Данный пример можно записать и другим способом: х+2=10.
Для математиков неизвестная разность — это просто число, которое нужно добавить к двум, чтобы получилось восемь. И никакого вычитания здесь не требуется, нужно просто найти подходящее числовое значение.
Умножение и деление рассматриваются так же. В примере 12:4=3 можно понять, что речь идет о разделении восьми предметов на две равные кучки. Но в действительности это просто перевернутая формула записи 3х4=12.Такие примеры на деление можно приводить бесконечно.
Примеры на деление на 0
Вот тут и становится понемногу понятным, почему нельзя делить на ноль. Умножение и деление на ноль подчиняется своим правилам. Все примеры на деление этой величины можно сформулировать в виде 6:0=х. Но это же перевернутая запись выражения 6 * х=0. Но, как известно, любое число, умноженное на 0, дает в произведении только 0. Это свойство заложено в самом понятии нулевой величины.
Выходит, что такого числа, которое при умножении на 0 дает какую-либо осязаемую величину, не существует, то есть данная задача не имеет решения.
Такого ответа бояться не следует, это естественный ответ для задач такого типа. Просто запись 6:0 не имеет никакого смысла, и она ничего не может объяснить. Кратко говоря, это выражение можно объяснить тем самым бессмертным «деление на ноль невозможно».
Существует ли операция 0:0? Действительно, если операция умножения на 0 законна, можно ли ноль разделить на ноль? Ведь уравнение вида 0х 5=0 вполне легально. Вместо числа 5 можно поставить 0, произведение от этого не поменяется.
Действительно, 0х0=0. Но поделить на 0 по-прежнему нельзя. Как было сказано, деление — это просто обратная операция умножения. Таким образом, если в примере 0х5=0, нужно определить второй множитель, получаем 0х0=5. Или 10. Или бесконечность. Деление бесконечности на ноль — как вам это понравится?
Но если в выражение подходит любое число, то оно не имеет смысла, мы не можем из бесконечного множества чисел выбрать какое-то одно. А раз так, это значит и выражение 0:0 не имеет смысла. Получается, что на ноль нельзя делить даже сам ноль.
Высшая математика
Деление на ноль — это головная боль для школьной математики. Изучаемый в технических вузах математический анализ немного расширяет понятие задач, которые не имеют решения. Например, к уже известному выражению 0:0 добавляются новые, которые не имеют решения в школьных курсах математики:
- бесконечность, разделенная на бесконечность: ∞:∞;
- бесконечность минус бесконечность: ∞−∞;
- единица, возведенная в бесконечную степень: 1 ∞ ;
- бесконечность, умноженная на 0: ∞*0;
- некоторые другие.
Элементарными методами решить такие выражения невозможно. Но высшая математика благодаря дополнительным возможностям для ряда подобных примеров дает конечные решения. Особенно это видно в рассмотрении задач из теории пределов.
Раскрытие неопределенности
В теории пределов значение 0 заменяется условной бесконечно малой переменной величиной. А выражения, в которых при подставлении нужного значения получается деление на ноль, преобразовываются.
Ниже представлен стандартный пример раскрытия предела при помощи обычных алгебраических преобразований:
Как видно в примере, простое сокращение дроби приводит ее значение к вполне рациональному ответу.
При рассмотрении пределов тригонометрических функций их выражения стремятся свести к первому замечательному пределу. При рассмотрении пределов, в которых знаменатель обращается в 0 при подставлении предела, используют второй замечательный предел.
Метод Лопиталя
В некоторых случаях пределы выражений можно заменить пределом их производных. Гийом Лопиталь — французский математик, основоположник французской школы математического анализа. Он доказал, что пределы выражений равны пределам производных этих выражений. В математической записи его правило выглядит следующим образом.
Если число разделить на бесконечность, то частное будет стремиться к нулю? Продолжение внутри и получил лучший ответ
Ответ от Оленька[новичек]
все 0
Krab Вark
Оракул
(56636)
Нет.
Точный нуль. При стремлении делителя к бесконечности частное будет стремиться к нулю. А, если делим не на стремящееся к бесконечности число, а на саму бесконечность (кстати, она, если говорить более точно, официально числом вообще не считается, а считается специальным символом, дополняющим обозначения чисел) — точно нуль.
Ответ от Ђугеус Владимир [гуру]
Нуль хоть дели, хоть умножай на любое число всё равно нуль будет!
Ответ от 1 23 [гуру]
если какая- херь стремится к нулю то умножать ее на что-то конечное (число или ограниченную функцию) беспалезна, патаму что все-рна ана стремится к нулю.
Ответ от Krab Вark [гуру]
При делении на бесконечность любого числа получится нуль. Точный нуль, никакого «стремления к нулю». И потом, на какое число его ни умножай, нуль. А результатом деления нуля на любое число, кроме нуля, будет нуль, только при делении нуля на нуль результат не определен, как частное будет годиться любое число.
Пример 4
Найти предел
Это более простой пример для самостоятельного решения. В предложенном примере снова неопределённость ( более высокого порядка роста, чем корень ).
Если «икс» стремится к «минус бесконечности»Призрак «минус бесконечности» уже давно витал в этой статье. Рассмотрим пределы с многочленами, в которых . Принципы и методы решения будут точно такими же, что и в первой части урока, за исключением ряда нюансов.
Рассмотрим 4 фишки, которые потребуются для решения практических заданий:
1) Вычислим предел
Значение предела зависит только от слагаемого , поскольку оно обладает самым высоким порядком роста. Если , то бесконечно большое по модулю отрицательное число в ЧЁТНОЙ степени , в данном случае – в четвёртой, равно «плюс бесконечности»: . Константа («двойка») положительна , поэтому:
2) Вычислим предел
Здесь старшая степень опять чётная , поэтому: . Но перед расположился «минус» (отрицательная константа –1), следовательно:
3) Вычислим предел
Значение предела зависит только от .
Как вы помните из школы, «минус» «выскакивает» из-под нечётной степени, поэтому бесконечно большое по модулю отрицательное число в НЕЧЁТНОЙ степени равно «минус бесконечности», в данном случае: .
Константа («четвёрка») положительна , значит:
4) Вычислим предел
Первый парень на деревне снова обладает нечётной степенью, кроме того, за пазухой отрицательная константа, а значит: Таким образом:
.
Пример 5
Найти предел
Используя вышеизложенные пункты, приходим к выводу, что здесь неопределённость . Числитель и знаменатель одного порядка роста, значит, в пределе получится конечное число. Узнаем ответ, отбросив всех мальков:
Решение тривиально:
Пример 6
Найти предел
Это пример для самостоятельного решения. Полное решение и ответ в конце урока.
А сейчас, пожалуй, самый тонкий из случаев:
Пример 7
Найти предел
Рассматривая старшие слагаемые, приходим к выводу, что здесь неопределённость .
Решаем:
Разделим числитель и знаменатель на
Пример 15
Найти предел
Это пример для самостоятельного решения. Примерный образец чистового оформления в конце урока.
Ещё пара занятных примеров на тему замены переменной:
Пример 16
Найти предел
При подстановке единицы в предел получается неопределённость . Замена переменной уже напрашивается, но сначала преобразуем тангенс по формуле . Действительно, зачем нам тангенс?
Заметьте, что , поэтому . Если не совсем понятно, посмотрите значения синуса в тригонометрической таблице . Таким образом, мы сразу избавляемся от множителя , кроме того, получаем более привычную неопределённость 0:0. Хорошо бы ещё и предел у нас стремился к нулю.
Проведем замену:
Если , то
Под косинусом у нас находится «икс», который тоже необходимо выразить через «тэ».
Из замены выражаем: .
Завершаем решение:
(1) Проводим подстановку
(2) Раскрываем скобки под косинусом.
(4) Чтобы организовать первый замечательный предел , искусственно домножаем числитель на и обратное число .
Задание для самостоятельного решения:
Пример 17
Найти предел
Полное решение и ответ в конце урока.
Это были несложные задачи в своём классе, на практике всё бывает хуже, и, помимо формул приведения , приходится использовать самые разные тригонометрические формулы , а также прочие ухищрения. В статье Сложные пределы я разобрал пару настоящих примеров =)
В канун праздника окончательно проясним ситуацию ещё с одной распространённой неопределённостью:
Устранение неопределённости «единица в степени бесконечность»Данную неопределённость «обслуживает» второй замечательный предел , и во второй части того урока мы очень подробно рассмотрели стандартные примеры решений, которые в большинстве случаев встречаются на практике.
Сейчас картина с экспонентами будет завершена, кроме того, заключительные задания урока будут посвящены пределам-«обманкам», в которых КАЖЕТСЯ, что необходимо применить 2-й замечательный предел, хотя это вовсе не так.
Недостаток двух рабочих формул 2-го замечательного предела состоит в том, что аргумент должен стремиться к «плюс бесконечности» либо к нулю. Но что делать, если аргумент стремится к другому числу?
На помощь приходит универсальная формула (которая на самом деле является следствием второго замечательного предела):
Неопределённость можно устранить по формуле:
Где-то вроде уже пояснял, что обозначают квадратные скобки. Ничего особенного, скобки как скобки. Обычно их используют, чтобы чётче выделить математическую запись.
Выделим существенные моменты формулы:
1) Речь идёт только о неопределённости и никакой другой .
2) Аргумент «икс» может стремиться к произвольному значению (а не только к нулю или ), в частности, к «минус бесконечности» либо к любому конечному числу.
С помощью данной формулы можно решить все примеры урока Замечательные пределы , которые относятся ко 2-му замечательному пределу. Например, вычислим предел :
В данном случае , и по формуле :
Правда, делать так не советую, в традициях всё-таки применять «обычное» оформление решения, если его можно применить. Однако
Производная от функции недалеко падает, а в случае правил Лопиталя она падает точно туда же, куда падает исходная функция. Это обстоятельство помогает в раскрытии неопределённостей вида 0/0 или ∞/∞ и некоторых других неопределённостей, возникающих при вычислении предела отношения двух бесконечно малых или бесконечно больших функций. Вычисление значительно упрощается с помощью этого правила (на самом деле двух правил и замечаний к ним):
Как показывает формула выше, при вычислении предела отношений двух бесконечно малых
или бесконечно больших функций предел отношения двух функций можно заменить пределом отношения их производных и, таким
образом, получить определённный результат.
Перейдём к более точным формулировкам правил Лопиталя.
Правило Лопиталя для случая предела двух бесконечно малых величин . Пусть функции f (x ) и g (x a . А в самой точке a a производная функции g (x ) не равна нулю (g «(x a равны между собой и равны нулю:
.
Правило Лопиталя для случая предела двух бесконечно больших величин . Пусть функции f (x ) и g (x ) имеют производные (то есть дифференцируемы) в некоторой окрестности точки a . А в самой точке a они могут и не иметь производных. При этом в окрестности точки a производная функции g (x ) не равна нулю (g «(x )≠0 ) и пределы этих функций при стремлении икса к значению функции в точке a равны между собой и равны бесконечности:
.
Тогда предел отношения этих функций равен пределу отношения их производных:
Иными словами, для неопределённостей вида 0/0 или ∞/∞ предел отношения двух функций
равен пределу отношения их производных, если последний существует (конечный, то есть равный определённому
числу, или бесконечный, то есть равный бесконечности).
Замечания .
1. Правила Лопиталя применимы и тогда, когда функции f (x ) и g (x ) не определены при x = a .
2. Если при вычисления предела отношения производных функций f (x ) и g (x ) снова приходим к неопределённости вида 0/0 или ∞/∞, то правила Лопиталя следует применять многократно (минимум дважды).
3. Правила Лопиталя применимы и тогда, когда аргумент функций (икс) стремится не к конечному числу a , а к бесконечности (x → ∞).
К неопределённостям видов 0/0 и ∞/∞ могут быть сведены и неопределённости других видов.
Раскрытие неопределённостей видов «ноль делить на ноль» и «бесконечность делить на бесконечность»
Пример 1.
x =2 приводит к неопределённости вида 0/0. Поэтому производную каждой функции и получаем
В числителе вычисляли производную многочлена, а в знаменателе — производную сложной
логарифмической функции .
Перед последним знаком равенства вычисляли обычный предел , подставляя вместо
икса двойку.
Пример 2. Вычислить предел отношения двух функций, пользуясь правилом Лопиталя:
Решение. Подстановка в заданную функцию значения x
Пример 3. Вычислить предел отношения двух функций, пользуясь правилом Лопиталя:
Решение. Подстановка в заданную функцию значения x =0 приводит к неопределённости вида 0/0. Поэтому вычисляем производные функций в числителе и знаменателе и получаем:
Пример 4. Вычислить
Решение. Подстановка в заданную функцию значения икса, равного плюс бесконечности, приводит к неопределённости вида ∞/∞. Поэтому применим правило Лопиталя:
Замечание. Переходим к примерам, в которых правило Лопиталя приходится применять дважды, то есть приходить к пределу отношений вторых производных, так как предел отношения первых производных представляет собой неопределённость вида 0/0 или ∞/∞.
Раскрытие неопределённостей вида «ноль умножить на бесконечность»
Пример 12.
Вычислить
.
Решение. Получаем
В этом примере использовано тригонометрическое тождество .
Раскрытие неопределённостей видов «ноль в степени ноль», «бесконечность в степени ноль» и «один в степени бесконечность»
Неопределённости вида , или обычно приводятся к виду 0/0 или ∞/∞ с помощью логарифмирования функции вида
Чтобы вычислить предел выражения , следует использовать логарифмическое тождество , частным случаем которого является и свойство логарифма .
Используя логарифмическое тождество и свойство непрерывности функции (для перехода за знак предела), предел следует вычислять следующим образом:
Отдельно следует находить предел выражения в показателе степени и возводить e в найденную степень.
Пример 13.
Решение. Получаем
.
.
Пример 14. Вычислить, пользуясь правилом Лопиталя
Решение. Получаем
Вычисляем предел выражения в показателе степени
.
.
Пример 15. Вычислить, пользуясь правилом Лопиталя
Почему на ноль делить нельзя простыми словами
Что такое деление?Прежде чем пытаться делить на ноль, нужно понять, что вообще такое деление и как оно работает. Возьмем для примера число восемь и поделим его на несколько чисел: 8:8 = 1, 8:4 = 2, 8:2 = 4, 8:1 = 8. Можно заметить, что чем меньше число, на которое мы делим, тем больше получается результат от деления. Логично предположить, что, если делитель уменьшить еще сильнее, до нуля, частное вырастет до бесконечности. Но так ли это на самом деле?
Математики знают лишь то, что, если делитель стремится к нулю, частное стремится к бесконечности. Но это вовсе не значит, что результат деления на ноль равен бесконечности.
Давайте введем еще одно понятие — обратные числа. Что это?Посмотрим на те же примеры с другой стороны. При делении восьми на два получается четыре. Тот же самый результат можно получить, умножив восемь на одну вторую: 8:2 = 4 → 8 × ½ = 4.
А чтобы из восьми получить единицу, можно либо разделить восемь на восемь, либо умножить восемь на одну восьмую. Получается, что деление можно заменить умножением — для этого достаточно заменить второе число в примере на «перевернутую» версию себя или на обратное число: 8:8 = 1 → 8 × ⅛ = 1.
Взаимно обратные числа обладают еще одним важным свойством: их произведение всегда равно одному: 8 × ⅛ = 1; 5 × ⅕ = 1; 2 × ½ = 1. Значит, вместо того, чтобы пытаться разделить какое-то число на ноль, достаточно умножить его же на обратное нулю число. Какое число обратно нулю? Такое, которое при умножении на ноль давало бы единицу: 0 × ? = 1. Но не существует числа, которое при умножении на ноль дало бы что-то кроме нуля!
Можно ли ввести специальное число, обратное нулю?В математике так нередко делают — например, нельзя извлечь квадратный корень из -1. Но математики ввели специальное число i = √-1, которое открыло много возможностей работы со сложными числами.
Мы могли бы договориться, что знак бесконечность ∞ означает нужное нам обратное нулю число: ∞ = 1/0. Можно ли таким числом пользоваться и совершать операции?
0 × ∞ = 1. Пока все в порядке. Тогда 1+1 = 2 можно представить как (0 × ∞) + (0 × ∞) = 2. Это выражение можно сократить до (0 + 0) × ∞ = 2. Но получившееся выражение 0 × ∞ = 2 противоречит нашим изначальным условиям!
Число, обратное нулю, не работает в привычной нам математике и нарушает все ее правила.
Позволяет ли математика делить сам ноль на ноль?
Если попытаться разделить ноль на ноль, ситуация меняется: в таком случае нужно подобрать число, которое при умножении на ноль дало бы ноль: 0 × ? = 0. Получаем проблему, противоположную предыдущей, ведь на этот раз под интересующее нас условие подходит любое число. А так как однозначный ответ выбрать невозможно, говорят, что результат деления нуля на ноль не определен.
Получается, что разделить ноль на ноль нам мешает отсутствие однозначного результата.
Любое другое число разделить на ноль не получается из-за самого определения деления как действия, обратного умножению: нет таких чисел, которые при умножении на ноль давали бы не ноль. А значит, и деление на ноль в обычной математике просто не имеет смысла.
мягкий вопрос — Почему $\infty \cdot 0$ явно не равно $0$?
спросил
Изменено 1 год, 3 месяца назад
Просмотрено 187 тысяч раз
$\begingroup$
Я немного занимался математикой в школе, и кажется, что это легко — что я упускаю?
$$n\times m = \underbrace{n+n+\cdots +n}_{m\text{times}}$$
$$\quad n\times 0 = \underbrace{0 + 0 + \ cdots+ 0}_{n\text{ times}} = 0$$
(т.е. добавьте $0$ к $0$ сколько угодно раз, результат будет $0$)
Итак, я подумал, что бесконечное число $0$’ s не может быть ничем иным, как $0$? Но кто-то утверждает другое, но не может дать разумного объяснения, почему.
Результаты Google кажутся немного сомнительными по этому вопросу — надеюсь, этот вопрос изменит это.
- мягкий вопрос
- бесконечность
- неопределенные формы
$\endgroup$
6
$\begingroup$
Проблема в том, что используемые вами законы сложения и умножения справедливы для натуральных чисел , но бесконечность не является натуральным числом, поэтому эти законы не применимы. Если бы они это сделали, вы могли бы использовать аналогичный аргумент, что умножение чего-либо на бесконечность, независимо от того, насколько оно мало, дает бесконечность, таким образом, $\infty \times 0 = \infty$. Можно использовать и более сложные аргументы, например $\infty \times 0 = \lim_{x \to \infty} (x \times 1/x) = 1$. Ясно, что все эти разные значения для $\infty \times 0$ означают, что с $\infty$ нельзя обращаться как с другими числами.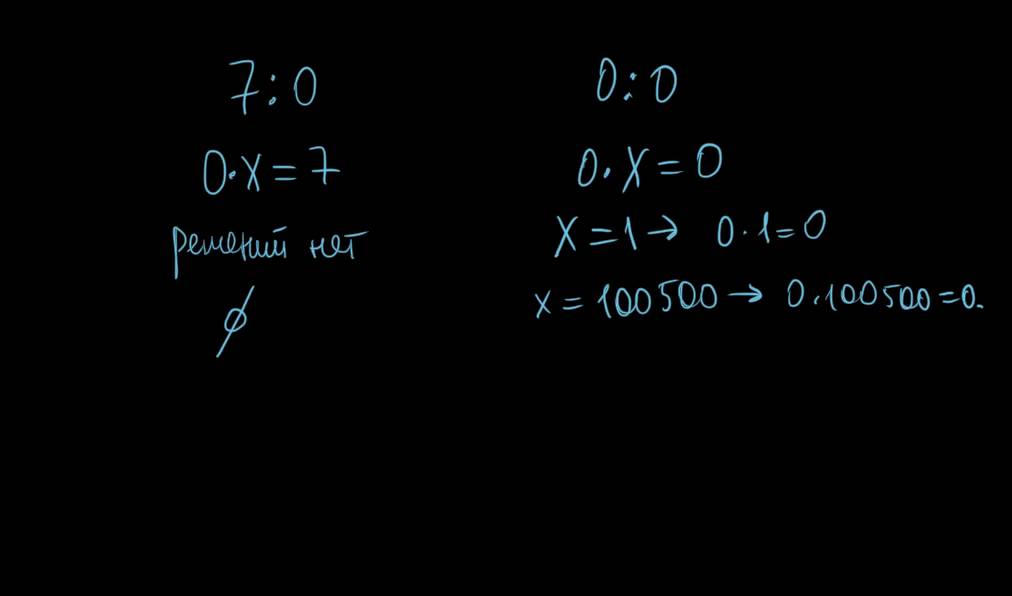
Чтобы работать с бесконечностью, вы должны сначала определить ее. Вы можете думать, что знаете, что такое бесконечность, но на самом деле у вас нет конкретного определения. На самом деле существует многих различных определений бесконечности, которые вы могли бы использовать, каждое из которых приводит к разному поведению. Например, реальная проективная прямая имеет такое понятие бесконечности, что $1/\infty = 0$, в то время как, говоря о бесконечных множествах, для представления размеров этих множеств используются кардинальных чисел (другой тип бесконечности). Вы должны ясно дать понять, о какой бесконечности вы говорите, чтобы работать с ней.
Таким образом, выражение $\infty \times 0$ с использованием умножения, определенного для натуральных чисел, не имеет никакого смысла, поэтому нельзя сказать, что оно равно $0$.
$\endgroup$
12
$\begingroup$
Вы должны помнить, что бесконечность — это не число.
Это скорее концепт. Когда вы пишете
$$n \times 0 = 0 + 0 + 0 +\cdots+ 0 = 0$$
вы выполняете конечную операцию. Невозможно продолжать добавлять ноль, пока вы не достигнете бесконечности, потому что вы не можете достичь бесконечности. Именно эта неспособность «достичь» бесконечности заставляет операции нарушать вашу интуицию. Традиционная алгебра/арифметика не работает с бесконечностью. Вот почему мы используем концепцию пределов, которая хорошо определена математически и позволяет нам выполнять алгебраические операции с бесконечностями.
$\endgroup$
4
$\begingroup$
Как указывали некоторые другие, $\infty$ не является числом. Поэтому вам нужно относиться к этому с некоторой осторожностью.
Чтобы прояснить ваши сомнения, способ, которым вы написали, состоит в том, чтобы посмотреть на $n \times 0$, а затем позволить $n \rightarrow \infty$.
Таким образом, верно, что $$\displaystyle \lim_{n \rightarrow \infty}\left( n \times 0 \right)= 0$$
Однако, когда люди пишут $\infty \times 0$, обычно это сокращенно для обозначения неопределенной формы, когда одна величина стремится к бесконечности, а другая к нулю в предельном смысле, т.е. выражения вида $$\lim_{x \rightarrow 0} \left( f(x) \times g(x ) \right)$$, где $\displaystyle \lim_{x \rightarrow 0} f(x) = \infty$ и $\displaystyle \lim_{x \rightarrow 0} g(x) = 0$.
(Обратите внимание, что $\infty$ не является числом в общепринятом смысле. Это просто сокращение для обозначения того, что что-то неограниченно растет, т. е. при любом числе ваша функция может принимать значение, превышающее это число.)
Например, пусть $f(x) = \frac{1}{x}$, поскольку $g(x) = x$, тогда $f(x) \times g(x) = 1$, $\forall x \neq 0$ и, следовательно, $$\displaystyle \lim_{x \rightarrow 0} \left( f(x) \times g(x)\right) = \lim_{x \rightarrow 0} 1 = 1$$ Однако $\displaystyle \ lim_{x \rightarrow 0} f(x) = \infty$ и $\displaystyle \lim_{x \rightarrow 0} g(x) = 0$ и, следовательно, в этом случае неопределенная форма оценивается как $1$.
+} \frac{1}{\sqrt{x}} = \infty$$
Следовательно, вы не можете связать уникальное значение с $\infty \times 0$. Это зависит от решаемой проблемы. Подробнее о неопределенной форме можно прочитать здесь. (Как всегда с Википедией, прочитайте ее, чтобы получить общее представление.)
$\endgroup$
4
$\begingroup$
Как указано в других ответах, проблема заключается в интерпретации того, что вы подразумеваете под $\infty \cdot 0$. Строго говоря, $0+0+\cdots+0$, когда количество членов стремится к бесконечности, ЯВЛЯЕТСЯ 0 (это просто сумма ряда).
Но посмотрите на этот пример
\begin{eqnarray} \начать{разделить} 1&=&1 \\ \frac{1}{2}+\frac{1}{2}&=&1 \\ \frac{1}{3}+\frac{1}{3}+\frac{1}{3} &={}&1 \\ \vdots\\ \frac{1}{n}+\frac{1}{n}+\cdots+\frac{1}{n} &={}&1 \\ \конец{разделить} \end{eqnarray}
Повторяя процесс, с каждым шагом я получаю больше чисел, каждое из которых ближе к нулю.
.. Это также то, что мы можем понимать под $\infty \cdot 0$, но это $1$ , не так ли?
$\endgroup$
3
$\begingroup$
Это просто общий комментарий относительно таких вопросов:
Когда вы сталкиваетесь с определениями и результатами, с которыми, как вам кажется, вы можете не согласиться, постарайтесь обдумать определения. В таком случае, как бы вы определили умножение на $\infty$? Более фундаментально, как бы вы определили $\infty$? Один из подходов состоит в том, чтобы формально определить $\infty$ как такой символ, что $a \infty = \infty$ для всех чисел $a$, но тогда нам придется исключить $0$ и установить $0 \infty = 0$. Однако это вызывает проблемы (если мы хотим, чтобы закон распределения выполнялся): $0=(a-a)\infty =\infty-\infty$. И как бы вы это определили?
Короче говоря, попытка выполнить арифметические действия с этим новым символом вызывает много проблем.
Всякий раз, когда вы имеете дело с «необычными» объектами, вы должны определить, что они из себя представляют и как они взаимодействуют с другими математическими объектами.
Таким же образом мы могли бы спросить, как определить бесконечно малые числа, которые меньше любого другого числа. Скажем, число $\epsilon$ такое, что $|\epsilon| < a$ для всех действительных ненулевых чисел $a$. Такого числа не существует в реальной системе счисления, но определить такую систему можно. (нестандартный анализ Google) Теперь задача определить, как делать арифметику с бесконечно малыми числами... (но это действительно не по теме)
Подводя итог этому несколько неорганизованному ответу: попробуйте продумать последствия определения $0 \infty = 0$. (то есть попытаться довести до абсурда ). Подумайте, какие определения вы используете, и попытайтесь найти примеры.
$\endgroup$
$\begingroup$
Символ $\infty$ впервые был введен Уоллисом в 17 веке.
Он использовал его для обозначения определенного бесконечного числа и продолжил рассмотрение разбиения интервалов на $\infty$ частей ширины $\frac{1}{\infty}$ в таких приложениях, как вычисление площадей плоских фигур.
Такие гиганты, как Лейбниц, Эйлер и Коши использовали бесконечные количества для получения результатов в анализе. Более подробную информацию можно найти, например, в недавней статье здесь.
В обогащенной системе счисления, содержащей такие бесконечные числа, верно, что бесконечное число, умноженное на $0$, действительно является «простым нулевым ответом». Можно было бы принять такую систему счисления за гиперреальные числа, но таких систем счисления много. Пока система счисления является полем, любое произведение, умноженное на $0$, обязательно даст $0$, даже если «что угодно» — бесконечное число.
Привычная интерпретация выражения «бесконечность, умноженная на ноль» относится к так называемым «неопределенным формам» (см. также Что бесконечность делится на бесконечность?), и тогда ответ далеко не прост и на самом деле не равен нулю в общем.
Однако, если интерпретировать буквально, догадка ОП о том, что $\infty \times 0=0$ «просто», может быть полностью оправдана, как указано выше.
Связанный с этим вопрос о «бесконечности, умноженной на бесконечно малую», см. «бесконечность, умноженная на бесконечно малую». Что происходит?
$\endgroup$
11
$\begingroup$
Это также может быть связано с противоречивыми определениями: вообще говоря, для некоторого числа n n * 0 = 0, а n * бесконечность = бесконечность. Так что же такое бесконечность * 0? Это не определено.
Кроме того, как указал Алекс, бесконечность не является натуральным числом, поэтому те же правила не применяются. И он прав, существуют разные определения бесконечности, так что не думайте о ней как о числе с реальным значением. Например, множество всех действительных чисел и множество всех рациональных чисел бесконечны, но множество всех действительных чисел представляет собой «большую» бесконечность.
5}{5!}
\end{выравнивание}
То, что «$0\cdot\infty$» является «неопределенной формой», означает именно то, что если вы умножаете что-то, что приближается к $0$, на что-то, что приближается к $\infty$, то произведение может приближаться к $0$ или $\infty$ или какое-то число между этими крайними значениями, в зависимости от того, каковы два перемножаемых фактора.
$\endgroup$
$\begingroup$
Проблема в том, что нет способа расширить обычные операции сложения и умножения на $\mathbb R$ так, чтобы $\mathbb R \cup \{\infty,-\infty\}$ образовывало поле. Техническая сложность на самом деле с добавить бесконечностей, не вычитая их. Что такое $\infty + \infty$? Ну, это не может быть $\infty$, потому что тогда мы вычтем $\infty$ с обеих сторон и получим $\infty = 0$. У нас не может быть $\infty + \infty = -\infty$, потому что тогда мы получим $3\infty = 0$, поэтому $\infty = 0$.
И у нас не может быть $\infty+\infty = r$ для реального $r$, потому что тогда у нас было бы $\infty = r/2$. Таким образом, вообще невозможно сделать арифметику только с положительной и отрицательной бесконечностью. Так что, если для удобства вы хотите использовать ограниченный вид арифметики с бесконечностями, вы должны заблаговременно изложить правила, которые вы выбрали для использования — настоящего стандарта не существует. Однако, как подсказывают некоторые другие ответы, можно восстановить смысл, добавив лотов бесконечных чисел, таких как $2\infty$, $\frac 2 3 \infty$ и т. д., и соответствующие им «бесконечно малые», но это выходит за рамки моих собственных знаний.
$\endgroup$
1
$\begingroup$
Проблема с большинством неопределенных чисел заключается в том, что им нельзя присвоить уникальное значение.
Существует бесконечно много чисел, удовлетворяющих этим свойствам.
Начните с $\frac{0}{0}$. Допустим, оно равно $x$, что означает $0\cdot x=0$. Таким образом, для каждого значения $x$ это уравнение выполняется, поэтому мы не можем получить уникальный $x$.
Другой $\frac{\infty}{\infty}$ равен $\frac{\frac{1}{\infty}}{\frac{1}{\infty}}$=$\frac{ 0}{0}$, поэтому по тем же причинам это тоже нельзя определить однозначно. 90$. Так как каждый $x$ удовлетворяет и этому, мы не можем получить уникальный $x$ и в этом случае.
Еще один $0\cdot \infty$. Допустим, $0\cdot \infty=x$ или $\frac{x}{\infty}=0$, или $x\cdot 0=0$, потому что $\frac{1}{\infty}\rightarrow 0$. Так что и в этом случае мы не можем получить уникальный $x$.
Фактически, $$\infty\cdot 0=\infty\cdot \frac{1}{\infty} (\text{потому что } \frac{1}{\infty}\rightarrow 0) =\frac{\ infty}{\infty} =\frac{0}{0}=\text{undefined}$$ (потому что всем им нельзя присвоить уникальное значение).
Таким образом, кажется, что все эти неопределенные формы в основном одно и то же.
0$ не определено? 9{2x}-1)}$$
Я предполагал, что любое число, умноженное на 0, даст ответ 0. Это оказалось не так. Есть ли простое объяснение, почему бесконечность, умноженная на 0, не равна 0?
- исчисление
- пределы
- бесконечность
$\endgroup$
2
$\begingroup$
Любое число при умножении на 0 дает 0. Однако бесконечность не является действительным числом. Когда мы пишем что-то вроде $\infty \cdot 0$, это ничего не значит напрямую; скорее, это сокращение для определенного типа лимита, где первая часть 92}$).
$\endgroup$
1
$\begingroup$
«Бесконечность умножить на ноль» или «ноль умножить на бесконечность» — это «битва двух гигантов».
0$, которые, как говорит Любош, более или менее одно и то же (просто возьмите $\log$ или $\exp$). 9+$, что означает, что ваш лимит становится равным $0/0$.
Несколько более очевидно, почему $0/0$ неопределенно, потому что решение для $x=0/0$ — это решение для $0x=0$, и каждое число решает эту проблему.
$\endgroup$
$\begingroup$
Вот очень простой случай: $\lim\limits_{x\to 0+} x\cdot\frac{6}{x}$. Ясно, что $x$ превращается в $0$.
Но $x\cdot\frac{6}{x} = 6$ всякий раз, когда $x\neq0$. Итак, $\lim\limits_{x\to 0+} x\cdot\frac{6}{x} = \lim\limits_{x\to0+} 6 = 6$. Этот лимит не равен $0$.
$\endgroup$
1
$\begingroup$
Если $f(x) \to 0$ и $g(x) \to \infty$, то произведение $f(x) g(x)$ может вообще приближаться к любому числу.
Например, произведение может приближаться к 0:
$$
\begin{массив}{с|с|с|с|с|с}
f(x) и 0,01, и 0,0001, и 0,000001, и 0,00000001, и \cdots \\
\hline
g(x) & 10 & 100 & 1000 & 10 000 & \cdots \\
\hline
f(x) g(x) & 0,1 & 0,01 & 0,001 & 0,0001 & \cdots \\
\конец{массив}
$$
или произведение может приближаться к бесконечности:
$$
\begin{массив}{с|с|с|с|с|с}
f(x) & 0,1 & 0,01 & 0,001 & 0,0001 & \cdots \\
\hline
g(x) & 100 & 10 000 & 1 000 000 & 100 000 000 & \cdots \\
\hline
f(x) g(x) & 10 & 100 & 1000 & 10 000 & \cdots \\
\конец{массив}
$$
Он также может приблизиться к чему-то промежуточному. Например, в пределе
$$
\lim_{x\to\infty} (x)\left(\frac{5}{x}\right)
$$
$x$ приближается к $\infty$, а $\dfrac{5}{x}$ приближается к $0$, но произведение равно $5$. В общем случае предел вида $0\cdot\infty$ представляет собой конкуренцию двух факторов:
Если первый фактор достигает $0$ быстрее, то ограничение составляет $0$.
Если второй множитель достигает $\infty$ быстрее, то ограничение равно $\infty$.
