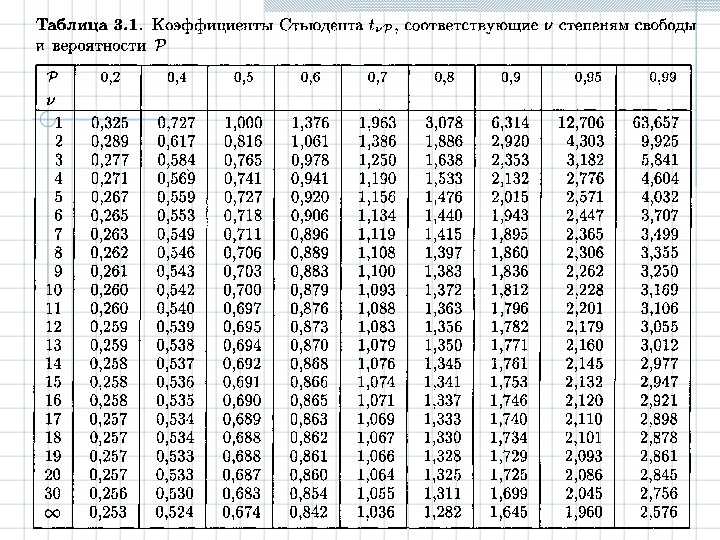
Таблица критических значений t критерия стьюдента: Т-критерий (табличные значения коэффициента Стьюдента) | Таблицы | Справочные материалы

Содержание

t критерий стьюдента таблица

Вы искали t критерий стьюдента таблица? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и t критерия стьюдента таблица, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «t критерий стьюдента таблица».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как t критерий стьюдента таблица,t критерия стьюдента таблица,коэф стьюдента,коэф стьюдента таблица,коэффициент стьюдента,коэффициент стьюдента для 3 измерений,коэффициент стьюдента для 50 измерений,коэффициент стьюдента как найти,коэффициент стьюдента как определить,коэффициент стьюдента онлайн,коэффициент стьюдента таблица,коэффициенты стьюдента,коэффициенты стьюдента таблица,критерий стьюдента таблица,критические значения t критерия стьюдента,критические значения критерия t стьюдента,критические значения критерия стьюдента определяются по,распределение стьюдента t,распределение стьюдента таблица,степень свободы стьюдента,стьюдента таблица,стьюдента таблицы,т критерий стьюдента таблица,таблица t критерия стьюдента,таблица значение коэффициента стьюдента,таблица значений критерия стьюдента t критерия,таблица коэф стьюдента,таблица коэффициентов стьюдента,таблица критериев стьюдента,таблица критерий стьюдента,таблица критерия стьюдента,таблица критических значений стьюдента,таблица распределение стьюдента,таблица распределения стьюдента,таблица стьюдента,таблица стьюдента полная,таблица т критерий стьюдента,таблицы стьюдента,табличное значение критерия стьюдента.

На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и t критерий стьюдента таблица. Просто введите задачу в окошко и нажмите «решить» здесь (например, коэф стьюдента).

Решить задачу t критерий стьюдента таблица вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.

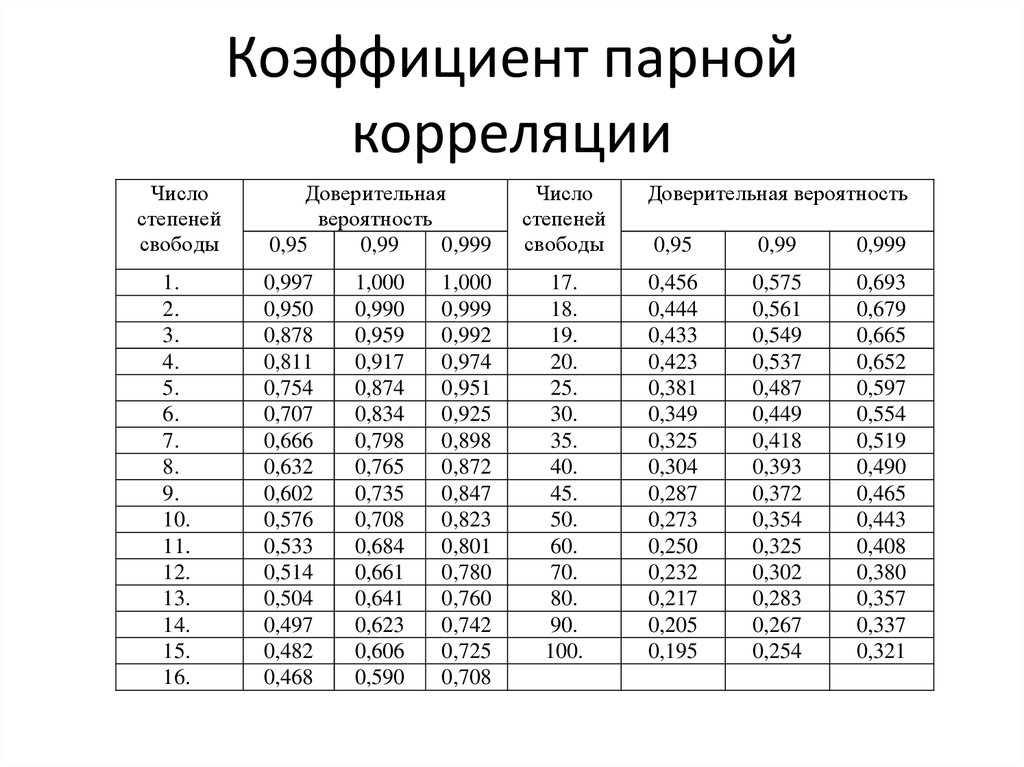
Таблицы критических значений — Методы математической статистики — — Каталог статей

Таблицы критических значений

Таблица критических значений для углового преобразования Фишера
Скачать: http://psystat. at.ua/Articles/FisherPHICritTable.xls

Критические значения коэффициента линейной корреляции Пирсона.

Скачать: http://psystat.at.ua/Articles/Table_Pearson.PDF

Инструкция №1.

Чаще всего используется такой алгоритм.

1. Вычислите коэффициент корреляции.

2. Выберите необходимый уровень ошибки. В психологии при выборке более 30 чел. традиционно используется p≤0,05 (two-tailed).

3. Посчитайте df (степени свободы) по формуле N – 2, где N – размер выборки.

4. На совмещении строки с вычисленным df и выбранным p найдите критический коэффициент корреляции.
5. Если вычисленный коэффициент больше критического, делаем вывод, что полученное значение достоверно с p≤0,05.
Инструкция №2.
Инструкция для поиска вероятности ошибки (p) для вычисленного коэффициента.
1. Решите, какой тест вы будете использовать – односторонний или двухсторонний.
Односторонний (one-tailed) если Вы имеете априорную гипотезу о направлении корреляции. Двусторонний (two-tailed) если вы не имеете гипотезы о направлении корреляции. Чаще всего нас интересует значимость корреляции без учёта знака, поэтому в таблице смотрим Two-tailed.
2. Рассчитайте df (степени свободы) по формуле N – 2, где N – размер выборки.
3. Найдите в таблице строчку с соответствующим либо наиболее близким df .

4. В найденной строке найдите значение коэффициента корреляции большее либо равное тому, которое Вы рассчитали. Таким образом, определите необходимый столбец.
5. Значение в заглавии столбца (0,1; 0,05; 0,02; 0,01; 0,001) будет вероятностью ошибки.
Критические значения коэффициента ранговой корреляции Спирмена.
Скачать: http://psystat.at.ua/Articles/Table_Spearman.pdf
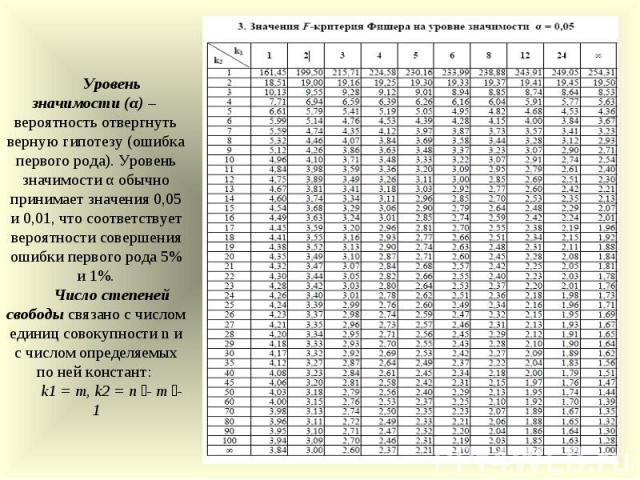
Инструкция. На пересечении строки n (количество человек) и столбца с уровнем значимости находим критическое значение. Если вычисленное значение больше критического, принимаем решение о его значимости на уровне p≤уровень значимости.
Критические значения t-критерия Стьюдента.
Скачать: http://psystat.at.ua/Articles/Table_t_Student.pdf
Инструкция.
1. Вычисляем df по формуле df = N1 + N2 – 2 , где N1 – объем первой выборки, N2 – объем второй выборки.

2. На пересечении строки с вычисленным df и уровня значимости находим критическое значение.
3. Сравниваем полученное значение t-критерия без учёта знака с критическим. Если полученное больше критического – различия достоверны на уровне p≤уровень значимости.
Критические значения F-критерия Фишера (дисперсионный анализ).
Скачать: http://psystat.at.ua/Articles/Table_F.pdf
Документ содержит 2 таблицы: для уровней значимости p=0.05 и p=0,01.
Инструкция.
1.     Вычисляем df between = кол-во групп – 1.
2.     Вычисляем df within = кол-во человек – 1.
3.     В нужной таблице на пересечении df between и df within находим критическое значение.
4.     Если рассчитанное значение больше критического – влияние фактора достоверно.

Критические значения коэффициента хи-квадрат (chi—square).
Скачать: http://psystat.at.ua/Articles/Table_Chi-Square.pdf
Инструкция.
1а. Расчет df. Если коэффициент использовался для сравнения одного эмпирического распределения с теоретическим, то df = C-1, где С – количество вариантов или групп.
1б. Расчет df. Если сравнивалось два и более эмпирических распределения, то df = (R-1)*(C-1), где R – количество строк в таблице частот, С – количество столбцов.
2. На пересечении вычисленного df и уровня значимости находим критическое значение. Если полученное эмпирическое значение больше критического – делаем вывод о достоверном отличии распределений.
Критические значения коэффициента Манна-Уитни.
Скачать: http://psystat.at.ua/Articles/Table_Man-Whitney-U.pdf
Инструкция.
Число на пересечении размера наибольшей выборки (size of the largest sample) и и наименьшей выборки (size of the smallest sample) является критическим значением коэффициента Манна-Уитни.

Вам нужны качественные расчеты с аналитическими выводами? Обращайтесь!

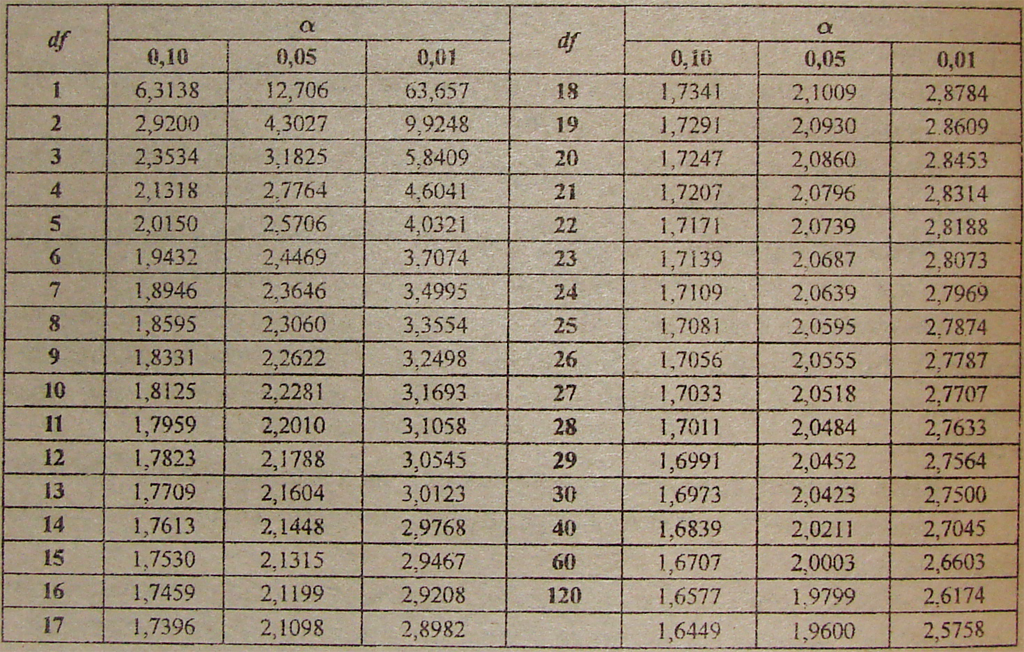
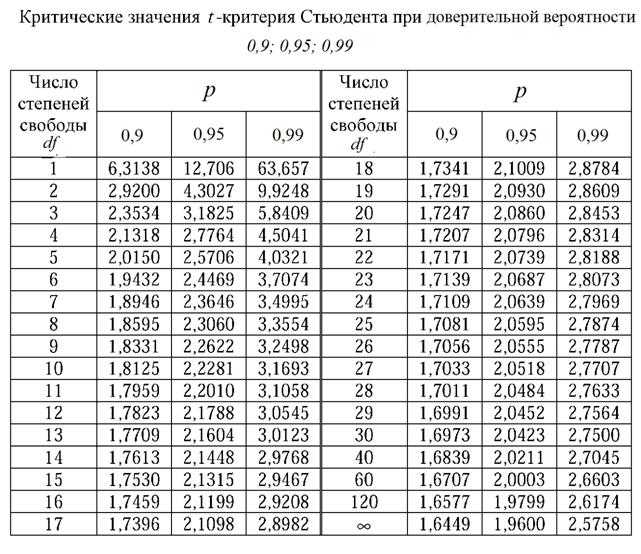
1.3.6.7.2. Верхние критические значения распределения Стьюдента t

1.3.6.7.2. Верхние критические значения Стьюдента-t Распределение

1. Исследовательский анализ данных
1.3. Методы ЭДА
1.3.6. Распределения вероятностей
1.3.6.7. Таблицы распределения вероятностей

1.3.6.7.2. Верхние критические значения Стьюдента-t Распределение

Как использовать эту таблицу

Эта таблица содержит верхние критические значения Студенческая т -раздача. Верхний критические значения рассчитываются с помощью функция процентной точки. Ввиду симметрии t -распределения эту таблицу можно использовать как для односторонних (нижний и верхний), так и для двусторонних тестов с использованием соответствующее значение .

Уровень значимости, , равен продемонстрировано на графике ниже, на котором показано распределение t с 10 степени свободы. Наиболее часто используемый уровень значимости = 0,05. Для двустороннего теста мы вычисляем функцию процентной точки в /2 (0,025). Если абсолютное значение тестовой статистики больше верхнего критическое значение (0,025), то мы отвергаем нулевую гипотезу. Из-за симметрии t -распределения, мы только табулируем верхние критические значения в таблице ниже.

Учитывая указанное значение для :

Для двустороннего теста найдите столбец, соответствующий /2 и отклонить нулевая гипотеза, если абсолютное значение тестовой статистики равно больше, чем значение в таблицу ниже.
Для верхнего одностороннего теста найдите столбец, соответствующий и отвергнуть ноль гипотеза, если тестовая статистика больше табличной стоимость.
Для нижнего одностороннего теста найдите столбец, соответствующий и отвергнуть ноль гипотеза, если тестовая статистика меньше, чем отрицательная табличное значение.

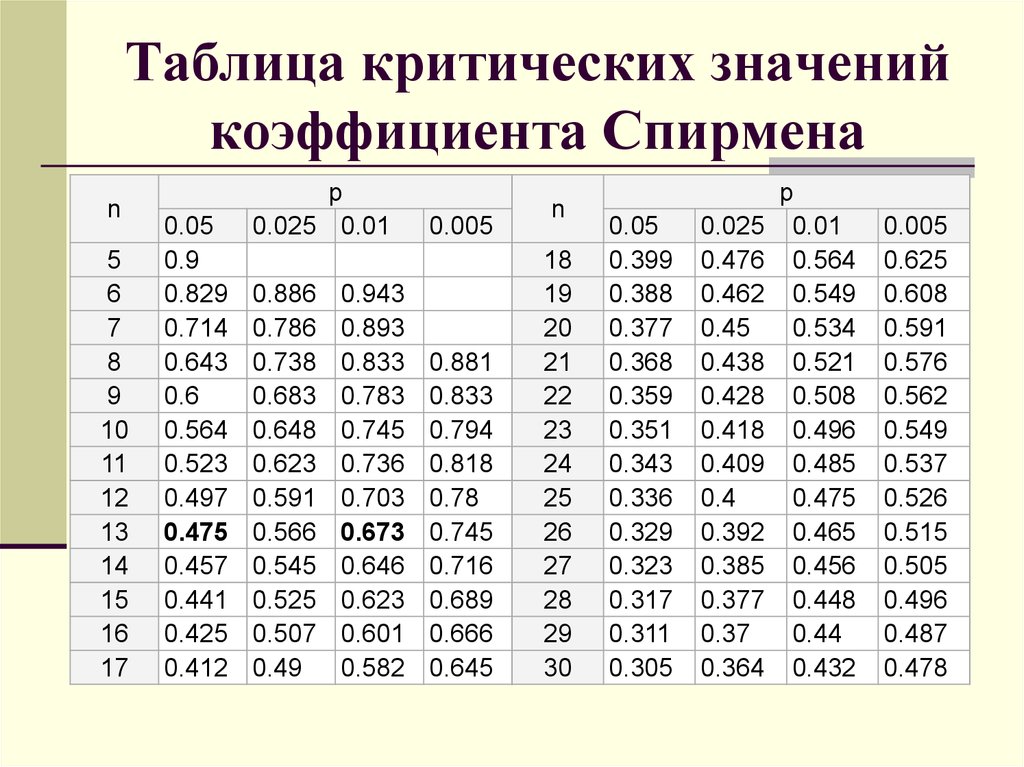
Верхние критические значения распределения Стьюдента со степенями свобода

           Вероятность превышения критического значения
           0,10 0,05 0,025 0,01 0,005 0,001
 
 
  1. 3,078 6,314 12,706 31,821 63,657 318,313
  2. 1,886 2,920 4,303 6,965 9,925 22,327
  3. 1,638 2,353 3,182 4,541 5,841 10,215
  4. 1,533 2,132 2,776 3,747 4,604 7,173
  5. 1,476 2,015 2,571 3,365 4,032 5,893
  6. 1,440 1,943 2,447 3,143 3,707 5,208
  7. 1,415 1,895 2,365 2,998 3,499 4,782
  8. 1,397 1,860 2,306 2,896 3,355 4,499
  9. 1,383 1,833 2,262 2,821 3,250 4,296
 10. 1,372 1,812 2,228 2,764 3,169 4,143
 11. 1,363 1,796 2,201 2,718 3,106 4,024
 12. 1,356 1,782 2,179 2,681 3,055 3,929
 13. 1,350 1,771 2,160 2,650 3,012 3,852
 14. 1,345 1,761 2,145 2,624 2,977 3,787
 15. 1,341 1,753 2,131 2,602 2,947 3,733
 16. 1,337 1,746 2,120 2,583 2,921 3,686
 17. 1,333 1,740 2,110 2,567 2,898 3,646
 18. 1,330 1,734 2,101 2,552 2,878 3,610
 19.  1,328 1,729 2,093 2,539 2,861 3,579
 20. 1,325 1,725 2,086 2,528 2,845 3,552
 21. 1,323 1,721 2,080 2,518 2,831 3,527
 22. 1,321 1,717 2,074 2,508 2,819 3,505
 23. 1,319 1,714 2,069 2,500 2,807 3,485
 24. 1,318 1,711 2,064 2,492 2,797 3,467
 25. 1,316 1,708 2,060 2,485 2,787 3,450
 26. 1,315 1,706 2,056 2,4792,779 3,435
 27. 1,314 1,703 2,052 2,473 2,771 3,421
 28. 1,313 1,701 2,048 2,467 2,763 3,408
 29. 1,311 1,699 2,045 2,462 2,756 3,396
 30. 1,310 1,697 2,042 2,457 2,750 3,385
 31. 1,309 1,696 2,040 2,453 2,744 3,375
 32. 1,309 1,694 2,037 2,449 2,738 3,365
 33. 1,308 1,692 2,035 2,445 2,733 3,356
 34. 1,307 1,691 2,032 2,441 2,728 3,348
 35. 1,306 1,690 2,030 2,438 2,724 3,340
 36. 1,306 1,688 2,028 2,434 2,7193.333
 37. 1,305 1,687 2,026 2,431 2,715 3,326
 38. 1,304 1,686 2,024 2,429 2,712 3,319
 39. 1,304 1,685 2,023 2,426 2,708 3,313
 40. 1,303 1,684 2,021 2,423 2,704 3,307
 41. 1,303 1,683 2,020 2,421 2,701 3,301
 42. 1,302 1,682 2,018 2,418 2,698 3,296
 43. 1,302 1,681 2,017 2,416 2,695 3,291
 44.  1,301 1,680 2,015 2,414 2,692 3,286
 45. 1,301 1,679 2,014 2,412 2,690 3,281
 46. 1.300 1.679 2.013 2.410 2.687 3.277
 47. 1.300 1.678 2.012 2.408 2.685 3.273
 48. 1,299 1,677 2,011 2,407 2,682 3,269
 49. 1,299 1,677 2,010 2,405 2,680 3,265
 50. 1,299 1,676 2,009 2,403 2,678 3,261
 51. 1,298 1,675 2,008 2,402 2,676 3,258
 52. 1,298 1,675 2,007 2,400 2,674 3,255
 53. 1,298 1,674 2,006 2,399 2,672 3,251
 54. 1,297 1,674 2,005 2,397 2,670 3,248
 55. 1,297 1,673 2,004 2,396 2,668 3,245
 56. 1,297 1,673 2,003 2,395 2,667 3,242
 57. 1,297 1,672 2,002 2,394 2,665 3,239
 58. 1,296 1,672 2,002 2,392 2,663 3,237
 59. 1,296 1,671 2,001 2,391 2,662 3,234
 60. 1,296 1,671 2,000 2,390 2,660 3,232
 61. 1,296 1,670 2,000 2,389 2,659 3,229
 62. 1,295 1,670 1,999 2,388 2,657 3,227
 63. 1,295 1,669 1,998 2,387 2,656 3,225
 64. 1,295 1,669 1,998 2,386 2,655 3,223
 65. 1,295 1,669 1,997 2,385 2,654 3,220
 66. 1,295 1,668 1,997 2,384 2,652 3,218
 67. 1,294 1,668 1,996 2,383 2,651 3,216
 68. 1,294 1,668 1,995 2,382 2,650 3,214
 69.  1,294 1,667 1,995 2,382 2,649 3,213
 70. 1,294 1,667 1,994 2,381 2,648 3,211
 71. 1,294 1,667 1,994 2,380 2,647 3,209
 72. 1,293 1,666 1,993 2,379 2,646 3,207
 73. 1,293 1,666 1,993 2,379 2,645 3,206
 74. 1,293 1,666 1,993 2,378 2,644 3,204
 75. 1,293 1,665 1,992 2,377 2,643 3,202
 76. 1,293 1,665 1,992 2,376 2,642 3,201
 77. 1,293 1,665 1,991 2,376 2,641 3,199
 78. 1,292 1,665 1,991 2,375 2,640 3,198
 79. 1,292 1,664 1,990 2,374 2,640 3,197
 80. 1,292 1,664 1,990 2,374 2,639 3,195
 81. 1,292 1,664 1,990 2,373 2,638 3,194
 82. 1,292 1,664 1,989 2,373 2,637 3,193
 83. 1,292 1,663 1,989 2,372 2,636 3,191
 84. 1,292 1,663 1,989 2,372 2,636 3,190
 85. 1,292 1,663 1,988 2,371 2,635 3,189
 86. 1,291 1,663 1,988 2,370 2,634 3,188
 87. 1,291 1,663 1,988 2,370 2,634 3,187
 88. 1,291 1,662 1,987 2,369 2,633 3,185
 89. 1,291 1,662 1,987 2,369 2,632 3,184
 90. 1,291 1,662 1,987 2,368 2,632 3,183
 91. 1,291 1,662 1,986 2,368 2,631 3,182
 92. 1,291 1,662 1,986 2,368 2,630 3,181
 93. 1,291 1,661 1,986 2,367 2,630 3,180
 94.  1,291 1,661 1,986 2,367 2,629 3,179
 95. 1,291 1,661 1,985 2,366 2,629 3,178
 96. 1,290 1,661 1,985 2,366 2,628 3,177
 97. 1,290 1,661 1,985 2,365 2,627 3,176
 98. 1,290 1,661 1,984 2,365 2,627 3,175
 99. 1,290 1,660 1,984 2,365 2,626 3,175
100. 1,290 1,660 1,984 2,364 2,626 3,174
         1,282 1,645 1,960 2,326 2,576 3,090

Выбранные критические значения t-распределения



Дом	Лаборатория Исследования	Ведение учета, Письмо, и анализ данных	Лаборатория Методы
	Обзор Микроскоп исследования Жгутики эксперимент Лаборатория математика Кровь фракционирование Гель электрофорез Белок гель-анализ Митохондрии Концепции/ теория	Обзор Хранение лабораторный блокнот Написание исследований бумаги Размеры и единицы измерения Использование рисунки (графики) Примеры графиков Экспериментальный ошибка Представление ошибка Подача заявки статистика	Обзор Принципы микроскопии Растворы и разведения Белок анализы Спектрофотометрия Фракционирование и центрифугирование Радиоизотопы и обнаружение

Статистические тесты Непарный (независимый) t-тест парный t-тест Учебное пособие по использованию t-тестов Тест хи-квадрат примеры задач решения типовых задач Столы Критические значения (хи-квадрат) Критические значения (t-критерий)	Тест является двусторонним, если вы задаете вопрос: «Отличается ли популяция 1 от население 2′. Тогда, если среднее значение для населения 1 значительно больше или меньше чем для населения 2, вы отвергаете нулевую гипотезу. Если вы спросите просто, истинное среднее значение для населения 1 больше, чем для населения 2, то вы отвергаете нулевую гипотезу, только если экспериментальное среднее для популяция 1 оказалась значительно больше. Это может быть значительно меньше, но вы не задавали этот вопрос. Это было бы однобоко тестовое задание. Для двустороннего теста, если вычисленное значение t превышает табличное значение, затем укажите значение p в таблице. Для одностороннего теста значение p делится на два. Итак, п В таблицу следует включить значения для p=0,1, чтобы односторонний тест можно провести на уровне p=0,05, но мы никогда не делаю таких тестов в моем классе, так зачем загромождать стол?
	Авторское право и предполагаемое использование посетителей: чтобы гарантировать, что ваше сообщение не будет ошибочно принято за СПАМ, в теме письма укажите аббревиатуру «Bios211». No related posts. Навигация по записям Предыдущая статья0 5 м это сколько см: 0.5 м сколько см — решение и ответ! Следующая статья0 умножить на бесконечность равно: Неопределенность вида ноль умножить на бесконечность Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт Найти: Рубрики Геометрия Математика Физика Химия Школьная жизнь Разное © 2015 - 2019 Муниципальное казённое общеобразовательное учреждение «Таловская средняя школа» Карта сайта

t критерий стьюдента таблица

Таблицы критических значений — Методы математической статистики — — Каталог статей

1.3.6.7.2. Верхние критические значения распределения Стьюдента t

1.3.6.7.2.

Верхние критические значения Стьюдента-t Распределение

Выбранные критические значения t-распределения

Статистические тесты

Столы

Добавить комментарий Отменить ответ