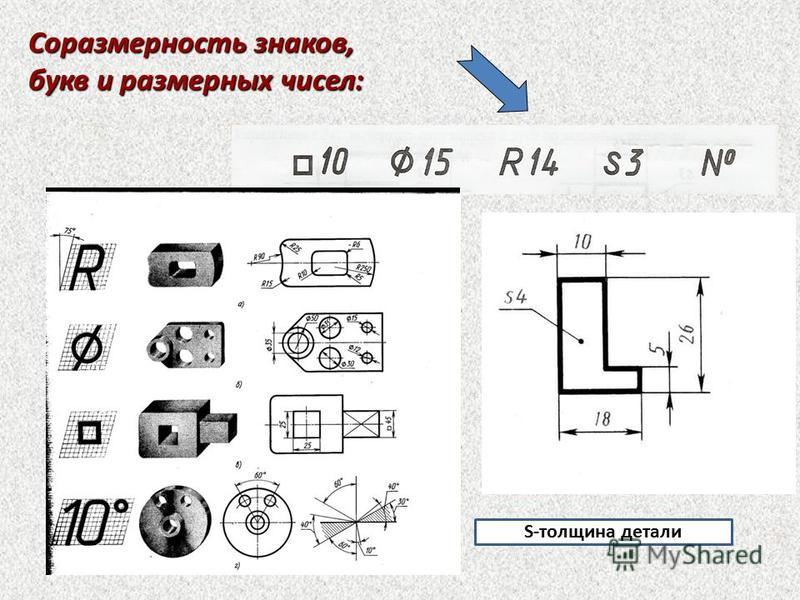
Диаметр — что это такое
Обновлено 22 июля 2021 Просмотров: 126 876 Автор: Дмитрий ПетровЗдравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Сегодня мы поговорим о том, что такое ДИАМЕТР. Это одно из базовых понятий в математике, которое начинают изучать еще в 3-м классе.
Но и повседневной жизни он встречается настолько часто, что знать его просто необходимо.
Диаметр — это…
Диаметр – это в первую очередь, хорда. Так называют отрезок (что это?) прямой, который соединяет две определенные точки. В нашем случае эти точки располагаются на максимально отдаленном друг от друга расстоянии на окружности, благодаря чему хорда проходит через ее центр.
В то же время диаметром еще называют и длину это самой хорды. Кстати, аналогичные определения применимы не только к окружностям, но и к другим геометрическим фигурам, таким как шар или сфера.
Графически это выглядит вот так:
Само слово «диаметр», как и многие термины в нашем языке, пришло из Древней Греции. Ведь именно в этой стране жили прославленные математики, такие как Евклид, Пифагор, Архимед, Платон. Так вот, греческое слово можно перевести как «поперечник».
Ведь именно в этой стране жили прославленные математики, такие как Евклид, Пифагор, Архимед, Платон. Так вот, греческое слово можно перевести как «поперечник».
Интересно, что во многих современных языках есть также похожие слова. Например, на латыни это «diametrus». А в русском языке мы нередко употребляем слово «диаметральный».
Например, говорим «диаметральные взгляды» или «диаметральные точки зрения», подразумевая совершенно противоположное отношение к чему-либо. Ну, точно как противоположные точки на окружности, разделенные диаметром.
Обозначения и символ диаметра
Диаметр имеет несколько сокращенных обозначений.
Например, если речь идет о математике, то в ней чаще всего употребляется латинская буква «D». Причем допускается как прописное написание этой буквы, так и строчное – «d». Второй вариант даже чаще встречается в задачках.
Например, это может выглядеть так:
d = 12 см или D = 12 см
А вот если говорить о бытовом понятии «диаметра», то тут уже чаще используется другой символ. Это – перечеркнутая буква «О».
Это – перечеркнутая буква «О».
Именно такой знак вы наверняка увидите, когда речь идет о трубах, о размере сверла и так далее. И записываются они так:
Ø6, Ø8, Ø12, Ø15, Ø20, Ø100
По умолчанию считается, что подобные обозначения всегда считаются в миллиметрах.
Стоит сказать, что символа «Ø» нет на обычной раскладке клавиатуры. И чтобы напечатать его в тексте, нужно или открыть специальный раздел «дополнительные символы» в программе Word, или просто скопировать откуда-нибудь, а потом вставить.
Радиус и другие величины, связанные с диаметром
Главной величиной, которая неизменно связана с диаметром, является радиус.
Радиус – это расстояние от центра окружности до любой точки на дуге окружности. Соответственно, радиусом также называют и длину этого отрезка.
Радиус обозначается буквой «R» или «r». И он всегда равен половине диаметра. В математике это уравнение записывают как:
D = 2R или R = D/2
Еще одна важная величина – длина окружности. Это расстояние всей дуги окружности. Оно обозначается буквой «С». Чтобы рассчитать ее, нужно пользоваться простой формулой:
Это расстояние всей дуги окружности. Оно обозначается буквой «С». Чтобы рассчитать ее, нужно пользоваться простой формулой:
С = 2πR или С = πD
Где «π», как многие знают, это математическая константа. И считать ее принято как 3,14, хотя после запятой там бесконечное количество знаков.
И наконец, еще одна величина – площадь окружности (круга). Это размер всего, что находится внутри ее границ. Обозначается она буквой «S». И чтобы ее вычислить, опять же надо воспользоваться определенной формулой:
S=πR²
Соответственно, эти формулы можно и перевернуть. То есть, зная длину или площадь окружности, всегда можно высчитать ее диаметр.
Интересные факты о диаметре
Первое документальное упоминание слова «диаметр» в России относится к 1720 году. И записано оно было в морском уставе. Хотя это неудивительно, так как моряки просто обязаны были разбираться в подобных математических задачах.
И записано оно было в морском уставе. Хотя это неудивительно, так как моряки просто обязаны были разбираться в подобных математических задачах.
Диаметр Земли составляет 12 543 километра. Это огромное расстояние. Но и оно кажется маленьким, если сравнить, например, с Солнцем. А у него диаметр составляет 1 390 000 километров, что в 109 раз больше земного.
Диаметр 10-копеечных монет в нашей стране не менялись на протяжении сотни лет. Он составляет 17,5 миллиметров. Таким он был еще при Николае II, таким же и в советское время, таким же остался и сейчас.
Вот и все, что мы хотели рассказать о таком понятии, как диаметр. До новых встреч на страницах нашего блога.
Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru
Эта статья относится к рубрикам:
- Математика
Обозначение: высота, ширина, длина. Ширина
Построение чертежей — дело непростое, но без него в современном мире никак. Ведь чтобы изготовить даже самый обычный предмет (крошечный болт или гайку, полку для книг, дизайн нового платья и подобное), изначально нужно провести соответствующие вычисления и нарисовать чертеж будущего изделия. Однако часто составляет его один человек, а занимается изготовлением чего-либо по этой схеме другой.
Однако часто составляет его один человек, а занимается изготовлением чего-либо по этой схеме другой.
Чтобы не возникло путаницы в понимании изображенного предмета и его параметров, во всем мире приняты условные обозначения длины, ширины, высоты и других величин, применяемых при проектировании. Каковы они? Давайте узнаем.
Величины
Площадь, длина, ширина, высота и другие обозначения подобного характера являются не только физическими, но и математическими величинами.
Единое их буквенное обозначение (используемое всеми странами) было уставлено в середине ХХ века Международной системой единиц (СИ) и применяется по сей день. Именно по этой причине все подобные параметры обозначаются латинскими, а не кириллическими буквами или арабской вязью. Чтобы не создавать отдельных трудностей, при разработке стандартов конструкторской документации в большинстве современных стран решено было использовать практически те же условные обозначения, что применяются в физике или геометрии.
Любой выпускник школы помнит, что в зависимости от того, двухмерная или трехмерная фигура (изделие) изображена на чертеже, она обладает набором основных параметров. Если присутствуют два измерения — это ширина и длина, если их три – добавляется еще и высота.
Итак, для начала давайте выясним, как правильно длину, ширину, высоту обозначать на чертежах.
Ширина
Как было сказано выше, в математике рассматриваемая величина является одним из трех пространственных измерений любого объекта, при условии что его замеры производятся в поперечном направлении. Так чем знаменита ширина? Обозначение буквой «В» она имеет. Об этом известно во всём мире. Причем, согласно ГОСТу, допустимо применение как заглавной, так и строчной латинских литер. Часто возникает вопрос о том, почему именно такая буква выбрана. Ведь обычно сокращение производится по первой букве латинского, греческого или английского названия величины. При этом ширина на английском будет выглядеть как «width».
Вероятно, здесь дело в том, что данный параметр наиболее широкое применение изначально имел в геометрии.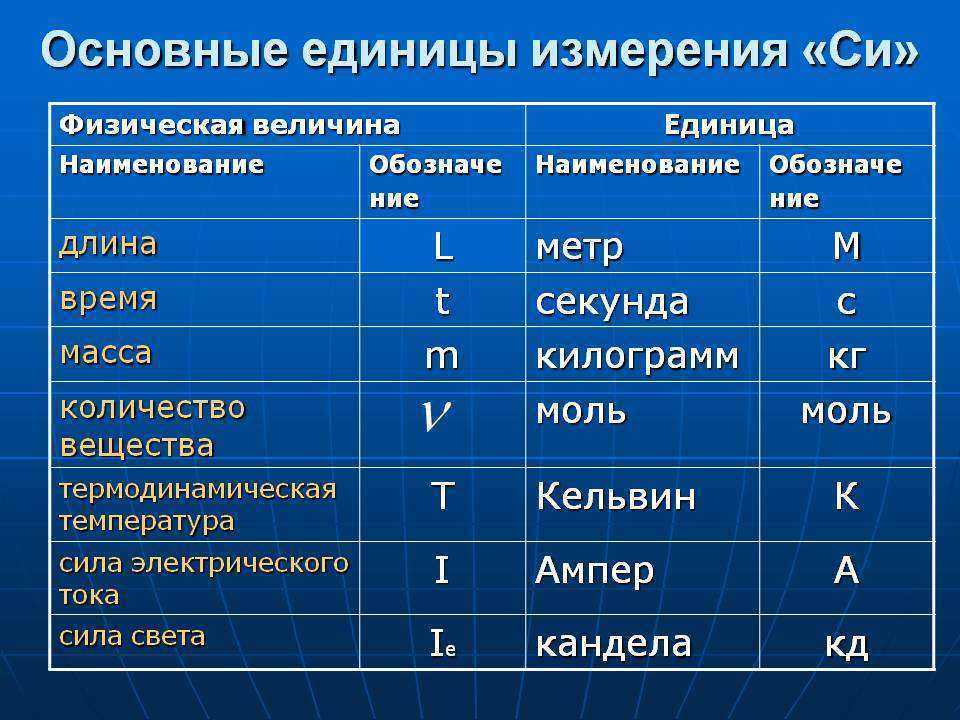 В этой науке, описывая фигуры, часто длину, ширину, высоту обозначают буквами «а», «b», «с». Согласно этой традиции, при выборе литера «В» (или «b») была заимствована системой СИ (хотя для других двух измерений стали применять отличные от геометрических символы).
В этой науке, описывая фигуры, часто длину, ширину, высоту обозначают буквами «а», «b», «с». Согласно этой традиции, при выборе литера «В» (или «b») была заимствована системой СИ (хотя для других двух измерений стали применять отличные от геометрических символы).
Большинство полагает, что это было сделано, дабы не путать ширину (обозначение буквой «B»/«b») с весом. Дело в том, что последний иногда именуется как «W» (сокращение от английского названия weight), хотя допустимо использование и других литер («G» и «Р»). Согласно международным нормам системы СИ, измеряется ширина в метрах или кратных (дольных) их единицах. Стоит отметить, что в геометрии иногда также допустимо использовать «w» для обозначения ширины, однако в физике и остальных точных науках такое обозначение, как правило, не применяется.
Длина
Как уже было указано, в математике длина, высота, ширина – это три пространственных измерения. При этом, если ширина является линейным размером в поперечном направлении, то длина — в продольном. Рассматривая ее как величину физики можно понять, что под этим словом подразумевается численная характеристика протяжности линий.
Рассматривая ее как величину физики можно понять, что под этим словом подразумевается численная характеристика протяжности линий.
В английском языке этот термин именуется length. Именно из-за этого данная величина обозначается заглавной или строчной начальной литерой этого слова — «L». Как и ширина, длина измеряется в метрах или их кратных (дольных) единицах.
Высота
Наличие этой величины указывает на то, что приходится иметь дело с более сложным — трехмерным пространством. В отличие от длины и ширины, высота численно характеризует размер объекта в вертикальном направлении.
На английском она пишется как «height». Поэтому, согласно международным нормам, ее обозначают латинской литерой «Н»/«h». Помимо высоты, в чертежах иногда эта буква выступает и как глубины обозначение. Высота, ширина и длина – все все эти параметры измеряются в метрах и их кратных и дольных единицах (километры, сантиметры, миллиметры и т. п.).
Радиус и диаметр
Помимо рассмотренных параметров, при составлении чертежей приходится иметь дело и с иными.
Например, при работе с окружностями возникает необходимость в определении их радиуса. Так именуется отрезок, который соединяет две точки. Первая из них является центром. Вторая находится непосредственно на самой окружности. На латыни это слово выглядит как «radius». Отсюда и общепринятое сокращение: строчная или заглавная «R»/«r».
Чертя окружности, помимо радиуса часто приходится сталкиваться с близким к нему явлением – диаметром. Он также является отрезком, соединяющим две точки на окружности. При этом он обязательно проходит через центр.
Численно диаметр равен двум радиусам. По-английски это слово пишется так: «diameter». Отсюда и сокращение – большая или маленькая латинская буква «D»/«d». Часто диаметр на чертежах обозначают при помощи перечеркнутого круга – «Ø».
Хотя это распространенное сокращение, стоит иметь в виду, что ГОСТ предусматривает использование только латинской «D»/«d».
Толщина
Большинство из нас помнят школьные уроки математики. Ещё тогда учителя рассказывали, что, латинской литерой «s» принято обозначать такую величину, как площадь. Однако, согласно общепринятым нормам, на чертежах таким способом записывается совсем другой параметр – толщина.
Ещё тогда учителя рассказывали, что, латинской литерой «s» принято обозначать такую величину, как площадь. Однако, согласно общепринятым нормам, на чертежах таким способом записывается совсем другой параметр – толщина.
Почему так? Известно, что в случае с высотой, шириной, длиной, обозначение буквами можно было объяснить их написанием или традицией. Вот только толщина по-английски выглядит как «thickness», а в латинском варианте — «crassities». Также непонятно, почему, в отличие от других величин, толщину можно обозначать только строчной литерой. Обозначение «s» также применяется при описании толщины страниц, стенок, ребер и так далее.
Периметр и площадь
В отличие от всех перечисленных выше величин, слово «периметр» пришло не из латыни или английского, а из греческого языка. Оно образовано от «περιμετρέο» («измерять окружность»). И сегодня этот термин сохранил свое значение (общая длина границ фигуры). Впоследствии слово попало в английский язык («perimeter») и закрепилось в системе СИ в виде сокращения буквой «Р».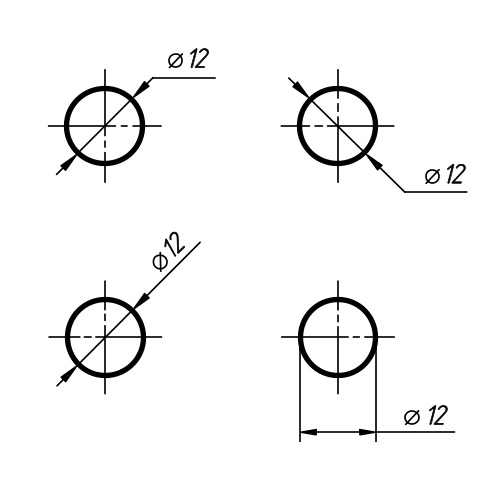
Площадь — это величина, показывающая количественную характеристику геометрической фигуры, обладающей двумя измерениями (длиной и шириной). В отличие от всего перечисленного ранее, она измеряется в квадратных метрах (а также в дольных и кратных их единицах). Что касается буквенного обозначения площади, то в разных сферах оно отличается. Например, в математике это знакомая всем с детства латинская литера «S». Почему так – нет информации.
Некоторые по незнанию думают, что это связано с английским написанием слова «square». Однако в нем математическая площадь – это «area», а «square» — это площадь в архитектурном понимании. Кстати, стоит вспомнить, что «square» — название геометрической фигуры «квадрат». Так что стоит быть внимательным при изучении чертежей на английском языке. Из-за перевода «area» в отдельных дисциплинах в качестве обозначения применяется литера «А». В редких случаях также используется «F», однако в физике данная буква означает величину под названием «сила» («fortis»).
Другие распространенные сокращения
Обозначения высоты, ширины, длины, толщины, радиуса, диаметра являются наиболее употребляемыми при составлении чертежей. Однако есть и другие величины, которые тоже часто присутствуют в них. Например, строчное «t». В физике это означает «температуру», однако согласно ГОСТу Единой системы конструкторской документации, данная литера — это шаг (винтовых пружин, заклепочных соединений и подобного). При этом она не используется, когда речь идет о зубчатых зацеплениях и резьбе.
Заглавная и строчная буква «A»/«a» (согласно все тем же нормам) в чертежах применяется, чтобы обозначать не площадь, а межцентровое и межосевое расстояние. Помимо различных величин, в чертежах часто приходится обозначать углы разного размера. Для этого принято использовать строчные литеры греческого алфавита. Наиболее применяемые — «α», «β», «γ» и «δ». Однако допустимо использовать и другие.
Какой стандарт определяет буквенное обозначение длины, ширины, высоты, площади и других величин
Как уже было сказано выше, чтобы не было недопонимания при прочтении чертежа, представителями разных народов приняты общие стандарты буквенного обозначения. Иными словами, если вы сомневаетесь в интерпретации того или иного сокращения, загляните в ГОСТы. Таким образом вы узнаете, как правильно обозначается высота, ширины, длина, диаметр, радиус и так далее.
Иными словами, если вы сомневаетесь в интерпретации того или иного сокращения, загляните в ГОСТы. Таким образом вы узнаете, как правильно обозначается высота, ширины, длина, диаметр, радиус и так далее.
Для Российской Федерации таким нормативным документом является ГОСТ 2.321-84. Он был внедрен еще в марте 1984 г. (во времена СССР), взамен устаревшего ГОСТа 3452—59.
Значение, определение, свойства и примеры решения
Геометрия — это предмет, связанный с математикой. Благодаря этому предмету мы выучили различные формы и фигуры, изучили различные из них. Как геометрия помогает нам? Что ж, если вы стремитесь стать инженером, то это первый и основной шаг к вашему стремлению.
Диаметр – тема, которую мы подхватили, так как важность диаметра в геометрии нельзя недооценивать или недооценивать. В этом разделе мы узнаем о диаметре, определении диаметра, его свойствах и формуле. Мы также представим решенные примеры в этом содержании, чтобы учащиеся получили пользу.
Определение диаметра
Диаметр определяется как удвоенная длина радиуса окружности. Радиус измеряется от центра круга до конечной точки круга, тогда как расстояние диаметра измеряется от одного конца круга до другой точки на другом конце круга, это будет сделано с помощью прохождение через центр.
Диаметр обозначается буквой «D». На окружности круга есть и другие бесконечные точки, а это значит, что круг имеет бесконечное число диаметров, и каждый из этих диаметров круга имеет одинаковую длину. Здесь мы узнали определение диаметра, теперь мы узнаем определение диаметра в других аспектах следующим образом.
Диаметр круга
После изучения значения диаметра нам нужно наблюдать и изучать то же самое в других аспектах.
В геометрии круг — это двумерная фигура, в которой набор точек на поверхности круга находится на равном расстоянии от центральной точки. Расстояние, измеряемое от центра до любой точки поверхности, называется радиусом. Точно так же расстояние, измеренное от одной точки на поверхности круга до другой точки на поверхности круга, проходящей через центр, называется диаметром. Иными словами, диаметр в два раза больше радиуса. Следовательно, можно сказать, что диаметр — это самая длинная хорда окружности. Обозначения, которые используются для обозначения диаметра: «d», «φ», «D», «Dia».
Точно так же расстояние, измеренное от одной точки на поверхности круга до другой точки на поверхности круга, проходящей через центр, называется диаметром. Иными словами, диаметр в два раза больше радиуса. Следовательно, можно сказать, что диаметр — это самая длинная хорда окружности. Обозначения, которые используются для обозначения диаметра: «d», «φ», «D», «Dia».
Изображение Просмотр диаметра окружности
Определение диаметра Математика
Простейшее определение – Диаметр – это расстояние от одной точки окружности через центр окружности до другой точки на окружности. Это также самое длинное расстояние, измеренное по кругу. Кроме того, это в два раза больше радиуса.
Свойства диаметра
Свойства диаметра круга записываются следующим образом:
Диаметр — это самая длинная хорда любого круга.
Хорда диаметра делит окружность на две равные половины и таким образом образует две равные полуокружности.

Середина диаметра точно совпадает с центром окружности.
Радиус равен половине диаметра.
Символ диаметра
Φ — это символ, который используется в технике для обозначения диаметра. Этот символ обычно используется в технических спецификациях и чертежах. Φ25 мм означает, что диаметр круга равен 25 мм.
Диаметр круга с использованием длины окружности
Здесь мы можем легко вывести формулу диаметра через длину окружности. Формула для длины окружности $C=\pi d$ здесь, C обозначает длину окружности, d обозначает диаметр окружности, $\pi$ обозначает константу (3,141)
Формула диаметра, которая выполняется с использованием окружности: Диаметр = Окружность$\div\pi$
Диаметр окружности Используя радиус
Радиус — это длина отрезка, который проходит от центра круга до другой конечной точки на круге, а диаметр равен дважды — это измерение длины радиуса окружности.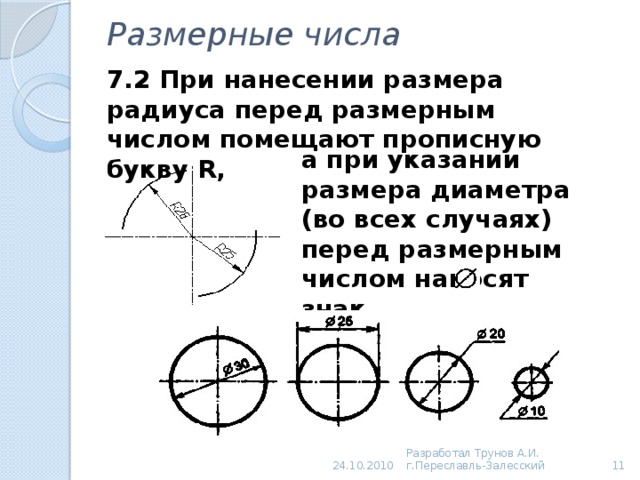 Здесь, следуя определению, формула для диаметра: $\mathtt{Диаметр} = \mathtt{Радиус}\times 2$. Мы подробно обсудим формулу диаметра в следующем разделе. 9{2}$.
Здесь, следуя определению, формула для диаметра: $\mathtt{Диаметр} = \mathtt{Радиус}\times 2$. Мы подробно обсудим формулу диаметра в следующем разделе. 9{2}$.
$\Rightarrow \frac{D}{2} = \sqrt{\frac{A}{\pi}} \\$
$\Rightarrow D = 2\times \sqrt{\frac{A}{\ pi}}$
Следовательно, формула диаметра круга с использованием площади $D = 2\times \sqrt{\frac{A}{\pi}}$, где A — площадь.
Решенные примеры
Ниже приведены задачи на нахождение диаметра круга.
Пример 1: Найдите диаметр круга, если его радиус равен 6 см.
Решение:
Дан радиус, R = 6 см
Мы знаем, что, если радиус известен, формула для расчета диаметра:
Д = 2р.
Подставляем в формулу R = 6 см, получаем
D = 2(6)
D = 12 см.
Пример 2: длина окружности 30 см. Вычислите диаметр круга.
Решение:
Дано: Окружность, C = 30 см.
Мы знаем, что
$D =\dfrac{C}{\pi}$
Теперь подставим C = 30 см и π= 3,14 в формулу,
$D =\dfrac{30}{3,14 }$
D = 9,55 (приблизительно)
Следовательно, диаметр круга равен 90,55 см (приблизительно).
Пример 3: Диаметр круглого бассейна составляет 7 футов. Какова окружность бассейна? Ответьте через число π.
Решение:
Дано: Диаметр = 7 футов
Мы знаем, что длина окружности = $\pi\times d$
Таким образом, длина окружности бассейна = $\pi\times 7$
Следовательно, окружность бассейна = $7\pi $ футов.
Практические задачи
1. Найдите радиус и диаметр следующей окружности.
A) Радиус 9 см, диаметр 18 см
B) Радиус 18 см, диаметр 9 см
C) Радиус 36 см, диаметр 18 см
D) Радиус 16 см, диаметр 38 см
2. Найдите радиус и диаметр следующего круга.
Найдите радиус и диаметр следующего круга.
A) Радиус 23 м, диаметр 98 м
B) Радиус 12 м, диаметр 24 м
C) Радиус 24 м, диаметр 24 м
D) Радиус 22 м, диаметр 23 м
3. Определите радиус, диаметр и хорда из заданной окружности.
A) Радиус LK, диаметр MK
B) Радиус LK, диаметр MN
C) Радиус LK, диаметр KN
D) Радиус MN, диаметр LK
3) B
Заключение
В этой статье мы узнали, что диаметр – это расстояние от одной точки окружности через центр окружности до другой точки на окружности. Это также самое длинное расстояние, измеренное по кругу. Диаметр в два раза больше радиуса окружности. Мы также узнали о диаметре, используя окружность, радиус и площадь круга. Надеюсь, вам понравилось!
Расмус — Математика, геометрия, урок 4
Расмус — Математика, геометрия, урок 4| 2006 Расмус Эхф | Геометрия — район | Печать |
Урок 4
Площадь и окружность круга
Длина черной линии, образующей окружность, называется
длина окружности.
Обозначается символом C.
Диаметр указан синей линией, показанной выше. это линия, проведенная через центр круга и обозначенная символом d
Радиус — это красные линии, показанные выше. радиус окружности — это расстояние от центра до края окружности. Это 1 / 2 диаметра и обозначен символом r.
Если измерить окружность и диаметр круга и разделить длину окружности на диаметр, вы получите число Пи, которое составляет около 3.14.
Пи часто обозначается греческой буквой π .
Древние греки использовали символ π для обозначения отношения длины окружности к диаметр круг. Если в вашем калькуляторе нет символ π , вы можете использовать округленное число 3.14 для π .
Некоторые формулы, которые полезно знать и понять.
| Символ | Имя | Формула | ||
π | Пи | |||
| д | Диаметр | и | ||
| С | Окружность | |||
| р | Радиус | |||
| А | Район | |||
Некоторые примеры
Пример 1.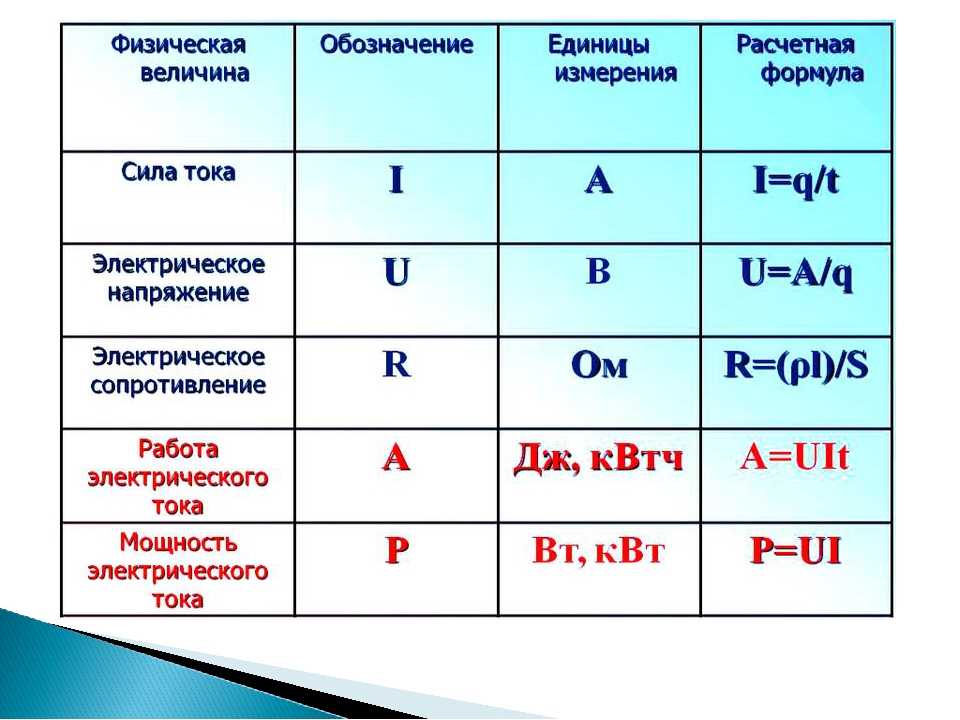
Найдите диаметр. д = 2 3 см = 6 см
Пример 2.
Найдите длину окружности. С = д пи = 6 см 3,14 = 18,8 см
Пример 3.
Найдите диаметр.
д= 18,8 3,14 = 6 см
Пример 4.
Площадь круга:
A = 5 м 5 м 3,14 78,5 м 2 (Примечание: символ означает примерно то же, что и).
На приведенной выше диаграмме площадь малого желтый квадрат составляет четверть площади большого квадрата.
| Если площадь заштрихованного квадрата равна | А = 5 м 5 м = 25 м 2 |
| то площадь г. большой квадрат | А = 4 25 м 2 =100 м 2 |
Вы видите, что площадь круга
меньше, чем у квадрата, так как круг помещается внутри него.