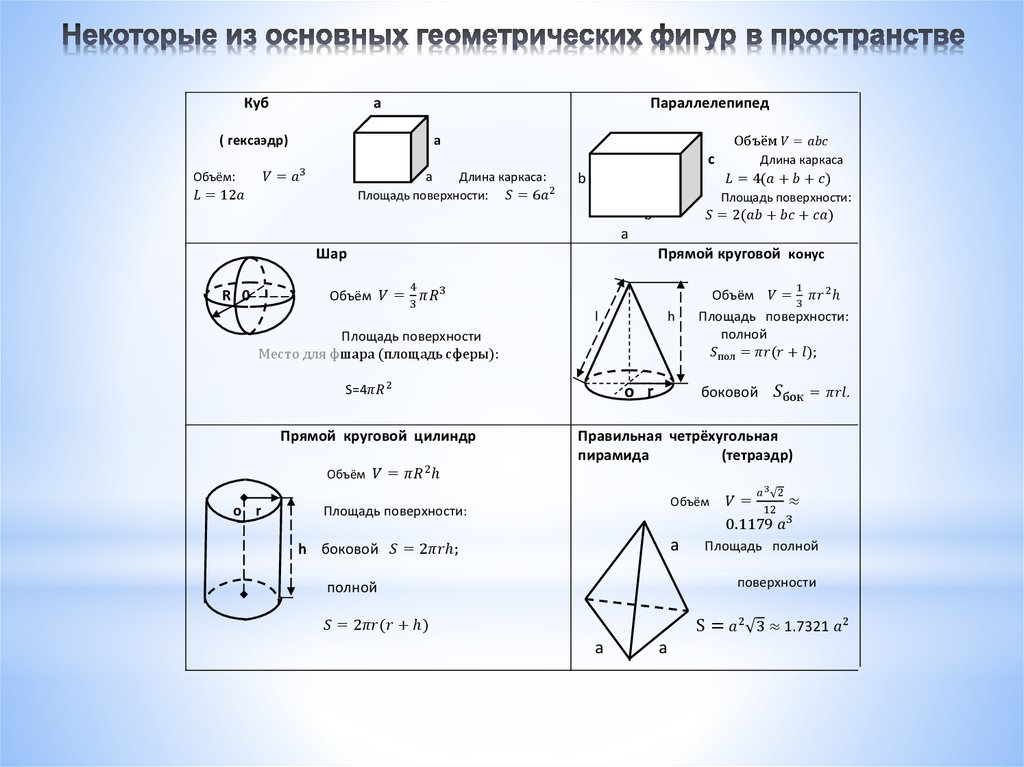
Раздел недели: Плоские фигуры. Свойства, стороны, углы, признаки, периметры, равенства, подобия, хорды, секторы, площади и т.д. | ||||
| Поиск на сайте DPVA Поставщики оборудования Полезные ссылки О проекте Обратная связь Ответы на вопросы. Оглавление Таблицы DPVA.ru — Инженерный Справочник | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация/ / Математический справочник / / Геометрические фигуры. Свойства, формулы: периметры, площади, объемы, длины. Треугольники, Прямоугольники и т. Поделиться:
Поиск в инженерном справочнике DPVA. Введите свой запрос: | |||
Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста. | ||||
Коды баннеров проекта DPVA.ru Консультации и техническая | Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса. Free xml sitemap generator Free xml sitemap generator | |||
Площади и объемы геометрических фигур
Похожие презентации:
Площадь фигуры. Измерение и единицы площади
Площади фигур
Площадь. Равновеликие и равносоставленные фигуры
Площади и объемы. Контрольный вопрос
Объемы геометрических тел
Единицы площади: квадратный километр, квадратный миллиметр, ар, гектар
Решение задач на нахождение площади геометрических фигур на сетке. ОГЭ . Задание № 19
Решение задач на нахождение площади геометрических фигур на сетке. ОГЭ
Единицы измерения площадей
Площадь. Равновеликие и равносоставленные фигуры
Математика
5 класс
Расшифруйте ребус:
Расшифруйте ребус:
18.05.20
Площади и
объемы
Расшифруйте ребус:
v = 15 км/ч
Формула пути
s = ? км
s = vt
t =4ч
Формулы
Запись какого-нибудь правила с помощью букв
называют формулой
v = 60 км/ч
t=?ч
s = 600 км
t=s:v
Формулы
v = ? км/ч
t=4ч
s = 24 км
v=s:t
Площадь.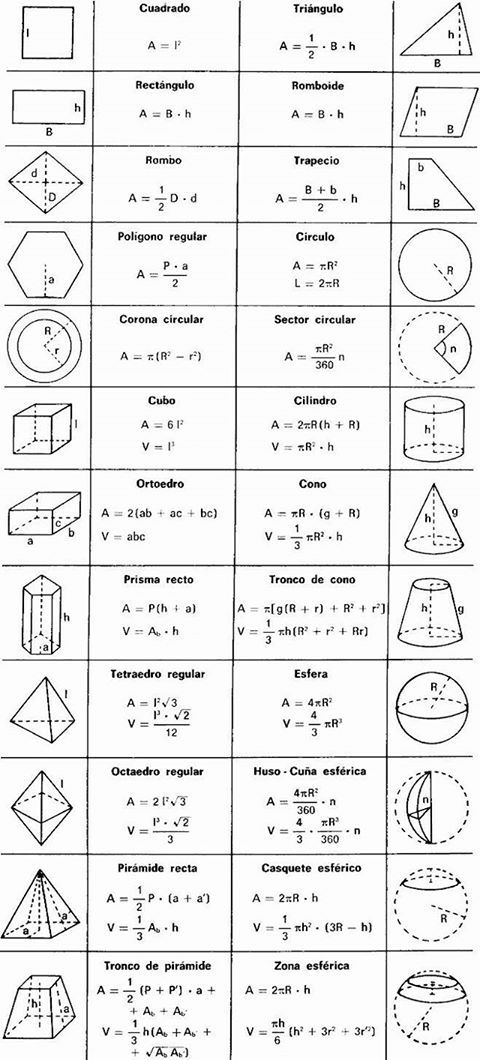 Формула площади прямоугольника
Формула площади прямоугольника
1 см
1 см
S= 1 см2
Площадь квадрата со стороной 1 см
называют квадратным сантиметром
S= 21 см2
квадратов со стороной 1 см, то её площадь
равна р см2
Площадь. Формула площади прямоугольника
4 см
а
b
S = ab
5 см
Чтобы найти площадь прямоугольника надо
умножить его длину на ширину
S = 5 ∙ 4 = 20 см2
Площадь. Формула площади прямоугольника
Две фигуры называются равными, если одну из
них можно так наложить на вторую, что эти
фигуры совпадут
Площади равных фигур равны.
Их периметры тоже равны.
Найдите одинаковые фигуры
Площадь. Формула площади прямоугольника
D
S
С
Q
R
P
А
N
M
В
Площадь всей фигуры равна сумме площадей её
частей
Площадь. Формула площади треугольника
С
D
b
А
а
В
Площадь треугольника равна половине площади
всего прямоугольника
S = ab : 2
Площадь.
 Формула площади квадрата
Формула площади квадратаКвадрат – это прямоугольник с равными сторонами
а
а
Площадь квадрата равна квадрату его стороны
S = a ∙ а = а2
Ответьте на вопросы:
1. Чему равна площадь фигуры, если эту фигуру
можно разбить на 18 квадратов со стороной 1см?
2. Назовите формулу площади прямоугольника.
3. Какие измерения надо провести, чтобы найти
площадь прямоугольника?
4. Какие фигуры называют равными?
5. Могут ли равные фигуры иметь различные
площади? А периметры?
6. Как найти площадь всей фигуры, зная площади
всех ее частей?
7. Назовите формулу площади квадрата.
Единицы измерения площадей
квадратный миллиметр – 1 мм2
квадратный сантиметр – 1 см2
квадратным дециметр – 1 дм2
квадратный метр – 1 м2
квадратный километр – 1 км2
гектар – 1 га
сотка – ар – 1 ар
Гектар – это площадь квадрата со стороной 100 м
Ар (сотка) – площадь квадрата со стороной 10 м
Единицы измерения площадей
1 см2 = 100 мм2
1 м2 = 100 дм2 = 10 000 см2 = 1 000 000 мм2
1 км2 = 100 га = 1 000 000 м2 = 100 000 000 дм2
1 а = 100 м2 = 10 000 дм2 = 1 000 000 см2
1 га = 10 000 м2 = 1 000 000 дм2
Если длина и ширина прямоугольника измерены в
разных единицах, то их надо выразить в одних
единицах
Единицы измерения площадей
С
D
14 см
8 м 30 см
А
В
а = 8 м 30 см = 830 см
b = 14 см
S − ? см2
S = ab
S = 830 ∙ 14 = 11 620 см2
Ответ: 11 620 см2
Единицы измерения площадей
С
D
30 см
А
6 дм
а = 6 дм
b = 30 см = 3 дм
S − ? дм2
S = ab
S = 6 ∙ 3 = 18 дм2
Ответ: 18 дм2
В
Ответьте на вопросы:
1.
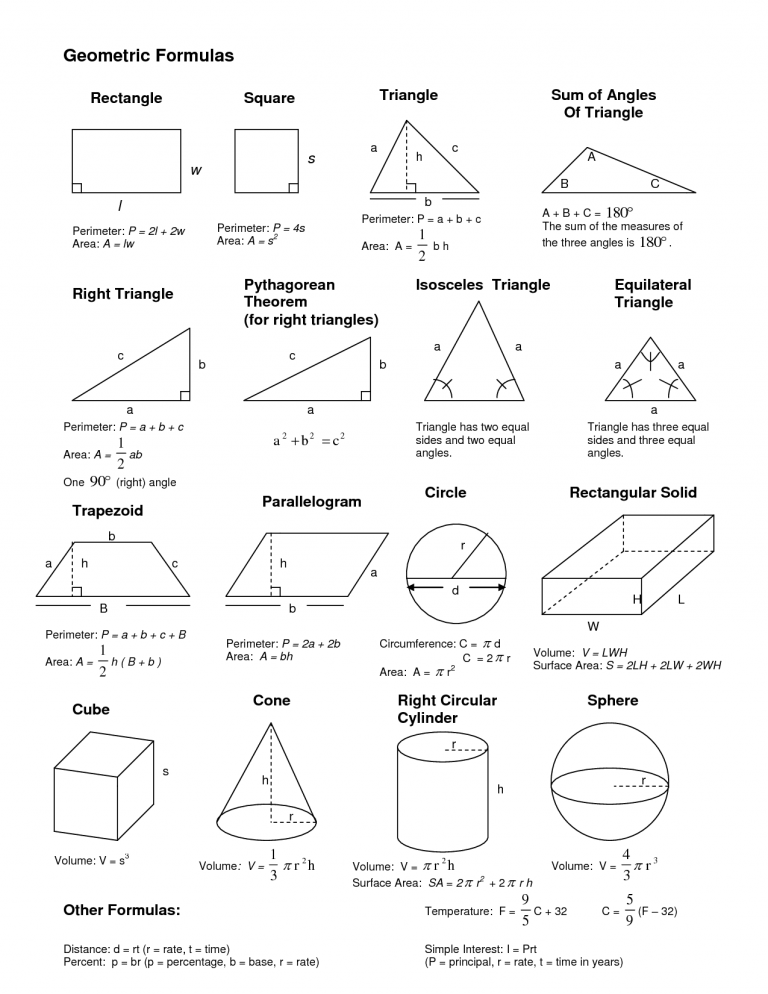 Назовите единицы измерения площадей.
Назовите единицы измерения площадей.2. Что такое квадратный метр; квадратный
дециметр; квадратный километр?
3. В каких единицах измеряют площади земельных
участков?
4. Что такое гектар?
5. Что такое ар (сотка)?
6. Сколько квадратных метров в гектаре?
7. Сколько гектаров в квадратном километре?
8. Объясните, почему 1 дм2 = 100 см2 = 10 000 мм2;
почему 1 км2 = 1 000 000 м2.
Найдите площади фигур
3 см
С
2 см
В
5 см
Н
D
3 см
4 см
4 см
А
F
E
Найдите площади фигур
4 см
X
2 см 1 см
T
3 см
S
M 2 см
2 см
K
2 см
Y
Z
4 см
3 см
R
P
N
Прямоугольный параллелепипед
Прямоугольный параллелепипед
Грани (6)
Поверхность прямоугольного параллелепипеда
состоит из 6 прямоугольников, каждый из
которых называют гранью прямоугольного
параллелепипеда.
Прямоугольный параллелепипед
Вершины (8)
Ребра (12)
Противоположные грани прямоугольного
параллелепипеда равны.
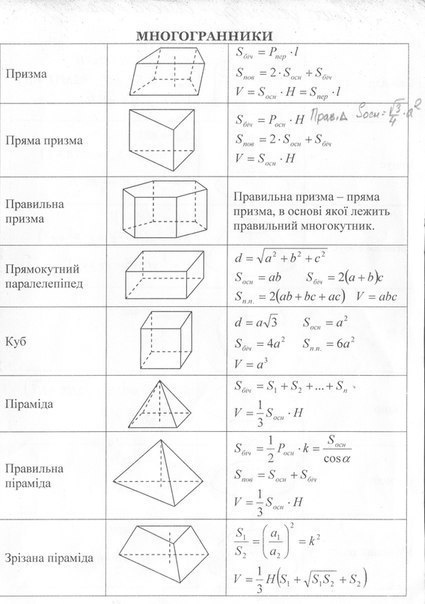
Стороны граней называют ребрами
параллелепипеда, а вершины граней – вершинами
параллелепипеда.
Прямоугольный параллелепипед
высота
ширина
длина
Прямоугольный параллелепипед имеет три
измерения – длину, ширину и высоту
КУБ
Куб – это прямоугольный параллелепипед, у
которого все измерения одинаковы
Ответьте на вопросы:
1. Приведите примеры предметов, имеющих форму
прямоугольного параллелепипеда.
2. Сколько граней имеет прямоугольный
параллелепипед?
3. Какую форму имеют эти грани?
4. Сколько ребер у прямоугольного параллелепипеда?
5. Сколько у него вершин?
6. Является ли куб прямоугольным
параллелепипедом?
7. Назовите единицы измерения площадей.
Важным свойством тела
является его вместимость.
Вместимость фигуры
характеризуют объемом.
За единицу измерения
объема принимают объем
единичного куба.
33. ЕДИНИЦЫ ОБЪЁМА
кубический миллиметр (1 мм3)кубический сантиметр (1 см3)
Объемы
кубическийединичных
дециметр
(1 дм3)
кубов
получают
кубический
метр
(1 м3)
названия
в
кубический километр
(1 км3)
1 дм³=1 л (литр) от
зависимости
выбранной единицы
длины ребра:
1
cм
1
см²
1
см³
1
см³
1
см³
1
см³
1
см³
35.
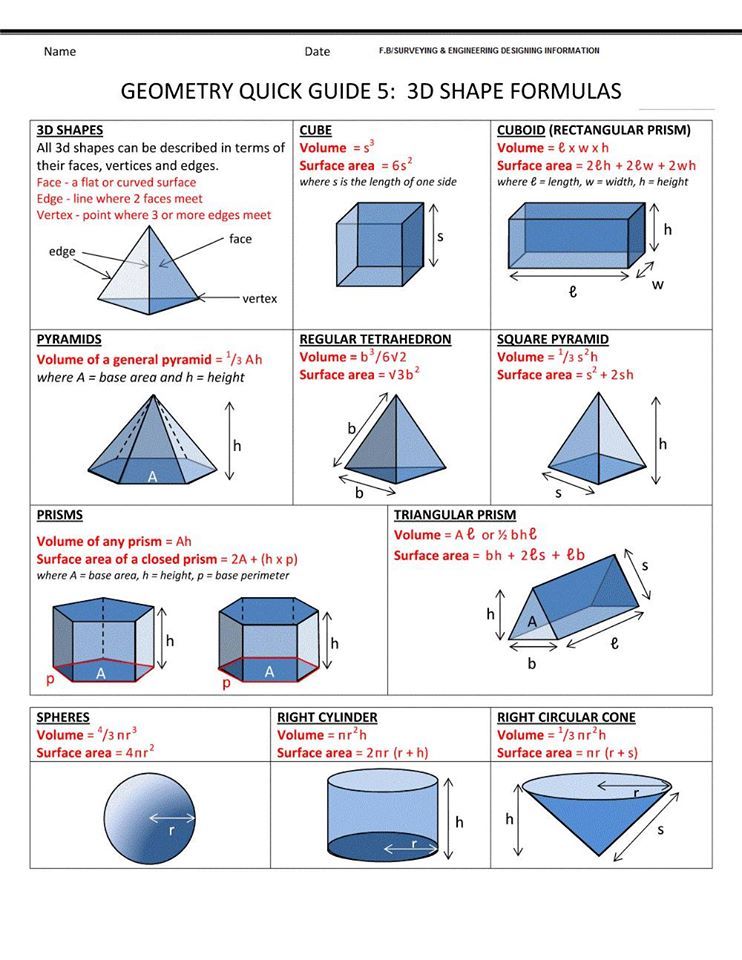 ЗАДАЧА 4
ЗАДАЧА 4(4×3)×2=24
см³
2
3
3
1 см³
4
3
4×3=12
cм³
а
а
с
в
V=abc
а
а
V=a³
Внимание! При вычислениях все
измерения должны быть выражены в
одинаковых единицах.
Урок окончен
До свидания!!!!
Спасибо за работу!
English Русский Правила
TIMES MODULE M11 — Площадь, объем и площадь поверхности
Проект улучшения математического образования в школах (TIMES)
вернуться к индексу
Площадь, объем и площадь поверхности
Измерение и геометрия: Модуль 11Year: 8-10
Июнь 2011 г.
PDF-версия модуля
Предполагаемые знания
- Знание площадей прямоугольников, треугольников, кругов и составных фигур.
- Определения параллелограмма и ромба.
- Знакомство с основными свойствами параллельных прямых.
- Знакомство с объемом прямоугольной призмы.
- Базовые знания о конгруэнтности и подобиях.

- Поскольку будут задействованы некоторые формулы, учащимся потребуется некоторый опыт работы с подстановкой, а также с дистрибутивным законом.
Мотивация
Площадь плоской фигуры является мерой пространства внутри нее. Вычисление площадей — важный навык, используемый многими людьми в повседневной работе. Строителям и торговцам часто необходимо продумать площади и размеры возводимых ими сооружений, а также архитекторам, дизайнерам и инженерам.
Хотя прямоугольники, квадраты и треугольники обычно встречаются в окружающем нас мире, встречаются и другие формы, такие как параллелограмм, ромб и трапеция. Рассмотрим, например, этот вид крыши с высоты птичьего полета.
Вид состоит из двух трапеций и двух треугольников.
Точно так же часто встречаются твердые тела, отличные от прямоугольной призмы. Пакет Toblerone ©
(с основанием на конце) является примером треугольной призмы, а масляный барабан
имеет форму цилиндра.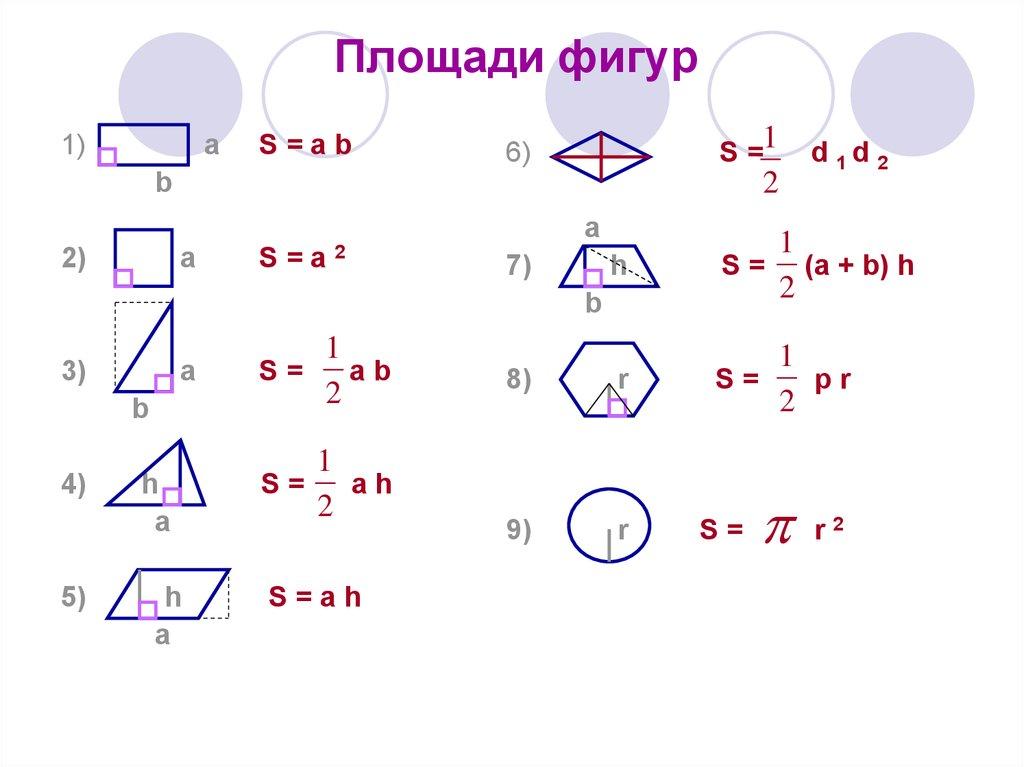 Важно уметь находить объемы таких твердых тел.
Важно уметь находить объемы таких твердых тел.
Медицинские специалисты измеряют такие параметры, как скорость кровотока (что делается с использованием скорости жидкости и площади поперечного сечения потока), а также размер опухолей и новообразований.
В физике площадь под графиком скорость-время показывает пройденное расстояние.
В этом модуле мы будем использовать простые идеи для получения ряда фундаментальных формул
для площадей и объемов. Учащиеся должны понять, почему формулы верны, и запомнить их.
Содержание
Площадь параллелограмма
Параллелограмм – это четырехугольник, у которого противоположные стороны равны и параллельны.
Мы можем легко найти площадь параллелограмма, зная его основание b и высоту h.
На приведенном ниже рисунке мы проводим диагональ BD и делим фигуру на два треугольника, каждый с длиной основания b и высотой h. Поскольку площадь каждого треугольника равна bh, общая площадь A равна
A= bh.
Обратите внимание, что два треугольника на диаграмме не только имеют одинаковую площадь, но и являются конгруэнтными треугольниками.
Некоторые учителя могут предпочесть установить формулу площади параллелограмма без использования формулы площади треугольника, чтобы вычислить площадь треугольника, используя формулу площади параллелограмма.
Это можно сделать, показав, что треугольник справа на левой диаграмме ниже можно расположить слева, чтобы сформировать прямоугольник, основание и высота которого такие же, как у параллелограмма, так что снова площадь равна равно бх.
Площадь трапеции
Трапеция – это четырехугольник, у которого одна пара противоположных сторон параллельна. (Название происходит от греческого слова, означающего стол.)
Мы можем найти площадь трапеции, если знаем длины двух параллельных сторон и перпендикулярное расстояние между этими двумя сторонами.
Как и в случае с параллелограммом, проводим одну из диагоналей.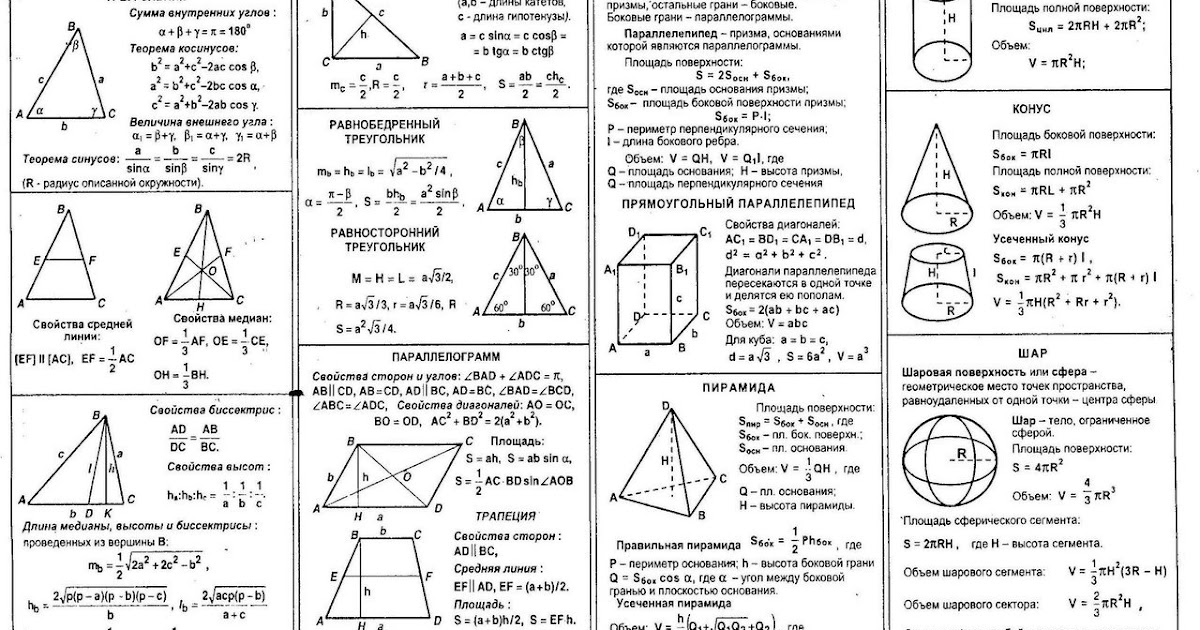 У нас тогда есть два треугольника, оба с высотой h, и один с основанием a, и один с основанием b.
У нас тогда есть два треугольника, оба с высотой h, и один с основанием a, и один с основанием b.
Таким образом, площадь трапеции A равна
А | = ах + чч | |
= ч(а+б). |
Таким образом, формула площади трапеции с параллельными сторонами a и b и перпендикулярным расстоянием h между ними равна
А = ч(а +b).
Это можно представить как «высоту, умноженную на среднее значение параллельных сторон».
щелкните для просмотра экрана
Упражнение 1
Вот еще один вывод формулы площади трапеции. Предположим, что ABCD
— трапеция.
Возьмем F за середину CD и проведем через нее прямую EG, параллельную AB.
а Объясните, почему треугольники CFG и DFE равны.
b Что это говорит нам о CG и ED?
cОбъясните, почему AE = (BC +AD).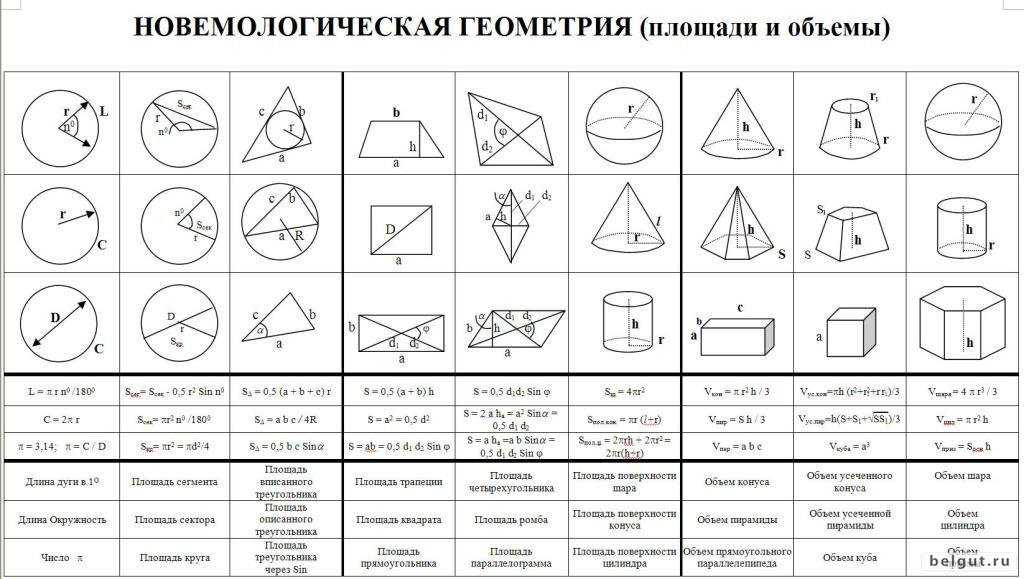
d Используйте формулу площади параллелограмма, чтобы вывести формулу площади трапеции.
щелкните для просмотра экрана
Упражнение 2
(В этом упражнении используются подобные треугольники).
На рисунке ABCD представляет собой трапецию, в которой AB параллельна DC, а расстояние между ними h. Точки E и F являются серединами AD и BC соответственно. AG перпендикулярна DC в G и пересекает EF в H. Пусть a = AB, b = DC и = EF.
а Покажите, что EF параллелен DC.
b Рассматривая треугольники AEH и ADG, покажите, что AH = HG = .
c Сравнивая площади трех образованных таким образом или иначе
трапеций, покажите, что площадь трапеции ABCD равна h.
Площадь ромба и воздушного змея
Ромб – четырехугольник, у которого все стороны равны. В модуле Ромбы, Воздушные змеи и Трапеции с помощью простых геометрических рассуждений мы показали
- противоположные стороны параллельны
- диагонали делят друг друга пополам под прямым углом
Таким образом, ромб является параллелограммом, и мы можем вычислить площадь ромба, используя формулу площади параллелограмма.
Теперь возьмем ромб с диагоналями длины x и y.
Поставив ромб на один угол, мы видим, что две диагонали разрезают ромб на четыре прямоугольных треугольника, из которых можно составить четыре прямоугольника внутри
большой прямоугольник.
Поскольку площадь восьми треугольников одинакова (действительно, все они конгруэнтны), площадь ромба равна половине площади большого прямоугольника, т. е. xy.
Следовательно, если x и y длины диагоналей ромба, то
Площадь ромба = xy.
Площадь ромба равна половине произведения длин его диагоналей.
щелкните для просмотра экрана
Упражнение 3
Предположим, что ABCD представляет собой ромб с одной диагональю 8 см и одной стороной 5 см, как показано на рисунке.
a Используйте теорему Пифагора, чтобы найти
длину другой диагонали.
b Отсюда найдите площадь ромба.
щелкните для просмотра экрана
Упражнение 4
Воздушный змей – это четырехугольник, у которого две пары смежных сторон равны.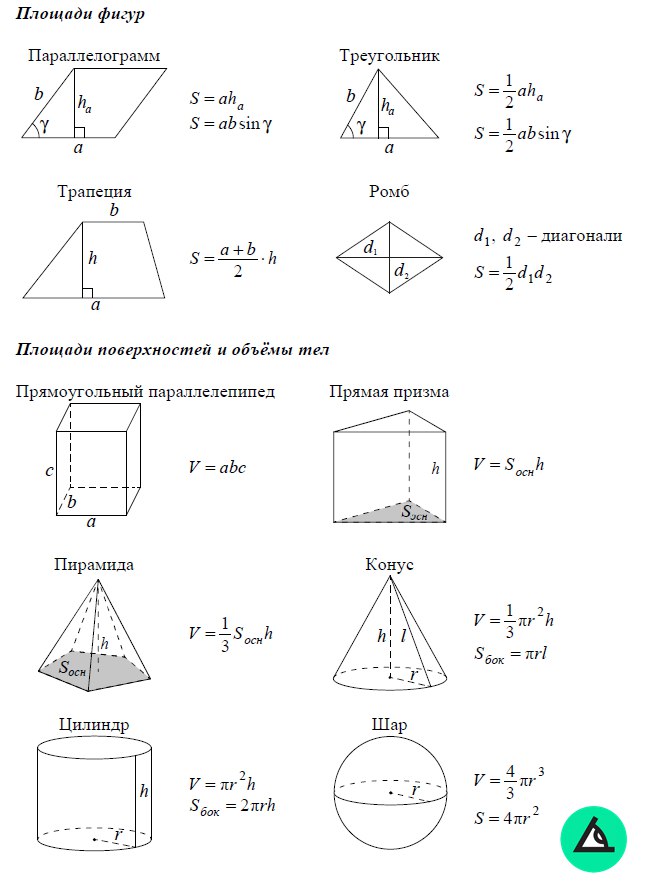
a Используйте конгруэнтность и два равнобедренных треугольника, чтобы показать, что диагонали воздушного змея перпендикулярны.
b Ясно, что мы можем собрать воздушного змея в форме
прямоугольник, площадь которого в два раза больше площади воздушного змея,
поэтому
площадь воздушного змея = xy,
, где x и y — длины диагоналей воздушного змея.
Пример
Найдите площадь каждой фигуры: (Все измерения даны в сантиметрах.)
a b c
Решения
a Площадь = × (13 + 3) × (6 + 6) = 96 см2.
b Площадь = × 5 × (7 + 15) = 55 см2.
c Площадь = × (8 + 8) × (6 + 6) = 96 см2.
Площадь полигонов
Любой многоугольник можно разбить на треугольники. Следовательно, площадь любого многоугольника определена и может быть рассчитана путем вычисления площади каждого треугольника.
Объем призмы
Многогранник – это тело, ограниченное многоугольниками. Прямая призма — это многогранник, у которого две конгруэнтные и параллельные грани (называемые основанием и вершиной), а все остальные грани — прямоугольники.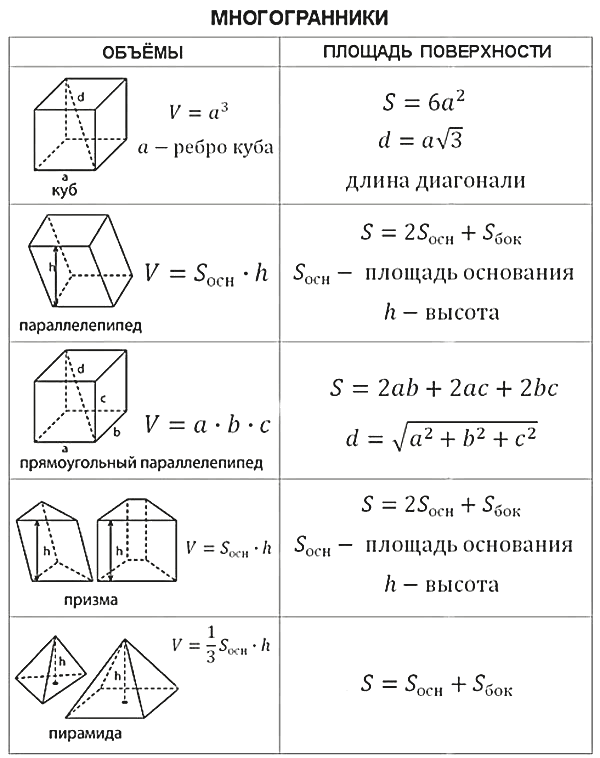 Это означает, что когда на основание поставлена прямая призма, все стенки представляют собой вертикальные прямоугольники. Обычно мы говорим «призма», когда на самом деле имеем в виду «правильную призму». Призма имеет однородное поперечное сечение. Это означает, что когда вы делаете срезы твердого тела параллельно основанию, вы получаете многоугольники, конгруэнтные основанию. Таким образом, площадь каждого среза всегда одинакова. В прямоугольной призме поперечное сечение всегда прямоугольник.
Это означает, что когда на основание поставлена прямая призма, все стенки представляют собой вертикальные прямоугольники. Обычно мы говорим «призма», когда на самом деле имеем в виду «правильную призму». Призма имеет однородное поперечное сечение. Это означает, что когда вы делаете срезы твердого тела параллельно основанию, вы получаете многоугольники, конгруэнтные основанию. Таким образом, площадь каждого среза всегда одинакова. В прямоугольной призме поперечное сечение всегда прямоугольник.
В модуле Введение в измерения мы видели, что объем прямоугольной призмы определяется произведением площади основания на высоту, или
Объем = lwh, где l и w — длина и ширина призмы. призмы и h высота.
Треугольные призмы
В треугольной призме каждое поперечное сечение, параллельное треугольному основанию, представляет собой треугольник, конгруэнтный основанию.
Предположим, у нас есть треугольная призма длиной 4 см, как показано на рисунке.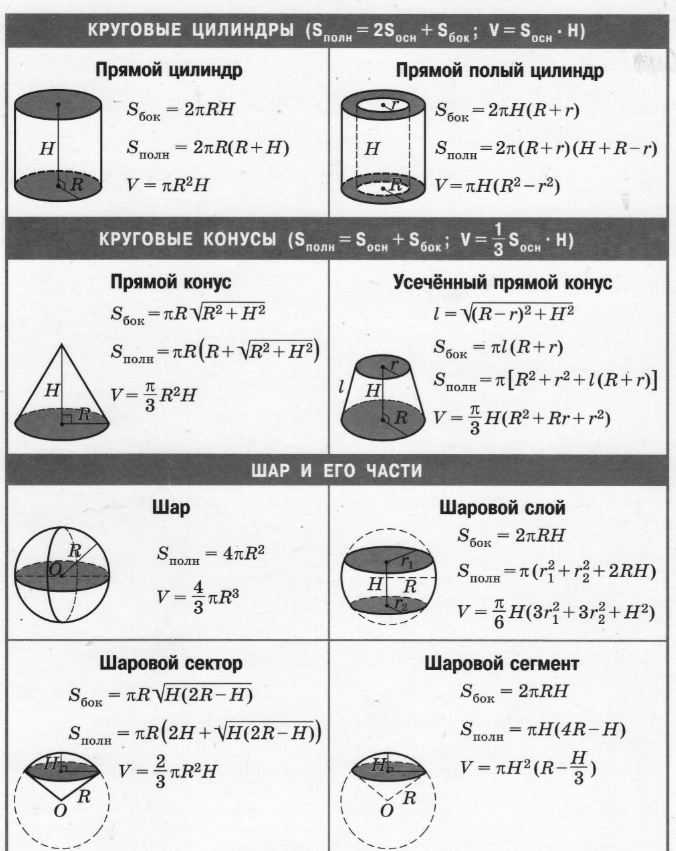
Мы можем разрезать призму на слои, каждый из которых имеет длину 1 см.
Ранее мы видели, что из остроугольного треугольника можно составить прямоугольник с удвоенной площадью.
Точно так же мы можем собрать треугольную призму, чтобы сформировать прямоугольную призму. Объем каждого из 1 см слоев равен половине объема соответствующей прямоугольной призмы, т.е.
Объем каждого слоя = × 3 × 2 см3.
Отсюда объем треугольной призмы | = × 3 × 2 × 4 | |
|
Таким образом, объем треугольной призмы равен
Объем = площадь треугольного поперечного сечения × перпендикулярная высота = Ah.
Поскольку любой многоугольник можно разрезать на треугольники, объем любой призмы с многоугольным основанием равен площади A многоугольного основания, умноженной на высоту h, то есть
Объем = Ah
, где A — площадь многоугольного основания, а h — высота, когда призма стоит на своем основании.
Пример
Найдите объем призмы, изображенной на рисунке.
Решение
Поперечное сечение представляет собой переднюю грань призмы и состоит из треугольника и прямоугольника.
А | = × 8 × 4 + (8 × 6) | |
= 64 см2. | ||
Том | = Ач | |
= 64 × 5 | ||
= 320 см3. |
щелкните для просмотра экрана
Упражнение 5
Большой пьедестал имеет форму призмы, лицевая сторона которой представляет собой трапецию.
а Найдите площадь передней грани.
b Найдите объем пьедестала.
Объем цилиндра
Цилиндры используются повсеместно в повседневной жизни. Например, консервы обычно поставляются в банках цилиндрической формы.
Например, консервы обычно поставляются в банках цилиндрической формы.
Если мы разрежем цилиндр параллельно его основанию, то каждое поперечное сечение будет окружностью того же размера, что и основание.
Таким образом, цилиндр обладает тем же основным свойством, что и призма, и мы возьмем формулу объема цилиндра как произведение площади круглого основания на высоту. Мы не можем строго доказать эту формулу на данном этапе, потому что доказательство включает в себя построение цилиндра как предела призм.
Если окружность основания цилиндра имеет радиус r, то мы знаем, что площадь окружности равна
А =π r2. Если высота цилиндра h, то его объем равен
Объем = π r2 × h = π r2h.
Пример
Для цилиндра радиусом 7 см и высотой 3 см найдите:
a точный объем, выраженный в π .
b приблизительное значение объема с использованием π .
Раствор
и | В | = π r2h | б | В | = π r2h | |||
= π × 49 × 3 | ≈ × 49 × 3 | |||||||
= 147π см3 | = 462 см3. |
Задание 6
Термос высотой 30 см имеет форму двух цилиндров, один внутри другого. Он имеет внутренний радиус 8 см и внешний радиус 10 см. Какой объем между двумя цилиндрами?
Площадь поверхности призмы
Предположим, мы возьмем прямоугольную призму размером 3 см на 4 см на 5 см и раскроем ее, как показано ниже.
Мы можем найти площадь сплющенной прямоугольной призмы, сложив площади шести прямоугольников. Имеются три пары равных прямоугольников, поэтому общая площадь равна
A = 2 × (3 × 4 + 3 × 5 + 4 × 5) = 94 см2.
Это называется площадью поверхности призмы.
Таким образом, площадь поверхности призмы равна сумме площадей ее граней. Действительно, площадь поверхности многогранника также равна сумме площадей всех его граней.
Пример
Найдите площадь поверхности треугольной призмы
, показанной напротив.
Раствор
Площадь лицевой стороны = × 12 × 16 = 96 см2.
Площадь спинки = 96 см2.
Площадь трех прямоугольных граней | = (9 × 20) + (9 × 12) + (9 × 16) |
= 432 см2. |
Общая площадь поверхности | = 96 + 96 + 432 |
= 624 см2. |
Длина ребра
Длина ребра призмы равна сумме длин всех его ребер.
щелкните для просмотра экрана
Упражнение 7
Найдите общую длину ребра призмы в приведенном выше примере.
Упражнение 8
Палатка, изготовленная из ситца, включая настил
, имеет форму треугольной призмы с размерами, как показано на рисунке. Сколько бязи нужно для изготовления палатки?
Ссылки Вперед
Площади
Теперь мы можем найти площади основных геометрических фигур. Мы также видели в модуле по кругам, что площадь круга определяется выражением A = π r2, где r — радиус. Чтобы понять площадь фигуры, которая не ограничена ни прямыми линиями, ни дугами окружности, нам понадобится интегральное исчисление. Хотя эти идеи восходят к Архимеду и Евдоксу, систематическое развитие интегрального исчисления принадлежит Ньютону и Лейбницу.
Мы также видели в модуле по кругам, что площадь круга определяется выражением A = π r2, где r — радиус. Чтобы понять площадь фигуры, которая не ограничена ни прямыми линиями, ни дугами окружности, нам понадобится интегральное исчисление. Хотя эти идеи восходят к Архимеду и Евдоксу, систематическое развитие интегрального исчисления принадлежит Ньютону и Лейбницу.
Мы можем использовать тригонометрию, чтобы найти площади различных фигур, имея достаточно информации об их сторонах и углах.
Объемы: пирамиды и призмы
Можно показать, что объем квадратной пирамиды составляет одну треть объема соответствующей прямой призмы с такими же высотой и основанием.
Объем пирамиды = Ah,
, где A — площадь основания
, а h — высота перпендикуляра
, измеренная от основания.
Эта формула верна для пирамид с многоугольным основанием площадью A.
Поперечные сечения конуса (или сферы) представляют собой окружности, но радиусы сечений различаются. Объем конуса равен одной трети объема соответствующего цилиндра той же высоты и радиуса.
Объем конуса равен одной трети объема соответствующего цилиндра той же высоты и радиуса.
Объем конуса = π r2h,
, где r — радиус основания
, а h — высота.
Наконец, объем сферы равен
Объем сферы = π r3,
где r — радиус сферы.
Это завершает формулу объема для основных твердых тел. Тела с неправильными границами можно рассматривать с помощью интегрального исчисления. Все они рассматриваются в модуле Конусы, пирамиды и сферы .
Площадь поверхности
Точно так же, как мы «разрезали» призму, чтобы найти площадь поверхности, мы можем «разрезать» цилиндр радиусом r и высотой h, чтобы показать, что площадь искривленной поверхности равна 2π rh . Добавляя два круглых конца, мы получаем формулу A = 2π rh + 2π r2 для общей площади поверхности цилиндра. Формула площади поверхности конуса: A = π r2 + π rl, где r — радиус, а l — наклонная высота. Наконец, площадь поверхности сферы определяется выражением A = 4π r2, где r — радиус сферы.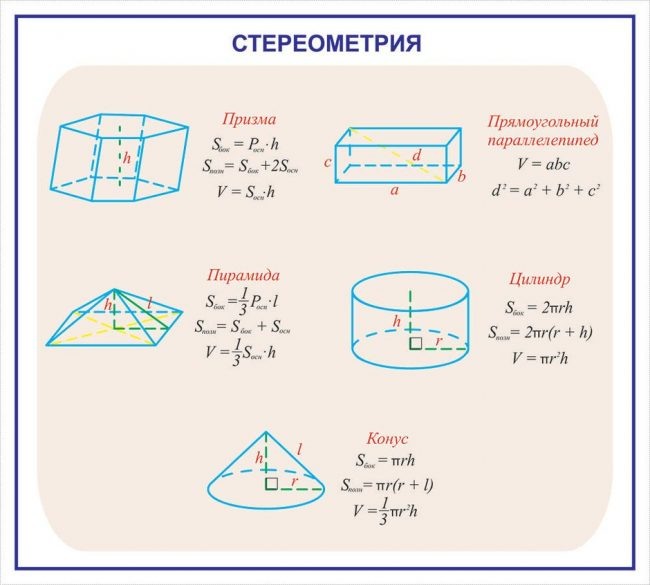
История и применение
Многие названия фигур и тел, площадь и объем которых мы нашли, происходят от греч. Например, слово «трапеция» (несмотря на латинское окончание) происходит от греческого слова «стол», тогда как «призма» происходит от греческого слова, означающего «пилить» (поскольку поперечные сечения или разрезы конгруэнтны), а слово «цилиндр» происходит от слова «стол». Греческое слово, означающее катиться. Древние греки первыми систематически исследовали площади и объемы плоских фигур и тел.
В эллинистический период великий математик Архимед (ок. 287–212 г. до н. э.) аппроксимировал площадь круга, используя вписанные многоугольники, и нашел очень хорошие приближения к π . Он также вывел формулы объема и площади поверхности шара. Архимед разработал метод нахождения площадей и объемов, названный «методом исчерпания», который был близок к идеям, используемым в современном исчислении.
До разработки интегрального исчисления, которое вывело площади и объемы на новый уровень абстракции, итальянский математик Бонавентура Франческо Кавальери (1598-1647) вывел результат, известный как принцип Кавальери, который утверждает, что два тела имеют одинаковый объем, если площади их соответствующих поперечных сечений равны во всех случаях.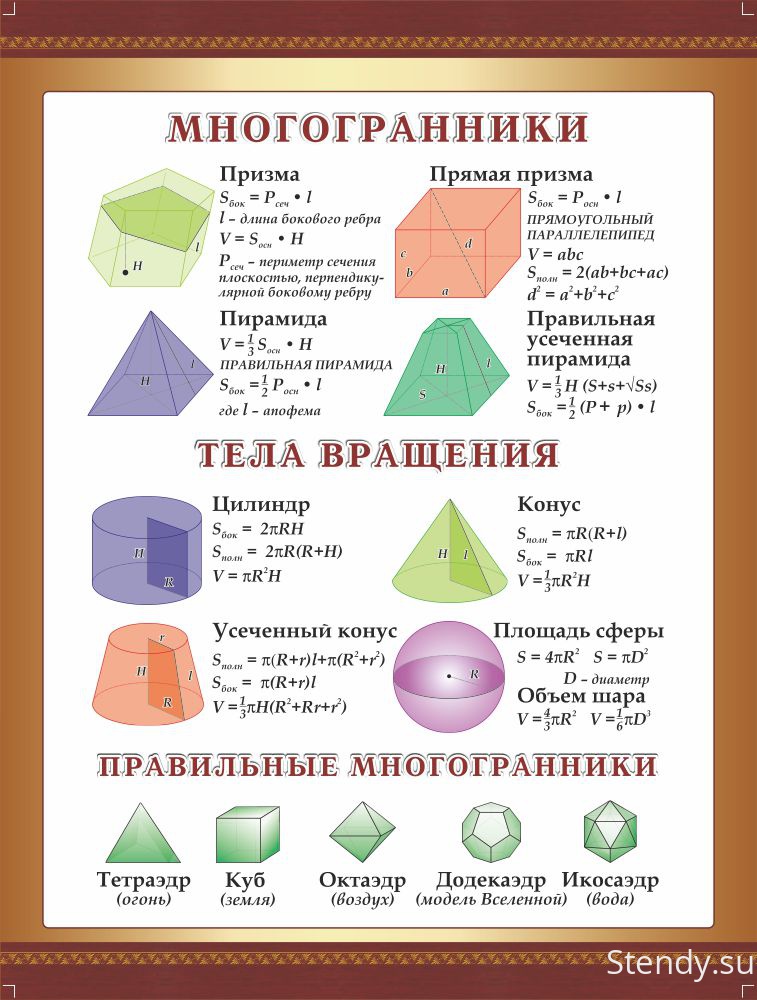 (Тот же принцип был ранее открыт Цзу Гэнчжи (480–525 гг.) в Китае.) Умное использование этого метода показывает, что объем полусферы радиусом r равен объему твердого тела, полученного путем удаления конуса из радиуса r и высоты r из цилиндра той же высоты и радиуса, таким образом показывая, что объем полушария равен π r3.
(Тот же принцип был ранее открыт Цзу Гэнчжи (480–525 гг.) в Китае.) Умное использование этого метода показывает, что объем полусферы радиусом r равен объему твердого тела, полученного путем удаления конуса из радиуса r и высоты r из цилиндра той же высоты и радиуса, таким образом показывая, что объем полушария равен π r3.
Принцип Кавальери можно использовать для нахождения объема наклонных тел (в отличие от прямых тел). Таким образом, косая призма имеет параллельные горизонтальные основание и вершину, но стороны не вертикальны. Такое твердое тело называется параллелепипедом (другое греческое слово, означающее параллельные плоскости). × перпендикулярная высота.
Следующим большим достижением стало интегральное исчисление, когда можно было придать смысл понятию площади под кривой, используя идеи предела. Хотя Ферма и Декарт добились в этом значительного прогресса, именно (независимая) работа Ньютона и Лейбница привела к современной теории интеграции.
Существуют приближенные методы нахождения площади фигуры с неровной границей.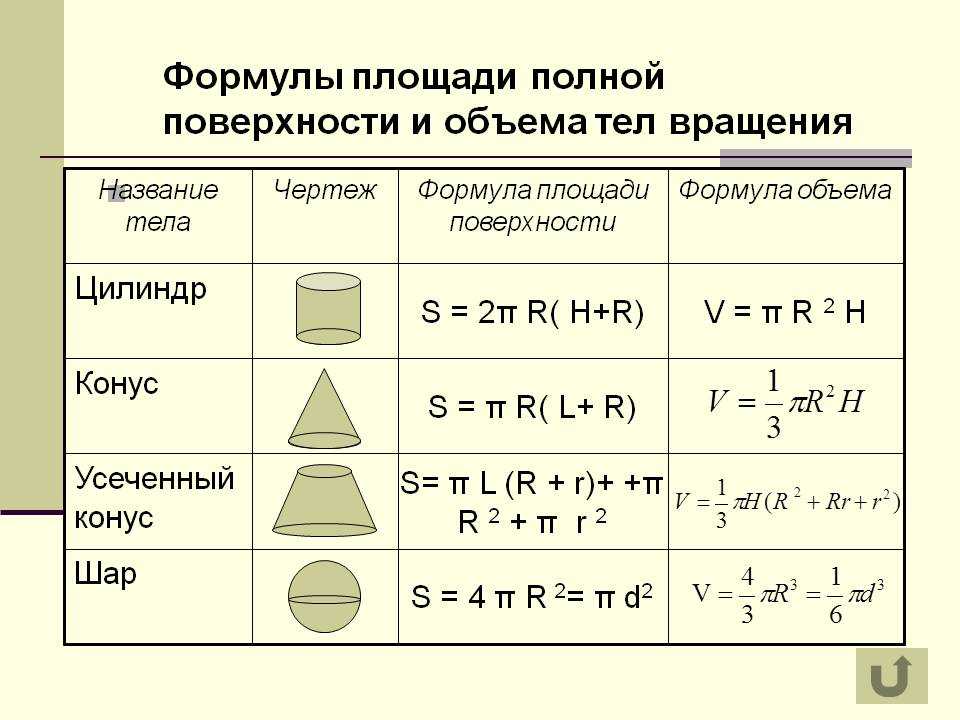 Одно довольно точное из них называется правилом Симпсона, которое было известно Кавальери, заново открыто Грегори (1638-1675) и приписано Томасу Симпсону (1710-1761). Это правило позволяет найти приблизительное значение площади неправильной фигуры, производя измерения поперек фигуры в различных точках вдоль некоторой оси. Сегодня он используется кардиологами для измерения, например, объема правого желудочка (ПЖ), связанного с кровотоком в сердце.
Одно довольно точное из них называется правилом Симпсона, которое было известно Кавальери, заново открыто Грегори (1638-1675) и приписано Томасу Симпсону (1710-1761). Это правило позволяет найти приблизительное значение площади неправильной фигуры, производя измерения поперек фигуры в различных точках вдоль некоторой оси. Сегодня он используется кардиологами для измерения, например, объема правого желудочка (ПЖ), связанного с кровотоком в сердце.
Ответы на упражнения
Упражнение 1
| a | КФ = ДФ | (F — середина CD) | |
КФГ = DFE | (вертикально противоположные углы) | ||
GCF = EDF | (переменные углы) | ||
Треугольник CFG конгруэнтен треугольнику DFE (SAS) | |||
b CG = ED (соответствие сторон равных треугольников)
в | 2АЭ = АЭ + БГ | = AD — ED + CG + BG | |
| = AD + БГ | |||
| AE = ( AD + BG ) |
|
D Площадь трапеции = площадь параллелограмма
= AE × H
= ( AD + BG ). ADG и BCK вместе образуют треугольник ACD ( B и A совпадают). E и F являются средними точками AC и AD соответственно. Треугольник AFE подобен треугольнику ACD и, таким образом, EF параллелен DC (соответствующие углы равны).
ADG и BCK вместе образуют треугольник ACD ( B и A совпадают). E и F являются средними точками AC и AD соответственно. Треугольник AFE подобен треугольнику ACD и, таким образом, EF параллелен DC (соответствующие углы равны).
b Треугольник AEH подобен треугольнику ADG (AAA)
AH = HG =
Зона | = (АВ + CD) | ||
= (2(ГД + ЭГ + ДФ)) | |||
= гл |
Упражнение 3
a 6 см
b 24 см2
Упражнение 4
| a | Треугольник CBA соответствует CDA (SSS) | |
| Треугольник BCE конгруэнтен треугольнику DCE (SAS) | ||
| CEB = CED = 90° | ||
б | Площадь прямоугольника = xy . | |
Упражнение 5
a 31,5 м2 b 94,5 м3
Упражнение 6
1080π см3
7Упражнение0003
123 см
Упражнение 8
60 м2
Проект улучшения математического образования в школах (TIMES) 2009–2011 гг. финансировался Министерством образования, занятости и трудовых отношений правительства Австралии.
Мнения, выраженные здесь, принадлежат автору и не обязательно отражают точку зрения Министерства образования, занятости и трудовых отношений правительства Австралии.
© Мельбурнский университет от имени Международного центра передового опыта в области образования в области математики (ICE-EM), образовательного подразделения Австралийского института математических наук (AMSI), 2010 г. (если не указано иное). Эта работа находится под лицензией Creative Commons Attribution-NonCommercial-NoDerivs 3. 0 Unported License.
0 Unported License.
https://creativecommons.org/licenses/by-nc-nd/3.0/
Объем геометрических фигур – формулы и примеры
Объем геометрических фигур является одним из наиболее важных измерений трех- объемные фигуры. Объем — это мера пространства, занимаемого объектом в трехмерном пространстве. Поскольку объем является трехмерной мерой, для его измерения мы используем кубические единицы. Формула объема зависит от формы фигуры и различных ее размеров.
Здесь мы узнаем о формулах важнейших трехмерных фигур. Затем мы будем использовать эти формулы для решения некоторых задач.
ГЕОМЕТРИЯ
Актуально для …
Изучение формул объема геометрических фигур.
См. формулы
Содержание
ГЕОМЕТРИЯ
Актуально для …
Изучение формул объема геометрических фигур.
См. формулы
Определение объема
Объем геометрической фигуры определяется как количество места, занимаемого объектом или фигурой в трехмерном пространстве.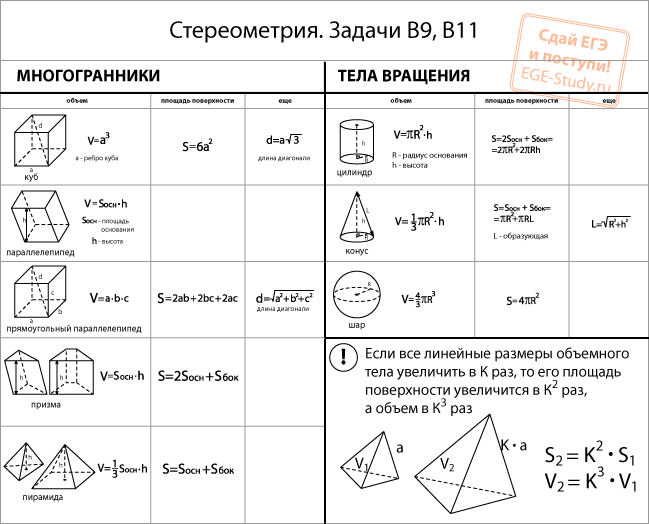 Объем измеряется в кубических единицах, например, м³, см³ и так далее. Объем можно рассматривать как способность контейнера вмещать некоторое количество жидкости (газа или жидкости).
Объем измеряется в кубических единицах, например, м³, см³ и так далее. Объем можно рассматривать как способность контейнера вмещать некоторое количество жидкости (газа или жидкости).
Объем можно рассчитать арифметически путем перемножения его различных измерений и, в некоторых случаях, с использованием некоторых констант. Две геометрические фигуры могут иметь одинаковый объем в зависимости от их размеров и формы.
Формулы объема геометрических фигур
Формула объема геометрических фигур зависит от формы и размеров фигуры. Существует большое количество объемных геометрических фигур, однако наиболее важными из них являются куб, прямоугольная призма, цилиндр, сфера, пирамида и тетраэдр.
Объем прямоугольной призмы
Прямоугольный штрих – это призма с прямоугольными основаниями и прямоугольными боковыми гранями. Объем этих призм зависит от их трех измерений.
Объем прямоугольной призмы = l bh
где l длина ширины призмы, b 6 длина основания и h 901 1 901 .
Объем куба
Куб — это трехмерная фигура, все стороны которой имеют одинаковую длину. Всего у куба шесть квадратных граней.
Объем куба = a³
, где a – длина одной из сторон куба.
Объем цилиндра
Цилиндр характеризуется наличием двух круглых оснований и поверхности, соединяющей эти два основания.
Объем цилиндра = πr²h
, где r — радиус оснований, а h — высота цилиндра.
Объем шара
Шар — это полностью круглая трехмерная фигура. Сфера определяется радиусом. 93}}{6 \sqrt{2}}$
, где a – длина одной из сторон тетраэдра.
Table of formulas for the volume of geometric figures
| Figure | Volume |
| Rectangular prism | V = lbh |
| Cube | V = a³ |
| Цилиндр | V = πr²h |
, где r – радиус, a и l – разные длины фигур, представляет собой площадь основания.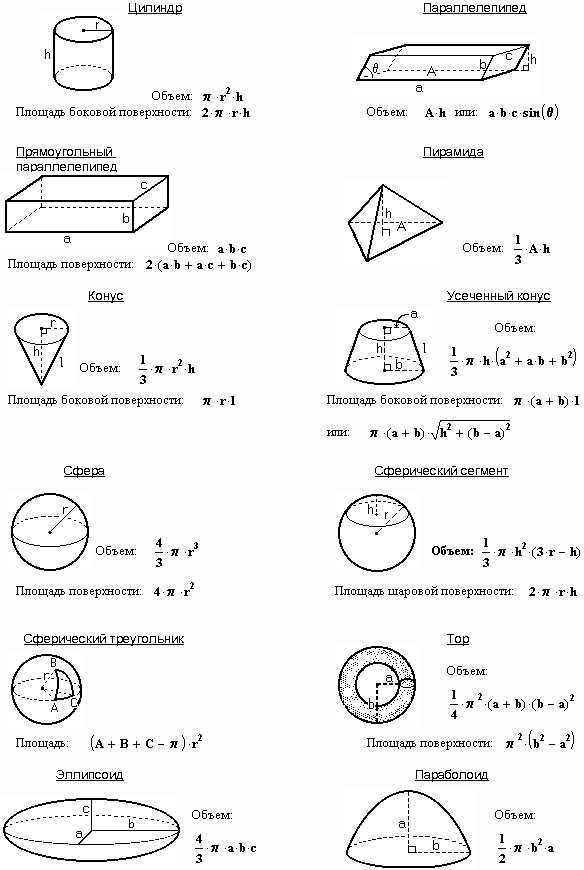

 д. Градусы в радианы. / / Плоские фигуры. Свойства, стороны, углы, признаки, периметры, равенства, подобия, хорды, секторы, площади и т.д.
д. Градусы в радианы. / / Плоские фигуры. Свойства, стороны, углы, признаки, периметры, равенства, подобия, хорды, секторы, площади и т.д.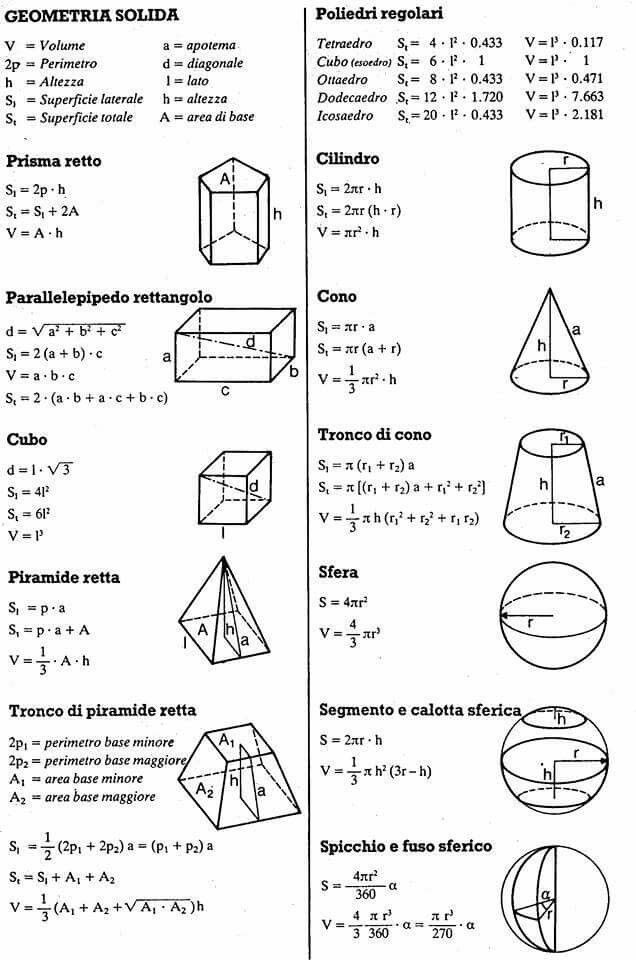
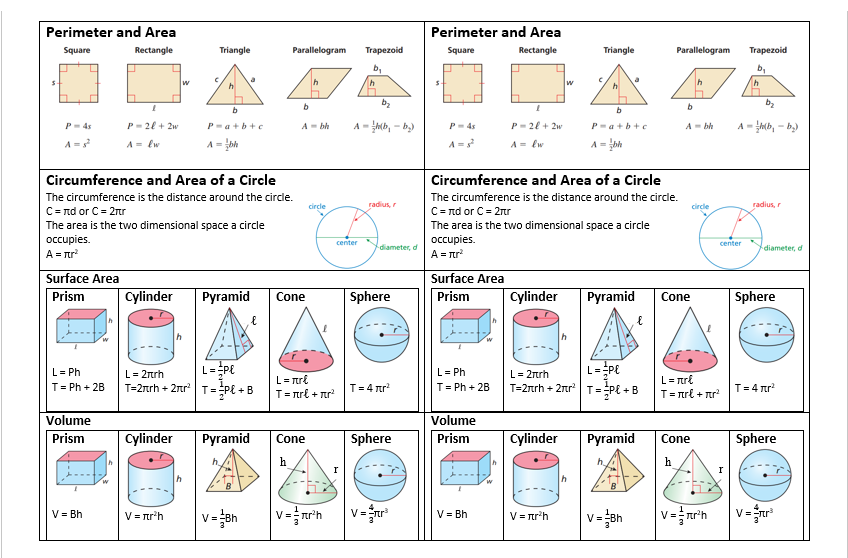
 Введите свой запрос:
Введите свой запрос: