Формулы по геометрии — Понятные формулы с рисунками по геометрии
Теоремы по геометрии
Теорема Виета
05
Рассмотрим квадратное уравнение где a – коэффициент при x2 b – коэффициент при x c – свободный член Теорема Виета – сумма корней X1, X2 приведенного квадратного
Теоремы по геометрии
Теорема Чевы
07
Рассмотрим произвольный треугольник АВС. A, B, C – вершины треугольника A1 – точка, лежащая на стороне BC треугольника B1 – точка, лежащая на стороне AC
Теоремы по геометрии
Теорема Фалеса
06
Рассмотрим параллельные прямые c, d, e и произвольные прямые, секущие их. c, d, e – параллельные прямые a, b – произвольные прямые, секущие параллельные
Теоремы по геометрии
Теорема о биссектрисе
08
Рассмотрим произвольный треугольник АВС. α – угол треугольника α/2 – угол между биссектрисой и стороной треугольника AD – биссектриса треугольника A, B
Теоремы по геометрии
Теорема о медианах треугольника
08
Рассмотрим произвольный треугольник АВС. ma – медиана треугольника, проведенная к стороне BC mb – медиана треугольника, проведенная к стороне AC mc– медиана
Теоремы по геометрии
Теорема о сумме углов многоугольника
06
Рассмотрим произвольный многоугольник АВСDEF. α – углы правильного многоугольника A, B, C, D, E, F – вершины многоугольника n – количество сторон многоугольника
Теоремы по геометрии
Теорема о сумме углов треугольника
05
Рассмотрим произвольный треугольник АВС. α, β, γ – углы треугольника A, B, C – вершины треугольника Теорема о сумме углов треугольника формулируется следующим
Теоремы по геометрии
Обратная теорема Пифагора
07
Рассмотрим прямоугольный треугольник АВС. a, b – катеты прямоугольного треугольника c – гипотенуза прямоугольного треугольника A, B, C – вершины треугольника
Теоремы по геометрии
Теорема тангенсов
05
Рассмотрим прямоугольный треугольник АВС. a, b, с – стороны треугольника α – угол треугольника, противолежащий стороне a β – угол треугольника, противолежащий
Теоремы по геометрии
Теорема косинусов
05
Рассмотрим прямоугольный треугольник АВС.
a, b, с – стороны треугольника α – угол треугольника, противолежащий стороне a β – угол треугольника, противолежащий
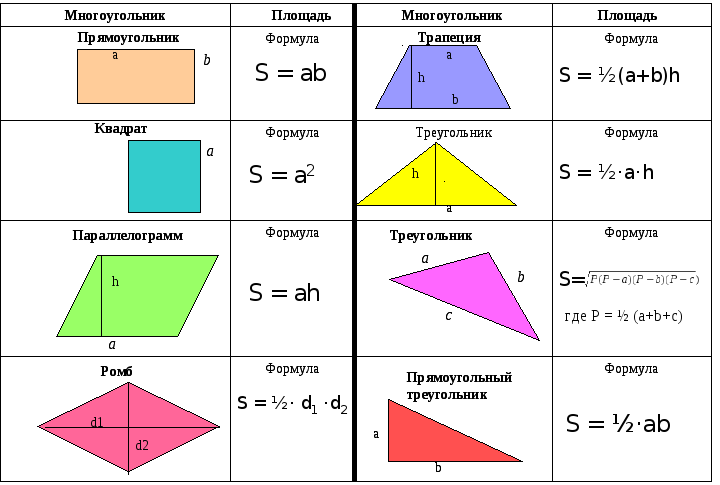
Формулы нахождения площадей фигур.
Чтобы решить задачи по геометрии, надо знать формулы — такие, как площадь треугольника или площадь параллелограмма — а также простые приёмы, о которых мы расскажем.
Для начала выучим формулы площадей фигур. Мы специально собрали их в удобную таблицу. Распечатайте, выучите и применяйте!
Конечно, не все формулы по геометрии есть в нашей таблице. Например, для решения задач по геометрии и стереометрии во второй части профильного ЕГЭ по математике применяются и другие формулы площади треугольника. О них мы обязательно расскажем.
А что делать, если надо найти не площадь трапеции или треугольника, а площадь какой-либо сложной фигуры? Есть универсальные способы! Покажем их на примерах из банка заданий ФИПИ.
1. Как найти площадь нестандартной фигуры? Например, произвольного четырёхугольника? Простой приём — разобьём эту фигуру на такие, о которых мы всё знаем, и найдем её площадь — как сумму площадей этих фигур.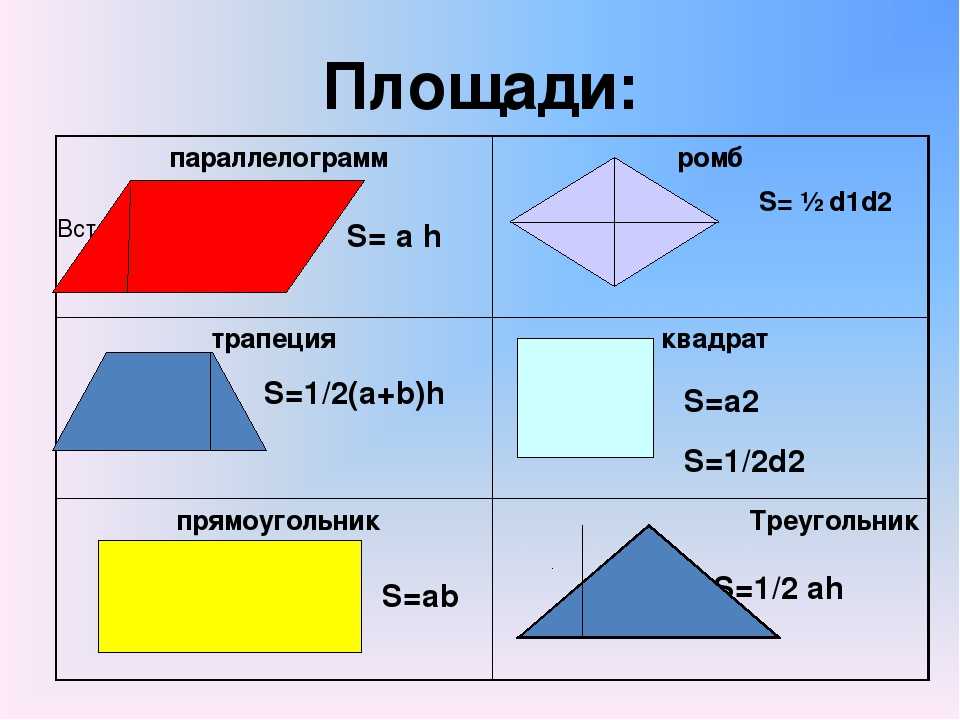
Разделим этот четырёхугольник горизонтальной линией на два треугольника с общим основанием, равным . Высоты этих треугольников равны и . Тогда площадь четырёхугольника равна сумме площадей двух треугольников: .
Ответ: .
2. В некоторых случаях площадь фигуры можно представить как разность каких-либо площадей.
Не так-то просто посчитать, чему равны основание и высота в этом треугольнике! Зато мы можем сказать, что его площадь равна разности площадей квадрата со стороной и трёх прямоугольных треугольников. Видите их на рисунке? Получаем: .
Ответ: .
3. Иногда в задании надо найти площадь не всей фигуры, а её части. Обычно речь здесь идет о площади сектора — части круга.Найдите площадь сектора круга радиуса , длина дуги которого равна .
На этом рисунке мы видим часть круга. Площадь всего круга равна , так как . Остается узнать, какая часть круга изображена. Поскольку длина всей окружности равна (так как ), а длина дуги данного сектора равна , следовательно, длина дуги в раз меньше, чем длина всей окружности.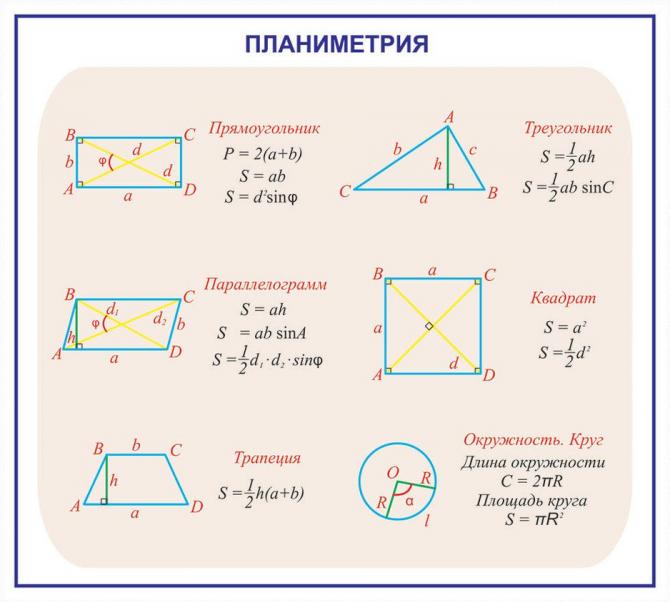
Площадь геометрической фигуры — численная характеристика геометрической фигуры показывающая размер этой фигуры (части поверхности, ограниченной замкнутым контуром данной фигуры). Величина площади выражается числом заключающихся в нее квадратных единиц.
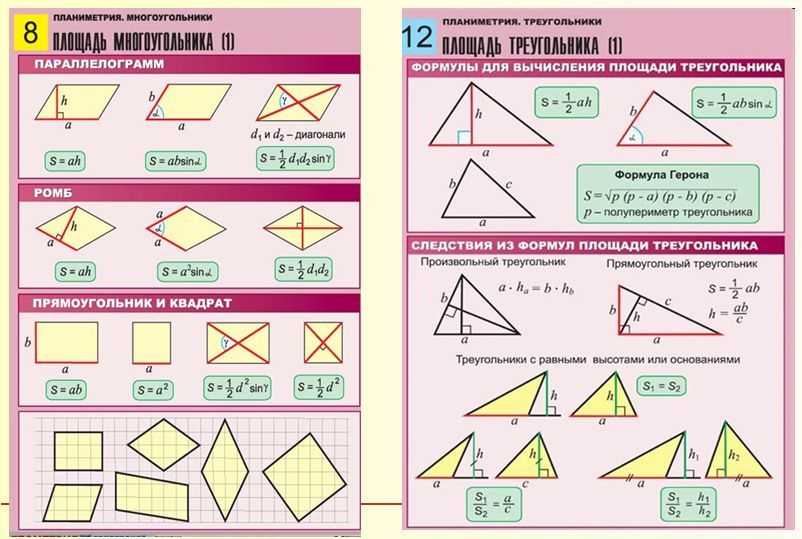
Формулы площади треугольника
- Формула площади треугольника по стороне и высоте
Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты - Формула площади треугольника по трем сторонам и радиусу описанной окружности
- Формула площади треугольника по трем сторонам и радиусу вписанной окружности
Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности. где S — площадь треугольника,
— длины сторон треугольника,
— высота треугольника,
— угол между сторонами и,
— радиус вписанной окружности,
R — радиус описанной окружности,
Формулы площади квадрата
- Формула площади квадрата по длине стороны
Площадь квадрата равна квадрату длины его стороны.
- Формула площади квадрата по длине диагонали
Площадь квадрата равна половине квадрата длины его диагонали.S = 1 2 2 где S — Площадь квадрата,
— длина стороны квадрата,
— длина диагонали квадрата.
Формула площади прямоугольника
- Площадь прямоугольника равна произведению длин двух его смежных сторон
где S — Площадь прямоугольника,
— длины сторон прямоугольника.
Формулы площади параллелограмма
- Формула площади параллелограмма по длине стороны и высоте
Площадь параллелограмма - Формула площади параллелограмма по двум сторонам и углу между ними
Площадь параллелограмма равна произведению длин его сторон умноженному на синус угла между ними.a · b · sin α
где S — Площадь параллелограмма,
— длины сторон параллелограмма,
— длина высоты параллелограмма,
— угол между сторонами параллелограмма.
Формулы площади ромба
- Формула площади ромба по длине стороны и высоте
Площадь ромба равна произведению длины его стороны и длины опущенной на эту сторону высоты. - Формула площади ромба по длине стороны и углу
Площадь ромба равна произведению квадрата длины его стороны и синуса угла между сторонами ромба. - Формула площади ромба по длинам его диагоналей
Площадь ромба равна половине произведению длин его диагоналей. где S — Площадь ромба,
— длина стороны ромба,
— длина высоты ромба,
— угол между сторонами ромба,
1 , 2 — длины диагоналей.
Формулы площади трапеции
- Формула Герона для трапеции
Где S — Площадь трапеции,
— длины основ трапеции,
— длины боковых сторон трапеции,
Все формулы площади плоских фигур
Площадь равнобедренной трапеции
1.
Формула площади равнобедренной
трапеции через стороны и угол
а — нижнее основание
b — верхнее основание
с — равные боковые стороны
α — угол при нижнем основании
Формула площади равнобедренной трапеции через стороны, (S):
Формула площади равнобедренной трапеции через стороны и угол, (S):
2. Формула площади равнобедренной трапеции через радиус вписанной окружности
R- радиус вписанной окружности
D- диаметр вписанной окружности
O- центр вписанной окружности
H- высота трапеции
α, β — углы трапеции
Формула площади равнобедренной трапеции через радиус вписанной окружности, (S):
СПРАВЕДЛИВО, для вписанной окружности в равнобедренную трапецию:
3. Формула площади равнобедренной трапеции через диагонали и угол между ними
d- диагональ трапеции
α,β- углы между диагоналями
Формула площади равнобедренной трапеции через диагонали и угол между ними, (S):
4.
c- боковая сторона
m- средняя линия трапеции
α, β — углы при основании
Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании,
(S):
5. Формула площади равнобедренной трапеции через основания и высоту
a — нижнее основание
b — верхнее основание
h — высота трапеции
Формула площади равнобедренной трапеции через основания и высоту, (S):
Площадь треугольника по стороне и двум углам, формула.
a, b, c- стороны треугольника
α, β, γ- противолежащие углы
Площадь треугольника через сторону и два угла (S):
Формула площади правильного многоугольника
a — сторона многоугольника
n — количество сторон
Площадь правильного многоугольника, (S):
Формула (Герона) площади треугольника через полупериметр (S):
Площадь равностороннего треугольника равна:
Формулы расчета, площади равностороннего
треугольника.
a — сторона треугольника
h – высота
Как вычислить площадь равнобедренного треугольника?
b — основание треугольника
a — равные стороны
h – высота
3. Формула площади трапеции через четыре стороны
a — нижнее основание
b — верхнее основание
c , d — боковые стороны
Радиус описанной окружности трапеции по сторонам и диагонали
a — боковые стороны трапеции
c — нижнее основание
b — верхнее основание
d — диагональ
h — высота
Формула радиуса описанной окружности трапеции, (R)
найти радиус описанной окружности равнобедренного треугольника по сторонам
Зная стороны равнобедренного треугольника, можно по формуле, найти, радиус описанной окружности около этого треугольника.
a, b — стороны треугольника
Радиус описанной окружности равнобедренного треугольника (R):
Радиус вписанной окружности в шестиугольник
a — сторона шестиугольника
Радиус вписанной окружности в шестиугольник, (r):
Радиус вписанной окружности в ромб
r — радиус вписанной окружности
a — сторона ромба
D, d — диагонали
h — высота ромба
Радиус вписанной окружности в равнобочную трапецию
с — нижнее основание
b — верхнее основание
a — боковые стороны
h — высота
Радиус вписанной окружности в прямоугольный треугольник
a, b — катеты треугольника
с — гипотенуза
Радиус вписанной окружности в равнобедренный треугольник
a, b — стороны треугольника
Доказать, что площадь вписанного четырёхугольника равна
\/(р — а)(р — b) (р — с) (р — d),
где р — полупериметр и а, b, с и d —
стороны четырёхугольника.
Доказать, что площадь вписанного в круг четырёхугольника равна
1/2 (ab + cb) · sin α , где а, b, с и d — стороны четырёхугольника и α — угол между сторонами а и b.
S = √[ a ƀ c d] sin ½ (α + β). — Читайте подробнее на FB.ru:
Площадь произвольного четырёхугольника (рис. 1.13) можно выразить через его стороны а, b, c и сумму пары противоположных углов:
где р – полупериметр четырёхугольника.
Площадь вписанного в окружность четырёхугольника () (рис. 1.14, а) вычисляется по формуле Брахмагупты
а описанного (рис. 1.14, б) () – по формуле
Если же четырёхугольник вписан и описан одновременно (рис. 1.14, в), то формула становится совсем простой:
Формула Пика
Чтобы оценить площадь многоугольника
на клетчатой бумаге, достаточно
подсчитать, сколько клеток покрывает
этот многоугольник (площадь клетки мы
принимаем за единицу). Точнее, если S –
площадь многоугольника, — число клеток,
которые целиком лежат внутри многоугольника,
и — число клеток, которые имеют с
внутренностью многоугольника хоть одну
общую точку.
Будем рассматривать ниже только такие многоугольники, все вершины которых лежат в узлах клетчатой бумаги – в таких, где пересекаются линии сетки. Оказывается, что для таких многоугольников можно указать такую формулу:
где — площадь, r – число узлов, которые лежат строго внутри многоугольника.
Эту формулу называют «формула Пика» — по имени математика, открывшего её в 1899 году.
Измерьте площадь прямоугольника с разными сторонами. Формулы Square Trapezia
Прямоугольник является частным случаем четырехугольника. Это означает, что прямоугольник имеет четыре стороны. Его противоположные стороны равны: Например, если одна из его сторон равна 10 см, то и противоположная ей сторона тоже будет равна 10 см. Особым случаем прямоугольника является квадрат. Квадрат – это прямоугольник, у которого все стороны равны. Для вычисления площади квадрата можно использовать тот же алгоритм, что и для вычисления площади прямоугольника.
Как узнать площадь прямоугольника по двум сторонам
Для того чтобы найти площадь прямоугольника, нужно умножить его длину на ширину: площадь = длина × ширина.
В указанном ниже случае: Площадь = АВ × ВС.
Как узнать площадь прямоугольника по стороне и длине диагонали
В некоторых задачах необходимо найти площадь прямоугольника по длине диагонали и одной из сторон . Диагональ прямоугольника делит его на два равных прямоугольных треугольника. Следовательно, вы можете определить вторую сторону прямоугольника, используя теорему Пифагора. После этого задача сводится к предыдущему пункту. 92 × sin (острый угол между диагоналями) / 2.
Что такое площадь и что такое прямоугольник
Площадь – это такая геометрическая величина, по которой можно определить размер любой поверхности геометрической фигуры.
На протяжении многих веков было так необходимо, что расчет площади называли квадратурой. То есть, чтобы узнать площади простых геометрических фигур, достаточно подсчитать количество одиночных квадратов, которые были условно покрыты фигурами. А фигура, имевшая площадь, называлась квадратичной.
Таким образом, можно подытожить, что площадь – это такая величина, которая показывает нам размер плоскости, соединенной между собой отрезками.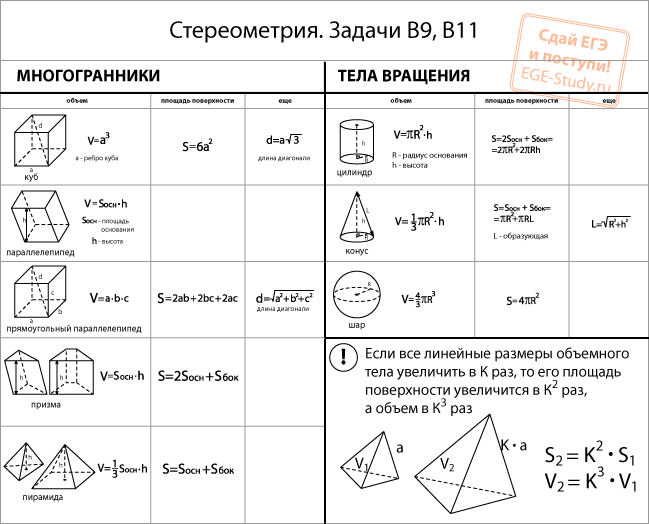
Прямоугольник – это такой четырехугольник, у которого все углы прямые. То есть четырехугольник, у которого четыре прямых угла и противоположные стороны, называется прямоугольником.
Как найти площадь прямоуголь к изображению прямоугольника. Количество заполненных квадратиков и будет площадью в квадратных сантиметрах. Например, на рисунке видно, что прямоугольник приходится на 12 квадратов, значит, его площадь равна 12 квадратным метрам. см.
Но для нахождения площади больших объектов, например квартиры, нужен более универсальный метод, поэтому доказана формула нахождения площади прямоугольника, чтобы умножить его длину на ширина.
А теперь попробуем ответить на правило нахождения площади прямоугольника в формуле. Обозначим площадь нашей фигуры буквой S, буквой А будет обозначена ее длина, а буквой В ширина.
В итоге получаем такую формулу:
S = а*б.
Если наложить эту формулу на рисунок прямоугольника выше, то мы получим те же 12 кв.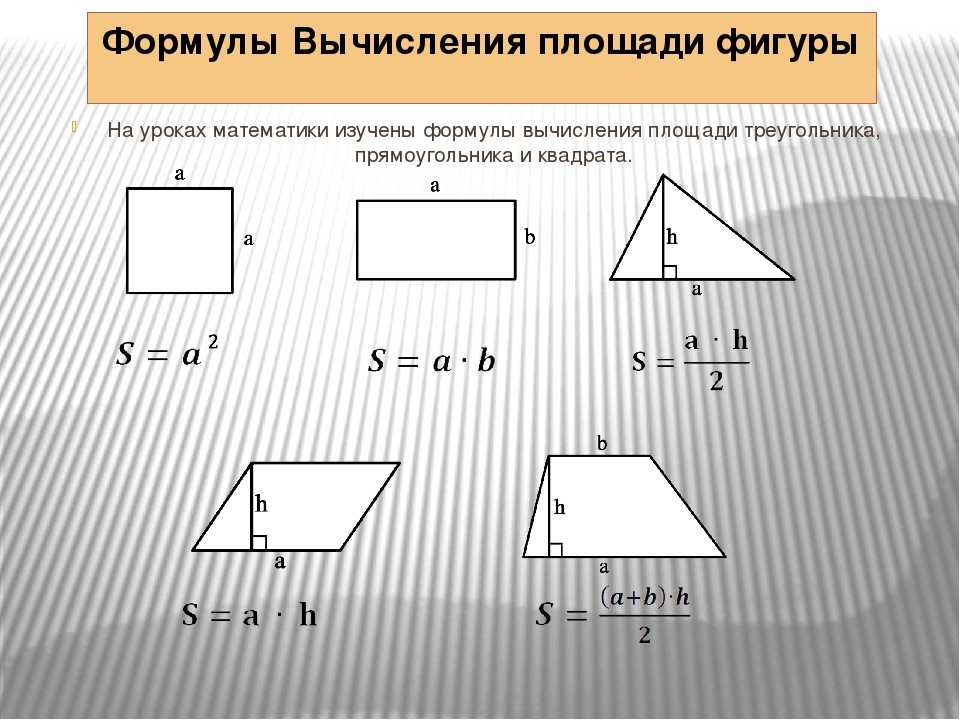
см, потому что а=4 см, b=3 см, а S=4*3=12 кв. .м.
Если взять две одинаковые фигуры и наложить их одну на другую, то они совпадут, но будут называться равными. Такие равные фигуры также будут равны своей площади и периметру.
Зачем уметь находить площадь
Во-первых, если вы знаете, как найти площадь какой-то фигуры, то с помощью ее формулы вы сможете решать любые задачи по геометрии и тригонометрии.
Во-вторых, научившись находить площадь прямоугольника, вы сначала сможете решать простые задачи, а со временем перейдете к решению более сложных, и научитесь находить площади фигур, которые вписанный в прямоугольник или около него.
В-третьих, зная такую простую формулу, как s=a*b, вы получаете возможность без особых проблем решать любые несложные бытовые задачи (например, найти s квартиры или дома), а со временем и применить их к решать сложные архитектурные проекты.
То есть, если совсем упростить формулу Квадрата, то она будет выглядеть так:
N = d x sh
Что обозначает n — искомая площадь, D — ее длина, w — обозначает ее ширину, а x — знак умножения.
Известно ли вам, что площадь любого полигона можно освятить на определенное количество квадратных блоков, находящихся внутри этого полигона? Чем отличается площадь от периметра
Попробуем понять разницу между периметром и площадью. Например, наша школа находится на участке, который огорожен забором — общая длина этого забора будет периметром, а пространство, которое находится внутри забора, — площадью.
Единицы измерения Квадрат
Если периметр измеряется в линейных единицах, такими как дюймы, футы и метры, то s относится к двумерному исчислению и имеет длину и ширину.
И измеряется в квадратных единицах, например:
Один квадратный миллиметр, где s квадрат имеет сторону, равную одному миллиметру;
Квадратный сантиметр, имеет такой квадрат, у которого сторона равна одному сантиметру;
Квадратный дециметр — это площадь этого квадрата со стороной в один дециметр;
Квадратный метр имеет площадь S, сторона которой равна одному метру;
Наконец, у квадратного километра есть квадрат, сторона которого равна одному километру.
Для измерения площадей больших участков на поверхности Земли применяют такие единицы, как:
Один АР или плетение — если s квадрат имеет сторону десять метров;
Один гектар равен квадрату, сторона которого равна ста метрам.
Задания и упражнения
А теперь рассмотрим несколько примеров.
На рисунке 62 нарисована фигура, которая состоит из восьми квадратов и каждая сторона этих квадратов равна одному сантиметру. Следовательно, S такого квадрата будет квадратным сантиметром.
Если записать, то это будет выглядеть так:
1 см2. А s всей этой фигуры, состоящей из восьми квадратов, будет 8 кв.м.
Если взять какую-нибудь фигуру и разбить ее на «р» квадратов со стороной, равной одному сантиметру, то ее площадь будет равна:
Р см2.
Посмотрим на прямоугольник, изображения на рисунке 63. Этот прямоугольник состоит из трех полос, и каждая такая полоса разделена на пять равных квадратов со стороной 1 см.
Попробуем найти его площадь. И так берем пять квадратов, и умножаем на три полоски и получаем площадь равную 15 кв.м.:
Рассмотрим следующий пример. На рис. 64 показан прямоугольник ABCD, ломаная линия KLMN разбита на две части. Его первая часть равна площади 12 см2, а вторая имеет площадь 9 см2. Теперь найдем площадь всего прямоугольника:
Итак, берем три и умножаем семь и получаем 21 кв.см:
3 7 = 21 кв.м. При этом 21 = 12 + 9.
И делаем вывод, что площадь всей нашей фигуры равна сумме площадей отдельных ее частей.
Рассмотрим другой пример. И так на рисунке 65 изображен прямоугольник, который разбит на два равных треугольника ABC и ADC с отрезком АС
А так как мы уже знаем, что квадрат это такой же прямоугольник, только имеющий равные стороны, то площадь \ каждый треугольник будет равен половине площади всего прямоугольника.
Представим, что сторона квадрата равна, тогда:
S = A A = A2.
Делаем вывод, что формула квадрата квадрата будет иметь такой вид:
А запись A2 называется квадратом числа a.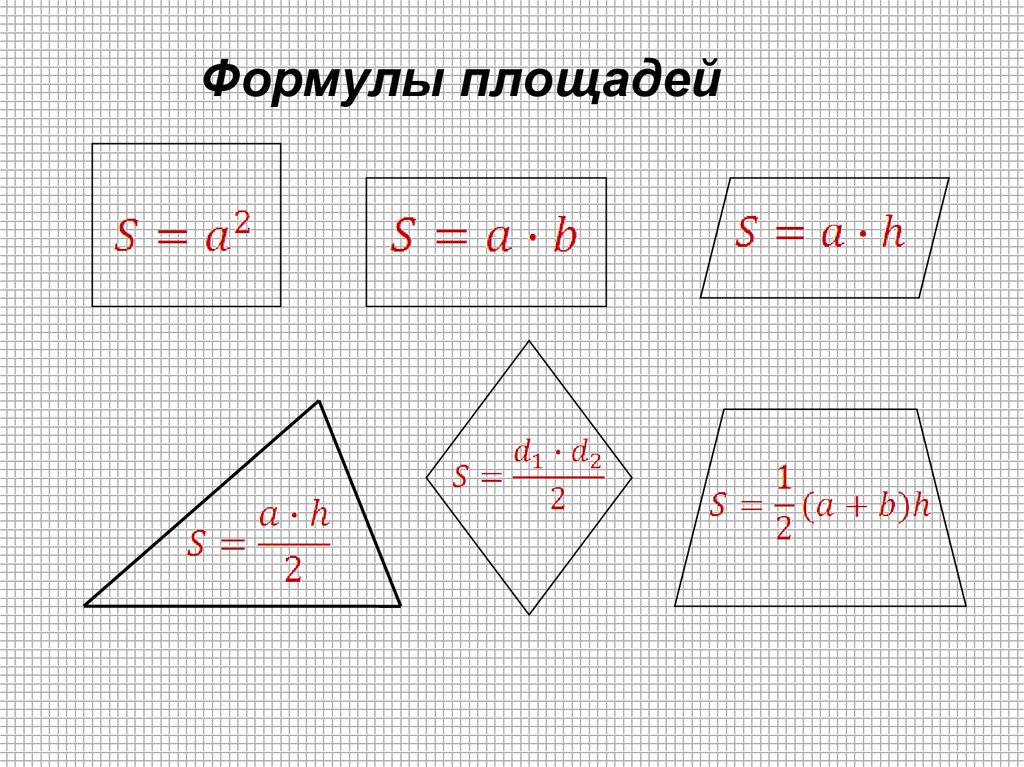
Итак, если сторона нашего квадрата равна четырем сантиметрам, то его площадь будет:
4 4, то есть 4*2=16 кв.м.
Вопросы и задания
Найдите фигуру фигуры, которая разбита на шестнадцать квадратов, сторона которых равна одному сантиметру.
Запомните формулу прямоугольника и запишите ее.
Какие измерения нужно произвести, чтобы узнать площадь прямоугольника?
Дайте определение равным фигурам.
Могут ли быть одинаковые фигуры разных площадей? А периметры?
Если известны площади отдельных частей фигуры, как узнать ее общую площадь?
Слово и запиши чему равен квадрат.
Историческая справка
А знаете ли вы, что древние люди в Вавилоне умели вычислять площадь прямоугольника. Также древние египтяне производили расчеты различных цифр, но так как точных формул они не знали, то в расчетах были небольшие погрешности.
В своей книге «Начало» известный древнегреческий математик Евклид описывает различные способы вычисления площадей различных геометрических фигур.
Урок на тему: «Формулы определения площади треугольника, прямоугольника, квадрата»
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания. Все материалы проверяются антивирусной программой.
Учебные пособия и тренажеры в интернет-магазине «Интеграл» для 5 класса
Тренажер к учебнику И.И. Зубарева и А.Г. Мордкович
Тренажер к учебнику Г.В.Дорофеева и Л.Г.Петерсона
Определение и понятие Квадрата Рисунок
Чтобы лучше понять, что такое площадь фигуры, рассмотрим чертеж.
Эта произвольная фигура разбита на 12 маленьких квадратиков. Сторона каждого квадрата равна 1 см. А площадь каждого квадрата равна 1 квадратному сантиметру, что записывается так: 1 см 2.
Тогда площадь фигуры равна 12 квадратных сантиметров. В математике площадь обозначается латинской буквой S.
Итак, площадь нашей фигуры равна: S Цифры = 12 см 2 .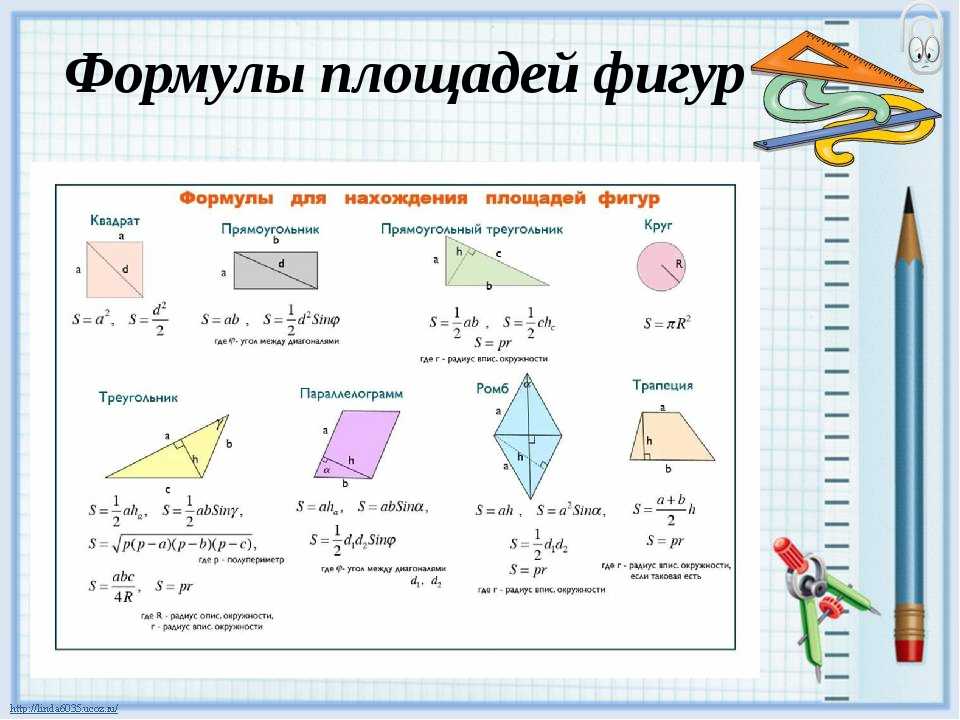
Площадь фигуры равна площади всех маленьких квадратов, из которых она состоит!
Ребята, помните!
Площадь измеряется в квадратных единицах длины. Единицы измерения площади:
1. Квадратный километр — км 2 (когда площадь очень большая, например, страна или море).
2. Квадратный метр — м 2 (вполне подходит для того, чтобы измерить площадь участка или квартиры).
3. Квадратный сантиметр — см 2 (обычно используется на уроках математики, когда фигуры рисуются в тетради).
4. Квадратный миллиметр — мм 2 .
Площадь треугольника
Рассмотрим два вида треугольников: прямоугольный и произвольный.
Чтобы найти площадь прямоугольного треугольника нужно знать длину основания и высоту. В прямоугольном треугольнике высота заменяет одну из сторон. Поэтому в формуле площади треугольника вместо высоты подставляем одну из сторон.
В нашем примере стороны 7 см и 4 см. Формула вычисления площади треугольника записывается так:
S прямоугольного треугольника ABC = Солнце * SA: 2
S прямоугольный треугольник ABC = 7 см * 4 см: 2 = 14 см 2
Теперь рассмотрим произвольный треугольник.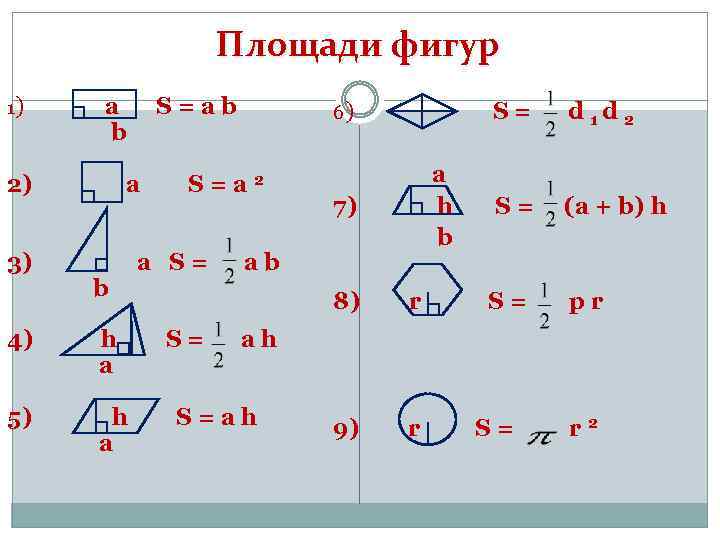
Для такого треугольника необходимо провести высоту до основания.
В нашем примере высота 6 см, а основание 8 см. Как и в предыдущем примере, вычисляем площадь по формуле:
S произвольный треугольник АВС = Солнце*Н:2.
Подставляем наши данные в формулу и получаем:
S произвольный треугольник ABC = 8 см * 6 см: 2 = 24 см 2 .
Прямоугольник и квадрат Квадрат
Возьмите прямоугольник AVD со сторонами 5 см и 8 см.
Формула вычисления площади прямоугольника записывается так:
S Прямоугольник AVD = AV*Sun.
S Прямоугольник AVD = 8 см * 5 см = 40 см 2.
Теперь посчитаем площадь квадрата. В отличие от прямоугольника и треугольника, чтобы найти площадь квадрата, нужно знать только одну сторону. В нашем примере сторона квадрата ABCD равна 9 см. S квадрат AVD = AB * Sun = AB 2.
Подставляем наши данные в формулу и получаем:
S Квадрат ABSD = 9 см * 9 см = 81 см 2.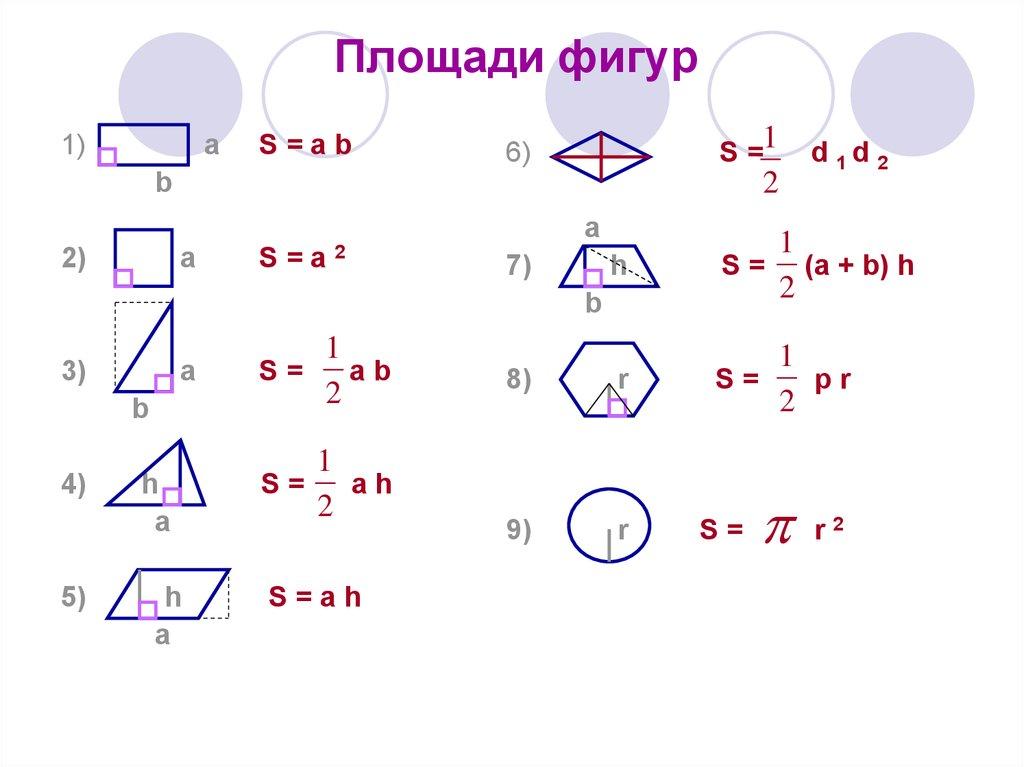
Мы уже познакомились с понятием квадрат Цифра , узнали одну из единиц измерения Площадь — квадратных сантиметра . На уроке выводим правило, как вычислить площадь прямоугольника.
Мы уже умеем находить площади фигур, которые делятся на квадратные сантиметры.
Например:
Определим, что площадь первой фигуры 8 см 2 , площадь второй фигуры 7 см 2 .
Как найти площадь прямоугольника, длина стороны которого равна 3 см и 4 см?
Для решения задачи ломаем прямоугольник на 4 полоски по 3 см 2 каждая.
Тогда площадь прямоугольника будет 3*4 = 12 см 2 .
Тот же прямоугольник можно разделить на 3 полосы по 4 см 2 . прямоугольник будет 4 * 3 = 12 см 2 .
В обоих случаях для нахождения площади прямоугольника перемножаются числа, выражающие длины сторон прямоугольника.
Находим площадь каждого прямоугольника.
Рассмотрим прямоугольник Акмо.
В одной полоске 6 см 2 , а таких полосок в этом прямоугольнике 2.
Следовательно, мы можем сделать следующее:
Цифра 6 обозначает длину прямоугольника, а 2 — ширину прямоугольника. Таким образом, мы изменили сторону прямоугольника, чтобы найти площадь прямоугольника.
Рассмотрим прямоугольник KDCO.
В прямоугольнике КДКО в одной полоске 2см 2 , а таких полосок 3. Следовательно, мы можем выполнить действие
Цифра 3 обозначает длину прямоугольника, а 2 — ширину прямоугольника. Мы изменили их и узнали площадь прямоугольника.
Можно сделать вывод: чтобы найти площадь прямоугольника, не нужно каждый раз разбивать цифру на квадратные сантиметры.
Для вычисления площади прямоугольника необходимо найти его длину и ширину (длины сторон прямоугольника должны быть выражены в одинаковых единицах измерения), а затем вычислить произведение полученные числа (площадь будет выражена в соответствующих единицах площади)
Обобщая: площадь прямоугольника равна произведению его длины на ширину.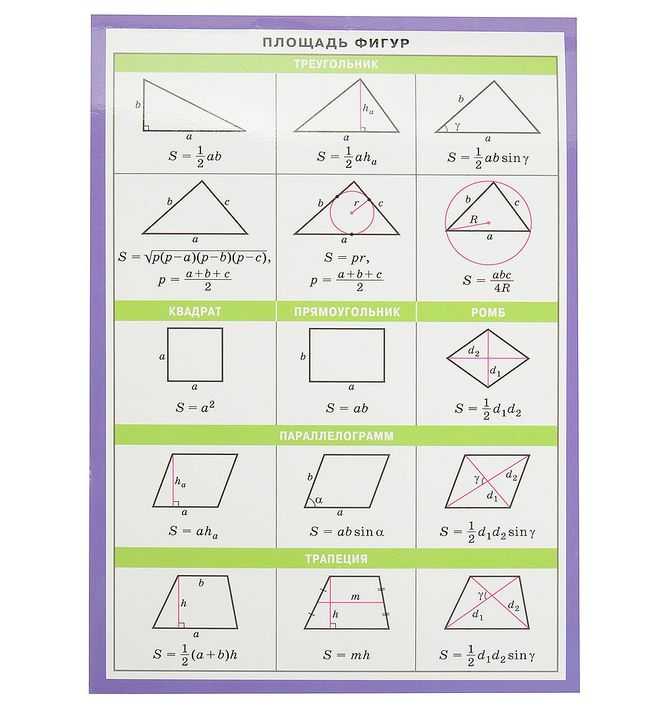
Решить задачу.
Вычисли площадь прямоугольника, если длина прямоугольника 9см, а ширина 2см.
Мы так спорим. В этой задаче известны длина и ширина прямоугольника. Поэтому действуем по правилу: площадь прямоугольника равна произведению его длины на ширину.
Записываем решение.
Ответ: Площадь прямоугольника 18 см 2
Как вы думаете, какой еще может быть длина стороны прямоугольника с такой площадью?
Ты можешь так говорить. Так как площадь есть произведение длин прямоугольника, значит нужно вспомнить таблицу умножения. При умножении каких чисел получится 18?
Правильно, при умножении 6 и 3 тоже получится 18. Значит, прямоугольник может быть частью 6см и 3см и его площадь тоже будет равна 18см2.
Решить задачу.
Длина прямоугольника 8см, ширина 2см. Найдите его площадь и периметр.
Мы знаем длину и ширину прямоугольника. Необходимо помнить, что для нахождения площади необходимо найти произведение ее длины на ширину, а для нахождения периметра нужна сумма длины и ширины умноженная на два.
Записываем решение.
Ответ: Площадь прямоугольника 16 см 2 , а периметр прямоугольника 20 см.
Решить задачу.
Длина прямоугольника 4см, ширина 3см. Что такое треугольный квадрат? (см. рисунок)
Чтобы ответить на вопрос задачи, сначала нужно найти площадь прямоугольника. Мы знаем, что для этого нужно длину умножить на ширину.
Посмотрите на рисунок. Вы заметили, что диагональ делит прямоугольник на два равных треугольника? Следовательно, площадь одного треугольника в 2 раза меньше площади прямоугольника. Значит, надо уменьшить 12 в 2 раза.
Ответ: Площадь треугольника равна 6 см 2.
Сегодня на уроке мы познакомились с правилом, как вычислить площадь прямоугольника и научились применять это правило при решение задач на нахождение площади прямоугольника.
1. М.И. Моро, М.А.Бантова и др. Математика: Учебник. 3 класс: В 2-х частях, часть 1. М., «Просвещение», 2012.
2.
М.И. Моро, М.А.Бантова и др. Математика: Учебник. 3 класс: В 2 ч., ч. 2. М., «Просвещение», 2012.
3. М.И. Моро. Уроки математики: Методические рекомендации для учителя. 3 класс. — М.: Просвещение, 2012.
4. Нормативный документ. Контроль и оценка результатов обучения. М., «Просвещение», 2011.
5. Школа России: Программы начальной школы. — М.: «Просвещение», 2011.
6. Волков С.И. Математика: контрольная работа. 3 класс. — М.: Просвещение, 2012.
7. В.Н. Лодницкая. Тесты. М., «Экзамен», 2012 (127С.)
2. Издательство «Просвещение» ()
1. Длина прямоугольника 7 см, ширина 4 см. Найдите площадь прямоугольника.
2. Сторона квадрата 5 см. Найдите площадь квадрата.
3. Наклоните возможные варианты прямоугольников, площадь которых 18 см. 2.
4. Составьте задание по теме урока для своих товарищей.
Квадрат геометрической формы — Числовая характеристика геометрической фигуры, показывающая размер этой фигуры (части поверхности, ограниченной замкнутым контуром этой фигуры).
Величина площади выражается количеством квадратных единиц, входящих в нее.
Формулы квадрата треугольника
- Формула площади треугольника по стороне и высоте
Площадь треугольника равна половине произведения длины стороны треугольника на длину высоты израсходовано - Формула площади треугольника по трем сторонам и радиусу описанной окружности
- Формула площади треугольника по трем сторонам и радиусу вписанной окружности
Площадь треугольника Равен произведению полуверсионера треугольника на радиус вписанной окружности. где S — площадь треугольника,
— длина стороны треугольника,
— высота треугольника,
— угол между сторонами и
— радиус вписанной окружности,
R — радиус описанной окружности ,
Формулы квадрат квадрат
- Формула квадрат квадрат сторона
Площадь квадрата равна квадрату длины его стороны. - Формула Квадратная диагональ квадрата
Площадь квадрата Равна половине длины его диагонали.S =. 1 2 2 где S — площадь квадрата,
— длина стороны квадрата,
— длина диагонали квадрата.
Формула квадрата прямоугольника
- Квадратный прямоугольник равен произведению длины двух его смежных сторон
где S — площадь прямоугольника,
— Длина сторон прямоугольника.
Формулы площади паралилограммы
- Формула Квадрат Поллограмма сторона и высота
Квадрат Поллограмма - Формула параллелограмма по двум сторонам и углу между ними
Поллограмма квадрата Равен произведению его длин на угол между ними.
