соответствующий рисунок 6.
 
Рис 6: Гипербола и ее директрисы.
 
Это уравнение, напомним, выполняется в специальной системе координат, которая называется канонической. Числа $a, \, b$ называются вещественной и мнимой полуосями гиперболы. Точки $(\pm a, \, 0)$ называются вершинами гиперболы. Выпишем элементарные свойства гиперболы.
1. Из уравнения следует, что $|x| \geq a$.
2. Так как переменные $x,y$ входят в уравнение гиперболы только в квадратах, то из того, что $(x,y)$ лежат на гиперболе следует, что точки $(\pm x, \, \pm y)$ также лежат на гиперболе при любом выборе знаков. Это означает, что гипербола симметрична при отражении относительной осей координат и имеет центр симметрии, точку $O$.
3. Гипербола состоит из двух ветвей, содержит точки, сколь угодно далекие от начала координат.
 
Теорема. Для того, чтобы точка лежала на гиперболе, необходимо и достаточно, чтобы отношение расстояния от этой точки до фокуса к расстоянию до соответствующей директрисы было равно эксцентриситету гиперболы, \begin{equation} r_2/d_2=\varepsilon. (24) \label{hyp3} \end{equation}  
Доказательство.
1. Достаточность. Пусть $r_2=\varepsilon d_2$. Из рисунка следует, что $d_2=a/ \varepsilon -x$, так что
\[
\sqrt{(x-c)^2+y^2}=a-\varepsilon x.
 
3.5 Эллипс 3.7 Парабола
 
Гипербола: формулы, примеры решения задач
- Определение гиперболы, решаем задачи вместе
- Решить задачи на гиперболу самостоятельно, а затем посмотреть решение
Определение гиперболы. Гиперболой называется множество всех точек плоскости, таких, для которых модуль разности расстояний от двух точек, называемых фокусами, есть величина постоянная и меньшая, чем расстояние между фокусами.
Каноническое уравнение гиперболы имеет вид:
,
где a и b — длины полуосей, действительной и мнимой.
На чертеже ниже фокусы обозначены как и .
На чертеже ветви гиперболы — бордового цвета.
При a = b гипербола называется равносторонней.
Пример 1. Составить каноническое уравнение гиперболы, если его действительная полуось a = 5 и мнимая = 3.
Решение. Подставляем значения полуосей в формулу канонического уравения гиперболы и получаем:
.
Точки пересечения гиперболы с её действительной осью (т. е. с осью Ox) называются вершинами. Это точки (a, 0) (- a, 0), они обозначены и надписаны на рисунке чёрным.
Точки и , где
,
называются фокусами гиперболы (на чертеже обозначены зелёным, слева и справа от ветвей гиперболы).
Число
называется эксцентриситетом гиперболы.
Гипербола состоит из двух ветвей, лежащих в разных полуплоскостях
относительно оси ординат.
Пример 2. Составить каноническое уравнение гиперболы, если расстояние между фокусами равно 10 и действительная ось равна 8.
Решение.
Если действительная полуось равна 8, то её половина, т. е. полуось a = 4,
Если расстояние между фокусами равно 10, то число c из координат фокусов равно 5.
То есть, для того, чтобы составить уравнение гиперболы, потребуется вычислить квадрат мнимой полуоси b.
Подставляем и вычисляем:
Получаем требуемое в условии задачи каноническое уравнение гиперболы:
.
Пример 3. Составить каноническое уравнение гиперболы, если её действительная ось равна 48 и эксцентриситет .
Решение. Как следует из условия, действительная полуось a = 24. А эксцентриситет — это пропорция и
так как a = 24, то коэффициент пропорциональности
отношения с и a равен 2. Следовательно, c = 26.
Из формулы числа c выражаем квадрат мнимой полуоси и
вычисляем:
Следовательно, c = 26.
Из формулы числа c выражаем квадрат мнимой полуоси и
вычисляем:
.
Результат — каноническое уравнение гиперболы:
Нет времени вникать в решение? Можно заказать работу!
К началу страницы
Пройти тест по теме Кривые второго порядка
Если — произвольная точка левой ветви гиперболы () и — расстояния до этой точки от фокусов , то формулы для расстояний — следующие:
.
Если — произвольная точка правой ветви гиперболы () и — расстояния до этой точки от фокусов , то формулы для расстояний — следующие:
.
На чертеже расстояния обозначены оранжевыми линиями.
Для каждой точки, находящейся на гиперболе, сумма расстояний от фокусов есть величина постоянная, равная 2a.
Прямые, определяемые уравнениями
,
называются директрисами гиперболы (на чертеже — прямые ярко-красного
цвета).
Из трёх вышеприведённых уравнений следует, что для любой точки гиперболы
,
где — расстояние от левого фокуса до точки любой ветви гиперболы, — расстояние от правого фокуса до точки любой ветви гиперболы и и — расстояния этой точки до директрис и .
Пример 4. Дана гипербола . Составить уравнение её директрис.
Решение. Смотрим в уравнение директрис и обнаруживаем, что требуется найти эксцентриситет гиперболы, т. е. . Вычисляем:
.
Получаем уравнение директрис гиперболы:
Многие задачи на директрисы гиперболы аналогичны задачам на директрисы эллипса. В уроке «Эллипс» это пример 7.
Характерной особенностью гиперболы является наличие асимптот — прямых, к которым приближаются точки гиперболы при удалении от центра.
Асимптоты гиперболы определяются уравнениями
.
На чертеже асимптоты — прямые серого цвета, проходящие через начало координат O.
Уравнение гиперболы, отнесённой к асимптотам, имеет вид:
, где .
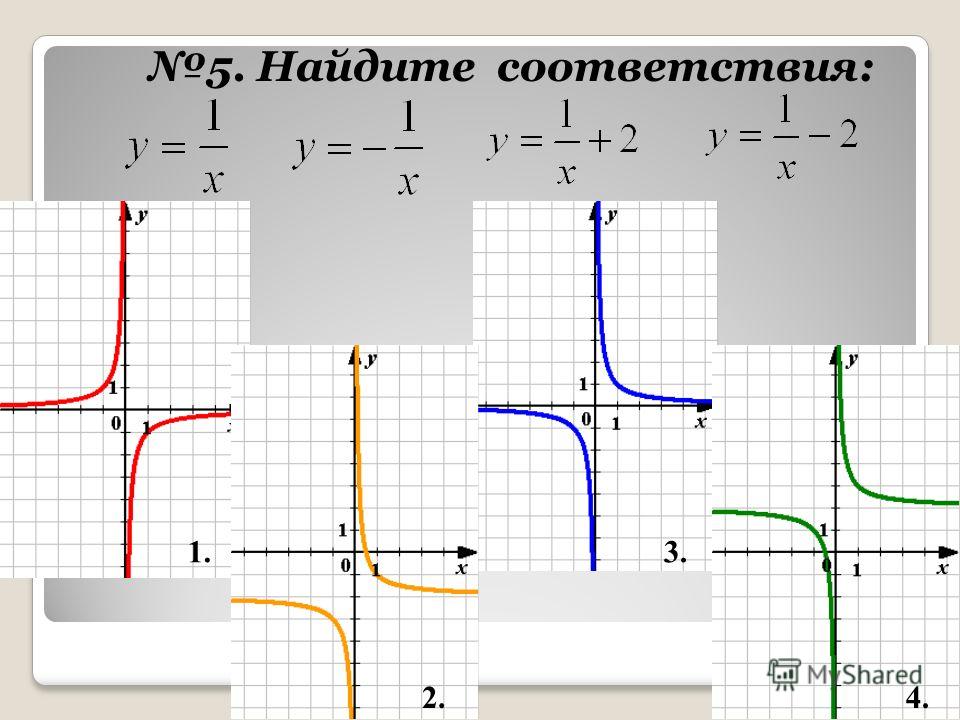
В том случае, когда угол между асимптотами — прямой, гипербола называется равнобочной, и если асимптоты равнобочной гиперболы выбрать за оси координат, то её уравнение запишется в виде y = k/x, то есть в виде уравения обратной пропорциональной зависимости.
Пример 5. Даны уравнения асимптот гиперболы и координаты точки , лежащей на гиперболе. Составить уравнение гиперболы.
Решение. Дробь в уравнении асимптот гиперболы — это пропорция, следовательно,
нужно сначала найти коэффициент пропорциональности отношения .
Для этого подставляем в формулу канонического уравнения гиперболы координаты точки 
.
Теперь имеем все данные, чтобы получить каноническое уравнение гиперболы. Получаем:
Гипербола обладает оптическим свойством, которое описывается следующим образом: луч, исходящий из источника света, находящегося в одном из фокусов гиперболы, после отражения движется так, как будто он исходит из другого фокуса.
Пример 6. Фокусы эллипса расположены на оси Ox симметрично относительно начала координат. Составить каноническое уравнение эллипса, если:
1) b = 4, а один из фокусов в точке (5; 0)
посмотреть правильное решение и ответ,
2) действительная ось 6, расстояние между фокусами 8
посмотреть правильное решение и ответ,
3) один из фокусов в точке (-10; 0), уравнения асимптот гиперболы
посмотреть правильное решение и ответ.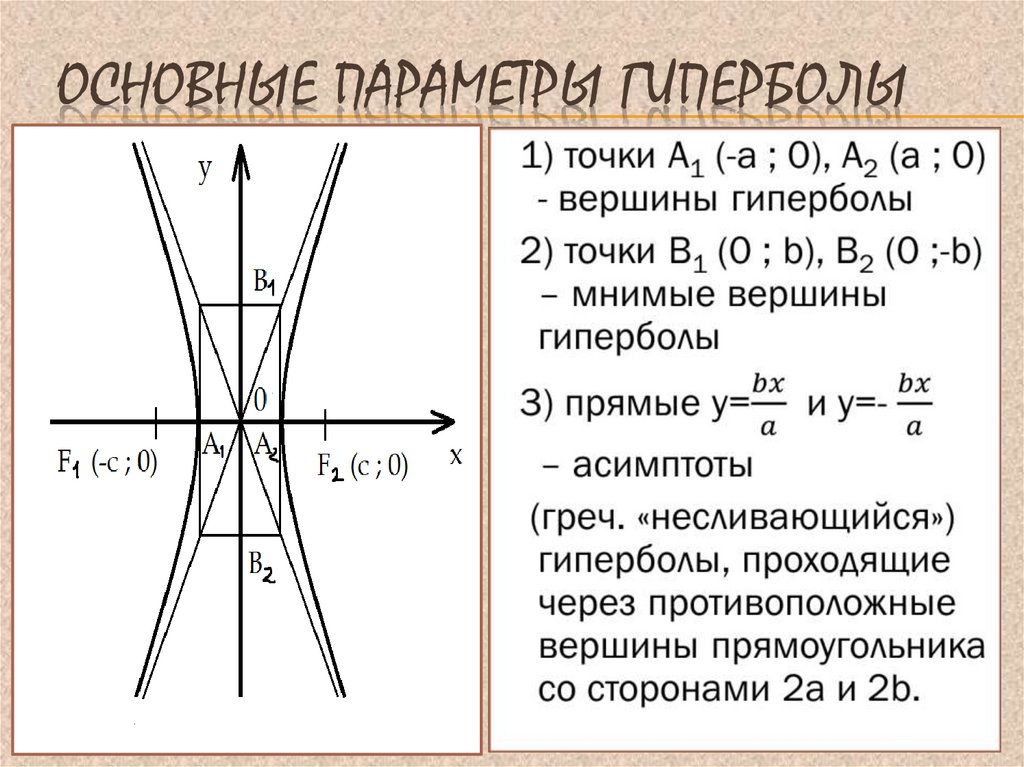
| Назад | Листать | Вперёд>>> |
Нет времени вникать в решение? Можно заказать работу!
К началу страницы
Пройти тест по теме Кривые второго порядка
Поделиться с друзьями
Другие материалы по теме Кривые второго порядка
Эллипс
Парабола
| § 4.3. Гипербола Гиперболой называется геометрическое место точек плоскости, разность расстояний которых от двух данных точек той же плоскости, называемых фокусами гиперболы, постоянна. Для вывода простейшего уравнения
гиперболы расположим оси координат по отношению к ее фокусам
и
так же, как мы это делали в предыдущем параграфе для эллипса. Сохраним для
гиперболы те же обозначения: 2а для постоянной величины, упоминаемой
в определении гиперболы, 2с для расстояния между фокусами
и . Возьмем произвольную точку , лежащую на гиперболе. По определению гиперболы для точек кривой, лежащих в I и IV четвертях имеем: (3.18), а для точек, лежащих во II и III четвертях: (3.18`). Заметим, что для гиперболы в отличие от эллипса (2а есть разность двух сторон треугольника , а 2с – его третья сторона). Выражая через координаты точек , и длины отрезков и оба равенства (3.18) и (3.18′) можно записать в виде: (3.19). Производя над этим уравнением те же преобразования, что и над уравнением (3.6) в случае эллипса (см. § 4.2), мы в конечном счете придем к тому же самому уравнению (3.10): , в котором, однако, теперь . Деля левую и правую части уравнения (3.10) на и учитывая, что теперь , запишем результат в виде: Наконец, полагая , получим окончательно простейшее (каноническое) уравнение гиперболы: (3.21). Можно доказать, что равенство (3.21) равносильно объединенному равенству (3.19). Для построению гиперболы по ее уравнению (3.21) заметим прежде всего, что первый член левой части этого уравнения не меньше его правой части, т. е. единицы (поскольку из вычитается неотрицательная величина ): . Отсюда . Таким образом, в вертикальной полосе между параллельными оси Oy прямыми и точек кривой нет. Отмечаем далее, что, так же как и для эллипса, оси координат служат осями симметрии гиперболы, так как в уравнении (3. Решим уравнение гиперболы (3.21) относительно y: , выберем в правой части знак плюс, поскольку в I четверти : , (3.22). При ; при возрастании x возрастает и y: ветвь гиперболы, подымаясь от оси Ox, уходит на плоскости все дальше и дальше, или, как говорят в геометрии, уходит «в бесконечность». Но при этом, как нетрудно показать, ветвь кривой все ближе и ближе подходит к прямой . В самом деле, разность между ординатами точек этой прямой и гиперболы (обозначим ее через ), соответствующих одному и тому же значению абсциссы х, имеем следующее выражение: (3.23) Из последнего выражения видно,
что когда х неограниченно возрастает, то ,
оставаясь положительным, стремится к нулю, что и подтверждает высказанную
нами мысль: ветвь гиперболы, лежащая в I
четверти неограниченно приближается (и притом снизу, так как )
к прямой ,
когда абсцисса х точки гиперболы неограниченно возрастает. Таким образом, прямая является асимптотой гиперболы. В силу симметрии гиперболы у нее есть и вторая асимптота: . Наличие асимптот и соображения симметрии позволяют нам построить всю гиперболу (рис. 5): кривая состоит из двух не смыкающихся ветвей, лежащих в углах между прямыми и и неограниченно приближаются к этим прямым. В отношении гиперболы используется следующая терминология. Отрезок
называют вещественной, а
– мнимой осью гиперболы; их длины равны соответственно 2а и 2b (а – вещественная полуось, b – мнимая полуось). Точки гиперболы
и ,
лежащие на вещественной оси, – вершины гиперболы. Точка О – центр гиперболы. Изображенный на рис. Для построения фокусов гиперболы и полезно знать, что основное соотношение между величинами , и у гиперболы можно записать в виде: (3.24). Поэтому расстояние от центра гиперболы до ее фокуса равно половине длинны диагонали осевого прямоугольника : в прямоугольном треугольнике катеты , , а следовательно, его гипотенуза . Форма гиперболы зависит от угла
наклона асимптоты к вещественной оси, т. е. от величины отношения :
чем эта величина меньше, тем меньше угол между асимптотами, в котором заключена
гипербола, и тем более сжата сама гипербола; чем больше величина ,
тем круче располагаются ветви гиперболы. Но, так же как и для эллипса, в качестве характеристики формы гиперболы в аналитической геометрии пользуются не величиной отношения , а величиной , называемой эксцентриситетом гиперболы и обозначают той же буквой , как и для эллипса: (3.25). Так как у гиперболы , то эксцентриситет гиперболы . Из прямоугольного треугольника , в котором острый угол наклона асимптоты к вещественной оси обозначен через , находим: и, следовательно: (3.26), т. е. эксцентриситет гиперболы равен секансу угла наклона асимптоты к вещественной оси. Важным частным случаем гиперболы является равносторонняя (равноосная) гипербола – такая гипербола, у которой равны длины вещественной и мнимой полуосей: . Уравнение этой гиперболы имеет вид: (3. У равносторонней гиперболы, как нетрудно показать, угол между асимптотами прямой, и . Для гиперболы, у которых оси совпадают и равны, но вещественная ось одной служит мнимой осью другой и наоборот, называются сопряженными; асимптоты таких гипербол также совпадают (поскольку совпадают их осевые прямоугольники), но гиперболы располагаются в смежных углах между асимптотами. Нетрудно видеть, что если уравнением одной из сопряженных гипербол является уравнение (3.21): , то уравнение второй будет иметь вид: , или (3.28), поскольку меняются ролями оси Ox и Oy и полуоси гипербол а и b. Отметим, что расстояние с от центра до фокусов у обеих сопряженных гипербол одно и то же, определяемое
формулой (3.24), но эксцентриситеты различные: ,
;
(если только обе гиперболы не являются равносторонними).
|
Гипербола — уравнение, свойства, примеры
В математике гипербола — это важное коническое сечение, образованное пересечением двойного конуса плоской поверхностью, но не обязательно в центре. Гипербола симметрична вдоль сопряженной оси и имеет много общего с эллипсом. Такие понятия, как фокус, директриса, широкая прямая кишка, эксцентриситет, применимы к гиперболе. Несколько распространенных примеров гиперболы включают путь, по которому следует кончик тени солнечных часов, траектория рассеяния субатомных частиц и т. д.
Здесь мы будем стремиться понять определение, формулу гиперболы, вывод формулы и стандартные формы гиперболы, используя решенные примеры.
| 1. | Что такое гипербола? |
| 2. | Части гиперболы |
| 3. | Стандартная форма уравнения гиперболы |
4. | Вывод уравнения гиперболы |
| 5. | Формула гиперболы |
| 6. | График гиперболы |
| 7. | Свойства гиперболы |
| 8. | Часто задаваемые вопросы о Hyperbola |
Что такое гипербола?
Гипербола, тип гладкой кривой, лежащей на плоскости, состоит из двух частей, называемых связными компонентами или ответвлениями, которые являются зеркальным отображением друг друга и напоминают две бесконечные дуги. Гипербола — это множество точек, разность расстояний которых от двух фокусов является постоянной величиной. Эта разница берется из расстояния от дальнего фокуса, а затем из расстояния от ближнего фокуса. Для точки Р(х, у) гиперболы и двух фокусов F, F’ геометрическое место гиперболы равно PF — PF’ = 2a.
Гипербола Определение
Гипербола в аналитической геометрии — это коническое сечение, которое образуется при пересечении плоскостью двойного прямого кругового конуса под таким углом, что обе половины конуса пересекаются.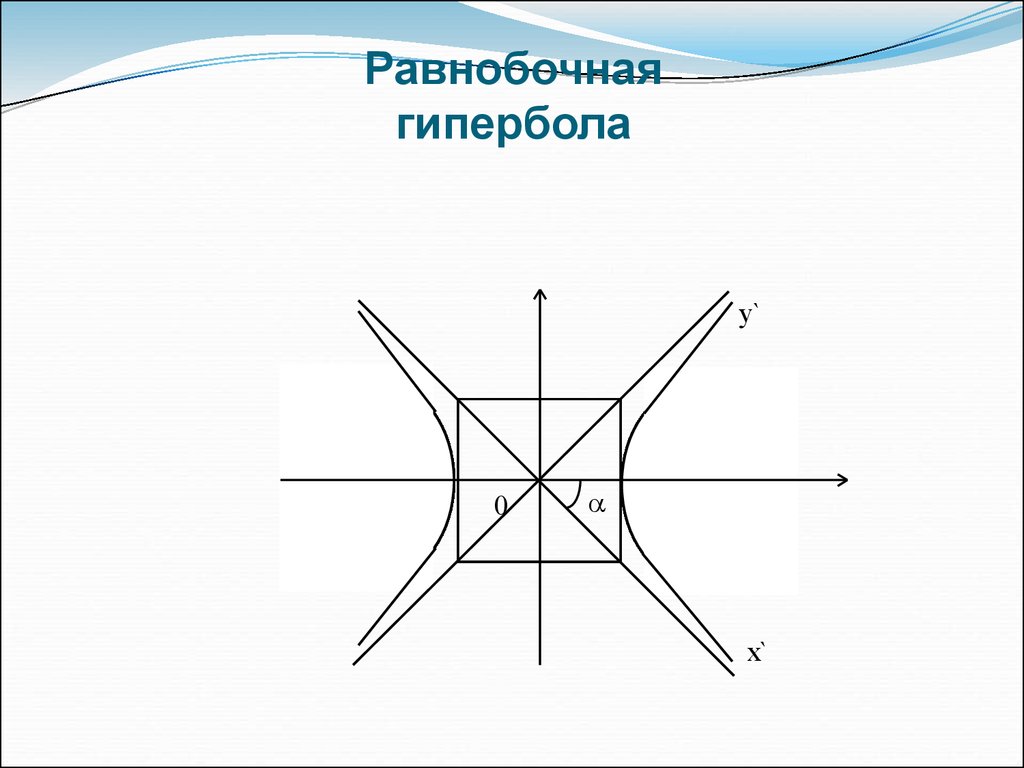 Это пересечение плоскости и конуса дает две отдельные неограниченные кривые, которые являются зеркальным отображением друг друга, называемые гиперболой.
Это пересечение плоскости и конуса дает две отдельные неограниченные кривые, которые являются зеркальным отображением друг друга, называемые гиперболой.
Части гиперболы
Давайте проверим несколько важных терминов, относящихся к различным параметрам гиперболы.
Фокусы гиперболы: Гипербола имеет два фокуса и их координаты F(c, o) и F'(-c, 0).
Центр гиперболы: Середина линии, соединяющей два фокуса, называется центром гиперболы.
Большая ось: Длина большой оси гиперболы составляет 2a единиц.
Малая ось: Длина малой оси гиперболы составляет 2b единиц.
Вершины: Точки, в которых гипербола пересекает ось, называются вершинами. Вершины гиперболы равны (а, 0), (-а, 0).
Широкая прямая кишка гиперболы: Широкая прямая кишка представляет собой линию, проведенную перпендикулярно поперечной оси гиперболы и проходящую через фокусы гиперболы. Длина широкой прямой кишки гиперболы 2b 2 /а.
Длина широкой прямой кишки гиперболы 2b 2 /а.
Поперечная ось: Линия, проходящая через два фокуса и центр гиперболы, называется поперечной осью гиперболы.
Сопряженная ось: Прямая, проходящая через центр гиперболы и перпендикулярная поперечной оси, называется сопряженной осью гиперболы.
Эксцентриситет гиперболы: (e > 1) Эксцентриситет представляет собой отношение расстояния фокуса от центра гиперболы и расстояния вершины от центра гиперболы. Расстояние до фокуса составляет c единиц, а расстояние до вершины равно a единиц, следовательно, эксцентриситет равен e = c/a.
Уравнение гиперболы
Приведенное ниже уравнение представляет собой общее уравнение гиперболы. Здесь ось x является поперечной осью гиперболы, а ось y является сопряженной осью гиперболы. 92} = 1\) и имеет поперечную ось как ось у, а ее сопряженная ось — ось х. На изображении ниже показаны две стандартные формы уравнений гиперболы.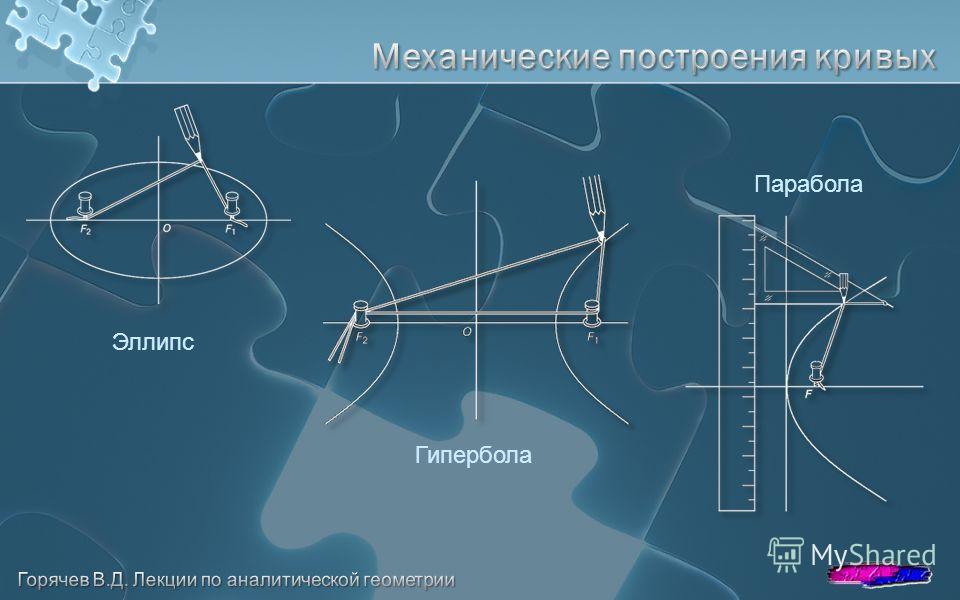
Вывод уравнения гиперболы
Согласно определению гиперболы, рассмотрим точку P на гиперболе, и разница ее расстояний от двух фокусов F, F’ равна 2а.
PF’ — PF = 2a
Пусть координаты точки P равны (x, y), а фокусы равны F(c, o) и F'(-c, 0) 92} =1\)
Следовательно, выводится стандартное уравнение гиперболы.
Формула гиперболы
Гипербола — это незамкнутая кривая, имеющая две ветви, которые выглядят как зеркальные отражения друг друга. Для любой точки любой из ветвей абсолютная разность между точкой и фокусами постоянна и равна 2а, где а — расстояние ветви от центра. Формула гиперболы помогает нам найти различные параметры и связанные части гиперболы, такие как уравнение гиперболы, большую и малую оси, эксцентриситет, асимптоты, вершину, фокусы и полуширотную прямую кишку. 92} \),y\(_0\))
Semi-latus rectum(p) формулы гиперболы:
p = b 2 / a
, где
- x\(_0\), y\(_0\) — центральные точки.

- а = большая полуось.
- b = малая полуось.
Пример: Уравнение гиперболы задается как (x — 5) 2 /4 2 — (y — 2) 2 / 2 2 = 1. Используйте формулы гиперболы, чтобы найти длина большой оси и малой оси.
Решение:
Используя формулу гиперболы для длины большой и малой оси
Длина большой оси = 2a и длина малой оси = 2b
Длина большой оси = 2 × 4 = 8, и Длина малой оси = 2 × 2 = 4
Ответ: Длина большой оси 8 единиц, а длина малой оси 4 единицы.
График гиперболы
Все гиперболы имеют общие черты, состоящие из двух кривых, каждая из которых имеет вершину и фокус. Поперечная ось гиперболы — это ось, проходящая через обе вершины и фокусы, а сопряженная ось гиперболы перпендикулярна ей. Мы можем наблюдать графики стандартных форм уравнения гиперболы на рисунке ниже. Если уравнение данной гиперболы имеет нестандартную форму, то нам необходимо дополнить квадрат, чтобы привести его к стандартной форме. 92} = 1\)
92} = 1\)
Свойства гиперболы
Следующие важные свойства, связанные с различными концепциями, помогают лучше понять гиперболу.
Асимптоты: Пара прямых, проведенных параллельно гиперболе и предположительно касающихся гиперболы на бесконечности. Уравнения асимптот гиперболы имеют вид y = bx/a и y = -bx/a соответственно.
Прямоугольная гипербола: Гипербола, имеющая поперечную ось и сопряженную ось одинаковой длины, называется прямоугольной гиперболой. Здесь мы имеем 2a = 2b или a = b. Следовательно, уравнение прямоугольной гиперболы равно x 2 — y 2 = a 2
Параметрические координаты: Точки на гиперболе могут быть представлены параметрическими координатами (x, y) = (asecθ, btanθ). Эти параметрические координаты, представляющие точки на гиперболе, удовлетворяют уравнению гиперболы.
Эти параметрические координаты, представляющие точки на гиперболе, удовлетворяют уравнению гиперболы.
Вспомогательная окружность: Окружность, нарисованная с конечными точками поперечной оси гиперболы в качестве ее диаметра, называется вспомогательной окружностью. Уравнение вспомогательной окружности гиперболы x 2 + у 2 = а 2 .
Направление окружности: Геометрическое место точки пересечения перпендикулярных касательных к гиперболе называется направляющей окружностью. Уравнение окружности директора гиперболы: x 2 + y 2 = a 2 — b 2 .
Связанные статьи о гиперболе:
Следующие темы помогут лучше понять гиперболу и связанные с ней концепции.
- Координатная геометрия
- Коники в реальной жизни
- Декартовы координаты
- Парабола
Примеры гиперболы
Пример 1: Уравнение гиперболы записывается как [(x — 5) 2 /4 2 ] — [(y — 2) 2 / 6 2 ] = 1.
 Найдите асимптота этой гиперболы.
Найдите асимптота этой гиперболы.Решение:
Используя одну из формул гиперболы (для нахождения асимптот):
y = y\(_0\) — (b/a)x + (b/a)x\(_0\) и y = y\(_0\) + (b/a)x — (b/a)x \(_0\)у = 2 — (6/4)х + (6/4)5 и у = 2 + (6/4)х — (6/4)5
Ответ: Асимптоты: y = 2 — (3/2)x + (3/2)5 и y = 2 + 3/2)x — (3/2)5.
Пример 2: Уравнение гиперболы задается как [(x — 5) 2 /6 2 ] — [(y — 2) 2 / 4 2 ] = 1. Используйте формулы гиперболы, чтобы найти длину большой оси и малой оси.
Решение:
Используя формулу гиперболы для длины большой и малой оси
Длина большой оси = 2a и длина малой оси = 2b
Длина большой оси = 2 × 6 = 12, и Длина малой оси = 2 × 4 = 8
Ответ: Длина большой оси 12 единиц, а длина малой оси 8 единиц.
Пример 3: Уравнение гиперболы записывается как (x — 3) 2 /5 2 — (у — 2) 2 / 4 2 = 1.
 Найдите асимптоту этой гиперболы.
Найдите асимптоту этой гиперболы.Решение:
Используя одну из формул гиперболы (для нахождения асимптот):
y = y\(_0\) — (b/a)x + (b/a)x\(_0\) и y = y\(_0\) — (b/a)x + (b/a)x \(_0\)y = 2 — (4/5)x + (4/5)5 и y = 2 + (4/5)x — (4/5)5
Ответ: Асимптоты у = 2 — (4/5)х + 4, и у = 2 + (4/5)х — 4.
перейти к слайдуперейти к слайдуперейти к слайду
Разложите сложные концепции с помощью простых визуальных эффектов.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Записаться на бесплатный пробный урок
Практические вопросы по гиперболе
перейти к слайдуперейти к слайду
Часто задаваемые вопросы по Hyperbola
Что такое гипербола в коническом сечении?
А гипербола 92} = 1\). Здесь «а» — большая полуось, а «b» — малая полуось. Существуют две стандартные формы уравнений гиперболы. Эксцентриситет гиперболы больше 1. (e > 1). Эксцентриситет — это отношение расстояния фокуса от центра эллипса и расстояния вершины от центра эллипса. Расстояние до фокуса составляет c единиц, а расстояние до вершины равно a единиц, следовательно, эксцентриситет равен e = c/a. Также здесь у нас есть c 92} = 1\) имела ось абсцисс в качестве своей поперечной оси. В аналитической геометрии гипербола представляет собой коническое сечение, образованное пересечением прямого кругового конуса с плоскостью под углом, при котором обе половины конуса пересекаются. Гипербола Как и эллипс, гипербола также может быть определена как набор точек на координатной плоскости. Гипербола — это множество всех точек [латекс]\слева(х,у\справа)[/латекс] на плоскости, таких, что разность расстояний между [латекс]\слева(х,у\справа)[/латекс ], а фокусы — положительная постоянная. Обратите внимание, что определение гиперболы очень похоже на определение эллипса. Отличие состоит в том, что гипербола определяется в терминах разности двух расстояний, тогда как эллипс определяется в терминах суммы двух расстояний. Как и эллипс, каждая гипербола имеет две оси симметрии . Поперечная ось представляет собой отрезок, который проходит через центр гиперболы и имеет вершины в качестве своих концов. Фокусы лежат на линии, содержащей поперечную ось. Сопряженная ось перпендикулярна поперечной оси и имеет ковершины в качестве своих конечных точек. Ключевые особенности гиперболы В этом разделе мы ограничим наше обсуждение гиперболами, расположенными вертикально или горизонтально в координатной плоскости; оси будут лежать или быть параллельными осям x и y . Мы рассмотрим два случая: те, которые сосредоточены в начале координат, и те, которые сосредоточены в точке, отличной от начала координат. Пусть [латекс]\влево(-c,0\вправо)[/латекс] и [латекс]\влево(с,0\вправо)[/латекс ] быть фокусов гиперболы с центром в начале координат. Если [латекс]\влево(а,0\вправо)[/латекс] является вершиной гиперболы, расстояние от [латекс]\влево(-c,0\вправо)[/латекс] до [латекс] \left(a,0\right)[/latex] равно [latex]a-\left(-c\right)=a+c[/latex]. Расстояние от [латекс]\слева(с,0\справа)[/латекс] до [латекс]\слева(а,0\справа)[/латекс] равно [латекс]с-а[/латекс]. Разность расстояний от фокусов до вершины равна [латекс]\влево(а+с\вправо)-\влево(с-а\вправо)=2а[/латекс] Если [латекс]\влево(х,у\вправо)[/латекс] является точкой на гиперболе мы можем определить следующие переменные: [латекс]\begin{align}&{d}_{2}=\text{расстояние от }\left(-c,0\right)\text{ до }\left(x,y\right)\\ &{d}_{1}=\text{расстояние от }\left(c,0\right)\text{ до }\left(x,y\ right)\end{align}[/latex] По определению гиперболы [latex]\lvert{d}_{2}-{d}_{1}\rvert[/latex] постоянна для любой точки [латекс]\влево(х,у\вправо)[/латекс] на гиперболе. Показать решение Как и в случае с эллипсами, запись уравнения гиперболы в стандартной форме позволяет вычислить ключевые характеристики: ее центр, вершины, ко-вершины, фокусы, асимптоты, длины и положения поперечной и сопряженной осей. И наоборот, уравнение гиперболы можно найти, учитывая ее ключевые особенности. Начнем с нахождения стандартных уравнений для гипербол с центром в начале координат. Затем мы обратим наше внимание на поиск стандартных уравнений для гипербол с центром в какой-либо точке, отличной от начала координат. 9{2}[/латекс]. Это соотношение используется для записи уравнения гиперболы при заданных координатах ее фокусов и вершин. Какова стандартная форма уравнения гиперболы с вершинами right)[/latex] и фокусы [latex]\left(\pm 2\sqrt{10},0\right)?[/latex] Показать решение Уравнение стандартной формы гиперболы, имеющей вершины [латекс]\влево(0,\pm 2\справа)[/латекс] и фокусы [латекс]\влево(0,\pm 2\ sqrt{5}\справа)?[/latex] Показать решение Как и графики для других уравнений, график гиперболы можно трансформировать. Асимптоты гиперболы совпадают с диагоналями центрального прямоугольника. Длина прямоугольника равна [латекс]2а[/латекс], а ширина — [латекс]2b[/латекс]. Наклоны диагоналей равны [латекс]\pm \frac{b}{a}[/латекс], и каждая диагональ проходит через центр [латекс]\влево(ч,к\вправо)[/латекс]. Используя формулу точек-наклонов , легко показать, что уравнения асимптот таковы: [latex]y=\pm \frac{b}{a}\left(x-h\right)+k[/latex]. 9{2}[/латекс] Используя приведенные выше рассуждения, уравнения асимптот таковы: [латекс]y=\pm \frac{a}{b}\left(x-h\right)+k[/latex].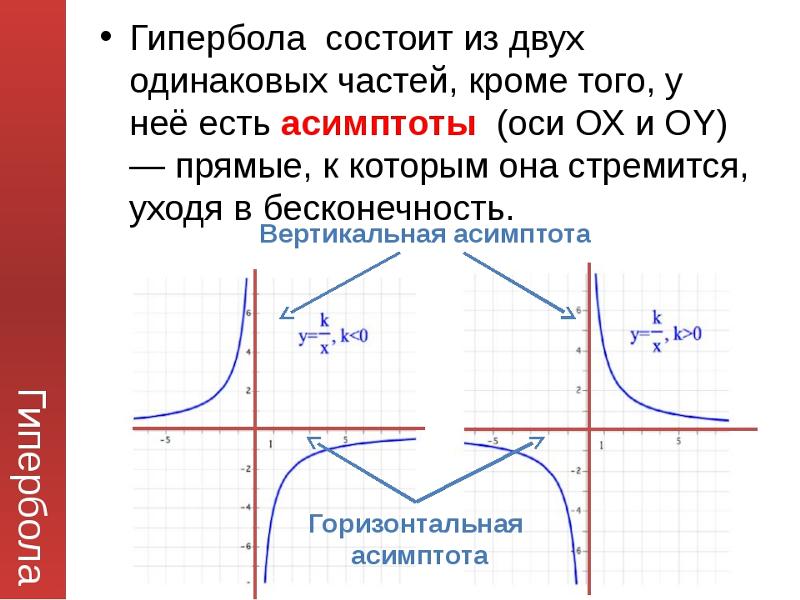 2} = 1\). 92} = 1\), для гиперболы, имеющей поперечную ось в качестве оси у, а сопряженной ей осью является ось х.
2} = 1\). 92} = 1\), для гиперболы, имеющей поперечную ось в качестве оси у, а сопряженной ей осью является ось х. Что такое эксцентриситет гиперболы?
Уравнения гиперболы | Колледж Алгебра
Результаты обучения
 Это пересечение дает две отдельные неограниченные кривые, которые являются зеркальным отображением друг друга.
Это пересечение дает две отдельные неограниченные кривые, которые являются зеркальным отображением друг друга. центр гиперболы является серединой поперечной и сопряженной осей, где они пересекаются. Каждая гипербола также имеет две асимптоты , которые проходят через ее центр. При удалении гиперболы от центра ее ветви приближаются к этим асимптотам. Центральный прямоугольник гиперболы имеет центр в начале координат со сторонами, которые проходят через каждую вершину и ковершину; это полезный инструмент для построения графиков гиперболы и ее асимптот. Чтобы начертить асимптоты гиперболы, просто нарисуйте и продлите диагонали центрального прямоугольника.
центр гиперболы является серединой поперечной и сопряженной осей, где они пересекаются. Каждая гипербола также имеет две асимптоты , которые проходят через ее центр. При удалении гиперболы от центра ее ветви приближаются к этим асимптотам. Центральный прямоугольник гиперболы имеет центр в начале координат со сторонами, которые проходят через каждую вершину и ковершину; это полезный инструмент для построения графиков гиперболы и ее асимптот. Чтобы начертить асимптоты гиперболы, просто нарисуйте и продлите диагонали центрального прямоугольника. Стандартная форма уравнения гиперболы с центром в начале координат
 Гипербола — это множество всех точек [латекс]\слева(х,у\справа)[/латекс], таких что разность расстояний от [латекс]\слева(х,у\справа)[/латекс] до очаги постоянны.
Гипербола — это множество всех точек [латекс]\слева(х,у\справа)[/латекс], таких что разность расстояний от [латекс]\слева(х,у\справа)[/латекс] до очаги постоянны.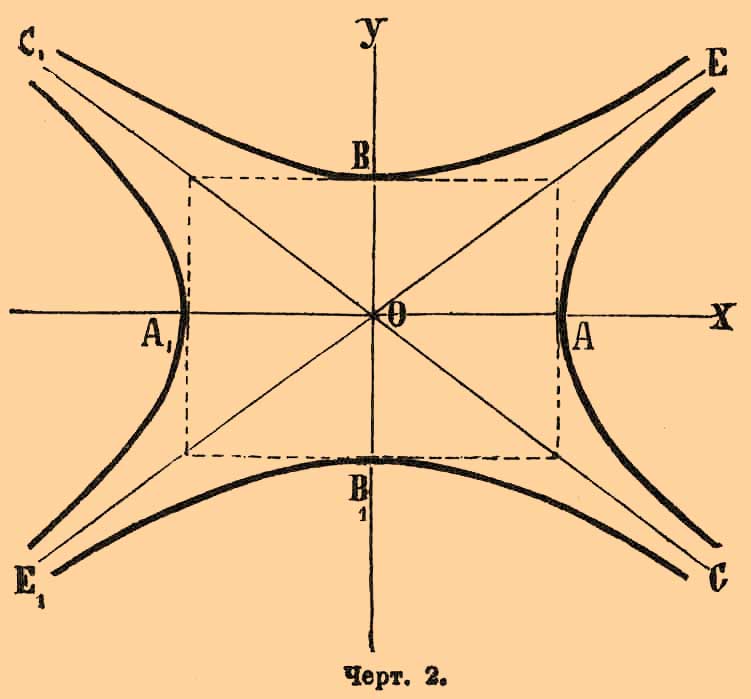 {2}[/latex] всегда находится под переменной с положительным коэффициентом. Итак, если вы установите другую переменную равной нулю, вы можете легко найти точки пересечения. В случае, когда центр гиперболы находится в начале координат, точки пересечения совпадают с вершинами. 9{2}}{25}=1[/латекс].
{2}[/latex] всегда находится под переменной с положительным коэффициентом. Итак, если вы установите другую переменную равной нулю, вы можете легко найти точки пересечения. В случае, когда центр гиперболы находится в начале координат, точки пересечения совпадают с вершинами. 9{2}}{25}=1[/латекс]. Запись уравнений гиперболы в стандартной форме

Как сделать: Имея вершины и фокусы гиперболы с центром в точке [латекс]\влево(0,\текст{0}\вправо)[/латекс], запишите ее уравнение в стандартной форме.
Пример. Нахождение уравнения гиперболы с центром в точке (0,0) при заданных фокусах и вершинах
Попробуйте
Гиперболы, не центрированные в начале координат
 Если перевести гиперболу [latex]h[/latex] единиц по горизонтали и [latex]k[/latex] единиц по вертикали, центр гиперболы будет [latex]\left(h,k\right)[/ латекс]. Этот перевод приводит к стандартной форме уравнения, которое мы видели ранее, с заменой [latex]x[/latex] на [latex]\left(x-h\right)[/latex] и [latex]y[/latex] на [латекс]\влево(у-к\вправо)[/латекс]. 9{2}[/латекс]
Если перевести гиперболу [latex]h[/latex] единиц по горизонтали и [latex]k[/latex] единиц по вертикали, центр гиперболы будет [latex]\left(h,k\right)[/ латекс]. Этот перевод приводит к стандартной форме уравнения, которое мы видели ранее, с заменой [latex]x[/latex] на [latex]\left(x-h\right)[/latex] и [latex]y[/latex] на [латекс]\влево(у-к\вправо)[/латекс]. 9{2}[/латекс] {2}[/латекс]. Мы можем использовать это соотношение вместе с формулами средней точки и расстояния, чтобы найти стандартное уравнение гиперболы, когда заданы вершины и фокусы. 9{2}[/latex] в стандартную форму уравнения, определенного на шаге 1.
{2}[/латекс]. Мы можем использовать это соотношение вместе с формулами средней точки и расстояния, чтобы найти стандартное уравнение гиперболы, когда заданы вершины и фокусы. 9{2}[/latex] в стандартную форму уравнения, определенного на шаге 1. Пример: нахождение уравнения гиперболы с центром в точке (
h , k ) с учетом ее фокусов и вершин ,-2\вправо)[/латекс] и [латекс]\влево(6,-2\вправо)[/латекс] и фокусы в [латекс]\влево(-2,-2\вправо)[/латекс] и [латекс]\влево(8,-2\вправо)?[/латекс]
Показать решение
Попробуйте
Уравнение стандартной формы гиперболы с вершинами [латекс]\влево(1,-2\вправо)[/латекс] и [латекс]\влево(1,\текст{8}\вправо) )[/latex] и фокусы [латекс]\левый(1,-10\правый)[/латекс] и [латекс]\левый(1,16\правый)?[/латекс]
Показать решение
Решение прикладных задач, связанных с гиперболами
Как мы обсуждали в начале этого раздела, гиперболы находят практическое применение во многих областях, таких как астрономия, физика, инженерия и архитектура. Эффективность конструкции гиперболических градирен особенно интересна. Градирни используются для передачи отработанного тепла в атмосферу и часто рекламируются за их способность эффективно генерировать энергию. Из-за своей гиперболической формы эти конструкции способны противостоять сильным ветрам, при этом требуя меньше материала, чем любые другие формы их размера и прочности. Например, 500-футовая башня может быть сделана из железобетонной оболочки шириной всего 6 или 8 дюймов!
Эффективность конструкции гиперболических градирен особенно интересна. Градирни используются для передачи отработанного тепла в атмосферу и часто рекламируются за их способность эффективно генерировать энергию. Из-за своей гиперболической формы эти конструкции способны противостоять сильным ветрам, при этом требуя меньше материала, чем любые другие формы их размера и прочности. Например, 500-футовая башня может быть сделана из железобетонной оболочки шириной всего 6 или 8 дюймов!
Градирни на электростанции Drax в Северном Йоркшире, Великобритания (фото: Les Haines, Flickr)
Первые гиперболические градирни были спроектированы в 1914 году и имели высоту 35 метров. Сегодня самые высокие градирни находятся во Франции, их высота составляет 170 метров. В Примере 6 мы будем использовать проектную схему градирни, чтобы найти гиперболическое уравнение, моделирующее ее стороны.
Пример: решение прикладных задач, связанных с гиперболой
Схема градирни показана ниже. Башня стоит 179.6 метров в высоту. Диаметр вершины 72 метра. Ближайшие стороны башни находятся на расстоянии 60 метров друг от друга.
Башня стоит 179.6 метров в высоту. Диаметр вершины 72 метра. Ближайшие стороны башни находятся на расстоянии 60 метров друг от друга.
Проект градирни с естественной тягой
Найдите уравнение гиперболы, моделирующей стороны градирни. Предположим, что центр гиперболы , обозначенный на рисунке пересечением пунктирных перпендикулярных линий, является началом координатной плоскости. Округлите окончательные значения до четырех знаков после запятой.
Показать решение
Попробуйте
Ниже показан проект градирни. Найдите уравнение гиперболы, моделирующей стороны градирни. Предположим, что центр гиперболы, обозначенный на рисунке пересечением пунктирных перпендикулярных линий, является началом координатной плоскости.
Показать решение
Поддержите!
У вас есть идеи по улучшению этого контента? Мы будем признательны за ваш вклад.
Улучшить эту страницуПодробнее
Коники:
Гиперболы: Введение (стр. Разделы: Введение, Нахождение информацию из уравнения, Нахождение уравнение из информации Гиперболы, по крайней мере, не часто всплывают не то, чтобы я замечал на других уроках математики, но если вы освещаете conics, вам нужно знать их основы. Гипербола выглядит примерно так две зеркальные параболы с двумя «половинками» называются «ветвями». Как эллипс, гипербола имеет два фокуса и две вершины; в отличие от эллипса, фокусы в гиперболе дальше от центра гиперболы, чем ее вершины: Гипербола центрируется в точке ( ч , k ), который является « центр »
гиперболы. Точка на каждой ветке, ближайшая к центру, такова, что
ветка « вершина «.
Вершины находятся на некотором фиксированном расстоянии от до от центра. Для любой точки эллипса сумма расстояний от этой точки до каждого из фокусов есть некоторая фиксированная величина;
для любой точки гиперболы это разность расстояний
из двух фиксированных фокусов. Глядя на график выше и позволяя
«точка» должна быть одной из вершин, это фиксированное расстояние должно
быть (расстояние до дальнего фокуса) меньше (расстояние до ближнего
фокус) или ( + )
( в в ) = 2 в . Как и в случае с эллипсами, существует связь
между и , б ,
и c ,
и, как и в случае с эллипсами, вычисления долгие и мучительные. Так что доверяй
мне, что для гипербол (где < c ), соотношение в 2 а 2 = б 2 или, что означает
то же самое, c 2 = б 2 + а 2 .
(Да, для доказательства этой связи используется теорема Пифагора. Да,
это те же самые буквы, которые используются в теореме Пифагора. Нет,
это не то же самое, что теорема Пифагора.
В «конической» форме гипербола уравнение всегда «=1». Значение b дает «высоту» «фундаментальной коробки» для гипербола ( отмечено серым цветом на первой картинке выше), и 2 б — длина «сопряженной» оси. Эта информация не помочь вам построить гиперболы, хотя. Авторские права Элизабет Стапель 2010-2011 Все права защищены По причинам, которые вы узнаете из анализа,
график гиперболы становится довольно плоским и прямым, когда он удаляется
от его центра. Если «уменьшить масштаб» графика, он будет выглядеть
очень похоже на «X», с небольшим изгибом около
середина.
Обратите внимание, что единственная разница в асимптоте
уравнения выше находится в наклонах прямых: Если a 2 это знаменатель для x часть уравнения гиперболы, тогда a все еще находится в знаменателе наклона уравнений асимптот;
если а 2 идет с и часть уравнения гиперболы, то и входит в числитель наклона в уравнениях асимптот. Гиперболы могут быть довольно «прямыми». или еще довольно «гибкий»:
Мера величины кривизны
это «эксцентриситет» e ,
где e = c / a .
Так как фокусы находятся дальше от центра гиперболы, чем
вершин (таким образом, c > и для гипербол), затем и > 1. |

 Координаты фокусов те же, что и для эллипса в предыдущем параграфе:
и .
Координаты фокусов те же, что и для эллипса в предыдущем параграфе:
и .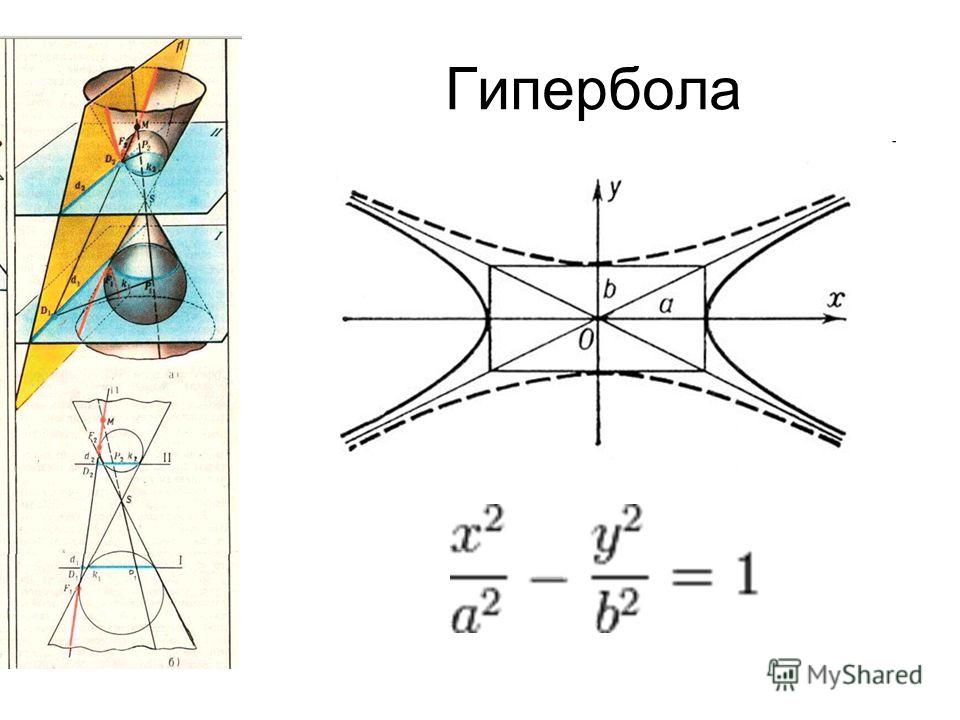 (Рекомендуется читателю произвести это преобразование самостоятельно.)
(Рекомендуется читателю произвести это преобразование самостоятельно.) 21) x и y входят лишь в четных степенях. Поэтому достаточно построить часть гиперболы, лежащую в I четверти.
21) x и y входят лишь в четных степенях. Поэтому достаточно построить часть гиперболы, лежащую в I четверти. Такие прямые,
к которым неограниченно приближаются уходящие в бесконечность ветви кривых,
называются асимптотами этих кривых.
Такие прямые,
к которым неограниченно приближаются уходящие в бесконечность ветви кривых,
называются асимптотами этих кривых.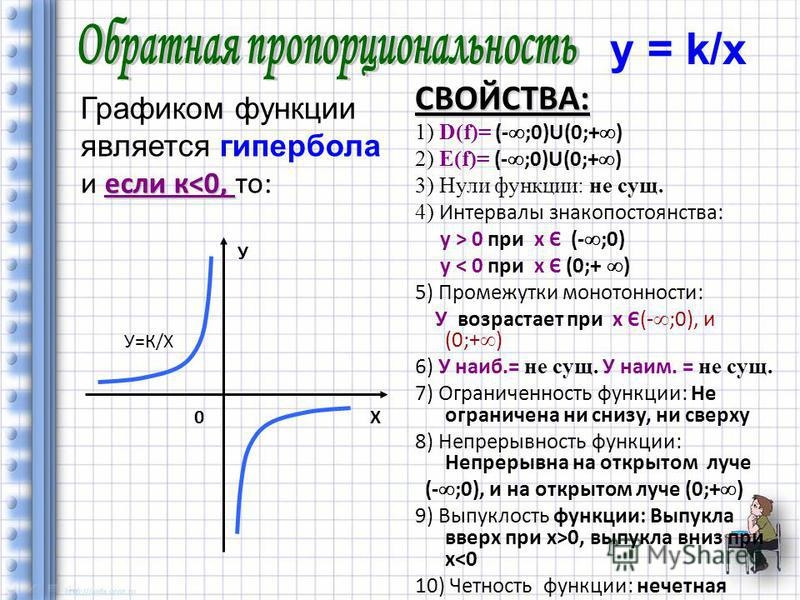 3.5 пунктиром прямоугольник
с центром в точке О и сторонами ,
и ,
параллельными осями симметрии гиперболы, называют осевым прямоугольником гипербол; его построение облегчает построение гиперболы; сама гипербола касается
вертикальных сторон этого прямоугольника в их серединах, являющихся вершинами
гиперболы.
3.5 пунктиром прямоугольник
с центром в точке О и сторонами ,
и ,
параллельными осями симметрии гиперболы, называют осевым прямоугольником гипербол; его построение облегчает построение гиперболы; сама гипербола касается
вертикальных сторон этого прямоугольника в их серединах, являющихся вершинами
гиперболы.
 27).
27).

 Найдите асимптота этой гиперболы.
Найдите асимптота этой гиперболы. Найдите асимптоту этой гиперболы.
Найдите асимптоту этой гиперболы. 1 из 3)
1 из 3)  Линия, идущая из одной вершины через центр и
оканчивающаяся в другой вершине, называется «поперечной» осью. очаги »
гиперболы находятся «внутри» каждой ветви, и каждый фокус
находится на некотором фиксированном расстоянии c от центра. (Это означает, что а < c для гипербол.)
Значения a и c будет
варьируются от одной гиперболы к другой, но они будут фиксированными значениями для
любая заданная гипербола.
Линия, идущая из одной вершины через центр и
оканчивающаяся в другой вершине, называется «поперечной» осью. очаги »
гиперболы находятся «внутри» каждой ветви, и каждый фокус
находится на некотором фиксированном расстоянии c от центра. (Это означает, что а < c для гипербол.)
Значения a и c будет
варьируются от одной гиперболы к другой, но они будут фиксированными значениями для
любая заданная гипербола. Это свойство фиксированной разницы можно использовать для определения местоположений:
два маяка размещаются в известных и фиксированных положениях, разница в
время, в которое их сигналы принимаются, скажем, кораблем в море, может
Сообщите экипажу, где они.
Это свойство фиксированной разницы можно использовать для определения местоположений:
два маяка размещаются в известных и фиксированных положениях, разница в
время, в которое их сигналы принимаются, скажем, кораблем в море, может
Сообщите экипажу, где они. Да, это очень
сбивает с толку. Просто запомните его и двигайтесь дальше.)
Да, это очень
сбивает с толку. Просто запомните его и двигайтесь дальше.) 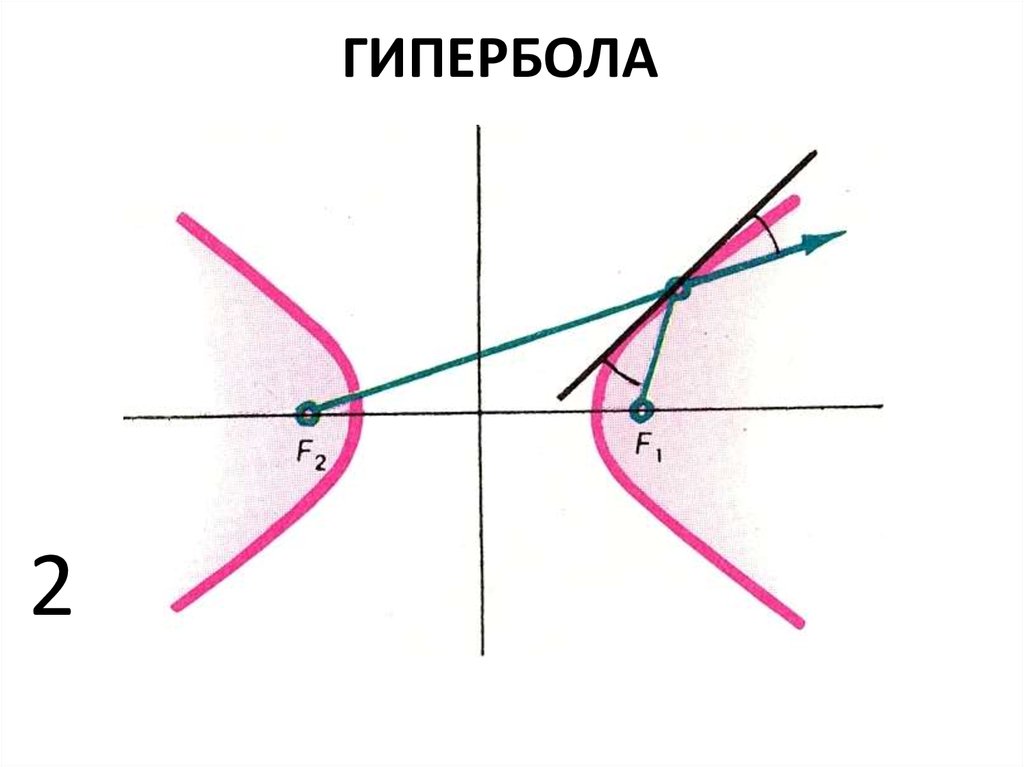
 Эти «почти прямые» части очень близки к тому, что
называются «асимптотами»
гипербола. Для гиперболы с центром в ( ч , k ) и имеющие фиксированные значения a и б ,
асимптоты задаются следующими уравнениями:
Эти «почти прямые» части очень близки к тому, что
называются «асимптотами»
гипербола. Для гиперболы с центром в ( ч , k ) и имеющие фиксированные значения a и б ,
асимптоты задаются следующими уравнениями:
