| Главная Контакты Случайная статья
|
gif» bgcolor=»#FDFCF7″/> | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Ключи, критерии оценивания заданий школьного этапа Всероссийской олимпиады школьников 2020-2021 учебный год Математика 8 класс Максимальный балл – 35 баллов Задача 1 (7 б.) Определите, какой цифрой оканчивается число 21999 Решение: Так как степени двойки заканчиваются на цифры 2, 4, 8, 6 с периодом 4 и 1999 = 4∙994 + 3, то 21999 оканчивается цифрой 8. Ответ: 8
Задача 2 (7 б. Решение: Пусть х метров – расстояние от гнезда до места, в котором лежит орех. Тогда секунд это время, которое потребуется белке для того, чтобы она добежала до ореха, а обратно она пробежит за секунд. По условию задачи белка добежит до ореха и вернется обратно за 60 ∙ 20 = 1200 секунд. Составим уравнение: + = 1200 3х + 5х = 1200 ∙ 15 8х = 18000 х = 2250 значит, белка пробегает от гнезда до места, в котором лежит орех – 2250 метров. Ответ: 2250 метров
Задача 3 (7 б. Решение: Так как стрелок выбил 90 очков и из них за 4 раза набрал 40 очков, то в другие 6 раз он набрал оставшиеся 50 очков. Так как стрелок попадал лишь в семерку, восьмерку и девятку в остальные 6 выстрелов, то за три выстрела (по одному разу в семерку, восьмерку и девятку) он наберет 24 очка. Тогда за оставшиеся 3 выстрела надо набрать 26 очков, что возможно только при единственной комбинации цифр 7, 8, 9: 8 + 9 + 9 = 26. Таким образом, в семерку стрелок попал 1 раз, в восьмерку – 2 раза, а в девятку – 3 раза.
Задача 4 (7 б.) Один из внешних углов равнобедренного треугольника равен 34°.
Решение: Данный угол не может быть при основании равнобедренного треугольника, так как в этом случае сумма внутренних углов треугольника была бы больше 180°. Значит, данный угол находится при вершине. Тогда смежный с ним, внутренний угол треугольника, будет равен 146°, соответственно углы при основании будут по 17°. Значит, угол между основанием треугольника и высотой треугольника, проведенной из вершины угла при основании, будет равен: 180° – 90° – 17° = 73°.
Ответ: 73°
Задача 5 (7б.) Построить график функции Решение:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Михаил Гуров — Учитель года
Обо мне
Гуров Михаил Николаевич, учитель математики высшей квалификационной категории.- Образование
- Дополнительное образование
- Курсы повышения квалификации
- Опыт работы
- Дипломы и грамоты
- Отраслевые и государственные награды
- Научно-исследовательская деятельность
- 2009 г., Южный федеральный университет (РГУ), факультет математики, механики и компьютерных наук, бакалавр математики по направлению «01.01.00 Математика», диплом с отличием.
- 2011 г., Южный федеральный университет, факультет математики, механики и компьютерных наук, магистр математики по направлению «01.
 01.02 Математика», диплом с отличием.
01.02 Математика», диплом с отличием. - 2013 г., Южно-Российский гуманитарный институт, экономический факультет, магистр по направлению «080100.68 Экономика», диплом с отличием.
- 2016 г., Южный федеральный университет, Институт математики механики и компьютерных наук, кандидат физико-математических наук (01.01.01 – вещественный, комплексный и функциональный анализ).
- 2017 г., Южный федеральный университет, Академия психологии и педагогики, магистр по направлению «44.04.01 Педагогическое образование».
- 2011 г., Южный федеральный университет, факультет математики, механики и компьютерных наук, дополнительно к степени магистра математики присвоена дополнительная квалификация «Преподаватель».
- 2015 г., Ростовский государственный экономический университет (РИНХ), программа профессиональной переподготовки «Государственное и муниципальное управление» (510 ч.).
- 2012 г., повышение квалификации в ГБОУ ДПО РО «Ростовский институт повышения квалификации и профессиональной переподготовки работников образования» по проблеме «Профессиональная компетентность и результативность профессиональной деятельности педагога как объекты экспертизы в ходе аттестации педагогических работников».

- 2015 г., повышение квалификации в ГБОУ ДПО РО «Ростовский институт повышения квалификации и профессиональной переподготовки работников образования» по проблеме «Совершенствование подходов к оцениванию развернутых ответов экзаменационных работ участников ЕГЭ экспертами предметных комиссий Ростовской области».
- 2015 г., повышение квалификации в ГБОУ ДПО РО «Ростовский институт повышения квалификации и профессиональной переподготовки работников образования» по проблеме «Обеспечение качества педагогической деятельности в контексте реализации деятельностной парадигмы».
- 2016 г., повышение квалификации в Образовательном Фонде «Талант и успех» (образовательный центр «Сириус», городской округ Сочи) по программе «Региональный, муниципальный и школьный этапы ВсОШ по математике: составление заданий, проведение, проверка и оценка работ».
- 2016 г., повышение квалификации в АНО ВПО «Европейский Университет «Бизнес Треугольник» по дополнительной профессиональной программе «Учитель математики.
 Подготовка экспертов ЕГЭ по математике».
Подготовка экспертов ЕГЭ по математике». - 2016 г., повышение квалификации в ФГБНУ «ФИПИ» по дополнительной профессиональной программе «Подготовка экспертов для работы в региональной предметной комиссии при проведении государственной итоговой аттестации по образовательным программам среднего общего образования» по предмету «Математика».
- 2017 г., повышение квалификации в ООО ЦПО «Развитие» по дополнительной профессиональной программе «Основы оказания первой помощи работниками сферы образования».
- 2019 г., повышение квалификации в ГБОУ ДПО РО «Ростовский институт повышения квалификации и профессиональной переподготовки работников образования» по программе дополнительного профессионального образования «Совершенствование подходов к оцениванию развернутых ответов экзаменационных работ участников ЕГЭ экспертами предметных комиссий Ростовской области».
- 2019 г., повышение квалификации в ЧОУ ДПО «Академия повышения квалификации и профессиональной переподготовки» по дополнительной профессиональной программе «Психологическое консультирование».

- 2012 г., повышение квалификации в ГБОУ ДПО РО «Ростовский институт повышения квалификации и профессиональной переподготовки работников образования» по проблеме «Профессиональная компетентность и результативность профессиональной деятельности педагога как объекты экспертизы в ходе аттестации педагогических работников».
- 2010 – 2017 гг., ГБУ ДО РО «Областной центр дополнительного образования детей», педагог дополнительного образования.
- 2012 – 2013 гг., Южный федеральный университет, ассистент кафедры дифференциальных и интегральных уравнений.
- 2012 – 2013 гг., МКУ «Информационно – аналитический центр образования» г. Ростова-на-Дону, методист по математике.
- 2012 – 2013 гг., МАОУ «Лицей № 11» г. Ростова-на-Дону, учитель математики.
- 2012 – 2016 гг., Южный математический институт (ЮМИ ВНЦ РАН), младший научный сотрудник, научный сотрудник.
- 2012 г. – настоящее время, ГБУ РО «Ростовский областной центр обработки информации в сфере образования», старший эксперт областной предметной комиссии по математике.
- 2013 – 2018 гг., МБОУ «Гимназия № 95» г. Ростова-на-Дону, учитель математики.
- 2016 г. – настоящее время, ЧОУ «Лицей КЭО», учитель математики.
- 2021 – 2022 гг., советник Министра просвещения РФ на общественных началах.

- 2016 г., благодарственное письмо Министерства общего и профессионального образования Ростовской области за обеспечение проведения ЕГЭ на территории Ростовской области в 2016 году в соответствии с установленными требованиями на высоком организационном уровне в качестве эксперта (Приказ от «05» сентября 2016 г., № 14-н).
- 2017 г., благодарственное письмо Губернатора Ростовской области за большой вклад в развитие системы образования Ростовской области (Распоряжение от 18 июля 2017 г., № 168).
- 2019 г., благодарность заместителя председателя Комитета Государственной Думы Федерального Собрания Российской Федерации по образованию и науке Л. Н. Тутовой.
- 2019 г., диплом лауреата премии Губернатора Ростовской области (Лауреат областного конкурса «Учитель года Дона – 2019») (Распоряжение Правительства Ростовской области от 30.05.2019 № 308).
- 2020 г., диплом лауреата премии Губернатора Ростовской области за достижения в педагогической деятельности на территории Ростовской области в 2020 году (Распоряжение Правительства Ростовской области от 24.
 09.2020 № 3).
09.2020 № 3). - 2021 г., абсолютный победитель Всероссийского конкурса «Учитель года России — 2020».
Сфера моих научных интересов напрямую связана с тематикой моего диссертационного исследования «Операторы свёртки с осциллирующими ядрами или символами в пространствах Харди — Лебега и пространствах гёльдеровских функций». К настоящему моменту имею более двадцати опубликованных научных работ.
Как педагог считаю, что необходимо вовлекать мотивированных школьников в научно-исследовательскую деятельность, как можно раньше. Именно поэтому, помимо учебной работы и подготовки обучающихся к олимпиадам, я активно участвую в подготовке школьников к научным конкурсам и конференциям в качестве научного руководителя. За последнее время под моим руководством было выполнено несколько научных работ по геометрии, теории чисел и информатике. Все они были успешно представлены на региональном, федеральном и международном уровнях.
СПИСОК ОПУБЛИКОВАННЫХ НАУЧНЫХ И УЧЕБНО – МЕТОДИЧЕСКИХ РАБОТ
- Гуров М.
 Н., Задорожный А. И. Определение спектра тороидальных волновых движений в шаровом слое самогравитирующей вязкой жидкости. Математические методы в современных и классических моделях экономики и естествознания: материалы региональной научно – практической конференции профессорско- преподавательского состава / Ростовский государственный экономический университет «РИНХ». – Ростов н/Д, 2008. С. 5 – 7.
Н., Задорожный А. И. Определение спектра тороидальных волновых движений в шаровом слое самогравитирующей вязкой жидкости. Математические методы в современных и классических моделях экономики и естествознания: материалы региональной научно – практической конференции профессорско- преподавательского состава / Ростовский государственный экономический университет «РИНХ». – Ростов н/Д, 2008. С. 5 – 7. - Гуров М. Н., Задорожный А. И. Магнитогидродинамическая задача Ламба с учетом молекулярной вязкости и конечной электропроводимости. Исследования по дифференциальным уравнениям и математическому моделированию / отв. Ред. С. Б. Климентов, Е. С. Каменский. – Владикавказ: ВНЦ РАН и РСО – А, 2009. С. 43 – 51.
- Гуров М. Н., Задорожный А. И. Магнитогидродинамическая задача Ламба о волнах в вязкой жидкости конечной электрической проводимости. Современные проблемы прикладной математики и математического моделирования: Материалы III Международной научной конференции. Часть 1.
 – Воронеж: «Научная книга», 2009. С. 126 – 130.
– Воронеж: «Научная книга», 2009. С. 126 – 130. - Гуров М. Н., Дрей Я. В., Задорожный А. И. Самосогласованная задача о спектре коротких магнитогидродинамических волн с учетом диссипации. Материалы Научной конференции [«Ломоносовские чтения» 2009 года] и международной научной конференции студентов, аспирантов и молодых ученых [«Ломоносов — 2009»] / под. ред. В. А. Иванова, В. А. Трифонова, В. И. Кузищина, Н. Н. Миленко, В. В. Хапаева – Севастополь: Филиал МГУ в г. Севастополе, 2009. С. 211 – 212.
- Гуров М. Н., Задорожный А. И. Исследование влияния конечной электропроводимости на поверхностные МГД – волны в глубоководной морской среде. Системы контроля окружающей среды/ Сб. науч. Тр. МГИ НАНУ. – Севастополь: МГИ НАНУ, 2010. – Вып. 14. С. 95 – 104.
- Гуров М. Н., Задорожный А. И. Характеристики длинных внутренних магнитогидродинамических волн в равномерно стратифицированном море с учетом вязкости. Материалы научной конференции «Ломоносовские чтения» 2010 года и международной конференции студентов, аспирантов и молодых ученых «Ломоносов — 2010» / под ред.
 А. И. Иванова, В. А. Трифонова, В. И. Кузищина, Н. Н. Миленко, В. В. Хапаева – Севастополь: Филиал МГУ в г. Севастополе, 2010. С. 314 – 315.
А. И. Иванова, В. А. Трифонова, В. И. Кузищина, Н. Н. Миленко, В. В. Хапаева – Севастополь: Филиал МГУ в г. Севастополе, 2010. С. 314 – 315. - Гуров М. Н., Задорожный А. И. Спектральная задача Ламба теории МГД волн с учетом молекулярной и магнитной вязкости. Исследования по дифференциальным уравнениям и математическому моделированию / отв. Ред. С. Б. Климентов, Е. С. Каменский. – Владикавказ: ВНЦ РАН и РСО – А, 2011. С. 67 – 71.
- Гуров М. Н., Ногин В. А. О дифференциальных свойствах обобщенных потенциалов Стрихарца с — плотностями. Изв. вузов. Сев. — Кавк. регион. Естеств. науки. 2012. № 6. С. 15 – 21.
- Гуров М. Н., Ногин В. А. О гёльдеровости обобщенных потенциалов Стрихарца с плотностями из пространств Харди. Изв. вузов. Сев.-Кавк. Регион. Естеств. науки. 2013. № 5. С. 14 – 19.
- Гуров М. Н., Ногин В. А. О гёльдеровости некоторых потенциалов с осциллирующими символами. Математический форум. Т. 7. Исследования по математическому анализу. — Владикавказ: ЮМИ ВНЦ РАН и РСО-А, 2013.
 С. 67 – 79.
С. 67 – 79. - Гуров М. Н., Ногин В. А. О гёльдеровости обобщенных потенциалов Стрихарца по шаровому слою. Порядковый анализ и смежные вопр. матем. моделирования: тез. докл. междунар. науч. конф. (Владикавказ, 14-20 июля 2013 г.). – Владикавказ: ЮМИ ВНЦ РАН и РСО-А, 2013. С. 55.
- Гуров М. Н., Ногин В. А. О дифференциальных свойствах обобщенных потенциалов Стрихарца по шаровому слою. Материалы Воронежской зимней математической школы «Современные методы теории функций и смежные проблемы» / Воронежский государственный университет; Московский государственный университет им. М. В. Ломоносова; Математический институт им. В. А. Стеклова РАН. – Воронеж. Издательско-полиграфический центр Воронежского государственного университета, 2013. – 310 с.
- Гуров М. Н., Ногин В. А. Оценки для некоторых операторов типа потенциала с особенностями ядер на сферах. Владикавк. мат. журн. 2014. Т. 16, №1. С. 12 – 23.
- Гуров М. Н. О гёльдеровости обобщенных потенциалов Стрихарца по единичному шару.
 Математический форум. Т. 8. Порядковый анализ и смежные вопросы математического моделирования. — Владикавказ: ЮМИ ВНЦ РАН и РСО-А, 2014. С. 239 – 250.
Математический форум. Т. 8. Порядковый анализ и смежные вопросы математического моделирования. — Владикавказ: ЮМИ ВНЦ РАН и РСО-А, 2014. С. 239 – 250. - Гуров М. Н. О преобразовании Фурье одной осциллирующей функции. Изв. вузов. Сев.-Кавк. Регион. Естеств. науки. 2014. № 5. С. 11 – 14.
- Гуров М. Н., Ногин В. А. Lp-Lq – оценки для некоторых операторов типа потенциала с осциллирующими ядрами. Теория операторов, комплексный анализ и математическое моделирование: тезисы докладов международной научной конференции (пос. Дивноморское, 7 – 13 сентября 2014 г.). – Владикавказ: ЮМИ ВНЦ РАН и РСО – А. 2014. С. 43.
- Гуров М. Н., Карасёв Д. Н., Ногин В. А. Об одном Фурье- мультипликаторе. Владикавк. мат. журн. 2015. Т. 17, №1. С. 14 – 20.
- Гуров М. Н., Ногин В. А. Обращение и описание образов некоторых операторов свёртки с осциллирующими ядрами и символами. Международная научная конференция «Современные методы и проблемы теории операторов и гармонического анализа и их приложения — V» в г.
 Ростове-на-Дону. Тезисы докладов. Издательский центр ДГТУ, Ростов н/Д. – 2015. С. 25.
Ростове-на-Дону. Тезисы докладов. Издательский центр ДГТУ, Ростов н/Д. – 2015. С. 25. - Гуров М. Н., Ногин В. А. Оценки для операторов типа потенциала с осциллирующими ядрами и символами и их приложения к описанию образов этих потенциалов. Изв. вузов. Сев.-Кавк. Регион. Естеств. науки. 2016. № 4. С. 12 – 16.
- Гуров М. Н., Ногин В. А. Lp-Lq – оценки для обобщенных потенциалов Рисса с осциллирующими ядрами. Владикавк. мат. журн. 2017. Т. 19, №2. С. 3 – 10.
- Gurov M. N., Volkov M. A. Chains of tangent circles inscribed in curvilinear triangles. International journal of geometry. Vol. 7 (2018), No. 1, pp. 105 – 118.
- Гуров М. Н., Ногин В. А. Lp-Lq – оценки для операторов типа потенциала с осциллирующими ядрами. Владикавк. мат. журн. 2018. Т. 20, №4. С. 35 – 42.
- Гуров М. Н., Жмурова И. Ю. Применение систем компьютерной алгебры для визуализации математических объектов и их преобразований на уроках математики // Актуальные задачи педагогики: материалы XI Междунар.
 науч. конф. (г. Краснодар, февраль 2020 г.). — Краснодар: Новация, 2020. — С. 22-26.
науч. конф. (г. Краснодар, февраль 2020 г.). — Краснодар: Новация, 2020. — С. 22-26.
- Гуров М.
Достижения учеников
- 2010-2011
- 2011-2012
- 2012-2013
- 2013-2014
- 2014-2015
- 2015-2016
- 2016-2017
- 2017-2018
- 2018-2019
- 2019-2020
- 2020-2021
- 2021-2022
- Курситыс Владимир, 8 класс, муниципальный этап ВсОШ по математике, призер.
- Курситыс Владимир, 8 класс, региональный этап ВсОШ по математике (олимпиада им. Л. Эйлера), призер.
- Курситыс Владимир, 8 класс, областная олимпиада для школьников по математике «Универсиада-2011», призер.
- Курситыс Владимир, 9 класс, муниципальный этап ВсОШ по математике, победитель.

- Курситыс Владимир, 9 класс, региональный этап ВсОШ по математике, призер.
- Курситыс Владимир, 9 класс, областная олимпиада для школьников по математике «Универсиада-2012», призер.
- Курситыс Владимир, 9 класс, муниципальный этап ВсОШ по математике, победитель.
- Курситыс Владимир, 10 класс, муниципальный этап ВсОШ по математике, призер.
- Курситыс Владимир, 10 класс, региональный этап ВсОШ по математике, призер.
- Курситыс Владимир, 10 класс, областная олимпиада для школьников по математике «Универсиада-2013», победитель.
- Скобелев Дмитрий, 10 класс, муниципальный этап ВсОШ по математике, призер.
- Кириченко Анастасия, 10 класс, муниципальный этап ВсОШ по математике, победитель.
- Кириченко Анастасия, 10 класс, региональный этап ВсОШ по математике, призер.
- Курситыс Владимир, 11 класс, муниципальный этап ВсОШ по математике, призер.
- Курситыс Владимир, 11 класс, региональный этап ВсОШ по математике, призер.
- Курситыс Владимир, 11 класс, областная олимпиада для школьников по математике «Универсиада-2014», призер.

- Курситыс Владимир, 11 класс, олимпиада «Физтех» по математике, призёр, диплом 2 степени.
- Скобелев Дмитрий, 11 класс, муниципальный этап ВсОШ по математике, призер.
- Кириченко Анастасия, 11 класс, муниципальный этап ВсОШ по математике, победитель.
- Белкин Дмитрий (7 класс), Посохов Константин (7 класс), Тынянко Роман (8 класс), Борисов Михаил (8 класс), II Международный Математический Турнир им. М. В. Ломоносова (г. Барселона, Испания), общий зачет – диплом III степени, личный зачет: Тынянко Роман – диплом I степени, Борисов Михаил – диплом II степени, Посохов Константин – похвальная грамота.
- Сафронов Руслан (9 класс), Клименко Олег (10 класс), Водясов Алексей (11 класс), XXII Международная олимпиада «Интеллектуальный марафон — 2013», общий зачет – диплом II степени, личный зачет: Сафронов Руслан – диплом I степени, Клименко Олег – диплом II степени, Водясов Алексей – диплом III степени.
- Ерешко Владислав (7 класс), Заиченко Илья (7 класс), Посохов Константин (8 класс), Туманова Анастасия (8 класс), III Международный Математический Турнир им.
 М.В. Ломоносова, общий зачет – диплом I степени, личный зачет: Туманова Анастасия – диплом I степени, Посохов Константин – диплом I степени.
М.В. Ломоносова, общий зачет – диплом I степени, личный зачет: Туманова Анастасия – диплом I степени, Посохов Константин – диплом I степени. - Тынянко Роман (9 класс), Волков Макар (9 класс), Сафронов Руслан (10 класс), XXIII Международная олимпиада «Интеллектуальный марафон — 2014», общий зачет – диплом II степени, личный зачет: Сафронов Руслан – диплом II степени.
- Яшина Виолетта, 10 класс, муниципальный этап ВсОШ по математике, победитель.
- Волков Макар, 9 класс, областная олимпиада для школьников по математике «Универсиада-2015», победитель.
- Волков Макар, 9 класс, XXI межрегиональная физико-математическая олимпиада школьников, призер.
- Волков Макар, 9 класс, муниципальный этап ВсОШ по математике, победитель.
- Волков Макар, 9 класс, региональный этап ВсОШ по математике, призер.
- Волков Макар, 9 класс, межрегиональная олимпиада школьников «САММАТ», победитель.
- Ерешко Владислав (7 класс), Заиченко Илья (7 класс), Посохов Константин (8 класс), Туманова Анастасия (8 класс), III Международный Математический Турнир им.
- Волков Макар, 10 класс, XXII межрегиональная физико-математическая олимпиада школьников, победитель.

- Волков Макар, 10 класс, муниципальный этап ВсОШ по математике, победитель.
- Волков Макар, 10 класс, региональный этап ВсОШ по математике, призер.
- Волков Макар, 10 класс, международный дистанционный блиц-турнир по математике «Математика – царица наук», победитель.
- Волков Макар, 10 класс, международный дистанционный конкурс по математике «Олимпис-2015 – Осенняя сессия», победитель.
- Волков Макар, 10 класс, международная онлайн-олимпиада «Фоксфорд», II сезон, призер.
- Волков Макар, 10 класс, олимпиада школьников «Физтех», призер.
- Кащеев Владислав, 10 класс, муниципальный этап ВсОШ по математике, победитель.
- Зудин Роман, 11 класс, муниципальный этап ВсОШ по математике, призер.
- Белов Борис, 11 класс, муниципальный этап ВсОШ по математике, призер.
- Волков Макар, 10 класс, XXII межрегиональная физико-математическая олимпиада школьников, победитель.
- Волков Макар, 11 класс, областная олимпиада для школьников по математике «Универсиада-2017», победитель.
- Волков Макар, 11 класс, олимпиада школьников «Физтех», призер.

- Волков Макар, 11 класс, многопрофильная инженерная олимпиада «Звезда», призер.
- Волков Макар, 11 класс, муниципальный этап ВсОШ по математике, победитель.
- Зудин Роман, 11 класс, муниципальный этап ВсОШ по математике, победитель.
- Курочка Константин, 11 класс, муниципальный этап ВсОШ по математике, призер.
- Белов Борис, 11 класс, муниципальный этап ВсОШ по математике, призер.
- Кащеев Владислав, 11 класс, муниципальный этап ВсОШ по математике, победитель.
- Белов Борис, 11 класс, объединенная межвузовская математическая олимпиада, призер II степени.
- Белов Борис, 11 класс, межрегиональная отраслевая олимпиада школьников «Паруса надежды», призер.
- Курочка Константин, 11 класс, объединенная межвузовская математическая олимпиада, призер II степени.
- Курочка Константин, 11 класс, турнир им. М. В. Ломоносова, призер III степени.
- Курочка Константин, 11 класс, олимпиада школьников «Ломоносов», призер III степени.

- Кирдеев Александр, Болошко Анастасия, 11 класс, Межрегиональная олимпиада школьников по математике и криптографии, призеры.
- Альберштейн Герман, 7 класс, муниципальный этап ВсОШ по математике, призер.
- Абгарян Екатерина, 7 класс, муниципальный этап ВсОШ по математике, призер.
- Самолётова Ульяна, 7 класс, муниципальный этап ВсОШ по математике, призер.
- Селезнёва Алена, 10 класс, муниципальный этап ВсОШ по математике, победитель.
- Алёхин Артем, 10 класс, муниципальный этап ВсОШ по математике, призер.
- Алехин Артем, 10 класс, межрегиональная олимпиада школьников «САММАТ», победитель.
- Алехин Артем, 10 класс, олимпиада школьников «Физтех», призер.
- Алехин Артем, 10 класс, открытая олимпиада школьников по математике (университет ИТМО), призер.
- Буртаков Илья, 11 класс, объединенная межвузовская математическая олимпиада, призер II степени.
- Буртаков Илья, 11 класс, олимпиада «Росатом», призер II степени.

- Литовченко Павел, 11 класс, многопрофильная инженерная олимпиада «Звезда», победитель.
- Абгарян Екатерина, Альберштейн Герман, Артемьев Иван, Астахов Владимир, Геворгян Арташес, Геворгян Эдуард, Жукова Яна, Карапетян Александр, Коновко Анастасия, Найда Анастасия, Самолётова Ульяна, Шпигорь Ева, 7 класс, 57-я Выездная физико-математическая олимпиада МФТИ, призеры.
- Алехин Артем, 11 класс, региональный этап ВсОШ по математике, победитель.
- Алехин Артем, 11 класс, муниципальный этап ВсОШ по математике, призер.
- Алехин Артем, 11 класс, межрегиональная олимпиада школьников «САММАТ», призер.
- Алехин Артем, 11 класс, объединенная межвузовская математическая олимпиада, призер III степени.
- Алехин Артем, 11 класс, олимпиада школьников «Физтех», призер.
- Альберштейн Герман, Астахов Владимир, Артемьев Иван, 8 класс, муниципальный этап ВсОШ по математике, призеры.
- Артемьев Иван, 8 класс, региональный этап олимпиады им.
 Л. Эйлера, призер.
Л. Эйлера, призер. - Артемьев Иван, 8 класс, международная олимпиада «Кавказская математическая олимпиада», похвальная грамота.
- Астахов Владимир, 8 класс, международная олимпиада «Кавказская математическая олимпиада», призер.
- Зобов Даниил, 11 класс, олимпиада «Росатом», призер.
- Мисюра Елена, 11 класс, объединенная межвузовская математическая олимпиада, призер II степени.
- Ушаков Ярослав, 7 класс, муниципальный этап ВсОШ по математике, победитель.
- Цыпочка Даниил, Галкина Мария, Кадомцев Кирилл, Швец Андрей, 7 класс, муниципальный этап ВсОШ по математике, призеры.
- Мартынова Анна, 8 класс, муниципальный этап ВсОШ, победитель;
- Швец Андрей, 8 класс, муниципальный этап ВсОШ, призер;
- Астахов Владимир, 9 класс, муниципальный этап ВсОШ, победитель;
- Артемьев Иван, 9 класс, муниципальный этап ВсОШ, победитель;
- Карапетян Александр, 9 класс, муниципальный этап ВсОШ, призер;
- Обревская Вероника, 11 класс, муниципальный этап ВсОШ, призер;
- Швыдко Алексей, 11 класс, муниципальный этап ВсОШ, призер.

- Артемьев Иван, 9 класс, региональный этап ВсОШ, победитель.
- Астахов Владимир, 9 класс, региональный этап ВсОШ, призер.
- Карапетян Александр, 9 класс, региональный этап ВсОШ, призер.
- Альберштейн Герман, 9 класс, региональный этап ВсОШ, призер.
- Артемьев Иван, 9 класс, международная олимпиада «Кавказская математическая олимпиада», призер II степени;
- Альберштейн Герман, 9 класс, международная олимпиада «Кавказская математическая олимпиада», призер III степени;
- Астахов Владимир, 9 класс, международная олимпиада «Кавказская математическая олимпиада», похвальная грамота;
- Роман Букреев, 11 класс, Межрегиональная олимпиада школьников им. И.Я. Верченко по математике и криптографии, призёр;
- Обревская Вероника, 11 класс, Межрегиональная олимпиада школьников им. И.Я. Верченко по математике и криптографии, призёр;
- Роман Букреев, 11 класс, Олимпиада «Миссия выполнима. Твое призвание — финансист!», победитель;
- Анисимов Александр, 11 класс, Олимпиада «Миссия выполнима.
 Твое призвание — финансист!», победитель;
Твое призвание — финансист!», победитель; - Королева Валерия, 11 класс, Олимпиада «Миссия выполнима. Твое призвание — финансист!», победитель;
- Обревская Вероника, 11 класс, Олимпиада «Миссия выполнима. Твое призвание — финансист!», призер;
- Касимов Владислав, 11 класс, Олимпиада «Миссия выполнима. Твое призвание — финансист!», призер;
- Кислая Софья, 11 класс, Олимпиада «Миссия выполнима. Твое призвание — финансист!», призер;
- Королев-Зеленый Кирилл, 11 класс, олимпиада «Росатом», призер;
- Величко Божена, 11 класс, олимпиада «Росатом», призер;
- Глушко Антон, 11 класс, олимпиада «Росатом», призер;
- Ушаков Ярослав, 8 класс, олимпиада ИТМО, призер.
- Быстров Максим, 8 класс, муниципальный этап ВсОШ, победитель;
- Липский Андрей, 8 класс, муниципальный этап ВсОШ, призер;
- Мартынова Анна, 9 класс, муниципальный этап ВсОШ, призер;
- Альберштейн Герман, 10 класс, муниципальный этап ВсОШ, призер;
- Агошкин Никита Витальевич, 9 класс, муниципальный этап ВСОШ, призер;
- Быстров Максим, 8 класс, региональный этап олимпиады им.
 Л. Эйлера, призер;
Л. Эйлера, призер; - Мартынова Анна, 9 класс, региональный этап ВсОШ, призер;
- Альберштейн Герман, 10 класс, региональный этап ВсОШ, призер;
- Альберштейн Герман, 10 класс, Открытая олимпиада школьников по математике (ИТМО), призер;
- Альберштейн Герман, 10 класс, Выездная олимпиада Физтех, победитель;
- Альберштейн Герман, 10 класс, Phystech international, победитель;
- Альберштейн Герман, 10 класс, Саммат, призер;
- Альберштейн Герман, 10 класс, Миссия Выполнима твое призвание финансист, призер;
- Мартынова Анна, 9 класс, Олимпиада школьников «Физтех» по математике, призер;
- Мартынова Анна, 9 класс, «Открытая олимпиада школьников» по математике, призер.
- Альберштейн Герман, 11 класс, Муниципальный этап ВСОШ, призер;
- Кнышев Глеб, 11 класс, Муниципальный этап ВСОШ, призер;
- Цыпочка Даниил, 10 класс, Муниципальный этап ВСОШ, призер;
- Мартынова Анна, 10 класс, Муниципальный этап ВСОШ, призер;
- Дымченко Светлана, 10 класс, Муниципальный этап ВСОШ, призер;
- Агошкин Никита, 10 класс, Муниципальный этап ВСОШ, призер;
- Карапетян Акоп, 10 класс, Муниципальный этап ВСОШ, призер;
- Ушаков Ярослав, 10 класс, Муниципальный этап ВСОШ, призер;
- Швец Андрей, 10 класс, Муниципальный этап ВСОШ, призер;
- Быстров Максим, 9 класс, Муниципальный этап ВСОШ, призер;
- Липский Андрей, 9 класс, Муниципальный этап ВСОШ, призер;
- Бартенев Владимир, 9 класс, Муниципальный этап ВСОШ, призер;
- Альберштейн Герман, 11 класс, Региональный этап ВСОШ, призер;
- Мартынова Анна, 10 класс, Региональный этап ВСОШ, призер;
- Быстров Максим, 9 класс, Региональный этап ВСОШ, победитель;
- Липский Андрей, 9 класс, Региональный этап ВСОШ, призер;
- Бартенев Владимир, 9 класс, Региональный этап ВСОШ, призер;
- Альберштейн Герман, 11 класс, Межрегиональная олимпиада школьников по математике и криптографии, призер;
- Альберштейн Герман, 11 класс, Олимпиада «Миссия выполнима.
 Твое призвание — финансист!», победитель;
Твое призвание — финансист!», победитель; - Агошкин Никита, 10 класс, Олимпиада «Миссия выполнима. Твое призвание — финансист!», победитель.
- 2012-2013
- 2013-2014
- 2014-2015
- 2015-2016
- 2016-2017
- 2017-2018
- Белкин Дмитрий и Борисов Михаил, 6 и 7 класс, XVII Международный Фестиваль «Дети. Интеллект. Культура» (о. Мальта), диплом I степени.
- Сафронов Руслан, 8 класс, XVII Международный Фестиваль «Дети. Интеллект. Культура» (о. Мальта), диплом II степени.
- Кузнецов Владимир, 10 класс, научно-практическая конференция ДАНЮИ имени Ю. А. Жданова (г. Ростов-на-Дону), диплом III степени.
- Сафронов Руслан, 9 класс, Всероссийский конкурс достижений талантливой молодежи «Национальное Достояние России» (Московская обл., ДО «Непецино» УД Президента РФ), диплом I степени.

- Сафронов Руслан, 10 класс, Всероссийский конкурс достижений талантливой молодежи «Национальное Достояние России» (Московская обл., ДО «Непецино» УД Президента РФ), диплом II степени.
- Арутюнян Артем, 11 класс, Всероссийский конкурс достижений талантливой молодежи «Национальное Достояние России» (Московская обл., ДО «Непецино» УД Президента РФ), победитель.
- Хан Евгений, 10 класс, научно-практическая конференция ДАНЮИ имени Ю. А. Жданова (г. Ростов-на-Дону), диплом I степени.
- Волков Макар, 10 класс, Всероссийский конкурс научных работ школьников «Юниор» (г. Москва), диплом III степени.
- Хан Евгений, 11 класс, научно-практическая конференция ДАНЮИ имени Ю. А. Жданова (г. Ростов-на-Дону), диплом I степени.
- Хан Евгений, 11 класс, Всероссийский конкурс достижений талантливой молодежи «Национальное Достояние России» (Московская обл., ДО «Непецино» УД Президента РФ), победитель.
- Волков Макар, 11 класс, Всероссийский конкурс научных работ школьников «Юниор» (г.
 Москва), сертификат финалиста.
Москва), сертификат финалиста. - Волков Макар, 11 класс, научно-инженерный конкурс «Ученые Будущего» (г. Москва), диплом II степени основного жюри, диплом IV степени молодежного жюри.
- Волков Макар, 11 класс, суперфинал научно-инженерного конкурса «Ученые Будущего» (г. Москва), победитель.
- Волков Макар, 11 класс, Intel International Science and Engineering Fair (Intel ISEF), Лос-Анджелес, США, сертификат финалиста.
- Васильева Кристина, 11 класс, научно-практическая конференция ДАНЮИ имени Ю. А. Жданова (г. Ростов-на-Дону), диплом I степени.
- 2015-2016
- 2016-2017
- 2018-2019
- 2019-2020
- Арутюнян Артем (2016).
- Щербакова Елизавета (2016).
- Волков Макар (2017).
- Артем Алехин (2019).
- Роман Букреев (2020).

- Роман Букреев (2020).
Учебные материалы
1. Тематическая подборка задач с параметром (по разделам), на основе которой ведется подготовка в ЧОУ «ЛИЦЕЙ КЭО»:
- Задачи с параметром. Раздел №1
- Задачи с параметром. Раздел №2
- Задачи с параметром. Раздел №3
- Задачи с параметром. Раздел №4
- Задачи с параметром. Раздел №5
- Задачи с параметром. Раздел №6
- Задачи с параметром. Раздел №7
- Задачи с параметром. Раздел №8
- Задачи с параметром. Раздел №9
- Авторские задачи с параметром. Раздел №10
2. Подборка вариантов, содержащих как задачи из открытого банка ФИПИ, так и авторские задачи:
- Вариант №1
- Вариант №2
- Вариант №3
- Вариант №4
- Вариант №5
- Вариант №6
- Вариант №7
- Вариант №8
3.
 Тематическая подборка олимпиадных задач:
Тематическая подборка олимпиадных задач:- 1. Логика
- 2. Четность
- 3. Инварианты
- 4. Признаки делимости
- 5. Математическая индукция
- 6. Комбинаторика
- 7. Принцип Дирихле
- 8. Теория чисел
- 9. Основная теорема арифметики
- 10. Линейные уравнения в ЦЧ
- 11. Нелинейные уравнения в ЦЧ
- 12. Неравенства
- 13. Теория множеств
- 14. Многочлены
- 15. Окружность
- 16. Медианы треугольника
- 17. Оценка Пример
- 18. Теорема Виета
- 19. Теоремы Чевы, Менелая и Ван-Обеля
- 20. Параметр и многочлены
4. Подборка олимпиадных задач по классам:
7 класс
- Вариант №7_1
- Вариант №7_2
- Вариант №7_3
- Вариант №7_4
- Вариант №7_5
- Вариант №7_6
8 класс
- Вариант №8_1
- Вариант №8_2
- Вариант №8_3
- Вариант №8_4
- Вариант №8_5
- Вариант №8_6
- Вариант №8_7
9 класс
- Вариант №9_1
- Вариант №9_2
- Вариант №9_3
- Вариант №9_4
- Вариант №9_5
- Вариант №9_6
- Вариант №9_7
10 класс
- Вариант №10_1
- Вариант №10_2
- Вариант №10_3
- Вариант №10_4
- Вариант №10_5
- Вариант №10_6
- Вариант №10_7
11 класс
- Вариант №11_1
- Вариант №11_2
- Вариант №11_3
- Вариант №11_4
- Вариант №11_5
- Вариант №11_6
- Вариант №11_7
5.
 Цифровая библиотека:
Цифровая библиотека:1. Геометрический смысл производной
2. Множество касательных
3. Нули параболы и дискриминант
4. Основное тригонометрическое тождество
5. Постоянный периметр
6. Построение синусоиды
* Раздел «Учебные материалы» будет пополняться.
Галерея
Официальные ресурсы
Информатика и математика в Акимовской школе Нижнегорского района: 9 класс, алгебра
12 декабря 2019
олимпиадные задачи
№1
В прямоугольнике ABCD сторона AB равна 6, сторона BC равна 11. Из вершин B и C проведены биссектрисы углов, пересекающие сторону AD в точках X и Y соответственно. Найдите длину отрезка XY .
Ответ: 1.
Решение. Углы AXB и XBC равны как накрест лежащие при параллельных прямых AD и BC и секущей BX. Углы XBC и XBA равны, так как BX — биссектриса угла ABC. Получаем, что ∠AXB = ∠XBA, откуда следует, что треугольник AXB — равнобедренный, AB = AX = 6;
XD = AD — AX = 11 — 6 = 5. Аналогично получаем, что AY = 5. Тогда XY = AD — AY — XD = 11 — 5 — 5 = 1.
№2
В треугольнике ABC провели медиану AM. Найдите угол AMC, если углы BAC и BCA равны 45° и 30° соответственно.
Ответ: 135°.
Решение. Пусть BH — высота треугольника ABC. По условию угол BAC равен 45°, поэтому BH = AH. В треугольнике CBH катет BH лежит против угла 30°, поэтому BC = 2BH. Медиана HM прямоугольного треугольника BHC равна половине гипотенузы BC.
В треугольнике CBH катет BH лежит против угла 30°, поэтому BC = 2BH. Медиана HM прямоугольного треугольника BHC равна половине гипотенузы BC.
Собирая все равенства отрезков воедино, получаем
AH = BH = HM = MB = MC.
Значит, треугольник MBH равносторонний, и угол CMH равен 120°. Кроме того, треугольник AHM равнобедренный, его угол AHM равен 90° + 60° = 150°, поэтому угол AMH равен 15°. Таким образом,
∠AMC = ∠AMH + ∠HMC = 120° + 15° = 135°
Загадка №2
Сколько двоек будет в разложении на простые множители числа 1984!,? (Примечание: 1984! = 1 • 2 • 3 • … • 1984).
Загадка №3
Все натуральные числа поделены на хорошие и плохие. Известно, что если число A хорошее, то и число A + 6 тоже хорошее, а если число B плохое, то и число B + 15 тоже плохое. Может ли среди первых 2000 чисел быть ровно 1000 хороших?
Может ли среди первых 2000 чисел быть ровно 1000 хороших?
ОТВЕТЫ загадок:
Загадка 2
Среди чисел от 1 до 1984 существует 992 четных. Каждое из них дает по крайней мере одну двойку в разложение на простые множители числа 1984!,. Две двойки в это разложение дадут числа, делящиеся на 4 (их всего 496). Далее, по 3, 4, 5, 6, 7, 8, 9 и 10 двоек соответственно дадут 248, 124, 62, 31, 15, 7, 3 и 1 чисел делящихся на 8, 16, 32, 64, 128, 256, 512 и 1024 соответственно. Сложив полученные числа, мы и получим искомую степень: 992 + 496 + 248 + 124 + 62 + 31 + 15 + 7 + 3 + 1 = 1979.
Загадка 3
Докажем, что числа C и C + 3 являются одновременно либо хорошими, либо плохими при любом значении C. Предположим для этого, что число C — хорошее, а C + 3 — плохое. Тогда с одной стороны, число C + 18 = (C + 3) + 15 должно быть хорошим, а с другой стороны, это же число C + 18 = ((C + 6) + 6) + 6 должно быть плохим. Если же предположить, что число C — плохое, а C + 3 — хорошее, то число C + 15 = ((C + 3) + 6) + 6 должно быть одновременно и плохим и хорошим. Полученное в обоих случаях противоречие доказывает, что числа C и C + 3 всегда принадлежат одному классу. Из этого следует, что любой класс вычетов по модулю 3 (см. Т5) является либо целиком хорошим, либо целиком плохим.
Полученное в обоих случаях противоречие доказывает, что числа C и C + 3 всегда принадлежат одному классу. Из этого следует, что любой класс вычетов по модулю 3 (см. Т5) является либо целиком хорошим, либо целиком плохим.
Среди первых 2000 чисел каждый такой класс содержит 666 или 667 чисел. Любой класс содержит меньше 1000 чисел, а любые два класса — больше 1000 чисел. Поэтому ровно 1000 хороших чисел быть не может.
Задача №1
Можно ли представить дробь 2/7 в виде суммы двух дробей, числители которых равны 1, а знаменатели — различные целые числа?
Задача №2
Токарь и его ученик, работая одновременно, обычно выполняют задание за 4 часа. При этом производительность труда токаря в 2 раза выше производительности ученика. Получив такое же задание, и, работая по очереди, они справились с заданием за 9 часов работы. Какую часть задания выполнил ученик токаря.
Задача №3
Стрелок десять раз выстрелил по стандартной мишени и выбил 90 очков. Сколько попаданий было в семерку, восьмерку и девятку, если десяток было четыре, а других попаданий и промахов не было?
Сколько попаданий было в семерку, восьмерку и девятку, если десяток было четыре, а других попаданий и промахов не было?
Задача №4
На столе лежат 2005 монет. Двое играют в следующую игру: ходят по очереди; за ход первый может взять со стола любое нечетное число монет от 1 до 99, второй – любое четное число монет от 2 до 100. Проигрывает тот, кто не сможет сделать ход. Кто выиграет при правильной игре?
Ответы
Задача 1
Можно. Например, 2/7=1/4+1/28.
Задача 2
Ученик выполнит 1\2 часть задания
Задача 3
Так как стрелок попадал лишь в семерку, восьмерку и девятку в остальные шесть выстрелов, то за три выстрела (по одному разу в семерку, восьмерку и девятку) он наберет 24 очка. Тогда за оставшиеся 3 выстрела надо набрать 26 очков. Что возможно при единственной комбинации 8 + 9 + 9 = 26. Итак, в семерку стрелок попал 1 раз, в восьмерку – 2 раза, в девятку – 3 раза.
Задача 4
Опишем стратегию первого игрока. Первым ходом он должен взять со стола 85 монет. Каждым следующим, если второй игрок берет х монет, то первый игрок должен взять 101 – x монет (он всегда может это сделать, потому что если х – четное число от 2 до 100, то (101 – x) – нечетное число от 1 до 99). Так как 2005 = 101 × 19 + 85 + 1, то через 19 таких «ответов» после хода первого на столе останется 1 монета, и второй не сможет сделать ход, т. е. проиграет.
Олимпиадные задачи по геометрии
1. В четырехугольнике АВСD проведены диагонали ВD и АС, пересекающиеся в точке О. При этом ВО=ОD=АО, АВD= АСD. Докажите, что АВСD — прямоугольник.
2. Пусть АМ медиана треугольника АВС, точка Р середина медианы АМ. И пусть луч ВР пересекает сторону АС в точке N. Найдите углы треугольника АВС, если известно, что NР- биссектриса угла АNМ и ВАС = NМС.
3. В треугольнике АВС биссектриса AD угла А в точке своего пересечения с медианой угла В делит ее пополам, при этом АD=DС. Найдите углы треугольника АВС.
Найдите углы треугольника АВС.
2 октября 2019
Неизвестное двузначное число представим аb=10*а+b, где а — количество десятков, эта цифра может принимать значения от 1 до 9, b -количество единиц данного двузначного числа и может эта цифра принимать значения от 0 до 9. Из условия задачи получаем уравнение
404 — СТРАНИЦА НЕ НАЙДЕНА
Почему я вижу эту страницу?
404 означает, что файл не найден. Если вы уже загрузили файл, имя может быть написано с ошибкой или файл находится в другой папке.
Другие возможные причиныВы можете получить ошибку 404 для изображений, поскольку у вас включена защита от горячих ссылок, а домен отсутствует в списке авторизованных доменов.
Если вы перейдете по временному URL-адресу (http://ip/~username/) и получите эту ошибку, возможно, проблема связана с набором правил, хранящимся в файле .htaccess. Вы можете попробовать переименовать этот файл в .htaccess-backup и обновить сайт, чтобы посмотреть, решит ли это проблему.
Также возможно, что вы непреднамеренно удалили корневую папку документа или ваша учетная запись должна быть создана заново. В любом случае, пожалуйста, немедленно свяжитесь с вашим веб-хостингом.
Вы используете WordPress? См. Раздел об ошибках 404 после перехода по ссылке в WordPress.
Как найти правильное написание и папку
Отсутствующие или поврежденные файлыКогда вы получаете ошибку 404, обязательно проверьте URL-адрес, который вы пытаетесь использовать в своем браузере. Это сообщает серверу, какой ресурс он должен использовать попытка запроса.
http://example.com/example/Example/help.html
В этом примере файл должен находиться в папке public_html/example/Example/
Обратите внимание, что CaSe важен в этом примере. На платформах с учетом регистра e xample и E xample не совпадают.
Для дополнительных доменов файл должен находиться в папке public_html/addondomain. com/example/Example/, а имена чувствительны к регистру.
com/example/Example/, а имена чувствительны к регистру.
Если на вашем сайте отсутствует изображение, вы можете увидеть на своей странице поле с красным цветом X , где изображение отсутствует. Щелкните правой кнопкой мыши X и выберите «Свойства». Свойства сообщат вам путь и имя файла, который не может быть найден.
Это зависит от браузера. Если вы не видите на своей странице поле с красным X , попробуйте щелкнуть правой кнопкой мыши на странице, затем выберите «Просмотреть информацию о странице» и перейдите на вкладку «Мультимедиа».
http://example.com/cgi-sys/images/banner.PNG
В этом примере файл изображения должен находиться в папке public_html/cgi-sys/images/
Обратите внимание, что в этом примере важен CaSe . На платформах с учетом регистра символов PNG и png не совпадают.
404 Ошибки после перехода по ссылкам WordPress
При работе с WordPress часто могут возникать ошибки 404 Page Not Found, когда была активирована новая тема или когда были изменены правила перезаписи в файле . htaccess.
htaccess.
Когда вы сталкиваетесь с ошибкой 404 в WordPress, у вас есть два варианта ее исправления.
Вариант 1: Исправьте постоянные ссылки- Войдите в WordPress.
- В меню навигации слева в WordPress нажмите Настройки > Постоянные ссылки (Обратите внимание на текущую настройку. Если вы используете пользовательскую структуру, скопируйте или сохраните ее где-нибудь.)
- Выберите По умолчанию .
- Нажмите Сохранить настройки .
- Верните настройки к предыдущей конфигурации (до того, как вы выбрали «По умолчанию»). Верните пользовательскую структуру, если она у вас была.
- Нажмите Сохранить настройки .
Во многих случаях это сбросит постоянные ссылки и устранит проблему. Если это не сработает, вам может потребоваться отредактировать файл .htaccess напрямую.
Вариант 2. Измените файл . htaccess
htaccess Добавьте следующий фрагмент кода 9index.php$ — [L]
RewriteCond %{REQUEST_FILENAME} !-f
RewriteCond %{REQUEST_FILENAME} !-d
RewriteRule . /index.php [L]
# Конец WordPress
Если ваш блог показывает неправильное доменное имя в ссылках, перенаправляет на другой сайт или отсутствуют изображения и стиль, все это обычно связано с одной и той же проблемой: в вашем блоге WordPress настроено неправильное доменное имя.
Как изменить файл .htaccess
Файл .htaccess содержит директивы (инструкции), которые сообщают серверу, как вести себя в определенных сценариях, и напрямую влияют на работу вашего веб-сайта.
Перенаправление и перезапись URL-адресов — это две очень распространенные директивы, которые можно найти в файле .htaccess, и многие скрипты, такие как WordPress, Drupal, Joomla и Magento, добавляют директивы в .htaccess, чтобы эти скрипты могли работать.
Возможно, вам потребуется отредактировать файл . htaccess в какой-то момент по разным причинам. В этом разделе рассматривается, как редактировать файл в cPanel, но не то, что может потребоваться изменить. статьи и ресурсы для этой информации.)
htaccess в какой-то момент по разным причинам. В этом разделе рассматривается, как редактировать файл в cPanel, но не то, что может потребоваться изменить. статьи и ресурсы для этой информации.)
- Отредактируйте файл на своем компьютере и загрузите его на сервер через FTP
- Использовать режим редактирования программы FTP
- Используйте SSH и текстовый редактор
- Используйте файловый менеджер в cPanel
Самый простой способ отредактировать файл .htaccess для большинства людей — через диспетчер файлов в cPanel.
Как редактировать файлы .htaccess в файловом менеджере cPanelПрежде чем что-либо делать, рекомендуется сделать резервную копию вашего веб-сайта, чтобы вы могли вернуться к предыдущей версии, если что-то пойдет не так.
Откройте файловый менеджер- Войдите в cPanel.
- В разделе «Файлы» щелкните значок «Диспетчер файлов ».

- Установите флажок для Корень документа для и выберите доменное имя, к которому вы хотите получить доступ, из раскрывающегося меню.
- Убедитесь, что установлен флажок Показать скрытые файлы (точечные файлы) «.
- Нажмите Перейти . Файловый менеджер откроется в новой вкладке или окне.
- Найдите файл .htaccess в списке файлов. Возможно, вам придется прокрутить, чтобы найти его.
- Щелкните правой кнопкой мыши файл .htaccess и выберите Редактировать код в меню. Кроме того, вы можете щелкнуть значок файла .htaccess, а затем Редактор кода Значок вверху страницы.
- Может появиться диалоговое окно с вопросом о кодировании. Просто нажмите Изменить , чтобы продолжить. Редактор откроется в новом окне.
- При необходимости отредактируйте файл.

- Нажмите Сохранить изменения в правом верхнем углу, когда закончите. Изменения будут сохранены.
- Протестируйте свой веб-сайт, чтобы убедиться, что ваши изменения были успешно сохранены. Если нет, исправьте ошибку или вернитесь к предыдущей версии, пока ваш сайт снова не заработает.
- После завершения нажмите Закрыть , чтобы закрыть окно диспетчера файлов.
Почему стрельба на поражение не имеет научного, юридического или тактического смысла
Действительно ли полицейские должны убивать людей, когда стреляют в них? Разве они не могли быть более гуманными и просто целиться в руки или ноги?
Как сообщалось в Force Science News, сенатор штата Нью-Йорк Дэвид Патерсон [D.-Harlem] обдумывал эти вопросы в 2006 году и пришел к выводу, что полицейские напрасно убивали подозреваемых. В ответ он ввел закон, который требует от офицеров стрелять в конечности преступников вместо того, чтобы нацеливаться на места, которые с большей вероятностью предотвратят угрозу, но также могут привести к смерти. Патерсон предложил, чтобы любой офицер, который применил силу, превышающую минимальную, необходимую, чтобы остановить опасного для жизни подозреваемого, был обвинен в непредумышленном убийстве. Правоохранительные органы взорвались протестами, и Патерсон отозвал законопроект.
Патерсон предложил, чтобы любой офицер, который применил силу, превышающую минимальную, необходимую, чтобы остановить опасного для жизни подозреваемого, был обвинен в непредумышленном убийстве. Правоохранительные органы взорвались протестами, и Патерсон отозвал законопроект.
Но битва еще не окончена.
Газета New York Post только что сообщила, что члены Бруклинской ассамблеи Аннет Робинсон [Д.-Бедфорд Стайвесант] и Дэррил Таунс [Д.-Восток Нью-Йорка] внесли законопроект о «минимальной силе», который требует от офицеров «застрелить подозреваемого». в руку или ногу» и использовать огнестрельное оружие «с намерением остановить, а не убить».
«Когда я сталкиваюсь с реакцией гражданского населения на стрельбу с участием офицеров, я очень часто спрашиваю: «Почему они просто не выстрелили ему в ногу?», — сказал Force Science News доктор Билл Левински, исполнительный директор Force Science Institute. интервью 2006 года было посвящено законопроекту, предложенному Патерсоном. «Когда гражданские лица судят о расстрелах полицией — присяжных, наблюдательных советах, в средствах массовой информации, в обществе — часто выдвигается тот же самый аргумент. Стрельба на поражение наивно считается разумным средством пресечения опасного поведения.
«Когда гражданские лица судят о расстрелах полицией — присяжных, наблюдательных советах, в средствах массовой информации, в обществе — часто выдвигается тот же самый аргумент. Стрельба на поражение наивно считается разумным средством пресечения опасного поведения.
«На самом деле такое мышление является результатом «обучения в Голливуде», когда полицейские из кино и телевидения могут делать все, что угодно, чтобы контролировать исход событий, которые служат драматическим интересам режиссера. Это отражает неправильное представление о реальной динамике и в конечном итоге навязывает нереалистичные ожидания навыков от реальных офицеров».
Вице-президент Джо Байден соглашается. Когда Майкл Паладино, президент Нью-Йоркской ассоциации благотворительных организаций детективов, показал ему законопроект, он, как сообщается, высмеял его и предложил назвать его «Билль Джона Уэйна» из-за нереалистичных, как в кино, навыков меткой стрельбы, которые он требует от офицеров.
В свете возрождения ошибочного мышления «выстрелить в рану» Force Science News переиздает «документ с изложением позиции», первоначально представленный после законопроекта, предложенного Патерсоном в 2006 году, в котором обсуждается, почему стрельба в рану и стрельба в практично и нежелательно в качестве стандарта производительности. Мы надеемся, что эта информация окажется полезной для вас при рассмотрении любой правозащитной деятельности, которая может возникнуть в вашей юрисдикции.
Мы надеемся, что эта информация окажется полезной для вас при рассмотрении любой правозащитной деятельности, которая может возникнуть в вашей юрисдикции.
Практические вопросы
Законопроект Робинсона и Таунса был составлен после неоднозначного выстрела в Шона Белла, который погиб после того, как нью-йоркские полицейские произвели в общей сложности 50 выстрелов в него и двух других мужчин. Сенатор Патерсон сказал, что его законопроект, предложенный в 2006 году, был мотивирован смертельной стрельбой в Нью-Йорке Амаду Диалло, в которого попали 19 человек.пули, когда офицеры ошибочно подумали, что он тянется за оружием, когда подошли к нему для допроса. Патерсон считал, что выстрел в руку или ногу, как правило, останавливает угрожающие действия подозреваемого, исключая необходимость стрелять в голову или грудь, где смерть более вероятна. Требуя минимального количества силы, необходимой для контроля над подозреваемым, он, по-видимому, надеялся снизить вероятность «чрезмерных» выстрелов.
Исследования, проведенные Исследовательским центром Силы, выявили некоторые практические проблемы с этими позициями. Левински объясняет некоторые основы динамики и анатомии человека, а также относительный риск промахов и попаданий:
«Кисти и предплечья могут быть самыми быстро движущимися частями тела. Например, средний подозреваемый может двигать рукой и предплечьем по всему телу под углом 90 градусов за 12/100 секунды. Он может переместить руку от бедра до уровня плеча за 18/100 секунды.
«Среднему офицеру, который нажимает на спусковой крючок так быстро, как только может, на Glock, одном из самых быстродействующих полуавтоматов, требуется 1/4 секунды для выстрела каждого выстрела.
«Офицер не может отреагировать, выследить, выстрелить и надежно поразить угрожающего подозреваемого предплечья или оружия в руке подозреваемого за требуемый промежуток времени.
«Даже если подозреваемый держит руку с оружием ровно полсекунды или больше, точное попадание маловероятно, а в полицейских перестрелках подозреваемый и его оружие редко остаются неподвижными. Кроме того, сам офицер может двигаться во время стрельбы.
Кроме того, сам офицер может двигаться во время стрельбы.
«Предплечья двигаются медленнее, чем предплечья и кисти. Но стреляя в предплечья, вы с большей вероятностью попадете в плечевую артерию подозреваемого или центральную массу тела, в области с высокой вероятностью летального исхода. Так при чем тут стрельба только по ране, когда даже области, которые некоторые считают «безопасными» от смертельного риска, на самом деле могут нести тот же уровень риска, что и прицеливание в центральную массу?
«Ноги изначально двигаются медленнее, чем руки, и занимают более статичное положение. Однако области нижней части туловища и верхней части бедра богаты васкуляризацией. Подозреваемый, получивший ранение, может истечь кровью за считанные секунды, если одна из основных артерий будет повреждена, поэтому повторная стрельба только для того, чтобы ранить, может не привести к простому ранению.
«С другой стороны, если офицеру удается без смертельного исхода отрубить подозреваемому ноги, у преступника остаются руки для стрельбы. Его способность угрожать жизни не обязательно была остановлена».
Его способность угрожать жизни не обязательно была остановлена».
Что касается предотвращения так называемого «избыточного поражения» от выстрелов после нейтрализации угрозы, Левински приводит следующие наблюдения:
«Двадцать лет назад офицеров обучали «выстрелить, а затем оценить». затем остановился, чтобы увидеть эффект. На это требовалось от 1/4 до 1/2 секунды, в течение которых подозреваемый мог продолжать стрелять, если он не был выведен из строя.
«Теперь их учат «стрелять и оценивать», оценивать эффективность своих выстрелов по мере того, как они продолжают стрелять, — это непрерывный процесс. Это позволяет полицейскому постоянно защищаться, но, поскольку мозг пытается делать две вещи одновременно — стрелять и оценивать, — для того, чтобы полицейский осознал изменение обстоятельств, в поведении преступника должно произойти очень существенное изменение.
«Подозреваемый, упавший на землю от выстрела, был бы существенным изменением. Но анализируя то, как люди падают, мы определили, что человеку требуется от 2/3 секунды до полной секунды или больше, чтобы человек упал на землю из положения стоя. И это происходит, когда они поражены в двигательном центре, что вызывает мгновенную потерю мышечного напряжения.
И это происходит, когда они поражены в двигательном центре, что вызывает мгновенную потерю мышечного напряжения.
«Пока офицер замечает это изменение, он будет продолжать стрелять, если он стреляет так быстро, как только может, под давлением попытки спасти свою жизнь. В среднем, с момента, когда офицер воспринимает изменение стимула, до того момента, когда он способен обработать это и фактически прекратить стрельбу, расходуется от 2 до 3 дополнительных патронов.
«Стрельба после момента нейтрализации угрозы в большинстве случаев не является умышленным злонамеренным действием. Это непроизвольный фактор человеческой динамики.
«Учитывая то, что наука говорит нам о вооруженных столкновениях, это последнее предложение является фантазией, как и закон Патерсона до него. Они принуждали бы офицеров к сверхчеловеческим способностям и наказывали бы их в уголовном порядке за то, что они не могли этого добиться».
Юридические вопросы
Постановление о стрельбе по ране «недействительно с юридической точки зрения», поскольку оно устанавливает стандарт, выходящий далеко за рамки того, что установлено в деле Грэм против Коннора, эталонном решении Верховного суда США о применении силы полицией, говорит бывший прокурор Джефф Чадвин, ныне начальник полиции Олимпия Филдс (Иллинойс) и президент Ассоциации тактических офицеров штата Иллинойс.
Признавая, что столкновения с применением насилия являются «напряженными, неопределенными и быстро развивающимися», Суд «не требует от офицеров использовать наименее навязчивый метод» принудительного контроля угрожающего подозреваемого, а «только то, что разумно», объясняет Чадвин. Когда жизнь офицера или третьего лица находится под угрозой, стрельба может быть оправдана как разумная.
Согласно юридическому определению, возможные последствия применения смертоносной силы включают как смерть, так и тяжкие телесные повреждения. «Закон никогда не разделял эти два понятия», — говорит Чадвин, что и пытались сделать эти предложения. «Политики, которые предлагают такое законодательство, говорят, что полиция должна стрелять в кого-то совсем чуть-чуть. Смертельная сила — это не «всего лишь немного». Каждый раз, когда вы стреляете из огнестрельного оружия, существует значительный риск серьезных телесных повреждений или смерти. Закон даже не предполагает, что смертоносной силы должно быть достаточно только для того, чтобы ранить, но без вероятности смерти. Это совершенно неправильно с юридической и тактической точек зрения и посылает неверный сигнал».
Это совершенно неправильно с юридической и тактической точек зрения и посылает неверный сигнал».
Адвокат Билл Эверетт, бывший руководитель отдела управления рисками, инструктор по применению силы, бывший LEO и член Национального консультативного совета Force Science, соглашается. Как он объясняет, применение силы с юридической точки зрения — это вопрос «соразмерности», и есть два способа его измерения: необходимый и разумный.
Он проводит аналогию с горящим домом. «Пожарные могут вылить на него количество воды, которое на данный момент кажется достаточным, чтобы остановить огонь, вместо того, чтобы не использовать ни одной капли воды больше, чем необходимо, даже задним числом, чтобы потушить огонь». Первое соответствует «разумному» подходу, второе является «необходимой» точкой зрения и является сутью законопроекта о стрельбе по ране/минимальной силе.
«Когда вы вводите стандарт строгой необходимости, вы требуете от офицеров много думать в ситуации, когда Верховный суд признает, что времени на размышления не так много», — заявляет Эверетт. Согласно директиве о стрельбе по ране, «ожидается, что офицер, столкнувшись с подозреваемым, бегущим на него с зазубренной бутылкой, подумает о том, чтобы попасть в цель на руке или ноге, в то время как его собственная жизнь находится в опасности». Нерешительность, которую это может вызвать, только повысит его риск.
Согласно директиве о стрельбе по ране, «ожидается, что офицер, столкнувшись с подозреваемым, бегущим на него с зазубренной бутылкой, подумает о том, чтобы попасть в цель на руке или ноге, в то время как его собственная жизнь находится в опасности». Нерешительность, которую это может вызвать, только повысит его риск.
Если оставить в стороне критическую проблему выживания офицеров, Эверетт предсказывает, что предлагаемый закон «существенно расширит гражданскую и уголовную ответственность полицейских». Он спрашивает: «Что, если полицейский попытается надуть подозреваемого и в итоге ударит невиновного прохожего? А что там с ответственностью? Что, если офицер попытается выстрелить преступнику в конечность, но вместо этого выстрелит ему в грудь? Как можно судить о его истинных намерениях?
«Прямо сейчас в соответствии с преобладающим стандартом Верховного суда адвокаты и судьи в большом проценте полицейских перестрелок могут посмотреть на факты и сделать вывод, что нет никаких оснований для передачи гражданского иска в суд. Но если вы измените стандарт, присяжным предстоит оценить гораздо больше дел: 1) намеревался ли офицер ранить или он намеревался убить подозреваемого и 2) была ли смерть подозреваемого абсолютно необходимой. Суд станет правилом, а не исключением.
Но если вы измените стандарт, присяжным предстоит оценить гораздо больше дел: 1) намеревался ли офицер ранить или он намеревался убить подозреваемого и 2) была ли смерть подозреваемого абсолютно необходимой. Суд станет правилом, а не исключением.
«Кто в здравом уме стал бы офицером полиции в юрисдикции, где стрельба на поражение и нормы строгой необходимости стали законом? Эти идеи могут иметь некоторую гуманитарную привлекательность, но как только вы выходите за рамки диснеевской привлекательности и смотрите в глаза реальности, поддержка этого мышления должна испариться».
Тактические вопросы
Современная подготовка учит, что когда офицер применяет смертоносную силу, его цель должна состоять в том, чтобы как можно быстрее остановить угрожающее поведение подозреваемого.
По словам инструктора по огнестрельному оружию Рона Эйвери, который сам является чемпионом по стрельбе, руководителем Академии практической стрельбы и членом Технического консультативного совета Force Science, стрельба по центру массы нападавшего обычно считается наиболее эффективным первым вариантом, поскольку верхняя туловище сочетает в себе концентрацию жизненно важных областей и основных кровеносных сосудов в пределах самой большой цели тела. «Когда риск неудачи — смерть, офицеру нужен самый высокий процент шансов на успех, который он может получить», — отмечает Эверетт.
«Когда риск неудачи — смерть, офицеру нужен самый высокий процент шансов на успех, который он может получить», — отмечает Эверетт.
Вместо этого стрельба по меньшей, но более быстрой руке или ноге с намерением ранить, а не вывести из строя, приводит к множеству тактических дилемм.
Например:
• Инстинкт выживания офицера может оказать решающее влияние на выбор цели. «Меня не волнует, насколько хорошо вы стреляете, — говорит Эйвери, — если вашей жизни угрожает опасность, вы в первую очередь пойдете на более надежное дело, а уже потом будете беспокоиться о спасении жизни нападавшего. Если парень бежит на меня с лезвием, последнее, о чем я буду думать, это «я прострелю ему руку».
• Плохая меткость выстрела будет увеличиваться. Даже когда офицеры пытаются стрелять в центр масс, они часто промахиваются. Левински вспоминает случай, в котором он участвовал, когда офицер, стрелявший в состоянии сильного стресса всего в 5 футах от преступника, вообще не попал в него из первых 5 выстрелов, а следующие четыре попали только потому, что подозреваемый перешел на его линию огня.
«Ударить рукой или ногой движущегося подозреваемого с хирургической точностью будет практически невозможно», — утверждает Эйвери. «Возможно, я мог бы пересчитать по пальцам одной руки людей, которые могут сделать такой бросок под давлением своей жизни на линии. Нелепо ожидать такого уровня работы полицейских в масштабах всего ведомства». Промахи вполне могут ранить или убить кого-то еще.
• Использование некоторых видов оружия может не поощряться. «Из-за рассредоточенности офицеру может быть запрещено брать дробовик из-за боязни поразить жизненно важные области, когда он попытается выстрелить, чтобы ранить», — предполагает Эверетт. «Если у преступника есть, скажем, полностью автоматическое оружие, следует ли запрещать офицеру использовать лучшее защитное оружие, которое у него может быть, потому что оно может иметь размах или подъем?»
• «Удачные» выстрелы могут быть опасны для людей, кроме подозреваемого, из-за сквозного проникновения. «Практически каждый полицейский снаряд сегодня предназначен для пробивания тяжелой одежды и баллистического геля толщиной от 10 до 12 дюймов», — объясняет Чадвин.
«Снаряды с такой способностью пробивают даже самые большие руки» и могут, как и промахи, затем двигаться дальше, чтобы поразить непреднамеренные цели на заднем плане.
• «Успешные» выстрелы, которые не убеждают преступника сдаться, оставляют офицера в опасности. Когда мы знаем из уличного опыта, что даже многократные попадания в центральную массу не всегда останавливают решительных, невменяемых или под действием наркотиков нападавших, «сколько офицеров будет убито преступниками, получившими ранение в конечность и все еще полностью способными стрелять в ответ?» — спрашивает Чадвин. Действительно, Эйвери считает, что выстрел в преступника без выведения его из строя «может просто разозлить его, поэтому он удваивает свои усилия, чтобы убить вас. Нет надежной корреляции между ранением кого-то и остановкой».
• «Стрельба в рану свидетельствует о неправильном применении полицейского оборудования. «Менее смертоносные варианты следует применять только с инструментами, предназначенными для этой цели», — говорит Эйвери.
«Если вы намеренно применяете смертоносную силу, чтобы арестовывать людей, не выводя их из строя, вы используете неправильный инструмент для этой работы. Кроме того, если вы выстрелите им в руку или ногу и разрушите мышечную ткань, сломаете кость или нарушите функцию нерва, вы покалечите этого человека на всю жизнь. Теперь адвокаты могут использовать аргумент о «жестоком и необычном наказании» и добиваться штрафных санкций за то, что ваша «жертва» не может получать заработную плату и так далее. Вы не пытаетесь просто ранить людей из пистолета. Период.»
Эксперты, с которыми мы консультировались, согласились с тем, что адвокаты, продвигающие программу «стрельба в рану», похоже, мало понимают в человеческой динамике, баллистике, тактике, силовых законах или проблемах, с которыми офицеры сталкиваются на улице. Чадвин обнаружил, что эти критики полицейской практики часто могут быть просвещены, если им предлагается испытать сценарии принятия силовых решений на симуляторе огнестрельного оружия.
У Эйвери есть более драматичная, хотя и причудливая идея. «Посадите их в клетку со львом», — предлагает он. «Тогда посмотрим, будут ли они стрелять на поражение».
Особая благодарность Рону Барберу из In the Line of Duty, чей электронный информационный бюллетень предупредил Force Science об этом недавнем законопроекте Ассамблеи.
Об авторе
Force Science Institute (FSI) состоит из группы врачей, юристов, психологов, ученых, полицейских инструкторов и специалистов правоохранительных органов, занимающихся углублением знаний и обучением в вопросах уголовного правосудия.
FSI проводит сложные научные исследования человеческого поведения, документируя физическую и психическую динамику, связанную с социальными потребностями функции по поддержанию мира, включая ситуации с высоким давлением и инциденты с применением силы. Его выводы применимы к применению силы гражданами, а также влияют на расследования применения силы офицерами. Исследования FSI применительно к обучению повышают эффективность работы офицеров и общественную безопасность.
Полиция Акрона стреляет в новые вопросы об обучении офицеров: NPR
Противостояние демонстрантов с офицерами возле мэрии Акрона в воскресенье, когда они протестуют против смертельного выстрела полицией в Джейленда Уокера. Мэтью Хэтчер/AFP через Getty Images скрыть заголовок
переключить заголовок
Мэтью Хэтчер/AFP через Getty Images
Противостояние демонстрантов с офицерами возле мэрии Акрона в воскресенье, когда они протестуют против убийства полицией Джейленда Уокера со смертельным исходом.
Мэтью Хэтчер/AFP через Getty Images
Джейланд Уокер, 25-летний темнокожий мужчина, который был безоружен в момент, когда он был убит полицией в Акроне, штат Огайо, на прошлой неделе, получил не менее 60 выстрелов, как заявили власти в выходные, когда они выпустили нательную камеру кадры со стрельбы.
Огромное количество пуль, выпущенных восемью офицерами, участвовавшими в стрельбе, вызвало новые вопросы со стороны политиков и активистов, которые критикуют то, что они считают чрезмерным применением силы полицией.
Правоохранительные органы и эксперты в области полицейского права, просмотревшие кадры стрельбы с нательной камеры, говорят, что реакция офицеров отражает стандартную полицейскую подготовку.
«Офицеров учат стрелять до тех пор, пока не прекратится угроза, которую они ощущают или в которой они обоснованно верят», — сказал Лэнс ЛоРуссо, юрист, специализирующийся на делах о применении силы.
Но другие эксперты предупреждают, что подготовка полицейских в США отстает от других стран, когда речь идет о психологических и физиологических аспектах применения силы.
WKSU: город Акрон вводит комендантский час, начиная с ночи понедельника
Полиция стреляет до тех пор, пока предполагаемая угроза не исчезнет
Стивен Майлетт, начальник полиции Акрона, заявил об этом на воскресной действующие полицейские протоколы для ситуаций, когда несколько полицейских стреляют в подозреваемого, и сколько пуль должно быть выпущено.
Хотя расследование стрельбы все еще продолжается, Майлетт сообщила, что офицеры независимо друг от друга сообщили, что они ощущали такую угрозу.
То, что началось как обычная остановка движения, превратилось в проблему общественной безопасности, сообщила полиция, когда во время преследования из машины Уокера, похоже, был произведен выстрел. Хотя власти заявили, что Уокер оставил свой пистолет, когда вышел из машины, чтобы бежать пешком, офицеры заявили, что после неудачной попытки использовать электрошокер они опасались, что подозреваемый готовился стрелять, когда они стреляли из своего оружия.
Майлетт сказал, что не знает, сколько выстрелов было произведено в Уокера, но он ожидает, что число будет «большим».
Юридически количество выстрелов в таких случаях не имеет значения, отметил ЛоРуссо. Верховный суд США согласился с тем, что в соответствии с Четвертой поправкой «если офицеры имеют право стрелять в подозреваемого, чтобы устранить серьезную угрозу общественной безопасности, им не нужно прекращать стрельбу до тех пор, пока угроза не будет устранена». Суды должны решить, была ли обоснованной оценка офицерами угрозы.
Суды должны решить, была ли обоснованной оценка офицерами угрозы.
Полиция не обучена стрелять на поражение
Большое количество пуль и смертельных исходов, которые часто являются результатом сценариев применения силы, сводятся к меткой стрельбе, говорит Эдвард Обаяши, заместитель шерифа округа Плумас, Калифорния
«Несмотря на то, что изображают в Голливуде, например, «Смертельное оружие », «Грязный Гарри » и все эти другие фильмы и телешоу, ни один полицейский не сравнится с таким мастерством стрельбы, — сказал Обаяши.
Добавьте к этому движущуюся цель, плохое освещение и быстро меняющиеся обстоятельства, ЛоРуссо сказал: «Нацеливание на самую большую доступную цель — самый безопасный метод избежать попадания в непреднамеренные цели».
С юридической точки зрения, говорит адвокат, нет никакой разницы между выстрелом подозреваемому в бедро и в грудь.
«Стрельба в человека в любую часть тела представляет собой один и тот же уровень силы — смертоносную силу — и должна быть оправдана в соответствии с законодательством штата», — сказал он, добавив, что любой выстрел несет в себе одинаковую степень риска «серьезных телесных повреждений». травмы или смерть», что является стандартом для оправдания применения смертоносной силы.
травмы или смерть», что является стандартом для оправдания применения смертоносной силы.
В состоянии стресса человеческое тело не отличает правильное от неправильного
Сегодня многие офицеры вооружены полуавтоматическим оружием, способным разрядить весь магазин — обычно около 15 или 17 патронов — за секунды, сказал Обаяши, который также работает в качестве консультанта по применению силы в правоохранительных органах.
Это означает, что к тому времени, когда офицер поймет, что пора прекращать стрельбу, может быть выпущено необоснованное количество пуль в быстрой последовательности, сказал он.
«Потребуется еще некоторое время, чтобы ваше зрение передало сигнал в мозг: «О, хорошо, угроза миновала. Я прекращаю стрелять».
Нельзя недооценивать физиологическую реакцию, говорит Мария «Маки» Хаберфельд, профессор полицейских наук в Колледже уголовного правосудия Джона Джея.
«К сожалению, адреналин и стресс берут верх, и это нельзя просто клинически объяснить с точки зрения того, что правильно, а что нет», — сказала она.

 ) Белка за 20 минут приносит орех в гнездо. Какое расстояние она при этом пробегает, если без ореха белка бежит со скоростью 5 м/с, а с орехом – 3 м/с?
) Белка за 20 минут приносит орех в гнездо. Какое расстояние она при этом пробегает, если без ореха белка бежит со скоростью 5 м/с, а с орехом – 3 м/с? ) Стрелок 10 раз выстрелил по стандартной мишени и выбил 90 очков. Сколько было попаданий в семерку, восьмерку и девятку, если десяток было четыре, а других попаданий и промахов не было.
) Стрелок 10 раз выстрелил по стандартной мишени и выбил 90 очков. Сколько было попаданий в семерку, восьмерку и девятку, если десяток было четыре, а других попаданий и промахов не было. Также указано, что стрелок точно по одному разу попал в семерку, восьмерку и девятку, что в сумме будет 24 очка, значит, останется «выбить» 26 очков. А дальше в решении не указано, что 26 очков можно набрать только при единственной комбинации цифр: 8 + 9 + 9.
Также указано, что стрелок точно по одному разу попал в семерку, восьмерку и девятку, что в сумме будет 24 очка, значит, останется «выбить» 26 очков. А дальше в решении не указано, что 26 очков можно набрать только при единственной комбинации цифр: 8 + 9 + 9.

 е. рассмотрен случай когда внешний угол расположен при основании треугольника и доказано, что такое решение невозможно
е. рассмотрен случай когда внешний угол расположен при основании треугольника и доказано, что такое решение невозможно
 ..
..
 01.02 Математика», диплом с отличием.
01.02 Математика», диплом с отличием.
 Подготовка экспертов ЕГЭ по математике».
Подготовка экспертов ЕГЭ по математике».
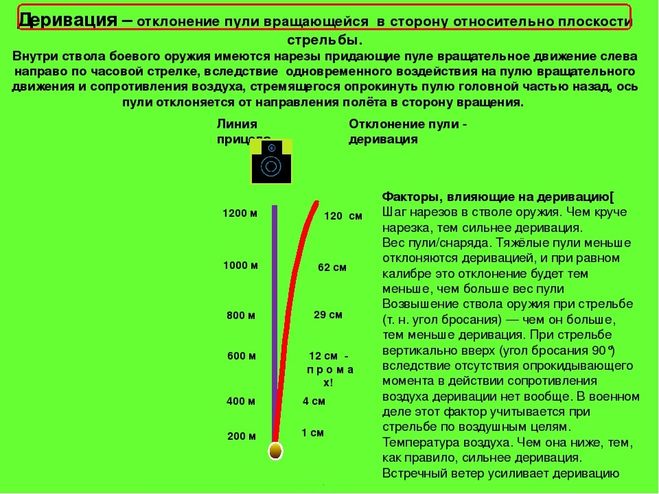
 09.2020 № 3).
09.2020 № 3). Н., Задорожный А. И. Определение спектра тороидальных волновых движений в шаровом слое самогравитирующей вязкой жидкости. Математические методы в современных и классических моделях экономики и естествознания: материалы региональной научно – практической конференции профессорско- преподавательского состава / Ростовский государственный экономический университет «РИНХ». – Ростов н/Д, 2008. С. 5 – 7.
Н., Задорожный А. И. Определение спектра тороидальных волновых движений в шаровом слое самогравитирующей вязкой жидкости. Математические методы в современных и классических моделях экономики и естествознания: материалы региональной научно – практической конференции профессорско- преподавательского состава / Ростовский государственный экономический университет «РИНХ». – Ростов н/Д, 2008. С. 5 – 7. – Воронеж: «Научная книга», 2009. С. 126 – 130.
– Воронеж: «Научная книга», 2009. С. 126 – 130. А. И. Иванова, В. А. Трифонова, В. И. Кузищина, Н. Н. Миленко, В. В. Хапаева – Севастополь: Филиал МГУ в г. Севастополе, 2010. С. 314 – 315.
А. И. Иванова, В. А. Трифонова, В. И. Кузищина, Н. Н. Миленко, В. В. Хапаева – Севастополь: Филиал МГУ в г. Севастополе, 2010. С. 314 – 315. С. 67 – 79.
С. 67 – 79. Математический форум. Т. 8. Порядковый анализ и смежные вопросы математического моделирования. — Владикавказ: ЮМИ ВНЦ РАН и РСО-А, 2014. С. 239 – 250.
Математический форум. Т. 8. Порядковый анализ и смежные вопросы математического моделирования. — Владикавказ: ЮМИ ВНЦ РАН и РСО-А, 2014. С. 239 – 250. Ростове-на-Дону. Тезисы докладов. Издательский центр ДГТУ, Ростов н/Д. – 2015. С. 25.
Ростове-на-Дону. Тезисы докладов. Издательский центр ДГТУ, Ростов н/Д. – 2015. С. 25. науч. конф. (г. Краснодар, февраль 2020 г.). — Краснодар: Новация, 2020. — С. 22-26.
науч. конф. (г. Краснодар, февраль 2020 г.). — Краснодар: Новация, 2020. — С. 22-26.

 М.В. Ломоносова, общий зачет – диплом I степени, личный зачет: Туманова Анастасия – диплом I степени, Посохов Константин – диплом I степени.
М.В. Ломоносова, общий зачет – диплом I степени, личный зачет: Туманова Анастасия – диплом I степени, Посохов Константин – диплом I степени.



 Л. Эйлера, призер.
Л. Эйлера, призер.
 Твое призвание — финансист!», победитель;
Твое призвание — финансист!», победитель; Л. Эйлера, призер;
Л. Эйлера, призер; Твое призвание — финансист!», победитель;
Твое призвание — финансист!», победитель;
 Москва), сертификат финалиста.
Москва), сертификат финалиста.


 «Ударить рукой или ногой движущегося подозреваемого с хирургической точностью будет практически невозможно», — утверждает Эйвери. «Возможно, я мог бы пересчитать по пальцам одной руки людей, которые могут сделать такой бросок под давлением своей жизни на линии. Нелепо ожидать такого уровня работы полицейских в масштабах всего ведомства». Промахи вполне могут ранить или убить кого-то еще.
«Ударить рукой или ногой движущегося подозреваемого с хирургической точностью будет практически невозможно», — утверждает Эйвери. «Возможно, я мог бы пересчитать по пальцам одной руки людей, которые могут сделать такой бросок под давлением своей жизни на линии. Нелепо ожидать такого уровня работы полицейских в масштабах всего ведомства». Промахи вполне могут ранить или убить кого-то еще. «Снаряды с такой способностью пробивают даже самые большие руки» и могут, как и промахи, затем двигаться дальше, чтобы поразить непреднамеренные цели на заднем плане.
«Снаряды с такой способностью пробивают даже самые большие руки» и могут, как и промахи, затем двигаться дальше, чтобы поразить непреднамеренные цели на заднем плане. «Если вы намеренно применяете смертоносную силу, чтобы арестовывать людей, не выводя их из строя, вы используете неправильный инструмент для этой работы. Кроме того, если вы выстрелите им в руку или ногу и разрушите мышечную ткань, сломаете кость или нарушите функцию нерва, вы покалечите этого человека на всю жизнь. Теперь адвокаты могут использовать аргумент о «жестоком и необычном наказании» и добиваться штрафных санкций за то, что ваша «жертва» не может получать заработную плату и так далее. Вы не пытаетесь просто ранить людей из пистолета. Период.»
«Если вы намеренно применяете смертоносную силу, чтобы арестовывать людей, не выводя их из строя, вы используете неправильный инструмент для этой работы. Кроме того, если вы выстрелите им в руку или ногу и разрушите мышечную ткань, сломаете кость или нарушите функцию нерва, вы покалечите этого человека на всю жизнь. Теперь адвокаты могут использовать аргумент о «жестоком и необычном наказании» и добиваться штрафных санкций за то, что ваша «жертва» не может получать заработную плату и так далее. Вы не пытаетесь просто ранить людей из пистолета. Период.»