Что такое круг: определение, свойства, формулы
Sign in
Password recovery
Восстановите свой пароль
Ваш адрес электронной почты
MicroExcel.ru Математика Геометрия Что такое круг: определение, свойства, формулы
В данной публикации мы рассмотрим определение и свойства одной из основных геометрических фигур – круга. Также приведем формулы, с помощью которых можно найти его радиус, диаметр, периметр и площадь (полную и сектора).
- Определение круга
- Свойства круга
- Свойство 1
- Свойство 2
- Свойство 3
- Свойство 4
- Формулы
Определение круга
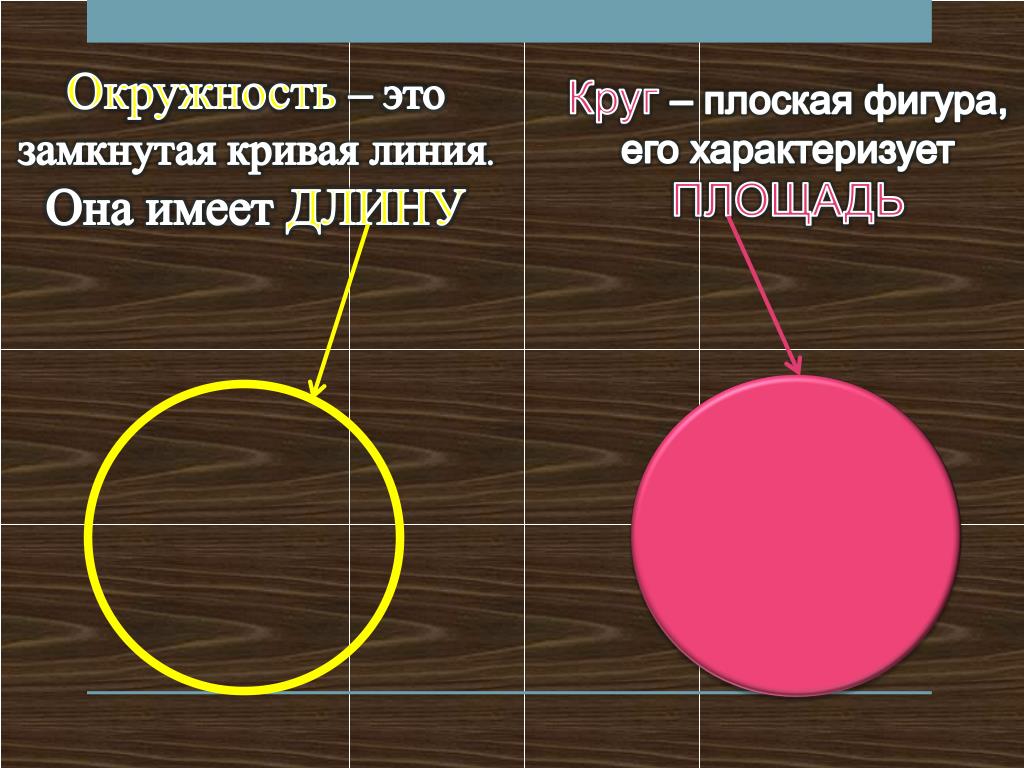
Круг – это множество точек на плоскости, ограниченных окружностью (т.е. лежащих внутри окружности). На рисунке ниже всё, что закрашено бирюзовым цветом, является кругом.
Сектор круга – область внутри круга, которая образована двумя радиусами и дугой между ними.
Сегмент круга – область, образованная в результате деления круга хордой, которая в свою очередь является частью секущей (прямой), пересекающей круг.
- AB – секущая;
- CD – хорда (отрезок, соединяющий две любые точки окружности).
Свойства круга
Свойство 1
Центр круга совпадает с центром ограничивающей его окружности. Чаще всего, обозначается буквой O.
Свойство 2
Радиус круга (R) является, в т.ч., радиусом граничной окружности. Это отрезок, соединяющий центр круга с любой точкой, лежащей на его границе, т.е. на окружности.
Хорда, проходящая через центр круга называется его диаметром (d).
Свойство 3
Периметр круга равняется длине ограничивающей его окружности.
Свойство 4
Круг по сравнению с другими фигурами имеет наибольшую площадь при заданном периметре.
Формулы
1. Периметр круга (L):
2. Радиус круга (R):
3. Диаметр круга (d):
4. Площадь круга (S):
Площадь круга (S):
5. Площадь сектора (S):
ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ
Таблица знаков зодиака
Нахождение площади трапеции: формула и примеры
Нахождение длины окружности: формула и задачи
Римские цифры: таблицы
Таблица синусов
Тригонометрическая функция: Тангенс угла (tg)
Нахождение площади ромба: формула и примеры
Нахождение объема цилиндра: формула и задачи
Тригонометрическая функция: Синус угла (sin)
Геометрическая фигура: треугольник
Нахождение объема шара: формула и задачи
Тригонометрическая функция: Косинус угла (cos)
Нахождение объема конуса: формула и задачи
Таблица сложения чисел
Нахождение площади квадрата: формула и примеры
Что такое тетраэдр: определение, виды, формулы площади и объема
Нахождение объема пирамиды: формула и задачи
Признаки подобия треугольников
Нахождение периметра прямоугольника: формула и задачи
Формула Герона для треугольника
Что такое средняя линия треугольника
Нахождение площади треугольника: формула и примеры
Нахождение площади поверхности конуса: формула и задачи
Что такое прямоугольник: определение, свойства, признаки, формулы
Разность кубов: формула и примеры
Степени натуральных чисел
Нахождение площади правильного шестиугольника: формула и примеры
Тригонометрические значения углов: sin, cos, tg, ctg
Нахождение периметра квадрата: формула и задачи
Теорема Фалеса: формулировка и пример решения задачи
Сумма кубов: формула и примеры
Нахождение объема куба: формула и задачи
Куб разности: формула и примеры
Нахождение площади шарового сегмента
Что такое окружность: определение, свойства, формулы
Окружность и круг — геометрия и искусство
- Окружность и круг
- Взаимное расположение окружностей
- круг и окружность в искусстве
- Эллипс
Плоские фигуры > Окружность
Окружность – это плоская замкнутая линия, все точки которой находятся на одинаковом расстоянии от некоторой точки (точки О), которая называется центром окружности.
(Окружность — геометрическая фигура, состоящая из всех точек, расположенных на заданном расстоянии от данной точки.)
Круг – это часть плоскости, ограниченная окружностью.Точка О также называется центром круга.
Расстояние от точки окружности до её центра, а также отрезок, соединяющий центр окружности с её точкой, называется радиусом окружности/круга.
Хорда — греческое — струна, стягивающая что-то
Диаметр — «измерение через»
КРУГЛАЯ ФОРМА
Углы могут встречаться во все более возрастающем количестве, приобретать, соответственно, все больший разворот – пока не исчезнут окончательно и плоскость не станет кругом. Это очень простой и одновременно очень сложный случай, о котором мне хотелось бы поговорить подробно. Здесь необходимо отметить, что как простота, так и сложность обусловлены отсутствием углов. Круг прост, поскольку давление его границ, в сравнении с прямоугольными формами, нивелировано – различия здесь не так велики. Он сложен, поскольку верх неощутимо перетекает в левое и правое, а левое и правое – в низ.
Он сложен, поскольку верх неощутимо перетекает в левое и правое, а левое и правое – в низ.
В. Кандинский
В Древней Греции круг и окружность считались венцом совершенства. Действительно, в каждой своей точке окружность устроена одинаковым образом, что позволяет ей двигаться самой по себе. Это свойство окружности сделало возможным возникновение колеса, поскольку ось и втулка колеса должны все время быть в соприкосновении.
В школе изучается много полезных свойств окружности. Одной из самых красивых теорем является следующая: проведем через заданную точку прямую, пересекающую заданную окружность, тогда произведение расстояний от этой точки до точек пересечения окружности с прямой не зависит от того, как именно была проведена прямая. Этой теореме около двух тысяч лет.
На рис. 2 изображены две окружности и цепочка окружностей, каждая из которых касается этих двух окружностей и двух соседей по цепочке. Швейцарский геометр Якоб Штейнер около 150 лет назад доказал следующее утверждение: если при некотором выборе третьей окружности цепочка замкнется, то она замкнется и при любом другом выборе третьей окружности.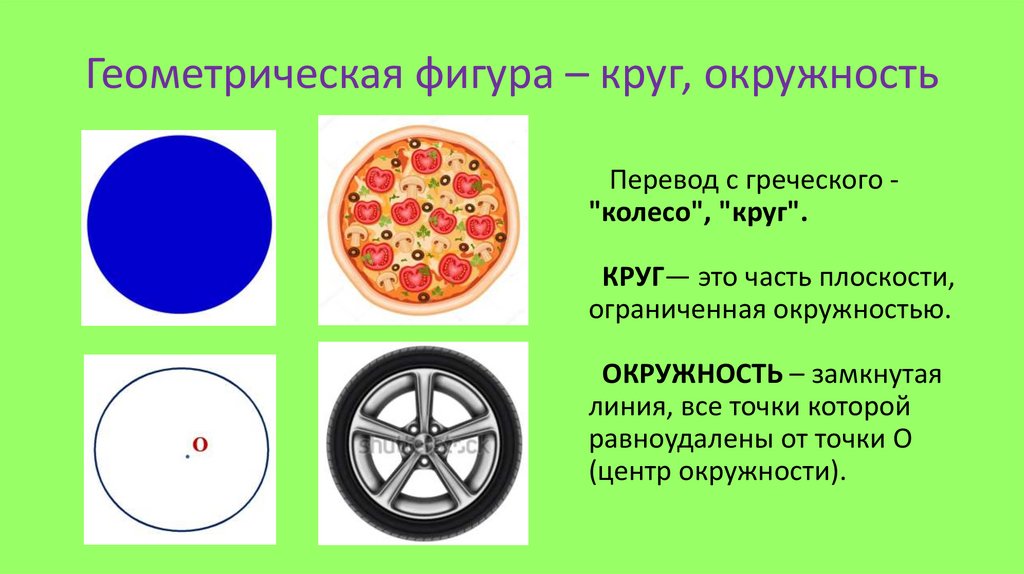
Вначале мы упомянули о колесе, но еще до колеса люди использовали круглые бревна — катки для перевозки тяжестей.
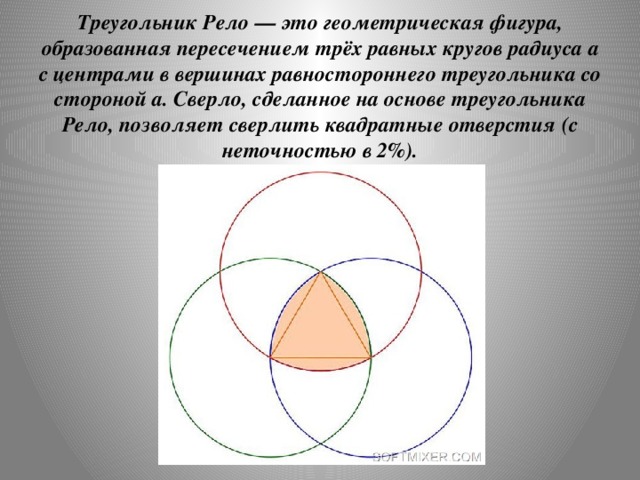
А можно ли использовать катки не круглой, а какой-нибудь другой формы? Немецкий инженер Франц Рело обнаружил, что таким же свойством обладают катки, форма которых изображена на рис. 3. Эта фигура получается, если провести дуги окружностей с центрами в вершинах равностороннего треугольника, соединяющие две другие вершины. Если провести к этой фигуре две параллельные касательные, то расстояние между ними будет равно длине стороны исходного равностороннего треугольника, так что такие катки ничем не хуже круглых. В дальнейшем были придуманы и другие фигуры, способные выполнять роль катков.
Энц. «Я познаю мир. Математика», 2006
У каждого треугольника имеется, и притом единственная, окружность девяти точек. Это окружность, проходящая через следующие три тройки точек, положение которых определено для треугольника : основания его высот D1 D2 и D3, основания его медиан D4, D5 и D6 середины D7, D8 и D9 отрезков прямых от точки пересечения его высот Н до его вершин.
Эта окружность, найденная в XVIII в. великим ученым Л. Эйлером (поэтому ее часто также называют окружностью Эйлера), была заново открыта в следующем столетии учителем провинциальной гимназии в Германии. Звали этого учителя Карл Фейербах (он был родным братом известного философа Людвига Фейербаха). Дополнительно К. Фейербах выяснил, что окружность девяти точек имеет еще четыре точки, тесно связанные с геометрией любого данного треугольника. Это -точки ее касания с четырьмя окружностями специального вида. Одна из этих окружностей вписанная, остальные три — вневписанные. Они вписаны в углы треугольника и касаются внешним образом его сторон.
Окружность эту очень легко построить, если знать два ее свойства. Во-первых, центр окружности девяти точек лежит в середине отрезка, соединяющего центр описанной около треугольника окружности с точкой Н- его ортоцентром (точка пересечения его высот). Во-вторых, ее радиус для данного треугольника равен половине радиуса описанной около него окружности.
Энц. справочник юного математика, 1989
Главная | Геометрия и искусство | Плоские фигуры | Пространственные фигуры | Движения и преобразования | Орнаменты и стили | Доклад | Разное | Галерея | Главная Карта Сайта
Круги – объяснение и примеры
Одной из важных фигур в геометрии является круг. На экзамене по геометрии большинство вопросов будет состоять из прямоугольников, треугольников и кругов.
Все мы уже видели круги. У них идеально круглая форма, что делает их идеальными для хула-хупов! В этой статье объясняется, что такое круг, его свойства и составные части.
Что такое круг в геометрии?
Слово ‘ круг «происходит от греческого слова, означающего « обруч » или « кольцо «. В геометрии круг определяется как замкнутая двумерная фигура, в которой множество всех точек на плоскости равноудалено от данная точка называется « центр ».
Никогда не путайте круг с многоугольником. Круг не является многоугольником, потому что он состоит из кривых.
История круга древняя. Раньше люди верили, что луна, солнце и другие планеты имеют круглую форму, потому что не существовало представления о трехмерных формах — математики изучают круги, что помогло им развить исчисление и астрономию.
В 1700 г. до н.э. Райнд Папирус предложил метод нахождения площади круга. В то время значение числа пи не было точным. В 300 г. до н.э. Евклид в своей книге изложил свойства кругов. Наконец, в 1880 году нашей эры немецкий математик Линдеманн решил проблему со значением числа пи и доказал, что число пи является трансцендентным (не корнем какого-либо многочлена с рациональными коэффициентами).
В то время значение числа пи не было точным. В 300 г. до н.э. Евклид в своей книге изложил свойства кругов. Наконец, в 1880 году нашей эры немецкий математик Линдеманн решил проблему со значением числа пи и доказал, что число пи является трансцендентным (не корнем какого-либо многочлена с рациональными коэффициентами).
Круги вокруг нас! Некоторые из реальных примеров кругов:
- Колесо велосипеда
- Монета
- Обеденная тарелка
- Настенные часы
- Колеса обозрения
Таким образом, круг является важной формой в области геометрии. Посмотрим на стороны и свойства окружности.
Части круга
- Центр: Центр — это середина круга. На приведенной выше диаграмме центр окружности указывает « O» .
- Радиус : Это отрезок от центра круга, соединяющий любую точку на самом круге. Радиус окружности обозначается либо буквой « r ” (строчные буквы) или “ R ” (верхние буквы).

Линия ОТ – это радиус описанной выше окружности.
- Диаметр : Диаметр круга — это отрезок, проходящий через центр круга и имеющий обе конечные точки круга. Математически диаметр в два раза больше радиуса окружности. Диаметр окружности обозначается « D » или «»
Линия PQ — это диаметр окружности.
- Хорда : Хорда представляет собой отрезок с обеими концами на окружности. Линия RS является хордой окружности выше. Диаметр окружности — самая длинная хорда.
- Секанс : Секанс представляет собой удлиненную хорду окружности.
Строка 2 ( l 2 ) является секущей круга выше.
- Дуга : Дуга представляет собой кривую вдоль внешней линии окружности
- Касательная : Тангенс окружности — это прямая линия, которая снаружи касается окружности, внешней линии окружности.
 Линия 2 ( l 2 ) является касательной окружности.
Линия 2 ( l 2 ) является касательной окружности. - Сегмент : Сегмент представляет собой область, ограниченную дугой и хордой.
- Сектор : Сектор представляет собой область по дуге и двум радиусам. Регион OTP — это сектор круга, как показано выше.
- Окружность : Окружность круга – это общее расстояние вокруг внешней линии круга
- Площадь круга : Область, ограниченная внешней линией круга
- Кольцо : Кольцо представляет собой кольцо -образный объект, образованный между двумя концентрическими (окружностями с общим центром) окружностями. Например, заштрихованная область в круге ниже называется кольцом.
Свойства круга
Существует несколько фактов о кругах. Эти факты о кругах известны как свойства круга. Давайте рассмотрим их.
- Окружности с равными радиусами или диаметрами конгруэнтны.

- Самая длинная хорда окружности называется диаметром.
- Диаметр круга в два раза больше радиуса самого круга.
- Диаметр делит круг на две равные половины.
- Внешняя линия круга равноудалена от центра.
- Независимо от меры радиуса или диаметра, все окружности подобны.
- Радиус представляет собой серединный перпендикуляр к хорде.
- Две или более хорды равны по длине, если все они равноудалены от центра окружности.
- Угол между радиусом и касательной всегда равен 90 градусов (прямой угол).
- Две касательные равны, если они имеют общую точку начала.
- Угол, образуемый в центре круга его окружностью, равен четырем прямым углам.
- Длина окружности двух или более разных кругов пропорциональна их соответствующим радиусам.
- Дуги одной и той же окружности пропорциональны соответствующим углам.
- Радиусы равных окружностей или одной и той же окружности равны.
- Равные круги имеют площадь и длину окружности.

- Расстояние между самой длинной хордой и центром окружности равно нулю.
- Перпендикулярное расстояние от центра окружности до хорды увеличивается по мере уменьшения длины хорды, и наоборот.
- Окружность может описывать многоугольники, такие как треугольник, трапеция, прямоугольник и т. д.
- Точно так же окружность может быть вписана внутрь многоугольника, такого как прямоугольник, воздушный змей, квадрат, трапеция и т. д.
- Касательные, проведенные на обоих концах диаметра, всегда параллельны друг другу.
- Два радиуса, соединяющие концы хорды с центром окружности, образуют равнобедренный треугольник.
- Равные дуги образуют равные углы в центре окружности.
Пример 1
Какой из следующих предметов имеет круглую форму?
- Пицца
- Футбол
- Апельсин
- Все это.
Решение
Все упомянутые формы имеют круглую форму.
Следовательно, правильный выбор D.
Пример 2
Круглая чаша имеет диаметр 9 дюймов. Каков радиус чаши?
Решение
Мы знаем, что радиус круга равен половине диаметра.
Следовательно,
Радиус = 9/2 = 4,5 дюйма
Пример 3
Какая из следующих частей окружности также может быть хордой окружности?
- Радиус
- Диаметр
- Дуга
- Сектор
Решение
Хорда — это отрезок, оба конца которого лежат на окружности. Диаметр окружности — самая длинная хорда.
Решение геометрических задач с кругами
Key Terms
o Circle
o Radius
o Diameter
o Arc
o Subtend
o Sector
o Chord
o Secant
o Tangent
o Circumference
Цели
o Знать, как дать основное определение окружности
o Определите различные части кругов
o Расчет области и окружности круга или его части
Введение в круги
A Circle — просто показанная на всех очках, которые являются точками, которые являются точками равноудалены от заданной центральной точки.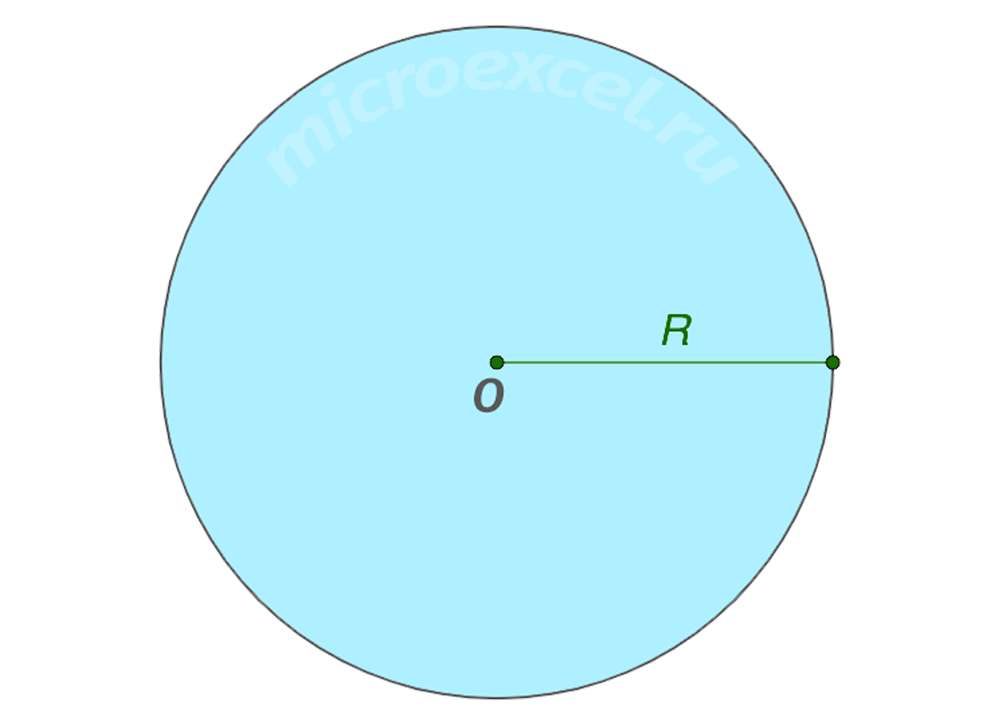
Обратите внимание, что независимо от того, какая точка на окружности выбрана, она всегда находится на расстоянии r от центральной точки C. Каждый из отрезков, проведенных от C до окружности, называется радиусом. (другими словами, ни один сегмент не определяется как радиуса
, поскольку все такие сегменты равны по длине). Сама окружность не показывает никаких углов или сторон, которые мы можем использовать, чтобы определить, сколько градусов составляет фигура (как мы сделали с многоугольниками), но мы можем видеть, что любые два радиуса действительно образуют угол α , как показано ниже.
Используя наше измерение градусов, этот угол α может (однозначно) принимать любое значение от 0° до 360°. Мы также можем определять углы как с положительными, так и с отрицательными числами, в зависимости от направления измерения от определенного радиуса — положительный угол традиционно измеряется в направлении против часовой стрелки, а отрицательный угол традиционно измеряется в направлении по часовой стрелке, как показано ниже. .
Любые два радиуса окружности (составляющие угол α ), такие как показанные ниже, образуют дугу и сектор. Дуга — это часть окружности, противоположная углу α (или , на который опирается ) и между конечными точками радиусов. Сектор — это область, ограниченная дугой и радиусами. Дуга A на приведенной ниже схеме показана жирной линией, а сектор S показан заштрихованной областью.
Дуга — это часть окружности, противоположная углу α (или , на который опирается ) и между конечными точками радиусов. Сектор — это область, ограниченная дугой и радиусами. Дуга A на приведенной ниже схеме показана жирной линией, а сектор S показан заштрихованной областью.
Хотите узнать больше? Почему бы не пройти онлайн-курс по геометрии?
Любой отрезок, соединяющий две точки на окружности, называется хордой . Обратите внимание, что диаметр — это хорда (самая длинная возможная хорда окружности!). Хорда D показана ниже жирной линией.
Другими специальными фигурами, относящимися к окружностям, являются секущие и тангенсы. Секанс — это просто линия, пересекающая две точки окружности (хорда — это отрезок секанса). Касательная — это прямая, пересекающая окружность ровно в одной точке.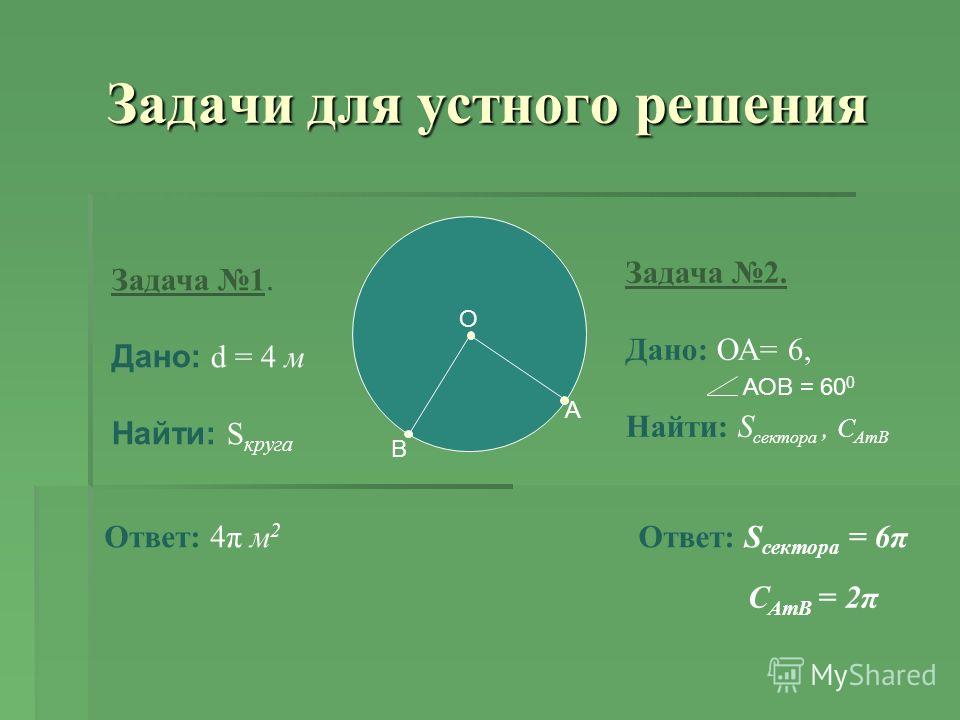 секанс E и касательная T показаны на диаграмме ниже жирными линиями.
секанс E и касательная T показаны на диаграмме ниже жирными линиями.
Практическая задача : Определите каждую часть (от A до E) круга ниже.
Решение : Каждую часть круга или другую линию можно определить по ее отношению ко всему кругу. Каждая из этих фигур обсуждалась и определялась выше. Заштрихованная область А является сектором. Прямая (или отрезок) B является касательной (обратите внимание, что она пересекает окружность только в одной точке). C — диаметр, D — хорда, E — радиус.
Основные характеристики кругов
Теперь, когда мы идентифицировали некоторые компоненты кругов, мы можем теперь начать получать некоторые из их характеристик, используя инструменты, которые мы разработали до сих пор. Для вывода некоторых свойств окружностей требуется тригонометрия (например, длина хорды, опирающейся на угол α ), но другие мы можем вывести или просто сформулировать основные формулы, которые можно использовать для решения задач.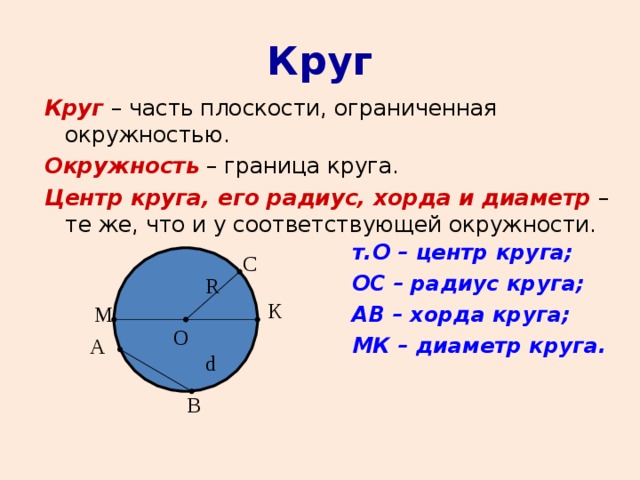 Начнем с длины окружности и площади круга. окружность круга — это просто длина границы (то есть периметра) круга. Мы просто сформулируем формулу для длины окружности C через радиус ( r ) или диаметр ( d ):
Начнем с длины окружности и площади круга. окружность круга — это просто длина границы (то есть периметра) круга. Мы просто сформулируем формулу для длины окружности C через радиус ( r ) или диаметр ( d ):
Обратите внимание, что с формулой для длины окружности мы вводим число π . Поскольку π (большинство математиков считают) является иррациональным числом, мы не можем точно записать его в десятичной форме и не можем точно записать в виде дроби. Однако мы можем записать десятичную оценку π , что достаточно для наших целей.
π ≈ 3,1416
Многие калькуляторы имеют встроенный ключ для числа π (хотя калькулятор по-прежнему просто использует приближение 3 π ). Для многих расчетов приблизительное значение π , равное 3,14, дает достаточную точность. Оказывается, π также фигурирует в формуле площади круга. Запишем площадь A через радиус р . A = πr 2 Заметим еще раз, что на самом деле мы не вывели эти формулы; мы просто констатируем их как фундаментальные факты, на которых мы будем основывать остальную часть нашего исследования характеристик кругов. Практическая задача : Найдите площадь и длину окружности круга диаметром 4 дюйма. Решение : Одно из первых правил решения подобных задач, связанных с окружностями, состоит в том, чтобы тщательно отмечать, имеем ли мы дело с радиусом или с диаметром. В этой задаче окружность описывается с помощью диаметра, который равен 4 дюймам. Таким образом, радиус составляет 2 дюйма. Давайте теперь вычислим площадь A и длину окружности C , используя приведенные выше формулы. А = πr 2 = π (2 дюйма) 2 ≈ (3,14)(4 дюйма 2 ) = 12,56 дюйма 2 C = πd = 9,04 дюйма (1,4 903) = 12,56 in Так совпало, что площадь и окружность имеют одинаковые числовые значения (но разные единицы измерения!). Давайте посмотрим на характеристики других частей круга. Например, теперь, когда мы знаем, как вычислить длину окружности, мы можем также вычислить длину дуги (которая является просто частью окружности). Угол α определяется двумя радиусами, стягивающими дугу. Давайте рассмотрим несколько примеров, из которых мы можем определить закономерность. Дуга K в каждом случае показана жирной кривой. Длина окружности равна C . 
 Обычно это не так, конечно.
Обычно это не так, конечно.
Выражения в каждом примере могут быть получены путем проверки. Мы знаем, что если угол α равен 90° (четверть полных 360° окружности), то стягиваемая дуга составляет четверть окружности. Те же рассуждения применимы к определению длины дуги K и для двух других случаев. Таким образом, мы можем видеть, что длина дуги связана с окружностью, как угол α связан с 360°. Но это просто отношение, которое мы можем записать следующим образом.
. Поперечное умножение мы получаем формулу выше для длины дуги K С точки зрения окружности C и угла подношения α . Мы можем использовать тот же тип рассуждений, чтобы определить площадь сектора С . Снова обратите внимание на приведенные ниже примеры, где S — заштрихованная область, а круг имеет площадь A .
Таким образом, площадь сектора S связана с площадью A соотношением α 3 3. Мы снова можем вывести формулу.
Практическая задача : Центральный угол γ в окружности радиусом 10 единиц образует сектор площадью 2,62 квадратных единиц. Найдите меру γ .
Решение : Начнем с рисования схемы задачи. Эта диаграмма не обязательно должна быть в масштабе — мы можем просто использовать ее, чтобы легче идентифицировать части круга, обсуждаемые в задаче.

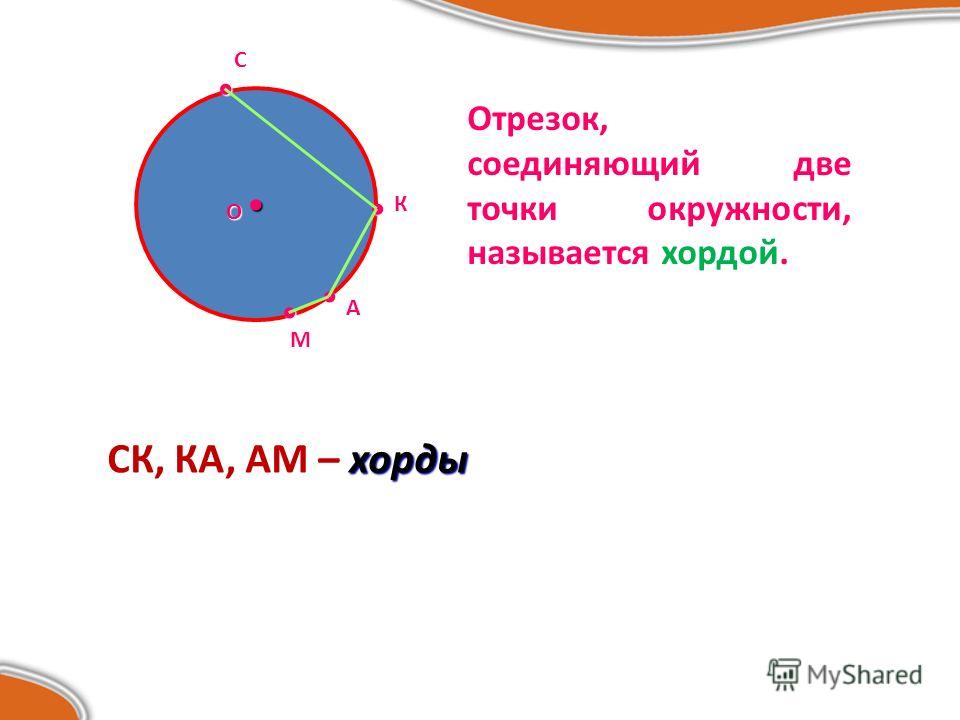 Линия 2 ( l 2 ) является касательной окружности.
Линия 2 ( l 2 ) является касательной окружности.
