В треугольнике sin – Синус, косинус и тангенс острого угла прямоугольного треугольника

Как найти синус угла в треугольнике

Как найти синус угла в треугольнике, причем в произвольном
Чтобы узнать sin любого из углов в любом (то есть произвольном) треуг-ке, принято применять теорему косинусов (важно заметить, что используется теорема cos, но не sin). Согласно этой теореме квадрат любой из сторон треуг-ка равен сумме квадратов второй и третьей стороны, если вычесть из этой суммы два произведения размеров этих сторон на cos угла, который они образуют:

   

Рассматриваемая формула позволяет получить значение cos угла, используя значения всех трех сторон треуг-ка:

   

Из тригонометрического равенства, которое принято называть основным, зная, что сумма квадрата sin и квадрата cos одного из углов равна 1, можно без трудностей вычислить и значение sin угла.
К тому же можно получить такую формулу для sin, используя выше приведенные формулы:

   

Выведем из этой формулы выражение для sin угла:

   

   

Подставим полученное значение для cos угла в эту формулу:

   

Формула для отыскания sin угла в любом из треугольников.

ru.solverbook.com

Как найти синус угла по сторонам треугольника

Синус – это одна из базовых тригонометрических функций. Изначально формула ее нахождения была выведена из соотношений длин сторон в прямоугольном треугольнике. Ниже приведены как эти базовые варианты нахождения синусов углов по длинам сторон треугольника, так и формулы для больше трудных случаев с произвольными треугольниками.

Инструкция

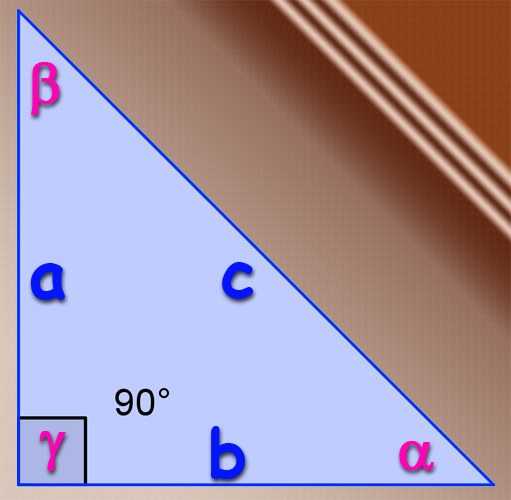
1. Если рассматриваемый треугольник является прямоугольным, то дозволено применять базовое определение тригонометрической функции синуса для острых углов. По определению синусом угла называют соотношение длины катета, лежащего наоборот этого угла, к длине гипотенузы этого треугольника. То есть, если катеты имеют длину А и В, а длина гипотенузы равна С, то синус угла ?, лежащего наоборот катета А, определяйте по формуле ?=А/С, а синус угла ?, лежащего наоборот катета В – по формуле ?=В/С. Синус третьего угла в прямоугольном треугольнике находить нет необходимости, потому что угол, лежащий наоборот гипотенузы неизменно равен 90°, а его синус неизменно равен единице.

2. Для нахождения синусов углов в произвольном треугольнике, как это ни необычно, проще применять не теорему синусов, а теорему косинусов. Она гласит, что возведенная в квадрат длина всякий стороны равна сумме квадратов длин 2-х других сторон без удвоенного произведения этих длин на косинус угла между ними: А?=В?+С2-2*В*С*cos(?). Из этой теоремы дозволено вывести формулу для нахождения косинуса: cos(?)=(В?+С?-А?)/(2*В*С). А от того что сумма квадратов синуса и косинуса одного и того же угла неизменно равна единице, то дозволено вывести и формулу для нахождения синуса угла ?: sin(?)=?(1-(cos(?))?)= ?(1-(В?+С?-А?)?/(2*В*С)?).

3. Воспользуйтесь для нахождения синуса угла двумя различными формулами расчета площади треугольника, в одной из которых задействованы только длины его сторон, а в иной – длины 2-х сторон и синус угла между ними. Потому что итоги их будут равны, то из тождества дозволено выразить синус угла. Формула нахождения площади через длины сторон (формула Герона) выглядит так: S=?*?((А+В+С)*(В+С-А)*(А+С-В)*(А+В-С)). А вторую формулу дозволено написать так: S=А*В*sin(?). Подставьте первую формулу во вторую и составьте формулу для синуса угла, лежащего наоборот стороны С: sin(?)= ?*?((А+В+С)*(В+С-А)*(А+С-В)*(А+В-С)/(А*В)). Синусы 2-х других углов дозволено обнаружить по аналогичным формулам.

Прямоугольным треугольником считается треугольник, у которого один из углов прямой. Для подсчета синуса его острых углов, а также прямого угла, довольно владеть данными о его сторонах.

Вам понадобится

• Размеры сторон прямоугольного треугольника.

Инструкция

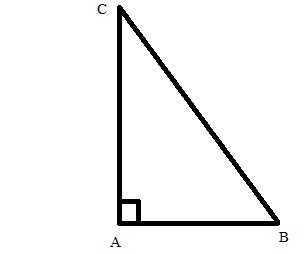
1. Отношение противолежащего катета к гипотенузе прямоугольного треугольника именуется синусом острого угла прямоугольного треугольника :Sin A = ABBCSin B = ACCBСинус 90 градусов равен 1.

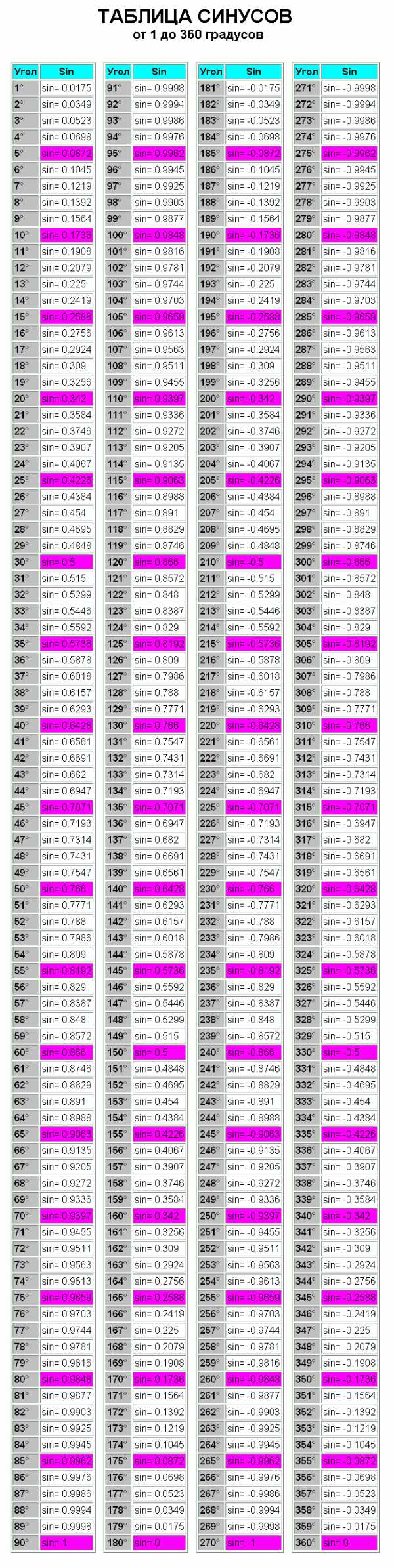
2. Для того, дабы подсчитать синус того либо другого угла, дозволено воспользоваться таблицей синусов. Она представляет собой сводную таблицу из значений углов от 0 до 360 градусов и соответствующие им размеры углов.

Видео по теме

«Четырехзначные математические таблицы» Брадиса, невзирая на огромное число современных средств вычисления тригонометрических функций, не выходят из употребления. С их поддержкой дозволено стремительно обнаружить необходимое значение, не прилагая специальных усилий. Но для этого нужно обучиться пользоваться этими таблицами.

Вам понадобится

• – данный угол;
• – «Четырехзначные математические таблицы».

Инструкция

1. Откройте «Четырехзначные математические таблицы. Они есть как в печатном варианте, так и в интернете. Пользуются ими в обоих случаях идентично, только в книге необходимо заглянуть в оглавление, а на сайте — в меню. Обнаружьте главу «Синусы» и откройте надобную страницу.

2. Посмотрите, какой угол вам дан. Таблицами Брадиса дозволено пользоваться и в том случае, если угол дробный, то есть измеряется в градусах и минутах. Если размер угла дан в радианах, переведите его в градусы. Он равен произведению размера в радианах, умноженному на отношение 180° на показатель ? и выражается формулой ?1=?*180°/?, где ? — величина угла в градусах, а ?1 — в радианах.

3. В таблице вы видите горизонтальные и вертикальные ряды. Посмотрите на самый крайний ряд слева. В верхнем левом углу стоит слово sin, а под ним — столбик цифр с обозначением градуса. Это целое число градусов. Обнаружьте число, которое соответствует числу целых градусов в заданном вам угле. Скажем, вам дан угол размером 27°18′. Обнаружьте в крайней левой колонке число 27. После этого в верхней строке разыщите число 18. На пересечении надобных строки и столбца обнаружьте надобное значение.

4. Обратите внимание на то, что градусы в таблице идут подряд, а минуты — через шесть. То есть 18 минут обнаружить непринужденно в таблице дозволено, а 19 — нет. Для того дабы обнаружить синус угла, число минут которого не кратно шести, существуют поправки. Они находятся в правой стороне таблицы. Вычислите разницу между числом минут в заданном угле и ближайшем, где число минут кратно 6. Если эта разность составляет 1, 2 либо 3 минуты, легко приплюсуйте надобное значение к последней цифре величины синуса меньшего угла. Если разность составляет 4 либо 5, возьмите величину ближайшего большего угла и отнимите от последней цифры значение первой либо 2-й поправок.

Видео по теме

В математике существует несколько различных подходов, с поддержкой которых даются определения всякой из тригонометрических функций – через решение дифференциальных уравнений, через ряды, решение функциональных уравнений. Есть и два варианта геометрических трактовок таких функций, один из которых определяет их через соотношения сторон и острых углов в прямоугольном треугольнике.

Инструкция

1. Используйте базовое определение

синуса острого угла в треугольнике, если из условий вестимо, что это прямоугольный треугольник, а также даны длины его гипотенузы (С) и того катета (А), тот, что лежит наоборот необходимого угла (?). Согласно определению, синус этого угла должен быть равен соотношению длины вестимого катета к длине гипотенузы: sin(?)=А/С.

2. Если треугольник является прямоугольным, длина его гипотенузы вестима (С), но и из катетов есть только длина (В) прилежащего тому углу (?), синус которого нужно вычислить, то в дополнение к определению из предыдущего шага дозволено задействовать еще и теорему Пифагора. Из нее вытекает, что длина неведомого катета равна квадратному корню из разности возведенных в квадрат длин гипотенузы и иного катета. Подставьте это выражение в полученную выше формулу: sin(?)=v(С?-В?)/С.

3. Используйте теорему Пифагора и в том случае, если в прямоугольном треугольнике вестимы только длины обоих катетов (А и В). Длина гипотенузы, согласно теореме, равна квадратному корню из суммы квадратов длин катетов. Замените этим выражением длину гипотенузы в формуле из первого шага: sin(?)=А/v(А?+В?).

4. Если длины сторон прямоугольного треугольника неведомы, но дана величина одного из его острых углов (?), то вычислить синус иного острого угла (?) дозволено с применением таблиц тригонометрических функций либо калькулятора. Исходите из теоремы о сумме углов треугольника в евклидовой геометрии – она заявляет, что эта сумма неизменно должна быть равна 180°. Потому что в прямоугольном треугольнике один из углов по определению равен 90°, а иной дан в условиях задачи, то величина надобного угла будет равна 180°-90°- ?. Значит вам останется только вычислить значение синуса угла : sin(90°-?).

5. Для вычисления значения синуса при знаменитой величине

угла воспользуйтесь, скажем, калькулятором, встроенным в операционную систему вашего компьютера. Если это ОС Windows, то запустить такое приложение дозволено, нажав сочетание клавиш Ctrl + R, введя команду calc, а после этого кликнув кнопку ОК. Для доступа к тригонометрическим функциям в калькуляторе переключите его в «инженерный» либо «ученый» режим – соответствующий пункт есть в разделе «Вид» меню этой программы.

Видео по теме

Видео по теме

jprosto.ru

Как найти синус угла треугольника?

Чтобы найти синус угла прямоугольного треугольника, нужно вспомнить, что такое синус по определению. А определение очень простое: синус угла равен отношению противолежащего катета к гипотенузе.

Как вычислять синусы

Если мы имеем треугольник АВС, у которого А – прямой угол, то стороны АВ и АС будут катетами, а сторона ВС – гипотенузой. Значит, по определению, синус угла В равен отношению катета АС к гипотенузе: sinB = AC/BC, а синус другого угла sinC = AB/BC.

В прямоугольном треугольнике функции углов вычислять удобно: не нужны никакие дополнительные построения. Достаточно знать длины нужных сторон. Но чаще известна только часть необходимых данных, остальные нужно искать. Рассмотрим, как это сделать. 

Ищем синус по двум катетам

Берём тот же самый треугольник АВС с прямым углом А, в котором нам известны размеры катетов: AB=a, AC=c. Чтобы вычислить синус угла С, нужно катет поделить на гипотенузу:

Но гипотенузу придётся считать по теореме Пифагора:

• BC=√(AB²+AC²)=√(a²+b²). (2)

Поставляем найденное значение гипотенузы (2) в выражение (1), получаем ответ:

Ищем синус по гипотенузе и прилегающему катету

Теперь в том же треугольнике нам нужно найти синус того же угла С, но известны при этом гипотенуза BC=b и катет AC=с. С помощью теоремы Пифагора: AB²+AC²=BC² ищем катет AB:

Теперь подставляем найденное значение АВ в формулу для синуса:

• sinC = AB/b = √(b²-c²)/b.

Вычисление синуса по одной стороне и острому углу

В треугольнике АВС с прямым углом А известен угол В=β и катет АC=c. Нужно найти синус угла С.

Способ 1.

Самое простое – если вспомнить, что сумма всех углов в треугольнике равна 180°:

• А+В+С=180°.
• Угол А=90°, В = β, значит,
• С=180°-90°- β = 90°- β.
• Отсюда sinC=sin(90°- β).

Способ 2.

Но можно пойти и другим путём:

• Sinβ=AC/BC; Sinβ =c/BC. Отсюда:
• BC= с/Sinβ.

Из теоремы Пифагора AB²+AC²=ВС&su

elhow.ru

Найдите синус угла A в треугольнике

27392. Найдите синус угла A в треугольнике АВС, угол С равен 90⁰, косинус внешнего угла при вершине А равен –7/25.

Углы ∠ВАС и  ∠ВАD и смежные. Это  значит, что ∠ВАD = 180⁰–∠ВАС.

По свойству косинуса cos BAD = cos (180⁰–∠ВАС) = – cos ВАС

Найдём sin BAC   Из основного тригонометрического тождества

Ответ: 0,96

27403. В треугольнике ABC угол C равен 90⁰, тангенс внешнего угла при вершине A равен –2. Найдите tg B.

Углы ∠ВАС и  ∠ВАD и смежные. Это  значит, что  ∠ВАD = 180⁰–∠ВАС.

По свойству косинуса tg BAD = tg (180⁰–∠ВАС) = – tg ВАС .

Значит  tg ВАС = – tg ВАD = –(–2) =2. Из свойств прямоугольного треугольника tg AВС = ctg ВАC. Известно, что tg ВАC∙ ctg ВАC = 1, значит

Ответ: 0,5

27406. В треугольнике ADC угол C равен 90⁰, косинус внешнего угла при вершине A равен –0,5; АВ=8. Найдите AC.

Углы Углы ∠ВАС и  ∠ВАD и смежные. Это значит, что ∠ВАD=180⁰–∠ВАС.

По свойству косинуса cos BAD=cos (180⁰–∠ВАС)=–cos ВАС.

Значит cos BAC=–cos ВАD=–(–0,5)=0,5…

По определению косинуса в прямоугольном треугольнике:

Значит АС=АВ∙cos BAC=8 ∙ 0,5=4.

Ответ: 4

27413. В треугольнике АВС угол С равен 90⁰, косинус внешнего угла при вершине А равен –(√17)/17, АС=0,5. Найдите BC.

Углы ∠ВАС и ∠ВАD и смежные. Это  значит, что ∠ВАD=180⁰–∠ВАС.

По свойству косинуса cos BAD = cos (180⁰–∠ВАС)=–cos ВАС.Значит

В треугольнике нам известен cos BAС и сторона,  по определению косинуса  найдём АВ:

Теперь известны АВ и АС  По теореме Пифагора:

Таким образом, ВС=2

Ответ: 2

matematikaege.ru

Как найти синус угла в треугольнике? Не в прямоугольном, в любом

Если рассматриваемый треугольник является прямоугольным, то можно использовать базовое определение тригонометрической функции синуса для острых углов. По определению синусом угла называют соотношение длины катета, лежащего напротив этого угла, к длине гипотенузы этого треугольника. То есть, если катеты имеют длину А и В, а длина гипотенузы равна С, то синус угла α, лежащего напротив катета А, определяйте по формуле α=А/С, а синус угла β, лежащего напротив катета В — по формуле β=В/С. Синус третьего угла в прямоугольном треугольнике находить нет необходимости, так как угол, лежащий напротив гипотенузы всегда равен 90°, а его синус всегда равен единице. 2 Для нахождения синусов углов в произвольном треугольнике, как это ни странно, проще использовать не теорему синусов, а теорему косинусов. Она гласит, что возведенная в квадрат длина любой стороны равна сумме квадратов длин двух других сторон без удвоенного произведения этих длин на косинус угла между ними: А²=В²+С2-2*В*С*cos(α). Из этой теоремы можно вывести формулу для нахождения косинуса: cos(α)=(В²+С²-А²)/(2*В*С) . А поскольку сумма квадратов синуса и косинуса одного и того же угла всегда равна единице, то можно вывести и формулу для нахождения синуса угла α: sin(α)=√(1-(cos(α))²)= √(1-(В²+С²-А²)²/(2*В*С) ²). 3 Воспользуйтесь для нахождения синуса угла двумя разными формулами расчета площади треугольника, в одной из которых задействованы только длины его сторон, а в другой — длины двух сторон и синус угла между ними. Так как результаты их будут равны, то из тождества можно выразить синус угла. Формула нахождения площади через длины сторон (формула Герона) выглядит так: S=¼*√((А+В+С) *(В+С-А) *(А+С-В) *(А+В-С)) . А вторую формулу можно написать так: S=А*В*sin(γ). Подставьте первую формулу во вторую и составьте формулу для синуса угла, лежащего напротив стороны С: sin(γ)= ¼*√((А+В+С) *(В+С-А) *(А+С-В) *(А+В-С) /(А*В)) . Синусы двух других углов можно найти по аналогичным формулам.

touch.otvet.mail.ru

Ребят, как найти cos и sin в прямоугольном треугольнике…

Своими словами: В прямоугольном треугольнике есть прямой угол. Две стороны, которые образуют этот прямой угол назвали катетами. Третью сторону назвали гипотенузой. В прямоугольном треугольнике кроме прямого угла есть еще два угла, они острые. Если взять длину катета, который находится напротив острого угла треугольника (назовем этот угол А) и разделить ее на длину гипотенузы — то вот это отношение назвали синусом угла А sinA = противолежащий углу А катет / гипотенуза А косинусом назвали отношение прилежащего к этому углу катета к гипотенузе. cosA= катет, прилежащий к углу А / гипотенуза. Если ты знаешь длины сторон прямоугольного треугольника, ты можешь найти эти отношения, разделить тот или другой катет на гипотенузу. Это и будет sin или cos. Назвали их так, для краткости. Чтобы не говорить длинное предложение : отношение прилежащего к углу А катета к гипотенузе…. Короче ведь сказать или написать —cosA Всё! Свои слова кончились 🙂

Косинус и синус это числа, которые получаются, если разделить одну сторону треугольника на его самую большую сторону. В прямоугольном треугольнике она находиться напротив угла 90

Своими словами — это в любви объясняться. а в определении понятий таких важных нужны строгость и четкость. для каждого острого угла один из катетов является ПРОТИВОлежащим. другой-ПРИлежащим. отношение ПРО к Гипотенузе это синус отношение ПРИ к гипот. это косинус того же угла отношение ПРО к ПРИ — это ТАНГЕНС. тангенс определяется еще как отношение синуса к косинусу. смотри таблицу и возьми на вооружение — сокращения ПРО и ПРИ. <img src=»//otvet.imgsmail.ru/download/94b45cf5e57c5b1baffcbe79a9b5efe6_i-87.jpg» >

touch.otvet.mail.ru