Площади геометрических фигур. 8-й класс
- Потёмкина Наталья Борисовна, учитель
Разделы: Математика, Конкурс «Презентация к уроку»
Класс: 8
Презентация к уроку
Загрузить презентацию (2 МБ)
Цели: закреплять навыки в решении задач по теме “Площади” и готовиться к ОГЭ.
Задачи:
Образовательные:
- обобщить знания и умения учащихся по теме “Площадь”.
Развивающие:
- формировать умения ясно и четко излагать свои мысли;
- формировать навыки публичного выступления и
умения отстаивать самостоятельное суждение.
Воспитательные:
- создавать условия для реальной самооценки учащихся, реализации его как личности;
- воспитывать познавательный интерес к предмету;
- воспитывать эстетический вкус.
Оборудование: компьютер, проектор, экран, раздаточный материал.
План урока:
- Организационный. Постановка цели урока.
- Повторение. Устная работа.
- Решение задач.
- Заключительная часть. Подведение итогов урока.
- Домашнее задание.
Ход урока
I. Организационный. Постановка цели урока
Мы заканчиваем изучение темы: “ Площади”. Сегодня на уроке мы вспомним, как вычисляются площади различных фигур. Решим задачи, опираясь на наши знания по этой теме.
II. Устная работа
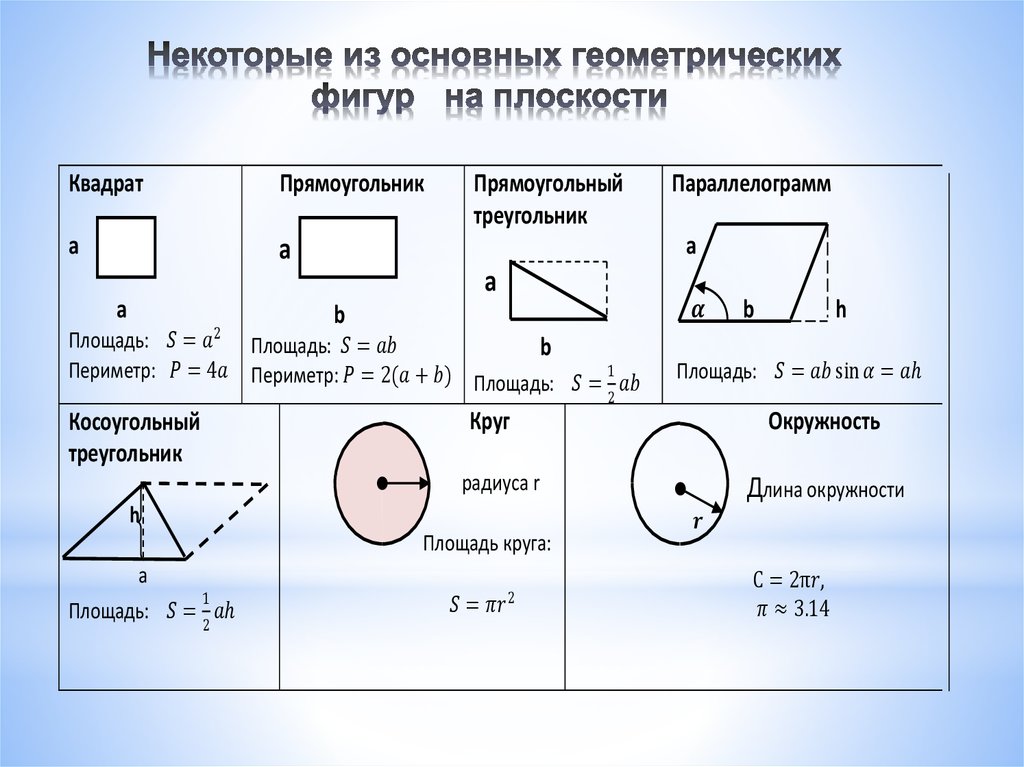
На доске подготовлена таблица.
| № | фигура | формулы |
| 1 | квадрат | |
| 2 | прямоугольник | |
| 3 | параллелограмм | |
| 4 | ромб | |
| 5 | треугольник | |
| 6 | трапеция |
По окончании устно работы таблица имеет такой
вид.
| № | фигура | формулы |
| 1 | квадрат | |
| 2 | прямоугольник | |
| 3 | параллелограмм |
|
| 4 | ромб | |
| 5 | треугольник |
|
| 6 | трапеция |
Для проведения устной работы используется
презентация
Приложение слайд 1
Задача 1. Используя слайды, учащиеся должны выбрать формулу для вычисления площади изображенной фигуры и обосновать свой ответ.
Пример.
Фигура ABCD – квадрат, т.к. на чертеже показано, что у данного четырёхугольника все стороны равны и все углы по 90°. Значит, для вычисления площади воспользуемся формулой под номером.
Слайд 1 включает в себя 4 задачи подобного
типа, решение которых позволяет не только ещё раз
вспомнить формулы, но и III.
Сейчас мы с вами будем решать задачи, которые в
экзаменационных работах стоят в блоке
“Геометрия” № 11. Предлагаю вам разделиться на
группы. На экране будут появляться задачи, та
группа, которая первая найдет решение, отвечает у
доски, остальные помогают.
За каждый правильный
полный ответ группа получает 5 баллов. За не
достаточные обоснования снимается 1 балл и
передается той группе, которая сможет дополнить.
Для решения задач используется презентация.
Приложение слайд 2 – 9
На каждом слайде есть кнопка “Подсказка” с указанием количества подсказок. Ей имеет смысл воспользоваться, если возникают затруднения с решением задач.
IV. Заключительный этап.
Подведение итогов
Домашняя работа
1. Задание 11 № 195. Найдите площадь параллелограмма, изображённого на рисунке.2. Задание 11 № 333013. Основания трапеции равны 1 и 11. Найдите бoльший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.
3. Задание 11 № 323902. Основания
равнобедренной трапеции равны 5 и 17, а ее боковые
стороны равны 10. Найдите площадь трапеции.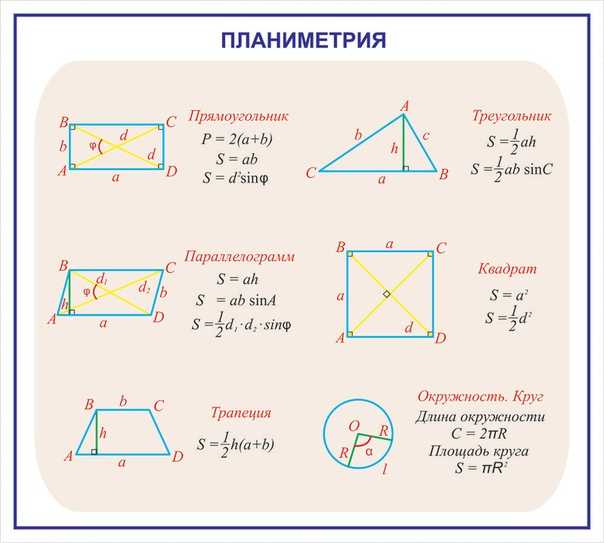
Ресурсы Интернет.
- http://100formul.ru
- http://sdamgia.ru/
Площадь фигуры | это… Что такое Площадь фигуры?
У этого термина существуют и другие значения, см. Площадь (значения).
Пло́щадь плоской фигуры — аддитивная числовая характеристика фигуры, целиком принадлежащей одной плоскости. В простейшем случае, когда фигуру можно разбить на конечное множество единичных квадратов, площадь равна числу квадратов.
Содержание
|
Об определении
Формальное введение понятия площадь и объём можно найти в статье мера Жордана, здесь мы приводим лишь намётки определения с комментариями.
Площадь — это вещественнозначная функция, определённая на определённом классе фигур евклидовой плоскости, такая что:
- (положительность) площадь неотрицательна;
- (нормировка) квадрат со стороной единица имеет площадь 1;
- конгруэнтные фигуры имеют равную площадь;
- (аддитивность) площадь объединения двух фигур без общих внутренних точек равна сумме площадей.
Определённый класс должен быть замкнут относительно пересечения и объединения, а также относительно движений плоскости и включать в себя все многоугольники. Из этих аксиом следует монотонность площади, то есть
- Если одна фигура принадлежит другой фигуре, то площадь первой не превосходит площади второй:
Чаще всего за «определённый класс» берут множество квадрируемых фигур. Фигура называется квадрируемой, если для любого существует пара многоугольников и , такие что и , где обозначает площадь .
Связанные определения
- Две фигуры называются равновеликими, если они имеют равную площадь.
Комментарии
На самом деле, есть довольно неестественный и неоднозначный способ определить площадь для всех ограниченных подмножеств плоскости. На множестве всех ограниченных подмножеств плоскости существуют различные функции площади, т. е. не равные функции, удовлетворяющие вышеприведённым аксиомам, а множество квадрируемых фигур является максимальным множеством фигур, на которых функционал площади определяется однозначно.
То же самое можно сделать для длины на прямой, но нельзя для объёма в евклидовом пространстве и также нельзя для площади на единичной сфере в евклидовом пространстве, (смотри соответственно парадокс Банаха — Тарского и парадокс Хаусдорфа).
Площади некоторых фигур
Формулы для нахождения площадей различных фигур
| Фигура | Формула | Комментарий |
|---|---|---|
| Правильный треугольник | — длина стороны треугольника. | |
| Треугольник | Формула Герона.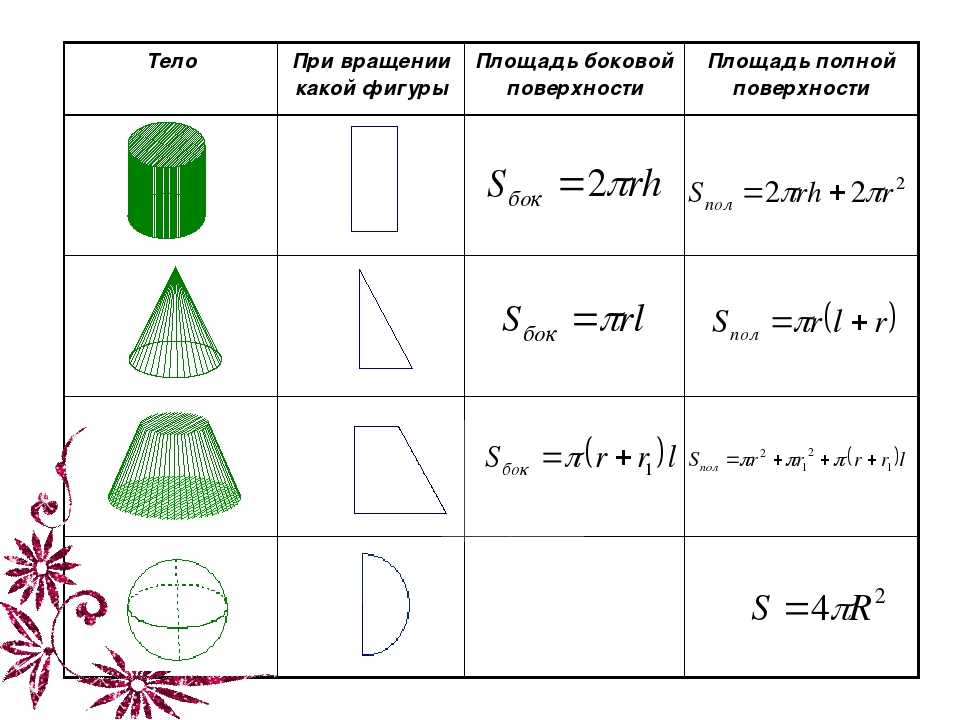 — полупериметр, , и — длины сторон треугольника. | |
| Треугольник | и — две стороны треугольника, а — угол между ними. | |
| Треугольник | и — сторона треугольника и высота, проведённая к этой стороне. | |
| Квадрат | — длина стороны квадрата. | |
| Прямоугольник | и — длины сторон прямоугольника. | |
| Ромб | и — длины диагоналей ромба. | |
| Параллелограмм | — длина одной из сторон параллелограмма, а — высота, проведённая к этой стороне. | |
| Трапеция | и — длины параллельных сторон, а — расстояние между ними (высота). | |
| Правильный шестиугольник | — длина стороны шестиугольника. | |
| Правильный восьмиугольник | — длина стороны восьмиугольника. | |
| Правильный многоугольник | — длина стороны многоугольника, а — количество сторон многоугольника. | |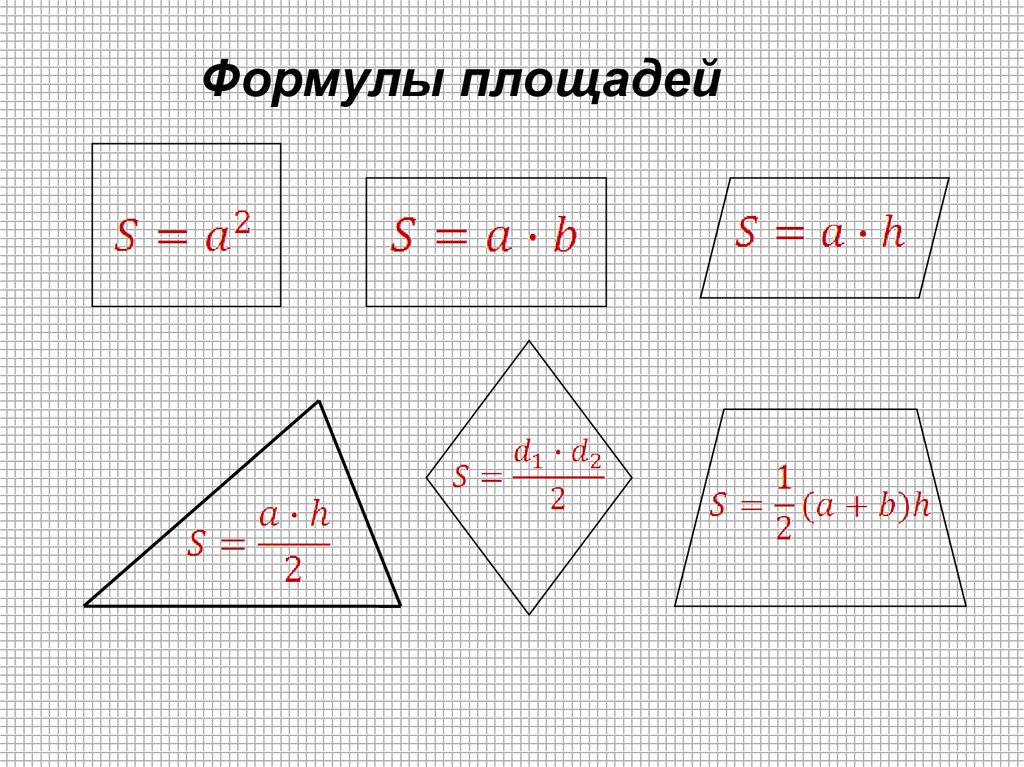
| — апофема (или радиус вписанной в многоугольник окружности), а — периметр многоугольника. | ||
| Круг | или | — радиус окружности, а — её диаметр. |
| Сектор круга | и — соответственно радиус и угол сектора (в радианах). | |
| Эллипс | и — большая и малая полуоси эллипса. | |
| Поверхность Цилиндра | и — радиус и высота цилиндра соответственно. | |
| Боковая поверхность цилиндра | и — радиус и высота цилиндра соответственно. | |
| Поверхность конуса | и — радиус и длина образующей соответственно. | |
| Боковая поверхность конуса | и — радиус и длина образующей соответственно. | |
| Поверхность сферы | и — радиус и диаметр соответственно. | |
| Поверхность эллипсоида | См. статью. |
- Площадь треугольника равна половине произведения стороны на высоту, проведенную к этой стороне:
- Площадь прямоугольника равна произведению его смежных сторон:
- Площадь произвольного четырехугольника ABCD равна половине произведения диагоналей и синуса угла между ними:
- ,
- где — угол между диагоналями.
- Площадь ромба ABCD равна половине произведения диагоналей:
- Площадь параллелограмма равна произведению стороны на высоту, проведенную к этой стороне:
- Площадь трапеции равна произведению полусуммы оснований на высоту:
См. также
- Площадь
- Мера Бореля
- Мера Жордана
- Мера Лебега
- Ориентированная площадь
- Площадь поверхности
- Теорема Бойяи — Гервина о равносоставленности равновеликих многоугольников
- Исчезновение клетки
Ссылки
- В.Болтянский, О понятиях площади и объёма. Квант, № 5, 1977
- Б. П. Гейдман, Площади многоугольников, Библиотека «Математическое просвещение», выпуск 16, (2002).
- В. А. Рохлин, Площадь и объём, Энциклопедия элементарной математики, Книга 5, Геометрия, под редакцией П. С. Александрова, А. И. Маркушевича и А. Я. Хинчина.
геометрия — Среди всех фигур с одинаковой площадью круг имеет самый короткий периметр
Это верно и классически, и не так тривиально, как можно было бы подумать.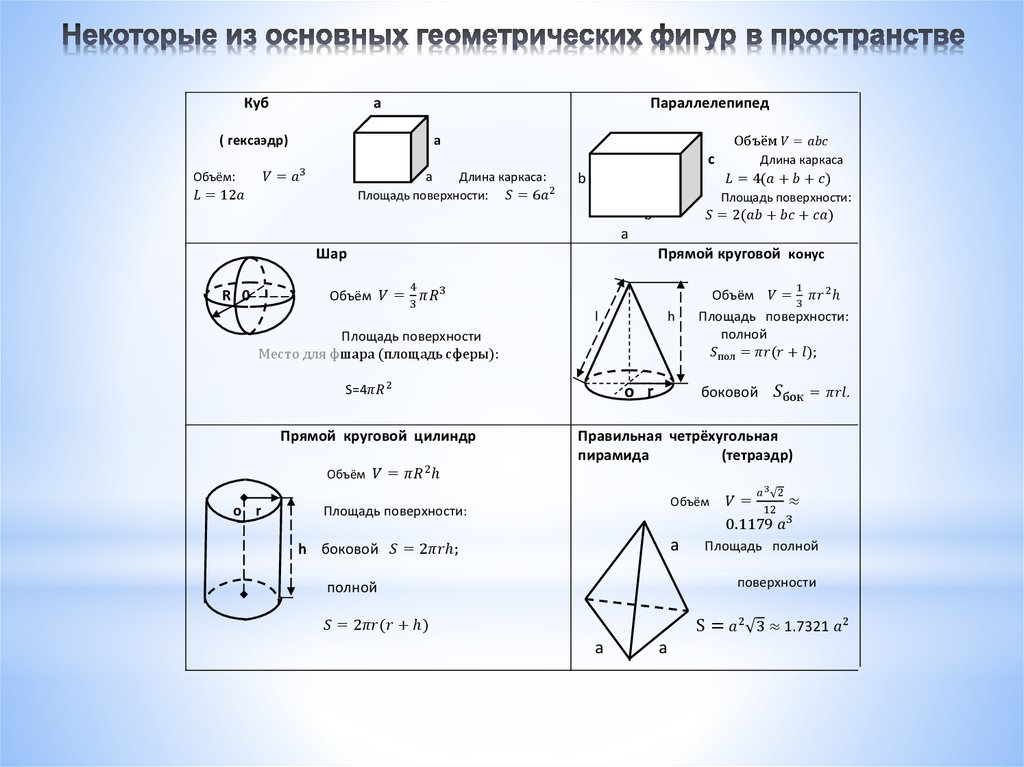
Это также работает в более высоких измерениях.
Для реального спора — посмотрите, какую форму принимают капли воды! Или еще более убедительно: посмотрите на мыльные пузыри (спасибо fgp за этот пример).
Чтобы понять, почему это должно быть верно математически, попробуйте следующее рассуждение:
Пусть $F$ будет фигурой с кратчайшим периметром среди фигур с заданной площадью. Попробуйте разрезать фигуру $F$ линией $l$ так, чтобы обе части имели одинаковую площадь. Назовите эти части $F_1$ и $F_2$.
Поучительное наблюдение состоит в том, что теперь вы можете построить другую фигуру $F’$ той же площади, что и $F$. Это достигается заменой $F_2$ отражением $F_1$ относительно $l$; т. е. возьмем $F’ := F_1 \cup R_l(F_1)$, где $R_l$ — отражение относительно $l$. Конечно, можно взять и $F» := F_2 \cup R_l(F_2)$. Поскольку площади $\operatorname{Area}(F_1)$ и $\operatorname{Area}(F_2)$ равны (и имеют значение $\frac{1}{2} \operatorname{Area}(F)$) , новые фигуры имеют области $\operatorname{Area}(F’) = \operatorname{Area}(F») = \operatorname{Area}(F) $.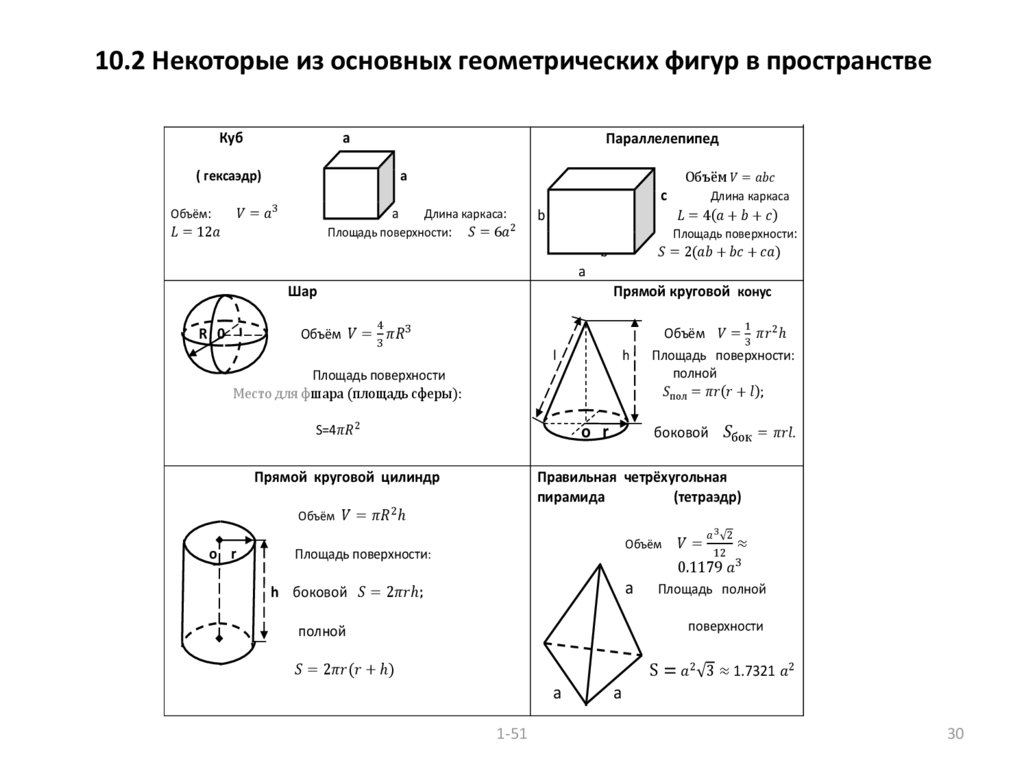
Аналогично имеем $\operatorname{Периметр}(F’) = 2 \operatorname{Периметр}(F_1)$ (здесь не учитывается часть периметра, лежащая на $l$), $\operatorname{Периметр }(F») = 2 \operatorname{Периметр}(F_2)$ и, конечно же:
$$\operatorname{Периметр}(F) = \operatorname{Периметр}(F_1) + \operatorname{Периметр}(F_2) = \frac{\operatorname{Периметр}(F’) + \operatorname{Периметр}(F’ ‘)}{2} $$
Если бы $F_1$ и $F_2$ имели разные периметры, то один из $F’$, $F»$ имел бы меньший периметр, чем $F$, и ту же площадь. Но мы предположили, что $F$ оптимальна, поэтому $\operatorname{Perimeter}(F_1) = 2 \operatorname{Perimeter}(F_2)$.
Давайте продвинем эту идею немного дальше. Обратите внимание, что $F’$ и $F»$ теперь снова оптимальны в том смысле, что они имеют ту же площадь, что и $F$. Это означает, что они должны быть выпуклыми (если фигура не выпуклая, то можно сделать «срез» на ее вогнутости, сделав периметр короче, а площадь больше; но от лишней площади легко избавиться, не увеличивая периметр , например, путем масштабирования).
Это означает, среди прочего, что прямые, перпендикулярные $l$, проходящие через точки пересечения с $F$, касаются $F$ (поэтому, если $F$ имеет четко определенную касательную в этих точках, касательная перпендикулярна $ л$). Это еще не показывает, что $F$ должен быть кругом, но мы видим, что $F$ имеет много симметрии, которая, кажется, есть только у круга.
Немного поработав, мы почти подошли бы к решению. Заметим, что вместо работы с $F$ можно работать с $F’$, т.е. можно считать, что фигура симметрична относительно $l$. Но это эквивалентно простому рассмотрению $F_1$. Обозначим две точки пересечения $l$ с $F$ через $A,B$ и пусть $C$ — точка на границе $F_1$. Прямые $AB,BC,CA$ делят $F_1$ на три области: треугольник $ABC$ и две неправильные фигуры, касающиеся прямых $AC$ и $BC$. Теперь мы можем сделать две вещи. Идея от Разрубить узел означает преобразовать $ABC$, изменив длину $AB$. Поскольку $\operatorname{Area}(ABC) = \frac{1}{2} |AC| \cdot |CB| \cdot \sin \angle C$, можно считать, что $\angle C = \pi/2$.
Другая возможность состоит в том, чтобы отразить площадь, прилегающую к $AC$, и сделать вывод, что касательная к $F$ в точке $C$ пересекает $AC$ под тем же углом, что и касательная в точке $A$ пересекает $AC$. Делая то же самое для $BC$, считая углы, снова приходим к выводу, что $\angle C = \pi/2$. Но $\angle C = \pi/2$ означает, что $C$ лежит на полуокружности, основанной на $F_1$. Итак, $F_1$ — это полукруг, и мы закончили!
Конечно, в предположении, что лучшая фигура существует, есть некоторый обман. Также в нескольких шагах я предположил наличие касательных. Это можно объяснить, но я не уверен, что это представляет интерес здесь.
Для подробного обсуждения это кажется уместным: разрубите узел (что я сильно использовал здесь, но большинство идей — математический фольклор).
Область простых фигур | Мир математики Пасси
Источник изображения: http://rackcdn.com
Периметр — это расстояние вокруг внешней стороны объекта, а площадь — это количество пространства внутри двумерного плоского объекта.
В этом посте мы рассмотрим площади геометрических фигур. Однако мы не рассматриваем составные области или круги, так как они будут рассмотрены в других статьях.
Области важны для геодезистов, градостроителей и советов.
Источник изображения: http://clcreport.files.wordpress.com
Авиационные инженеры определяют площади крыльев самолетов при исследовании аэродинамических свойств и конструкций.
Источник изображения: http://www.grc.nasa.gov
Площадь также очень важна для строителей при расчете стоимости материалов.
Источник изображения: http://www.ebricksolutions.com
Люди, работающие с осветительными и медиа-проекторами, должны понимать математику, связанную с дисперсией и интенсивностью света.
Источник изображения: http://www.sciencebuddies.org
Теперь, когда мы знаем, насколько важна площадь в нашей повседневной жизни, давайте рассмотрим математику вычисления площадей.
Вот отличное музыкальное видео, чтобы посмотреть все о Периметре и площади.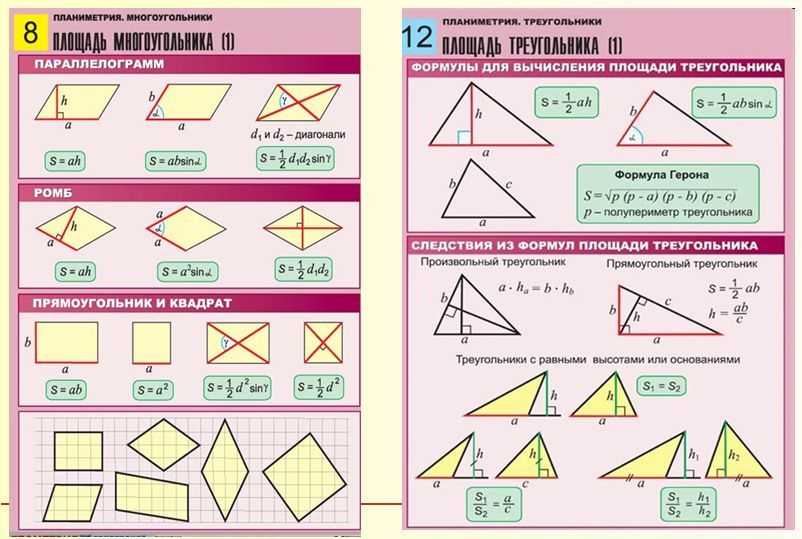
[youtube http://www.youtube.com/watch?v=D5jTP-q9TgI]
Различные формы имеют разные формулы площади.
Площадь прямоугольника
Очень простой фигурой является «Прямоугольник».
Прямоугольник имеет площадь основания x высоту, что иногда называют длиной x шириной или длиной x высотой.
Источник изображения: http://www.k6-geometric-shapes.com
Мы можем доказать эту формулу, нарисовав целую кучу прямоугольников и подсчитав, сколько квадратов находится внутри них.
Источник изображения: http://www.geom.uiuc.edu
Однако не все формы так просты, как прямоугольник. Если мы сдвинем прямоугольник в сторону, мы получим параллелограмм.
Площадь параллелограмма
Площадь параллелограмма равна площади = основание x высота
Вот видео о площади параллелограмма.
[youtube http://www.youtube.com/watch?v=dLZd1MD9kaw]
Как вам такой параллелограмм в реальной жизни!
Источник изображения: http://www.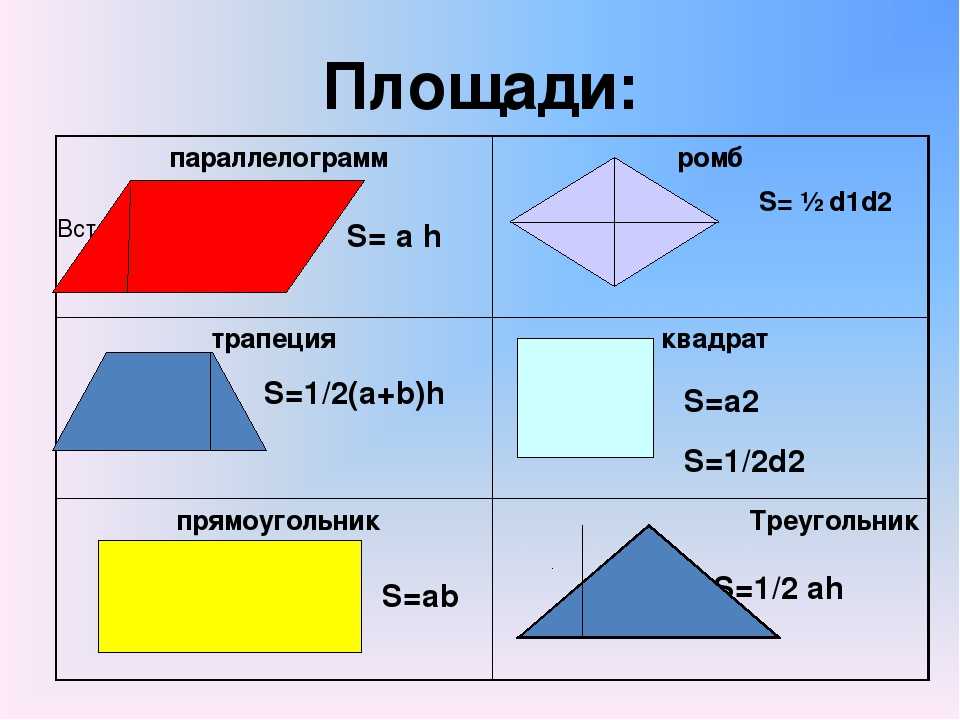
elec-intro.com
Площадь треугольника
Мы могли бы вычислить площадь треугольника, нарисовав его в масштабе на сетке и подсчитав квадраты.
Источник изображения: http://www.geom.uiuc.edu
Но гораздо проще измерить основание и высоту треугольника и использовать математическую формулу для вычисления площади.
Эту формулу очень легко вычислить, потому что треугольник — это половина параллелограмма.
Площадь любого параллелограмма равна площади = основание x высота.
Итак, площадь любого треугольника: Площадь = 1/2 x основание x высота.
Вот видео, объясняющее, как это работает.
[youtube http://www.youtube.com/watch?v=2avSR3Izbss]
Вот пример того, как мы вычисляем площадь треугольника.
Источник изображения: http://www.loisterms.com
Обратите внимание, что в приведенном выше примере использовались этапы разработки «FISC».
Формула
Информационная диаграмма
Подстановка значений в формулу
Вычислите окончательный ответ и убедитесь, что в нем есть квадратные единицы.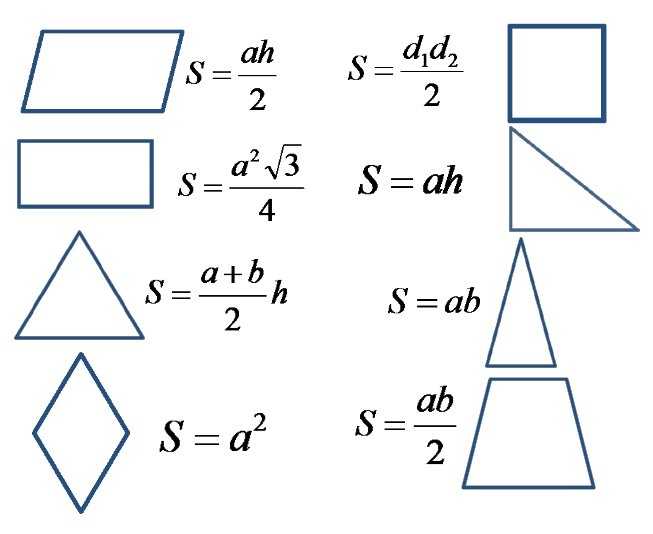
Например. кв см, кв дюйм, кв км и так далее.
Крайне важно всегда показывать эти шаги при расчете площади любой формы.
Площадь трапеции (или трапеции).
Эта фигура немного похожа на параллелограмм, за исключением того, что у нее только две параллельные стороны.
Австралийцы называют его «трапецией», а американцы — «трапецией».
Источник изображения: http://www.mathwarehouse.com
Вот небольшой видеоролик, который поможет запомнить, как вычислять площадь трапеции.
[youtube http://www.youtube.com/watch?v=qlxawNewXiY]
Площадь ромба
Ромб — это параллелограмм, у которого все четыре стороны равны. Мы можем вычислить его площадь, используя основание x высоту, но мы также можем вычислить ту же площадь, перемножив две внутренние диагонали вместе и разделив на 2.
Источник изображения: http://www.thefreemathtutor.com
Ответы на вопросы по ромбу:
Q1. 418 кв.см, 41600 кв.мм, 0,0006 кв.м.
Q2.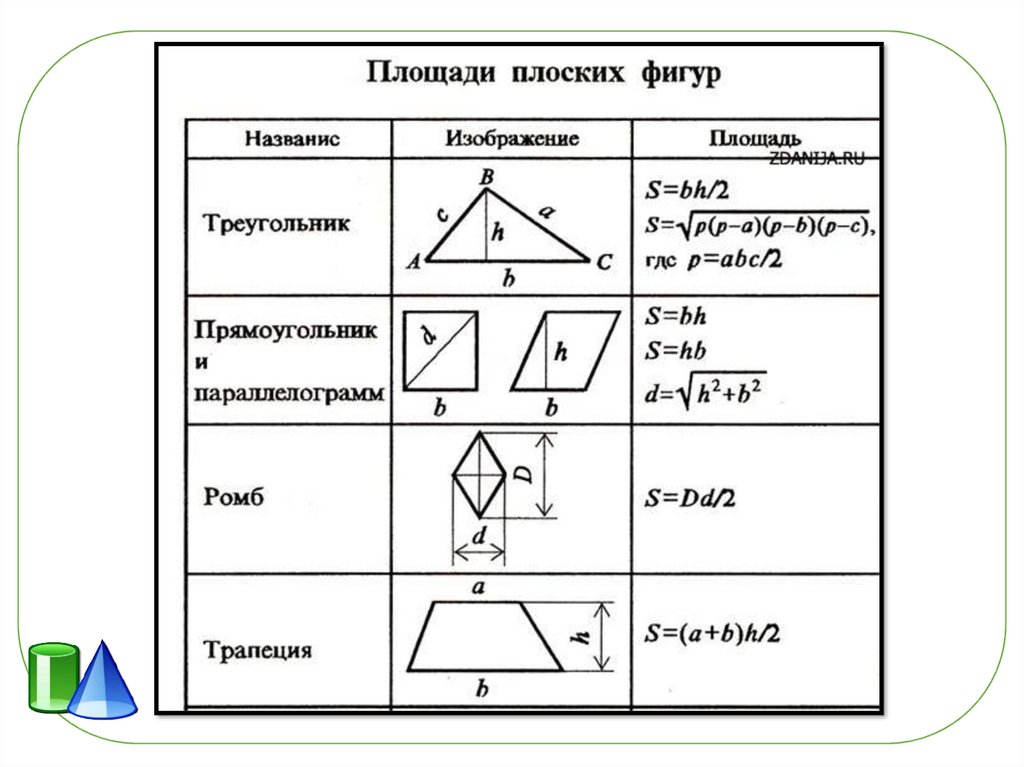
91 кв см
Q3. (1000×2) / 10 = 200 мм.
Q4. (120×2)/30=8м.
Площадь воздушного змея
Воздушный змей имеет форму, аналогичную ромбу, и его площадь получается путем перемножения его диагоналей.
Источник изображения: http://www.coolmath.com
Краткое изложение формул площади
Вот набор формул, которые используются в математике для нахождения площадей.
Источник изображения: http://www.math-videos-online.com
Источник изображения: http://www.grc.nasa.gov
Онлайн-мероприятия
Вот онлайн-обучение, посвященное периметру и площади
http://www.bgfl.org/bgfl/custom/resources_ftp/client_ftp/ks2/maths/perimeter_and_area/index.html
Вот задание по площадям прямоугольников, треугольников и параллелограммов.
(Для загрузки требуется некоторое время).
Нажмите на вопросительный знак, чтобы ввести свой ответ, затем нажмите «ОК», чтобы проверить свой ответ.
http://www.bbc.co.uk/schools/ks3bitesize/maths/measures/area/activity.shtml
Онлайн-игры с площадью и периметром
Сыграйте в эту забавную игру, в которой мы используем базовые навыки площади и периметра для проектирования вольеров зоопарка для экспонатов животных:
http://www.mrnussbaum.com/zoo/index.html
Сыграйте в эту интересную игру, чтобы найти взаимосвязь между периметром и площадью.
http://pbskids.org/cyberchase/games/perimeterarea/index.html
Получайте удовольствие от изучения областей неправильной формы в этой игре Tangrams.
http://pbskids.org/cyberchase/games/area/index.html
Сложная игра «Площадь и периметр»
Нужно попасть прямо по углам начальных символов, получить руку символ, а затем перетащите элементы по сетке, чтобы они соответствовали заданным правилам периметра и площади.
Обратите внимание, что конечные области элементов не могут перекрываться.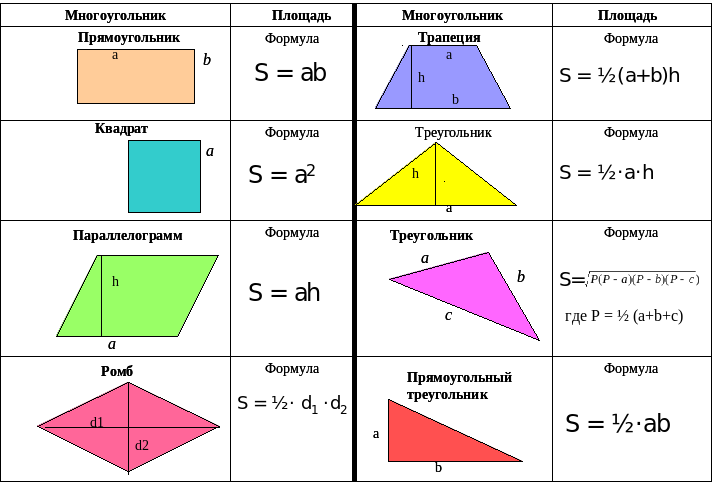
Тем не менее, может возникнуть необходимость сделать некоторое перекрытие при создании фигур.
http://www.mathplayground.com/PartyDesigner/PartyDesigner.html
Проверь себя онлайн
Щелкните ссылку ниже, чтобы перейти к онлайн-уроку по площади треугольников, и прокрутите страницу вниз, чтобы выполнить онлайн-тест из пяти вопросов. .
http://www.mathgoodies.com/lessons/vol1/area_triangle.html
Нажмите на ссылку ниже, чтобы перейти к онлайн-уроку по площади параллелограммов и онлайн-тесту из пяти вопросов.
http://www.mathgoodies.com/lessons/vol1/area_parallelogram.html
Нажмите на ссылку ниже, чтобы перейти к онлайн-уроку по площади трапеций и онлайн-тесту из пяти вопросов.
http://www.mathgoodies.com/lessons/vol1/area_trapezoid.html
Вот онлайн-викторина по площадям прямоугольников и параллелограммов, которая включает в себя нахождение неизвестных сторон, если площадь известна.
http://au.ixl.com/math/year-7/area-of-rectangles-and-parallelograms
Попробуйте эти смешанные практические вопросы по периметру и площади.
http://www.mathgoodies.com/lessons/vol1/practice_unit1.html
Вот последний набор смешанных задач.
http://www.bbc.co.uk/scotland/learning/bitesize/standard/maths_i/measure/quiz/area_general/
Надеюсь, это охватило все области!
Связанные элементы
Периметр
Окружность
Площадь круга
Интересные круги
Составные площади
Формулы измерения
Высокие здания и огромная плотина
Мой виртуальный дом
Если вам понравился этот пост, почему бы не получить бесплатную подписку на наш Веб-сайт.
После этого вы сможете получать уведомления о новых страницах прямо на свой адрес электронной почты.
Просто найдите область подписки на правой боковой панели, введите свой адрес электронной почты и нажмите кнопку «Подписаться».
Чтобы точно узнать, как работает бесплатная подписка, нажмите на следующую ссылку:
Как работает бесплатная подписка
Enjoy,
Passy
Эта запись была размещена в разделе Площадь, Площадь простых фигур, Измерение, Онлайн-уроки математики, Периметр.