Практика. Решение задач 8 класс онлайн-подготовка на Ростелеком Лицей
Центральный и вписанный углы
Вспомним определение и свойства центрального и вписанного углов (см. рис. 1): центральный угол – это угол, вершина которого совпадает с центром окружности; вписанный угол – это угол, вершина которого принадлежит окружности.
Рис. 1. Центральный угол и вписанный угол
При этомвписанный угол равен половине градусной меры дуги окружности, на которую он опирается, а центральный угол равен этой дуге:
Одним из следствий является то, что два вписанных угла, опирающихся на одну дугу (или одну хорду), равны друг другу (см. рис. 2).
Рис. 2. Вписанные углы , опирающиеся на одну дугу
Угол, вершина которого лежит внутри окружности
А как обстоит дело с остальными углами, опирающимися на дугу, но вершина которых не лежит ни на окружности, ни в ее центре?
Понятно, что в этом случае вершина лежит либо внутри окружности (см.
рис. 3), либо снаружи (см. рис. 4).
Рис. 3. Вершина угла лежит внутри окружности
Рис. 4. Вершина угла лежит вне окружности
Рассмотрим случай, когда вершина лежит внутри окружности. Угол опирается на дугу (см. рис. 5).
Рис. 5. Угол опирается на дугу
Интуитивно понятно, что угол больше вписанного, опирающегося на ту же самую дугу. Продлим стороны угла и до пересечения с окружностью (см. рис. 6) и попробуем выразить сам угол через величины дуг, на которые разбита окружность.
Рис. 6. Стороны угла и продлили до пересечения с окружностью
Наш угол является внешним для треугольника . А раз так, то он равен сумме двух внутренних углов, не смежных с ним (см. рис. 7):
Рис. 7. Угол , являющийся внешним для треугольника , равен сумме двух внутренних углов, не смежных с ним
Но углы и уже являются вписанными, а значит, каждый из них равен половине дуги, на которую опирается:
Уберем лишнее с рисунка (см.
рис. 8).
Рис. 8. Угол равен полусумме дуг и
Итак: если через точку внутри окружности проведены две секущие, то угол между ними равен полусумме дуг, на которые опираются сам угол и ему вертикальный.
Легко проверить, что это выполняется и для центрального, и для вписанного углов (как для предельных случаев). Т. е. мы обобщили теорему о центральном и вписанном угле (как раньше обобщили теорему Пифагора теоремой косинусов).
Второй случай, когда вершина угла лежит вне окружности, а стороны угла пересекают эту окружность. Попробуйте самостоятельно изобразить этот случай и выразить величину угла через дуги, на которые окружность поделилась сторонами угла. А решение можно посмотреть ниже.
Угол, вершина которого лежит вне окружности
Итак, постановка задачи: через точку, лежащую вне окружности, проходят две секущие (см. рис. 9). Выразить величину угла через полученные дуги окружности.
Рис. 9. Через точку, лежащую вне окружности, проходят две секущие
Посмотрим на две дуги, которые лежат внутри угла : дуги и .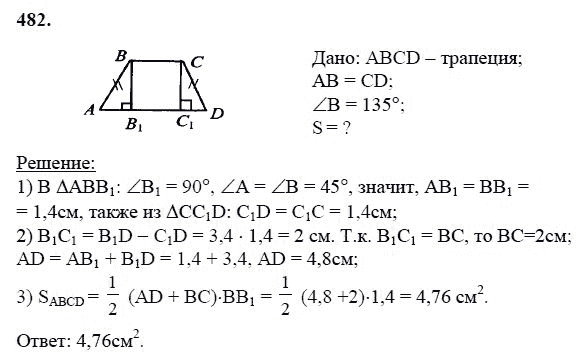
Мы знаем, как выразить через дуги вписанные углы, которые на них опираются. Поэтому попробуем выразить угол через вписанные углы. Для этого соединим точки и . Получим два вписанных угла и (см. рис. 10).
Рис. 10. Соединили точки и , получили два вписанных угла и
Угол опирается на дугу , угол опирается на дугу . Эти углы равны половине соответствующих дуг. И при этом исследуемый угол выражается через эти два угла.
В самом деле, угол является внешним для треугольника , значит:
Тогда:
Вспомним теперь, что эти углы равны половинам своих дуг:
Таким образом, угол равен полуразности дуг, заключенных внутри угла.
Свойство вписанного четырехугольника
При изучении новых объектов мы обычно формулируем два типа утверждений: свойства (то, что мы всегда можем сказать об этом объекте) и признаки (благодаря чему мы можем узнать именно этот объект).
Например: у каждой лошади есть голова.
Это свойство лошадей или их необходимый признак. Но назвать признаком наличие головы нельзя: она есть у людей, у собак и т. д.
Умение читать книги – достаточный признак человека (если кто-то умеет читать, то это точно человек). Если признак работает в обе стороны, то он так и называется – необходимым и достаточным. Молния – необходимый и достаточный признак грозы (если гроза, то обязательно есть молния, но если видим молнию, значит, точно гроза).
Итак, ранее мы убедились, что, в отличие от треугольников, далеко не все четырехугольники можно вписать в окружность (и, соответственно, любой четырехугольник можно вписать в окружность). Например, квадрат можно вписать в окружность, а ромб, не являющийся квадратом, нельзя.
Оказалось, что можно сформулировать признаки вписанного и описанного четырехугольников (т. е. то свойство, которым обладают только такие четырехугольники и не обладают остальные).
Свойство вписанного четырехугольника: если четырехугольник вписан в окружность, то суммы противоположных углов в нем равны (см.
рис. 11).
Рис. 11. Если четырехугольник вписан в окружность, то суммы противоположных углов в нем равны
Признак вписанного четырехугольника
Доказать это свойство оказалось несложно (Окружность и многоугольники). Но оно не поможет нам, если мы не докажем, что у любого другого не вписанного четырехугольника суммы противоположных углов не равны . Вспомните пример с лошадью: отсутствие головы точно говорит нам, что данный объект не лошадь, но вот ее наличие еще ничего не говорит.
Итак, в свое время мы доказали свойство, а обратное утверждение приняли на веру. Сейчас у нас есть все инструменты, чтобы вернуться и доказать признак вписанного четырехугольника.
Теорема
Если в четырехугольнике сумма противоположных углов равна , то он вписанный (вокруг него можно описать окружность).
Доказательство
Рассмотрим четырехугольник , у которого углы и в сумме равны (см. рис. 12).
Рис.
12. Четырехугольник , где сумма углов и равна
Вокруг любого треугольника можно описать окружность. Опишем ее вокруг треугольника (см. рис. 13) и докажем, что она пройдет обязательно и через точку .
Рис. 13. Вокруг треугольника описана окружность
Будем доказывать методом от противного. Предположим, что окружность не проходит через точку . Тогда точка может оказаться внутри или вне окружности.
Рассмотрим случай, когда она находится внутри (см. рис. 13).
Рис. 13. Точка находится внутри окружности
Продлим стороны до пересечения с окружностью:
Но тогда он больше, чем просто половина дуги :
При этом угол вписанный и равен половине дуги, на которую опирается:
Если к обеим частям неравенства прибавить равные выражения, то получим эквивалентное неравенство:
Таким образом:
Но это противоречит условию. Таким образом, точка не может лежать внутри окружности.
Самостоятельно рассмотрите случай, когда точка лежит вне окружности, и докажите, что это невозможно.
Там рассуждения совершенно аналогичны (изменится только знак неравенства).
Доказано.
Итак, равенство суммы противоположных углов является теперь необходимым и достаточным признаком вписанного четырехугольника.
Нахождение значений тригонометрических функций
Мы с вами успели убедиться, что тригонометрические функции очень удобный инструмент для решения геометрических задач. Во многом это связано с тем, что значение тригонометрической функции зависит только от величины угла и не зависит от типа треугольника.
В произвольном треугольнике есть три угла и для каждого угла можно посчитать значение синуса, косинуса, тангенса и котангенса (или указать, что тангенс не определен – для прямого угла).
Мы нашли значения тригонометрических функций для некоторых углов. Обычно их сводят в такую таблицу (см. рис. 15).
Рис. 15. Таблица значений основных тригонометрических функций
Запоминать ее не обязательно (хотя при решении большого количества задач вы это сделаете непроизвольно), лучше помнить, как можно их получить (Тригонометрические функции произвольных углов.
Теоремы синусов и косинусов).
Значения разных тригонометрических функций для одного угла связаны между собой основными тригонометрическими тождествами:
Зная значение одной тригонометрической функции угла, можно найти все остальные.
Задача 1. Найти неизвестные тригонометрические функции угла, если:
Решение
Можно, конечно, найти угол, зная, что угол лежит в интервале от до , а его косинус равен (см. рис. 16).
Рис. 16. Иллюстрация к задаче 1
Зная определение тригонометрической функции (косинус – абсцисса соответствующей точки на окружности) (см. рис. 17), несложно получить, что:
Т. е. .
Рис. 17. Иллюстрация к задаче 1
Но мы рассмотрим общий способ, ведь нам не обязательно «повезет» с табличным значением тригонометрической функции.
Чтобы найти синус, зная, косинус, воспользуемся тождеством, которое их связывает, а именно:
Выразим из него синус:
Мы получили два возможных значения синуса.
Как быть? Если бы у нас не было больше никакой информации об угле, то на этом нам бы пришлось остановиться. Действительно, при данном значении косинуса у синуса может быть два значения (вертикальная прямая пересекает окружность в двух точках с противоположными ординатами) (см. рис. 18).
Рис. 18. Иллюстрация к задаче 1
Но у нас есть дополнительная информация: угол лежит в четвертой четверти (см. рис. 19).
Рис. 19. Иллюстрация к задаче 1
В этой четверти у всех точек окружности ордината отрицательная, значит, синус будет иметь знак «минус»:
Осталось найти тангенс и котангенс, зная синус и косинус:
Ответ: .
Обратите внимание: если бы в условии речь шла об угле треугольника, то мы бы сами ограничили величину угла: , и сказали бы, что т. к. его косинус положительный, то угол лежит в первой четверти (тогда и все остальные тригонометрические функции данного угла были бы положительными).
Задача 2. Найти неизвестные тригонометрические функции угла, если:
Решение
Мы знаем, что, по определению, синус угла – это ордината соответствующей точки окружности.
Видим, что окружность пересекается горизонтальной прямой в двух точках (см. рис. 20).
Рис. 20. Иллюстрация к задаче 2
Значит, условию соответствуют два угла: в первой четверти и во второй (больше никакой информации об угле, в отличие от предыдущей задачи, нет).
Соответственно, у нас будут два разных значения косинуса. По рисунку видно, что по модулю эти значения равны и отличаются только знаком (см. рис. 21).
Рис. 21. Иллюстрация к задаче 2
Снова воспользуемся основным тригонометрическим тождеством:
Тогда:
В такой постановке мы бы должны были получить и два возможных значения тангенса и котангенса (с точностью до знака). Давайте добавим информацию о величине угла, чтобы получить однозначный ответ: пусть (или, по-другому, угол находится во второй четверти).
Косинус, который ему соответствует, имеет знак «минус» (т. к. абсциссы точек окружности во второй четверти отрицательные):
Осталось найти тангенс и котангенс:
Ответ: .
Теоремы синусов и косинусов
Кроме непосредственно тригонометрических функций, у нас есть еще два очень мощных инструмента, которые помогают нам находить недостающие элементы треугольников: теорема синусов и теорема косинусов. Вспомним обе теоремы.
Теорема синусов: отношение сторон к синусам противолежащих углов постоянно для данного треугольника и равно диаметру описанной окружности:
Возьмем первую часть этого утверждения:
Зная три элемента в этой пропорции, мы можем найти четвертый.
Например, если мы знаем две стороны и один противолежащий угол, то можем найти второй угол:
Или знаем одну сторону и два угла, найдем вторую сторону:
Теорема косинусов: квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними:
С помощью этой теоремы мы находим третью сторону, если знаем две стороны и угол между ними.
Или, зная три стороны, можно найти каждый угол, точнее – его косинус.
Задача 3. Выяснить тип треугольника (остроугольный, прямоугольный, тупоугольный), если его стороны равны:
Решение
Тип треугольника определяется его наибольшим углом, а наибольший угол лежит напротив наибольшей стороны (см. рис. 22). Зная три стороны, мы можем найти угол, используя теорему косинусов.
Рис. 22. Иллюстрация к задаче 3
1. Стороны треугольника равны , значит, наибольший угол лежит напротив стороны . По теореме косинусов имеем:
Выразим косинус:
Косинус положительный, соответствующий ему угол треугольника может быть только острым (у тупых углов косинус отрицательный – соответствующие им точки окружности расположены во второй четверти) (см. рис. 23). Т. е. наибольший угол треугольника острый, остальные тем более острые. Треугольник остроугольный.
Рис. 23. Иллюстрация к задаче 3
Остальные два случая решаются аналогично.
Выполните их самостоятельно. У вас должно получиться, что во втором случае косинус наибольшего треугольника равен (треугольник прямоугольный), а в третьем – косинус угла отрицательный (треугольник тупоугольный).
Ответ: остроугольный, прямоугольный, тупоугольный.
Свойство биссектрисы угла треугольника
Биссектриса делит угол пополам – это ее определение. Но, оказывается, противоположную сторону треугольника она тоже делит всегда не пополам, но в определенном соотношении.
Биссектриса треугольника делит противоположную сторону на два отрезка. Обозначим их как и (см. рис. 24). Углы , и, конечно, .
Рис. 24. Биссектриса треугольника делит противоположную сторону на отрезки и
Кроме того, углы и смежные (см. рис. 25):
Рис. 25. Смежные углы и
Но у таких углов синусы тоже равны (в самом деле, на единичной окружности двум таким углам соответствует одно и то же значение синуса) (см.
рис. 26).
Рис. 26. На единичной окружности углам и соответствует одно и то же значение синуса
Тогда имеем:
Применим к двум треугольникам теоремы синусов. Для треугольника имеем:
Для треугольника имеем:
Но правые части в обеих пропорциях равны, следовательно, равны и левые:
Или:
Таким образом, мы доказали, что биссектриса угла треугольника делит его противоположную сторону на отрезки, пропорциональные прилежащим сторонам. Этот факт сам по себе полезный инструмент, который мы будем использовать для решения различных задач.
Решение практической задачи с использованием теоремы синусов
Задача 4. На горе находится башня, высота которой равна м. Некоторый предмет у подножия горы наблюдают сначала с вершины башни под углом к горизонту, а потом с ее основания под углом . Найдите высоту горы (см. рис. 27).
Рис. 27. Иллюстрация к задаче 4
Решение.
Рассмотрим прямоугольный треугольник (см. рис. 28):
Рис. 28. Иллюстрация к задаче 4
Тогда:
Теперь рассмотрим треугольник . В нем мы знаем:
Тогда:
Используем теорему синусов:
м
Ответ: м.
Чтобы потренироваться использовать рассмотренные инструменты для решения других задач, используйте наши тренажеры и тесты. Чем больше вы практикуетесь, тем легче вам будет «увидеть», какой инструмент лучше всего применить для решения той или иной задачи и как именно это сделать.
Список литературы
- Александров А.Д., Вернер А.Л., Рыжик В.И. Геометрия, 8 класс. Учебник. – М.: «Просвещение», 2018.
- Бутузов В.Ф., Кадомцев С.Б., Прасолов В.В./Под ред. Садовничего В.А. Геометрия, 8 класс. Учебник. – М.: «Просвещение», 2018.
- Мерзляк А.Г., Полонский В.Б., Якир М.С., Геометрия. 8 класс. Учебник. – М.: издательский центр «ВЕНТАНА-ГРАФ», 2018.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал tmath.ru (Источник)
- Интернет-портал cleverstudents.ru (Источник)
- Интернет-портал схемо.рф (Источник)
Домашнее задание
- Доказать, что если в параллелограмм можно вписать окружность и можно описать около него окружность, то этот параллелограмм – квадрат.
- Найти угол между лучом и положительной полуосью , если точка имеет координаты .
- В равнобедренной трапеции меньшее основание равно боковой стороне, большее основание равно см, а угол при основании равен . Найти периметр трапеции.
школьная программа и отзывы учеников
- Главная
- Для детей
- 8 класс
- Математика/Алгебра/Геометрия 8 класс
На дистанционных курсах по математике для 8 класса можно изучать не только школьную программу, но и познакомиться с новыми разделами геометрии и алгебры, о которых не расскажут на обычных уроках.
Мы собрали онлайн-сервисы с занятиями для восьмиклассников по алгебре и геометрии. Актуальность учебных программ и их стоимость проверяются каждый день.
Все курсы алгебры и геометрии для учеников 8 класса
Фильтры
По возрастанию ценыПо рейтингу отзывовРекомендованныеПо возрастанию ценыПо убыванию цены
Алгебра для 8 класса (базовый уровень)
4 390 р./курс
4.9 / 5
25 отзывов о школе
Формат: Курс включает 30 занятий в записи, каждое длится 2 академических часа. Доступ к новому вебинару открывают 1 раз в неделю. У всех уроков есть конспект и домашнее задание в форме теста с автопроверкой.
Особенности: На курсе ученик познакомится с алгебраическими дробями, квадратными корнями, уравнениями, графиками функций, неравенствами. Программа содержит большое количество задач разного уровня сложности под любую образовательную цель.
4 390 р.
/курс
Геометрия для 8 класса (базовый уровень)
4 390 р./курс
Фоксфорд
4.9 / 5
25 отзывов о школе
Формат: Курс включает 30 занятий в записи, каждое длится 2 академических часа. Доступ к новому вебинару открывают 1 раз в неделю. У всех уроков есть конспект и домашнее задание в форме теста с автопроверкой.
Особенности: На курсе ученик познакомится с четырехугольниками и окружностью, научится находить площадь параллелограмма, трапеции, ромба, квадрата, узнает про подобные треугольники и решение задачи с помощью подобия.
4 390 р./курс
Повторение математики за 8 класс
390 р./курс
Фоксфорд
4.9 / 5
25 отзывов о школе
Формат: Курс включает 22 занятия в записи. Каждый вебинар длится от 5 до 15 минут. У всех уроков есть наглядная презентация, конспект и проверочное задание.
Особенности: На занятиях преподаватель заново объяснит тему вписанных и описанных многоугольников, напомнит, как решать квадратные уравнения и использовать теорему Пифагора, как выполнять действия с алгебраическими дробями.
390 р./курс
Математика для 8 класса (продвинутый уровень)
9 990 р./курс
Фоксфорд
4.9 / 5
25 отзывов о школе
Формат: Более 30 живых вебинаров, которые проводятся 1 раз в неделю и длятся 2 ак. часа, чат для общения с учителем, домашние задания с проверкой. В личном кабинете остаются записи уроков и конспекты.
Особенности: Курс поможет глубже изучить понятия и теоремы из математики. На занятиях ученик познакомится с новыми методами решения задач по алгебре, конструкциями из геометрии, формулами для корней квадратных уравнений, вписанными и описанными четырехугольниками.
9 990 р./курс
Математика для 8 класса
23 990 р.
/курс
14 790 р./курс
TutorOnline
4.6 / 5
31 отзыв о школе
Формат:
30 занятий по 1 академическому часу. Уроки проходят в группе 1 раз в неделю, в режиме реального времени. Можно задавать преподавателю вопросы в общем чате. Домашние задания после каждого урока.Особенности: 2 первых занятия бесплатно. Все видеолекции остаются в записи. Профессиональный преподаватель с современным подходом к обучению. Дополнительные занятия с психологом курса.
Скидка 38%
Рассрочка 4 мес.
23 990 р./курс
14 790 р./курс
Курсы математики для учеников 8 класса в Skysmart
Индивидуальное занятие
от 790 ₽/урок
Skysmart
4.8 / 5
40 отзывов о школе
Особенности:
- Школьная программа или продвинутый уровень.
- Онлайн-доска для занятий с преподавателем.
- Записи уроков сохраняются в личном кабинете.
- Ежемесячные отчеты для родителей.
- Можно переносить уроки.
Первый урок — бесплатно!
Курс на сайте школы
Курсы математики для восьмиклассников в Skysmart
Групповое занятие
от 499 ₽/урок
Skysmart
4.8 / 5
40 отзывов о школе
Особенности:
- Школьная программа или продвинутый уровень.
- Онлайн-доска для занятий с преподавателем.
- Записи уроков сохраняются в личном кабинете.
- Ежемесячные отчеты для родителей.
- Можно переносить уроки.
Первый урок — бесплатно!
Курс на сайте школы
Курсы математики для 8 класса в Тетрике
Индивидуальное занятие
от 890 ₽/урок
Тетрика
4.
9 / 5
Особенности:
- Индивидуальная программа.
- Фундаментальная проработка всех тем.
- Для разных целей — улучшить оценки, подготовка к контрольной и т.д.
- Научат решить задачи любого уровня.
- Опытные преподаватели.
Первый урок — бесплатно!
Курс на сайте школы
Курс подготовки к ВПР для 8 класса в Тетрике
Индивидуальное занятие
от 1 490 ₽/урок
Групповое занятие
от 650 ₽/урок
Тетрика
4.9 / 5
23 отзыва о школе
Особенности:
- Помощь в решении самых сложных заданий.
- Улучшение общей успеваемости.
- Занятия с интерактивной доской.
- Можно учиться с компьютера, планшета или смартфона.
- Записи уроков сохраняются в личном кабинете.
Первое занятие — бесплатно!
Курс на сайте школы
Сравнение всех курсов
Сравните все онлайн-курсы в одной таблице, чтобы выбрать лучший для себя.
Сортировать по:
Цене
Сроку
| Курс | Школа | Цена | Для кого | Срок | После обучения | Сайт курса |
|---|---|---|---|---|---|---|
| Алгебра для 8 класса (базовый уровень) | 4.8 / 5 26 отзывов | 4 390 р./курс | 8 месяцев | Сертификат | Открыть | |
| Геометрия для 8 класса (базовый уровень) | 4.8 / 5 26 отзывов | 4 390 р./курс | 8 месяцев | Сертификат | Открыть | |
| Повторение математики за 8 класс | 4. | 390 р./курс | 4 дня | Сертификат | Открыть | |
| Математика для 8 класса (продвинутый уровень) | 4.8 / 5 26 отзывов | 9 990 р./курс | 7 месяцев | Сертификат | Открыть | |
| Математика для 8 класса | 4.7 / 5 30 отзывов | 14 790 р./курс 23 990 р./курс В рассрочку от 3 990 р./мес. (4 мес.) | Сертификат | Открыть | ||
Индивидуальные занятия Курсы математики для учеников 8 класса в Skysmart | 4.8 / 5 40 отзывов | Индивидуальное занятие | 50 минут | Сертификат | Открыть | |
Групповое занятие Курсы математики для восьмиклассников в Skysmart | 4. | Групповое занятие | 50 минут | Сертификат | Открыть | |
Индивидуальные занятия Курсы математики для 8 класса в Тетрике | 4.9 / 5 23 отзыва | Индивидуальное занятие | 55 минут | Открыть | ||
Групповое занятие Индивидуальные занятия Курс подготовки к ВПР для 8 класса в Тетрике | 4.9 / 5 23 отзыва | Индивидуальное занятие Групповое занятие | 60 минут | Открыть |
8 / 5
8 / 5Рейтинг онлайн-школ
Подробнее о школе
4.
9 / 5
23 отзыва
Тетрика — это онлайн-сервис, где можно подготовиться к школе, подтянуть оценки по всем школьным предметам, пройти подготовку к ОГЭ или ЕГЭ. А также Tetrika проводит дистанционные уроки английского для детей и взрослых. В онлайн-школе есть бесплатные курсы и платные обучающие программы. Ниже мы собрали все ее курсы и отзывы реальных учеников. Вы можете оставить свой отзыв о Тетрике и поделиться опытом, что будет полезно для потенциальных учеников.
Раскрыть курсы
Скрыть курсы
Все курсы алгебры и геометрии для учеников 8 класса в Тетрика
| Название | Цена | Срок | Скидка |
|---|---|---|---|
| Курсы математики для 8 класса в Тетрике На сайте школы | Индивидуальное занятие | 55 минут | Нет |
| Курс подготовки к ВПР для 8 класса в Тетрике На сайте школы | Индивидуальное занятие Групповое занятие | 60 минут | Нет |
Подробнее о школе
4.
8 / 5
40 отзывов
Skysmart — онлайн-школа от создателей Skyeng (крупнейшей онлайн-школы английского в Европе), работает с 2019 года. Здесь обучают детей от 4 до 18 лет.
Раскрыть курсы
Скрыть курсы
Все курсы алгебры и геометрии для учеников 8 класса в Skysmart
| Название | Цена | Срок | Скидка |
|---|---|---|---|
| Курсы математики для учеников 8 класса в Skysmart На сайте школы | Индивидуальное занятие | 50 минут | Нет |
| Курсы математики для восьмиклассников в Skysmart На сайте школы | Групповое занятие | 50 минут | Нет |
Подробнее о школе
4.8 / 5
26 отзывов
Фоксфорд — это онлайн-школа для детей 1-11 классов, работает с 2009 года.
Здесь можно подготовиться к ЕГЭ, ОГЭ и олимпиадам на курсах, улучшить оценки по школьным предметам, пройти подготовку к поступлению в ВУЗ, а также школа подойдет для тех, кто выбрал домашнее/семейное обучение (экстернат). Фоксфорд ведет свою деятельность на основании государственной лицензии, входит в состав онлайн-университета Нетология и является участником Сколково.
Раскрыть курсы
Скрыть курсы
Все курсы алгебры и геометрии для учеников 8 класса в Фоксфорд
| Название | Цена | Срок | Скидка |
|---|---|---|---|
| Алгебра для 8 класса (базовый уровень) На сайте школы | 4 390 р./курс | 8 месяцев | Нет |
| Геометрия для 8 класса (базовый уровень) На сайте школы | 4 390 р./курс | 8 месяцев | Нет |
| Повторение математики за 8 класс На сайте школы | 390 р. | 4 дня | Нет |
| Математика для 8 класса (продвинутый уровень) На сайте школы | 9 990 р./курс | 7 месяцев | Нет |
/курсПодробнее о школе
4.7 / 5
30 отзывов
TutorOnline работает с 2011 года. В онлайн-школе можно обучаться всем школьным предметам с 1 по 11 классы, иностранным языкам (английскому, французскому, немецкому, итальянскому, китайскому и др.), а также здесь готовят к ОГЭ и ЕГЭ — всего больше 170 дисциплин. Средний балл по ЕГЭ выпускников TutorOnline — 80 баллов.
Раскрыть курсы
Скрыть курсы
Все курсы алгебры и геометрии для учеников 8 класса в TutorOnline
| Название | Цена | Срок | Скидка |
|---|---|---|---|
| Математика для 8 класса На сайте школы | 14 790 р. 23 990 р./курс В рассрочку от 3 990 р./мес. (4 мес.) | 8 месяцев | 38% |
/курсСтатьи по теме
Все статьи
Все статьи
Все категории раздела «8 класс» Перейти в раздел
Часто задаваемые вопросы
Кому будут полезны онлайн-курсы по алгебре и геометрии?
На дополнительных занятиях восьмиклассники разберут новые способы решения задач и узнают об интересных разделах математики, которые не охватывает школьная программа.
Удаленные курсы по алгебре и геометрии подойдут ученикам 8 класса, которые хотят подготовиться к урокам и контрольным работам, улучшить оценки, выучить новые формулы, проявляют интерес к точным наукам, а также для общего развития.
Как проходят занятия по математике для учеников 8 класса?
Формат занятий по математике может быть разным:
- тренажеры для решения задач на логику — можно проходить сколько угодно заданий в любое время;
- видео в записи — тоже можно смотреть, когда удобно;
- онлайн-уроки с преподавателем в режиме реального времени — проходят по расписанию, но пропущенные занятия можно посмотреть через личный кабинет.
При первом варианте преподавателя нет — ребенок занимается самостоятельно, выбирая правильный ответ. В двух других — есть чат для связи с учителем. Он не только ответит на вопросы во время урока, но и вышлет подробный комментарий по ошибкам в домашней работе.
Как узнать, подойдут ли дистанционные курсы восьмикласснику?
В большинстве онлайн-школ есть пробные уроки по алгебре и геометрии — за них не нужно платить. Вы сможете посмотреть занятие вместе с ребенком, оценить качество учебных материалов и профессионализм преподавателя. Для прохождения вводного урока достаточно указать электронную почту.
Плюс дистанционного обучения математике в том, что подростки могут заниматься из дома, в привычной обстановке, а также совмещать курсы со школой и секциями.
Нужно ли покупать учебники по алгебре и геометрии?
Для онлайн-обучения математике не нужно покупать детские учебники и тетради. Все необходимые пособия будут загружены в личный кабинет, их можно посмотреть в любое время.
Домашние задания тоже сдаются онлайн.
Оцените полезность страницы
Общая оценка 4 / 5
Нашли неточность или ошибку?
Не нашли подходящий курс?
Воспользуйтесь поиском
Поищите в рубрикаторе
Математика для восьмиклассников ⭐ Курс математики для детей 8-го класса
Brighterly — это онлайн-платформа, предлагающая уроки математики. Это фантастический сайт для восьмиклассников с профессиональными опытными учителями математики. Если вы зарегистрируетесь, наиболее подходящий учитель будет отвечать за улучшение успеваемости вашего ребенка по математике в 8 классе.
Получить бесплатный урок
Изучите образовательные модули для 8-го класса
Как работает ярче?
Brighterly — один из лучших математических сайтов для восьмиклассников. Прежде чем записать своего ребенка на вводный курс по математике в Brighterly, вы должны знать, как работает эта онлайн-платформа.
Бесплатная пробная версия
У Brighterly есть бесплатный пробный урок математики, и вы можете начать с записи на занятие. Это будет полноценный урок математики, который позволит детям понять, нравится ли им подход репетитора, и определить, удовлетворят ли курсы их потребностям.
Заполнение бланка заказа
Далее вы должны оформить заказ, заполнив необходимую информацию в бланке заказа, указав класс и уровень вашего ребенка и запланировав будущие уроки математики. Вам будет назначен лучший репетитор, который научит вашего ребенка математике.
Начало класса
Во время онлайн-обучения ваши дети будут наслаждаться персонализированным уроком математики. Они могут присоединиться к обсуждениям с репетитором, посмотреть видеоуроки, просмотреть учебный план по математике и спланировать последующие уроки математики.
Продолжайте учиться с Brighterly
Дети начнут с демонстрационных занятий, которые заставят их полюбить математику и продолжить обучение с Brighterly.
Теперь, чтобы получить все преимущества, вы должны подписаться на один из онлайн-курсов по математике и согласовать график обучения и учебный план по математике с репетиторами.
Получить бесплатный урок
Что о нас говорят родители
Ивонн
Мама Бена, 2-й класс
У моего сына всегда были проблемы с математикой, пока я не наткнулась на рекламу Brighterly на Facebook. После заказа класса его знания по математике значительно увеличились. Я определенно буду продолжать бронировать занятия, чтобы помочь ему.
Джесс
Мама Цири, 3 класс
Я всегда сижу на уроках своих детей. Это мой способ попытаться понять их уроки, чтобы стать лучшим опекуном. Однако до Brighterly было трудно запланировать урок, который бы соответствовал моему времени.
Рэй
Отец Финна, 2-й класс
Признаюсь, поначалу я скептически относился к использованию игр и видео для изучения математики. По моему опыту, я ожидал, что математика будет сложной для изучения детьми.
Но после наблюдения за тем, как мой сын быстро выучил математику благодаря этим методам обучения, я убежден, что Брайтерли точно знает, что делает.
Вики
Мама Дэнни, 4-й класс
Я всегда искала способ научить Дэнни математике после уроков в школе, но я запуталась из-за новых общих базовых стандартов. Брайтерли очень помог ему на уроке, что сделало его лучшим учеником по математике в школе. Я буду продолжать заказывать для него дополнительные занятия, пока он занимается математикой.
Фейри
Опекун Нины, 2-й класс
Смотреть, как Нина повторяет игры и математические задания, которые она выучила на уроках Brighterly, было захватывающим. Кажется, ее математические познания расширились с тех пор, как мы подписались на них. Мне нравится, как она любит свои занятия и повторяет все, чему научилась.
Джейсон
Папа Дейва, 4 класс
Будучи одиноким работающим отцом, я иногда возвращаюсь домой и слишком устаю, чтобы помогать Дейву с домашним заданием, из-за чего мне становится плохо.
Однако с тех пор, как мы подписались на Brighterly, я больше не думаю об этом, потому что Brighterly помогает с домашним заданием.
Карлтон
Отец Дианы, 3-й класс
Учитель математики Дианы жаловался, что Диана считает математику скучной и часто отсыпается во время уроков. Этот отчет меня обеспокоил, поэтому я решил подписать ее на Brighterly. Вскоре я понял, что метод преподавания в ее школе был проблемой, потому что ей нравится учиться с Брайтерли. Она не выглядит скучающей или уставшей и более вовлечена, чем когда-либо.
Детский класс
- Класс 1
- 2 класс
- 3 класс
- 4 класс
- 5 класс
- 6 класс
- 7 класс
- 8 класс
О процессе обучения Brighterly
Чтобы убедить родителей в том, что Brighterly — лучший поставщик математических онлайн-курсов для детей, необходимо объяснить, как работает платформа.
Вот причины, по которым это место особенное:
Интерактивное обучение
Участвуя в веселых и интерактивных уроках математики, дети поймут, как математика связана с реальным миром. Преподаватели Brighterly понимают, что прежде чем учить детей математике, им нужно поговорить со своими учениками и завоевать доверие. Благодаря этому методу дети находят уроки приятными.
Комплексная учебная программа (соответствует школьным стандартам США)
У каждого ребенка есть свой стиль обучения и темп, в котором он может освоить и понять математические понятия. Поэтому учителя используют адаптивные методы обучения и комплексную учебную программу, чтобы дети полностью понимали материал. Воспитатели не торопятся, чтобы определить, что лучше для ребенка.
Индивидуальное внимание (занятия 1:1)
В Brighterly дети пользуются преимуществами индивидуального обучения. Учителя адаптируют свои уроки к индивидуальным учебным потребностям своих учеников, позволяя детям прогрессировать в своем собственном темпе без необходимости прыгать вперед или назад, чтобы следовать за сверстниками.
Учись, где бы ты ни был
Отчеты о проделанной работе — важная функция для родителей, чьи дети изучают математику. Репетиторы Brighterly регулярно сообщают родителям новости и отзывы об успехах их детей, что доказывает, что Brighterly — лучший выбор для родителей.
Отчеты о проделанной работе для родителей
Отчеты об успеваемости являются важной функцией для родителей, чьи дети изучают математику. Репетиторы Brighterly регулярно сообщают родителям новости и отзывы об успехах их детей, что доказывает, что Brighterly — лучший выбор для родителей.
Получить бесплатный урок
Преимущества Brighterly
С Brighterly вашему ребенку предлагается:
Эффективный учебный процесс
Во время онлайн-уроков математики учителя тратят достаточно времени на объяснение математических понятий для детей. Они дают детям одну или несколько точек зрения на решение математических задач. Учебная программа является всеобъемлющей и своевременной, что помогает детям развивать знания и навыки по математике 8 класса.
Такой подход делает обучение более эффективным.
Упрощение сложных математических понятий для учащихся старших классов
Что вы изучаете в 8 классе по математике? Большинство детей изучают пространственное чувство, анализ данных, чувство числа и т. д. Но из-за сложной природы этих понятий детям часто требуются дополнительные математические занятия, чтобы ускорить их.
На курсах математики Brighterly для детей учителя представляют эти сложные математические задачи легко усваиваемыми частями. Студенты наслаждаются лекциями, не чувствуя себя перегруженными. И эта легкость обычно резко контрастирует с тем, что чувствуют дети во время обучения в обычных классах.
Творческие способы решения задач
Критическое мышление является важным навыком для изучения математики, а повторяющийся характер большинства теоретических математических уравнений не позволяет детям овладеть этим навыком. Если у ребенка проблемы с математикой, есть два варианта: использовать известное решение или найти альтернативное.
Дети развивают творческие способности, находя уникальные способы решения математических задач 8-го класса.
Почему математика может быть трудной для восьмиклассников?
Математика в средней школе может оказаться сложной для учащихся, и они могут расстроиться. Чтобы определить, нужна ли ребенку помощь в изучении предмета, вы можете задать такие вопросы, как «Что вы изучаете в 8-м классе по математике?» и «Вам нужна помощь по математике для 8-го класса?» Вот некоторые факторы, которые вызывают чувство раздражения у детей:
Большинство уроков математики начинаются с того, что учитель представляет задачи и предлагает пошаговый процесс, который поможет ученикам 8-го класса решить их. После того, как учитель покажет, как решить задачу определенным образом, дети могут почувствовать себя достаточно уверенно, чтобы попробовать решить ее самостоятельно. Но позже, когда дети сталкиваются с более сложными проблемами, они понимают, что не понимают того, чему их учили учителя в классе, что снижает их уверенность в себе.
Дети также могут избегать разговоров со своим учителем, потому что им стыдно, что они не понимают методов решения математических задач.
Если ученик 8-го класса нервничает или напрягается при выполнении математики, процесс обучения может быть для него непростым. Математическая тревога — это фобия, которая возникает, когда человек сталкивается с проблемой в математике. Обычно это происходит на уроке математики или домашнем задании. Математическая тревога проявляется во многих формах. Ученик 8-го класса может казаться беспокойным и беспокойным во время урока математики или экзаменов и может не хотеть ходить в школу. У них также могут проявляться физические симптомы, такие как тошнота и тремор.
Занятия математикой онлайн и офлайн для восьмиклассников
Всегда будут споры о предпочтительном режиме занятий: онлайн или офлайн. Структура класса зависит от предпочтений, поскольку два типа классов работают вместе. Кроме того, каждая модель обучения имеет свои преимущества и недостатки и нуждается друг в друге для существования.
Обучение в автономном режиме требует, чтобы участники отправились в место обучения, такое как аудитория, классная комната или холл. Офлайн-курсы можно проводить только в стенах классной комнаты, а дети участвуют в физико-математических упражнениях, таких как подвижные игры, которые поддерживают физическое и умственное развитие. Наоборот, онлайн-обучение доступно практически в любой точке мира. Участникам нужен только доступ к Интернету из дома. Во время онлайн-занятий репетиторы могут обучать студентов в виртуальных классах.
Когда дело доходит до онлайн-обучения, учебный процесс становится все более цифровым. Учителя могут использовать инструменты онлайн-обучения, такие как аудиоклипы, видеоролики, виртуальные доски, анимацию, беседы и виртуальные конференц-залы, чтобы облегчить процесс обучения. Напротив, автономное обучение позволяет учащимся учиться в более практической среде, взаимодействуя с учителями и сверстниками и активно участвуя в практическом обучении.
Ярко помогает детям изучать математику!
Потребности детей 8-го класса в математике могут различаться, и учителя хорошо понимают, как помочь учащимся в этой области.
Если вам нужен эксперт, который поможет вашему ребенку в изучении математики, загляните в Brighterly. Их онлайн-курс по математике для 8-го класса может сделать обучение детей увлекательным и увлекательным.
Ярче предоставляет учащимся ценную информацию о математических понятиях, чтобы стимулировать активное обучение. Некоторые учащиеся могут быть пассивными учениками, которые не задают вопросы в классе, даже если у них возникают проблемы с математическими понятиями 8-го класса. Тем не менее, преподаватели знают, что лучший способ учиться — это учиться в привлекательной среде. Педагоги Brighterly помогают детям понять математику 8-го класса | используя забавные ресурсы, такие как игры, красочные рабочие листы и видео на YouTube.
Учителя Brighterly знакомы с лучшими учебными материалами, которые необходимы для улучшения понимания детьми математики. Даже если дети могут показаться расстроенными и неспособными правильно ответить на вопросы, их учителя достаточно терпеливы и никогда не расстроят ребенка.
Да, конечно. За исключением 5-го класса, Brighterly предлагает уроки математики для 1-го, 2-го, 3-го, 4-го, 5-го, 6-го и 7-го классов.
Детский класс
- Класс 1
- 2 класс
- 3 класс
- 4 класс
- 5 класс
- 6 класс
- 7 класс
- 8 класс
Электронная почта родителей
Успешно отправлено
math-7-unit-5 — Googlesuche
AlleBilderShoppingNewsMapsVideosBücher
suchoptionen
Математика 7 класс, Раздел 5 — Open Up Resources
access.
openupresources.org › curricula › unit-5
Unit 5. 7.5 Арифметика рациональных чисел… Урок 1 · Интерпретация отрицательных чисел… Урок 7 · Сложение и вычитание для решения задач …
N- Gen Math 7.Unit 5.Lesson 1.The Properties of Real Numbers
www.youtube.com › смотреть
19.12.2019 · В этом уроке мы рассмотрим ассоциативные и коммутативные свойства сложения и…
Дауэр: 18:27
Прислан: 19.12.2019
N-Gen Math 7.Unit 5.Lesson 5.Combining LikeTerms – YouTube
www.youtube.com › смотреть
27.01.2020 · На этом уроке учащиеся повторяют понятия коэффициентов и подобных терминов. Тогда они понимают…
Dauer: 20:26
Прислан: 27.01.2020
Модуль 5 — Линейные выражения — eMATHinstruction
www.emathinstruction.com › … › N-Gen Math™ 7
Unit 5 – Линейные выражения. Урок 1. Свойства действительных чисел. УРОК/ДОМАШНЕЕ ЗАДАНИЕ … Урок 7. Факторинг биномов. УРОК/ДОМАШНЕЕ ЗАДАНИЕ.
ЛЕКЦИОН/ТАРЕЯ.
Математика 7, раздел 5 — Альта Сьерра промежуточный — Объединенный школьный округ Кловис
altasierra.cusd.com › Math7Unit5
7 класс Иллюстративная математика — Раздел 5: Арифметика рациональных чисел. Загрузить студенческое издание в формате PDF · Загрузить практическую работу учащегося в формате PDF (домашнее задание).
Веб-страница г-жи Клеменс-Брентон — Математика 7, раздел 5 — Сайты Google
site.google.com › nlesd.ca › math-7 › class-notes
NLESD Resources · Math 9· Заметки о классе · Домашнее задание/Задания/Объявления. Блок 5 — Дроби, десятичные дроби и проценты. НАЗАД. Сообщить о нарушении.
Справка по математике мистера Моргана — Раздел 5 — Арифметика рациональных чисел
site.google.com › illustrative-mathematics › math-7 Math 7 Unit 5 — Complete Student Edition.pdf.
Математика 7: Повторение карточек для Темы 5 — Quizlet0003
Математика 7: Обзор единицы 5 .