Триг таблица: Таблица значений тригонометрических функций

Вопросы для проверки

Формулы тройных углов

Обратные тригонометрические функции

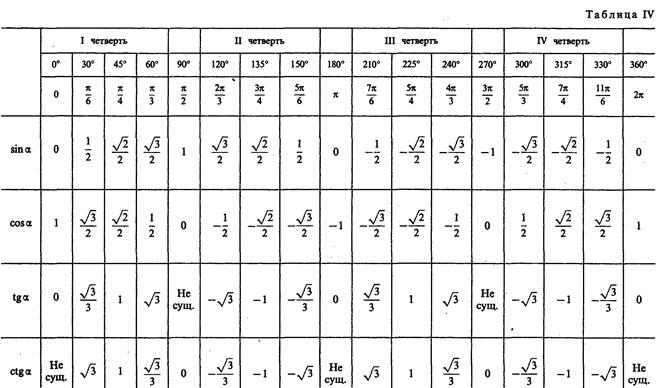
Некоторые значения тригонометрических функций

таблица 3

Аргумент	Функция
	sin 	cos 	tg 	ctg 
15
18
36
54
72
75

1. Что такое числовая окружность?

2. Перечислите признаки числовой окружности.

3. Какая величина принимается за единицу измерения при градусном измерении углов?

4. Что такое радиан?

5. По каким формулам переводят градусную меру угла в радианную и наоборот?

6. Выразите в радианах углы, равные 30, 45, 60, 90, 180, 270, 360.

7. Почему ошибочна запись  = 180?

8. При каком условии длина дуги равна ее радианной мере?

9. Какой угол называется углом поворота?

10. Какой угол поворота называется положительным? отрицательным?

11. Задайте формулой общий вид углов поворота.

12. Сформулируйте правило «полного оборота».

13. Какие функции называются тригонометрическими?

14. Дайте определение функции синус; косинус; тангенс; котангенс.

15. При каких углах не определен тангенс? котангенс?

16.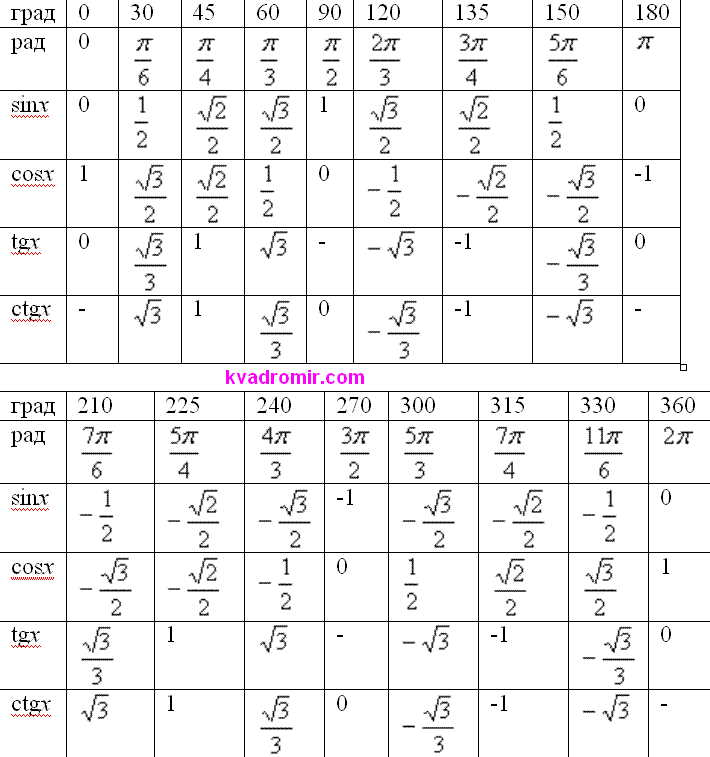 Назовите значения тригонометрических функций углов 30, 45, 60.

17. Какие значения может принимать синус? косинус? тангенс? котангенс?

18. Определите знаки тригонометрических функций в зависимости от того, в какой четверти находится аргумент.

19. Какие из тригонометрических функций являются четными, какие – нечетными?

20. Чему равен период синуса? косинуса? тангенса? котангенса?

1. Числовая прямая

Алгебраические функции — это функции, заданные аналитическим выражением, в записи которого используются алгебраические операции над числами и переменной (сложение, вычитание, умножение, деление, возведение в степень, извлечение корня).

у = 2х + 3,

Числовая прямая — это математическая модель для представления чисел, в которой каждое число соответствует точке на прямой, причем расстояние от точки до начала отсчета равно модулю числа:

Признаки числовой прямой:

1) начало отсчета;

2) единичный отрезок;

3) положительное направление (стрелка).

11. Простейшие тригонометрические неравенства

Чтобы решить простейшее тригонометрическое неравенство нужно:

1. Провести прямую к линии соответствующей функции.

2. Выделить дугу, на которой лежат решения неравенства.

3. Найти концы этой дуги, помня, что обход совершается против часовой стрелки от меньшего числа к большему.

4. Прибавить к концам интервала числа, кратные периоду функции.

Решить неравенство .

Решение.

Все решения, удовлетворяющие заданному неравенству, лежат на дугеl. Найдем ее концы:

С учетом периода синуса, запишем ответ:

.

Ответ:

10. Простейшие тригонометрические уравнения

Если правая часть уравнения — отрицательное число, то следует воспользоваться свойствами соответствующих обратных тригонометрических функций, тогда:

При а = 1; 0; –1 решение уравнения записывается в виде (n  Z):

2.

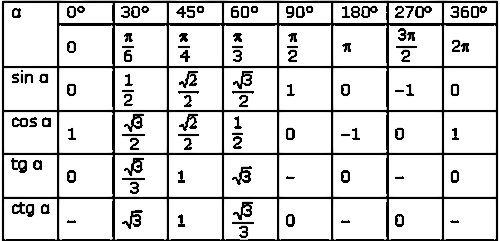Числовая окружность

Единичная окружность — это окружность, радиус которой принят за единицу измерения.

Числовая окружность — это единичная окружность с установленным соответствием между действительными числами и точками окружности:

Указанное соответствие можно определить следующим образом: каждому числу  соответствует такая точка Р числовой окружности, чтобы дуга ОР имела длину || и была отложена в положительном направлении если  > 0 и в отрицательном, если  < 0:

Признаки числовой окружности:

1) начало отсчета – правый конец горизонтального диаметра;

2) единичный отрезок – длина радиуса окружности;

3) положительное направление – против часовой стрелки.

Откладывать можно дуги какой угодно длины. То есть числовую окружность можно рассматривать как окружность радиуса 1, на которую «намотана» числовая прямая:

Интегрирование тригонометрических рациональных функций

Методы интегрирования тригонометрических рациональных функций

Рассмотрим интегралы от тригонометрических рациональных функций:
,
где R – рациональная функция, то есть функция, составленная из операций сложения, деления и возведения в целочисленную степень. Сюда также могут входить тангенсы и котангенсы (поскольку они получаются операциями деления синуса и косинуса). Их, чаще всего, стоит преобразовать через синусы и косинусы.

В зависимости от вида подынтегральной функции, применяют несколько методов интегрирования тригонометрических рациональных функций.

Подстановки t = sin x или t = cos x

Если R( cos x, sin x ) умножается на   –1 при замене
cos x  →  – cos x или sin x  →  – sin x ,
то полезно другую из них обозначить через t.

Так, при подстановке
t = cos x ,
dt = (cos x )′ dx = – sin x dx,
sin² x = 1 – cos² x = 1 – t ².

При подстановке
t = sin x ,
dt = (sin x )′ dx = cos x dx,
cos² x = 1 – sin² x = 1 – t ².

Подстановка t = tg x

Если R( cos x, sin x ) не меняется при одновременной замене
cos x  →  – cos x и sin x  →  – sin x ,
то полезно положить tg x = t или ctg x = t.

Пусть t = tg x, тогда
,
,
,
.

Подстановка t = tg(x/2)

Подстановка

во всех случаях приводит к интегралу от рациональной дроби.

При этом
,
,
,
,
,
.

Итак,
.

Эта подстановка является универсальной и позволяет во всех случаях привести интегралы от тригонометрических рациональных функций к интегралам от рациональных функций. К сожалению, эта подстановка приводит к более длинным вычислениям, чем предыдущие, если они применимы.

Интегралы с произведением степенных функций от cos x и sin x

Часто встречаются интегралы, в которых подынтегральная функция является произведением степенных функций от синуса и косинуса:

При целых m и n подынтегральная функция является тригонометрической рациональной функцией и, для ее интегрирования, применимы перечисленные выше методы. Однако, в виду особенности, существует ряд дополнительных методов, которые, в некоторых случаях, позволяют упростить вычисление таких интегралов.
Подробнее >>>

Примеры

Ниже подробно рассмотрены три примера интегрирования рациональных тригонометрических функций.

Пример 1

Вычислить интеграл

Решение

Подынтегральная функция

является дробью, состоящей из многочленов от тригонометрических функций sin x и cos x. Поэтому она является рациональной функцией от sin x и cos x.

Заменим cos x на – cos x:

Вся функция умножилась на   –1 .

По правилу 1, делаем подстановку:
t = sin x.
Тогда
dt = (sin x)′ dx = cos x dx.

Подставляем в интеграл:

Получили интеграл от рациональной функции (дроби из многочленов). Выделяем целую часть и разложим дробь на простейшие:
.
Интегрируем:

Ответ

Пример 2

Определить интеграл

Решение

Подынтегральная функция

является дробью, состоящей из многочленов от тригонометрической функции sin x. Поэтому она является рациональной функцией от sin x и cos x.

Заменим sin x на – sin x:

Функция не изменилась.

Заменим cos x на – cos x. Поскольку подынтегральная функция не зависит от cos x, то при этой замене она также не меняется.

Согласно второму правилу, приведенному выше, делаем подстановку:
t = tg x.
;
;
.
Применим формулу sin² x + cos² x = 1 и разделим числитель и знаменатель на cos² x.
.
Подставляем и раскладываем дробь на простейшие:
.

Ответ

Пример 3

Решить интеграл

Решение

Подынтегральная функция

является дробью, состоящей из многочлена от тригонометрических функций sin x и cos x. Поэтому она является рациональной функцией от sin x и cos x.

Если заменить sin x на – sin x или cos x на – cos x, то функция меняет вид, поэтому правила 1 или 2 не применимы.

Согласно третьему правилу, приведенному выше, делаем подстановку:
.
;
.
Преобразуем знаменатель, применяя формулы:
,
,
.
.

.

Приводим знаменатель к сумме квадратов:
.

Подставляем:

Ответ

Использованная литература:
Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.

Тригонометрия | Определение, формулы, отношения и тождества

тригонометрические функции

Просмотреть все СМИ

Ключевые люди:

Гиппарх Леонард Эйлер Региомонтан Абу аль-Вафах Франсуа Виет, сеньор де ла Биготьер

Похожие темы:

тригонометрическая таблица сферическая тригонометрия плоская тригонометрия аналитическая тригонометрия сферический треугольник

Просмотреть весь соответствующий контент →

Резюме

Прочтите краткий обзор этой темы

тригонометрия , раздел математики, связанный со специфическими функциями углов и их применением в вычислениях. В тригонометрии обычно используются шесть функций угла. Их названия и сокращения: синус (sin), косинус (cos), тангенс (tan), котангенс (cot), секанс (sec) и косеканс (csc). Эти шесть тригонометрических функций по отношению к прямоугольному треугольнику показаны на рисунке.

Например, треугольник содержит угол А , а отношение стороны, противолежащей А и стороны, противоположной прямому углу (гипотенузе), называется синусом А , или синусом А ; аналогично определяются другие тригонометрические функции. Эти функции являются свойствами угла A , не зависящими от размера треугольника, и расчетные значения для многих углов были сведены в таблицы до того, как компьютеры сделали тригонометрические таблицы устаревшими. Тригонометрические функции используются для получения неизвестных углов и расстояний от известных или измеренных углов в геометрических фигурах.

Тригонометрия возникла из-за необходимости вычислять углы и расстояния в таких областях, как астрономия, картографирование, геодезия и дальномер артиллерийских орудий. Задачи, связанные с углами и расстояниями в одной плоскости, рассматриваются в плоской тригонометрии. Приложения к подобным задачам более чем в одной плоскости трехмерного пространства рассматриваются в сферической тригонометрии.

История тригонометрии

Классическая тригонометрия

Слово тригонометрия происходит от греческих слов тригонон («треугольник») и метрон («для измерения»). Примерно до 16 века тригонометрия в основном занималась вычислением числовых значений отсутствующих частей треугольника (или любой формы, которую можно разбить на треугольники), когда были даны значения других частей. Например, если известны длины двух сторон треугольника и величина прилежащего к нему угла, можно вычислить третью сторону и два оставшихся угла. Такие вычисления отличают тригонометрию от геометрии, которая исследует главным образом качественные отношения. Конечно, это различие не всегда абсолютно: теорема Пифагора, например, представляет собой утверждение о длинах трех сторон прямоугольного треугольника и, таким образом, носит количественный характер. Тем не менее, в своем первоначальном виде тригонометрия в целом была потомком геометрии; только в 16 веке эти две науки стали отдельными разделами математики.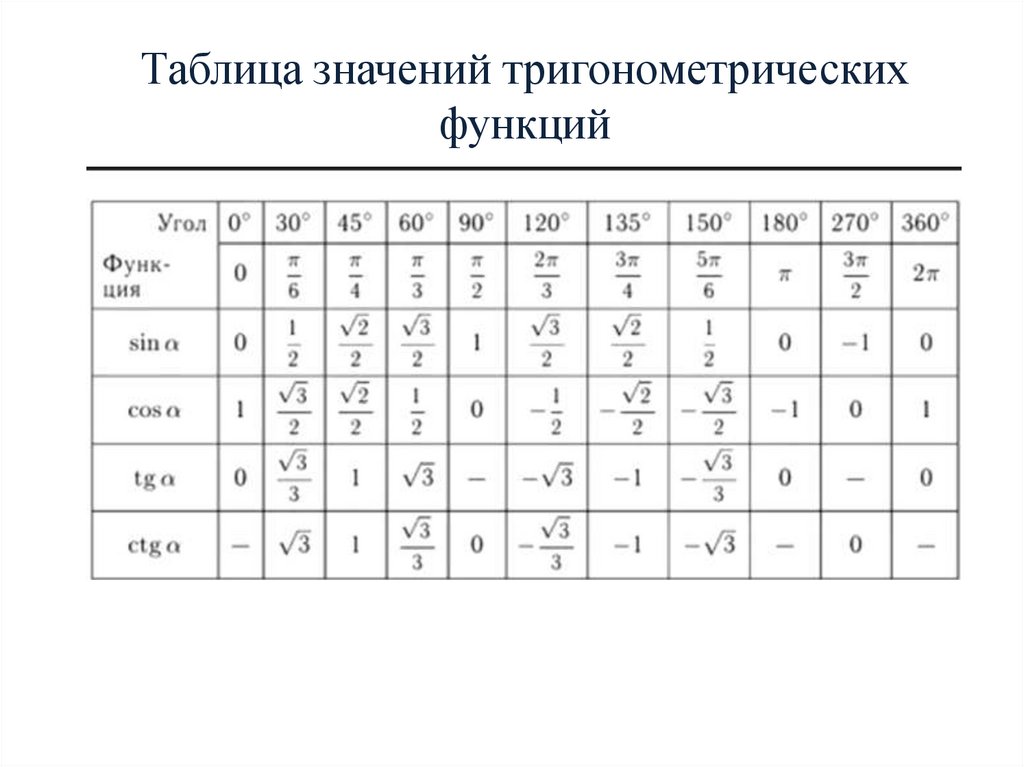

Древний Египет и Средиземноморье

Несколько древних цивилизаций — в частности, египетская, вавилонская, индуистская и китайская — обладали значительными познаниями в практической геометрии, включая некоторые понятия, которые были прелюдией к тригонометрии. Папирус Райнда, египетский сборник из 84 задач по арифметике, алгебре и геометрии, датируемый примерно 1800 г. до н. э., содержит пять задач, касающихся секед . Тщательный анализ текста и сопровождающих его рисунков показывает, что это слово означает наклон склона — важное знание для крупных строительных проектов, таких как пирамиды. Например, в задаче 56 спрашивается: «Если высота пирамиды 250 локтей, а длина стороны ее основания 360 локтей, какова ее 9 локтей?0027 секед

? Решение дается как 5 ¹ / ₂₅ ладони на локоть, и, поскольку один локоть равен 7 ладоням, эта дробь эквивалентна чистому отношению ¹⁸ / ₂₅ . На самом деле это отношение «длины к высоте» рассматриваемой пирамиды — по сути, котангенс угла между основанием и гранью. Это показывает, что египтяне хотя бы немного знали числовые отношения в треугольнике, своего рода «прототригонометрию».

Викторина по Британике

Числа и математика

Тригонометрия в современном понимании началась с греков. Гиппарх (

г. ок. г., 190–120 гг. до н. э.) первым составил таблицу значений тригонометрической функции. Он рассматривал каждый треугольник — плоский или сферический — как вписанный в круг, так что каждая сторона становится хордой (то есть прямой линией, соединяющей две точки на кривой или поверхности, как показано вписанным треугольником A ). Б C на рисунке). Чтобы вычислить различные части треугольника, нужно найти длину каждой хорды как функцию центрального угла, который ее стягивает, или, что то же самое, длину хорды как функцию соответствующей ширины дуги. Это стало главной задачей тригонометрии на следующие несколько столетий. Как астронома Гиппарха в основном интересовали сферические треугольники, такие как воображаемый треугольник, образованный тремя звездами на небесной сфере, но он также был знаком с основными формулами плоской тригонометрии.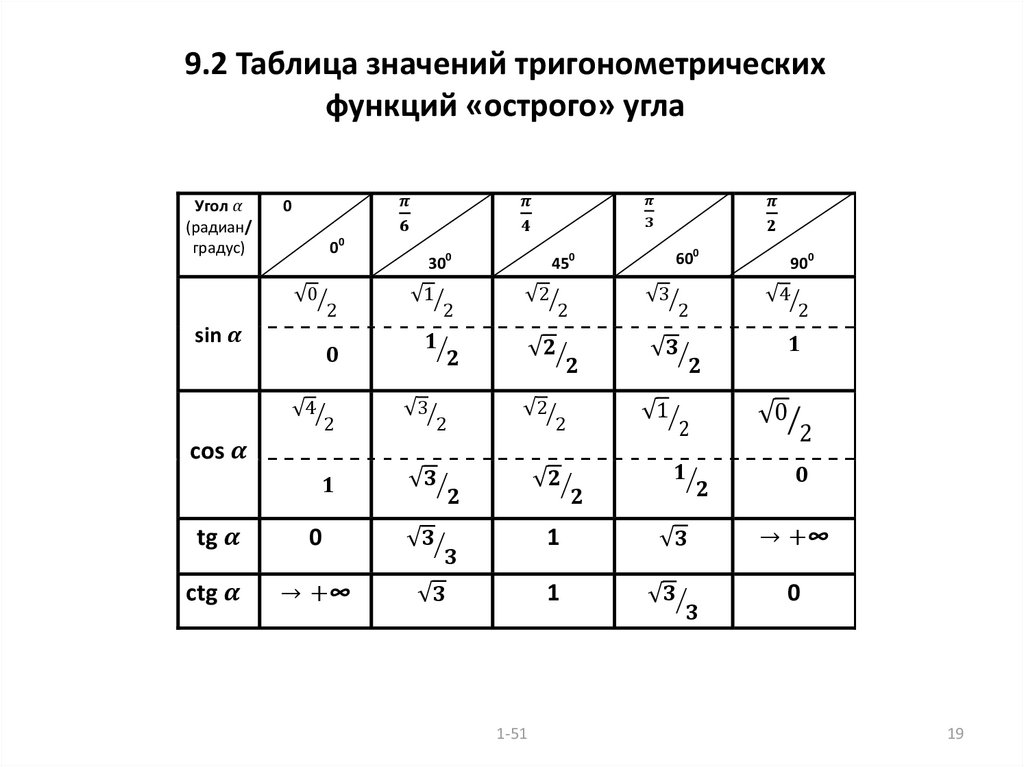 Во времена Гиппарха эти формулы выражались в чисто геометрических терминах как отношения между различными хордами и углами (или дугами), которые их стягивают; современные символы для тригонометрических функций не вводились до 17 века.

Изучите, как Птолемей пытался использовать деференты и эпициклы для объяснения ретроградного движения

Просмотреть все видео к этой статье

Щелкните здесь, чтобы просмотреть таблицу в полном размереПервой крупной древней работой по тригонометрии, дошедшей до Европы в целости и сохранности после Средневековья, был Альмагест Птолемея ( ок. 100–170 н.э.). Он жил в Александрии, интеллектуальном центре эллинистического мира, но больше о нем мало что известно. Хотя Птолемей написал работы по математике, географии и оптике, в основном он известен своими Альмагест , сборник из 13 книг по астрономии, который стал основой для картины мира человечества, пока гелиоцентрическая система Николая Коперника не начала вытеснять геоцентрическую систему Птолемея в середине 16 века.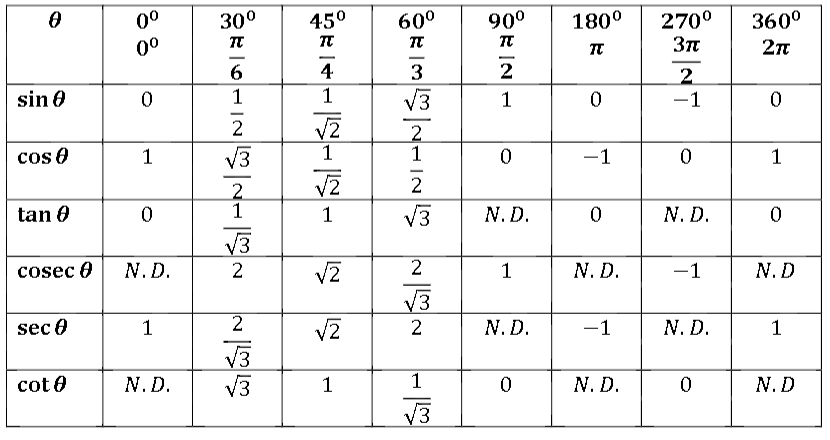 Чтобы развить эту картину мира, сущностью которой была неподвижная Земля, вокруг которой по круговым орбитам движутся Солнце, Луна и пять известных планет, Птолемею пришлось использовать некоторую элементарную тригонометрию. Главы 10 и 11 первой книги Альмагеста касается построения таблицы хорд, в которой длина хорды в окружности дана как функция центрального угла, который ее стягивает, для углов в диапазоне от 0 ° до 180 ° с интервалами в полградуса. . По сути, это таблица синусов, которую можно увидеть, обозначив радиус r , дугу A и длину стягиваемой хорды c , чтобы получить c = 2 r sin ^А / ₂ . Поскольку Птолемей использовал вавилонские шестидесятеричные числа и системы счисления (основание 60), он провел свои вычисления со стандартным кругом радиуса 9.0027 r = 60 единиц, так что c = 120 sin ^A / ₂ . Таким образом, помимо коэффициента пропорциональности 120, это была таблица значений sin ^A / ₂ и, следовательно, (удвоением дуги) sin A . 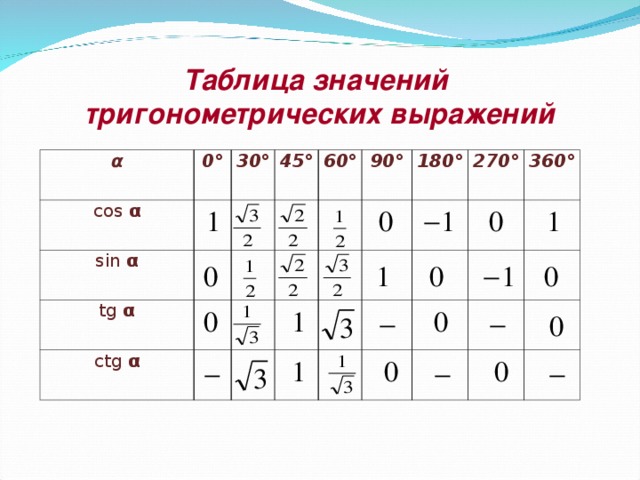С помощью своей таблицы Птолемей усовершенствовал существующие геодезические меры мира и уточнил Гиппархову модель движения небесных тел.

Оформите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишитесь сейчас

Не поддавайтесь рекламе вавилонской тригонометрии

Возможно, вы видели заголовки о древней месопотамской табличке. «Математические секреты древней таблички раскрыты после почти столетнего изучения», — говорится в сообщении The Guardian. «Эта загадочная древняя табличка может научить нас кое-чему по математике», — говорится в журнале Popular Science, добавляя: «Некоторые исследователи говорят, что вавилоняне изобрели тригонометрию — и сделали это лучше». National Geographic был немного более осмотрителен: «Новое исследование утверждает, что планшет может быть одним из старейших вкладов в изучение тригонометрии, но некоторые по-прежнему настроены скептически». Дэниел Мэнсфилд и Норман Вильдбергер, безусловно, проделали хорошую работу, продав свою новую статью в обычно более солидном журнале Historia Mathematica. Я хотел бы помочь отделить факты от домыслов и откровенной чепухи, когда дело доходит до этой новой статьи.

Что такое Плимптон 322?

Plimpton 322, планшет, о котором идет речь, безусловно, является заманчивым артефактом. Это осколки глины размером примерно с открытку. Он был заполнен четырьмя столбцами клинописных чисел около 1800 г. до н.э., вероятно, в древнем городе Ларса (ныне в Ираке) и был удален в 1920-х годах. Джордж Плимптон купил его в 1922 году и завещал Колумбийскому университету, который владеет им с 1936 года. С тех пор многие ученые изучали Плимптон 322, поэтому любая фотография Мэнсфилда и Уайлдбергера, стоящих на четвереньках в жарком пыльном археологических раскопок, или даже рыться в заплесневелых, заброшенных архивах и выкапывать это сокровище неточно. Мы знали об артефакте и о том, что на нем было, на протяжении десятилетий. Исследователи утверждают, что у них есть новая интерпретация того, как использовался артефакт, но я настроен скептически.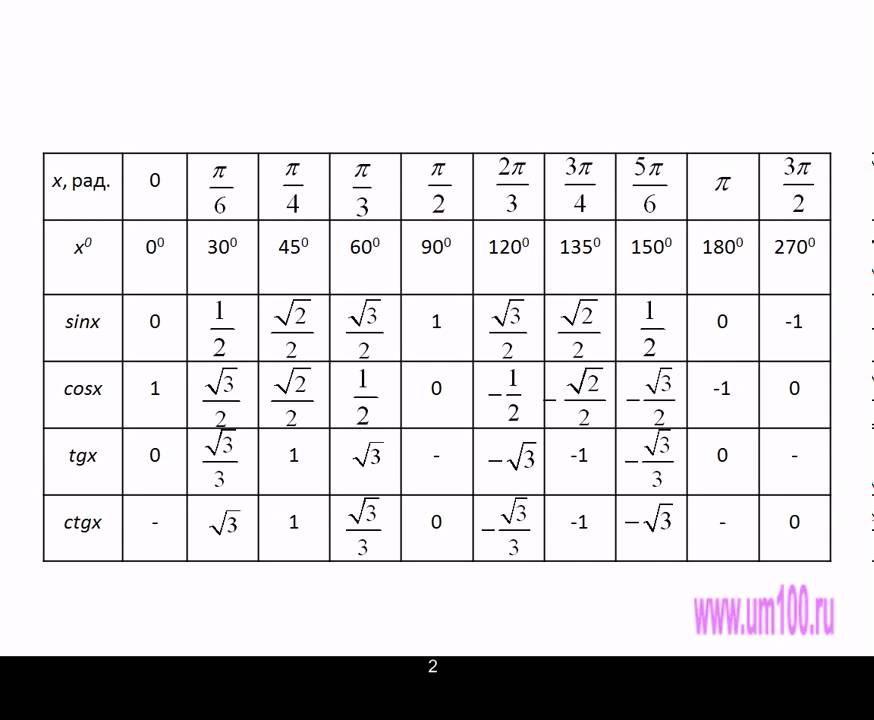

Ученые знали с 1940-х годов, что Плимптон 322 содержит числа, входящие в тройки Пифагора, то есть целые решения уравнения a ² +b ² =c ² . Например, 3-4-5 является тройкой Пифагора, потому что 3 ² +4 ² =9+16=25=5 ² . 15 августа этого года некоторые праздновали как «Пифагорейский тройной день», потому что 8-15-17 — еще одна, немного более сексуальная, такая тройка.

Крайний правый столбец состоит из чисел от 1 до 15, так что это просто перечисление. Два средних столбца Plimpton 322 содержат одну сторону и гипотенузу пифагорейского треугольника, или a и c в уравнении a ² +b ² =c ² . (Обратите внимание, что a и b взаимозаменяемы.) Но они немного мощнее, чем пифагорейские тройки, которые вы изучаете в школе. Первые записи 119 и 169 соответствуют тройке Пифагора 119 ² +120 ² = 169 ² . Крайний левый столбец — это отношение квадратов сторон треугольников. Какие именно стороны немного зависят от того, что содержится в отсутствующем осколке с левой стороны артефакта, но это не имеет большого значения. Это либо квадрат гипотенузы, деленный на квадрат оставшегося катета, либо квадрат одного катета, деленный на квадрат другого катета. На современном математическом жаргоне это квадраты касательной или секущей угла в треугольнике.

Мы можем интерпретировать один из столбцов как содержащий тригонометрические функции, так что в некотором смысле это таблица триггеров. Но несмотря на то, что заголовки хотели бы заставить вас поверить, люди знали это на протяжении десятилетий. Загадка заключается в том, для какой цели в свое время служила табличка. Почему он был создан? Почему именно эти треугольники были включены в таблицу? Как вычислялись столбцы? В статье 1980 года под названием «Шерлок Холмс в Вавилоне» Р. Крейтон Бак намекнул, что с помощью математики и хитрого наблюдения можно выяснить значение таблички, и предложил объяснение, которое, по его мнению, соответствовало данным.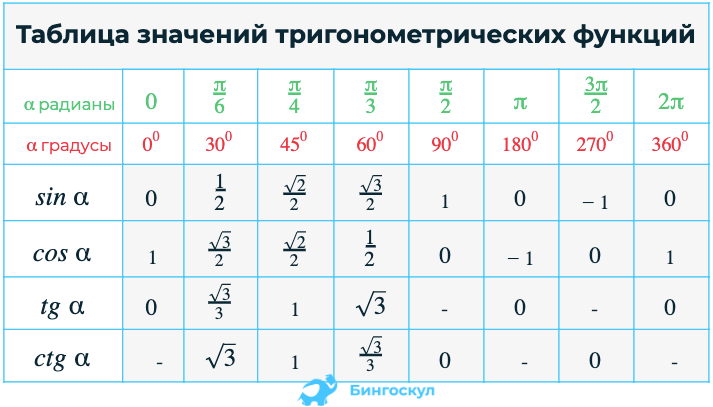 Но Элеонора Робсон в «Ни Шерлоке Холмсе, ни Вавилоне» пишет: «Древние математические тексты и артефакты, если мы хотим понять их полностью, должны рассматриваться в свете их математико-исторического контекста, а не рассматриваться как искусственные, самостоятельные. -содержащие творения в стиле детективов». Высокомерно и, вероятно, приведет к неправильным выводам смотреть на древние артефакты прежде всего  через призму нашего современного понимания математики.

Что он сделал?

Существует несколько теорий о том, как Plimpton 322 был создан и использовался человеком или людьми, которые его построили. Мэнсфилд и Уайлдбергер не первые, кто считает, что это какая-то триггерная таблица. С другой стороны, некоторые считают, что она связывает теорему Пифагора (известную этим древним жителям Месопотамии и многим другим цивилизациям задолго до Пифагора) с методом завершения квадрата для решения квадратного уравнения, обычной задачей в математических текстах того времени и места. . Некоторые считают, что тройки были сгенерированы с использованием различных чисел, не включенных в таблицу, «теоретико-числовым» способом. Некоторые считают, что числа произошли от так называемых обратных пар, которые использовались для умножения. Некоторые думают, что планшет был педагогическим инструментом, возможно, источником упражнений для студентов. Некоторые считают, что он использовался в чем-то больше похожем на оригинальное математическое исследование. Академическую, но удобочитаемую информацию об этих интерпретациях можно найти в статьях Бака в 1980, Робсоном в 2001 и 2002 годах, а также Джоном П. Бриттоном, Кристин Пруст и Стивом Шнайдером в 2011 году.

Если это тригонометрическая таблица, то лучше ли она современных тригонометрических таблиц?

Вклад Мэнсфилда и Уайлдбергера в исследования Плимптона 322, похоже, является предположением о том, что артефакт можно использовать для тригонометрии более точным способом, чем мы это делаем сейчас. В рекламном видео UNSW, которое, должно быть, сопровождало пресс-релизы, разосланные многим математическим и научным журналистам (но не мне — что дает, UNSW?), Мэнсфилд заявляет, что эта таблица «в некотором роде превосходит современную тригонометрию». и «единственно полностью точная тригонометрическая таблица».

Трудно понять, с чего начать с этой части их заявлений. Во-первых, табличка содержит некоторые хорошо известные ошибки, поэтому заявления о том, что это самая точная или точная таблица триггеров, просто не соответствуют действительности. Но даже исправленная версия Plimpton 322 не станет революционной заменой современным триггерным таблицам.

Если вы, как и я, не выросли с использованием триггерных таблиц, они станут отличным инструментом, если у вас нет компьютера, который выполняет вычисления с точностью до 10 разрядов за доли секунды. Триггерная таблица будет включать столбцы с синусом, косинусом, тангенсом и, возможно, другими тригонометрическими функциями углов.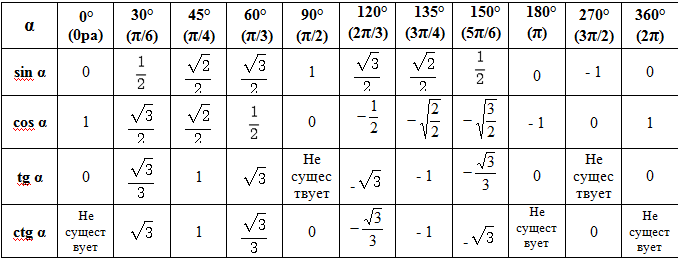 Кто-то или группа людей выполняли эти кропотливые вычисления вручную, а затем вы могли просто найти значение, когда, скажем, в вычислении возникало значение cos(24°). Сегодня компьютеры обычно используют формулы для триггерных функций, а не вызывают список всех значений, а людям вообще не нужно знать много значений. Эти формулы основаны на исчислении и могут быть настолько точными, насколько это необходимо. Нужен правильный ответ на 50 цифр? Ваш компьютер может сделать это, вероятно, довольно быстро.

Если вы запомнили «soh cah toa» или мнемоническое выражение о «каком-то старом хиппи», вы, возможно, помните, что основные триггерные функции — это отношения длин сторон треугольников. Синус угла — это противолежащий катет, деленный на гипотенузу, косинус — это противолежащий катет, деленный на гипотенузу, а тангенс — противолежащий катет, деленный на прилежащий. Значения триггерных функций большинства углов не являются рациональными числами. Их нельзя записать как отношение двух целых чисел, поэтому записи, которые вы найдете в таблицах триггеров, обрезаются после некоторого количества десятичных знаков. Мэнсфилд и Уайлдбергер, кажется, сосредоточились на наблюдении, что, когда все длины сторон прямоугольного треугольника являются целыми числами, все эти отношения рациональны. Plimpton 322 — это «точная» тригонометрическая таблица, потому что она имеет только тригонометрические функции, основанные на треугольниках с целыми длинами сторон. (И на самом деле создатель таблицы настроил ее так, что знаменатели всех дробей легко представить в базе 60.) 

Современные триггерные таблицы основаны на углах, которые увеличиваются с постоянной скоростью. Они могут давать синусы 1°, 2°, 3° и т. д. или 0,1°, 0,2°, 0,3° и т. д. или даже более тонкие градации углов. Поскольку, как и другие древние жители Месопотамии, люди, создавшие Плимптона 322, думали о треугольниках с точки зрения длин сторон, а не углов, углы не изменяются постоянно. В этом разница между этой триггерной таблицей и современными триггерными таблицами. Ни один из способов не является превосходным по своей сути. Если бы мы захотели сделать современные триггерные таблицы с углами, которые имели бы только рациональные триггерные функции, мы могли бы, но это не сделало бы вычисления значительно более точными.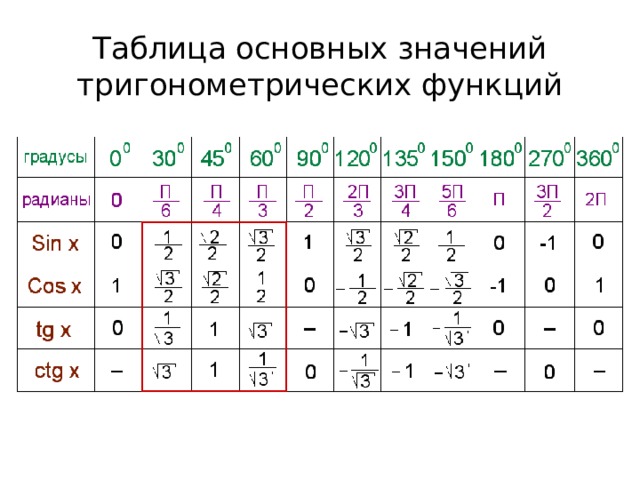 В любом случае мы могли бы получить точность, необходимую для любого конкретного приложения.

Небольшие раскопки показывают, что у Вильдбергера есть любимая идея под названием «рациональная тригонометрия». Кажется, он несколько скептически относится к вещам, связанным с бесконечностью, включая иррациональные числа, которые имеют бесконечные неповторяющиеся десятичные представления. Бегло прочитав написанную им главу о рациональной тригонометрии, я не вижу ничего вопиюще неправильного в этой теории, но она кажется решением проблемы, которой не существует. Тот факт, что большинство углов имеют иррациональные синусы, косинусы и тангенсы, не беспокоит подавляющее большинство математиков, физиков, инженеров и других, использующих тригонометрию. Трудно не заметить, что их работа над Plimpton 322 мотивирована желанием узаконить подход, который почти не пользуется популярностью в математическом сообществе.

Основание 60 лучше, чем основание 10?

Возможно, полезность различных типов триггерных таблиц зависит от мнения, но в видео UNSW также есть несколько откровенных ложных сведений о точности в системе с основанием 60 по сравнению с системой с основанием 10, которую мы сейчас используем. Примерно на отметке 1:10 Мэнсфилд говорит: «Мы считаем по основанию 10, которое имеет только две точные дроби: 1/2, что равно 0,5, и 1/5». Мое первое возражение состоит в том, что любая дробь точна. Число 1/3 как раз и есть 1/3. Мэнсфилд ясно дает понять, что под 1/3, не являющейся точной дробью, он подразумевает то, что она имеет бесконечное число (0,333…), а не конечную десятичную дробь. А как же 1/4? Это 0,25, что означает окончание, и все же Мэнсфилд не считает это точной дробью. А как насчет 1/10 или 2/5? Их можно записать как 0,1 и 0,4, что кажется довольно точным.

Неоправданно, когда он восхваляет множество «точных дробей», доступных в базе 60, он не применяет те же стандарты. В системе счисления 60 1/8 будет записано как 7/60+30/3600, что является той же идеей, что и запись 0,25 или 2/10+5/100 для 1/4 в базе 10. Почему 1/8 является точным в основание 60, но 1/4 не точно в основании 10? Трудно поверить, что это честная ошибка математика, и вместо этого я еще больше подозреваю, что его работа мотивирована повесткой дня.