Решить онлайн задачу по геометрии бесплатно: геометрии калькулятор

1. Как быстрее всего решать задачи по геометрии?

Одним из самых быстрых и простых способов решения задачи по геометрии является использование онлайн-калькуляторов геометрии.

2. Существуют ли приложения или веб-сайты для решения геометрических задач?

Да, Onlinecalculator.guru — лучший веб-сайт, помогающий учащимся решать задачи по геометрии. Он предлагает различные бесплатные онлайн-калькуляторы концепций геометрии для всех вас, чтобы упростить ваши расчеты.

3. Где я могу найти подробные шаги, чтобы понять решения расчета геометрии?

С помощью калькулятора геометрии вы можете легко найти решение и подробные шаги, чтобы понять концепцию расчета задачи.

4. Как решать задачи по геометрии на калькуляторе?

Просто введите числа или уравнения в поля ввода калькулятора и нажмите кнопку расчета, чтобы мгновенно получить результат вместе с подробным объяснением.

Помощь с домашним заданием по геометрии | Наймите онлайн-помощника по геометрии

Больше не нужно нервничать: получите помощь по домашнему заданию по геометрии, которая вам нужна

Даже самый успешный и преданный ученик может столкнуться с трудностями при решении сложных задач, связанных с геометрией. Будь то отдельная концепция в рамках этого курса или весь предмет целиком, студентам часто нужна рука помощи. И обращение за помощью к домашним заданиям по геометрии, которая вам нужна сейчас, а не позже, может сохранить ваши оценки на высоком уровне и вашу карьеру в колледже.

Почему наша помощь в выполнении задания по геометрии — это отличное жизненное решение

В StudyGate мы серьезно относимся к нашей приверженности успеху учащихся. Мы понимаем, что у вас нет времени ждать ответов от преподавателей и вы не хотите отправлять некачественные задания. Вот почему мы создали платформу, которая мгновенно реагирует на ваши потребности. Быстрые клики, удобный интерфейс и бесперебойная работа обеспечивают обмен сообщениями между вами и вашим преподавателем со скоростью света.

Но не только технология отличает StudyGate; наша команда помощников по геометрии прошла строгий процесс проверки, который гарантирует, что они знают свои предметы. Они также понимают серьезность вашего положения. Если у вас есть крайний срок на следующий день или два, вам нужно работать с экспертами, которые могут выполнить то, что они обещают. Мы позволяем вам выбирать, с кем вы будете работать над ответами на домашнее задание по геометрии, и если вы недовольны возвращенной вам работой, мы все исправим.

Мы в StudyGate верим в простую концепцию: вы платите за помощь в выполнении домашнего задания по геометрии и заслуживаете уважения. Это то, что вы всегда получите от членов нашей команды — уважение, прозрачность и доступ к обширным знаниям.

Взгляд на аналитическую геометрию

Эта область исследования опирается на систему координат для изучения геометрических построений и фигур. В частности, он моделирует основные и сложные геометрические объекты, включая окружности, прямые линии и точки. Наша команда экспертов прекрасно понимает необходимость точности ответов на домашние задания по геометрии. Их не пугают сложные концепции, и они могут упростить их для понимания.

Ясность дифференциальной геометрии

Эта область геометрии изучает линии, поверхности и плоскости в трехмерном пространстве. Курсы дифференциальной геометрии известны тем, что они математически строгие, но при этом подчеркивают геометрические принципы. Другими словами, многим студентам приходится нелегко на этом курсе. Наши преподаватели, однако, ждут от любой помощи в выполнении домашних заданий по геометрии и приветствуют ваши самые сложные вопросы.

Алгебраическая геометрия

Принципы алгебраической геометрии используются для планирования экспериментов и проверки гипотез в исследовательских целях. Если вы не знаете, что это за принципы, наши эксперты готовы помочь вам с домашним заданием по геометрии. Они также могут помочь в других областях, включая евклидову и неевклидову геометрию. Это означает, что на любой вопрос можно ответить понятным для вас образом и в соответствии с требованиями вашего инструктора.

Получите самую точную помощь для домашнего задания по геометрии

Ранее мы упоминали, что геометрия — это область точности. Наши специалисты уже изучили этот предмет, а некоторые даже специализировались на нем, и могут дать столь необходимый толчок к отстающим оценкам или неясности. Не тратьте еще одну бессонную ночь, беспокоясь об ответах на домашнее задание по геометрии. Надежная помощь на расстоянии одного клика.

Несколько советов от наших экспертов

Учащиеся часто теряются во множестве различных деталей геометрии. Мы хотим облегчить ваше разочарование и предлагаем бесплатную онлайн-помощь в выполнении домашних заданий по геометрии. Например, наши эксперты рекомендуют вам понять пять постулатов Евклида, первый из которых гласит, что можно провести прямую линию, соединяющую любые две точки. Как только они будут поняты, другие концепции будут иметь больше смысла.

Вам также следует выучить теорему Пифагора и различные типы треугольников. Наконец, делайте тщательные заметки в классе. Даже если вы несколько раз выберете StudyGate для помощи в задании по геометрии, эти заметки будут полезны как вам, так и нашей команде. Мы можем использовать их, чтобы понять методы обучения вашего преподавателя и то, что он или она ожидает увидеть в каждом задании.

См. пример вопроса и ответа по геометрии для себя, если одного раза было недостаточно, мы снова предоставляем бесплатную онлайн-помощь по геометрии, чтобы вы могли увидеть наших преподавателей в действии.

Вопрос

Преобразуйте следующие градусы в радианы и радианы в градусы. Обязательно укажите единицы измерения, либо градусы, либо радианы (используйте аббревиатуру «рад» для радианов).

A. 40°
B. /10
C. 150°

Ответы

A. 40° = /180 = 40/180 = 4/18 рад
B. /10 = 180/ = 180/10 = 18°
C. 150° = /180 = 150/160 = 5/6 рад

Веские причины выбрать нашу доступную помощь для домашнего задания по геометрии

Поиск правильных ответов по любому вопросу требует много времени. Но когда ваш преподаватель дал вам задание к определенной дате, вы должны выполнить его. Не рискуйте получить плохую оценку, просто пропустив крайний срок; Получите необходимую помощь по геометрии в домашней работе по математике от уважаемой команды.

Дай 10 долларов, получи 10 долларов

Давайте немного поговорим о том, как положить дополнительные деньги в карман. Будучи студентом колледжа, мы знаем, что вам нужно хотя бы немного денег, чтобы пойти куда-нибудь с друзьями, купить припасы и поесть. Благодаря нашей программе «Подари 10 долларов, получи 10 долларов» мы будем загружать 10 долларов на ваш бумажник StudyGate каждый раз, когда вы приглашаете другого студента, который зарегистрируется у нас. Ваш друг также получит 10 долларов, и вы оба сможете использовать эти средства в следующий раз, когда вам понадобится помощь с домашним заданием по геометрии.

Обещание никакой ерунды

Мы не любим путаницы, и мы держим пари, что вы тоже. Наше обещание «Нет ерунде» делает вещи ясными и простыми, начиная с ценообразования. Мы не взимаем ежемесячные членские взносы, плату за использование или другие скрытые платежи. Вы будете точно знать, сколько берет ваш репетитор, еще до того, как начнете сотрудничать с ним или с ней для помощи в задании по геометрии.
После того, как нужная помощь с домашним заданием по геометрии будет доставлена, мы задержим ваш платеж на 14 дней. Используйте это время, чтобы убедиться, что вы получили правильный ответ и что ваш преподаватель доволен. Только после того, как вы одобрите работу вашего репетитора, мы разблокируем оплату. Это обеспечивает вам полную защиту; поверьте нам, когда мы говорим, что вам не о чем беспокоиться с домашней работой по геометрии от StudyGate.

Если вы недовольны нашей работой, мы вернем вам деньги. Например, если ответы на домашнее задание по геометрии были правильными менее чем на 80 % или были выполнены за пределами ваших временных параметров, вы ничего не платите. Наша цель — предоставить выдающуюся помощь в выполнении домашних заданий по геометрии, и если мы не справимся, нам не нужны ваши деньги.

Мы упомянули эти факторы только потому, что вы должны быть уверены в помощи по заданию геометрии, которую мы предоставляем. Наш уровень удовлетворенности клиентов составляет около 97%, а это означает, что мы редко сталкиваемся с недовольным студентом. На самом деле, большинство из них возвращаются к нашим преподавателям за дополнительной помощью в задании по геометрии.

Помощь предоставляется круглосуточно и без выходных

Поздно ночью, рано утром и даже в выходные дни. Всякий раз, когда вам нужны ответы на домашние задания по геометрии, мы здесь. И то же самое верно, если вам нужно уточнить детали вашего задания или предоставить нам дополнительную информацию. Работаем по удобному для вас графику.

Удивительная команда репетиторов наготове

У нас есть много репетиторов, с которыми вы можете работать. Некоторые, как Анита С., преподают студентам информатику и математику. Другие, такие как Игнатий Н., занимают профессиональные должности и имеют опыт репетиторства по таким предметам, как статистика, физика и т. д. Это всего лишь два эксперта в огромном сообществе, стремящемся поделиться своими знаниями. Проявив немного юмора, много терпения и дополнительную дозу доброты, наша команда может превратить срочную потребность в помощи с заданием по геометрии в удивительно приятное занятие.

Мы знаем, что у вас есть крайний срок, и мы его выполним

Необходимость укладываться в сроки возникает довольно рано, сопровождая большинство из нас в колледже и в нашей профессиональной карьере. Имея это в виду, мы не подведем вас, когда вы обратитесь к нам за помощью в домашнем задании по геометрии. Мы знаем, что вы хотите произвести впечатление на своего преподавателя, продемонстрировав приверженность своевременному и качественному выполнению заданий. Помощь с домашним заданием по геометрии, которую мы предоставляем, поддержит ваши усилия и докажет, что вы добросовестный ученик.

Мы помним свои студенческие годы

Не так давно мы тоже учились в колледже. На самом деле, некоторые из наших преподавателей даже сейчас получают ученые степени в таких областях, как математика и естественные науки. Это люди, с которыми вы хотите работать вместе — те, кто понимает необходимость академической честности и ответов на домашние задания по геометрии, подкрепленных доказательствами.
Члены команды, с которыми мы работали, являются экспертами в своих областях. Если вы думаете о том, чтобы попросить помощи с домашним заданием по геометрии, не бойтесь. Вам нечем рисковать, и вы можете получить все. StudyGate может облегчить ваши заботы, снять стресс и дать вам возможность насладиться студенческими годами. Задайте свой вопрос сегодня – наши преподаватели ждут вас.

Часто задаваемые вопросы

и

Как я могу улучшить свою геометрию?

В отличие от некоторых ответов на домашние задания по геометрии, ответ на этот вопрос прост: наймите репетитора из StudyGate.

Наши профессионалы могут превратить сложные концепции в идеи, которые легко понять. Ваши ответы на домашнее задание по геометрии будут выполнены правильно и, благодаря лаконичному изложению, будут иметь для вас смысл. Вы сможете точно увидеть, что сделал ваш наставник и почему он или она это сделали. А если вам нужна дополнительная помощь, наши онлайн-репетиторы помогут вам пройти этот курс и подготовиться к следующему семестру.

и

Может ли Google решать математические задачи?

У Google есть довольно большие возможности, но, в конце концов, он работает на искусственном интеллекте. Это означает, что ему не хватает человеческого сочувствия и терпения, которые необходимы, чтобы помочь вам по-настоящему понять геометрические принципы. Поэтому мы рекомендуем вам придерживаться рекомендаций экспертов и доверить домашнее задание по геометрии тем, кто был на вашем месте.

и

Какой сайт решает любую математическую задачу?

Мы понимаем, что у вас есть много вариантов, но преподаватели StudyGate любят сложные задачи.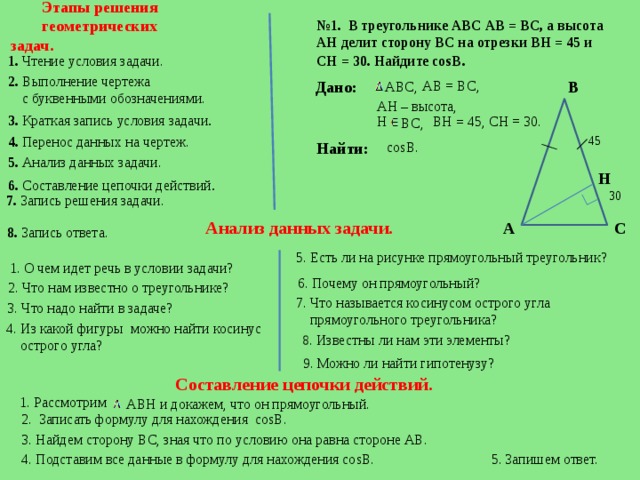 Мы не только можем решить любую математическую задачу, но и с нетерпением ждем этого. Вот почему мы делаем то, что делаем. Если бы мы не любили математику, мы бы не посвящали время таким ученикам, как вы. Так что давай, отправь нам запрос на помощь с домашним заданием по геометрии, который кажется невозможным. Мы уверены, что видели это или что-то подобное раньше, и с нетерпением ждем возможности использовать наш мозг для разработки новых ответов на домашнее задание по геометрии.

и

Какая математика является геометрией?

Этот раздел математики изучает размеры, углы, положения, формы и размеры многих элементов. Большое внимание уделяется плоским формам, таким как треугольники и квадраты, которые известны как 2D-формы.

и

С какой онлайн-репетиторской компанией лучше работать?

Это еще один простой ответ. Любая ваша потребность в помощи по математике по геометрии лучше всего решается с помощью StudyGate. Мы занимаемся этим уже некоторое время — восемь лет — и помогли бесчисленному количеству учеников получить отличные оценки. У нас есть надежный процесс для обеспечения быстрой связи между вами и вашим преподавателем, и наши цены доступны. Мы также гарантируем точность. О чем еще ты можешь попросить?

и

Как решить задачу по геометрии?

Сначала мы рассмотрим ваш уникальный проект, чтобы понять характер вашей помощи в выполнении домашнего задания по геометрии. Участвуют ли чертежи? Нужно ли давать письменное объяснение? Нам ничего не передается, и если нам понадобится дополнительная информация, мы без колебаний обратимся к вам. Как только у нас будут свои утки в ряду, мы продолжим разработку тщательного и краткого ответа. Любые источники, которые мы используем, будут задокументированы, и шаги, которые мы предприняли из точки А в точку Б, будут понятны.

и

Какие три типа геометрии существуют?

Три основных типа: евклидовы, гиперболические и эллиптические. И будьте уверены, мы можем помочь с домашним заданием по геометрии в каждой из этих областей.