Построить график функции f x y: математика — Как построить график функции f(x,y) = 0?

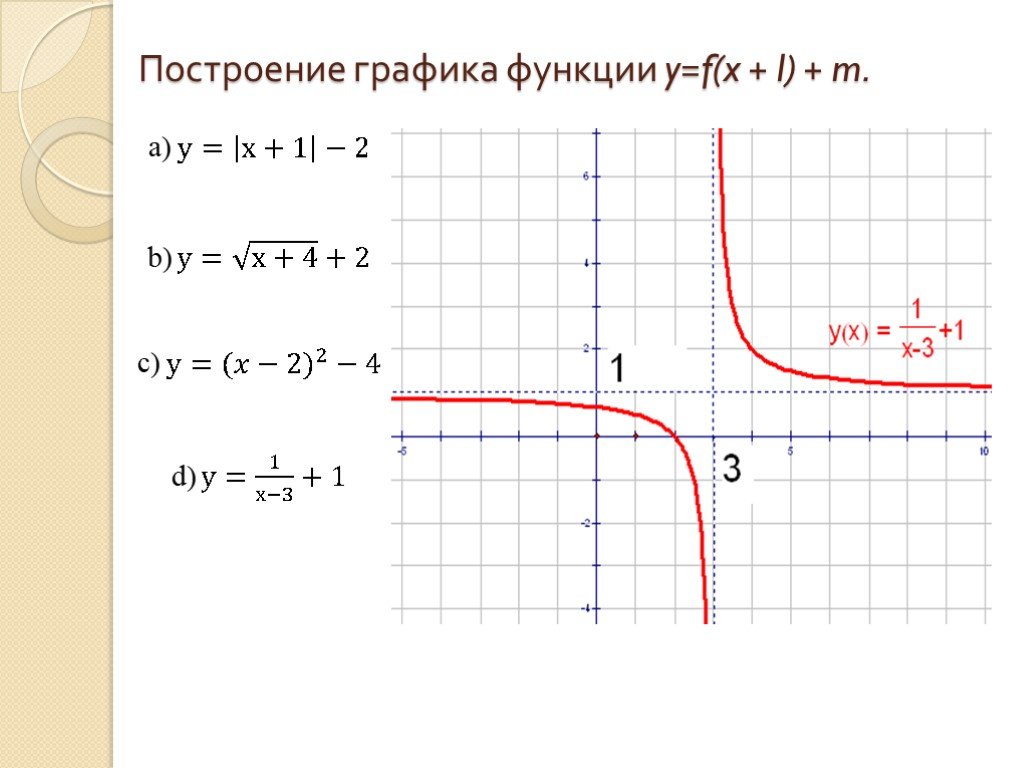
НОУ ИНТУИТ | Лекция | Графика

< Дополнительный материал  || Лекция 3: 123456

Аннотация: В лекции представлены методы построения типичных графиков функций на плоскости и в пространстве, а также инструменты их редактирования, форматирования и настройки. Описаны разные технологические приемы построения графиков функций: автоматически, с помощью сетки и с применением специальных функций.

Ключевые слова: программа, координаты, панель инструментов, графика, меню, список, шаблон, прямоугольник, имя функции, курсор, область определения, функция, график, множества, значение, опция, радиус, массив

Цель лекции. Научить строить графики функций в разных системах координат с помощью различных технологических приемов. Показать способы форматирования и настройки разных типов графиков и диаграмм.

3.1. Инструменты графики

MathCAD предоставляет широкие возможности для построения графиков. Графические построения являются универсальными и легкими в использовании. Программа позволяет строить графики на плоскости и в трехмерном пространстве. Можно использовать декартовы и полярные координаты на плоскости, сферическую и цилиндрическую систему координат в пространстве.

Панель Математика содержит панель инструментов графики. Для построения графиков используются шаблоны. Большинство параметров графического процессора, необходимых для построения графиков, по умолчанию задается автоматически. Поэтому для начального построения графика того или иного вида достаточно задать тип графика. На панели Graph (Графика) или в меню Insert/ Graph (Вставка/Графика) содержится список из семи основных типов графиков.

Рис. 3.1. Панель Графика

1. Декартов график [@] —шаблон двухмерного графика;
2. intuit.ru/2010/edi»>Полярный график [Ctrl+ 7] —шаблон графика в полярной системе координат;
3. График поверхности [Ctrl+ 2] — шаблон для построения трехмерного графика;
4. Карта линий уровня [Ctrl+ 5] —шаблон для контурного графика трехмерной поверхности;
5. 3D точечный график –шаблон для графика в виде точек в трехмерном пространстве;
6. 3D столбиковая гистограмма –шаблон для изображения в виде совокупности столбиков в трехмерном пространстве;
7. Векторное поле— создать шаблон для графика векторного поля на плоскости.

Для вывода шаблона двухмерной графики в декартовой системе координат служит кнопка декартов график на панели Graph [3, 8]. Она выводит в текущее положение курсора шаблон графиков в декартовых координатах (Рис.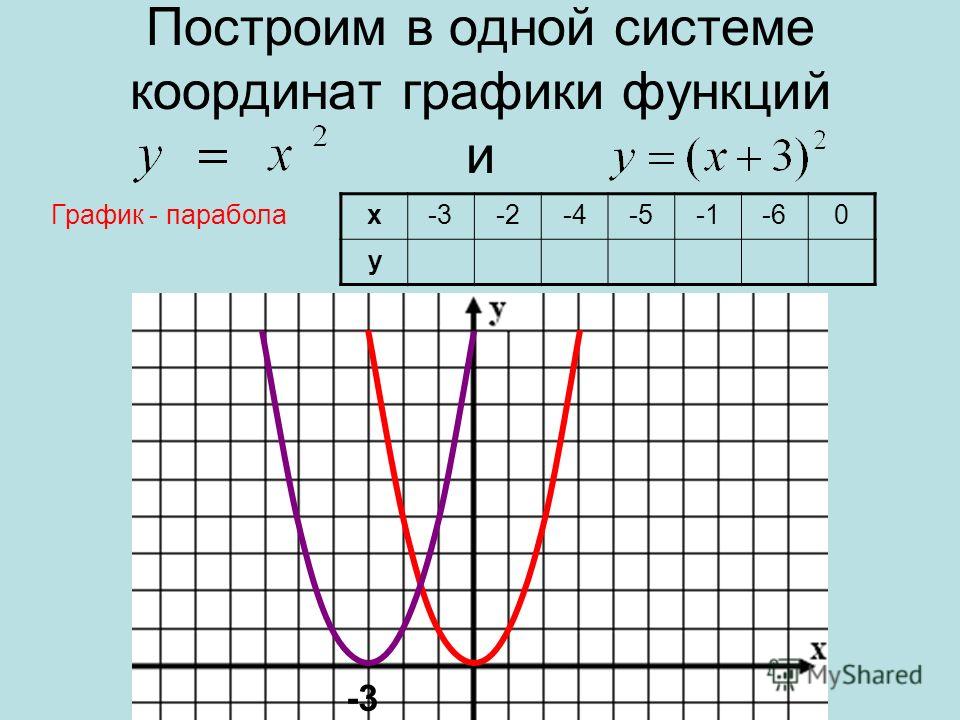

3.2). Незаполненный шаблон графика — пустой прямоугольник с шаблонами данных в виде темных маленьких прямоугольников, расположенных около осей абсцисс и ординат будущего графика.

Рис. 3.2. Шаблон графика в декартовых координатах

В средние шаблоны данных надо поместить имя функции F(x) оси абсцисс x. Если строятся графики нескольких функций в одном шаблоне, то для их разделения следует использовать запятые. Крайние шаблоны данных служат для указания предельных значений абсцисс и ординат, т. е. они задают масштабы графика. Если оставить эти шаблоны незаполненными, то масштабы по осям графика будут устанавливаться автоматически. Масштабы, могут оказаться неудобными для представления целиком всего графика в максимальном размере. Рекомендуется всегда вначале использовать автоматическое масштабирование, а затем изменять масштабы на более подходящие.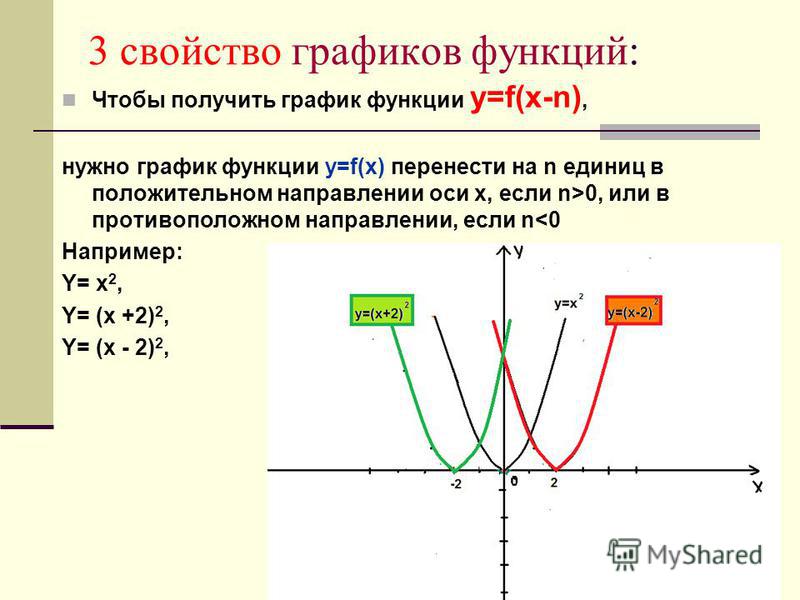

Для построения графика достаточно вывести курсор за пределы графического объекта.

3.2. Построение графиков функций на плоскости

Для построения графика функции надо написать функцию, выбрать интервалы построения графика по оси X и Y и обозначить параметры графика. При этом следует учитывать область допустимых значений существования функции или область определения. Если функция задана формулой, то область определения состоит из всех значений независимой переменной, при которых формула имеет смысл. График функции может быть представлен в различных системах координат. Наиболее употребительна прямоугольная координатная система – декартова. На плоскости применяют полярные системы координат, а в пространстве, наряду с декартовыми, цилиндрические и сферические системы координат.

3.2.1.Декартов график

Пример 3.1. Построить графики функций : , , . Функция не существует в точке . Но график строится и никаких дополнительных действий предпринимать не нужно. В отличие от построения графиков поверхности. Но эту проблему рассмотрим ниже.

Построение графика

Форматирование графика

Параметры изображения (цвет и толщина линий, координатная сетка, разметка осей, надписи на графиках и др.) можно изменить, вызвав команду меню Format/Graph/X-Y Plot (Формат/График/декартов график) или щелкнув дважды по полю графика. Появится окно Formatting Currently Selected X-Y Plot (Форматирование выбранного графика), в котором устанавливаются настройки в соответствующих вкладках (Рис.3.7).

Рис. 3.7. Окно форматирования декартова графика

• Вкладка X-Y оси устанавливает для осей X и Y : тип шкалы: логарифмическая Log scale, цифровая Numbered), линии сетки (Grid Lines), Сетку автоматическую (Auto Grid) или режим задания количества меток (Number of Grid). Внизу устанавливается стиль вида осей (Axes Style)/
• Вкладка Traces устанавливает условные обозначения различных кривых графика.
• Вкладка Надпись (Labels) расположение надписей.

Установка границ на осях координат

MathCAD обеспечивает следующие возможности устанавливать границы на осях координат:

• Автоматически, с включенным режимом Авто масштаб (Autoscale)(см. закладка » X-Y Оси » ).
• Автоматически, с выключенным режимом Авто масштаб.
• Вручную, вводя границы непосредственно на графике.

При включенном режиме Авто масштаб MathCAD устанавливает границу на каждой оси соответствующей первому главному делению, выходящему за пределы значений данных

intuit.ru/2010/edi»>При выключенном режиме Авто масштаб MathCAD устанавливает границы на осях точно равными пределам данных.

Добавление горизонтальных и вертикальных линий

Чтобы добавить горизонтальную или вертикальную линию к графику:

• вызвать окно форматирования графика в декартовых координатах,
• в диалоговом окне Форматирование— закладка » X-Y Оси » ,
• щёлкнуть » Нанести риски » (для X-оси, или Y-оси). MathCAD показывает два дополнительных пустых поля на каждой оси, для которой включена опция » Нанести риски «,
• впечатать значение, для которого нужно провести линию,
• чтобы удалить линию, удалить это число или щёлкните на поле » Нанести риски «

Дальше >>

< Дополнительный материал  || Лекция 3: 123456

Преобразования графиков функций

Преобразования графиков функций Исследовательская работа

y=f(x)

y=|f(x)|

y=f(|x|)

|y|=f(x)

y=|f(|x|)|

|y|=|f(x)|

Актуальность: Эта тема актуальна, т. к. в конце 11 класса необходимо сдавать единый государственный экзамен по математике, куда будут включены задания, связанные с преобразованием графиков функций.

Нами были проанализированы различные собрания с экзаменационными заданиями.

Вывод: в сборниках КИМ единого государственного экзамена по математике встречаются задания на использование знаний о различных преобразованиях графиков функций.

Цель: Изучение способов построения графиков функций с помощью различных преобразований.

Задачи:

• Исследовать взаимосвязь графика функции y = f ( x ) с графиками функций y =| f ( x )|, y=f(|x|) , y=f(kx), y=kf(x), y= -f(x), y=f(x)+b, y=f(x-a).
• Рассмотреть задания на построение графиков функций с помощью преобразований.
• Попробовать создать рисунок, используя исследуемые функции.
• Узнать, есть ли более профессиональные и эффективные системы для построения графиков в декартовых системах координат кроме E xcel и C alc, которые мы использовали для построения в прошлой работе.
• Выявить в чём преимущества и недостатки этих компьютерных программ.

Рабочая гипотеза : графики сложных функций, можно построить с помощью преобразований графика исходной функции.

Объект – графики функций.

Предмет – построение графиков сложных функций с помощью преобразования графика исходной функции.

Методы исследования: наблюдения, сравнения, анализ, обобщение, прогнозирование, знаковое моделирование.

y= -f( х )

y=f( х )

Симметрия относительно оси «ох»

Сохраняя ту часть, где х ≥0, выполнить её симметрию относительно оси «оу»

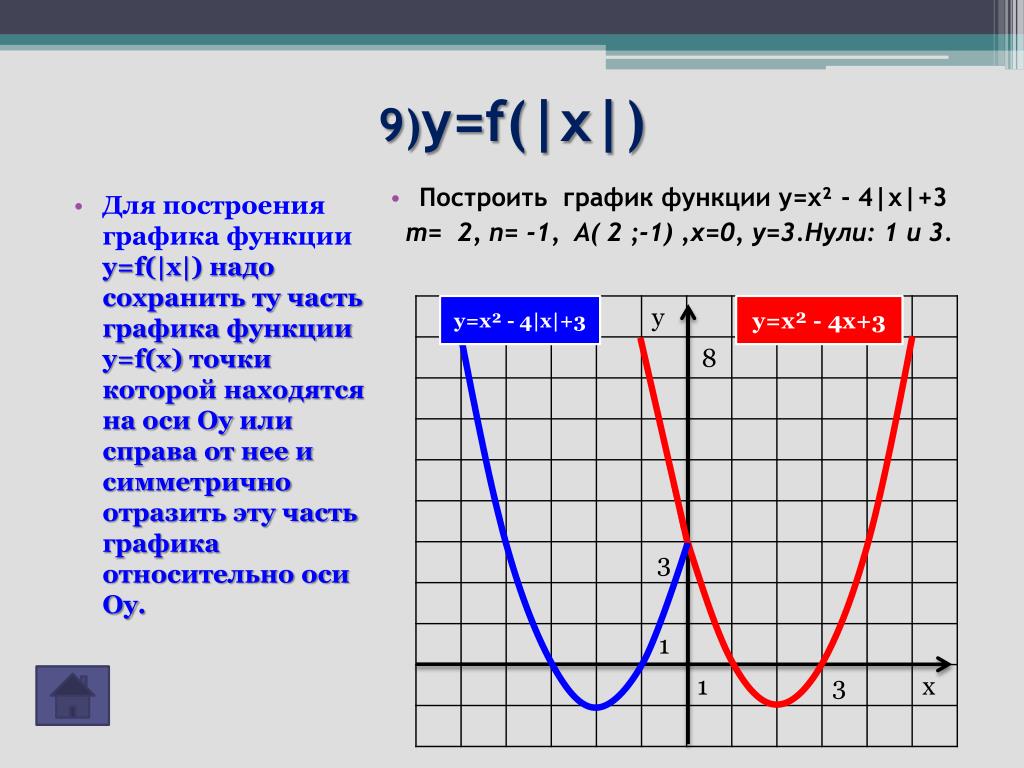
y=f(| х |)

y=f( х )

y=f( х )

Сохраняя ту часть, где у ≥0, выполнить симметрию относительно «ох» той части, где у

y = |f( х )|

?

y=cos х y= -cos x

?

y=cos х y=cos |x|

?

y=cos х y=|cos x|

y=cos х

Графиком является косинусоида, проходящая через точки:

x

0

y

1

0,5

0

-0,5

-1

y=cos х

?

y=cos х y= -cos x

y=cos х

y= -cos x

Для того, чтобы из графика функции y = cos x получить график функции y = — cos x , необходимо выполнить симметрию исходного графика относительно оси «ох».

?

y=cos х y=cos |x|

y=cos х

y=cos |x|

Для того, чтобы из графика функции y = cos x получить график функции y = cos | x |, необходимо сохранить ту часть исходного графика, где х≥0, и выполнить её симметрию относительно «оу», а это и будет сам график y = cos x .

?

y=cos х y=|cos x|

y=|cos x|

y=cos х

Для того, чтобы из графика функции y = cos x получить график функции y =| cos x |, необходимо сохранить ту часть исходного графика, где у≥0, и выполнить симметрию относительно «ох» той части, где у

?

y=cos х y=|cos |x||

y=|cos | х ||

y=cos | х |

y=cos х

y=|cos | х ||

y=cos х

y=cos | х |

Для того, чтобы из графика функции y = cos x получить график функции y =| cos | x ||, необходимо сохранить ту часть исходного графика, где х≥0, и выполнить её симметрию относительно «оу», а затем сохранить ту часть получившеюся графика, где у≥0, и выполнить её симметрию относительно «ох» той части, где у

y=cos х y=cos 3 x

?

y=cos 3 x

График этой функции проходит через точки:

х

у

0

1

0

-1

0

1

0

-1

0

-1

0

1

0

-1

?

y=cos х y=cos 3 x

y=cos х

y=cos 3 x

Вывод: Для того, чтобы из графика функции y = cos x получить график функции y = cos 3 x , необходимо сжать исходный график в 3 раза вдоль «ох».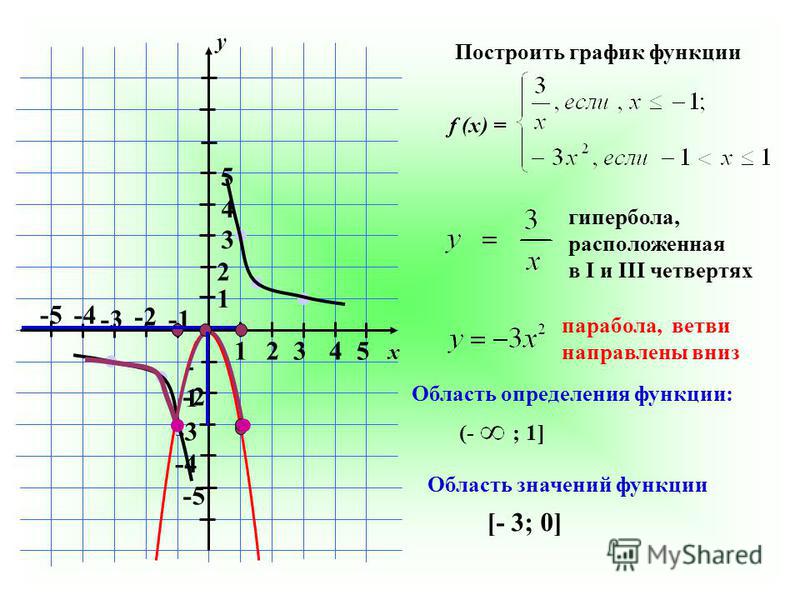

y=cos х y=cos x /3

?

y=cos x /3

График этой функции проходит через точки:

х

у

0

1

0,5

?

y=cos х y=cos x /3

y=cos x /3

y=cos х

Вывод : Для того, чтобы из графика функции y = cos x получить график функции y = cos x /3, необходимо выполнить растяжение исходного графика в 3 раза вдоль оси «ох».

y=cos х y= 3 cos x

?

y= 3 cos x

График проходит через точки:

х

у

0

3

1,5

0

-1,5

-3

1,5

0

-1,5

-3

?

y=cos х y= 3 cos x

y= 3 cos x

y=cos х

Вывод: Для того, чтобы из графика функции y = cos x получить график функции y =3 cos x , необходимо растянуть исходный график в 3 раза вдоль оси «оу».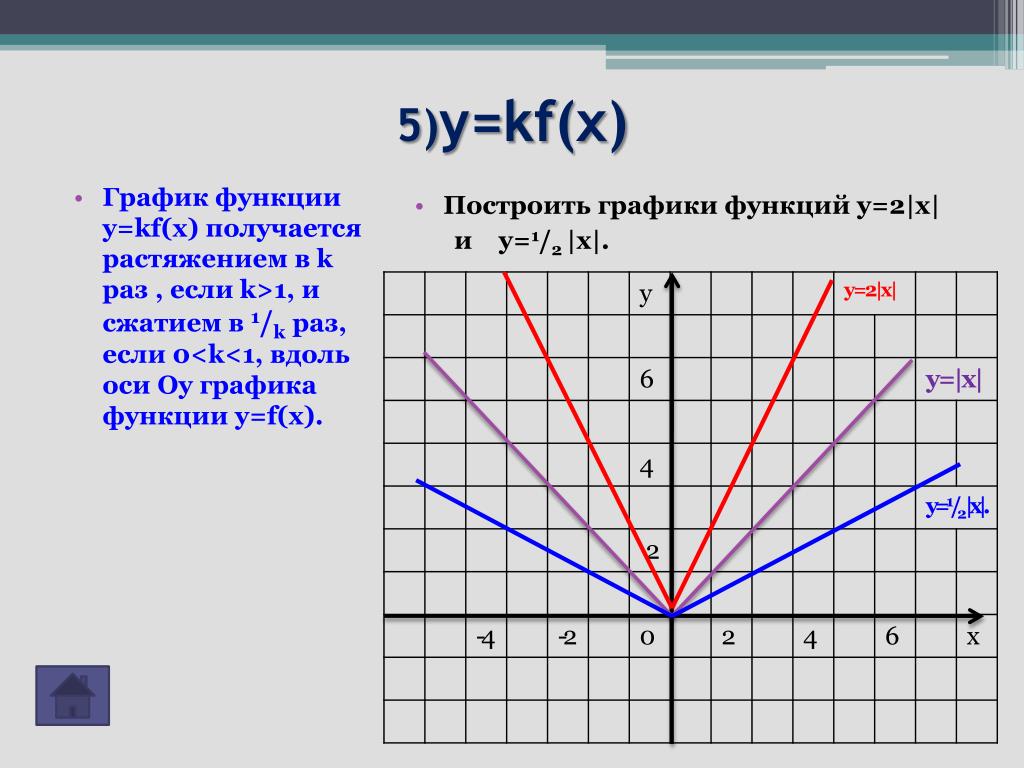

y=cos х y=cos ( x +2)

?

y=cos ( x +2)

Графиком является косинусоида, проходящая через точки:

х

у

0

-0,5

1

-0,5

0

0,5

0

0,5

1

0,5

?

y=cos х y=cos ( x +2)

y=cos ( x +2)

y=cos х

Вывод: Для того, чтобы из графика функции y = cos x получить график функции y = cos ( x +2) , необходимо сдвинуть исходный график вдоль оси «ох» на 2 единицы влево.

y=cos х y=cos x -3

?

y=cos x -3

Графиком является косинусоида, проходящая через точки:

х

у

0

-2

-2,5

-3

-3,5

-4

-2,5

-3

-3,5

-4

?

y=cos х y=cos x -3

Вывод: Для того, чтобы из графика функции y = cos x получить график функции y = cos x -3, необходимо сдвинуть исходный график вдоль оси «оу» на 3 единицы вниз.

1 , то сжатие исходного графика в k раз вдоль оси «ох», если 0 y=f(kx) y=f(x) Если k 1 , то растяжение исходного графика в k раз вдоль оси «оу», если 0 y=f(x) y=kf(x) Симметрия исходного графика относительно оси «ох» y= — f(x) y=f(x) Сдвиг вдоль оси «ох», если а ≥0, то на а единиц вправо, если а а единиц влево y=f(x — a) y=f(x) Сдвиг вдоль оси «оу», если b ≥0, то на b единиц вверх, если bb единиц вниз y=f(x) + b y=f(x) «

Итог:

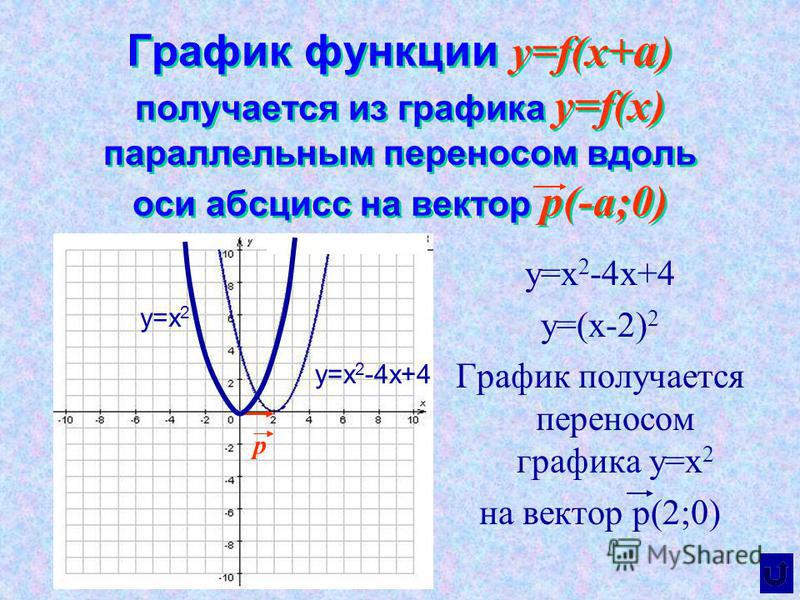
Сохраняя ту часть исходного графика, где х ≥0, выполнить её симметрию относительно оси «оу»

y=f(x)

y=f(|x|)

Сохраняя ту часть, где у ≥0, выполнить симметрию относительно оси «ох» той части, где у

y=|f(x)|

y=f(x)

Если k 1 , то сжатие исходного графика в k раз вдоль оси «ох», если 0

y=f(kx)

y=f(x)

Если k 1 , то растяжение исходного графика в k раз вдоль оси «оу», если 0

y=f(x)

y=kf(x)

Симметрия исходного графика относительно оси «ох»

y= — f(x)

y=f(x)

Сдвиг вдоль оси «ох», если а ≥0, то на а единиц вправо, если а а единиц влево

y=f(x — a)

y=f(x)

Сдвиг вдоль оси «оу», если b ≥0, то на b единиц вверх, если bb единиц вниз

y=f(x) + b

y=f(x)

Исследование количества корней уравнения:

y=a

1.

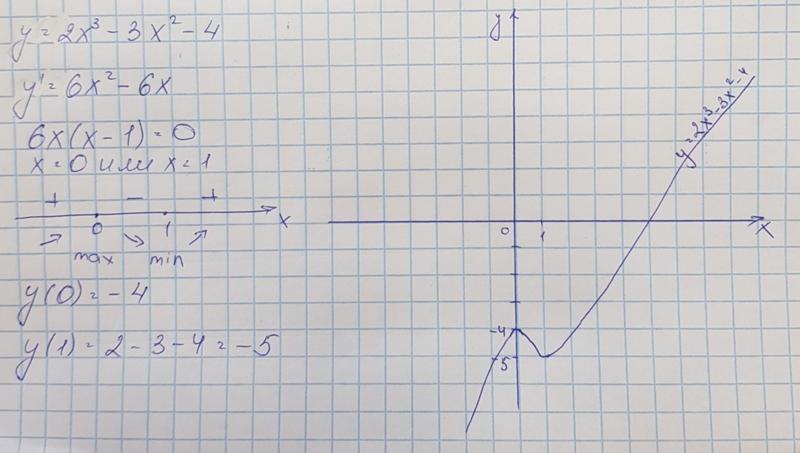
Мы знаем, что для того, чтобы из графика функции получить график функции необходимо растянуть исходный график в 4 раза вдоль оси «оу».

Графиком является косинусоида, проходящая через точки:

х

0

у

1

0,5

0

-0,5

-1

2. у=а – линейная функция.

Графиком является прямая, параллельная оси «ох» и проходящая через точки (2;а) и (0;а).

y=6

y=4

y=4cos x

а) Уравнение 4cos x =a имеет бесконечное множество корней при

б) Уравнение 4cos x =a не имеет корней при

y=1

y=-4

y=-6

Исследование количества корней уравнения:

|cos 2x| =x ²

• y=|cos 2x|

y=cos x y=cos 2x y=|cos 2x |

Мы знаем, что для того, чтобы из графика функции y=cos x получить график функции y=cos 2x , необходимо сжать исходный график в 2 раза вдоль оси «ох», а затем, чтобы получить график функции y=|cos 2x | , необходимо сохранить ту часть графика, где у ≥ 0, и выполнить симметрию относительно оси «ох» той части, где у

y=cos x

Графиком является косинусоида, проходящая через точки:

y=x² — квадратичная функция.

Графиком является парабола, ветви которой направлены вверх.

(0;0) – вершина параболы.

«оу» — ось симметрии параболы.

y=|cos 2x|

y=x²

х

0

у

1

0,5

0

-0,5

-1

х

0

у

1

0

2

1

3

4

9

-1

-2

1

-3

4

9

y=x ²

Т.к. графики функций y=|cos 2x| и y=x² пересекаются в двух точках, то уравнение |cos 2x| =x ² имеет 2 корня.

y=|cos 2x |

Функции, использованные для построения рисунка

Microsoft Office Excel и Open Office Calc

Wolfram Mathematica

1. Чтобы построить график функции необходимо указать список значений переменной «х», а затем ввести формулу для вычисления переменной «у». Только потом можно строить график.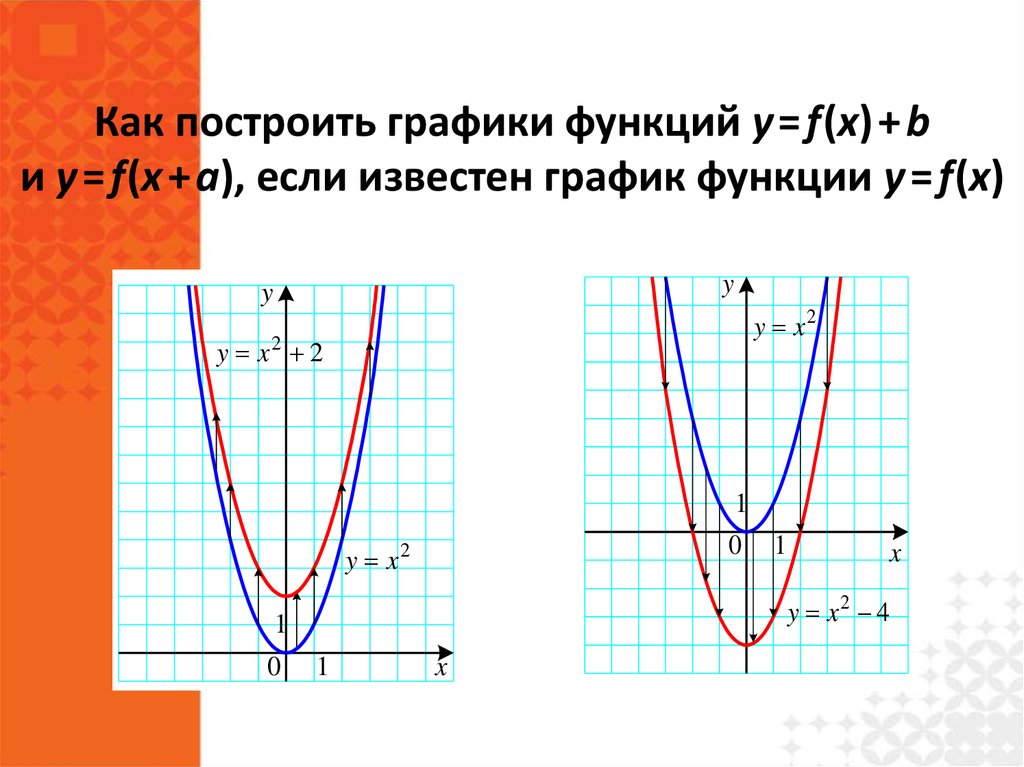

1. В отличие от других систем Mathematica применяет разумную автоматизацию. То есть достаточно выбрать необходимую команду, ввести функцию и указать её область значений, а затем программа сама построит график.

2. Как следствие из первого пункта, на построение графиков затрачивается большое количество времени. —

2. Исходя из первого пункта, можем сделать вывод, что на построение графиков затрачивается совсем немного времени.

3. Существует один способ построения графиков (мастер диаграмм – график или точечная)

3. Есть несколько способов построения графиков функций ( Plot , ListPlot и т.д.).

4. Чтобы каким-либо образом видоизменить график, необходимо зайти в меню «Диаграмма». Там указаны все возможные способы видоизменений графика.

4. Большинство различных видоизменений графика соответствует определённой опции, наименование которой необходимо знать наизусть или найти в справочном материале.

5. Интерфейс сложнее, чем в Mathematica и занимает большее пространство.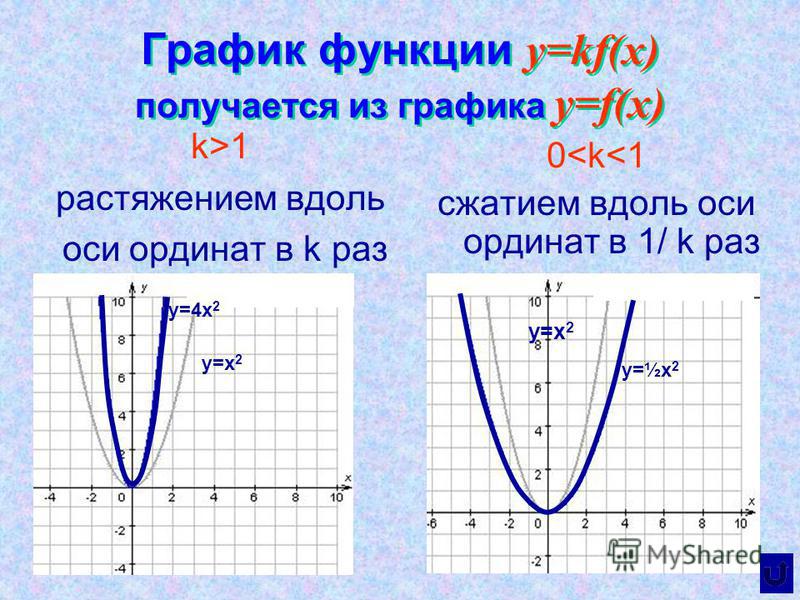

5. Интерфейс пакета значительно упрощён по сравнению с другими программами. Он строится из нескольких базовых понятий: Тетрадь, Ячейка и Палитра.

Поэтому, работая в этой системе, можно убрать всё ненужное и оставить только необходимое.

6. Не возникло трудностей с построением, т.к. всё уже знакомо. + и —

6. При построении графиков у меня возникли трудности, потому что мы впервые столкнулись с этой программой, многое расположено в других местах и метод построения графиков совершенно новый.

и

Но с опытом работы этот способ построения стал доступным и более лёгким.

Заключение

Цель достигнута , мы изучили способы построения графиков функций с помощью различных преобразований.

Задачи выполнены , мы исследовали взаимосвязь графика функции y = f ( x ) с графиками функций y =| f ( x )|, y=f(|x|) , y=f(kx), y=kf(x), y= -f(x), y=f(x)+b, y=f(x-a) ,научились строить эти графики, рассмотрели задания с применением таких функций, построили лицо мушкетёра, используя исследуемые функции, выяснили с помощью каких программных средств кроме Excel и Calc можно строить графики функций, выявили, в чём их преимущества и недостатки.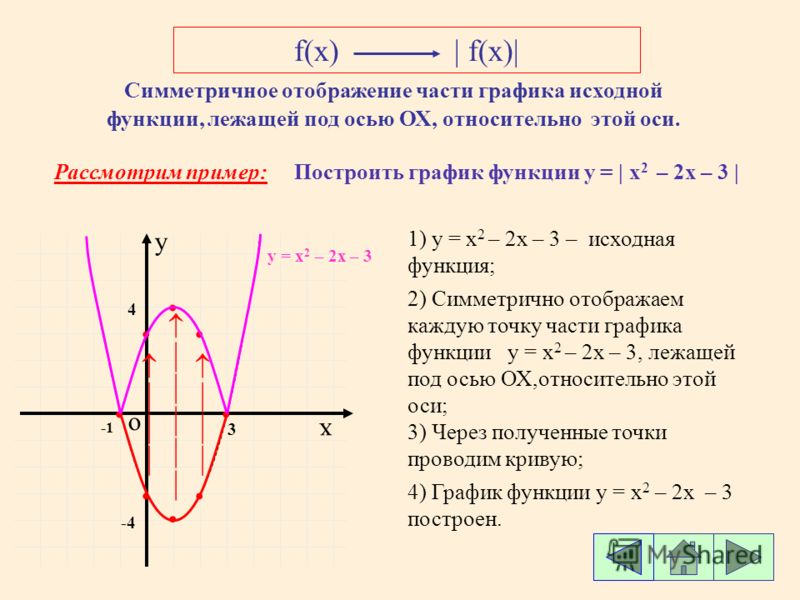

Теперь мы знаем, что для построения графиков используется не только Microsoft Office Excel и Open Office Calc , но есть и другие программы, не только не уступающие по возможностям этим программам, но и превышающие их, например, Wolfram Mathematica.

Значимость полученных результатов: сейчас нам стало известно, как строить графики сложных функций с помощью преобразований графика исходной функции, и если встретятся задания с применением этих функций, то мы будем знать, как они выполняются.

Использовать эти результаты можно при решении заданий единого государственного экзамена.

Спасибо за внимание!

2$

Загрузка…

Mathematics Stack Exchange — это сайт вопросов и ответов для людей, изучающих математику на любом уровне, и профессионалов в смежных областях. Регистрация занимает всего минуту.

Зарегистрируйтесь, чтобы присоединиться к этому сообществу

Любой может задать вопрос

Любой может ответить

Лучшие ответы голосуются и поднимаются на вершину 92$? Я могу построить функции одной переменной, но я не знаю, как построить функцию многих переменных.

• вычисления с несколькими переменными
• функции
• графические функции

$\endgroup$

3

$\begingroup$

Ваш участок имеет три измерения. Вы можете построить его в перспективе, в контурных линиях или в различных других представлениях. Альфа дает следующее: 9{2}}$ граф будет поверхностью!! Если вы хотите визуализировать любую такую ​​функцию, вы можете использовать https://www.wolframalpha.com/, и ваш график будет выглядеть как https://www.wolframalpha.com/input/?i=plot+x%5E2%2By%5E2.

PS:Я бы посоветовал вам использовать LaTeX для ввода вопросов.

$\endgroup$

 

неявный — Как построить конкретное решение в форме f (x, y) = 0 на Gnuplot

спросил 1 год, 7 месяцев назад

Изменено 1 год, 7 месяцев назад

Просмотрено 211 раз

Мне нужно построить функцию двух переменных в Gnuplot, когда она пересекается с 0, то есть: f(x,y)=0.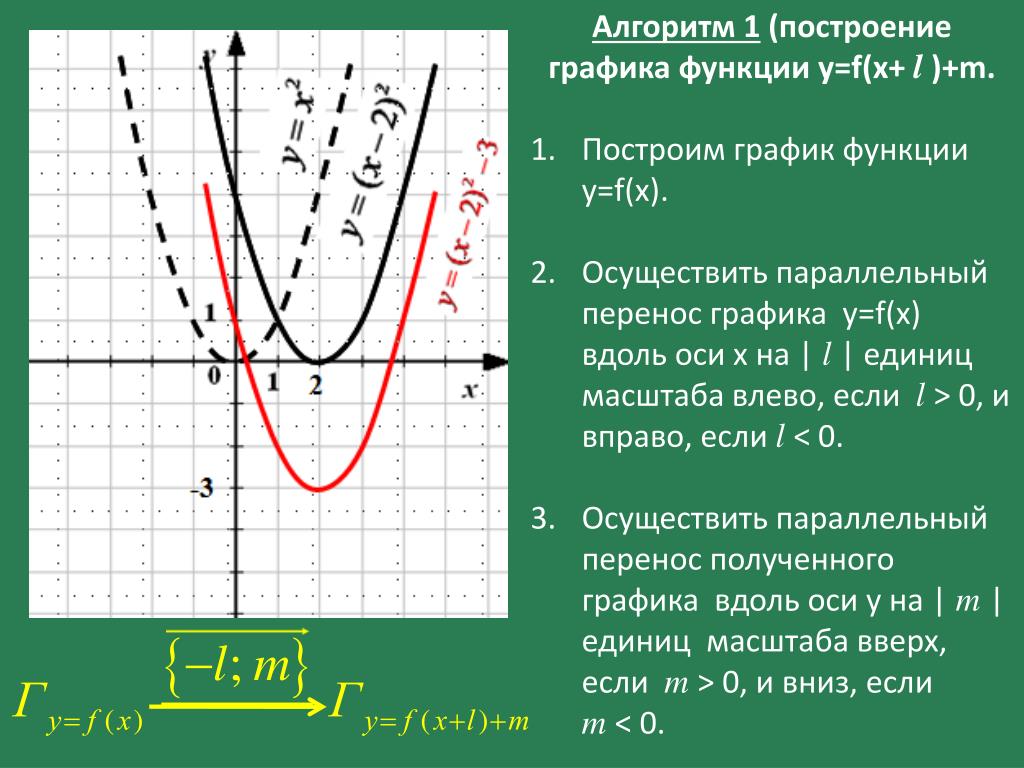 Это будет означать 2D-сюжет, а не 3D. Моя попытка до сих пор:

 набор сроков cairolatex eps автономный размер 6 дюймов, 6 дюймов lw 7
установить ключевой ящик непрозрачный образец 6
установить расстояние между клавишами 1,5
установить ключ вправо
установить высоту ключа 2
установить ширину ключа 3
е (х, у) =...
установить вывод 'V.tex'
график f (x, y) = 0 title '\ small $ {\ hat {V} = 2} $' lc rgb "черный"
установить
 

, но он возвращает функцию для построения ожидаемого .

На всякий случай обходной путь , приведенный в разделе 5.2 часто задаваемых вопросов Gnuplot в http://www.gnuplot.info/faq/faq.html , не создает файл .tex, который я могу скомпилировать.

• gnuplot
• неявный

3

Я попытался объединить код из FAQ (@gdupras’s answer) с кодом, который вы показали вначале.

 набор сроков cairolatex eps автономный размер 6 дюймов, 6 дюймов lw 7
установить ключевой ящик непрозрачный образец 6
установить расстояние между клавишами 1,5
установить ключ вправо
установить высоту ключа 2
установить ширину ключа 3
f(x,y) = y - x**2 / тангенс (y)
установить контурную базу
установить уровни cntrparam дискретно 0. 0
незакрепленная поверхность
настроить таблицу $TEMP
график f (х, у)
сбросить таблицу
установить вывод 'V.tex'
plot $TEMP w l title '\small${\hat{V}=2}$' lc rgb "черный"
установить
 

В моей среде этот код генерирует «V.tex», и после компиляции я получаю следующий рисунок (PDF, преобразованный в PNG).

0

Это задокументировано в часто задаваемых вопросах gnuplot: http://www.gnuplot.info/faq/faq.html

С этой страницы:

5.2 Неявно определенные графы

Неявные графики или кривые не могут быть построены непосредственно в gnuplot. Однако есть обходной путь.

 gnuplot> # Пример. Поместите свое определение в следующую строку:
gnuplot> f(x,y) = y - x**2 / tan(y)
gnuplot> установить базу контура
gnuplot> установить уровни cntrparam дискретно 0.0
gnuplot> неустановленная поверхность
gnuplot> установить таблицу $TEMP
gnuplot> график f(x,y)
gnuplot> сбросить таблицу
gnuplot> график $TEMP w l
 

Хитрость заключается в том, чтобы нарисовать одну контурную линию z=0 поверхности z=f(x,y) и сохранить полученную контурную кривую во временный файл или блок данных.

No related posts.