Треугольник в геометрии это: Треугольник (в геометрии) | это… Что такое Треугольник (в геометрии)?

ТРЕУГОЛЬНИК – ПРОСТЕЙШИЙ И НЕИСЧЕРПАЕМЫЙ

• Авторы
• Руководители
• Файлы работы
• Наградные документы

Годовикова Д.И. 1

---

1МБОУ «Коношская СШ»

Пономарева Е.В. 1

---

1МБОУ «Коношская СШ»

Автор работы награжден дипломом победителя III степени

Диплом школьникаСвидетельство руководителя

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF

Введение

Ум заключается не только в знании, но и в умении приложить знание на делеАристотель

Высшее проявление духа – это разум. Высшее проявление разума – это геометрия. Клетка геометрии – треугольник. Он так же неисчерпаем, как и вселенная”

Иван Федорович Шарыгин

Начиная с седьмого класса, в расписании уроков появляется новый предмет — геометрия.

Геометрия, наверное, самая древняя наука. Геометрами называли себя математики древности. Некоторые теоремы геометрии являются древнейшими памятниками мировой культуры, возможно старше самой Библии[2]. Геометрия – необычайно важный и интересный предмет, и каждый человек может найти в ней уголок по душе.

Геометрия – это не совсем математика. В традиционном понимании, математика — это вычисления, действия с числами. А геометрия – это предмет для тех, кому нравится что-то представлять, рассматривать картинки, наблюдать, выполнять чертежи, замечать, и делать выводы.

Замечательный русский ученый-геометр Иван Федорович Шарыгин сказал: ”Высшее проявление духа – это разум. Высшее проявление разума – это геометрия. Клетка геометрии – треугольник. Он так же неисчерпаем, как и вселенная”[4]. Исследование свойств треугольника послужило началом для создания новой ветви элементарной математики — «геометрии треугольника» или «новой геометрии треугольника», одним из родоначальников которой стал Леонард Эйлер [3].

Треугольник – самая простая замкнутая прямолинейная фигура, одна из первых, свойства которых человек узнал еще в глубокой древности, поэтому эта фигура всегда имела широкое применение в практической жизни и до сих пор используется человеком.

В самом начале седьмого класса изучаются три признака равенства треугольника. После рассмотрения третьего признака равенства треугольников (по трем сторонам) сделан вывод о том, что треугольник – жесткая фигура, и его практическое применение достаточно широко.

Актуальность работы в том, что свойство жесткости треугольника — это геометрические понятия, знания которых имеют огромное значение для решения практических задач и в наше время. Данное исследование, которое выходит за рамки нашей школьной программы, поможет нам определить значимость данной простейшей фигуры и её свойства жесткости для человечества.

Цель исследования – установить, что треугольник являясь жесткой фигурой, нашел широкое практическое применение в жизни человека. Задачи:

1. Изучить литературу о треугольнике;

2. Изучить свойство треугольника – жесткость и исследовать применение свойства жесткости на практике;

3. Проанализировать применение треугольника в жизни человека;

4. Углубить имеющиеся знания по геометрии;

5. Обобщить собранную информацию и познакомить с ней своих одноклассников.

Гипотеза: мы предполагаем, что сможем найти подтверждающие доказательства о том, что обладая таким свойством как жесткость, треугольник является простейшим и неисчерпаемым.

Объект исследования: свойство жесткости треугольника.

Практическая значимость: обобщённый материал данного исследования можно применять как на уроках математики, так и во внеурочное время для развития интереса к математике. Данный материал способствует формированию представления о прикладных возможностях математики.

Методы исследования: анкетирование, сбор информации, анализ, наблюдение, изучение литературы.

Теория. Понятие жесткости треугольника.

Из учебника геометрии Л.С. Атанасяна за 7 класс из параграфа 14 [1]:

Отметим какие-нибудь три точки, не лежащие на одной прямой, и соединим их отрезками. Получим геометрическую фигуру, которая называется треугольником. Отмеченные точки называются вершинами, а отрезки – сторонами треугольника.

Из параграфа 20:

Третий признак равенства треугольников. Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.

Из третьего признака равенства треугольников следует, что треугольник — жёсткая фигура.

Что такое жесткая фигура? Почему треугольник — жесткая фигура? Жесткая фигура — это фигура, не подверженная деформации.

И действительно:

• если вырезать из картона 4 полоски и соединить их между собой булавками или декоративными кнопками в четырехугольник, а затем попробовать изменить форму четырехугольника (просто взявшись руками за две противоположные стороны и покачать вверх-вниз). Получаем, что можно изменять градусную меру углов четырехугольника, не меняя длины его сторон. Можно менять величины углов у пятиугольников, шестиугольников и многоугольников с большим количеством сторон.

• С треугольником так поступить не удастся. Из 3-х полосок сложим треугольник и соединим кнопками или булавками и попробуем изменить форму треугольника.

Стороны треугольника определяют его углы однозначно.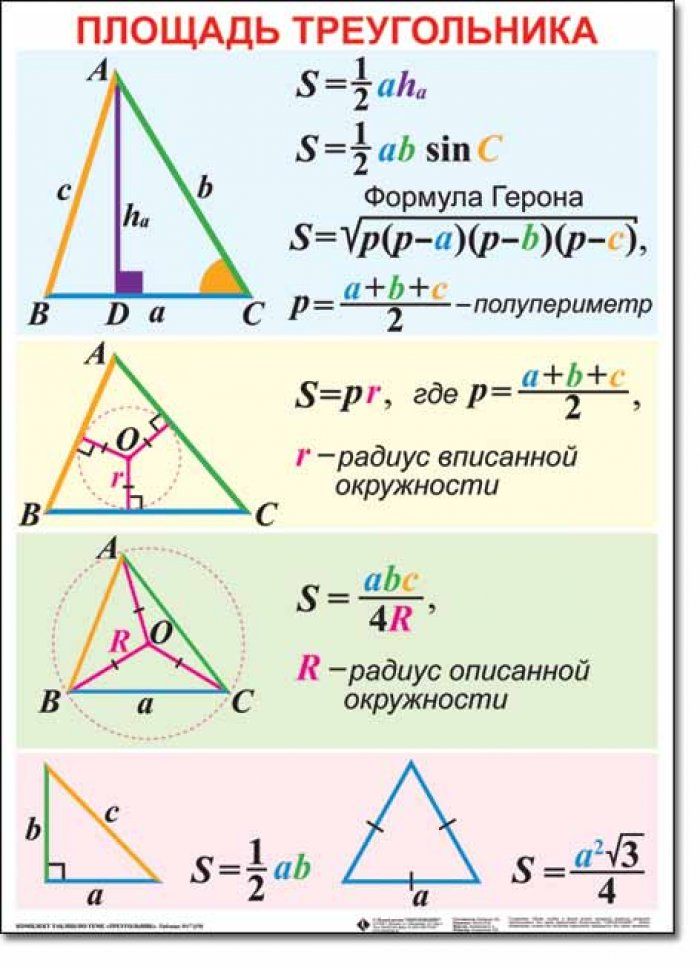

Треугольник не подвержен деформации. В нём нельзя сдвинуть или раздвинуть никакие две стороны, т. е. нельзя изменить ни один угол. Действительно, если бы это удалось, то мы получили бы новый треугольник, не равный исходному. Но это невозможно, так как новый треугольник должен быть равен исходному по третьему признаку равенства треугольников. Поэтому треугольник — жесткая фигура. Из всех многоугольников только треугольник является жесткой фигурой.

Это свойство треугольника используется, в частности, при создании железных ажурных конструкций. Мосты, башни, подъемные краны, каркасы зданий, опоры для высоковольтных линий электропередач изготавливают таким образом, чтобы они содержали как можно больше треугольных элементов.

Вывод: Треугольник — фигура жёсткая. Если заданы три его стороны, то форма треугольника уже не может измениться. Жёсткостью треугольника пользуются в строительстве, при конструировании механизмов, различных приспособлений.

Практика.

Применение свойства жесткости треугольника на практике.

В школьной программе свойство жесткости треугольника подробно не рассматривается и более детальное практическое изучение не предусмотрено. После рассмотрения третьего признака равенства треугольников, заинтересовавшись данной проблемой, я провела анкетирование обучающихся своего класса. В анкетировании приняли участие 22 ученика, им были предложены вопросы:

1. Что, по – вашему означает слово жесткость? Ответы: что-то крепкое, неизменяемое; крепкое тело, состоящее из чего- либо; это фигуры, которые не могут сломаться.

2. Что, по-вашему, означает жесткость фигуры? Ответы: означает устойчивое состояние фигуры; означает твердость фигуры; означает что фигура, не изменяет свою форму; означает неподвижность.

3. Какая из известных Вам фигур самая жесткая? Ответы: Треугольник – 12; точка — 2; ромб – 5; нет жестких фигур – 3.

4. Почему у велосипеда треугольная рама? Ответы: Не знаю; так правильнее делать; велосипед становиться легче.

5. Знаете ли вы, где применяется свойство жесткости треугольника? Ответ: в геометрии, в физике, в строительстве (опоры, подставки).

6. Что в жизни вы встречали в форме треугольника? Ответ:

   крыши домов; подставка для подтягивания; музыкальные инструменты; сыр; украшения; линейка; дорожный знак; окна и т.п.

7. Согласны ли Вы с утверждением, что треугольник – простейший и неисчерпаемый? Ответы: Да – 12; Нет — 10.

После проведенного опроса я сделала вывод, что одноклассники совсем не знают самого свойства жесткости треугольника и применения его на практике. Тогда я решила более подробно исследовать данный вопрос и ознакомить ребят с результатами.

Свою работу начала с изучения информации в сети Интернет[5], где довольно широко освещается этот вопрос. Свойство жесткости треугольника широко используется на практике.

1. Символ Франции, знаменитая Эйфелева башня — самая узнаваемая архитектурная достопримечательность Парижа. Огромная железная башня не особо страдает от ветра. Даже самый сильный ветер, случившийся в Париже (примерно 180 км/ч), отклонил верхушку башни лишь на 12 см. Это объясняется тем, что вся конструкция башни сплетена из треугольников, обладающих жёсткостью

1.

2. Линии электропередачи. Ажурная конструкция, составленная из треугольников, обладает повышенной устойчивостью. Треугольники делают конструкции надежными².

3. Геодезический купол (геокупол, геодом) — сферическое архитектурное сооружение, собранное из стержней, образующих геодезическую структуру, благодаря которой сооружение в целом обладает хорошими несущими качествами. Геодезический купол является несущей сетчатой оболочкой, составленной из треугольников.

4. Во время Великой Отечественной войны для сохранения стекол во время бомбежки их заклеивали бумажными полосками, чтобы получился треугольник.

5. При строительстве любых мостов в их конструкциях также присутствуют треугольники.

Дальше я решила проанализировать – встречается ли свойство жесткости треугольника в моей повседневной жизни, в моем поселке. Для этого я провела наблюдение, рассматривала всевозможные конструкции и пыталась найти треугольник и его применение.

1. Спортивный зал МБОУ «Коношская СШ»:

а) шведская стенка	б) крепеж баскетбольного кольца

2. Железнодорожная станция³.

 

3. Велосипед.

4. Так, чтобы закрепить столб в вертикальном положении, к нему ставят подпорку. Телеграфные столбы с подпоркой называют анкерными⁴.Коноша. Ул. Травница, 34

5. Антенные мачты. Широкое применение нашли в свете развития сотовой связи и цифрового телерадиовещания.

На территории Коноши установлены мачты сотовой связи известных провайдеров МТС, Мегафон, Билайн, Ростелеком⁵.

6. Делая садовую калитку, обязательно прибивают планку, чтобы получить треугольник. Это придаёт ей прочность, иначе калитку перекосит.

7. При строительстве домов на помощь человеку вновь приходит треугольник, так как стропила зданий имеют вид треугольников. Это придаёт им крепость и устойчивость. Именно для усиления даже временных конструкций используют укосы⁶. При установке или пристройке балконов используются кронштейны в форме треугольников⁷.

8. Широкое применение свойство жесткости треугольника находит и при работе по сборке мебели.

Усиление углов стола

 

 

Крепления для полок

 

9. Жесткость треугольников применяется при строительстве подъемных кранов, которых очень часто сейчас можно увидеть на строительных площадках Коноши.

10. Стремянки — это специальные, как правило, переносные лестницы, раскладывающиеся для выполнения определённой задачи. Лестница, в разложенном виде образующая равнобедренный треугольник: по его сторонам находятся одна или две лестницы (одностороннее или двустороннее восхождение), между ними для жёсткости конструкции ближе к вершине раскладывается площадка, предназначенная для опоры ног или устанавливаются растяжки. Надёжность такой лестницы определяется углом её раскрытия: чем шире раскрытие, тем она устойчивее, а, следовательно, и надёжнее.

11. Свойство жесткости треугольника приносит радость детям. Что может быть интереснее, чем качаться на качелях.

Приводить примеры использования свойства жесткости треугольника можно очень долго. Человечество активно применяет свойство в своей повседневной жизни⁸.

Вывод: свойство жесткости треугольника нашло широкое применение в жизни человека. Наиболее часто данное свойство встречается при установке столбов и строительстве домов и металлических конструкций.

Заключение

Форму треугольника невозможно изменить, если заданы все три стороны треугольника. В треугольнике нельзя изменить ни один из углов. В противном случае, идет противоречие с третьим признаком равенства треугольника — равенство по трем сторонам. В результате исследования можно сделать вывод, что треугольник — геометрическая фигура, которая обладает свойством жёсткости, широко используемым человеком в своей деятельности.

Треугольник всегда имел широкое применение в практической жизни. Так, в строительном искусстве испокон веков используется свойство жесткости треугольника для укрепления различных строений и их деталей. Вокруг нас очень много предметов, имеющих форму треугольника (эстетическое направление), поэтому треугольник применяется в архитектуре, в быту, при строении чертежа, в мореплаванье, в моде и т.п.

Слова, сказанные великим французским архитектором Ле Корбюзье, в начале ХХ века, справедливы и в наше время: «Я думаю, что никогда до настоящего времени мы не жили в такой геометрический период. Стоит поразмыслить о прошлом, вспомнить то, что было ранее, и мы будем ошеломлены, видя, что окружающий нас мир – это мир геометрии, чистой, истинной, безупречной в наших глазах. Всё вокруг – геометрия. Прошли века, но роль геометрии не изменилась. Она по-прежнему остается грамматикой архитектора».

Список литературы

[1] Атанасян Л.С. Геометрия, 7 -9. М, Просвещение, 2009.

[2 ]Глейзер Г. И. История математики в школе. М, Просвещение, 1993.

[3]Панов В. Ф. Математика древняя и юная/ Под ред. В. С. Зарубина. – 2-е изд., испр. – М.: Изд-во МГТУ им. Н. Э. Баумана, 2006. – 648с.

[4] Шарыгин И.Ф. Первые шаги в геометрии. Изд-тво КЛАССИКС СТИЛЬ, 2003 — 80 с.

[5 ]Интернет – ресурсы.

http://www.treugolniki.ru/treugolnik-zhestkaya-figura/

https://yandex.ru/images/

http://fizmat.by

http://matznanie.ru

http://www.home-edu.ru/user/f/00000568/zpt/lesson1.htm

https://ru. wikipedia.org

Приложение

рис.1. Эйфелева башня.

рис.2. Линии электропередачи.

рис.3. На железнодорожной станции Коноша.

рис.4. Установка столбов в вертикальном положении.

рис.5. Мачты сотовой связи.

рис. 6. Восстановление воинского обелиска в центре Коноши.

рис.7. Пристройка балкона на 1 этаже в г. Архангельск.

рис.8.

1 ^{Приложение, рис.1.}

2 ^{Приложение, рис.2.}

3 ^{Приложение, рис.3.}

4 ^{Приложение, рис.4.}

5 ^{Приложение, рис.5.}

6 ^{Приложение, рис.6.}

7 ^{Приложение, рис. 7.}

8 ^{Приложение, рис.8.}

Просмотров работы: 3426

Проектная работа по геометрии «Треугольник в жизни человека»

Муниципальное бюджетное общеобразовательное учреждение «Средняя общеобразовательная школа №199»

Проектная работа по геометрии

Авторы проекта: Учащиеся 9 «Б» класса:

Цалман Никита

Адамович Семен Руководитель проекта:

Копылова Вера Егоровна

Новосибирск 2020

Содержание

Введение

Глава 1. История треугольника

Глава 2. Треугольники в жизни человека

Глава 3. Треугольники в строительстве

Заключение

Введение

Геометрия начинается с треугольника. Вот уже два тысячелетия треугольник является служит одним из символов геометрии, но на самом деле он гораздо большее: треугольник – это атом геометрии.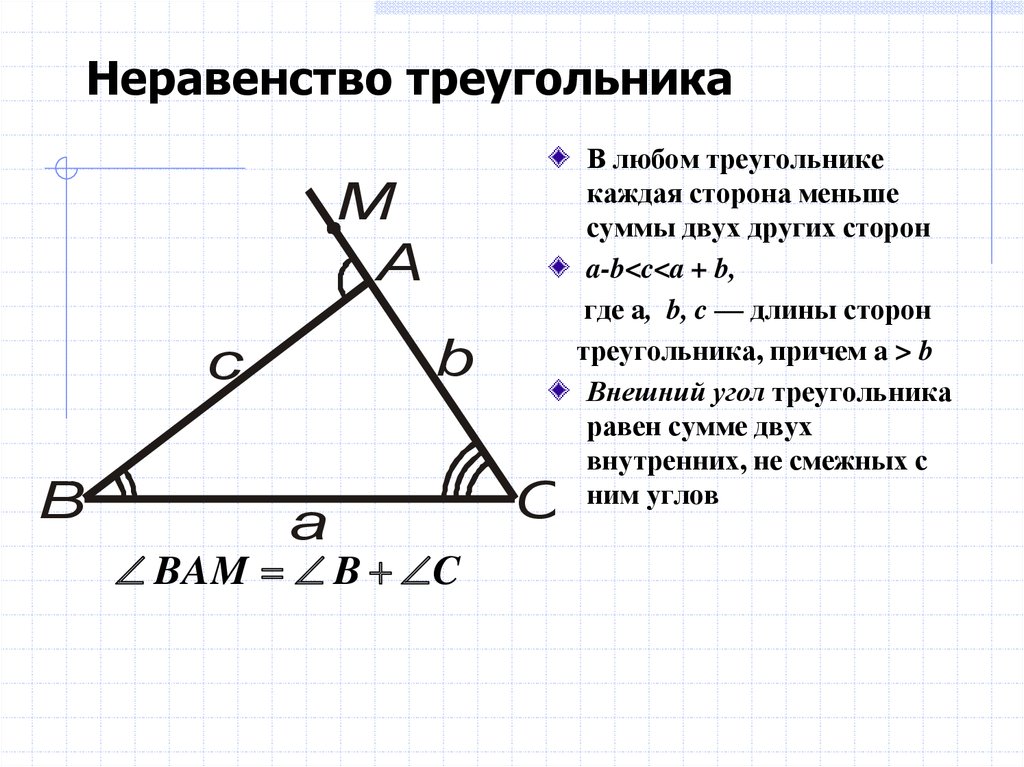

Он постоянно встречается нам не только на уроках, но и в жизни: в нашей одежде, в рисунке улиц, хитросплетении переулков и архитектуре домов — везде. Задумывались ли вы хотя бы один раз когда-либо  о значении треугольника в жизни человека? Что скрывается в столь казалось бы незамысловатом предмете? И почему треугольник так часто встречается в повседневной жизни?

Эти и другие похожие вопросы и породили у нас желание заняться этим проектом. Мы захотели попытаться разобраться в основах теории треугольника.

Цель работы: расширить представления о треугольниках и их значимости.

Задачи:

•  Изучение исторических сведений о треугольниках;

•  Изучение сведений о нахождении треугольников в окружающем мире;

•  Исследование свойств треугольника и применения их в практической жизни

Проблема: показать связь геометрической фигуры с окружающими нас предметами.

Актуальность данной темы определяется важностью умения видеть математику в мире, в котором мы живем, необходимостью добывать знания о треугольниках, а также применением полученных знаний в повседневной жизни.

Продукт проекта: звездчатый октаэдр – макет

Глава 1. История треугольника

Треугольник – геометрическая фигура, состоящая из трех точек, не лежащих на одной прямой и соединенных отрезками. Одна из первых, свойства которой человек узнал еще в глубокой древности, так как эта фигура всегда имела широкое применение в практической жизни.

Крупнейший древнегреческий историк Геродот (V век до нашей эры) оставил описание того, как египтяне после каждого разлива Нила заново размечали плодородные участки его берегов, с которых ушла вода. По Геродоту, с этого и началась геометрия – «землемерие» (от греческого «гео» –»земля» и «метрео» – «измеряю»).

Древние землемеры выполняли геометрические построения, измеряли длины и площади; астрологи рассчитывали расположение небесных светил –все это требовало весьма обширных познаний о свойствах плоских и пространственных фигур, и в первую очередь о треугольнике.

Треугольник по праву считается простейшей из фигур: любая плоская, то есть простирающаяся в двух измерениях, фигура должна содержать хотя бы три точки, не лежащие на одной прямой. Если соединить эти точки попарно прямолинейными отрезками, то построенная фигура и будет треугольником. Так же называют и заключенную внутри образовавшегося контура часть плоскости. Таким образом, любой плоскостной многоугольник может быть разбит на треугольники.

Треугольник всегда имел широкое применение в практической жизни. Так, в строительном искусстве испокон веков используется свойство жесткости треугольника для укрепления различных строений и их деталей.

Из всех многоугольников только треугольник является жесткой фигурой, поскольку его углы невозможно изменить, не изменив длины его сторон. Это свойство треугольника используется во многих конструкциях (мосты, башенные краны, опоры линий электропередач).

Стропила зданий имеют вид треугольников. Это придаёт им крепость и устойчивость.

При устройстве садовой калитки обязательно прибивают планку (доску), иногда две планки, чтобы получились треугольники. Это придаёт крепость калитке, иначе её скоро перекосит.

Изображения треугольников и задачи на треугольники встречаются в папирусах, в старинных индийских книгах и в других древних документах. В Древней Греции учение о треугольниках развивалось в ионийской школе, основанной в VII веке до н.э. Фалесом, и в школе Пифагора. Уже Фалес доказал, что треугольник определяется одной стороной и двумя прилежащими к ней углами. Учение о треугольниках было, затем полностью изложено в первой книге “Начал” Евклида.

Понятие о треугольнике исторически развивалось так: сначала рассматривались лишь равносторонние, затем равнобедренные и, наконец, разносторонние треугольники.

Равнобедренный треугольник обладает рядом геометрических свойств, которые привлекли к себе внимание еще в древности._{На практике часто применялось свойство медианы равнобедренного треугольника, являющейся одновременно и высотой и биссектрисой. То, что углы при основании равнобедренного треугольника равны, было известно еще древним вавилонянам 4 000 лет назад. А землемеры и поныне прибегают к прямоугольному треугольнику для определения расстояний.}

Глава 2. Треугольник в жизни человека

Человека окружает множество предметов треугольной формы. Например, предметы мебели, подошва утюга, элементы орнаментов, элементы одежды (концы мужского галстука, косынки, треуголки, пилотки, колпаки и т.п.), линии электропередач. И даже для выпечки пирожков нередко используют данную форму.

Мы даже не задумываемся о том, что иногда безопасность человека на дороге зависит от знаков дорожного движения, имеющих треугольную форму – это некоторые знаки приоритета и предупреждающие знаки, регулирующие дорожное движение.

Первоначальное положение шаров в бильярде, кеглей в боулинге задается треугольной формой.

             

Существует немало музыкальных инструменты, в основе которых заложена форма треугольника.

Наша флора и фауна переполнена треугольными формами: форма деревьев, форма крыльев насекомых, подвижная голова богомолов, уши у куницы и соболя, клювы птиц, листья некоторых растений, например, кислица, крапива.

Форма некоторых растений подобна треугольнику, например, кипарис, ель. Цветы и соцветия многих цветковых растений также напоминают треугольник.

Причина популярности треугольника: это простота, красота, и значимость. Таким образом, мир треугольника разнообразен. Они широко используются человеком и украшают его жизнь.

Глава 3. Значение треугольников в строительстве

Жесткая фигура – это фигура не подверженная деформации. Из всех многоугольников только треугольник является жесткой фигурой. Это свойство треугольника используется, в частности, при создании железных ажурных конструкций.

Жёсткость — это способность конструктивных элементов сопротивляться деформации при внешнем воздействии. Если возьмём три металлические или деревянные планки, закрепим их концы булавками или гвоздиками так, чтобы получить треугольник.  – треугольник – будет жесткой. В полученной конструкции нельзя сдвинуть или раздвинуть никакие две стороны, т. е. нельзя изменить ни один угол.

Действительно, по третьему признаку равенства треугольников невозможно изменить величины его углов, не изменив длины сторон. Таким образом, треугольник не подвержен деформации при сохранении в целостности его составных элементов (сторон).

Дощечки, собранные в форме квадрата, могут сместиться после приложения силы, т. к. меняются внутренние углы. Таким образом, четырехугольник (квадрат) не является жесткой фигурой, то есть подвержен деформации.

Мосты, башни, подъемные краны, каркасы зданий, вышки сотовой связи, опоры для высоковольтных линий электропередач изготовляют таким образом, чтобы они содержали как можно больше треугольных элементов. Устойчивы они потому, что через три точки всегда проходит плоскость.

Эйфелева башня самая узнаваемая архитектурная достопримечательность. Колебания башни во время бурь не превышает 15 см. Вся конструкция башни сплетена из треугольников, обладающих свойством жесткой фигуры.

При строительстве крыши небольших домов и многоэтажных зданий зачастую используют стропила. Можно сказать, что стропильная система это каркас скатной крыши, её основа (скелет). Стропила выполняют несущую функцию в системе крыши. Вес от крыши через стропильную систему передаётся на несущие стены строения.

В зависимости от вида и типа строения крыши, в состав стропильной системы могут входить стропила, мауэрлаты, подстропильные горизонтальные балки (ригеля), прогоны, лежни и стойки на них, а так же подкосы и прочие элементы.

Элементы треугольника можно наблюдать в чертежах при строительстве самых древних домов и замков. Неизменный атрибут треугольника в крышах домов, на фасадах зданий, оконных проемов и дверей. Некоторые жилища имеют форму треугольника: вигвам, палатка,  юрта.

        

При строительстве мостов, установке ЛЭП и вышек сотовой и телевизионной связи используется не только форма, но и свойства треугольников.

Заключение

Геометрия играет большую роль в жизни каждого человека. С ней мы встречаемся не только на уроках, она находится вокруг нас. Геометрия несет красоту в нашу жизнь, она же участвует во многих сферах человеческой жизни и вносит свой вклад в ряд наук.

Треугольники окружают нас повсюду: детские игрушки, архитектурные сооружения, дорожные знаки, музыкальные инструменты. В повседневной жизни мы перестали их замечать, а ведь это очень интересно, знать историю привычных для всех предметов, тем более, если она так увлекательна. С одной стороны, треугольники имеют тысячелетнюю историю, с другой – это современный раздел математики. Теория треугольника имеет большое значение не только для теоретических исследований по геометрии, но и для других наук.

В ходе нашего исследования мы пришли к выводу, что треугольник действительно является интересной и важной фигурой. Мир треугольников разнообразен. Человека окружает множество предметов быта, одежды, музыкальные инструменты, имеющие треугольную форму.

Треугольник используется человеком с древних времен и до наших дней. Это единственная фигура, которая обладает свойством жёсткости, которое_{нашло широкое применение в жизни человека. Оно встречается наиболее часто в строительстве}

Список литературы

1.                 https://mybiblioteka.su/tom2/8-62542.html-История возникновения треугольника

2.                 https://school-science.ru/2/7/29646-Тайны и загадки треугольника

3.                 http://alltriangles.blogspot.com/- Изучение треугольников

4.                 https://doklad-i-referat.ru/- Треугольник (история треугольника)

5.                 https://ru.wikipedia.org/wiki/- Треугольник

6.                 https://mybiblioteka.su/tom2/8-62547.html — Применение треугольника в жизни человека.

7.                 http://www.treugolniki.ru/treugolnik — Треугольник — жесткая фигура

8.                 https://mnogogranniki.ru/ — Самая прочная конструкция

9.                 Е. Е.Семенов. Изучаем геометрию. Москва  «Просвещение» 1987г.

Приложение 1. Наиболее известные здания, использующие треугольные формы в своей архитектуре

Сиднейский оперный театр – визитная карточка Австралии

 Астана – пирамида, Дворец мира и согласия

 

«Парижский Треугольник», вход в Лувр (Париж)

Арктический собор

        ТЦ «Бутон»                                 Павильон «Шар»

Биотехнопарк «Кольцово»

GRE Геометрия | Треугольники — GeeksforGeeks

Треугольник — одна из основных двумерных фигур в геометрии. Он состоит из трех углов, трех сторон и трех вершин, например,

На основе измерения сторон и углов существуют различные типы треугольников, перечисленных ниже:  

1. Равносторонний треугольник:  
равны, все углы также равны 60°, например,

2. Равнобедренный треугольник:  
Два ребра равны, следовательно, два угла также равны или стороны, противоположные равным сторонам, равны, например, 

3. Разносторонний треугольник:  
Все ребра различны, следовательно, все углы также различны, например,

4. Треугольник с прямым углом:
Один угол составляет 90 °, а сторона, противоположная 90 °, является гипотенузой, например,

5. Треусный треугольник:
Один угол равен, например,

5.

6. Остроугольный треугольник:  
Все углы острые, например,

Важные свойства треугольника:

• Сумма углов треугольника больше 9 0 0 0 5 9 ° 0 0 5 9 ° разность двух других сторон и меньше суммы двух других сторон.
• Площадь треугольника = (1 / 2) * основание * высота.
• В прямоугольном треугольнике, гипотенуза ² = основание ² + перпендикуляр ² . [ Теорема Pythagoras ]
• Площадь равенственного треугольника = (√3 / 4) Сторона ²

Конглина и сходство в треугольниках:

1. Конгрессионный триангл:

1. Конгрессионный триангл: 9001 3. и размер двух треугольников одинаков или два треугольника имеют одинаковые углы и одинаковые стороны, например,

Треугольники ABC и XYZ конгруэнтны.
или △ABC ≅△XYZ 

Правила соответствия: 

• (i) Правило SSS (сторона – сторона – сторона):  
  Если все стороны треугольника равны всем сторонам другого треугольника. Тогда эти два треугольника конгруэнтны друг другу по правилу SSS, например,

• (ii) правило SAS (сторона – угол – сторона):  
  Если две стороны треугольника равны двум сторонам другого треугольник и угол между ними равен углу между равными сторонами в другом треугольнике, то эти два треугольника конгруэнтны друг другу по правилу SAS, например,
   

• (iii) Правило ААА (угол – угол – угол): Если все углы треугольника равны всем углам другого треугольника, то эти два треугольника конгруэнтны друг другу по правилу ААА, т. е. , 
   

• (iv) Правило ASA (угол – сторона – угол):  
  Если два угла треугольника равны двум углам в другом треугольнике и сторона между ними равна стороне между равными углами в другого треугольника, то эти два треугольника конгруэнтны друг другу по правилу ASA, например,
   

• (v) Правило AAS (угол – угол – сторона):  
  Если два угла и одна сторона треугольника равны двум углам и одной стороне в другом треугольнике, то эти треугольники равны друг другу другое по правилу AAS, например,
   

2. Подобные треугольники:  
Два треугольника подобны, если их форма одинакова, но не обязательно, чтобы их размер был одинаковым. Чтобы доказать, что два треугольника подобны масштабный коэффициент подобия используется, этот коэффициент проверяет эквивалентность отношений соответствующих сторон и соответствующих углов, например,

 △ABC подобен △XYZ.  

Поскольку △ABC подобен △XYZ, мы можем записать масштабный коэффициент подобия как: 

 XY / AB = XZ / AC = YZ / BC. 

Чтобы получить AB/AC, просто перемножьте

 XY / AB = XZ / AC.
АВ/АС=ХУ/ХZ. 

Свойства треугольника в геометрии

Треугольники — одна из самых узнаваемых фигур в геометрии. Хотя некоторые могут подумать, что все треугольники одинаковы, на самом деле в этой простой форме есть довольно много разнообразия. В этом сообщении блога мы рассмотрим свойства треугольника, связанные с геометрией, и почему важно понимать эти свойства.

Определение треугольника

Треугольник — это двумерная фигура, состоящая из трех прямых линий, соединенных вместе. Важно отметить, что сумма любых двух сторон треугольника должна быть больше, чем третья сторона, чтобы он считался правильным треугольником. Кроме того, сумма всех углов внутри треугольника должна составлять 180, чтобы он считался действительным. Это свойство известно как теорема о сумме углов треугольника и применимо ко всем типам треугольников.

Типы треугольников

Существует несколько различных типов треугольников в зависимости от их сторон и углов. Равнобедренные треугольники имеют три равные стороны и три равных угла, каждый из которых равен 60. Равнобедренные треугольники имеют две равные стороны и два равных угла, причем третий угол отличается от других. Разносторонние треугольники имеют три неравные стороны и три неравных угла, причем никакие две стороны или углы не равны друг другу. Эти свойства можно применять ко всем типам треугольников независимо от их размера или ориентации.

Использование треугольников в геометрии

Треугольники являются неотъемлемой частью геометрии, поскольку они обеспечивают структуру и устойчивость при построении других форм, таких как квадраты и прямоугольники. Кроме того, понимание того, как стороны и углы связаны друг с другом внутри треугольника, помогает нам понять, как эти отношения применяются при создании других геометрических фигур, таких как круги или многоугольники. Эти знания также пригодятся при решении сложных задач, таких как вычисление площади или поиск недостающих измерений в геометрических фигурах.

Заключение

В заключение, треугольники являются важными компонентами при изучении геометрии, потому что они обеспечивают структуру и стабильность при построении других фигур, таких как квадраты и прямоугольники, что позволяет нам понять, как эти отношения применяются при создании других геометрических фигур, таких как круги или многоугольники. Кроме того, понимание того, как стороны и углы соотносятся друг с другом в треугольниках, помогает нам решать сложные задачи, такие как вычисление площади или поиск недостающих измерений в геометрических фигурах. Обладая этими знаниями, учащиеся будут хорошо подготовлены к пониманию того, почему знание свойств треугольника важно для дальнейшего изучения математики!

Часто задаваемые вопросы

Какими свойствами обладает треугольник в геометрии?

Свойства треугольника в геометрии включают наличие трех прямых сторон, трех углов, сумма которых равна 180, и двух сторон, имеющих одинаковую длину.