Гипербола
Определение гиперболы. Гиперболой называется множество всех точек плоскости, таких, для которых модуль разности расстояний от двух точек, называемых фокусами, есть величина постоянная и меньшая, чем расстояние между фокусами.
Каноническое уравнение гиперболы имеет вид:
,
где a и b — длины полуосей, действительной и мнимой.
На чертеже ниже фокусы обозначены как и .
На чертеже ветви гиперболы — бордового цвета.
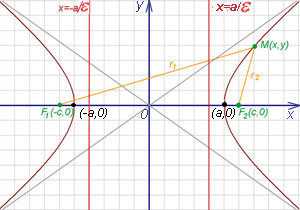
При a = b гипербола называется равносторонней.
Пример 1. Составить каноническое уравнение гиперболы, если его действительная полуось a = 5 и мнимая = 3.
.
Точки пересечения гиперболы с её действительной осью (т. е. с осью Ox) называются вершинами. Это точки (a, 0) (- a, 0), они обозначены и надписаны на рисунке чёрным.
Точки и , где
,
называются фокусами гиперболы (на чертеже обозначены зелёным, слева и справа от ветвей гиперболы).
Число
называется эксцентриситетом гиперболы.
Гипербола состоит из двух ветвей, лежащих в разных полуплоскостях относительно оси ординат.
Пример 2. Составить каноническое уравнение гиперболы, если расстояние между фокусами равно 10 и действительная ось равна 8.
Решение.Если действительная полуось равна 8, то её половина, т. е. полуось a = 4,
Если расстояние между фокусами равно 10, то число c из координат фокусов равно 5.
То есть, для того, чтобы составить уравнение гиперболы, потребуется вычислить квадрат мнимой полуоси b.
Подставляем и вычисляем:
Получаем требуемое в условии задачи каноническое уравнение гиперболы:
.
Пример 3. Составить каноническое уравнение гиперболы, если её действительная ось равна 48 и эксцентриситет .
Решение. Как следует из условия, действительная полуось
a = 24. А эксцентриситет — это пропорция и
так как a = 24, то коэффициент пропорциональности
отношения с и a
равен 2. Следовательно,
.
Результат — каноническое уравнение гиперболы:
На чертеже расстояния обозначены оранжевыми линиями.
Для каждой точки, находящейся на гиперболе, сумма расстояний от фокусов есть величина постоянная, равная 2a.
Прямые, определяемые уравнениями
,
называются директрисами гиперболы (на чертеже — прямые ярко-красного цвета).
Пример 4. Дана гипербола . Составить уравнение её директрис.
Решение. Смотрим в уравнение директрис и обнаруживаем, что требуется найти эксцентриситет гиперболы, т. е. . Вычисляем:
.
Получаем уравнение директрис гиперболы:Многие задачи на директрисы гиперболы аналогичны задачам на директрисы эллипса. В уроке «Эллипс» это пример 7.
Характерной особенностью гиперболы является наличие асимптот — прямых, к которым приближаются точки гиперболы при удалении от центра.
Асимптоты гиперболы определяются уравнениями
.
На чертеже асимптоты — прямые серого цвета, проходящие через начало координат O.
Уравнение гиперболы, отнесённой к асимптотам, имеет вид:
, где .
В том случае, когда угол между асимптотами — прямой, гипербола называется равнобочной, и если асимптоты равнобочной гиперболы выбрать за оси координат, то её уравнение запишется в виде y = k/x, то есть в виде уравения обратной пропорциональной зависимости.
Пример 5. Даны уравнения асимптот гиперболы и координаты точки , лежащей на гиперболе. Составить уравнение гиперболы.
Решение. Дробь в уравнении асимптот гиперболы — это пропорция, следовательно, нужно сначала найти коэффициент пропорциональности отношения . Для этого подставляем в формулу канонического уравнения гиперболы координаты точки M x и y и значения числителя и знаменателя из уравнения асимптоты, кроме того, умножаем каждую дробь в левой части на коэффициент пропорциональности k.
.
Теперь имеем все данные, чтобы получить каноническое уравнение гиперболы. Получаем:
Гипербола обладает оптическим свойством, которое описывается следующим образом: луч, исходящий из источника света, находящегося в одном из фокусов гиперболы, после отражения движется так, как будто он исходит из другого фокуса.
Поделиться с друзьями
Другие материалы по теме Кривые второго порядка
function-x.ru
Гипербола (математика) — это… Что такое Гипербола (математика)?
У этого термина существуют и другие значения, см. Гипербола. Гипербола и её фокусы Сечения конусов плоскостью (с эксцентриситетом, большим единицы)Гипе́рбола (др.-греч. ὑπερβολή, от ὑπερ — «верх» + βαλειν — «бросать») — геометрическое место точек M Евклидовой плоскости, для которых абсолютное значение разности расстояний от M до двух выделенных точек и (называемых фокусами) постоянно. Точнее,
- причем
Наряду с эллипсом и параболой, гипербола является коническим сечением и квадрикой. Гипербола может быть определена как коническое сечение с эксцентриситетом, большим единицы.
История
Термин «гипербола» (греч. ὑπερβολή — избыток) был введён Аполлонием Пергским (ок. 262 год до н. э. — ок. 190 год до н. э.), поскольку задача о построении точки гиперболы сводится к задаче о приложении с избытком.
Определения
Гипербола может быть определена несколькими путями.
Коническое сечение
Три основных конических сеченияГипербола может быть определена, как множество точек, образуемое в результате сечения кругового конуса плоскостью, отсекающей обе части конуса. Другими результатами сечения конуса плоскостью являются парабола, эллипс, а также такие вырожденные случаи, как пересекающиеся и совпадающие прямые и точка, возникающие, когда секущая плоскость проходит через вершину конуса. В частности, пересекающееся прямые можно считать вырожденной гиперболой, совпадающей со своими асимптотами.
Как геометрическое место точек
Через фокусы
Гипербола может быть определена, как Геометрическое место точек, абсолютная величина разности расстояний от которых до двух заданных точек, называемых фокусами, постоянна.
Для сравнения: кривая постоянной суммы расстояний между двумя точками — эллипс, постоянного отношения — окружность Аполлония, постоянного произведения — овал Кассини.
Через директрису и фокус
Геометрическое место точек, для которых отношение расстояния до фокуса и до заданной прямой, называемой директрисой, постоянно и больше единицы, называется гиперболой. Заданная постоянная называется эксцентриситетом гиперболы.
Связанные определения
 Асимптоты гиперболы (красные кривые), показанные голубым пунктиром, пересекаются в центре гиперболы, C. Два фокуса гиперболы обозначены как F1 и F2. Директрисы гиперболы обозначены линиями двойной толщины и обозначены D1 и D2. Эксцентриситет ε равен отношению расстояний точки P на гиперболе до фокуса и до соответствующей директрисы (показаны зелёным). Вершины гиперболы обозначены как ±
Асимптоты гиперболы (красные кривые), показанные голубым пунктиром, пересекаются в центре гиперболы, C. Два фокуса гиперболы обозначены как F1 и F2. Директрисы гиперболы обозначены линиями двойной толщины и обозначены D1 и D2. Эксцентриситет ε равен отношению расстояний точки P на гиперболе до фокуса и до соответствующей директрисы (показаны зелёным). Вершины гиперболы обозначены как ±a — расстояние от центра C до каждой из вершин
b — длина перпендикуляра, опущенного из каждой из вершин на асимптоты
c — расстояние от центра C до любого из фокусов, F1 и F2,
θ — угол, образованный каждой из асимптот и осью, проведённой между вершинами
- Гипербола состоит из двух отдельных кривых, которые называют ветвями.
- Ближайшие друг к другу точки двух ветвей гиперболы называются вершинами.
- Кратчайшее расстояние между двумя ветвями гиперболы называется большой осью гиперболы.
- Середина большой оси называется центром гиперболы.
- Расстояние от центра гиперболы до одной из вершин называется большой полуосью гиперболы.
- Обычно обозначается a.
- Расстояние от центра гиперболы до одного из фокусов называется фокальным расстоянием .
- Обычно обозначается c.
- Оба фокуса гиперболы лежат на продолжении большой оси на одинаковом расстоянии от центра гиперболы. Прямая, содержащая большую ось гиперболы, называется действительной или поперечной осью гиперболы.
- Прямая, перпендикулярная действительной оси и проходящая через её центр называется мнимой или сопряженной осью гиперболы.
- Отрезок между фокусом гиперболы и гиперболой, перпендикулярный её действительной оси, называется фокальным параметром.
- Расстояние от фокуса до асимптоты гиперболы называется прицельным параметром.
- Обычно обозначается b.
- В задачах, связанных с движением тел по гиперболическим траекториям расстояние от фокуса до ближайшей вершины гиперболы называется перицентрическим расстоянием
- Обычно обозначается ..
Соотношения
Для характеристик гиперболы определённых выше подчиняются следующим соотношениям
Типы гипербол
Равнобочная гиперболаГиперболу, у которой , называют равнобочной. Равнобочная гипербола в некоторой прямоугольной системе координат описывается уравнением
при этом фокусы гиперболы располагаются в точках (a, a) и (−a,−a).
Гиперболы, связанные с треугольником
См. также Треугольник#Эллипсы, параболы и гиперболы
Уравнения
Декартовы координаты
Гипербола задаётся уравнением второй степени в декартовых координатах (x, y) на плоскости:
- ,
где коэффициенты Axx, Axy, Ayy, Bx, By, и C удовлетворяют следующему соотношению
и
Канонический вид
Перемещением центра гиперболы в начало координат и вращением её относительно центра уравнение гиперболы можно привести к каноническому виду
- ,
где a и b — полуоси[источник?].
Полярные координаты
График гиперболы в полярных координатахЕсли полюс находится в фокусе гиперболы, а вершина гиперболы лежит на продолжении полярной оси, то
Если полюс находится в фокусе гиперболы, а полярная ось параллельна одной из асимптот, то
Уравнения в параметрической форме
Подобно тому, как эллипс может быть представлен уравнениями в параметрической форме, в которые входят тригонометрические функции, гипербола в прямоугольной системе координат, центр которой совпадает с её центром, а ось абсцисс проходит через фокусы, может быть представлена уравнениями в параметрической форме, в которые входят гиперболические функции[1].
В первом уравнении знак «+» соответствует правой ветви гиперболы, а «-» — её левой ветви.
Свойства
- Оптическое свойство. Свет от источника, находящегося в одном из фокусов гиперболы, отражается второй ветвью гиперболы таким образом, что продолжения отраженных лучей пересекаются во втором фокусе.
- Иначе говоря, если и фокусы гиперболы, то касательная в любой точки гиперболы является биссектрисой угла .
- Для любой точки лежащей на гиперболе отношение расстояний от этой точки до фокуса к расстоянию от этой же точки до директрисы есть величина постоянная.
- Гипербола обладает зеркальной симметрией относительно действительной и мнимой осей, а также вращательной симметрией при повороте на угол 180° вокруг центра гиперболы.
- Каждая гипербола имеет сопряженную гиперболу, для которой действительная и мнимая оси меняются местами, но асимптоты остаются прежними. Это соответствует замене a и b друг на друга в формуле, описывающей гиперболу. Сопряженная гипербола не является результатом поворота начальной гиперболы на угол 90°; обе гиперболы различаются формой.
Асимптоты
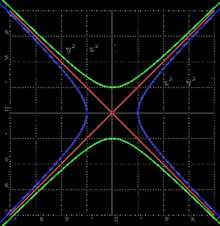 Две сопряженные гиперболы (голубая и зелёная) обладают совпадающими асимптотами (красные). Эти гиперболы единичные и равнобочные, так как a = b = 1
Две сопряженные гиперболы (голубая и зелёная) обладают совпадающими асимптотами (красные). Эти гиперболы единичные и равнобочные, так как a = b = 1Для гиперболы, заданной в каноническом виде
уравнения двух асимптот имеют вид:
- .
Диаметры и хорды
Диаметры гиперболыДиаметром гиперболы, как и всякого конического сечения, является прямая, проходящая через середины параллельных хорд. Каждому направлению параллельных хорд соответствует свой сопряженный диаметр. Все диаметры гиперболы проходят через её центр. Диаметр, соответствующий хордам, параллельным мнимой оси, есть действительная ось; диаметр соответствующий хордам, параллельным действительной оси, есть мнимая ось.
Угловой коэффициент параллельных хорд и угловой коэффициент соответствующего диаметра связан соотношением
Если диаметр a делит пополам хорды, параллельные диаметру b, то диаметр b делит пополам хорды, параллельные диаметру a. Такие диаметры называются взаимно сопряженными. Главными диаметрами называются взаимно сопряженные и взаимно перпендикулярные диаметры. У гиперболы есть только одна пара главных диаметров — действительная и мнимая оси.
Определение центра гиперболы по её графикуКасательная и нормаль
Поскольку гипербола является гладкой кривой, в каждой её точке (x0, y0) можно провести касательную и нормаль. Уравнение касательной к гиперболе, заданной каноническим уравнением, имеет вид:
- ,
или, что то же самое,
- .
Уравнение нормали к гиперболе имеет вид:
- .
| Вывод уравнения нормали |
|---|
Уравнение нормали произвольной плоской линии имеет вид
Каноническое уравнение гиперболы можно представить в виде пары функций
Тогда производная этих функций имеет вид
Подставив это уравнение в общее уравнение нормали, получим
|
Кривизна и эволюта
Синим цветом показана гипербола. Зелёным цветом — эволюта правой ветви этой гиперболы (эволюта левой ветви вне рисунка. Красным цветом показан круг, соответствующий кривизне гиперболы в ей вершине)Кривизна гиперболы в каждой её точке (x, y) определяется из выражения:
- .
Соответственно, радиус кривизны имеет вид:
- .
В частности, в точке (a, 0) радиус кривизны равен
- .
| Вывод формулы для радиуса кривизны |
|---|
Формула для радиуса кривизны плоской линии, заданной параметически, имеет вид:
Воспользуемся параметрическим представлением гиперболы: Тогда, первая производная x и y по t имеет вид
а вторая производная — Подставляя эти значения в формулу для кривизны получаем:
|
Координаты центров кривизны задаются парой уравнений:
Подставив в последнюю систему уравнений вместо x и y их значения из параметрического представления гиперболы, получим пару уравнений, задающих новую кривую, состоящую из центров кривизны гиперболы. Эта кривая называется эволютой гиперболы.
Применения
- Другие ортогональные двумерные координатные системы, построенные с помощью гипербол, могут быть получены с помощью других конформных преобразований. Например, преобразование w = z² отображает декартовы координаты в два семейства ортогональных гипербол.
См. также
Примечания
Литература
dic.academic.ru
Графики математических функций Гипербола ИСТОРИЯ ПРОИСХОЖДЕНИЯ ГИПЕРБОЛЫ
 Графики математических функций. Гипербола
Графики математических функций. Гипербола
 ИСТОРИЯ ПРОИСХОЖДЕНИЯ ГИПЕРБОЛЫ Одним из первых, кто начал изучать конические сечения — эллипс, парабола, гипербола, был ученик знаменитого Платона, древнегреческий математик Менехм (IV в. до н. э. ). Решая задачу об удвоении куба, Менехм задумался: «А что случится, если разрезать конус плоскостью, перпендикулярной его образующей? »
ИСТОРИЯ ПРОИСХОЖДЕНИЯ ГИПЕРБОЛЫ Одним из первых, кто начал изучать конические сечения — эллипс, парабола, гипербола, был ученик знаменитого Платона, древнегреческий математик Менехм (IV в. до н. э. ). Решая задачу об удвоении куба, Менехм задумался: «А что случится, если разрезать конус плоскостью, перпендикулярной его образующей? »
 ИСТОРИЯ ПРОИСХОЖДЕНИЯ ГИПЕРБОЛЫ Так, изменяя угол при вершине прямого кругового конуса, Менехм получил три вида кривых: эллипс — если угол при вершине конуса острый; парабола — если угол прямой; одну ветвь гиперболы — если угол тупой. Название этих кривых придумал не Менехм.
ИСТОРИЯ ПРОИСХОЖДЕНИЯ ГИПЕРБОЛЫ Так, изменяя угол при вершине прямого кругового конуса, Менехм получил три вида кривых: эллипс — если угол при вершине конуса острый; парабола — если угол прямой; одну ветвь гиперболы — если угол тупой. Название этих кривых придумал не Менехм.
 ИСТОРИЯ ПРОИСХОЖДЕНИЯ ГИПЕРБОЛЫ Названия предложил один из крупнейших геометров древности Аполлоний Пергский, посвятивший замечательным кривым трактат из восьми книг «Конические сечения» ( «О кониках» ). Семь книг сохранились, три из них — в арабском переводе. Первые четыре книги содержат начало теории и основные свойства конических сечений. Это — трактат об эллипсе, параболе и гиперболе, определяемых как сечения кругового конуса, где изложение доведено до исследования эволют конического сечения.
ИСТОРИЯ ПРОИСХОЖДЕНИЯ ГИПЕРБОЛЫ Названия предложил один из крупнейших геометров древности Аполлоний Пергский, посвятивший замечательным кривым трактат из восьми книг «Конические сечения» ( «О кониках» ). Семь книг сохранились, три из них — в арабском переводе. Первые четыре книги содержат начало теории и основные свойства конических сечений. Это — трактат об эллипсе, параболе и гиперболе, определяемых как сечения кругового конуса, где изложение доведено до исследования эволют конического сечения.
 ИСТОРИЯ ПРОИСХОЖДЕНИЯ ГИПЕРБОЛЫ Аполлоний показал, что кривые можно получить, проводя различные сечения одного и того же кругового конуса, причем любого. При надлежащем наклоне секущей плоскости удается получить все типы конических сечений. Если считать, что конус не заканчивается в вершине, а проектируется на нее, тогда у некоторых сечений образуется две ветви.
ИСТОРИЯ ПРОИСХОЖДЕНИЯ ГИПЕРБОЛЫ Аполлоний показал, что кривые можно получить, проводя различные сечения одного и того же кругового конуса, причем любого. При надлежащем наклоне секущей плоскости удается получить все типы конических сечений. Если считать, что конус не заканчивается в вершине, а проектируется на нее, тогда у некоторых сечений образуется две ветви.
 МАТЕМАТИЧЕСКАЯ ГИПЕРБОЛА Из школьного курса математики известно, что кривая, задаваемая уравнением , называется гиперболой. Однако это —частный случай гиперболы (равносторонняя гипербола). Определение: гиперболой называется множество точек плоскости, абсолютная величина разности которых до двух данных точек (F 1 и F 2), называемых фокусами, есть величина постоянная (ее обозначают через 2 а), причем эта постоянная меньше расстояния между фокусами (2 c).
МАТЕМАТИЧЕСКАЯ ГИПЕРБОЛА Из школьного курса математики известно, что кривая, задаваемая уравнением , называется гиперболой. Однако это —частный случай гиперболы (равносторонняя гипербола). Определение: гиперболой называется множество точек плоскости, абсолютная величина разности которых до двух данных точек (F 1 и F 2), называемых фокусами, есть величина постоянная (ее обозначают через 2 а), причем эта постоянная меньше расстояния между фокусами (2 c).
 ЭЛЕМЕНТЫ ГИПЕРБОЛЫ Гипербола имеет две оси симметрии (главные оси гиперболы) и центр симметрии (центр гиперболы). При этом одна из этих осей пересекается с гиперболой в двух точках, называемых вершинами гиперболы. Она называется действительной осью (2 а) гиперболы (ось Ох для канонического выбора координатной системы), а половина действительной оси – действительной полуосью (а). Другая ось не имеет общих точек с гиперболой и называется ее мнимой осью (2 b) (в канонических координатах – ось Оу), а половина мнимой оси – мнимой полуосью (b). По обе стороны от нее расположены правая и левая ветви гиперболы. Фокусы гиперболы располагаются на ее действительной оси. Прямоугольник со сторонами 2 а и 2 b называется основным прямоугольником гиперболы.
ЭЛЕМЕНТЫ ГИПЕРБОЛЫ Гипербола имеет две оси симметрии (главные оси гиперболы) и центр симметрии (центр гиперболы). При этом одна из этих осей пересекается с гиперболой в двух точках, называемых вершинами гиперболы. Она называется действительной осью (2 а) гиперболы (ось Ох для канонического выбора координатной системы), а половина действительной оси – действительной полуосью (а). Другая ось не имеет общих точек с гиперболой и называется ее мнимой осью (2 b) (в канонических координатах – ось Оу), а половина мнимой оси – мнимой полуосью (b). По обе стороны от нее расположены правая и левая ветви гиперболы. Фокусы гиперболы располагаются на ее действительной оси. Прямоугольник со сторонами 2 а и 2 b называется основным прямоугольником гиперболы.
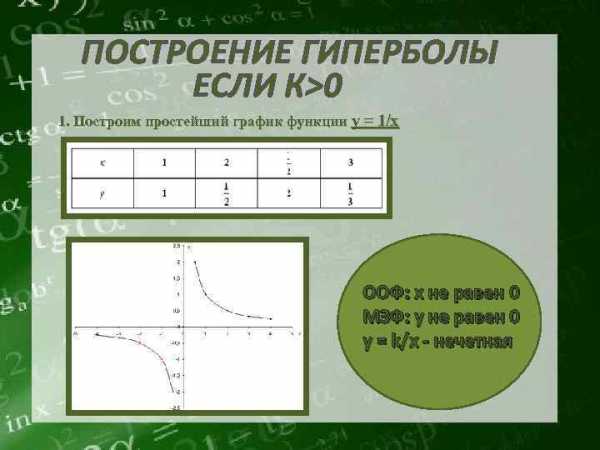 ПОСТРОЕНИЕ ГИПЕРБОЛЫ ЕСЛИ К>0 1. Построим простейший график функции y = 1/x ООФ: х не равен 0 МЗФ: у не равен 0 y = k/x — нечетная
ПОСТРОЕНИЕ ГИПЕРБОЛЫ ЕСЛИ К>0 1. Построим простейший график функции y = 1/x ООФ: х не равен 0 МЗФ: у не равен 0 y = k/x — нечетная
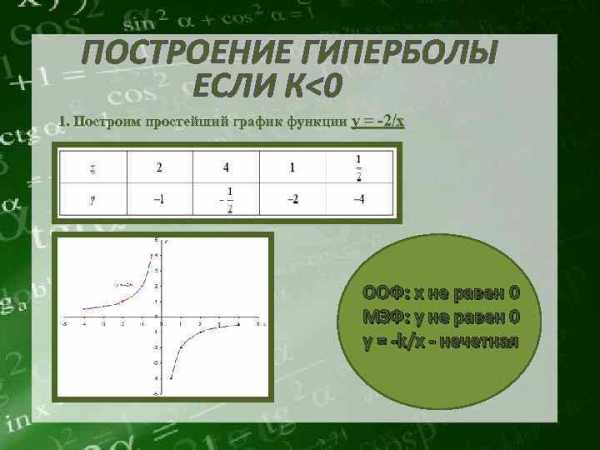 ПОСТРОЕНИЕ ГИПЕРБОЛЫ ЕСЛИ К
ПОСТРОЕНИЕ ГИПЕРБОЛЫ ЕСЛИ К
 АСИМПТОТА Прямая L называется асимптотой неограниченной кривой K, если расстояние d от точки M кривой K до этой прямой стремится к нулю при неограниченном удалении точки M вдоль кривой K от начала координат (см. рис. 1). Асимптота кривой, имеющая бесконечную ветвь — это прямая, которая обладает тем свойством, что когда точка по кривой удаляется в бесконечность, ее расстояние до этой прямой стремится к нулю.
АСИМПТОТА Прямая L называется асимптотой неограниченной кривой K, если расстояние d от точки M кривой K до этой прямой стремится к нулю при неограниченном удалении точки M вдоль кривой K от начала координат (см. рис. 1). Асимптота кривой, имеющая бесконечную ветвь — это прямая, которая обладает тем свойством, что когда точка по кривой удаляется в бесконечность, ее расстояние до этой прямой стремится к нулю.
 СВЯЗАННЫЕ ОПРЕДЕЛЕНИЯ Гипербола состоит из двух отдельных кривых, которые называют ветвями. Ближайшие друг к другу точки двух ветвей гиперболы называются вершинами. Кратчайшее расстояние между двумя ветвями гиперболы называется большой осью гиперболы. Середина большой оси называется центром гиперболы. Расстояние от центра гиперболы до одной из вершин называется большой полуосью гиперболы. ◦Обычно обозначается a. Расстояние от центра гиперболы до одного из фокусов называется фокальным расстоянием. ◦Обычно обозначается c.
СВЯЗАННЫЕ ОПРЕДЕЛЕНИЯ Гипербола состоит из двух отдельных кривых, которые называют ветвями. Ближайшие друг к другу точки двух ветвей гиперболы называются вершинами. Кратчайшее расстояние между двумя ветвями гиперболы называется большой осью гиперболы. Середина большой оси называется центром гиперболы. Расстояние от центра гиперболы до одной из вершин называется большой полуосью гиперболы. ◦Обычно обозначается a. Расстояние от центра гиперболы до одного из фокусов называется фокальным расстоянием. ◦Обычно обозначается c.
 СВЯЗАННЫЕ ОПРЕДЕЛЕНИЯ Оба фокуса гиперболы лежат на продолжении большой оси на одинаковом расстоянии от центра гиперболы. Прямая, содержащая большую ось гиперболы, называется действительной или поперечной осью гиперболы. Прямая, перпендикулярная действительной оси и проходящая через её центр называется мнимой или сопряженной осью гиперболы. Отрезок между фокусом гиперболы и гиперболой, перпендикулярный её действительной оси, называется фокальным параметром: Расстояние от фокуса до асимптоты гиперболы называется прицельным параметром. ◦Обычно обозначается b. • Уравнения директрис:
СВЯЗАННЫЕ ОПРЕДЕЛЕНИЯ Оба фокуса гиперболы лежат на продолжении большой оси на одинаковом расстоянии от центра гиперболы. Прямая, содержащая большую ось гиперболы, называется действительной или поперечной осью гиперболы. Прямая, перпендикулярная действительной оси и проходящая через её центр называется мнимой или сопряженной осью гиперболы. Отрезок между фокусом гиперболы и гиперболой, перпендикулярный её действительной оси, называется фокальным параметром: Расстояние от фокуса до асимптоты гиперболы называется прицельным параметром. ◦Обычно обозначается b. • Уравнения директрис:
 ПРАКТИЧЕСКОЕ ПРИМЕНЕНИЕ Примером является зона слышимости звука пролетающего самолета. Если самолет движется со сверхзвуковой скоростью, то в воздухе зона слышимости образует конус. Поверхность Земли может приближенно считаться плоскостью, рассекающей этот конус. Если гиперболу вращать вокруг ее оси, проходящей через фокусы, то получающаяся поверхность будет называться двуполостным гиперболоидом, потому что состоит из двух полостей: одна – рассмотренная нами, а вторая получается от вращения второй ветви гиперболы. Если же вращать гиперболу вокруг второй ее оси, то получится поверхность, называемая однополостным гиперболоидом. Такую форму имеют секции Шаболовской радиобашни в Москве.
ПРАКТИЧЕСКОЕ ПРИМЕНЕНИЕ Примером является зона слышимости звука пролетающего самолета. Если самолет движется со сверхзвуковой скоростью, то в воздухе зона слышимости образует конус. Поверхность Земли может приближенно считаться плоскостью, рассекающей этот конус. Если гиперболу вращать вокруг ее оси, проходящей через фокусы, то получающаяся поверхность будет называться двуполостным гиперболоидом, потому что состоит из двух полостей: одна – рассмотренная нами, а вторая получается от вращения второй ветви гиперболы. Если же вращать гиперболу вокруг второй ее оси, то получится поверхность, называемая однополостным гиперболоидом. Такую форму имеют секции Шаболовской радиобашни в Москве.
 ПРЕЗЕНТАЦИЮ ВЫПОЛНИЛИ: УЧЕНИЦЫ 10 «Б» КЛАССА ЯКУБОВСКАЯ КСЕНИЯ ЛЕПЕШКО ЕКАТЕРИНА
ПРЕЗЕНТАЦИЮ ВЫПОЛНИЛИ: УЧЕНИЦЫ 10 «Б» КЛАССА ЯКУБОВСКАЯ КСЕНИЯ ЛЕПЕШКО ЕКАТЕРИНА
present5.com
Построение гиперболы, с примерами
Схема построения графика гиперболы
Функцию, которую можно задать формулой вида называют обратной пропорциональностью. Кривая, которая является графиком функции , называется гиперболой.

Гипербола состоит из двух частей – веток гиперболы. Если , то ветви гиперболы расположены в I и III координатных четвертях, а если – то в II и IV четвертях.
Областью определения и областью значений функции , где , есть все числа, кроме 0. Гипербола не имеет общих точек с осью ординат.
Функция – нечетная функция, поскольку
значит, график функции симметричен относительно начала координат.
Если , то функция убывает на промежутке .
Если , то функция возрастает на промежутке .
Примеры решения задач
| Понравился сайт? Расскажи друзьям! | |||
ru.solverbook.com
Что такое гипербола: уравнения и свойства
Определение 1
Гипербола в математике – это множество всех точек на плоскости, для любой из которых абсолютная разность расстояния между двумя точками $F_1$ и $F_2$, называемыми фокусами, всегда равна одному и тому же значению и равна $2a$.
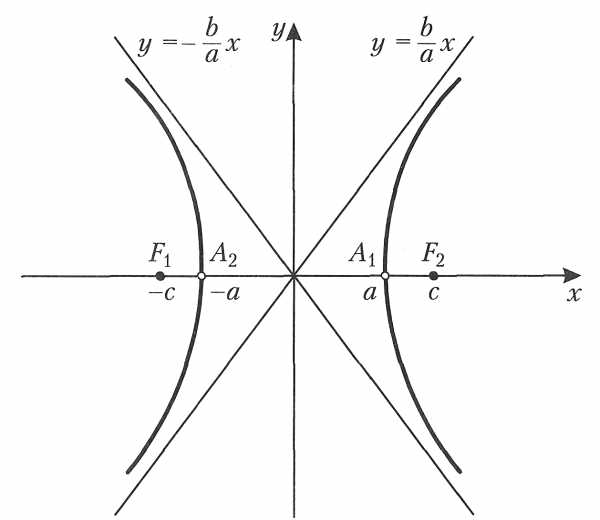
Рисунок 1. Как выглядит гипербола: пример гиперболы
Свойства гиперболы
- Если точки $F_1$ и $F_2$ являются фокусами гиперболы, то касательная, проведённая через любую точку $A$, принадлежащую кривой, является биссектрисой угла $F_1AF_2$;
- Отношение расстояний от точки на гиперболе до фокуса и от этой же точки до директрисы – это константа, называемая эксцентриситетом $ε$;
- Гиперболе свойственна зеркальная симметричность относительно действительной и мнимой осей, а также вращательная к центру при повороте на 180°;
- Ограниченный действительными осями отрезок касательной, проведённой через точку $M$, делится пополам точкой $M$;
- У каждой гиперболы есть сопряжённая гипербола, которая располагается в незанятых четвертях графика.
Основные определения
- Ветви гиперболы – это две непересекающиеся кривые;
- Вершинами гиперболы называются две ближайшие точки на разных ветвях гиперболы;
- Формула для определения расстояния между вершинами гиперболы выглядит как $2\cdot a$;
- Большой действительной осью называется прямая, проложенная через две ближайшие точки на гиперболе. На половине этого расстояния расположен центр гиперболы;
- Полуосями гиперболы называется половина расстояния между вершинами гиперболы, формула для его определения $2\cdot a/2 = a$;
- Мнимая ось – это прямая, проложенная через центр гиперболы и перпендикулярная действительной оси;
- Геометрическое построение гиперболы производится по заданным вершинам и фокусам с помощью циркуля.
Уравнение гиперболы
Общая формула гиперболы и функция гиперболы описывается следующим уравнением: $\frac{x^2}{a^2} — \frac{y^2}{b^2} = 1$, где $a, b$ — положительные действительные числа.
Уравнение вырожденной гиперболы выглядит как уравнение двух асимтот к гиперболе: $\frac{x}{a} — \frac{y}{b} = 0$
Уравнение гиперболы со смещенным центром $\frac{(x — x_0)^2}{a^2} — \frac{(y — y_0)^2}{b^2} = 1$, где $x_0, y_0$ — координаты центра гиперболы.
Для нахождения уравнения смещенной гиперболы по графику сначала определяют смещение центра относительно оси координат, оно равно координатам центра. Затем по асимтоптам определяют значения $a$ и $b$.
Пример вывода формулы параметрического уравнения гиперболы в математике
Пример 1
Рассмотрим уравнение: $5x^2 – 4y^2 = 20$
Для того чтобы привести его к каноничному виду, сначала разделим всё на 20:
$\frac{5x^2}{20} — \frac{4y^2}{20} = 1$
Теперь сократим числители и знаменатели: $\frac{x^2}{4} — \frac{y^2}{5} = 1$
Для получения каноничной формы выразим в знаменателе квадрат:
$\frac{x^2}{2^2} — \frac{y^2}{\sqrt(5)^2} = 1$
spravochnick.ru
Презентация на тему: Что такое гипербола?

Гипербола |
|
проявлялась в |
|
человеческом |
|
мышлении и |
|
сознании с |
|
первобытного |
|
строя. | Гипербола в литературе |
|
Гипербола в математике | Сергеева Евгения | |
Ученица 8 класса | ||
|

История происхождения гиперболы
Одним из первых, кто начал изучать конические сечения — эллипс, парабола, гипербола, был ученик знаменитого Платона, древнегреческий математик Менехм (IV в. до н.э.). Решая задачу об удвоении куба, Менехм задумался: «А что случится, если разрезать конус плоскостью, перпендикулярной его образующей?». Так, изменяя угол при вершине прямого кругового конуса, Менехм получил три вида кривых: эллипс — если угол при вершине конуса острый; парабола — если угол прямой; одну ветвь гиперболы — если угол тупой.
Название этих кривых придумал не Менехм. Их предложил один из крупнейших геометров древности Аполлоний Пергский, посвятивший замечательным кривым трактат из восьми книг «Конические сечения» («О кониках»). Семь книг сохранились, три из них — в арабском переводе. Первые четыре книги содержат начало теории и основные свойства конических сечений. Это — трактат об эллипсе, параболе и гиперболе, определяемых как сечения кругового конуса, где изложение доведено до исследования эволют конического сечения. Аполлоний показал, что кривые можно получить, проводя различные сечения одного и того же кругового конуса, причем любого.
При надлежащем наклоне секущей плоскости удается получить все типы конических сечений. Если считать, что конус не заканчивается в вершине, а проектируется на нее, тогда у некоторых сечений образуется две ветви.

Описывая кривые языком алгебры, математик выберет в плоскости сечения такую прямоугольную систему координат, в которой уравнения кривых имеют наиболее простой вид. Если направить ось абсцисс по оси симметрии конического сечения и поместить начало координат на саму кривую.
Происхождение названия объясняется следующим рисунком.
Построим в вершине любой прямоугольник. К нему приставим квадрат, касающийся вертикальной кривой, а стороной — оси симметрии. Тогда в гиперболе площадь квадрата больше, чем прямоугольника.
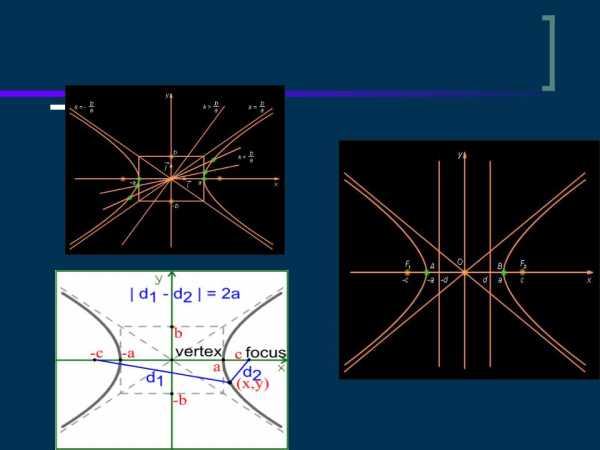
Математическая гипербола

Определение
•Обратной пропорциональностью называют функцию, заданную формулой y = k/x где k неравно 0. Число k называется коэффициентом обратной пропорциональности.
•Если считать х независимой переменной, а у — зависимой, то формула y = k/x определяет у как функцию от х. График функции y = k/x называют гиперболой.
•Гипербола имеет две ветви, которые расположены в первом и третьем квадратах, если k > 0, и во втором и четвертом квадрантах, если k > 0.
•Функция y = k/x , где k > 0 обладает следующими свойствами:
•область определения функции — множество всех действительных чисел, за исключением числа 0
•множество значений функции, все числа кроме числа 0
•y = k/x — нечетная
•принимает положительные значения при х > 0 и отрицательные — при x < 0
•убывает на промежутках х < 0 и х > 0.
Если k < 0, то функция y = k/x обладает свойствами 1—3, а свойства 4—5 формулируются так: принимает положительные значения при х < 0 и отрицательные при х > 0
•возрастает на промежутках х < 0 и х > 0.
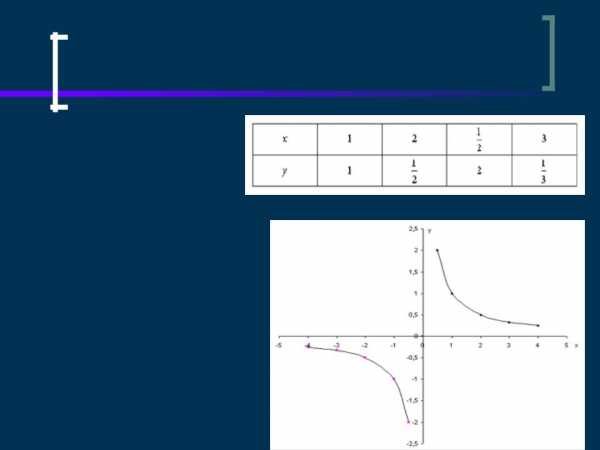
Строение графика если K>0
Построим график функции y = 1/x
ООФ: х неравен 0 МЗФ: у неравен 0 y = k/x — нечетная
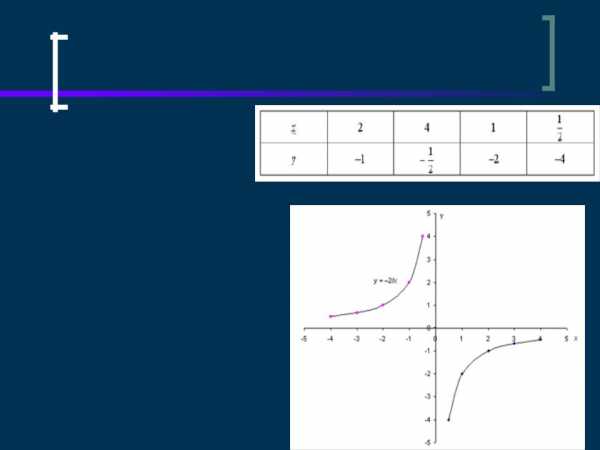
Строение графика ели К<0
Построим график функции y = k/x
При k = 2 y = -2/x ООФ: х неравен 0 МЗФ: у неравен 0 y = k/x — нечетная

Вот мы и узнали, что называют гиперболой в математике
А где же еще применяют гиперболу?

Примеры стилистической гиперболы
Толковый словарь русского языка гиперболу математическую и стилистическую практикует, как слова — амонимы, но исходя из выше приведенных фактов мы можем говорить о сходстве понятий гиперболы в математике и литературе.
Например, в «Повести о том, как поссорился Иван Иванович с Иваном Никифоровичем» Н. В. Гоголя основным художественным средством выразительности служит гипербола, использование которой придает сатирический эффект всему произведению. Например, «Иван Иванович несколько боязливого характера. У Ивана Никифоровича, напротив того. Шаровары в таких широких складках, что если бы раздуть их, то в них можно было бы поместить весь двор с амбаром и строениями».
У Гоголя гипербола вообще является излюбленным средством выразительности. Например, в повести «Тарас Бульба» автор использует следующие гиперболы: «Вся поверхность земли представлялась зелено-золотым океаном, по которому брызнули миллионы разных цветов…»; «Он веял холодными веками и расстилался ближе, ближе и, наконец, охватил половину всей поверхности земли…»; «…запорожец, как лев, растянулся на дороге. Закинутый гордо чуб его захватывал на пол-аршина земли».
В комедии «Ревизор», усиливая эффект вранья Хлестакова, Гоголь вкладывает в его уста следующую фразу: «Курьезы, курьезы … тридцать пять … тысяч курьезов». Автор прибегает к гиперболе для усиления впечатления, для заострения образа важный способ передачи авторской мысли построение сюжета образной системы

Литературная гипербола
Гипербола — образное выражение, содержащие непомерное преувеличение размера, силы, значения какого-либо предмета, явления. Например: «В сто сорок солнца закат пылал» (Маяковский). Используется гипербола для усиления эмоционального воздействия на читателя, а также для того, чтобы ярче выделить в изображаемом явлении те или иные стороны. Например: «И ядрам пролетать мешала гора кровавых тел» (М. Ю. Лермонтов). Или у Н. В. Гоголя: «Шаровары, шириной в Черное море»; «Рот величиной в арку Главного штаба». Наибольшую роль гипербола приобретает в сатире. Гипербола может быть идеализирующей и уничтожающей.
studfiles.net
Гипербола
Из школьного курса математики известно, что кривая, задаваемая уравнением , где- число, называется гиперболой. Однако это — частный случай гиперболы (равносторонняя гипербола).
Определение 2.5.Гиперболойназывается геометрическое место точек плоскости, для каждой из которых абсолютная величина разности расстояний до двух фиксированных точек той же плоскости, называемыхфокусамигиперболы, есть величина постоянная.
Так же, как и в случае эллипса, для получения уравнения гиперболы выберем подходящую систему координат. Начало координат расположим на середине отрезка между фокусами, ось направим вдоль этого отрезка, а ось ординат — перпендикулярно к нему.
Теорема 2.3. Пусть расстояние между фокусами игиперболы равно, а абсолютная величина разности расстояний от точки гиперболы до фокусов равна. Тогда гипербола в выбранной выше системе координат имеет уравнение:
-,
где (2.9)
Доказательство.Пусть- текущая точка гиперболы (рисунок 2.9).
Рисунок 2.9
Так как разность двух сторон треугольника меньше третьей стороны, то , то есть,. В силу последнего неравенства вещественное число, определяемое формулой (2.9), существует.
По условию, фокусы — ,. По формуле для случая плоскости получаем:
, .
По определению гиперболы
.
Это уравнение запишем в виде:
.
Обе части возведем в квадрат:
.
После приведения подобных членов и деления на 4, приходим к равенству:
.
Опять обе части возведем в квадрат:
.
Раскрывая скобку и приводя подобные члены, получим
.
С учетом формулы (2.9) уравнение принимает вид
Разделим обе части уравнения на и получим уравнение (2.8).
Уравнение (2.8) называетсяканоническимуравнением гиперболы.
Предложение 2.3Гипербола обладает двумя взаимно перпендикулярными осями симметрии, на одной из которых лежат фокусы гиперболы, и центром симметрии. Если гипербола задана каноническим уравнением, то ее осями симметрии служат координатные оси и, а начало координат — центр симметрии гиперболы.
Доказательство.Проводится аналогично доказательствупредложения 2.1.
Проведем построение гиперболы, заданной уравнением (2.8). Заметим, что из-за симметрии достаточно построить кривую только в первом координатном угле. Выразим из канонического уравнениякак функцию, при условии, что,
и построим график этой функции.
Область определения — интервал ,, функция монотонно растет. Производная
существует во всей области определения, кроме точки . Следовательно, график — гладкая кривая (без углов). Вторая производная
во всех точках интервала отрицательна, следовательно, график — выпуклый вверх.
Проверим график на наличие асимптоты при . Пусть асимптота имеет уравнение. Тогда по правилам математического анализа
,
.
Выражение под знаком предела домножим и разделим на . Получим
.
Итак, график функции имеет асимптоту . Из симметрии гиперболы следует, что- тоже асимптота. Остается неясным характер кривой в окрестности точки, а именно, образует ли графики симметричная ему относительно осичасть гиперболы в этой точке угол или гипербола в этой точке — гладкая кривая (есть касательная). Для решения этого вопроса выразим из уравнения (2.8)xчерезy:
Очевидно, что данная функция имеет производную в точке y=0,x’(0)=0, и в точкеу гиперболы есть вертикальная касательная. По полученным данным рисуем график функции(рисунок 2.10).
Рисунок 2.10 — График функции
Окончательно, используя симметрию гиперболы, получаем кривую рисунка 2.11.

Рисунок 2.11 — Гипербола
Определение 2.6.Точки пересечения гиперболы, заданной каноническим уравнением (2.8), с осьюназываютсявершинамигиперболы, отрезок между ними называетсядействительной осьюгиперболы. Отрезок оси ординат между точкамииназываетсямнимой осью. Числаaиbназываются соответственнодействительнойимнимой полуосямигиперболы. Начало координат называется ее центром. Величинаназывается эксцентриситетом гиперболы.
Замечание 2.3.Из равенства (2.9) следует, чтоc > a, то есть у гиперболы. Эксцентриситетхарактеризует угол между асимптотами, чем ближек 1, тем меньше этот угол.
Замечание 2.4.В отличие от эллипса в каноническом уравнении гиперболы соотношение между величинамиaиbможет быть произвольным. В частности, приa = bмы получим равностороннюю гиперболу, известную из школьного курса математики. Ее уравнение имеет знакомый вид, если взять, а осиинаправить по биссектрисам четвертого и первого координатных углов (рисунок 2.12).

Рисунок 2.12 — Равносторонняя гипербола
Для отражения на рисунке качественных характеристик гиперболы достаточно определить ее вершины, нарисовать асимптоты и нарисовать гладкую кривую, проходящую через вершины, приближающуюся к асимптотам и похожую на кривую рисунка 2.10.
Пример 2.4.Постройте гиперболу, найдите ее фокусы и эксцентриситет.
Решение.Разделим обе части уравнения на 4. Получим каноническое уравнение
a = 1, b = 2.Проводим асимптотыи строим гиперболу (рисунок 2.13).
Рисунок 2.13 – Гипербола
Из формулы (2.9) получим. Тогда фокусы -,,.
Пример 2.5.Постройте гиперболу. Найдите ее фокусы и эксцентриситет.
Решение.Преобразуем уравнение к виду
Данное уравнение не является каноническим уравнением гиперболы, так как знаки перед ипротивоположны знакам в каноническом уравнении. Однако, если переобозначить переменные,, то в новых переменных получим каноническое уравнение
Действительная ось этой гиперболы лежит на оси , то есть на осиисходной системы координат, асимптоты имеют уравнение, то есть уравнениев исходных координатах. Действительная полуось равна 5, мнимая — 2. В соответствии с этими данными проводим построение (рисунок 2.14).
Рисунок 2.14 — Гипербола с уравнением
Из формулы (2.9) получим,, фокусы лежат на действительной оси -,,где координаты указаны в исходной системе координат.
studfiles.net
