что такое? Как найти синус, косинус и тангенс?
что такое? Как найти синус, косинус и тангенс?
Одним из разделов математики, с которыми школьники справляются с наибольшими трудностями, является тригонометрия. Неудивительно: для того чтобы свободно овладеть этой областью знаний, требуется наличие пространственного мышления, умение находить синусы, косинусы, тангенсы, котангенсы по формулам, упрощать выражения, уметь применять в вычислениях число пи. Помимо этого, нужно уметь применять тригонометрию при доказательстве теорем, а это требует либо развитой математической памяти, либо умения выводить непростые логические цепочки.
Истоки тригонометрии
Знакомство с данной наукой следует начать с определения синуса, косинуса и тангенса угла, однако прежде необходимо разобраться, чем вообще занимается тригонометрия.
Исторически главным объектом исследования данного раздела математической науки были прямоугольные треугольники. Наличие угла в 90 градусов дает возможность осуществлять различные операции, позволяющие по двум сторонам и одному углу либо по двум углам и одной стороне определять значения всех параметров рассматриваемой фигуры. В прошлом люди заметили эту закономерность и стали активно ею пользоваться при строительстве зданий, навигации, в астрономии и даже в искусстве.
Начальный этап
Первоначально люди рассуждали о взаимоотношении углов и сторон исключительно на примере прямоугольных треугольников. Затем были открыты особые формулы, позволившие расширить границы употребления в повседневной жизни данного раздела математики.
Изучение тригонометрии в школе сегодня начинается с прямоугольных треугольников, после чего полученные знания используются учениками в физике и решении абстрактных тригонометрических уравнений, работа с которыми начинается в старших классах.
Сферическая тригонометрия
Позже, когда наука вышла на следующий уровень развития, формулы с синусом, косинусом, тангенсом, котангенсом стали использоваться в сферической геометрии, где действуют иные правила, а сумма углов в треугольнике всегда больше 180 градусов. Данный раздел не изучается в школе, однако знать о его существовании необходимо как минимум потому, что земная поверхность, да и поверхность любой другой планеты, является выпуклой, а значит, любая разметка поверхности будет в трёхмерном пространстве «дугообразной».
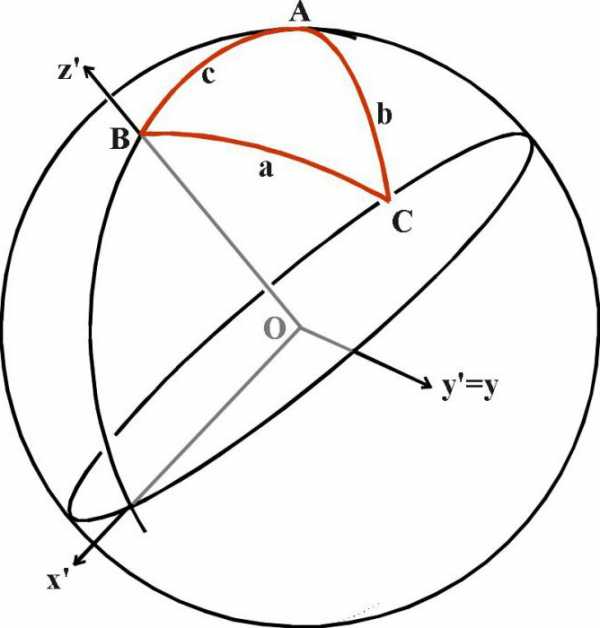Возьмите глобус и нитку. Приложите нитку к двум любым точкам на глобусе, чтобы она оказалась натянутой. Обратите внимание – она обрела форму дуги. С такими формами и имеет дело сферическая геометрия, применяющаяся в геодезии, астрономии и других теоретических и прикладных областях.
Прямоугольный треугольник
Немного узнав про способы применения тригонометрии, вернемся к базовой тригонометрии, чтобы в дальнейшем разобраться, что такое синус, косинус, тангенс, какие расчёты можно с их помощью выполнять и какие формулы при этом использовать.
Первым делом необходимо уяснить понятия, относящиеся к прямоугольному треугольнику. Во-первых, гипотенуза – это сторона, лежащая напротив угла в 90 градусов. Она является самой длинной. Мы помним, что по теореме Пифагора её численное значение равно корню из суммы квадратов двух других сторон.
Например, если две стороны равны 3 и 4 сантиметрам соответственно, длина гипотенузы составит 5 сантиметров. Кстати, об этом знали ещё древние египтяне около четырех с половиной тысяч лет назад.
Две оставшиеся стороны, которые образуют прямой угол, носят название катетов. Кроме того, надо помнить, что сумма углов в треугольнике в прямоугольной системе координат равняется 180 градусам.
Определение
Наконец, твердо понимая геометрическую базу, можно обратиться к определению синуса, косинуса и тангенса угла.
Синусом угла называется отношение противолежащего катета (т. е. стороны, располагающейся напротив нужного угла) к гипотенузе. Косинусом угла называется отношение прилежащего катета к гипотенузе.
Запомните, что ни синус, ни косинус не может быть больше единицы! Почему? Потому что гипотенуза – это по умолчанию самая длинная сторона прямоугольного треугольника. Каким бы длинным ни был катет, он будет короче гипотенузы, а значит, их отношение всегда будет меньше единицы. Таким образом, если у вас в ответе к задаче получился синус или косинус со значением, большим, чем 1, ищите ошибку в расчётах или рассуждениях. Этот ответ однозначно неверен.
Наконец, тангенсом угла называется отношение противолежащей стороны к прилежащей. Тот же самый результат даст деление синуса на косинус. Посмотрите: в соответствии с формулой мы делим длину стороны на гипотенузу, после чего делим на длину второй стороны и умножаем на гипотенузу. Таким образом, мы получаем т
10i5.ru
зная cos как найти sin
Зная косинус угла находим угол через функцию, обратную косинусу — это арккосинус, зная угол находим синус.. . Так надежнее, чем через sin^2(x) + cos^2(x) = 1
неправильно. cos^2+sin^2 = 1 sin=(1-cos)^(1/2)
по основному тригонометрическому тождеству. соs в квадрате + sin в квадрате=1 отсюда выводишь что соs= под корнем выражение: 1-sin в квадрате
основное тригонометрическое тождество sin2+cos2=1; sin=квадратный корень (1-cos2) sin x = tg x / cos x
touch.otvet.mail.ru
Как найти синус угла
Рассмотрим вопрос о том, как найти синус угла.
Первый из способов, который будем рассматривать, это традиционный тригонометрический метод нахождения синуса острого угла из прямоугольного треугольника.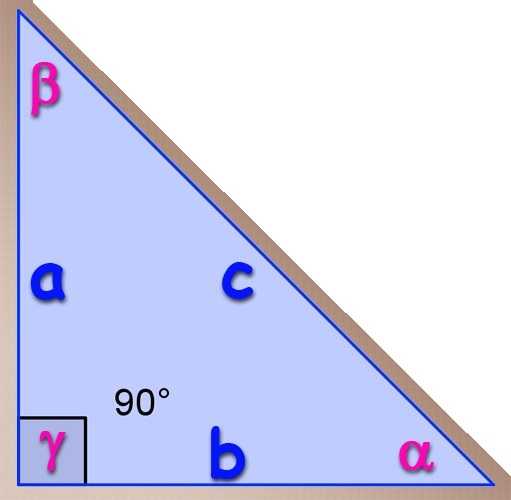
Из прямоугольного треугольника проще простого найти значение синуса острого угла, если известна длина катета, который лежит напротив необходимого угла, и длина гипотенузы.
В таком случае синус угла рассчитывается как отношение длины такого катета к длине гипотенузы.
Например, если нужно найти синус угла альфа, то формула для нахождения синуса будет следующей:
Соответственно, для синуса угла бета запишем:
Синус третьего угла, который в прямоугольном треугольнике является прямым, находить нет необходимости, так как синус 90 градусов равен единице:
Второй способ касается вычисления синуса угла в произвольном треугольнике. Для этого используется теорема косинусов, что кажется немного странным (что не теорема синусов).
Согласно теореме запишем выражение:
Выведем из этого выражения формулу для косинуса альфа:
Чтобы найти синус альфа, нужно использовать основное тригонометрическое тождество, в котором сумма квадратов синуса альфа и косинуса альфа равна единице:
Подставив найденное значение косинуса в формулу можно вычислить синус.
ru.solverbook.com