Этап урока | Образовательная задача этапа урока | Образовательная технология, Методы и приемы обучения | Деятельность учителя | Деятельность обучающихся | Форма организации учебной деятельности (Ф-фронтальная, И-индивидуальная, П-парная, Г-групповая) | Дидактические средства, интерактивное оборудование | Формы контроля, взаимоконтроля и самоконтроля | Планируемые результаты | ||
Предметные | Метапредметные (П-познавательные, Р – регулятивные, К– коммуникативные) | Личностные | ||||||||
Мотивация (самоопределение к учебной деятельности) | Создать условия для возникновения внутренней потребности включения в учебную деятельность | Здоровьесберегающая, ИКТ Включение в урок через движение под речетатив. Проверка посадки детей. Показ слайдов. | Здравствуйте, меня зовут Юлия Игоревна, и сегодня я проведу у вас урок. Если я пришёл учиться, если ты пришёл учиться, мы не будем все лениться, А друг другу помогать. Давайте проверим, у вас на столах должны лежать: тетради, учебники, пенал и дневник, остальное уберите в портфель, чтобы эти предметы вам не мешали. Молодцы, мы готовы приступить к уроку. | Приветствуют учителя и маршируют под речёвку. Настраиваются на работу | Ф | Интерактивная доска | Р: волевая саморегуляция | развитие мотивов учебной деятельности | ||
Актуализация и фиксирование индивидуального затруднения в пробном действии | подготовка мышления учащихся и организация осознания ими внутренней потребности к построению учебных действий | ИКТ, Словесный метод Фронтальная работа Наглядный материал | Играют в игру, где проходят разные препятствия. 1 препятствие: «Устный счет» Читают стихотворение, которое написано на доске. Учащимся предлагается посчитать Сколько на картинке утят, которые бегут за мячом? сколько утят хотят поймать кота? Сколько все утят, как это узнать? 2 препятствие: учащиеся смотрят на доску — Как нам узнать какое число предшествует 37? -Так какой у нас ответ? | Выполняют задание. (читают стихотворение) — двое утят — трое — сложить утят? — нужно от 37 отнять единицу 37-1= 36 | Отвечают на вопросы учителя. | Интерактивная доска | Контроль, самоконтроль | Распознавание ранее изученных приемов счета. | Р: овладение логическими действиями сравнения, анализа К: умение выражать свои мысли П: закрепит вычислительные навыки; овладение логическими операциями анализа и сопоставления | Развитие навыков сотрудничества со взрослыми и сверстниками |
Выявление места и причины затруднения | Создать проблемную ситуацию, зафиксировать новую проблемную задачу | Проблемное обучение, ИКТ, здоровьесберегающая Фронтальный метод Словесный метод Наглядный метод Практический метод | Учащиеся рассматривают следующую запись: 3-1=2 4-11 3+12 5-1 4+1=5 1+1=2 — Что заметили? — Какие две группы можно выделить? — Запишите первую группу выражений в столбик в ваших тетрадях. — Как бы вы назвали выражения, записанные в первом столбике? — Как можно назвать записи второго столбика? — Правильно, ребята, вы молодцы! — Как вы думаете какая тема нашего урока? Чтобы узнать правильный ответ на этот вопрос давайте откроем учебник на странице 48 и прочитаем тему. | Рассматривают примеры, записанные на доске. Мы заметили, что одни выражения равны, а другие нет(учащиеся записывают в тетрадях,а учитель – на доске. Один из учеников комментирует) — Выражения в первом столбике называются равенства. — Записи второго столбика можно назвать неравенства. Открывают учебник, читают тему урока. | Ф | Интерактивная доска, | Взаимоконтроль | формирование мыслительных операций: анализ, сравнение, обобщение | П: осознание того, что уже усвоено и что ещё нужно усвоить Р: К: умение выражать свои мысли | развитие самостоятельного критического мышления контролировать свои действия |
Построение проекта выхода из затруднения | Зафиксировать причину затруднения при сравнивании чисел | ИКТ, проблемное обучение Практический метод | — Какую цель ставим? — Наметим план наших действий: 1. 2. Сопоставим свои предположения с учебником, спросим у учителя; 3. устраним затруднения; 4. применим новые знания. — Как вы думаете, что нам в этом поможет? | — Узнать что такое равенство и неравенство и их виды. С помощью этих операций, мы сможем сравнивать числа и выражения. — Наверное, нам поможет в этом учебник, учитель, свой опыт. | Ф | учебник | Контроль. | Умение строить план действий и пути его осуществления. | П: осознание того, что уже усвоено и что ещё нужно усвоить Р: волевая саморегуляция в ситуации затруднения, определение и формулировка цели и планирование учебной деятельности К: умение выражать свои мысли и учитывать разные мнения | развитие самостоятельного критического мышления контролировать свои действия |
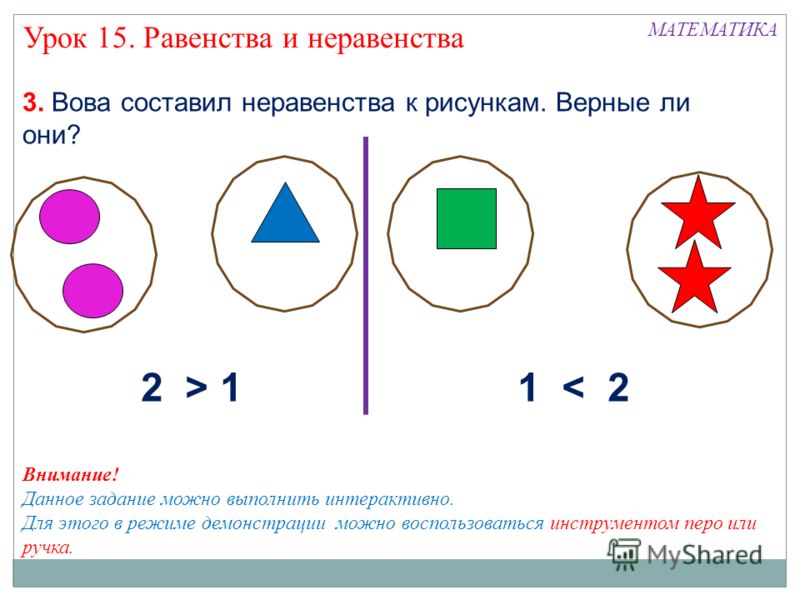
Первичное закрепление с проговариванием во внешней речи | ИКТ Практический метод | -Сейчас мы разделимся по парам. -Давайте вспомним правила работы в парах. — Откройте учебник на странице 48 и рассмотрите задание №4. Вам дан рассказ, по нему вы должны составить равенства. Теперь проверим, что у вас получилось. Следующее задание №5. — Рассмотрите рисунки, которые даны в задании №5 и запишите лишние выражения. И докажите, свою точку зрения. | Учащиеся отвечают на вопрос: -не шуметь; — не мешать остальным; — слушать друг друга; — не перебивать соседа. Учащиеся работают по учебнику, выполняют задание №4. Некоторые по желанию зачитывают свои равенства. Выполняют задание №5. Записывают в тетрадь лишние выражение и высказывают свое мнение. | Парная работа. И. | Самоконтроль. Взаимоконтроль. | Уметь различать равенства и неравенства. Уметь оформлять на письме запись числовых выражений. | К: уметь взаимодействовать с соседом по парте. Слушать и понимать речь других. П: уметь использовать знаково-символичные средства. Уметь оформлять свои мысли в устной и письменной форме. | Развитие навыков сотрудничества со взрослыми и сверстникам | ||
Самостоятельная работа с самопроверкой по эталону | Самостоятельное выполнение заданий. | ИКТ Н Дидактический материал | — Сейчас я вам раздам карточки, в них вы увидите выражения и числа, которые вы должны сравнить. Эталон для самопроверки на доске. — У кого все правильно? — У кого одна ошибка? Две? Больше двух? — Какие затруднения возникли? | Учащиеся выполняют задания на карточках. После того, как сделали, сверяют свои ответы с доской. Отвечают на вопросы учителя. | И. Ф | Интерактивная доска. Карточки. | Самоконтроль. | Развитие умения оформлять решение задачи; применять на практике знания о «Равенстве. Неравенстве». | Р: умение планировать свое действие в соответствии с поставленной задачей. Л: проявлять инициативу в оказании помощи; способность к самооценке на основе критерия успешной учебной деятельности. П: умение проговаривать последовательность действий | развитие самостоятельного критического мышления, развитие умения контролировать свои действия. |
Включение в систему знания и повторения | ИКТ. Проблемное обучение. | Давайте вспомним, с чем мы сегодня познакомились. — Что нового вы узнали? — Выполнили мы наш план? — Какие задания вызвали у вас затруднения? — Как вы думаете, как исправить ваши затруднения? | Отвечают на вопросы учителя. | Ф | Учебник. Интерактивная доска. | Взаимоконтроль. | формирование мыслительных операций: анализ, сравнение, обобщение | П:осознание усвоенного материала; Уметь добывать новые знания, находить ответы на вопросы в учебнике, используя полученную информацию. Р:умение высказывать свои предположения. | Способность строить грамотные полные ответы на вопросы. | |
Рефлексия учебной деятельности на уроке | Организация рефлексии и самооценки учебной деятельности. | ИКТ. | -Теперь давайте подведём итоги нашего урока -Какую цель мы с вами ставили? Достигли поставленной цели? -Ребята, обратите внимание на доску. Весь собранный материал у нас расположен в строгой последовательности. Это и есть наш проект, которой мы должны были составить к концу урока. -А теперь нужно одному ученику рассказать всё то, что мы добились всем классом, т.е выступить с сообщением , как это делают настоящие взрослые учёные. -Молодец! Хорошее выступление. -А теперь давайте оценим свою деятельность на уроке, использую прием лесенка. Урок окончен. | Учащиеся отвечают на поставленные вопросы учителем. | Ф | Интерактивная доска | Взаимоконтроль. | Умение анализировать свою работу и работу других. | Р: умение оценивать правильность выполнения действий на уровне адекватной оценки. Л: способность к самооценке на основе критерия успешной учебной деятельности. К: умение правильно и грамотно стоить ответы на вопросы. | Развитие способности адекватно оценивать мебя и окружающих. |
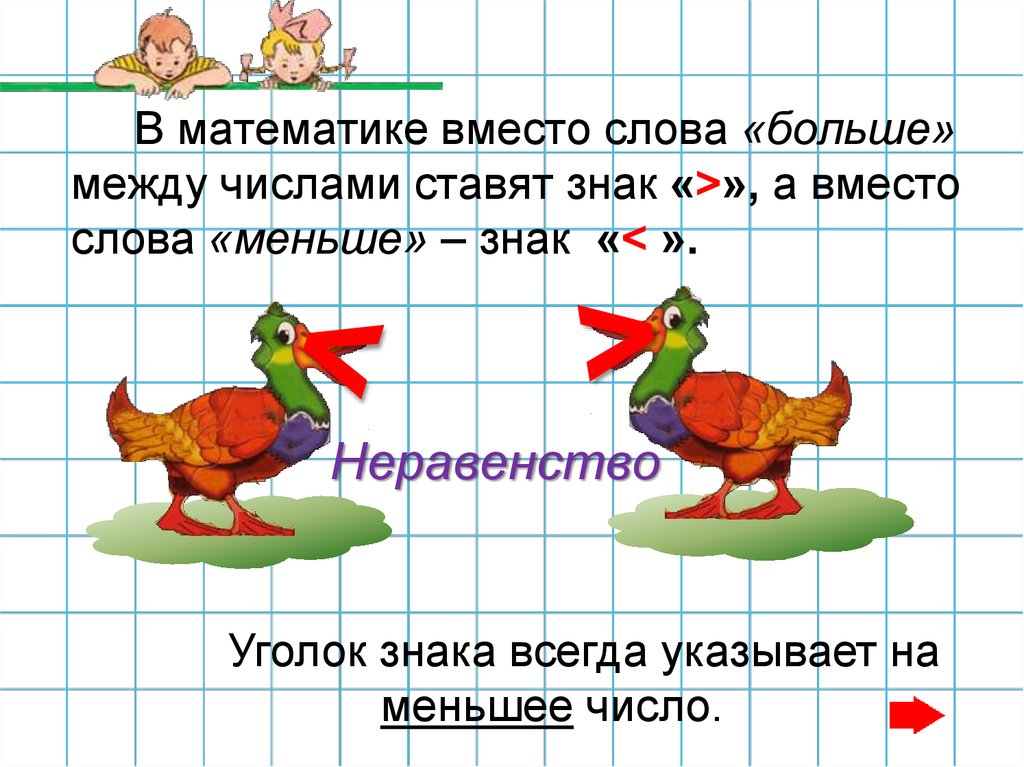
Что такое равенство в математике 2 класс?
Что такое равенство в математике 2 класс?
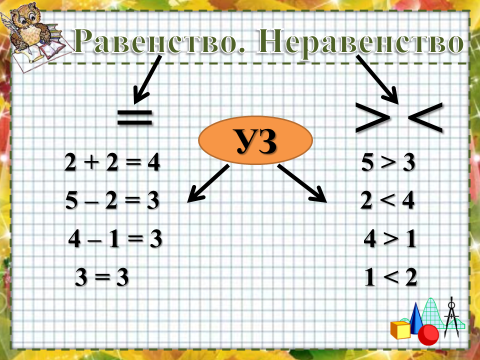
Равенство – это когда одно количество равно другому. Неравенство – это когда одна сторона выражения не равна второй.
Что такое равенство в математике 3 класс?
Чтобы получить запись, называемую числовым равенством, надо два числовых выражения соединить знаком равенства (=). … Если числовое равенство верно, то прибавив к обеим частям этого равенства одно и тоже число мы получим верное числовое равенство.
… Если числовое равенство верно, то прибавив к обеим частям этого равенства одно и тоже число мы получим верное числовое равенство.
Что значит решить уравнение?
Значения неизвестных переменных, при которых это равенство достигается, называются решениями или корнями данного уравнения. … Решить уравнение означает найти множество всех его решений (корней) или доказать, что корней нет вовсе (либо нет тех, что удовлетворяют заданным условиям).
В каком случае одно уравнение является следствием другого?
два уравнения называют равносильными, если они имеют одинаковые корни, или если оба уравнения не имеют корней. Определение 2. то уравнение (2) называют следствием уравнения (1). … два уравнения равносильны тогда и только тогда, когда каждое из них является следствием другого.
Какое уравнение называется следствием другого уравнения?
Если каждый корень уравнения f(x)=g(x) является в то же время корнем уравнения p(x)=h(x), то уравнение p(x)=h(x) называют следствием уравнения f(x)=g(x) [3, с. Если все корни первого уравнения являются корнями второго уравнения, то второе уравнение называется следствием первого уравнения [4, с. …
Если все корни первого уравнения являются корнями второго уравнения, то второе уравнение называется следствием первого уравнения [4, с. …
Как найти равносильное уравнение?
Если какой-либо член уравнения перенести из одной части уравнения в другую с противоположным знаком, то получится уравнение, равносильное данному. Теорема 2. Если обе части уравнения возвести в одну и туже нечетную степень, то получится уравнение, равносильное данному. равносильно уравнению f(x) = g(х).
Какие преобразования приводят к равносильным уравнениям?
Такую замену называют равносильным преобразованием уравнения. Основные равносильные преобразования: 1) перенос членов уравнения из одной части уравнения в другую с противоположными знаками. 2) Умножение или деление обеих частей уравнения на одно и то же отличное от нуля число или выражение.
Какое уравнение называется показательным?
Показательными называются уравнения, в которых неизвестное содержится в показателе степени. Простейшее показательное уравнение имеет вид: ах = аb, где а> 0, а 1, х — неизвестное. Основные свойства степеней, при помощи которых преобразуются показательные уравнения: а>0, b>0.
Простейшее показательное уравнение имеет вид: ах = аb, где а> 0, а 1, х — неизвестное. Основные свойства степеней, при помощи которых преобразуются показательные уравнения: а>0, b>0.
Какое уравнение называется Биквадратным?
Биквадратным называется уравнение вида ax 4 + bx 2 + c =0 , где a 0 . Биквадратное уравнение решается методом введения новой переменной: положив x 2 = y , прийдем к квадратному уравнению ay 2 + by + c =0 . Пример: Решить уравнение x 4 +4 x 2 -21=0 .
Как называется уравнение которое содержит переменные только в показателе степени?
ПОКАЗАТЕЛЬНЫЕ УРАВНЕНИЯ — уравнения, в которых неизвестное (переменная) содержится в показателе степени.
Когда показательное уравнение не имеет корней?
При каких условиях уравнение (1) не имеет корней? Если D уравнение не имеет корней. Если D ≥ 0.
Когда уравнение имеет один корень?
При a = 1 уравнение имеет вид 2x = 0 и, очевидно, имеет единственный корень x = 0. Если a № 1, то данное уравнение является квадратным и имеет единственный корень при тех значениях параметра, при которых дискриминант квадратного трехчлена равен нулю.
Если a № 1, то данное уравнение является квадратным и имеет единственный корень при тех значениях параметра, при которых дискриминант квадратного трехчлена равен нулю.
Когда уравнение имеет единственное решение?
Уравнение (1) имеет единственное решение, если уравнение (2) имеет один положительный корень. Это возможно в следующих случаях. 1. Если D = 0, то есть p = 1, тогда уравнение (2) примет вид t2 – 2t + 1 = 0, отсюда t = 1, следовательно, уравнение (1) имеет единственное решение x = 0.
Какие способы решения показательных уравнений вы знаете?
Методы решения уравнений
- Одним из методов решения показательных уравнений является метод логарифмирования.
- Следующим методом решения показательного уравнения является введение новой переменной: …
- Метод вынесения общего множителя за скобки
- Метод использования монотонности показательной функции
Что называется показательным неравенством?
Показательными называются неравенства, в которых неизвестное содержится в показателе степени.
В чем заключается графический метод решения показательных уравнений?
Теория Графический метод решения уравнений, в том числе и показательных, предполагает построение в одной системе координат графиков функций, отвечающих левой и правой части решаемого уравнения, с целью определения количества всех точек пересечения и абсцисс этих точек.
Что называется показательной функцией?
е. функция вида y = a x , где a — заданное число, x — переменная. Такие функции называют показательными. Это название объясняется тем, что аргументом показательной функции является показатель степени, а основанием степени — заданное число.
Как определить область значения показательной функции?
Функцию вида y=ax, где а>0, a≠1, х – любое число, называют показательной функцией. Область определения показательной функции: D (y)=R – множество всех действительных чисел. Область значений показательной функции: E (y)=R+ — множество всех положительных чисел.
Когда показательная функция убывает?
Если же a показательная функция убывает при возрастании ее аргумента; она больше единицы при x 0 и при неограниченном возрастании аргумента неограниченно приближается к нулю, а при его неограниченном убывании неограниченно возрастает (рис.
мат-гр. 1. Равенство и неравенство, гр. 2. Округление – г-жа Чин
1-й класс: равенство и неравенство
Сегодня я хочу, чтобы вы попрактиковались в определении, является ли уравнение равным или нет. Например, вы привыкли видеть такие уравнения, как 5+5=10 и 8-5=3. Теперь представьте, что знак = похож на стену. Когда мы пытаемся увидеть, равны ли вещи в математических уравнениях, мы хотим знать, одинаковы ли значения чисел на каждой стороне стены со знаком =. Например, для уравнения 5+5=10. С левой стороны 5+5, мы знаем, что это равно 10. С правой стороны у нас есть число 10. Таким образом, на каждой стороне стены значение одинаковое. Опять же, с 8-5=3. Представьте, что знак = — это стена. На левой стороне стены у нас есть 8-5, что, как мы знаем, равно 3. На правой стороне стены у нас есть 3, поэтому на каждой стороне стены значение одинаково. В обеих этих ситуациях есть равенство.
На левой стороне стены у нас есть 8-5, что, как мы знаем, равно 3. На правой стороне стены у нас есть 3, поэтому на каждой стороне стены значение одинаково. В обеих этих ситуациях есть равенство.
А как насчет 4+5=10? С левой стороны стены мы знаем, что 4+5=9. Таким образом, на левой стороне стены значение чисел равно 9. На правой стороне стены со знаком = 9. Равно ли это уравнение? Ответ — нет. 4+5 не равно 10. Значения на каждой стороне стены неравны, поэтому возникает неравенство . Для этого уравнения мы покажем, что это неравенство, используя этот знак: ≠.
Мы также можем сделать это с помощью простых уравнений.
Если у меня 5+5=6+4, это правильно? Должен ли быть знак = или знак ≠?
С левой стороны стены со знаком = есть 5+5, что, как мы знаем, равно 10. С правой стороны есть 6+4, что тоже равно 10. Так есть ли равенство или неравенство? Существует равенство, потому что обе стороны равны 10.
Попробуйте эти рабочие листы и посмотрите, сможете ли вы выяснить, используете ли вы знак = или знак ≠!
Рабочие листы:
Введение Рабочий лист равенства и неравенства
Равенство и неравенство Простые уравнения
2 класс: Округление
Сегодня мы попрактикуемся в округлении до десятых. Что такое округление? Округление — это когда мы берем число и находим ближайшее число 10, 20, 30, 40, 50, 60, 70, 80, 90, 100, рядом с которым оно находится. Мы делаем это, когда оцениваем измерение или нуждаемся в общем представлении о том, сколько чего-то есть или какова его длина. Например, если у меня есть число 26, я должен подумать, между какими числами оно находится или близко к ним (которые кратны десяти)? Что ж, на числовой прямой 26 находится между 20 и 30. Теперь, какова середина пути между 20 и 30?
Что такое округление? Округление — это когда мы берем число и находим ближайшее число 10, 20, 30, 40, 50, 60, 70, 80, 90, 100, рядом с которым оно находится. Мы делаем это, когда оцениваем измерение или нуждаемся в общем представлении о том, сколько чего-то есть или какова его длина. Например, если у меня есть число 26, я должен подумать, между какими числами оно находится или близко к ним (которые кратны десяти)? Что ж, на числовой прямой 26 находится между 20 и 30. Теперь, какова середина пути между 20 и 30?
20, 21, 22, 23, 24, 25 , 26, 27, 28, 29, 30.
25 находится прямо между ними. Теперь я должен подумать, 26 ниже или выше, до или после 25? Оно выше 25, потому что 26 больше 25, оно стоит после него на числовой прямой. На числовой прямой видно, что 26 ближе к 30. Поэтому, если бы я округлял до ближайших десяти, 26 округлилось бы до 30.
Мы также можем округлить до ближайших сотых. Например, если у меня есть число 123. Я должен подумать, ближе ли оно к 100 или 200? На числовой прямой это число было бы ближе к 100, чем к 200.
Я должен подумать, ближе ли оно к 100 или 200? На числовой прямой это число было бы ближе к 100, чем к 200.
Посмотрите это видео, чтобы получить полное объяснение того, что такое округление и как это сделать!
Округление до ближайших 10
Вот диаграмма, которая может вам помочь.
Округление до ближайших 10 и 100 Диаграмма
Теперь я хочу, чтобы вы попробовали. Вот несколько рабочих листов, чтобы попробовать. Если у вас нет принтера, попробуйте сделать это устно. Используйте числовые линии, чтобы помочь вам, если вам это нужно!
Округлить до ближайшей десятки Введение
Округление до ближайшего 10-го рабочего листа
Математика, 6 класс, уравнения и неравенства, представление неравенства на числовой прямой
Обзор
Учащиеся изображают неравенства на числовой прямой, находят хотя бы одно значение, которое делает неравенство верным, и записывают неравенство словами.
SWD: Когда вы звоните учащимся, обязательно звоните ELL и призывайте их к активному участию. Поймите, что их темп может быть медленнее, они могут быть застенчивыми или более неохотно вызываться добровольцами из-за более слабого владения языком.
SWD: Мысли вслух — это один из способов сделать обучение видимым. Когда учителя думают вслух, они воплощают свои внутренние мыслительные процессы вовне. Это может дать учащимся представление о математическом мышлении и способах решения проблем. Это также помогает моделировать точный математический язык.
Неравенства, как и уравнения, имеют решения. Стрелку на числовой прямой, указывающую вправо для больших значений и влево для меньших значений, можно использовать, чтобы показать, что существует бесконечно много решений неравенства.
Решения x < a представлены на числовой прямой стрелкой, указывающей влево от незакрашенного кружка на a .
Пример: x < 2
Решения x > a представлены на числовой прямой стрелкой, указывающей вправо от незакрашенного кружка a .
Пример: x > 2
Решения задачи x ≤ a представлены на числовой прямой стрелкой, указывающей влево от замкнутого круга a .
Пример: x ≤ 2
Решения x ≥ a представлены на числовой прямой стрелкой, указывающей вправо от замкнутого круга на a .
Пример: x ≥ 2
- Представьте неравенство на числовой прямой с помощью слов.
- Поймите, что неравенства имеют бесконечно много решений.
Предложите учащимся поработать в парах, чтобы сопоставить неравенства с их представлениями на числовой прямой и написать неравенство словами.
Поделитесь с учениками неравенствами из открытия и правильными соответствующими числовыми линиями, чтобы они могли легко обращаться к ним в будущем.
ELL: Изучение новых способов построения графиков неравенства может стать проблемой для ELL. Просмотрите и/или предварительно изучите новые понятия в этом уроке. Содействуйте связям с базовыми знаниями учащихся и с предыдущими уроками в этом разделе.
Просмотрите и/или предварительно изучите новые понятия в этом уроке. Содействуйте связям с базовыми знаниями учащихся и с предыдущими уроками в этом разделе.
Учащиеся будут рассуждать, чтобы сопоставить числовые строки с правильными неравенствами. Им нужно будет объяснить, что открытый кружок означает, что число не включено в неравенство, а закрытый кружок указывает, что оно включено. Не сообщайте эту информацию учащимся. Если изначально не все в классе согласны с этим соглашением, позвольте учащимся отстаивать свои позиции до тех пор, пока все не поймут, почему это соглашение имеет смысл.
- х < 2: Б." x меньше 2″.
- x > 2: C. » x больше 2″.
- x ≥ 2: D. » x больше или равно 2 .»
- x ≤ : A. « x меньше или равно 2.»
Открытие
- Сопоставьте каждое неравенство с числовой прямой.
- Запишите неравенство словами в отведенном месте; например, « x меньше 5″.

ИНТЕРАКТИВНЫЙ: сопоставление неравенств с графиками
Обсудить математическую миссию. Учащиеся представят неравенства на числовой прямой и найдут хотя бы одно значение, которое делает неравенство верным.
Открытие
Представьте неравенства на числовой прямой и найдите хотя бы одно значение, которое делает неравенство верным.
Предложите учащимся поработать в парах над задачами 3 и 4. Определите любые неверные представления учащихся, которые следует устранить в разделе «Способы мышления».
SWD: Пройдитесь по классу, прежде чем ваши ученики поделятся. Помогите учащимся определить идеи из своих заметок и мыслей, которые можно использовать в ходе этой части обсуждения «Пути мышления».
Математическая практика 3: Создание убедительных аргументов и критика рассуждений других.
Слушайте разговоры учащихся о том, применяются ли правила или соглашения к отрицательным значениям так же, как и к положительным значениям.
Слушайте разговоры учащихся о том, должны ли кружки быть открытыми или закрытыми.
Слушайте разговоры студентов о том, в каком направлении должны быть стрелки.
Студент не понимает, как пользоваться интерактивом.
- Попросите своего партнера продемонстрировать, как пользоваться интерактивом.
Студент борется с отрицательными значениями и направлением стрелок.
- Число слева больше или меньше числа справа?
Учащийся не понимает правил использования открытых и закрытых кружков на числовой прямой.
- Просмотрите ответы на Открытие.
- Как математические соглашения связаны с языком: больше или меньше, и больше или равно или меньше или равно ?
Учащийся не знает, как найти одно значение, которое делает неравенство верным.
- Посмотрите на незамкнутый (или замкнутый) круг. Это число делает неравенство верным?
- Будут ли числа, подтверждающие истинность неравенства, находиться слева или справа от открытого (или закрытого) круга?
Рабочее время
Для каждого неравенства выполните следующие действия.
- Представьте неравенство на числовой прямой с помощью интерактивной числовой строки.
- Запишите одно значение, которое делает неравенство верным.
- Запишите неравенство словами.
- x ≥ –2
- x < 4
- 12 ≥ x
- x ≤ −3.5
- x < 1.5
INTERACTIVE: Inequalities and Number Lines
Hint:
- Где находится число на числовой прямой?
- Должна ли начальная точка быть замкнутым кругом или незамкнутым кругом?
- Какое значение делает неравенство верным? Это значение заштриховано на числовой прямой?
Смотреть для учащихся, которые:
- Не могут описать реальную ситуацию, чтобы представить числовую прямую.

Математическая практика 1: Разбираться в задачах и настойчиво решать их.
Ищите множество реальных сценариев.
Математическая практика 3: Создание убедительных аргументов и критика рассуждений других.
Слушайте разговоры учащихся о том, применяются ли правила или соглашения к отрицательным значениям так же, как и к положительным значениям.
- Детям должно быть не менее 5 лет, чтобы они могли посещать час рассказов.
- Минимальная цена футболки в этом магазине — 5 долларов.
- Эта коробка с книгами весит 5 фунтов или больше.
Рабочее время
- Напишите о реальной ситуации, которая может быть представлена этой числовой линией.
Подсказка:
Подумайте о ситуациях, связанных с возрастом, деньгами или весом.
Часы для студентов, которые:
- Неверно используйте открытые и закрытые кружки на диаграмме с числовыми линиями для представления утверждений о неравенстве.

- Покажите стрелку в неправильном направлении на их диаграммах с числовыми линиями.
- Проблемы с отрицательными значениями.
- Возникают проблемы, когда переменная находится справа от символа неравенства.
- Невозможно определить значение, которое делает неравенство верным.
- Невозможно точно записать неравенство словами.
- Невозможно записать реальную ситуацию для представления числовой линейной диаграммы.
Шаг 1: Рабочее время
- Объясните, как вы представили неравенство на числовой прямой.
- Подтвердите свое объяснение своей работой.
- Не согласен; -2 не меньше -5. Я знаю, что -2 больше, чем -5, потому что -2 находится справа от -5 на числовой прямой.
Шаг 2: Рабочее время
Дензел говорит, что поскольку 2<5, это означает −2<−5.
- Вы согласны? Объясните, почему да или почему нет.
Подчеркните тот факт, что стрелки на числовых линиях в первой задаче представляют решения утверждений о неравенстве, и облегчите понимание того, что существует бесконечно много решений каждого неравенства.
Спросите учащихся:
- Сколько решений имеют эти утверждения?
- Почему вы используете линию со стрелкой для представления этих решений?
Воспользуйтесь идеями и диаграммами одного или двух учащихся, которые работали над задачей-вызовом. Сосредоточьтесь на 2 < 5 и −2 > −5, чтобы обрамить первую часть обсуждения способов мышления.
Спросите учащихся:
- Как числовой ряд помогает понять, что происходит?
- Что больше, –10 или –10,5? Представьте эти числа на числовой прямой. Затем сравните свои результаты с утверждением о неравенстве 10 < 10,5.
В оставшейся части обсуждения сосредоточьтесь на ситуациях, соответствующих числовой прямой, позволяя как можно большему количеству учащихся поделиться своими реальными ситуациями.
ELL: Как и в случае с другими устными инструкциями, убедитесь, что темп вашей речи подходит для ELL. Часто делайте паузы, чтобы учащиеся могли задать вопросы. Кроме того, контролируйте понимание учащимися, задавая вопросы по ходу объяснения.
Performance Task
Делайте заметки о том, как ваши одноклассники представляют неравенства на числовой прямой.
Подсказка:
В присутствии одноклассников задавайте вопросы, например:
- Почему кружок закрашен?
- Почему круг разомкнут?
- Почему линия идет в этом направлении?
- Объясните, почему –4 меньше –3,5.
- Каким наибольшим числом может быть x?
Пусть пары тихо обсудят информацию о неравенствах. Попросите их привести дополнительные примеры реальных ситуаций для каждого типа неравенства.
Пока учащиеся работают вместе, прислушивайтесь к учащимся, у которых могут быть неверные представления, чтобы вы могли обсудить их в ходе обсуждения в классе.
Через несколько минут обсудите резюме всем классом. Просмотрите следующие пункты.
Неравенства, как и уравнения, имеют решения.
Стрелку на числовой прямой, указывающую вправо для больших значений и влево для меньших значений, можно использовать, чтобы показать, что существует бесконечно много решений неравенства.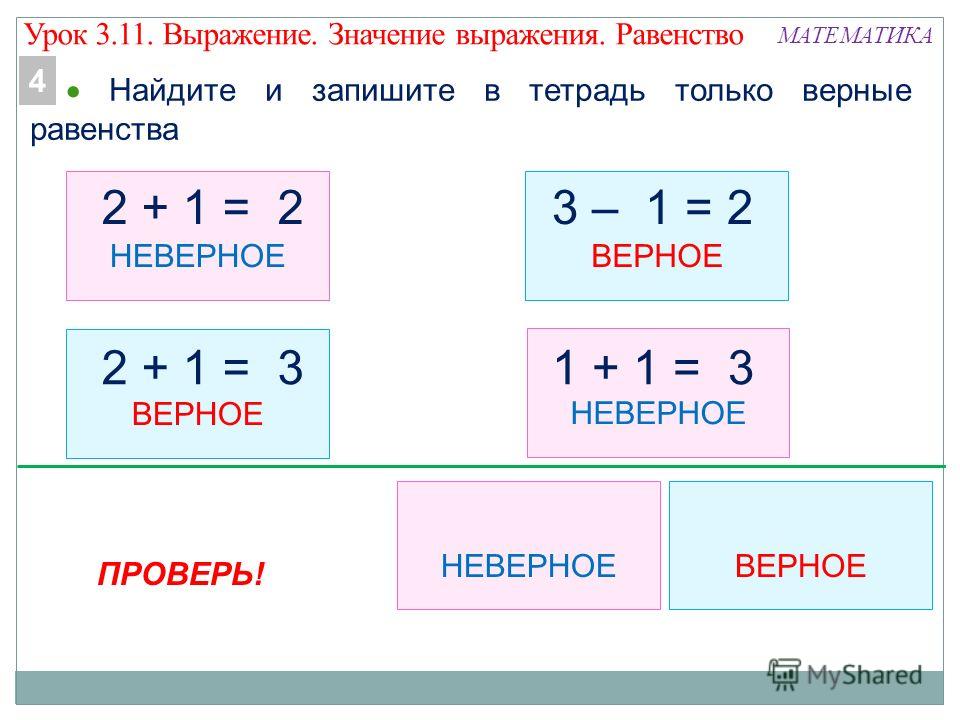
Решения задачи x < a x < a ( x x меньше, чем a a ) представлены стрелкой, указывающей влево от строки к числу. открытый круг на .
Решения для x > A x > A ( x x больше, чем A A . вправо от открытого круга на .
The solutions to x ≤ a x ≤ a ( x x is less than or equal to a a ) представлены на числовой прямой стрелкой, указывающей влево от замкнутого круга a a .
Решения x ≥ a x ≥ a ( x x больше или равно a a ) представлены на числовой прямой стрелкой, указывающей вправо от замкнутого круга a a .

Формирующее оценивание
Прочтите и обсудите
Неравенство — это связь между двумя различными значениями.
a < b означает, что a меньше b (или, что то же самое, b больше a ).
a > b означает, что a больше b (или, что то же самое, что b меньше a ).
a ≤ b означает, что a меньше или равно b (или, что то же самое, что b больше или равно и ).
a ≥ b означает, что a больше или равно b (или, что то же самое, что b меньше или равно a ).
Подсказка:
Можете ли вы:
- Объяснить значение каждого символа неравенства?
- Покажите, как каждый вид неравенства представлен на числовой прямой?
Это задание позволяет оценить работу учащихся и определить, какие трудности у них возникают. Результаты самопроверки помогут вам определить, какие учащиеся должны работать над галереей, а какие учащиеся получат пользу от проверки перед оцениванием. Предложите учащимся работать над самопроверкой индивидуально.
Результаты самопроверки помогут вам определить, какие учащиеся должны работать над галереей, а какие учащиеся получат пользу от проверки перед оцениванием. Предложите учащимся работать над самопроверкой индивидуально.
Попросите учащихся отправить вам свои работы. Делайте заметки о том, что их работа говорит об их текущем уровне понимания и различных подходах к решению проблем.
Не оценивайте работу учащихся. Поделитесь с каждым учащимся наиболее подходящими вмешательствами, чтобы направить их мыслительный процесс. Также отметьте студентов с определенной проблемой, чтобы вы могли работать с ними на следующем уроке «Собери все вместе».
SWD: разместите выступления в классе, чтобы учащиеся могли использовать их в качестве ресурса во время работы. Создайте и предоставьте расширенную версию интервенций со встроенными текстовыми структурами (метки, выделения, слова, выделенные жирным шрифтом), чтобы учащиеся обращали больше внимания на определенные термины.
Учащийся использует неправильное свойство или неправильно определяет свойство.
- Используйте свойство равенства сложения для уравнений типа x + 4 = 10.
- Используйте свойство равенства умножения для уравнений типа 2 x = 10 или 12 x = 9 или для решения пропорций.
Ученик неправильно решает уравнение.
- Правильно ли вы использовали операцию для изоляции x ?
- Вы подставили решение в уравнение, чтобы проверить его?
Студент не включает текстовые задачи.
- Попробуйте эти стартеры:
- Рубашка стоит на 5 долларов больше, чем …
- Четыре книги стоят 22 доллара …
- Фиолетовая краска смешана в соотношении … приведено уравнение.
- Работа в обратном направлении. Прочтите слово «проблема», которое вы написали. Напишите уравнение, которое его представляет. Соответствует ли оно уравнению, которое вам дали?
- x+5−5=17−5Дополнительное свойство равенстваx=12
Задачи Word будут разными.
 Возможный ответ: Рубашка стоит на 5 долларов больше, чем пара шорт. Рубашка стоит 17 долларов. Сколько стоит пара шорт? Ответ: Пара шорт стоит 12 долларов.
Возможный ответ: Рубашка стоит на 5 долларов больше, чем пара шорт. Рубашка стоит 17 долларов. Сколько стоит пара шорт? Ответ: Пара шорт стоит 12 долларов. - 14⋅4x=14⋅22Свойство умножения равенстваx=512
Словесные задачи будут разными. Возможный ответ: Четыре книги стоят 22 доллара. Каждый стоит одинаковую сумму. Сколько стоит одна книга? Ответ: Одна книга стоит 5,50 долларов.
- x6⋅6=58⋅6Свойство умножения равенстваx=334
Словесные задачи будут разными. Возможный ответ: Фиолетовую краску смешивают в пропорции 5 частей синей на 8 частей красной. Сколько синей краски нужно смешать с 6 стаканами красной краски, чтобы получить такой же оттенок фиолетового? Ответ: Вам нужно смешать 334 стакана синей краски.
Формирующее оценивание
Пройдите эту самопроверку самостоятельно.
Для каждого уравнения сделайте следующее.
- Решите уравнение. Назовите свойство равенства, которое вы используете, и покажите каждый шаг.






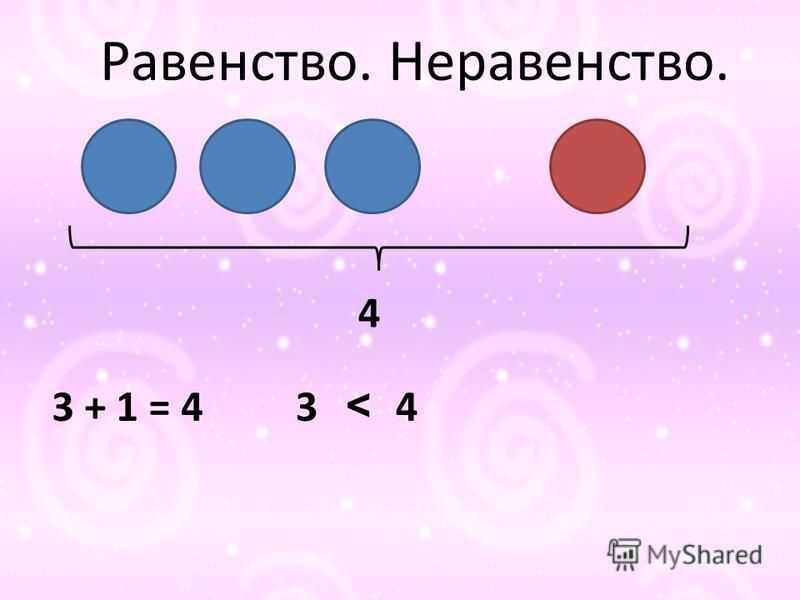
 Сами попробуем выполнить задание: узнать, что такое равенство и неравенство;
Сами попробуем выполнить задание: узнать, что такое равенство и неравенство; Первая парта- 1 пара; вторая парта – 2 и т.д
Первая парта- 1 пара; вторая парта – 2 и т.д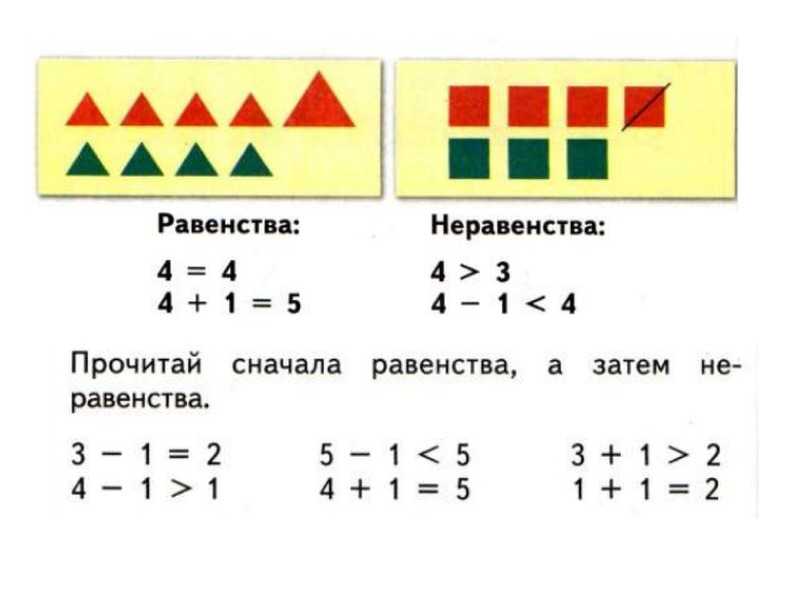





 Возможный ответ: Рубашка стоит на 5 долларов больше, чем пара шорт. Рубашка стоит 17 долларов. Сколько стоит пара шорт? Ответ: Пара шорт стоит 12 долларов.
Возможный ответ: Рубашка стоит на 5 долларов больше, чем пара шорт. Рубашка стоит 17 долларов. Сколько стоит пара шорт? Ответ: Пара шорт стоит 12 долларов.