что это такое простыми словами
Частное чисел в математике: что это такое? В школе учат действие деление, где есть делимое, делитель и частное. Что означают эти названия? Давайте разбираться!
Содержание статьи:
Частное чисел в математике: что это такоеОднажды клоун Бим решил выучить математическое действие деление и нашел для себя в интернете вот такое определение:
Определение. Говорят, что a делится на b, если существует натуральное число с, при умножении которого на b получается а: a=b*c. При этом записывают: a:b=с, — и называют а — делимым, b — делителем, с — частным.
Как мне это понять? — задумался Бим. — Но скоро представление, пойду ребят к нам приглашать.
Как найти частное чиселПришли в цирк трое ребят: Вася, Коля и Оля. На входе их встречал клоун Бим, который дарил детям шарики. У него в руках было 6 шариков, но дарил он их за отгадки. Клоун спросил у ребят:
У него в руках было 6 шариков, но дарил он их за отгадки. Клоун спросил у ребят:
— Мне надо подарить вам шарики, какое математическое действие я буду применять?
— Деление! — быстро ответил Коля. — Ты же будешь делить шарики между нами.
Клоун хитро прищурился:
— А как называются члены деления?
— Мы недавно это изучали! — воскликнула Оля. — Всё количество шариков, которое ты будешь делить, называется делимое. У тебя сейчас 6 шариков, значит здесь делимое — 6!
— А то, на сколько ребят ты их разделишь, называется делитель, — вмешался Вася. — Нас трое ребят, значит делитель — 3!
Коля продолжил:
— У каждого из нас будет часть шариков, и результат от деления называется частным.
— Какое же здесь будет частное? — спрашивает Бим.
— Два! — не сговариваясь, хором ответили ребята.
— Правильно, каждому из вас достанется по два шарика, это и есть частное.
Ребята ответили на все вопросы Бима, и каждый получил по два шарика — как результат деления:
6 (делимое) : 3 (делитель) = 2 (частное).
Запишем цифрами:
6:3=2
| Делимое | Делитель | Частное |
| 6 | 3 | 2 |
В этом выражении 6 (делимое) стоит самым первым, 3 (делитель) — на втором месте. А частное (2) — после знака равенства справа.
Итак, частное — это число, которое получается в результате деления делимого на делитель.
Полное и неполное частноеА потом было замечательное представление.
В антракте дети пошли в буфет. На подносе лежало семь пирожных. Как же их разделить поровну на трёх ребят?
Друзья задумались и взяли по 2 пирожных, а последним, которое было в остатке, угостили клоуна Бима.
— Теперь я понял! — воскликнул Бим. — Если нельзя всё число пирожных поделить между ребятами без остатка, то такой результат от деления называется неполным частным. А то, что осталось после деления, так и называется остатком и записывается это вот так:
А то, что осталось после деления, так и называется остатком и записывается это вот так:
7:3=2(1)
| Делимое | Делитель | Неполное частное | Остаток |
| 7 | 3 | 2 | 1 |
Здесь 7 (делимое) по-прежнему стоит в начале выражения, 3 (делитель) — в середине, 2 (неполное частное) — справа. Но после неполного частного ещё пишем в скобках остаток (1).
- Полное частное — результат деления, когда делимое делится нацело на делитель (остаток равен 0, его и писать незачем).
- Неполное частное — это результат деления с остатком (когда делимое не делится нацело на делитель).
Когда дети ушли занимать свои места, буфетчица подошла к Биму и спросила:
— Я забыла, сколько было ребят. Помню только, что каждый из них съел по два пирожных, а всего им досталось 6 штук. Сколько же посетителей было у меня?
Помню только, что каждый из них съел по два пирожных, а всего им досталось 6 штук. Сколько же посетителей было у меня?
Тут в буфет заглянул дрессировщик Бом и быстренько решил эту задачку. Он разделил 6 (делимое) на 2 (частное) и получил 3 (делитель).
— Всего было трое ребят, — ответил Бом.
— Верно! — вспомнил Бим.
Для того чтобы найти делитель, надо делимое разделить на частное.
6:2=3
Здесь 6 – делимое, 2 – частное, а 3 – делитель.
Как найти делимое— А сколько ты подарил всего шариков трём ребятам? — спросил Бом.
— Забыл, — ответил Бим. — Помню только, что детей было трое, и каждому досталось по два шарика.
Бом и говорит:
— Тогда надо 3 (делитель) умножить на 2 (частное), получится 6.
Для того чтобы найти делимое, надо делитель умножить на частное.
Запишем это цифрами:
3*2=6.
3 — наш делитель, 2 — частное, а 6 — делимое.
Проверка деления умножением— Я что-то не пойму. Это уже умножение, а не деление! — говорит Бим. — Выходит, что деление — действие обратное умножению. То есть, мы можем проверить деление умножением?
— Да, — ответил Бом.
Деление — действие, обратное умножению. Для того чтобы проверить деление, надо провести умножение.
А клоун для себя сделал плакаты и теперь каждый день может сразу вспомнить, что:
Определение. Говорят, что а делится на b, если существует число с, при умножении которого на b получается а: a= b*c. При этом записывают: a:b=с, — и называют а — делимым, b — делителем, с — частным.
- Деление — действие, обратное умножению;
- умножение проверяет правильность математического действия — деления;
- для того чтобы найти делимое, надо делитель умножить на частное;
- для того чтобы найти делитель, надо делимое разделить на частное.

Итак, теперь мы знаем, что же такое частное в математике. Оказывается, оно бывает полным и неполным! Кроме того, нетрудно будет найти делитель, делимое и проверить деление умножением. И если учитель спросит в школе: «Частное чисел в математике: что это такое?» — сможем ответить сразу. И пусть любой пример или задача на эту тему будет вам по плечу!
Учим правила деления и умножения на 0 вместе с клоуном Бимом и Бомом.
Оригинальная идея подачи материала принадлежит Стуловой Лилии Валериевне (преподаватель математики от 5 лет и старше).
Не забудьте оценить наши старания. Комментарии приветствуются! По желанию подписывайтесь на нас в Яндекс.Дзен и в других социальных сетях!!!)))
Дважды два – четыре, или Умножение и деление
Наряду со сложением, важными операциями является умножение и деление. Вспомним хотя бы задачи на определение, во сколько раз у Маши яблок больше, чем у Саши, или на нахождение количества произведенных деталей в год, если известно количество производимых в сутки деталей.
Умножение – это одно из четырех основных арифметических действий, в ходе которого одно число умножаемся на другое. Иными словами, запись 5 · 3 = 15 значит, что число 5 было сложено 3 раза, т.е. 5 · 3 = 5 + 5 + 5 = 15.
Умножение регулируется системой правил.
1. Произведение двух отрицательных чисел равно положительному числу. Чтобы найти модуль произведения, необходимо перемножить модули этих чисел.
(—6) · (—6) = 36; (—17,5) · (—17,4) = 304,5
2. Произведение двух чисел с разными знаками равняется отрицательному числу. Чтобы найти модуль произведения, необходимо перемножить модули этих чисел.
(—5) · 6 = —30; 0,7 · (—8) = —21
3. Если один из множителей равен нулю, то произведение равно нулю. Верно и обратное: произведение равно нулю только в том случае, если один из множителей равен нулю.
Если один из множителей равен нулю, то произведение равно нулю. Верно и обратное: произведение равно нулю только в том случае, если один из множителей равен нулю.
2,73 · 0 = 0; (—345,78) · 0 = 0
Опираясь на изложенный материал, попробуем решить уравнение 4 ∙ (х – 5) = 0.
1. Раскроем скобки и получим 4х – 20 = 0.
2. Перенесем (-20) в правую часть (не забудем при этом поменять знак на противоположный) и
получим 4х = 20.
3. Найдем х, сократив обе части уравнения на 4.
4. Итого: х = 5.
Но, зная правило № 3, мы можем гораздо быстрее решить наше уравнение.
1. Наше уравнение равно 0, а по правилу № 3 произведение равно 0, елси один из множителей равен 0.
2. Множителя у нас два: 4 и (х – 5). 4 не равно 0, значит, х – 5 = 0.
3. Решаем получившееся простое уравнение: х – 5 = 0. Значит, х = 5.
Умножение опирается на два закона – переместительный и сочетательный законы.
Переместительный закон: для любых чисел а и b верно равенство ab = ba:
(—
Сочетательный закон: для любых чисел a, b и c верно равенство (ab)c = a(bc).
(—3) · (—5) · 2 = (—3) · (2 · (—5)) = (—3) · (—10) = 30.
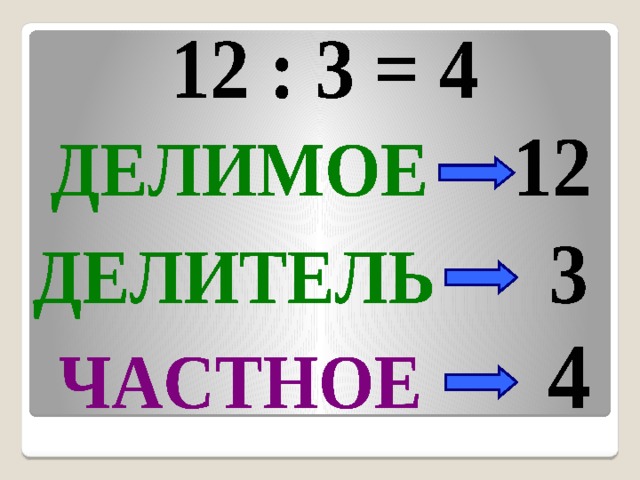
Арифметическое действие, обратное умножению, это деление. Если компоненты умножения называются множителями, то у деления число, которое делится, называется делимым, число, на которое делим, – делителем, а результат – частным.
12 : 3 = 4, где 12 – это делимое, 3 – делитель, 4 – частное.
Деление, аналогично умножению, регулируется правилами.
1. Частное двух отрицательных чисел есть число положительное. Чтобы найти модуль частного, нужно модуль делимого разделить на модуль делителя.
—12 : (—3) = 4
2. Частное двух чисел с разными знаками есть число отрицательное. Чтобы найти модуль частного, нужно модуль делимого разделить на модуль делителя.
—12 : 3 = —4; 12 : (—3) = —4.
3. При делении нуля на любое число, не равное нулю, получится нуль. Делить на нуль нельзя.
0 : 23 = 0; 23 : 0 = ХХХХ
Основываясь на правилах деления, попробуем решить пример —4 х (—5) – (—30) : 6 = ?
1. Выполняем умножение: -4 х (-5) = 20. Значит, наш пример примет вид 20 – (-30) : 6 = ?
2. Выполняем деление (-30) : 6 = -5. Значит, наш пример примет вид 20 – (-5) = ?.
3.
Итак, наш ответ 25.
Знание умножения и деления, наряду со сложением и вычитанием, позволяет решать разнообразные уравнения и задачи, а также отлично ориентироваться в окружающем нас мире цифр и операций.
Закрепим материал, решив уравнение 3 ∙ (4х – 8) = 3х – 6.
1. Раскроем скобки 3 ∙ (4х – 8) и получим 12х – 24. Наше уравнение приобрело вид 12х – 24 = 3х – 6.
2. Приведем подобные. Для этого перенесем все компоненты с х влево, а все числа вправо.
Получим 12х – 24 = 3х – 6 → 12х – 3х = -6 + 24 →9х = 18.
!!! НЕ забываем при перенесении компонента из одной части уравнения в другую менять знаки на противоположные.
3. Решаем получившееся уравнение 9х = 18, откуда х = 18 : 9 = 2. Итак, наш ответ 2.
4. Чтобы убедиться в правильности нашего решения, проведем проверку:
3 ∙ (4х – 8) = 3х – 6
3 · (4 ∙ 2 – 8) = 3 ∙ 2 – 6
3 ∙ (8 – 8) = 6 – 6
3 ∙ 0 = 0
0 = 0, значит, наш ответ верен.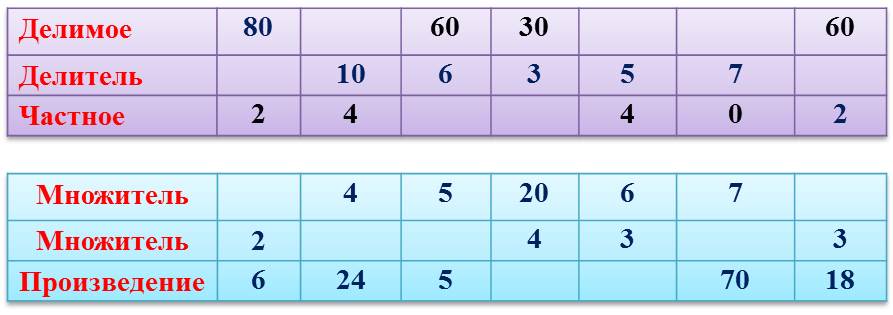
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Что такое дивиденд? — Определение, факты и примеры
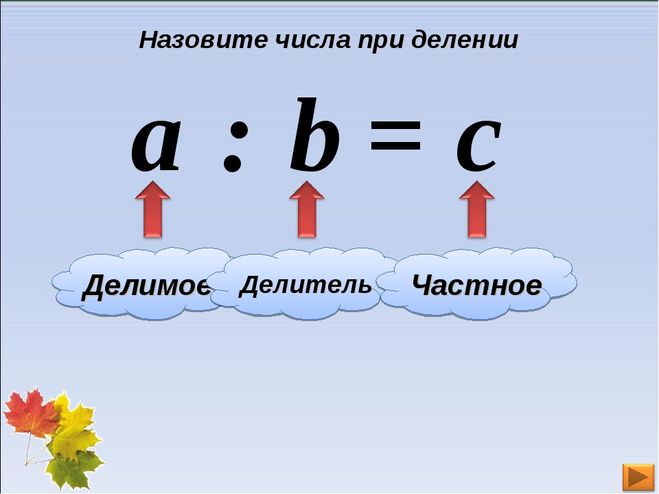
В элементарной математике четыре основных арифметических действия: сложение, вычитание, умножение и деление. Деление — это метод, при котором мы пытаемся разделить определенное количество вещей на равные части. Например, Разделение 20 яблок между 5 людьми означает, что мы должны распределить 20 яблок таким образом, чтобы у всех 5 человек было одинаковое количество яблок.
В задаче на деление число, которое нужно разделить или разделить на определенное количество равных частей, называется делимым. Как и в приведенном выше примере, когда мы делим 20 яблок на 5 человек, делимое равно числу 20; а число 5 называется делителем.
Когда делимое полностью делится на делитель, полученное таким образом число называется частным. Разделив 20 яблок между 5 людьми, мы видим, что каждому досталось по 4 яблока. Мы запишем это в виде уравнения как
Мы запишем это в виде уравнения как
В случае, когда делимое не делится на делитель целиком, мы получаем некоторую оставшуюся сумму.
Например, если бы мы разделили 21 яблоко между 5 людьми, мы смогли бы дать только 4 яблока каждому человеку, и тогда у нас осталось бы 2 яблока.
Это соотношение между четырьмя условиями операции деления задается формулой
Это соотношение можно использовать для проверки процесса деления или для нахождения делимого, когда даны только делитель, частное и остаток.
Например, в некоторой задаче на деление частное равно 4, остаток равен 2, а делитель равен 5.
Решение: доступное количество автобусов.
1 Найдите дивиденд в разделении Факт: 90 ÷ 9 = 10.9 10 90 1 Правильный ответ: 90 2 Что такое дивиденд: 1537?7 153 21,85 6 Правильный ответ: 153 Найдите делимое, если делитель равен 5, частное равно 3, а остаток равен 1. получаем Дивиденд = 16.4 20 шоколадок распределяются между 4 детьми так, что каждый ребенок получает по 5 шоколадок. Каков дивиденд в этом примере?20 4 5 Правильный ответ: 20 |
Может ли 0 быть делимым?
Да, однако деление 0 на любое число всегда дает 0.
Как проверить правильность деления?
Это соотношение можно использовать для проверки процесса деления или для нахождения делимого, если известны только делитель, частное и остаток.
Дивиденд = Делитель × Частное + Остаток
Как найти делимое, если остаток равен нулю?
Если остаток равен нулю, делимое можно найти по следующей формуле:
Дивиденд = делитель x частное
Может ли делитель быть больше делимого?
Да, делитель может быть больше делимого. В этом случае частное будет десятичным числом. Например, 85 ÷ 1000 = 0,085.
В этом случае частное будет десятичным числом. Например, 85 ÷ 1000 = 0,085.
Финансы: что такое математика реинвестирования дивидендов? Видео
Что такое математика реинвестирования дивидендов? При принятии решения о реинвестировании дивидендов, полученных от акций, в покупку дополнительных акций, дробные акции имеют право на будущие дивиденды в дополнение к выгоде от любого дальнейшего прироста капитала по акциям. В результате окупаемость инвестиций может ускориться без дополнительных брокерских сборов и может быстро привести к двузначному увеличению рентабельности инвестиций.
вы хотите с ним, но вы также можете реинвестировать его
which means buying mawr of the stock you already own
So the concept may seem boring but it’s good way
to increase your акции И это как ваши акции
или рождение дочерних акций, и все это без вашего вклада в MOHR
ваших собственных денег в процессе. 0003
0003
move around a lot and as such the math behind
dividend reinvestment can get complex ish or well sometimes just
plain ugly So давайте решим задачу здесь Вы покупаете
тыс. акций Alpaca Corp и альтернативного поставщика молока, право
Они дают молоко от альпак, конечно, но также и от лам
коз и якс хорошо, вот и акции. Производительность
Два года или восемь кварталов, которые вы держали на складе
В конце первого квартала запас был
в час два пятьдесят, затем в конце
91216 90: 04Акции Que Tu выросли на одну или пять и
акции продолжали расти в третьем квартале, достигнув одного из
семь пять к концу периода
queue for alpaca reached one ten by the end of
that year Right next year Same basic story of stock
reach one twenty поделиться после окончания второй
год, и это его производительность, акции продолжают платить
его пятьдесят процент на акцию каждая квартала в Dividend Doe
дивиденды стабильны в течение полных двух лет
поэтому каждый квартал компания отправляет вам пятьдесят долларов
цента на акцию на каждую из ваших тысяч акций
five hundred bucks each quarter You can choose to reinvest
that dividend each quarter The amount of stock that those
dividend repurchase sings
это зависит от цены акций в тот момент, когда
вы получили первую выплату дивидендов, когда акции стоили
ОДИН О ДВА Пятьдесят пятьсот, разделенные на один или
. реинвестирование дивидендов у вас есть тысяча четыре
реинвестирование дивидендов у вас есть тысяча четыре
целых восемь десятых акций И да, вы можете получить
восемь акций или что-то в этом роде.0003
Работает ОК. у вас больше нет тысячи акций
У вас есть тысяча четыре целых восемь десятых акций из-за
реинвестирования дивидендов в первом квартале.0003
time around you get five hundred two dollars forty ish
sense in dividends Reinvest those dividends and while you get
another approximately four точка восемь акций что-то вроде этого может
быть немного больше Процесс продолжается Пока
вы поддерживаете реинвестирование дивидендов, вы покупаете акции с
Дивиденды, придающие вам акции MOHR, которые затем увеличивают ваши
Dividend, который дает вам больше денег, чтобы купить больше акций
 усложняющим фактором в этом расчете является то, что
усложняющим фактором в этом расчете является то, чтоцена акции продолжает двигаться.0003
Вы получите на некоторую установленную сумму выплаты дивидендов. в чем преимущество всего этого Но
зачем реинвестировать, а не просто брать наличные, упрощая наш пример
из них Вы получаете около пяти акций в квартал за
eight quarters in reinvesting your dividends So at the end
of two years you have forty more shares of alpaca
instead of having kept
тысяч акций по пятьдесят центов за акцию каждый квартал свыше
восемь четвертей Это четыре штуки Также у вас все еще есть
тысяча акций, которыми вы владели первоначально, теперь они стоят
Прибавьте четыре к дивидендам, и вы получите один
сто двадцать четыре тысячи Посмотрите, как это работает Это
map But here with dividend reinvestment and ignoring all kinds
of taxes and commissions and other you know realistic noise
well you’ d иметь тысячу сорок акций по сто
по двадцать долларов каждая на общую сумму сто
двадцать четыре тысячи восемьсот баксов и сдачу У вас будет
made another eight hundred ish dollars by reinvesting your dividend
and this presumes that you spent all of the cash
dividends out to ты, когда не выкупил акции
Раван реинвестирует эти деньги куда-нибудь, ты знаешь, что это полезно Так почему
имеет ли все это значение Ну S и P пять
hundred pays about a two percent dividend in the modern
era Maybe three That is The median company pays about
that amount The SNP — это Индекс Джастина.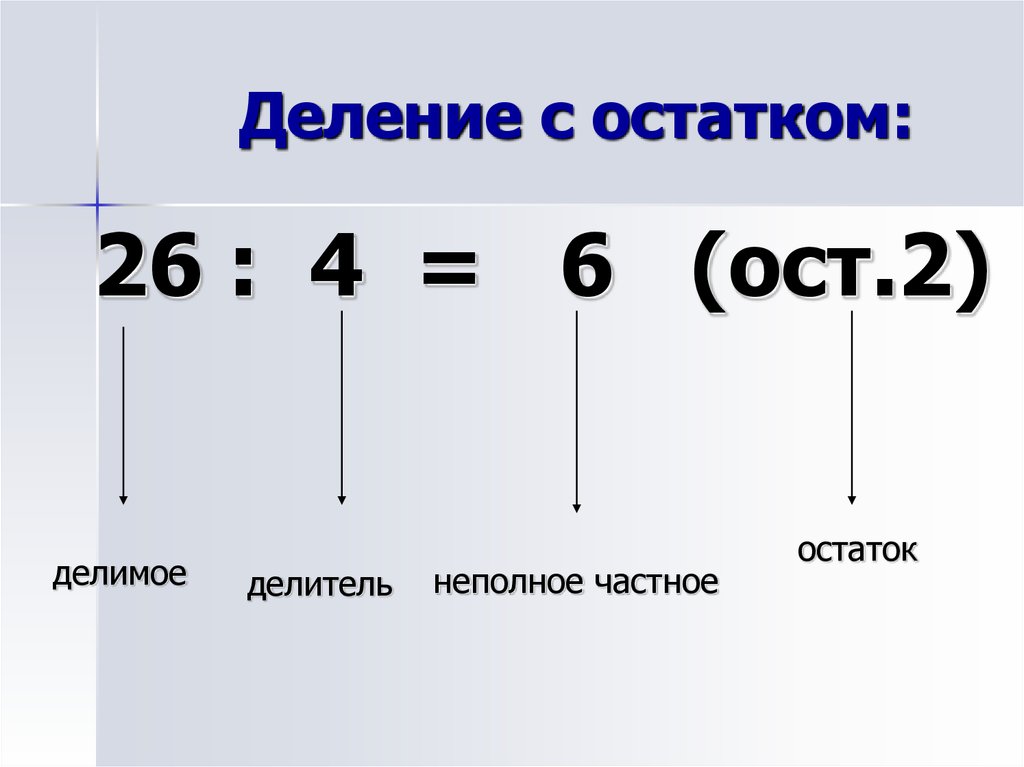


 0003
0003