Что называется частным. Частное — это что такое? Частное числа: значение
Частное в математике на
Давайте вспомним определение, что называется частным чисел. Частное чисел — это результат деления одного числа на другое. Таким образом, частное чисел а и b будет число c, которое равно c = a: b. При этом число a будет делимым, а число — b делителем. Иными словами, частное чисел — это математическая величина, которая получается в результате деления одного числа на другое. Частное двух чисел показывает нам, во сколько раз одно число больше другого. a: b = c, где a — делимое; b — делитель; c — частное.
Частное чисел
1. Введем определение этого понятия. Частным чисел называется результат деления одного из чисел на другое. Частное чисел — это математическая величина.
- а — делимое; b — делитель; c — частное.
3. Пример 1. 156 / 2. Если поделить число 156 на 2, то в результатом будет число 78. В этом случае число 78 представляет собой частное двух чисел, результат от деления числа 156 на 2. 156 — делимое, 2 — делитель. Число 156 больше, чем число 2, в 78 раз. Данные умозаключения можно проверить, достаточно лишь выполнить операцию, обратную делению. 78 * 2 = 156. Верно.
156 — делимое, 2 — делитель. Число 156 больше, чем число 2, в 78 раз. Данные умозаключения можно проверить, достаточно лишь выполнить операцию, обратную делению. 78 * 2 = 156. Верно.
4. Усложненный пример. 153214 / 2. 153214 — делимое, 2 — делитель.
- Делим 15 на 2. Берем по 7. 7 * 2 = 14. Вычитаем из 15 полученное значение и получаем 1. Спускаем 3. 13 делим на 2. Берем по 6. 6 * 2 = 12. Вычитаем из 13 полученное значение и получаем 1. Спускаем 2. 12 делим на 2. Берем по 6. 6 * 2 = 12. Вычитаем из 12 полученное значение и получаем 0. Спускаем единицу, прописываем ноль. Спускаем 4. 14 делим на 2. Берем по 7. 7 * 2 = 14. Вычитаем из 14 полученное значение и получаем 0.
Неполное частное
Пример пункта 3 довольно прост. Так число 2 содержится в числе 156 ровно 78 раз.
Приведем пример: 157 / 3. 157 — делимое, 3 — делитель. При делении мы получаем, что число 3 содержится в числе 157, 52 раза, но образуется еще и остаток, который равен единице. В данном случае число 52 будем называть неполным частным. Число 1 — это остаток от деления числа 157 на 3.
Число 1 — это остаток от деления числа 157 на 3.
Подписаться на сайт
Ребята, мы вкладываем душу в сайт. Cпасибо за то,
Что открываете эту красоту. Спасибо за вдохновение и мурашки.
Присоединяйтесь к нам в Facebook и ВКонтакте
Математика – уникальная наука, которая привлекает точностью и последовательностью. Каждый, кто начал изучать эту важную дисциплину, должен разобраться, что такое частное в математике.
Деление
В математике есть четыре простейших операции:
- Сложение Вычитание Деление Умножение
Если мы говорим о частном, то нас будет интересовать такая операция, как деление.
Деление всегда обратно умножению. Это математическая величина, которую мы получим, разделив одно число на другое . Есть ряд символов, которые обозначают его:
- Двоеточие (:) Косая черта (/) Обелюс (тире между двумя точками ÷)
В учебных пособиях для учеников 1 – 5 классов есть простое и точное определение этого понятия. Деление – это операция, в результате которой мы получаем число, которое при умножении на делитель дает делимое. Число, о котором говорится в первой части определения, и есть частное.
Деление – это операция, в результате которой мы получаем число, которое при умножении на делитель дает делимое. Число, о котором говорится в первой части определения, и есть частное.
Частное рассказывает, во сколько раз одно число больше другого.
Наглядные примеры
Чтобы лучше понять, что такое частное чисел в математике, следует обратиться к примерам. Они помогут разложить знания по полочкам в вашей голове. Решение примеров – это лучший тренажер для усвоения новых знаний. Приступим к их решению.
Итак, частное получается, если делимое поделить на делитель. При помощи символов эту операцию можно записать следующим образом:
Запишем простой пример из математики:
80 – делимое (оно делится)
2 – это делитель (на него разделяют)
Восемьдесят больше, чем сорок, в два раза.
Другой пример выглядит так:
Сто двадцать больше, чем шестьдесят, в два раза.
Проверка
Если вы провели операцию деления и сомневаетесь в результате, на помощь придет проверка. Для этого умножьте делитель на частное. Если в результате вы получили делимое, то пример решен верно:
Для этого умножьте делитель на частное. Если в результате вы получили делимое, то пример решен верно:
Если после знака равно вы увидели знакомое вам делимое, то можете поставить себе твердую пятерку. Вы научились находить частное чисел и делать проверку. Это очень важно, чтобы в дальнейшем освоить более сложные понятия в алгебре и геометрии.
Частное – это основа математики. Если ученик не смог понять его суть, то двигаться дальше просто бессмысленно. Обратитесь к учителю, если это понятие так и осталось для вас туманным. Педагог разъяснит все ошибки и укажет на подводные камни.
Полное и неполное частное
В результате проведения математических подсчетов частное может быть двух видов:
- Полное. В результате деления мы получаем целое число:
50 – полное частное
- Неполное. Если в результате мы получаем остаток:
51:2=25 (остаток 1)
25 – неполное частное
1 – остаток от деления
Если вы откроете учебник математики, то увидите, что частное в задачах обозначают при помощи различных символов (переменных). Для этого используют латинские буквы:
Для этого используют латинские буквы:
Чтобы найти частное, следует делимое разделить на делитель:
Ответ 5 – это частное в данном примере.
Абстрактные определения и туманные рассуждения плохо усваиваются мозгом школьника. Поэтому всегда держите под рукой задачник со списком упражнений по математике. Он поможет понять различные математические категории на практике. Конкретные цифры, записанные в тетради, станут главными помощниками.
Частное, как результат деления Частное, как противопоставление общему Частное, как принадлежащее Частному лицу … Википедия
— [сн], частного, ср. (мат.). Число, полученное от деления одного числа на другое. Толковый словарь Ушакова. Д. Н. Ушаков. 1935 1940 … Толковый словарь Ушакова
ЧАСТНОЕ, ого, ср. Результат, итог деления. Толковый словарь Ожегова. С. И. Ожегов, Н. Ю. Шведова. 1949 1992 … Толковый словарь Ожегова
Сущ., кол во синонимов: 1 термин (18) Словарь синонимов ASIS. В. Н. Тришин. 2013 … Словарь синонимов
Обвинение особый порядок производства в судебныхустановлениях дел о Ч. преступлениях; в более общем значении термин: Ч. обвинение обнимает собой все формы участия Ч. лиц в возбужденииуголовного преследования и в обличении обвиняемого на суде.… … Энциклопедия Брокгауза и Ефрона
преступлениях; в более общем значении термин: Ч. обвинение обнимает собой все формы участия Ч. лиц в возбужденииуголовного преследования и в обличении обвиняемого на суде.… … Энциклопедия Брокгауза и Ефрона
Частное — частное. Произносится [часное] … Словарь трудностей произношения и ударения в современном русском языке
Частное — отношение коэффициент — [Л. Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом Синонимы отношениекоэффициент EN quotient … Справочник технического переводчика
ЧАСТНОЕ — результат операции деления; обозначается а:b, а/b или … Большая политехническая энциклопедия
Ого; ср. 1. Матем. Результат деления одной величины на другую. Найти ч. В частном получилось слишком большое число. 2. То, что представляет собой отдельную часть, особенность чего л. От частного к общему. Уделить внимание частному. * * * частное… … Энциклопедический словарь
Частное — вынести частное определение существование / создание … Глагольной сочетаемости непредметных имён
Книги
- Частное право Древнего Рима, В.
 В. Макеев, А. Г. Головко. Предлагаемое издание является учебным пособием по римскому частному праву. Новационность содержания и структуры не имеет на сегодняшний день аналога, так как охватывает буквально все стороны… Частное расследование, Фридрих Незнанский. Талантливый ученый и инженер А. Н. Грамов создает уникальный психотропный генератор, при помощи которого можно влиять на человека, где бы он ни находился. По сути им создано новейшее…
В. Макеев, А. Г. Головко. Предлагаемое издание является учебным пособием по римскому частному праву. Новационность содержания и структуры не имеет на сегодняшний день аналога, так как охватывает буквально все стороны… Частное расследование, Фридрих Незнанский. Талантливый ученый и инженер А. Н. Грамов создает уникальный психотропный генератор, при помощи которого можно влиять на человека, где бы он ни находился. По сути им создано новейшее…1. Введем определение этого понятия. Частным чисел называется результат деления одного из чисел на другое. Частное чисел — это математическая величина.
2. Наглядное представление: a / b = c.
- а — делимое; b — делитель; c — частное.
3. Пример 1. 156 / 2. Если поделить число 156 на 2, то в результатом будет число 78. В этом случае число 78 представляет собой частное двух чисел, результат от деления числа 156 на 2. 156 — делимое, 2 — делитель. Число 156 больше, чем число 2, в 78 раз. Данные умозаключения можно проверить, достаточно лишь выполнить операцию, обратную делению.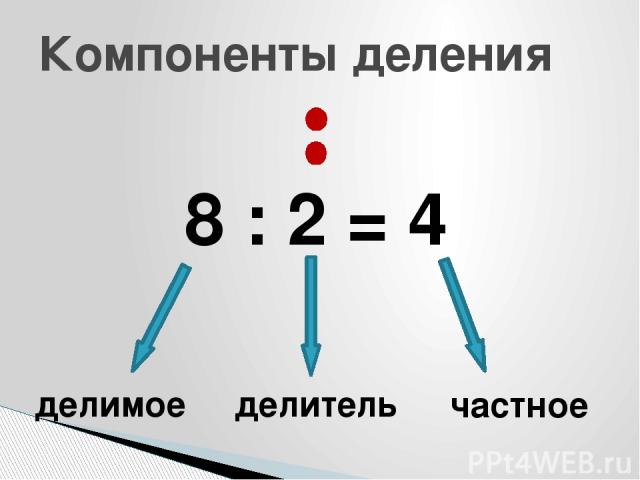
4. Усложненный пример. 153214 / 2. 153214 — делимое, 2 — делитель.
- Делим 15 на 2. Берем по 7. 7 * 2 = 14. Вычитаем из 15 полученное значение и получаем 1. Спускаем 3. 13 делим на 2. Берем по 6. 6 * 2 = 12. Вычитаем из 13 полученное значение и получаем 1. Спускаем 2. 12 делим на 2. Берем по 6. 6 * 2 = 12. Вычитаем из 12 полученное значение и получаем 0. Спускаем единицу, прописываем ноль. Спускаем 4. 14 делим на 2. Берем по 7. 7 * 2 = 14. Вычитаем из 14 полученное значение и получаем 0.
Неполное частное
Пример пункта 3 довольно прост. Так число 2 содержится в числе 156 ровно 78 раз.
Приведем пример: 157 / 3. 157 — делимое, 3 — делитель. При делении мы получаем, что число 3 содержится в числе 157, 52 раза, но образуется еще и остаток, который равен единице. В данном случае число 52 будем называть неполным частным. Число 1 — это остаток от деления числа 157 на 3.
Давайте вспомним определение, что называется частным чисел.
Частное чисел — это результат деления одного числа на другое. Таким образом, частное чисел а и b будет число c, которое равно c = a: b. При этом число a будет делимым, а число — b делителем.
Таким образом, частное чисел а и b будет число c, которое равно c = a: b. При этом число a будет делимым, а число — b делителем.
Иными словами, частное чисел — это математическая величина, которая получается в результате деления одного числа на другое.
Частное двух чисел показывает нам, во сколько раз одно число больше другого.
Давайте вспомним определение, что называется частным чисел. Частное чисел — это результат деления одного числа на другое. Таким образом, частное чисел а и b будет число c, которое равно c = a: b. При этом число a будет делимым, а число — b делителем. Иными словами, частное чисел — это математическая величина, которая получается в результате деления одного числа на другое. Частное двух чисел показывает нам, во сколько раз одно число больше другого. a: b = c, где a — делимое; b — делитель; c — частное.
1. Введем определение этого понятия. Частным чисел называется результат деления одного из чисел на другое. Частное чисел — это математическая величина.
- а — делимое; b — делитель; c — частное.
3. Пример 1. 156 / 2. Если поделить число 156 на 2, то в результатом будет число 78. В этом случае число 78 представляет собой частное двух чисел, результат от деления числа 156 на 2. 156 — делимое, 2 — делитель. Число 156 больше, чем число 2, в 78 раз. Данные умозаключения можно проверить, достаточно лишь выполнить операцию, обратную делению. 78 * 2 = 156. Верно.
4. Усложненный пример. 153214 / 2. 153214 — делимое, 2 — делитель.
- Делим 15 на 2. Берем по 7. 7 * 2 = 14. Вычитаем из 15 полученное значение и получаем 1. Спускаем 3. 13 делим на 2. Берем по 6. 6 * 2 = 12. Вычитаем из 13 полученное значение и получаем 1. Спускаем 2. 12 делим на 2. Берем по 6. 6 * 2 = 12. Вычитаем из 12 полученное значение и получаем 0. Спускаем единицу, прописываем ноль. Спускаем 4. 14 делим на 2. Берем по 7. 7 * 2 = 14. Вычитаем из 14 полученное значение и получаем 0.
Сто двадцать больше, чем шестьдесят, в два раза.
Kerchtt. ru
ru
08.11.2017 8:12:26
2017-11-08 08:12:26
Источники:
Https://kerchtt. ru/chto-nazyvaetsya-chastnym-chastnoe—eto-chto-takoe-chastnoe/
Урок 55. название чисел при делении — Математика — 2 класс — Российская электронная школа » /> » /> .keyword { color: red; }
Частное в математике на
2. Как называется числовое выражение со знаком деление?
Глоссарий по теме:
Деление — это арифметическое действие, обратное умножению. С помощью деления по произведению и одному из множителей определяется второй множитель.
Делимое — это число стоящее слева от знака деления, которое делим.
Делитель — это число стоящее справа от знака деления, число на которое делим делимое. (какими частями делим, дробим)
Частное — это число стоящее после знака равно, результат деления, числовое выражение со знаком деление.
Обязательная литература и дополнительная литература:
Моро М. И., Бантова М. А. и др. Математика 2 класс. Учебник для общеобразовательных организаций. М.; Просвещение, 2017. – с. 62. С. И. Волкова. Математика 2 класс. Тетрадь учебных достижений. Учебное пособие для общеобразовательных организаций. М.; Просвещение, 2018. – с. 44-47.
А. и др. Математика 2 класс. Учебник для общеобразовательных организаций. М.; Просвещение, 2017. – с. 62. С. И. Волкова. Математика 2 класс. Тетрадь учебных достижений. Учебное пособие для общеобразовательных организаций. М.; Просвещение, 2018. – с. 44-47.
Теоретический материал для самостоятельного изучения
Запишем равенство, используя необходимое арифметическое действие:
10 яблок разложили на две тарелки поровну.
9 конфет раздали трём детям поровну.
8 тетрадей раздали четырём ученикам поровну.
Для того, чтобы выполнит задание, нам понадобилось действие деление.
Вы уже знаете, как называются числа при сложении и вычитании, недавно вы познакомились с названиями чисел при умножении.
Вы умеете называть выражения со знаками «плюс», «минус», со знаком умножения. Сегодня вы узнаете, как называются числа при делении. Выражение со знаком деления тоже имеет своё название. Хотите узнать? Вперёд!
Числа при делении имеют свои названия.
8 листьев раздали детям, по 2 листа каждому.
4 человека получили листья.
Число, которое делят, называется делимым. 8 – это делимое. Число, на которое делят делимое, называется делитель. 2 – это делитель Результат действия деления называется частным. 4 – это частное. Выражение 8 разделить на 2 тоже называется частным.
Компоненты деления: делимое, делитель, частное.
Найдите частное, если делимое – 6, делитель – 3.
Проверьте: 6 : 3 = 2
Найдите частное чисел 12 и 6. Проверьте: 12 : 6 = 2
Решим задачу: 12 клубничек раздали 4 детям поровну. По сколько клубничек получил каждый ребёнок?
Для решения задачи выберем действие деление, так как надо узнать, сколько раз по 4 содержится в числе 12.
Ответ: по 3 клубнички получил каждый ребёнок.
Вспомним название чисел при делении. 12 – делимое, 4 – делитель. 3 – частное. 12 : 4 – это частное.
Вывод: компоненты действия деление – делимое, делитель, результат деления – частное.
Ответим на вопросы, поставленные в начале урока.
Число, которое делят, называется делимое.
Число, на которое делят делимое, называется делитель.
Результат деления – частное.
Числа, которые соединены знаком деления, тоже называются частное.
Выполним несколько тренировочных заданий.
1. По рисунку составьте задачи на деление. Запишите решение. Назовите компоненты действия деление.
А) 15 яблок разложили в 3 вазы, в каждую вазу поровну. Сколько яблок положили в одну вазу?
Проверьте: 15 : 3 = 5 (яб.).
15 – делимое. 3 – делитель. 5 – частное. Выражение 15:3 – частное.
Б) 15 яблок разложили в вазы, по 5 штук в каждую. Сколько ваз заняты яблоками?
9 конфет раздали трём детям поровну.
Resh. edu. ru
13.04.2018 1:09:46
2018-04-13 01:09:46
Источники:
Https://resh. edu. ru/subject/lesson/4303/conspect/
Что такое частное чисел? ответ на » /> » /> .keyword { color: red; }
Частное в математике на
Давайте вспомним определение, что называется частным чисел.
Частное чисел — это результат деления одного числа на другое. Таким образом, частное чисел а и b будет число c, которое равно c = a : b. При этом число a будет делимым, а число — b делителем.
Иными словами, частное чисел — это математическая величина, которая получается в результате деления одного числа на другое.
Частное двух чисел показывает нам, во сколько раз одно число больше другого.
A : b = c, где a — делимое; b — делитель; c — частное.
Частное чисел
1. Введем определение этого понятия. Частным чисел называется результат деления одного из чисел на другое. Частное чисел — это математическая величина.
2. Наглядное представление: a / b = c.
- а — делимое; b — делитель; c — частное.
3. Пример 1. 156 / 2. Если поделить число 156 на 2, то в результатом будет число 78. В этом случае число 78 представляет собой частное двух чисел, результат от деления числа 156 на 2. 156 — делимое, 2 — делитель. Число 156 больше, чем число 2, в 78 раз. Данные умозаключения можно проверить, достаточно лишь выполнить операцию, обратную делению. 78 * 2 = 156. Верно.
Данные умозаключения можно проверить, достаточно лишь выполнить операцию, обратную делению. 78 * 2 = 156. Верно.
4. Усложненный пример. 153214 / 2. 153214 — делимое, 2 — делитель.
- Делим 15 на 2. Берем по 7. 7 * 2 = 14. Вычитаем из 15 полученное значение и получаем 1. Спускаем 3. 13 делим на 2. Берем по 6. 6 * 2 = 12. Вычитаем из 13 полученное значение и получаем 1. Спускаем 2. 12 делим на 2. Берем по 6. 6 * 2 = 12. Вычитаем из 12 полученное значение и получаем 0. Спускаем единицу, прописываем ноль. Спускаем 4. 14 делим на 2. Берем по 7. 7 * 2 = 14. Вычитаем из 14 полученное значение и получаем 0.
Неполное частное
Пример пункта 3 довольно прост. Так число 2 содержится в числе 156 ровно 78 раз.
Приведем пример: 157 / 3. 157 — делимое, 3 — делитель. При делении мы получаем, что число 3 содержится в числе 157, 52 раза, но образуется еще и остаток, который равен единице. В данном случае число 52 будем называть неполным частным. Число 1 — это остаток от деления числа 157 на 3.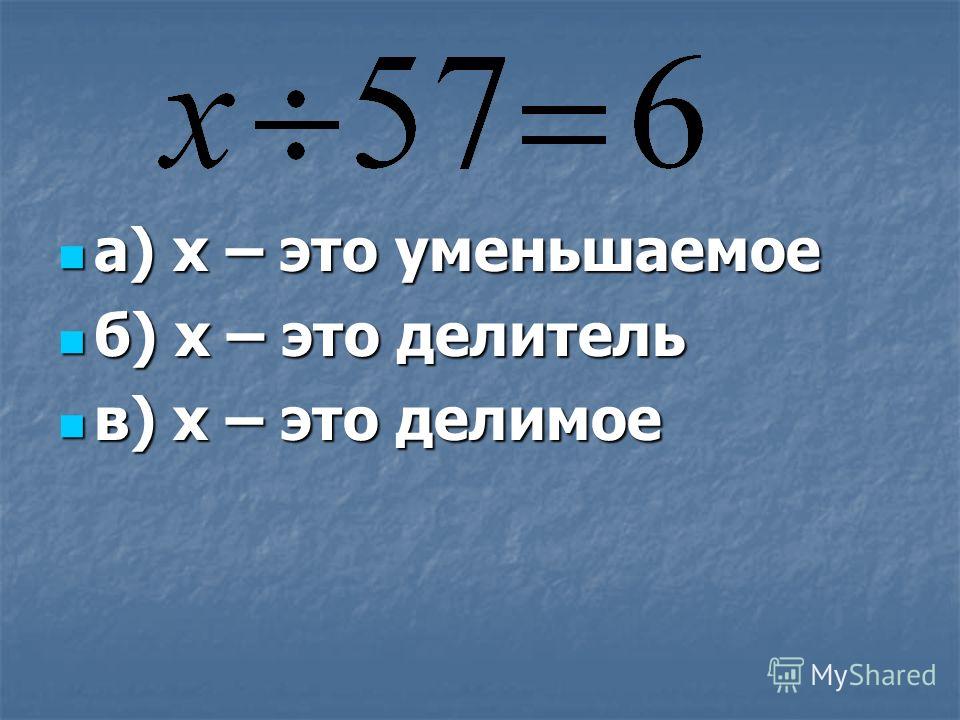
Наглядное представление a b c.
Uchi. ru
28.05.2018 13:32:44
2018-05-28 13:32:44
Источники:
Https://uchi. ru/otvety/questions/chto-takoe-chastnoe-chisel-aa08a141-2003-4380-bcc6-b54db38c5e5f
Деление правила математика — Тур-инфо
Деление правила математика
Определить, сколько раз нужно взять слагаемым меньшее число 2, чтобы получить большее число 6, значит определить, сколько раз число 2 содержится в 6, или сколько раз число 6 содержит 2.
Число 2 содержится в 6 три раза, ибо, чтобы получить 6, нужно взять сумму трех равных слагаемых:
Найти, сколько раз число 2 содержится в 6, значит Разделить 6 на 2.
Определение. Деление есть такое действие, в котором по двум данным числам определяют, сколько раз одно число содержится в другом.
Данные числа в делении называются Делимым и Делителем, искомое называется Частным.
Делимое есть то число, которое содержит другое.
Делитель есть то число, которое содержится в другом.
Частное показывает, сколько раз делитель содержится в делимом.
В данном примере делимое есть 6, делитель 2, частное 3.
Разделить 6 на 2 значит также разбить 6 на 2 равных слагаемых и отыскать их величину. Число 6 представится при помощи двух равных слагаемых в виде:
Каждое из равных слагаемых называется частью делимого.
Посредством деления целых чисел также узнается, как велико каждое слагаемое, если делимое разобьется на столько равных слагаемых, сколько в делителе единиц.
В этом случае Делимое есть то число, которое делится или разбивается на равные части. Делитель показывает, на сколько равных частей делится делимое. Частное показывает, сколько приходится на каждую часть.
Способы деления
Имея два числа 12 и 4, мы можем разделить 12 на 4 различными способами.
С помощью сложения мы можем определить, сколько раз нужно взять 4 слагаемым для того, чтобы получить в сумме 12. Так, взяв 4 слагаемым 3 раза, находим в сумме:
Следовательно, 4 содержится в 12 три раза.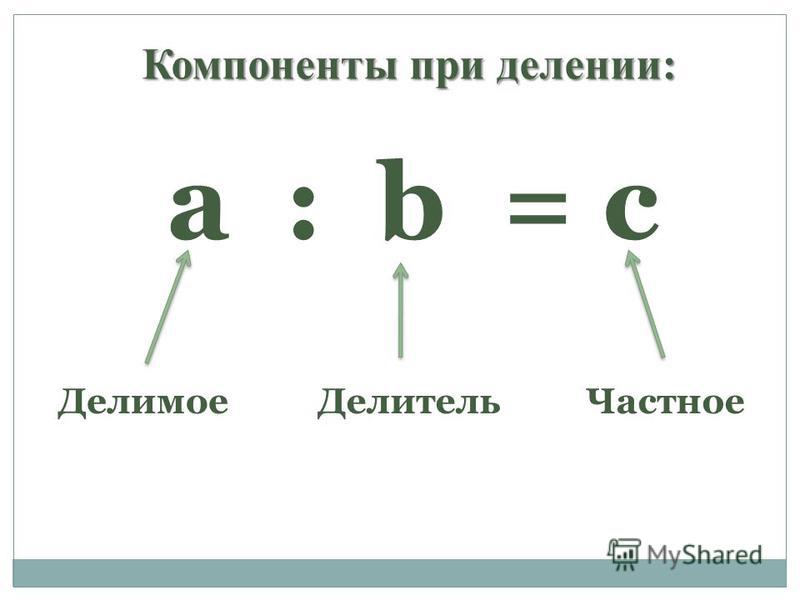
С помощью вычитания определяем, сколько раз можно из большего числа 12 вычесть меньшее 4. При этом мы вычитаем делитель до тех пор, пока это возможно. Так, вычитая последовательно из 12 по 4, имеем:
12 — 4 = 8
8 — 4 = 4
4 — 4 = 0
Отсюда находим, что можно вычесть 4 из 12 ровно три раза.
Деление есть сокращенное вычитание равных вычитаемых.
Наконец, Посредством умножения, мы можем определить, на какое число нужно помножить 4, чтобы получить 12. Умножая последовательно 4 на 1, 2, 3, находим, что для того, чтобы получить 12, нужно 4 помножить на 3.
Различные случаи при делении
При делении целых чисел бывают два случая:
Разделяя 12 на 4, мы находим в частном 3. Делитель 4 содержится ровно 3 раза в делимом 12. Вычитая последовательно из 12 по 4, мы могли вычесть число 4 ровно три раза и не получили никакого остатка. В этом случае говорят, что Деление совершилось нацело или без остатка. Умножив частное 3 на делитель 4, получаем делимое 12.
Разделяя 26 на 8, мы при последовательном вычитании получаем:
26 — 8 = 18
18 — 8 = 10
10 — 8 = 2
Далее нельзя продолжать вычитания, потому что из 2 нельзя вычесть делитель 8. Число 2 называют Остатком.
Остаток всегда меньше делителя. В этом случае говорят, что Деление не совершается нацело или Деление совершается с остатком.
Разделяя 26 на 8, мы могли вычесть делитель 8 три раза, и у нас получился остаток 2. Число 3 мы будем называть целым частным. Целое частное есть не полное частное, ибо оно не выражает вполне, сколько раз меньшее число содержится в большем. Число 8 не содержится в 26 ровно 3 раза. В этом случае говорят: число 8 содержится в 26 три раза и еще получается остаток. Умножив делитель 8 на целое частное 3, мы не получим делимого 26, а число 24 — меньшее делимого. Чтобы получить делимое, нужно к этому произведению прибавить еще остаток 2.
Целое частное иногда называют просто частным.
Итак, при делении мы имеем два случая:
Деление нацело или без остатка. Когда делитель содержится в делимом ровное число раз, тогда деление совершается нацело или без остатка. Частное выражает, сколько раз делитель содержится в делимом. Делимое равно делителю, умноженному на частное. В этом случае деление есть действие в котором по данному произведению и одному из производителей находится другой производитель.
Когда делитель содержится в делимом ровное число раз, тогда деление совершается нацело или без остатка. Частное выражает, сколько раз делитель содержится в делимом. Делимое равно делителю, умноженному на частное. В этом случае деление есть действие в котором по данному произведению и одному из производителей находится другой производитель.
Если дается произведение и множимое, отыскивают множитель, то есть число равных слагаемых; если дается произведение и множитель, отыскивают множимое, то есть величину равных слагаемых.
Деление с остатком. Когда делитель не содержится в делимом ровное число раз, тогда деление не совершается нацело, или деление совершается с остатком. Остаток всегда меньше делителя и делимое равно произведению делителя на целое частное, сложенное с остатком.
При делении целых чисел делимое всегда уменьшается во столько раз, сколько в делителе единиц, поэтому Деление есть действие, обратное умножению.
Знак деления
Действие деления изображается знаком двоеточия ÷, который ставится между делимым и делителем.
Деление числа 6 на 2 изображают письменно:
6 ÷ 2 = 3 частное.
Действие деления обозначается также начертанием |–, где вертикальная черта отделяет делимое, а горизонтальная делитель от частного.
В данном примере имеем:
В нашем примере деление изображается письменно:
Знак деления прешел к нам от древних математиков.
Основные приемы при делении
Делить значит последовательно вычитать делитель из делимого, пока это возможно. Этот способ деления можно считать общим. Прием этот, однако, приводит к длинным вычислениям, если делимое очень велико, поэтому существуют различные сокращенные приемы деления.
Чтобы определить частное в том случае, когда оно выражается одной цифрой, прибегают к таблице умножения.
Чтобы разделить 27 на 3 мы пишем
Для частного выбираем такое число, чтобы, умножив делитель на частное, получить делимое. Чтобы найти цифру частного, мы пробуем умножать делитель на разные числа или, как обыкновенно говорят, задаемся разными числами, и сравниваем произвдение делителя на частное с делимым.
Разделяя 27 на 3 и перебирая в уме все произведения 3 на разные числа, содержащиеся в таблице умножения, находим, что произведение 3 × 9 составляет 27 и потому пишем в частном 9. Вычитая произведение делителя на частное из делимого, получаем в остатке нуль.
Само вычисление выражают письменно:
Деление совершилось нацело.
Иногда делитель не содержится в делимом ровное число раз; так, разделяя 27 на 4, мы не находим в таблице целого числа, которое, будучи помножено на 4, дало бы 27; тогда деление не совершается нацело.
Отыскивая целое частно, мы имеем при этом три случая:
Или мы задаемся очень малым числом; так, для данного примера, задавшись в частном 5 и умножив 4 на 5, имеем 20. Подписав произведение 20 под делимым и вычитая из 27, имеем:
В остатке число 7 больше делителя 4. Это показывает, что частное 5 мало и его нужно увеличить.
Или, взяв для частного 7 и умножив его на делителя 4, получаем произведение 28 больше делимого, что показывает, что мы задались в частно очень большим числом. В таком случае нужно уменьшить цифру частного 7.
В таком случае нужно уменьшить цифру частного 7.
Взяв для частного 6, мы ход вычисления выражаем письменно:
Словесно: 4 в 27 содержится 6 раз, 4 * 6 = 24, подписываем 24 под делимым, вычитаем и получаем остаток 3. Остаток 3 меньше делителя, следовательно, цифра частного верна. Отсюда выводим следующее:
Правило определения частного:
Если при делении остаток более или равен делителю, цифра частного мала и ее нужно увеличить.
Если произведение делителя на частное больше делимого, цифра частно велика и ее нужно уменьшить.
Если остаток меньше делителя, цифра частного верна.
Это правило показывает, что При делении нужно для частного выбирать такое число, чтобы остаток был меньше делителя. Задаваться так, значит задаваться наибольшим целым числом.
В данном примере 27 не делится нацело на 4, а получается остаток 3; число 6 есть целое частное и
27 = 4 × 6 + 3 = 24 + 3
Делимое 27 равно произведению делителя 4 на целое частное 6, сложенному с остатком 3.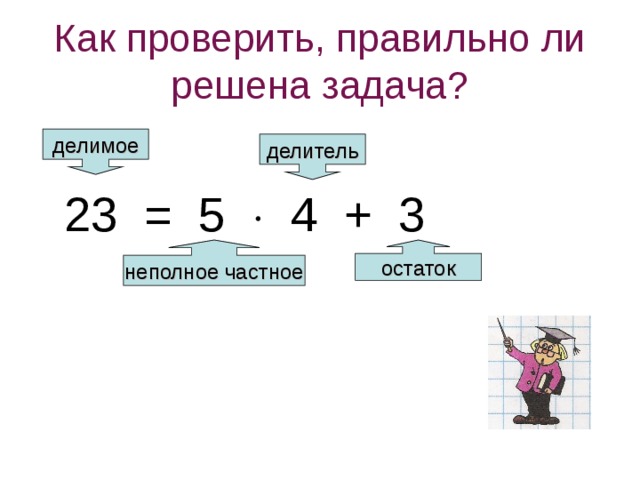
Деление многозначного числа на однозначное
Частное от деления многозначного числа на однозначное иногда выражается числом, состоящим также из нескольких цифр. В этом случае деление распадается на несколько отдельных действий.
Разделим 702 на 3. Частное содержит три цифры. Оно больше 100 и меньше 1000, ибо делимое больше 300 (3 × 100) и меньше 3000 (3 × 1000). Включая три цифры, частное содержит сотни, десятки и единицы. В данном случае разбиваем деление на три отдельных действия, то есть отыскиваем последовательно сотни, потом десятки и, наконец, единицы частного. Самое действие начинаем с сотен.
Отыскиваем сотни частного. Цифра сотен частного может происходить от деления сотен делимого на делитель 3. Десятки и единицы делимого не имеют никакого влияния на сотни частного, поэтому на них пока не обращаем внимания. Наибольшее число сотен в частном есть 2, ибо 3 содержится в 7 сотнях 2 сотни раз; пишем в частном 200. Умножая 200 на 3 и вычитая произведение 600 из делимого, получаем первый остаток 132.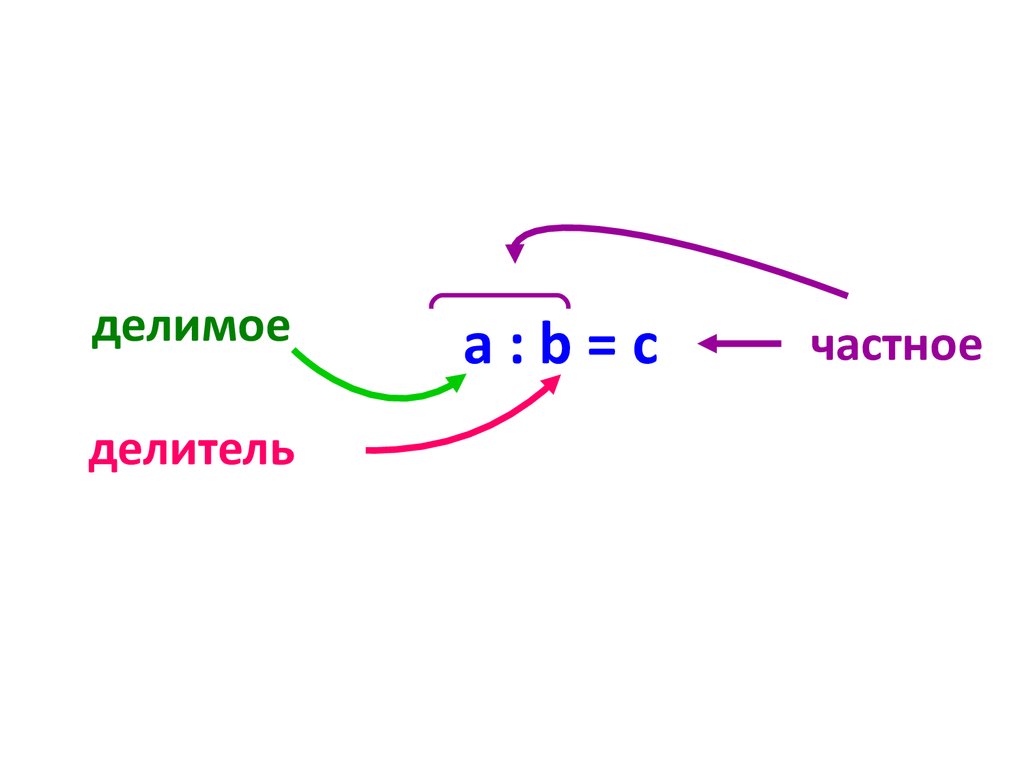
Отыскиваем десятки частного. В остатке 132 находится 12 десятков. Единицы делимого не имеют влияния на десятки частного. Разделив 13 на 3, находим, что в частном могут быть только 4 десятка, — пишем 40 в частном. Умножая 40 на 3 и вычитая произведение 120, получаем в остатке 12.
Отыскиваем единицы частного. Разделив 12 на 3, находим для единиц частного 4. Умножая 4 на 3 и вычитая произведение 12, получаем в остатке 0.
Если не писать каждый раз лишних нулей и принимать в соображение только те цифры делимого, которые имеют влияние на частное, деление изобразится письменно:
Отделяем 7 — одну цифру делимого; 3 в 7 содержится 2 раза, — пишем в частном 2; умножая на нее делителя 3 и вычитая произведение 6 из 7, получаем первый остаток 1.
Сносим 3 — следующую цифру делимого; 3 в 13 содержится 4 раза, 3-жды 4 составляет 12; вычитая 12 из 13, получаем в остатке 1.
Сносим 2 следующую цифру делимого; 3 в 12 содержится 4 раза, пишем в частном 4; 3-жды 4 составляет 12. Вычитая 12, получаем в остатке нуль и в частном 244.
Вычитая 12, получаем в остатке нуль и в частном 244.
Пример. Разделить 2417 на 3. Ход вычисления выразится письменно:
Отделив одну цифру 2, мы видим, что 3 в 2 не содержится целое число раз, поэтому нужно отделить две цифры; 3 в 24 содержится 8 раз, — пишем 8 в частном. Умножив 8 на делителя 3 и вычитая произведение 24, получаем в остатке нуль.
Сносим следующую цифру 1; 3 в 1 не содержится, — пишем в частном нуль.
Сносим следующую цифру 7; 3 в 17 содержится 5 раз, — пишем в частном 5; 3-жды 5 составляет 15; вычитая 15 из 17, получим в остатке 2 и целое частное 805.
Деление многозначного числа на многозначное
При делении многозначного числа на многозначное поступаем точно так же, как поступали при делении многозначного числа на однозначное.
Разделяя число 37207 на 47, мы прежде всего определяем, из скольких цифр состоит частное. Частное меньше 1000 и больше 100, ибо 37207 меньше 47000 (47 × 1000) и больше 4700 (47 × 100), следовательно, частное состоит из сотен, десятков и единиц. Начиная с сотен, мы определяем каждую цифру частного отдельно:
Начиная с сотен, мы определяем каждую цифру частного отдельно:
Определяем сотни частного:
Делимое 37207 имеет 372 сотни. Десятки и единицы делимого не имеют влияния на цифру сотен частного. В частном может быть только 7 сотен, ибо 47 содержится в 372 семь раз; пишем в частном 700.
Умножая делитель на частное и вычитая из делимого, получаем первый остаток 4307.
Определяем десятки частного:
Остаток 4307 содержит 430 десятков. Единицы не имеют влияния на цифру десятков частного. Делитель 47 содержится в 430 девять раз; пишем в частном 90.
Умножая 90 на частное 47 и вычитая произведение 4330, получаем в остатке 77.
Определяем единицы частного:
47 содержится в 77 один раз. Пишем в частном 1 и, вычитая из 77 произведение единицы на делитель, получаем в остатке 30.
Итак, после деления имеем в целом частном 791 и в остатке 30.
Если не писать каждый раз лишних нулей и принимать в соображение только те цифры делимого, которые имеют влияние на частное, ход вычисления изобразится письменно:
Отделяем в делимом от левой руки к правой столько цифр, чтобы делитель мог содержаться в отделенной части делимого. В данном случае отделяем 3 цифры, 47 содержится в 372 семь раз; умножаем делитель 47 на 7, цифру частного, и, вычитая произведение 47 × 7 = 329 из 372, получаем в остатке 43.
В данном случае отделяем 3 цифры, 47 содержится в 372 семь раз; умножаем делитель 47 на 7, цифру частного, и, вычитая произведение 47 × 7 = 329 из 372, получаем в остатке 43.
К остатку 43 сносим 0, следующую цифру делимого; 47 содержится в 430 девять раз, пишем в частном 9. Умножая 47 на 9 и вычитая произведение 423 из 430, получаем остаток 7.
Сносим к остатку следующую цифру частного 7; 47 содержится в 77 один раз. Пишем единицу в частном.
Умножая ею делитель и вычитая 47 из 77, получаем в остатке 30 и в целом частно 791.
Пример. Разделить 671064 на 335. Деление изобразится письменно:
Отделяем 671 в делимом; 335 содержится в 671 два раза, пишем в частном 2. Умножая 335 на 2 и вычитая произведение 670, получим в остатке 1.
Сносим 0, следующую цифру делимого; 335 не содержится в 10, — пишем для второй цифры частного 0.
Сносим 6, следующую цифру делимого; 335 не содержится в 106, — пишем для третьей цифры частного 0.
Сносим следующую цифру делимого 4; 335 содержится в 1064 три раза, — пишем в частном 3. Умножая делитель на 3 и вычитая произведение, получим в остатке 59 и в целом частном 2003.
Умножая делитель на 3 и вычитая произведение, получим в остатке 59 и в целом частном 2003.
Из предложенных примеров выводим следующее правило:
Чтобы разделить многозначное число на однозначное или многозначное, нужно отделить в делимом от левой руки к правой столько цифр, сколько их находится в делителе. Если делитель не содержится, отделяют в делимом одной цифрой больше. Разделив отделенное число на делитель, получают первую цифру частного, умножают ей делитель и полученное произведение вычитают из отделенной части делимого.
К остатку сносят следующую цифру делимого и снова задаются.
Если при этом получается число меньше делителя, пишут в частном нуль, сносят следующую цифру и снова задаются.
Получив новую цифру частного, поступают с нею так же, как и с первой цифрой.
Деление продолжают до тех пор, пока не снесут всех цифр делимого и не получат таким образом всех цифр частного.
Всякий раз, когда приходится делить, нужно задаваться в частном такою цифрой, чтобы остаток был меньше делителя. Чтобы легче найти такую цифру частного, при делении многозначного числа на многозначное обращают внимание на одну или две старшие цифры делителя и задаются только ими в соответствующей части делимого. При этом в делимом и в делителе отделяют от правой руки к левой одинаковое число цифр. Так, определяя, сколько раз содержится 6373 в 27302, мы задаемся четырьмя, ибо 6 в 27 содержится 4 раза.
Чтобы легче найти такую цифру частного, при делении многозначного числа на многозначное обращают внимание на одну или две старшие цифры делителя и задаются только ими в соответствующей части делимого. При этом в делимом и в делителе отделяют от правой руки к левой одинаковое число цифр. Так, определяя, сколько раз содержится 6373 в 27302, мы задаемся четырьмя, ибо 6 в 27 содержится 4 раза.
Полученная при этом цифра частного будет или равна или больше действительной. В последнем случае ее нужно уменьшить.
Иногда при делении не подписывают произведение цифры частного на делитель, а, подразумевая его в уме, подписывают один остаток. Сокращая таким образом деление, изображают его письменно:
8 в 43 содержится 5 раз; 5-ю 8 — сорок. Вычитая 40 из 43, получаем в остатке 3.
Сносим 2; 8 в 32 содержится 4 раза; 4-жды 8 составляет 32. Вычитая 32, получим в остатке нуль.
Сносим 8; 8 в 8-ми содержится 1 раз, 1-жды 8 составляет 8. Вычитая 8, получаем в остатке нуль и в частном 541.
Деление на 10, 100, 1000 и т. д.
Разделяя число на 10, мы десятки делимого обращаем в единицы, сотни в десятки, тысячи в сотни, вообще понижаем на единицу все порядки делимого. Этого мы достигаем, отделяя запятою цифру единиц. Число до запятой будет выражать частное, а после запятой — остаток.
Разделяя на 100, мы понижаем все порядки делимого на две единицы, для чего отделяем запятою от правой руки к левой две цифры и т. д. Отсюда правило:
Чтобы разделить какое-нибудь число на единицу с нулями, нужно от правой руки к левой отделить столько цифр, сколько нулей в делителе; тогда число до запятой выражает целое частное, а после запятой — остаток.
Пример. Разделяя 30207 на 100. Отделяя справа 2 цифры, находим 302,07. Целое частное будет 302, а остаток 7.
Деление на число, оканчивающееся нулями
Разделяя число 27057 на 400 и поступая при этом по общему правилу
Мы замечаем, что две последние цифры делимого не оказывают никакого влияния на частное. Они являются в остатке без всякой перемены. Откуда правило:
Они являются в остатке без всякой перемены. Откуда правило:
Если делитель оканчивается нулями, отделяют в делимом запятою от правой руки к левой столько цифр, сколько зачеркнуто нулей в делителе, и делят часть делимого до запятой на значащие цифры делителя. Отделенные цифры делимого приписывают к остатку.
В данном примере деление представится в виде
F
Если делимое и делитель оканчиваются нулями, их зачеркивают поровну в делимом, делителе и производят деление; зачеркнутые нули делимого приписывают к остатку.
Чтобы разделить 27300 на 4100, делим 273 на 41:
Частное будет 6, а остаток 2700.
Число цифр частного. При делении отделяют в делимом от левой руки к правой столько цифр, сколько их находится во делителе, или одною больше. Каждой оставшейся цифре делимого соответствует особая цифра частного, следовательно, Число цифр частного будет равно или разности числа цифр делимого и делителя или на единицу больше этой разности .
Зависимость между данными и искомыми деления
При делении целых чисел мы имеем два случая: а) Деление нацело, или без остатка, и б) Деление с остатком.
Каждому из этих случаев соответствует особая зависимость между данными и искомыми деления.
Деление нацело или без остатка
При делении нацело
Частное равно делимому, разделенному на делитель.
Разделяя 42 на 7, имеем в частном 6; следовательно,
42 ÷ 7 = 6, или 6 = 42 ÷ 7
Делимое равно делителю, умноженному на частное.
Так как делитель и частное — два множителя, произведение которых равно делимому, то Делитель равен делимому, разделенному на частное.
Деление с остатком
При делении с остатком
Делимое равно произведению делителя на целое частное, сложенное с остатком.
При делении 47 на 6, имеем в целом частном 7, в остатке 5.
Делимое 47 = 6 × 7 + 5.
Делимое без остатка делится нацело на делитель и на целое частное.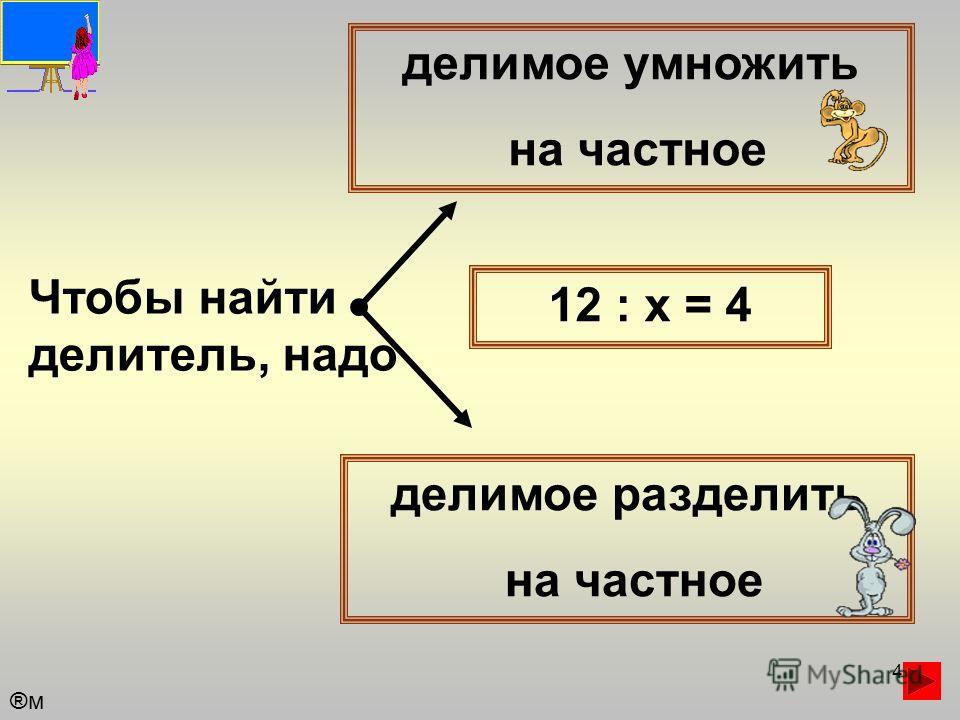
Разность делимого без остатка равна произведению делителя на целое частное, то есть эта разность при делении на делитель дает целое частное, при делении на целое частное дает делитель.
f
Чтобы получить делимое, нужно к этому произведению прибавить еще остаток 2.
Maths-public. ru
22.05.2020 5:47:34
2020-05-22 05:47:34
Источники:
Https://maths-public. ru/arithmetic/division
Деление целых чисел: правила, примеры, как делить целые числа, деление нуля на число » /> » /> .keyword { color: red; }
Деление правила математика
Данная статья рассказывает о том, как делить без остатка целые числа, то есть нацело. Будут введены термины и обозначения для дальнейшего описания чисел, деление положительных и отрицательных чисел. В итоге произведем проверку вычислений.
Термины и обозначения
При делении целых чисел используются те же термины, что и при описании натуральных чисел.
Делимое – это число, над которым совершают деление.
Делитель – число, на которое делят.
Частное – результат деления.
Знак деления обозначают двоеточием « : » или знаком ÷ . Его расположение после делимого и перед делителем. Запись с использованием символов выглядит так: a : b. Результат записывается после знака равно « = ». Если при делении числа а на b получаем с, тогда запись выглядит в виде равенства a : b = c. Деление иначе называют частным.
Деление целых чисел
Между умножением и делением натуральных чисел существует связь. Это связано с тем, что при делении можно найти частное, которое при обратном действии будет считаться множителем. Иначе можно записать, что деление целых чисел служит нахождением одного из целых множителей.
Отсюда делаем вывод, что произведение целых чисел a и b с частным, равным с, можно представить обратным действием деления с на b с частным равным а. Если произведение чисел 5 и — 7 равна — 35 , отсюда имеем, что частное ( − 35 ) : 5 равняется — 7 , а ( − 35 ) : ( − 7 ) с результатом 5 .
Частное от деления считается целым тогда, когда получается результат без остатка, то есть целое число a должно делиться на число b с целым частным в результате.
Правила деления целых чисел
Смысл деления необходим для утверждения того, что одним из двух множителей является частным, а другой просто множителем. Таким образом не найти неизвестный множитель, имея известный множитель и произведение. Равенство 6 · ( − 7 ) = − 42 говорит о том, что результаты ( − 42 ) : 6 и ( − 42 ) : ( − 7 ) равняются — 7 и 6 соответственно. При известном произведении 45 , а одного из множителей — 5 , то смысл деления не даст прямого результата другого множителя.
Можно сделать вывод, что необходимо использовать правила, которые позволяют производить деление целых чисел. Они позволят делить целые и натуральные числа.
Деление целых положительных чисел
Целыми положительными числами называют натуральные числа, поэтому деление целых положительных чисел производится, исходя из правил деления натуральных чисел. Рассмотрим несколько примеров для детального просмотра деления целых положительных чисел.
Рассмотрим несколько примеров для детального просмотра деления целых положительных чисел.
Произвести деление целого положительного 104 на целое положительное 8 .
Для упрощения процесса деления можно представить число 104 в виде суммы 80 + 24 ,теперь необходимо применить правило деления суммы на данное число. Получим 104 : 8 = ( 80 + 24 ) : 8 = 80 : 8 + 24 : 8 = 10 + 3 = 13 .
Ответ: 104 : 8 = 13 .
Найти частное от деления 308 716 : 452 .
Решение
Когда имеем большое число, деление лучше всего производить в столбик:
Ответ: 308 716 : 452 = 683 .
Правило деления целых отрицательных чисел, примеры
Для формулировки правила необходимо применить рассуждения. Если необходимо поделить целые отрицательные числа a на b, то искомое частное получится равным с. Форма записи: a : b = c. После чего можно выяснить, чему равна абсолютная величина с.
Исходя из смысла деления равенство b · c = a справедливо. Значит, b · c = a. Благодаря свойствам модуля, можно записать равенство b · c = b · c, значит, и b · c = a.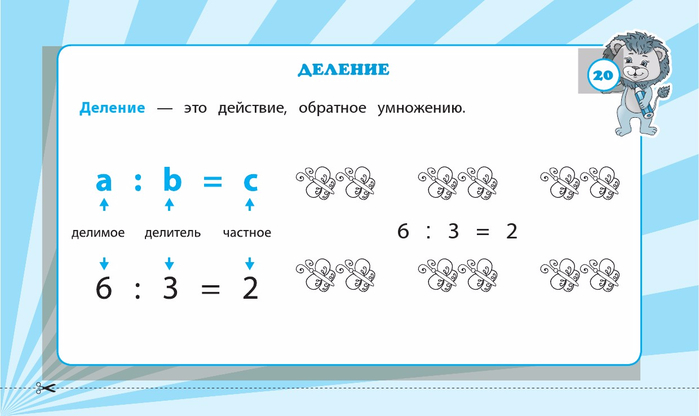 Отсюда получаем, что c = a : b. Абсолютная величина частного от деления равняется частному от деления модулей делимого и делителя.
Отсюда получаем, что c = a : b. Абсолютная величина частного от деления равняется частному от деления модулей делимого и делителя.
Для определения знака числа с необходимо выяснить, какие знаки находятся перед делимым и делителем.
Исходя из смысла деления целых чисел, равенство b · c = a справедливо. Правило умножения целых чисел говорит о том, что частное должно быть положительным. Иначе, b · c будет производиться по правилам целых отрицательных чисел. Частное с от деления целых отрицательных целых чисел является положительным числом.
Объединить в правило деления: чтобы разделить целое отрицательное число на отрицательное, необходимо разделить делимый на делитель по модулю. Эта запись будет выглядеть так a : b = a : b, при а и b равными отрицательным числам.
Рассмотрим несколько примеров деления отрицательных чисел.
Разделить — 92 на — 4 .
Используя правила деления целых отрицательных чисел, получим, что следует делить по модулю. Получим, что — 92 : — 4 = — 92 : — 4 = 92 : 4 = 23
Ответ: ( − 92 ) : ( − 4 ) = 23 .
Вычислить — 512 : ( — 32 ) .
Решение
Для решения необходимо разделить числа по модулю. Деление производится столбиком.
Ответ: ( − 512 ) : ( − 32 ) = 16 .
Правило деления целых чисел с разными знаками, примеры
Выделим правило деления целых чисел, содержащих разные знаки.
Если делим целое числа a и b с разными знаками, то получаем число с. Необходимо определить знак получаемого числа. Следует записать c = a : b.
Чтобы определить смысл деления равенства b · c = a, необходимо рассмотреть два варианта. Предположительно существует вариант, когда а – отрицательное, b – положительное или а – положительное, а b – отрициательное. Любой из случаев в итоге имеет отрицательный результат. Следуя из правил умножения, имеем, что b и с отрицательные, тогда произведение будет являться положительным. Если b положительное, с – отрицательное, тогда произведение является отрицательным числом.
Для формулировки применимо правило деления целых чисел с разными знаками. Отсюда получим: чтобы разделить целые числа с разными знаками, необходимо разделить делимое на делитель по модулю, перед полученным результатом поставить « — ». Получаем, что a и b являются целыми числами с разными знаками. Это запишем, как a : b = — a : b.
Отсюда получим: чтобы разделить целые числа с разными знаками, необходимо разделить делимое на делитель по модулю, перед полученным результатом поставить « — ». Получаем, что a и b являются целыми числами с разными знаками. Это запишем, как a : b = — a : b.
Детально разберем примеры, где необходимо применить правило деления целых чисел с разными знаками.
Разделить 56 на — 4 .
Решение
Исходя из правила, имеем, что 56 необходимо разделить на 4 по модулю. Значит, получим, что 56 : 4 = 14 . Для определения знака результата необходимо посмотреть наличие « — » перед делителем и делимым. Если имеется только один знак минуса, то результат запишем как отрицательное значение. То есть, — 14 .
Ответ: 56 : ( − 4 ) = − 14 .
Выполнить деление — 1625 на 25 .
Данный пример показывает правильное деление целых чисел с разными знаками. Для этого необходимо применить правило
— 1625 : 25 = — — 1625 : 25 = — 1625 : 25 = — 65
Деление числа 1625 можно производить в столбик или с помощью представления его в виде суммы 1500 + 125 , применив правило деления полученной суммы на число.
Ответ: ( − 1 625 ) : 25 = − 65 .
Деление нуля на целое число
Деление нуля на любое целое число рассматривается как отдельная тема, так как имеет свои нюансы. По правилу частное от деления на любое целое число, отличное от нуля, равно нулю. Иначе можем записать, что 0 : b = 0 , где значение числа b отлично от нуля.
Для углубления в правило рассмотрим некоторые пояснения.
Допустим, что результат деления нуля на целое число равен с, тогда равенство b · c = 0 считается верным. Произведение в итоге дает ноль тогда, когда хотя бы один из них равен нулю. Если по условию b не равно нулю, тогда множитель с = 0 . Отсюда следует, что частное, полученное делением нуля на целое число, отличное от нуля, равняется нулю.
Например, при делении нуля на целое число, частное получаем равное нулю: 0 : 4 или 0 : — 908 . Оба результаты будут равны нулю.
Не делить на нуль
Деление целого числа на нуль не определяется, поэтому и запрещено производить деление на 0 .
Например, если при делении целого числа а на ноль получим число с, то из смысла деления должно быть справедливо равенство c · 0 = a. Правило умножения на нуль говорит о том, что c · 0 = 0 при любом значении с. Сравнивая оба равенства, получим, что, если делимое анне равно нулю, тогда равенство c · 0 = a считается неверным. Поэтому можно делать вывод о том, что деление на нуль производить нельзя.
Возможно ли деление нуля на самого себя? Допустим, что при делении получаем целое число с, тогда равенство c · 0 = 0 должно быть верным. Оно считается действительным при любом значении с. Результат деления 0 на 0 принимается любое значение. Для уменьшения многозадачности данный вариант не рассматривается.
Проверка результата деления целых чисел
Проверку осуществляют умножением. Чтобы произвести проверку деления, нужно полученное частное умножить на делитель, если в результате получается число, равное делимому, тогда результат считается правильным.
Рассмотрим на примере решение с проверкой результата.
Результат деления 72 на — 9 равен — 7 . Произвести проверку данного выражения.
Решение
Выполняем проверку деления. Необходимо произвести умножение полученного частного и делителя, то есть ( − 7 ) · ( − 9 ) = 63 . Проверка показала, что 63 отлично от 72 , значит действие выполнено неверно.
Данная статья рассказывает о том, как делить без остатка целые числа, то есть нацело. Будут введены термины и обозначения для дальнейшего описания чисел, деление положительных и отрицательных чисел. В итоге произведем проверку вычислений.
При делении целых чисел используются те же термины, что и при описании натуральных чисел.
Делимое – это число, над которым совершают деление.
Делитель – число, на которое делят.
Частное – результат деления.
Знак деления обозначают двоеточием « : » или знаком ÷ . Его расположение после делимого и перед делителем. Запись с использованием символов выглядит так: a : b. Результат записывается после знака равно « = ». Если при делении числа а на b получаем с, тогда запись выглядит в виде равенства a : b = c. Деление иначе называют частным.
Если при делении числа а на b получаем с, тогда запись выглядит в виде равенства a : b = c. Деление иначе называют частным.
Если по условию b не равно нулю, тогда множитель с 0.
Zaochnik. com
01.04.2020 23:08:08
2020-04-01 23:08:08
Источники:
Https://zaochnik. com/spravochnik/matematika/dejstvitelnye-ratsionalnye-irratsionalnye-chisla/delenie-tselyh-chisel/
Деление рациональных чисел (6 класс, математика) – правило » /> » /> .keyword { color: red; }
Деление правила математика
Деление рациональных чисел подразумевает вообще любое деление, где не используется корень. Сюда входит как деление целых чисел, так и деление дробей. Этот обширный пласт знаний курса математики 6 класса крайне важен, поскольку без деления не обходятся не только точные науки, но и гуманитарные и естественные науки: биология, химия, экономика.
Что такое деление?
Первое, что необходимо узнать в теме деление рациональных чисел – это что такое деление.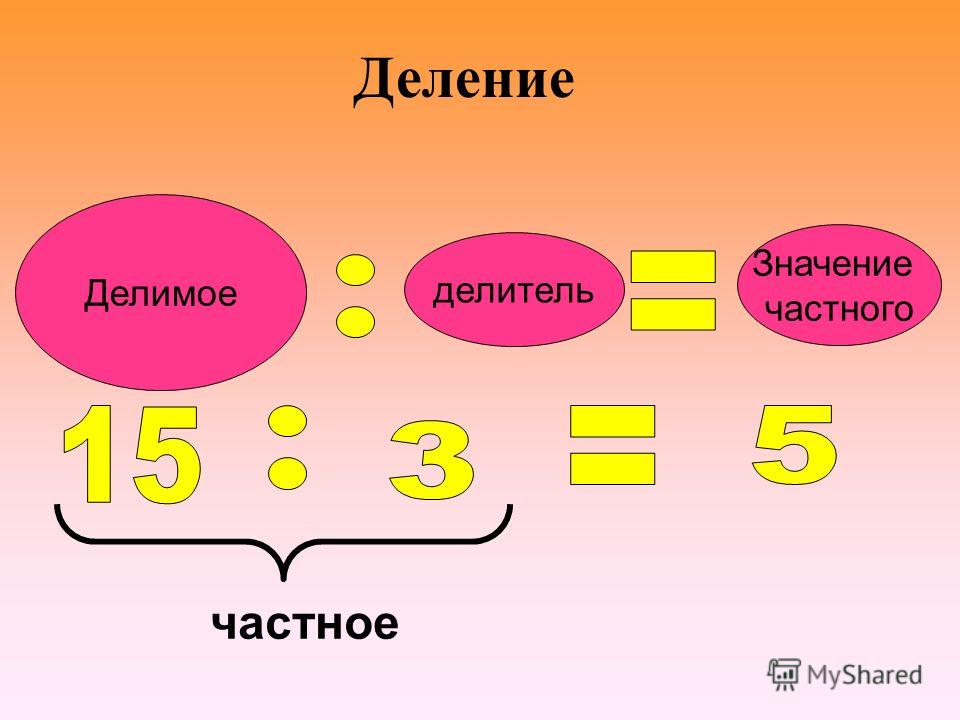 Деление – это операция обратная умножению. Деление подразумевает под собой, что в результате вычисления мы должны узнать, сколько раз в делимом поместился делитель. Иначе говоря, сколько раз нужно сложить делитель с самим собой, чтобы получить делимое. Или же на какое число нужно умножить делимое, чтобы получить делитель. Именно последнее определение чаще всего используется в современных учебниках математики.
Деление – это операция обратная умножению. Деление подразумевает под собой, что в результате вычисления мы должны узнать, сколько раз в делимом поместился делитель. Иначе говоря, сколько раз нужно сложить делитель с самим собой, чтобы получить делимое. Или же на какое число нужно умножить делимое, чтобы получить делитель. Именно последнее определение чаще всего используется в современных учебниках математики.
Деление нацело
Деление нацело – это деление без остатка. Для того, что овладеть этим подвидом деления, для начала, нужно наизусть выучить таблицу умножения. Математика редко требует слепого заучивания, но это один из этих случаев. После этого простейшие примеры деления нацело станут, действительно, простейшими. Приведем пример.
$6*7=42$ – это один из столбцов таблицы умножения. Соответственно:
$42:7=6$ – вот соответствующая этой строке процедура деления. Более большие числа делятся в столбик.
Деление с остатком
Деление нацело подразумевает деление без остатка. Деление с остатком также имеет место быть. Это процедура, которая регулярно выполнятся во множестве самых обычных продуктовых магазинов при подсчете сдачи от покупки.
Деление с остатком также имеет место быть. Это процедура, которая регулярно выполнятся во множестве самых обычных продуктовых магазинов при подсчете сдачи от покупки.
Для того, чтобы разделить одно число на другое с остатком придется подобрать число, меньше делимого, которое делиться на делитель с остатком. Результат деления этого числа на делитель и будет результатом деления, а остаток это разность изначального делимого и найденного. Приведем пример:
$53:5$ – ближайшее число, которое меньше, чем 53 и делится на 5 это 50.
$50:5=10$ – это результат.
$53-50=3$ – это остаток. Теперь запишем выражение полностью без промежуточных вычислений:
Деление дробных чисел
Числа бывают как целые, так и дробные. Причем последние также могут подвергаться процедуре деления. Рациональные дроби делятся с помощью переворачивания делителя.
Дробь делитель преображается так, что числитель становится знаменателем, а знаменатель числителем. Деление изначальных чисел будет равняться умножению делимого на перевернутую дробь.
Таким же способом можно делить и десятичные дроби после преобразования их в натуральные.
Десятичные дроби делятся с помощью перенесения запятой. Делимое и делитель домножаются на 10 в такой степени, чтобы оба числа стали целыми.
Домножить необходимо на одинаковое число, чтобы не нарушить тождество выражения.
Правило деления рациональных чисел распространяется как на целые, так и на дробные числа..
Что мы узнали?
Мы рассмотрели все виды деления, привели общие принципы и приемы, которые применяют для правильного выполнения этой операции.
Что такое деление?
Первое, что необходимо узнать в теме деление рациональных чисел – это что такое деление. Деление – это операция обратная умножению. Деление подразумевает под собой, что в результате вычисления мы должны узнать, сколько раз в делимом поместился делитель. Иначе говоря, сколько раз нужно сложить делитель с самим собой, чтобы получить делимое. Или же на какое число нужно умножить делимое, чтобы получить делитель. Именно последнее определение чаще всего используется в современных учебниках математики.
Именно последнее определение чаще всего используется в современных учебниках математики.
Деление нацело – это деление без остатка. Для того, что овладеть этим подвидом деления, для начала, нужно наизусть выучить таблицу умножения. Математика редко требует слепого заучивания, но это один из этих случаев. После этого простейшие примеры деления нацело станут, действительно, простейшими. Приведем пример.
$6*7=42$ – это один из столбцов таблицы умножения. Соответственно:
$42:7=6$ – вот соответствующая этой строке процедура деления. Более большие числа делятся в столбик.
6 7 42 это один из столбцов таблицы умножения.
Obrazovaka. ru
13.08.2018 7:59:46
2018-08-13 07:59:46
Источники:
Https://obrazovaka. ru/matematika/delenie-racionalnyh-chisel-6-klass. html
Частное чисел в арифметике — Тур-инфо
Частное математика что это
Частное — это результат процесса деления. Делением называется такая операция, которая обратна умножению, то есть показывает, сколько одинаковых чисел способно содержаться в другом.
Буквенный вид этого действия выглядит следующим образом: A: b = c, где:
- a – это делимое (число, которое делят) b – это делитель (число, которым делят) с – это частное (результирующее число деления) : — арифметический знак, с помощью которого обозначается деление
Важно! Число 0 никогда не может быть делителем
Нахождение значения частного чисел
Пример:
12 : 3 = 4 (в числе 12 4 раза содержится по 3)
15 : 5 = 3 (в числе 15 5 раз содержится по 5)
Нужно знать, что правильность определения частного от деления числа всегда можно проверить путем перемножения его на делитель, либо делимое поделить на частное и получить делитель.
Перемножим частное двух чисел на делитель и получим делимое:
Разделим делимое на частное и получим делитель:
Таким образом, мы доказали правильность определения частного.
Что такое частное значение чисел с остатком?
Иногда при делении от делимого остается остаток, который меньше делителя, но более нуля. Приведем выражение частного чисел:
Приведем выражение частного чисел:
Это значит, что делимое 8 поделилось 2 раза по 3 и остался остаток 2, который меньше трех, но больше нуля.
Основные понятия о частном суммы и разности чисел
Что такое частное суммы чисел?
Частное от деления суммы чисел – это когда делимое либо делитель выступает в роли суммы двух слагаемых.
Общий вид: (a+b):(c+d), где сумма чисел (a+b) – делимое, а сумма (c+d) – делитель
Важно, в подобных примерах последовательность решения определяется следующим образом: сначала решаются выражения в скобочках, потом выражения со знаками деления или умножения, после – вычитание или сложение.
Нужно знать, что правильность определения частного от деления числа всегда можно проверить путем перемножения его на делитель, либо делимое поделить на частное и получить делитель.
Www. napishem. ru
21.01.2019 19:33:02
2019-01-21 19:33:02
Источники:
Https://www. napishem. ru/spravochnik/matematika/chastnoe-chisel. html#:~:text=%D0%9E%D0%BF%D1%80%D0%B5%D0%B4%D0%B5%D0%BB%D0%B5%D0%BD%D0%B8%D0%B5%20%D0%A7%D0%B0%D1%81%D1%82%D0%BD%D0%BE%D0%B5%20%E2%80%94%20%D1%8D%D1%82%D0%BE%20%D1%80%D0%B5%D0%B7%D1%83%D0%BB%D1%8C%D1%82%D0%B0%D1%82%20%D0%BF%D1%80%D0%BE%D1%86%D0%B5%D1%81%D1%81%D0%B0%20%D0%B4%D0%B5%D0%BB%D0%B5%D0%BD%D0%B8%D1%8F.%20%D0%94%D0%B5%D0%BB%D0%B5%D0%BD%D0%B8%D0%B5%D0%BC,%D0%BF%D0%BE%D0%BA%D0%B0%D0%B7%D1%8B%D0%B2%D0%B0%D0%B5%D1%82%2C%20%D1%81%D0%BA%D0%BE%D0%BB%D1%8C%D0%BA%D0%BE%20%D0%BE%D0%B4%D0%B8%D0%BD%D0%B0%D0%BA%D0%BE%D0%B2%D1%8B%D1%85%20%D1%87%D0%B8%D1%81%D0%B5%D0%BB%20%D1%81%D0%BF%D0%BE%D1%81%D0%BE%D0%B1%D0%BD%D0%BE%20%D1%81%D0%BE%D0%B4%D0%B5%D1%80%D0%B6%D0%B0%D1%82%D1%8C%D1%81%D1%8F%20%D0%B2%20%D0%B4%D1%80%D1%83%D0%B3%D0%BE%D0%BC.
html#:~:text=%D0%9E%D0%BF%D1%80%D0%B5%D0%B4%D0%B5%D0%BB%D0%B5%D0%BD%D0%B8%D0%B5%20%D0%A7%D0%B0%D1%81%D1%82%D0%BD%D0%BE%D0%B5%20%E2%80%94%20%D1%8D%D1%82%D0%BE%20%D1%80%D0%B5%D0%B7%D1%83%D0%BB%D1%8C%D1%82%D0%B0%D1%82%20%D0%BF%D1%80%D0%BE%D1%86%D0%B5%D1%81%D1%81%D0%B0%20%D0%B4%D0%B5%D0%BB%D0%B5%D0%BD%D0%B8%D1%8F.%20%D0%94%D0%B5%D0%BB%D0%B5%D0%BD%D0%B8%D0%B5%D0%BC,%D0%BF%D0%BE%D0%BA%D0%B0%D0%B7%D1%8B%D0%B2%D0%B0%D0%B5%D1%82%2C%20%D1%81%D0%BA%D0%BE%D0%BB%D1%8C%D0%BA%D0%BE%20%D0%BE%D0%B4%D0%B8%D0%BD%D0%B0%D0%BA%D0%BE%D0%B2%D1%8B%D1%85%20%D1%87%D0%B8%D1%81%D0%B5%D0%BB%20%D1%81%D0%BF%D0%BE%D1%81%D0%BE%D0%B1%D0%BD%D0%BE%20%D1%81%D0%BE%D0%B4%D0%B5%D1%80%D0%B6%D0%B0%D1%82%D1%8C%D1%81%D1%8F%20%D0%B2%20%D0%B4%D1%80%D1%83%D0%B3%D0%BE%D0%BC.
Что такое частное чисел и деление с остатком, как их вычислить? читай ответы на Справочник24 » /> » /> .keyword { color: red; }
Частное математика что это
Деление – это действие в арифметике, которое противоположное умножению, и при помощи этих результатов можно узнать, сколько раз одно число может содержаться в другом.
Делимым числом называют то, которое делят, делитель – это число на которое делят, а результатом такого деления является частное числа. Например, если число 26 разделить на 13, тогда можно узнать определение частного числа 26 и 13, в результате оно будет равно 2.
Важно запомнить, что частное число имеет одну очень важную особенность, оно не изменяется при делении или умножении делимого и делителя, на одно и то же число. Для того чтобы понять, данное определение, мы предлагаем рассмотреть пример, и можно все увидеть:
И в случае, если вы ошиблись при делении чисел, все легко можно проверить путем умножения частного числа на делитель, если получаем число равно делимому, тогда все верно.
Но есть такие случаи в математике, что делении чисел не всегда получается их полностью разделить, тогда остается остаток. Деление с остатком – это такое деление чисел, при котором остаток больше нуля. Вот рассмотрим такой случай, здесь хорошо понятно, где берется остаток, и почему так получается:
И при этом нужно запомнить такое правило математики, что остаток, не должна быть больше делителя. Здесь мы получим остаток число 1, который меньше чем делитель 2, а число 6 можно назвать неполным частным.
Здесь мы получим остаток число 1, который меньше чем делитель 2, а число 6 можно назвать неполным частным.
Например, если число 26 разделить на 13, тогда можно узнать определение частного числа 26 и 13, в результате оно будет равно 2.
Spravochnick. ru
30.05.2018 20:58:47
2018-05-30 20:58:47
Источники:
Https://spravochnick. ru/vopros/5263/
Частное чисел: понятие частного числа, примеры решения задач » /> » /> .keyword { color: red; }
Частное математика что это
Частное — это результат процесса деления. Делением называется такая операция, которая обратна умножению, то есть показывает, сколько одинаковых чисел способно содержаться в другом.
Буквенный вид этого действия выглядит следующим образом: A: b = c, где:
- a – это делимое (число, которое делят) b – это делитель (число, которым делят) с – это частное (результирующее число деления) : — арифметический знак, с помощью которого обозначается деление
Важно! Число 0 никогда не может быть делителем
Нахождение значения частного чисел
Пример:
12 : 3 = 4 (в числе 12 4 раза содержится по 3)
15 : 5 = 3 (в числе 15 5 раз содержится по 5)
Нужно знать, что правильность определения частного от деления числа всегда можно проверить путем перемножения его на делитель, либо делимое поделить на частное и получить делитель.
Перемножим частное двух чисел на делитель и получим делимое:
Разделим делимое на частное и получим делитель:
Таким образом, мы доказали правильность определения частного.
Что такое частное значение чисел с остатком?
Иногда при делении от делимого остается остаток, который меньше делителя, но более нуля. Приведем выражение частного чисел:
Это значит, что делимое 8 поделилось 2 раза по 3 и остался остаток 2, который меньше трех, но больше нуля.
Основные понятия о частном суммы и разности чисел
Что такое частное суммы чисел?
Частное от деления суммы чисел – это когда делимое либо делитель выступает в роли суммы двух слагаемых.
Общий вид: (a+b):(c+d), где сумма чисел (a+b) – делимое, а сумма (c+d) – делитель
Важно, в подобных примерах последовательность решения определяется следующим образом: сначала решаются выражения в скобочках, потом выражения со знаками деления или умножения, после – вычитание или сложение.
Перемножим частное двух чисел на делитель и получим делимое.
Www. napishem. ru
08.03.2019 7:55:59
2019-03-08 07:55:59
Источники:
Https://www. napishem. ru/spravochnik/matematika/chastnoe-chisel. html
Дивиденд в делении – значение, формула, примеры
Дивиденд – это целое число или количество вещей, которые необходимо разделить на определенные равные части. Деление — это процесс деления числа на равные части с оставлением остатка, если данное число не может быть разделено на части поровну. Дивиденды являются важной частью операции деления.
| 1. | Что такое Дивиденды в разделе Значение? |
| 2. | Как определить дивиденд? |
| 3. | Формула дивидендов |
| 4. | Дивиденд в дробях |
| 5. | Разница между дивидендом и делителем |
6. | Часто задаваемые вопросы о дивидендах |
Что такое Дивиденды в разделе Значение?
Когда мы делим любое число p на число q (p ÷ q), здесь в этом делении факт ‘p’ относится к делимому. Давайте разберемся в этом на примере. Разделите число 20 на 5. Запишем факт деления для данного примера.
Факт деления = 20 ÷ 5. Здесь 20 — делимое.
Определение дивиденда
В процессе деления делимое — это число, которое полностью делится на делитель, оставляя результат в виде остатка. Другими словами, это целое, которое нужно разделить на части. Например, 15 яблок нужно разделить между 3 детьми. Здесь 15 — делимое. Деление может быть выполнено в различных формах. Разберемся, как идентифицировать делимое в разных представлениях.
Как определить дивиденд?
При делении делимое делится на равные группы по делителю. Число, которое делится в задаче на деление, называется делимым , а число, на которое делится делимое, называется делителем . Существует 3 различных способа представления факта деления. Во всех соответствующих формах результаты остаются одинаковыми. Давайте в общих чертах посмотрим на изображение ниже, на котором показаны различные методы записи дивидендов.
Существует 3 различных способа представления факта деления. Во всех соответствующих формах результаты остаются одинаковыми. Давайте в общих чертах посмотрим на изображение ниже, на котором показаны различные методы записи дивидендов.
На изображении выше 32 — это делимое, представленное в трех разных формах.
Формула дивидендов
Без дивидендов операция деления невозможна. Предположим, нам нужно разделить число 75 на 5. Математически это можно представить как факт деления, например, 75 ÷ 5 = 15. В этом факте деления:
- Число 75 является делимым. Это число, которое нужно разделить.
- Число 5 равно Делитель. Это число, которое делит делимое.
- Число 15 — это частное.
- Остаток для вышеуказанного случая равен нулю.
Чтобы провести тщательную проверку деления, мы можем использовать формулу для нахождения дивидендов или, другими словами, формулу деления. Посмотрите на формулу, упомянутую ниже.
Дивиденд = (Делитель × Частное) + Остаток.
Рассмотрим еще один пример, где мы найдем делимое по указанной формуле.
- делимое = х
- делитель = 6
- частное = 6
- остаток = 0
Подставляя значение в формулу, получаем x = (6×6)+0 = 36. Следовательно, значение делимого равно 36.
Разберемся с формулой нахождения дивидендов, когда остаток равен нулю. Для этого конкретного случая формула будет такой:
- Если остаток равен 0, то Дивиденд = (Делитель × Частное).
Дивиденд в дробях
Дроби — это числа, представленные в виде p/q. Например, ¼, ½, ¾ и т. д. Когда группа предметов или коллекция разбита на равные части или части, мы называем это частью целого. Все дроби состоят из числителя и знаменателя.
- Числитель дроби является делимым.
- Знаменатель дроби является делителем.
Разница между дивидендом и делителем
Дивиденд и делитель являются основными частями факта деления. Без делителя мы не можем разделить делимое, а без делимого мы не можем выполнить деление. Делитель делит делимое на равные части, тогда как делимое делится поровну на делитель. Поясним этот факт с помощью иллюстрации.
Без делителя мы не можем разделить делимое, а без делимого мы не можем выполнить деление. Делитель делит делимое на равные части, тогда как делимое делится поровну на делитель. Поясним этот факт с помощью иллюстрации.
Пример: разделить 52 на 4
Факт деления = 52 ÷ 4
Здесь 52 — делимое, а 4 — делитель. Если какой-либо член отсутствует, мы не можем выполнить деление с одним термином. Следовательно, 52 ÷ 4 = 13. Здесь 13 — частное.
Факты о дивидендах
Ниже приведены факты, связанные с дивидендами в подразделении.
- Когда делимое и делитель равны в задаче на деление, результат такой задачи на деление всегда равен 1. Например, 75 ÷ 75 = 1
- Когда остаток равен нулю, это означает, что делимое полностью делится на делитель.
- Если делимое и частное факта деления равны, то значение делителя равно 1. Например, 75 ÷ 1 = 75
- Если делитель больше делимого, то результирующее число будет десятичным числом. Например, 75 ÷ 1000 = 0,075· .

☛Статьи по теме
Ознакомьтесь с интересными темами, чтобы узнать больше о дивидендах.
- Длинная часть
- Остаток
- Дивизион Формула
- Частное
Часто задаваемые вопросы о дивидендах
Что такое дивиденд в математике?
Число, которое делится на другое число (делитель), называется делимым. Например, разделите 24 на 4. Здесь 4 — это число, на которое делится число 24, поэтому 24 называется делимым, а 4 — делителем.
Как рассчитать дивиденды в подразделении?
Если известны другие части факта деления, такие как делитель, частное и остаток, то мы можем найти делимое, используя данную формулу:
Дивиденд = делитель x частное + остаток.
Какая формула для нахождения дивиденда, когда остаток равен нулю?
Если в остатке 0, то формула нахождения дивиденда = (Делитель × Частное).
Куда мы пишем дивиденды в подразделении?
При выполнении длинного деления делимое записывается внутри знака деления, а делитель вне его, слева.
Что такое дивиденд в дроби?
Дробь представлена в виде p/q,(q не равно 0). Все дроби состоят из двух частей: числителя и знаменателя. Здесь числитель — делимое. Например, 8/2, числитель 8 — это делимое.
Что такое Дивиденд в разделе?
Когда любой общий факт деления представлен как A ÷ B = C, в таком случае A является дивидендом соответствующего факта деления.
Чему равно число 24, разделенное на 3?
Данный пример можно представить как 24 ÷ 3. В этом случае 24 — это делимое, а 3 — делитель.
Какой дивиденд в 72/8?
72/8 записывается в форме дроби, здесь числитель равен 72, а в форме дроби часть числителя известна как делимое.
Каков дивиденд деления Факт 45 ÷ 15 дает 3?
Делимое — это число, которое делится поровну на делитель. Здесь 45 делится на 15. Следовательно, 45 — делимое.
Определение и значение дивидендов | Dictionary.com
- Верхние определения
- Синонимы
- Викторина
- Связанный контент
- Примеры
- British
- Scientific
- Cultural
This Louse Louse на уровне.
[ div-i-dend ]
/ ˈdɪv ɪˌdɛnd /
Сохранить это слово!
См. синонимы для: дивиденд / дивиденды на Thesaurus.com
Показывает уровень оценки в зависимости от сложности слова.
сущ.
Математика. число, которое нужно разделить на делитель.
Право. сумма из неплатежеспособного имущества, выплаченная кредиторам.
Финансы.
- пропорциональная часть распределяемой суммы.
- сумма денег, выплачиваемая акционерам корпорации из прибыли.
Страхование. (в страховании с участием) распределение держателю полиса части премии, не необходимой компании для оплаты требований или покрытия расходов.
доля чего-либо разделенного.
все, что получено в качестве бонуса, вознаграждения или в дополнение к ожидаемому или сверх того, что ожидается: плавание — это весело и дает вам дивиденды в виде улучшения здоровья.
ДРУГИЕ СЛОВА ДЛЯ ДИВИДЕНА
5 надел, порция.
См. синонимы слова «дивиденд» на Thesaurus.com
ВИКТОРИНА
Сыграем ли мы «ДОЛЖЕН» ПРОТИВ. «ДОЛЖЕН» ВЫЗОВ?
Следует ли вам пройти этот тест на «должен» или «должен»? Это должно оказаться быстрым вызовом!
Вопрос 1 из 6
Какая форма обычно используется с другими глаголами для выражения намерения?
Происхождение дивидендов
1470–80; <Латинское dīvidendum то, что нужно разделить, средний герундий слова dīvidere, чтобы разделить
ДРУГИЕ СЛОВА ОТ СЛОВА дивиденд
над·пер·дел·и·денд, существительноеСлова рядом с дивидендом
делимый, разделяй, разделяй и властвуй, разделенный, разделенное шоссе, дивиденд, покрытие дивидендов, дивиденд на, дивидендус, делитель , разделители
Dictionary.com Unabridged На основе Random House Unabridged Dictionary, © Random House, Inc., 2022
Слова, относящиеся к дивидендам
надбавка, премия, купон, прибыль, премия, выручка, перевод, вознаграждение, излишек, выделение, присвоение, пряник, чек, сокращение , диспенсация, дивви, экстра, подливка, гердон, интерес
Как использовать «дивиденд» в предложении
Компания «Аврора» надеется, что ее узкая ориентация на «Водителя» — аппаратно-программную систему для управления автомобилем — а не на создание самого транспортного средства или обслуживание службы совместного использования, будет выплачивать дивиденды.

Последний выживший единорог: сможет ли выжить этот самоуправляемый новатор?|Чару Кастури|27 августа 2020 г.|Ози
Итак, в долгосрочной перспективе стратегия борьбы с действующими лицами может принести дивиденды левым.
Прогрессивные группы становятся более избирательными в отношении действующих лиц. Это работает?|Натаниэль Ракич ([email protected])|21 августа 2020 г.|FiveThirtyEight
Если вы потратите немного своего времени и усилий на эти списки, они принесут большие дивиденды в виде поиска. кампании.
Как использовать аудиторию заинтересованных покупателей для улучшения поисковых кампаний|Харикришна Кундария|18 августа 2020 г.|Наблюдение за поисковыми системами
Джордж Цугрос, исполнительный директор Совета по искусству штата Висконсин Такие инициативы приносят дивиденды.
Может ли искусство спасти сельскую Америку от рецессии?|Чару Кастури|16 августа 2020 г.|Ози
длительный срок.

Расширенный поиск Google: шесть мощных советов по улучшению SEO|Адитья Шет|30 июня 2020 г.|Search Engine Watch
С тех пор все выплаты дивидендов были заморожены, и Иран не получает «никакого урана или доходов от шахты».
Маккейн помогает бизнес-партнеру из Ирана|Бен Джейкобс|13 ноября 2014|DAILY BEAST
В обмен на наличные Fannie и Freddie выпустили привилегированные акции Казначейству, которые должны были выплачивать 10-процентные дивиденды.
Помните спасение AIG на 182 миллиарда долларов? Это было недостаточно щедро|Дэниел Гросс|15 октября 2014 г.|DAILY BEAST
Fannie Mae в сентябре выплатила дивиденды в размере 10,2 миллиарда долларов, а Freddie Mac выплатила дивиденды в размере 4,4 миллиарда долларов.
Правительство закрывается, и частный сектор тоже чувствует боль | Дэниел Гросс | 4 октября 2013 г. | DAILY BEAST
Во вторник компания также объявила, что поднимет свои квартальные дивиденды на 26,7 процента, с 30 центов до 38 процентов.
 .
.Джейми Даймон — акционерам: сосать|Дэниел Гросс|21 мая 2013|DAILY BEAST
Большая часть этих денег будет отправлена домой в США и передана акционерам по чрезвычайно выгодным ставкам налогообложения дивидендов.
Конгресс на гриль Генеральный директор Apple о налогах|Меган Макардл|21 мая 2013|DAILY BEAST
Финансовая депрессия сменила период дикого возбуждения, и дивиденды Мидленда упали с семи до двух процентов.
Пятьдесят лет железнодорожной жизни в Англии, Шотландии и Ирландии|Джозеф Татлоу
Он предстал перед акционерами и предложил, если его советы и методы будут приняты, гарантировать двойные дивиденды.
Пятьдесят лет железнодорожной жизни в Англии, Шотландии и Ирландии | Джозеф Татлоу
Но банк может удержать дивиденды, которые были объявлены, чтобы уменьшить задолженность владельца перед банком за его акции.
Удобная книга законов Патнэма для неспециалистов|Альберт Сидни Боллес
Одно из самых приятных действий, которое может сделать корпорация, — это объявить дивиденды, особенно если они будут крупными.

Удобная юридическая книга Патнэма для неспециалистов|Альберт Сидни Боллз
Вопрос о том, следует ли объявлять дивиденды, а также о сумме, в значительной степени находится на усмотрении директоров.
Putnam’s Handy Law Book for the Layman|Albert Sidney Bolles
British Dictionary definitions for dividend
dividend
/ (ˈdɪvɪˌdɛnd) /
noun
finance
- a distribution from the net profits of a компания своим пайщикам
- пропорциональная часть этого распределения, полученная пайщиком
доля прибыли кооператива, распределенная в конце периода между членами
страхование сумма денег, распределяемая из чистой прибыли компании среди держателей определенных полисов
что-то дополнительное; премия
число или количество, которое должно быть разделено на другое число или количествоСравнить делитель
закон доля неплатежеспособного имущества, подлежащего выплате кредиторам
Слово Происхождение для дивиденда
C15: от латинского dīvidendum то, что должно быть разделено; см. раздел
раздел
Английский словарь Коллинза — полное и полное цифровое издание 2012 г. © William Collins Sons & Co. Ltd. 1979, 1986 © HarperCollins Publishers 1998, 2000, 2003, 2005, 2006, 2007, 2009, 2012
Научные определения дивиденда
дивиденда
[див’и-денд’]
. В уравнении 15 ÷ 3 = 5 15 — делимое.
Научный словарь American Heritage® Авторские права © 2011. Опубликовано издательством Houghton Mifflin Harcourt Publishing Company. Все права защищены.
Культурные определения дивидендов
дивидендов
Выплата акционерам корпорации из прибыли корпорации.
Новый словарь культурной грамотности, третье издание Авторское право © 2005 г., издательство Houghton Mifflin Harcourt Publishing Company. Опубликовано издательством Houghton Mifflin Harcourt Publishing Company. Все права защищены.
ТОП 8 что такое дивиденды в математике ЛУЧШИЕ и НОВЕЙШИЕ
ТОП 8 что такое дивиденды в математике САМЫЕ ЛУЧШИЕ и НОВЕЙШИЕ0086 Вы задаетесь вопросом что такое дивиденды в математике но в настоящее время нет ответа, поэтому позвольте kienthuctudonghoa. com обобщить и перечислить лучшие статьи с вопросом. ответьте на вопрос, что такое дивиденд в математике, что поможет вам получить наиболее точный ответ. Следующая статья призвана помочь вам сделать более правильный выбор и получить больше полезной информации.
com обобщить и перечислить лучшие статьи с вопросом. ответьте на вопрос, что такое дивиденд в математике, что поможет вам получить наиболее точный ответ. Следующая статья призвана помочь вам сделать более правильный выбор и получить больше полезной информации.
Краткое содержание
- 1 1. Что такое дивиденды? – Факты и примеры определений – SplashLearn
- 2 2. Дивиденд в математике – определение, формула, примеры, как найти
- 3 3. Определение дивиденда – математика – это весело
- 4 4. Что такое дивиденд в математике? – Video & Lesson Transcript – Study.com
- 5 5.Дивиденд в делении – Значение, формула, примеры – Cuemath
- 6 6.делим, деление, делимое, делитель – Математический словарь для детей
- 7 7.Дивиденд – Определение, формула и важные правила — Веданту
- 8 8. Дивиденд — Math.net
1.Что такое дивиденды? — Определение Факты и пример — Splashlearn
- Автор: www.
 splashlearn.com
splashlearn.com - Дата поста: 30 вчера
- : 5 (1700 Reviews)
- . Низкий рейтинг: 2
- Суммарно: В задаче на деление число, которое нужно разделить или разделить на определенное количество равных частей, называется делимым. Как и в приведенном выше примере …
См. Подробности
2. Dividend in Mathematics — определение, формула, примеры, как найти
- Автор: Byjus.com
- Post Date: 13 вчера
- : 5441 5 ( 5 ( 13
- : 5 ( 5 ( 13
- : 5 ( 5 ( 13
- . отзывы)
- Высшая оценка: 3
- Низкая оценка: 2
- Резюме: В математике делимое — это значение, которое делится на другое значение, чтобы получить результат.
 Делимое является основой любого метода деления.
Делимое является основой любого метода деления.
См. Подробная информация
3. Определение дивидендов — математика — это веселье
- Автор: www.mathsisfun.com
- Дата почты: 8 вчера
- rating: 1 (1)
- : 1 ()
- : 1 ()
- : 1 ()
- : 1 ()
- : 1 ()
- : 1 () Самый высокий рейтинг: 5
- Низкий рейтинг: 3
- Итог: Сумма, которую вы хотите разделить. делимое ÷ делитель = частное. Пример: в 12 ÷ 3 = 4 делимое равно 12. Разделение.
Подробнее
4.Что такое дивиденд в математике? — Стенограмма видео и урока — исследование.com
- Автор: Исследование.

- Пост дата: 11 Вчера
- Рейтинг: 1 (1518 Обзоры)
- HOSTORST: 3
- 60. Низкий рейтинг: 2
- Резюме:
Подробнее
0046
- Автор: www.cuemath.com
- Дата: 12 вчера
- Оценка: 1 (236 Обзоры)
- СВОЙСТВЕННА Резюме: Делимое – это целое число или количество вещей, которые необходимо разделить на определенные равные части. Деление — это процесс деления числа на равные …
Подробнее
6.делить, делить, делимое, делитель — Математический словарь для детей
- Автор: www.amathsdictionaryforkids.com
- Пост Дата: 0 вчера
- Оценка: 3 (247 Обзоры)
- . Резюме: число на равные части.
 • делимое: делимое число. • делитель или множитель: число, на которое делимое точно делится. ПРИМЕРЫ:
• делимое: делимое число. • делитель или множитель: число, на которое делимое точно делится. ПРИМЕРЫ:
Подробнее
7.Дивиденд – определение, формула и важные правила – Веданту
- Автор: www.vedantu.com
- Дата поста: 26 вчера
- Оценка: 4 (715 Обзоры)
- СВОЙСТВЕННА Резюме: Делимое – это целое число или количество вещей, которые необходимо разделить на определенные равные части. Существует четыре основных операции над числами, называемыми …
См. подробности
8. Дивиденд – Math.net
- Автор: www.math.net
- Дата поста: 10 вчера
- Оценка: 4 (212 Обзоры)
- Высокий рейтинг: 4
- . Резюме: В контексте математики делимым называется число, которое делится в задаче на деление.

