Как решать функция: Ошибка: 404 Материал не найден

Содержание

Как решать типовые задачи при помощи функций в «МойОфис Таблица»

Электронные таблицы удобны для упорядочивания данных и незаменимы для вычислений. Рассмотрим несколько основных функций, которые помогут в решении повседневных задач.

Принцип ввода функций и основные понятия

Ввод любых формул в «МойОфис Таблица» всегда начинается с нажатия символа «=» (равно) и доступен как в строке формул, расположенной ниже меню команд, так и в самой ячейке таблицы. Например, если вы в ячейке D5 введете =A1+B2*C3, и затем нажмете клавишу [Enter], то редактор умножит содержимое ячейки B2 на C3, затем прибавит значение из ячейки A1 и отразит результат в ячейке D5.

В «МойОфис Таблица» при вводе формул пользователям также доступен ввод функций. Вы можете ввести функцию двумя способами: при помощи инструментов ячейки или панели инструментов. В первом случае вам потребуется выполнить следующие действия:

выделите ячейку, в которую необходимо ввести функцию,

в строке формул или в ячейке введите «=»,
начните вводить название функции, чтобы вызвать список с подсказками,

кликните мышкой по нужному названию и введите аргументы функции,
завершите ввод функции, нажав зеленую галочку в правом верхнем углу таблицы или клавишу [Enter].

Чтобы ввести функцию через боковую панель таблицы, вам также нужно начать с выделения ячейки и ввода знака «=». Далее вам потребуется развернуть панель формул одним из следующих способов:

выберите пункт командного меню «Вставка»> «Формулы»,
на боковой панели или в строке для ввода формул нажмите кнопку fx.

Как и в первом случае, выберите нужную функцию, введите аргументы и завершите ввод функции зеленым значком или клавишей [Enter].

Функция СУММ

Предположим, что вы ведете проект и вам нужно рассчитать, сколько времени ваша команда на него потратила и сколько дней осталось до сдачи.

Выделим ячейку, где должен располагаться результат вычислений.
Введем «=», щелкнем по ячейке с датой окончания проекта и введем «-» клавиатурой.
Кликнем на ячейку с датой начала проекта и добавим единицу, чтобы первый день работы над проектом учитывался, нажмем [Enter].

Мы работали с датами, поэтому и результат вычислений отображен в формате даты. Присвоим ячейке числовой формат и увидим, что команда работает над проектом 145 дней.

Если вы хотите применить функцию к другим периодам, просто «захватите» угловой маркер и протяните его вниз левой кнопкой мыши.

Теперь сложим дни всех периодов и рассчитаем общее количество использованных дней при помощи

функции СУММ. СУММ позволяет складывать не только отдельные значения, но и диапазоны ячеек, что особенно удобно при работе с большими массивами данных.

Поставим знак «=» в ячейке E2 и вызовем функцию СУММ.
Для суммирования диапазона ячеек кликнем на ячейку C2, которая содержит первое необходимое нам значение, поставим знак «:» и кликнем на последнюю ячейку диапазона – С4.

Нажмем [Enter] или зеленую галочку, чтобы завершить вычисление. Получилось 375 дней.

Чтобы просуммировать диапазон, вы также можете выделить диапазон ячеек мышкой или вбить номера ячеек вручную.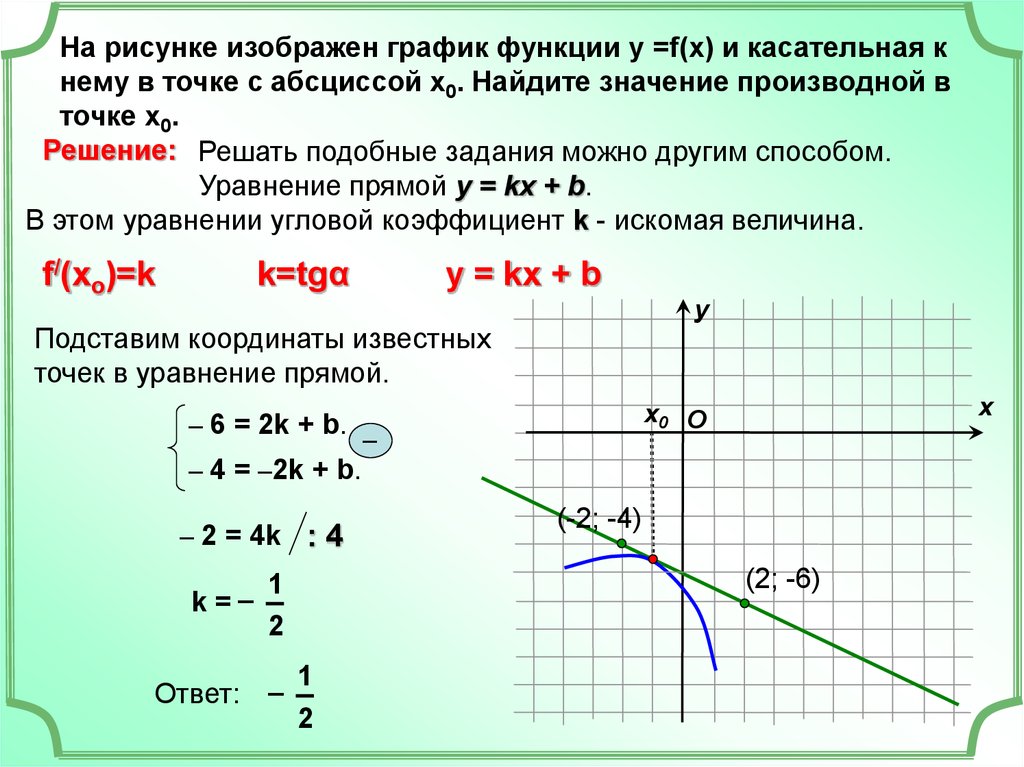

Функция СЕГОДНЯ

Теперь узнаем, сколько дней осталось до окончания работы над проектом и будем отслеживать эти изменения каждый день. Если мы введем число вручную, то придется обновлять данные каждый день. Чтобы всегда видеть текущую дату, используем функцию СЕГОДНЯ.

Введем знак «=» в нужной ячейке и введем название функции. Обратите внимание, что после ввода функции редактор ожидает ввод аргументов и самостоятельно добавляет открывающую скобку. Однако у функции СЕГОДНЯ их нет, и для завершения работы с ней достаточно просто нажать [Enter], после чего программа автоматически подставит закрывающую скобку и функция будет корректно работать.

Текущая дата появится в ячейке B1. В соседней ячейке B2 укажите дату сдачи проекта и рассчитайте количество оставшихся до дедлайна дней с помощью простой формулы. Для этого, вычтем из даты окончания дату начала — введите в ячейке B3 следующее выражение: =B2-B1 и нажмите [Enter].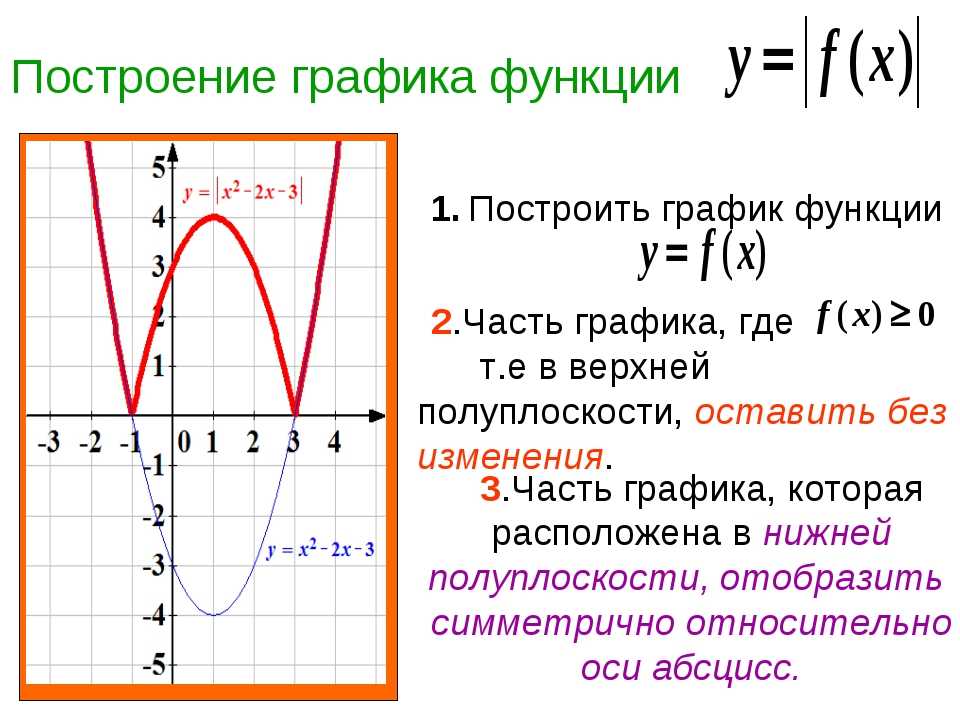

Чтобы увидеть количество дней, осталось только присвоить ячейке числовой формат. Теперь функция СЕГОДНЯ будет обновлять значение в ячейке B1 каждый день при открытии файла.

Функция ЕСЛИ

Допустим, ваша команда приняла участие в проверочном тесте, и вы хотите узнать, как много сотрудников набрали проходной балл. В этом поможет функция ЕСЛИ – она выполняет логические сравнения значений и ожидаемых результатов.

Зададим условие: если сотрудник набрал меньше 100 баллов, то будем считать, что он не справился с тестом. Если же баллов больше 100 – тест успешно пройден. Вынесем параметр – 100 – в отдельную ячейку для наглядности и отразим условия в аргументах функции ЕСЛИ, которую введем в ячейке С2 и нажмем [Enter].

Теперь в ячейке B2 появился результат «не пройден». Растянем эту ячейку, чтобы увидеть результаты других участников.

Если вы измените исходные данные, результат обновится автоматически.

График линейной функции y kx. Как решать линейные функции

1) Область определения функции и область значений функции .

Область определения функции — это множество всех допустимых действительных значений аргумента x (переменной x ), при которых функция y = f(x) определена. Область значений функции — это множество всех действительных значений y , которые принимает функция.

В элементарной математике изучаются функции только на множестве действительных чисел.

2) Нули функции .

Нуль функции – такое значение аргумента, при котором значение функции равно нулю.

3) Промежутки знакопостоянства функции .

Промежутки знакопостоянства функции – такие множества значений аргумента, на которых значения функции только положительны или только отрицательны.

4) Монотонность функции .

Возрастающая функция (в некотором промежутке) — функция, у которой большему значению аргумента из этого промежутка соответствует большее значение функции.

Убывающая функция (в некотором промежутке) — функция, у которой большему значению аргумента из этого промежутка соответствует меньшее значение функции.

5) Четность (нечетность) функции .

Четная функция — функция, у которой область определения симметрична относительно начала координат и для любого х из области определения выполняется равенство f(-x) = f(x) . График четной функции симметричен относительно оси ординат.

Нечетная функция — функция, у которой область определения симметрична относительно начала координат и для любого х из области определения справедливо равенство f(-x) = — f(x ). График нечетной функции симметричен относительно начала координат.

6) Ограниченная и неограниченная функции .

Функция называется ограниченной, если существует такое положительное число M, что |f(x)| ≤ M для всех значений x . Если такого числа не существует, то функция — неограниченная.

7) Периодическость функции .

Функция f(x) — периодическая, если существует такое отличное от нуля число T, что для любого x из области определения функции имеет место: f(x+T) = f(x). Такое наименьшее число называется периодом функции. Все тригонометрические функции являются периодическими. (Тригонометрические формулы).

19. Основные элементарные функции, их свойства и графики. Применение функ-ций в экономике.

Основные элементарные функции. Их свойства и графики

1. Линейная функция.

Линейной функцией называется функция вида , где х — переменная, а и b — действительные числа.

Число а называют угловым коэффициентом прямой, он равен тангенсу угла наклона этой прямой к положительному направлению оси абсцисс. Графиком линейной функции является прямая линия. Она определяется двумя точками.

Свойства линейной функции

1. Область определения — множество всех действительных чисел: Д(y)=R

2. Множество значений — множество всех действительных чисел: Е(у)=R

3. Функция принимает нулевое значение при или.

4. Функция возрастает (убывает) на всей области определения.

5. Линейная функция непрерывная на всей области определения, дифференцируемая и .

2. Квадратичная функция.

Функция вида , где х — переменная, коэффициенты а, b, с — действительные числа, называетсяквадратичной.

Инструкция

Если графиком является прямая линия, проходящая через начало координат и образующая с осью ОX угол α (угол наклона прямой к положительной полуоси ОХ). Функция, описывающая эту прямую, будет иметь вид y = kx. Коэффициент пропорциональности k равен tg α. Если прямая проходит через 2-ю и 4-ю координатные четверти, то k 0 и функция возрастает.Пусть представляет собой прямую линию, располагающуюся различным образом относительно осей координат. Это линейная функция, и она имеет вид y = kx + b, где переменные x и y стоят в первой степени, а k и b могут принимать как положительные, так и отрицательные значения или равны нулю.

Прямая параллельна прямой y = kx и отсекает на оси |b| единиц. Если прямая параллельна оси абсцисс, то k = 0, если оси ординат, то уравнение имеет вид x = const.

Кривая, состоящая из двух ветвей, располагающихся в разных четвертях и симметричных относительно начала координат, гиперболой. Этот график обратную зависимость переменной y от x и описывается уравнением y = k/x. Здесь k ≠ 0 — коэффициент пропорциональности. При этом если k > 0, функция убывает; если же k

Квадратичная функция имеет вид y = ax2 + bx + с, где a, b и c – величины постоянные и a  0. При выполнении условия b = с = 0, уравнение функции выглядит, как y = ax2 (простейший случай ), а ее график является параболой, проходящей через начало координат. График функции y = ax2 + bx + с имеет ту же форму, что и простейший случай функции, однако ее вершина (точка пересечения с осью OY) лежит не в начале координат.

Параболой является также график степенной функции, выраженной уравнением y = xⁿ, если n – любое четное число.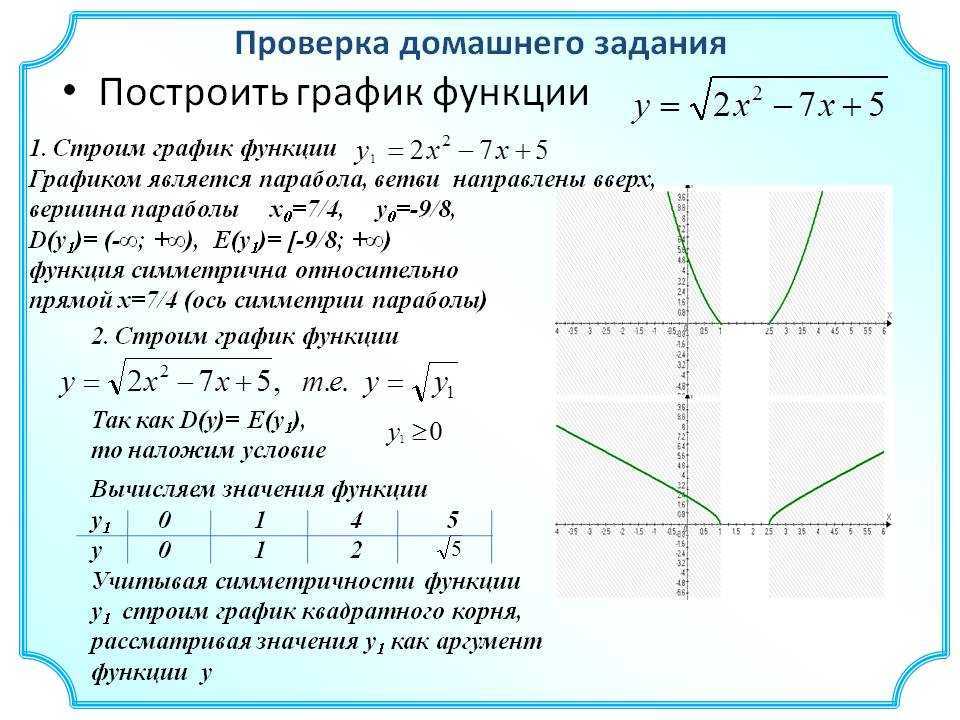 Если n — любое нечетное число, график такой степенной функции будет иметь вид кубической параболы.
В случае, если n – любое , уравнение функции приобретает вид. Графиком функции при нечетном n будет гипербола, а при четном n их ветви будут симметричны относительно оси ОУ.

Еще в школьные годы подробно изучаются функции и строятся их графики. Но, к сожалению, читать график функции и находить ее тип по представленному чертежу практически не учат. В действительности это довольно просто, если помнить основные виды функций.

Инструкция

Если представленным графиком является , которая через начало координат и с осью ОX угол α (который является углом наклона прямой к положительной полуоси), то функция, описывающая такую прямую, будет представлена как y = kx. При этом коэффициент пропорциональности k равен тангенсу угла α.

Если заданная прямая проходит через вторую и четвертую координатные четверти, то k равен 0, и функция возрастает. Пусть представленный график является прямой линией, располагающейся любым образом относительно осей координат.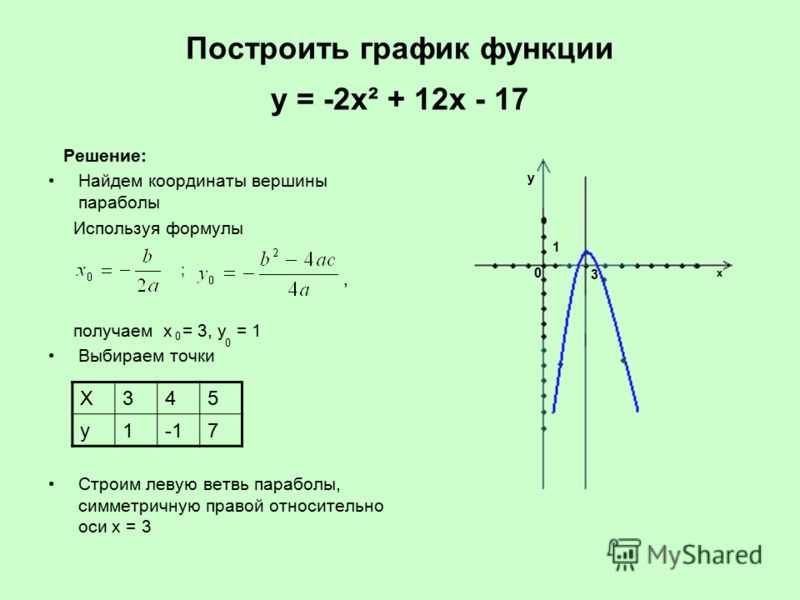 Тогда функцией такого графика будет линейная, которая представлена видом y = kx + b, где переменные y и х стоят в первой , а b и k могут принимать как отрицательные, так и положительные значения или .

Если прямая параллельна прямой с графиком y = kx и отсекает на оси ординат b единиц, тогда уравнение имеет вид x = const, если график параллелен оси абсцисс, то k = 0.

Кривая линия, которая состоит из двух ветвей, симметричных относительно начала координат и располагающихся в разных четвертях, гиперболой. Такой график показывает обратную зависимость переменной y от переменной x и описывается уравнением вида y = k/x, где k не должен быть равен нулю, так как является коэффициентом обратной пропорциональности. При этом, если значение k больше нуля, функция убывает; если же k меньше нуля – возрастает.

Если предложенным графиком является парабола, проходящая через начало координат, ее функция при выполнении условия, что b = с = 0, будет иметь вид y = ax2. Это самый простой случай квадратичной функции.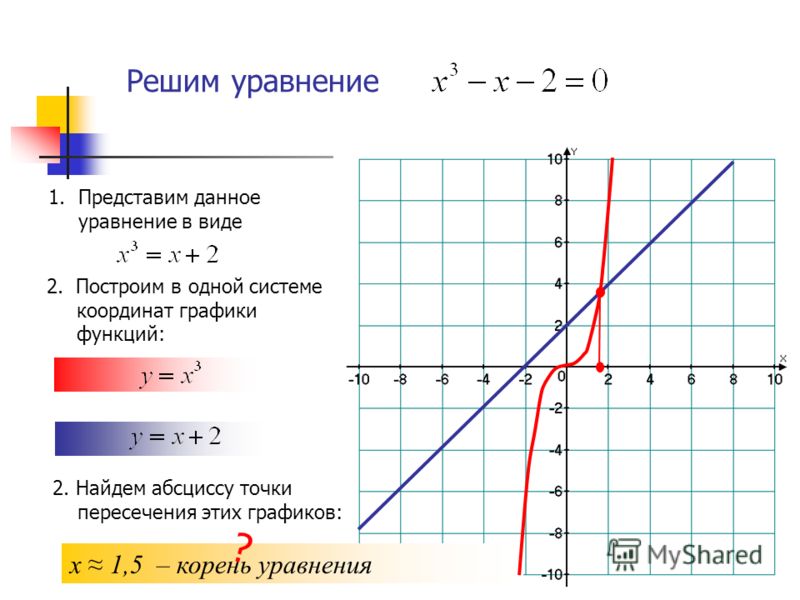 График функции вида y = ax2 + bx + с будет иметь такой же вид, что и простейший случай, однако вершина (точка, где график пересекается с осью ординат) будет находиться не в начале координат. В квадратичной функции, представленной видом y = ax2 + bx + с, значения величин a, b и c – постоянные, при этом a не равно нулю.

Параболой также может являться график степенной функции, выраженной уравнением вида y = xⁿ, только если n является любым четным числом. Если же значение n — нечетное число, такой график степенной функции будет представлен кубической параболой. В случае, если переменная n является любым отрицательным числом, уравнение функции приобретает вид .

Видео по теме

Координата абсолютно любой точки на плоскости определяется двумя ее величинами: по оси абсцисс и оси ординат. Совокупность множества таких точек и представляет собой график функции. По нему вы видите, как меняется значение Y в зависимости от изменения значения Х. Также вы можете определить, на каком участке (промежутке) функция возрастает, а на каком убывает.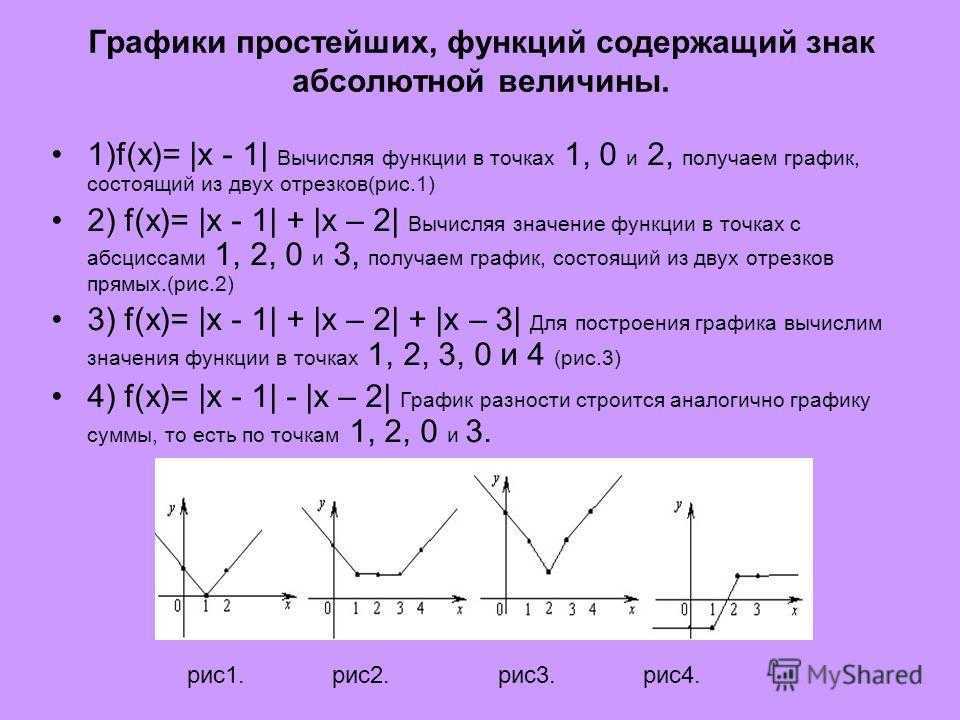

Инструкция

Что можно сказать о функции, если ее график представляет собой прямую линию? Посмотрите, проходит ли эта прямая через точку начала отсчета координат (то есть, ту, где величины Х и Y равны 0). Если проходит, то такая функция описывается уравнением y = kx. Легко понять, что чем больше будет значение k, тем ближе к оси ординат будет располагаться эта прямая. А сама ось Y фактически соответствует бесконечно большому значению k.

Линейная функция – это функция вида

x-аргумент (независимая переменная),

y- функция (зависимая переменная),

k и b- некоторые постоянные числа

Графиком линейной функции является прямая .

Для построения графика достаточно двух точек, т.к. через две точки можно провести прямую и притом только одну.

Если k˃0, то график расположен в 1-й и 3-й координатных четвертях. Если k˂0, то график расположен в 2-й и 4-й координатных четвертях.

Число k называют угловым коэффициентом прямой графика функции y(x)=kx+b.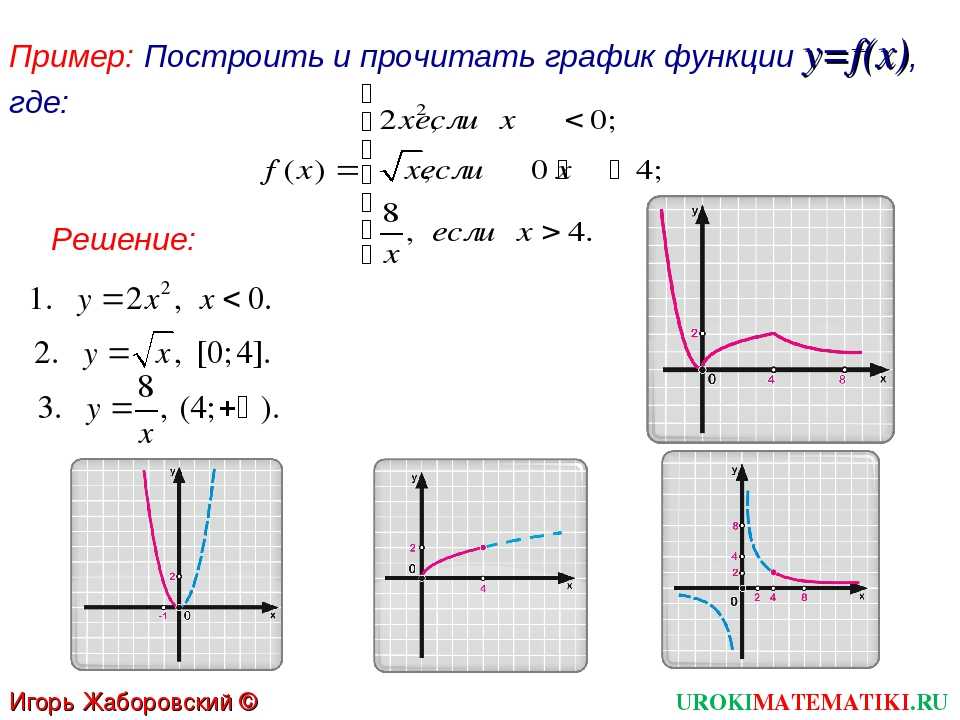 Если k˃0, то угол наклона прямой y(x)= kx+b к положительному направлению Ох — острый; если k˂0, то этот угол- тупой.

Коэффициент b показывает точку пересечения графика с осью ОУ (0; b).

y(x)=k∙x— частный случай типичной функции носит название прямая пропорциональность. Графиком является прямая, проходящая через начало координат, поэтому для построения этого графика достаточно одной точки.

График линейной функции

Где коэффициент k = 3, следовательно

График функции будет возрастать и иметь острый угол с осью Ох т.к. коэффициент k имеет знак плюс.

ООФ линейной функции

ОЗФ линейной функции

Кроме случая, где

Так же линейная функция вида

Является функцией общего вида.

Б) Если k=0; b≠0,

В этом случае графиком является прямая параллельная оси Ох и проходящая через точку (0;b).

В) Если k≠0; b≠0, то линейная функция имеет вид y(x)=k∙x+b.

Пример 1 . Построить график функции y(x)= -2x+5

Пример 2 .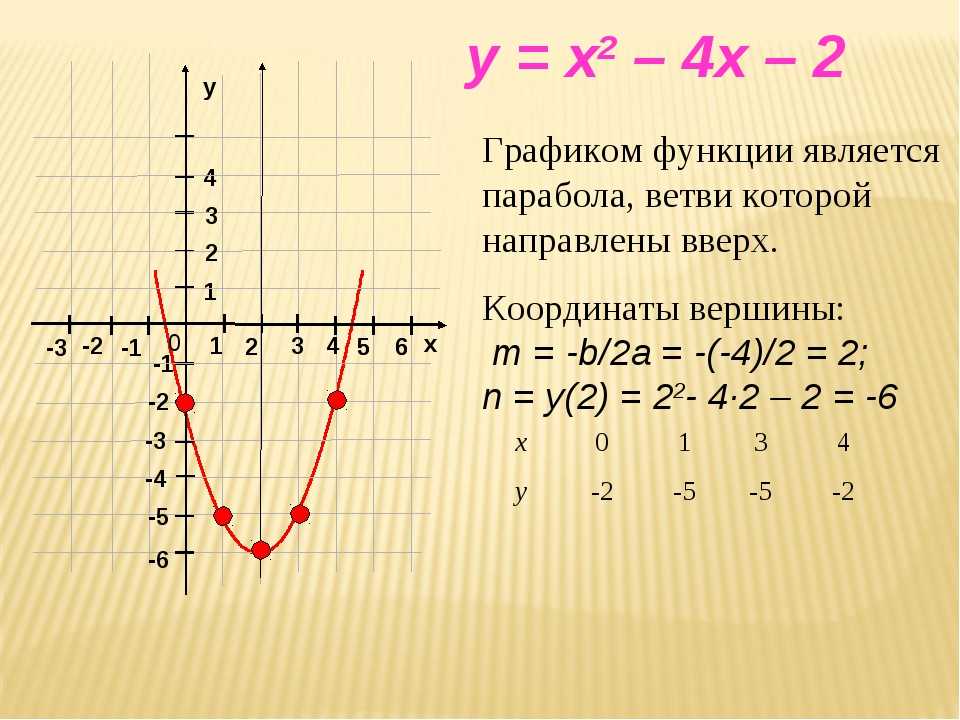 Найдём нули функции у=3х+1, у=0;

– нули функции.

Ответ: или (;0)

Пример 3 . Определить значение функции y=-x+3 для x=1 и x=-1

y(-1)=-(-1)+3=1+3=4

Ответ: y_1=2; y_2=4.

Пример 4 . Определить координаты их точки пересечения или доказать, что графики не пересекаются. Пусть даны функции y 1 =10∙x-8 и y 2 =-3∙x+5.

Если графики функций пересекаются, то значение функций в этой точке равны

Подставим х=1, то y 1 (1)=10∙1-8=2.

Замечание. Подставить полученное значение аргумента можно и в функцию y 2 =-3∙x+5, тогда получим тот же самый ответ y 2 (1)=-3∙1+5=2.

y=2- ордината точки пересечения.

(1;2)- точка пересечения графиков функций у=10х-8 и у=-3х+5.

Ответ: (1;2)

Пример 5 .

Построить графики функций y 1 (x)= x+3 и y 2 (x)= x-1.

Можно заметить, что коэффициент k=1 для обеих функций.

Из выше сказанного следует, что если коэффициенты линейной функции равны, то их графики в системе координат расположены параллельно.

Пример 6 .

Построим два графика функции.

Первый график имеет формулу

Второй график имеет формулу

В данном случае перед нами график двух прямых, пересекающихся в точке (0;4). Это значит, что коэффициент b, отвечающий за высоту подъёма графика над осью Ох, если х=0. Значит мы может полагать, что коэффициент bу обоих графиков равен 4.

Редакторы: Агеева Любовь Александровна, Гаврилина Анна Викторовна

Инструкция

Существует несколько способов решения линейных функций. Приведем наиболее из них. Чаще всего используется пошаговый метод подстановки. В одном из уравнений необходимо выразить одну переменную через другую, и подставить в другое уравнение. И так до тех пор, пока в одном из уравнений не останется лишь одна переменная. Чтобы решить его необходимо с одной стороны знака равенства оставить переменную (она может быть с коэффициентом), а на другую сторону знака равенства все числовые данные, не забыв при переносе поменять знак числа на противоположный.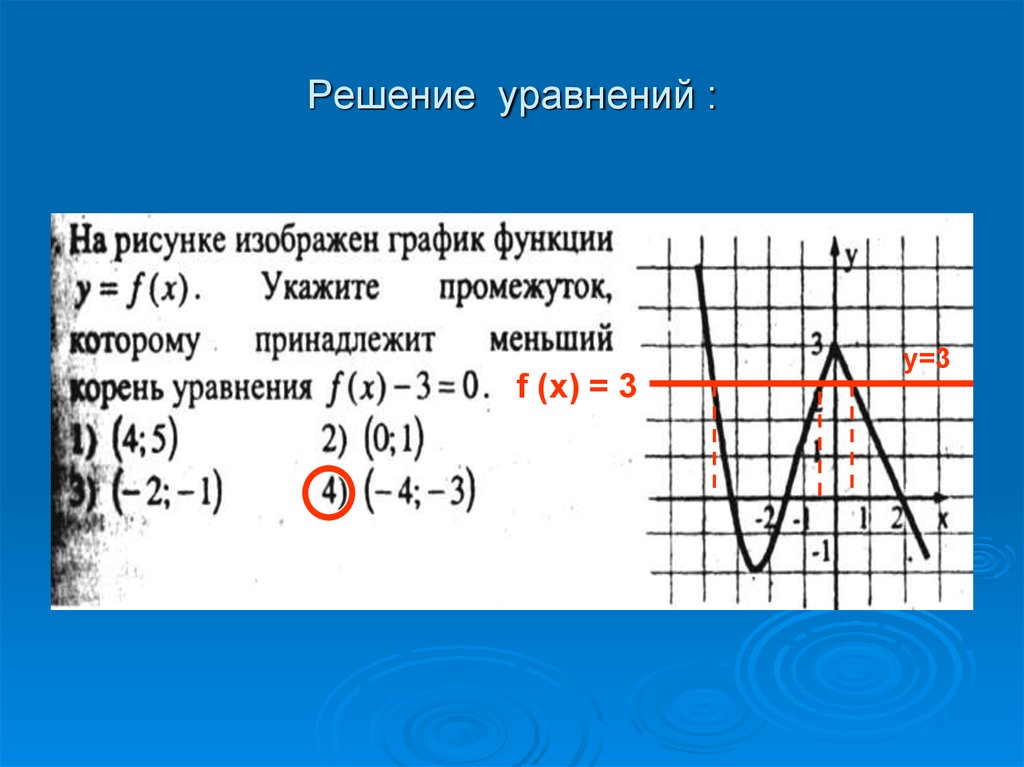 Вычислив одну переменную, подставьте ее в другие выражения, продолжите вычисления по такому же алгоритму.

Для примера возьмем систему линейной функции , состоящую из двух уравнений:
2х+у-7=0;
х-у-2=0.
Из второго уравнения удобно выразить х:
х=у+2.
Как видите, при переносе из одной части равенства в другую, у и переменных поменялся знак, как и было описано выше.
Подставляем полученное выражение в первое уравнение, таким образом исключая из него переменную х:
2*(у+2)+у-7=0.
Раскрываем скобки:
2у+4+у-7=0.
Компонуем переменные и числа, складываем их:
3у-3=0.
Переносим в правую часть уравнения, меняем знак:
3у=3.
Делим на общий коэффициент, получаем:
у=1.
Подставляем полученное значение в первое выражение:
х=у+2.
Получаем х=3.

Еще один способ решения подобных — это почленное двух уравнений для получения нового с одной переменной. Уравнение можно умножить на определенный коэффициент, главное при этом умножить каждый член уравнения и не забыть , а затем сложить или вычесть одно уравнение из .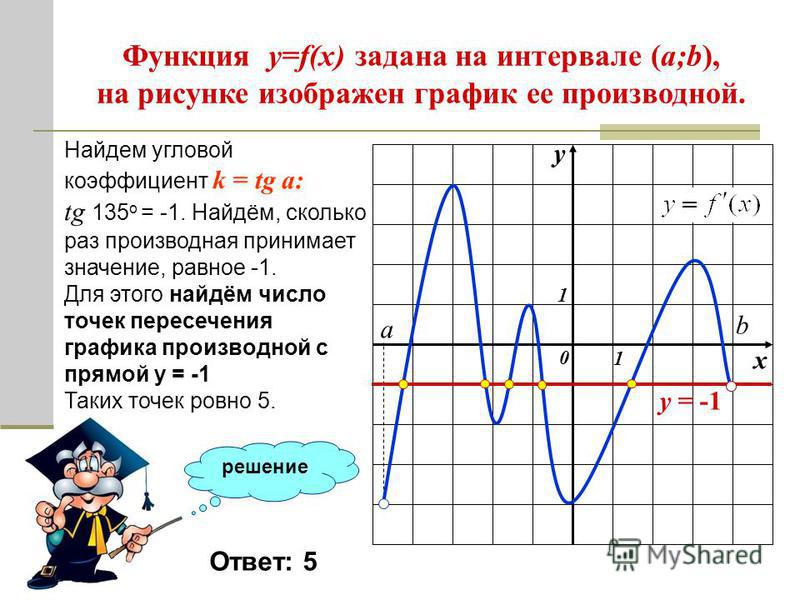 Этот метод очень экономит при нахождении линейной функции .

Возьмем уже знакомую нам систему уравнений с двумя переменными:
2х+у-7=0;
х-у-2=0.
Легко заметить что коэффициент при переменной у идентичен в первом и втором уравнении и отличается лишь знаком. Значит, при почленном сложении двух этих уравнений мы получим новое, но уже с одной переменной.
2х+х+у-у-7-2=0;
3х-9=0.
Переносим числовые данные на правую сторону уравнения, меняя при этом знак:
3х=9.
Находим общий множитель, равный коэффициенту, стоящему при х и дели обе части уравнения на него:
х=3.
Полученный можно подставить в любое из уравнений системы, чтобы вычислить у:
х-у-2=0;
3-у-2=0;
-у+1=0;
-у=-1;
у=1.

Также вы можете вычислять данные, построив точный график. Для этого необходимо найти нули функции . Если одна из переменных равняется нулю, то такая функция называется однородной. Решив такие уравнения, вы получите две точки, необходимые и достаточные для построения прямой — одна из них будет располагаться на оси х, другая на оси у.

Берем любое уравнение системы и подставляем туда значение х=0:
2*0+у-7=0;
Получаем у=7. Таким образом первая точка, назовем ее А, будет иметь координаты А(0;7).
Для того чтобы вычислить точку, лежащую на оси х, удобно подставить значение у=0 во второе уравнение системы:
х-0-2=0;
х=2.
Вторая точка (В) будет иметь координаты В (2;0).
На координатной сетке отмечаем полученные точки и поводим через них прямую. Если вы построите ее довольно точно, другие значения х и у можно будет вычислять прямо по ней.

Гипербола. График функции и свойства.

теория по математике 🎲 функции

Определение

Графиком функции у=kx.., где k≠0 число, а х – переменная, является кривая, которую называют гиперболой.

Гипербола имеет две ветви и может располагаться в 1 и 3 координатных четвертях, либо во 2 и 4. Это зависит от знака числа k. Рассмотрим данную кривую на рисунке, где показано ее расположение в зависимости от знака k.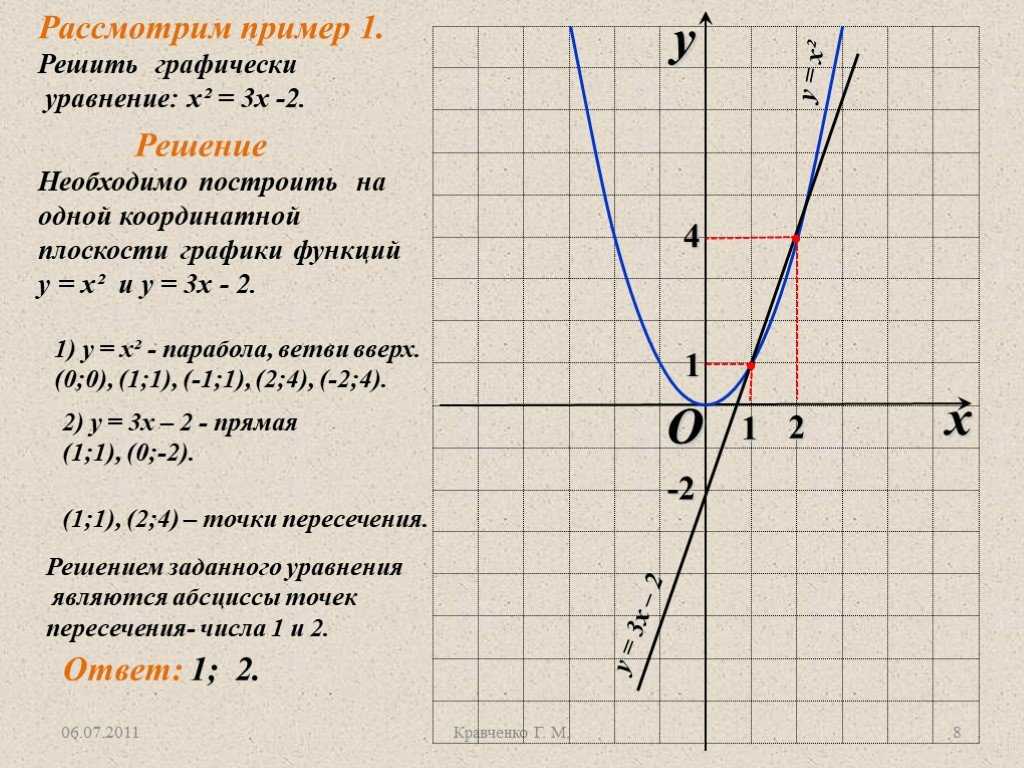

График функции симметричен относительно начала координат (0;0). Поэтому функцию еще называют – обратная пропорциональность.

Область определения – любое число, кроме нуля.
Область значения – любое число, кроме нуля.
Функция не имеет наибольших или наименьших значений.

Построение графика функции

Для построения графика функции необходимо подбирать несколько положительных и несколько отрицательных значений переменной х, затем подставлять их в заданную функцию для вычисления значений у. После этого по найденным координатам построить точки и соединить их плавной линией. Рассмотрим построение графиков на примерах.

Построить график функции у=10x…

Для этого построим две таблицы для положительных и отрицательных значений х. Подбирать желательно такие значения х, чтобы число 10 на них делилось

х	1	2	4	5	10
у

х	–1	–2	–4	–5	–10
у

Теперь делим на эти числа 10, получим значения у:

х	1	2	4	5	10
у	10	5	2,5	2	1

х	–1	–2	–4	–5	–10
у	–10	–5	–2,5	–2	–1

Выполняем построение точек, они будут располагаться в первой и третьей координатных четвертях, так как число k положительное.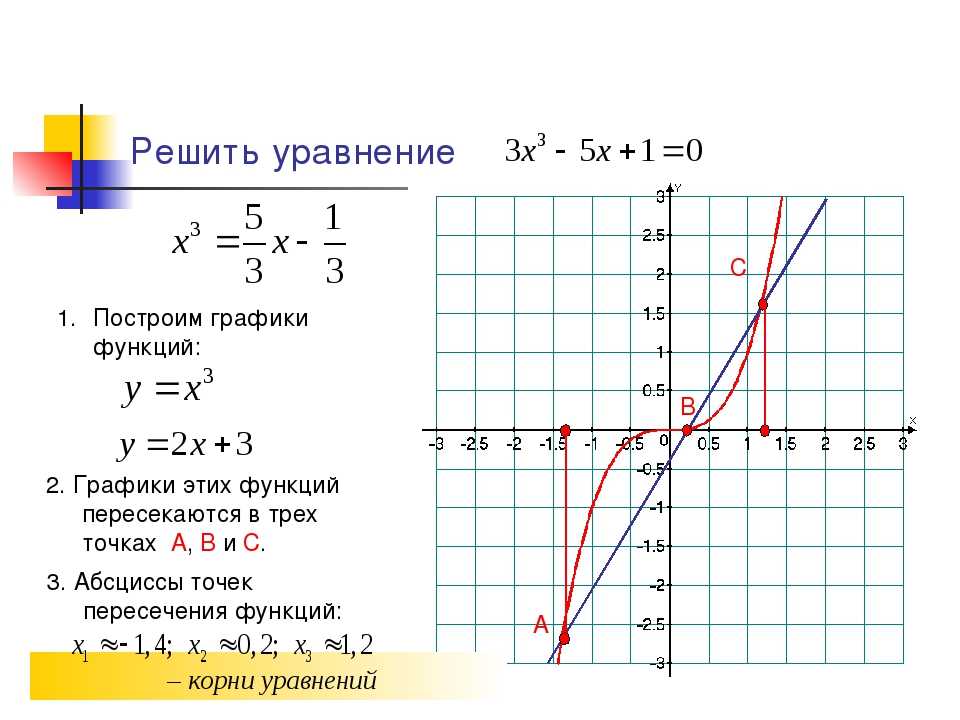

Теперь для построения гиперболы соединим точки плавной линией.

Построить график функции у=−5x…

Для этого построим также две таблицы для положительных и отрицательных значений х. Подбирать желательно такие значения х, чтобы число минус 5 на них делилось. Выполняем деление и получаем значения у. При делении обращаем внимание на знаки, чтобы не допускать ошибок.

х	1	2	5	10
у	–5	–2,5	–1	–0,5

х	–1	–2	–5	–10
у	5	2,5	1	0,5

Теперь отмечаем точки во 2 и 4 координатных четвертях (число k отрицательное) и соединяем их для получения ветвей гиперболы.

Задание OM1104o

Установите соответствие между графиками функций и формулами, которые их задают.

1) y = x²

2) y = x/2

3) y = 2/x

Для решения данной задачи необходимо знать вид графиков функций, а именно:

y = x² – парабола, в общем виде это y = ax²+bx+c, но в нашем случае b = c = 0, а а = 1

x/2 – прямая, в общем виде график прямой имеет вид y = ax + b, в нашем случае b = 0, а = 1/2

y = 2/x – гипербола, в общем виде график функции y = a/x + b, в данном примере b = 0, a = 2

Парабола изображена на рисунке А, гипербола на рисунке Б, а прямая – В.

Ответ:

А 1

Б 3

В 2

Ответ: 132

pазбирался: Даниил Романович | обсудить разбор | оценить

Задание OM1102o

Установите соответствие между функциями и их графиками.

Функции:

A) y = -3/x

Б) y = 3/x

В) y = 1/(3x)

Графики:

В данной ситуации можно воспользоваться двумя подходами — можно руководствоваться общими соображениями, а можно просто решить задачу подстановкой. Я рекомендую решать задачу общими соображениями, а проверять подстановкой.

Общие правила:

если уравнение гиперболы положительное (то есть не стоит знак -, как во втором и третьем случае), то график функции лежит в первой и третьей координатной четверти
если перед уравнением гиперболы стоит знак — (как в первом случае), то график лежит во второй и четвертой четвертях

Таким образом можно сразу определить, что первое уравнение соответствует графику под номером 2.

Второе правило, которым я пользуюсь, звучит так:

чем больше число в знаменателе гиперболы (рядом с x), тем сильнее гипербола жмется к осям координатной плоскости

и наоборот:

чем больше число в числителе уравнения гиперболы, тем слабее и медленнее график функции прижимается к осям

Следовательно, функция Б слабее прижимается к осям и ей соответствует график 3, а функции В соответствует график 1, так как она сильнее прижимается к осям.

Ответ:

A) 2

Б) 3

В) 1

Ответ: 231

pазбирался: Даниил Романович | обсудить разбор | оценить

Даниил Романович | Просмотров: 6.4k | Оценить:

Решение уравнений с абсолютными значениями — ChiliMath

Решение уравнений абсолютного значения так же просто, как работа с обычными линейными уравнениями. Единственный дополнительный ключевой шаг, который вам нужно запомнить, — это разделить исходное уравнение абсолютного значения на две части: положительную и отрицательную ( ± ) составляющие.

Ниже приведен общий подход к тому, как разбить их на два уравнения:

Кроме того, нам также необходимо помнить о следующих ключевых моментах относительно приведенной выше настройки:

Ключевой момент № 2: X внутри символа абсолютного значения, \left| {\,\,\,\,\,} \right|, могут быть любыми выражениями.

Ключевой момент № 3: a в правой части уравнения должно быть либо положительным числом , либо нулем , чтобы было решение.

Ключевой момент № 4: Если a в правой части является отрицательным числом , то оно не имеет решения.

Примеры решения уравнения абсолютного значения

Пример 1: Решите уравнение абсолютного значения \left| х \ справа | =\, — 5 .

Абсолютное значение любого числа либо положительное, либо нулевое. Но это уравнение предполагает, что существует число, абсолютное значение которого отрицательно. Можете ли вы придумать какие-либо числа, которые могут сделать уравнение верным? Нет его.

Поскольку нет значения x, удовлетворяющего уравнению, мы говорим, что оно имеет нет решения .

Фактически, следующие уравнения абсолютного значения также не имеют решений.

Пример 2: Решите уравнение абсолютного значения — \left| х \ справа | =\, — 5 .

Не спешите делать вывод, что это уравнение не имеет решения. Хотя правая часть уравнения отрицательна, само выражение абсолютного значения должно быть положительным. Но это не так, верно?

Прежде чем мы сможем продолжить, нам нужно удалить отрицательный знак символа абсолютного значения.

Заметим, что данное уравнение имеет коэффициент −1 . Разделите обе части уравнения на это значение, чтобы избавиться от отрицательного знака.

Поскольку выражение абсолютного значения и число оба положительны, теперь мы можем применить процедуру, чтобы разбить его на два уравнения.

Следовательно, решение задачи становится

Вы можете проверить наши ответы, подставив их обратно в исходное уравнение. Я оставлю это вам.

Пример 3: Решите уравнение абсолютного значения \left| {х — 5} \право| = 3 .

Эта проблема становится интересной, поскольку выражение внутри символа абсолютного значения больше не является просто одной переменной. Не волнуйся; установка остается прежней. Просто будьте осторожны, когда вы разбиваете заданное уравнение абсолютного значения на два более простых линейных уравнения, а затем действуйте, как вы обычно решаете уравнения.

Вы можете сверить ответы с исходным уравнением.

Пример 4: Решите уравнение абсолютного значения \left| { — 2x + 7} \право| = 25 .

Вы можете подумать, что эта задача сложная из-за -2 рядом с переменной x. Однако это не должно вас пугать, потому что ключевая идея остается прежней. У нас есть символ абсолютного значения, изолированный с одной стороны, и положительное число с другой. Решение этой проблемы похоже на еще один день в парке!

Разбейте его на компоненты + и -, затем решите каждое уравнение.

Пример 5 : Решить уравнение абсолютного значения \left| { — 6x + 3} \право| — 7 = 20.

Этот не готов еще не разделен на два компонента. Почему? Это потому, что символ абсолютного значения сам по себе не находится на одной стороне уравнения. Если вы посмотрите на это, слева будет -7 , которую нужно устранить в первую очередь. Как только мы избавимся от этого, мы сможем продолжать как обычно.

Удалите -7 с левой стороны, добавив с обеих сторон \color{blue}7.

Теперь у нас есть уравнение абсолютного значения, которое можно разбить на две части.

Пример 6 : Решить уравнение абсолютного значения — 7\left| {9\, — 2x} \право| + 9 =\, — 12.

Выражение абсолютного значения еще не изолировано. Удалите сначала +9, а затем -7, которые в настоящее время умножают выражение абсолютного значения.

Теперь давайте разделим их на два случая и решим каждое уравнение. 92} + 2x — 4} \право| = 4.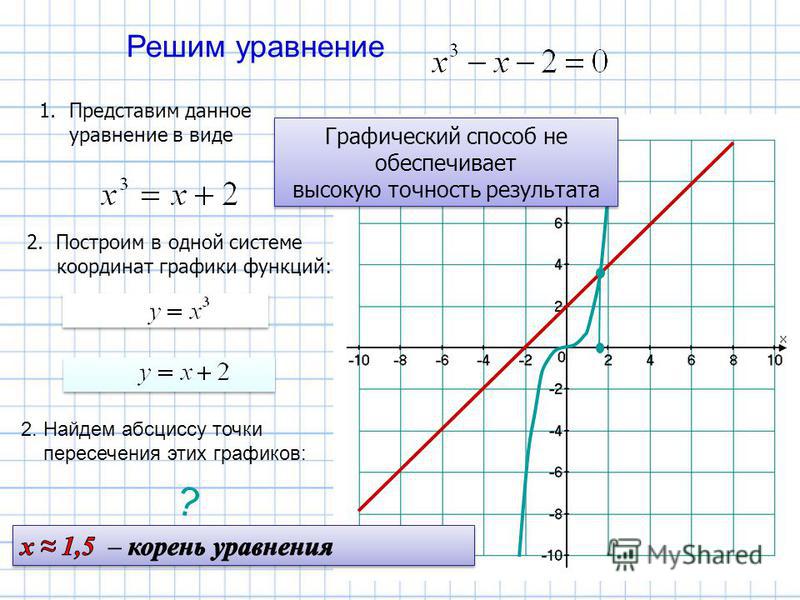

Это интересная задача, потому что у нас есть квадратное выражение внутри символа абсолютного значения. Надеюсь, вас не отвлекает то, как это выглядит! Если вы столкнулись с ситуацией, в которой вы не знаете, как поступить, придерживайтесь основ и вещей, которые вы уже знаете.

Нам все равно, что внутри символа абсолютного значения. Пока оно изолировано, а другая сторона является положительным числом, мы определенно можем применить правило, чтобы разделить уравнение на два случая.

На самом деле, единственное отличие этой задачи от того, что вы делали до сих пор, заключается в том, что вы будете решать квадратные уравнения, а не линейные уравнения.

Мы можем убедиться, что наши четыре ответа или решения равны x = -1,4,-2, 0 и 2, построив графики двух функций и посмотрев на их точки пересечения.

Вас также могут заинтересовать:

Сложные уравнения с абсолютными значениями

Графики функций с абсолютными значениями
Решение неравенств с абсолютными значениями

Решение логарифмических функций — объяснение и примеры

В этой статье мы узнаем, как вычислять и решать логарифмические функции с неизвестными переменными.

Логарифмы и экспоненты — две тесно связанные темы в математике. Поэтому полезно сделать краткий обзор показателей.

Показатель степени — это форма записи многократного умножения числа на себя. Показательная функция имеет вид f (x) = b ^y , где b > 0 < x и b ≠ 1. Величина x — это число, b — основание, а y — показатель степени или степень.

Например, , 32 = 2 × 2 × 2 × 2 × 2 = 2 ² .

Экспоненциальная функция 2 ² читается как « два в степени пяти » или « два в степени пять » или « два в пятой степени». ”

С другой стороны, логарифмическая функция определяется как обратная функция возведения в степень. Рассмотрим снова экспоненциальную функцию f(x) = b ^y , где b > 0 < x и b ≠ 1. Мы можем представить эту функцию в логарифмической форме как:

y = log _b x

Тогда логарифмическая функция имеет вид;

f(x) = log _b x = y, где b — основание, y — показатель степени, x — аргумент.

Функция f (x) = log _b x читается как «логарифмическая база b числа x». Логарифмы полезны в математике, потому что они позволяют нам производить вычисления с очень большими числами.

Для решения логарифмических функций важно использовать показательные функции в данном выражении. Натуральное бревно или в является инверсией e . Это означает, что можно отменить другое, то есть

ln (e ^x) = x

e ^{ln x} = x

Чтобы решить уравнение с логарифмами, важно знать их свойства.

Свойства логарифмических функций

Свойства логарифмических функций — это просто правила упрощения логарифмов, когда входные данные представлены в форме деления, умножения или возведения в степень логарифмических значений.

Некоторые свойства перечислены ниже.

Правило произведения

Правило произведения логарифма гласит, что логарифм произведения двух чисел, имеющих общее основание, равен сумме индивидуальных логарифмов.

⟹ log _a (p q) = log _a p + log _a q.

Правило частных

Правило частных логарифмов гласит, что логарифм отношения двух чисел с одинаковыми основаниями равен разности каждого логарифма.

⟹ log _a (p/q) = log _a p – log _a q

Степенное правило

равно произведению показателя степени на ее логарифм.

⟹ log _A (стр. ^Q) = Q log _A P

Изменение базового правила

⟹ log _A P = log _{x 9016 P ⋅ 9016 P ⋅ 9016 P ro log _A P = log _{x 9016 x 9016 P ⋅ 9016.0161 a} x}

⟹ log _q p = log _x p / log _x q

Zero Exponent Rule

⟹ log _p 1 = 0.

Other properties of логарифмические функции включают:

Основания экспоненциальной функции и эквивалентной ей логарифмической функции равны.
Логарифмы положительного числа по основанию того же числа равны 1.

log _A A = 1

Логарифмы 1 к любой базе: 0.

log _A 1 = 0

log _A 0 — это не определено _a 0. — это не определено _A 0.
Основание логарифма никогда не может быть отрицательным или равным 1.
Логарифмическая функция с основанием 10 называется десятичным логарифмом. Всегда принимайте основание 10 при решении с логарифмическими функциями без маленького нижнего индекса для основания.

Сравнение экспоненциальной функции и логарифмической функции

Всякий раз, когда вы видите логарифмы в уравнении, вы всегда думаете о том, как отменить логарифм, чтобы решить уравнение. Для этого вы используете экспоненциальную функцию . Обе эти функции взаимозаменяемы.

В следующей таблице указан способ записи и перестановки экспоненциальных функций и логарифмических функций .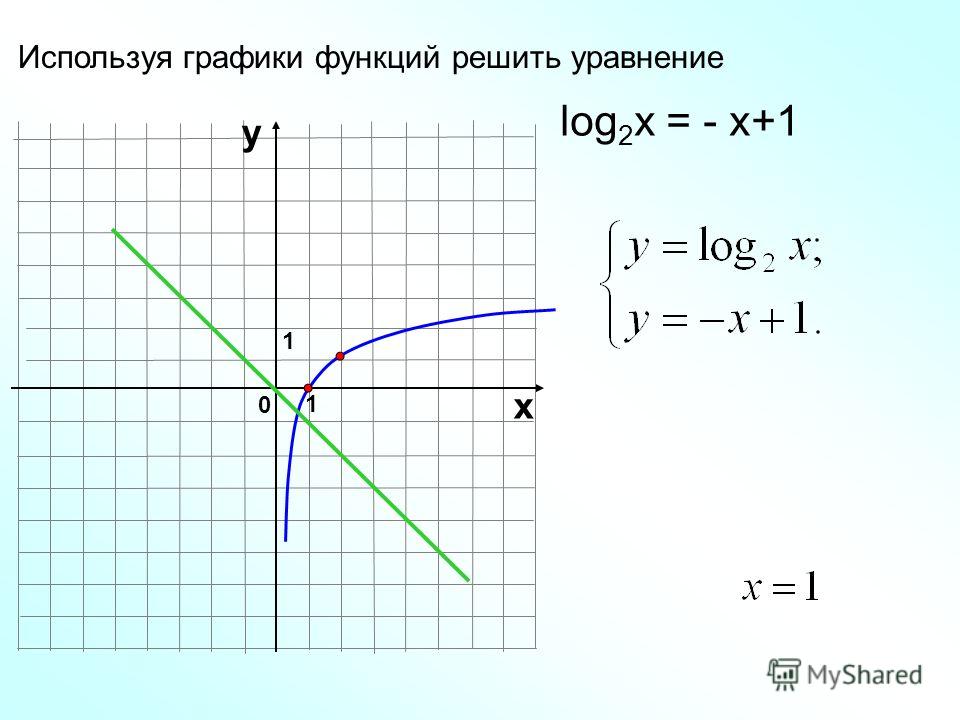 В третьем столбце рассказывается о том, как читать обе логарифмические функции.

Exponential function	Logarithmic function	Read as
8 ² = 64	log ₈ 64 = 2	log base 8 of 64
10 ³ = 1000	log 1000 = 3	log base 10 of 1000
10 ⁰ = 1	log 1 = 0	log base 10 of 1
25 ^{2 =} 625	log ₂₅ 625 = 2	log base 25 of 625
12 ² = 144	log ₁₂ 144 = 2	log base 12 of 144

Давайте воспользуемся этими свойствами для решения нескольких задач, связанных с логарифмическими функциями.

Пример 1

Преобразуйте экспоненциальную функцию 7 ² = 49 в эквивалентную ей логарифмическую функцию.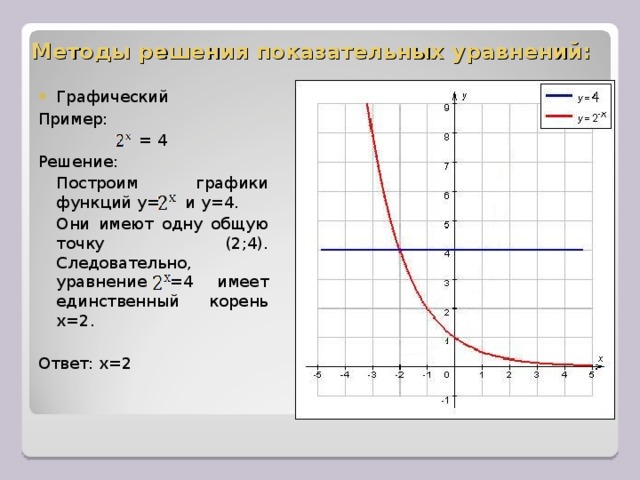

Решение

Дано 7 ² = 64.

Здесь основание = 7, показатель степени = 2 и аргумент = 49. Следовательно, 7 ² = 64 в логарифмической функции есть;

⟹ log ₇ 49 = 2

Пример 2

Напишите логарифмический эквивалент 5 ³ = 125.

Solution

= 55.

Раствор

= 5; 5; 5; 5; 5; 5; 5; 5; 5; 5; 5; 5; 5; 5; 5; 5; 5; 5; 5; 5; 5;

показатель степени = 3;

и аргумент = 125

5 ³ = 125 ⟹ log ₅ 125 = 3

Пример 3

Решение для x in log ₃ x = 2

раствор

_{_{2 _{2 _{2 _{2 _{2 _{2 _{2 _{2 _{2 _{2 _{2 _{2 _{2 _{2 _{2 _{2 _{2 _{2 _{2 _{2 _{2
. ² = x
⟹ x = 9
Пример 4
Если 2 log x = 4 log 3, то найдите значение «x».
Решение
2 log x = 4 log 3
Разделите каждую сторону на 2.
log x = (4 log 3) / 2
log x = 2 log 3
log x = log 3 ²
log x = log
x =
Пример 5
Найдите логарифм 1024 на базу 2.
Решение
1024 = 2 ¹⁰
log ₂ 1024 = 10
Пример 6
Найти значение X в Log ₂
.
Раствор
Переписать логарифмическую функцию log ₂ ( x ) = 4 в экспоненциальную форму.
2 ⁴ = x
16 = x
Пример 7
Решение для x в следующем логарифментном журнале ₂
(x – 1) = 5.
116 (x – 1) = 5.
161 (x –1
6 (x –1 (x – 1) =
16 (x – 1) =
6 (x – 1). Решение
Перепишите логарифм в экспоненциальной форме как;
логарифм ₂ (х – 1) = 5 ⟹ х – 1 = 2 ⁵
Теперь найдите x в алгебраическом уравнении.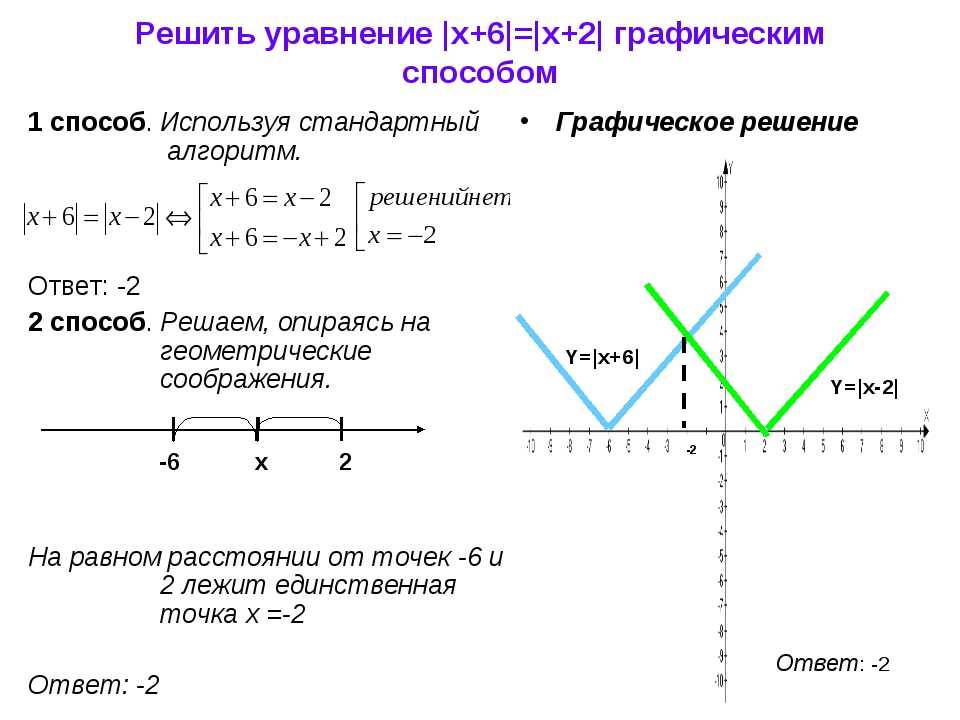 Пример 8
Найдите значение x в log x 900 = 2.
x ² = 900
Найдите квадратный корень из обеих частей уравнения, чтобы получить;
x = -30 и 30
Но так как основание логарифма никогда не может быть отрицательным или равным 1, то правильный ответ 30.
Example 9
Solve for x given, log x = log 2 + log 5
Solution
Using the product rule Log _b (m n) = log _b m + log _b n получаем;
⟹ журнал 2 + журнал 5 = журнал (2 * 5) = журнал (10). Пример 100002 Перепишите логарифм в экспоненциальной форме, чтобы получить;
x ² = 4x – 3
Теперь решите квадратное уравнение.
x ² = 4x – 3
x ² – 4x + 3 = 0
(x -1) (x – 3) = 0
x = 1 или 3
Поскольку основание логарифма никогда не может быть 1, то единственным решением будет 3.

Как использовать поиск цели и решатель Excel для поиска неизвестных переменных
Excel — мощный инструмент, когда ваши данные полны. Но было бы неплохо, если бы он мог найти неизвестные переменные ?
С Goal Seek и надстройкой Solver это возможно. И мы покажем вам, как это сделать. Читайте полное руководство о том, как решить одну ячейку с помощью Goal Seek или более сложное уравнение с помощью Solver.
Как использовать поиск цели в Excel
Поиск цели уже встроен в Excel. Он находится на вкладке Data в меню What-If Analysis :
В этом примере мы будем использовать очень простой набор чисел. У нас есть данные о продажах за три квартала и цель на год. Мы можем использовать поиск цели, чтобы выяснить, какие числа должны быть в Q4, чтобы достичь цели.
Как видите, текущий объем продаж составляет 114 706 единиц. Если мы хотим продать 250 000 к концу года, сколько нам нужно продать в четвертом квартале? Поиск цели Excel расскажет нам.
Вот как использовать поиск цели, шаг за шагом:
Щелкните Данные > Анализ возможных вариантов > Поиск цели . Появится окно поиска цели.
Поместите «равно» часть вашего уравнения в поле Установить ячейку . Это число, которое Excel попытается оптимизировать. В нашем случае это промежуточная сумма продаж в ячейке A5.
Введите значение цели в поле До значения . Мы ищем в общей сложности 250 000 проданных единиц, поэтому мы поместим «250 000» в это поле.
Сообщите Excel, какую переменную нужно найти в поле . Путем изменения поля ячейки . Мы хотим увидеть, какими должны быть наши продажи в четвертом квартале. Итак, мы скажем Excel решить для ячейки D2. Когда он будет готов к работе, он будет выглядеть так:
Нажмите OK , чтобы решить свою задачу. Когда все выглядит хорошо, просто нажмите OK . Excel сообщит вам, когда Goal Seek найдет решение.
Щелкните OK еще раз, и вы увидите значение, которое решает ваше уравнение, в ячейке, которую вы выбрали для . Путем изменения ячейки .
В нашем случае решение составляет 135 294 единицы. Конечно, мы могли бы просто найти это, вычтя промежуточную сумму из годовой цели. Но поиск цели также можно использовать в ячейке, в которой уже есть данные . И это более полезно.
Обратите внимание, что Excel перезаписывает наши предыдущие данные. Это хорошая идея запустить поиск цели на копии ваших данных . Также неплохо отметить в скопированных данных, что они были сгенерированы с помощью поиска цели. Вы не хотите путать его с текущими, точными данными.
Итак, поиск цели — полезная функция Excel, но она не так уж впечатляет. Вы можете использовать его только в одной ячейке за раз. Если вы хотите использовать поиск цели Excel одновременно в нескольких ячейках, вам понадобится гораздо более мощный инструмент. К счастью, один из таких инструментов поставляется вместе с Excel. Давайте посмотрим на надстройку Solver.
Что делает решатель Excel?
Короче говоря, Solver похож на многомерную версию Goal Seek . Если вам интересно, как использовать поиск цели в Excel для нескольких ячеек одновременно, вот оно. Он берет одну целевую переменную и регулирует ряд других переменных, пока не получит желаемый ответ.
Он может найти максимальное значение числа, минимальное значение числа или точное число. И он работает в пределах ограничений, поэтому, если одна переменная не может быть изменена или может изменяться только в указанном диапазоне, Solver примет это во внимание.
Это отличный способ найти несколько неизвестных переменных в Excel. Но найти и использовать его не так просто. Давайте взглянем на загрузку надстройки «Поиск решения», а затем перейдем к тому, как использовать «Поиск решения» в текущей версии Microsoft 365 Excel.
Как загрузить надстройку Solver
Excel не имеет Решателя по умолчанию.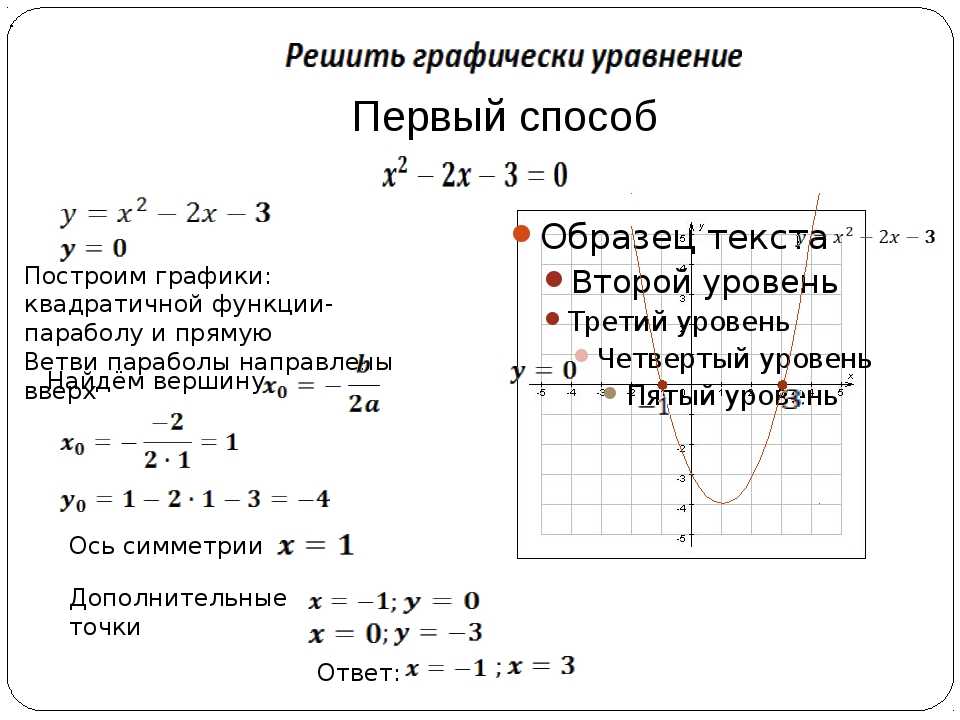 Это надстройка, поэтому сначала ее нужно загрузить. К счастью, он уже есть на вашем компьютере.
Перейдите к Файл > (Дополнительно… >) Параметры > Надстройки . Затем нажмите Перейти рядом с Управление: надстройки Excel .
Если в этом раскрывающемся списке указано что-то отличное от «Надстройки Excel», вам нужно изменить его:
В появившемся окне вы увидите несколько вариантов. Убедитесь, что установлен флажок рядом с надстройкой Solver , и нажмите OK .
Теперь вы увидите кнопку Solver в группе Analysis на вкладке Data :
Если вы уже использовали пакет инструментов анализа данных, вы увидите кнопку Анализ данных. Если нет, Solver появится сам по себе.
Теперь, когда вы загрузили надстройку, давайте посмотрим, как ее использовать.
Как использовать решатель в Excel
Любое действие Решателя состоит из трех частей: цель, переменные ячейки и ограничения. Мы пройдемся по каждому из шагов.
Щелкните Данные > Решатель . Ниже вы увидите окно Solver Parameters. (Если вы не видите кнопку решателя, см. предыдущий раздел о том, как загрузить надстройку «Поиск решения».)
Установите цель ячейки и сообщите Excel свою цель. Цель находится в верхней части окна Решателя и состоит из двух частей: ячейка цели и выбор максимизации, минимизации или конкретного значения. Если вы выберете Макс. , Excel настроит ваши переменные, чтобы получить максимально возможное число в целевой ячейке. Мин. наоборот: Решатель минимизирует целевой номер. Значение позволяет указать конкретное число, которое будет искать Solver.
Выберите ячейки переменных, которые Excel может изменить. Ячейки переменных устанавливаются с помощью поля By Changeable Variable Cells . Щелкните стрелку рядом с полем, затем щелкните и перетащите, чтобы выбрать ячейки, с которыми должен работать Solver. Обратите внимание, что это все ячейки которые могут варьироваться. Если вы не хотите, чтобы ячейка изменялась, не выбирайте ее.
Установка ограничений для нескольких или отдельных переменных. Наконец, мы подошли к ограничениям. Вот где Solver действительно силен. Вместо того, чтобы изменять любую из переменных ячеек на любое желаемое число, вы можете указать ограничения, которые должны быть соблюдены. Дополнительные сведения см. в разделе о том, как установить ограничения ниже.
Когда вся эта информация будет на месте, нажмите Решить , чтобы получить ответ. Excel обновит ваши данные, включив в них новые переменные (поэтому мы рекомендуем сначала создать копию ваших данных).
Вы также можете создавать отчеты, которые мы кратко рассмотрим в нашем примере с Солвером ниже.
Как установить ограничения в Solver
Вы можете указать Excel, что одна переменная должна быть больше 200. При попытке использовать разные значения переменных Excel не будет опускаться ниже 201 с этой конкретной переменной.
Чтобы добавить ограничение, нажмите кнопку Добавить рядом со списком ограничений. Вы получите новое окно. Выберите ячейку (или ячейки) для ограничения в Cell Reference , затем выберите оператора.
Доступные операторы:
<= (меньше или равен)
= (равна)
=> (больше или равна)
INT (должен быть интуитивным (должно быть либо 1, либо 0)
AllDifferent
AllDifferent немного сбивает с толку. Он указывает, что каждая ячейка в диапазоне, который вы выбираете для Ссылка на ячейку должна быть другим номером. Но также указывается, что они должны быть между 1 и количеством ячеек. Итак, если у вас есть три ячейки, вы получите числа 1, 2 и 3 (но не обязательно в таком порядке)
. Наконец, добавьте значение ограничения.
Важно помнить, что вы можете выбрать несколько ячеек для ссылки на ячейку. Например, если вы хотите, чтобы шесть переменных имели значения больше 10, вы можете выбрать их все и указать Solver, что они должны быть больше или равны 11. Вам не нужно добавлять ограничение для каждой ячейки.
Вы также можете установить флажок в главном окне Решателя, чтобы убедиться, что все значения, для которых вы не указали ограничения, неотрицательны. Если вы хотите, чтобы ваши переменные стали отрицательными, снимите этот флажок.
Пример решателя
Чтобы увидеть, как все это работает, мы воспользуемся надстройкой Solver для быстрого расчета. Вот данные, с которых мы начинаем:
. В ней у нас есть пять разных заданий, каждое из которых оплачивается по разным ставкам. У нас также есть количество часов, которое теоретический рабочий отработал на каждой из этих работ в данную неделю. Мы можем использовать надстройку Solver, чтобы узнать, как максимизировать общую оплату, удерживая определенные переменные в некоторых ограничениях.
Вот ограничения, которые мы будем использовать:
Нет рабочих мест может быть менее четырех часов.
Задание 4 должно быть больше 12 часов .
Работа 5 должна быть менее одиннадцати часов .
Общее количество отработанных часов должно быть равно 40 .
Может быть полезно записать ваши ограничения перед использованием Solver.
Вот как мы настроили это в Солвере:
Во-первых, обратите внимание, что Я создал копию таблицы , поэтому мы не перезаписываем исходную таблицу, которая содержит наши текущие рабочие часы.
И, во-вторых, обратите внимание, что значения в ограничениях больше и меньше на единицу больше или меньше , чем то, что я упомянул выше. Это потому, что нет вариантов больше или меньше. Есть только больше-или-равно и меньше-или-равно.
Нажмем Решим и посмотрим, что получится.
Solver нашел решение! Как вы можете видеть в левой части окна выше, наша прибыль увеличилась на 130 долларов. И все ограничения соблюдены.
Чтобы сохранить новые значения, установите флажок Keep Solver Solution и нажмите OK .
Если вам нужна дополнительная информация, вы можете выбрать отчет в правой части окна. Выберите все отчеты, которые вы хотите, сообщите Excel, хотите ли вы, чтобы они были выделены в общих чертах (я рекомендую это), и нажмите OK .
Отчеты создаются на новых листах в вашей рабочей книге и содержат информацию о процессе, через который надстройка «Поиск решения» прошла, чтобы получить ваш ответ.
В нашем случае отчеты не очень интересные, да и интересной информации там не много. Но если вы запустите более сложное уравнение Solver, вы можете найти полезную отчетную информацию в этих новых рабочих листах. Просто нажмите кнопку + сбоку от любого отчета, чтобы получить дополнительную информацию:
Дополнительные параметры решателя
Если вы мало разбираетесь в статистике, вы можете игнорировать дополнительные параметры Солвера и просто запустить его как есть. Но если вы выполняете большие и сложные вычисления, вы можете изучить их.
Самый очевидный метод решения:
Вы можете выбрать между GRG Nonlinear, Simplex LP и Evolutionary. Excel предоставляет простое объяснение того, когда вы должны использовать каждый из них. Лучшее объяснение требует некоторого знания статистики Excel и регрессии.
Чтобы настроить дополнительные параметры, просто нажмите кнопку Options . Вы можете сообщить Excel об оптимальности целых чисел, установить временные ограничения вычислений (полезно для больших наборов данных) и настроить методы решения GRG и Evolutionary для выполнения своих вычислений.
Опять же, если вы не знаете, что это означает, не беспокойтесь об этом. Если вы хотите узнать больше о том, какой метод решения использовать, у Engineer Excel есть хорошая статья, в которой он изложен для вас. Если вам нужна максимальная точность, Evolutionary, вероятно, является хорошим выбором. Просто знайте, что это займет много времени.
No related posts.}}}}}}}}}}}}}}}}}}}}}}