Делитель в математике это: Делители и кратные — урок. Математика, 6 класс.

Содержание

Теория чисел. Делители и кратные OTUS

В школе даются начальные знания по основным наукам. Огромную роль играет математика. Она используется не только при расчетах, но и в программировании.

В данной статье рассмотрена теория чисел. Она является своеобразной «базой», помогающей более подробно рассматривать математические действия и операции. В ней особую роль играют делители чисел. Зная о них, можно достаточно быстро и точно провести большинство операций. Пример – посчитать дроби и выделить грамотно доли.

Делители чисел – это такие значения, при делении на которые у «первоначального» числового компонента не будет остатка. Является целым в обязательном порядке. Пример – у 21 два делителя: 3 и 7. Проверить это можно по таблице умножения, которая изучается в начальных классах. Других упомянутых компонентов к 21 нет. В остальных случаях при делении будет получаться остаток.

Кратные

С делителями чисел познакомились. Теперь стоит обратить внимание на еще один момент, изучаемый в младших классах. Речь идет о кратных.

Краткое – это ситуация, при которой какое-нибудь значение удалось поделить без остатка на другое. Кратным a будет называться значение, которое без остатка делится на a.

Каждая «цифра» в математике имеет бесконечно много кратных. Пример – 5. Сюда можно отнести: 5, 10, 15, 20, 25, 100, 1005 и так далее. Все они будут без остатка делиться на пятерку.

Простые и составные

В начальных классах учителя говорят, что в математике есть простые числа и составные. Тут необходимо запомнить:

Простые – это натуральное число, которое делится только на себя и единицу.
Единица не включена в ряд простых.
Составное число – это непростой элемент в математике. Единица сюда тоже не включена. Имеет несколько делителей. Согласно информации, подаваемой в начальных классах – больше двух.

Если интересует, сколько делителей у простого заданного числа, ответ будет очевиден – их всего два. И найти таковые проще простого. Эта информация очевидна из самого определения.

Составные числа могут иметь бесконечное количество делителей. Ответить, сколько именно, невозможно – все зависит от конкретной ситуации. Главное – чтобы их в конечном итоге оказалось больше двух.

В программировании найти «простую цифру» достаточно легко. Операция с легкостью проводится за O(N), где N – это проверяемый элемент. Достаточно проверить, будет ли оно делиться без остатка хотя бы на один элемент среди цепочки: 2, 3, 4, …, N-1. В школьных классах соответствующая информация не изучается. Она пригодится непосредственным программистам.

Вот – пример реализации. Этот код нужно просто обработать компилятором и посмотреть на выданные результаты. N – подставить свое значение.

Делимость – признаки

В разных классах начальной школы (иногда – в среднем звене) активно рассматриваются не только делители числа, но и признаки делимости. Эта информация тоже включена в рассматриваемую теорию. Она помогает найти простые делители заданного числа намного быстрее. А еще – понять, простое оно или сложное. Узнать количество делителей, которые имеют числа, будет намного проще.

На десятку

Если «цифра» заканчивается на 0, она может делиться без остатка на 10. Это – правило, которое нужно запомнить в младших классах. Обычно такие элементы относятся к сложным/составным. Об этом учителя говорят еще в начальных классах. Связано это с тем, что «цифра», которая делится на 10, обычно может быть поделена:

сама на себя;
на десятку;
на пятерку.

Из ранее изученных определений следует достоверность последнего утверждения.

Делимость на 5 и 2

Теперь стоит изучить более сложные варианты. Они тоже рассматриваются в начальных классах и позволяют понять, сколько делителей будет у «цифры», заданной в примере. Среди основных знаний, которые нужно освоить в начальной школе, выделяют признаки делимости на двойку и пятерку.

Тут в начальных классах требуется запомнить, что:

Любая «цифра», которая заканчивается на 0, делится без остатка на 5 и 2.
Если в конце стоит 0 или 5, то возможно деление без остатков на «пятерку».
Когда «цифра» заканчивается на 0, 2, 4, 6, 8 – оно будет делиться на 2. Остаток не предусматривается.

Все это поможет быстрее найти делитель числа в начальных классах. Но есть и иные признаки делимости. Они тоже необходимы для нахождения рассматриваемых элементов.

Согласно установленным правилам, если сумма цифр в заданном элементе делится на 3, то все оно тоже разделяется без остатка на «тройку». Пример – 27. Сумма его составляющих будет равна 9. Оно делится на 3. Отсюда следует, что 27 при делении на «тройку» остатка не образовывается.

Рассматривая делители числа, стоит обратить внимание на еще один признак делимости. Речь идет о 9. Если сумма цифр в заданном компоненте делится на «девятку», то и все оно тоже не образовывает остатка вследствие выполняемых математических манипуляций. Соответствующий принцип тоже изучается в младших классах.

Разложение на множители

Разложение на простые множители – еще одна операция, которая изучается в рассматриваемой теории в начальных классах.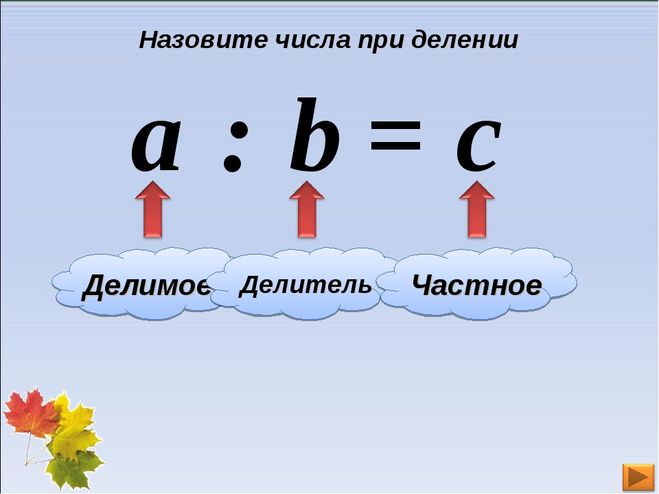 Можно провести разложение любого натурального числа, которое входит в заданное выражение им же, но представленном в ином виде. Для этого требуется изучить делители чисел. Они пригодятся в соответствующей операции.

Суть приема заключается в том, что нужно представить «цифру» в виде произведения нескольких простых множителей (делителей заданных чисел). Пример – дана «шестерка». Находим делители этого числа. Справиться с соответствующей задачей сможет ученик младших классов:

В поиске натуральных множителей теперь не будет никаких проблем. И в представлении «цифры» соответствующей записью – тоже. Шестерка – это 3*2 и 6*1.

Стоит обратить внимание – согласно правилам, продиктованным математикой в начальных классах, разложить на множители удастся только составную «цифру». У него будет простой делитель натурального заданного числа. Простая заданная «цифра» не подлежит разложению.

Данный вариант разложения – элементарный. Его легко освоить даже в начальных классах, после изучения таблицы умножения. Подходит для небольших «цифр». Когда дело доходит до больших значений, стоит воспользоваться иным методом:

Провести вертикальную линию.
Слева написать делимые.
Справа прописать делители заданного числа.
Собрать полученные сведения во множители.

Правила, изучаемые в начальных классах, указывают на то, что тут на помощь приходят признаки делимости.

Выше – пример реализации приема с числом 180.

Правило обнаружения делителей

Чтобы найти простые делители числа, в начальных классах необходимо запомнить следующий принцип (правило):

Записать в качестве первого делителя единицу.
Исходный элемент разложить на простые множители.
Выписать из соответствующих делителей те, на которые без остатка делится заданная изначально «цифра». При повторении повторно записывать его не потребуется.
Отыскать все произведения полученных простых множителей между собой.

Полученные ответы – это остальные искомые компоненты. Если этот принцип усвоить в младших классах школы, удастся достаточно быстро разобраться в математике и счете.

Дроби

Ближе к средним классам школьная программа начинает предлагать дроби. Там рассмотренная тема будет особо актуальна. Одно и то же число можно записать десятично (15 – 3*5) и в виде дроби.

У дробей есть:

числитель – то, что написано над чертой-разделителем;
знаменатель – нижняя часть записи.

Чтобы в любом классе без проблем привести дроби к общему знаменателю, потребуется:

Найти общее кратное знаменателей. Эта запись будет общим знаменателем.
Разделить общий знаменатель на знаменатель каждой отдельно взятой дроби. Получится дополнительный множитель.
Умножить числитель каждой дроби на дополнительный множитель.

Лишь после этого можно проводить сложение и вычитание дробей. Соответствующая информация пригодится в любом классе школы и даже во взрослой жизни при разнообразных вычислениях.

Хотите освоить современную IT-специальность? Огромный выбор курсов по востребованным IT-направлениям есть в Otus!

Делители и кратные числа: определения и примеры

Эта статья посвящена делителям и кратным. Здесь мы объясним данные понятия, сформулируем определения, приведем примеры делителей и различных кратных чисел (рассмотрим пока только целые числа). Отдельно остановимся на делителях 1 и -1, а также делителях и кратных 0.

Основные определения

Для начала сформулируем определения для целого числа.

Определение 1

Делитель целого числа a есть такое число b, на которое можно разделить a без остатка.

Если вспомнить такое понятие, как делимость, то данную формулировку можно слегка изменить.

Определение 2

Делитель целого числа a – это такое число b, которое в сочетании с некоторым числом q делает справедливым равенство a=b·q.

Когда мы говорим о числе b, являющимся делителем целого числа a, это значит, что b делит a, что можно записать кратко как b|a или b\a.

Согласно определению целых чисел, а также свойствам умножения целых чисел, любое целое число можно разделить на единицу и на себя, то есть a=a·1 и a=1·a. Зная свойства умножения, мы можем также вывести равенства a=(−a)·(−1) и a= (−1)·(−a). Из них следует, что у a будет еще два делителя, равных −a и −1. Следовательно, целое число a мы всегда можем разделить на a, −a, 1 и −1. К примеру, число 12 делится на 12, -12, 1 и -1.

Остановимся на делителях таких чисел, как нуль, единица и минус единица. Поскольку нам знакомы свойства делимости, то мы можем заключить, что делителем 0 может стать любое целое число (включая сам 0), а единица и минус единица имеют только делители, равные 1 и −1 соответственно.

Таким образом, 0 всегда будет иметь бесконечно большое число делителей в виде целых чисел (сюда входит и нуль), а у 1 и −1 будут только 2 делителя – единица и минус единица. Минимальное количество делителей для любого целого числа a равно четырем. В их число входят a, −a, 1 и −1.

Какие еще можно привести примеры делителей в случае с целыми числами?

Пример 1

Так, 8 можно разделить на -2, поскольку равенство 8= (−2)·(−4) верное (если нужно, повторите материал об умножении целых чисел). Восьмерку мы также можем разделить на −8, −4, −1, 1, 2, 4, 8, а вот -3 не входит в состав делителей, поскольку числа q, при котором равенство

8= (−3)·q было бы верным, не существует. То есть разделить 8 на -3 мы можем только с остатком. Кроме указанных делителей, мы не можем разделить восьмерку ни на какие целые числа без остатка.

Рассмотренные выше примеры говорят нам о том, что в качестве делителей целого числа могут выступать не только положительные, но и отрицательные целые числа. Эта возможность обоснована одним из свойств делимости: если b – делитель целого числа a, то и противоположное число -b тоже будет его делителем. Следовательно, можно разбирать только случаи с положительными делителями и просто распространять полученные результаты на отрицательные.

Вспомним также и другое свойство делимости, которое гласит, что если целое число b будет делителем a, то a можно разделить и на -b, следовательно, множества делителей для положительного и отрицательного a будут совпадать. Это правило опять же подтверждает возможность работы только с положительными числами для простоты и краткости вычислений.

Далее мы будем говорить лишь о положительных делителях целых положительных (натуральных) чисел.

У единицы есть только один положительный делитель – сама единица. Этим 1 отличается от остальных натуральных чисел, поскольку другие имеют не меньше 2 делителей: кроме единицы их можно разделить на числа, равные им самим. В зависимости от того, имеются ли делители, отличные от самого числа и единицы, различают числа простые и составные.

Наименьший положительный делитель числа a – это единица (если само число a не равно 1),
а число a – наибольший положительный делитель самого себя (подробнее о сравнении трех и более натуральных чисел мы писали в отдельной статье). Таким образом, для любого натурального a положительный делитель b будет соответствовать условию 1≤b≤a. Важную роль здесь также играет наибольший общий делитель (НОД), о котором мы поговорим отдельно.

Понятие кратных чисел

Начнем, как всегда, с определения.

Определение 3

Число a называется кратным b, если его можно разделить на b без остатка.

Другими словами, кратное b число является некоторым числом a, для которого будет верным равенство a=b·q(здесь q – некоторое целое число). Если у нас есть a, которое по отношению к b является кратным, мы говорим, что a кратно b. Записать это можно так: a⋮b.

Между кратным и делимым существует вполне определенная связь. На самом деле, если a является кратным b, то b будет делителем данного числа, и наоборот.

Возьмем несколько примеров кратных чисел.

Пример 2

Так, -12 будет кратно трем, поскольку −12=3·(−4). У тройки есть много других кратных, например, 0, 3, −3, 6, −6, 9, −9 и др. А 5 не будет кратным 3, поскольку нет такого q, при котором было бы верным равенство 5=3·q.

Согласно определению кратных чисел, 0 будет кратным по отношению к любому b, в том числе и нулевому. Доказательством является равенство 0=b·0, ведь умножение любого числа на нуль дает в итоге нуль.

Также уточним, что для любого целого числа b существует бесконечно много кратных, и любое целое число, соответствующее произведению b·q, где q – любое целое число, будет кратным b.

Наименьшее положительное кратное положительного числа есть само это число. Обратите внимание, что наименьшее кратное в этом случае не нужно путать с наименьшим общим кратным для нескольких чисел (НОК).

Далее будут рассмотрены другие случаи с натуральными кратными целых положительных чисел.

Делитель

Определение и значение — Merriam-Webster

разделитель də-vī-zər

: число, на которое делится делимое

Примеры предложений

Недавние примеры в Интернете Но чтобы такие вещи, как дробление акций и изменения в составляющих его акциях, не искажали индекс Доу-Джонса, его администраторы создали нечто, называемое делителем Доу-Джонса . — Аллан Слоан, Washington Post , 16 декабря 2022 г. Дрейер начал урок с того, что написал пример оценки частного с двузначным числом 9.0011 делитель на доске и попросил учеников поднять руку и поделиться своими наблюдениями, включая возможные пути решения проблемы. — Кливленд , 18 ноября 2022 г. Например, для деления в длинное учащиеся использовали цветные карандаши, чтобы сопоставить штрихи делителя и в делимом. — Алена Найден, Anchorage Daily News , 7 ноября 2022 г. Используя этот новый делитель , ожидаемая продолжительность жизни будет уменьшаться на единицу каждый год. — Джули Джейсон, Jd, Forbes , 7 марта 2022 г. Текущий делитель промышленного индекса Доу-Джонса равен 0,1517. — Q.ai — Движение за личное богатство, Forbes , 9 октября 2022 г. Дивидендная доходность в целом не изменится, но дивиденд на акцию может уменьшиться на те же делитель как раскол. — Ли Клиффорд, Fortune , 10 марта 2022 г. Дивидендная доходность в целом не изменится, но дивиденд на акцию может быть уменьшен на тот же делитель , что и дробление. — Ли Клиффорд, Fortune , 10 марта 2022 г. Дивидендная доходность в целом не изменится, но дивиденд на акцию может уменьшиться на те же делитель как раскол. — Ли Клиффорд, Fortune , 10 марта 2022 г. Узнать больше

Эти примеры предложений автоматически выбираются из различных онлайн-источников новостей, чтобы отразить текущее использование слова «делитель». Мнения, выраженные в примерах, не отражают точку зрения Merriam-Webster или ее редакторов. Отправьте нам отзыв.

История слов

Первое известное использование

15 век, в значении, определенном выше

Путешественник во времени

Первое известное использование делителя было в 15 веке

Посмотреть другие слова из того же века вызывающий разногласия

делитель

разделяющий

Посмотреть другие записи поблизости

Процитировать эту запись «Дивизор».

Словарь Merriam-Webster.com , Merriam-Webster, https://www.

merriam-webster.com/dictionary/divisor. По состоянию на 30 января 2023 г.

Копировать цитирование

Детское определение

Делитель

существительное

разделитель də-vī-zər

: Число, по которому дивиденд делится

больше от Merriam-Webster на

Divisor

Nglish: Перевод Divisor для испанских спикеров

Britannica.com: Encyclopedia. Последнее обновление: 26 дек. 2022 — Обновлены примеры предложений

Подпишитесь на крупнейший словарь Америки и получите тысячи дополнительных определений и расширенный поиск без рекламы!

Merriam-Webster без сокращений

D: Иллюстрированный математический словарь — Enchanted Learning.com

D: Иллюстрированный математический словарь — Enchanted Learning.com Реклама.

EnchantedLearning.com — это сайт, поддерживаемый пользователями.
В качестве бонуса участники сайта получают доступ к версии сайта без баннерной рекламы и страницам, удобным для печати.
Щелкните здесь, чтобы узнать больше.

(Уже зарегистрированы? Нажмите здесь.)

Вам также может понравиться:

J: Иллюстрированный математический словарь — Enchanted Learning.

com

H: Illustrated Math Dictionary — Enchanted Learning.com

H: Illustrated Math Dictionary -Enchanted.

K: Иллюстрированный математический словарь — Enchanted Learning.com

L: Иллюстрированный математический словарь — Enchanted Learning.com

Сегодняшняя избранная страница: Книги по математике

Оценочный уровень наших подписчиков для этой страницы: 4-й

+ , —

EnchantedLearning.com
Математический словарь

х , ÷

Дж

D для . ..

десятиугольник

Десятиугольник — десятигранная геометрическая фигура.

деци

деци — это префикс, означающий одну десятую. Например, дециметр — это одна десятая метра.

1.33
десятичное число

Десятичное число — это число с основанием 10, которое записывается с десятичной точкой. Например, 1,1, 10,43 и 0,01 — десятичные числа.

десятичная точка

Десятичная точка — это точка, которая разделяет число на целую часть числа (слева от десятичной точки) и дробь (справа от десятичной точки). Например, в 21,46 21 — это целое число, а 0,46 (сорок шесть сотых) — дробь.

неполноценное число

Неполноценное число — это целое число, у которого сумма собственных множителей (делителей) меньше самого числа. 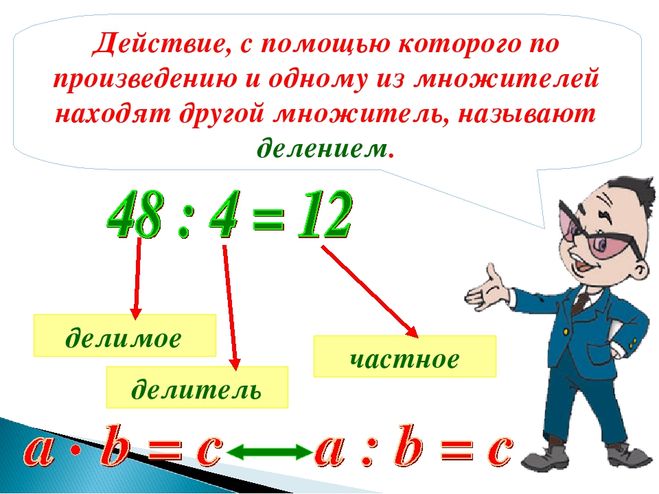Например, 9является недостаточным числом, потому что правильными делителями 9 являются 1 и 3, которые в сумме дают 4, что меньше 9. Сравните с обильным числом, совершенным числом.

градус

Градус — это мера температуры или угла. В окружности 360 градусов. Каждый градус делится на 60 минут, представленных символом апострофа «. 1°=60′.

знаменатель

Знаменатель — это нижнее число в дроби.

Декарт

Рене Декарт (31 марта 1596 — 11 февраля 1650) — французский математик и философ. Декарт изобрел декартову систему координат и многие принципы философии.

диагональ

Диагональ — это линия, соединяющая две непоследовательные вершины многоугольника.

диаметр

Диаметр — это наибольшее расстояние от одной стороны круга (или сферы) до другой.

ромб

Алмаз представляет собой четырехугольник (четырехугольник), все стороны которого имеют одинаковую длину.

Люди играют в бейсбол на ромбовидном поле.

игральные кости

Игральные кости — это кубики с числами на каждой стороне, которые используются в играх. Один называется кубиком.

разница

Разница есть ответ в задаче на вычитание.

цифра

Цифра — это одна цифра в числе. Например, число 153 — это трехзначное число.

дайм

Десять центов — монета достоинством в десять центов.

Директриса

Директриса — это линия, которая помогает построить параболу или гиперболу. Например, парабола — это набор точек (P), таких, что расстояние от директрисы до P равно расстоянию от P до фокуса F.

делимое

Делимое — это число, которое делится (в длинном делении).

Делимое, деленное на делитель, есть частное (плюс остаток).

деление

Деление — это операция деления числа на части. Любое число, деленное на единицу, равно исходному числу. Нельзя делить любое число на ноль. Деление обратное умножению. В длинном делении делимое делится на делитель, в результате чего получается частное плюс остаток. Символ ÷ называется обелюсом.

делитель

Делитель — это число, на которое делится делимое (в длинном делении). Делимое, деленное на делитель, есть частное (плюс остаток).

додекагон

Додекагон — это многоугольник с двенадцатью сторонами (рисунок).

додекаэдр

Додекаэдр представляет собой двенадцатигранное геометрическое тело, грани которого представляют собой пятиугольники.

доллар

Один доллар стоит 100 центов.

домино

Домино — это игра, в которой используются плитки с точками.

точка

Точка — это крошечное пятнышко или точка.

****
****
****
12
дюжина
Дюжина — это другое слово, обозначающее двенадцать.

+ , —

EnchantedLearning.com
Математический словарь

х , ÷

Дж

Подсчет

Дополнение

Вычитание

Умножение

Подразделение

Номер строки

Дроби

Десятичные числа

Графики

Измерение

Округление

Нажмите на подчеркнутое слово, чтобы получить дополнительную информацию по этому вопросу.