Формулы по математике: Ошибка: 404 Материал не найден

Как запоминать формулы? Лайфхаки для ЕГЭ и ОГЭ

Анна Малкова

Что проще запомнить с первого раза и пересказать другу – сюжет интересного фильма или большую таблицу с формулами по геометрии?

Мы хорошо запоминаем сюжеты и истории. А однообразная и скучная информация быстро вылетает из головы.

Можно запоминать формулы «как буковки». Долго, трудно и напряженно. Результат – вы сами знаете, какой.

А можно придумать историю. Понять, почему формула именно такая. Как она получилась. На что она похожа.

Например, формулы для площадей геометрических фигур. Они есть в нашем ЕГЭ-Справочнике

 

Площадь прямоугольника равна произведению его сторон:

Чем больше стороны, тем больше площадь. Проверяйте, чтобы площадь была выражена в квадратных единицах.

Отрежем от нашего прямоугольника треугольник. И переставим этот треугольник, как на рисунке, получим параллелограмм.

Площадь параллелограмма:

Поделим параллелограмм пополам. Получим два равных треугольника и формулу для  площади треугольника:

Теперь трапеция. Поделим ее на два треугольника с основаниями   и  .

Площадь трапеции

 

В формулы для длины окружности и площади круга входит число .

Длина окружности 

.

Число  – это отношение длины окружности к ее диаметру.

.

Число известно с глубокой древности. С давних времен – с доисторических – люди плели круглые корзины и лепили из глины круглые тарелки и миски. Во всяком случае, старались сделать их круглыми.

Нарисуйте древнего человека, который плетет корзинку. Он смотрит на небо и видит на нем круглое солнце. Он старается, чтобы его корзина получилась круглой, как солнце. Измерив диаметр своего изделия, наш первобытный труженик осознает, что диаметр укладывается на окружности корзины три раза, и еще немного остается! Причем это справедливо и для маленькой корзины, и для большой. Удивительное открытие!

Во сколько же раз длина окружности больше, чем ее диаметр? В  раз.

площадь выражается в квадратных единицах, значит, в формуле должен быть квадрат радиуса.

Площадь круга

Формулу для площади сектора запомнить легко. Кусочки, на которые вы нарезаете круглую пиццу, – это секторы.

Вспомним, что 1 градус – это  часть полного круга. Тогда площадь сектора в 1 градус равна части полного круга. А площадь сектора в градусов равна части полного круга.

Точно так же для длины дуги:

Есть отличная «запоминалка», и ее все знают.

Биссектриса – это крыса, которая бегает по углам и делит угол пополам.

Нарисуем угол, который крыса делит пополам, и эта крыса тащит за собой (на хвосте) круглый сыр. Центр окружности, вписанной в угол, лежит на биссектрисе угла.

Прогоним крысу, оставим вписанную в угол окружность. Отрезки касательных, проведенных из одной точки к окружности, равны.

А поскольку прямоугольные треугольники АОВ и СОВ на рисунке равны – значит, равны расстояния от точки  до точек  и . Биссектриса угла треугольника – это множество точек, равноудаленных от сторон угла.

Впишем в треугольник окружность. Окружность касается всех сторон треугольника – значит, ее центр одинаково удален от сторон АВ, ВС и АС. Центр окружности, вписанной  в треугольник, – это  точка пересечения его биссектрис.

А где же находится центр окружности, описанной вокруг треугольника? Очевидно, что расстояние от этой точки до всех вершин треугольника одинаково и равно радиусу описанной окружности.

Где находятся точки, равноудаленные от концов отрезка, вы знаете. На серединном перпендикуляре к отрезку.

Вот и нарисуем три серединных перпендикуляра к сторонам треугольника. А в точке, где все они пересекаются, уселась киса, чтобы быть на одинаковом расстоянии от вершин треугольника. А что делает киса? – правильно, писает! Хочет до всех вершин треугольника достать. И получается окружность, описанная вокруг треугольника.

Чтобы легко запоминать формулы, придумывайте истории. Глупые, смешные, даже неприличные.  И картинки к ним рисуйте!

Теперь стереометрия. Будем искать логические связи. Ассоциации. Придумываеть себе «запоминалки».

Посмотрим на таблицу с формулами для объемов и площадей поверхности многогранников  и тел вращения.

С призмой и цилиндром все просто – их объем равен произведению площади основания на высоту.

Чем больше площадь основания, тем больше объем.

Чем больше высота, тем больше объем.

 

Объем призмы

Объем цилиндра

С объемами пирамиды и конуса тоже просто: умножаем  на площадь основания и на высоту. Как вы думаете, почему у пирамиды и у конуса похожие формулы для объема?

Объем пирамиды

Объем конуса

Площадь боковой поверхности многогранника равна сумме площадей всех его граней. Сложные формулы здесь не нужны.

Теперь цилиндр. В его основаниях – два круга. Как запомнить, чему равна площадь поверхности цилиндра? Развернем боковую поверхность цилиндра и получим  прямоугольник, одна сторона которого равна , а другая равна .

Площадь боковой поверхности цилиндра

Как запомнить формулу для площади боковой поверхности конуса?*

Нарисуем ракушку в форме конуса. Вот у него какая красивая боковая поверхность.

А в ракушке что бывает? – жемчужинка! По-английски жемчужина: pearl. Вот и запомним формулу для площади боковой поверхности конуса:

Остались объем шара  и площадь поверхности сферы .

Что же, две формулы можно и просто выучить.

Хорошо, а как выучить формулы тригонометрии?

Есть отличный способ. Вырежьте из плотной бумаги карточки. На одной пишете левую часть формулы. На другой – правую. Перемешиваете. И собираете. Любые формулы запоминаются  легко и быстро!

И конечно, чем больше решаете задач, тем лучше запоминаются формулы.

*Лайфхак преподавателя ЕГЭ-Студии А.В. Фомичевой

Формулы по математике и физике: инструкция по запоминанию

Помните ли вы формулу Закона всемирного притяжения или скорости с постоянным ускорением? Остались ли у вас в памяти формулы суммы кубов или произведения косинусов? Наверняка, вы либо вовсе не помните, что означает этот набор слов, либо что-то припоминаете, либо не помните формулы, но понимаете, о чем мы. Если же вы без проблем сможете написать хотя бы пару из этих формул, значит, вы скорее всего, технарь, и ваша работа связана с математическими или физическими расчетами. Конечно, есть еще вариант, что у вас феноменальная память, но это встречается довольно редко.

Совершенно логично у вас может возникнуть вопрос: а зачем мне вообще помнить эту информацию, если она никак не пригодится мне в жизни? Что ж, здесь нам есть, что ответить:

• Во-первых, главная причина – это тренировка памяти, а это в свою очередь развитие системного, аналитического, ассоциативного мышления. Более подробно о пользе и способах развития памяти читайте здесь.
• Во-вторых, запоминая формулы, вы способны быстрее выполнять вычисления, что заметно облегчает работу, особенно связанную с какими-либо подсчетами.
• В-третьих, несмотря на то, что ваша работа никак не связана с вычислениями и подсчетами, в бытовой жизни вам нет-нет да приходится что-то складывать, вычитать, умножать или делить, и чтобы не попасть впросак, нужно тренировать этот навык.

Кстати, отличным бонусом развития памяти становится выясненное канадскими учеными замедление процессов старения головного мозга. Любое упражнение, в том числе заучивание стихотворений, воспоминание прошедших событий, изучение иностранных слов и т.д. этому способствует.

Итак, давайте приступим к способам запоминания формул. Сначала перечислим наиболее общеизвестные способы запоминания формул по математике и физике.

Решаем, решаем и еще раз решаем

Конечно! А как вы думали? Давайте порассуждаем: конечная цель запоминания формул – это решение поставленной задачи. Следовательно, идем от противного: чтобы запомнить формулу, её нужно как можно чаще применять. Соответственно, практика – лучшее средство.

С каждым разом формула запоминается все лучше и лучше, оседает в памяти, ведь напоминание – это лучшая техника при борьбе с забыванием. Еще лучше, если вы будете выполнять задания с перерывами в полчаса, 8 часов, день, 5 дней и т.д. Тогда формула навсегда останется с вами. Более подробно о кривой забывания можно почитать в этой статье.

Плюсом данного метода является и то, что с наработанными примерами по одной формуле вы прокачиваете умение решать задачи подобного вида. Особенно актуально это для школьников и студентов.

Давайте посмотрим, какие еще способы можно применять при запоминании математических и физических формул.

Пишем на карточках

Не преуменьшайте значение визуального контакта. Чем чаще вы встречаетесь глазами со своей формулой, тем более родной она становится для вас, и собственно вероятность её забывания снижается.

Также очень полезно среди большого количества разных формул сгруппировать их по определенному критерию и составить «тематические» карточки. К примеру, вы можете сделать заготовки формул квадратного уравнения, составить список карточек по тригонометрии или начертить трапецию с поясняющими равенствами. Точно так же это работает и с физикой. В этой области знаний можете выбрать, допустим, формулы, начинающиеся с ½, или все равенства, где есть масса. Так запоминать будет увлекательнее и эффективнее!

Карточки желательно не сложить в одно место и забыть, а разложить по разным местам комнаты или даже квартиры (только предупредите домочадцев, чтобы они не удивились). Нежданная встреча с той или иной формулой добавит в процесс запоминания эмоции (неожиданность), а это всегда усиливает воздействие.

Более стандартным подходом является использование карточек с целью проверки. Для этого одна их сторона должна быть подписана названием, а другая (перевернутая и не видная вам) должна содержать непосредственно саму формулу.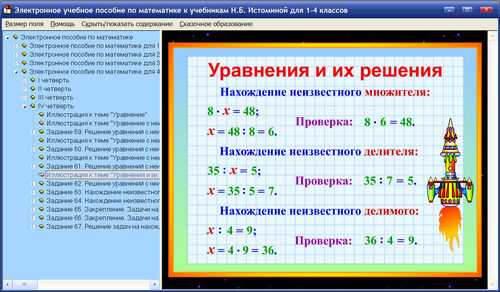 Когда вам попадается, к примеру, «Потенциальная энергия тела, поднятого на высоту», вы пытаетесь вспомнить, что же там было (если что, это Ep = mgh). Если вспоминаете без труда, значит, откладываете её в сторону. С теми карточками, с которыми возникают сложности, вы не прощаетесь, а берете их на вооружение и обязательно возвращаетесь к ним впоследствии.

«Сейчас будет метод для умных», – подумаете вы.

Выводим сами

Но на самом деле, этот способ подвластен всем. Если уж вы решили изучать формулы, то наверняка вам знакомы базовые знания по элементарным арифметическим операциям. Если же нет, советуем вам этому научиться, это совершенно просто.

А работает это так. Допустим, вы однозначно знаете, что формула Закона всеобщего тяготения – это F = G(Mm/r2), G = 6,673 × 10 в -11-й степени , поэтому вам не составит труда вычислить массу первого объекта: M = Fr²/Gm².

Чтобы прийти к этому результату, необходимо стремиться к тому, чтобы m₁ с каждым последующим шагом оставался в одиночестве в левой (или правой) стороне уравнения. Следовательно, мы перенесли r² к F в числитель, а G и m₂отправились в знаменатель. Собственно, так и получилась новая формула.

Или, к примеру, вы позабыли формулу нахождения высоты правильной четырехугольной пирамиды. Изобразив пирамиду (ABCDS), прочертив её высоту (SO) и соединив точку пересечения высоты и основания (O) с одной из точек нижнего квадрата (возьмем B) получится прямоугольный треугольник (SOB) (см. рис. 1). Далее вы можете вывести формулу высоты пирамиды из площади прямоугольного треугольника либо как высоту равнобедренного треугольника, либо из теоремы Пифагора. Выбирайте и считайте:

Таким образом, данный способ заставляет не только тренировать память, но и развивать логическое мышление, мыслить структурированно и рационально. Минусом этого метода является то, что у вас должны быть все же какие-то знания, ведь выводить новую формулу нужно из чего-то, из уже имеющихся равенств, которыми можно воспользоваться.

Медитируем над формулой

Не переживайте, благовония или успокаивающая музыка вам не понадобятся. Достаточно лишь хорошо вглядеться в формулу, разобраться, какой символ что означает, подумать над тем, почему эти символы связаны именно таким путем, и – вуаля! – вы придете к осознанному пониманию того, что пытаетесь вычислить.

Снова не обойтись без примера. Возьмем формулу связи давления, площади и силы, выглядит она так: p = F/S . Теперь вдумайтесь, ведь на самом деле когда мы на что-то давим, нужно, главным образом, учитывать три фактора:

1. То, с какой силой мы давим (F).
2. То, какая поверхность оказывается под воздействием этой силы (S).
3. То, что чем больше площадь поверхности, на которую оказывают действие, тем менее заметно это воздействие, т.е. сила обратно пропорциональна площади поверхности (F/S).

Аналогично можно проанализировать и разобрать остальные не слишком комплексные формулы. Но что же делать, если формула гораздо более сложная, длинная и содержащая большее количество параметров? В таком случае обычно применяют мнемотехники.

Даем волю фантазии

Слово мнемоника (равнозначна мнемотехнике) – это совокупность специальных приемов, помогающих увеличить объем запоминаемой информации, подчас в разы. Может показаться, что это панацея для забывчивых и ленивых товарищей, однако мнемотехника требует активного включения воображения, фантазии, креативности, долгих часов тренировок и, конечно же, самой памяти. Посмотрим, как мнемоника помогает на практике с математическими и физическими формулами.

Суть этой техники заключается в присвоении какой-либо единице информации определенного образа, его последующем кодировании, запоминании связей между кодированными данными и последовательной расшифровке. В этом сложно сформулированном алгоритме на самом деле все очень просто.

Помните, сколько цветов и какие конкретно заложены в радуге? Наверняка в ответе на этот вопрос вам поможет детская присказка «Каждый Охотник Желает Знать, Где Сидит Фазан». Таким образом, посредством акростиха (как вариант мнемотехники) вы запомнили, что радуга содержит красный, оранжевый, желтый и другие цвета.

Точно так же можно пофантазировать и на тему формул, а именно придумать символические образы для каждого параметра или цифры, соединить их каким-либо действием или ситуацией и запомнить. Допустим, мы говорим о цифрах, тогда мы можем использовать следующие образы:

1 — свеча;

2 – лебедь;

3 – скрученная змея;

4 – перевернутый стул;

5 – дяденька с пузом, стоящий вбок;

6 – вишенка;

7 – флаг;

8 – бесконечность;

9 – рыбка.

Все это нужно хорошенько визуализировать, представить и запомнить.

Далее мы начинаем вводить параметры. Чтобы быть более конкретными, давайте выберем формулу механической работы, которая выглядит следующим образом:

 Какую тут можно придумать технику? Можно подобрать какие-нибудь слова, фразу, связывающую параметры. В конце концов, это буквы, и, связав их, можно получить что-то со смыслом. Например, буквы «А», «Ф», «С» содержатся в имени АФанаСий. Если у Афанасия появляется коза, то и запоминать становится почти нечего: только лишь рельсы (знак равенства) со звездой (знак умножения).

Теперь представьте: стоит некий Афанасий на железнодорожных путях рядом с козой вечерком, а над ними ярко-ярко горит звезда и освещает их. Представили? Подержите у себя в голове Афанасия с козой секунд пять, постарайтесь разглядеть их подробно, увидеть то, как свет играет по шерсти козы и волосам Афанасия. Теперь вероятность того, что вы вспомните формулу механической работы гораздо выше.

Если вдруг вы обладаете знаниями в английском языке или латыни, это может помочь во многом. В частности, вышеупомянутая формула давления содержит в себе первые буквы таких слов как pressure (давление), force (сила), square (площадь поверхности). Другие слова, такие как volume (объем), height (высота), mass (масса), time (время), acceleration (ускорение) несомненно будут большой подсказкой. Учите иностранный язык, эти знания пригодятся в нужный момент.

Техниками мнемоники пользуется большое количество людей, существуют даже специальные школы по подготовке именно с использованием этой методики. На 4brain также есть онлайн-программа «Мнемотехника», благодаря которой вы сможете в увлекательной форме научиться запоминать большой массив данных, перестанете забывать имена, адреса, телефоны, дни рождения и многое другое.

Другие мнемотехники, связанные с ассоциативным мышлением, поэтапным запоминанием, можно посмотреть в этом видеоролике:

Тренируйте память, учите формулы, заставляйте работать головной мозг, потому что, как показывает практика, это идет только на пользу организму, да и жизни в целом.

Желаем вам успехов!

Другие мнемотехники, связанные с ассоциативным мышлением, поэтапным запоминанием, можно посмотреть в этом видеоролике:

Тренируйте память, учите формулы, заставляйте работать головной мозг, потому что, как показывает практика, это идет только на пользу организму, да и жизни в целом.

Желаем вам успехов!

Ключевые слова:1Мнемотехники

Фото: Наука: Наука и техника: Lenta.ru

Нейробиологи из Великобритании провели эксперимент, в ходе которого попросили 15 математиков оценить красоту математических формул, предложив им список из 60 штук. После этого участникам эксперимента по очереди показывали красивые и некрасивые формулы. За откликом их мозга наблюдали при помощи функциональной магнитно-резонансной томографии (fMRI).

Как обнаружили нейробиологи, просмотр красивых, с точки зрения математиков, формул вызывает отклик в префронтальной коре головного мозга, отвечающей за сложные когнитивные функции и эмоции. Проанализировав отклик, ученые пришли к выводу, что восприятие красоты математики очень похоже на ощущение, возникающее во время прослушивания музыки или просмотра произведений живописи.

«Лента.ру» предлагает читателям самостоятельно оценить красоту некоторых математических формул, использовавшихся в этом эксперименте.

Тождество Эйлера

Тождество Эйлера является следствием формул Эйлера, связывающих экспоненту комплексного числа с тригонометрическими функциями. Эта формула является основной для экспоненциального представления комплексных чисел и формул Муавра для выражения синусов и косинусов кратных углов (в школе проходят частные случаи этой формулы для удвоенных и утроенных углов). Именно это тождество было признано участниками опыта самым красивым.

Основное тригонометрическое тождество

Эта формула связывает две основные тригонометрические функции. Обычно ее выводят геометрически, из теоремы Пифагора для прямоугольного треугольника с гипотенузой, равной единице: синус угла при гипотенузе будет в этом случае отношением противолежащего катета к гипотенузе, а косинус — прилежащего.

Формула для эйлеровой характеристики

В простейшем случае эта формула связывает между собой количество вершин (V), ребер (E) и граней (F) произвольного выпуклого многогранника.

Формула Гаусса-Бонне

В частном случае эта формула связывает локальную характеристику поверхности под названием гауссова кривизна (она является мерой того, насколько поверхность отличается от плоскости) и ее глобальную, топологическую характеристику — количество сквозных дырок. Такая интерпретация подходит для двумерной поверхности, изготовленной из единого «куска» — например, сферы или тора. У сферы, кстати, сквозных дырок нет, а у тора она одна.

Формула Эйлера

Та самая формула Эйлера, о которой говорилось вначале. Тождество Эйлера является ее частным случаем, если вместо x подставить «пи».

Гауссов интеграл (также известный как интеграл Эйлера-Пуассона)

Это выражение является инструментом для подсчета вероятностей в случае, когда речь идет о распределении Гаусса.

Формула Римана-Дирихле-Мёбиуса

В этой формуле слева стоит знаменитая дзета-функция Римана, а справа — ряд Дирихле для функции Мёбиуса. Функция Мёбиуса определена для натуральных чисел и возвращает 1, если число состоит из четного числа простых множителей, среди которых нет одинаковых, -1, если число состоит из нечетного числа таких множителей, и 0 — во всех остальных случаях. Эта формула демонстрирует глубокую связь дзета-функции с теорией чисел.

Формула для экспоненты

Представление экспоненты в виде ряда.

Преобразование Фурье от функции Гаусса

Эта формула показывает, что преобразование Фурье (используется, например, в радиотехнике, но далеко не только в ней) от гауссовой функции — это снова функция Гаусса, правда, с численным коэффициентом и другим множителем у показателя.

Число e

Определение числа e как предела некоторой числовой последовательности.

Теорема Кантора для натуральных чисел

Для сравнения двух бесконечных множеств в математике используется понятие биекции. Говорят, что два множества равномощны, если между их элементами можно установить взаимнооднозначное соответствие. Если, например, множество A равномощно некоторому подмножеству множества B, а B не равномощно A, то говорят, что B — мощнее. Теорема Кантора в данном случае утверждает, что множество точек отрезка мощнее множества натуральных чисел.

Квадратичный итерационный процесс

Бенуа Мандельброт обнаружил, что с помощью таких, казалось бы, простых процессов можно строить очень сложные множества. Он назвал их фракталами. Квадратичный итерационный процесс позволяет строить множество Мандельброта, названное в честь математика.

Дельта-функция Дирака

Дельта-функция является на самом деле не функцией, а обобщенной функцией. Приведенный интеграл можно использовать как ее определение. Такие функции очень активно используются в физике.

Формула Рамануджана

Эта формула для числа «пи» примечательна своей относительно быстрой (на момент открытия, конечно, то есть начала XX века) сходимостью ряда в правой части.

Минимальное число такси

Однажды математик Годфри Харди отправился навестить приболевшего математика Сриниваса Рамануджана. По прибытии Харди заметил, что приехал на такси «с достаточно скучным номером» 1729. На это Рамануджан немедленно возразил, что 1729 — очень интересное число. Это минимальное число из натуральных, для которого существует больше одного разложения в сумму двух кубов. Благодаря этой истории такие числа (то есть представимые в виде суммы двух кубов несколькими способами) получили наименования чисел такси.

Теорема Пифагора

Сумма квадратов катетов равна квадрату гипотенузы. Эта теорема была известна еще в Междуречье примерно за 1800 лет до нашей эры.

Первообразная и производная

Эта формула является частным случаем формулы Ньютона-Лейбница. Она позволяет связать две важнейшие операции математического анализа — дифференцирование и интегрирование.

Теорема Коши о вычетах

Теорема утверждает, что, когда речь идет о комплексных функциях, для подсчета интеграла по замкнутому контуру достаточно вычислить некоторые величины в особых точках функции, именуемые вычетами, которые попали в ограниченную контуром область. Благодаря этой теореме, например, становится возможным подсчет разных бесконечных сумм.

Модель Лотки-Вольтерры

Эта система нелинейных дифференциальных уравнений описывает динамику в простейшей экосистеме, состоящей из одного вида хищников и одного вида жертв. Часто используется как пример сравнительной неустойчивости равновесия в таких экосистемах — достаточно сильное возмущение может приводить к вымиранию видов.

Уравнение диффузии

Уравнение описывает процесс диффузии — то есть постепенного взаимного проникновения — двух сред.

Формула для «пи»

Пожалуй, самая главная формула для числа «пи». Здесь c — длина окружности, а d — ее диаметр.

Дифференцирование экспоненты

Одно из замечательнейших свойств экспоненты: ее производная равна ей самой. Легко показать, что экспонента — единственная с точностью до умножения на константу функция, обладающая таким свойством.

Ряд Тейлора-Маклорена

Представление аналитической функции в виде ряда в нуле. Вообще говоря, такой ряд можно построить для более широкого класса функций, называемых гладкими, однако в этом случае в формуле нельзя ставить знак равенства.

Уравнение для собственного вектора оператора

Понятие собственного вектора оператора, то есть вектора, который при действии этого оператора просто растягивается, является одним из ключевых в линейной алгебре. Это понятие крайне полезно, например, в квантовой механике — состояния квантовых систем есть собственные вектора в некотором (правда, бесконечномерном) пространстве.

Неравенство треугольника

Неравенство треугольника для нормированных пространств. Простейший пример такой нормы — это корень квадратный из суммы квадратов координат вектора в трехмерном пространстве. В этом случае это неравенство превращается в обычное неравенство треугольника: сумма двух сторон не меньше третьей.

Асимптотика пи-функции

Пи-функцией называется функция, которая возвращает количество простых чисел меньше данного действительного x или равных ему. Как показал в XIX веке Жак Адамар, эта функция растет примерно как отношение в правой части. Это означает, что простых чисел, не превосходящих x, примерно x/log x.

Формула Эйлера для дзета-функции Римана

Как оказалось, иногда бывает полезно работать не с бесконечными суммами, а с бесконечными произведениями. В правой части стоит произведение по всем простым числам p — еще один замечательный факт, связывающий дзета-функцию и теорию чисел.

Пифагорова тройка

Тройки натуральных чисел, которые могут быть сторонами прямоугольного треугольника, получили название пифагоровых. Считается, что тройка (3, 4, 5) была известна еще древним египтянам.

Интегральная формула Коши

Формула позволяет связать кратные производные комплексно-аналитической функции с интегралом по контуру. Благодаря этой формуле доказывается эквивалентность нескольких определений комплексно-аналитической функции. В частности, если она дифференцируема, то немедленно раскладывается в сходящийся ряд.

Число «пи» в виде ряда

Представление числа «пи» в виде ряда от дробей с нечетными знаменателями.

Эйлерова сумма обратных квадратов

В возрасте 28 лет Леонард Эйлер доказал, что сумма обратных квадратов связана с числом «пи». Это немедленно принесло ему славу — на тот момент задача о суммировании считалась крайне сложной, над ней безуспешно бились лучшие умы того времени.

Сумма геометрической прогрессии

Геометрической прогрессией называется последовательность чисел, в которой каждое следующее получается из предыдущего умножением на некоторое фиксированное число r.

Неравенство для средних, открытое Коши

Неравенство связывает среднее арифметическое и среднее геометрическое чисел.

Формула Стирлинга

Формула Стирлинга позволяет оценить скорость роста такой функции, как факториал n!

Объем n-мерного шара радиусом r

В формулу для объема n-мерного шара входит гамма-функция.

Уравнение Лапласа

Это уравнение возникает в задачах механики, теплопроводности, электростатики, гидравлики. Оператор Лапласа, стоящий в левой части, играет важную роль в квантовой механике. Там с его помощью определяется уравнение Шрёдингера.

Великая теорема Ферма

Утверждение великой теоремы Ферма, доказанной в 1995 году Эндрю Уайлзом, говорит, что записанное уравнение не разрешимо для целых ненулевых a, b, c.

Функциональное уравнение на гамма- и дзета-функции

Это уравнение позволяет, среди прочего, формализовать понятие «суммы всех натуральных чисел», которое возникает в теории струн.

Математические формулы GRE [10 уравнений, которые необходимо знать] 2022 Памятка GRE

Какие формулы GRE должны знать и запоминать учащиеся?

Раздел GRE Math охватывает различные темы, включая системы координат, таблицы, символы и фигуры.

Поэтому очень важно знать, что от вас ожидается во время экзамена, чтобы помочь вам ознакомиться с жизненно важными формулами для успешной сдачи теста.

Вот обзор математических/количественных рассуждений формул на экзамене GRE , которые вы должны запомнить.

---

Темы математического раздела GRE

Математический раздел GRE называется Quantitative Reasoning или Quant, и он входит в число трех разделов, тестируемых в GRE General Test. В каждом разделе есть два раздела Quant, каждый из которых состоит из 20 вопросов, которые вы должны ответить в течение 35 минут на каждый раздел.

У вас будет экранный калькулятор, если вы выполняете компьютерный тест, а если вы выполняете бумажный тест, калькулятор будет предоставлен в центре Prometric. Для многих это самый сложный раздел GRE.

Квантовый раздел охватывает математические понятия, изучаемые в средней и старшей школе, и не проверяет понятия более высокого уровня, такие как тригонометрия. Однако в Quant рассматриваются четыре основные темы: алгебра, арифметика, анализ данных и геометрия.

Алгебра

Алгебра включает в себя то, где в игру вступают неизвестные и известные числа. Тестируемые концепции включают неравенства, уравнения, выражения, константы и переменные, функции, геометрию координат, системы координат, факторизации, а также линии и наклоны.

Арифметика

Арифметика — это основа всего, что изучают в математике, и в основном это манипуляции с числами. Раздел Quant в основном касается умножения, деления, сложения и вычитания. Рассматриваемые темы включают абсолютные числа, квадратные корни и показатели степени, простые числа, порядок операций, дроби, десятичные и целые числа, последовательности, процентные изменения, отношения и пропорции.

Геометрия

Геометрия в основном имеет дело с углами и формами. Вопросы охватывают типы углов, соотношения углов, параллельные и перпендикулярные линии, окружности, секторы и дуги. Другими темами являются многоугольники, включая прямоугольники, квадраты, трапеции, треугольники и параллелограммы, периметр, площадь, окружность и площадь поверхности, а также твердые тела и подобные формы.

Анализ данных

Анализ данных включает интерпретацию данных, и вопросы будут касаться частоты и распределения данных, стандартного отклонения, факториалов, комбинаций и перестановок, процентилей и квартилей, статистики, графиков, вероятности и нормального распределения.

---

Какие распространенные математические формулы GRE следует запомнить?

Очень важно запомнить Математические формулы , если вы хотите получить хороший результат в разделе GRE Quant. Понимание формул и знание того, когда их применять, помогут вам быстро и точно отвечать на вопросы, что приведет к высокому баллу.

Кроме того, высокие баллы по Quant повышают ваши шансы на поступление в аспирантуру. Уравнения иногда являются ключом к решению какой-либо квантовой задачи. К сожалению, если вы не помните количественную формулу, вам будет сложно ответить на вопрос, и в конечном итоге вы можете выбрать неправильный ответ.

Хотя иногда запоминание математических формул не обязательно для решения задачи, понимание уравнений может сэкономить время и сократить сложные вычисления. Вы идете в ногу со временем, и вам не следует тратить много времени на один вопрос.

---

Список математических формул GRE

Вот список из 10 математических формул GRE , которые вы должны знать для теста GRE:

1. Площадь треугольника
2. Теорема Пифагора
3. Площадь прямоугольника
4. Площадь круга
5. Площадь трапеции
6. Площадь цилиндра
7. Формула уклона
8. Уравнения интегрирования
9. Формулы дифференциации
10. Грех, загар, детская кроватка

---

Шпаргалка по математическим формулам GRE

Вот шпаргалка для запоминания математических формул на тесте GRE .

Каждый раздел разбит по темам экзамена, включая геометрию, алгебру, исчисление и дифференцирование.

---

Геометрия

Треугольник

Площадь треугольника рассчитывается:

Площадь = ½ базовой высоты x (½ млн. Б.0009 высота

Теорема Пифагора используется для вычисления длины стороны прямоугольного треугольника. Квадрат наибольшей стороны равен сумме двух коротких сторон.

Мера внутренних углов n-стороннего многоугольника: (n-2)x180/n.

---

Прямоугольник

Площадь прямоугольника вычисляется путем умножения длины и ширины.

A= длина x ширина (lw) или A=½(диагональ)²

Периметр прямоугольника равен сумме длины и ширины, умноженной на 2

P= 2(длина + ширина)

---

Окружность

Площадь окружности вычисляется путем умножения числа пи (π ) с радиусом (r ² )

Площадь = πr ²

Где π — константа, представленная числом 3,14159, а r — половина длины линии, делящей окружность (диаметр) на две половины

Окружность круга — это расстояние по окружности, рассчитанное путем умножения числа пи на диаметр.

Длина окружности = πD или 2πr

---

Трапеция

Площадь трапеции: A=½(основание₁+основание₂)(высота).

Площадь = ½ (a+b)h

Это распространенная математическая формула в тесте GRE, которую неправильно понимают. Обратите особое внимание на то, как использовать это в различных типах задач.

---

Цилиндр

Площадь поверхности цилиндра с верхом и низом.

Площадь = 2πrh+2πr²

Где π= 3,14159, r — радиус цилиндра, а h — высота цилиндра

Эта формула используется в различных практических задачах.

---

Алгебра

Наклон

Наклон — это градиент только по представленному m, который является функцией изменения по оси Y, деленного на изменение по оси x. Если линия имеет две точки (X ₁ , Y ₁₎ и (X ₂ , Y ₂ )

Уравнение линии: Y= MX =C

Где Y — координата, x — координата x, M — уклон, c — Y -intercept

Расстояние между двумя точками на графике равно √( x2- x1)+(y2-y1)

---

Исчисление

Интегрирование – это процесс непрерывного сложения с переменной C, представляющей константу интегрирования. Интегральные уравнения, которые вы должны помнить, чтобы помочь вам в Quant, включают:

xn dx = x(n+1) / (n+1) + C,(n -1)

bx dx = bx / ln(b) + C

sin x dx = -cos x + C

tan x dx = -ln|COs x| + C

---

Дифференцирование

Дифференцирование включает в себя нахождение производной функции, которая определяется как Y=f(X). это мера скорости изменения переменной y относительно изменения переменной x. Некоторые дифференциальные формулы, которые следует запомнить, включают:

sin x = cos x

cot x = – csc2 x

кроватка h x = 1 – кроватка h3 x

sinx x = ch x

---

GRE Math & Quantic Formula Study Tips

Главный совет – это знание основ путем знакомства с математическими понятиями, правилами и формулами, относящимися к геометрии. , арифметика, алгебра и анализ данных.

Всегда старайтесь запоминать стандартные формулы, потому что они жизненно важны для решения задач Quant. В отличие от других стандартизированных тестов, в математическом разделе GRE нет списка формул. Постарайтесь понять, где применяются формулы, чтобы сэкономить время.

Вы можете сделать карточки для изучения определенных понятий и уравнений. Самое главное, вы можете использовать их при изучении символов и математических терминов. В равной степени отработка реалистичных практических количественных вопросов может помочь вам освоить формулы.

 

Учебник — Математические уравнения в LaTeX

Содержание

LaTeX предоставляет функцию специального инструмента редактирования для научного инструмента для математических уравнений в LaTeX. В этом статье вы узнаете, как писать основные уравнения и конструкции в LaTeX, о выравнивании уравнений, растягиваемые горизонтальные линии, операторы и разделители, дроби и двучлены.

Для написания математических уравнений в LaTeX существует два режима записи: встроенный режим и режим отображения. встроенный режим используется для записи формул, которые являются частью текста, а режим отображения используется для записи выражения, которые не являются частью текста и, следовательно, располагаются на разных строках. 2.

2. Уравнение: Математические выражения, представленные в строке, называются выражениями. Они в основном размещены в центре страницы, и уравнения являются важными, которые заслуживают внимания. выделено. Встроенное выражение должно быть помещено между \[ и \].

3. Стиль отображения: Команда \displaystyle используется для получения полноразмерного встроенного выражение.

Формула состоит из комбинации различных конструкций. Некоторые из них объясняются ниже:

1. Арифметические операции:

• Арифметические уравнения печатаются со знаком доллара. Например, $a + b$, $a — b$, $-a$, $a / b$, $a б$. Существуют разные формы умножения и деления: $a \cdot b$, $a \times b$, $a \дел б$.

• Дроби набираются командой \frac путем подстановки знаменателя и числителя с отдельными фигурными скобками. 9{\dagger}$, где {} означает пустую группу.
  

• Команды \sb и \sp используются для нижних и верхних индексов соответственно.
  

2. Биномиальные коэффициенты:

3. Эллипсы:

• Имеются два эллипса внизу или на линии эллипсы и эллипсы по центру.

• Низкие эллипсы или эллипсы на линии имеют тип F(x_{1}, x_{2}, \dots, x_{n}) и центрированные эллипсы вводятся как x_{1} + x_{2} + \dots + x_{n}.
  

• LaTeX дает команду \ldots для различения низких и \bdots для центрированных эллипсов.
  

Другие варианты команды \dots: \dotsc для эллипса, за которым следует запятая, \dotsb для эллипса за которым следует бинарная операция, \dotsm, если следует умножение, \dotsi для эллипса с интегралом и \dotso для «другого» эллипса. {2}}$ дают и соответственно.

Можно ввести с помощью выражения $\sqrt[g]{5}$, а положение «g» можно изменить, предоставив дополнительные команды: \leftroot перемещает ‘g’ влево или вправо с отрицательным аргументом, а \uproot перемещает «g» вверх или вниз с отрицательным атрибутом.

Мы используем среду уравнений, чтобы обернуть наше уравнение, или мы можем использовать уравнение, если мы хотим, чтобы оно было пронумеровано. Разделение среды используется внутри среды уравнения для разделения уравнения на более мелкие части, которые будет выровнено соответственно. 92 \конец{разделить} \end{уравнение} \конец{документ}

Вывод вышеуказанного кода

Уравнения, в которых используется более одной строки, используют многострочную среду. Мы используем двойную обратную косую черту, чтобы установить точка, где уравнение должно быть нарушено. 2 — х \end{многострочный*} \конец{документ}

Вывод приведенного выше кода

Мы используем среду выравнивания с * для определения того, пронумеровано уравнение или нет.

\documentclass{статья}
\usepackage[utf8]{inputenc}
\usepackage{аммат}
\начать{документ}
\начать{выравнивать*}
а+б и а-б и (а+б)(а-б)\\
х+у и х-у и (х+у)(х-у)\\
p+q & p-q & (p+q)(p-q)
\конец{выравнивание*}
\конец{документ}

 

Вывод вышеуказанного кода

Математическое уравнение в LaTeX предоставляет три растягиваемые линии/стрелки, которые появляются над или под уравнением: фигурные скобки, бары и стрелки. Команда \overbrace помещает фигурную скобку над выражением (или переменные), а команда \underbrace ставит фигурную скобку под выражением. Команда \overline и \underline помещает строку выше или ниже выражения. Команда \overleftarrow а \overrightarrow помещает стрелку выше или ниже выражения. Выражение должно быть пишется между фигурными скобками. 92-2аб \end{собрать*} \конец{документ}

Вывод вышеуказанного кода

Круглые скобки очень часто встречаются в математических уравнениях. Мы можем изменить размер скобки в математические уравнения в LaTeX.

\documentclass{статья}
\usepackage[utf8]{inputenc}
\usepackage{аммат}
\начать{документ}
\[
\оставил \{
\begin{табличный}{ccc}
1 и 5 и 8 \\
0 и 2 и 4 \\
3 и 3 и -8
\end{табличный}
\Правильно \}
\]
\конец{документ}

 92(а) = 1
\]
\конец{документ}

 

Вывод вышеуказанного кода

Операторы, принимающие параметры, написаны особым образом. Например, в предельном уравнении предел объявление включает индекс.

\documentclass{статья}
\usepackage[utf8]{inputenc}
\usepackage{аммат}
\начать{документ}
\[
\lim_{h \rightarrow 0 } \frac{f(x+h)-f(x)}{h}
\]
Этот оператор изменяется при использовании вместе с
текст \( \lim_{x \rightarrow h} (xh) \).
\конец{документ}

 

Вывод вышеуказанного кода

Пользователь может определить или персонализировать своего оператора с помощью команды \DeclareMathOperator который принимает два параметра, первый — имя нового оператора, а второй — текст для отображаться. Если оператор использует индексы, используется команда \DeclareMathOperator*.

Дроби и биномиальные коэффициенты математических уравнений в LaTeX записываются с использованием \frac и \бином 9команда 0010 соответственно.

\documentclass{статья}
\usepackage[utf8]{inputenc}
\usepackage{аммат}
\начать{документ}
\[
\binom{n}{k} = \frac{n!}{k!(n-k)!}
\]
\конец{документ}

 

Вывод приведенного выше кода

Мы используем команду \frac для отображения дробей. Выражение между первой парой в скобках числитель, а во второй знаменатель. Размер текста дроби меняется судя по тексту рядом. Вы также можете установить размер текста дроби вручную с помощью команды \displaystyle.

\documentclass{статья}
\usepackage[utf8]{inputenc}
\usepackage{аммат}
\начать{документ}
\[ f(x)=\frac{P(x)}{Q(x)} \ \ \textrm{and}
\ \ f(x)=\textstyle\frac{P(x)}{Q(x)} \]
\конец{документ}

 

Вывод вышеуказанного кода

Дроби могут быть вложены друг в друга для получения сложных выражений. Команда \cfrac отображает вложенные дроби без изменения размера текста. Пример этого приведен ниже:

\documentclass{статья}
\usepackage[utf8]{inputenc}
\usepackage{аммат}
\начать{документ}
\[ \frac{1+\frac{a}{b}}{1+\frac{1}{1+\frac{1}{a}}} \]
\конец{документ}

 

Вывод вышеуказанного кода

Не хотите тратить время на верстку документов вручную?

Конвертируйте Word в LaTeX прямо сейчас

Скопировано в буфер обмена!

9 распространенных математических формул в сфере недвижимости, которые вы должны знать

Независимо от того, готовитесь ли вы сдать экзамен по недвижимости или рассчитываете платеж по ипотеке для клиента, вам необходимо знать базовый уровень математики в сфере недвижимости агент.

Это руководство познакомит вас с типом математических навыков в сфере недвижимости, которые вы обнаружите на государственном экзамене, а также в каждой сделке с недвижимостью, которую вы совершаете после получения лицензии.

Если вы предпочитаете смотреть или слушать этот контент, посмотрите видео или подкаст ниже!

Математика недвижимости: что нужно знать для работы агентом

1. Отношение кредита к стоимости

Это самая распространенная математическая задача, с которой вы, вероятно, столкнетесь в своей карьере в сфере недвижимости. Соотношение кредита к стоимости следует следующей формуле:

Сумма кредита / оценочная стоимость имущества = отношение кредита к стоимости

Ответ на эту основную математическую задачу выражается в процентах. Таким образом, дом стоимостью 100 000 долларов и кредит в размере 80 000 долларов будет иметь отношение кредита к стоимости 80%, потому что 80 000/100 000 равно 0,8 или 80%.

2.

Правило 28/36 (соотношение квалификаций)

При работе с покупателем жилья чрезвычайно важно знать, на какую сумму он может претендовать. Сторона 28 правила 28/36 гласит, что покупатель может претендовать на 28 процентов своего валового ежемесячного дохода (до вычета налогов). Так, например, если покупатель жилья зарабатывает 10 000 долларов в месяц, он может претендовать на ипотечный платеж в размере около 2800 долларов.

36-я сторона правила учитывает дополнительные долговые платежи (автокредиты, студенческие кредиты, кредитные карты и т. д.). Здесь вы все еще можете умножить 10 000 долларов на 36 процентов, чтобы получить 3 600 долларов. Это означает, что их общая сумма платежей по долгу плюс ипотека должна быть ниже 3600 долларов.

3. Первоначальный взнос

Независимо от того, покупает ли покупатель инвестиционную недвижимость или дом для проживания, ему потребуется первоначальный взнос.

Для определения первоначального взноса используйте следующую математическую формулу:

Цена продажи x Процент авансового платежа = Сумма первоначального взноса

Таким образом, если цена покупки составляет 100 000 долларов США и покупатель использует традиционный первоначальный взнос в размере 20%, у вас будет:

100 000 долларов США x 0,2 = 20 000 долларов США Ставка

В инвестиционной собственности ставка капитализации представляет собой сумму, которую инвестор зарабатывает и получает домой в качестве дохода от собственности. Знание ставки капитализации помогает инвестору рассчитывать доход и поддерживать положительный денежный поток при управлении сдаваемой в аренду недвижимостью.

Используйте эту формулу:

Чистый операционный доход / Цена покупки = Максимальная ставка

Например, предположим, что у вас есть доходная сдаваемая в аренду собственность, которая стоит 500 000 долларов и приносит 50 000 долларов в виде арендной платы. Тем не менее, его обслуживание в течение года стоит 15 000 долларов. Расчет ставки капитализации будет выглядеть следующим образом:

(50 000–15 000 долл. США) / 500 000 долл. США = 7%

5. Возврат инвестиций

ROI показывает, сколько вы зарабатываете на конкретной инвестиции при ее продаже. Рассчитайте рентабельность инвестиций по этой формуле:

ROI = (Окончательная стоимость – Первоначальная стоимость) / Стоимость

Таким образом, если вы покупаете недвижимость за 250 000 долларов, а затем продаете ее за 280 000 долларов, ваш ROI будет выглядеть следующим образом:

(280 000–250 000 долларов) / 000 000 долларов США 12%

Имейте в виду, что это валовой доход от продажи. Любой ремонт, который инвестор сделал в собственности, также повлияет на то, сколько вы заработаете на продаже.

6. Пропорциональные налоги

Обычно большинство покупателей уплачивают пропорциональную сумму налога при закрытии сделки. Чтобы пропорционально распределить налоги, вы должны определить, какая сумма налога остается на недвижимость за календарный год.

Для этого найдите оставшееся количество дней в году и разделите его на 365. Это даст вам процент налога, который должен заплатить покупатель.

Затем возьмите этот процент и умножьте его на сумму, оставшуюся в налоговом счете. Это даст вам сумму налога на недвижимость, подлежащую уплате при закрытии.

7. Расчет платежей по ипотеке

Основная сумма и проценты

Основная сумма ипотечного кредита — это другое название первоначальной суммы кредита. Это полная сумма, которую покупатель занимает в банке. Например, если у покупателя есть 150 000 долларов наличными для внесения 25% первоначального взноса за дом стоимостью 600 000 долларов, ему потребуется первоначальная сумма кредита в размере 450 000 долларов в банке.

Чтобы определить ежемесячную процентную ставку по дому, вам необходимо знать годовую процентную ставку по ипотечным кредитам в вашем регионе. Вы можете получить этот номер у любого ипотечного кредитора на вашем рынке.

Затем разделите это число на 12, чтобы получить месячный процент. Так, например, если годовая процентная ставка составляла 3%, то месячная ставка была бы 0,25%.

Расчет ежемесячного платежа по ипотеке

Для расчета ежемесячного платежа по ипотеке (без учета страховки и налогов) вы можете использовать следующую формулу: 9360-1)

М = 2416 долларов

Очевидно, что если вы работаете с клиентом и не отвечаете на вопрос экзамена по недвижимости, гораздо проще просто использовать калькулятор выплат по ипотеке. Мне нравится использовать калькулятор ипотечных платежей Zillow, так как вы можете добавить PMI, страхование, ТСЖ, налоги и т. д. Или, если вы хотите загрузить приложение на свой телефон, вот приложение для iPhone и Android.

Ипотечное страхование

Частное ипотечное страхование (PMI) требуется, если покупатель вносит первоначальный взнос менее 20% от покупной цены дома. Эта стоимость добавляется к ежемесячным платежам по ипотеке.

Стоимость PMI будет зависеть от того, что кредитор указывает в оценке кредита, но обычно она составляет от 0,2% до 2% от основной суммы ипотечного кредита. Обычно PMI заканчивается, когда у покупателя остается 20% акций дома.

Некоторые факторы, определяющие стоимость PMI:

• Срок кредита – более короткий срок означает, что ежемесячные платежи будут выше, но 20% собственного капитала будет достигнуто раньше.
• Соотношение кредита к стоимости – если покупатель вносит первоначальный взнос более 20%, PMI вообще не нужен.
• Кредитный рейтинг — более высокий кредитный рейтинг позволит покупателю получить более выгодную сделку по стоимости PMI.

Существует четыре типа PMI, о которых вам обычно следует знать:

• Ипотечное страхование, оплачиваемое заемщиком
• Ипотечное страхование с единой премией
• Ипотечное страхование с раздельной премией
• Страхование ипотечного кредита, оплачиваемое кредитором

24

Далее необходимо определить стоимость страховки домовладельца. Это будет зависеть от множества факторов, в том числе:

• Местоположение дома
• Потенциальная экспозиция стихийных бедствий
• Стоимость дома
• Уровень покрытия
• Суммаруемое количество
. )

В среднем домовладельцы в США могут рассчитывать на выплату около 1000 долларов в год за страхование домовладельца. Но чтобы получить точную оценку того, сколько это будет стоить вашему покупателю, вам нужно будет получить предложение от страховой компании.

Покупатели также могут претендовать на более низкие страховые ставки, добавив в свои дома некоторые средства безопасности, такие как детекторы дыма, штормовые жалюзи или новую крышу. Однако в конечном итоге цена будет зависеть от вышеперечисленных факторов.

Налоги на имущество

Наконец, вам нужно знать, как рассчитать налоги на имущество. Хотя правительство будет взимать налоги на недвижимость автоматически, все же полезно понимать, на какую сумму покупатель может рассчитывать заплатить.

Размер долга покупателя будет зависеть от двух цифр: ставки налога в районе, в котором он живет, и стоимости дома.

Стоимость дома — это не только цена покупки, которую заплатил покупатель. Чтобы узнать оценочную стоимость дома, вам нужно будет связаться с налоговым инспектором, который определил его стоимость, или просмотреть соответствующие записи об имуществе.

Получив оценочную стоимость, умножьте ее на налоговую ставку, чтобы получить годовой счет по налогу на недвижимость. Затем это число делится на 12, чтобы получить ежемесячную сумму, которая будет добавлена ​​к ипотечному платежу покупателя.

Имейте в виду, что в некоторых регионах также взимается налог на передачу собственности при продаже дома. Как правило, это оплачивает продавец, но вам все же следует об этом знать.

8. Множитель брутто-арендной платы

Множитель брутто-арендной платы (GRM) — это расчет, используемый для определения стоимости недвижимости. Он учитывает годовой доход от аренды и стоимость покупки недвижимости.

Чтобы использовать МРЖ, вам необходимо знать следующее:

• Годовой доход от аренды
• Цена покупки

Формула МРЖ: МРЖ = Цена покупки или стоимость / Валовой доход от аренды

Например, если недвижимость куплена за 200 000 долл. США, а годовой доход от аренды составляет 24 000 долл. США, МРЖ будет равен: МРЖ = 200 000 / 24 000 = 8,3·9.0005

Затем этот номер можно сравнить с аналогичными объектами недвижимости в этом районе, чтобы убедиться, что цена покупки справедлива. Вообще говоря, чем ниже GRM, тем лучше, так как это указывает на то, что недвижимость недооценена.

9. Цена за квадратный фут

Вероятно, это одна из самых простых, но наиболее часто используемых математических задач, которые вам придется решать на протяжении всей вашей карьеры. Вы будете использовать его при оценке как коммерческой, так и жилой недвижимости. Чтобы рассчитать цену за квадратный фут, просто возьмите продажную цену или стоимость недвижимости и разделите ее на квадратные метры.

Например, если дом площадью 2 000 квадратных футов куплен за 400 000 долларов, цена за квадратный фут будет следующей: 400 000 / 2 000 = 200 долларов

Этот расчет также можно использовать для определения стоимости квадратного фута недвижимости. . Поэтому, если вы знаете цену продажи или стоимость, вы можете использовать это уравнение, чтобы узнать приблизительную площадь недвижимости в квадратных футах.

Математика в сфере недвижимости: что нужно знать для подготовки к экзамену

Существует множество ипотечных калькуляторов, которые можно использовать, чтобы перепроверить свои математические расчеты и убедиться, что вы на правильном пути.

Однако вам необходимо знать все эти математические понятия, связанные с недвижимостью, чтобы успешно сдать экзамен на получение лицензии на недвижимость. Вы можете легко подготовиться, купив рабочие тетради или пройдя практические тесты, чтобы решить примеры математических задач по недвижимости.

Прочтите мой другой пост, чтобы узнать больше советов по сдаче экзамена по недвижимости.

No related posts.