Что такое молярный объем и в каких единицах он выражается: Что такое молярный объем и в каких единицах он выражается?…

Содержание

формулы чисел и молярная масса газа

Объем 1 моль вещества называют Молярным объемом Молярная масса 1 моль воды = 18 г/моль 18 г воды занимают объём 18 мл. Значит молярный объем воды равен 18 мл. 18 г воды занимают объем равный 18 мл, т.к. плотность воды равна 1 г/мл ВЫВОД: Молярный объем зависит от плотности вещества (для жидкостей и твердых веществ).

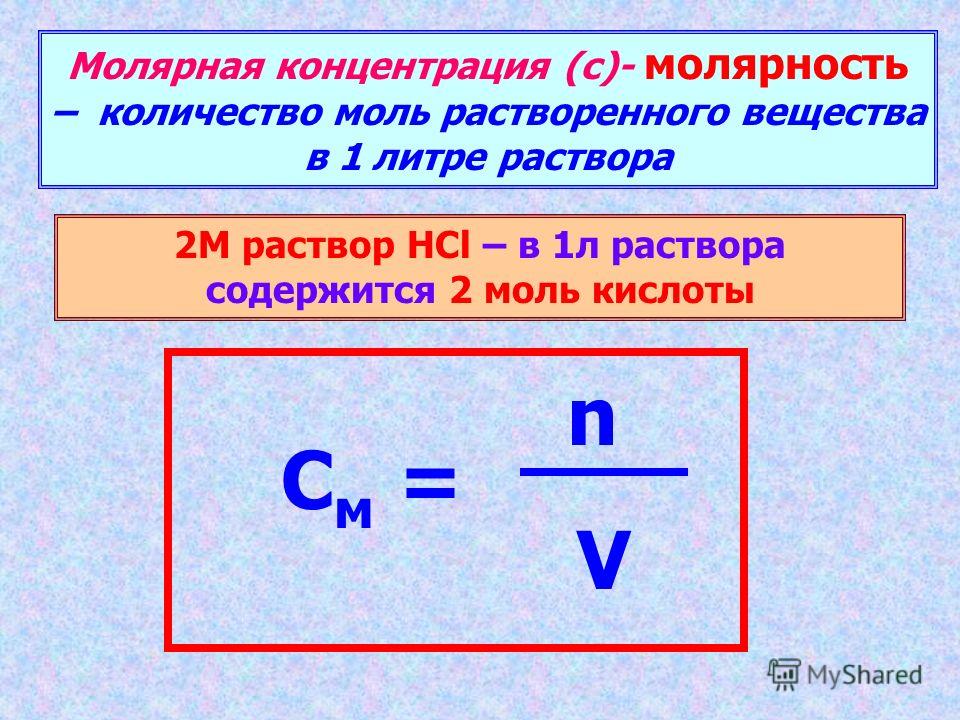
1 моль любого газа при нормальных условиях занимает один и тот же объем равный 22,4 л. Нормальные условия и их обозначения н.у. (0 0 С и 760 мм.рт.ст.; 1 атм.; 101,3 к Па). Объем газа количеством вещества 1 моль называют молярным объемом и обозначают – V m

Решение задач Задача 1 Дано: V(NH 3) н.у. = 33,6 м 3 Найти: m — ? Решение: 1. Рассчитываем молярную массу аммиака: М(NH 3) = = 17 кг/кмоль

ВЫВОДЫ 1. Объем 1 моль вещества называется молярным объемом V m 2. У жидких и твердых веществ молярный объем зависит от их плотности 3. V m = 22,4 л/моль 4. Нормальные условия (н.у.): и давление 760 мм.рт.ст., или 101,3 к Па 5. Молярный объем газообразных веществ выражается в л/моль, мл/ммоль,

Где m-масса,M-молярная масса, V- объем.

4. Закон Авогадро. Установлен итальянским физиком Авогадро в 1811 г. Одинаковые объемы любых газов, отобранные при одной температуре и одинаковом давлении, содержат одно и тоже число молекул.

Таким образом, можно сформулировать понятие количества вещества: 1 моль вещества содержит число частиц, равное 6,02*10 23 (называемое постоянной Авогадро)

Следствием этого закона является то, что 1 моль любого газа занимает при нормальных условиях (Р 0 =101,3кПа и Т 0 =298К) объём, равный 22,4л.

5. Закон Бойля-Мариотта

При постоянной температуре объем данного количества газа обратно пропорционален давлению, под которым он находится:

6. Закон Гей-Люссака

При постоянном давлении изменение объема газа прямо пропорционально температуре:

V/T = const.

7. Зависимость между объемом газа, давлением и температурой можно выразить объединенным законом Бойля-Мариотта и Гей-Люссака, которым пользуются для приведения объемов газа от одних условий к другим:

P 0 , V 0 ,T 0 -давление объема и температуры при нормальных условиях: P 0 =760 мм рт. ст. или 101,3 кПа; T 0 =273 К (0 0 С)

8. Независимая оценка значения молекулярноймассы М может быть выполнена с использованием так называемого уравнения состояния идеального газа или уравнения Клапейрона-Менделеева :

pV=(m/M)*RT=vRT. (1.1)

где р — давление газа в замкнутой системе, V — объем системы, т — масса газа, Т — абсолютная температура, R — универсальная газовая постоянная.

Отметим, что значение постоянной R может быть получено подстановкой величин, характеризующих один моль газа при н.у., в уравнение (1.1):

r = (р V)/(Т)=(101,325кПа 22. 4 л)/(1 моль 273К)=8.31Дж/моль.К)

Примеры решения задач

Пример 1. Приведение объема газа к нормальным условиям.

Какой объем (н.у.) займут 0,4×10 -3 м 3 газа, находящиеся при 50 0 С и давлении 0,954×10 5 Па?

Решение. Для приведения объема газа к нормальным условиям пользуются общей формулой, объединяющей законы Бойля-Мариотта и Гей-Люссака:

pV/T = p 0 V 0 /T 0 .

Объем газа (н.у.) равен , где Т 0 = 273 К; р 0 = 1,013×10 5 Па; Т = 273 + 50 = 323 К;

м 3 = 0,32×10 -3 м 3 .

При (н.у.) газ занимает объем, равный 0,32×10 -3 м 3 .

Пример 2. Вычисление относительной плотности газа по его молекулярной массе.

Вычислите плотность этана С 2 Н 6 по водороду и воздуху.

Решение. Из закона Авогадро вытекает, что относительная плотность одного газа по другому равна отношению молекулярных масс (М ч ) этих газов, т.е. D=М 1 /М 2 . Если М 1 С2Н6 = 30, М 2 Н2 = 2, средняя молекулярная масса воздуха равна 29, то относительная плотность этана по водороду равна D Н2 = 30/2 =15.

Относительная плотность этана по воздуху: D возд = 30/29 = 1,03, т.е. этан в 15 раз тяжелее водорода и в 1,03 раза тяжелее воздуха.

Пример 3. Определение средней молекулярной массы смеси газов по относительной плотности.

Вычислите среднюю молекулярную массу смеси газов, состоящей из 80 % метана и 20 % кислорода (по объему), используя значения относительной плотности этих газов по водороду.

Решение.

Часто вычисления производят по правилу смешения, которое заключается в том, что отношение объемов газов в двухкомпонентной газовой смеси обратно пропорционально разностям между плотностью смеси и плотностями газов, составляющих эту смесь. Обозначим относительную плотность газовой смеси по водороду через D Н2 . она будет больше плотности метана, но меньше плотности кислорода:

80D Н2 – 640 = 320 – 20D Н2 ; D Н2 = 9,6.

Плотность этой смеси газов по водороду равна 9,6. средняя молекулярная масса газовой смеси М Н2 = 2D Н2 = 9,6×2 = 19,2.

Пример 4. Вычисление молярной массы газа.

Масса0,327×10 -3 м 3 газа при 13 0 С и давлении 1,040×10 5 Па равна 0,828×10 -3 кг. Вычислите молярную массу газа.

Решение. Вычислить молярную массу газа можно, используя уравнение Менделеева-Клапейрона:

где m – масса газа; М – молярная масса газа; R – молярная (универсальная) газовая постоянная, значение которой определяется принятыми единицами измерения.

Если давление измерять в Па, а объем в м 3 , то R =8,3144×10 3 Дж/(кмоль×К).

Цель урока: сформировать понятие о молярном, миллимолярном и киломолярном объемах газов и единицах их измерения.

Задачи урока:

Обучающие – закрепить ранее изученные формулы и найти связь между объемом и массой, количеством вещества и числом молекул, закрепить и систематизировать знания учащихся.
Развивающие – развивать умения и навыки решать задачи, способности к логическому мышлению, расширять кругозор учащихся, их творческие способности, умения работать с дополнительной литературой, долговременную память, интерес к предмету.
Воспитательные

– воспитывать личности с высоким уровнем культуры, формировать потребность в познавательной деятельности.

Тип урока: Комбинированный урок.

Оборудование и реактивы: Таблица «Молярный объем газов», портрет Авогадро, мензурка, вода, мерные стаканы с серой, оксидом кальция, глюкозы количеством вещества 1 моль.

План урока :

Организационный момент (1 мин.)
Проверка знаний в виде фронтального опроса (10 мин.)
Заполнение таблицы (5 мин.)
Объяснение нового материала (10 мин.)
Закрепление (10 мин.)
Подведение итогов (3 мин.)
Домашнее задание (1 мин.)

Ход урока

1. Организационный момент.

2. Фронтальная беседа по вопросам.

Как называется масса 1 моля вещества?

Как связать молярную массу и количество вещества?

Чему равно число Авогадро?

Как связано число Авогадро и количество вещества?

А как связать массу и число молекул вещества?

3.

А теперь заполните таблицу, решив задачи – это групповая работа.

Формула, вещества	Масса, г	Молярная масса, г/моль	Количество вещества, моль	Число молекул	Число Авогадро, молекул/моль
ZnO	?	81 г/моль	? моль	18 10 23 молекул	6 10 23
MgS	5,6г	56 г/моль	? моль	?	6 10 23
BaCl 2	?	? г/моль	0,5 моль	3 10 23 молекул	6 10 23

4.

Изучение нового материала.

«…Мы хотим не только знать, как устроена природа (и как происходят природные явления), но и по возможности достичь цели, может быть, утопической и дерзкой на вид, – узнать, почему природа является именно такой, а не другой. В этом ученые находят наивысшее удовлетворение.»
Альберт Эйнштейн

Итак, наша цель найти наивысшее удовлетворение, как настоящие ученые.

А как называется объем 1 моля вещества?

От чего зависит молярный объем?

Чему будет равен молярный объем воды, если ее M r = 18, а ρ = 1 г/мл?

(Конечно 18 мл).

Для определения объема вы пользовались формулой известной из физики ρ = m / V (г/мл, г/см 3 , кг/м 3)

Отмерим этот объем мерной посудой. Отмерим молярные объемы спирта, серы, железа, сахара. Они разные, т.к. плотность разная, (таблица различных плотностей).

А как обстоит дело у газов? Оказывается, 1 моль любого газа при н.у. (0°С и 760 мм.рт.ст.) занимает один и тот же объем молярный 22,4 л/моль (показывается на таблице).

А как будет называться объем 1 киломоля? Киломолярным. Он равен 22,4 м 3 /кмоль. Миллимолярный объем 22,4 мл/моль.

Откуда взялось это число?

Оно вытекает из закона Авогадро. Следствие из закона Авогадро: 1 моль любого газа при н.у. занимает объем 22,4 л/моль.

Немного о жизни итальянского ученого мы сейчас услышим. (сообщение о жизни Авогадро)

А теперь посмотрим зависимость величин от разных показателей:

Формула вещества	Агрегатное состояние (при н.у.)	Масса, г	Плотность, г/мл	Объем порций в 1 моль, л	Количество вещества, моль	Зависимость между объемом и количеством вещества
NaCl	Твердое	58,5	2160	0,027	1	0,027
H 2 O	Жидкое	18	1000	0,018	1	0,18
O 2	Газ	32	1,43	22,4	1	22,4
H 2	Газ	2	0,09	22,4	1	22,4
CO 2	Газ	44	1,96	22,4	1	22,4
SO 2	газ	64	2,86	22,4	1	22,4

Из сравнения полученных данных сделайте вывод (зависимость между объемом и количеством вещества для всех газообразных веществ (при н. у.) выражается одинаковой величиной, которая называется молярным объемом.)

Обозначается V m и измеряется л/моль и т.д. Выведем формулу для нахождения молярного объема

V m = V/ v , отсюда можно найти количество вещества и объем газа. А теперь вспомним ранее изученные формулы, можно ли их объединить? Можно получить универсальные формулы для расчетов.
m/M = V/V m ;
V/V m = N/Na

5. А теперь закрепим полученные знания с помощью устного счета, чтобы знания через умения стали применятся автоматически, то есть превратились в навыки.

За правильный ответ вы будите получать балл, по количеству баллов получите оценку.

Назовите формулу водорода?
Какова его относительная молекулярная масса?
Какова его молярная масса?
Сколько молекул водорода будет в каждом случае?
Какой объем займут при н.у. 3 г H 2 ?
Сколько будут весить 12 10 23 молекул водорода?
Какой объем займут эти молекулы в каждом случае?

А теперь решим задачи по группам.

Задача №1

Образец: Какой объем занимает 0,2 моль N 2 при н.у.?

Какой объем занимают 5 моль O 2 при н.у.?
Какой объем занимают 2,5 моль H 2 при н.у.?

Задача №2

Образец: Какое количество вещества содержит водород объемом 33,6 л при н.у.?

Задачи для самостоятельного решения

Решите задачи по приведённому образцу:

Какое количество вещества содержит кислород объемом 0,224 л при н.у.?
Какое количество вещества содержит углекислый газ объемом 4,48 л при н.у.?

Задача №3

Образец: Какой объем займут 56 г. газа СО при н.у.?

Задачи для самостоятельного решения

Решите задачи по приведённому образцу:

Какой объем займут 8 г. газа O 2 при н.у.?
Какой объем займут 64 г. газа SO 2 при н.у.?

Задача №4

Образец: В каком объеме содержится 3·10 23 молекул водорода H 2 при н.у.?

Задачи для самостоятельного решения

Решите задачи по приведённому образцу:

В каком объеме содержится 12,04 ·10 23 молекул водорода СO 2 при н. у.?
В каком объеме содержится 3,01·10 23 молекул водорода O 2 при н.у.?

Понятие относительной плотности газов следует дать на основании их знаний о плотности тела: D = ρ 1 /ρ 2 , где ρ 1 – плотность первого газа, ρ 2 – плотность второго газа. Вы знаете формулу ρ = m/V. Заменив в этой формуле m на М, а V на V m , получим ρ = М/V m . Тогда относительную плотность можно выразить, используя правую часть последней формулы:

D = ρ 1 /ρ 2 = М 1 /М 2 .

Вывод: относительная плотность газов – число, показывающее, во сколько раз молярная масса одного газа больше молярной массы другого газа.

Например, определите относительную плотность кислорода по воздуху, по водороду.

6. Подведение итогов.

Решите задачи для закрепления:

Найдите массу (н.у.): а) 6 л. О 3 ; б) 14 л. газа H 2 S?

Какой объём водорода при н.у. образуется при взаимодействии 0,23 г натрия с водой?

Какова молярная масса газа, если 1 л. его имеет массу 3,17 г. ? (Подсказка! m = ρ·V)

Для того, чтобы узнать состав любых газообразных веществ необходимо уметь оперировать такими понятиями, как молярный объем, молярная масса и плотность вещества. В данной статье рассмотрим, что такое молярный объем, и как его вычислить?

Количество вещества

Количественные расчеты проводят с целью, чтобы в реальности осуществить тот или иной процесс или узнать состав и строение определенного вещества. Эти расчеты неудобно производить с абсолютными значениями массы атомов или молекул из-за того, что они очень малы. Относительные атомные массы также в большинстве случаев невозможно использовать, так как они не связаны с общепринятыми мерами массы или объема вещества. Поэтому введено понятие количество вещества, которое обозначается греческой буквой v (ню) или n. Количество вещества пропорционально числу содержащихся в веществе структурных единиц (молекул, атомных частиц).

Единицей количества вещества является моль.

Моль – это такое количество вещества, которое содержит столько же структурных единиц, сколько атомов содержится в 12 г изотопа углерода.

Масса 1 атома равна 12 а. е. м., поэтому число атомов в 12 г изотопа углерода равно:

Na= 12г/12*1,66057*10в степени-24г=6,0221*10 в степени 23

Физическая величина Na называется постоянной Авогадро. Один моль любого вещества содержит 6,02*10 в степени 23 частиц.

Рис. 1. Закон Авогадро.

Молярный объем газа

Молярный объем газа – это отношение объема вещества к количеству этого вещества. Эту величину вычисляют при делении молярной массы вещества на его плотность по следующей формуле:

где Vm – молярный объем, М – молярная масса, а p – плотность вещества.

Рис. 2. Молярный объем формула.

В международной системе Си измерение молярного объема газообразных веществ осуществляется в кубических метрах на моль (м 3 /моль)

Молярный объем газообразных веществ отличается от веществ, находящихся в жидком и твердом состоянии тем, что газообразный элемент количеством 1 моль всегда занимает одинаковый объем (если соблюдены одинаковые параметры).

Объем газа зависит от температуры и давления, поэтому при расчетах следует брать объем газа при нормальных условиях. Нормальными условиями считается температура 0 градусов и давление 101,325 кПа. Молярный объем 1 моля газа при нормальных условиях всегда одинаков и равен 22,41 дм 3 /моль. Этот объем называется молярным объемом идеального газа. То есть, в 1 моле любого газа (кислород, водород, воздух) объем равен 22,41 дм 3 /м.

Рис. 3. Молярный объем газа при нормальных условиях.

Таблица «молярный объем газов»

В следующей таблице представлен объем некоторых газов:

Газ	Молярный объем, л
H 2	22,432
O 2	22,391
Cl 2	22,022
CO 2	22,263
NH 3	22,065
SO 2	21,888
Идеальный	22,41383

Что мы узнали?

Молярный объем газа, изучаемый по химии (8 класс) наряду с молярной массой и плотностью являются необходимыми величинами для определения состава того или иного химического вещества. Особенностью молярного газа является то, что в одном моле газа всегда содержится одинаковый объем. Этот объем называется молярным объемом газа.

Тест по теме

Оценка доклада

Средняя оценка: 4.3 . Всего получено оценок: 70.

Урок 1.

Тема: Количество вещества. Моль

Химия – это наука о веществах. А как измерять вещества? В каких единицах? В молекулах, из которых состоят вещества, но сделать это очень сложно. В граммах, килограммах или миллиграммах, но так измеряют массу. А что если объединить массу, которую измеряют на весах и число молекул вещества, возможно ли это?

а) H-водород

А н = 1а.е.м.

1а.е.м = 1,66*10 -24 г

Возьмем 1г водорода и подсчитаем количество атомов водорода в этой массе (предложите это сделать ученикам с помощью калькулятора).

N н = 1г / (1,66*10 -24) г = 6,02*10 23

б) O-кислород

А о = 16а.е.м = 16*1.67* 10 -24 г

N o = 16г / (16 *1.66 * 10 -24) г =6,02 * 10 23

в) C-углерод

А с = 12а. е.м = 12*1.67*10 -24 г

N c = 12г / (12* 1.66*10 -24) г = 6,02*10 23

Сделаем вывод: если мы возьмем такую массу вещества, которая равна атомной массе по величине, но взята в граммах, то там будет всегда (для любого вещества) 6.02 *10 23 атомов этого вещества.

H 2 O — вода

18г / (18* 1.66*10 -24) г =6,02*10 23 молекул воды и т.д.

N а = 6,02*10 23 — число или постоянная Авогадро .

Моль — количество вещества, в котором содержится 6,02 *10 23 молекул, атомов или ионов, т.е. структурных единиц.

Бывает моль молекул, моль атомов, моль ионов.

n – число молей,(число молей часто обозначают- ню),
N — число атомов или молекул,
N а = постоянная Авогадро.

Кмоль = 10 3 моль, ммоль = 10 -3 моль.

Показать портрет Амедео Авогадро на мультимедийной установке и кратко рассказать о нем, или поручить ученику подготовить небольшой доклад о жизни учёного.

Урок 2.

Тема « Молярная масса вещества»

Чему же равна масса 1 моля вещества? (Вывод учащиеся часто могут сделать сами. )

Масса одного моля вещества равна его молекулярной массе, но выражена в граммах. Масса одного моля вещества называется молярной массой и обозначается – M.

Формулы:

М — молярная масса,
n — число молей,
m — масса вещества.

Масса моля измеряется в г/моль, масса кмоля измеряется в кг/кмоль, масса ммоля измеряется в мг/моль.

Заполнить таблицу (таблицы раздаются).

Вещество	Число молекул N= N a n	Молярная масса M= (рассчитывается по ПСХЭ)	Число молей n ()=	Масса вещества m = M n
			5моль
Н 2 SO 4
	12 ,0 *410 26**

Урок 3.

Тема: Молярный объем газов

Решим задачу. Определите объем воды, масса которой при нормальных условиях 180 г.

Дано:

Т.е. объем жидких и твердых тел считаем через плотность.

Но, при расчёте объёма газов не обязательно знать плотность. Почему?

Итальянский ученый Авогадро определил, что в равных объемах различных газов при одинаковых условиях (давлении, температуре) содержится одинаковое число молекул — это утверждение называется законом Авогадро.

Т.е. если при равных условиях V(H 2) =V(O 2) , то n(H 2) =n(O 2), и наоборот если при равных условиях n(H 2) =n(O 2) то и объемы этих газов будут одинаковы. А моль вещества всегда содержит одно и тоже число молекул 6,02 *10 23 .

Делаем вывод – при одинаковых условиях моли газов должны занимать один и тот же объем.

При нормальных условиях (t=0, P=101,3 кПа. или 760 мм рт. ст.) моли любых газов занимают одинаковый объем. Этот объем называется молярным.

V m =22,4 л/моль

1кмоль занимает объём -22,4 м 3 /кмоль, 1ммоль занимает объем -22,4 мл/ммоль.

Пример 1. (Решается на доске):

Пример 2. (Можно предложить решить ученикам):

Дано:	Решение:
m(H 2)=20г V(H 2)=?

Предложить учащимся заполнить таблицу.

Вещество	Число молекул N = n N a	Масса вещества m = M n	Число молей n =	Молярная масса M= (можно определить по ПСХЭ)	Объем V=V m n

ХИМИЧЕСКИЙ ЭКВИВАЛЕНТ

Эквивалент – это реальная или условная частица, которая в кислотно-основных реакциях присоединяет (или отдает) один ион Н⁺ или ОН^–, в окислительно-восстановительных реакциях принимает (или отдает) один электрон, реагирует с одним атомом водорода или с одним эквивалентом другого вещества.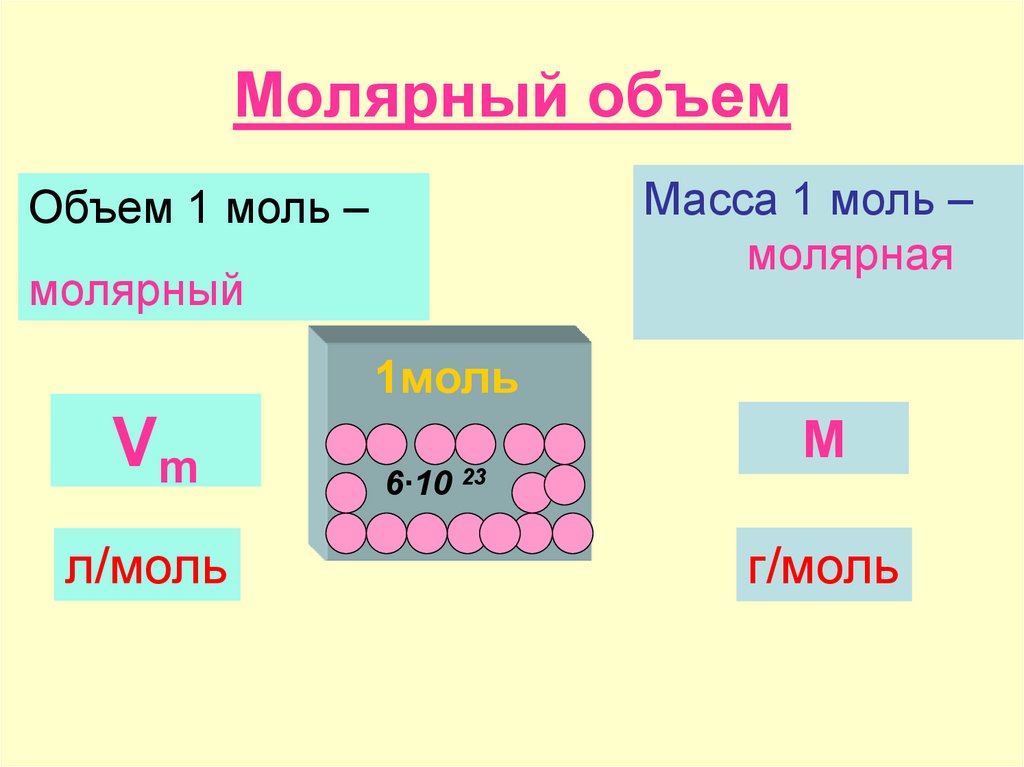 Например, рассмотрим следующую реакцию:

H₃PO₄ + 2KOH ® K₂HPO₄ + 2H₂O.

В ходе этой реакции только два атома водорода замещаются на атомы калия, иначе, в реакцию вступают два иона Н⁺(кислота проявляет основность 2). Тогда по определению эквивалентом H₃PO₄ будет являться условная частица 1/2H₃PO₄, т.к. если одна молекула H₃PO₄ предоставляет два иона Н⁺, то один ион Н⁺ дает половина молекулы H₃PO₄.

С другой стороны, на реакцию с одной молекулой ортофосфорной кислотой щелочь отдает два иона ОН^–, следовательно, один ион ОН^– потребуется на взаимодействие с 1/2 молекулы кислоты. Эквивалентом кислоты является условная частица 1/2Н₃РО₄, а эквивалентом щелочи частица КОН.

Число, показывающее, какая часть молекулы или другой частицы вещества соответствует эквиваленту, называется фактором эквивалентности (f_Э). Фактор эквивалентности – это безразмерная величина, которая меньше, либо равна 1. Формулы расчета фактора эквивалентности приведены в таблице 1.1.

Таким образом, сочетая фактор эквивалентности и формульную единицу вещества, можно составить формулу эквивалента какой-либо частицы, где фактор эквивалентности записывается как химический коэффициент перед формулой частицы:

f_Э (формульная единица вещества) º эквивалент

В примере, рассмотренном выше, фактор эквивалентности для кислоты, соответственно, равен 1/2, а для щелочи КОН равен 1.

Между H₃PO₄ и КОН также могут происходить и другие реакции. При этом кислота будет иметь разные значения фактора эквивалентности:

H₃PO₄ + 3KOH ® K₃PO₄ + 3H₂O f_Э(H₃PO₄) = 1/3

H₃PO₄ + KOH ® KН₂PO₄ + H₂O f_Э(H₃PO₄) = 1.

Следует учитывать, что эквивалент одного и того же вещества может меняться в зависимости от того, в какую реакцию оно вступает. Эквивалент элемента также может быть различным в зависимости от вида соединения, в состав которого он входит. Эквивалентом может являться как сама молекула или какая-либо другая формульная единица вещества, так и ее часть.

Таблица 1.1 – Расчет фактора эквивалентности

Частица

Фактор эквивалентности

Примеры

Элемент

где В(Э) – валентность элемента

Простое вещество

где n(Э) – число атомов элемента (индекс в химической формуле), В(Э) – валентность элемента

f_Э(H₂) = 1/(2×1) = 1/2;

f_Э(O₂) = 1/(2×2) = 1/4;

f_Э(Cl₂) = 1/(2×1) = 1/2;

f_Э(O₃) = 1/(3×2) = 1/6

Оксид

где n(Э) – число атомов элемента (индекс в химической формуле оксида), В(Э) – валентность элемента

f_Э(Cr₂O₃) = 1/(2×3) = 1/6;

f_Э(CrO) = 1/(1×2) = 1/2;

f_Э(H₂O) = 1/(2×1) = 1/2;

f_Э(P₂O₅) = 1/(2×5) = 1/10

Кислота

где n(H⁺) – число отданных в ходе реакции ионов водорода (основность кислоты)

f_Э(H₂SO₄) = 1/1 = 1 (основность равна 1)

или

f_Э(H₂SO₄) = 1/2

(основность равна 2)

Основание

где n(ОH^–) – число отданных в ходе реакции гидроксид-ионов (кислотность основания)

f_Э(Cu(OH)₂) = 1/1 = 1 (кислотность равна 1) или

f_Э(Cu(OH)₂) = 1/2

(кислотность равна 2)

Соль

где n(Ме) – число атомов металла (индекс в химической формуле соли), В(Ме) – валентность металла; n(А) – число кислотных остатков, В(А) – валентность кислотного остатка

f_Э(Cr₂(SO₄)₃) = 1/(2×3) = 1/6 (расчет по металлу) или

f_Э(Cr₂(SO₄)₃) = 1/(3×2) = 1/6 (расчет по кислотному остатку)

Частица в окислительно-восстановительных реакциях

где – число электронов, участвующих в процессе окисления или восстановления

Fe²⁺ + 2® Fe⁰

f_Э(Fe²⁺) =1/2;

MnO₄^– + 8H⁺ + 5 ® ® Mn²⁺ + 4H₂O

f_Э(MnO₄^–) = 1/5

Ион

где z – заряд иона

f_Э(SO₄^2–) = 1/2

Пример. Определите фактор эквивалентности и эквивалент у солей: а) ZnCl₂, б) КНСО₃, в) (MgOH)₂SO₄.

Решение: Для расчетов воспользуемся формулами, приведенными в таблице 1.1.

а) ZnCl₂ (средняя соль):

f_Э(ZnCl₂) = 1/2, поэтому эквивалентом ZnCl₂ является частица 1/2ZnCl₂.

б) КНСО₃ (кислая соль):

f_Э(КНСО₃) = 1, поэтому эквивалентом КНСО₃ является частица КНСО₃.

в) (MgOH)₂SO₄ (основная соль):

f_Э( (MgOH)₂SO₄ ) = 1/2, поэтому эквивалентом (MgOH)₂SO₄ является частица 1/2(MgOH)₂SO₄.

Эквивалент, как частица, может быть охарактеризован молярной массой (молярным объемом) и определенным количеством вещества n_э. Молярная масса эквивалента (М_Э) – это масса одного моль эквивалента. Она равна произведению молярной массы вещества на фактор эквивалентности:

М_Э = М×f_Э.

Молярная масса эквивалента имеет размерность «г/моль».

Молярная масса эквивалента сложного вещества равна сумме молярных масс эквивалентов образующих его составных частей, например:

М_Э(оксида) = М_Э(элемента) + М_Э(О) = М_Э(элемента) + 8

М_Э(кислоты) = М_Э(Н) + М_Э(кислотного остатка) = 1 + М_Э(кислотного остатка)

М_Э(основания) = М_Э(Ме) + М_Э(ОН) = М_Э(Ме) + 17

М_Э(соли) = М_Э(Ме) + М_Э(кислотного остатка).

Газообразные вещества помимо молярной массы эквивалента имеют молярный объем эквивалента ( или V_Э) – объем, занимаемый молярной массой эквивалента или объем одного моль эквивалента. Размерность «л/моль». При н.у. получаем:

Закон эквивалентов был открыт в 1792 г. И. Рихтером. Современная формулировка закона: вещества реагируют и образуются согласно их эквивалентам. Все вещества в уравнении реакции связаны законом эквивалентов, поэтому:

n_э(реагента₁) = … = n_э(реагента_n) = n_э(продукта₁) = … = n_э(продукта_n)

Из закона эквивалентов следует, что массы (или объемы) реагирующих и образующихся веществ пропорциональны молярным массам (молярным объемам) их эквивалентов. Для любых двух веществ, связанных законом эквивалентов, можно записать:

или или ,

где m₁ и m₂ – массы реагентов и (или) продуктов реакции, г;

, – молярные массы эквивалентов реагентов и (или) продуктов реакции, г/моль;

V₁, V₂ – объемы реагентов и (или) продуктов реакции, л;

,– молярные объемы эквивалентов реагентов и (или) продуктов реакции, л/моль.

Л.А. Яковишин

Объемный и массовый расход газа

Расход газа – это количество газа, прошедшего через поперечное сечение трубопровода за единицу времени. Вопрос в том, что принять за меру количества газа. В этом качестве традиционно выступает объем газа, а получаемый расход называют объемным. Не случайно чаще всего расход газа выражают в объемных единицах (см3/мин, л/мин, м3/ч и т.д.). Другой мерой количества газа является его масса, а соответствующий расход называется массовым. Он измеряется в массовых единицах (например, г/с или кг/ч), которые на практике встречаются значительно реже.

Как объем связан с массой, так и объемный расход связан с массовым через плотность вещества:
, где – массовый расход, – объемный расход, – плотность газа в условиях измерения (рабочие условия). Пользуясь этим соотношением, для массового расхода переходят к использованию объемных единиц (см3/мин, л/мин, м3/ч и т.д.), но с указанием условий (температуру и давление газа), определяющих плотность газа. В России применяют «стандартные условия» (ст.): давление 101,325 кПа (абс) и температура 20°С. Помимо «стандартных», в Европе используют «нормальные условия» (н.): давление 101,325 кПа (абс) и температура 0°С. В результате, получаются единицы массового расхода н.л/мин, ст.м3/ч и т.д.

Итак, расход газа бывает объемным и массовым. Какой из них следует измерять в конкретном применении? Как наглядно увидеть разницу между ними? Давайте рассмотрим простой эксперимент, где три расходомера последовательно установлены в магистраль. Весь газ, поступающий на вход схемы, проходит через каждый из трех приборов и выбрасывается в атмосферу. Утечек или накопления газа в промежуточных точках системы не происходит.

Источником сжатого воздуха является компрессора, от которого под давлением 0,5…0,7 бар (изб) газ подаётся на вход поплавкового ротаметра. Выход ротаметра подключен ко входу теплового регулятора расхода газа серии EL-FLOW, производства компании Bronkhorst. В нашей схеме именно он регулирует количество газа, проходящее через систему. Далее газ подаётся на вход второго поплавкового ротаметра, абсолютно идентичного первому. При задании расхода 2 н.л/мин с помощью расходомера EL-FLOW первый поплавковый ротаметр дает показания 1,65 л/мин, а второй – 2,1 л/мин.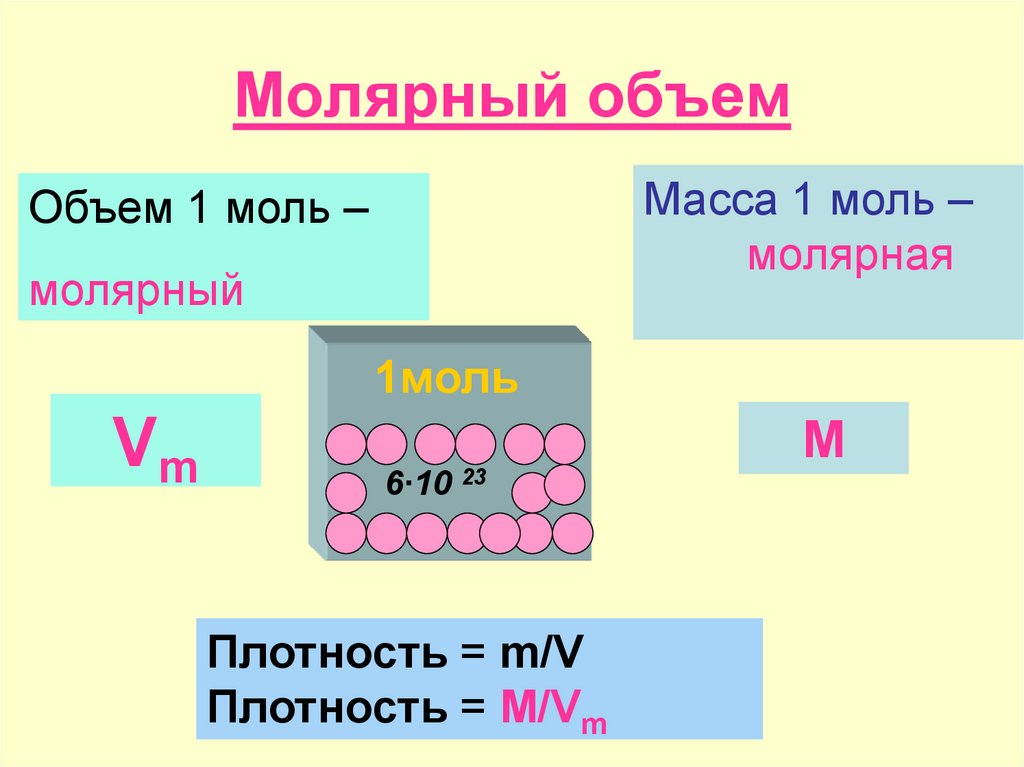 Все три расходомера дают различные показания, причем разница достигает 30%. Хотя через каждый прибор проходит одно и то же количество газа.

Попробуем разобраться. Какая мера количества газа в данной ситуации остается постоянной: объем или масса? Ответ: масса. Все молекулы газа, попавшие на вход в систему, проходят через нее и выбрасываются в атмосферу после прохождения второго поплавкового ротаметра. Молекулы как раз и являются носителями массы газа. При этом удельный объем (расстояние между молекулами газа) в разных частях системы изменяется вместе с давлением.

Здесь следует вспомнить, что газы сжимаемы, чем выше давление, тем меньше объем занимает газ (закон Бойля-Мариотта). Характерный пример: цилиндр емкостью 1 литр, герметично закрытый подвижным поршнем малого веса. Внутри него содержится 1 литр воздуха при давлении порядка 1 бар (абс). Масса такого объема воздуха при температуре равной 20°С составляет 1,205 г. Если переместить поршень на половину расстояния до дна, то объем воздуха в цилиндре сократится наполовину и составит 0,5 литра, а давление повысится до 2 бар (абс), но масса газа не изменится и по-прежнему составит 1,205 г. Ведь общее количество молекул воздуха в цилиндре не изменилось.

Возвратимся к нашей системе. Массовый расход (количество молекул газа, проходящих через любое поперечное сечение в единицу времени) в системе постоянен. При этом давление в разных частях системы отличается. На входе в систему, внутри первого поплавкового ротаметра и в измерительной части расходомера EL-FLOW давление составляет порядка 0,6 бар (изб). В то время, как на выходе EL-FLOW и внутри второго поплавкового ротаметра давление практически атмосферное. Удельный объем газа на входе ниже, чем на выходе. Получается, что и объемный расход газа на входе ниже, чем на выходе.

Эти рассуждения подтверждаются и показаниями расходомеров. Расходомер EL-FLOW измеряет и поддерживает массовый расход воздуха на уровне 2 н.л/мин. Поплавковые ротаметры измеряют объемный расход при рабочих условиях. Для ротаметра на входе это: давление 0,6 бар (изб) и температура 21°С; для ротаметра на выходе: 0 бар (изб), 21°С. Также понадобится атмосферное давление: 97,97 кПа (абс). Для корректного сравнения показаний объемного расхода, все показания должны быть приведены к одним и тем же условиям. Возьмем в качестве таковых «нормальные условия» расходомера EL-FLOW: 101,325 кПа (абс) и температура 0°С.

Пересчет показаний поплавковых ротаметров в соответствии с методикой поверки ротаметров ГОСТ 8.122-99 осуществляется по формуле:

, где Q – расход при рабочих условиях; Р и Т – рабочие давление и температура газа; Q_С – расход при условиях приведения; Рс и Тс – давление и температура газа, соответствующие условиям приведения.

Пересчет показаний ротаметра на входе к нормальным условиям по этой формуле даёт значение расхода 1,985 л/мин, а ротаметра на выходе – 1,990 л/мин. Теперь разброс показаний расходомеров не превышает 0,75%, что при точности ротаметров 3% ВПИ является отличным результатом.

Из приведенного примера видно, что объемный расход сильно зависит от рабочих условий. Мы показали зависимость от давления, но в той же мере объемный расход зависит и от температуры (закон Гей-Люссака). Даже в технологической схеме, имеющей один вход и один выход, где отсутствуют утечки и накопление газа, показания объемного расходомера будут сильно зависеть от конкретного места установки. Хотя массовый расход будет одним и тем же в любой точке такой схемы.

Хорошо понимать физику процесса. Но, все же, какой расходомер выбрать: объемного расхода или массового? Ответ зависит от конкретной задачи. Каковы требования технологического процесса, с каким газом необходимо работать, величина измеряемого расхода, точность измерений, рабочие температура и давление, особые правила и нормы, действующие в Вашей сфере деятельности, и, наконец, отведенный бюджет. Также следует учитывать, что многие расходомеры, измеряющие объемный расход, могут комплектоваться датчиками температуры и давления. Они поставляются вместе с корректором, который фиксирует показания расходомера и датчиков, а затем приводит показания расходомера к стандартным условиям.

Но, тем не менее, можно дать общие рекомендации. Массовый расход важен тогда, когда в центре внимания находится сам газ, и необходимо контролировать количество молекул, не обращая внимания на рабочие условия (температура, давление). Здесь можно отметить динамическое смешение газов, реакторные системы, в том числе каталитические, системы коммерческого учета газов.

Измерение объемного расхода необходимо в случаях, когда основное внимание уделяется тому, что находится в объеме газа. Типичные примеры – промышленная гигиена и мониторинг атмосферного воздуха, где необходимо проводить количественную оценку загрязнений в объеме воздуха в реальных условиях.

Молярный объем — Citizendium

Основной артикул

Обсуждение

Статьи по теме ^[?]

Библиография ^[?]

Внешние ссылки ^[?]

Версия для цитирования ^[?]

Эта редактируемая основная статья в разработке и подлежит отказу от ответственности . [изменить введение]

Молярный объем (обозначение V _м ) вещества – это объем, занимаемый одним молем вещества при данной температуре и давлении. ^[1] ^[2] Равен молекулярной массе ( M ) вещества, деленной на его плотность ( ρ ) при заданных температуре и давлении:

Vm = Mρ {\ displaystyle V _ {\ mathrm {m}} = {M \ over \ rho}}

Он имеет единицу СИ кубических метров на моль (м ³ /моль ). ^[1] ^[2] Однако молярные объемы часто выражаются в кубических метрах на 1000 молей (м ³ /кмоль) или кубических дециметрах на моль (дм ³ /моль) для газов и в сантиметрах на моль (см ³ /моль) для жидкостей и твердых тел. 9{N}x_{i}M_{i}}{\rho _{\mathrm {смесь} }}}}

где x _i — мольная доля i-го компонента, M _i – молекулярная масса i-го компонента, ρ _смеси – плотность смеси при данных температуре и давлении.

При указании числовых значений молярного объема важно также указать заданные условия температуры и давления. В противном случае числовые значения не имеют смысла.

Идеальные газы

Уравнение закона идеального газа можно изменить, чтобы получить следующее выражение для молярного объема идеального газа:

Где в Единицы СИ:

Р	= абсолютное давление газа в Па
нет	= количество молей в молях
В _м	= молярный объем газа, м ³ /моль
Т	= абсолютная температура газа в K
Р	= универсальная газовая постоянная 8,314472 м ³ ·Па·моль ^-1 ·K ^-1

Где в американских единицах измерения:

90 165 = количество молей в фунт-моль

нет
Р	= абсолютное давление газа в фунтах на квадратный дюйм
В _м	= молярный объем газа в футах ³ /фунт-моль
Т	= абсолютная температура газа в градусах Ренкина (°R)
Р	= универсальная газовая постоянная 10,7316 футов ³ ·psia·фунт-моль ^-l ·°R ^-1

Пример расчета молярных объемов идеального газа:

в метрических единицах SI:

В _M = 8,314472 × 273,15 / 10115 = 0,022414 M 2 ^{3 ^{3 ^{3 ^{3 ^{3 ^{3 ^{3 ^{3 ^{3 ^{3 ^{3 ^{3 ^{3 ^{3 ^{3 ^{3 ^{3 ^{3 ^{3 ^{3 ³ / 273,15 / 10115 = 0,1115.} /кмоль при 0 °C (273,15 K) и абсолютном давлении 101,325 кПа}}}}}}}}}}}}}}}}}}}

В _M = 8,314472 × 273,15 /100 000 = 0,022711 M ³ /KMOL при 0 ° C и 100 000 PA Абсолютное давление = 22,711 M ³ /KMOL при 0 ° C (273,15 K) и 100 KPA.

в обычных единицах США:

V _M = 10,7316 × 519,67 / 14,696 = 379,48 FT ^{3 ^{3 ³. psia}}

Примечания:

фунт-моль — это сокращение от фунт-моль
°R — это градусы Ранкина (абсолютная температурная шкала), а °F — градусы Фаренгейта (температурная шкала).
°R = °F + 459,67
Техническая литература может сбивать с толку, потому что некоторые авторы часто не могут объяснить, используют ли они универсальную газовую постоянную R , которая применима к любому идеальному газу, или используют конкретную газовую постоянную R _s , который применяется только к конкретному отдельному газу. Соотношение между двумя константами составляет R _с = R / M , где M — молекулярная масса газа.

Реальные газы

Реальные газы — это газы, поведение которых не является идеальным газом. Для таких газов простейшим методом определения молярных объемов является использование коэффициентов сжимаемости, как в следующем выражении:

где Z — коэффициент сжимаемости газа, который является полезным термодинамическим свойством для модификации закона идеального газа с учетом поведения реальных газов. ^[3] Приведенное выше уравнение в основном представляет собой простое уравнение состояния (УС). Основное ограничение этого уравнения состояния состоит в том, что коэффициент сжимаемости газа Z , не является постоянной величиной, а изменяется от одного газа к другому, а также в зависимости от температуры и давления рассматриваемого газа.

Более точные значения реальных молярных объемов газа можно получить, используя уравнения состояния, такие как уравнение Ван-дер-Ваальса, разработанное в 1873 г., уравнение Редлиха-Квонга, разработанное в 1949 г., уравнение Соава-Редлиха-Квонга, разработанное в 1972 г., и уравнение состояния. Уравнение Пенга-Робинсона разработано в 1976 г. ^[3]

Литература

↑ ^1.0 ^1.1 Международный союз теоретической и прикладной химии (IUPAC): количества, единицы и символы в физической химии, 2-е издание, 1993 г.
↑ ^2.0 ^2.1 Руководство NIST по СИ, пункт 8.6.3 в разделе 8
↑ ^3.0 ^3.1 Определение значений сжимаемости газа Информация о том, как определить коэффициенты сжимаемости газа и молярные объемы.

Молярный объем | Что это такое, для чего используется, формула, символ, примеры

Химия

В химии очень важно знать объем веществ, используемых для научных экспериментов, требующих предельной точности. Так как моль является одной из семи единиц измерения основных физических величин Международной системы единиц (СИ) , то необходимо знать объем, занимаемый молем вещества , чтобы уметь работать с это в области химии. В частном случае молекулярных газов моль содержит значение числа Авогадро (Na) и в соответствии с законом Авогадро, если идеальный газ находится в середине тех же условий давления и температуры, молярный объем этого газа будет равен молярному объему другого идеального газа при тех же условиях.

Обозначение : Vm
Единица измерения : л/моль

Что такое молярный объем?

Молярный объем – это пространство, занимаемое одним молем вещества. Этот термин используется в химии для определения молекулярного объема, выраженного в кубических метрах на моль (м ³ x моль ^-1 ). Моль — это единица измерения, предусмотренная Международной системой единиц, которая позволяет измерять и выражать определенное количество вещества. молярный объем идеального газа при нормальных условиях (давление 1 атмосфера и температура 0°C) равен 22,4 л/моль . Молярный объем можно вычислить в веществах в жидком, твердом и газообразном состояниях.

Важно отметить, что существует закон, определяющий, какие идеальные или совершенные газы и обычные или несовершенные газы, в которых значение молярного объема, равное 22,4 литра , не выполняется. Для других веществ в твердом или жидком состоянии молярный объем отличается и меньше, чем у газообразных веществ.

Какой молярный объем используется для
Символ
Формула молярного объема
Примеры

Какой молярный объем используется для

Он служит для определения объема, который вещество занимает в определенном пространстве 420 90. Это вещество может находиться в газообразном , жидком или твердом состоянии .

Обозначение

Обозначение молярного объема V _м .

Формула молярного объема

химическая формула для расчета объема: V= M/D . В случае молярного объема необходимо учитывать, являются ли эти вещества смесями газообразных или негазообразных элементов.

Для газообразных веществ формула V _m = V/N. Где V — объем, а N — число моль/грамм.

Важно помнить, что для расчета N используется формула N= m/M. Где m — вес образца, а M — его молекулярная масса. Другой способ расчета N — по формуле N = число молекул / N _и . Где N _a — это число Авогадро, равное 6,02 x 10 ²³ .

В смесях или негазообразных веществах они рассчитываются по формуле V _m = M (масса, выраженная в молях) / D (плотность, выраженная в см ³ ) .

Примеры

Ниже приведены некоторые примеры молярных объемов газа, этанола и кислорода.

Пример 1: молярный объем газа

При определении молярного объема газа 95 паскалей), а температура (273,15 К = 0 °С) равна 22,4 литра . Это значение является нормальным молярным объемом газа.

Существует закон идеальных газов, позволяющий распознать этот тип газа.

В случае обычных или неидеальных газов их молярный объем немного отличается от значения идеального газа. Это касается таких газов, как: диоксид серы (SO ₂ ) с молярным объемом 21,9 л или диоксид углерода (CO ₂ ) с молярным объемом 22,3 л. 9³ . Это вещество состоит из водорода (H), углерода (C) и кислорода (O).

Формула для веществ: масса/плотность . В этом смысле, чтобы узнать молярный объем этана, эта формула применяется со значениями этанола.

Vm= 46,07 г/моль/0,789г/см ³

Vm= 59,188 см ³ / моль

Пример 3: Молярный объем кислорода

Кислород считается идеальным газом, и по этой причине его молярный объем при нормальных условиях составляет 22,4 л на моль. Это означает, что если вы хотите рассчитать его точный объем в количестве X литров кислорода, вы должны применить правило трех, подобное следующему: у вас есть.

Автор: Габриэла Брисеньо В.

Объяснение урока: Молярный объем газа

В этом объяснении мы узнаем, как использовать молярный объем газа при стандартных условиях для расчета объема и количества молей газа.

В 1811 году Амедео Авогадро выдвинул гипотезу о том, что газы одинакового объема при одинаковых температурах и давлениях содержат такое же количество частиц газа. Эта гипотеза породила то, что мы теперь называем законом Авогадро. Закон Авогадро гласит, что объем образца газа прямо пропорциональна количеству молей газа при постоянном температура и давление.

Закон: Закон Авогадро

Закон Авогадро гласит, что при постоянной температуре и давлении объем и количество молей газа прямо пропорциональны.

Мы можем представить закон Авогадро с заявлением о пропорциональности 𝑉∝𝑛, где 𝑉 — объем газа, а 𝑛 — количество родинки.

Мы всегда должны понимать, что эта пропорция верна только до тех пор, пока температура и давление остаются постоянными. Заявление о пропорциональности показывает, что с увеличением количества молей газа увеличивается и объем, занимаемый газа, и наоборот.

Пример 1: Использование закона Авогадро для определения зависимости между объемом и количеством молей газа

Согласно закону Авогадро, что происходит с объемом, который занимает газ, если количество родинки увеличиваются?

Остается прежним.
Увеличивается.
Уменьшается.

Ответ

Закон Авогадро гласит, что объем и количество молей газа прямо пропорциональны при постоянной температуре и давлении. Мы можем выразить это как 𝑉∝𝑛.

Когда переменные прямо пропорциональны, увеличение количества одной переменной приведет к увеличению количества другой переменной на постоянная ставка. Следовательно, если количество молей газа увеличивается, объем газа также увеличится. Правильный ответ — выбор B.

Рассмотрим следствие закона Авогадро для следующей реакции при постоянной температуре и давлении: 2H()+O()2HO()222ggg

Согласно уравнению, два моля газообразного водорода и один моль газообразного кислорода соединяется с образованием два моля водяного пара. По количеству молей газа пропорциональна объему газа, уравнение также показывает два объема газообразного водорода (в литрах или миллилитров, например) смешиваются с одним объемом газообразного кислорода для получения двух объемы водяного пара.

Отношение h3 к O2 к HO2 будет 2∶1∶2 независимо от того, выражено ли оно в молях или единицах объема.

В дополнение к заявлению о пропорциональности 𝑉∝𝑛, Закон Авогадро можно представить в виде пропорционального уравнения 𝑉=𝑛𝑉, где 𝑉 — молярный объем, константа пропорциональности. Молярный объем обычно выражается в единицах л/моль и указывает объем, занимаемый один моль газа при удельном температура и давление. Молярный объем изменится при изменении температуры и/или давления газа. Если мы измерим объем и количество молей газа при определенной температуре и давлении, мы можем определить молярный объем.

Определение: Молярный объем (𝑉

_𝑚 )
Молярный объем — это объем, занимаемый одним молем газа при определенной температуре и давлении.
Пример 2. Расчет количества молей газа в заданном объеме путем определения молярного объема газа
Баллон объемом 12 л содержит 0,52 моля газообразного гелия. Второй баллон той же температуры и давление имеет объем 18 л.
Сколько молей газообразного гелия содержит второй баллон? Дайте ваш ответ с точностью до двух знаков после запятой.
Ответ
Объем и количество молей газа связаны уравнением 𝑉=𝑛𝑉, где 𝑉 — объем, 𝑛 — количество молей, 𝑉 – молярный объем. молярный объем — это константа пропорциональности, которая указывает объем одного моля любого газа при определенной температуре и давлении.
Мы можем заменить объем и количество молей газообразного гелия в первом шар в уравнение, чтобы дать нам 12=0,52⋅𝑉.Lмоль
Тогда мы можем определить молярный объем следующим образом: 120,52=0,52⋅𝑉0,5223,0769…=𝑉.LmolmolmolLmol
Молярный объем газа равен 23,077 л/моль. Поскольку второй воздушный шар находится в том же температура и давление, как в первом баллоне, газ в двух баллонах будет иметь одинаковый молярный объем. Это означает, что мы можем заменить объем второго баллона и молярный объем в уравнение 𝑉=𝑛𝑉 дать нам 18=𝑛⋅23.077.LLмоль
Тогда мы можем определить количество молей гелия во втором баллоне следующим образом: 1823,077=𝑛⋅23,07723,0770,7799…=𝑛.LmolLmolLmolLmol
Количество молей газообразного гелия во втором баллоне, округленное до двух знаков после запятой, равно 0,78 моль.
Поскольку объем и, следовательно, плотность газа зависят от температуры и давления, полезно определить стандартную температуру и давление, которое можно использовать в качестве эталонных условий при сравнении различных газов. Стандартная температура определяется как 0∘C, а стандартное давление определяется как 1 атм. В совокупности стандартная температура и давление обозначаются аббревиатурой STP.
Определение: Стандартная температура и давление (STP)
Стандартная температура равна 0∘C, стандартное давление равно 1 атмосфера (атм).
Как оказалось, один моль любого газа на СТП будет иметь объем 22,4 литра.
Gas O()2g Ar()g CH()4g
Temperature 0∘C 0∘C 0∘C
Pressure 1 атм 1 atm 1 atm
Amount 1 mole 1 mole 1 mole
Mass 32 g 40 g 16 g
Number of Particles 6.022×10 molecules 6.022×10 atoms 6.022×10 molecules
Volume 22. 4 L 22.4 L 22.4 L
Example 3: Determining Which Количество газа займет наибольший объем на ПГУ
Какое из следующих количеств газа займет наибольший объем при стандартной температуре и давлении (STP)?
1 моль Ch34
5 моль h3
0,5 моль N2
2 моль Cl2
3 моль O2
1 атм), один моль газа займет 22,4 литра. Это верно независимо от используемого газа. Поскольку объем и количество молей газа напрямую пропорционально, два моля любого газа при нормальных условиях должны иметь удвоить объем как один моль: 22,41×2=44,8,лмольмольл
В STP следующий график объема и количества молей можно построить.
Используя график, мы можем определить объем, занимаемый каждым из вариантов, следующим образом:
1 моль Ch34 имеет объем 22,4 л.
5 молей h3 имеют объем 112 л.
0,5 моля N2 имеют объем 11,2 л.
2 моля Cl2 имеют объем 44,8 л.
3 моля O2 имеют объем 67,2 л.
Количество газа, которое будет занимать наибольший объем при СТП, равно 5 молям h3, что является выбором B.
Для любого газа при стандартной температуре и давлении мы можем заменить объем 22,4 литра и один моль в пропорциональном уравнении 22,4=1⋅𝑉лмоль и определить молярный объем любого газа при нормальных условиях следующим образом: 22,41=1⋅𝑉122,4=𝑉.LmolmolmolLmol
Молярный объем любого газа при нормальных условиях составляет 22,4 л/моль. Это стандартный моляр объем газа. Так, на СТП 𝑉=𝑛⋅22,4.Lмоль
Это уравнение можно использовать для определения объема или количества молей газа при стандартных температуре и давлении. Это важно признать, что стандартный молярный объем может быть использован только тогда, когда газ поддерживается при постоянной температуре 0∘C и постоянное давление 1 атм.
Пример 4: Расчет количества молей молекул газа при STP при заданном объеме
При стандартной температуре и давлении (STP) газ занимает объем 2 л. Сколько имеется молей молекул газа? Дайте ответ с точностью до 2 знаков после запятой.
Ответ
Объем и количество молей газа связаны уравнением 𝑉=𝑛𝑉, где 𝑉 — объем, 𝑛 — количество молей, 𝑉 – молярный объем. Молярный объем – это константа пропорциональности, которая указывает объем один моль любого газа при определенной температуре и давлении.
В этой задаче газ находится при стандартной температуре и давлении (STP). Стандартная температура и давление 0∘С и 1 атм соответственно. Любой газ на СТП будет иметь стандартный молярный объем 22,4 л/моль.
Мы можем подставить объем газа, указанный в вопросе, и стандартный молярный объем в уравнение, чтобы получить 2=𝑛⋅22,4.LLmol
Тогда мы можем найти количество в молях следующим образом: 222. 4=𝑛⋅22.422.40.08928…=𝑛.LmolLmolLmolLmol
Два литра газа при СТП будут содержать 0,08928 моль молекул газа. Округляя до двух знаков после запятой, получаем, что наш окончательный ответ равен 0,09 моль. молекул газа.
Пример 5. Расчет объема газообразного аммиака при нормальных условиях с учетом массы
Какой объем заняли бы 8,5 г газа Nh4 при стандартная температура и давление (СТД), принимая молярный объем газа равным 22,4 л/моль? Дайте ответ в литрах. [N = 14 г/моль, H = 1 г/моль]
Ответ
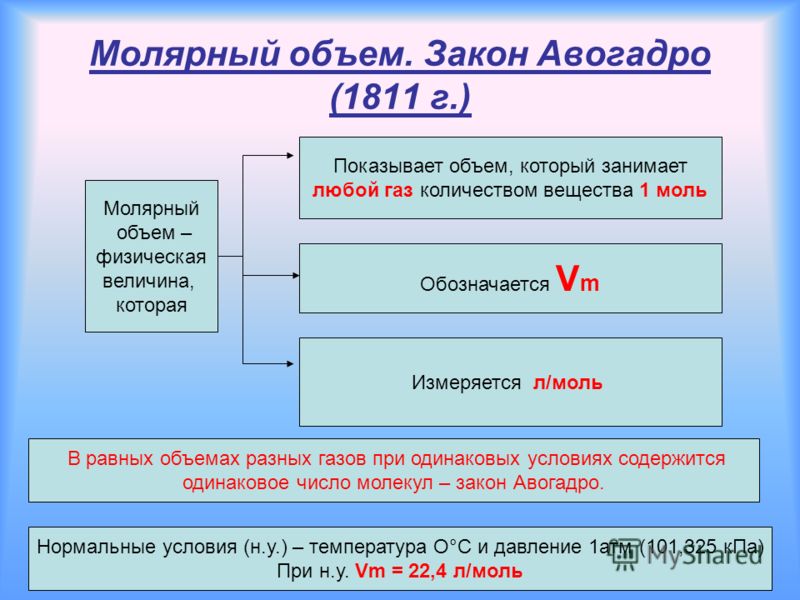
Объем и число молей газа связаны уравнением 𝑉=𝑛𝑉, где 𝑉 — объем, 𝑛 — количество моли, а 𝑉 – молярный объем. Нам нужно решить за объем аммиака (Nh4). Нам дан молярный объем газа при нормальных условиях, но мы не знаем количество молей аммиака. Однако мы можем преобразовать массу аммиака в моли аммиака по уравнению 𝑛=𝑚𝑀, где 𝑛 представляет количество молей, 𝑚 — масса в граммах, а 𝑀 — молярная масса в г/моль.
No related posts.

формулы чисел и молярная масса газа

Ход урока

1. Организационный момент.

2. Фронтальная беседа по вопросам.

3.

4.

5. А теперь закрепим полученные знания с помощью устного счета, чтобы знания через умения стали применятся автоматически, то есть превратились в навыки.

6. Подведение итогов.

Количество вещества

Молярный объем газа

Таблица «молярный объем газов»

Что мы узнали?

Тест по теме

Оценка доклада

ХИМИЧЕСКИЙ ЭКВИВАЛЕНТ

Объемный и массовый расход газа

Молярный объем — Citizendium

Идеальные газы

Реальные газы

Литература

Молярный объем | Что это такое, для чего используется, формула, символ, примеры

Что такое молярный объем?

Какой молярный объем используется для

Обозначение

Формула молярного объема

Примеры

Пример 1: молярный объем газа

Пример 3: Молярный объем кислорода

Объяснение урока: Молярный объем газа

Закон: Закон Авогадро

Пример 1: Использование закона Авогадро для определения зависимости между объемом и количеством молей газа

Ответ

Определение: Молярный объем (𝑉

Пример 2. Расчет количества молей газа в заданном объеме путем определения молярного объема газа

Ответ

Определение: Стандартная температура и давление (STP)

Example 3: Determining Which Количество газа займет наибольший объем на ПГУ

Пример 4: Расчет количества молей молекул газа при STP при заданном объеме

Ответ

Пример 5. Расчет объема газообразного аммиака при нормальных условиях с учетом массы

Ответ

Добавить комментарий Отменить ответ