Как находится вероятность в математике: Классическое определение вероятности — урок. Алгебра, 9 класс.

Задачи по теории вероятностей-1. Решение задания В10

Во всех заданиях В6 на теорию вероятностей, которые представлены в  Открытом банке заданий для подготовки к ЕГЭ  по математике, требуется найти вероятность какого-либо события.

Нужно знать всего лишь одну формулу,  с помощью которой вычисляется вероятность:

В этой формуле р — вероятность события,

k —  число событий, которые нас «устраивают», на языке теории вероятностей они называются благоприятными исходами.

n — число всех возможных событий, или число всех возможных исходов.

Очевидно, что число всех возможных событий больше, чем число благоприятных исходов, поэтом вероятность — это величина, которая меньше или равна 1.

Если вероятность события равна 1, это значит, что данное событие обязательно произойдет. Такое событие называется достоверным. Например, то, что после воскресенья будет понедельник, является, к сожалению, достоверным событием и  его вероятность  равна 1.

Наибольшие сложности при решении задач возникают именно с нахождением чисел k и n.

Разумеется, как при решении любых задач, при решении задач на теорию вероятностей нужно внимательно читать условие, чтобы правильно понять что дано, и что требуется найти.

Рассмотрим несколько примеров решения задач из из  Открытого банка заданий для подготовки к ЕГЭ  по математике.

Пример1.  В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 8 очков. Результат округлите до сотых.

Пусть на первой кости выпало одно очко, тогда на второй может  выпасть 6 различных вариантов. Таким образом, поскольку у первой кости 6 различных граней, общее число различных вариантов равно 6х6=36.

Но нас устраивают не все. По условию задачи, сумма выпавших очков должна быть равна 8. Составим таблицу благоприятных исходов:

Мы видим, что число исходов, которые нас устраивают, равно 5.

Таким образом, вероятность того,  что в сумме выпадет 8 очков равна 5/36=0,13(8).

Еще раз читаем вопрос задачи: требуется результат округлить до сотых.

Вспомним правило округления.

Нам нужно округлить до сотых. Если в следующем после сотых долей разряде (то есть  в разряде тысячных)  стоит число, которое больше  или равно 5, то к числу, стоящему в разряде сотых прибавляем  1, если это число меньше 5, то число в разряде сотых оставляем без изменения.

В нашем случае в разряде тысячных стоит 8, поэтому число 3, которое стоит в разряде сотых, увеличиваем на 1.

Итак, p=5/36 ≈0,14

Ответ: 0,14

Пример 2. В чемпионате по гимнастике участвуют 20 спортсменок: 8 из России, 7 из США, остальные — из Китая. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется из Китая.

В этой задаче число возможных исходов равно 20 — это число всех спортсменов.

n=20

Найдем число благоприятных исходов. Оно равно числу спортсменок из Китая.

k= 20-8-7=5

Таким образом,

p=k/n=5/20=0,25

Ответ: 0,25 

Пример 3. В среднем из 1000 садовых насосов, поступивших в продажу, 5 подтекают. Найдите вероятность того, что один случайно выбранный для контроля насос не подтекает.

В этой задаче n=1000.

Нас интересуют насосы, которые не подтекают. Их число равно 1000-5=995. Т.е.

k=995.

n=k/p=995/1000=0,995.

Ответ: 0,995 

 Решение более сложных задач по теории вероятностей  мы рассмотрим в следующий раз.

Вероятно, Ваш браузер не поддерживается. Попробуйте скачать
Firefox или
Chrome

И.В. Фельдман, репетитор по математике.

Геометрические вероятности.

Решение типовых задач #1

Высшая математика / Справочник по теории вероятностей

07.06.201525.11.2015

Геометрические вероятности. Решение типовых задач. Часть 1
Пусть отрезок l составляет часть отрезка L. На отрезок L наудачу поставлена точка. Предполагается, что вероятность попадания точки на отрезок l пропорциональна длине этого отрезка и не зависит от его разложения относительно отрезка L. В этих предположениях вероятность попадания точки на отрезок l определяется равенством

Р = Длина l/Длина L. (1)

Пусть плоская фигура g составляет часть плоской фигуры G. На фигуру G наудачу брошена точка. Предполагается, что вероятность попадания брошенной точки на фигуру g пропорциональна площади Sg этой фигуры и не зависит ни от ее расположения относительно фигуры G, ни от формы фигур G и g.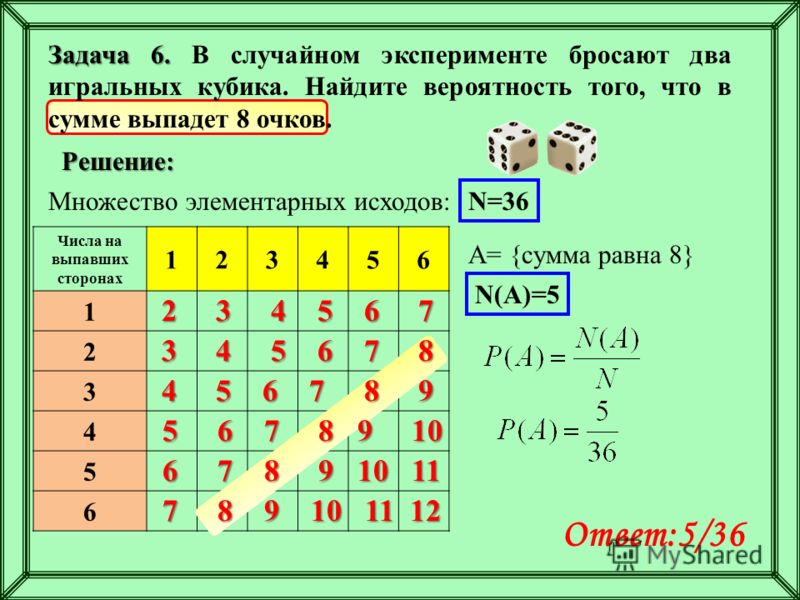 в этих предположениях вероятность попадания точки на фигуру g определяется равенством

где — площадь фигуры G.
Аналогично определяется вероятность попадания точки в пространственную фигуру v, которая составляет часть фигуры V.

Задача №1. На отрезок L, имеющий длину 40 см, помещен меньший отрезок l длиной 15 см. Найти вероятность того, что точка, наудачу поставленная на больший отрезок, попадет также и на меньший отрезок. Предполагается, что вероятность попадания точки на отрезок l пропорциональна длине этого отрезка и не зависит от его расположения на отрезке L.
Решение. Обозначим событие: А — точка, наудачу поставленная на отрезок L, попадает также и на отрезок l.
Найдем вероятность события А, применив формулу (1):

Задача №2. Внутрь круга радиуса R наудачу брошена точка. Найти вероятность того, что точка окажется внутри вписанного в этот круг правильного треугольника. Предполагается, что вероятность попадания точки в треугольник пропорциональна площади треугольника и не зависит от его расположения относительно круга.
Решение. Обозначим событие: В — точка, наудачу брошенная в круг, окажется внутри вписанного в этот круг правильного треугольника.
Найдем вероятность события В, применив формулу (2).
Площадь круга радиуса R равна

; площадь вписанного в круг правильного треугольника равна , где a — сторона треугольника. Известно, что , поэтому . Следовательно, вероятность события А равна

Тегигеометрическая вероятностьГеометрические вероятностигеометрическое определение вероятностиКакова вероятностьнайти вероятностьОтносительная частотарешение задач по теории вероятностей

Объяснение урока: Расчет вероятности с помощью диаграмм Венна

В этом объяснении мы узнаем, как использовать диаграммы Венна для организации информации и расчета вероятностей.

В теории вероятности диаграмма Венна представляет собой фигуру с одним или несколькими кругами внутри прямоугольника, которая описывает логические отношения между событиями. Прямоугольник на диаграмме Венна представляет пространство выборки или универсальный набор, то есть набор всех возможных результатов. Круг внутри прямоугольника представляет событие, то есть подмножество выборочного пространства.

Рассмотрим следующую диаграмму Венна, включающую два события, 𝐴 и 𝐵.

На диаграмме выше у нас есть два события 𝐴 и 𝐵 в демонстрационном пространстве (или универсальном множестве) 𝑆. Иногда пространство выборки обозначается 𝜎 или 𝜉 вместо 𝑆. Цветные области на этой диаграмме Венна представляют следующие события: Зеленые и фиолетовые регионыСиние и фиолетовые регионыФиолетовый регионЗеленые, фиолетовые и синие регионыЖелтые регионы, альтернативно, ∶𝐴, ∶𝐵, ∶𝐴∩𝐵, ∶𝐴∪𝐵, ∶𝐴∪𝐵, (𝐴∪𝐵)′.

Определение: диаграммы Венна с двумя событиями

Пусть 𝐴 и 𝐵 события, описанные на диаграмме Венна. Тогда

• кружки не перекрываются, если 𝐴 и 𝐵 взаимоисключающие события, то есть 𝐴∩𝐵=∅;
• окружности перекрываются, если 𝐴∩𝐵≠∅, и в этом случае пересечение 𝐴∩𝐵 представлено перекрывающейся областью;
• область за пределами обоих кругов, но внутри прямоугольника представляет собой дополнение объединения обоих событий, то есть 𝐴∪𝐵 или, альтернативно, (𝐴∪𝐵)′.

Внутри каждой разделенной области диаграммы Венна мы можем добавить данные одним из следующих способов:

• исходы события,
• количество исходов в событии,
• вероятность события.

В первом примере мы будем использовать диаграмму Венна для организации наших данных и использовать ее для вычисления вероятности события.

Пример 1. Организация данных с использованием диаграмм Венна для поиска вероятностей

В классе 100 учащихся; 70 из них любят математику, 60 — физику и 40 — и то, и другое. Если учащийся выбран случайным образом, используя диаграмму Венна, найдите вероятность того, что ему нравится математика, но не физика.

Ответ

Начнем с рисования пустой диаграммы Венна для представления этого примера.

Мы знаем, что перекрывающаяся область на диаграмме Венна представляет собой пересечение событий. Нам дано, что 40 учеников относятся к этому перекрестку, так как им нравится и математика, и физика.

70 школьников любят математику, 40 из них еще и физику. Это говорит нам о том, что количество студентов, которым нравится только математика, составляет 70−40=30. Точно так же мы можем сделать вывод, что 60−40=20 студентов любят только физику. Это приводит к следующей диаграмме Венна.

Заметим, что число 10 снаружи должно гарантировать, что сумма всех значений на диаграмме Венна равна 100, так как в классе всего 100 учеников. Мы ищем вероятность того, что случайно выбранный ученик любит математику, но не любит физику. Область диаграммы Венна, представляющая это событие, выделена ниже.

Из диаграммы Венна видно, что 30 школьников любят математику, но не любят физику. Поскольку студент выбирается случайным образом, мы можем получить вероятность этого события, разделив это число на общее количество студентов, которое равно 100.

Следовательно, вероятность того, что случайно выбранный ученик любит математику, но не любит физику, равна 30100=0,3.

В нашем следующем примере мы будем использовать диаграмму Венна для вычисления вероятности события.

Пример 2. Использование диаграмм Венна для расчета вероятности

Yara нарисовала эту диаграмму Венна, чтобы записать результат случайного выбора числа от 1 до 12.

1. Какова вероятность выбора числа, которое является кратным 20 ? Дайте ответ в виде дроби в простейшей форме.
2. Какова вероятность выбрать число, которое является коэффициентом 20 и кратным 3? Дайте ответ в виде дроби в простейшей форме.
3. Какова вероятность выбрать число, не кратное 3? Дайте ответ в виде дроби в простейшей форме.

Ответ

На данной диаграмме Венна кружками представлены два события: «Множитель 20» и «Кратность 3». Демонстрационное пространство этой диаграммы Венна представляет собой набор целых чисел от 1 до 12. Другими словами, эталонное пространство (или универсальное множество) задается выражением 𝑆={1,2,3,…,12}.

Часть 1

Поскольку мы случайным образом выбираем число от 1 до 12, вероятность события можно получить, разделив размер события на размер выборки, который равен 12. Другими словами , 𝑃(20)=2012.factorofnumberoffactorsof

Из диаграммы Венна видно, что существует 5 различных множителей 20 между 1 и 12.

Следовательно, вероятность выбора числа между 1 и 12, которое является множителем 20 512.

Часть 2

Отметим, что эти два события исключают друг друга, поскольку кружки на диаграмме Венна не перекрываются. Другими словами, между 1 и 12 не существует числа, которое одновременно является множителем 20 и кратно 3.

Следовательно, вероятность этого события равна 0.

Часть 3

Из Венна На диаграмме числа от 1 до 12, не кратные 3, лежат вне круга. Мы видим, что этому случаю принадлежат 8 чисел.

Следовательно, вероятность того, что случайно выбранное число от 1 до 12 не кратно 3, равна 812, что можно упростить до 23.

Мы также можем использовать диаграмму Венна для вычисления условных вероятностей. В нашем следующем примере мы организуем данные с помощью диаграммы Венна и используем ее для вычисления вероятности события при заданном условии.

Пример 3. Нахождение условной вероятности события

На выпускных экзаменах 40 % учащихся не сдали экзамен по химии, 25 % – по физике и 19% провалили и химию, и физику. Какова вероятность того, что случайно выбранный студент не сдал физику, если он сдал химию?

Ответ

Начнем с рисования пустой диаграммы Венна.

Мы можем использовать данную информацию, чтобы добавить относительную долю каждого региона. Поскольку 40 % учащихся не сдали экзамен по химии, а 19 % — и по химии, и по физике, мы можем сделать вывод, что 40–19 % = 21 % учащихся не сдали только по химии. Точно так же мы можем получить, что 25%−19%=6% учеников не сдали только физику. Тогда у нас есть следующие данные:

• 21% студентов не прошли химию, но не физику;
• 6% учащихся не прошли физику, но не химию;
• 19% учащихся не сдали ни физику, ни химию.

Оставшаяся относительная доля приходится на учащихся, сдавших оба предмета. Поскольку сумма всех относительных долей должна равняться 100 %, процент учащихся, сдавших оба предмета, равен 100%-21%-6%-19%=54%.

Мы добавляем эти проценты на диаграмму Венна следующим образом.

Мы хотим найти вероятность того, что случайно выбранный студент не сдал физику, если он сдал химию. Процент учащихся, успешно сдавших экзамен по химии, указан за пределами кружка с надписью «Неудовлетворительно по химии» на приведенной выше диаграмме Венна. Это область, заштрихованная фиолетовым цветом ниже. Кроме того, мы знаем, что область, заштрихованная зеленым цветом, представляет учащихся, которые не сдали физику и сдали химию.

Обратите внимание, что нам дано, что студент сдал химию. Это означает, что мы выбираем ученика из группы учеников, сдавших химию, а не из всего класса. Другими словами, наше выборочное пространство (или универсальное множество) — это область, заштрихованная фиолетовым, а не прямоугольник.

Процент учащихся, сдавших химию, определяется путем суммирования процентов в пределах фиолетовой области, что дает 6%+54%=60%. Среди учащихся, сдавших химию, процент учащихся, не сдавших физику, находится в зеленой области, что составляет 6%. Итак, вероятность случайного выбора студента, не сдавшего физику, из группы студентов, сдавших химию, определяется выражением процент учащихся, не сдавших физику, но сдавших химию, процент учащихся, сдавших химию=6%60%=0,1.

Проверим этот ответ по формуле условной вероятности события 𝐴 при заданном событии 𝐵: 𝑃(𝐴∣𝐵)=𝑃(𝐴∩𝐵)𝑃(𝐵).

В нашем примере эта формула может быть записана как 𝑃(∣)=𝑃()𝑃().студенты, не сдавшие физикустуденты, сдавшие химиюстуденты, не сдавшие физику и сдавшие химиюстуденты, сдавшие химию 𝑃()=0,06, 𝑃()=0,06+0,54=0,60. Студенты, не сдавшие физику и сдавшие химию Студенты, сдавшие химию

Подставляя эти значения в приведенное выше уравнение, мы получаем 𝑃(∣)=0,060,60=0,1.студенты, не сдавшие физикустуденты, сдавшие химию

Следовательно, вероятность того, что случайно выбранный учащийся не сдал физику при условии, что он сдал химию, равна 0,1.

В предыдущем примере мы вычислили условную вероятность, используя диаграмму Венна. В общем, условная вероятность события 𝐴 при наличии другого события 𝐵 может быть вычислена с помощью диаграммы Венна и следующих аналогичных шагов.

Практическое руководство. Вычисление условных вероятностей с использованием диаграммы Венна

Чтобы вычислить условную вероятность события 𝐴 при наличии другого события 𝐵 с помощью диаграммы Венна, нам нужно

1. определить область, представляющую событие 𝐵, на диаграмме Венна, и вычислить вероятность of 𝐵,
2. определяют область, представляющую пересечение 𝐴∩𝐵, и вычисляют вероятность 𝐴∩𝐵,
3. вычисляют 𝑃(𝐴∩𝐵)𝑃(𝐵).

Заметим, что этот процесс приводит к стандартной формуле 𝑃(𝐴∣𝐵)=𝑃(𝐴∩𝐵)𝑃(𝐵), где 𝑃(𝐴∣𝐵) — условная вероятность события 𝐴 при наличии другого события 𝐵.

Мы также можем использовать диаграмму Венна для описания отношений между тремя событиями. В двух особых случаях, перечисленных ниже, мы имеем особое представление диаграммы Венна с тремя событиями.

Рассмотрим пример, в котором мы используем диаграмму Венна с тремя событиями, где одно из событий является взаимоисключающим по отношению к двум другим событиям.

Пример 4. Использование диаграммы Венна для определения вероятности объединения двух событий

Используйте диаграмму выборочного пространства 𝑆 для определения 𝑃(𝐵∪𝐶).

Ответ

Из данной диаграммы Венна мы можем сказать, что событие 𝐶 является взаимоисключающим по отношению к событиям 𝐵 и 𝐶. Напомним, что вероятность события может быть получена с помощью диаграммы Венна путем вычисления относительной доли события по отношению к выборочному пространству.

На диаграмме Венна выборочное пространство обозначено 𝑆 и содержит 10 различных результатов. Таким образом, мы можем вычислить вероятность нашего события, разделив количество исходов события на 10. Событие 𝐵∪𝐶 выделено фиолетовым цветом ниже.

На приведенной выше диаграмме видно, что в области, представляющей 𝐵∪𝐶, есть 6 различных исходов.

Таким образом, вероятность определяется выражением 𝑃(𝐵∪𝐶)=610=35.

Если одно из трех событий не является взаимоисключающим по отношению к двум другим событиям, мы используем следующее соглашение для диаграммы Венна с тремя событиями.

Заметим, что все три круга пересекаются над серединой стандартной трехсобытийной диаграммы Венна. Эта область представляет собой пересечение всех трех событий, 𝐴∩𝐵∩𝐶.

Рассмотрим пример вычисления вероятности с использованием стандартной трехсобытийной диаграммы Венна.

Пример 5: Использование диаграммы Венна для определения пересечения событий

271 ученик проголосовал за музыку, которую они хотели на школьных танцах. Результаты показаны на диаграмме Венна. Найти вероятность того, что случайно выбранный студент проголосовал за рок, а не за джаз.

Ответ

В этом примере нам дана диаграмма Венна с тремя событиями. Поскольку учащийся выбирается случайным образом, мы знаем, что вероятность события определяется путем деления числа учащихся, участвующих в событии, на общее число учащихся, которое равно 271. Другими словами, 𝑃()=271.eventnumberofstudents, принадлежащих к событию

Итак, нам нужно найти количество студентов, проголосовавших за рок, но не за джаз. На данной диаграмме Венна область, представляющая это событие, выделена черным цветом:

Используя диаграмму Венна, мы можем видеть, что количество студентов для этого события составляет 70+7=77. Разделив это число на 271, вы получите вероятность этого события.

Следовательно, вероятность того, что случайно выбранный студент проголосовал за рок, а не за джаз, равна 77271.

В нашем последнем примере мы организуем данные о трех событиях, используя стандартную диаграмму Венна с тремя событиями, и используем ее для определения вероятности.

Пример 6. Организация данных с помощью диаграмм Венна для поиска вероятностей

В выборке из 100 студентов, поступающих в университет, анкета показала, что 45 из них изучали английский язык, 40 изучали французский язык, 35 изучали немецкий язык, 20 изучали английский и французский языки. 23 человека изучали английский и немецкий языки, 19 — французский и немецкий, а 12 — все три языка.

Используя диаграмму Венна, найдите вероятность того, что случайно выбранный студент изучал только один из трех языков.

Ответ

Начнем с рисования пустой стандартной трехсобытийной диаграммы Венна.

Чтобы заполнить эту диаграмму, мы начнем с середины, где все три круга перекрываются. Середина диаграммы Венна с тремя событиями представляет пересечение всех трех событий. В нашем примере это представляет учащихся, изучавших все три языка, которых всего 12.

Далее мы рассмотрим другие перекрывающиеся регионы. Мы знаем, что 20 студентов изучали и английский, и французский языки, но мы также знаем, что 12 из этих студентов изучали все три предмета, а значит, они также изучали немецкий язык. Отсюда мы можем сделать вывод, что 20−12=8 студентов изучали английский и французский языки, но не немецкий. Точно так же мы можем собрать следующие данные:

• Студенты, изучавшие английский и немецкий, но не французский: 23−12=11 студентов,
• Студенты, изучавшие французский и немецкий языки, но не английский: 19−12=7 студентов.

Теперь добавим эти цифры в соответствующие регионы.

Приступим к получению значений для части каждого круга, не перекрывающей два других круга. Нам дано, что 45 студентов изучали английский язык, но 8+12+11 из них также изучали французский или немецкий языки. Таким образом, число студентов, изучавших английский язык, но не изучавших французский или немецкий, определяется выражением 45−8−12−11=14.

Аналогичным образом получаем следующие данные:

• Студенты, изучавшие французский, но не английский или немецкий язык: 40−8−12−7=13 студентов,
• Студенты, изучавшие немецкий язык, но не английский или французский: 35−7− 12−11=5 учеников.

Теперь добавим эти цифры к диаграмме Венна.

На этой диаграмме Венна область, представляющая учащихся, изучавших только один из трех языков, заштрихована ниже желтым цветом.

Тогда количество таких студентов равно 13+14+5=32.

Поскольку студент выбран случайно, мы можем получить вероятность нашего события, разделив 32 на общее количество студентов, которое равно 100.

Вероятность того, что случайно выбранный студент изучал только один из трех языков 32100=0,32.

Давайте резюмируем несколько важных понятий из этого объяснения.

Ключевые точки

• Каждая из разделенных областей диаграммы Венна может содержать одну из следующих данных:
  • исходы события,
  • количество исходов события,
  • вероятность или относительная доля события.
• Диаграмма Венна с двумя событиями описывает отношения между двумя событиями следующими способами:
  • Если два события исключают друг друга, то круги, представляющие каждое событие, не перекрываются.
  • Если два события не исключают друг друга, то два круга перекрываются. Перекрывающаяся область представляет собой пересечение двух событий.
• Чтобы вычислить условную вероятность события 𝐴 для другого события 𝐵 с помощью диаграммы Венна, нам нужно
  • определить область, представляющую событие 𝐵, на диаграмме Венна, и вычислить вероятность 𝐵,
  • определить область, представляющую пересечение 𝐴∩𝐵 и вычислить вероятность 𝐴∩𝐵,
  • вычислить 𝑃(𝐴∩𝐵)𝑃(𝐵).
• В диаграмме Венна с тремя событиями мы можем следовать соглашению о диаграмме Венна с двумя событиями, когда одно событие является взаимоисключающим для двух других событий. В противном случае мы используем следующую стандартную трехсобытийную диаграмму Венна.
• Середина стандартной трехсобытийной диаграммы Венна, где все три круга перекрываются, представляет пересечение всех трех событий. При организации данных в стандартную диаграмму Венна с тремя событиями мы можем начать с определения середины.

Объяснение

диаграмм дерева вероятностей! — Mashup Math

Это краткое введение научит вас рассчитывать вероятности с помощью древовидных диаграмм.

Вычисление вероятностей в математике может сбить с толку, особенно учитывая множество правил и процедур. К счастью, есть визуальный инструмент под названием 9.0283 диаграмма дерева вероятностей , которую вы можете использовать, чтобы организовать свое мышление и упростить вычисление вероятностей.

На первый взгляд древовидная диаграмма может показаться сложной, но эта страница научит вас читать древовидную диаграмму и использовать ее для простого расчета вероятностей. Следуйте шаг за шагом, и вскоре вы станете мастером чтения и создания диаграмм дерева вероятностей.

Что такое диаграмма дерева вероятностей?

Пример 01: Вероятность однократного подбрасывания монеты

Начнем с обычного вероятностного события: подбрасывание монеты, у которой с одной стороны решка, а с другой решка:

Эта простая диаграмма дерева вероятностей имеет две ветви : по одному для каждого возможного исхода орел или решка. Обратите внимание, что результат расположен в конечной точке ветви (здесь заканчивается древовидная диаграмма).

Также обратите внимание, что вероятность каждого исхода записывается в виде десятичной дроби на каждой ветви. В этом случае вероятность любого исхода (выпадение монеты и выпадение орла или решки) равна 9.0307 пятьдесят на пятьдесят , что равно 0,5 или 1/2.

Пример 02: Вероятность подбрасывания монеты дважды

Теперь давайте посмотрим на диаграмму дерева вероятностей для подбрасывания монеты дважды!

Обратите внимание, что эта древовидная диаграмма изображает два последовательных события (первый бросок и второй бросок), поэтому имеется второй набор ветвей.

Используя древовидную диаграмму, вы можете видеть, что существует четыре возможных исхода при двойном подбрасывании монеты: «Орел/Орел», «Орел/Решка», «Решка/Орел», «Решка/Решка».

А так как возможных исходов четыре, вероятность каждого исхода составляет 0,25 (или ¼). Так, например, вероятность выпадения орла два раза подряд составляет 0,25.

Как найти вероятность

Правило для нахождения вероятности конкретного события на диаграмме дерева вероятности состоит в том, чтобы умножить вероятности соответствующих ветвей.

Например, чтобы доказать, что вероятность выпадения двух орлов подряд равна 0,25, нужно умножить 0,5 х 0,5 (поскольку вероятность выпадения орла при первом подбрасывании равна 0,5, а вероятность выпадения орла при втором подбрасывании равна также 0,5).

0,5 x 0,5 = 0,25

Повторите этот процесс для трех других исходов следующим образом, а затем сложите все вероятности исходов следующим образом:

Обратите внимание, что сумма вероятностей всех исходов всегда должна быть равна единице.

С этого момента вы можете использовать диаграмму дерева вероятностей, чтобы сделать несколько выводов, таких как:

·       Вероятность выпадения орла сначала и решки во вторую составляет 0,5×0,5 = 0,25

·       Вероятность выпадения хотя бы одной решки при двух последовательных бросках равна 0,25 + 0,25 + 0,25 = 0,75

·       Вероятность выпадения орла и решки равна 0,25 + 0,25 = 0,5

Независимые события и зависимые события

Что такое независимое мероприятие?

Обратите внимание, что в примере с древовидной диаграммой подбрасывания монеты результат каждого подбрасывания монеты не зависит от результата предыдущего подбрасывания. Это означает, что исход первого броска не повлиял на вероятность исхода второго броска. Эта ситуация известна как независимое событие .

 Что такое зависимое событие?

В отличие от независимого события, зависимое событие — это результат, который зависит от события, которое произошло до него. Такие ситуации немного сложнее, когда дело доходит до расчета вероятности, но вы все равно можете использовать диаграмму дерева вероятностей, чтобы помочь вам.

Давайте рассмотрим пример того, как можно использовать древовидную диаграмму для расчета вероятностей при наличии зависимых событий.

Как сделать древовидную диаграмму

Пример 03:

Грег — бейсбольный питчер, который бросает два вида подачи: фастбол и наклбол. Вероятность броска страйка различна для каждого шага:

·       Вероятность броска фастбола для страйка равна 0,6

·       Вероятность броска наклбола для страйка 0,2

Грег чаще бросает фастболы, чем наклболы. В среднем на каждые 10 бросков, которые он бросает, приходится 7 фастболов (вероятность 0,7) и 3 наклбола (вероятность 0,3).

Итак, какова вероятность того, что питчер выполнит страйк на любой данной подаче?

 Чтобы найти вероятность того, что Грег выполнит страйк, начните с построения древовидной диаграммы, показывающей вероятность того, что он выполнит фастбол или наклбол

Вероятность того, что Грег бросит фастбол, равна 0,7, а вероятность того, что он бросит наклбол, равна 0,3. Обратите внимание, что сумма вероятностей исходов равна 1, потому что 0,7 + 0,3 равно 1,00.

 Далее добавьте ветви для каждой подачи, чтобы показать вероятность того, что каждая подача будет страйком, начиная с фастбола:

Помните, что вероятность того, что Грег бросит фастбол для страйка, равна 0,6, поэтому вероятность того, что он не бросит мяч для страйка, равна 0,4 (поскольку 0,6 + 0,4 = 1,00)

Повторите этот процесс для наклбола:

Помните, что вероятность того, что Грег бросит наклбол для страйка, равна 0,2, поэтому вероятность того, что он не бросит его для страйка, равна 0,8 (поскольку 0,2 + 0,8 = 1,00)

Теперь, когда диаграмма дерева вероятностей была завершено, вы можете выполнить свои расчеты результатов. Помните, что сумма вероятностных исходов должна равняться единице:

Так как вы пытаетесь вычислить вероятность того, что Грег выполнит страйк на любом данном поле, вы должны сосредоточиться на результатах, которые приводят к тому, что он пробьет страйк: фастбол для страйка или наклбол для страйка:

Последним шагом является сложение вероятностей исхода удара:

0,42 + 0,06 = 0,48

 Вероятность того, что Грег нанесет удар, составляет 0,48 или 48%.

Диаграммы дерева вероятностей: ключевые выводы

·      Диаграмма дерева вероятностей — это удобный визуальный инструмент, который можно использовать для расчета вероятностей как зависимых, так и независимых событий.

·      Чтобы рассчитать вероятность исходов, умножьте значения вероятности связанных ветвей.

·      Чтобы рассчитать вероятность нескольких исходов, сложите вероятности вместе.

·      Вероятность всех возможных исходов всегда должна быть равна единице. Если вы получили какое-либо другое значение, вернитесь и проверьте на наличие ошибок.

 

Посмотрите анимированные видеоуроки и сохраните

Посмотрите видеоуроки ниже , чтобы узнать больше о том, как использовать древовидные диаграммы и вычислять вероятность в математике:

Есть мысли? Поделитесь своим мнением в разделе комментариев ниже!

(Никогда не пропустите блог Mashup Math — щелкните здесь, чтобы получать наш еженедельный информационный бюллетень!)

Автор: Энтони Персико. Вы часто можете увидеть, как я с радостью разрабатываю анимированные уроки математики, которыми я делюсь на моем канале YouTube . Или проводить слишком много времени в тренажерном зале или играть на своем телефоне.