Как можно решить задачу по математике
Многие из нас хотя бы раз сталкивались со сложной задачей по математике, решения которой, кажется, не существует вовсе. Специально для людей, которые не оставляют дела на полпути, мы разработали общую схему решения задач по математике, которая не только поможет вам прийти к правильному ответу, но и сбережет вашу нервную систему.
О чем статья
Какие бывают задачи по математике
Задачи по математике классифицируются по разным признакам. Например, по содержанию они бывают текстовые, вычислительные, задачи на доказательство или комбинированный тип.
По функциям можно выделить дидактические задачи, а также развивающие и контролирующие.
По роли в обучении задачи бывают на усвоение материала, на изучение математической символики, на получение математических навыков, а также общие задачи на развитие.
Спешим вас обрадовать: любую из вышеперечисленных задач можно решить при помощи правильного алгоритма, который предложен нами ниже.
Нужна помощь в написании работы?
Мы — биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.
Цена работы
Как можно решить задачу по математике
Чтобы самостоятельно прийти к правильному решению, воспользуйтесь нашим алгоритмом.
Во-первых, определите, задачу на какую тему вы решаете. Это задача на нахождение неизвестного, задача с дробями, задание на логику или же закрепление знаний о квадратных или кубических уравнениях? Вы должны четко понимать, чего именно от вас хотят, формулами из какой темы вы будете пользоваться.
Теперь сосредоточьтесь на условии задания. В математических задачах, как правило, не бывает лишней информации. Это значит, что условие содержит только сведения, которые обязательно нужно использовать.
Изучайте условие до тех пор, пока вы четко не осознаете, с чем имеете дело и не представите, сколько вам придется выполнить действий и на какие формулы ссылаться.
Теперь сформулируйте условие своими словами, чтобы вы руководствовались собственными мыслями и знаниями при решении. Лучше всего после изложения записать вашу формулировку в кратком виде, выписав важную информацию, чтобы не упустить ее из виду при решении. Просто в виде заметок выпишите основные сведения.
Теперь изобразите задачу в виде рисунка. Это не относится к задачам на логику, но другие математические задачи легче воспринимаются, когда перед глазами есть конкретные образы. Сравните готовый рисунок с условием задачи и исправьте помарки, если они есть. Рисунок может быть диаграммой или графиком. Можно просто изобразить несколько линий. Решать вам.
Попробуйте вспомнить, не решали ли вы подобные задания в прошлом. Скорее всего, хотя бы часть задачи уже была решена в подобном задании, вам просто нужно провести параллель с ним. Для этого попробуйте выбрать формулы, на которые вы полагаетесь при решении. Если ранее вы уже использовали эти формулы, поступите по такому же принципу.
Если вы все еще не видите ни одного решения, изучите похожие задачи с решением в интернете. Как правило, после этого процесса люди осознают, с чем столкнулись и продвигаются в решении.
Выбираем нужную информацию
Итак, вы уже определились, какими формулами пользоваться. Выпишите эти формулы, даже если вы их знаете наизусть. Информация, которую мы видим, лучше перерабатывается нашим мозгом.
Возможно, что для данного типа задач в учебнике уже предусмотрен определенный алгоритм. Если его нет, то запишите, как вы собираетесь решить задачу. Записывайте последовательно каждый свой шаг.
Если вы не можете сориентироваться в решении задания, найдите в учебнике или в интернете похожую задачу, но на уровень легче, и решите сперва ее.
Теперь проверьте, всю ли информацию, данную в условии, вы собираетесь использовать. Возможно, вы упустили из виду деталь, которая изменит ход решения или ответит на ваши вопросы.
Попробуйте представить, каким должен быть ответ. Любая задача не может иметь бесконечное количество ответов. Какие-нибудь ограничения (отрицательное число, определенный диапазон) должны присутствовать.
Любая задача не может иметь бесконечное количество ответов. Какие-нибудь ограничения (отрицательное число, определенный диапазон) должны присутствовать.
Рекомендации по ходу решения
Когда решаете задачу, не уходите от намеченного плана. Если вы зашли в тупик, то вернитесь в место, которое вызвало сомнения, и перепишите ваш план заново, начиная с этого места.
Когда вы пришли к ответу, сравните его с тем ответом, который вы предполагали ранее. Если результат значительно отличается от ожидаемого, возможно, где-то вы допустили ошибку.
Если вы не смогли получить ответ, попробуйте составить другой план решения. Наверняка тема, которую вы не понимаете, предоставляет множество формул, попробуйте использовать другие. Вполне вероятно, что вы просто не решились пойти по более сложному пути.
Типичные ошибки при решении задач
Чтобы лучше понять суть алгоритма, рассмотрим самые распространенные ошибки учащихся, которые заводят их в тупик и не дают получить верный ответ.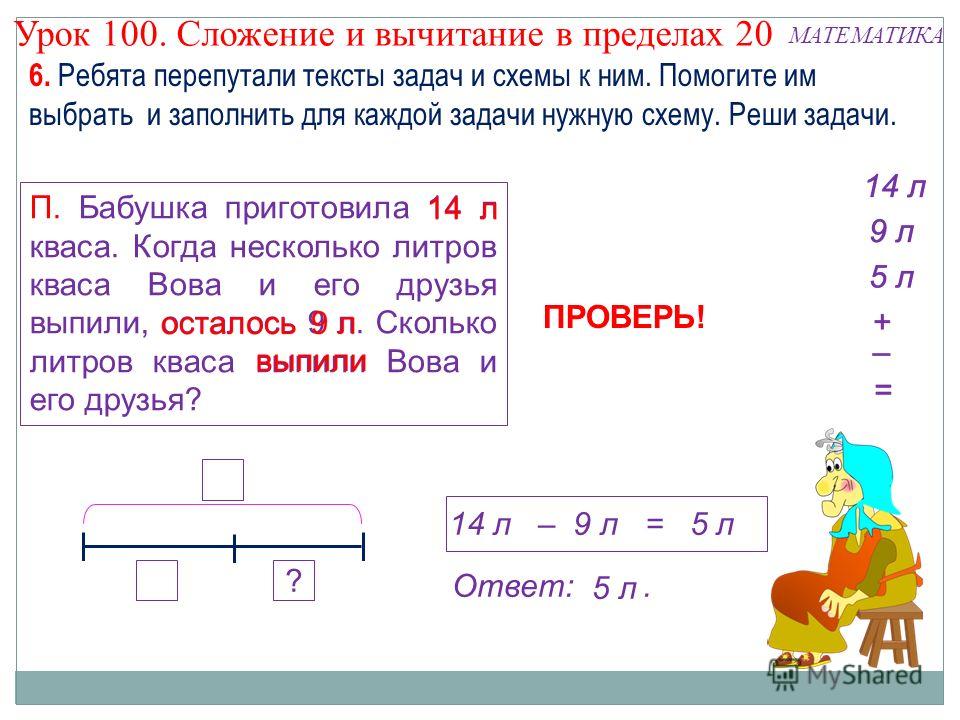
Во-первых, многие принимаются за решение, не зная общепринятых правил, определений или формул. Изучите материал по теме полностью, прежде чем приступать к решению.
Часто учащиеся знают правила и формулы, но попросту не понимают их. Вы должны не просто изучить материал, вы должны в него вникнуть и осознать цель применения полученной информации.
Бывает, что человек прекрасно владеет всем материалом и понимает его, но для конкретной задачи выбирает совсем не ту формулу. Попрактикуйтесь на более легких задачах, чтобы научиться выбирать правильные формулы для решения.
Одна из самых распространенных ошибок – это пренебрежение внимательным изучением условия задачи. Как говорят многие опытные педагоги, половина ответа уже дана в задании, и это абсолютная правда. Верное понимание условия дает правильное направление мыслей при решении.
Очень обидной, но распространенной проблемой многих учащихся, является постоянное допущение вычислительных ошибок. Профессиональные педагоги отмечают, что много талантливых учеников просто не обращают внимания на элементарные вычисления, вследствие чего и приходят к неправильному ответу.
Распространенная ошибка при решении геометрических задач – это пренебрежение свойствами геометрических фигур. Часто такие задачи основаны на этих свойствах, поэтому это первое, на что следует обратить внимание.
Когда учащиеся производят определенные действия по формулам, нужно помнить о свойствах математических операций. Так, скобки раскрываются в начале, после чего идет умножение с делением, а потом – сложение и вычитание. Этот материал преподается еще в начальной школе, но многие люди забывают о нем.
Полезные советы
Теперь, когда вы знаете, как решить задачу по математике, попытайтесь понять, что сильная усталость или нервное перенапряжение будут большой помехой правильному ходу решения. Дождитесь, когда вы будете отдохнувшим и сможете сконцентрироваться на задании полностью, а уже тогда приступайте к решению.
Кроме того, придумайте себе мотивацию для качественной работы. Именно она дает нам силы и заставляет выполнять задания, которые мы считали слишком сложными для себя.
Руководство по решению 📝 задач по математике
- Понимание задачи
- Графическое изображение задачи
- Составление плана
- Получение результатов
Существует множество типов задач по математике, а способов их решения и того больше. Так, к примеру, метод визуализации помогает просчитывать скорость движения в разных условиях или расстояние. При этом, даже при условии нескольких переменных, такие задачи можно развязать, если правильно их визуализировать.
При регулярном решении задач по математике учащиеся приобретают новые знания и навыки. Это однозначно поможет детям успешно сдать ЕГЭ, ну а студентам — успешно закрыть сессию. Не забывайте также о том, что самые успешные в области математики ученики и студенты могут посетить олимпиады. Олимпиада позволяет не только проверить свои знания и умения решать задачи, но и принесет много бонусов в виде автоматических зачетов, хороших оценок, высокого престижа, а в некоторых случаях даже финансовое вознаграждение.
Хотя видов и способов решения задач очень много, существует единая схема, для решения задач. Для начала следует определить тип задачи, чтобы понимать, что с ней делать дальше. Если в ней присутствует переменная «х», то возможно вам пригодятся формулы сокращенного умножения. Задачи на поиск скорости движения, расстояния или времени потребуют от вас знаний формул по физике. При работе с дробями потребуется вспомнить правила переноса числителя и знаменателя через знак равенства. Задачи по геометрии чаще всего требуют визуализации условия, поэтому запаситесь линейкой и циркулем, чтобы начертить необходимые фигуры.
В школе ученики учат только два крупных раздела математики: элементарную алгебру и элементарную геометрию. Поэтому им необходимо понимать исключительно базовые арифметические формулы, а также правила решения геометрических фигур. В высших учебных заведениях математика делится уже на большее количество разделов. Тут можно встретить математический анализ с его дифференциалами, функциями и интегралами; аналитическую геометрию, где простые и сложные геометрические фигуры можно решать алгебраическими методами; дискретную математику с изучением конечной структуры; статистику и даже теорию вероятности.
И хотя разделов в математике слишком много, а говорить о них можно вечно, но принцип решения задач остается неизменным, начиная с пятого класса и заканчивая аспирантурой и докторантурой. Детям и взрослым одинаково сложно могут даваться те или иные решения. Итак, вы выяснили к какой области математики относится задача, теперь можно приступать к поиску способа решения.
Перечитайте несколько раз текстовые условия задач. На первый взгляд задача может выглядеть элементарно, но не надо заблуждаться, поскольку каждая может содержать свои подводные камни. Не поленитесь и уделите время условию задачи.
Найдите в условии численные значения, которые уже известно, а также значения, которые легко высчитать. Например: «…вторая машина едет на 5 км в час быстрее первой…». Такие значения необходимо вынести в виде тезисов отдельно. Детям в школе на уроках рассказывают, как правильно оформлять задачу, и что начинать следует с такого структурного элемента, как «Дано». Это и есть тезисное изложение условия задачи. Также следует выделить такой элемент, как «Найти». В некоторых условиях задач он может быть не очевиден, но структурирование условия позволит быстро определить искомое.
Мы уже говорили о важности визуализации математических задач. Изобразить условие можно рисунком или таблицей, а также с помощью простой схемы. Не нужно детально вырисовывать каждые элемент. Если в условии задачи идет речь о корабле, который плывет с определенной скоростью за течением и против него, то вам не нужно рисовать корабль с масштабированием, просто изобразите это схематически.
Не забудьте нанести все известные числовые значения на рисунок. Так, к примеру, в средней школе на уроках геометрии, детей учат подписывать известные стороны прямоугольного треугольника для поиска неизвестной стороны. Такой подход значительно облегчает решение задач и позволяет визуально определить метод решения задачи.
Так, к примеру, в средней школе на уроках геометрии, детей учат подписывать известные стороны прямоугольного треугольника для поиска неизвестной стороны. Такой подход значительно облегчает решение задач и позволяет визуально определить метод решения задачи.
Создав схематическое изображение задачи внимательно сверьтесь с условием и, убедитесь, что все данные перенесены правильно. Если же чего-то не хватает или вы сомневаетесь, то перечитайте условие еще раз.
Еще небольшой совет: сложные объекты можно изображать исключительно схематически, в виде элементарных геометрических фигур. В некоторых ситуациях такой метод даже поможет найти решение или метод решения задачи.
Чем больше задач вы будете изучать, тем проще в дальнейшем будет искать решение в других задачах. Математика построена так, что многие задачи очень схожи между собой, поэтому, читая очередное условие, вы можете вспомнить, что как раз на днях решали подобную задачу и тогда решение придет к вам само собой. Не исключен и такой вариант, что вы сможете вспомнить аналогичное условие и сразу получите ответ, даже без сложного поиска решения.
В иных случаях вы можете воспользоваться методом поиска похожих задач, просмотреть варианты решения других людей и придете к определенному выводу. На контрольной работе у вас не будет возможности воспользоваться поиском в интернете или учебнике, и тогда пригодятся личные знания.
Когда схема вашей задачи готова, можно приступать к созданию плана решения.
Контрольная работа по определенной теме значительно упрощает момент поиска необходимого уравнения для решения задачи. Так, к примеру, если последнюю неделю вы изучали формулы сокращенного умножения, то и задачи на контрольной работе необходимо решать по одной из этих формул. Семестровая или годовая контрольная работа могут включать в себя все темы, пройденные за определенный период. Крайне важно выяснить, какое уравнение или теорема пригодится для решения вашей задачи.
Готовясь к экзамену обязательно выпишите отдельно на листок все основные математические формулы и уравнения, которые могут пригодиться. Это поможет их быстрее запомнить, а такие знания пригодятся, ведь вам не придется тратить время на подбор метода решения.
Если вы понимаете, как решать задачу, но вам сложно вычислить результат из-за дроби, отрицательных чисел, сложной переменной или наличия нескольких переменных, то потренируйтесь на более простых примерах. Подставьте натуральные числа вместо сложных переменных и решите уравнение. Придя к определенному результату, вы поймете, по какому принципу решать задачу и сможете решить ее уже по условию.
Не отступайте от намеченного плана и обязательно проверяйте правильность результата на каждом этапе. Небольшая ошибка в первой строке решения приведет к неверному итоговому ответу. Будет обидно, если вы неверно вычислите дискриминант, а в итоге получите два варианта скорости с отрицательным ответом.
Некоторые задачи можно перепроверить, подставив полученный результат в первое уравнение. Это отличный способ, когда вы ищете переменную «х». Обязательно убедитесь, что ответ имеет право на существование. Помните, что скорость или вес не могут быть отрицательными.
Если вы сомневаетесь в правильности решения задачи или получили результат, который не может существовать, то попробуйте изменить схему решения задачи. Неудачная попытка — это не проблема, а возможность поиска новых решений. Для того все и учатся, ведь допускать ошибки лучше в процессе обучения, а не на экзамене или работе. Не огорчайтесь, если у вас что-то не получилось с первого раза, никто не идеален.
Если все ваши усилия оказались безрезультатными, и вы никак не можете продвинуться в решении задачи, то обратитесь за помощью к тем, кто точно знает правильный ответ. Не стесняйтесь подойти к преподавателю, а иногда даже обратиться к репетитору. Вам помогут провести разбор ошибок и объяснят, как их исправить.
Не забывайте регулярно заниматься, чтобы не утратить навыки решения задач. Старайтесь выписывать основные правила и формулы, так вы со временем запомните их и сможете свободно применять в любой ситуации.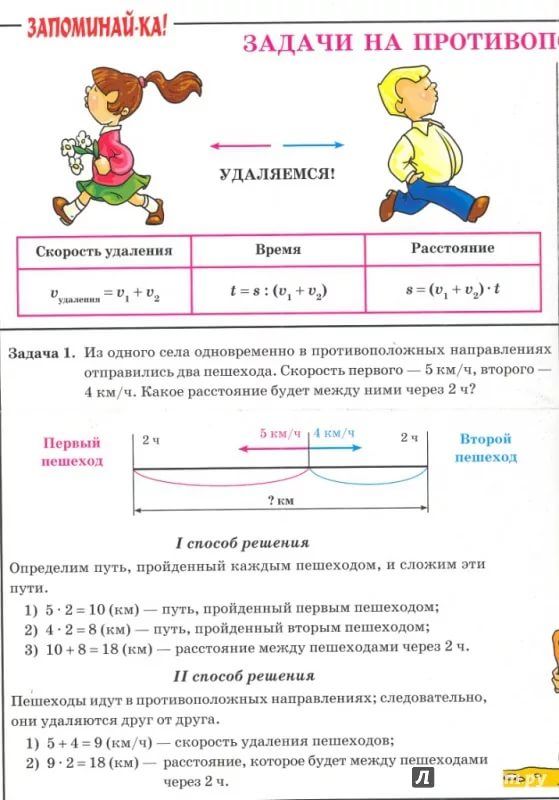
Как научить детей решать задачи по математике: советы именитых педагогов и простых мам
Научить детей решать задачи по математике — дело учителя, но и родители не должны оставаться в стороне, если их чадо «тормозит» в этом вопросе. Одним учебником математики сыт не будешь. Ведь если научить ребенка самостоятельно решать задачи в 1-3 классах, дальше он будет щелкать как семечки не только задачи по математике, но и по физике, химии, геометрии и др. И самое главное — этот навык пригодится ребенку в жизни!
vogazeta.ru
В статье Как научить ребенка математике мы подробно писали, из каких 4 частей состоит любая задача и что нужно сделать в первую очередь, чтобы ребенок понял, чего от него хотят и как ответить на вопрос задачи. Уяснив алгоритм решения задач, ребенок сможет самостоятельно решить практически любую задачу, даже несмотря на то, что они все кажутся такими разными.
Основные типы задач по математике: краткий конспект
Небольшой ликбез, т. к. далеко не все родители учились в педагогических ВУЗах и владеют методикой преподавания. Пробежимся по теории, чтобы понимать, кто, кому и чего «должен». Зная ключевые моменты, вам будет проще помочь ребенку в решении задач, которые вызывают у него сложности, вы сможете определить, где пробелы в знаниях и что нужно «подтянуть» в каждом конкретном случае.
к. далеко не все родители учились в педагогических ВУЗах и владеют методикой преподавания. Пробежимся по теории, чтобы понимать, кто, кому и чего «должен». Зная ключевые моменты, вам будет проще помочь ребенку в решении задач, которые вызывают у него сложности, вы сможете определить, где пробелы в знаниях и что нужно «подтянуть» в каждом конкретном случае.
iqsha.ru
Рассмотрим самые распространенные виды задач в начальных классах.
1. Простые задачи на сложение и вычитаниеК этой группе относятся несколько задач, но для всех есть общие рекомендации:
- Решаются в одно действие.
- Иногда удобно составить уравнение.
- На их примере ребенок должен научится выполнять краткую запись.
- Если краткого условия недостаточно, нарисовать рисунок. Если не помог рисунок, показываем на конкретных предметах и производим действия с ними.
- Четко усвоить, что «+» — это прибавить, увеличить, а «-» — уменьшить, отнять, вычесть.

- Хорошо запомнить компоненты арифметических действий:
слагаемое + слагаемое = сумма
уменьшаемое — вычитаемое = разность
- Понять разницу между словами «стало» и «осталось». Четко понимать, что значит «на … меньше», «на … больше».
- Важно понять и запомнить: чтобы узнать, НА СКОЛЬКО одно число больше или меньше другого, нужно из большего числа вычесть меньшее.
- Важно понять и запомнить: чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое.
- Важно понять и запомнить: чтобы найти неизвестное уменьшаемое, нужно к вычитаемому прибавить разность.
- Важно понять и запомнить: чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть разность.
Задачи с косвенным вопросом
Это самые коварные задачи из этой группы. Внимательно прочитайте условие — и поймете почему.
На стоянке у первого подъезда 7 машин. Это на 2 машины больше, чем на стоянке у второго подъезда. сколько машин на стоянке у второго подъезда.
Это на 2 машины больше, чем на стоянке у второго подъезда. сколько машин на стоянке у второго подъезда.
Эти задачи решаются двумя и более действиями.
Есть несколько способов решения:
- по действиям с пояснениями;
- по действиям с вопросами;
- выражением.
В решении таких задач главное:
- найти главное и сделать краткую запись;
- разложить эту задачу на несколько простых и составить план решения;
- помнить главное: по двум данным находим третье.
- Важно запомнить названия компонентов действий и понять их смысл:
1-й множитель х 2-й множитель = произведение
делимое : делитель =частное
- Ребенок должен понимать, что 1-й множитель показывает, КАКОЕ число повторяется а 2-й множитель показывает — СКОЛЬКО РАЗ оно повторяется.

Это очень важно для правильной записи в задачах, иначе получится бессмыслица.
Советы о том, как научить ребенка осознанно относиться к умножению и делению, вы найдете в нашей статье Как научить детей быстро считать: математика до школы. Если возникли проблемы с решением задач на умножение — сдайте чуть-чуть назад, закрепите осознание этого арифметического действия.
4. Простые задачи на умножение и деление
- Очень важно понять и запомнить разницу «в «, «на».
«Во сколько раз» или «на сколько»? Предлог «на» — это сложение или вычитание, а «в» — умножение или деление.
- Важно понять и запомнить: чтобы узнать, во сколько раз одно число больше или меньше другого, нужно большее число разделить на меньшее.
5. Составные задачи на все 4 арифметические действия
6. Задачи на цену, количество, стоимость
7. Задачи на движение
Это отдельная обширная тема, вернемся к ней позже.
Типичные ошибки в решении задач
Ошибка №1. Ребенок невнимательно прочитал условие задачи.
Ребенок невнимательно прочитал условие задачи.
Часто бывает так, что ошибки возникают от невнимательности. Так часто бывает в задачах с косвенным вопросом. Ребенок смотрит на цифры, вроде все логично, но… не верно.
Например: «У Маши 8 конфет, это на 2 меньше, чем у Кати. Сколько конфет у Кати».
Ребенок видит «на 2 меньше» и делает «логичный» вывод, что надо отнять. Отнять можно от бОльшего числа, т.е. сразу напрашивается решение 8-2=6. И ответ: 6 конфет у Кати. А ответ-то не тот! Если внимательно почитать условие, то станет понятно, что у Кати конфет больше чем у Маши. И вовсе тут не отнимать надо.
Как исправить ошибку. Сразу разберитесь с условием, поможет краткая запись.
Ошибка №2. Ребенок допустил ошибку в решении.
Когда в задаче несколько неизвестных, решение затрудняется, требуется выполнить не одно действие, а придумать целую цепочку рассуждений.
Как исправить ошибку. Для начала определим, каких данных нам не хватает. Решаем по действиям. Находим нужные числа (помним правило: по двум неизвестным находим третье), подставляем их и отвечаем на вопрос задачи.
Решаем по действиям. Находим нужные числа (помним правило: по двум неизвестным находим третье), подставляем их и отвечаем на вопрос задачи.
Ошибка №3. Неправильная запись ответа.
Часто ребенок пишет не то пояснение.
Как исправить ошибку. Нужно внимательно прочитать вопрос задачи. Уяснить раз и навсегда, что ответ начинается с числа, а дальше пишем, что требовалось найти (переписываем формулировку вопроса задачи).
Творческий подход в решении задач
www.craftykidsathome.com
- Учите ребенка рассуждать.
- Придумывайте задачи с лишними или недостающими данными.
Пусть ребенок сам вычеркнет лишнее, те данные, которые не влияют на решение.
- Дайте условие, а ребенок пусть сам придумает ответ.
- Пусть ребенок сам составит обратную задачу.
- Придумать несколько задач на одно решение.
- Придумать, как решить задачу другим способом и объяснить его.
На школу надейся, а сам не плошай
Заглянем в педагогику и «расшифруем» мысли умных и заслуженных, исходя из сегодняшних реалий.
В далеком 1867 году К. Ушинский сказал: «У хороших преподавателей дело выходит так, что арифметическая задача есть вместе занимательный рассказ, урок сельского хозяйства или домашней экономии, или историческая или статистическая тема и упражнение в языке».
«Расшифровка» следующая.
- Ученика нужно поставить в такие условия, чтобы он оказался в эпицентре событий, т.е., решая задачу, видел ее применение в жизни.
Не всегда задачи в школьном учебнике «вдохновляют» современных школьников. Многим не ясно условие по одной простой причине: ребенок не имеет представления о том, что говорится. Например, задача про надои и бидоны с молоком, а городской «деть» и корову-то в глаза не видел, не то, что тонны молока в бидонах. Или в задаче использованы такие значения, которые в жизни нереальны — это затрудняет восприятие, т.к. ребенок все воспринимает буквально.
Задача родителей — помочь ребенку ПОНЯТЬ условие. Любым способом: хоть рисуй, хоть танцуй.
- К решению задач нужно подходить творчески.
Интерес заставляет ребенка быть активным, а активность в свою очередь усиливает внимание.
В каждодневной жизни нам то и дело приходится решать задачи. Привлекайте ребенка, задавайте вопросы, просите совета. Например, тема ремонта. Вычислить метраж комнаты; просчитать нужное количество краски, зная расход на метр квадратный; купить линолеум, зная длину и ширину комнаты; просчитать, какой метраж выгоднее, если есть напольное покрытие шириной 2, 5 метра и 3 метра, чтобы меньше остатков было и по цене вышло выгоднее. Купить ткань на пошив постельного белья, зная размеры матраса. Примеров масса! И это работает гораздо эффективнее, чем «бездушная» задача в учебнике, которая совершенно не привязана к жизни и не вызывает эмоциональный отклик.
- При решении жизненных задач у ребенка помимо всего прочего развивается наблюдательность, речь, появляется рабочее настроение, развиваются творческие способности и самостоятельность.

Через некоторое время вы заметите, что ребенок различными способами комбинирует информацию, с легкостью составляет задачи сам, находя идеи в окружающем мире, а не высасывая из пальца.
- Когда ребенка просят составить собственную задачу, нужно следить и за содержанием, и за решением. Задача должна быть осмысленной и целесообразной.
Например, нельзя допускать таких «ляпов», как «Я съел 13 желтых груш и 20 зеленых яблок. Сколько фруктов я съел?» Задача теряет смысл, если она оторвана от жизни.
- От задачи надо идти к примеру, а не наоборот.
Дети мыслят не абстрактно, а конкретными образами. Пример 12-6 ни о чем не говорит, а вот ситуация, когда из 12 человек 6 уже купили билеты на футбольный матч — это совсем другое дело. Тут ребенок не задумываясь ответит, что оставшиеся шестеро очень рискуют, нужно поторопиться, иначе билетов может не хватить и придется сидеть у телевизора, вместо того, чтобы активно скандировать на трибунах в поддержку любимой команды.
Лебединцев в своей книге «Введение в современную методику математики» писал: «То влияние, которое может оказывать обучение счислению и вообще математике на умственное развитие детей, находится в прямой зависимости от материала, которым мы пользуемся при обучении; если в учебном материале будут преобладать отвлеченные упражнения в действиях и хитроумные задачи с условиями, лишенными внутренней связи и, по существу, далекими от жизни, то, упражняя учащихся на таком материале, мы, может быть, и выработаем у них формальные навыки в вычислениях и, пожалуй, изощрим их ум для разгадывания разных ребусов и головоломок, но отнюдь не сделаем их более способными к правильному мышлению в жизни или какой-либо области знания…».
Французский педагог Жан Мосе тоже был уверен, что «заставлять ребенка начинать с отвлеченного правила и затем предлагать ему задачи — это значит идти наперекор ходу развития человеческого ума…».
Практические советы по решению задач от реальных мам
fb. ru
ru
Что нам Ушинский, Лебединцев и Мосе, спросим у тех, кто «из нашей песочницы». Как они помогают своим детям решать задачи по математике, что «работает», какие приемы на практике доказали свою эффективность и помогли повысить успеваемость.
Татьяна, мама учеников 4 кл. и 6 кл.
«Я знаю, что особую сложность у детей вызывают задачи на скорость, поэтому начала готовить своих мальчишек к этому уже с 1 класса. Когда ехали к бабушке в Пинск, говорили о скорости, засекали время, считали сколько мы проехали км, смотрели на знаки и вычисляли сколько нам останется времени, если мы будем ехать с такой же скоростью и сколько, если папа будет ехать с другой. В общем, я очень удивлялась, когда мои пацаны на скорость задачи решали как орехи. Я поняла, что в моем детстве не хватало практического представления того, о чем говорилось в задачах».
Ольга, мама ученика 1 кл. и ученицы 4 кл.
«С задачами старшая плохо дружит)) Почти всегда приходит за помощью. Стараюсь выработать алгоритм решения, но частенько упираюсь в «лень подумать». Если совсем «затык», рисуем схемы. На дополнительные задачи совсем нет времени, а сама по своей воле заниматься ими дочь точно не будет)) Иногда встречаются задачи с некорректно поставленным вопросом, тут приходится помогать с формулировкой ответа.
Стараюсь выработать алгоритм решения, но частенько упираюсь в «лень подумать». Если совсем «затык», рисуем схемы. На дополнительные задачи совсем нет времени, а сама по своей воле заниматься ими дочь точно не будет)) Иногда встречаются задачи с некорректно поставленным вопросом, тут приходится помогать с формулировкой ответа.
Младшего усадить за математику очень сложно. В те редкие моменты, когда дело доходит до задач, он их решает в уме и выдает ответ устно).»
Вероника, мама учеников 2 кл. и 4 кл.
«Младший задачи решает без проблем, но ненавидит чертить схемы к ним и писать пояснения. Старший ходит на факультатив по математике, дома домашку сам делает».
Катерина, мама ученика 2 кл. и ученицы 5 кл.
«Сын отлично справляется сам. Он такие схемы рисует, что я иногда в шоке)). Если за помощью обращается дочь, стараюсь упростить условие задачи до понятных образов, а потом она сама догадывается, как сложную модель решить».
Татьяна, мама ученицы 5 кл.
«Чаще всего прибегаем к рисованию. Прямо вот как по условию… садимся и рисуем, как есть. Так сказать, наглядность помогает. Велосипедист выехал… значит рисуем человечка на велосипеде, город из которого он выехал и тд)))) Если катер плывет по течению, рисуем море, волны)))))) С пояснениями никогда исправлений со стороны учителя не было, да и у нас, собственно, тоже вопросов не возникало. Смотри по условию, что спрашивают — и пиши ответы возле каждого действия».
Наталья, мама ученика 5 кл.
«Приходилось объяснять дроби на примере сломанных карандашей, порванных в клочья бумажек. В гостях в тот момент был друг-проектировщик, он именно так решил наглядно пояснить сыну задачу. Я обычно прибегаю к помощи рисования. В задачах на скорость/время/расстояние рисовали целые истории: кто куда и на чем поехал, кого встретил по дороге и в какой момент. Порой решение задач превращалось в мультфильм, одного черновика обычно мало. Несколько раз решали задачи всей семьей: мама отдельно от папы, потом сравнивали результаты и каждый объяснял ребенку свой «самый рациональный и простой» способ. Как правило, у мужчин своя логика)), мое решение обычно отличается от папиного».
Несколько раз решали задачи всей семьей: мама отдельно от папы, потом сравнивали результаты и каждый объяснял ребенку свой «самый рациональный и простой» способ. Как правило, у мужчин своя логика)), мое решение обычно отличается от папиного».
Уважаемые читатели! Делитесь в комментариях своими находками и сложностями в решении задач по математике с детьми. будем разы разобраться вместе и помочь советами и полезными статьями на интересующие вас темы.
Как научить ребенка решать любые задачи: логические, математические, олимпиадные
Дети с развитой логикой смогут решить любую задачу
Развивать логическое мышление учащихся начальных классов необходимо постоянно. Регулярные тренировки в решении головоломок, нестандартных задач, ребусов и задач на смекалку полезны и необходимы для ума ребенка.
Для развития логического мышления младших школьников используются несложные задания, например, найти лишнее, продолжить ряд знаков, найти числа или недостающие фигуры и т. д. Даже самые простые логические задачи для детей помогают избавить мышление от шаблонов.
д. Даже самые простые логические задачи для детей помогают избавить мышление от шаблонов.
Что должен уметь школьник для успешного выполнения заданий на логику?
- рассуждать, используя доказательства и аргументы;
- последовательно мыслить;
- выстраивать гипотезы;
- оценивать важность условий задачи, их истинность;
- аргументированно опровергать чужие неверные выводы;
- выбирать и использовать разные способы для решения конкретного вида задач.
Способы решения задач на логику
Условно их можно поделить на стандартные и нестандартные.
Стандартные методы
К традиционным методам относятся популярный метод проб и ошибок, который может потребовать много времени и терпения, и метод шаблонов, к которому в основном прибегают при решении школьных задач.
Мы знаем, что абсолютное большинство взрослых захотят решить предложенную задачу с помощью уравнения. Неплохой способ, но зачастую обыкновенные логические рассуждения помогают найти ответ быстрее, без ручки и бумаги, просто в уме.
Рекомендуем ознакомиться с несколькими популярными методами, описанными на примерах в материале «Как решать логические задачи»:
- метод последовательных рассуждений;
- «с конца»;
- с помощью таблиц истинности;
- метод блок-схем.
Нестандартные методы
Среди популярных, нестандартных — целенаправленный поиск «ключа» («ключей») и метод «игры в создателя» (т.е. моделирования различных вариантов принципов, использованных для создания задачи). А если подсказки, шаблоны решения отсутствуют, применяется самый сложный метод – поиска метода.
Для быстрого и правильного решения различных логических головоломок и задач на смекалку ребенку необходимо:
- знать виды логических задач;
- владеть возможными методами решения задач;
- уметь классифицировать задачу и выбирать самый простой и «красивый» способ ее решения.

Алгоритм решения задач на логику и смекалку
Основные шесть этапов, которые последовательно должен пройти ученик, решая логическую задачу:
- Ознакомление с условиями задачи.
- Понимание содержания задачи, анализ условий, моделирование.
- Поиск метода решения.
- Применение метода решения, поиск правильного ответа.
- Проверка правильности решения и оформление ответа.
- Анализ проведенного решения.
- Отработка и закрепление навыков решения аналогичных задач.
1. Внимательно прочитайте условие задачи, лучше несколько раз. Четко уясните вопрос или проблему, которую нужно разрешить. Чаще всего ошибки в решении появляются от невнимательности. Особенно это касается задач с подвохом.
2. Кратко запишите условия задачи, по возможности, опишите задачу схематически (в виде рисунка, схемы, графика, дерева, чертежа и т. д.). Наглядное представление задачи не только способствует более быстрому уяснению содержания задачи, но и поможет выявить новые связи между элементами задачи или увидеть скрытые свойства объектов. Выделите существенные и несущественные условия задачи и попробуйте упростить задачу, абстрагироваться от действительности, мысленно смоделировать описанную в задаче ситуацию.
д.). Наглядное представление задачи не только способствует более быстрому уяснению содержания задачи, но и поможет выявить новые связи между элементами задачи или увидеть скрытые свойства объектов. Выделите существенные и несущественные условия задачи и попробуйте упростить задачу, абстрагироваться от действительности, мысленно смоделировать описанную в задаче ситуацию.
3. Попытайтесь определить тип задачи и соответственно подобрать метод решения, который обычно применяется для решения этого вида заданий. Например, для решения задач на определение истинности или ложности высказывания удобно использовать таблицу. Для решения задач с большим количеством взаимосвязанных условий лучше использовать метод графов и т.д.
4. Используя выбранный метод, решите задачу.
5. Проверьте ваш вариант ответа. В случае письменного решения задачи надлежащим образом запишите правильный ответ.
6. Анализ проведенного решения представляет собой обсуждение всего хода мыслительных действий в процесс решения логической задачи. Это завершающий и необходимый этап решения любой задачи, не только логической. Он включает:
Анализ проведенного решения представляет собой обсуждение всего хода мыслительных действий в процесс решения логической задачи. Это завершающий и необходимый этап решения любой задачи, не только логической. Он включает:
- поиск альтернативного, более рационального, красивого способа решения;
- анализ всего процесса, моментов, которые вызвали затруднения;
- выделение важных признаков данного типа задач;
- составление алгоритма их решения;
- систематизация полученных знаний.
Школьнику полезно записывать свои решения, алгоритмы и рассуждения в отдельную тетрадь, например, специально для занятий на ЛогикЛайк. Таким образом он будет «пропускать через моторику» свои рассуждения и всегда сможет вернуться к своим наработкам.
7. Чтобы закрепить свое умение решать головоломки определенного типа, необходимо не откладывая решить еще ряд подобных, однотипных задач с постепенным усложнением набора условий.
В учебной программе образовательной платформы LogicLike логические задачи распределены по 15 тематическим разделам. Каждая категория содержит задания разного уровня сложности.
Таким образом осуществляется последовательное и системное развитие логического мышления младших школьников. Подробнее о курсе развития логического мышления.
Чтобы занятия ребенка логикой были эффективнее, рекомендуем родителям дошкольников и первоклассников заниматься вместе с детьми.
Правильный подход к учебному процессу поможет научить ребенка решать логические задачи и воспитать полезные ему качества.
В ходе обучения на ЛогикЛайк дети становятся более самостоятельными и уверенными в себе, воспитывают в себе ответственность за принимаемые решения, усидчивость и настойчивость.
Как научить ребенка решать задачи по математике
Решение задач – одна из неотъемлемых составляющих школьного процесса обучения. В начальных классах дети решают простенькие арифметические задачи, потом наступает пора задач по алгебре и геометрии, физике, химии, биологии.
В начальных классах дети решают простенькие арифметические задачи, потом наступает пора задач по алгебре и геометрии, физике, химии, биологии.
Содержание:
- Почему важно научить школьника решать задачи?
- Пошаговый алгоритм действий
- Шаг 1. Чтение условия
- Шаг 2. Составление краткого описания
- Шаг 3. Поиск алгоритма решения
- Шаг 4. Запись ответа
- Какие навыки необходимы для решения задач
Почему важно научить школьника решать задачи?
Условия задач по разным предметам совершенно не похожи друг на друга, однако методы и приемы решения имеют много общего. И если ребенок не научится решать задачи по арифметике в младшей школе, он будет испытывать нарастающие сложности по мере перехода из класса в класс.
Проблемы с математическими задачами в младших классах – прямой путь к тому, что ребенок сопротивляется изучению точных наук в средней и старшей школе. Преподаватели и родители «записывают» таких учеников в гуманитарии и считают, что им «не дано» научиться решать задачи. А в учебниках написаны сухие формальные правила, которые никак не помогают и не мотивируют учащихся.
А в учебниках написаны сухие формальные правила, которые никак не помогают и не мотивируют учащихся.
На самом деле, умение логически мыслить и решать задачи необходимо все ученикам, даже абсолютным гуманитариям. Без этого во взрослом возрасте невозможно решать даже простейшие бытовые вопросы – к примеру, посчитать количество стройматериалов для ремонта или пропорции ингредиентов при приготовлении блюд. А для программиста, инженера или управленца логическое и аналитическое мышление – неотъемлемая составляющая профессии.
Пошаговый алгоритм действий
Родителям необходимо ребенка учить решать задачи уже с первого класса, причем делать это надо в доброжелательной форме. Нельзя кричать, сердиться или решать задания вместо школьника, как бы вам этого не хотелось. Не ругайте ребенка за ошибки, ведь в процессе обучения они неизбежны, без этого невозможно научиться делать что-либо в принципе.
Функция родителей – объяснить условие задачи и алгоритм рассуждений, который позволяет получить ответ. Стоит сразу запастись терпением, просто не будет. Это кропотливая и длительная работа, за один раз даже самого талантливого ребенка невозможно научить решать задачи.
Стоит сразу запастись терпением, просто не будет. Это кропотливая и длительная работа, за один раз даже самого талантливого ребенка невозможно научить решать задачи.
Шаг 1. Чтение условия
Умение читать условие и вникать в детали – обязательный навык для успешного решения задачи. Попросите ребенка прочитать условие вслух и задайте ему вопросы, чтобы убедиться в понимании текста. Если в задаче употребляются незнакомые понятия и формулировки, объясните их значения.
Особое внимание обратите на то, правильно ли ребенок понял вопрос. Зачастую сложности проистекают из того, что школьник путает математические понятия «больше в», «больше на» и прочие.
Шаг 2. Составление краткого описания
В школе детей учат составлять описание по определенным правилам, что вызывает у них сложности. Помимо того, что надо понять смысл задачи, школьник вынужден думать, как это записать в соответствии с требованиями учителя.
Значительно проще для ребенка нарисовать условие задачи. Графическая схема позволяет наглядно увидеть связи между элементами задачи и разобраться в условии. Очень часто алгоритм решения становится понятен ребенку уже на этом этапе.
Графическая схема позволяет наглядно увидеть связи между элементами задачи и разобраться в условии. Очень часто алгоритм решения становится понятен ребенку уже на этом этапе.
Шаг 3. Поиск алгоритма решения
Наглядная графическая схема в большинстве случаев наталкивает школьника на правильный ход рассуждений. Но что делать, если этого не происходит? В этом случае попробуйте иллюстрировать задачу подручными предметами, разыграйте с ними сценку, задайте наводящие вопросы. Единого метода не существует, вам нужно будет найти подход к ребенку.
Схему решения нужно подробно записать и убедиться, что школьник понимает общий принцип. Тогда он сможет пользоваться в дальнейшем для аналогичных задач.
Шаг 4. Запись ответа
Ответ нужно формулировать полно и точно. Убедитесь, что ребенок отвечает именно на тот вопрос, который спрашивается в задаче. Если это не так, нужно вернуться на первый шаг и заново пройти всю цепочку.
youtube.com/embed/cFZKykOE-Wc» frameborder=»0″ allow=»accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»» loading=»lazy»>Какие навыки необходимы для решения задач
Для нахождения ответа во многих задач нужно выполнить несколько действий. Убедитесь, что ребенок усвоил правила нахождения слагаемого, уменьшаемого, вычитаемого, множителя, делителя, делимого. Он должен уметь вычислять эти данные на «автомате».
Чтобы сохранить мотивацию, проявите творческий подход. К примеру, замените груши и яблоки любимыми лакомствами ребенка, а поезда и катера – космическими кораблями.
Развитая логика и аналитическое мышление – помощники в решении задач. Обязательно решайте с ребенком логические задания, разгадывайте головоломки и ребусы, учите его анализировать окружающие предметы и явления.
Рейтинг: 5/5 — 2 голосов
Как научить ребенка решать задачи по математике 1-4 класс?
Если ребенка научить решать задачи по математике с 1 по 4 класс, то дальше ему будет не сложно постигать другие точные предметы и не только в школе. Ведь практически в любой сфере жизни нужны навыки измерений, определений, расчетов, и сделать это без знания математики крайне сложно. Начиная с первых уроков арифметики, следует донести эту мысль малышам, чтобы они понимали — задача не живет только на страницах учебника, она входит в повседневную жизнь и влияет на нее.
Ведь практически в любой сфере жизни нужны навыки измерений, определений, расчетов, и сделать это без знания математики крайне сложно. Начиная с первых уроков арифметики, следует донести эту мысль малышам, чтобы они понимали — задача не живет только на страницах учебника, она входит в повседневную жизнь и влияет на нее.
Способов, как правильно научить ребенка решать и понимать задачи по математике, существует несколько, элементы каждого из них можно применять не только во 2 и 3 классе, но даже в старшем возрасте. Формировать такие навыки необходимо, они во многом повлияют на дальнейшие успехи в учебе.
Содержание статьи:
- 1 Как научить решать задачи по математике ребенка 1-4 классов
- 1.1 Для чего необходим навык
- 1.2 Общий алгоритм обучения
- 1.3 Распространенные ошибки в решении задач
- 2 Особенности решения задач в 1 классе
- 3 Что делать, если ребенок не понимает задачи по математике во 2 классе
- 4 Специфика обучению решения математических задач в 3 классе
- 5 Как просто решать задачи в 4 классе
- 6 Как учить ребенка решать задачи, если математика ему трудно дается
- 7 Как научить ребенка решать логические задачи по математике
Как научить решать задачи по математике ребенка 1-4 классов
Поскольку знакомство с математикой начинается в начальной школе, то и приобретение навыка справляться с такими головоломками происходит в данный период.
Для чего необходим навык
Важно понимать, что научившись справляться с математическими заданиями в начальной школе, ребенок сможет успешно овладеть химией, физикой, астрономией и другими предметами в старших классах. Родители просто обязаны помочь своему чаду с математикой в первых классах, поскольку данный вид занятий напрямую связан с четким логическим мышлением, способностью анализировать, делать выводы.
Полезно знать!
Кроме этого, задания на счет тренируют память, внимание, развивают способность рассуждать, положительно сказываются на когнитивных способностях в целом.
Общий алгоритм обучения
Следует придерживаться такой последовательности шагов, чтобы научить детей правильно выполнять математические задания:
- Внимательное чтение условий и разложение заданий на этапы: условие, вопрос, решение, ответ.
- Составление плана для выяснения неизвестного. Для маленьких хорошо применять рисунки — схемы на данном этапе, приводить примеры из личного опыта, которые аналогичны условию задачи, для лучшего ее восприятия.

Также уместно использование простеньких сценариев, которые позволяют детям «быть внутри задания».
- Акцент на тексте головоломки и поиск ответа в нем. Важно научить тому, что в математике нет лишних фраз, все они важны и используются для нахождения ответа, который заложен в формулировку предложений.
- Практика и еще раз практика. Для того, чтобы дети успешно овладели навыками сложения, вычитания, умножения, им необходимо довести эти действия до автоматизма.
Распространенные ошибки в решении задач
Главные ошибки в процессе поиска ответа следующие:
- беглое чтение условия задачи, которое не позволяет определить, какой именно ответ нужен;
- неправильное понимание последовательности действий, особенно при поиске нескольких неизвестных;
- некорректный ответ может быть формальным, когда перепутаны единицы измерения или же неправильно вычисленным.
Запомните!
Важно научить малыша самостоятельно исправлять и находить ошибки, перепроверять задачу, а не просто откладывать ее в сторону, если что-то не получилось.
Особенности решения задач в 1 классе
На начальном этапе используются так называемые «текстовые» задания, которые знакомят малышей в 1 классе с арифметикой и проблематикой поиска неизвестных данных. Для таких заданий характерно:
- описание простых сюжетов в задании, которые понятны и знакомы ребенку;
- решение таких головоломок помогает осознать важность математических знаний;
- формирование ключевых умений: выделение условия и вопроса, установление зависимости между понятиями и данными, построение логической цепочки решения, проверка результата.
Для того, чтобы научить первоклашек таким понятиям как «условие», «ответ», «неизвестное» следует использовать такие методы:
- дополнительные, наводящие вопросы по условиям;
- составление схем — рисунков условий;
- перевод текста в схематическую модель;
- объяснение значений фраз в условии задания;
- выбор варианта решения, исходя из схемы;
- обозначение в схеме известных и неизвестных разными способами.

Успешное получение навыков в решении простых задач поможет освоить математическую дисциплину в последующих этапах обучения.
Что делать, если ребенок не понимает задачи по математике во 2 классе
В математике второго года обучения также основными остаются текстовые задачи, которые требуют найти неизвестное при наличии двух известных чисел. Если ребенок не понимает, как следует работать с задачами по математике во 2 классе, то не следует паниковать и критиковать его. Еще вполне можно наверстать то, что упущено. Рекомендовано пройтись по основам данной проблемы и разобраться с ней:
При последовательной работе и выполнении подобных заданий, дети начинают запоминать их и понимают причинно-следственные связи между действиями и результатами, что в конечном итоге и требуется для работы с арифметикой.
Специфика обучению решения математических задач в 3 классе
Важной возрастной особенностью третьеклассника является активное развитие мыслительных процессов, что позволяет усваивать большие объемы информации и понимать сложные действия. Особенностями обучения решению арифметических заданий на данном этапе можно назвать следующие:
Особенностями обучения решению арифметических заданий на данном этапе можно назвать следующие:
Как просто решать задачи в 4 классе
В это период очень важно закрепить навыки работы с задачами разной степени сложности, чтобы применять их в дальнейшем. В 4 классе следует развивать не только автоматизацию процесса решения математических заданий, но и стимулировать интерес к ним разными способами:
- изменение условий, предполагающее нахождение нескольких способов решения;
- модификация числовых данных и единиц измерения;
- использование кратких схем и чертежей вместо текстовых условий;
- обнаружение ошибок в уже решенной задаче;
- замена цифр на буквы.
Только используя различные альтернативные варианты обучения можно подвести ребенка к простому алгоритму, применяемому к любой задаче:
- Ознакомление с условием.
- Определение неизвестных и способы их поиска.
- Анализ и вычисление.

- Ответ на главный вопрос.
- Проверка корректности найденного числового значения.
- Оформление задания письменно.
Если учителю и родителям удалось привести ученика к данному алгоритму работы с математическими головоломками, то он сможет успешно решать простые и сложные задачи.
Как учить ребенка решать задачи, если математика ему трудно дается
Доказано, что школьный курс математики способен освоить любой школьник, у которого нормально развита логика и работают мыслительные процессы. Зачастую родители предпочитают считать, что если ребенку трудно дается математика, то у него просто гуманитарный склад ума и эта дисциплина ему не нужна.
Важно!
Такая точка зрения в корне неверна, поскольку именно математика развивает логическое и критичное мышление, без которых ни один гуманитарий не может быть успешным.
Скорее всего, трудности связаны с психологическими проблемами. Для обучения детей, у которых есть проблемы с арифметикой в начальной школе, можно применять такие приемы:
Для обучения детей, у которых есть проблемы с арифметикой в начальной школе, можно применять такие приемы:
- акцентировать внимание на смысле фраз, а не числах;
- учить малыша отличать главную и второстепенную информацию;
- использовать рисование схем, моделей решения;
- применять цветовую гамму для создания контраста известных и неизвестных величин;
- описывать вместо условий задания ситуации, знакомые ребенку в его жизненном опыте;
- привлекать внимание к возможности применить знание математических действий и правил в реальной жизни;
- использовать образы и условных героев-помощников.
Как научить ребенка решать логические задачи по математике
Такая разновидность заданий дает возможность развивать логику детей и позволяет им обретать навыки нестандартного мышления. Постановка логических задач часто предполагает изобретение особого способа их решения, но все же существуют некоторые разработанные методы их решения, которым и следует обучить школьников:
Постановка логических задач часто предполагает изобретение особого способа их решения, но все же существуют некоторые разработанные методы их решения, которым и следует обучить школьников:
- метод рассуждений;
- таблицы истинности;
- метод блок — схем;
- средства алгебры высказываний;
- графический метод;
- математический бильярд.
При использовании рассуждений важно разделить условие задания на маленькие фрагменты и сделать последовательные выводы из каждого из них, таким образом ребенок приходит к ответу. Данный вариант решения можно также применять, начиная с конца условия, что тоже приводит к решению, но другим путем.
Применение таблиц истины дает возможность разделить все данные в тексте задачи на истинные и ложные, сравнить их наглядным образом и сделать соответствующие умозаключения о варианте ответа.
Для успешного овладения навыками решения математических головоломок детям требуется разный подход и приемы в зависимости от возраста и индивидуальных особенностей.
Решение задач со словами в современном математическом образовании: призыв к обучению навыкам понимания прочитанного
Введение
В последние десятилетия решение математических задач со словами привлекло большое внимание как исследователей, так и практикующих педагогов (Campbell, 1992; Hegarty et al., 1995; Hajer, 1996; Depaepe et al., 2010; Hickendorff, 2011, 2013; Moreno et al., 2011; Boonen et al., 2013; Swanson et al., 2013). Математические текстовые задачи относятся к математическим упражнениям, которые представляют соответствующую информацию по проблеме в виде текста, а не в форме математических обозначений (Расмуссен и Кинг, 2000; Тиммерманс и др., 2007). Следовательно, предполагается, что эффективное решение математической текстовой задачи зависит не только от способности учащихся выполнять необходимые математические операции, но и от того, в какой степени они способны точно понять текст текстовой задачи (Lewis and Mayer, 19).87; Хегарти и др., 1995; Ван дер Шут и др. , 2009 г.; Джитендра и Стар, 2012). Оба эти аспекта связаны таким образом, что более глубокое понимание текста задачи на слово служит решающим шагом перед тем, как можно будет выполнить правильные математические вычисления. Следовательно, ключевой задачей для решателей текстовых задач является адекватное понимание постановки задачи (Lee et al., 2009; Thevenot, 2010; Boonen et al., 2013).
, 2009 г.; Джитендра и Стар, 2012). Оба эти аспекта связаны таким образом, что более глубокое понимание текста задачи на слово служит решающим шагом перед тем, как можно будет выполнить правильные математические вычисления. Следовательно, ключевой задачей для решателей текстовых задач является адекватное понимание постановки задачи (Lee et al., 2009; Thevenot, 2010; Boonen et al., 2013).
В этом отношении важны два индивидуальных навыка. Во-первых, важным фактором, способствующим более глубокому пониманию текста словесной задачи, является способность построить богатое и связное мысленное представление, содержащее все (отношения между) релевантные для решения элементы, которые получены из текстовой основы слова. проблема (Де Корте и др., 1985; Хегарти и др., 1995; Пап, 2003). То есть решатели словесных задач должны использовать стратегию модели проблемы, в которой они переводят постановку задачи в качественное мысленное представление проблемной ситуации, скрытой в тексте (Pape, 2003; Van der Schoot et al. , 2009). Это мысленное представление впоследствии позволяет им составить план решения и выполнить необходимые математические операции. Хотя успешные решатели словесных задач, по-видимому, используют такую стратегию модели задач, опираясь на свои навыки мысленного представления, менее успешные решатели задач часто используют импульсивную, поверхностную стратегию прямого перевода, в которой они сосредотачиваются только на выборе представленных чисел, которые, в свою очередь, , составляют основу их математических расчетов (Verschaffel et al., 1992; Хегарти и др., 1995).
, 2009). Это мысленное представление впоследствии позволяет им составить план решения и выполнить необходимые математические операции. Хотя успешные решатели словесных задач, по-видимому, используют такую стратегию модели задач, опираясь на свои навыки мысленного представления, менее успешные решатели задач часто используют импульсивную, поверхностную стратегию прямого перевода, в которой они сосредотачиваются только на выборе представленных чисел, которые, в свою очередь, , составляют основу их математических расчетов (Verschaffel et al., 1992; Хегарти и др., 1995).
Вторым важным индивидуальным умением в успешном решении текстовых задач, подтвержденным данными исследований, является влияние способности учащегося понимать прочитанное (Pape, 2003; Van der Schoot et al., 2009; Boonen et al., 2013). Было высказано предположение, что способности к пониманию прочитанного особенно полезны при работе с семантико-лингвистическими характеристиками словесных задач, такими как последовательность известных элементов в тексте словесной задачи, степень, в которой семантические отношения между заданными и неизвестными количествами слова. проблема делается явной, а актуальность информации в тексте слова проблема (De Corte et al., 1985, 1990; Вершаффель и др., 1992; Marzocchi и др., 2002).
проблема делается явной, а актуальность информации в тексте слова проблема (De Corte et al., 1985, 1990; Вершаффель и др., 1992; Marzocchi и др., 2002).
Более того, навыки понимания прочитанного, по-видимому, более важны для преодоления таких текстовых сложностей, чем способность использовать свои навыки мысленного представления (De Corte et al., 1985, 1990). Это может объяснить, почему использование стратегии проблемной модели недостаточно во всех обстоятельствах. То есть текстовые задачи, содержащие семантически сложные признаки, требуют как точных навыков мысленного представления, так и навыков понимания прочитанного, тогда как для текстовых задач с более низкой семантико-лингвистической сложностью может быть достаточно хорошо развитых навыков мысленного представления.
Эти данные свидетельствуют о том, что для обучения учащихся тому, как эффективно решать математические текстовые задачи, навыки представления в уме и навыки понимания прочитанного должны быть частью программы обучения математике. В частности, внимание к семантико-лингвистическим особенностям текстовых задач важно, чтобы помочь учащимся улучшить свои успехи в решении текстовых задач, поскольку текстовые задачи становятся семантически более сложными по мере того, как учащиеся продвигаются в своей образовательной карьере, например, когда они переходят в среднюю школу. . Словесные задачи, предлагаемые по таким предметам средней школы, как геометрия, физика и биология, содержат больше вербальной информации и, как правило, содержат более сложные семантико-лингвистические характеристики текста (Сильвер и Цай, 19).96; Хельвиг и др., 1999).
В частности, внимание к семантико-лингвистическим особенностям текстовых задач важно, чтобы помочь учащимся улучшить свои успехи в решении текстовых задач, поскольку текстовые задачи становятся семантически более сложными по мере того, как учащиеся продвигаются в своей образовательной карьере, например, когда они переходят в среднюю школу. . Словесные задачи, предлагаемые по таким предметам средней школы, как геометрия, физика и биология, содержат больше вербальной информации и, как правило, содержат более сложные семантико-лингвистические характеристики текста (Сильвер и Цай, 19).96; Хельвиг и др., 1999).
Нидерланды, как и многие другие страны, в настоящее время уделяют большое внимание обучению решению текстовых задач в современном математическом образовании (Ruijssenaars et al., 2004; Elia et al., 2009). Преподавание математики в Нидерландах происходит в контексте предметно-ориентированного учебного подхода, называемого реалистическим математическим образованием (RME, Van den Heuvel-Panhuizen, 2003), где важную роль играет процесс решения математических задач со словами (Van den Boer, 2003; Barnes, 2005; Prenger, 2005; Van den Heuvel-Panhuizen, 2005; Hickendorff, 2011). Исследования, изучающие образовательную практику RME, показывают, что обучению навыкам мысленного представления уделяется большое внимание при обучении решению словесных задач (Van den Heuvel-Panhuizen, 2003; Van Dijk et al., 2003; Elia et al., 2009).). Тем не менее, навыки понимания прочитанного, позволяющие учащимся стать чувствительными к семантико-лингвистическим сложностям в словесной задаче, по-видимому, тренируются все меньше и меньше в учебной практике RME, несмотря на ее доказанную важность в предыдущих исследованиях (например, De Corte et al. ., 1985, 1990; Hegarty et al., 1992). Вероятно, это связано с тем, что учителя могут недооценивать или не знать о важности навыков понимания прочитанного для решения текстовых задач (Hajer, 1996; Van Eerde, 2009).). Таким образом, текущий подход к обучению решению текстовых задач, по-видимому, делает упор на развитие навыков мысленного представления, но, по-видимому, уделяет меньше внимания роли навыков понимания прочитанного. В этом отношении способ обучения решению текстовых задач в учебной программе RME, по-видимому, не соответствует тому, что в настоящее время известно из исследований о факторах, участвующих в эффективном решении текстовых задач.
Исследования, изучающие образовательную практику RME, показывают, что обучению навыкам мысленного представления уделяется большое внимание при обучении решению словесных задач (Van den Heuvel-Panhuizen, 2003; Van Dijk et al., 2003; Elia et al., 2009).). Тем не менее, навыки понимания прочитанного, позволяющие учащимся стать чувствительными к семантико-лингвистическим сложностям в словесной задаче, по-видимому, тренируются все меньше и меньше в учебной практике RME, несмотря на ее доказанную важность в предыдущих исследованиях (например, De Corte et al. ., 1985, 1990; Hegarty et al., 1992). Вероятно, это связано с тем, что учителя могут недооценивать или не знать о важности навыков понимания прочитанного для решения текстовых задач (Hajer, 1996; Van Eerde, 2009).). Таким образом, текущий подход к обучению решению текстовых задач, по-видимому, делает упор на развитие навыков мысленного представления, но, по-видимому, уделяет меньше внимания роли навыков понимания прочитанного. В этом отношении способ обучения решению текстовых задач в учебной программе RME, по-видимому, не соответствует тому, что в настоящее время известно из исследований о факторах, участвующих в эффективном решении текстовых задач.
Основываясь на приведенном выше анализе учебного плана RME, представляется правомерным предположить, что учащиеся, посещающие такой учебный план, могут оказаться в невыгодном положении, когда необходимо принимать во внимание семантико-лингвистические характеристики словесной задачи. То есть учащиеся учебной программы RME, скорее всего, будут испытывать трудности, когда их попросят решить математические текстовые задачи с высокой семантико-лингвистической сложностью. Чтобы проверить это предположение, мы сравнили результаты учащихся в решении текстовых задач, полученных при выполнении учебной программы RME, с их результатами в самостоятельном решении текстовых задач. Во-первых, мы классифицировали учащихся как успешных или менее успешных в решении текстовых задач с помощью теста по математике, который является частью учебной программы RME, а именно теста CITO по математике. Этот тест можно рассматривать как тест по математике, специфичный для метода (т. е. специфичный для RME), для оценки успеваемости учащихся в решении текстовых задач, поскольку он основан на используемом в настоящее время учебном методе решения текстовых задач. Следовательно, этот тест отражает навыки, которые учащиеся изучают в классе RME для решения текстовых задач (Doorman et al., 2007; Hickendorff, 2011). Во-вторых, мы изучили результаты учащихся в независимом тесте на решение задач со словами, который содержал либо задачи со словами, которые они могли решить, используя только свои навыки мысленного представления, либо задачи со словами, которые требовали от них также полагаться на свои навыки понимания прочитанного для обработки семантических слов. лингвистические сложности в текстовых задачах. Эта процедура имеет преимущество по сравнению с предыдущими исследованиями, проведенными, в частности, Hegarty et al. (1995), Pape (2003) и Van der Schoot et al. (2009), в которых обычно использовалась основная зависимая переменная исследования (т. е. успешность решения задач) в качестве меры результата, а также в качестве средства для классификации учащихся на успешных и менее успешных решателей текстовых задач. Классификация, используемая в настоящем исследовании, с другой стороны, основана на внешней, хорошо зарекомендовавшей себя мере решения математических задач со словами, которая не зависит от основной зависимой переменной исследования (т.
Следовательно, этот тест отражает навыки, которые учащиеся изучают в классе RME для решения текстовых задач (Doorman et al., 2007; Hickendorff, 2011). Во-вторых, мы изучили результаты учащихся в независимом тесте на решение задач со словами, который содержал либо задачи со словами, которые они могли решить, используя только свои навыки мысленного представления, либо задачи со словами, которые требовали от них также полагаться на свои навыки понимания прочитанного для обработки семантических слов. лингвистические сложности в текстовых задачах. Эта процедура имеет преимущество по сравнению с предыдущими исследованиями, проведенными, в частности, Hegarty et al. (1995), Pape (2003) и Van der Schoot et al. (2009), в которых обычно использовалась основная зависимая переменная исследования (т. е. успешность решения задач) в качестве меры результата, а также в качестве средства для классификации учащихся на успешных и менее успешных решателей текстовых задач. Классификация, используемая в настоящем исследовании, с другой стороны, основана на внешней, хорошо зарекомендовавшей себя мере решения математических задач со словами, которая не зависит от основной зависимой переменной исследования (т. е. успешности решения задач со словами). Это позволило нам сделать более значимые групповые сравнения.
е. успешности решения задач со словами). Это позволило нам сделать более значимые групповые сравнения.
Как упоминалось ранее, ключевой аспект, который отличает успешных решателей словесных задач от менее успешных, касается их способности построить точное мысленное представление текста задачи. Предыдущие исследования показали, что просьба к учащимся решить задачи на сравнение, особенно непоследовательные задачи на сравнение (см. пример 1), является подходящим методом для проверки того, насколько эффективно они построили точное мысленное представление постановки задачи (например, Pape, 2003; Ван дер Шут и др., 2009 г.).
[Пример 1 – проблема с несоответствием слов]
В продуктовом магазине бутылка оливкового масла стоит 7 евро.
Это на 2 евро больше, чем в супермаркете.
Если вам нужно купить семь бутылок оливкового масла, сколько это будет стоить в супермаркете?
[Пример 2 – проблема с согласованными словами]
В продуктовом магазине бутылка оливкового масла стоит 7 евро.
В супермаркете бутылка оливкового масла стоит 2 евро дороже в продуктовом магазине.
Если вам нужно купить 7 бутылок оливкового масла, сколько вы заплатите в супермаркете?
В несогласованных текстовых задачах, таких как представленная в примере 1, процесс перевода требует идентификации местоименной ссылки «то есть» как индикатора отношения между значением первой переменной («цена бутылки оливок масла в бакалейном магазине») до второго («цена бутылки оливкового масла в супермаркете»). Это отождествление необходимо для осознания того факта, что в задаче противоречивого сравнения относительный термин «более чем» относится к операции вычитания, а не к операции сложения. Таким образом, несовместимые текстовые задачи создают большую когнитивную сложность, чем последовательные текстовые задачи (см. пример 2), требуя от учащихся игнорировать устоявшуюся связь между больше с увеличением и сложением, а меньше с уменьшением и вычитанием (Шумахер и Фукс, 2012). Эмпирические данные подтверждают эту интерпретацию, показывая, что решатели текстовых задач делают больше (обратных) ошибок в непоследовательных, чем в последовательных текстовых задачах (например, эффект согласованности, Льюис и Майер, 1987; Папе, 2003; Ван дер Шут и др., 2009). Особенно учащиеся, которым не удается построить точное мысленное представление постановки задачи и, таким образом, сразу же начинают считать с заданными числами и относительным термином, менее успешны в решении непоследовательных текстовых задач (Hegarty et al., 19).95).
Эмпирические данные подтверждают эту интерпретацию, показывая, что решатели текстовых задач делают больше (обратных) ошибок в непоследовательных, чем в последовательных текстовых задачах (например, эффект согласованности, Льюис и Майер, 1987; Папе, 2003; Ван дер Шут и др., 2009). Особенно учащиеся, которым не удается построить точное мысленное представление постановки задачи и, таким образом, сразу же начинают считать с заданными числами и относительным термином, менее успешны в решении непоследовательных текстовых задач (Hegarty et al., 19).95).
В настоящем исследовании мы не ожидали, что ни успешные, ни менее успешные решатели проблем не столкнутся с трудностями при решении задач на последовательное сравнение слов. Тем не менее, мы предполагали, что успешные решатели текстовых задач в учебной программе RME будут испытывать меньше трудностей с правильным решением непоследовательных задач сравнения в результате их зависимости от навыков ментального представления (приобретенных во время обучения решению текстовых задач в RME), чем менее успешные решатели задач. которые используют более поверхностный подход к решению проблем (Verschaffel et al., 1992; Ван дер Шут и др., 2009).
которые используют более поверхностный подход к решению проблем (Verschaffel et al., 1992; Ван дер Шут и др., 2009).
Важно иметь в виду, что это справедливо только для последовательных и непоследовательных задач сравнения с низкой семантической сложностью; то есть проблемы, которые затрагивают только способность учащихся создавать точное мысленное представление. Мы ожидали, что если семантическая сложность задач на сравнение возрастет, даже учащиеся, классифицированные как успешно решающие задачи со словами (согласно нашей классификации, основанной на инструкции RME), могут столкнуться с трудностями при правильном решении непоследовательных задач на сравнение. В этом случае правильное решение словесной задачи требует, чтобы учащиеся использовали как навыки ментального представления, так и навыки понимания прочитанного, в то время как обучение решению словесных задач в RME (предположительно) предоставило учащимся значительную подготовку только в первом из этих двух навыков.
Относительно хорошо изученный и общепринятый способ усложнить семантическую сложность (несогласованных) задач сравнения — это манипулировать относительным термином (Lewis and Mayer, 1987; Van der Schoot et al.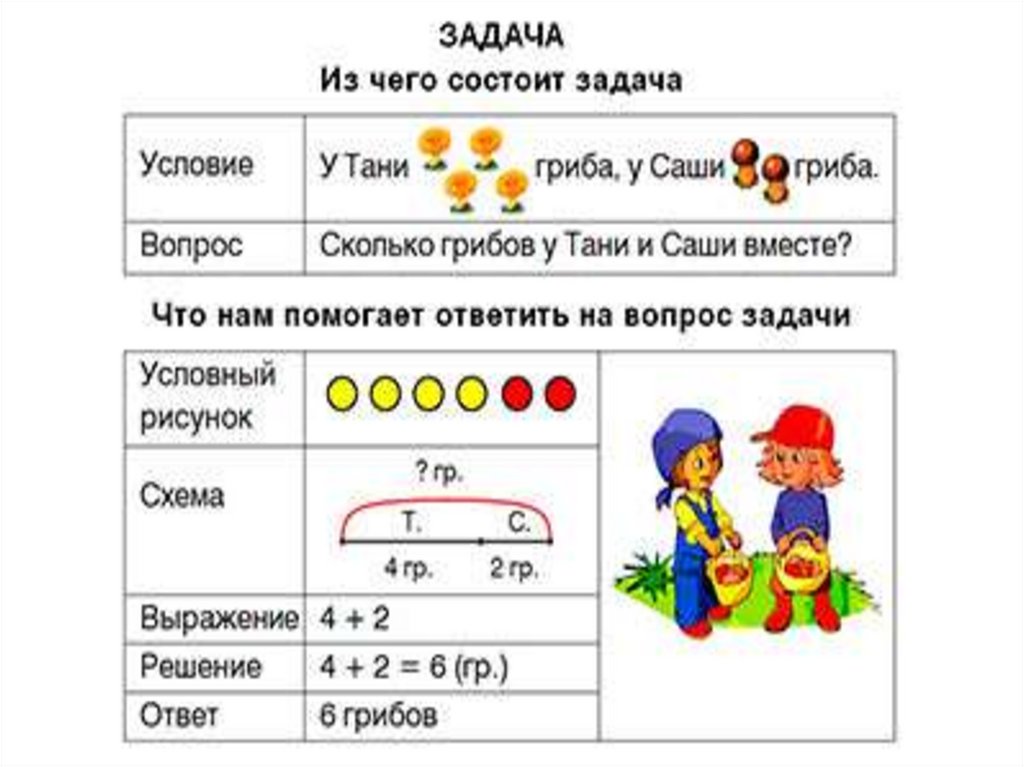 , 2009). В соответствии с принципом лексической маркировки (Кларк, 1969) труднее обрабатывать термины маркированных отношений (например, «меньше» в паре антонимов «более-менее», «узкий» в «широкий-узкий» или «короткий»). в «высокий-короткий»), чем немаркированные относительные термины (например, больше, широкий, высокий). В соответствии с этим исследование показало, что учащимся легче преобразовать неотмеченный относительный термин «больше чем» в операцию вычитания, чем отмеченный относительный термин «меньше чем» в операцию сложения (Clark, 19).69; Льюис и Майер, 1987 г.; Кинч, 1998; Папе, 2003; Ван дер Шут и др., 2009). Поэтому в настоящем исследовании мы называем текстовые задачи, содержащие отмеченный относительный термин («больше чем»), семантически более сложными текстовыми задачами, тогда как текстовые задачи с немаркированным относительным термином («меньше чем») называются семантически менее сложными. словесные задачи (см. примеры 3 и 4 для примеров помеченных и неотмеченных словесных задач соответственно).
, 2009). В соответствии с принципом лексической маркировки (Кларк, 1969) труднее обрабатывать термины маркированных отношений (например, «меньше» в паре антонимов «более-менее», «узкий» в «широкий-узкий» или «короткий»). в «высокий-короткий»), чем немаркированные относительные термины (например, больше, широкий, высокий). В соответствии с этим исследование показало, что учащимся легче преобразовать неотмеченный относительный термин «больше чем» в операцию вычитания, чем отмеченный относительный термин «меньше чем» в операцию сложения (Clark, 19).69; Льюис и Майер, 1987 г.; Кинч, 1998; Папе, 2003; Ван дер Шут и др., 2009). Поэтому в настоящем исследовании мы называем текстовые задачи, содержащие отмеченный относительный термин («больше чем»), семантически более сложными текстовыми задачами, тогда как текстовые задачи с немаркированным относительным термином («меньше чем») называются семантически менее сложными. словесные задачи (см. примеры 3 и 4 для примеров помеченных и неотмеченных словесных задач соответственно). Важно отметить, что трудности, возникающие при решении отмеченных непоследовательных словесных задач, заключаются в том, что эти задачи основаны на использовании учащимися их навыков ментального представления, а также навыков понимания прочитанного. Соответственно, влияние навыков понимания прочитанного на решение текстовых задач может быть изучено только у студентов, которые мысленно точно представляют постановку задачи, то есть у группы успешных решателей задач в нашем исследовании. Таким образом, хотя наша группа успешных решателей словесных задач может опираться на свои навыки мысленного представления, недостаточное внимание к навыкам понимания прочитанного в образовательной практике RME, вероятно, вызовет у них трудности с правильным решением (семантически сложных) отмеченных противоречивых словесных задач. .
Важно отметить, что трудности, возникающие при решении отмеченных непоследовательных словесных задач, заключаются в том, что эти задачи основаны на использовании учащимися их навыков ментального представления, а также навыков понимания прочитанного. Соответственно, влияние навыков понимания прочитанного на решение текстовых задач может быть изучено только у студентов, которые мысленно точно представляют постановку задачи, то есть у группы успешных решателей задач в нашем исследовании. Таким образом, хотя наша группа успешных решателей словесных задач может опираться на свои навыки мысленного представления, недостаточное внимание к навыкам понимания прочитанного в образовательной практике RME, вероятно, вызовет у них трудности с правильным решением (семантически сложных) отмеченных противоречивых словесных задач. .
[Пример 3 – задача с выделенным словом]
В продуктовом магазине бутылка оливкового масла стоит 7 евро.
В супермаркете бутылка оливкового масла стоит на 2 евро меньше, чем в продуктовом магазине.
Если вам нужно купить семь бутылок оливкового масла, сколько вы заплатите в супермаркете?
[Пример 4 – задача с непомеченными словами]
В продуктовом магазине бутылка оливкового масла стоит 7 евро.
Это на 2 евро меньше, чем в супермаркете.
Если вам нужно купить семь бутылок оливкового масла, сколько это будет стоить в супермаркете?
По мнению некоторых исследователей, степень, в которой успешные решатели текстовых задач могут преодолевать трудности при правильном решении отмеченных несовместимых словесных задач, связана с их навыками понимания прочитанного (например, Lee et al., 2004; Van der Schoot et al. ., 2009). Было обнаружено, что перевод отмеченного реляционного термина, такого как «меньше, чем», в операцию сложения тесно связан с общими показателями понимания прочитанного (Lee et al., 2004; Van der Schoot et al., 2009).). Это говорит о том, что навыки понимания прочитанного вместе с навыками мысленного представления могут быть необходимы для решения семантически сложных словесных проблем. Таким образом, настоящее исследование также принимает во внимание общую способность учащихся к пониманию прочитанного.
Таким образом, настоящее исследование также принимает во внимание общую способность учащихся к пониманию прочитанного.
В целом, настоящее исследование было направлено на проверку следующих гипотез:
1. Мы предположили, что из-за трудностей с построением последовательного ментального представления текстовых задач менее успешные решатели текстовых задач в учебной программе RME сделают больше. ошибок как в непомеченных, так и в отмеченных несовместимых текстовых задачах, чем в непомеченных и отмеченных непротиворечивых текстовых задачах.
2. Мы предположили, что в результате недостаточного внимания к навыкам понимания прочитанного при обучении решению словесных задач, успешные решатели словесных задач в учебной программе RME будут испытывать трудности с решением семантически сложных, отмеченных непоследовательностью словесных задач, но не с решением семантически менее сложных, немаркированных, непоследовательных словесных задач.
3. Мы предположили, что в результате предполагаемой связи между способностью понимать прочитанное и способностью преодолевать семантико-лингвистические сложности словесной задачи, для успешных решателей задач существует положительная связь между способностью понимать прочитанное и количеством правильно решены отмеченные несовместимые словесные задачи.
Материалы и методы
Отбор участников
Были собраны данные от 80 голландских учащихся шестого класса (42 мальчика, 38 девочек) из восьми начальных школ в Нидерландах. Средний возраст этих студентов составлял 11,72 года ( SD = 0,40). Они были почти поровну разделены на две группы (методом медианного разделения) на основе их результатов теста по математике CITO (Институт измерения образования) (2008 г.). Эта процедура отбора привела к группе менее успешных решателей текстовых задач ( N = 41) и группа успешных решателей текстовых задач ( N = 39). Тест CITO по математике — это общенациональный стандартизированный тест, отражающий способ обучения решению текстовых задач в реалистическом математическом образовании. Тест содержит такие элементы, как арифметика в уме (сложение, вычитание, умножение и деление), сложные приложения (задачи, включающие несколько операций) и измерение и геометрия (знание измерительных ситуаций), все из которых предлагаются как математические текстовые задачи. Внутренняя согласованность этого теста была высокой (α Кронбаха = 0,9).5, Янссен и др., 2010).
Внутренняя согласованность этого теста была высокой (α Кронбаха = 0,9).5, Янссен и др., 2010).
Родители предоставили письменное информированное согласие на основании распечатанной информации о цели исследования. Это исследование было проведено в соответствии с этическими процедурами Свободного университета Амстердама.
Инструменты и процедура
Два измерительных прибора, которые использовались в этом исследовании, были предоставлены студентам тремя обученными независимыми ассистентами в течение примерно 45 минут.
Несоответствие Задача
Задача на несоответствие содержала восемь двухэтапных задач сравнения (см. Приложение в дополнительных материалах), которые были выбраны из исследования Hegarty et al. (1992) и были переведены на голландский язык. Все текстовые задачи состояли из трех предложений. Первое предложение каждой задачи сравнения представляло собой оператор присваивания, выражающий значение первой переменной, а именно цену продукта в известном голландском магазине или супермаркете (например, в Aldi бутылка вина стоит 4 евро). Второе предложение содержало реляционное утверждение, выражающее значение второй переменной (т. е. цену этого товара в другом магазине или супермаркете) по отношению к первой (например, в Boni бутылка вина стоит на 3 евро больше, чем в Алди). В третьем предложении решателю задачи было предложено найти кратное значение второй переменной (например, если вам нужно купить три бутылки вина, сколько вы заплатите в Бони?). Ответ на эти задачи сравнения всегда включал сначала вычисление значения второй переменной (например, 4 + 3 = 7), а затем умножение этого решения на величину, указанную в третьем предложении (например, 7 умножить на 3 = 21).
Второе предложение содержало реляционное утверждение, выражающее значение второй переменной (т. е. цену этого товара в другом магазине или супермаркете) по отношению к первой (например, в Boni бутылка вина стоит на 3 евро больше, чем в Алди). В третьем предложении решателю задачи было предложено найти кратное значение второй переменной (например, если вам нужно купить три бутылки вина, сколько вы заплатите в Бони?). Ответ на эти задачи сравнения всегда включал сначала вычисление значения второй переменной (например, 4 + 3 = 7), а затем умножение этого решения на величину, указанную в третьем предложении (например, 7 умножить на 3 = 21).
Восемь сравнительных задач были разделены на четыре разных типа текстовых задач (см. Приложение в дополнительных материалах) путем пересечения следующих двух внутрипредметных факторов: Согласованность (согласованное или непоследовательное) и Маркировка (неотмеченное и отмеченное). . Согласованность относится к тому, соответствует ли относительный термин во втором предложении требуемой арифметической операции или нет. Согласованное предложение явно выражает значение второй переменной (например, в Boni бутылка вина стоит на 3 евро [больше/меньше], чем в Aldi), представленной в предыдущем предложении (например, в Aldi бутылка вина стоит 4 евро). . Непоследовательное предложение связывало значение второй переменной с первой с помощью местоименной ссылки (например, Это на 3 евро [больше/меньше], чем в Aldi). Следовательно, реляционный термин в задаче согласованного сравнения указывает на соответствующую арифметическую операцию («больше чем», когда требуемой операцией является сложение, и «меньше чем», когда требуемой операцией является вычитание). Реляционный термин в непоследовательной задаче сравнения указывает на неподходящую арифметическую операцию («больше чем», когда требуемой операцией является вычитание, и «меньше чем», когда требуемой операцией является сложение). Маркированность относится к тому, является ли реляционный термин отмеченным (т. е. меньше чем) или немаркированным (т. е. больше чем) членом пары антонимов «более-менее».
Согласованное предложение явно выражает значение второй переменной (например, в Boni бутылка вина стоит на 3 евро [больше/меньше], чем в Aldi), представленной в предыдущем предложении (например, в Aldi бутылка вина стоит 4 евро). . Непоследовательное предложение связывало значение второй переменной с первой с помощью местоименной ссылки (например, Это на 3 евро [больше/меньше], чем в Aldi). Следовательно, реляционный термин в задаче согласованного сравнения указывает на соответствующую арифметическую операцию («больше чем», когда требуемой операцией является сложение, и «меньше чем», когда требуемой операцией является вычитание). Реляционный термин в непоследовательной задаче сравнения указывает на неподходящую арифметическую операцию («больше чем», когда требуемой операцией является вычитание, и «меньше чем», когда требуемой операцией является сложение). Маркированность относится к тому, является ли реляционный термин отмеченным (т. е. меньше чем) или немаркированным (т. е. больше чем) членом пары антонимов «более-менее». относительный термин. Отмеченный реляционный термин (т. е. меньше чем) семантически более сложен, чем непомеченный реляционный термин (т. е. больше чем). Следовательно, задачи с помеченными и непомеченными словами считались семантически более сложными и семантически менее сложными.
относительный термин. Отмеченный реляционный термин (т. е. меньше чем) семантически более сложен, чем непомеченный реляционный термин (т. е. больше чем). Следовательно, задачи с помеченными и непомеченными словами считались семантически более сложными и семантически менее сложными.
Стимулы были разделены на четыре набора материалов. Каждому участнику было предложено восемь текстовых задач, по две на каждый тип текстовых задач. Порядок, в котором текстовые задачи были представлены в каждом наборе, был псевдослучайным. Каждый набор был представлен 20 участникам. Во всех наборах и среди участников каждая проблема со словами возникала одинаково часто в версиях без пометок/постоянства, помеченных/последовательных, без пометок/непоследовательных и помеченных/непоследовательных, чтобы обеспечить полное сочетание условий и материалов. В задачах со словами мы контролировали сложность необходимых вычислений и количество букв в названиях переменных (то есть магазинов) и продуктов. Для того, чтобы выполнение необходимых арифметических операций не было определяющим фактором при решении словесных задач учащимися, операции были выбраны на основе следующих правил: (1) ответы на первый шаг операции были ниже 10; (2) окончательные ответы были от 14 до 40; (3) ни один из первых шагов или окончательных ответов не содержал части числа или отрицательного числа; (4) ни одно числовое значение не встречается дважды в одной и той же задаче; и (5) ни один из (возможных) ответов не был равен 1. Числовые значения, используемые в согласованных и несогласованных задачах каждого типа словесных задач, были сопоставлены по величине (см. Van der Schoot et al., 2009).).
Числовые значения, используемые в согласованных и несогласованных задачах каждого типа словесных задач, были сопоставлены по величине (см. Van der Schoot et al., 2009).).
Для анализа мы смотрели на точность учащихся (т. е. количество правильных ответов) по каждому из четырех типов текстовых задач: (1) неотмеченные/последовательные; (2) выраженный/постоянный; (3) немаркированный/непоследовательный; и (4) выраженный/непоследовательный. Внутренняя согласованность этой меры в настоящем исследовании была высокой (α Кронбаха = 0,90).
Понимание прочитанного
Нормированный стандартизированный тест на понимание прочитанного CITO (Институт измерения образования) (2010 г.) Голландского национального института измерения образования использовался для оценки уровня понимания прочитанного детьми. Этот тест является частью стандартной голландской системы мониторинга учащихся CITO и предназначен для определения общего уровня понимания прочитанного у детей начальной школы. Этот тест состоит из двух модулей, каждый из которых включает текст и 25 вопросов с несколькими вариантами ответов. Вопросы относились к уровню слова, предложения или текста и касались как текстовой базы, так и ситуационного представления, которое читатель построил из текста (Кинч, 19).98). В этом тесте уровень понимания прочитанного детьми выражается оценкой умения читать, которая в данном исследовании варьировалась от 15 до 95 ( M = 40,51, SD = 13,94). Внутренняя согласованность этого теста была высокой с альфа Кронбаха 0,89 (Weekers et al., 2011).
Вопросы относились к уровню слова, предложения или текста и касались как текстовой базы, так и ситуационного представления, которое читатель построил из текста (Кинч, 19).98). В этом тесте уровень понимания прочитанного детьми выражается оценкой умения читать, которая в данном исследовании варьировалась от 15 до 95 ( M = 40,51, SD = 13,94). Внутренняя согласованность этого теста была высокой с альфа Кронбаха 0,89 (Weekers et al., 2011).
Анализ данных
Дисперсионный анализ 2 × 2 × 2 (ANOVA) был проведен с последовательностью (постоянство против непостоянства) и маркировкой (неотмеченные против отмеченных) в качестве внутрисубъектных факторов и группы (менее успешные против удачных слов) решатели проблем) как межсубъектный фактор. Последующие тесты проводились с использованием парного образца 9.0025 т -испытания. Частичный эта-квадрат (ηp2) рассчитывался как мера величины эффекта (Pierce et al., 2004). Согласно Пирсу и др. (2004), значения 0,02, 0,13 и 0,26 представляют малую, среднюю и большую величину эффекта соответственно.
В настоящем исследовании роль понимания прочитанного в четырех типах задач со словами была изучена путем расчета корреляции «продукт-момент» ( r Пирсона) между пониманием прочитанного и оценкой разницы между немаркированными непоследовательными и согласованными типами задач со словами, и корреляция между пониманием прочитанного и оценкой разницы между отмеченными непоследовательными и последовательными типами словесных задач. Эти баллы различий отражают различия в производительности между последовательными и непоследовательными типами текстовых задач и могут быть приняты в качестве меры того, в какой степени учащиеся могут построить мысленное представление описанной проблемной ситуации. Чем ниже оценка разницы, тем меньше решатели словесных задач страдают от несоответствия. Корреляции были рассчитаны сначала для менее успешных и успешных решателей текстовых задач вместе, а затем, для проверки третьей гипотезы, для каждой из этих групп в отдельности.
Наш подход отличается от исследования Van der Schoot et al. , но дает важное преимущество. (2009), которые добавили понимание прочитанного в качестве ковариации в повторные измерения ANOVA. То есть результаты, полученные Van der Schoot et al. (2009) могли дать лишь ограниченное представление о точном местоположении эффекта ковариаты, поскольку было неизвестно, какая группа (менее успешные или успешные решатели словесных задач) или в каком типе словесных задач (постоянные неотмеченные/отмеченные или непоследовательные неотмеченные/отмеченные) понимание прочитанного сыграло свою роль. Более того, оказывается, что повторные измерения ANCOVA изменяют основные эффекты повторных измерений по сравнению с оценкой основных эффектов с помощью простого повторного анализа ANOVA (см. Thomas et al., 2009).). Таким образом, подход, использованный в настоящем исследовании, позволил нам получить более конкретное представление о точной роли понимания прочитанного в решении текстовых задач. Во всех анализах альфа 0,05 использовалась для проверки значимости результатов.
, но дает важное преимущество. (2009), которые добавили понимание прочитанного в качестве ковариации в повторные измерения ANOVA. То есть результаты, полученные Van der Schoot et al. (2009) могли дать лишь ограниченное представление о точном местоположении эффекта ковариаты, поскольку было неизвестно, какая группа (менее успешные или успешные решатели словесных задач) или в каком типе словесных задач (постоянные неотмеченные/отмеченные или непоследовательные неотмеченные/отмеченные) понимание прочитанного сыграло свою роль. Более того, оказывается, что повторные измерения ANCOVA изменяют основные эффекты повторных измерений по сравнению с оценкой основных эффектов с помощью простого повторного анализа ANOVA (см. Thomas et al., 2009).). Таким образом, подход, использованный в настоящем исследовании, позволил нам получить более конкретное представление о точной роли понимания прочитанного в решении текстовых задач. Во всех анализах альфа 0,05 использовалась для проверки значимости результатов.
Результаты
Общие средние значения ( M ) и стандартные отклонения ( SD ) для основных факторов в этом исследовании, а также их взаимные корреляции представлены в таблице 1. Как видно, имело место значительное главный эффект согласованности [ F (1,78) = 23,84, p = 0,00, ηp2 = 0,23], что указывает на то, что задачи на согласованные слова были решены точнее, чем задачи на несогласованные слова (т. е. эффект согласованности). Не было значительного основного эффекта от отмеченности [ F (1,78) = 2,64, p = 0,11], что позволяет предположить, что в целом в задачах с отмеченными словами было сделано не больше ошибок, чем в задачах с немаркированными словами. Основной эффект группы также не был значительным [(1,78) = 1,15, p = 0,29)], что указывает на то, что в целом успешные решатели проблем не демонстрировали более высокую эффективность решения проблем, чем менее успешные решатели проблем.
ТАБЛИЦА 1. Общие средние значения, стандартные отклонения и корреляции основных переменных.
Общие средние значения, стандартные отклонения и корреляции основных переменных.
Что касается взаимодействующих эффектов между Постоянством и Маркировкой, анализ выявил значительное взаимодействие [ F (1,78) = 7,64, p = 0,01, ηp2 = 0,09], показывающее, что в целом эффект согласованности присутствовал для отмеченных текстовые задачи, но отсутствуют для непомеченных текстовых задач. Более интересным в свете наших гипотез является то, что, как и ожидалось, взаимодействие «Состоятельность × Маркированность» отличалось для менее успешных и успешных решателей текстовых задач. Об этом свидетельствовало значительное трехстороннее взаимодействие между Последовательностью, Маркировкой и Группой [9].0025 F (1,78) = 4,32, p = 0,03, ηp2 = 0,05]. На рисунке 1 эффективность решения словесных задач представлена как функция согласованности (последовательное или непоследовательное) и маркировки (отмечено или не отмечено) для менее успешных решателей проблем (рисунок 1А) и для успешных решателей проблем (рисунок 1В) соответственно. .
.
РИСУНОК 1. Результаты четырех типов текстовых задач для менее успешных (A) и успешных решателей задач (B).
Как показано на рисунке 1А, основной эффект согласованности [ F (1,38) = 8,16, p = 0,01, ηp2 = 0,18] указывает на то, что менее успешные решатели текстовых задач продемонстрировали эффект согласованности. Учитывая незначительное взаимодействие Согласованность × Отмеченность [ F (1,38) = 0,25, p = 0,62], эффект согласованности присутствовал как для задач с помеченными, так и для немаркированных слов. Значимого основного эффекта маркировки обнаружено не было [ F (1,38) = 0,12, p = 0,74]. Таким образом, менее успешные решатели текстовых задач показали значительно более низкие результаты как в непоследовательных типах текстовых задач с немаркированными, так и в маркированных словах по сравнению с согласованными типами задач с немаркированными и маркированными словами [9].0025 т (38) = 1,86, р = 0,04; t (38) = 2,57, p = 0,01 соответственно].
Как видно из рисунка 1B, группа успешных решателей задач напоминала менее успешных решателей проблем в том, что наблюдался основной эффект согласованности [ F (1,40) = 16,29, p = 0,00, ηp2 = 0,29], но нет существенного основного эффекта маркировки [ F (1,40) = 0,27, p = 0,61]. Однако, в отличие от группы менее успешных решателей задач, эффект согласованности в группе успешных решателей задач присутствовал для помеченных словесных задач, но отсутствовал для непомеченных словесных задач [Последовательность × Взаимодействие маркировки: F (1,40) = 17,44, p = 0,00, ηp2 = 0,30]. Это указывает на то, что успешные решатели текстовых задач показали значительно более низкие результаты при решении задач с пометкой «несовместимость» по сравнению с задачами с пометкой «последовательность» [ t (40) = 5,07, p = 0,00], в то время как производительность при решении задач с непоследовательностью без пометки и непоследовательность без пометки не различалась. достоверно [ t (40) = 1,52, p = 0,13].
достоверно [ t (40) = 1,52, p = 0,13].
Таким образом, эти результаты показывают, что менее успешные решатели текстовых задач продемонстрировали эффект согласованности как в семантически-лингвистически простых (т. е. немаркированных), так и в сложных (т. текст словесной задачи содержал сложные семантико-лингвистические признаки (т. е. маркировался).
Относительно роли навыков понимания прочитанного при решении текстовых задач были получены следующие данные. В целом, наблюдалась значительная корреляция между пониманием прочитанного и оценками по математике, полученными с помощью теста RME для конкретной учебной программы ( r = 0,59, p = 0,00). Это говорит о том, что учащиеся с более высокими показателями понимания прочитанного также показали более высокие результаты в тесте по математике RME. Чтобы получить более подробное представление о роли навыков понимания прочитанного в решении задач с помеченными и немаркированными словами, баллы на понимание прочитанного были сопоставлены с баллами различия (непоследовательный – последовательный), рассчитанными для типов задач с помеченными и немаркированными словами. Результаты показали, что понимание прочитанного значительно коррелировало с разницей в задачах с неотмеченными словами (9).0,025 r = 0,19, p = 0,04) и имел незначительно значимую корреляцию с оценкой различий в задачах с размеченными словами ( r = 0,17, p = 0,06). Это говорит о том, что общие способности к пониманию прочитанного имеют отношение к решению задач как с помеченными, так и с немаркированными словами.
Результаты показали, что понимание прочитанного значительно коррелировало с разницей в задачах с неотмеченными словами (9).0,025 r = 0,19, p = 0,04) и имел незначительно значимую корреляцию с оценкой различий в задачах с размеченными словами ( r = 0,17, p = 0,06). Это говорит о том, что общие способности к пониманию прочитанного имеют отношение к решению задач как с помеченными, так и с немаркированными словами.
При отдельном рассмотрении успешных и менее успешных решателей задач результаты показали, как и общие результаты, что понимание прочитанного значительно коррелировало с баллами теста по математике, специфичного для RME, для обоих успешных ( r = 0,48, p = 0,00) и менее успешные решатели задач ( r = 0,64, p = 0,00). Таким образом, для успешных и менее успешных решателей задач более высокие способности понимания прочитанного были связаны с более высокими оценками по математике RME. Более того, успешно решающие текстовые задачи ( M = 46,42, SD = 2,66) набрали значительно более высокие баллы в стандартизированном тесте на понимание прочитанного, чем менее успешно решающие текстовые задачи ( M = 35,02, SD = 1,27) [ t (53,32) = 3,87, p = 0,00].
Более конкретный анализ, сфокусированный на гипотетической связи между навыками понимания прочитанного и решением задач с выраженным несоответствием слов, выявил следующую закономерность результатов. В соответствии с нашими ожиданиями, результаты корреляционного анализа между пониманием прочитанного и разницей в баллах для задач с помеченными и немаркированными словами показали, что только в группе успешно решавших текстовые задачи оценка разницы для типа задач с помеченными словами была значимо связана с чтением. понимание ( r = -0,40, p = 0,01). Важно отметить, что понимание прочитанного не коррелировало с баллами различий успешных решателей словесных задач для неотмеченных словесных задач ( r = -0,27, p = 0,10). Кроме того, в группе менее успешных решателей словесных задач понимание прочитанного также не коррелировало с разницей в баллах, рассчитанных как для задач без пометок ( r = -0,04, p = 0,76), так и для задач с пометками ( r = — 0,04, р = 0,83).
Таким образом, только в группе успешно решавших текстовые задачи более высокий балл понимания прочитанного был связан с меньшим баллом разницы. То есть уязвимость к эффекту согласованности в задачах с отмеченными словами была ниже для учащихся с более высокими способностями к пониманию прочитанного. Это говорит о том, что учащиеся с более высокими способностями к пониманию прочитанного, по-видимому, меньше страдают от того, что их подталкивают к непоследовательным арифметическим операциям (т. е. их направляют к операции вычитания с помощью «меньше, чем», когда требуется сложение) при решении отмеченных непоследовательных задач со словами.
Обсуждение
Это исследование было мотивировано наблюдением, что современные RME в первую очередь учат студентов использовать свои навыки ментального представления и гораздо меньше фокусируются на использовании навыков понимания прочитанного для решения математических текстовых задач. На этом фоне мы решили исследовать предположение о том, что учащиеся учебной программы RME испытывают трудности, когда им приходится решать математические задачи со словами, которые являются семантико-лингвистически сложными. Поэтому мы разработали исследование, в котором мы не только манипулировали степенью, в которой требовались навыки мысленного представления, но также варьировали семантическую сложность словесных задач, используя маркированные (т. е. высокой семантической сложности) или немаркированные (т. е. низкой семантической сложности) слова. ) относительный термин в тексте текстовой задачи. Кроме того, мы классифицировали учащихся как успешных и менее успешных в решении текстовых задач на основе их результатов в независимом и хорошо зарекомендовавшем себя тесте по математике, специфичном для RME.
Поэтому мы разработали исследование, в котором мы не только манипулировали степенью, в которой требовались навыки мысленного представления, но также варьировали семантическую сложность словесных задач, используя маркированные (т. е. высокой семантической сложности) или немаркированные (т. е. низкой семантической сложности) слова. ) относительный термин в тексте текстовой задачи. Кроме того, мы классифицировали учащихся как успешных и менее успешных в решении текстовых задач на основе их результатов в независимом и хорошо зарекомендовавшем себя тесте по математике, специфичном для RME.
Используя эту процедуру классификации, была выдвинута гипотеза, что менее успешные решатели текстовых задач будут испытывать трудности с правильным решением несовместимых текстовых задач независимо от их семантической сложности (гипотеза 1). Эта гипотеза была подтверждена нашим анализом, который показал, что менее успешные решатели словесных задач плохо справились как с отмеченными, так и с неотмеченными несовместимыми словесными задачами. Успешные решатели текстовых задач, с другой стороны, были способны эффективно решать непоследовательные текстовые задачи с низкой семантической сложностью. Таким образом, эти результаты показывают, что основанная на RME классификация успешных и менее успешных решателей проблем также нашла свое отражение в нашей экспериментальной задаче решения словесных задач.
Успешные решатели текстовых задач, с другой стороны, были способны эффективно решать непоследовательные текстовые задачи с низкой семантической сложностью. Таким образом, эти результаты показывают, что основанная на RME классификация успешных и менее успешных решателей проблем также нашла свое отражение в нашей экспериментальной задаче решения словесных задач.
Однако в семантически сложных текстовых задачах даже те, кто успешно решил задачи, испытывали трудности, о чем свидетельствует большое количество ошибок, которые они допускали в отмеченных несогласованных текстовых задачах (гипотеза 2). Более конкретно, успешным решателям словесных задач было труднее перевести помеченный реляционный термин («меньше чем») в операцию сложения, чем перевести немаркированный реляционный термин («больше чем») в операцию вычитания.
Эти результаты еще раз подтверждают предыдущие наблюдения о том, что (тонкие) семантико-лингвистические элементы словесной проблемы, в частности, отмеченный реляционный термин, влияют на успех решения словесной проблемы (Кларк, 1969; Льюис и Майер, 1987 г. ; Кинч, 1998; Папе, 2003; Ван дер Шут и др., 2009). Более того, они согласуются с эмпирической работой, последовательно сообщающей о проблемах обработки с отмеченными терминами, которые, как предполагается, вызваны семантическим представлением отрицательных полюсов пар антонимов (например, больше, чем против меньше чем), например, «меньше, чем» означает больше. фиксированный и сложный, и, следовательно, с меньшей вероятностью может быть изменен, чем положительный полюс, такой как «больше, чем» (например, Lewis and Mayer, 1987; подробное объяснение лежащего в основе механизма см., например, Clark, 19).69). Например, более ранние исследования показали, что учащиеся менее способны точно вспоминать помеченные термины в задачах на запоминание (Clark and Card, 1969), медленнее реагируют на называние помеченных терминов в задачах на называние (Schriefers, 1990), медленнее решают задачи. с маркированными прилагательными в задачах на рассуждения (French, 1979) и, как это было повторено в этом исследовании, испытывают проблемы с решением проблемы с маркированными несогласованными словами (например, Pape, 2003; Van der Schoot et al.
; Кинч, 1998; Папе, 2003; Ван дер Шут и др., 2009). Более того, они согласуются с эмпирической работой, последовательно сообщающей о проблемах обработки с отмеченными терминами, которые, как предполагается, вызваны семантическим представлением отрицательных полюсов пар антонимов (например, больше, чем против меньше чем), например, «меньше, чем» означает больше. фиксированный и сложный, и, следовательно, с меньшей вероятностью может быть изменен, чем положительный полюс, такой как «больше, чем» (например, Lewis and Mayer, 1987; подробное объяснение лежащего в основе механизма см., например, Clark, 19).69). Например, более ранние исследования показали, что учащиеся менее способны точно вспоминать помеченные термины в задачах на запоминание (Clark and Card, 1969), медленнее реагируют на называние помеченных терминов в задачах на называние (Schriefers, 1990), медленнее решают задачи. с маркированными прилагательными в задачах на рассуждения (French, 1979) и, как это было повторено в этом исследовании, испытывают проблемы с решением проблемы с маркированными несогласованными словами (например, Pape, 2003; Van der Schoot et al. , 2009).
, 2009).
Важно отметить, что наши результаты показывают интересную ситуацию, когда учащиеся, классифицированные как успешные решатели текстовых задач в учебной программе RME, не справляются с решением семантически сложных (непоследовательных) текстовых задач. Тот факт, что успешные решатели проблем смогли решить непоследовательные словесные задачи с более низкой семантической сложностью, предполагает, что такая плохая работа над семантически сложными словесными задачами не связана с недостатками их навыков мысленного представления. Скорее, кажется, что успешные решатели проблем особенно испытывают трудности с эффективным решением семантико-лингвистических сложностей в текстовых задачах. Это говорит о том, что учащимся не хватает навыков понимания прочитанного, необходимых для определения и перевода математической операции с грунтовкой в математическую операцию, «соответствующую словесной задаче». В случае отмеченных непоследовательных словесных задач это означает, что даже успешным учащимся будет трудно преобразовать «меньше чем» в операцию сложения.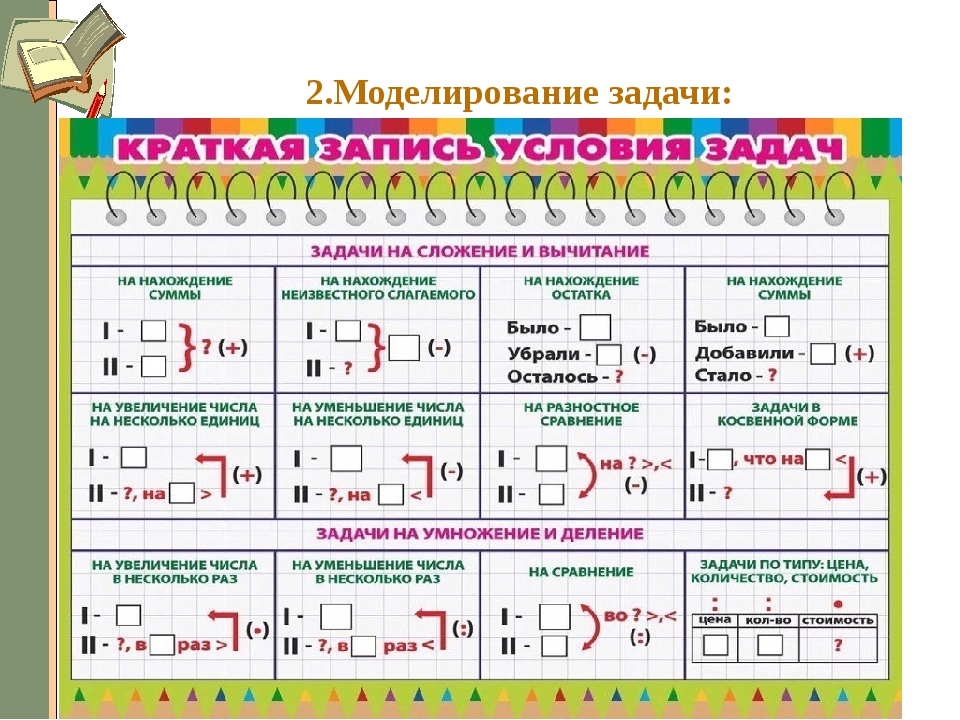 Хотя можно утверждать, что это, вероятно, является результатом относительно небольшого внимания к развитию навыков понимания прочитанного в контексте решения математических задач со словами в RME (например, Elia et al., 2009).), эта спекулятивная интерпретация нуждается в дальнейшем подтверждении в будущих исследованиях.
Хотя можно утверждать, что это, вероятно, является результатом относительно небольшого внимания к развитию навыков понимания прочитанного в контексте решения математических задач со словами в RME (например, Elia et al., 2009).), эта спекулятивная интерпретация нуждается в дальнейшем подтверждении в будущих исследованиях.
Основываясь на предыдущих исследованиях (например, Lee et al., 2004; Van der Schoot et al., 2009), еще одной целью этого исследования было выяснить, могут ли навыки понимания прочитанного помочь (успешно) решателям словесных задач преодолеть семантически сложный маркированный реляционный термин в непоследовательной текстовой задаче. В соответствии с нашими ожиданиями, понимание прочитанного было положительно связано с выполнением отмеченных (но не неотмеченных) непоследовательных текстовых задач для группы, успешно решавшей текстовые задачи, тогда как для менее успешной группы не было обнаружено значимых связей между пониманием прочитанного и текстовыми задачами. решение (гипотеза 3).
решение (гипотеза 3).
Эти результаты подтверждают, что общие навыки понимания прочитанного играют важную роль в способности учащихся правильно решать семантически сложные словесные задачи. Более того, наши результаты представляют собой прогресс по сравнению с предыдущей работой, поскольку они более конкретно определяют, какие типы текстовых задач и для каких учащихся способность понимания прочитанного может иметь эффект. Это исследование показывает, что навыки понимания прочитанного особенно полезны, когда дело доходит до улучшения производительности при решении семантически сложных текстовых задач успешными решателями текстовых задач (согласно классификации теста RME по математике). В частности, навыки понимания прочитанного важны для решения текстовых задач, прежде всего, помогая учащимся эффективно переводить сложные (т. Из этого становится очевидным, что навыки понимания прочитанного являются ценным дополнением к навыкам мысленного представления для решения словесных задач, и что просто полагаться на навыки мысленного представления недостаточно для правильного решения семантически сложных словесных задач. Это говорит о том, что в дополнение к обучению студентов использовать свои навыки ментального представления для решения текстовых задач, обучение решению текстовых задач должно уделять достаточное внимание развитию и использованию навыков понимания прочитанного, связанных с выявлением и обращением с семантико-лингвистическими особенностями в постановке задачи.
Это говорит о том, что в дополнение к обучению студентов использовать свои навыки ментального представления для решения текстовых задач, обучение решению текстовых задач должно уделять достаточное внимание развитию и использованию навыков понимания прочитанного, связанных с выявлением и обращением с семантико-лингвистическими особенностями в постановке задачи.
Важно начать развивать такие навыки в начальной школе, так как словесные задачи становятся семантически более сложными, когда учащиеся продвигаются в своей образовательной карьере, например, при переходе от начального к среднему образованию (Сильвер и Кай, 1996; Хелвиг и др.). др., 1999). В частности, в учебных подходах, ориентированных на решение текстовых задач, которые демонстрируют дисбаланс между количеством учебного времени, посвященным обучению навыкам мысленного представления, и навыкам понимания прочитанного, например, в RME, важно, чтобы учителя знали об этом неравное распределение. Поощрение их уделять больше внимания навыкам понимания прочитанного и обучение студентов тому, как обращаться с семантико-лингвистическими характеристиками в текстовых задачах, послужит хорошей отправной точкой для работы над более сбалансированными инструкциями по решению текстовых задач.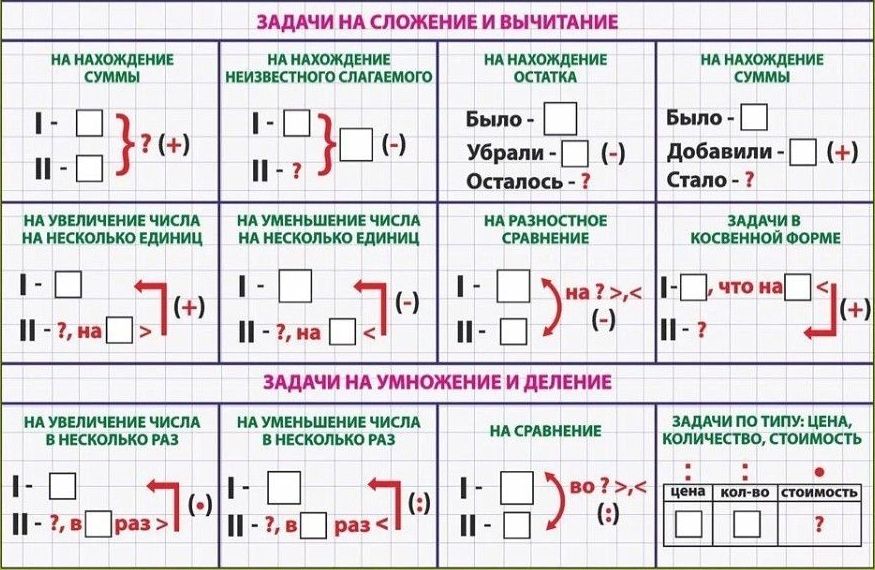 Более того, полезно проводить различие между обучением обработке более тонких семантико-лингвистических особенностей текста (таких как отмеченный термин отношения) и работой с более общими семантическими сложностями текста (такими как релевантность информации в текстовом задаче, эксплицитность и т. д.). описанных отношений и последовательности известных элементов в тексте текстовой задачи).
Более того, полезно проводить различие между обучением обработке более тонких семантико-лингвистических особенностей текста (таких как отмеченный термин отношения) и работой с более общими семантическими сложностями текста (такими как релевантность информации в текстовом задаче, эксплицитность и т. д.). описанных отношений и последовательности известных элементов в тексте текстовой задачи).
Эти и другие практические аспекты результатов, такие как поиск оптимального баланса между объемом обучения навыкам стратегического мысленного представления и навыкам понимания прочитанного, еще предстоит рассмотреть в будущих исследованиях. Предположительно, в настоящее время эффективные программы вмешательства, которые сосредоточены как на навыках стратегического мысленного представления, так и на навыках понимания прочитанного, такие как обучение на основе схем (например, Jitendra et al., 2002, 2011) и Solve It! Метод обучения (Montague et al., 2000; Krawec et al., 2013) может стать хорошей отправной точкой для решения этой задачи.
Вклад авторов
Все перечисленные авторы внесли существенный, непосредственный и интеллектуальный вклад в работу и одобрили ее для публикации.
Заявление о конфликте интересов
Авторы заявляют, что исследование проводилось при отсутствии каких-либо коммерческих или финансовых отношений, которые могли бы быть истолкованы как потенциальный конфликт интересов.
Дополнительный материал
Дополнительный материал к этой статье можно найти в Интернете по адресу: https://www.frontiersin.org/article/10.3389/fpsyg.2016.00191
Ссылки
Барнс, Х. (2005). Теория реалистического математического образования как теоретическая основа для обучения математике учащихся с низким уровнем успеваемости. Пифагор 61, 42–57.
Google Scholar
Бунен А. Дж. Х., Ван дер Шут М., Ван Весель Ф., Де Врис М. Х. и Джоллес Дж. (2013). Что лежит в основе успешного решения текстовых задач? Анализ пути у учащихся шестого класса. Контемп. Образовательный Психол. 38, 271–279. doi: 10.1016/j.cedpsych.2013.05.001
Образовательный Психол. 38, 271–279. doi: 10.1016/j.cedpsych.2013.05.001
Полнотекстовая перекрестная ссылка | Google Scholar
Кэмпбелл, JID (редактор) (1992). Природа и происхождение математических навыков. Амстердам: Издательство Elsevier Science.
Google Scholar
Clark, HH (1969). Лингвистические процессы в дедуктивных рассуждениях. Психолог. Ред. 76, 387–404. doi: 10.1037/h0027578
Полный текст CrossRef | Google Scholar
Кларк Х. Х. и Кард С. К. (1969). Роль семантики в запоминании сравнительных предложений. Дж. Эксп. Психол. 82, 545–553. doi: 10.1037/h0028370
Полный текст CrossRef | Google Scholar
Де Корте Э., Вершаффель Л. и Де Вин Л. (1985). Влияние переформулировки вербальных задач на представления детей о проблемах и их решения. Дж. Образовательный. Психол. 77, 460–470. doi: 10.1037/0022-0663.77.4.460
CrossRef Full Text | Google Scholar
Де Корте Э., Вершаффель Л. и Пауэлс А. (1990). Влияние семантической структуры текстовых задач на движения глаз второклассников. Дж. Образование. Психол. 82, 359–365. doi: 10.1037/0022-0663.82.2.359
и Пауэлс А. (1990). Влияние семантической структуры текстовых задач на движения глаз второклассников. Дж. Образование. Психол. 82, 359–365. doi: 10.1037/0022-0663.82.2.359
CrossRef Full Text | Google Scholar
Депаэпе Ф., Де Корте Э. и Вершаффель Л. (2010). Метакогнитивные и эвристические подходы учителей к решению текстовых задач: анализ и влияние на убеждения и успеваемость учащихся. ZDM Матем. Образовательный 42, 205–218. doi: 10.1007/s11858-009-0221-5
CrossRef Полный текст | Google Scholar
Швейцар М., Драйверс П., Деккер Т., Ван ден Хёвель-Панхуизен М., де Ланге Дж. и Вайерс М. (2007). Решение проблем как вызов математическому образованию в Нидерландах. ZDM Матем. Образовательный 39, 405–418. doi: 10.1007/s11858-007-0043-2
CrossRef Full Text | Google Scholar
Элиа И., Ван ден Хойвель-Панхуйзен М. и Коволу А. (2009). Изучение использования стратегии и гибкости стратегии в решении нестандартных задач у отличников начальной школы по математике. ЗДМ Междунар. Дж. Матем. Образовательный 41, 605–618. doi: 10.1007/s11858-009-0184-6
ЗДМ Междунар. Дж. Матем. Образовательный 41, 605–618. doi: 10.1007/s11858-009-0184-6
CrossRef Полный текст | Google Scholar
French, PL (1979). Лингвистическая маркировка, стратегия и аффект в силлогистических рассуждениях. Дж. Психолингвист. Рез. 8, 425–449.
Google Scholar
Хайер, М. (1996). Лерен в Эн Твид Таал. Interactie in Een Meertalige Mavo-Klas [Изучение второго языка. Взаимодействие в многоязычном классе. Гронинген: Уолтерс Нордхофф.
Хегарти, М., Майер, Р. Э., и Грин, К. Э. (1992). Понимание арифметических словесных задач: свидетельство фиксации глаз учащихся. Дж. Образовательный. Психол. 84, 76–84. дои: 10.1037/0022-0663.84.1.76
Полнотекстовая перекрестная ссылка | Google Scholar
Хегарти М., Майер Р. Э. и Монк К. А. (1995). Понимание арифметических словесных задач: сравнение успешных и неудачных решателей задач. Дж. Образовательный. Психол. 87, 18–32. doi: 10.1037/0022-0663. 87.1.18
87.1.18
CrossRef Полный текст | Google Scholar
Хельвиг Р., Розек-Тедеско М. А., Тиндал Г., Хит Б. и Алмонд П. Дж. (1999). Чтение как доступ к решению математических задач на тестах с несколькими вариантами ответов для учащихся шестого класса. Дж. Образование. Рез. 93, 113–125. doi: 10.1080/00220679
7635CrossRef Full Text | Google Scholar
Хикендорф, М. (2011). Моделирование объяснительных латентных переменных математических способностей в начальной школе: пересечение границы между психометрией и психологией. Докторская диссертация, Лейденский университет, Лейден.
Google Scholar
Хикендорф, М. (2013). Влияние представления многозначных математических задач в реалистичном контексте на решение задач шестиклассников. Познан. Инстр. 31, 314–344. doi: 10.1080/07370008.2013.799167
CrossRef Full Text | Google Scholar
Янссен Дж., Верхелст Н., Энгелен Р. и Шелтенс Ф. (2010). Wetenschappelijke Verantwoording Papieren Toetsen Rekenen-Wiskunde Groep 3 tot en met 8 [Научное обоснование. Тест по математике]. Арнем: Чито.
Тест по математике]. Арнем: Чито.
Джитендра, А., ДиПипи, К.М., и Перрон-Джонс, Н. (2002). Предварительное исследование обучения решению словесных задач на основе схем для учащихся средней школы с ограниченными возможностями обучения: акцент на концептуальном и процедурном понимании. J. Специальное образование. 36, 23–38. doi: 10.1177/002246660010301
CrossRef Full Text | Google Scholar
Джитендра А. Х. и Стар Дж. Р. (2012). Предварительное исследование, в котором сравниваются решения задач с процентом слов учащихся с высокой и низкой успеваемостью. Учиться. Индивид. Отличаться. 22, 151–158. doi: 10.1016/j.lindif.2011.11.003
CrossRef Полный текст | Google Scholar
Джитендра А.К., Стар Дж.Р., Родригес М., Линделл М. и Сомеки Ф. (2011). Улучшение пропорционального мышления учащихся с помощью обучения на основе схемы. Учиться. Инстр. 21, 731–745. doi: 10.1016/j.learninstruc.2011.04.002
CrossRef Full Text | Google Scholar
Кинч, В. (1998). Понимание: парадигма познания. Кембридж: Издательство Кембриджского университета.
(1998). Понимание: парадигма познания. Кембридж: Издательство Кембриджского университета.
Google Scholar
Кравец Дж. Л., Хуанг Дж., Монтегю М., Кресслер Б. и Мелия де Альба А. (2013). Влияние обучения когнитивной стратегии на знание процессов решения математических задач учащихся средней школы с ограниченными возможностями обучения. Учиться. Инвалид. Q. 36, 80–92. doi: 10.1177/0731948712463368
CrossRef Full Text | Google Scholar
Ли, К., Нг, Э.Л., и Нг, С.Ф. (2009). Вклад рабочей памяти и исполнительного функционирования в представление проблем и генерацию решений в алгебраических текстовых задачах. Дж. Образовательный. Психол. 101, 373–387. doi: 10.1037/a0013843
Полный текст CrossRef | Google Scholar
Lee, K., Ng, S.-W., Ng, E.-L., and Lim, Z.-Y. (2004). Рабочая память и грамотность как предикторы производительности в алгебраических текстовых задачах. Дж. Эксп. Детская психология. 89, 140–158. doi: 10. 1016/j.jecp.2004.07.001
1016/j.jecp.2004.07.001
PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
Льюис, А. Б., и Майер, Р. Е. (1987). Непонимание учащимися утверждений об отношениях в арифметических текстовых задачах. Дж. Образовательный. Психол. 79, 363–371. doi: 10.1037/0022-0663.79.4.363
CrossRef Full Text | Google Scholar
Marzocchi, G.M., Lucangeli, D., De Meo, T., Fini, F., and Cornoldi, C. (2002). Возмущающее влияние ненужной информации на решение арифметических задач у невнимательных детей. Дев. Нейропсихология. 21, 73–92. doi: 10.1207/S15326942DN2101_4
PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
Монтегю М., Варгер К. и Морган Т. Х. (2000). Реши! Инструкция стратегии для улучшения решения математических задач. Учиться. Инвалид. Рез. Практика. 15, 110–116. doi: 10.1207/SLDRP1502_7
CrossRef Full Text | Google Scholar
Морено Р., Озогул Г. и Рейслейн М. (2011). Обучение с использованием конкретных и абстрактных визуальных представлений: влияние на решение проблем учащихся, представление проблем и восприятие обучения.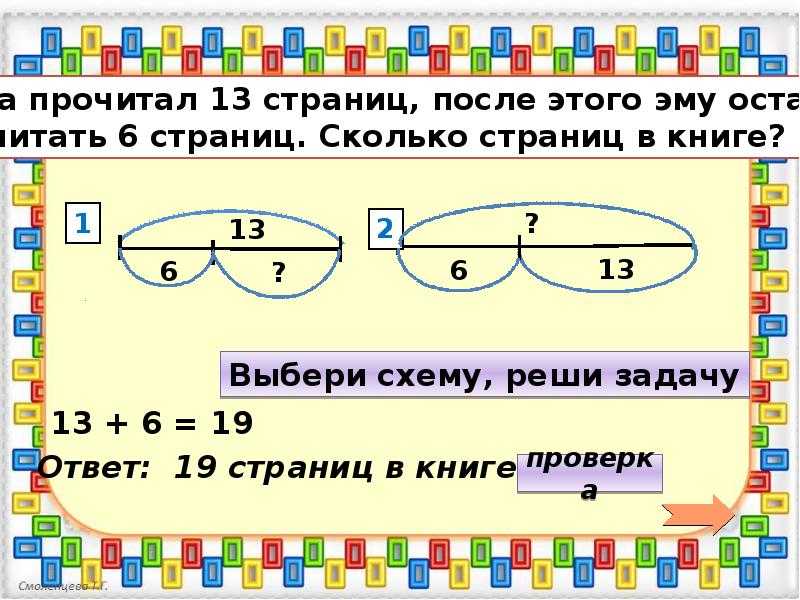 Дж. Образование. Психол. 103, 32–47. doi: 10.1037/a0021995
Дж. Образование. Психол. 103, 32–47. doi: 10.1037/a0021995
Полный текст CrossRef | Google Scholar
Pape, SJ (2003). Сравните текстовые задачи: пересмотр гипотезы согласованности. Контемп. Образовательный Психол. 28, 396–421. doi: 10.1016/S0361-476X(02)00046-2
CrossRef Full Text | Google Scholar
Пирс, К.А., Блок, Р.А., и Агуинис, Х. (2004). Предостережение относительно сообщения значений эта-квадрата из многофакторных планов дисперсионного анализа. Учеб. Психол. Изм. 64, 916–924. doi: 10.1177/0013164404264848
CrossRef Full Text | Google Scholar
Пренгер, Дж. (2005). Таал Телт! Een Onderzoek Naar де роль ван Taalvaardigheid en Textbegrip в его реалистических Rekenonderwijs. [Язык имеет значение! Исследование роли лингвистических навыков и понимания текста в реалистическом математическом образовании]. Докторская диссертация, Гронингенский университет, Гронинген.
Расмуссен, К.Л., и Кинг, К.Д. (2000). Поиск отправных точек в дифференциальных уравнениях: реалистичный подход к обучению математике. Междунар. Дж. Матем. Образовательный науч. Технол. 31, 161–172. doi: 10.1080/002073
Поиск отправных точек в дифференциальных уравнениях: реалистичный подход к обучению математике. Междунар. Дж. Матем. Образовательный науч. Технол. 31, 161–172. doi: 10.1080/002073
7219
CrossRef Полный текст | Google Scholar
Ruijssenaars, AJJM, Van Luit, H., and Van Lieshout, ECDM (ред.) (2004). Rekenproblemen en Dyscalculie [Арифметические задачи и дискалькулия]. Роттердам: Lemniscaat.
Google Scholar
Шриферс, Х. (1990). Лексические и понятийные факторы в именовании отношений. Познан. Психол. 22, 111–142. дои: 10.1016/0010-0285(90)
-OРезюме PubMed | Полный текст перекрестной ссылки | Google Scholar
Шумахер Р.Ф. и Фукс Л.С. (2012). Опосредует ли понимание реляционной терминологии влияние вмешательства на проблему сравнения слов? Дж. Экспл. Детская психология. 111, 607–628. doi: 10.1016/j.jecp.2011.12.001
PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
Сильвер, Э. А., и Кай, Дж. (1996). Анализ арифметической задачи, поставленной учащимися средней школы. Дж. Рез. Мат. Образовательный 27, 521–539. doi: 10.2307/749846
А., и Кай, Дж. (1996). Анализ арифметической задачи, поставленной учащимися средней школы. Дж. Рез. Мат. Образовательный 27, 521–539. doi: 10.2307/749846
CrossRef Полный текст | Google Scholar
Swanson, HL, Lussler, CM, и Orosco, MJ (2013). Когнитивные стратегии, рабочая память и рост в решении словесных задач у детей с математическими трудностями. Дж. Учись. Инвалид. ХХ, 1–20. doi: 10.1177/0022219413498771
PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
Thevenot, C. (2010). Решение арифметических задач со словами: данные для построения ментальной модели. Acta Psychol. 133, 90–95. doi: 10.1016/j.actpsy.2009.10.004
PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
Томас, М. С., Анназ, Д., Ансари, Д., Шериф, Г., Джарролд, К., и Кармилофф-Смит, А. (2009). Использование траекторий развития для понимания нарушений развития. J. Язык речи. Слышать. Рез. 52, 336–358. doi: 10. 1044/1092-4388(2009/07-0144)
1044/1092-4388(2009/07-0144)
CrossRef Full Text | Google Scholar
Тиммерманс, Р. Э., Ван Лисхаут, Э. Д. К. М., и Верховен, Л. (2007). Связанное с полом влияние современного обучения математике для слабоуспевающих на поведение при решении задач. Учиться. Инстр. 17, 42–54. doi: 10.1016/j.learninstruc.2006.11.005
CrossRef Full Text | Google Scholar
Ван ден Бур, К. (2003). Als je Begrijpt wat ik Bedoel. Een Zoektocht naar Verklaringen voor Achterblijvende Prestaties van Allochtone Leerlingen in het Wiskundeonderwijs [Если вы понимаете, что я имею в виду. В поисках объяснения более низких уровней успеваемости учащихся из числа меньшинств в области математического образования]. Утрехт: CD-ß Press.
Ван ден Хойвель-Панхуизен, М. (2003). Дидактическое использование моделей в реалистическом математическом образовании: пример продольной траектории в процентах. Учеб. Стад. Мат. 54, 9–35. doi: 10.1023/B:EDUC.0000005212.03219.dc
Полный текст CrossRef | Google Scholar
Ван ден Хойвель-Панхуизен, М. (2005). Роль контекстов в оценочных задачах по математике. Учиться. Мат. 25, 2–9.
(2005). Роль контекстов в оценочных задачах по математике. Учиться. Мат. 25, 2–9.
Google Scholar
Ван дер Шут, М., Баккер Аркема, А. Х., Хорсли, Т. М., и Ван Лисхаут, Э. Д. К. М. (2009). Эффект последовательности зависит от заметности в менее успешных, но не успешных решателях задач: исследование движения глаз у детей младшего школьного возраста. Контемп. Образовательный Психол. 34, 58–66. doi: 10.1016/j.cedpsych.2008.07.002
CrossRef Полный текст | Google Scholar
Van Dijk, I.M.A.W., Van Oers, HJM, and Terwel, J. (2003). Обеспечение или проектирование? Построение моделей в начальном математическом образовании. Учиться. Инстр. 13, 53–72. doi: 10.1016/S0959-4752(01)00037-8
CrossRef Полный текст | Google Scholar
Van Eerde, HAA (2009). Rekenen-wiskunde en taal: een didactisch duo [Арифметика и язык: дидактический дуэт]. Panama Post Reken Wiskunde Onderwijs Onderzoek Ontwikkeling Praktijk 28, 19–32.
Verschaffel, L. , De Corte, E., and Pauwels, A. (1992). Решение задач сравнения: тест движения глаз на соответствие гипотезе Льюиса и Майера. Дж. Образовательный. Психол. 84, 85–94. doi: 10.1037/0022-0663.84.1.85
, De Corte, E., and Pauwels, A. (1992). Решение задач сравнения: тест движения глаз на соответствие гипотезе Льюиса и Майера. Дж. Образовательный. Психол. 84, 85–94. doi: 10.1037/0022-0663.84.1.85
Полный текст CrossRef | Google Scholar
Уикерс А., Гроенен И., Кляйнтьес Ф. и Финстра Х. (2011). Wetenschappelijke Verantwoording Papieren Toetsen Begrijpend Lezen Voor Groep 7 en 8 [Научное обоснование теста на понимание прочитанного]. Арнем: Чито.
Google Scholar
Как решать математические задачи быстрее: 15 приемов для демонстрации учащимся
«Время теста. Никаких калькуляторов».
Вы запугаете многих учеников, сказав это, но обучение методам решения математических задач с легкостью и скоростью может сделать это менее пугающим.
Это также может сделать математику более полезной. Вместо того, чтобы полагаться на калькуляторы, учащиеся изучают стратегии, которые могут улучшить их навыки концентрации и оценки, одновременно развивая чувство числа. И хотя есть преподаватели, которые выступают против математических «трюков» по уважительным причинам, сторонники указывают на преимущества, такие как повышенная уверенность при решении сложных задач.
И хотя есть преподаватели, которые выступают против математических «трюков» по уважительным причинам, сторонники указывают на преимущества, такие как повышенная уверенность при решении сложных задач.
Вот 15 методов для демонстрации учащимся, помогающих им решать математические задачи быстрее:
Сложение и вычитание
это проще.
Первый шаг — добавить то, что легко. Второй шаг – добавить остальные.
Допустим, учащиеся должны найти сумму 393 и 89. Они должны быстро увидеть, что прибавление 7 к 393 будет равняться 400 — с ним проще работать. Чтобы сбалансировать уравнение, они могут затем вычесть 7 из 89.
В разбивке процесс выглядит следующим образом: 482 Благодаря этой быстрой технике большие числа теперь не будут выглядеть так страшно. Существует аналогичный метод для вычитания. Удалите то, что легко. Предположим, учащиеся должны найти разницу между 567 и 153. Большинству покажется, что 500 — более простое число, чем 567. Поэтому им просто нужно отнять 67 от уменьшаемого — 567 — и от вычитаемого — 153, прежде чем решать уравнение . Вот процесс: . один. С помощью этой быстрой техники вы можете придать учащимся уверенности в том, что они умеют обращаться с четырехзначными целыми числами. Чтобы вычесть число из 1000, вычтите первые две цифры этого числа из 9. Затем вычтите последнюю цифру из 10. Допустим, учащиеся должны решить 1000 – 438. 4 = 5 2. Двухэтапное вычитание
 Затем удалите то, что осталось.
Затем удалите то, что осталось.
9000 3. Вычитание из 1000
Умножение и деление
Когда учащимся нужно умножить два целых числа, они могут ускорить процесс, если одно из них является четным числом.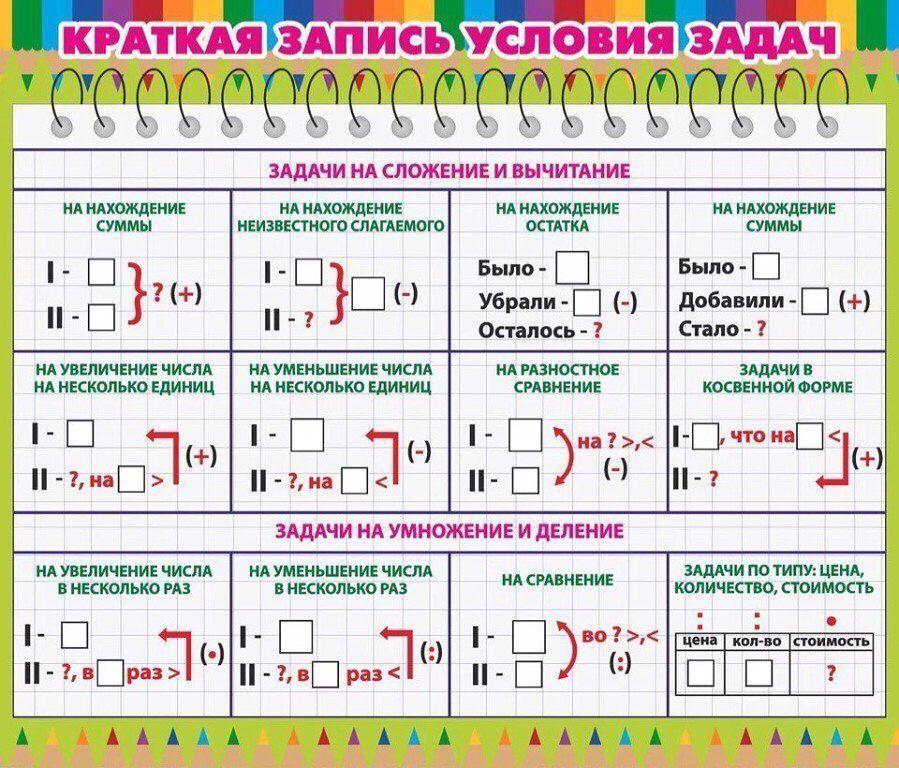 Им просто нужно 90 159 разделить пополам четное число и удвоить другое число.
Им просто нужно 90 159 разделить пополам четное число и удвоить другое число.
Учащиеся могут остановить процесс, когда они больше не могут делить пополам четное целое число или когда уравнение становится управляемым.
Используя 33 x 48 в качестве примера, вот процесс:
- 66 x 24
- 132 x 12
- 264 x 6
- 528 x 3
- 1,584
Единственным предварительным условием является понимание таблицы умножения на 2.
5. Умножение на степень двойки
Эта тактика представляет собой быстрый вариант удвоения и деления пополам.
Это упрощает умножение, если число в уравнении является степенью двойки, то есть оно работает для 2, 4, 8, 16 и так далее.
Вот что нужно сделать: Для каждой степени двойки, составляющей это число, удвойте другое число.
Например, 9 x 16 — это то же самое, что 9 x (2 x 2 x 2 x 2) или 9 x 24. Таким образом, учащиеся могут удвоить 9 четыре раза, чтобы получить ответ:
- 9 x 24
- 18 x 23
- 36 x 22
- 72 x 2
- 144
В отличие от удвоения и деления пополам, этот метод требует понимания показателей степени, а также уверенного владения таблицей умножения на 2.
6. Умножение на 9
Для большинства учащихся умножение на 9 — или 99, 999 и любое другое число, соответствующее этой схеме, — труднее, чем умножение на степень 10.
Но есть простой способ решить эту проблему, и он состоит из двух частей.
Во-первых, учащиеся округляют 9 до 10. Во-вторых, решив новое уравнение, они вычитают из ответа число, которое они только что умножили на 10.
Например, 67 x 9 приведет к тому же ответу, что и 67 x 10 – 67. Следование порядку операций даст результат 603. Точно так же 67 x 99 равно 67 x 100 – 67.
Несмотря на большее количество шагов, такое изменение уравнения обычно происходит быстрее.
Существует более простой способ умножения двузначных целых чисел на 11.
Предположим, учащиеся должны найти произведение 11 x 34.
Идея состоит в том, чтобы поставить пробел между цифрами, чтобы получилось 3_4. Затем сложите две цифры вместе и поставьте сумму в пробел.
Ответ: 374.
Что произойдет, если сумма будет двузначной? Студенты помещали вторую цифру в пробел и добавляли 1 к цифре слева от пробела. Например:
- 11 x 77
- 7_(7+7)_7
- 7_(14)_7
- (7+1)_4_7
- 847
Умножение без умножения.
8. Умножение четных чисел на 5
Для этого метода требуются только базовые навыки деления.
Есть два шага, и 5 x 6 служит примером. Сначала разделите число, умножаемое на 5, то есть 6, пополам. Во-вторых, добавьте 0 справа от числа.
Результат – 30 – правильный ответ.
Это идеальная и простая техника для учащихся, осваивающих таблицу умножения на 5.
9. Умножение нечетных чисел на 5
Это еще один способ сэкономить время, который хорошо работает при обучении учащихся таблице умножения на 5.
У этого есть три шага, , пример которых 5 x 7.
Сначала вычтите 1 из числа, умноженного на 5, чтобы получить четное число. Во-вторых, сократите это число вдвое — в данном случае с 6 до 3. В-третьих, добавьте 5 справа от числа.
Во-вторых, сократите это число вдвое — в данном случае с 6 до 3. В-третьих, добавьте 5 справа от числа.
Ответ: 35.
Кому нужен калькулятор?
10. Возведение в квадрат двузначного числа, оканчивающегося на 1
Возведение в квадрат большого двузначного числа может быть утомительным, но есть более короткий путь, если 1 является второй цифрой.
Этот ярлык состоит из четырех шагов. Дважды сложите целое число с полученным квадратом: 6 400 + 80 + 80 = 6 560 Этот обходной путь устраняет трудности, связанные со второй цифрой, позволяя учащимся работать с числами, кратными 10. Возведение в квадрат чисел, оканчивающихся на 5, проще, так как состоит только из двух частей процесса. Во-первых, студенты всегда будут составлять 25 последних цифр произведения. Во-вторых, чтобы определить первые цифры произведения, учащиеся должны умножить первую цифру числа — 9, например — на целое число на единицу больше — в данном случае 10. Итак, учащиеся решат число 952, назначив 25 в качестве двух последних цифр. Затем они должны были умножить 9 x 10, чтобы получить 90. Если сложить эти числа вместе, результат составит 9025. Таким образом, сложная задача становится простым умножением для многих учеников. Перекрестное умножение — важный навык, который нужно развивать, но есть более простой способ вычисления процентов. Например, если учащиеся хотят узнать, сколько составляет 65% от 175, они могут перемножить числа вместе и передвинуть десятичную цифру на две цифры влево. Результат 113,75, что действительно является правильным ответом. Этот ярлык помогает сэкономить время на тестах и викторинах. Чтобы определить среднее значение среди набора чисел, учащиеся могут балансировать их вместо использования сложной формулы. Предположим, студент хочет работать волонтером в среднем 10 часов в неделю в течение четырех недель. Чтобы определить количество часов, необходимых на четвертой неделе, учащийся должен добавить, насколько он или она превзошли или пропустили целевое среднее значение в другие недели: Чтобы узнать количество часов за последнюю неделю, учащийся должен вычесть сумму из целевого среднего: С практикой этот метод может даже не требовать карандаша и бумаги. Вот как это легко. 11. Возведение в квадрат двузначных чисел, оканчивающихся на 5

12. Вычисление процентов
13. Балансировка средних значений
 В первые три недели студент работал по 10, 12 и 14 часов.
В первые три недели студент работал по 10, 12 и 14 часов. Словесные задачи
14. Выявление модных словечек
Учащимся, которым сложно перевести словарные задачи в уравнения, будет полезно научиться определять модные словечки — фразы, обозначающие конкретные действия.
Это не уловка. Это тактика.
Научите учащихся искать эти модные слова, и какие навыки они соответствуют в большинстве контекстов:
Не забудьте включить модные словечки, которые обычно появляются в их учебниках (или других учебниках по математике в классе), а также те, которые вы используете в тестах и заданиях.
В результате им должно быть легче решать текстовые задачи.
15. Создание подвопросов
В сложных текстовых задачах покажите учащимся, как анализировать вопрос, ответив на три конкретных подвопроса.
Каждый учащийся должен задать себе вопрос:
- Что я ищу? — Учащиеся должны перечитывать вопрос снова и снова, отыскивая модные словечки и определяя важные детали.
- Какая информация мне нужна? — Учащиеся должны определить, какие факты, цифры и переменные им нужны для решения вопроса. Например, если они определяют, что вопрос основан на вычитании, им нужны уменьшаемое и вычитаемое.
- Какой информацией я располагаю? — Учащиеся должны быть в состоянии составить основное уравнение, используя информацию, содержащуюся в словесной задаче, после определения важных деталей.
Эти подвопросы помогают учащимся избежать перегрузки.
Вместо того, чтобы писать и анализировать каждую деталь вопроса, они смогут определить ключевую информацию.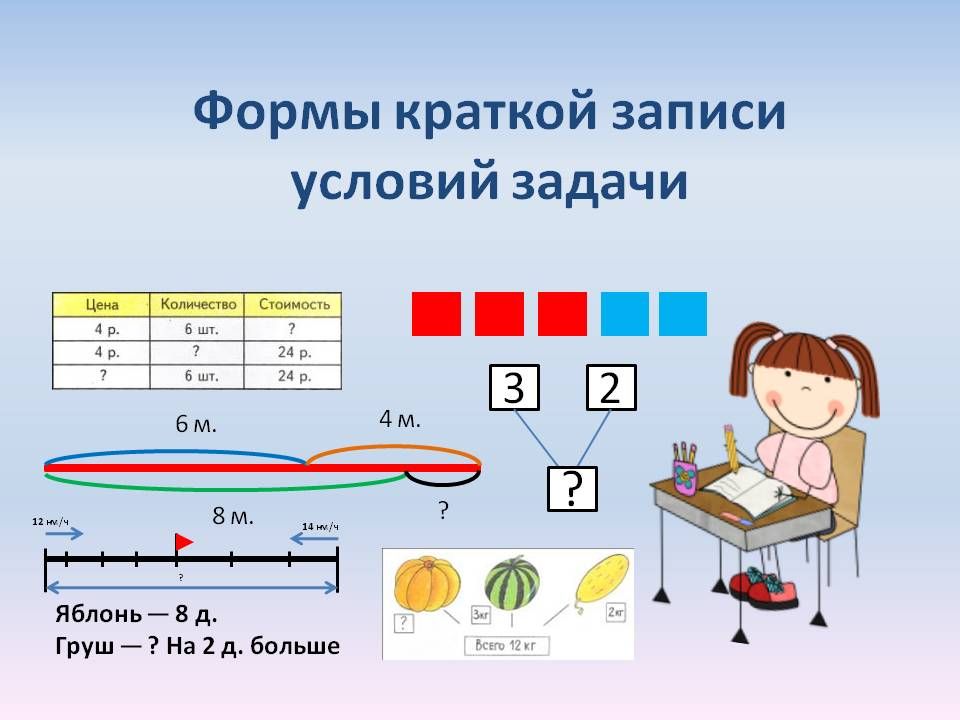 Если вы определите учащихся, которые борются с этим, вы можете использовать взаимное обучение по мере необходимости.
Если вы определите учащихся, которые борются с этим, вы можете использовать взаимное обучение по мере необходимости.
Чтобы получить более свежие подходы к преподаванию математики в классе, подумайте о том, чтобы предложить своим ученикам ряд увлекательных математических занятий.
Заключительные мысли об этих способах быстрого решения математических задач
Демонстрация этих 15 техник учащимся может придать им уверенности в решении сложных вопросов.
Это также упражнения по математике в уме , которые помогают им развивать навыки, связанные с концентрацией внимания, логикой и критическим мышлением.
Поощряющий класс равен вовлекающему классу. Это уравнение легко запомнить.
>Создайте или войдите в свою учетную запись учителя в Prodigy — бесплатной адаптивной математической игре, содержание которой настраивается с учетом проблемных мест и скорости обучения игрока. В соответствии с учебными планами США и Канады, его любят более 500 000 учителей и 15 миллионов учащихся.
Как решать задачи Word
По мере того, как ваш ребенок будет учиться в школе, он столкнется с несколькими камнями преткновения. Есть некоторые проблемы, которые трудно понять многим учащимся. Наиболее распространенная проблема связана с текстовыми задачами. Студенты изо всех сил пытаются увидеть математику за словами.
Проверенный пошаговый метод решения текстовых задач на самом деле довольно прост.
- Прочтите задачу вслух про себя
- Нарисуй картинку
- Подумайте: «Что мне нужно найти?»
- Список того, что дается
- Найдите ключевые слова
- Решить
- Проверьте свою работу
Давайте применим эти шаги на практике. Рассмотрим задачу со словами ниже.
Пример: Кевин любит читать. Ему нравятся разные книги. У него есть 3 больших книжных шкафа, в каждом по 9 полок, заполненных его книгами. Если на каждой полке может поместиться 16 книг, сколько книг у Кевина?
Прочтите задачу вслух
Дети склонны торопиться с каждой задачей. Это связано с ограничениями по времени на классные работы и тесты. Если ваш ребенок не знает, о чем спрашивает проблема, то он не может ее решить. Когда ваш ребенок читает задачу вслух, он говорит и слышит задачу. Они могут сформировать в голове более четкую картину проблемы и более подготовлены к ее решению.
Это связано с ограничениями по времени на классные работы и тесты. Если ваш ребенок не знает, о чем спрашивает проблема, то он не может ее решить. Когда ваш ребенок читает задачу вслух, он говорит и слышит задачу. Они могут сформировать в голове более четкую картину проблемы и более подготовлены к ее решению.
Нарисуй картинку
Учащиеся, особенно младшие школьники, должны визуализировать задачу, чтобы понять ее. Когда они становятся старше, они могут начать визуализировать в своей голове, но в юном возрасте они должны рисовать картинку, которая объясняет им, в чем проблема. Картина должна учитывать все аспекты проблемы.
Спросите: «Что мне нужно найти?»
Некоторые текстовые задачи прямолинейны со своими вопросами. Это может быть так просто, как «У Молли две собаки, у Джейсона три. Сколько собак у Молли и Джейсона вместе?» Однако об этом нам нужно подумать. Эта проблема состоит из более чем одного шага. Сначала нам нужно выяснить, сколько у него полок, а затем выяснить, сколько книг на всех полках, чтобы узнать, сколько всего у него книг.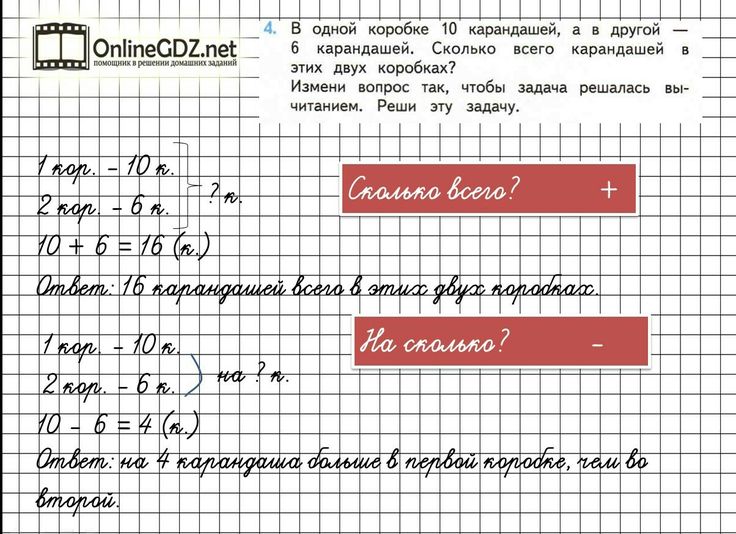
Перечислите то, что дано
Всегда хорошо начинать с перечисления вещей, которые вы знаете. Если вы попытаетесь решить проблему, не зная, какие инструменты вам даны для ее решения, вы не получите правильного ответа. Вспомните, когда вы в последний раз пытались заполнить пробелы или предположить ответ, не зная всех фактов. Ваш результат, вероятно, не обернулся хорошо. Именно по этой причине нам нужно перечислять то, что дано перед любой проблемой. Учащийся должен записать его вверху или сбоку на листе бумаги, чтобы он всегда имел его в качестве справочного материала при решении задачи. Для этой задачи мой список того, что дано, будет:
- У Кевина 3 книжных шкафа
- Каждый книжный шкаф имеет 9 полок
- На каждой полке 16 книг
Поиск ключевых слов
В каждом слове задача есть ключевые слова, на которые нужно обращать внимание, чтобы узнать, какую операцию нужно выполнить. По мере того, как ваш ребенок будет больше практиковаться в решении текстовых задач, поиск ключевых слов станет проще. Вот некоторые из самых популярных ключевых слов для текстовых задач:
Вот некоторые из самых популярных ключевых слов для текстовых задач:
Эксплуатация | Ключевые слова |
Дополнение | «все вместе», «оба», «вместе», «всего»* «дополнительно» |
Вычитание | «уменьшение», «разность», «меньше», «на сколько больше», «насколько больше», «ушли», «остались» |
Умножение | «удвоенный/утроенный», «каждый» «равные группы» «во всех», «из», «на» |
Подразделение | «равные части» «разделенные» «разделенные», «проценты» |
*это может быть ключевым словом для сложения и умножения
Решите
Согласно таблице выше, мы должны использовать умножение. Во-первых, мы должны умножить количество полок в ящике на количество ящиков. 9 полок на ящик x 3 книжных шкафа = 27 полок. Далее мы должны умножить количество книг на полке на количество полок. 27 полок x 16 книг на полке = 432 книги.
Во-первых, мы должны умножить количество полок в ящике на количество ящиков. 9 полок на ящик x 3 книжных шкафа = 27 полок. Далее мы должны умножить количество книг на полке на количество полок. 27 полок x 16 книг на полке = 432 книги.
Проверьте свой ответ
Последним шагом, конечно же, является проверка вашей работы на предмет соответствия ответа заданному вопросу. Математически мы можем проверить нашу работу, выполнив операцию, обратную той, которую мы использовали. Таким образом, для этой задачи мы можем разделить 432 на 16, и мы получим 27, затем разделим 27 на 3 и получим 9.
Какими бы сложными ни были задачи со словами для детей, выполнение этих простых 7 шагов поможет им лучше понять словесные задачи и видеть дальше сложных слов. Достаточно скоро мировые проблемы перестанут их беспокоить, и они вырастут, станут более уверенными в себе и готовыми учиться.
1
Темы: математика, Детское образование, математические навыки, Советы для родителей, Детская тревога, Математическая тревога, Текстовые задачи
3 шага к решению задачи по математике.
 Цените знания выше оценок
Цените знания выше оценокЛатрейл Джексон
Словесные задачи
Латрейл Джексон
Словесные задачи
Можешь даже не говорить мне.
Я знаю, что задачи со словами повышают уровень беспокойства по математике больше, чем любое другое математическое задание. Откуда я это знаю? Мои ученики, занимающиеся репетиторством по математике, каждый раз бросают на меня убийственный взгляд, когда приходит время поработать над разделом задач со словами в их домашнем задании по математике.
Честно говоря, у меня было некоторое опасение самому решать математические задачи, даже будучи математиком, специалистом по математике и учителем математики! Это кажется безумием, но это доказывает, что задачи со словами — это не только математика.
Задачи Word требуют хорошего понимания прочитанного, чтобы вы могли понять, о чем вас просит задача. Мое понимание прочитанного было самым слабым из двух предметов, как я объяснил в своем математическом муаре «История моей [математической] жизни» . Но мне нужно было практиковаться и буквально тренировать свой ум, чтобы я мог улучшить свое понимание прочитанного, если я хотел помочь другим студентам-математикам решать текстовые задачи.
Найдите минутку и подумайте о двух причинах, по которым вы избегаете словесных ошибок любой ценой.
Возможно, вы не понимаете, о чем вас спрашивают.
Может быть, вы не можете понять ситуацию.
Возможно, вы просто не знаете, как найти и применить операции, которые нужно использовать для решения.
Возможно, вы поняли вопрос, но не более того. Вы не знаете, что делать, чтобы ответить на него.
Я встречал студентов, которые приводили мне одну или все эти причины, которые помогли мне разработать стратегию, которая поможет вам решать текстовые задачи как чемпион! Мой метод описан во встроенном видео, а также в виде текста под видео.
3-шаговый процесс решения задач Word
Шаг 1: RRTR — понимание прочитанного
Шаг 2: поиск мусора из 4 частей
Шаг 3: решение с целью и стратегией
Шаг Давайте узнаем больше о каждом шаге
: RRTR — Понимание прочитанногоВам может понадобиться словарь для этой части.
1. Прочтите
Познакомьтесь со словом «проблема» и ознакомьтесь с ситуацией.
2. Перечитайте
Старайтесь читать медленно и намеренно, указывая конкретные детали, которые могут понадобиться для ответа на вопрос.
3. Подумайте
Замените числа пробелами , чтобы помочь вам сосредоточиться на ситуации, а не торопиться с решением проблемы.
Проиграйте в уме то, что происходит. Вы сталкивались с этой ситуацией раньше? Вы не в состоянии относиться к этому сценарию? Есть ли в этой задаче слова, с которыми вы не знакомы?
Если вы не можете понять, погуглите фразу в задаче, которая звучит незнакомо, и проведите небольшое исследование, чтобы лучше понять.

Если есть слова, которых вы не знаете, не пропускайте их. Возьмите словарь и запишите определение. Эти слова могут помочь вам правильно решить проблему слова. Руководство по предварительному алгебраическому переводу может помочь вам идентифицировать и перевести некоторые из этих устных слов и фраз в алгебраические выражения.
4. Перепишите задачу, используя эти три шага.
Перепишите задачу своими словами.
Переписав заданную вам словесную проблему своими словами, вы сделаете для себя много хорошего: проблема. Это также может напомнить вам о похожем сценарии, в котором вы действительно были.
Предлагаю вам написать задачу так, как вы обычно говорите.
Доказательство того, что вы понимаете ситуацию в слове проблема.
Настройте себя на то, чтобы меньше времени тратить на путаницу и больше времени на решение словесной задачи, правильно, так как теперь понятно, что вам нужно делать.

Это может помочь поговорить о проблеме вслух или с другом. Попытайтесь разбить его на части и объяснить устно, как будто вы пытаетесь помочь им понять это. Затем перепишите задачу именно так.
Нарисуйте рисунок или схему того, что происходит, и как вы можете организовать информацию, чтобы вы могли видеть, как ее нужно решить.
Замените числа в исправленной текстовой задаче.
Бесчисленные задачи со словами помогают нам решать задачи без «захвата чисел». #fcslearn @WeedenElem pic.twitter.com/eqYAVxYxjN
— Хизер Паундерс (@hgpounders) 24 сентября 2019 г.
Шаг 2. Охота за мусором из 4 частей
Возьмите четыре разноцветных маркера или маркера. Вы будете выделять каждый раздел ниже другим цветом.
Номера: Вы хотите знать, как каждый из этих номеров способствует решению проблемы.
 Ищите их определения в единицах измерения (граммы, секунды, галлоны и т. д.) и других контекстных подсказках.
Ищите их определения в единицах измерения (граммы, секунды, галлоны и т. д.) и других контекстных подсказках.Неизвестные и переменные: В каждой задаче со словами всегда есть хотя бы одно неизвестное. Иногда они замаскированы в слова и словосочетания, а иногда являются переменными. Задайте себе эти вопросы, чтобы найти неизвестную информацию в вашей текстовой задаче.
Что я пытаюсь найти?
Какое число отсутствует, чтобы решить эту задачу?
Есть ли какие-либо переменные уже в задаче (т.е. x, m, t и т.д.)?
Скрытые операции: Операции, которые необходимо использовать для решения задачи со словами, также будут скрыты в словах и фразах. Используйте свое руководство по предварительному алгебраическому переводу, чтобы определить словесные слова и фразы, которые можно перевести в алгебраические выражения.
Отдельные шаги: Иногда необходимо выполнить более одной задачи, чтобы полностью ответить на вопрос.

Спросите себя: Включает ли слово «проблема» более одной скрытой операции, требующей от меня выполнения более одной задачи, чтобы полностью ответить на вопрос?
Сделайте следующее: Напишите краткое описание (всего несколько слов) каждой задачи, перечислив их по порядку, чтобы не забыть ни одного шага.
Шаг 3: Решение с целью и стратегией
Вы не решаете эту задачу со словами просто для того, чтобы перетасовать несколько чисел на листе бумаги. Вы хотите получить правильный ответ на вопрос правильно? Выполните эти шаги, чтобы убедиться, что вы делаете.
Обрисуйте стратегию:
Назовите неизвестное с помощью переменной (т. е. t = время, затрачиваемое на дорогу до работы, измеряемое в минутах)
Соберите все свои записи и мысли воедино и подумайте о последних шагах, необходимых для решения проблемы.
 Используйте формулы, создавайте уравнения, применяйте правила и т. д.
Используйте формулы, создавайте уравнения, применяйте правила и т. д.
Номера меток: После того, как вы получили свой ответ, пометьте цифры единицами измерения и дайте краткое описание (т. е. t = 17 минут, потраченных на поездку на работу). ).
Дважды проверьте вопрос и убедитесь, что вы выполнили все шаги и полностью ответили на вопрос.
Обведите свой ответ , чтобы вы могли найти его, когда он вам понадобится. Также может помочь написать ответ в виде предложения, чтобы вы могли видеть, что ответ имеет смысл и что его легко найти.
Теперь, когда вы привыкнете решать математические задачи, вам, возможно, не придется каждый раз выполнять каждый шаг. (Вот как работает математика, иногда вы можете пропустить шаг или два, когда вы достаточно хорошо знаете содержание. Этих шагов будет 9.1191 подразумевало . ) Однако вы должны убедиться, что идея каждого шага учитывается в вашей стратегии решения проблем.
) Однако вы должны убедиться, что идея каждого шага учитывается в вашей стратегии решения проблем.
Этим же шагам я учу своих учеников. Я всегда задаю вопрос «Что означает это число?» Я хочу, чтобы вы и все другие студенты, изучающие алгебру, чувствовали себя комфортно и были способны решать текстовые задачи, особенно теперь, когда у вас есть ориентир, которым вы можете руководствоваться.
Хотите глубже погрузиться в решение математических задач? Примите участие в соревнованиях по словесным задачам!
Пожалуйста, дайте мне знать в комментариях, что вы думаете о моем трехэтапном процессе, и есть ли у вас процесс, который вы предпочитаете для решения текстовых задач. Хотелось бы узнать, что еще есть!
Используйте Руководство по предварительному алгебраическому переводу , чтобы понять, как словесные слова и фразы могут помочь вам решать математические задачи со словами.
С помощью этого руководства легко переводите язык словесный и математический!
Мне нужно это руководство!
Метки: Математическая стратегия, Процесс решения задач в 3 шага
Как превратить текстовые задачи в математические — Объяснение!
Примеры
Purplemath
Самое сложное в решении текстовых задач — использовать ту часть, где вам нужно взять английские слова и перевести их в математику. Обычно, как только вы получаете математическое уравнение, все в порядке; фактическая математика часто довольно проста. Но вычисление фактического уравнения может показаться почти невозможным. Далее следует список советов и подсказок. Однако имейте в виду: до действительно узнать, «как делать» словесные задачи, вам нужно будет практиковаться, практиковаться, практиковаться.
Обычно, как только вы получаете математическое уравнение, все в порядке; фактическая математика часто довольно проста. Но вычисление фактического уравнения может показаться почти невозможным. Далее следует список советов и подсказок. Однако имейте в виду: до действительно узнать, «как делать» словесные задачи, вам нужно будет практиковаться, практиковаться, практиковаться.
Как преобразовать текстовые задачи в математические?
Шаги для создания текстовых задач:
- Прочитайте упражнение полностью.
- Работать организованно.
- Найдите ключевые слова.
- Примените свои знания о «реальном мире».
Содержимое продолжается ниже
MathHelp.com
Словесные задачи по алгебре
Шаг 1 для эффективного перевода и решения текстовых задач — прочитать задачу полностью. Не начинайте пытаться решить что-либо, когда вы прочитали только половину предложения. Сначала попытайтесь прочувствовать всю проблему; попытайтесь сначала посмотреть, какая информация у вас есть, а затем выяснить, что вам еще нужно.
Сначала попытайтесь прочувствовать всю проблему; попытайтесь сначала посмотреть, какая информация у вас есть, а затем выяснить, что вам еще нужно.
Шаг 2 – работать организованно. Определите, что вам нужно, но чего у вас нет. Назовите вещи. Выберите переменные для обозначения неизвестных, четко обозначив эти переменные тем, что они обозначают. Аккуратно рисуйте и подписывайте картинки. Объясните свои рассуждения по ходу дела. И убедитесь, что вы точно знаете, о чем на самом деле просит проблема. Вам нужно сделать это по двум причинам:
- Четкая работа поможет вам ясно мыслить, а
- выяснение того, что вам нужно, поможет вам перевести ваш окончательный ответ обратно на английский язык.
Относительно пункта (а) выше:
Может быть очень неприятно (и смущающе) потратить пятнадцать минут на решение словесной задачи на тесте, только чтобы в конце понять, что вы больше не имеете ни малейшего представления о том, что » x » означает, поэтому вам придется решать всю задачу заново. Я сделал это на тесте по математике — слава богу, это был короткий тест! — и, поверь мне, ты не захочешь сделать это с собой. Потратить пятнадцать секунд на то, чтобы маркировать вещи, — это лучшее использование вашего времени, чем потратить пятнадцать секунд на то, чтобы пометить вещи.1191 минут переделки всего упражнения!
Я сделал это на тесте по математике — слава богу, это был короткий тест! — и, поверь мне, ты не захочешь сделать это с собой. Потратить пятнадцать секунд на то, чтобы маркировать вещи, — это лучшее использование вашего времени, чем потратить пятнадцать секунд на то, чтобы пометить вещи.1191 минут переделки всего упражнения!
Шаг 3 — поиск «ключевых» слов. Определенные слова обозначают определенные математические операции. Некоторые из этих слов легкие. Если в упражнении говорится, что один человек «добавил» свои шарики в кучку, принадлежащую кому-то другому, и спрашивается, сколько шариков сейчас в этой кучке, вы знаете, что будете складывать два числа.
Каковы общие ключевые слова для текстовых задач?
Ниже приводится список наиболее распространенных ключевых слов для текстовых задач:
Дополнение:
увеличено на
больше
вместе взятых, вместе
итого
сумма плюс
прибавлено к
сравнительные («больше чем» и т. д.)
д.)
Вычитание:
уменьшить на
минус, меньше
разница между/из
меньше, меньше чем
осталось, осталось после
сохранить (старомодный термин)
сравнительные («меньше чем» и т. д.)
Умножение:
из
раз, умноженное на
произведение
, увеличенное/уменьшенное на коэффициент (этот последний тип может включать как сложение, так и вычитание и умножения!) получил по три» и т. д.)
Деление:
на,
из
соотношение, частное
процентов (деление на 100)
равные части, разделенные
среднее
Равно
есть, есть, было, были, будут
дает, дает
продан за, стоимость
Обратите внимание, что «за» в «Подразделении» означает «разделить на», как в «Я проехал 90 миль на трех галлонах бензина, поэтому я получил 30 миль на галлон». Кроме того, «а» иногда означает «деленное на», например: «Когда я заправился, я заплатил 12,36 доллара за три галлона, поэтому бензин стоил 4,12 доллара за галлон».
Кроме того, «а» иногда означает «деленное на», например: «Когда я заправился, я заплатил 12,36 доллара за три галлона, поэтому бензин стоил 4,12 доллара за галлон».
Предупреждение: конструкция «меньше чем» в «вычитании» в английском языке является обратной по сравнению с математикой. Если вам нужно, например, перевести «1,5 меньше x «, возникает соблазн написать «1,5 − x «. Не делайте этого!
Вы можете увидеть, насколько это неправильно, используя эту конструкцию в ситуации «реального мира»: Рассмотрим утверждение, «Он зарабатывает на 1,50 доллара в час меньше, чем я». Вы не вычисляете его заработную плату, вычитая свою заработную плату из 1,50 доллара. Вместо этого вы вычитаете 1,50 доллара из своей заработной платы. Так что помните: конструкция «меньше чем» является обратной.
( Технически, конструкция «больше чем» в «Сложение» также является обратным по математике от английского, но порядок сложения не имеет значения, поэтому можно складывать в обратном порядке, потому что результат будет одинаковым в любом случае. .)
.)
Также обратите внимание, что порядок важен в конструкциях «частное/отношение» и «разность между/из». Если в задаче написано «отношение х и х », это означает « х разделить на х », а не « х разделить на х ». Если в задаче написано «разность x и y », это означает « x − y », а не « y − x ».
Иногда от вас ожидают, что вы привнесете свои знания «реального мира» в упражнение. Например, предположим, вам сказали, что «Шелби отработал восемь часов MTThF и шесть часов WSat». Вы должны были бы понять, что это означало, что она работала по восемь часов каждый из четырех дней в понедельник, вторник, четверг и пятницу; и шесть часов для каждого из двух дней среды и субботы. Предположим, вам сказали, что Шелби зарабатывает «полтора часа» за любые часы, которые она отработала больше сорока в данную неделю. Ожидается, что вы знаете, что «полтора раза» означает в 1,5 раза больше ее базовой ставки; если ее базовая ставка составляет двенадцать долларов в час, то она будет получать 1,5 × 12 = 18 долларов за каждый час сверхурочной работы.
Вы должны знать, что «дюжина» — это двенадцать; можно ожидать, что вы знаете, что «счет» равен двадцати. От вас потребуется знать количество дней в году, количество часов в сутках и другие основные единицы измерения.
Вы также должны знать, что «периметр» указывает длину вокруг внешней стороны плоской формы, такой как прямоугольник (поэтому вы, вероятно, будете добавлять длины), а «площадь» указывает размер внутренней части плоская форма (так что вы, вероятно, будете умножать длину на ширину или применять какую-то другую формулу). А «объем» — это внутренности трехмерной формы, такой как куб или сфера (так что вы, вероятно, будете умножать).
Вероятно, самым большим источником ошибок является использование переменных без определений. Когда вы выбираете букву для обозначения чего-либо, четко запишите, что означает эта последняя буква. «S» означает «Шелби» или «часы работы Шелби»? Если первое, то что это означает на практике? (И, если вы не можете придумать какое-либо осмысленное определение, то, возможно, вам нужно замедлиться и немного больше подумать о том, что происходит в слове «проблема». )
)
Во всех случаях не стесняйтесь использовать свои знания «реального мира». Иногда вы не будете уверены в своем переводе английского языка в математическое выражение или уравнение. В этих случаях попробуйте подставить числа. Например, если вы не уверены, следует ли вам делить или умножать, попробуйте выполнить этот процесс с обычными числами. Например, предположим, что вы не уверены, следует ли представлять «половину (неизвестной суммы)» умножением на половину или делением на половину. Если вы используете цифры, вы можете быть уверены. Выберите простое число, например десять. Половина десяти — это пять, поэтому мы ищем операцию (т.е. умножение или деление), которая дает нам ответ 5. Сначала попробуем деление:
десять разделить на половину:
10/(1/2) = (10/1)×(2/1) = 20
Что ж, это явно неправильно. Как насчет того, чтобы пойти другим путем?
десять умножить на половину:
(10)×(1/2) = 10 ÷ 2 = 5
Вот так! Вы знаете , что половина десяти равна пяти, и теперь вы можете видеть, какие математические операции дают вам правильное значение. Итак, теперь вы знаете, что выражение, которое вам нужно, определенно «(1/2) x «.
Итак, теперь вы знаете, что выражение, которое вам нужно, определенно «(1/2) x «.
У вас есть опыт и знания; не бойтесь применять свои навыки в этом новом контексте!
URL: https://www.purplemath.com/modules/translat.htm
Страница 2
Применение стратегии решения проблем к основным задачам со словами |
Подойдите к задачам со словами с позитивным настроем
Мир полон текстовых задач. Сколько денег мне нужно, чтобы заправить машину бензином? Сколько дать чаевых официанту в ресторане? Сколько носков взять с собой в отпуск? Насколько большую индейку мне нужно купить на ужин в честь Дня Благодарения и во сколько мне нужно поставить ее в духовку? Если мы с сестрой купим маме подарок, сколько каждый из нас заплатит?
Теперь, когда мы можем решать уравнения, мы готовы применить наши новые навыки для решения текстовых задач. Знаете ли вы кого-нибудь, у кого в прошлом был негативный опыт решения проблем со словами? Были ли у вас когда-нибудь мысли, как у студента в карикатуре ниже?
Знаете ли вы кого-нибудь, у кого в прошлом был негативный опыт решения проблем со словами? Были ли у вас когда-нибудь мысли, как у студента в карикатуре ниже?
Негативные мысли о задачах со словами могут стать препятствием на пути к успеху.
Когда мы чувствуем, что не можем себя контролировать, и продолжаем повторять негативные мысли, мы возводим барьеры на пути к успеху. Нам нужно успокоить наши страхи и изменить наши негативные чувства.
Начните с чистого листа и начните мыслить позитивно, как ученик на карикатуре ниже. Прочитайте положительные мысли и произнесите их вслух.
Когда дело доходит до текстовых задач, позитивный настрой — это большой шаг к успеху.
Если мы возьмем управление в свои руки и поверим, что сможем добиться успеха, мы сможем решать текстовые задачи.
Подумайте о том, что вы можете сделать сейчас, но не могли сделать три года назад. Будь то вождение автомобиля, катание на сноуборде, приготовление изысканной еды или говорение на новом языке, вы смогли изучить и освоить новый навык. Проблемы со словами ничем не отличаются. Даже если в прошлом вы боролись с текстовыми задачами, вы приобрели много новых математических навыков, которые помогут вам добиться успеха сейчас!
Проблемы со словами ничем не отличаются. Даже если в прошлом вы боролись с текстовыми задачами, вы приобрели много новых математических навыков, которые помогут вам добиться успеха сейчас!
Используйте стратегию решения задач Word
В предыдущих главах вы переводили словосочетания в алгебраические выражения, используя базовый математический словарь и символы. С тех пор вы увеличили свой математический словарный запас, поскольку узнали больше об алгебраических процедурах, и у вас было больше практики перевода слов в алгебру.
Вы также перевели словесные предложения в алгебраические уравнения и решили некоторые текстовые задачи. Словесные задачи применяли математику к повседневным ситуациям. Вы должны были переформулировать ситуацию в одном предложении, назначить переменную, а затем написать уравнение, которое нужно решить. Этот метод работает до тех пор, пока ситуация вам знакома и математика не слишком сложна.
Теперь мы разработаем стратегию, которую вы сможете использовать для решения любой текстовой задачи. Эта стратегия поможет вам добиться успеха в решении текстовых задач. Мы продемонстрируем стратегию при решении следующей задачи.
Эта стратегия поможет вам добиться успеха в решении текстовых задач. Мы продемонстрируем стратегию при решении следующей задачи.
Пример
Пит купил рубашку на распродаже за $
181818
, что составляет половину первоначальной цены. Какова была первоначальная цена рубашки?
Решение:
Шаг 1. Прочтите проблему. Убедитесь, что вы понимаете все слова и идеи. Возможно, вам придется прочитать задачу два или более раз. Если есть слова, которые вы не понимаете, поищите их в словаре или в Интернете.
- В этой задаче вы понимаете, о чем идет речь? Вы понимаете каждое слово?
Шаг 2. Определите , что вы ищете. Трудно найти что-то, если вы не уверены, что это такое! Прочитайте задачу еще раз и найдите слова, которые говорят вам, что вы ищете!
- В этой задаче слова «какова была первоначальная цена рубашки» говорят вам, что вы ищете: первоначальную цену рубашки.

Шаг 3. Назовите то, что вы ищете. Выберите переменную для представления этого количества. Вы можете использовать любую букву для переменной, но может помочь выбрать ту, которая поможет вам запомнить, что она представляет.
- Let
p=p=p=
первоначальная цена рубашки
Шаг 4. Преобразуйте в уравнение. Может помочь сначала переформулировать проблему в одном предложении со всей важной информацией. Затем переведите предложение в уравнение.
Шаг 5. Решите уравнение, используя хорошие методы алгебры. Даже если вы сразу знаете ответ, использование алгебры лучше подготовит вас к решению задач, на которые нет очевидных ответов.
| Напишите уравнение. | 18=12p18=\frac{1}{2}p18=21p |
| Умножьте обе стороны на 2. | 2⋅18=2⋅12p\color{red}{2}\cdot18=\color{red}{2}\cdot\frac{1}{2}p2⋅18=2⋅21p |
Упростить. | 36=p36=p36=p |
Шаг 6. Проверьте ответ в задаче и убедитесь, что он имеет смысл.
- Мы обнаружили, что
p=36p=36p=36
, означает, что первоначальная цена была$36\text{\$36}$36
. Имеет ли смысл$36\text{\$36}$36
в задаче? Да, потому что181818
составляет половину от363636
, и рубашка продавалась за половину первоначальной цены.
Шаг 7. Ответьте на вопрос полным предложением.
- Проблема спросила «Какова была первоначальная цена рубашки?» Ответ на вопрос: «Первоначальная цена рубашки была
$36\text{\$36}$36
».
Если бы это было домашнее задание, наша работа могла бы выглядеть так:
Перечислим шаги, которые мы предприняли для решения предыдущего примера.
Стратегия решения проблем
- Прочтите слово проблема. Убедитесь, что вы понимаете все слова и идеи. Возможно, вам придется прочитать задачу два или более раз. Если есть слова, которые вы не понимаете, поищите их в словаре или в Интернете.
- Определите , что вы ищете.
- Имя то, что вы ищете. Выберите переменную для представления этого количества.
- Переведите в уравнение. Может быть полезно сначала переформулировать проблему в одном предложении, прежде чем переводить.
- Решите уравнение, используя хорошие методы алгебры.
- Проверьте ответ в задаче. Убедитесь, что это имеет смысл.
- Ответьте на вопрос полным предложением.
Для обзора того, как перевести алгебраические утверждения в слова, посмотрите следующее видео.
youtube.com/embed/Hub7ku7UHT4?feature=oembed» allowfullscreen=»»>Давайте применим этот подход к другому примеру.
Пример
Яш принес на пикник яблоки и бананы. Количество яблок было на три больше, чем вдвое больше, чем количество бананов. Яш принес
111111
яблоки на пикник. Сколько бананов он принес?
Показать решение
Решение:
| Шаг 1. Прочтите задачу. | |
| Шаг 2. Определите , что вы ищете. | Сколько бананов он принес? |
| Шаг 3. Назовите то, что вы ищете. Выберите переменную для представления количества бананов. | Пусть b=количество банановb=\text{количество бананов}b=количество бананов |
Шаг 4. Перевести. Переформулируйте проблему в одном предложении со всей важной информацией. Перевести в уравнение. | 11⇒11\enspace\Rightarrow11⇒ Количество яблок=⇒=\enspace\Rightarrow=⇒ было3⇒3\enspace\Rightarrow3⇒ три+⇒+\enspace\Rightarrow+⇒ 9000 2b⇒2b\enspace\Rightarrow2b⇒ вдвое больше бананов |
| Шаг 5. Решите уравнение. | 11=2b+311=2b+311=2b+3 |
| Вычтите 3 с каждой стороны. | 11−3=2b+3−311\цвет{красный}{-3}=2b+3\цвет{красный}{-3}11−3=2b+3−3 |
| Упрощение. | 8=2b8=2b8=2b |
| Разделите каждую сторону на 2. | 82=2b2\frac{8}{\color{red}{2}}=\frac{2b}{\color{red}{2}}28=22b |
| Упрощение. | 4=b4=b4=b |
Шаг 6. Проверка: Во-первых, разумен ли наш ответ? Да, взять четыре банана на пикник кажется разумным. В задаче говорится, что яблок было на три больше, чем бананов. Если есть четыре банана, получается одиннадцать яблок? Дважды 4 банана равно 8. На три больше 8 равно 11. На три больше 8 равно 11. | |
| Шаг 7. Ответьте на вопрос. | Яш принес на пикник 4 банана. |
В следующем примере мы применим нашу стратегию решения проблем к применению процентов.
пример
Премия Нга по автострахованию увеличилась на
60$\text{\$60}60$
, что составило
8%\text{8\%}8%
от первоначальной стоимости. Какова была первоначальная стоимость премии?
Показать решение
Решение:
| Шаг 1. Прочтите проблему. Помните, если есть слова, которые вы не понимаете, поищите их. | |
| Шаг 2. Определите , что вы ищете. | первоначальная стоимость премиум |
Шаг 3. Имя. Выберите переменную для представления первоначальной стоимости премии. | Пусть c=первоначальная стоимостьc=\text{первоначальная стоимость}c=исходная стоимость |
| Шаг 4. Перевести. Переформулируйте одним предложением. Переведите в уравнение. | |
| Шаг 5. Решите уравнение. | 60=0,08с60=0,08с60=0,08с |
| Обе части разделить на 0,080.080,08 . | 600,08=0,08c0,08\frac{60}{\color{red}{0,08}}=\frac{0,08c}{\color{red}{0,08}}0,0860=0,080,08c |
| Упрощение. | с=750с=750с=750 |
| Шаг 6. Проверка: Разумен ли наш ответ? Да, $ 750 \ text {\ $ 750} $ 750 премия по автострахованию является разумной. Теперь давайте проверим нашу алгебру. 8% от 750 равно606060 ?750=c750=c750=c 0,08(750)=600,08(750)=600,08(750)=60 60=60✓60=60\quad\checkmark60=60✓ | |
Шаг 7. Ответьте на вопрос. |




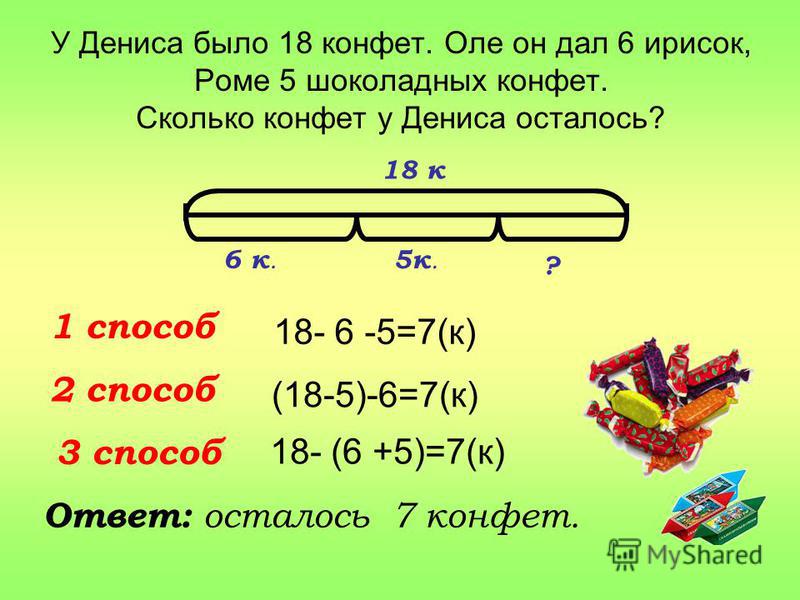



 Ищите их определения в единицах измерения (граммы, секунды, галлоны и т. д.) и других контекстных подсказках.
Ищите их определения в единицах измерения (граммы, секунды, галлоны и т. д.) и других контекстных подсказках.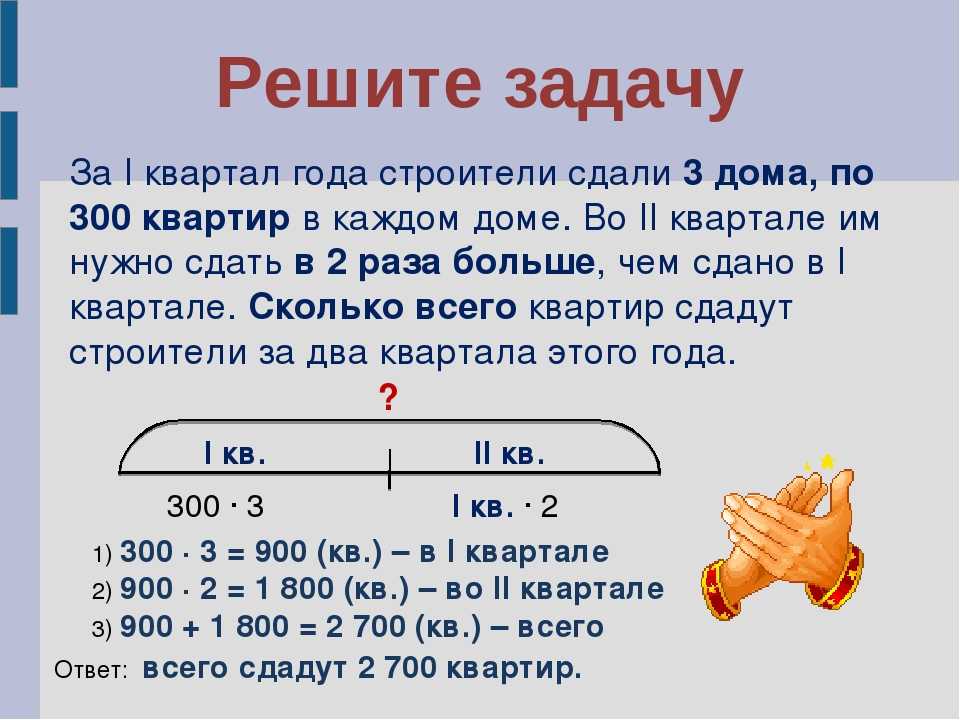
 Используйте формулы, создавайте уравнения, применяйте правила и т. д.
Используйте формулы, создавайте уравнения, применяйте правила и т. д.