Производная функции, заданной неявно
- Как найти производную функции, заданной неявно
- Решаем задачи вместе
- Решить задачи самостоятельно, а затем посмотреть решения
- Производная неявной функии онлайн
Будем учиться находить производные функций, заданных неявно. Что значит неявно? Сравним с обычной функцией. Обычная функция задана уравнением вида y=f(x), где игрек, то есть функция, задан некоторым выражением, в котором присутствует икс. Таким образом, из переменных в левой части — только игрек, в правой — только икс. Если же функция задана неявно, то в левой части различные слагаемые с игреком «смешаны» с различными слагаемыми с иксом (или переменной, обозначенной другой буквой). Примеры функций, заданных неявно:
,
,
,
,
.
При этом и икс, и игрек могут быть в различных степенях, а в одном слагаемом могут быть
и игрек, и икс.
Если функция задана неявно, то как получить игрек, то есть явную функцию? Просто: выразить игрек через другую переменную, то есть получить в левой части только игрек. А если нужно найти производную функции, заданной неявно, то есть получить в левой части только игрек со штрихом? Нужно сначала найти производные обеих частей уравнения, то есть продифференцировать их. А затем выразить производную игрека через производные других переменных.
Теперь приведенный выше «скелет» решения обрастет «мясом», то есть необходимыми
подробностями. Те слагаемые, в
которых присутствует только икс, обратятся в обычную производную функции от икса. А слагаемые, в которых
присутствуют и икс, и игрек, нужно дифференцировать, пользуясь правилом дифференцирования сложной функции,
то есть учитывать, что игрек — это функция от икса. Если совсем просто, то в полученной производной
слагаемого с иксом должно получиться: производная функции от игрека, умноженная на производную от игрека.
Пример 1. Найти производную функции, заданной неявно:
.
Решение. Дифференцируем обе части уравнения по иксу, считая, что игрек — функция от икса:
.
Отсюда получаем производную, которая требуется в задании:
.
Решение производной функции, заданной неявно, можно проверить на онлайн калькуляторе.
Пример 2. Найти производную функции, заданной неявно:
.
Решение. Дифференцируем обе части уравнения по иксу:
.
Выражаем игрек штрих и — на выходе — производная функции, заданной неявно:
.
Нет времени вникать в решение? Можно заказать работу!
Пример 3. Найти производную функции, заданной неявно:
.
Решение. Дифференцируем обе части уравнения по иксу:
.
Выражаем и получаем производную:
.
Решение производной функции, заданной неявно, можно проверить на онлайн калькуляторе.
Пример 4. Найти производную функции, заданной неявно:
.
Решение. Дифференцируем обе части уравнения по иксу:
.
Выражаем и получаем производную:.
Пример 5. Найти производную функции, заданной неявно:
.
Решение. Переносим слагаемые в правой части уравнение в левую часть и справа оставляем ноль. Дифференцируем обе части уравнения по иксу:
Путь к ответу и в конец сам ответ:
Пример 6.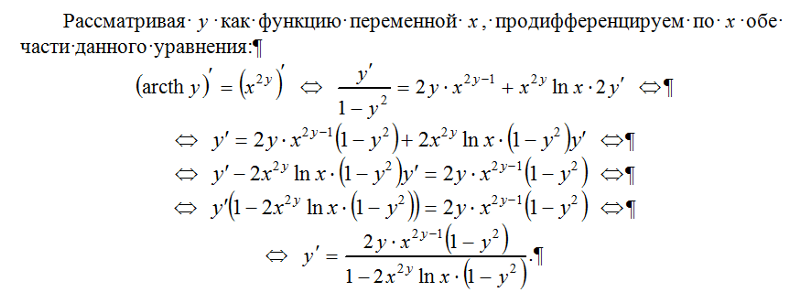 Найти производную функции, заданной неявно:
Найти производную функции, заданной неявно:
Правильное решение и ответ.
Пример 7. Найти производную функции, заданной неявно:
Правильное решение и ответ.
Пример 8. Найти производную функции, заданной неявно:
Правильное решение и ответ.
| Назад | Листать | Вперёд>>> |
К началу страницы
Пройти тест по теме Производная, дифференциал и их применение
Поделиться с друзьями
Производные
- Что такое производная
- Найти производную: алгоритм и примеры решений
- Производные произведения и частного функций
- Производная суммы дробей со степенями и корнями
- Производные простых тригонометрических функций
- Производная сложной функции
- Производная логарифмической функции
- Уравнение касательной и уравнение нормали к графику функции
- Дифференциал функции
- Дифференциал сложной функции, инвариантность формы дифференциала
- Правило Лопиталя
Функции несольких переменных
- Функции нескольких переменных
- Частные производные
- Экстремумы функции двух переменных
- Условные экстремумы и функция Лагранжа
Производные различных порядков от неявных функций
Используй поиск, чтобы найти научные материалы и собрать список литературы
База статей справочника включает в себя статьи написанные экспертами Автор24, статьи из научных журналов и примеры студенческих работ из различных вузов страны
Содержание статьи
1. {3} }{xy} -2xyy»=0\]
{3} }{xy} -2xyy»=0\]
Сообщество экспертов Автор24
Автор этой статьи Дата последнего обновления статьи: 15.12.2021
Выполнение любых типов работ по математике
Решение задач по комбинаторике на заказ Решение задачи Коши онлайн Математика для заочников Контрольная работа на тему числовые неравенства и их свойства Контрольная работа на тему умножение и деление рациональных чисел Контрольная работа на тему действия с рациональными числами Дипломная работа на тему числа Курсовая работа на тему дифференциальные уравнения Контрольная работа на тему приближенные вычисления Решение задач с инвариантами
Подбор готовых материалов по теме
Дипломные работы Курсовые работы Выпускные квалификационные работы Рефераты Сочинения Доклады Эссе Отчеты по практике Решения задач Контрольные работы
Производная неявной функции · Калькулятор Онлайн
Производная функции/ Неявной
Вы также можете построить график неявной функции. 2
2
Интегральные функции:
- Si(x)
- Интегральный синус от x
- Ci(x)
- Интегральный косинус от x
- Shi(x)
- Интегральный гиперболический синус от x
- Chi(x)
- Интегральный гиперболический косинус от x
В выражениях можно применять следующие операции:
- Действительные числа
- вводить в виде 7.
 3
3- — возведение в степень
- x + 7
- — сложение
- x — 6
- — вычитание
- 15/7
- — дробь
Другие функции:
- asec(x)
- Функция — арксеканс от x
- acsc(x)
- Функция — арккосеканс от x
- sec(x)
- Функция — секанс от x
- csc(x)
- Функция — косеканс от x
- floor(x)
- Функция — округление x в меньшую сторону (пример floor(4.5)==4.0)
- ceiling(x)
- Функция — округление
- sign(x)
- Функция — Знак x
- erf(x)
- Функция ошибок (или интеграл вероятности)
- laplace(x)
- Функция Лапласа
- asech(x)
- Функция — гиперболический арксеканс от x
- csch(x)
- Функция — гиперболический косеканс от x
- sech(x)
- Функция — гиперболический секанс от x
- acsch(x)
- Функция — гиперболический арккосеканс от x
Постоянные:
- pi
- Число «Пи», которое примерно равно ~3.
 14159..
14159.. - e
- Число e — основание натурального логарифма, примерно равно ~2,7183..
- i
- Комплексная единица
- oo
- Символ бесконечности — знак для бесконечности
Производная неявной функции — Энциклопедия по экономике
Производная неявной функции — Энциклопедия по экономикеПроизводная неявной функции 127 [c.127]
Производная неявной функции [c.127]
Производная неявной функции от одной переменной [c.296]
Таким образом, tga (и, следовательно, наклон касательной К-см. рис. 7.8), равный А (, °), может быть найден как отношение (первых) частных производных функции Дх,, х2) в точке (х,°, Xj0), взятое со знаком минус, т.е. без использования явного выражения А(х,). Выписанная формула называется производной неявной функции Xj = Л(х,). Эта формула играет важную роль в микроэкономическом анализе (в теории потребительского поведения и в теории фирмы).
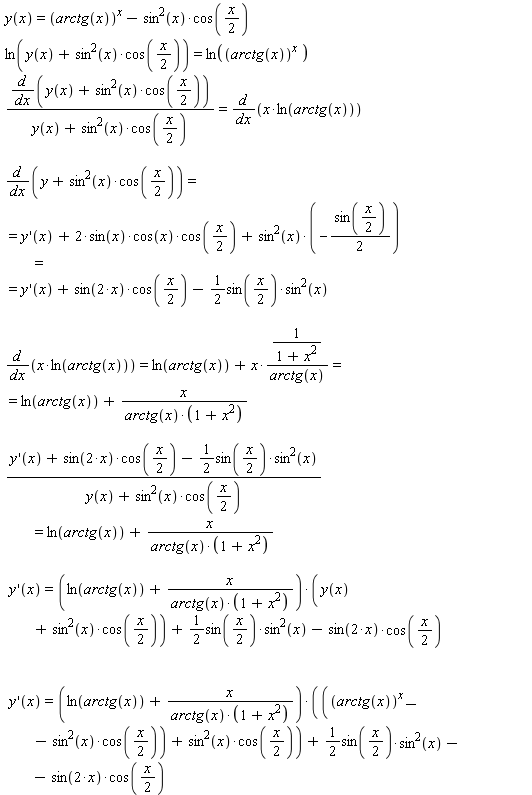 Производная неявной функции х, = g(x2) выписывается аналогично (числитель и знаменатель меняются местами).
[c.110]
Производная неявной функции х, = g(x2) выписывается аналогично (числитель и знаменатель меняются местами).
[c.110]Приведите формулу производной неявной функции. [c.119]
По правилу дифференцирования неявных функций найдем производные по рк [c.202]
Выше было рассмотрено дифференцирование явных функций и параметрических функций. Рассмотрим дифференцирование неявной функции, заданной уравнением F(x,y] = 0. Для нахождения производной функции у, заданной неявно, нет нужды искать явное выражение функции у = /(ж) нужно просто продифференцировать обе части уравнения, рассматривая у как функцию от ж, а затем из полученного уравнения найти производную у. [c.127]
Теорема однако не дает представления о способе вычисления производной от неявной функции у х. А это очень важно в социально-экономических исследованиях, так как использование производной позволяет более детально исследовать функцию определить интервалы ее возрастания и убывания, найти точки минимума и максимума.
 Поэтому ниже приводится простой прием, с помощью которого можно легко находить производную от неявной функции.
[c.298]
Поэтому ниже приводится простой прием, с помощью которого можно легко находить производную от неявной функции.
[c.298]Пусть выполнены условия теоремы. Согласно определению неявной функции у = /(ж) удовлетворяет уравнению (14.3). Левая часть этого уравнения представляет собой сложную функцию от ж, которая тождественно равна нулю. Тогда и производная ее по х также есть нуль. Воспользовавшись формулой (14.1) дифференцирования сложной функции, получаем [c.298]
Если функция F(x,y] имеет еще и непрерывные производные второго порядка, то выражение, стоящее в равенстве (14.6) справа, может быть продифференцировано по ж, следовательно существует и вторая производная у»ж от неявной функции у. [c.299]
Оно задает в виде неявной функции зависимость объема производства, выбираемого монополистом, от величины предельных издержек у» = у(с). В предположении существования производных обратной функции спроса р(у и функции у (с), продифференцируем по [c.483]
Производная неявно заданной функции
[c. 123]
123]
Иррациональные числа, а также возникшие по ходу развития математики такие понятия, как бесконечность, предел, явились следствием признания невозможности наглядно выразить кардинальные свойства фигуры большей размерности (например, прямоугольника) в понятиях фигуры меньшей размерности (например, отрезка), и желания, закодировав эту невозможность названиями, открыть путь к описанию и исследованию других последующих из доступных осознанию количественных свойств реальности. Свойство ее изменчивости (в частности, такое кардинальное для управленца понятие, как изменение во времени — движение) учитывается с помощью понятий переменная величина, функция, а также производная и интеграл, связывающие величину количества с характером его изменения в окрестности этой величины, дающих возможность получить аналитическое описание многих физических законов движения (например, в виде дифференциальных уравнений). Оценки более тонких количественных отношений реальности отражаются в таких разделах математики, как, например, вариационное исчисление, где независимой переменной является уже не число, а функция. Оценки качества количественных отношений — в таких понятиях, как явные и неявные зависимости, корректность, грубость и т.д.
[c.261]
Оценки качества количественных отношений — в таких понятиях, как явные и неявные зависимости, корректность, грубость и т.д.
[c.261]
Дискретный принцип максимума получается почти по такой же схеме, но вместо дифференциальных уравнений в выкладках участвуют их разностные аппроксимации. И вот здесь появляется упомянутое реальное следствие дискретной теории разностное уравнение для сопряженного уравнения является следствием того или иного выбора аппроксимаций для прямого уравнения и для интеграла в тождестве Лагранжа. Разностная аппроксимация уравнения в вариациях также однозначно определяется выбором аппроксимации исходного уравнения, но это не так важно, так как в вычислительных методах обычно это уравнение не интегрируется. Эту аппроксимацию сопряженного уравнения «мы будем называть согласованной с аппроксимациями исходного уравнения и интеграла в том смысле, что для конечно-разностных решений Sz и ф, полученных по согласованным аппроксимациям соответствующих уравнений, алгебраически точно выполняется тождество Лагранжа (тоже в соответствующей аппроксимации).
 Это и есть то единственное практическое следствие, которое автор смог извлечь из теории дискретного принципа максимума и которого в своих вычислениях никогда не использовал ни в явной, ни в неявной формах. Автор всегда выбирал для исходного и сопряженного уравнений независимые аппроксимации, причем сопряженное обычно интегрировалось более грубо, с большим шагом по времени. Дело в том, что использование согласованной > аппроксимации связано с определенными техническими неудобствами, необходимость преодоления которых не очевидна. Во всяком случае, автору неизвестны трудности численного решения задач оптимального управления, которые можно было бы преодолеть, используя согласованную аппроксимацию. Чтобы и здесь быть более конкретным, можно все же указать на некоторое следствие использования согласованной аппроксимации. Речь идет о получении минимума функционала с большим числом знаков. Используя для вычисления функциональной производной функцию , найденную по произвольной аппроксимации сопряженного уравнения, мы, разумеется, находим не точную производную, а лишь приближенную, искаженную влиянием ошибок аппроксимации.
Это и есть то единственное практическое следствие, которое автор смог извлечь из теории дискретного принципа максимума и которого в своих вычислениях никогда не использовал ни в явной, ни в неявной формах. Автор всегда выбирал для исходного и сопряженного уравнений независимые аппроксимации, причем сопряженное обычно интегрировалось более грубо, с большим шагом по времени. Дело в том, что использование согласованной > аппроксимации связано с определенными техническими неудобствами, необходимость преодоления которых не очевидна. Во всяком случае, автору неизвестны трудности численного решения задач оптимального управления, которые можно было бы преодолеть, используя согласованную аппроксимацию. Чтобы и здесь быть более конкретным, можно все же указать на некоторое следствие использования согласованной аппроксимации. Речь идет о получении минимума функционала с большим числом знаков. Используя для вычисления функциональной производной функцию , найденную по произвольной аппроксимации сопряженного уравнения, мы, разумеется, находим не точную производную, а лишь приближенную, искаженную влиянием ошибок аппроксимации. Поэтому получить минимум с очень большой точностью не удастся начиная с некоторого этапа минимизации (например, методом градиента в функциональном пространстве) мы будем в этом случав
[c.54]
Поэтому получить минимум с очень большой точностью не удастся начиная с некоторого этапа минимизации (например, методом градиента в функциональном пространстве) мы будем в этом случав
[c.54]В равновесии совокупный спрос должен быть равен выпуску и, таким образом, приравнивая их, мы получаем неявную зависимость между выпуском и ставкой процента. Совокупность всех комбинаций ставки процента выпуска, при которых рынок товаров уравновешен, дает нам кривую, которую мы будем называть кривой IS. Кривая IS имеет отрицательный наклон, то есть характеризуется отрицательной зависимостью между ставкой процента и выпуском. Действительно, если мы возьмем соответствующую производную, то она, в силу принятых гипотез относительно поведения функции инвестиций с учетом того, что предельная склонность к потреблению меньше единицы, имеет отрицательный знак [c.37]
Отметим основное отличие данной реализации метода динамического программирования от схемы вычислений 15. Оно связано с использованием интерполяции функции Беллмана F (х1, х ) с узлов сетки. Этим снимается ограничение на шаг сетки в фазовом пространстве типа h=o (t), необходимое в схеме метода Н. Н. Моисеева. Вместе с тем интерполяция является источником определенных ошибок, тем более, что сетки приходится брать сравнительно грубые. Кроме того, используя интерполяцию, неявно предполагают наличие у функции Беллмана таких свойств гладкости, которых может и не быть. Известны простые примеры задач, в которых функция Беллмана разрывна, а наличие разрывов производной может считаться почти общим явлением. Схема вычислений 15 может быть (при h=0 (t2)) обоснована без всяких предположений о свойствах функции Беллмана. Что касается реализации алгоритма на ЭВМ, то в данном случае наибольшие ограничения связаны с ресурсом памяти. Вычисления в [4] тре= буют N таблиц по 30×30 величин, однако при вычислении очередной функции Fn (х1, х2-) в оперативной памяти нужно иметь только две такие таблицы.
[c.307]
Этим снимается ограничение на шаг сетки в фазовом пространстве типа h=o (t), необходимое в схеме метода Н. Н. Моисеева. Вместе с тем интерполяция является источником определенных ошибок, тем более, что сетки приходится брать сравнительно грубые. Кроме того, используя интерполяцию, неявно предполагают наличие у функции Беллмана таких свойств гладкости, которых может и не быть. Известны простые примеры задач, в которых функция Беллмана разрывна, а наличие разрывов производной может считаться почти общим явлением. Схема вычислений 15 может быть (при h=0 (t2)) обоснована без всяких предположений о свойствах функции Беллмана. Что касается реализации алгоритма на ЭВМ, то в данном случае наибольшие ограничения связаны с ресурсом памяти. Вычисления в [4] тре= буют N таблиц по 30×30 величин, однако при вычислении очередной функции Fn (х1, х2-) в оперативной памяти нужно иметь только две такие таблицы.
[c.307]
Смотреть главы в:
Математика для социологов и экономистов Учебное пособие -> Производная неявной функции
Copyright © 2022 — economy-ru.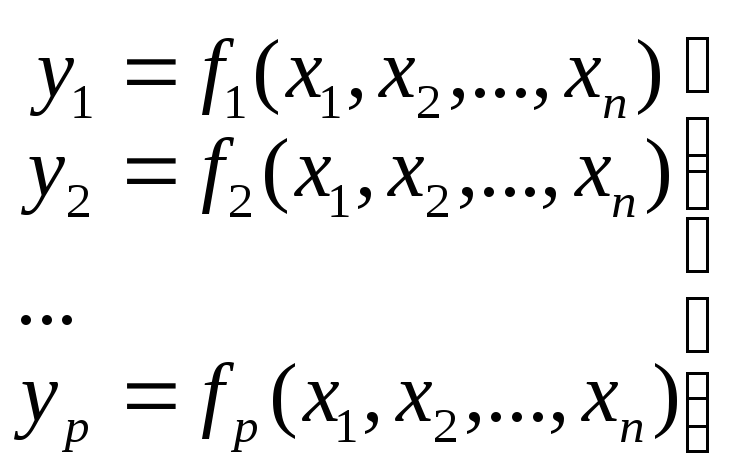 info
info
| 6.5.2. Производные неявных функций, заданных системой уравнений. Определитель Якоби |
Высшая математика > 6. Дифференциальное исчисление функций нескольких переменных > 6.5. Производные функций нескольких переменных, заданных неявно > 6.5.2. Производные неявных функций, заданных системой уравнений. Определитель Якоби Дифференциальное исчисление функций нескольких переменных > 6.5. Производные функций нескольких переменных, заданных неявно > 6.5.2. Производные неявных функций, заданных системой уравнений. Определитель Якоби
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Производная неявной функции — онлайн справочник для студентов
ОПРЕДЕЛЕНИЕ
Если функция \(\
y=y(x)
\)
задается уравнением \(\
F(x ; y(x))=0
\), то говорят, что она дается неявно. {3}}
\)
{3}}
\)
Физика
166
Реклама и PR
31
Педагогика
80
Психология
72
Социология
7
Астрономия
9
Биология
30
Культурология
86
Экология
8
Право и юриспруденция
36
Политология
13
Экономика
49
Финансы
9
История
16
Философия
8
Информатика
20
Право
35
Информационные технологии
6
Экономическая теория
7
Менеджент
719
Математика
338
Химия
20
Микро- и макроэкономика
1
Медицина
5
Государственное и муниципальное управление
2
География
542
Информационная безопасность
2
Аудит
11
Безопасность жизнедеятельности
3
Архитектура и строительство
1
Банковское дело
1
Рынок ценных бумаг
6
Менеджмент организации
2
Маркетинг
238
Кредит
3
Инвестиции
2
Журналистика
1
Конфликтология
15
Этика
9
Формулы дифференцирования Частные производные Таблица производных сложных функций Таблица производных Частные дифференциалы
Узнать цену работы
Узнай цену
своей работы
Имя
Выбрать тип работыЧасть дипломаДипломнаяКурсоваяКонтрольнаяРешение задачРефератНаучно — исследовательскаяОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерскаяНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация в ВАКПубликация в ScopusДиплом MBAПовышение оригинальностиКопирайтингДругоеПринимаю Политику конфиденциальности
Подпишись на рассылку, чтобы не пропустить информацию об акциях
Неявное дифференцирование — Примеры | Неявная производная
Неявное дифференцирование — это процесс нахождения производной неявной функции. т. е. этот процесс используется для нахождения неявной производной. Есть два типа функций: явная функция и неявная функция. Явная функция имеет вид y = f(x) с зависимой переменной «y» на одной из сторон уравнения. Но не обязательно всегда иметь «y» на одной стороне уравнения. Например, рассмотрим следующие функции:
т. е. этот процесс используется для нахождения неявной производной. Есть два типа функций: явная функция и неявная функция. Явная функция имеет вид y = f(x) с зависимой переменной «y» на одной из сторон уравнения. Но не обязательно всегда иметь «y» на одной стороне уравнения. Например, рассмотрим следующие функции:
- х 2 + у = 2
- ху + грех (ху) = 0
В первом случае, хотя ‘y’ не является одной из сторон уравнения, мы все же можем решить его, записав его как y = 2 — x 2 , и это явная функция. Но во втором случае мы не можем легко решить уравнение для «y», и этот тип функции называется неявной функцией, и на этой странице мы увидим, как найти производную неявной функции, используя процесс неявного дифференцирования.
| 1. | Что такое неявное дифференцирование? |
| 2. | Неявная производная |
| 3. | Неявное дифференцирование и цепное правило |
4. | Как сделать неявное дифференцирование? |
| 5. | Неявное дифференцирование обратных тригонометрических функций |
| 6. | Часто задаваемые вопросы о неявном дифференцировании |
Что такое неявное дифференцирование?
Неявное дифференцирование — это процесс дифференцирования неявной функции. Неявная функция — это функция, которая может быть выражена как f(x, y) = 0, т. е. ее нельзя легко решить для ‘y’ (или ее нельзя легко представить в виде y = f(x ). Рассмотрим пример нахождения dy/dx по заданной функции xy = 5. Найдем dy/dx двумя способами: (i) решая относительно y (ii) не решая относительно y.
- Метод — 1:
ху = 5
у = 5/х
у = 5x -1
Дифференцируя обе стороны по x:
dy/dx = 5(-1x -2 ) = -5/x 2 - Метод — 2:
ху = 5
Дифференцируя обе стороны по x:
д/дх (ху) = д/дх(5)
Используя правило произведения слева,
х d/dx(y) + y d/dx(x) = d/dx(5)
х (dy/dx) + у (1) = 0
х(dy/dx) = -y
dy/dx = -y/x
Из xy = 5 мы можем написать y = 5/x.
dy/dx = -(5/x)/x = -5/x 2
В методе -1 мы преобразовали неявную функцию в явную и нашли производную, используя степенное правило. Но в методе 2 мы дифференцировали обе части по x, рассматривая y как функцию от x, и этот тип дифференцирования называется неявным дифференцированием. Но для некоторых функций, таких как xy + sin (xy) = 0, запись в виде явной функции (Метод — 1) невозможна. В таких случаях только неявное дифференцирование (метод — 2) является способом нахождения производной.
Неявная производная
Производная, найденная с помощью процесса неявного дифференцирования, называется неявной производной. Например, производная dy/dx, найденная в методе 2 (в приведенном выше примере), сначала была dy/dx = -y/x и называется неявной производной. Это потому, что мы продифференцировали неявную функцию xy = 5 напрямую, не решая ее для y. Неявная производная обычно выражается как по x, так и по y.
Неявное дифференцирование и цепное правило
Цепное правило дифференцирования играет важную роль при нахождении производной неявной функции. Цепное правило гласит: d/dx (f(g(x)) = (f’ (g(x)) · g'(x). Всякий раз, когда мы сталкиваемся с производной членов y по x, цепное правило приходит в сцену и из-за цепного правила мы умножаем реальную производную (по формулам производных) на dy/dx. Вот пример.
Цепное правило гласит: d/dx (f(g(x)) = (f’ (g(x)) · g'(x). Всякий раз, когда мы сталкиваемся с производной членов y по x, цепное правило приходит в сцену и из-за цепного правила мы умножаем реальную производную (по формулам производных) на dy/dx. Вот пример.
Вот еще примеры, чтобы понять цепное правило в неявном дифференцировании.0003
- d/dx (y 2 ) = 2y dy/dx
- d/dx (sin y) = cos y dy/dx
- d/dx (ln y) = 1/y · dy/dx
- d/dx (tan -1 y) = 1/(1 + y 2 ) · dy/dx
Другими словами, везде, где y дифференцируется, также пишите dy/dx. Предлагается повторять эти примеры снова и снова, так как они очень полезны при неявном дифференцировании.
Как сделать неявное дифференцирование?
В процессе неявного дифференцирования мы не можем начать непосредственно с dy/dx, так как неявная функция имеет вид не y = f(x), а f(x, y) = 0. Примечание. что мы должны знать производные правила, такие как правило мощности, правило произведения, правило частного, правило цепи и т. д., прежде чем изучать процесс неявного дифференцирования. Вот блок-схема шагов для выполнения неявного дифференцирования.
д., прежде чем изучать процесс неявного дифференцирования. Вот блок-схема шагов для выполнения неявного дифференцирования.
Теперь эти шаги объясняются на примере, где мы собираемся найти неявную производную dy/dx, если функция y + sin y = sin x.
Формула неявного дифференцирования
Мы рассмотрели шаги для выполнения неявного дифференцирования. Сталкивались ли мы с какой-либо конкретной формулой на этом пути? Нет!! Не существует конкретной формулы для неявного дифференцирования, вместо этого мы выполняем шаги, описанные в блок-схеме выше, чтобы найти неявную производную.
Неявное дифференцирование обратных тригонометрических функций
Процесс неявного дифференцирования полезен при нахождении производных обратных триггерных функций. Найдем производную от y = tan -1 x с использованием неявного дифференцирования. Из определения arctan y = tan -1 x ⇒ tan y = x. Дифференцируя обе части этого уравнения по x,
сек 2 y × dy/dx = 1 (поскольку производная тангенса x равна sec 2 x)
dy/dx = 1/сек 2 y
dy/dx = 1 / (1 + tan 2 y) (по одному из тригонометрических тождеств)
dy/dx = 1 / (1 + x 2 ) (поскольку tan y = x)
Таким образом, процесс неявного дифференцирования можно использовать для нахождения производных любой обратной функции.
Важные замечания по неявному дифференцированию:
- Неявное дифференцирование — это процесс нахождения dy/dx, когда функция имеет вид f(x, y) = 0,
- Чтобы найти неявную производную dy/dx, просто продифференцируйте обе части и найдите dy/dx. Но в этом процессе пишите dy/dx везде, где мы дифференцируем y.
- Все производные формулы и приемы следует использовать и в процессе неявного дифференцирования.
☛ Связанные темы:
- Калькулятор производных
- Расчетный калькулятор
- Калькулятор второй производной
- Дифференциация
Часто задаваемые вопросы о неявном дифференцировании
Что такое определение неявного дифференцирования в исчислении?
Неявное дифференцирование — это процесс дифференцирования неявной функции, имеющей вид f(x, y) = 0, и нахождения dy/dx. Чтобы найти неявную производную,
- Продифференцировать обе части f(x, y) = 0 по x
- Применение обычных формул производных для дифференцирования членов x
- Применение обычных формул производной для дифференцирования членов по оси y с умножением производной на dy/dx
- Решите полученное уравнение для dy/dx (выделив dy/dx).

Как найти неявную производную?
Чтобы найти неявную производную уравнения, например, скажем, x 2 + sin(y) = 0:
- Возьмем производную по x с обеих сторон.
Тогда мы получаем d/dx(x 2 ) + d/dx (sin y) = 0, . - Умножать на dy/dx везде, где мы что-то дифференцируем с помощью y.
2x + cos y dy/dx = 0, - Решите для dy/dx.
cos y dy/dx = -2x
dy/dx = -2x/cos y
Как выполнить неявное дифференцирование с помощью триггерных функций?
Когда мы выполняем неявное дифференцирование тригонометрических функций, то просто применяем нормальные тригонометрические производные, такие как d/dx(sin x) = cos x, d/dx(cos x) = — sin x и т. д., а затем применяем цепное правило . Это означает, что мы должны умножить реальную производную на производную внутренней функции. Например, d/dx (sin y 2 ) = cos y 2 d/dx (y 2 ) = 2y cos y 2 dy/dx.
Что такое неявные правила дифференциации?
При нахождении неявной производной мы просто дифференцируем уравнение относительно x и y с обеих сторон относительно x, используем dy/dx также всякий раз, когда мы дифференцируем что-то с y, и решаем полученное уравнение относительно dy/dx.
Что такое неявное значение дифференциации?
Смысл неявного дифференцирования, как следует из его названия, заключается в процессе дифференцирования неявной функции f(x, y) = 0 и нахождения производной dy/dx. Чтобы узнать, как сделать неявное дифференцирование, нажмите здесь.
Как найти вторую неявную производную?
Если задана неявная функция f(x, y) = 0, используйте процесс неявного дифференцирования, чтобы найти первую производную dy/dx (или) y’. Затем мы дифференцируем первую производную y’ по x с обеих сторон, чтобы найти вторую неявную производную. В этом процессе нам, возможно, придется также использовать ответ y’.
Что такое неявная формула дифференцирования?
Специальной формулы для неявного дифференцирования не существует. Вместо этого мы просто дифференцируем функцию с обеих сторон, не игнорируя цепное правило, и решая полученное уравнение для dy/dx. Везде, где мы дифференцируем что-то с y, просто умножайте производную также на dy/dx.
Вместо этого мы просто дифференцируем функцию с обеих сторон, не игнорируя цепное правило, и решая полученное уравнение для dy/dx. Везде, где мы дифференцируем что-то с y, просто умножайте производную также на dy/dx.
8. Дифференцирование неявных функций
М. Борна
Мы встречаем много уравнений, где и не выражены явно только с точки зрения x , например:
f ( x , y ) = y 4 + 2 x 2 y 2 + 6 x 2 = 7
Вы можете увидеть несколько примеров таких выражений в разделе Polar Graphs.
Обычно трудно, если не невозможно, решить для y , чтобы мы могли найти `(dy)/(dx)`.
Нам нужно уметь находить производные таких
выражения, чтобы найти скорость изменения y как x изменений. Для этого нам нужно знать неявных
дифференциация .
Давайте узнаем, как это работает, на нескольких примерах.
Начнем с неявной функции y 4 + x 5 − 7 x 2 − 5 x -1 = 0,
Вот график этой неявной функции. Обратите внимание:
- Это не обычная функция, потому что существует более одного значения y для каждого значения x (для областей `x
- Кривая имеет два «плеча»
- Кривая вертикальна вблизи `x = -1` и `x = 2`
Найдите производную этой неявной функции и представьте ответ в виде `dy/dx`.
Ответ
y 4 + x 5 -7 x 2 -5 x -1 = 0
Мы видим, как вывести это выражение в момент. Мы просто выводите выражения по мере того, как мы подходим к ним слева направо. Правильно.
(В этом примере мы могли бы легко выразить функцию только через y , но это задумано как относительно простой первый пример. )
)
Часть A: Найдите производную относительно 93`
Пример 2
Найдите наклон касательной в точке `(2,-1)` для кривой:
2 y + 5 − x 2 − y 3 = 0,
Ответить
Работая слева направо, имеем:
Производное от `2y`:
`d/(dx)2y=2(dy)/(dx)`
Производная от «5» равна «0».
Производное от x 2 93=0`
и начертите касательную к кривой в точке `(2, -1)`. Мы видим, что действительно наклон равен «-4».
График, показывающий тангенс при `x=2`
Это работает!
Пример 3 (включает правило продукта)
Найдите выражение для `(dy)/(dx)` если:
y 4 + 2 x 2 y 2 + 6 x 2 = 30 7
(Это пример, приведенный вверху этой страницы. )
)
Ответить
Сначала построим график неявной функции, заданной в вопросе, чтобы увидеть, с чем мы работаем. Мы наблюдаем, что это просто эллипс:
График y 4 + 2 x 2 y 2 + 6 x 2 = 70003
до того, что мы срок разобью этот вопрос на части.
Часть A:
Найдите производную относительно x 93(дх)/(дх)`
Часть B:
Найдите производную относительно x от 2 x 2 y 2
Теперь найдем производную от 2 x 2 y 90 x мы должны признать, что это продукт .
Если мы допустим u = 2 x 2 и 92г)`
Производная неявной функции
Разница между явной и неявной функциями
В математике функция представляет отношение между двумя наборами значений таким образом, что каждое входное значение генерирует одно выходное значение. Есть два типа функций:
Есть два типа функций:
- Явная функция : Когда x известен, мы можем вычислить значение y. Оно выражается как у, равное некоторой функции переменной х.
- Неявная функция : Даже если значение x известно, мы не можем напрямую вычислить значение y.
Примеры
- — это пример явной функции, поскольку зная значение x напрямую, можно получить значение y.
- является примером неявной функции, потому что знание значения x не приводит нас напрямую к значению y. Это также не выражается как y, равный некоторой функции x.
Теперь, когда вы знаете разницу между явными и неявными функциями, вы можете легко обозначить, является ли данная функция явной или неявной формой.
Лучшие репетиторы по математике
Поехали
Дифференцирование неявных функций
Мы знаем, что нахождение производной функции является одним из фундаментальных понятий исчисления. Производная функции определяется как мгновенная скорость изменения функции в какой-то момент. Процесс нахождения производной функции известен как дифференцирование . Мы можем вычислить несколько производных одной и той же функции. Когда мы сначала дифференцируем функцию, результирующая производная известна как первая производная . Когда мы далее дифференцируем первую производную, результирующее выражение известно как вторая производная . В этой статье мы увидим только, как найти первую производную неявных функций.
Процесс нахождения производной функции известен как дифференцирование . Мы можем вычислить несколько производных одной и той же функции. Когда мы сначала дифференцируем функцию, результирующая производная известна как первая производная . Когда мы далее дифференцируем первую производную, результирующее выражение известно как вторая производная . В этой статье мы увидим только, как найти первую производную неявных функций.
Перед поиском производных функций необходимо ознакомиться с правилами дифференцирования. Некоторые из основных правил дифференциации приведены ниже.
- Правило констант:
- Правило степени:
- Правило сумм:
- Правило разности:
- Правило произведения:
- Правило частного (используется для дробей):
- Цепное правило:
Как выполнить неявное дифференцирование?
Вероятно, вы несколько раз проводили явное дифференцирование, потому что это основной вид дифференцирования, который включает применение производных правил. Вы когда-нибудь задумывались, как отличить неявную функцию и чем этот вид дифференциации отличается от явной? Что ж, в этом разделе мы узнаем, как найти производную неявной функции на примерах. Но прежде чем перейти к примерам, давайте сначала рассмотрим шаги, связанные с неявным дифференцированием функции.
Вы когда-нибудь задумывались, как отличить неявную функцию и чем этот вид дифференциации отличается от явной? Что ж, в этом разделе мы узнаем, как найти производную неявной функции на примерах. Но прежде чем перейти к примерам, давайте сначала рассмотрим шаги, связанные с неявным дифференцированием функции.
- Шаг 1: Первым шагом неявного дифференцирования является дифференцирование обеих частей функции по переменной . Следует помнить одну вещь: производную члена, включающего переменную, нужно умножить на .
- Шаг 2. На этом шаге мы решаем уравнение для путем выделения .
Другими словами, мы можем сказать, что когда нам дана неявная функция, мы используем цепное правило, чтобы дифференцировать функцию. Следующие примеры еще больше прояснят эту концепцию.
Пример 1
Дифференцировать
Решение
Для вашего удобства мы разбили решение этой задачи на несколько шагов.
Шаг 1. Продифференцируем обе части функции по переменной x
Применим правило производной мощности к левой части и правило производной константы к правой части функции.
Так как в правой части уравнения была только константа, то мы приравняли все уравнение к 0. Помимо дифференцирования каждого элемента в функции, производная y также умножается на .
Шаг 2: Упростите уравнение, решив для
На этом шаге мы решим уравнение для путем выделения левой части уравнения. Пример 2 Шаги для дифференциации этой функции по существу одинаковы.
Шаг 1. Продифференцируем обе части функции по переменной x
Найдем производную каждого члена, используя правила дифференцирования. В левой части уравнения мы будем использовать производную мощность и правило произведения. В правой части мы просто продифференцируем константу, используя правило производной константы.
Шаг 2: Упростите уравнение, найдя
Второй шаг включает упрощение уравнения путем выделения левой части уравнения. Пример 3 Широко используемые триггерные функции — это синус, косинус и тангенс. Всегда полезно запомнить производные общих тригонометрических функций. Мы также записали производные общих триггерных функций в конце этой статьи.
Всегда полезно запомнить производные общих тригонометрических функций. Мы также записали производные общих триггерных функций в конце этой статьи.
Шаг 1. Дифференцируем обе части функции по переменной x
Как обычно, мы найдем производную каждого элемента в обеих частях функции и умножим производную члена с переменной y по .
Перепишем уравнение следующим образом: уравнение. 9Пример 4 Процедура дифференцирования этой неявной функции такая же, как мы использовали в предыдущих примерах.
Шаг 1. Дифференцируем обе части функции по переменной x
Примените общее правило мощности, чтобы дифференцировать триггерные функции в левой части. Следует отметить, что общее силовое правило является особым видом цепного правила. Математическая обозначения этого правила приведена ниже:
Помните, что производная и производная
Шаг 2: Упрощение уравнения, решая для
Чтобы еще больше упростить уравнение, мы удалим общий член «-2» в числителе и знаменателе.
Производители общих тригонометрических функций
Производные общие тригонометрические функции приведены ниже:
Производная функция
0002
Производные неявных функций — Непрерывность и дифференцируемость | Класс 12 Математика
Неявные функции — это функции, в которых конкретная переменная не может быть выражена как функция другой переменной. Функция, зависящая более чем от одной переменной. Неявное дифференцирование помогает нам вычислить производную y по x без решения данного уравнения для y. Этого можно достичь с помощью цепного правила, которое помогает нам выразить y как функцию от x.
Неявное дифференцирование также можно использовать для вычисления наклона кривой, поскольку мы не можем следовать прямой процедуре дифференцирования функции y = f(x) и присвоения значения координаты x точки в dy/dx для получить наклон. Вместо этого нам придется следовать процессу неявного дифференцирования и найти dy/dx.
Вместо этого нам придется следовать процессу неявного дифференцирования и найти dy/dx.
Используемый здесь метод неявного дифференцирования является общим методом нахождения производных неизвестных величин.
Пример
x 2 y 2 + xy 2 + e xy = abc = константа
х.
Производная неявной функцииПоскольку функции не могут быть выражены через одну конкретную переменную, мы должны следовать другому методу, чтобы найти производную неявной функции:
При вычислении производной неявной функции функция, наша цель состоит в том, чтобы решить для dy/dx или любые производные более высокого порядка в зависимости от функции. Чтобы решить dy/dx через x и y, мы должны выполнить определенные шаги:
Шаги для вычисления производной неявной функции- Учитывая неявную функцию с зависимой переменной y и независимой переменной x ( или наоборот).

- Продифференцировать все уравнение по независимой переменной (это может быть x или y).
- После дифференцирования нам нужно применить цепное правило дифференцирования.
- Решите полученное уравнение для dy/dx (или dx/dy аналогично) или снова продифференцируйте, если нужны производные более высокого порядка.
«Некоторая функция от y и x равна чему-то другому». Знание x не поможет нам вычислить y напрямую. Например,
x 2 + y 2 = R 2 ( неявная функция)
Дифференциал с относительно X:
D (x 2 ) /dx + d (y (y y (y y (y y (x 2 ) /dx + d 2 )/ dx = d(r 2 ) / DXРешите каждый термин:
с использованием правила мощности : D (x 2 ) / dx = 2x
с использованием цепочки правило : d (y 2 ) / dx = 2y dydx
r 2 является константой, поэтому ее производная равна 0: d(r 2 )/ dx = 0
Что дает нам:
2x + 2y dy/dx = 0
9000dy /dx с одной стороныy dy/dx = −x
Решить для dy/dx:
dy/dx = −xy
Примеры задач на производную неявной функции
Пример 1. Найдите выражение для первой производной функции y(x), заданной неявно уравнением: x 2 y 3 – 4y + 3x 3 = 2.
Найдите выражение для первой производной функции y(x), заданной неявно уравнением: x 2 y 3 – 4y + 3x 3 = 2.
Решение:
Шаг 1: Дифференцируйте данное уравнение или функцию по x.
x 2 y 3 – 4y + 3x 3 = 2,
d(x 2 y 3 – 4y + 3x 3 ) / dx = d(2) / dx
Шаг 2: правая часть будет просто производной 0 постоянный.
Левая сторона после дифференциации:
2xy 3 + 3x 2 y 2 * DY/DX-4 * DY/DX + 2 = 0,
Шаг + 2 = 0,
. 3: Соберите члены, включающие dy/dx, на одной стороне и возьмите оставшиеся члены на другой стороне, чтобы получить:
DY/DX * (3x 2 Y 2 -4) = -9x 2 -2xy 3
DY/DX = -(9x 2 + 2xy 3 )// (3x 2 y 2 – 4 )
Это выражение для первой производной в любой точке кривой. Это выражение также помогает нам вычислить наклон касательной, проведенной в точке (x, y) к кривой.
Это выражение также помогает нам вычислить наклон касательной, проведенной в точке (x, y) к кривой.
Пример 2. Найдите первую производную y, заданную неявно как: y – tan -1 у = х.
Решение:
d(y – tan -1 y) /dx = d(x)/ dx.
dy/dx – (1/(1 + y 2 ) * dy/dx = 1
dy/dx = 1/(1 / (1–1/ (1 + y 2 ))
DY/DX = 1/Y 2 + 1
Пример 3. Найдите DY/DX, если x 2 Y 3 — XY = 10.
Решение:
/2xy 1. 3 + х 2 . 3 года 2 . dy/dx – у – х. dy/dx = 0
(3x 2 y 2 – x ). dy/dx = y – 2xy 3
dy/dx = (y – 2xy 3 ) / (3x 2 y 2 – x)
90 = sinx + cosy
Решение:
y – уют = sinx
dy/dx + siny.
dy/dx = cosx
dy/dx = cosx / (1 + siny)
Пример 5. Найти наклон касательной к кривой x 2 + y 2 = 25 в точке (3,−4).
Решение:
Обратите внимание, что наклон касательной к кривой является производной, неявно дифференцированной по x, что дает
2x + 2y. dy/dx = 0
dy/dx = -x/y
Следовательно, при (3,−4) y′ = −3/−4 = 3/4, а касательная имеет наклон 3/4 при точка (3,−4).
исчисление — Как я могу проверить правильность моей производной для неявной функции?
Спросил
Изменено 7 лет, 9 месяцев назад
Просмотрено 3к раз
$\begingroup$
Для явных функций я могу вычислить производную в определенной точке, используя исходную функцию: $$\frac{f(1+0. 1) — f(1)}{0.1}$$
1) — f(1)}{0.1}$$
И затем использовать $\frac{ d}{dx}f(1)$, чтобы проверить правильность функции. Но что я могу сделать для неявных функций? как я могу рассчитать изменение, а затем сравнить его с моей производной функцией 92-1)$$ и после того, как я продифференцирую его, как я могу проверить его правильность
- исчисление
- производные
$\endgroup$
7
$\begingroup$
Вы можете сначала вычислить действительную производную для пары $(x,y)$, которая удовлетворяет уравнению, затем выбрать $Δx$, затем проверить, если $\left(x+\Delta x,y+\Delta x\frac {dy}{dx}\right)$ приблизительно удовлетворяет уравнению.
Например, похоже, что $\left(0, -\pi/8\right)$ является корнем вашего уравнения. Таким образом, вы можете выбрать $x’ = 0,000001$ и найти соответствующий $y’$, используя производную: 9{-8}$$
И надеюсь, что это достаточно близко. ..
..
$\endgroup$
2
$\begingroup$
Отличный вопрос. Подобные вещи постоянно возникают при написании кода для решения задач оптимизации с ограничениями.
Стандартная стратегия такова. Во-первых, вам нужен механизм для нахождения $y$ при заданном $x$. Например, вы можете использовать метод Ньютона, поиск пополам или что-то еще. Я рекомендую метод Ньютона с линейным поиском с возвратом. Вы можете проверить правильность своего кода решателя, подставив $x,y$ в исходное уравнение и убедившись, что невязка равна нулю. 92 (х+ 2 у) ; $$
и подключите их, чтобы вычислить $\frac {dy}{dx}$ при любом (x,y).
Как получить этот результат?
Дифференцировать F(x,y)= 0 ; Суммарный дифференциал
$$ F_x dx + F_y dy = 0.$$
Чтобы проверить вычислением в любой точке, удерживайте x постоянным и вычисляйте $F_y $ дифференциал так, как вы указали, затем сохраняйте y постоянным и вычисляйте $ F_x $ то же самое кстати, используйте (1*).
$\endgroup$
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя адрес электронной почты и пароль
Опубликовать как гость
Электронная почта
Обязательно, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается 9y$ нам нужно знать, что функция $y$ имеет a
производная. y}\cr
}$$
$\квадрат$
9y=x$ для $y$, поэтому, возможно, после взятия производной мы получим
то, что трудно решить за $y’$. На самом деле это никогда
бывает. Все вхождения $y’$ происходят из применения цепного правила,
и всякий раз, когда используется цепное правило, он вносит один $y’$
умножить на какое-то другое выражение. Так что всегда можно будет
сгруппируйте термины, содержащие $y’$ вместе, и вынесите $y’$ на множители, просто
как в предыдущем примере. Если у вас когда-нибудь возникнет что-то более сложное
вы допустили ошибку и должны исправить ее, прежде чем пытаться продолжить.
y}\cr
}$$
$\квадрат$
9y=x$ для $y$, поэтому, возможно, после взятия производной мы получим
то, что трудно решить за $y’$. На самом деле это никогда
бывает. Все вхождения $y’$ происходят из применения цепного правила,
и всякий раз, когда используется цепное правило, он вносит один $y’$
умножить на какое-то другое выражение. Так что всегда можно будет
сгруппируйте термины, содержащие $y’$ вместе, и вынесите $y’$ на множители, просто
как в предыдущем примере. Если у вас когда-нибудь возникнет что-то более сложное
вы допустили ошибку и должны исправить ее, прежде чем пытаться продолжить.
Иногда бывает так, что ситуация естественным образом приводит к уравнение, которое неявно определяет функцию.
Пример 4.8.3
Рассмотрим все точки $(x,y)$, обладающие тем свойством, что
расстояние от $(x,y)$ до $\ds (x_1,y_1)$ плюс расстояние
от $(x,y)$ до $\ds (x_2,y_2)$ равно $2a$ ($a$ — некоторая константа). Эти
точки образуют эллипс, который, как и окружность, не является функцией, но может
рассматривается как две функции, склеенные вместе. 2}=2a.$$
Затем мы можем использовать неявное дифференцирование, чтобы найти наклон кривой.
эллипс в любой точке, хотя вычисления довольно беспорядочны.
$\квадрат$
92$
(отвечать)
2}=2a.$$
Затем мы можем использовать неявное дифференцирование, чтобы найти наклон кривой.
эллипс в любой точке, хотя вычисления довольно беспорядочны.
$\квадрат$
92$
(отвечать)
Пример 4.8.4 $\ds 4\cos x \sin y = 1$ (отвечать)
Пример 4.8.5 $\ds\sqrt{x} + \sqrt{y} = 9$ (отвечать)
Пример 4.8.6 $\ds \tan(x/y) = x+ y$ (отвечать)
Пример 4.8.7 $\ds\sin(x+y)=xy$ (отвечать)
Пример 4.8.8 $\ds{1\над х} + {1\над у} = 7$ (отвечать)
Пример 4.8.9 Гипербола, проходящая через $(8,6)$, состоит из всех точек, расстояние до которых от начала координат постоянная больше, чем его расстояние от точки (5,2). Найдите наклон касательной к гиперболе в точке $(8,6)$. (отвечать) 92 = 9$ — эллипс. Найдите прямые, касающиеся этой кривой в двух точках. точки пересечения с осью $x$. Покажите, что эти линии параллельно. (отвечать)
Пример 4.8.13 Повторите предыдущую задачу для точек, в которых
эллипс пересекает ось $y$.

 3
3 14159..
14159.. Получим , или . Если решить эту систему формулам Крамера относительно производных
и , то формулы для них будут иметь
вид
Получим , или . Если решить эту систему формулам Крамера относительно производных
и , то формулы для них будут иметь
вид




 dy/dx = cosx
dy/dx = cosx