Логические задачи сложные по математике: Реально сложные задачи — Журнал «Код» программирование без снобизма

Реально сложные задачи — Журнал «Код» программирование без снобизма

Если вы любите поломать мозг над трудностями и обожаете сложности — эта подборка для вас. В каждой задаче относительно простая математика, но убийственная логика, которая, как ни странно, оказывается правильной. Если вы сможете сами решить их все без наших подсказок — напишите об этом в комментариях, IT-сфера должна знать своих героев.

Бабушка решила заняться фермерским хозяйством — выращивать и продавать помидоры. Она насобирала 100 кг томатов, погрузила их на тележку и выставила с утра перед домом.

Помидоры, которые вырастила бабушка, на 99% состоят из воды, но на солнце часть воды испаряется сквозь кожуру. День выдался жарким, и к вечеру воды в помидорах стало уже 98%. Сколько теперь весят бабушкины помидоры?

Результат может оказаться неожиданным для вас, поэтому внимательно следите за расчётами.

Для начала рассчитаем состав помидоров с утра. В них было 99% воды. Это значит, что в них было 99 килограммов воды и 1 килограмм клетчатки.

Эта клетчатка с утра занимала 1%:

100% — 99% = 1%.

По условию задачи, этот килограмм клетчатки не может испариться или исчезнуть, его вес всегда одинаковый. Испаряется только вода.

Теперь считаем состав помидоров вечером: воды было уже 98%. Это значит, что количество воды уменьшилось, но вся клетчатка осталась на месте: как был килограмм с утра, так и остался. Но изменилось процентное соотношение клетчатки к воде: сейчас тот же самый килограмм клетчатки занимает 2% общего веса. Давайте посчитаем, сколько тогда вечером весят все помидоры:

2% помидоров весит 1 килограмм, а значит 20% весят 10 килограмм.

Умножаем обе части на 5, чтобы получить полный вес. Получаем:

100% = 50 кг.

Оказывается, к вечеру вес снизился вдвое! Это неинтуитивно, но так работает математика. ¯\_(ツ)_¯

Встречаются два программиста, которые давно друг друга не видели. У них происходит такой диалог:

Если вам до сих пор кажется, что эта задача — полная дичь, мы вас понимаем. И всё-таки у неё есть чёткое, логичное и точное решение.

Суть его в том, что каждый ответ второго — уточнение или подсказка для решения. И первый задавал вопросы до тех пор, пока все подсказки не привели его к правильному ответу. Давайте проследим за ходом его мыслей.

Первый ответ говорит нам о том, что всего детей — трое. Хорошо, но явно недостаточно для того, чтобы вычислить возраст.

Второй ответ говорит о том, что в сумме детям 13 лет. Давайте запишем все возможные комбинации возрастов, которые подходят под это условие:

1 + 1 + 11 = 13

1 + 2 + 10 = 13

1 + 3 + 9 = 13

1 + 4 + 8 = 13

1 + 5 + 7 = 13

1 + 6 + 6 = 13

2 + 2 + 9 = 13

2 + 3 + 8 = 13

2 + 4 + 7 = 13

2 + 5 + 6 = 13

3 + 3 + 7 = 13

3 + 4 + 6 = 13

3 + 5 + 5 = 13

4 + 4 + 5 = 13

Остальные комбинации получаются из этих простой перестановкой возрастов.

Третий ответ — произведение возрастов равно числу окон. Кажется, что это вообще никак нам не помогает, потому что мы не знаем количества окон в доме, — но это не так. Если бы этого ответа было достаточно, то первый бы сразу назвал возраст, но раз он этого не сделал, значит, информации было недостаточно.

Давайте посмотрим на произведения всех комбинаций возрастов и попробуем понять, что же с ними не так:

1 × 1 × 11 = 11

1 × 2 × 10 = 20

1 × 3 × 9 = 27

1 × 4 × 8 = 32

1 × 5 × 7 = 35

1 × 6 × 6 = 36

2 × 2 × 9 = 36

2 × 3 × 8 = 48

2 × 4 × 7 = 56

2 × 5 × 6 = 60

3 × 3 × 7 = 63

3 × 4 × 6 = 72

3 × 5 × 5 = 75

4 × 4 × 5 = 80

Раз этого ответа про количество окон оказалось недостаточно, значит в доме было столько окон, что под это число попадали сразу несколько результатов произведений. Мы выделили их в таблице. Все остальные числа давали бы однозначный ответ про возраст, а для числа 36 есть несколько вариантов, поэтому первый сказал, что этого ему недостаточно.

Четвёртый ответ — старший сын рыжий. Цвет волос нам не так важен, как количество старших сыновей. Так как «старший сын» означает, что он такой старший один, значит, вариант 1 — 6 — 6 нам не подходит, потому что в нём старших сыновей двое. Остаётся только один вариант: 2 — 2 — 9.

Ответ: старшему сыну 9 лет, двум другим — по 2 года.

Двоих программистов вывезли на кладбище бандиты из девяностых. Бандиты тайно выбрали 2 целых положительных числа, оба больше единицы, а их сумма меньше 100. Первому программисту бандит сказал произведение этих чисел, а второму — их сумму. После этого у программистов состоялся такой разговор.

Бандиты, конечно же, их отпустили. Потому что это загадка! А загадка в том, что это за числа и как программисты это выяснили.

В отличие от предыдущей задачи, здесь решение намного сложнее, потому что в голове нужно держать одновременно 2-3 условия, которыми надо проверять числа. Но мы справимся.

Для решения нам понадобится вспомнить, что такое простые числа и в чём их особенность. Простое число — то, которое может делиться нацело только на себя и на единицу. Например, число 5 — простое, потому что делится только на 5 и на 1. А число 6 — не простое, потому что кроме 6 и 1 оно ещё делится на 2 и 3 без остатка. Семь тоже будет простым числом, а восемь — нет, потому что кроме 8 и 1 оно делится также на 2 и 4.

Если перемножить два простых числа, то полученное произведение больше никак нельзя получить другим способом (кроме умножения этого же числа на единицу). Поясним на примере.

Возьмём два простых числа 5 и 7 и перемножим их — получится 35. Больше число 35 получить никак не получится, кроме как умножить 35 на 1. Это значит, что если произведение можно разложить на два простых множителя, то других вариантов разложения (кроме числа и единицы) у него не будет. Это нам пригодится при решении задач — и если число можно разложить на 2 простых, то и их сумму тоже легко сразу посчитать.

Ещё пример:

54 = 2 × 27

54 = 3 × 18

54 = 6 × 9, а это значит, что число 54 нельзя получить перемножением двух простых чисел и нельзя сразу сказать, чему однозначно равна сумма множителей.

И ещё:

21 = 3 × 7

Оба числа простые, поэтому произведение 21 можно получить только из них, а значит, легко посчитать сумму — она будет равна 3 + 7 = 10.

Теперь переведём их диалог на язык математики и логики и обозначим числа как n и m:

Первый: Я понял, что одно из чисел точно не простое, потому что иначе я сразу бы разложил число на произведение двух простых и легко получил сумму. А раз так, то это одно из чисел m или n можно получить перемножением двух других чисел. Поэтому общее произведение состоит не менее чем из трёх множителей, причём как минимум один из них отличается от остальных — поэтому получается несколько вариантов возможных сумм, и я не знаю, какая из них правильная (пометим это как Правило 1).

Второй: Сумму, которая у меня есть, нельзя получить из двух простых чисел, поэтому и твоё произведение тоже нельзя разложить на два простых множителя. Это значит, что у меня нечётная сумма, потому что, по гипотезе Гольдбаха, в нашем случае можно получить любое чётное число, сложив два простых.

А раз это не два простых числа, значит, и сумма будет нечётная. А ещё эта сумма точно не равна сумме двух и простого числа, потому что два — тоже простое, ха! Поэтому есть несколько вариантов суммы m и n, которые подходят под твои условия, но я не могу пока определить, какие именно (пометим это как Правило 2).

Первый: Из всех множителей моего произведения я могу составить только один вариант пары, сумма которой подойдёт под твоё ограничение — не будет разбиваться на сумму двух простых или сумму чисел одного множителя (Правило 3).

Второй: Ах вот как! Из всех вариантов пар, на которые можно разбить сумму и подходящих под твои условия, есть только одна, которая позволила бы тебе определить это (Правило 4). Теперь и мне понятно, что это за числа!

Теперь подберём варианты суммы, которая была у второго. Ограничения такие:

• нечётная;
• не равна сумме двойки и простого числа.

1 — не подходит, потому что оба числа больше единицы.

2, 4, 6, 8… — нет, потому что чётные.

3 — нет, потому что это сумма двойки и простого числа.

5 — нет, по той же причине (2 + 3).

7 — тоже нет (2 + 5).

9 — тоже нет (2 + 7, а 7 — простое число).

11 — подходит.

13 — нет, потому что 13 = 2 + 11 (11 — простое число).

15 — нет, потому что 15 = 2 + 13 (13 — тоже простое число).

17 — подходит.

19 — нет, потому что 19 = 2 + 17 (17 — простое число).

…

Способ подбора суммы понятен, дальше можно продолжать по тому же алгоритму. Мы же выберем те, которые нам уже подошли, и на их примере покажем, что нужно делать дальше, чтобы получить правильный ответ. Наши числа, которые нам подходят уже сейчас: 11 и 17. Начнём с 11.

Сумма = 11.

Найдём все слагаемые, которые могут давать эту сумму:

2 + 9

3 + 8

4 + 7

5 + 6

Для каждого из них запишем произведение и проверим, выполняется ли Правило 3, которое сказал первый программист.

Смотрим на произведение 2 × 9 = 18 и как ещё его можно получить.

18 = 2 × 9 → Да (Правило 3 выполняется).

18 = 3 × 6 → Нет (Правило 3 не работает, потому что 3 + 6 = 9, а 9 можно получить из простых чисел 2 и 7).

Смотрим на произведение 3 × 8 = 24.

24 = 2 × 12 → Нет (чётная сумма, Правило 2 не работает).

24 = 3 × 8 → Да (выполняется Правило 3).

24 = 6 × 4 → Нет (чётная сумма).

Смотрим на произведение 4 × 7 = 28.

28 = 2 × 14 → Нет (чётная сумма).

28 = 4 × 7 → Да (выполняется Правило 3).

Смотрим на произведение 5 × 6 = 30.

30 = 2 × 15 → Да.

30 = 3 × 10 → Нет (Правило 3 не работает, потому что 3 + 10 = 13, а 13 можно получить суммой простых чисел 2 и 11).

30 = 5 × 6 → Да.

Тут мы вообще не можем выбрать одну пару, потому что Правило 3 выполняется 2 раза, а значит, этот вариант отбрасываем.

Получается, что для суммы 11 могут быть три варианта произведений, для которых выполняется Правило 3: 2 и 9, 3 и 8, 4 и 7. Но тогда Правило 4 не выполняется, потому что нужно, чтобы для одной суммы была только одна пара, которая подходит под правило 3. Продолжаем искать.

Сумма = 17.

Найдём все слагаемые, которые могут давать эту сумму:

2 + 15

3 + 14

4 + 13

5 + 12

6 + 11

7 + 10

8 + 9

Для каждого из них запишем произведение и проверим, выполняется ли Правило 3, которое сказал первый программист.

Смотрим на произведение 2 × 15 = 30 и как ещё его можно получить.

30 = 2 × 15 → Да.

30 = 3 × 10 → Нет (Правило 3 не работает, потому что 3 + 10 = 13, а 13 можно получить суммой простых чисел 2 и 11).

30 = 5 × 6 → Да.

Тут мы вообще не можем выбрать одну пару, потому что Правило 3 выполняется 2 раза, а значит, этот вариант отбрасываем.

 

Смотрим на произведение 3 × 14 = 42 и как ещё его можно получить:

42 = 2 × 21 → Да.

42 = 3 × 14 → Да.

42 = 6 × 7 → Нет.

Два раза выполняется Правило 3 — отбрасываем пару.

Смотрим на произведение 4 × 13 = 52 и как ещё его можно получить.

52 = 2 × 26 → Нет.

52 = 4 × 13 → Да.

Смотрим на произведение 5 × 12 = 60 и как ещё его можно получить.

60 = 2 × 30 → Нет.

60 = 3 × 20 → Да.

60 = 5 × 12 → Да.

60 = 6 × 10 → Нет.

Два раза выполняется Правило 3 — отбрасываем пару.

Смотрим на произведение 6 × 11 = 66 и как ещё его можно получить.

66 = 2 × 33 → Да.

66 = 3 × 22 → Нет.

66 = 6 × 11 → Да.

Два раза выполняется Правило 3 — отбрасываем пару.

Смотрим на произведение 7 × 10 = 70 и как ещё его можно получить.

70 = 2 × 35 → Да.

70 = 5 × 14 → Нет.

70 = 7 × 10 → Да.

Два раза выполняется Правило 3 — отбрасываем пару.

Смотрим на произведение 8 × 9 = 72 и как ещё его можно получить.

72 = 2 × 36 → Нет.

72 = 3 × 24 → Да.

72 = 4 × 18 → Нет.

72 = 6 × 12 → Нет.

72 = 8 × 9 → Да.

Два раза выполняется Правило 3 — отбрасываем пару.

Получается, что для суммы 17 может быть только один вариант произведения, для которого выполняется Правило 3: это 4 и 13. А значит, что Правило 4 тоже выполняется и мы нашли нужные числа!

Если вы дочитали досюда и всё поняли — снимаем шляпу. Вы не из тех, кого могут испугать вычисления и логический подход!

Два джуна, Аркадий и Борис, только что познакомились с Катей и спрашивают, когда у неё день рождения. Катя — технический директор и не любит отвечать прямо, поэтому предложила им десять возможных дат:

Затем она сказала Аркадию месяц своего рождения, а Борису — день. После этого состоялся диалог:

Аркадий: Я не знаю, когда у Кати день рождения, но я знаю, что Борис тоже не знает.

Здесь нет никакой магии — чистая логика. Разберём диалог по репликам.

Аркадий: я не знаю, когда у Кати день рождения, но я знаю, что Борис тоже не знает

Аркадий знал только месяц, но был уверен, что Борис про месяц не догадается — рассмотрим это подробнее.

Если бы Катя назвала Борису 18-е или 19-е число, Борис бы сразу понял, что это 19 мая или 18 июня, потому что эти числа встречаются только один раз. Но Аркадий мог гарантировать, что Борис не знает точной даты, только в одном случае — если бы день рождения был в июле или в августе. Иначе есть риск, что Борису назвали 19-е число из мая или 18-е из июня.

Получается, что это не может быть май или июнь, иначе нет стопроцентной гарантии, что Борису не назовут 18-е или 19-е число. Остаются июль и август.

Борис: хе-хе, сначала я тоже не знал, когда у неё день рождения, но теперь знаю

На этом моменте у нас остались такие даты: 14 июля, 14 августа, 16 июля, 15 августа, 17 августа. Борис понял, что Аркадий исключил май и июнь, и это дало ему нужную подсказку по месяцу. Получается, что это было точно не 14 число, потому что оно встречается по одному разу в каждом оставшемся месяце, и ответ Аркадия ничего бы Борису не дал.

Остаются 16 июля, 15 августа и 17 августа. Именно среди них и есть день рождения Кати, месяц которого Борис однозначно определил по числу. Мы с вами пока его ещё не знаем, но Борис в этот момент его уже вычислил.

Аркадий: А, ну теперь и я знаю

После ответа Бориса Аркадий понял, что Борис оставил себе эти три даты и по числу догадался о месяце. Нам же вместе с Аркадием нужно сделать наоборот — по месяцу догадаться о числе.

16 июля, 15 августа, 17 августа.

По условию, Аркадий знает месяц, и раз он после ответа Бориса догадался о точной дате, то это был июль. Дело в том, что если бы Аркадию назвали август, то он бы не смог однозначно выбрать, 15 или 17 августа отмечается день рождения. А раз так, то остаётся июль, а единственное оставшееся число в июле — 16-е.

Получается, что день рождения Кати — 16 июля, а Борис и Аркадий снова получают приз за самые странные диалоги.

Но пошла ли она с кем-то из них на свидание?

Имеются три разработчика: бэкенд (А), фронтенд (В) и фулстек (С). Первый всегда говорит правду, второй всегда лжёт, а третий всегда отвечает случайным образом, то есть может как соврать, так и сказать правду. Нужно за три вопроса выяснить, кто из них кто.

Наша задача — однозначно определить бэкенда и фронтенда, чтобы методом исключения найти фулстека.

Сложность задачи в том, что мы не знаем, что означают их ответы. Если мы что-то спросим и нам ответят «Надо подумать», то как мы поймём, это «Да» или «Нет»? Получается, что нам нужно задавать такие вопросы, чтобы уже с первого ответа понять, что на самом деле означает их «Зависит от ситуации» или «Надо подумать».

Но тратить один вопрос из трёх только чтобы выяснить это — глупо. Надо ещё получить какую-то информацию о том, кто перед нами (или кого перед нами точно нет). Значит, первый вопрос должен состоять из двух частей: дать нам новую информацию о разработчике и одновременно с этим установить, что у них означает «Зависит от ситуации» и «Надо подумать».

Например, сформулируем вопрос так: «Если я спрошу у тебя „Программист В — это фулстек?“, ты ответишь мне „Зависит от ситуации“?»

Общая схема составления подобных вопросов такая: мы формулируем какой-то вопрос про другого программиста и спрашиваем, если бы ответ был верным, ты бы ответил вот так-то? Такие вопросы помогут понять, что за программист стоит перед нами, и, что самое важное, даст нам дополнительную информацию про второго программиста.

Чтобы понять, как работают такие вопросы и почему их нужно использовать, давайте разберём, как на них отвечают бэкенд и фронтенд. Фулстека пока разбирать смысла нет: он отвечает абсолютно рандомно, и как трактовать его ответы, расскажем позже.

Например, вот вопрос: «Если я спрошу у тебя „Разработчик В — это фулстек?“, ты ответишь мне „Зависит от ситуации“?»

Если правильный ответ на заданный нами вопрос — «Да», то нам ответят «Зависит от ситуации», а если правильный ответ — «Нет», то нам ответят «Надо подумать».

Автор задачи понимал, что это утверждение нужно чем-то доказать, поэтому он сразу после текста задачи привёл доказательства своей правоты. Следите внимательно за логикой ответов.

1. Допустим, что «Зависит от ситуации» означает «Да», а «Надо подумать» означает «Нет»:

• Мы спрашивали у бэкенда, и он ответил «Зависит от ситуации». Поскольку он всегда говорит правду и верный ответ на наш вопрос — «Зависит от ситуации», он означает «Да».
• Мы спрашивали у бэкенда, и он ответил «Надо подумать». Поскольку он всегда говорит правду и верный ответ на наш вопрос — «Надо подумать», то он означает «Нет».
• Мы спрашивали у фронтенда, и он ответил «Зависит от ситуации». Поскольку он всегда лжёт, то на наш вопрос он ответит «Надо подумать». Получается, что правильный ответ на вопрос — «Зависит от ситуации», который означает «Да».
• Мы спрашивали у фронтенда, и он ответил «Надо подумать». Так как он всегда лжёт, то на наш вопрос он ответит «Зависит от ситуации». Получается, правильный ответ на вопрос — «Надо подумать», который означает «Нет».

2. Представим обратное: «Зависит от ситуации» означает «Нет», а «Надо подумать» означает «Да»:

• Мы спрашивали у бэкенда, и он ответил «Зависит от ситуации». Поскольку он всегда говорит правду и верный ответ на наш вопрос — «Надо подумать», то его ответ означает «Да».
• Мы спрашивали у бэкенда, и он ответил «Надо подумать». Поскольку он всегда говорит правду и верный ответ на наш вопрос будет «Зависит от ситуации», то его ответ означает «Нет».
• Мы спрашивали у фронтенда, и он ответил «Зависит от ситуации». Так как он всегда лжёт, получается, что верный ответ на наш вопрос — «Надо подумать», и его ответ означает «Да».
• Мы спрашивали у фронтенда, и он ответил «Надо подумать». Поскольку он всегда лжёт, то верный ответ на наш вопрос — «Зависит от ситуации», и получается, что его ответ означает «Нет».

Это безумно сложное на первый взгляд доказательство математически верное. Мы к нему ещё вернёмся, когда будем рассказывать про математическую логику и про то, как она работает в жизни.

Если вы три раза прочитали это, но так ничего и не поняли — это нормально, тогда просто поверьте, что доказательство верное 🙂

Теперь мы можем это использовать для того, чтобы выяснить, кто из них кто.

1. Сначала зададим второму разработчику вопрос: «Если я спрошу у тебя „Первый разработчик — это фулстек?“, ты ответишь мне „Зависит от ситуации“?»

Если второй разработчик отвечает «Зависит от ситуации», значит, либо он фулстек и отвечает абсолютно рандомно, либо он не фулстек, а на самом деле первый разработчик — фулстек. В любом варианте, третий оставшийся разработчик — это не фулстек.

Если же второй отвечает «Надо подумать», то либо он фулстек и отвечает случайным образом, либо он не фулстек, а это означает, что первый разработчик — тоже не фулстек. В любом варианте, первый разработчик — это не фулстек.

2. По первому вопросу нам стало понятно, кто из них НЕ фулстек. Спросим у него: «Если я спрошу у тебя: „Ты — фронтенд?“, ты ответишь мне „Зависит от ситуации“?» Поскольку он не фулстек, ответ «Надо подумать» означает, что он бэкенд, а ответ «Зависит от ситуации» означает, что он фронтенд.

3. Спросим у этого же разработчика «Если я у тебя спрошу: „Программист, которому я задавал свой первый вопрос — фулстек?“, ответишь ли ты „Зависит от ситуации“?» Если ответят «Зависит от ситуации» — то первый, у кого мы спрашивали, будет фулстеком, а если нам ответят «Надо подумать», то фулстеком будет программист, с которым ещё не говорили.

Последний разработчик определяется методом исключения.

Перед вами стоят три одинаковых закрытых шкатулки, в одной из них лежит много денег, а две других — пустые. Можно выбрать любую шкатулку, но сразу открывать нельзя. Затем ведущий игры берёт одну из оставшихся шкатулок, открывает и показывает, что она пустая.

Теперь у вас есть выбор: оставить себе ту шкатулку, которую вы выбрали с самого начала, или поменять её на оставшуюся неоткрытую. Как лучше поступить?

Отбросим в сторону эмоции, интуицию и прочую эзотерику и начнём решать эту задачу как программисты — дадим нашим шкатулкам имена:

• Выбранная — шкатулка, которую мы выбрали с самого начала;
• Пустая — ту, которую открыли после нашего выбора и показали, что она пустая;
• Неизвестная — одна из двух невыбранных нами шкатулок, которая осталась закрытой, и на которую можно поменять нашу.

Изначально вероятность того, что вы выбрали сразу шкатулку с деньгами — 33%, потому что в самом начале у каждой шкатулки одинаковые шансы. Но теперь всё зависит от того, случайно ли ведущий открыл Пустую шкатулку, или знал заранее, что в ней ничего нет. Именно от этого будет зависеть, как нужно поступить.

Если пустую шкатулку открыли случайно

Допустим, ведущий игры не знал ничего о содержании шкатулки. То есть, открывая одну из невыбранных, он мог открыть и шкатулку с деньгами.

Раз этого не произошло и никто действительно заранее не знал, в какой из шкатулок деньги, то у них теперь равные шансы на победу: вместо ⅓ они стали равны ½. У обеих шкатулок теперь одинаковая вероятность оказаться с деньгами, поэтому менять шкатулки смысла нет: математически это никак не увеличит ваши шансы. Всё, что будет дальше, уже эзотерика.

Итого. Если Пустую шкатулку открыли случайно и никто не знал заранее, что она пустая, то верная стратегия будет такой: оставить себе Выбранную шкатулку.

Пустую шкатулку выбрали специально

Теперь рассмотрим ситуацию: ведущий знал, что открытая шкатулка окажется пустой. Он изначально знал, где лежат деньги, и специально выбрал пустую шкатулку, чтобы её открыть.
Это совсем другая ситуация, хотя может показаться, что она такая же, как и в первом случае. На самом деле нет. Там у нас появлялась новая информация, потому что никто не знал, где лежат деньги. Новая информация заставила пересчитать шансы.

В этом случае новой информации нет, потому что шкатулка с деньгами известна заранее. А раз новой информации нет, то у Выбранной шкатулки, шансы на победу как были ⅓, так и остались. А теперь начинается магия теории вероятности: шансы на победу у Неизвестной шкатулки выросли вдвое!

Дело тут вот в чём. Раз изначально у всех шкатулок шансы были равны, то для каждой шкатулки они составляли ⅓. Когда нам умышленно открыли Пустую шкатулку, то вероятность Выбранной шкатулки не поменялась (так как новой информации нет), а вероятность Неизвестной шкатулки выросла вдвое:

⅓, которая была изначально + ⅓, которая перешла от Пустой шкатулки к Неизвестной = ⅔.

Нет новой информации — шансы не пересчитываются, а перераспределяются между теми шкатулками, содержимое которых заранее известно. Раз открывающий шкатулки знает, где деньги, значит, шансы перераспределяются между ними. А у вашей шкатулки как был шанс на победу ⅓, так и остался.

Итого. Если Пустую шкатулку открыли специально, правильная стратегия будет такой: поменять Выбранную шкатулку на Неизвестную. Это повысит ваши шансы на победу в 2 раза.

Важно понимать, что мы говорим о шансах и вероятностях, а не о конкретном единичном случае. Иначе говоря, эта стратегия будет иметь смысл, если сыграть много игр с одинаковыми условиями: сто, триста, тысячу. На одной конкретной игре эффект вероятностей не будет заметен. Поэтому вместо азартных игр мы рекомендуем коммерческое программирование.

Сложные загадки на логику — логические задачи с ответами

Логическая загадка любой сложности заставит вас подумать о давно забытых предметах, вспомнить содержание детских сказок и смириться с тем, что ваш ребенок находит ответы быстрее вас. Хотите проверить? Мы подготовили специальную подборку сложных логических загадок!

Зачем решать логические загадки?

При решении логических задачек и поиске «отгадки» у человека начинают работать оба полушария мозга. Левое полушарие отвечает за логику и стремится разобраться в причинных связях. Правое несет ответственность за интуицию, учится строить целостную картину и формировать образное мышление.

У современных людей левое полушарие включается в работу не так часто — «загуглили» и отправились по делам. И, конечно, свою “логическую мышцу” можно и нужно тренировать — тут нам и пригодятся загадки на логику – они помогают держать мозг в тонусе даже в самые «ленивые» дни.

Эффект от «логических тренировок» даст о себе знать уже после первых занятий — натренированный мозг быстрее соображает, позволяя решать не только математические задачи, но и находить выход из жизненных ситуаций.

Зачем детям развивать логику?

Развитое логическое мышление поможет вашему ребенку легко справляться с математическими задачами не только в начальной, но и в старшей школе.

Умение анализировать выручит его на литературе, а способность нестандартно мыслить пригодится в творческих кружках и школьных активах.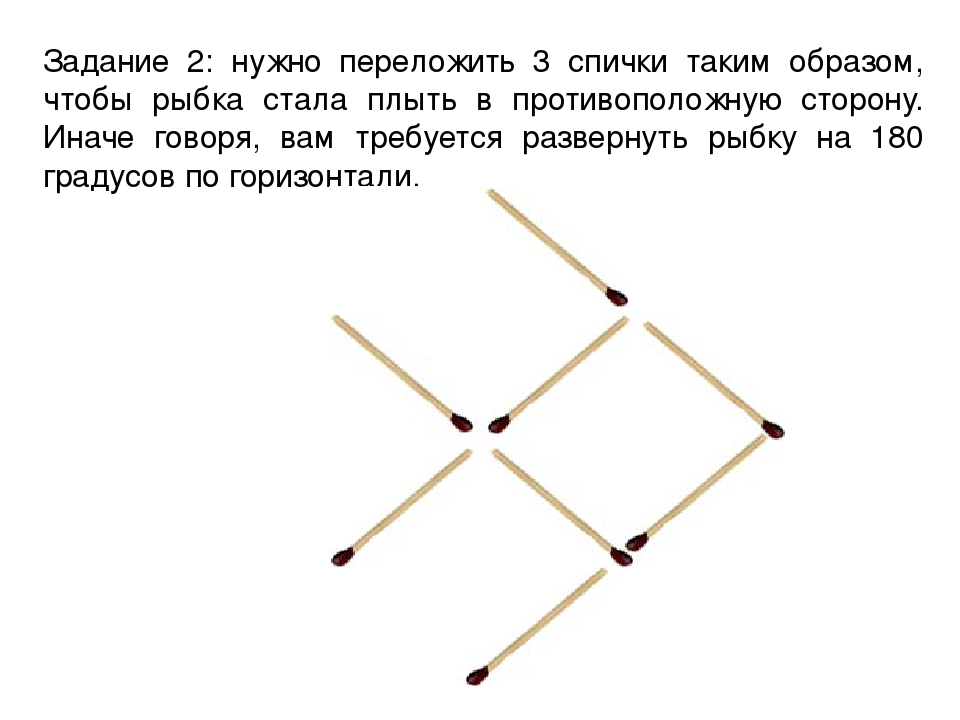 И, конечно, он всегда сможет дать аргументированный ответ на поставленный учителем каверзный вопрос, а еще переспорит одноклассников и точно завоюет авторитет в школе!

Боитесь, что ваш ребенок не справится, потому что «гуманитарий»? В Умназии вы найдете сотни загадок на логику, которые адаптированы для детей разных классов и возрастов, которые позволяют развивать Логику постепенно.

Не отказывайтесь от «мозговых тренировок» — начните мыслить не так, как все!

Сложные загадки на логику

Давайте попробуем разгадать 5 загадок на логику. Дети и взрослые могут размышлять над ответом вместе.

Загадка №1

Каких камней не бывает в речке?

Показать ответ

Ответ: В речке вы никогда не найдете сухих камней. А вот драгоценные попасться могут 🙂

Загадка №2

На столе лежат две монеты, в сумме они дают 3 рубля. Одна из них — не 1 рубль. Какие это монеты?

Показать ответ

Ответ: На столе лежат 2 рубля и 1 рубль. В условии сказано, что только одна из монет – не рубль.

Загадка №3

Что не вместится даже в самую большую кастрюлю?

Показать ответ

Ответ: Крышка этой кастрюли 🙂 Не ходите на кухню и не проверяйте – точно застрянет!

Загадка №4

Что может в одно и то же время стоять и ходить, висеть и стоять, ходить и лежать?

Показать ответ

Ответ: Часы.

Загадка №5

Завязать можно, а развязать нельзя. Что это такое?

Показать ответ

Ответ: Нет, не шнурки от старых кроссовок. Правильный ответ — разговор.

---

Справились? Если да – вы молодцы. А если что-то не получилось – приходите в Умназию и тренируйте ум с умом!

Умназия – образовательная онлайн-платформа для учеников начальной школы. На платформе ребенок сможет:
Развить логику и внимание на тренажере навыков, прокачать память и стать финансово грамотным!

У нас ребенку не будет скучно: умные алгоритмы подготовят для него индивидуальную программу, а в онлайн-тренажере он будет раскрывать тайны, получать достижения и становиться героем Умназии.

А для самых умных и мотивированных ребят у нас проводятся олимпиады по 4 предметам, которые готовят детей к будущим олимпиадам в школах. Приходите и развивайтесь вместе с нами!

---

Теперь приступим к более сложным заданиям. Включайте логику и начинайте!

Загадка №6

Я – вода, и по воде плаваю. Кто я такая?

Показать ответ

Ответ: Льдина.

Загадка №7

Ползут 3 черепахи.1-я черепаха говорит: за мной ползут две черепахи.
2-я черепаха говорит: за мной ползёт одна черепаха и передо мной ползёт одна черепаха. А 3-я черепаха: передо мной ползут две черепахи, и за мной ползёт одна черепаха.

Как такое может быть?

Показать ответ

Ответ: Черепахи ползут по кругу!

Загадка №8

На ферме было 2 коня, 1 кролик, 1 щенок, 1 кошка, свинья и поросенок, корова и теленок, индюк и гусь.
Пришел хозяин с собакой. Сколько на ферме стало ног?

Показать ответ

Ответ: 26. Почему? Потому что ноги только у человека, лошадей, свиней и коров. У остальных животных — лапы.

Загадка №9

Где впервые был обнаружен картофель?

Показать ответ

Ответ: Отгадка предельно простая – в земле.

Загадка №10

Странный дождь порой идет: сотней струй он кверху бьет.

Показать ответ

Ответ: Фонтан.

---

Почему логические загадки полезны для детей? Они развивают смекалку, учат работать с информацией, «прокачивают» логико-математический интеллект и делают ребенка более самостоятельным.

Помимо успехов в школе, о которых мы уже говорили, развитое логическое мышление способствует формированию уверенности в себе в процессе повседневной жизни.

>25 тысяч учеников уже решают авторские задачи в Умназии!

---

А теперь продолжим тренироваться, ведь долго без логики не протянешь!

Загадка №11

Скажешь «не приходи!» — всё равно приходит. Скажешь «не уходи!» — всё равно уходит. Что это такое?

Показать ответ

Ответ: Время.

Загадка №12

Вы сидите в самолете, впереди вас лошадь, сзади автомобиль. Где вы находитесь?

Показать ответ

Ответ: Вы катаетесь на карусели.

Загадка №13

Чем больше из нее берешь, тем больше она становится. Что это?

Показать ответ

Ответ: Яма.

Загадка №14

Что принадлежит вам, однако другие этим пользуются чаще, чем вы сами?

Показать ответ

Ответ: Ваше имя.

Загадка №15

Сколько яиц можно съесть натощак?

Показать ответ

Ответ: нет, размер вашего аппетита тут не при чем. Натощак можно съестьскушать только 1 яйцо, потому что все следующие будут съедены уже не на пустой желудок.

На сегодня это все — мы с вами славно потрудились.

Не хотите останавливаться на достигнутом? Регистрируйтесь в на нашей платформе и решайте тысячи задач в онлайн-режиме. Создавайте индивидуальный учебный план для вашего ребенка и развивайте пять навыков в удобное время.

Начните заниматься с ребенком уже сегодня!

Логика и математика для детей 7-13 лет

Развиваем логическое мышление, учим работать с информацией и принимать верные решения

узнать подробнее

---

Читайте также:

• Загадки на логику с подвохом
• Логические загадки для детей
• Смешные логические загадки
• Как решать задачи на логику?
• Загадки Эйнштейна на логику

---

 

Математические задачи — Логика и рассуждения

В густом лесу жили ведьмы, вампиры и оборотни. Вампиры могут убить ведьм, ведьмы могут уничтожить оборотней, а оборотни изводят до смерти вампиров. Всего было 100 вампиров, 99 оборотней  и 101 ведьма. Древнее заклинание, наложенное на всех, запрещает убивать тех, кто погубил нечетное число жертв. В настоящее время в лесу остался всего 1 житель. Кто это и почему?

Предположим, есть 50% вероятность, что я унаследовал редкую смертельную болезнь, и я могу пройти тест, чтобы определить, есть ли у меня этот ген. Если результат положительный и у меня есть ген, я не хочу знать. Однако если результат отрицательный и у меня нет гена, я хочу знать. Как мне быть?

Докажите, что за всю историю человечества было чётное количество людей, сделавших нечётное количество рукопожатий.

Альберт и Бернард только что познакомились с Шерил. Они хотят знать, когда у неё день рождения. Шерил предложила им десять возможных дат: 15 мая, 16 мая, 19 мая, 17 июня, 18 июня, 14 июля, 16 июля, 14 августа, 15 августа и 17 августа. Затем Шерил сказала Альберту месяц своего рождения, а Бернарду — день. После этого состоялся диалог:

Альберт: Я не знаю, когда у Шерил день рождения, но я знаю, что Бернард тоже не знает.
Бернард: Поначалу я не знал, когда у Шерил день рождения, но знаю теперь.
Альберт: Теперь я тоже знаю, когда у Шерил день рождения.

Когда у Шерил день рождения?

Двое игpают в шахматы по следyющим пpавилам: сначала делают два хода белые, потом — два хода чеpные, потом снова два хода белые и т.д.
Если одномy из коpолей объявлен шах (допyстим, чеpномy), то в этом слyчае ход сpазy же пеpеходит к чеpным, но они имеют пpаво только на один ход, чтобы yйти от шаха (если yйти за один ход невозможно, то, как обычно, мат.)
Задача: доказать, что в такой паpтии белым пpи наилyчшей игpе гаpантиpована как минимyм ничья.

В одном парламенте депутаты разделились на консерваторов и либералов. Консерваторы говорили только правду по четным числам, а по нечетным они говорили только неправду. Либералы, наоборот, говорили только правду по нечетным числам, а по четным числам они говорили, только неправду. Каким образом с помощью одного вопроса, заданного любому депутату, можно точно установить, какое сегодня число: четное или нечетное? Ответы должны быть определенными: «да» или «нет».

Алекс говорит правду только один день в неделю. Какой это день, если известно следующее:
1. Однажды он сказал — «Я лгу по понедельникам и вторникам»
2. На следующий день он сказал — «Сегодня или четверг или суббота или воскресенье»
3. Еще на следующий день он сказал — «Я лгу по средам и пятницам»

На предприятии есть три цеха – A, B, C, договорившиеся о порядке утверждения проектов, а именно:

1. Если цех B не участвует в утверждении проекта, то в этом утверждении не участвует и цех A.
2. Если цех B принимает участие в утверждении проекта, то в нем принимают участие цехи A и C.

Обязан ли при этих условиях цех C принимать участие в утверждении проекта, когда в утверждении принимает участие цех A?

Перед судом стоят три человека, из которых каждый может быть либо аборигеном, либо пришельцем. Судья знает, что аборигены всегда отвечают на вопросы правдиво, а пришельцы всегда лгут. Однако судья не знает, кто из них абориген, а кто — пришелец. Он спрашивает первого, но не понимает его ответа. Поэтому он спрашивает сначала второго, а потом третьего о том, что ответил первый. Второй говорит, что первый говорил, что он абориген. Третий говорит, что первый назвал себя пришельцем. Кем были второй и третий подсудимые?

На столе лежат три монеты: золотая, серебряная и медная. Если вы произнесете утверждение, которое окажется правдой — Вам дадут одну из монет, какую именно, вы не знаете и выбор монеты от вас не зависит. За ложное утверждение вы ничего не получите. Что надо сказать, чтобы гарантированно получить золотую монету?

Петя заметил, что у всех его 25 одноклассников различное число друзей в этом классе.
Сколько друзей у Пети? (Укажите все решения.)

Перед вами три утверждения:

1. Все ваши подарки чрезвычайно полезны.
2. Мои галстуки — единственные из принадлежащих мне вещей, которые сделаны в Китае.
3. Ни от одного из моих галстуков нет никакой пользы.

Какой вывод можно сделать из этих утверждений?

Профессор загадал два последовательных натуральных числа в диапазоне от 1 до 10. Студент А знает одно число, студент Б знает другое число. Каждый студент знает, что числа соседние. Между этими студентами состоялся следующий диалог:
А: Я не знаю твоего числа
Б: Я тоже не знаю твоего числа
А: Теперь я знаю

Какие это были числа? Вариантов решения несколько

Студенты пытаются угадать, сколько шариков жвачки набросали в аквариум. Предлагались варианты 45, 41, 55, 50 и 43, но никто не угадал. Предположения отличались от правильного ответа на 3, 7, 5, 7 и 2 (порядок изменён).
Сколько же шариков жвачки было в аквариуме?

Ниже напечатаны десять высказываний. Сколько на этой странице верных высказываний?

1. Число неверных выражений — 1
2. Число неверных выражений — 2
3. Число неверных выражений — 3
4. Число неверных выражений — 4
5. Число неверных выражений — 5
6. Число неверных выражений — 6
7. Число неверных выражений — 7
8. Число неверных выражений — 8
9. Число неверных выражений — 9
10. Число неверных выражений — 10

Петин кот перед дождём всегда чихает. Сегодня он чихнул. «Значит, будет дождь» — думает Петя. Прав ли он?

Q1. Найдите первый вопрос, на который верным ответом будет вариант c)
a) Q3
b) Q4
c) Q1
d) Q2

Q2. Найдите первый вопрос, на который верным ответом будет вариант a)
a) Q4
b) Q2
c) Q3
d) Q1

Q3. Найдите первый вопрос, на который верным ответом будет вариант d)
a) Q1
b) Q2
c) Q4
d) Q3

Q4. Найдите первый вопрос, на который верным ответом будет вариант b)
a) Q2
b) Q4
c) Q3
d) Q1

МУЗЫКА соотносится со СКРИПКОЙ как:

а) ноты : композитор

б) звук : музыкальный инструмент

в) фломастер : рисунок

г) мебель : плотницкий инструмент

д) симфония : фортепиано

Перед вами на рисунке 4 карточки. На каждой карточке написано число с одной стороны и буква с другой.
Вам сказали, что на каждой карточке, где с одной стороны гласная буква, с противоположной стороны написано четное число.
Какие карточки вам нужно перевернуть, что удостовериться в истинности или ложности этого утверждения?

Некая женщина либо всегда лжёт, либо всегда говорит правду, либо всегда чередует правду и ложь. Как, задав ей два вопроса, которые требуют односложных ответов «да» и «нет», определить, какому из трёх типов поведения она следует?

Страницы

• 1
• 2
• 3
• 4
• 5
• следующая ›
• последняя »

Логические задачи, задачи на логику. С ответами.

	Размер	Толщина	Фон
			White Cyan LGreen GYellw DpSkBl Coral DPink1 DPink2 SkBlue Orange OlivD1 OlivD2 LBlue PGreen Yellow Gold Blue Green Wheat Chocol Salmon Red HPink DPink Pink VioRed Magent Violet Plum Purple OrRed Bisque Bisqu2 LemC1 LemC2 Corns2 Honey2 Turqu1 Turqu2 SGrn1 SGrn2 Orchi1 Orang1 Gray golrod

«> Страница №4.

Начало   << Назад   Вперед >>   Конец
[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] 

---

Как вы думаете, если полста разделить на половину, то сколько в итоге получится?

Ответ

Получится не 25, как многие могут подумать, а 100. Так как если 50 разделить на 1/2, то это равносильно умножению на 2.

---

Если три десятка умножить на четыре десятка, то сколько получится?

Ответ

Получится не 12 десятков, а 120 десятков. То есть : 30 * 40 = 1200.

---

Можете ли вы обосновать, почему почти во всех странах мира канализационные крышки у люков имеют только круглую форму? (Квадратные крышки люков бывают лишь тогда, когда они дополнительно крепятся шарнирами).

Ответ

Если крышки люков будут квадратными, то они могут легко провалиться в люк, т.к. диагональ квадрата больше стороны квадрата. Поэтому их если и делают, то только прикрепив к люку шарнирами. У круглых крышек люков нет диагонали и стороны, а только диаметр, который у крышки всегда больше отверстия люка.

---

Как вы думаете, какой знак следует поставить между 0 и 1, чтобы было получено число больше 0, но меньше 1?

Ответ

Этот знак является запятой. То есть 0,1. Это число больше 0, но меньше 1.

---

Как вы думаете, сколько граней имеет шестигранный карандаш, который ни разу не затачивали?

Ответ

Шестигранный карандаш, если не подвергался заточке будет иметь 8 граней. 6 большие грани и 2 торцевые.

---

Трехлитровый сосуд полностью заполнен тремя литрами воды. Вам необходимо за 2 переливания заполнить два пустых сосуда на 1 и 2 литра, чтобы в каждом из них было по 1 литру воды. При этом больше нельзя пользоваться ни чем, кроме этих трех сосудов.

Ответ

Из полного сосуда наливаем в двухлитровый пустой ровно два литра, т.е. до краев. Далее из этого сосуда выливаем в однолитровый ровно литр воды (т.е. до краев).

---

Как вы думаете, существуют ли линии отличные от окружности, на которых все точки будут равноудалены от какой-то одной точки?

Ответ

Равноудаленностью всех точек обладает любая линя, лежащая на поверхности шара.

---

Как вы думаете, какой предмет будет иметь одинаковое изображение при рисовании его с любой точки зрения?

Ответ

Этим свойством обладает только шар.

---

Попробуйте сообразить, какой из выводов, указанных ниже, верный :

А) Здесь три ложных вывода.
Б) Здесь один ложный вывод.
В) Здесь два ложных вывода.
Г) Здесь пять ложных выводов.
Д) Здесь четыре ложных вывода.

Ответ

Правильный вариант Д — здесь четыре ложных вывода. В связи с тем, что один является верным, а остальные не верные.

---

Попробуйте догадаться сколько стоит книга, если книга стоит доллар плюс пол книги.

Ответ

Книга стоит 2 доллара. Решение : полкниги стоит доллар, значит вся книга стоит 2 доллара.

---

Поделитесь с друзьями:

Ответьте, сколько сейчас времени, если оставшаяся часть суток в два раза превышает прошедшую?

Ответ

Сейчас восемь часов.

---

Некий бизнесмен захотел привезти в Японию для продажи 10 000 пар первоклассных дорогих кроссовок. Но в Японии на такие кроссовки накладываются очень большие пошлины. Подумайте и скажите, как же хитроумный бизнесмен смог ввезти все эти кроссовки в Японию, при этом заплатил только очень небольшие деньги? (Никакой коррупционной и преступной составляющей здесь нет).

Ответ

Бизнесмен поступил очень хитро. Он разделил каждую пару кроссовок и отправил весь объем двумя партиями. То есть в одной партии были только кроссовки на левую ногу, во второй только на правую ногу. Одну партию он отправил в Токио, другую в Осака. В каждом из городов бизнесмен не заплатил пошлину и товары были конфискованы и выставлены на аукционе. В связи с тем, что никому не была нужна партия кроссовок только на одну ногу, то бизнесмен выкупил сам обе партии за мизерные деньги.

---

5 рыбаков съели 5 карпов за 5 дней. Как вы думаете, а за сколько дней 15 рыбаков съедят 15 карпов?

Ответ

15 рыбаков съедят 15 карпов тоже за 5 дней. Если 5 рыбаков съедают 5 карпов за определенный промежуток времени, то у 15 рыбаков скорость поедания карпов в 3 раза больше, следовательно за 5 дней они съедят 15 карпов.

---

В мешке имеется 9 кг сахара. Есть также и две гири по 50г и 200г. Подумайте, как за три взвешивания на чашечных весах отвесить 2кг сахара?

Ответ

Сперва необходимо на чашечных весах разделить содержимое мешка пополам на 4,5кг в каждой чашке. Далее одну чашу опустошаем, и снова 4,5кг делим пополам и получаем в каждой чаше весов по 2,25кг. В третье взвешивание уже нужно опустошить обе чаши, но из одной чаши 2,25кг сахара положить в отдельный мешок. И далее при помощи гирек в 200г и 50г (итого 250г) отвесить из пакета с 2,25кг ровно 250г. Тогда в пакете останется ровно 2 кг.

---

Два колхозника решили узнать, у кого больше овец. Первый из них сказал : «если ты дашь мне свою козу, то у меня будет их в два раза больше, чем у тебя». Второй ему говорит : «А давай лучше ты мне дашь свою одну овцу, тогда у меня овец будет столько же, сколько и у тебя». Сколько же овец у каждого из колхозников? (Передачи овец пока еще не было).

Ответ

У первого колхозника 7 овец, у второго только 5. Если первый колхозник отдает одну овцу второму и их становится поровну, то значит, что изначально у первого их на 2 больше. Если же второй колхозник отдает овцу первому, то их становится у первого в 2 раза больше, такое возможно, только если у первого изначально было 7 овец, а у второго 5.

---

В одном классе всего 36 учеников. Девочек на 3 больше, чем мальчиков. Сколько мальчиков и девочек в этом классе?

Ответ

Если разделить 36 пополам, то получим 18, т.е. две половины класса по 18 человек. Если из первой половины добавить школьника в другую, то получится разница в 2 человека. Если отнять еще одного и добавить снова в большую часть, то получим превышение на 4 человека. Следовательно задача не имеет решения.

---

Можете ли вы записать число 1000 при помощи только восьми восьмерок и арифметических знаков суммы?

Ответ

Получится равенство : 888 + 88 + 8 + 8 + 8 = 1000.

---

На столе лежат 4 монеты, из которых одна сделана из другого металла и отличается по весу, хотя внешне они все одинаковые. Как определить эту монету за 2 взвешивания на чашечных весах?

Ответ

Варианты взвешиваний : 1) ложем на весы 1 и 2 монеты, если они равны по весу, то одну монету заменяем на третью. Далее если они равны, то отличная монета 4-я, если не равны, то 3-я монета отличная от остальных. 2) ложем на весы 1 и 2 монеты, если они не равны по весу, то вместо одной монеты ложем 3-ю. Если уравновешиваются, то отличная убранная монета, если не уравновешиваются, то отличная от других монет оставшаяся на весах старая монета.

---

Как так могло оказаться, что половина числа 12 стало равно 7 ?

Ответ

Нужно написать число 12 римскими цифрами : IIX , далее провести посередине линию. Верхняя половина будет в виде VII, что соответствует цифре 7.

---

На праздничном столе горят 7 свечей. 3 из них потушили. Сколько свечей останется?

Ответ

Останутся 3 потушенные свечи, т.к. остальные 4 сгорят полностью.

---

Страница №4.

Начало   << Назад   Вперед >>   Конец
[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] 

Поделитесь с друзьями:

15 упражнений для тренировки мозга

Программистам без логики никуда. Поэтому время прокачать мозг: проверьте свои способности. Вам под силу эти логические задачи?

Полезно решать и логические задачи, и математические. Так вы развиваете логику и тренируете мозг. В силу профессии айтишнику крайне важно следить за тонусом своей главной «мышцы». Мозг любит задачки и головоломки, а ещё переключение внимания и отдых от рутины. Поэтому скорее приступим к развлечениям с пользой!

Логические задачи для разминки

1 задача

Поставьте правильное число вместо вопросительного знака:

4  5  6  7  8  9 
61 52 63 94 46 ?

Ответ

Числа нижнего ряда – квадраты чисел верхнего ряда с перестановкой цифр. Вместо знака ставьте число 18.

2 задача

Один парень в компании предложил друзьям такой спор:

– Спорим, я выставлю бутылку на середину комнаты и вползу в неё.

И получилось. Он победил.

Как парню посчастливилось это сделать?

Ответ

Он без труда вполз в неё – в комнату.

3 задача

Представьте ряд из шести чашек на столе. Три первые из них ничем не наполнены, а три следующие – с водой. Как добиться чередования пустых чашек и чашек с водой? Касаться разрешается только одной чашки. При этом толкать чашку чашкой запрещается.

Что вы предпримете?

Ответ

Возьмите пятую чашку, перелейте из неё воду во вторую и поставьте чашку на место.

4 задача

В санатории на лужайке двое мужчин заняты настольным теннисом. Один ударяет ракеткой так сильно, что теннисный шарик улетает далеко и попадает в трубу из стали. Труба зарыта в землю вертикально на три метра. Шарик лежит на дне трубы, то есть на расстоянии трёх метров от плоскости земли. У игроков нет другого шарика.

Ответьте, как спортсменам достать игральный шар без извлечения трёхметровой трубы из-под земли?

Ответ

Спортсмены наполнят трубу водой до краёв, и тогда шарик всплывёт.

5 задача

Получится ли у вас записать число 1000 с использованием только восьми восьмёрок и символов математического сложения?

Ответ

888 + 88 + 8 + 8 + 8 = 1000

Логические задачи основного комплекса

6 задача

Попробуйте установить принцип построения указанной последовательности:

8 2 9 0 1 5 7 3 4 6

Ответ

Последовательность цифр построена на основании алфавитного порядка их названий (восемь, два, девять, ноль и т. д.).

7 задача

Вообразите десятикилометровый мост через пролив. Максимальная нагрузка для него – 25 тонн. С начала этого моста стартовал грузовик, масса которого – ровно 25 тонн. Автомобиль продолжает движение к противоположному краю. Баланс моста пока не нарушен. Неожиданно, когда грузовик достиг середины этого путепровода, на него сел воробей со своим весом.

Вопрос к вам: приведёт ли вес птицы к нарушению балансировки и разрушению моста?

Ответ

Не приведёт. Так как грузовик преодолел путь до середины моста, что равно 5 км, расход потраченного топлива в разы превысил вес птицы.

8 задача

В одно и то же время к водному каналу приблизилось двое. Добраться до другого берега поможет лодка, которая рассчитана только на одну персону. Тем не менее, без стороннего участия оба переправились на противоположный берег на этой лодке.

Как люди справились?

Ответ

Люди приблизились к противоположным берегам водного канала.

9 задача

Отважного воина захватили слуги султана. Султан приказал отправить смельчака в темницу, где вместе с ним беспрерывно будут рядом два надзирателя. Один стражник исключительно правдив в разговоре, а второй лжёт. Внутри темницы оказались два закрытых входа. Войдёшь в один – выберешь «неволю навсегда», а в другой – «освобождение». Султан предложил воину избрать один вход: если это окажется «освобождение», то пленник свободен.

Воину позволили спросить надзирателей только один раз. То есть один вопрос на двоих надзирателей. Пленник не в курсе, кто из них лжец, а кто правдив. Надзиратели, несомненно, знают, какой вход подарит воину освобождение.

Какой вопрос задаст воин одному из стражников для достоверного определения входа, который означает «освобождение»?

Ответ

Воин задаст только один вопрос любому из надзирателей: «Если попросить твоего коллегу указать на вход «освобождение», то куда он направит меня?» В обеих ситуациях надзиратель укажет на «вход в неволю».

10 задача

В лесу десять родников с мёртвой водой: от первого до десятого. Мёртвая вода из родников с первого по девятый доступна каждому, а десятый родник во власти Кощея в пещере, в которую он никого не впускает. По вкусу и цвету мёртвую воду не отличить от обыкновенной, однако глоток воды из родника означает смерть. Спасёт только вода из родника с номером выше. Поэтому того, кто изначально выпьет десятую воду, ничего не спасёт.

Иванушка бросил вызов Кощею. Условились принести с собой чашку с водой и дать её осушить сопернику. Радости Кощея не было предела: «Ура! Я налью десятый яд, и Иванушка не спасётся! В то же время выпью то, что даст Иванушка, следом выпью десятый яд и останусь живым!»

В оговоренный день соперники столкнулись. Последовал честный обмен чашками. Содержимое выпито. При этом Кощей погиб, а Иванушка выжил.

Как Иванушка победил Кощея?

Ответ

Иванушка предложил Кощею обыкновенную воду. А Кощей, по неверным предположениям, «запил» её собственным десятым ядом. Перед встречей с соперником Иванушка выпил воду из любого родника. Вышло, что он запил яд Кощеевым десятым, что привело к нейтрализации яда.

Логические задачи для «растяжки»

11 задача

Отец решил задать своему сыну-школьнику каверзный вопрос: назови самое большое число. Ответ сына ошеломил отца, возразить было нечего.

Для программиста это дело лёгкое, правда? Но что сказал школьник?

Ответ

Тридцать первое. Предполагается число месяца.

12 задача

Воинственное племя захватило странника. Вождь хотел смерти страннику и позволил ему выбирать. Страннику разрешалось озвучить одну фразу. При правдивости фразы его сбросят с отвесной скалы. Окажись фраза лживая, и его отдадут львам на растерзание. Но странник подобрал такую фразу, которая подарила ему свободу.

Отгадайте, что это за фраза?

Ответ

Фраза: «Меня растерзают львы». Тогда, если бы вождь отдал странника львам на растерзание, то сказанная фраза стала бы правдивой, и его полагалось бы бросить с отвесной скалы. Но если странника сбросят со скалы, то фраза окажется лживой.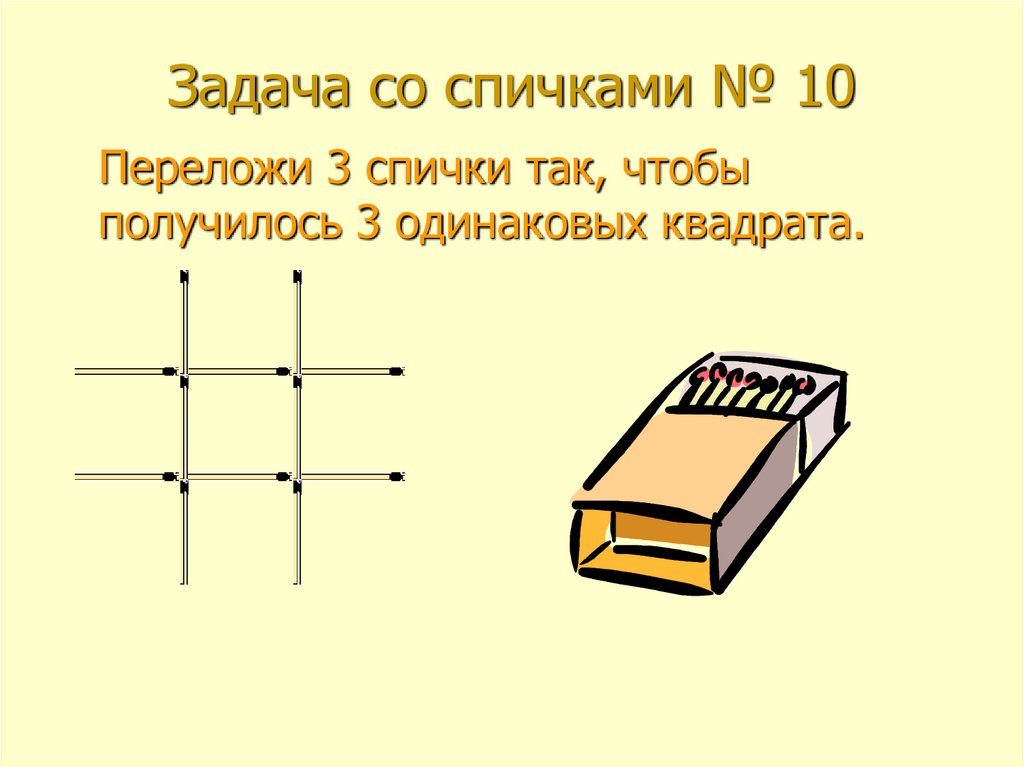 Вождь посчитал, что исключительно правильным исходом будет подарить свободу страннику.

13 задача

После гулянки мужчина направлялся домой слегка навеселе. Он шёл по центру песчаной проселочной дороги. Путь не освещался лунным светом. К тому же, на дороге отсутствовали фонари. Одежда мужчины была чёрной. Вдруг на дорогу выехал автомобиль с выключенными фарами. В конце концов, водитель заметил мужчину и свернул.

Как ему удалось увидеть пешехода?

Ответ

На улице стоял день.

Логические задачи для заминки

14 задача

Вам даётся три письма. Одно придётся незамедлительно проглотить. В каждом письме найдёте пару предложений. Два предложения в одном письме истинные, в другом – ложные, а в третьем – пополам – истинное и ложное. Смотрите, какие там предложения:

Первое письмо:

1. Не ешьте это письмо.
2. Непременно съешьте второе письмо.

Второе письмо:

1. Не стоит есть первое письмо.
2. Жуйте третье письмо.

Третье письмо:

1. Есть это письмо не стоит.
2. Скорее съедайте первое письмо.

Поделитесь своим мнением, какое письмо съесть?

Ответ

Третье письмо.

15 задача

Вы очутились в помещении, в котором четыре двери и крошечное окошко. Три двери фальшивые, то есть за ними сразу кирпичная кладка. И одна дверь с выходом на улицу. Вам дали ключ, который открывает все четыре двери, однако вы без понятия, какая дверь выведет на улицу. Попытаться можно один раз. При открывании одной двери оставшиеся замки блокируются механически и безвозвратно. Вдобавок комната тёмная и слегка озаряется светом одной свечи.

Какие вы примете меры, чтобы отыскать единственную дверь, которая ведёт на улицу?

Ответ

Стоит распахнуть окошко и подставлять свечу по очереди к дверям: к щелям или к замочной скважине. При этом внимательно смотреть на пламя свечи. Колебание пламени будет указывать на выход.

Эти логические задачи показались вам лёгкими или не очень?

Попробуйте другие логические задачи:

• Логика в программировании: логические задачи с собеседований
• Тренируй свои мозги или ТОП-15 логических задач

10 логических задач с собеседований, которые заставят застрелиться

Некоторые логические задачи с собеседований вгоняют в недоумение: зачем такое спрашивать? Чтобы создать сложную ситуацию и посмотреть, как быстро вы примете решение.

Разобраться и ответить правильно поможет наша подборка логических задач с собеседований.

Автомат с напитками

Начнём с простой логической задачи.

На склад привезли три машины для напитков. Одна из них выдаёт чай, вторая выдаёт кофе, а третья — чай или кофе (определяется случайно). Любой автомат продаст стакан напитка за одну монету. На каждом автомате приклеена этикетка с выдаваемым напитком. Но на заводе произошла ошибка, из-за чего на всех автоматах наклеены не те этикетки, которые должны быть.

Вопрос: сколько потребуется денег, чтобы определить, где какие автоматы?

Ответ

Потребуется одна монета, которую нужно бросить в автомат с наклейкой «случайный». Мы знаем, что это неправильная наклейка, поэтому это автомат с чаем либо кофе. После этого определяются остальные два автомата методом исключения. Например, если автомат выдал чай, то автомат с наклейкой «чай» на самом деле выдаёт кофе, а автомат с наклейкой «кофе» выдаёт случайный напиток.

Инопланетяне и десяток храбрецов

В нашу планету вторглась инопланетная раса, чтобы уничтожить всё человечество. Но перед этим они решили дать нам возможность проявить свои интеллектуальные способности. Они отобрали десять умнейших людей планеты, построив их в ряд в полностью тёмной комнате. Каждому они надели чёрную или белую шляпу. После этого свет включился.

Инопланетянин просит стоящего в конце ряда человека назвать цвет своей шляпы. Если ответ правильный — этот человек остаётся жить, если нет — погибает. Подсмотреть цвет своей шляпы нельзя, однако можно обсудить с остальными определённый принцип ответа, которого будут придерживаться все. Распределение цветов шляп случайное, но вам виден цвет шляп всех остальных людей.

Вопрос: каким должен быть ответ, чтобы в живых осталось как можно больше людей?

Ответ

Люди должны договориться о следующем принципе ответов: отвечающий считает количество чёрных шляп у остальных людей. Если шляп нечётное количество, он называет «чёрный», если чётное — «белый».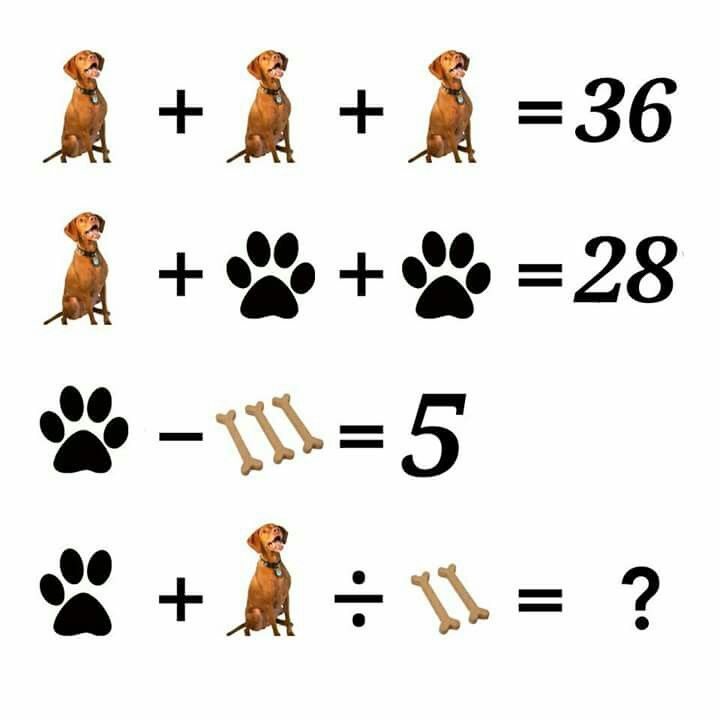 Следующий человек в ряду, видя шляпы остальных и зная чётность чёрных, может вычислить цвет своей шляпы. Например, если чёрных всё ещё нечетное количество, то на нём белая шляпа. С такой тактикой выживут 9 из 10 человек. Один же из них героически погибнет, спасая остальных.

Поездки на мотоциклах

У вас есть 50 мотоциклов с полным баком, которого хватает на 100 км езды.

Вопрос: используя все мотоциклы, какое максимальное расстояние вы сможете проехать? Все мотоциклы в начале пути находятся условно в одной точке.

Ответ

Самое простое решение, которое может прийти в голову — просто завести все мотоциклы и одновременно проехать на них 100 км. Но можно проехать и больше. Для этого сначала проедьте 50 км. Все мотоциклы будут с наполовину заполненными баками. Перелейте топливо с одной половины мотоциклов в другую половину. Теперь у вас 25 мотоциклов с полным баком. Проедьте ещё 50 км и повторите операцию. Таким образом можно проехать 350 км

3 лампы и 3 выключателя

Эта логическая задача особенно полюбилась на собеседованиях. Есть 2 комнаты. Первая комната закрыта дверью, в ней низкие потолки и висят 3 лампы накаливания. Во второй комнате есть 3 выключателя, подсоединённых к каждой из ламп. Можно как угодно переключать выключатели, но перейти из второй комнаты в первую можно лишь один раз.

Вопрос: как узнать, за какую лампу отвечает каждый из выключателей?

Ответ

Ситуацию спасут низкие потолки, которые позволят дотронуться до лампы. Ещё очень важная деталь — лампы накаливания, которые очень сильно нагреваются. Вам нужно, находясь во второй комнате, включить любую лампу на несколько минут, потом выключить её и включить любую из двух других. После этого переходите в комнату с лампами. Первый выключатель, который вы трогали, будет присоединён к лампе, которая ещё тёплая. Второй выключатель — к светящей лампе. А выключатель, который вы не трогали, будет подсоединён к выключенной холодной лампе.

Два стражника

А такая логическая задача часто встречается на интервью от Apple. Игрок дошёл до финального задания в квесте. Перед ним оказались две двери. Первая приведёт к богатству и победе, другая — к поражению. Под дверьми стоит по одному стражнику. Они знают, куда ведут их двери. Но один из них скажет неправду. Не известно, кто именно солжёт. Игрок может спросить одного стражника всего один раз.

Вопрос: что нужно спросить у стража, чтобы выйти к богатству и выиграть квест?

Ответ

У любого стражника нужно спросить: «какая дверь, по мнению другого стражника, ведёт к победе?». Если игрок спрашивает у правдивого стражника, то тот укажет на дверь с поражением, ведь второй стражник всегда врёт. Если же спросить у второго стражника, то он соврёт о мнении правдивого стражника и тоже укажет на дверь с поражением. Зная неправильную дверь, вам просто нужно выбрать другую.

Пьяные кролики

Как-то раз один наследник захотел убить своего короля, чтобы власть скорей перешла в его руки. У короля была 1000 бутылок вина его любимого сорта. 10) уникальных комбинаций состояний кроликов. Пронумеруем все бутылки в двоичной системе, для этого хватит 10 разрядов (в задаче нумерация регистров начинается с 1):

• 1-я бутылка = 0000000001
• 2-я бутылка = 0000000010
• 3-я бутылка = 0000000011
• …
• 999-я бутылка = 1111100111
• 1000-я бутылка = 1111101000

Кроликов нужно пронумеровать от 1 до 10. Каждый из них  будет соответствовать одному из 10 разрядов числа. Кроликов нужно поить из тех бутылок, где в соответствующем кролику разряде есть единица. Например, из первой бутылки пьёт только первый кролик; из третьей — первый и второй. Напоив кроликов из всех бутылок, нужно подождать один день. Номера кроликов, которые погибли, подскажут разряды числа, в которых должны быть единицы. Таким образом, если погибли только 3-й и 1-й кролики, то отравлена 5-я бутылка (0000000101 = 5).

Голодные белки

Данная логическая задача нередко задаётся на собеседованиях и выделяется среди прочих своей неординарностью. В её решении важны не особые математические способности, а умение абстрагироваться от странного условия. Полюбившаяся интервьюерам задача звучит так: 1,5 белки за 1,5 минуты поедают 1,5 жёлудя.

Вопрос: сколько желудей за 9 минут съедят 9 белок?

Ответ

Если вы не зависли на моменте «1.5 белки», то у вас есть все шансы осилить эту логическую задачку — завсегдатая собеседований. Нужно лишь иначе представить заданные условия. Если 1,5 белки съедают 1,5 жёлудя за 1,5 минуты, то 1 белка за 1,5 минуты съедает 1 жёлудь. Тогда 9 белок за 1,5 минуты съедают 9 желудей. Но по условию нужно узнать количество желудей, съедаемых за 9 минут:

1. 9 / 1,5 = 6 — во столько больше раз нам даётся времени;
2. 9 * 6 = 54 — столько желудей съедят 9 белок за 9 минут.

Треугольник муравьёв

Есть треугольник с равными углами. На углах стоят по одному муравью. В какой-то момент муравьи начинают идти в другой угол вдоль стороны треугольника. В какой именно — определяется случайно.

Вопрос: каков шанс того, что ни один муравей не столкнётся с другим муравьём?

Ответ

Может показаться, что вероятность 33%, но это не так. Есть два варианта необходимого движения муравьёв: по часовой стрелке и против. Давайте сконцентрируемся на одном муравье. После того, как он случайным образом выбрал направление, ему нужно, чтоб и остальные муравьи двигались в эту же сторону. Шанс того, что второй муравей пойдёт в его направлении — 50%. Аналогичная вероятность и у третьего муравья. Это значит, что общая вероятность того, что муравьи не столкнутся — 25%.

Котлета, котлета и ещё одна котлета

У вас есть 2 сковородки и 3 котлеты. На приготовление 1 котлеты с одной стороны уходит 1 минута. На одной сковороде вмещается лишь 1 котлета.

Вопрос: за какое минимальное время вы сможете полностью обжарить все 3 котлеты?

Ответ

Первым в голову приходит ответ — 4 минуты. Но можно уложиться и в 3 минуты. Для этого придерживайтесь следующей последовательности:

1. положите жариться по 1 котлете на две сковороды;
2. через минуту переверните первую котлету, а вторую уберите. На место второй котлеты положите третью;
3. ещё через минуту первая котлета будет полностью готова. На её место положите дожариваться вторую котлету, которую вы убрали, а третью котлету переверните;
4. спустя минуту все 3 котлеты будут полностью обжарены.

Необычная оплата

В поместье пришёл путник. В кармане — ни гроша, лишь одна золотая цепь из 6 звеньев. Хозяин поместья предложил брать плату в виде одного кольца с цепочки за один день проживания, при условии, что будет распилено только одно звено. Хозяин должен получать плату каждый день. Он не хочет принимать предоплату или давать в долг.

Вопрос: как путник должен распилить цепочку, чтобы вносить оплату за жильё каждый день в течение 5 дней?

Ответ

В условиях задачи не запрещался обмен звеньями цепи. Было лишь требование, чтобы с каждым днём у хозяина жилья прибавлялось одно звенье. Нужно распилить третье звено цепи, чтобы получить 3 части по 1, 2 и 3 звена. За 1-е сутки странник платит одним звеном. На 2-е сутки он платит куском из 2 звеньев и получает сдачу — одно звено (которым он расплатился за 1-е сутки). На 3-и сутки платит куском из 3 звеньев и забирает кусок из 2 звеньев. По такому принципу странник и должен оплатить все оставшиеся дни.

Заключение

Возможно, вы уже сталкивались с подобными логическими задачами на собеседованиях. Если так, поделитесь своим опытом: что это были за задачки и удалось ли их решить?

А для любителей поломать голову мы подготовили тест на проверку логики и математики.

20 лучших математических головоломок, чтобы увлечь и бросить вызов вашим ученикам

Пришло время урока математики, и ваши ученики скучают.

Это может показаться суровым, но это правда — только около половины учеников сообщают, что они вовлечены в школу, а уровень вовлеченности снижается только по мере того, как ученики становятся старше.

Математические головоломки — один из лучших и старейших способов поощрения участия учащихся. Головоломки, логические головоломки и математические загадки задают учащимся задачи, стимулирующие решение проблем и логическое мышление. Их можно использовать для геймификации в классе и для того, чтобы вдохновить учащихся на решение проблем, которые раньше казались им слишком сложными.

Пазлы для распечатки

Возьмите кроссворд и сделайте из него математику: такова основная концепция этого легко адаптируемого математического задания. Вместо слов учащиеся используют цифры для заполнения вертикальных и горизонтальных полос. Математические кроссворды можно адаптировать для обучения таким понятиям, как деньги, сложение или округление чисел. Решения могут быть произведениями уравнений или чисел, заданных подсказками.

2. Поиск математических задач

Предложите учащимся попрактиковаться в навыках сложения, вычитания, умножения и деления путем поиска скрытых математических уравнений в головоломке в стиле поиска слов. Его можно адаптировать к любому навыку, который вы хотите, чтобы учащиеся практиковали, и он способствует глубокому пониманию основных математических фактов.

3. Математические загадки

Ваши ученики любят текстовые задачи? Попробуйте дать им несколько математических загадок, которые сочетают критическое мышление с базовыми математическими навыками. Повесьте один на доске, чтобы учащиеся могли обдумать его перед началом урока, или раздайте его в качестве дополнительной практики после того, как они закончат свою работу.

4. Prodigy

Prodigy — увлекательная игровая платформа, превращающая математику в приключение! Хотя это и не математическая головоломка в традиционном смысле, Prodigy использует многие из тех же принципов для развития навыков критического мышления и беглости математики.

Учащиеся выполняют математические задания, соответствующие учебной программе, чтобы заработать монеты, собрать питомцев и выполнить квесты. Учителя могут предоставлять дифференцированный математический контент каждому учащемуся, готовиться к стандартизированным тестам и легко анализировать данные об успеваемости учащихся с помощью бесплатной учетной записи.

Зарегистрируйтесь сейчас

5. KenKen

KenKenKenKen

— это числовая головоломка на основе сетки, которая выглядит как комбинированный крест чисел и сетка судоку. Изобретенный в 2004 году известным японским учителем математики по имени Тэцуя Миямото, он ежедневно публикуется в The New York Times и другие газеты. Он предлагает учащимся практиковать свои основные математические навыки, применяя логику и навыки критического мышления для решения проблемы.

6. Предалгебраические головоломки

Предалгебраические головоломки используют забавные замены, чтобы подготовить учащихся к выполнению основных функций и побудить их развить навыки решения задач. Они способствуют абстрактному мышлению и побуждают учащихся критически относиться к стоящим перед ними задачам. В качестве дополнительного бонуса учащиеся, страдающие от математической тревожности, могут обнадежить отсутствие сложных уравнений и с большей готовностью попытаются найти решение.

7. Доска-головоломка домино

Игры 4 Gains

Существуют сотни способов использования домино на уроке математики, но эта головоломка дает учащимся возможность попрактиковаться в сложении и умножении в увлекательной игровой форме. Вы можете предложить учащимся работать в одиночку или в парах, чтобы собрать головоломку.

8. 2048

2048

В этой онлайн-игре и приложении игроки должны перемещать пронумерованные плитки по сетке, пока не достигнут числа 2048. Это очень затягивает и не так просто, как кажется, поэтому подумайте о том, чтобы отправить его домой со студентами или назначая его после того, как остальная часть урока закончена. Это побуждает студентов стратегически обдумывать свой следующий шаг, и это отличный инструмент для изучения экспонентов.

9. Какуро

Математика на английском языке

Какуро, также называемое «Перекрестные суммы», представляет собой еще один математический кроссворд. Игроки должны использовать числа от одного до девяти, чтобы добраться до «подсказок» за пределами ряда. Уменьшите размер сетки, чтобы упростить ее для младших игроков, или оставьте ее без изменений для учащихся, которым нужны задачи. Учащиеся могут сочетать дополнение и критическое мышление и развивать несколько навыков с помощью одного веселого задания.

10. Магический квадрат

Википедия

Магические квадраты существуют уже тысячи лет и были представлены западной цивилизации в переводе арабских текстов в эпоху Возрождения. В то время как магические квадраты могут быть самых разных размеров, сетка три на три является самой маленькой из возможных версий и наиболее доступна для младших школьников.

Это также отличная математическая головоломка, которую стоит попробовать, если ваши ученики учатся тактильно. Используя переработанные крышки от бутылок, пометьте каждую цифрой от одного до девяти. Попросите учащихся расположить их в виде квадрата три на три так, чтобы сумма любых трех заглавных букв в строке (по горизонтали, вертикали и диагонали) равнялась 15.

11. Магический треугольник с периметром

В этом упражнении используются те же материалы и концепция, что и в магическом квадрате, но учащимся предлагается расположить числа от одного до шести в треугольнике, все три стороны которого равны одному и тому же числу. У этой головоломки есть несколько различных решений, поэтому предложите учащимся посмотреть, сколько из них они смогут найти.

12. Судоку

Судоку — отличное занятие после уроков, которое развивает логическое мышление и решение проблем. Вы, наверное, уже играли в эту классическую головоломку, и это отличный выбор для ваших учеников. Головоломки судоку появляются в газетах по всему миру каждый день, и существуют сотни онлайн-ресурсов, которые создают головоломки в зависимости от сложности.

13. Flexagon

Есть большая вероятность, что к настоящему времени в ваш класс проникли спиннеры. Если вы хотите противостоять этому вторжению, подумайте о том, чтобы предложить своим ученикам создать флексагоны. Флексагоны — это объекты, сложенные из бумаги, которые можно трансформировать в различные формы, сжимая и складывая, и они будут держать блуждающие пальцы занятыми и сосредоточенными на чудесах геометрии.

14. Переверни рыбу

TransumЭта головоломка

кажется простым, но это может поставить ваших учеников в тупик. Расставив палочки в нужном порядке, дайте им задание заставить рыбу плыть в другом направлении, переместив всего три спички.

15. Соедини точки

Cool Math 4 Kids

В этой головоломке учащиеся должны соединить все точки в сетке три на три, используя только четыре прямые линии. Хотя это может показаться простым, есть вероятность, что вашему классу потребуется некоторое время, чтобы найти решение. (Подсказка: это требует некоторого «нестандартного» мышления.)

16. Головоломки

Хотя они не всегда связаны непосредственно с математическими навыками, головоломки могут быть важными инструментами в развитии навыков критического мышления ребенка. Включите головоломки в обсуждение в классе или используйте их в качестве подсказок к математическому журналу и предложите учащимся объяснить свое мышление.

Бонус: для обсуждения вероятности познакомьте старшего класса с проблемой Монти Холла, одной из самых противоречивых математических логических задач всех времен.

17. Ханойская башня

Эта интерактивная логическая головоломка была изобретена французским математиком Эдуардом Лукасом в 1883 году. .

Жрецы перемещают эти диски в соответствии с правилами игры, чтобы исполнить пророчество, согласно которому конец света наступит с последним ходом головоломки. Но не беспокойтесь — жрецам потребуется около 585 миллиардов лет, чтобы закончить, так что вы сможете вписаться в остальную часть вашего математического класса.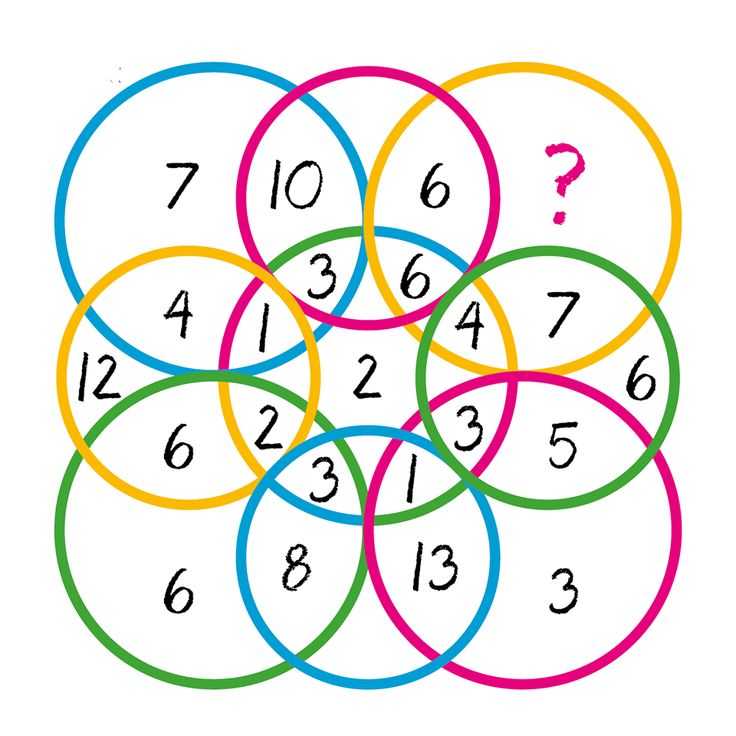

Начиная с трех дисков, поставленных друг на друга, учащиеся должны переместить все диски с первого столба на третий, не кладя больший диск поверх меньшего. Старшие школьники могут даже узнать о функциях, лежащих в основе решения: минимальное количество ходов можно выразить уравнением 2n-1, где n — количество дисков.

18. Танграм

Википедия

Головоломки Танграм, которые возникли в Китае и были привезены в Европу в начале 19 века.через торговые пути — используйте семь плоских геометрических фигур, чтобы составить силуэты. Хотя танграмы обычно делаются из дерева, вы можете сделать наборы для своего класса из цветной плотной бумаги или войлока.

Танграммы — отличный инструмент для учащихся, которым нравится управлять своей работой. Существуют тысячи опубликованных задач, чтобы занять ваших учеников.

19. Str8ts

Str8ts

Подобно судоку, Str8ts предлагает игрокам использовать свои логические навыки для размещения чисел в пустых квадратах. Числа могут быть последовательными, но могут появляться в любом порядке. Например, строка может быть заполнена 5, 7, 4, 6 и 8 . Эта головоломка больше подходит для учащихся старшего возраста, и ее можно использовать в качестве задания до или после урока, чтобы укрепить основные логические навыки.

20. Лента Мебиуса

Это магия? Это геометрия? Ваши ученики будут настолько поражены, что им может быть трудно понять это. Попросите их смоделировать задачу с помощью полосок бумаги и самим посмотреть, как это работает в реальной жизни. Со старшими учениками используйте ленты Мебиуса, чтобы говорить о геометрии и площади поверхности.

Зачем использовать математические головоломки для обучения?

Математические головоломки развивают критическое мышление.

Критическое мышление и логические навыки важны для всех профессий, а не только для тех, кто связан с STEM. Головоломки побуждают учащихся понимать структуру и применять навыки логического мышления для решения новых задач.

Исследование Eurasia Journal of Mathematics, Science and Technology Education показало, что головоломки «развивают логическое мышление, комбинаторные способности, усиливают способность к абстрактному мышлению и работе с пространственными образами, прививают критическое мышление и развивают математическую память».

Все эти навыки позволяют юным учащимся заложить фундамент навыков, которыми они будут пользоваться всю оставшуюся жизнь, независимо от того, какое высшее образование они выберут.

Они помогают улучшить беглость математики

Математические игры могут помочь учащимся получить базовое понимание основных математических понятий и, как показывает другое исследование, также могут помочь им дольше запоминать понятия.

В ходе исследования учащиеся начальных классов постепенно перешли от использования «счетной» части мозга для решения математических задач к «запоминающей» части, которую используют взрослые. Предполагается, что математические головоломки и повторяющиеся задачи могут помочь развить необходимый навык беглость математики .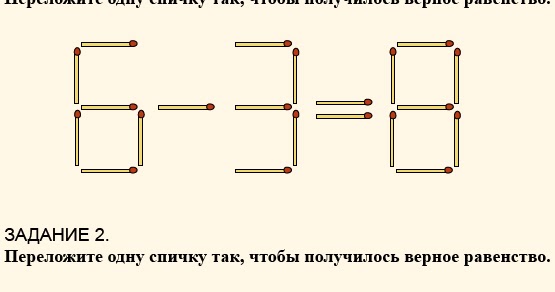

Многие из вышеперечисленных математических головоломок позволяют учащимся практиковать основные навыки сложения, вычитания, умножения и деления, а сложные или модифицированные задачи можно использовать для ознакомления с предалгебраическими понятиями и углубленными логическими навыками.

Математические головоломки связаны с существующими учебными планами

Независимо от того, какую учебную программу вы используете, есть большая вероятность, что она делает упор на решение проблем, критический анализ и абстрактное мышление. Это особенно верно в отношении математики Common Core и подобных учебных программ.

Как математические навыки влияют на развитие учащихся

Математические головоломки позволяют учащимся развивать базовые навыки в ряде ключевых областей и могут повлиять на практический и абстрактный подход учащихся к математике. Вы также можете связать их со стратегиями, такими как активное обучение и дифференцированное обучение.

Вместо того, чтобы просто учить факты и формулы, математические головоломки позволяют вам напрямую связываться с основными стандартами учебной программы. Вы также можете использовать их, чтобы предоставить ценную отправную точку для измерения того, насколько хорошо учащиеся развивают свои навыки критического мышления и абстрактного мышления.

Советы по использованию математических головоломок в классе

Теперь, когда у вас есть несколько отличных математических головоломок, может быть сложно понять, как лучше всего использовать их в классе. Вот несколько советов, как максимально эффективно использовать время урока:

Убедитесь, что уровень головоломок подходит для вашего класса

Если задачи слишком простые, учащимся станет скучно, и они отвлекутся от урока. Однако, если проблемы слишком сложны для решения, есть большая вероятность, что они разочаруются и сдадутся раньше времени.

Есть время и место

Хотя математические головоломки — отличный способ вовлечь учащихся в развитие навыков критического мышления, они не являются инструментом для обучения важным математическим понятиям.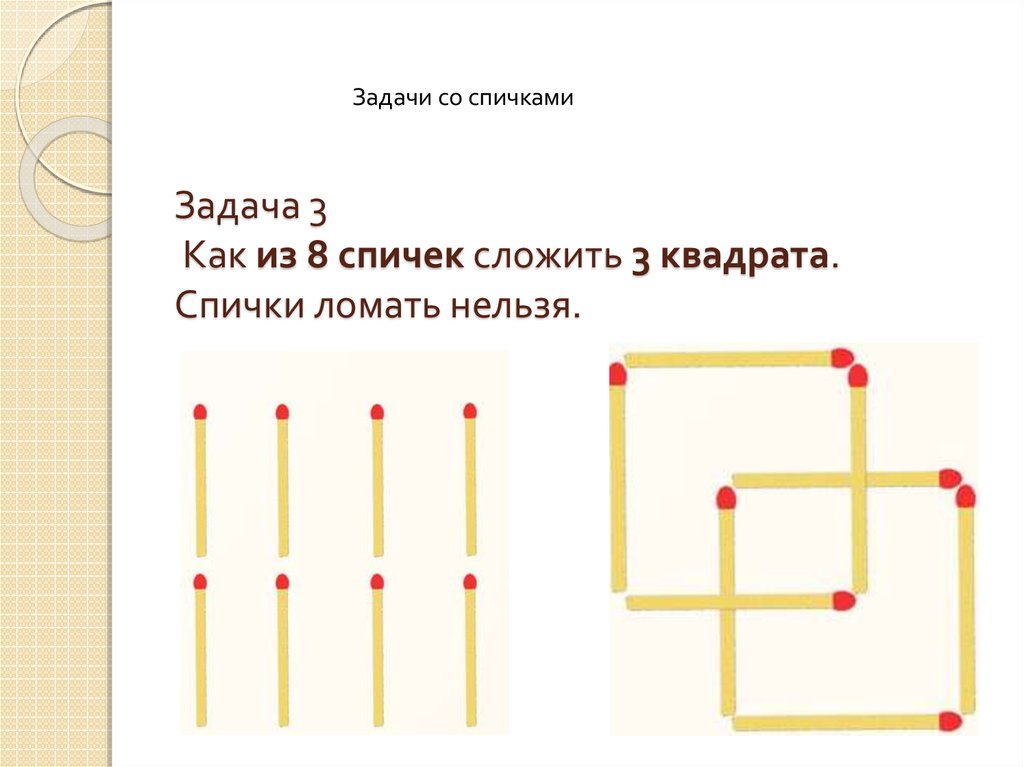 Вместо этого используйте их, чтобы закрепить понятия, которые они уже изучили.

Китти Резерфорд, консультант по математике из Северной Каролины, подчеркивает, что математические головоломки и игры должны основываться не только на математических способностях в уме, но и на «концептуальном понимании», которое со временем улучшает беглость речи. Математические головоломки помогают установить необходимый баланс между мышлением и запоминанием.

Дайте им пространство для размышлений

Рэйчел Кин из факультета психологии Университета Вирджинии провела исследование навыков решения проблем у дошкольников. Она обнаружила, что «игровое, исследовательское обучение приводит к более творческому и гибкому использованию материалов, чем явное обучение взрослых».

Дайте учащимся пространство для борьбы с проблемой и применения собственных решений, прежде чем броситься им на помощь. Если задача соответствует классу и решаема, учащиеся узнают больше, применяя к ней собственные рассуждения, а не просто наблюдая за тем, как вы решаете ее за них.

Моделирование головоломок для ваших учеников

Используйте такие задачи, как лента Мебиуса, чтобы вызвать благоговейный трепет и удивление ваших учеников, прежде чем вовлечь их в более масштабное обсуждение математической концепции, которую она представляет. Если возможно, сделайте математические головоломки физическими, используя переработанные материалы для рукоделия или модульные инструменты.

После этого проведите обсуждение в классе или разместите подсказки в журнале по математике. Какие методы пробовали ваши ученики? Какие инструменты они использовали? Что сработало, а что нет? Когда учащиеся четко указывают, как они пришли к своему решению (или даже где они застряли), это побуждает их исследовать свой процесс и делать выводы из своего опыта.

Заключительные мысли о математических головоломках

Имейте в виду, что может потребоваться некоторое время, чтобы собрать всех ваших учеников на борту — они могут сомневаться в подходе к незнакомым задачам или застрять в отсутствии энтузиазма, которое часто приносит урок математики. Рассмотрите возможность создания еженедельной таблицы лидеров в своем классе для учеников, которые решают больше всего головоломок, или проработайте несколько вместе с классом, прежде чем отправлять учеников самостоятельно.

Вместо зевоты и скучающих взглядов приготовьтесь к активным участникам и вдумчивой концентрации. Независимо от того, решите ли вы использовать их в качестве бонуса после уроков, в первый день школьных занятий или как часть целевого плана урока, математические головоломки порадуют ваших учеников, а также позволят им развить важные навыки, которые они будут использовать для остальных. их жизни.

Чего ты ждешь? Загадывайте!

>>Создайте или войдите в свою учетную запись учителя в Prodigy — увлекательной игровой платформе для обучения математике, которую легко использовать как преподавателям, так и учащимся. В соответствии с учебными планами англоязычного мира, его используют из более чем миллионов учителей и из 50 миллионов учащихся.

Зарегистрируйтесь сейчас

5 логических головоломок, которые сломают ваш мозг0003

Хочешь решить веселые и сложные логические головоломки и проверить свои умственные способности?

Попытки решить логические головоломки — один из лучших способов улучшить свои навыки решения проблем и логического мышления, одновременно получая массу удовольствия.

В сегодняшней публикации вы найдете коллекцию из 5 логических головоломок для детей и взрослых, сложность которых постепенно увеличивается, а также есть особая бонусная головоломка, которая ставит людей в тупик уже более 100 лет!

Обратите внимание, что решение каждой логической головоломки находится внизу поста (мы рекомендуем сначала решить все задачи самостоятельно, а затем проверить правильность ваших ответов).

Вы готовы начать?

5 логических головоломок, которые сломают ваш мозг

Некоторые из этих головоломок можно решить менее чем за одну минуту, в то время как другие достаточно сложны, чтобы поставить вас в тупик на весь день, подвергая ваш мозг испытанию!

Сегодня у вас будет возможность потренировать свой мозг, решив некоторые из этих знаменитых логических и числовых головоломок.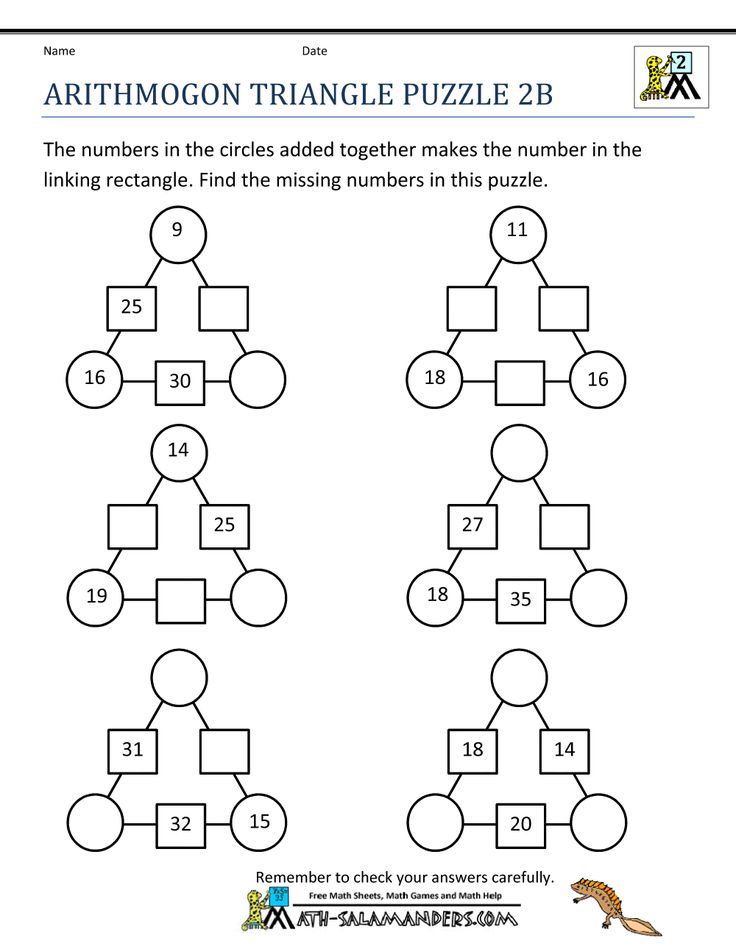

Итак, вы готовы принять вызов? И не забудьте решить бонусную головоломку — простую, но сложную загадку, которая существует уже более 100 лет.

А если вам нужны более подробные объяснения того, как решить каждую логическую головоломку, посмотрите наше видео 5 логических головоломок, которые сломают ваш мозг ниже, и обязательно нажмите кнопку «Нравится» и оставьте комментарий!

Посмотрите видео с 5 логическими головоломками:

Логическая головоломка #1

Сколько всего блоков на диаграмме ниже?

Продолжайте читать до конца этой страницы, чтобы увидеть ключ ответа И щелкните здесь, чтобы просмотреть видео, объясняющее решение этой проблемы.

Нажмите здесь, чтобы подписаться на нашу бесплатную еженедельную рассылку по электронной почте!

Логическая головоломка #2

Как далеко может пройти медведь в лесу?

Продолжайте читать до конца этой страницы, чтобы увидеть ключ ответа И щелкните здесь, чтобы просмотреть видео, объясняющее решение этой проблемы.

Логическая головоломка #3

Как перевернуть пирамиду мармеладных мишек вверх дном, перемещая только 3 мармеладных мишек?

Продолжайте читать до конца этой страницы, чтобы увидеть ключ ответа И щелкните здесь, чтобы просмотреть видео, объясняющее решение этой проблемы.

Вы ищете еще больше увлекательных математических загадок, головоломок и головоломок, чтобы поделиться ими со своими детьми?

Самая продаваемая рабочая тетрадь 101 математические загадки, головоломки и головоломки для детей от 10 лет! теперь доступен для загрузки в формате PDF. Вы можете получить свой сегодня, нажав здесь.

Логическая головоломка #4

Когда Берту исполнилось 14 лет, его младший брат Чип был вдвое моложе его. Если сегодня Берту 31 день рождения, то сколько лет Чипу?

Продолжайте читать до конца этой страницы, чтобы увидеть ключ ответа И щелкните здесь, чтобы просмотреть видео, объясняющее решение этой проблемы.

Логическая головоломка #5

Если в комнате 7 медведей, и каждый из них обнимает друг друга один и только один раз, сколько всего медвежьих объятий было всего?

Продолжайте читать до конца этой страницы, чтобы увидеть ключ ответа И щелкните здесь, чтобы просмотреть видео, объясняющее решение этой проблемы.

Бонусная логическая головоломка!

Исследователь, который проходит одну милю на юг, одну милю на восток и одну милю на север и в конечном итоге оказывается там же, где и начал. Пока он идет, он видит медведя. Какого цвета медведь?

Продолжайте читать до конца этой страницы, чтобы увидеть ключ ответа И щелкните здесь, чтобы просмотреть видео, объясняющее решение этой проблемы.

Готовы к ответам?

Помните, что нет необходимости спешить с ответами на сегодняшние логические задачи. Можно подождать, пока вы не найдете ответ на каждую проблему, прежде чем прокрутить вниз, чтобы увидеть ответы ниже.

КЛЮЧ ОТВЕТА:

1.) 11 блоков

2.) Полпути (после этого медведь идет из леса)

3.) Схема:

4.) Чипу 24 года

5.) 21 объятие

Бонус: Медведь белый (Белый медведь на Северном полюсе)

Вы ищете еще больше увлекательных математических головоломок, чтобы поделиться ими со своими детьми?

Моя самая продаваемая рабочая тетрадь 101 ежедневные задачи по математике для учащихся 3–8 классов  теперь доступна для скачивания в формате PDF. Вы можете получить свой сегодня, нажав здесь.

Я пропустил вашу любимую математическую загадку для детей? Поделитесь своими мыслями, вопросами и предложениями в разделе комментариев ниже!

(Никогда не пропустите блог Mashup Math-щелкните здесь, чтобы получить нашу еженедельную новостную рассылку!)

от Энтони Персико

Энтони-Content Crafter и Head Frediure для YouTube Mashup Math 3 и Head для YouTube Mashup Math и Head для YouTube’s Mashup Math и Head для YouTube’s Mashup Math и Head для YouTube’s Mashup Math и Head для You советник кампании Amazon Education « With Math I Can ». Вы часто можете увидеть, как я с радостью разрабатываю анимированные уроки математики, которыми я делюсь на своих Канал YouTube  . Или проводить слишком много времени в тренажерном зале или играть на своем телефоне.

Вам также может понравиться…

2 комментария

Опубликовано в ПОНИМАНИЕ УЧИТЕЛЯ

и

с тегами звездные войны математические игры, звездные войны математические игры бесплатно, последние математические игры джедаев, крутые звездные войны математические игры, звездные войны математические рабочие листы средней школы, звездные войны математика , математические задачи звездных войн, математические задачи на тему звездных войн, математические задачи последних джедаев, математические задачи звездных войн в средней школе, математические головоломки звездных войн, урок математики звездных войн в средней школе, урок математики звездных войн 4-й класс, урок математики звездных войн в 5-м классе, урок математики звездных войн 6-й класс, последние идеи математики джедая, последняя математика джедая, последние уроки математики джедая, математические действия супер марио, математические головоломки супер марио, математические игры супер марио, мир супер марио математики, математические игры нинтендо, урок математики супер марио, крутая математика супер Марио, урок математики nintendo, математические занятия на день святого патрика, математические занятия на день святого патрика для средней школы, математические занятия на день святого патрика для 4 класса, математические занятия на день святого патрика для 3 класса, день святого патрика Математические занятия на День Святого Патрика для 2 класса, Математические занятия на День Святого Патрика для 5 класса, Математические занятия на День Святого Патрика для 6 класса, Математические занятия на День Святого Патрика для 7 класса, Математические занятия на День Святого Патрика для 8 класса, Математические занятия на День Святого Патрика для 8 класса класс, математические занятия на день святого патрика для 7-го класса, математические занятия на день святого патрика для алгебры, математические занятия на день святого патрика для 6-го класса, математические занятия на день святого патрика для 5-го класса, математические занятия на день святого патрика для 4-го класса, математические занятия на день святого патрика для 4-го класса, математика на день святого патрика рабочие листы, математические листы ко дню святого патрика для средней школы, крутые математические игры день святого патрика, математическая головоломка ко дню святого патрика, снова в школу математические головоломки, снова в школу математические головоломки для детей, первый день в школе математическая головоломка, первый день в школе математика головоломки, снова в школу по математике, снова в школу по математике в средней школе, первая неделя школьных занятий по математике, бесплатно снова в школу по математике, бесплатно снова в школу по математике, снова в школу по математике по вечерам занятия, снова в школу элементарные математические занятия, снова в школу математические занятия 4 класс, снова в школу математические занятия 3 класс, снова в школу математические занятия 5 класс, снова в школу математические занятия 6 класс, снова в школу математические занятия 7 класс, назад в школу математические занятия 8-й класс, обратно в школу веселые математические занятия, снова в школу математические занятия для средней школы, первая неделя школьных математических занятий 4-й класс, разминка по математике для 3-го класса, разминка по математике для 4-го класса, теплая математика разминка по математике для 5 класса, разминка по математике для 6 класса, разминка по математике для 7 класса, разминка по математике для 8 класса, разминка по математике, разминка по математике, идея, разминка по математике, разминка по математике, разминка по математике идея деятельности, 2-й класс, 3-й класс, 4-й класс, 5-й класс, 6-й класс, 7-й класс, 8-й класс, разминка по математике для печати, топ3, covid, высший уровень, 10 логических головоломок, логические головоломки, логические головоломки, еще загадки

20 сложных загадок для взрослых

Кто сказал, что умопомрачительные логические головоломки только для детей? Мы придумали 20 совершенно новых загадок для взрослых, чтобы проверить ваше критическое мышление, математические и логические способности. Сложности варьируются от простых до умеренных и сложных — здесь каждый найдет что-то для себя.

Так что берите карандаш и лист бумаги для заметок и приготовьтесь рвать на себе волосы (и мы действительно имеем в виду это наилучшим образом). Когда вы думаете, что у вас есть правильный ответ, щелкните ссылку внизу каждой загадки, чтобы найти решение. Ошибся? Не беспокойтесь, у вас есть 19другие загадки, чтобы проверить.

Пройдите через наши загадки:

Приказы короля / Сколько яиц? / Золотая цепочка / Пиклбол / Автоматический выключатель / Два поезда, две бабушки / Муравьиная математика / Мятная лепешка / Великая американская железная дорога / Жестокая проблема SAT / Кинозвезды переходят реку / Дань уважения математическому гению / Один пояс, одна Земля / Постукивание локтем / Проблема с виски / Проблема с каракулями / Озадачивающие ученых / Что ‘ у нее на лбу? / Киану в президенты / Кто открыл шкафчики?

Загадка № 1: Приказы короля превращаются в адскую головоломку

Сложность: легкая

Король королевства Нупе Катан настолько обожает своих двух дочерей, что решает, что королевству будет лучше, если их станет больше девочек, чем мальчиков, и он издает следующий указ: все детородные пары должны продолжать рожать детей, пока у них не родится дочь!

Но, чтобы избежать перенаселения, он издает дополнительный указ: Все детородные пары будут прекратите иметь детей, как только у них появится дочь! Его подданные немедленно начинают выполнять его приказы.

Каково ожидаемое соотношение девочек и мальчиков в Катане спустя много лет?

Подсказка

Вероятность того, что каждый ребенок родится девочкой, составляет, конечно, 50 процентов.

Решение

Готовы к решению? Щелкните здесь, чтобы убедиться, что вы правы.

---

Загадка №2: Сколько яиц несет эта курица?

Сложность: Легко

Эта задача посвящена моему отцу, Гарольду Фейвсону. Благодаря ему я люблю математические головоломки, и это одна из первых задач (из многих), которые он дал мне, когда я рос.

Курица-полтора сносит полтора яйца за полтора дня. Сколько яиц несет одна курица за день?

Решение

Готовы к решению? Нажмите здесь, чтобы проверить, правы ли вы .

Загадка №3: ​​Математическая задача с золотой цепочкой обманчиво проста

Сложность: Средняя

Вы роетесь на чердаке своей прабабушки и находите пять коротких цепочек, каждая из которых состоит из четырех золотых звеньев. Вам приходит в голову, что если вы объедините их все в одну большую петлю из 20 звеньев, у вас получится невероятное ожерелье. Итак, вы приносите его ювелиру, который говорит вам, что стоимость изготовления ожерелья будет составлять 10 долларов за каждое золотое звено, которое она должна сломать, а затем снова запечатать.

Сколько это будет стоить?

Решение

Готовы к решению? Щелкните здесь, чтобы убедиться, что вы правы.

Загадка #4: Попробуйте решить эту головоломку с пиклболом

Сложность: 🚨СЛОЖНАЯ🚨 остается включенным после каждой игры, чтобы сыграть человека, который просидел эту игру.

В конце дня, когда они играли в пиклбол, Эбби измотана, сыграв последние семь игр подряд. Кенни, который менее запыхавшийся, подсчитывает количество сыгранных игр: 9.0003

Кенни сыграл восемь игр

Эбби сыграл 12 игр

Нед сыграл 14 игр

Кто у кого выиграл четвертую игру?

Подсказка

Сколько всего игр было сыграно?

Решение

Готовы к решению? Нажмите здесь, чтобы проверить, правы ли вы .

Загадка № 5: Загадка о нашем автоматическом выключателе — чистое зло. Извиняюсь.

Сложность: 🚨СЛОЖНАЯ🚨

Блок выключателя в вашем новом доме находится в неудобном углу подвала. К своему огорчению, вы обнаруживаете, что ни один из 100 автоматических выключателей не имеет маркировки, и вы сталкиваетесь с пугающей перспективой сопоставить каждый автоматический выключатель с соответствующей лампочкой. (Предположим, что каждый автоматический выключатель соответствует только одному источнику света.)

Для начала вы включаете все 100 светильников в доме, а затем направляетесь в свой подвал, чтобы начать обременительный процесс сопоставления. При каждой поездке в подвал вы можете включать и выключать любое количество автоматических выключателей. Затем вы можете бродить по коридорам своего дома, чтобы узнать, какие огни включены, а какие выключены.

Какое минимальное количество поездок вам нужно совершить в подвал, чтобы подключить каждый автоматический выключатель к каждому свету?

Подсказка

Решение , а не включает либо включение или выключение выключателей света в вашем доме, либо ощущение того, насколько нагрелись лампочки. Возможно, вы захотите сначала попробовать решить случай с 10 немаркированными автоматическими выключателями.

Решение

Готовы к решению? Нажмите здесь, чтобы убедиться, что вы правы .

---

Загадка №6: Два поезда. Две бабки. Сможете ли вы решить эту хитрую математическую загадку?

Сложность: Средняя

Две бабушки Джесси хотят видеть его каждые выходные, но живут в разных концах города. В качестве компромисса он говорит им, что каждое воскресенье он будет ходить на ближайшую к его квартире станцию ​​метро в случайное время дня и садиться на следующий прибывающий поезд.

Если это будет поезд, идущий на север, он навестит свою бабушку Эрику на окраине города, а если это окажется поезд, идущий на юг, он навестит свою бабушку Кару в центре города. Обе его бабушки согласны с этим планом, поскольку они знают, что поезда, идущие на север и юг, ходят каждые 20 минут.

Но через несколько месяцев бабушка Кара жалуется, что видит его только одно из пяти воскресений. Джесси обещает, что он действительно направляется на станцию ​​каждый день в случайное время. Как это может быть?

Подсказка

Поезда всегда прибывают в назначенное время.

Решение

Готовы к решению? Нажмите здесь, чтобы проверить, правы ли вы .

Загадка №7: вот чертовски сложная математическая задача о муравьях

Сложность: 🚨СЛОЖНАЯ🚨

Макс и Роуз — братья и сестры муравьи. Они любят гоняться друг с другом, но всегда равны, так как на самом деле ползут с одинаковой скоростью. Поэтому они решают создать гонку, в которой один из них (надеюсь) победит.

В этой гонке каждый из них начнет с нижнего угла прямоугольного параллелепипеда, а затем будет ползти со всей возможной скоростью, чтобы добраться до крошки в противоположном углу. Размеры их кубоидов как на картинке:

Лаура Фейвсон

Если они оба пойдут кратчайшим путем, чтобы добраться до своей крошки, кто первым доберется до своей крошки? (Не забывайте, что они муравьи, поэтому, конечно, они могут карабкаться по краям или поверхности прямоугольного параллелепипеда.)

Подсказка

Помните: мыслите нестандартно.

Решение

Готовы к решению? Нажмите здесь, чтобы убедиться, что вы правы .

Загадка №8: Эта загадка о мятной лепешке практически неразрешима

Сложность: 🚨СЛОЖНАЯ🚨

100 карамелек и один мятный пирожок. Вы и Кэрин будете ходить туда-сюда, беря не менее одной и не более пяти карамелек из кучи конфет за каждый ход. Тот, кто удалит последнюю карамель, также получит мятную лепешку. а ты любовь мятные пирожки.

Предположим, Кэрин позволяет вам решать, кто ходит первым. Кого выбрать, чтобы выиграть мятную лепешку?

Подсказка

Сначала найдите стопку из 10 карамелек.

Решение

Готовы к решению? Нажмите здесь, чтобы убедиться, что вы правы .

Загадка № 9: Сможете ли вы решить великую загадку американских железных дорог?

Сложность: Средняя

Эту задачу предложил физик П. Джеффри Унгар.

Наконец, Great American Rail-Trail по всей стране завершен! Вперед, похлопайте себя по плечу — вы только что установили самые длинные перила в истории мира — 4000 миль от начала до конца. Но сразу после церемонии открытия ваш помощник напоминает вам, что металл, который вы использовали для перил, летом немного расширяется, так что его длина в целом увеличивается на один дюйм.

«Ха!» вы говорите: «Один дюйм в перилах длиной 4000 миль? Это ничего!» Но… ты прав?

Предположим, что при расширении поручня он изгибается вверх в самой слабой точке, которая находится в центре. Насколько выше придется забираться пешеходам в центре страны летом, чтобы ухватиться за перила? То есть на рисунке ниже что такое h ? (Для целей этого вопроса игнорируйте кривизну Земли и предполагайте, что след представляет собой прямую линию.)

Лаура Фейвесон

Подсказка

Пифагор — увлекательная историческая личность.

Решение

Готовы к решению? Щелкните здесь, чтобы убедиться, что вы правы.

Загадка №10: Эта загадка похожа на особенно жестокую задачу SAT. Сможете ли вы найти ответ?

Сложность: Средняя

Аманда живет со своим сыном-подростком Мэттом в сельской местности — в нескольких минутах езды от школы Мэтта. Каждый день Аманда выходит из дома в одно и то же время, едет в школу с постоянной скоростью, забирает Мэтта ровно тогда, когда его шахматный кружок заканчивается в 5 часов вечера, а затем они сразу же вместе возвращаются домой с той же постоянной скоростью. Но однажды Мэтту стало нехорошо, поэтому он пораньше уходит с шахматной тренировки и едет домой на своем переносном скутере.

После того, как Мэтт ехал час, Аманда встречает его на своей машине (по своему обычному маршруту, чтобы забрать его), и они возвращаются вместе, прибывая домой на 40 минут раньше, чем обычно. Сколько шахматной практики пропустил Мэтт?

Подсказка

Рассмотрим случай, когда Аманда встречает Мэтта, когда выходит из их дома.

Решение

Готовы к решению? Нажмите здесь, чтобы проверить, правы ли вы .

Загадка №11: Сможете ли вы переправить этих трех кинозвезд через реку?

Сложность: Средняя

Три кинозвезды, Хлоя, Лекса и Джон, снимают фильм на Амазонке. Они очень известны и очень требовательны, поэтому их агенты всегда с ними. Однажды, отсняв сцену в глубине тропического леса, трое актеров и их агенты решают вернуться на базу пешком. Внезапно они подходят к большой реке.

На берегу реки они находят маленькую гребную лодку, но она достаточно большая, чтобы одновременно вместить двоих. Улов? Ни один из агентов не хочет оставлять свою кинозвезду с другими агентами, если их тоже нет. Они не верят, что другие агенты не попытаются переманить их звезду.

Например, с агентом Хлои все в порядке, если Хлоя и Лекса одни в лодке или на одном из берегов реки, но определенно не , если агент Лексы тоже с ними. Так как же им всем перебраться через реку?

Подсказка

Нет единственного способа решить эту проблему.

Решение

Готовы к решению? Нажмите здесь, чтобы проверить, правы ли вы .

Загадка № 12: Эта смехотворно сложная загадка — наша дань уважения позднему математическому гению. Можете ли вы понять это?

Сложность: 🚨HARD🚨

11 апреля Джон Хортон Конвей , блестящий математик, страстно любивший головоломки и игры, умер от осложнений, вызванных COVID-19. Конвей является изобретателем одной из моих любимых легендарных задач (не для слабонервных) и знаменитой игры Game of Life . Я создал эту проблему в его честь.

Кэрол создавала генеалогическое древо, но не смогла отследить дату рождения своей матери. Единственной зацепкой, которую она нашла, было письмо, написанное дедушкой бабушке в день рождения ее матери. К сожалению, некоторые символы были смазаны, представленные здесь «___» . (Длина строки не отражает количество смазанных символов.)

«Дорогая Вирджиния,

Я и не подозревала, отправляясь на работу в понедельник утром, что к вечеру у нас родится прекрасная девочка. И в годовщину свадьбы не меньше! Это заставляет меня вспомнить тот невероятный выходной день, J___ 27th, 19___ , когда мы впервые поделились нашей клятвой создать семью вместе, и вот мы здесь! С восьмой годовщиной, любовь моя.

С любовью, Эдвин»

Вопрос: Когда родилась мать Кэрол?

Подсказка

Эта задача навеяна Правилом судного дня Конвея .

Решение

Готовы к решению? Нажмите здесь, чтобы проверить, правы ли вы .

Загадка №13: Чтобы решить эту запутанную математическую загадку, вам нужен только один пояс и одна земля

Сложность: Средняя

Представьте, что у вас очень длинный пояс. Ну, очень длинный, на самом деле… на самом деле, он достаточно длинный, чтобы плотно обернуться вокруг всей нашей планеты. (Для простоты предположим, что Земля идеально круглая, без гор, океанов или других преград на пути пояса.)

Естественно, вы очень гордитесь своим поясом. Но тут появляется ваш брат Питер и, к вашему неудовольствию, достает ремень, который0043 просто немного длиннее вашего. Он хвастается, что его пояс длиннее ровно на его рост: 6 футов.

Если бы Питер тоже обернул свой пояс по окружности Земли, как высоко над поверхностью он мог бы подвесить пояс, если бы он туго и равномерно натянул его?

Подсказка

Окружность Земли составляет около 25 000 миль или 130 миллионов футов … но вам не нужно знать это, чтобы решить эту проблему.

Решение

Готовы к решению? Нажмите здесь, чтобы проверить, правы ли вы .

Загадка №14: Эта загадка с постукиванием локтя дьявольская. Удачи в ее решении.

Сложность: 🚨HARD🚨

Когда-нибудь в будущем, когда будут сняты запреты на самоизоляцию, супружеская пара, Флориан и Джулия, отправятся в бар, чтобы отпраздновать обретенную свободу.

Там они находят еще четыре пары, у которых была такая же идея.

Стремясь к общению, каждый человек в пяти парах с энтузиазмом постукивает локтями (новое рукопожатие) с каждому человеку, которого они еще не встретили .

На самом деле оказалось, что многие люди знали друг друга раньше, поэтому, когда Джулия спрашивает всех, сколько локтей они ударили, она получает девять разных ответов!

Вопрос: Сколько локтей постучал Флориан?

Подсказка

Какие девять ответов услышала Юля?

Решение

Готовы к решению? Нажмите здесь, чтобы проверить, правы ли вы .

Загадка №15: После того, как вы попытаетесь решить эту загадку о виски, вам понадобится выпить

Сложность: Легкая , ни воды без виски!» Итак, однажды, когда перед Аланом стоит стакан виски, а перед Клэр — стакан воды того же размера, Алан берет ложку своего виски и кладет ее в воду Клэр.

Клэр размешивает подкрашенную виски воду, а затем кладет ложку этой смеси обратно в виски Алана, чтобы убедиться, что они выпили точно такое же количество.

Итак: В виски Алана больше воды или в воде Клэр больше виски? И имеет ли значение, насколько хорошо Клэр перемешала?

Подсказка

Размер ложки имеет значение , а не .

Решение

Готовы к решению? Щелкните здесь, чтобы убедиться, что вы правы.

Загадка №16: Проблема с дудлом намного сложнее, чем кажется. Можете ли вы решить это?

Сложность: Средняя

Загадка этой недели относительно проста, но тем не менее зловеща.

Вопрос: можно ли составить 100, вставив любое количество плюсов и минусов в строку цифр 9 8 7 6 5 4 3 2 1? Вы не можете изменить порядок цифр! Итак, какое наименьшее количество плюсов и минусов нужно, чтобы получить 100?

Эндрю Дэниелс

Например, 98 — 7 — 6 + 54 — 32 показывает один из способов чередования плюсов и минусов, но поскольку оно равно 107, это не решение.

Я называю это «проблемой с каракулями»: над ней лучше всего работать во время собраний, где в противном случае вы могли бы рисовать.

Подсказка

Возможно, вы захотите начать искать решения, которые используют в общей сложности семь плюсов и минусов (хотя есть способы использовать меньше).

Решение

Готовы к решению? Щелкните здесь, чтобы убедиться, что вы правы.

Загадка №17: Эта математическая головоломка поставила в тупик всех ученых, кроме одного. Думаешь, сможешь взломать?

Уровень сложности: ВЫСОКИЙ

В честь Фримена Дайсона, известного физика , который умер в прошлом месяце , вот легендарная история, демонстрирующая его сообразительность и невероятную силу ума.

Однажды на собрании ведущих ученых один из них вслух спросил, существует ли целое число, которое можно было бы точно удвоить, переместив его последнюю цифру вперед. Например, 265 удовлетворило бы этому числу , если бы 526 было его точным дубликатом, а это не так.

Через , по-видимому, всего пять секунд , Дайсон ответил: «Конечно, есть, но самое маленькое такое число состоит из 18 цифр».

Это заставило некоторых из самых умных ученых в мире недоумевать, как он мог понять это так быстро.

Итак, учитывая подсказку Дайсона, какое наименьшее такое число?

Подсказка

Мой второклассник недавно научился складывать трехзначное число с помощью классического вертикального метода:

Эндрю Дэниелс

18-значные числа, разумеется, можно добавлять таким же образом.

Решение

Готовы к решению? Нажмите здесь, чтобы проверить, правы ли вы .

Загадка №18: Выясни, что у нее на лбу

Сложность: Средняя

Сесилия любит проверять логику своих очень логичных друзей Джаи, Джулиана и Леви, поэтому она объявляет: Я напишу положительное число на каждом из ваших лбов. Все числа не совпадают, а два числа дают в сумме третье».

Она записывает числа на их головах, затем поворачивается к Джае и спрашивает, какой у нее номер. Джайя видит, что у Джулиана 20 на лбу, а у Леви 30. Она задумалась на мгновение, а затем сказала: «Я не знаю, какой у меня номер». Джулиан трубит: «Я тоже не знаю своего номера», а затем Леви восклицает: «Я тоже!» Сесилия радостно говорит: «Я наконец поставила вас в тупик, ребята!»

«Не так быстро!» — говорит Джая. «Теперь я знаю свой номер!»

Какой у Джайи номер?

Подсказка

Джайя может быть одним из двух чисел, но только одно из этих чисел приведет к тому, что Джулиан и Леви не будут знать свои числа. Почему?

Решение

Готовы к решению? Нажмите здесь, чтобы проверить, правы ли вы .

Загадка №19: Сможете ли вы добиться избрания Киану Ривза президентом?

Сложность: Средняя

На дворе 2024 год, и в демократических праймериз участвуют пять кандидатов: Тейлор Свифт, Опра Уинфри, Марк Кьюбан, Киану Ривз и Дуэйн Джонсон. (Эй, такое может случиться.) Как обычно, первые предварительные выборы проходят в Айове.

В попытке преодолеть смущение после фиаско на закрытом собрании 2020 года Демократическая партия Айовы только что объявила о новом надежном способе поиска лучшего кандидата: выборы будут проводиться четыре раза подряд.

Сначала кандидат 1 будет баллотироваться против кандидата 2. Затем победитель будет баллотироваться против кандидата 3, затем этот победитель будет баллотироваться против кандидата 4, и, наконец, победитель этих выборов будет баллотироваться против финального кандидата. Согласно переходному свойству, победитель этих последних выборов должен быть лучшим кандидатом. .. так говорит Демократическая партия Айовы.

Кандидат Киану чувствует себя довольно плохо, так как он знает, что он находится в самом низу рейтинга большинства избирателей, и ни один из них не занимает первое место. На самом деле он знает, что население Айовы разделено на пять равных групп и что их предпочтения следующие:

.

Киану дружит с детства Биллом С. Престоном, эсквайром, новым главой Демократической партии Айовы. Престон, уверенный, что порядок кандидатов не имеет значения для результата, говорит Киану, что он может выбрать порядок голосования кандидатов.

Итак, какой порядок должен выбрать Киану?

Подсказка

Как поведет себя Киану в гонках один на один с каждым кандидатом?

Решение

Готовы к решению? Нажмите здесь, чтобы проверить, правы ли вы .

Загадка №20: Кто открыл все эти чертовы шкафчики?

Сложность: Средняя

В главном коридоре старшей школы Хелм стоят 100 шкафчиков. Каждую ночь директор школы следит за тем, чтобы все шкафчики были закрыты, чтобы следующий день начался организованно. Однажды 100 озорных школьников решают пошутить.

Все ученики встречаются перед началом занятий и выстраиваются в очередь. Затем первый ученик идет по коридору и открывает каждый шкафчик. Следующий ученик закрывает все остальные шкафчики (начиная со второго шкафчика). Затем ученик 3 подходит к каждому третьему шкафчику (начиная с третьего) и открывает его, если он закрыт, и закрывает, если он открыт. Затем ученик 4 открывает каждый четвертый шкафчик, если он закрыт, и закрывает его, если он открыт. Это продолжается до тех пор, пока Студент 100, наконец, не доходит до сотого шкафчика. Когда директор приходит поздно утром, какие шкафчики она находит открытыми?

Подсказка

Убедитесь, что вы обращаете внимание на все факторы.

Решение

Готовы к решению? Нажмите здесь, чтобы проверить, правы ли вы .

---

Лаура Фейвсон

Лаура Фейвсон — экономист в правительстве, рассказчик и энтузиаст математических головоломок. Она живет в Вашингтоне, округ Колумбия, с мужем и двумя дочерьми. 9Когда-то говорили, что 2 = -1$ не имеет решения. Затем было открыто (или изобретено?) число $i$, и наша система счисления обогатилась. В частности, в этом новом чудесном мире комплексных чисел мы можем доказать фундаментальную теорему алгебры, следствием которой является разрешимость любого многочлена в комплексной области.

Подобным образом логическое утверждение $P = \lnot P$ не имеет решения в множестве $\{True, False\}$. Это хорошо известный парадокс лжеца, который проявлялся в различных формах в логике, например. Парадокс Рассела, теорема Гёделя о неполноте.

Теперь предположим, что мы изобрели новое логическое значение $iTrue$, воображаемое, если хотите, которое определяется как решение уравнения $P = \lnot P$. Тогда наши предложения будут варьироваться в диапазоне $\{True, False, iTrue\}$.

Мой вопрос: Может ли эта новая система или подобная ей освободить нас от таких парадоксальных, неразрешимых логических утверждений подобно тому, как комплексные числа освободили нас от неразрешимых многочленов?

Мои мысли: Я скептически отношусь к вышеупомянутой системе. Я чувствую, что это может помочь нам «разрешить» некоторые парадоксы, но не все. Кроме того, не очевидно, что эти решения будут означает . С другой стороны, было бы прекрасно, если бы аналогия с комплексными числами работала на более строгой основе.

• логика
• программный вопрос

$\endgroup$

36

$\begingroup$

По многозначной логике имеется обширная литература. Первоначальная трехзначная логика Лукасевича, возможно, является самой простой такой логикой, и дополнительное истинностное значение $P$ удовлетворяет вашей формуле $P \iff \lnot P$.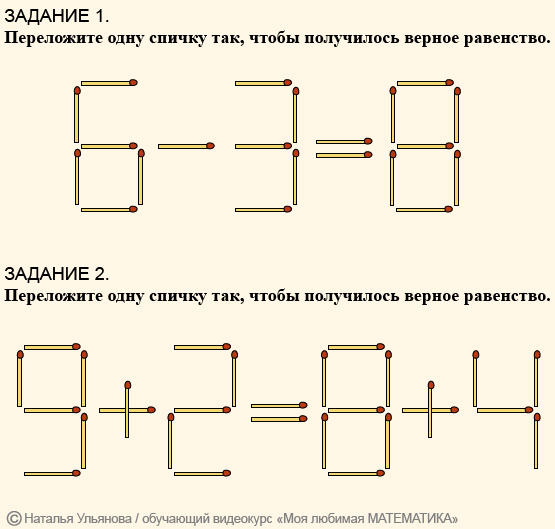 Лукасевич развил это в то, что сейчас называется логикой Лукасевича, которая интенсивно изучалась и обобщалась на протяжении многих лет. Одним из этих обобщений является предмет нечеткой логики, которая имеет практическое применение, например. моделировать ситуации, когда знания несовершенны. 92=-1$. Скорее важно, чтобы многое из того, что люди знали о действительных числах, также относилось к комплексным числам; в частности, $\mathbb C$ является полем нулевой характеристики (хотя и не упорядоченным). Таким образом, люди могли продолжать манипулировать уравнениями (но не неравенствами) с комплексными числами так же, как они это делали с действительными числами. Оказалось, что свойств действительных чисел, которые сохраняются при переходе к комплексным числам, достаточно, чтобы дать интересную и полезную теорию (а позже люди обнаружили дополнительные свойства $\mathbb C$, такие как алгебраическое замыкание, которые делают его еще более интересно и полезно).

Аналогично, было бы мало пользы от введения нового значения истинности и объявления его равным своему отрицанию. Нужно было бы показать, что новая система значений истинности сохраняет достаточно свойств традиционной системы, чтобы люди могли продолжать рассуждать более или менее так, как они привыкли.

$\endgroup$

3

$\begingroup$

Как говорит Роб Артан, на эту тему имеется обширная литература, и только некоторые из них касаются парадоксов.

Тем не менее, как решение парадоксов, подобных лжецу, введение третьего истинностного значения встречает немедленную трудность, так называемого «усиленного лжеца»:

Это предложение неверно.

$\endgroup$

2

$\begingroup$

Ваше введение в вопрос кажется очень похожим на мысли Л. Х. Кауфмана в «Виртуальной логике и мнимых значениях». Либо вы были вдохновлены ими, либо их стоит проверить.

Что касается вашего вопроса, похоже, вы ищете логику, в которой Закон исключенного третьего не является аксиомой. Итак, я бы предложил проверить поле паранепротиворечивой логики.

$\endgroup$

Твой ответ

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

Логика действительных и комплексных чисел

Мне всегда нравилась логика. Я изучал его кучу в средней школе и колледже. Сейчас это своего рода хобби. Я иногда обращаюсь к нему за облегчением, когда разочаровываюсь, пытаясь понять, что я могу сделать с глобальным потеплением. В последнее время я немного углубился в логику реальных и комплексных чисел. И этой осенью я веду курс по реальному анализу для выпускников, так что у меня есть небольшое оправдание для этого.

Есть что-то в логике, что одновременно завораживало и пугало меня с самого детства: это то, как мы не можем полностью определить бесконечные структуры, такие как действительные или комплексные системы счисления, используя язык с конечным числом символов и теорию с конечное число аксиом.

Ужасно, что мы не до конца понимаем, о чем говорим, когда говорим о числах! Но удивительно, что мы можем многое понять об ограничениях.

Об этом можно сказать по-разному, в зависимости от того, какие особенности этих систем счисления мы хотим описать и какую логику мы хотим использовать.

Может быть, мне стоит начать с натуральных чисел, так как эта история более известна. Это также может послужить беглым обзором некоторых основных понятий, которые, как я полагаю, вы уже смутно знаете: логика первого порядка и логика второго порядка, доказательства и модели и так далее. Если вы этого не знаете, вы можете либо притвориться, либо прочитать несколько ссылок в этой статье!

Натуральные числа

Когда Пеано первоначально описал натуральные числа, он сделал это, используя аксиомы, сформулированные в логике второго порядка. В логике первого порядка мы можем количественно оценить переменные: например, мы можем сказать

, что означает, что если предикат верен для всех, он верен для любой переменной. В логике второго порядка мы также можем количественно определять предикаты: например, мы можем сказать

, что говорит, что тогда и только тогда, когда для каждого предиката истинно именно тогда, когда правда. Лейбниц использовал этот принцип, называемый тождеством неразличимых, чтобы определить равенство… и это прекрасный пример большей силы логики второго порядка. В логике первого порядка мы обычно включаем равенство как часть языка и добавляем аксиомы, описывающие его свойства, например 9.0003

В логике второго порядка мы можем определить равенство и доказать эти свойства, исходя из свойств, которые мы уже имеем для

Так или иначе, в своих аксиомах для натуральных чисел Пеано использовал логику второго порядка, чтобы сформулировать принцип математической индукции следующим образом:

Это говорит о том, что если у вас есть какой-либо предикат, который истинен для и истинен для всякий раз, когда он истинен для, то он истинен для всех натуральных чисел.

В 1888 году Дедекинд показал, что исходные аксиомы Пеано для натуральных чисел равны категориальный , что означает, что все его модели изоморфны.

Понятие «модель» включает теорию множеств. В модели вы выбираете набор для ваших переменных, которые будут варьироваться, выбираете подмножество для каждого предиката, а именно подмножество, где этот предикат истинен, и так далее, таким образом, чтобы все аксиомы в этой теории были удовлетворены. Если две модели изоморфны, они одинаковы для всех практических целей.

Таким образом, грубо говоря, категориальная теория — это теория, которая дает полное описание математической структуры, о которой идет речь.

Таким образом, результат Дедекинда кажется отличной новостью. Похоже, что оригинальные аксиомы второго порядка Пеано для арифметики полностью описывают натуральные числа.

Однако есть важная загвоздка. В теории множеств есть много неопределенных по своей сути вещей! Так что на самом деле категориальная теория дает полное описание математической структуры, о которой идет речь , относительно выбора того, какие множества подобны 9.0044 .

Таким образом, результат Дедекинда просто запихивает под ковер все таинственное и неопределенное, связанное с натуральными числами: они становятся таинственным и неопределенным в теории множеств. Это стало ясно гораздо позже, благодаря Гёделю и другим. И в процессе стало ясно, что логика второго порядка немного проблематична по сравнению с логикой первого порядка.

Видите ли, в логике первого порядка есть набор правил вывода, а именно:

• звук : Каждое доказуемое предложение выполняется в любой модели.

• семантически завершено: Каждое предложение, содержащееся в любой модели, доказуемо.

• эффективное: Существует алгоритм, который может правильно решить, является ли любая заданная последовательность символов доказательством.

Логика второго порядка не работает! Он «слишком мощный», чтобы иметь все три этих приятных свойства.

Итак, в наши дни люди часто работают с версией аксиом Пеано первого порядка для арифметики. Вместо того, чтобы записать одну аксиому для математической индукции:

мы записываем схему аксиом — бесконечный список аксиом — с одной аксиомой вроде этой:

для каждой формулы, которую мы можем записать, используя язык арифметики.

Эта версия арифметики Пеано первого порядка является , а не категоричной: она имеет множество неизоморфных моделей. Люди часто делают вид, что существует одна «лучшая» модель: они называют ее «стандартными» натуральными числами, а все остальные называют «нестандартными». Но есть в этом что-то подозрительное.

Действительно, первая теорема Гёделя о неполноте говорит о том, что существует множество утверждений о натуральных числах, которые нельзя ни доказать, ни опровергнуть, исходя из аксиом Пеано. Отсюда следует, что для любого такого утверждения мы можем найти модель аксиом Пеано, в которой это утверждение выполняется, а также модель, в которой оно не выполняется.

Кроме того, это остается верным, даже если мы добавим любой список дополнительных аксиом к арифметике Пеано, пока существует какой-то алгоритм, который может перечислить все эти аксиомы.

Итак, я бы предпочел сказать, что существует множество различных «версий» натуральных чисел, так же как существует множество различных групп.

Мы можем изучать эти разные версии, и это увлекательная тема:

• Википедия, Нестандартные модели арифметики.

Тем не менее, я хочу поговорить о ситуации для других систем счисления!

Действительные числа

С действительными числами ситуация лучше — по крайней мере, если мы готовы думать о них «чисто алгебраически», оставляя большую часть анализа позади.

Для этого мы можем использовать теорию «реального замкнутого поля». Это список аксиом, сформулированных в логике первого порядка, которые описывают, как работают действительные числа. Вы можете представить себе эти аксиомы как состоящие из трех частей:

• поле аксиомы: обычные алгебраические тождества, включающие и вместе с законами, говорящими, что все имеет аддитивную обратную и все, кроме мультипликативной обратной.

• формально реальное поле аксиома, говорящая, что это не сумма квадратов. Это означает, что мы можем снабдить поле концепцией, превращающей его в упорядоченное поле, но не обязательно уникальным образом.

• реальное замкнутое поле аксиом, гласящих, что также для любого числа или или имеет квадратный корень, и каждый многочлен нечетной степени имеет корень. Помимо прочего, это означает, что наше поле можно уникальным образом превратить в упорядоченное поле. Для этого мы говорим, если и только если имеет квадратный корень.

Тарский показал, что эта теория полна : любое предложение первого порядка, включающее только операции и отношение, может быть либо доказано, либо опровергнуто, исходя из приведенных выше аксиом.

Тем не менее, теория реальных замкнутых полей не категорична: кроме реальных чисел существует множество других моделей! Все эти модели элементарно эквивалентны : любое предложение, включающее справедливую логику первого порядка, верное в одной модели, верное во всех остальных. Но не все эти модели изоморфны: мы не можем получить биекцию между ними, сохраняющую и

Действительно, только математические структуры конечного размера могут быть «прибиты» с точностью до изоморфизма теориями логики первого порядка. Видите ли, теорема Левенгейма–Скулема утверждает, что если теория первого порядка в счетном языке имеет бесконечную модель, то она имеет по крайней мере одну модель каждой бесконечной мощности. Итак, если мы пытаемся использовать такого рода теорию для описания бесконечно большой математической структуры, самое большее, на что мы можем надеяться, это то, что после того, как мы укажем его мощность , аксиомы его полностью определяют.

Однако настоящие аксиомы замкнутого поля не так хороши. Во-первых, у них есть бесконечно много неизоморфных счетных моделей. Вот некоторые из них:

• алгебраических действительных чисел : это действительные числа, которые подчиняются полиномиальным уравнениям с целыми коэффициентами.

• вычислимых действительных чисел : это действительные числа, которые могут быть вычислены с произвольной точностью с помощью компьютерной программы.

• действительных арифметических чисел : это числа, определяемые на языке арифметики. Точнее, действительное число является арифметическим , если существует формула на языке арифметики Пеано первого порядка с двумя свободными переменными такая, что

Каждое вычислимое действительное число является арифметическим, но не наоборот: просто потому, что можно определить действительное число указанным выше способом не означает, что вы можете вычислить его с произвольной точностью!

И в самом деле, существуют другие, еще более крупные исчисляемые действительные закрытые поля, состоящие из действительных чисел, которые можно определить с помощью более мощных методов, таких как арифметика Пеано второго порядка.

Мы также можем получить исчисляемые действительные закрытые поля, используя такие приемы: взять алгебраические действительные числа и добавить число вместе с достаточным количеством других чисел, чтобы снова получить действительное замкнутое поле. Или мы могли бы добавить и то, и другое, и это, вероятно, дает большее реальное замкнутое поле, но никто не знает, потому что, насколько нам известно, может быть равно плюс какое-то рациональное число! Все считает, что это ложь, но никто этого не доказал.

Существует также множество неизоморфных бесчисленных вещественных замкнутых полей, в том числе и таких, которые содержат обычные действительные числа.

Например, мы можем взять действительные числа и добавить элемент, который больше и так далее, а затем сделать все необходимое, чтобы получить еще одно реальное замкнутое поле. Это включает в себя добавление таких элементов, как

и так далее. Итак, мы получаем множество бесконечностей и бесконечно малых.

Здесь все немного запутанно, пытаясь понять, что чему равно. Но есть еще одно реально закрытое поле, содержащее бесконечный элемент, которым, кажется, легче управлять. Называется поле настоящей серии Puiseux . Это ряды вида

, где любое целое число, возможно, отрицательное, любое
положительное целое число, а коэффициенты действительны.

Что это? Это просто формальная переменная. Но настоящие ряды Пюизё представляют собой настоящее замкнутое поле и действуют так, как будто оно положительное, но меньше любого положительного действительного числа.

Приложив значительно больше усилий, мы можем составить реальное замкнутое поле, которое:

• содержит действительные числа,

• содержит элемент больше, чем

• подчиняется принципу переноса , который гласит, что первый- утверждение порядка, сформулированное на обычном языке теории множеств, верно для действительных чисел тогда и только тогда, когда оно верно для этой другой системы счисления.

Любое реальное замкнутое поле с такими свойствами называется системой гиперреальных чисел . В 1960-х годах логик Абрахам Робинсон использовал их, чтобы сделать старую идею Лейбница о бесконечно малых числах в исчислении полностью строгой. Полученная теория называется нестандартным анализом .

Итак, я надеюсь, вы видите захватывающее — или, возможно, пугающее — разнообразие реальных закрытых полей. Но не забывайте: все они элементарно эквивалентны. Если предложение, включающее справедливую логику первого порядка, выполняется в любом из этих реальных замкнутых полей, оно выполняется во всех них!

Вам может быть интересно, что говорит об этом логика второго порядка.

Здесь ситуация выглядит совсем иначе. В логике второго порядка мы можем проводить анализ, потому что мы можем количественно определить более предикатов , что позволяет нам говорить о подмножествах действительных чисел. А в логике второго порядка мы можем записать теорию действительных чисел, которая будет категоричной! Она называется теорией полных по Дедекинду упорядоченных полей . Опять же, мы можем сгруппировать аксиомы в три группы:

• поле аксиом: обычные алгебраические тождества, включающие и вместе с законами, говорящими, что все имеет аддитивную обратную и все, кроме мультипликативной обратной.

• упорядоченное поле аксиома, утверждающая, что существует такой полный порядок, что и подразумевает и подразумевает

• полнота Дедекинда аксиома, утверждающая, что каждое непустое подмножество с верхней границей имеет наименьшую верхнюю границу. Но вместо того, чтобы говорить о подмножествах, мы говорим о предикатах, которые относятся к этим подмножествам, поэтому мы говорим «для всех предикатов таких, что…»

Поскольку они категоричны, люди часто используют эти аксиомы для определения действительных чисел. Но поскольку они второго порядка, проблема многих неизоморфных моделей на самом деле просто заметена под ковер. Если мы будем использовать логику второго порядка, у нас не будет надежной, семантически полной и эффективной концепции «доказательства». И если мы будем использовать аксиомы первого порядка для теории множеств, чтобы явно говорить о подмножествах вместо предикатов, то наша теория множеств будет иметь много моделей! В каждой модели будет версия реальных чисел, уникальная с точностью до изоморфизма… но версии в разных моделях будут сильно отличаться.

На самом деле существует определенный смысл, в котором «стандартные действительные числа» в одной модели теории множеств могут быть «гипердействительными числами» в другой. Впервые это было показано Авраамом Робинсоном.

Комплексные числа

Я упоминал, что когда мы изучаем бесконечную математическую структуру с помощью логики первого порядка, лучшее, на что мы можем надеяться, это иметь одну модель каждого размера (с точностью до изоморфизма). Реальные числа далеко не так хороши… но комплексные числа гораздо ближе!

Точнее сказать какой-то кардинал. Теория первого порядка, описывающая структуру на одном множестве, называется κ-категоричной , если она имеет уникальную модель мощности. -категоричное для каждое неисчислимое Я не прорабатывал доказательство, которое, кажется, полно интересных идей. Но такие теории называются несчетно категоричный .

Отличным примером является «чисто алгебраическая» теория комплексных чисел. Под этим я подразумеваю, что мы записываем только аксиомы, включающие и не включаем ничего ни об этом времени, ни о сложном сопряжении. Видите ли, если мы начнем говорить о комплексном сопряжении, мы сможем выделить действительные числа среди комплексных чисел, а затем мы более или менее вернемся к истории, которая была у нас с действительными числами.

Эта теория называется теорией алгебраически замкнутое поле нулевой характеристики . И снова аксиомы делятся на три группы:

• поле аксиом.

• нулевая характеристика аксиом: это бесконечный список аксиом, утверждающих, что

• алгебраически замкнутых аксиом: они говорят, что каждый непостоянный многочлен имеет корень.

Почти любой достойный математик знает, что комплексные числа являются моделью этих аксиом, мощность которых соответствует континууму. Существует множество различных счетных моделей: алгебраические комплексные числа, вычислимые комплексные числа и так далее. Но поскольку приведенная выше теория неисчислимо категорична, существует ровно одно алгебраически замкнутое поле нулевой характеристики из каждое несчетной мощности… с точностью до изоморфизма.

Это подразумевает некоторые интересные вещи.

Например, мы можем взять комплексные числа, добавить дополнительный элемент и позволить ему свободно генерировать большее алгебраически замкнутое поле. Оно «больше» в том смысле, что содержит комплексные числа как правильное подмножество, даже подполе. Но поскольку оно имеет ту же мощность, что и комплексные числа, оно равно 9.0043 изоморфно комплексным числам!

И затем, поскольку это «большое» поле изоморфно комплексным числам, мы можем перевернуть этот аргумент. Мы можем взять комплексные числа, удалить множество тщательно отобранных элементов и получить подполе, изоморфное комплексным числам.

Или, если хотите, мы можем взять комплексные числа, присоединить к действительно огромному множеству дополнительных элементов и позволить им свободно порождать алгебраически замкнутое поле нулевой характеристики. Мощность этого поля может быть сколь угодно большой. Он будет определяться с точностью до изоморфизма своей мощностью.

Хорошая новость заключается в том, что благодаря результату Тарского теория алгебраически замкнутого поля нулевой характеристики завершена, а значит, все ее модели элементарно эквивалентны. Другими словами, все те же предложения первого порядка написаны на языке и выполняются в каждой модели.

А вот и кусочек странной новости.

Как я уже упоминал, теория реального замкнутого поля , а не неисчислимо категорична. Это подразумевает что-то действительно странное. Помимо «обычных» действительных чисел мы можем выбрать другое действительное замкнутое поле, не изоморфное ему, с той же мощностью. Мы можем построить комплексные числа, используя пары действительных чисел. Мы можем использовать тот же прием, чтобы построить поле с помощью пар фигур в Но легко проверить, что это забавное поле алгебраически замкнуто и имеет нулевую характеристику. Поскольку он имеет ту же мощность, что и должен быть изоморфен

Короче говоря, разные «версии» действительных чисел могут дать одну и ту же версию комплексных чисел!

Ссылки

Итак, я надеюсь, вы видите, что логические основы вещественных и комплексных систем счисления довольно скользкие… но с работой мы можем многое понять об этой скользкости.

Помимо ссылок, которые я дал, я просто хочу упомянуть еще две. Во-первых, вот бесплатный вводный учебник по математическому анализу, основанный на нестандартном анализе:

• Х. Джером Кейслер, Элементарное исчисление: инфинитезимальный подход , доступен на веб-сайте или в формате PDF.

А вот пояснительная статья, которая углубляется в бессчетно категоричные теории:

• Ник Рэмси, Теорема категоричности Морли.

Эта запись была опубликована в понедельник, 8 сентября 2014 г., в 1:00 и находится в разделе «Математика». Вы можете следить за любыми ответами на эту запись через ленту RSS 2.0. Вы можете оставить отзыв или вернуться со своего сайта.

Инвестиции в разум: математические и логические задачи

Обзор

Математика и логика в какой-то степени были с нами с самого начала цивилизации. Эволюция была интересной и привела нас к некоторым из самых сложных головоломок, проблем и загадок нашего времени.

В первые дни мы полагались на грубые рассуждения для решения наших проблем. С развитием сложного языка и культуры вскоре появились специалисты, а вместе с ними и язык чисел, которые формализовали большую часть нашей логики — математики. Таким образом, они всегда были связаны друг с другом; у вас не может быть математики без логики, а без математики рассуждать было бы еще труднее.

Позже, в 19 веке, мы познакомились с современной математической логикой, когда она расходилась с чистой логикой, поэтому она стала самостоятельным разделом математики. Это быстро просочилось в школьную программу и инженерию. С тех пор математические логические задачи дразнят мозг людей повсюду, от учеников начальной школы до математиков и даже экспертов по головоломкам.

Мы составили список сложных задач на математику, логику и математическую логику, которые могут попробовать все, от школьников до экспертов по головоломкам. Они обязательно дадут вашему мозгу тренировку. Веселитесь и удачи.

 

Начальный уровень (дети) – Математика и логические задачи

Математика и логика лучше всего знакомятся в раннем возрасте, чтобы помочь развивающемуся уму понять концепции и понять разницу между логикой и ошибками на раннем этапе. Воспользуйтесь любой из этих ссылок, чтобы ваши ученики встали на правильный путь в самом начале обучения.

• В NRICH есть двадцать две забавные игры и задачи, доступные в Интернете для решения юными учениками. Это простые задачи с базовыми изображениями, которые можно просмотреть в Интернете или распечатать для использования в классе.
• Государственные школы Арлингтона предлагают ссылки на множество математических задач для учащихся в разделе игр для мозга. Большинство их ссылок ведут на другие сайты, такие как PBS Kids и Британская радиовещательная корпорация.
• Организация Mathematics Education Collaborative составила список различных традиционных настольных и карточных игр, в которые можно играть в автономном режиме и которые развивают логическое мышление. Почему бы не перевести обучение в автономный режим, оставив его интересным?
• Управление энергетической информации США предлагает печатный документ о головоломках на логику ветра в качестве пособия для учителей для младших школьников. Пусть студенты узнают об окружающей среде, энергии и логике одновременно!
• В Национальном институте наук об окружающей среде и здоровье есть коробки-головоломки REBUS, которые нужно решить. По их словам, РЕБУС — это «изображение имени, произведения или фразы». Используйте эти визуальные головоломки, чтобы помочь расширить кругозор.

 

Промежуточный уровень (подростки и молодежь) – Математические и логические задачи

Вот еще несколько сложных математических и логических задач для учащихся следующего уровня. Важно практиковать логическое мышление на каждом этапе обучения.

• В Калифорнийском университете в Лос-Анджелесе есть раздаточный материал с несколькими головоломками, которые можно решить в классе или дома без использования компьютера.
• org содержит интерактивную трехмерную логическую игру, в которую можно играть в браузере без необходимости устанавливать или загружать что-либо.
• Центр математического и естественнонаучного образования AIMS предлагает шесть интересных и занимательных логических головоломок, направленных на работу ума.
• Университет Стетсона предлагает широкий выбор простых визуальных логических головоломок, которые больше похожи на игру, чем на работу.
• Университет Юты предлагает серию словесных головоломок, которые требуют только логического мышления. Никаких особых математических навыков не требуется!

 

Продвинутый уровень (подростки и молодые люди) — математические и логические задачи

Все еще готовы принять вызов? Вот еще четыре варианта для смелых.

• Cut the Knot содержит обширный интерактивный математический сборник и раздел головоломок, охватывающий несколько областей математики и логики. Они охватывают алгебру, арифметику, геометрию и многое другое.
• Wabash College публикует новую задачу каждые пару недель на случай, если у вас закончатся задачи. Доступ к предыдущим проблемам также доступен, если вы хотите наверстать упущенное.
• В Калифорнийском университете в Дэвисе есть распечатка нескольких сложных логических головоломок, которые вам предстоит решить. Почему бы не попробовать?
• Совет по образованию города Нью-Йорка предлагает пример логических головоломок, поскольку в настоящее время они необходимы для соответствия образовательным стандартам. Если вас интересуют текущие школьные требования, это может быть хорошим местом для посещения.

 

Только для экспертов – математические и логические задачи

Готовы ли вы к уровню эксперта? Несколько университетов, а также Агентство национальной безопасности предлагают сложные логические задачи на одних из самых сложных уровней. Вы все еще ищете больше после этого? Почему бы не подумать о том, чтобы создать несколько собственных логических задач, чтобы бросить вызов другим? Иногда настоящая проблема заключается в том, чтобы сделать идеальную головоломку.

• Университет Восточного Кентукки столкнулся с рядом трудностей, с которыми не справилось большинство людей. Вы готовы принять настоящий вызов?
• В Западно-семитском исследовательском проекте Университета Южной Калифорнии есть головоломка «Папирус» и обещание, что вы получите письмо, подтверждающее, что вы «мастер-папиролог», если вы отправите конверт с обратным адресом и маркой вместе с решенной головоломкой.

  No related posts.