Объединение это в математике: Пересечение и объединение множеств — урок. Алгебра, 9 класс.

Пересечение и объединение множеств: обозначение, правила решения

Решение некоторых математических задач предусматривает операции над множествами такие как пересечение, объединение, разность. Под множеством подразумевают объединение некоторых предметов в одно целое. Для совершения подобных действий требуется знание некоторых правил, которые позволят найти пересечение, объединение и разность множеств. О таких правилах пойдёт речь далее.

Обозначение множеств. Как записать объединение и пересечение множеств

Определения

Объединение множеств – это ряд таких элементов, при которым каждый из них представляет собой элемент одного из первоначальных множеств.

Пересечение множеств — заключает в себе все элементы, общие для первоначальных множеств.

При записи обозначения пересечения множеств и объединения множества чисел, используют специальный порядок символов. Самый лёгкий способ обозначить множество — это применение фигурных скобок, в середине которых элементы записаны через запятую.

А = {7, 3, 15, 31}

С помощью такой записи можно задать множество, если оно включает небольшое конечное число элементов. В связи с этим чаще применяется многофункциональный способ определения множеств – посредством характеристического свойства, которое свойственно всем элементам множества, которым не владеют объекты вне множества.

A = {x | P(x)} или A = {x : P(x)}

P(x) – характеристическое свойство множества A.

В таком виде объединение записывается следующим образом:

AUB={x|xєAvxєB}

Объединение множеств

а пересечение множеств записывается как:

AՈB={x|xєAᴧxєB}

Пересечение множеств

Где символы v / ᴧ, обозначают «или» / «и», символ | обозначает «таких что».

Чтобы обозначить множества, как числовые интервалы, при записи применяют скобки круглой и квадратной формы. К примеру, запись [4,24), выражает цифровой диапазон от 4 до 24, при этом число 4 входит в состав множества, а 24 нет. Числа менее 24 принадлежат этому множеству.

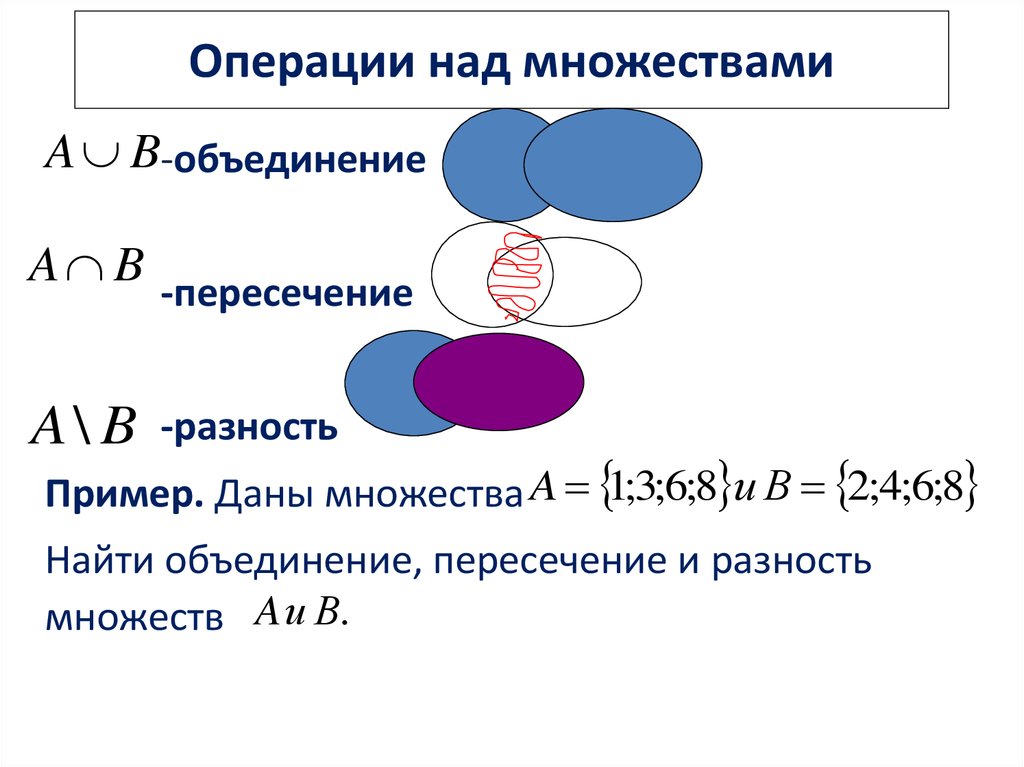
Найти пересечение и объединение множеств. Операции над множествами

Важно

U – обозначает объединение множеств A и B;

Ո – обозначает пересечение множеств A и B.

Чтобы легче запомнить данные знаки пересечения и объединения множеств, можно мысленно представить, что символ объединения U напоминает сосуд с открытым верхом, туда есть возможность что-то положить.

Символ пересечения Ո наоборот, выглядит как перевёрнутая ёмкость, в который невозможно поместить какой-либо предмет. Так же символ обозначающий пересечение Ո можно прочитать как «И».

Тогда выражение AՈB=C, читается так: “Все элементы, входящие в состав множества A и множества B, составляют элементы, которые принадлежат множеству C».

Правила нахождения объединения и пересечения и разности множеств

При формировании объединения числовых множеств, следует последовательно записать полностью части одного множества и их дополнить недостающими элементами из остальных. Операцию объединения в отдельных случаях называют сложением множеств и обозначают знаком «+».

Рассмотрим пример объединения числовых множеств A={0,1,2,3,4,5,6,7,8,9} и B={2,4,6,8,10}. К имеющимся числовым составляющим множества A 1,2,3,4,5,6,7,8,9 прибавим недостающую часть из множества B 10. Получившееся в результате объединения множество чисел будет выглядеть так {0,1,2,3,4,5,6,7,8,9,10}. Соответственно запись этого объединения:

AUB={0,1,2,3,4,5,6,7,8,9,10}

Чтобы составить пересечение числовых множеств, следует последовательно выбирать части одного множества и удостовериться, входят ли они в другие исследуемые множества, входящие в их число и составляют пересечение.

Для того, чтобы найти пересечение этих же множеств, друг за другом, последовательно проанализируем числа множества A на их наличие в множестве чисел B. Начнём проверку с самого первого числа в множестве A это число 0. В множестве B данное число отсутствует и не войдёт в совокупность пересечения.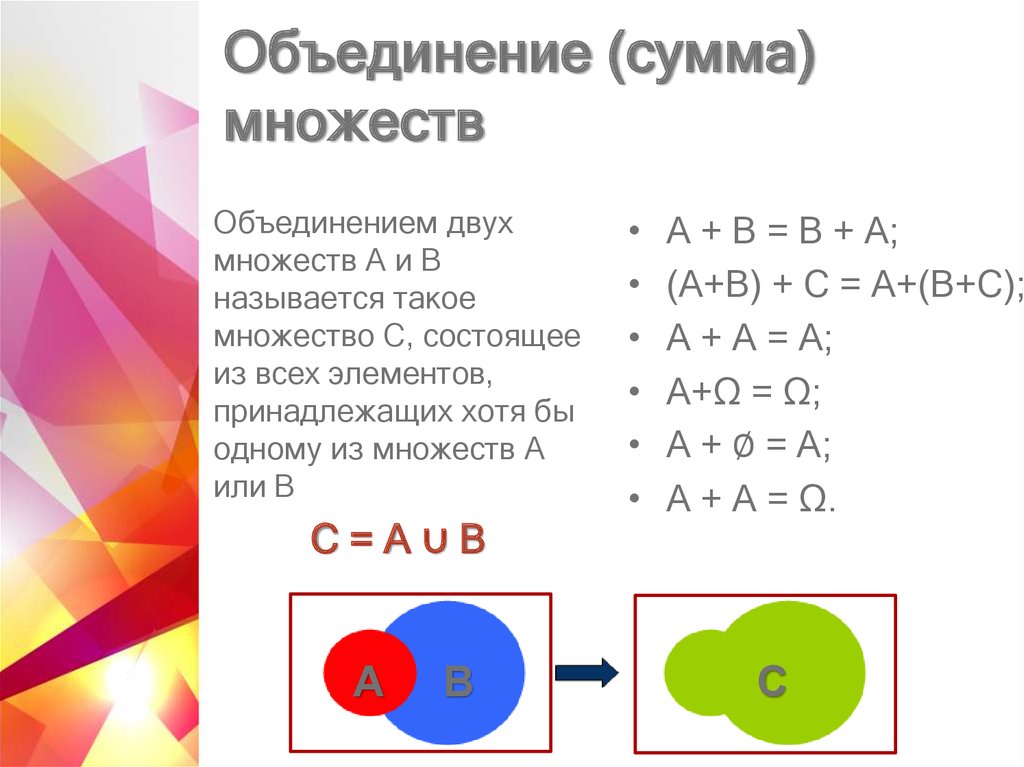 Смотрим далее, число 1 из множества A так же имеется в составе множества B. Затем следует число 2, которое принадлежит множеству B и, следовательно, пересечению. Идущее за ним 3 не принадлежит A и B не входит в перечисление. Число 4 входит в A и B, значит войдёт и в объединение. Далее продолжаем проверять числа по аналогии. Итак, пересечение множеств A={0,1,2,3,4,5,6,7,8,9} и B={2,4,6,8,10} состоит из чисел 2,4,6,8. При записи выглядит так:

AՈB={2,4,6,8}

Выполнение записи пересечения и объединения нескольких множеств

Если требуется выполнить операции с более чем двумя множествами, например: A, B, C, принцип действия подобный предыдущим примерам. В первую очередь находим пересечения A и B. Только затем пересечение полученного множества с C.

Следовательно, процесс нахождения пересечения более двух множеств осуществляется в несколько этапов.

Например, дано три множества A = {1,2,3,7,9}, B = {1,3,5,7,9} и C = {3,4,5,8,9}. Сначала находим пересечение AՈB = {3,9}, затем сравниваем полученное множество с C, это будут те же 3 и 9.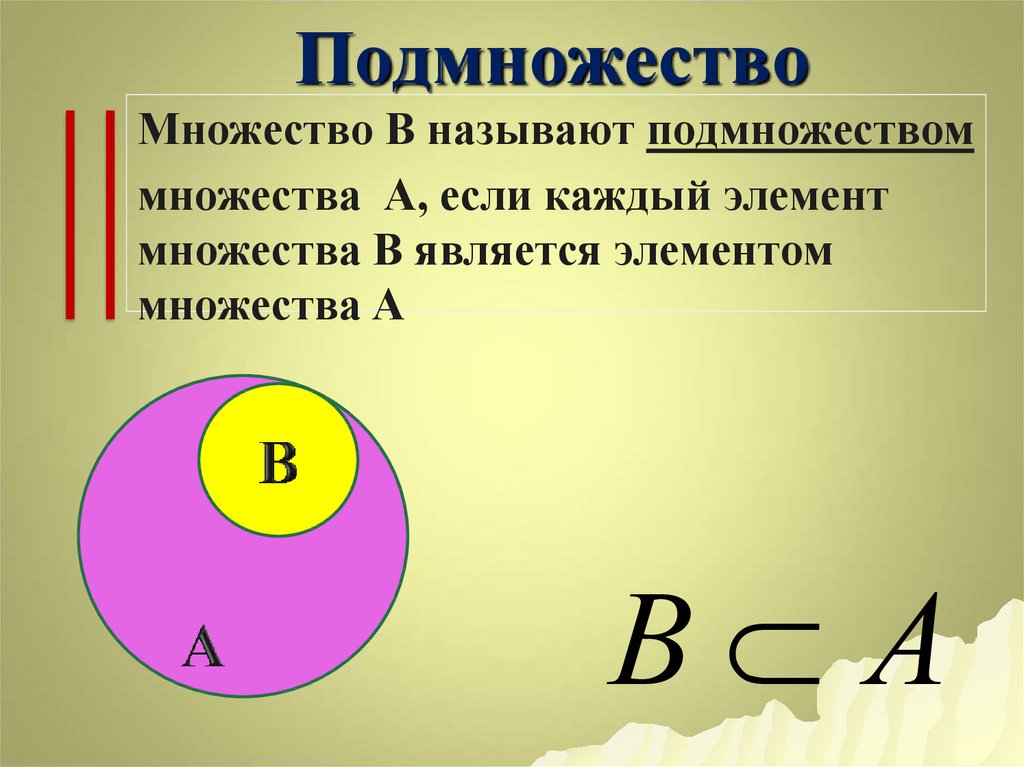 Получаем, что пересечение A, B, C выглядит следующим образом:

AՈBՈC={3,9}

При определении объединений двух и более множеств, к числам первого множества последовательно добавляют отсутствующие элементы из второго, третьего и последующих множеств. К примеру, даны следующее множества A = {1,4}, B = {4,3,} и C = {1,3,6,7}. К числовым элементам 1 и 4 из множества A, прибавляем число 4 из множества B. Теперь, к получившемуся множеству 1,3,4 прибавляем цифры 6 и 7 из множества C. В конечном результате получаем объединение:

AUBUC = {1,3,4,6,7}

Для нахождения пересечения совсем не нужно писать много букв. Когда элементов не много, то множество возможно задать элементарным перечислением. Например, первое множество включает в себя числа 1,3,5, второе состоит из элементов 2,3,5. В данном случае, пересечение будет состоять из элементов 3 и 5. Для записи можно использовать прямое перечисление: {1,3,5} Ո {2,3,5} = {3,5}

Основные свойства объединения и перечисления множеств

1. Коммутативность или перестановка. Распространяется на все компоненты при любом их количестве.
   • AUB = BUA
   • AՈB = BՈA
2. Ассоциативность или расстановка скобок. Позволяет опускать скобки и делать решение проще.
   • (AՈB)ՈC = AՈ(BՈC)
   • (AUB)UC = AU(BUC)
3. Раскрытие скобок или дистрибутивность.
   • (AUB)ՈC=(AՈC)U(BՈC)
   • (AՈB)UC=(AUC)Ո(BUC)

Разностью A и B называется множество, которое включает в себя все элементы, каждое из которых принадлежит множеству A и не принадлежит множеству B. Обозначается A\B. Приведём пример, найдём разность множеств A = {1,2,3,4,5} и множества B = {2,4,6,8}. Первый вариант находим разность множества A. Запись будет выглядеть так: A\B={1,3,5}, в которую не входят элементы, принадлежащие только B числа 6 и 8. Разность множества B при этом выглядит так: B\A={6,8}, сюда соответственно не входят числа, принадлежащие только A.

Для закрепления материала пройденных уроков, рассмотрим ещё несколько примеров. Дана задача: A = {0,5,8,10}, B = {3,6,8,9} и X = {0,1,3} Y = {2,4,6}.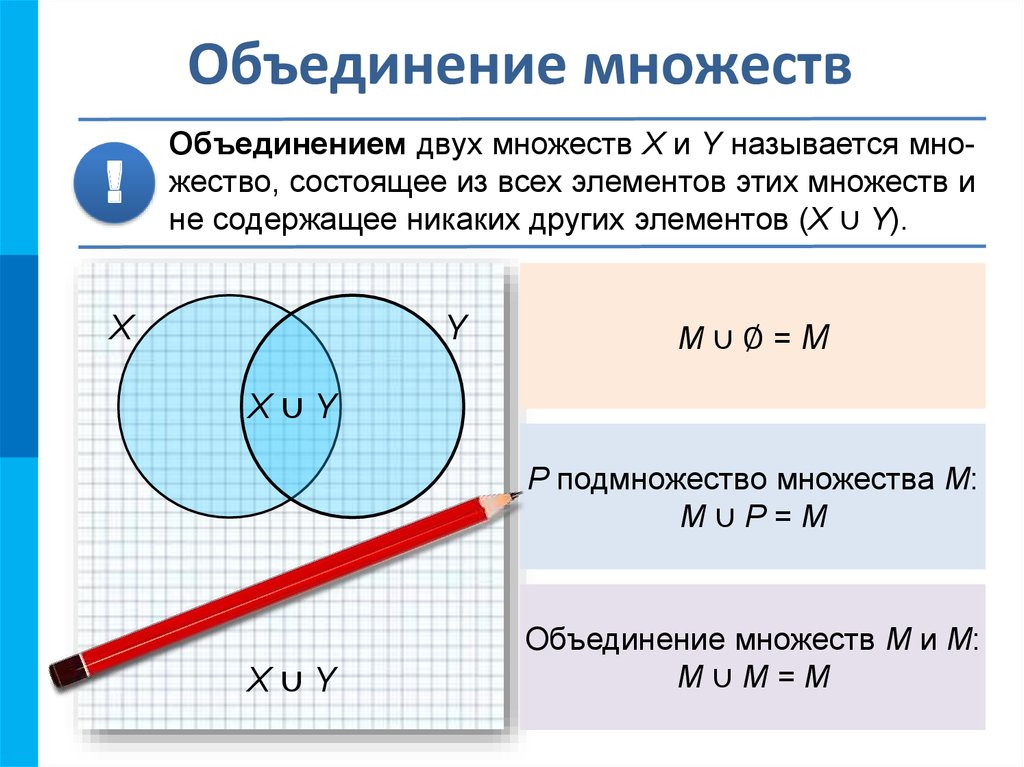 Найдите пересечение, объединение для A, B и разность множеств X, Y. Решение:

Сначала найдём объединение исходных множеств A U B = {0,3,5,6,8,9,10}.

Затем пересечение A Ո B = {8}

Разность X\Y = {0,1,3} Y\X = {2,4,6}

Для того, чтобы выполнить операции над множествами пересечения, объединения, разность в количестве больше двух, следует рассматривать элементы, входящие в первое их них. Затем определить, относится ли этот элемент к каждому из проверяемых множеств. Если данное обстоятельство не соблюдено, то элемент не относится к пересечению. При проверке, лучше выбирать множество с наименьшим количеством элементов в составе.

Кроме перечисленных действий пересечения и объедения существует дополнение множеств и многие другие операции.

Нет времени решать самому?

Наши эксперты помогут!

Контрольная

| от 300 ₽ |

Реферат

| от 500 ₽ |

Курсовая

| от 1 000 ₽ |

Отображение множеств с помощью координатной прямой

Для того, чтобы исследовать и обозначать множества, удобно применять выделение числовых промежутков на координатной прямой.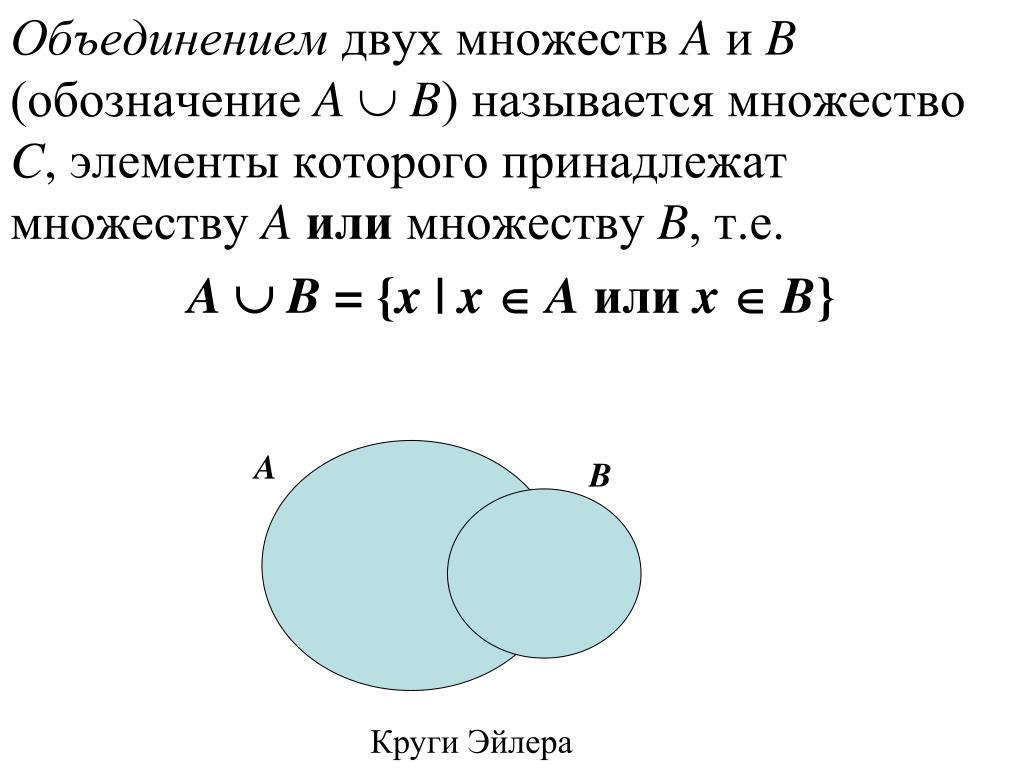 Каждая выбранная точка разделяет находящиеся на ней числа на два открытых луча. Приведём пример, точка с координатами 42,7 сформирует промежутки, которые можно записать как (-∞,42,7) и (42,7, +∞). Наше выражение заключено в круглые скобки, это значит, что сама точка 42,7 ни одному из этих промежутков не принадлежит. Числовая прямая, которая записывается как R = (-∞,+∞), при таком варианте из нашего примера, представляет объединение:

(-∞,42,7) U {42,7} U (42,7+∞).

При добавлении нашей рассматриваемой точки 42,7 к одному из представленных (-∞,42,7) или (42,7, +∞) числовых лучей, в таком случае промежуток перестанет быть открытым. При записи выражения нужно будет использовать квадратные скобки, которые обозначают, что точка входит в промежуток. Запись будет выглядеть так: (-∞,42,7] и [42,7+∞). Тем самым множество действительных чисел на координатной прямой будет выглядеть так:

(-∞,42,7] U (42,7+∞) или (-∞,42,7) U [42,7+∞).

На числовой прямой можно выполнять большое количество действий.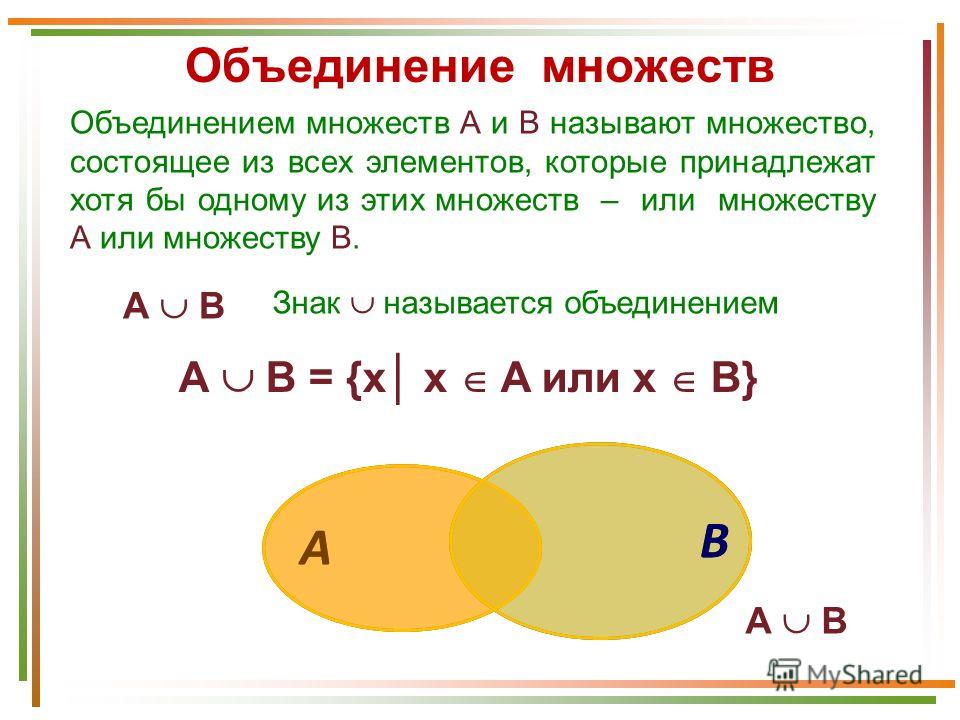 Такую прямую можно разделить на отрезки не точкой, как в предыдущем примере, а лучом или отрезком. Все выявленные закономерности так же будут соблюдены. Кроме того, они выполняются при разделении самих числовых промежутков. Рассмотрим пример, точка с координатой 18 на промежутке (8,34] разделит его на следующие промежутки (8,18) U {18} U (18,34]. Дополнив точкой, один из промежутков, получатся следующее записи: (8,18] U (18,34], (8,18) U [18,34]. Примем за разделяющую точку цифру 34, которая включается в состав рассматриваемого промежутка и ограничивает его справа. В результате получим объединение множеств {34} и интервала (8,34) либо (8,34] = (8,34) U {34}

Аналогичные закономерности объективны и в ситуации, когда координатная прямая разделяется на промежутки несколькими точками. К примеру, точки -5, 0 и 6 разделят её на промежутки (-∞,-5), (-5,0), (0,6), (6,+∞), при этом множество действительных чисел (-∞,-5) U {-5} U (-5,0) U {0} U (0,6) U {6} U (6,+∞).

Благодаря координатной прямой достаточно просто и легко рассматривать пересечения и объединения множеств.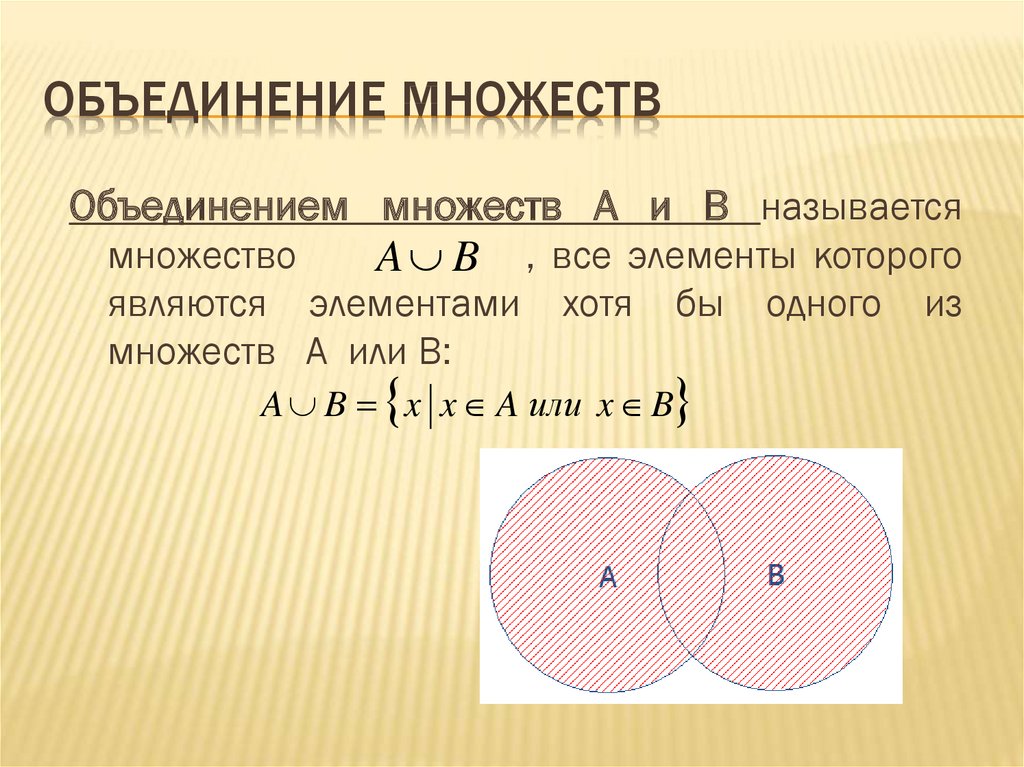 Они указываются друг под другом на координатных прямых с идентичными направлениями отсчёта и точками. При записи отображения множеств координатные прямые обозначают слева квадратной скобкой, фигурные скобки используются, чтобы показать пересечение.

С помощью дополнительной координатной прямой, которую располагают ниже исходной, показываются искомые пересечения или объединение. На ней поперечными чертами отмечают граничные точки первичных множеств, а после выяснения характера точек, их заменяют полями или сплошными. На рисунке вхождение промежутка в объединение показывается штриховкой, отсутствие вхождения – полой точкой, а вхождение – сплошной.

Графически пересечение A и B показывается промежутками, над которыми имеется штриховка, дополненная отдельными точками, которые принадлежат обоим множествам. На рисунке объединение проявляется там, где показана штриховка хотя бы у одного из множеств и сплошные точки.

В приведённых примерах объединения и пересечения множеств указаны только целые числа. Отрезкам на координатной прямой так же принадлежат и другие числа, которые целыми не являются, такие как десятичные дроби. При определении пересечения и определения множеств, класс чисел намного шире, чем представлен в упражнениях, они находятся между целыми числами и количество их очень велико, перечислять которые не представляется возможным.

Материал по математике «Пересечение и объединение множеств»

Что такое пересечение, объединение и разность множеств?

Пересечением двух множеств, называется третье множество, сформированное из элементов, которые входят в оба первых множества.

Например, если в одно множество входят числа от 1 до 10, а во второе — от 5 до 20, то пересечением этих множеств будут числа от 5 до 10, так как они входят в оба.

Пересечение множеств записывается так:

A ∩ B = {x | x ∈ A и x ∈ B}

На диаграмме Эйлера-Венна пересечение множеств обозначается общей частью кругов.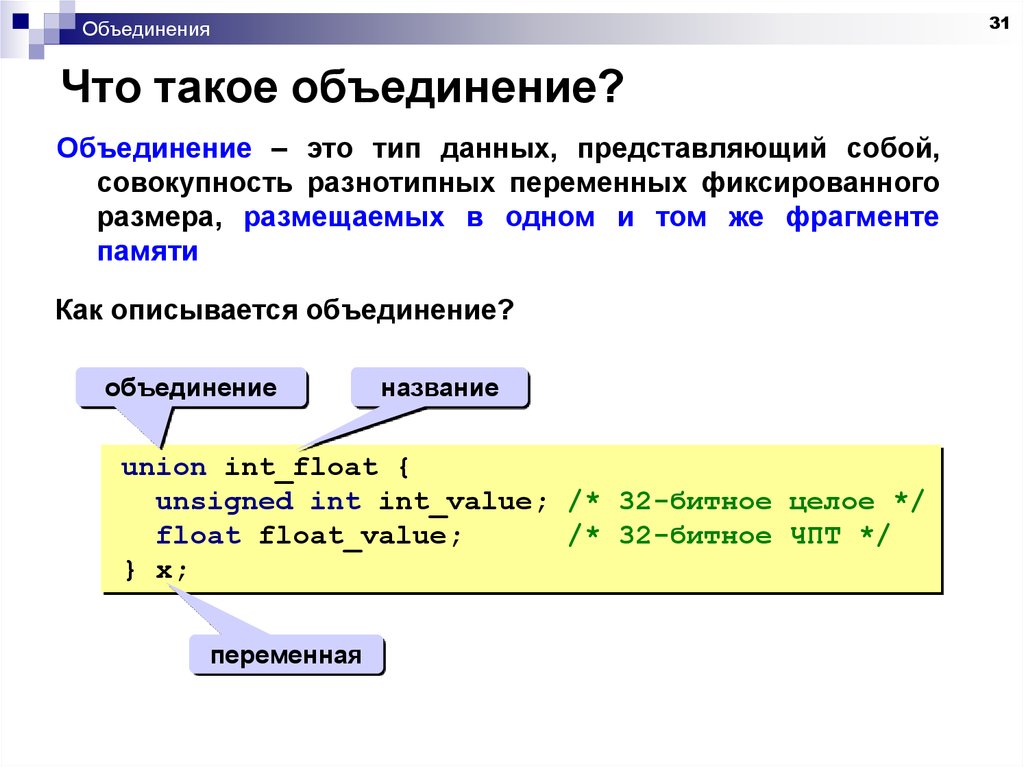

Множества могут не пересекаться вообще, одно может полностью включать другое.

Пересечение множеств может использоваться тогда, когда надо найти элементы, которые удовлетворяют нескольким условиям.

Объединением двух множеств, называется третье множество, сформированное из всех элементов обоих первых множеств. При этом если элемент входит в оба множества, то в объединенное он входит один раз. Это и понятно, так как множество по определению включает только разные элементы.

Например, объединением множества натуральных чисел от 1 до 10 и множества натуральных от 5 до 15 будет множество натуральных чисел от 1 до 15.

Объединение множеств описывается так:

A ∪ B = {x | x ∈ A или x ∈ B}

На диаграмме Эйлера-Венна объединение множеств обозначается всей областью кругов.

Разностью двух множеств, называют третье множество, в которое входят все элементы одного из двух множеств и не входят элементы принадлежащие обоим множествам.

Если результат пересечения и объединения двух множеств не меняется от перестановки множеств при выполнении операции, то результат разности зависит от того, какое множество из какого «вычитают».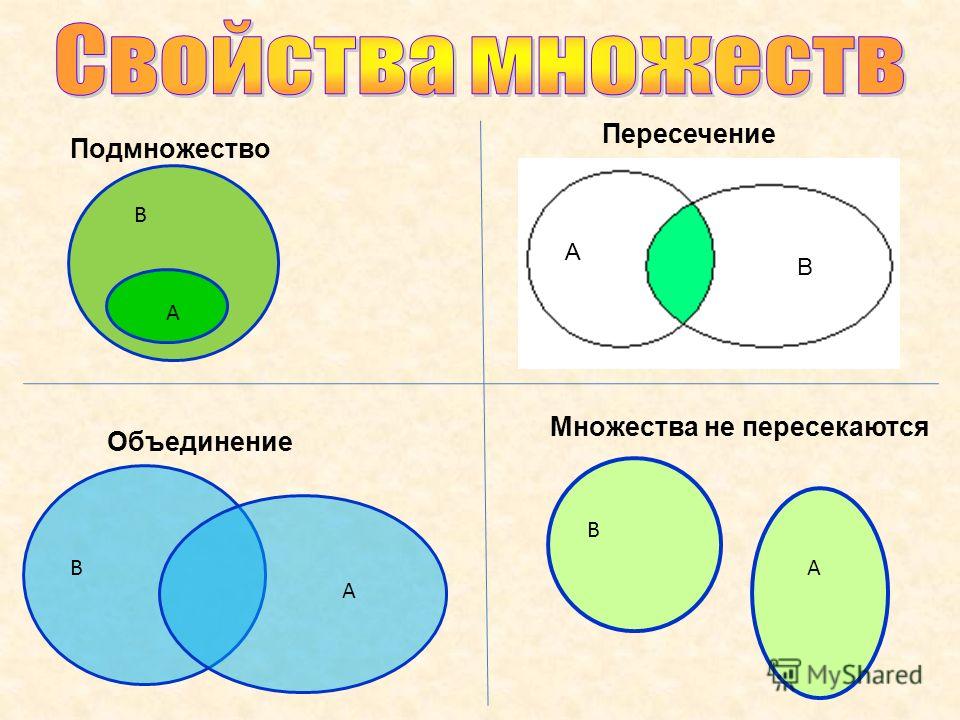

Сравните. Даны множества A = {1,2,3,4,5} и B = {4,5,8,9}. Разность множеств обозначается знаком \.
A \ B = {1,2,3}, т. к. 4 и 5 входят в множество B.
В то время как B \ A = {8,9}.

Понятно, что если у множеств нет общих элементов, то их разность будет равна «уменьшаемому», т. е. первому множеству. Если же множества полностью совпадают, то их разностью будет пустое множество.

Если все элементы «вычитаемого» множества B входят в состав «уменьшаемого» A (A \ B), то B называют дополнением некого множества C до A.

Пример: В классе 19 учеников: 10 девочек, 9 мальчиков.

10 девочек – это множество .

9 мальчиков – это множество .

Класс из 19 учеников – это множество С, которое объединяет два множества.

Пусть в классе 5 отличников – это множество D.

Из них 2 мальчика – это множество E.

Из какие элементов состоит множество

Е?

Мальчики входят в множества В, так как 2 мальчика – отличники, они входят в множество D.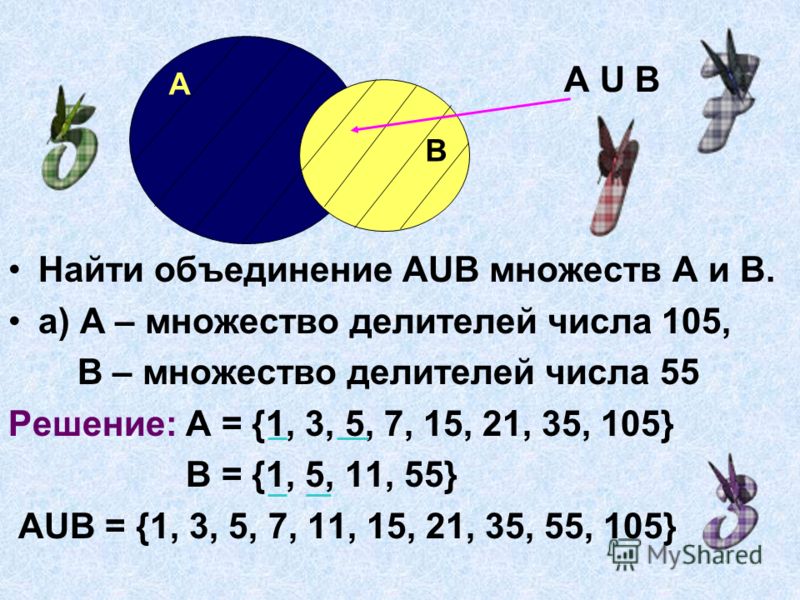

Рис. 1. Пересечение двух множеств

Множество Е есть пересечение двух множеств В и D(рис. 1).

Определение понятия объединение множеств

Определение: объединением множеств А и В называется новое множество, состоящее из тех и только тех элементов, которые входят хотя бы в одно из множеств А или В (рис. 3).

                                  

Рис. 2. Множества

Рис. 3. Объединение множеств

 – знак объединения.

Множество  состоит из всех элементов , которые входят или в множество , или в множество . Это можно записать следующим образом:

Пример № 1 на применение определения объединение множеств

Дано множество = и .

Найти объединение множеств .

Решение:

Пример № 2 на объединение бесконечных множеств

Дано множество  и .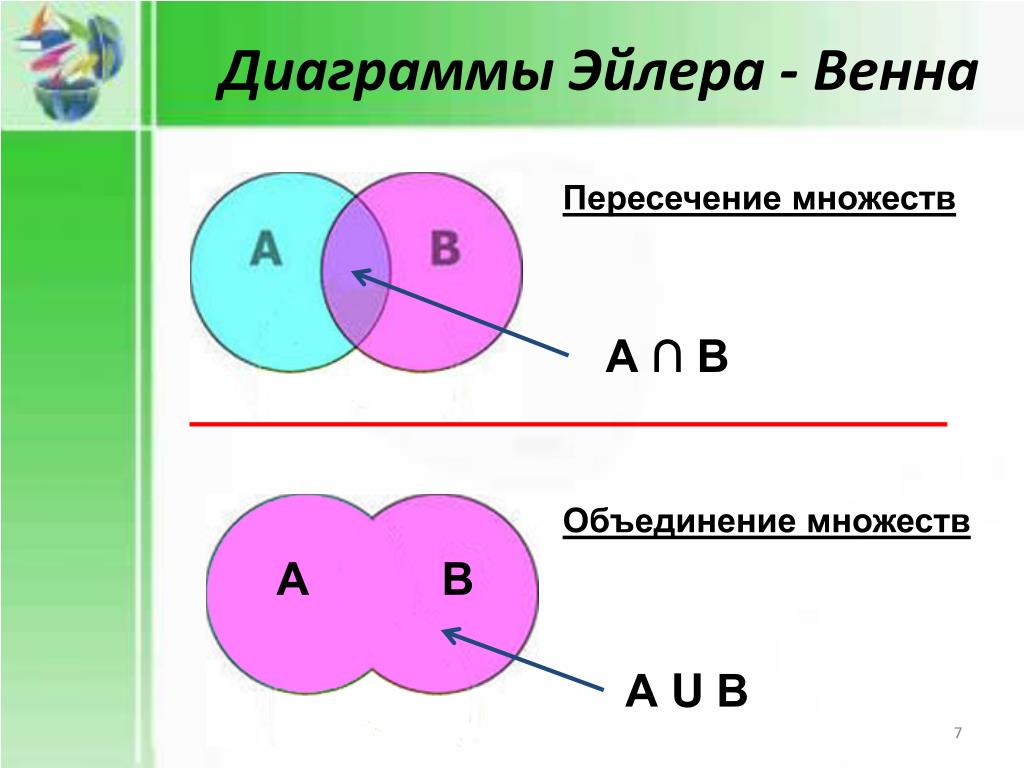

Найти объединение множеств .

Решение:

 

 

 

Имеем совокупность неравенств:

   

Пример № 3. Решение квадратного неравенства

Решить квадратное неравенство .

Решение:

Рассмотрим функцию .

Найдём корни функции .

По теореме Виета: .

Имеем объединение двух множеств .

Схематически изобразим график функции:

 при  или .

Ответ:.

Определение понятия пересечение множеств

Пересечение множеств

Пересечением множеств

Aи B называется новое множество, содержащее те и только те элементы, которые входят одновременно и в множество А, и в множество В.

 – знак пересечения

Рис. 4а. Пересечение множеств

– пересечение множеств на рис. 4а

Рис. 4б. Пересечения множеств нет

На рис. 4б множества не пересекаются, их пересечение – пустое множество 

Пример № 4 на применение определения пересечения множеств

Даны множества  и . Найти пересечение множеств .

Решение

По определению пересечения, решением будут те элементы, которые одновременно входят в оба множества:

 – пересечение множеств.

Сравним с объединением:

C= – объединение множеств.

Пример № 5 на пересечение бесконечных множеств

Найти пересечение бесконечных множеств

Решение

Нужно найти такие х, которые принадлежат пересечению :

 

 

 

Нужно решить систему неравенств. На оси изображаем множества и находим их пересечение

 

Ответ:

.

Сравним с объединением множеств:

Пример № 6. Решение системы неравенств

Решить систему неравенств

 

 

 

Решение:

Рассмотрим ось х:

 

Ответ:

Пересечением множеств будет:

 

Union

В теории множеств объединение (∪) набора множеств — это множество, содержащее все элементы набора.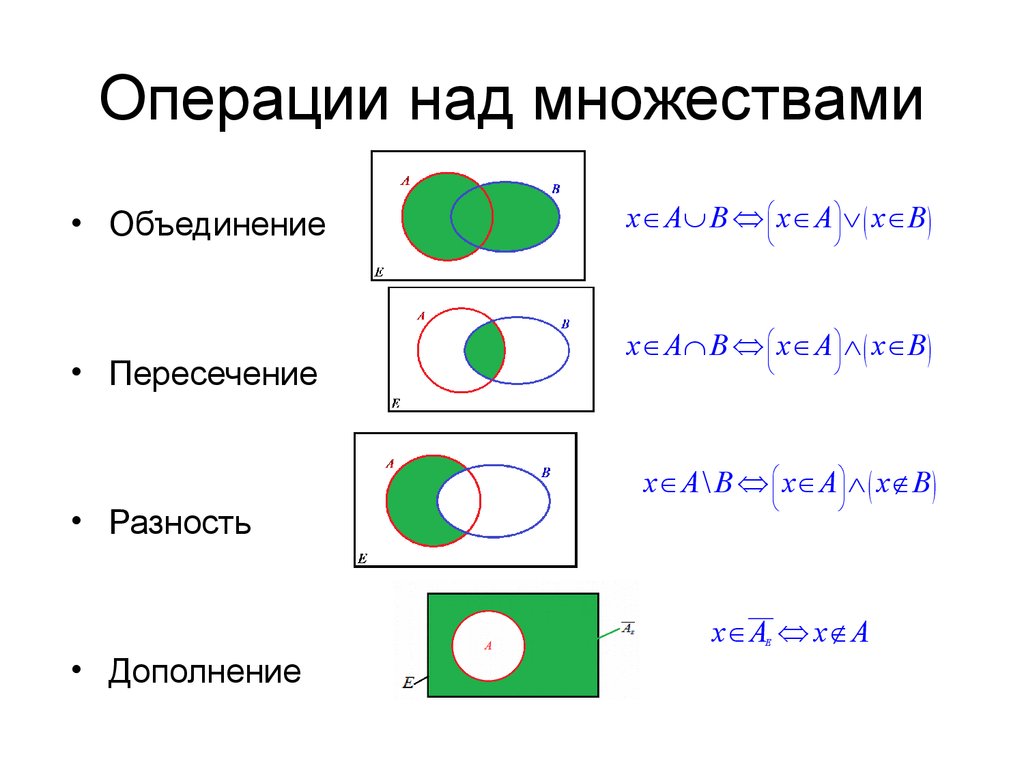 Например, для двух наборов A = {2, 2, 4, 6, 8, 10} и B = {1, 3, 5, 7, 9} их объединение выглядит следующим образом:

A ∪ B = { 1, 2, 3, 4, 5, 6, 7, 8, 9 10}

Обратите внимание, что хотя в A две двойки, в A ∪ B есть только одна двойка. Это связано с тем, что операция объединения включает только одну из каждый уникальный элемент.

Объединение двух множеств обычно изображается с помощью диаграммы Венна, на которой множество представлено кружком. Диаграмма Венна ниже показывает два множества: A = {a, b, c, d, e} и B = {d, e, f, g}. Их объединение представляет собой множество {a, b, c, d, e, f, g} и представлено на диаграмме Венна площадью, покрытой обеими окружностями.

Подобно другим базовым операциям, таким как сложение, операции над множествами, такие как объединение, также обладают определенными свойствами. При необходимости обратитесь к странице набора за таблицей символов, обычно используемых в теории множеств.

Объединения и подмножества

Если множество A является подмножеством множества B, то объединением двух множеств является множество B. Используя обозначение множества:

, если A ⊆ B, то A ∪ B = B

Например , если A = {2n|n ∈ ℕ} и B — множество целых чисел, то A ∪ B = B, поскольку множество A — это множество положительных четных целых чисел, которое является подмножеством всех целых чисел.

Коммутативный закон

Коммутативный закон гласит, что порядок объединения двух множеств не имеет значения. Даны два множества, A и B:

A ∪ B = B ∪ A

Пусть A = {1, 2, 3} и B = {3, 5, 7}. Наборы имеют 1 общий элемент. Объединение множеств включает в себя все уникальные элементы обоих множеств. Таким образом, A ∪ B = B ∪ A = {1, 2, 3, 5, 7}. Независимо от того, рассматривается ли первым A или B, результат один и тот же. Если бы элементы B были записаны первыми, объединение A и B можно было бы записать как {3, 5, 7, 1, 2}. Порядок, в котором элементы перечислены в наборе, не имеет значения; количество элементов и значения элементов определяют набор, поэтому 2 вышеуказанных набора равны, как и любые наборы, включающие все одинаковые элементы, записанные в разном порядке.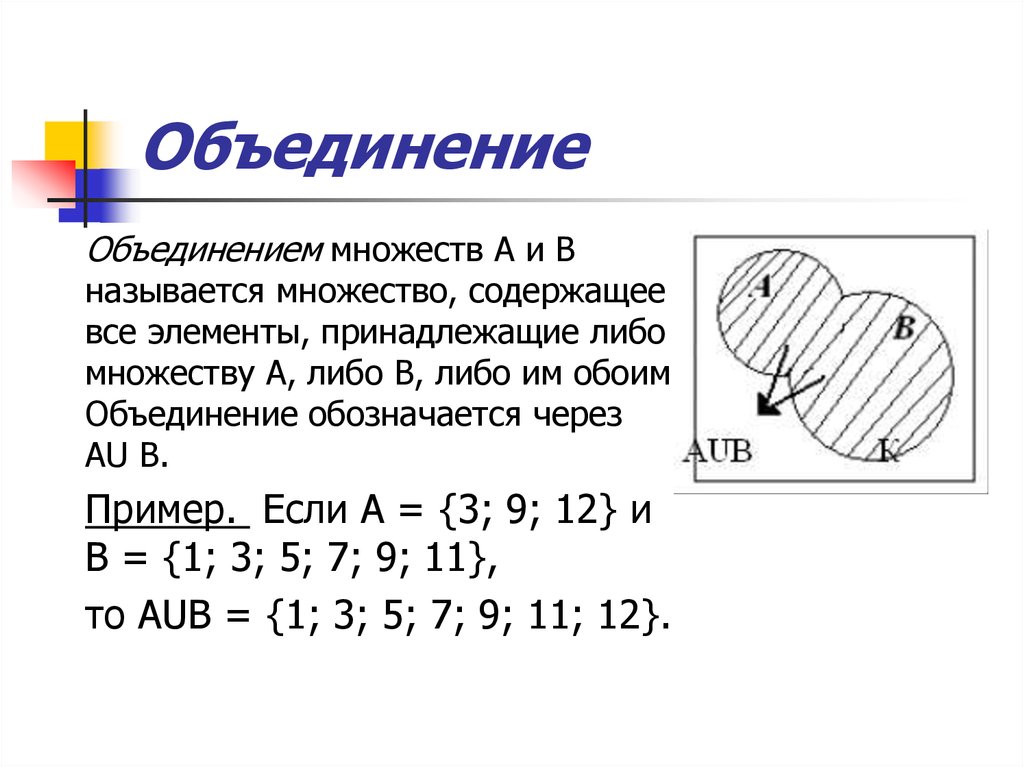

Ассоциативный закон

Ассоциативный закон гласит, что перестановка скобок в объединении множеств не меняет результат. Даны множества A, B и C:

(A ∪ B) ∪ C = A ∪ (B ∪ C)

Закон распределения

Для множеств A, B и C закон распределения гласит

A∪9000 (B ∩ C) = (A ∪ B) ∩ (A ∪ C)

A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)

3 аналогично дистрибутивному свойству умножения, при котором умножение распределяется над сложением.

Пример

Пусть A = {4, 6, 8, 10}, B = {8, 9, 10, 11} и C = {10, 11, 12}. Покажите, что A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C).

Вычислить левую часть уравнения: 6, 8, 10, 11}

Вычислите правую часть уравнения: 10, 11, 12}

(A ∪ B) ∩ (A ∪ C) = {4, 6, 8, 10, 11}

В обоих случаях результирующее множество равно {4, 6, 8, 10, 11}.

Законы Де Моргана

В теории множеств законы Де Моргана представляют собой набор правил, связывающих объединение и пересечение множеств через их дополнения.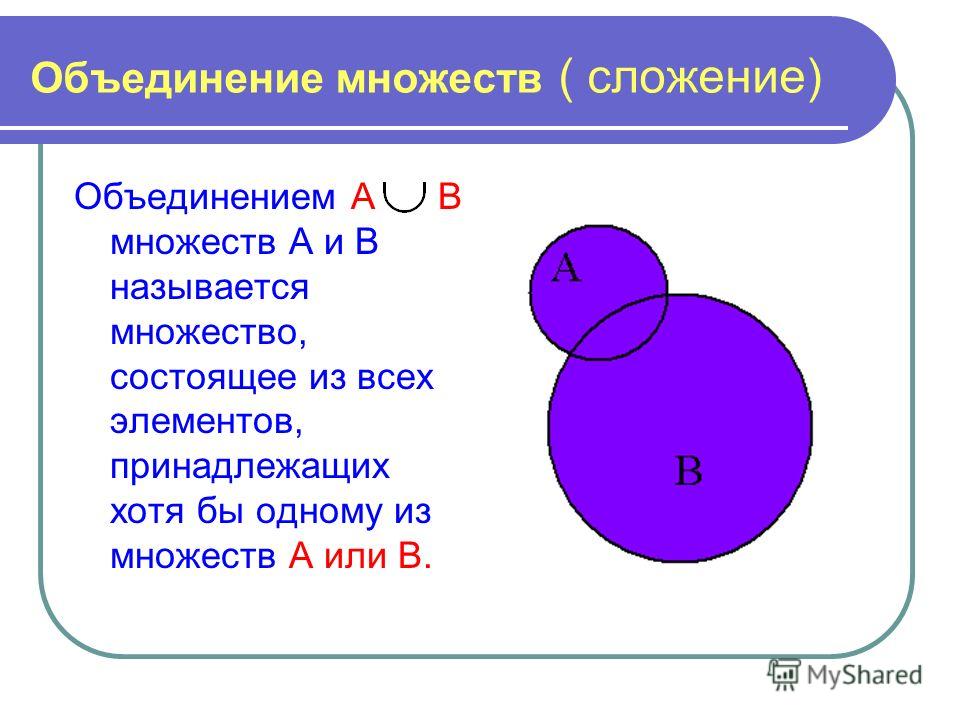

Объединение множеств:

Дополнение объединения двух множеств равно пересечению их дополнений:

(A ∪ B) ^C = A ^C  ∩ B ^C

3 90 Учитывая, что A и B являются подмножествами универсального множества 𝕌, эту связь можно увидеть на рисунке ниже:

Объединение A и B, A ∪ B, заштриховано синим цветом. Его дополнение (A ∪ B) ^C заштриховано желтым цветом. Пересечение дополнений A и B, A ^C  ∩ B ^C , также закрашено желтым цветом.

Пересечение множеств:

Дополнение пересечения двух множеств равно объединению их дополнений:

A ∩ B = A ^C  ∪ B ^C

Учитывая, что A и B являются подмножествами A и B универсальный набор 𝕌, это отношение можно увидеть на рисунке ниже:

Пересечение A и B, A ∩ B, заштриховано красным. Его дополнение (A ∩ B) ^C закрашено серым цветом. Объединение дополнений A и B, A ^C  ∪ B ^C , также закрашено серым цветом.

Математика | Union College

Major, Minor

Степень: Бакалавр

В старшей школе у ​​меня были проблемы с математикой. Но после того, как я прошел Calc I-III и увидел готовность профессоров помочь студентам добиться успеха и любовь, которую они питали к этому предмету, я решил не заниматься математикой. Это был один из лучших вариантов, которые я сделал».

-Stephany Heiberger ’22

Математика – одна из старейших изучаемых дисциплин, и Union College – одна из первых школ в стране, предложивших математику как часть своей учебной программы по гуманитарным наукам.

В Union вам понравится быть частью сообщества ученых, которые ценят и получают удовольствие от математических исследований и исследований. Мы стремимся помочь учащимся развивать способность логически рассуждать, понимать абстрактные концепции и решать задачи, а также готовить разносторонних математиков, которые понимают сложности в своей области.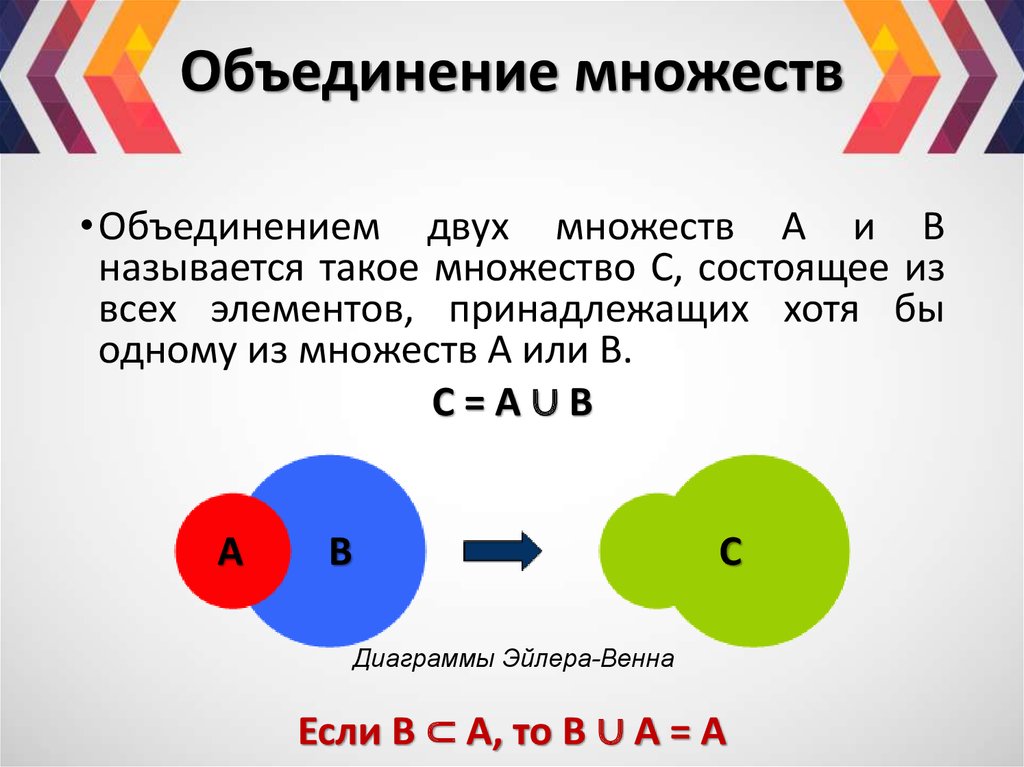

Мы также стремимся дать учащимся понимание эстетической стороны математики, которую можно оценить как интеллектуальную деятельность за ее красоту и способность оттачивать ум.

Курсы

Специалисты по математике в Union проходят базовые курсы, такие как исчисление, абстрактная алгебра и реальный анализ, а также выбирают курсы по криптологии, геометрии, дифференциальным уравнениям, дискретной математике, прикладной математике, вероятности, теории узлов, топологии и многим другим. другие. Их независимые исследования включали передовые темы реального анализа, математического изучения систем голосования и математической компьютерной графики. Статистика предлагается в качестве несовершеннолетнего на факультете математики.

• Курсы
  • Загрузка…
  • Загрузка. ..
• Главный

  Загрузка…

• Межфакультетская специальность

  Загрузка…

• Незначительный

  Загрузка…

Исследования преподавателей и студентов

Наши преподаватели проводят исследования в таких разнообразных областях, как коммутативная алгебра, топологический анализ данных, справедливое деление, теория голосования, статистика, алгебраическая топология, симплициальная и дифференциальная геометрия, медицинская визуализация и история математики. Они также направляют студентов в исследовательские проекты в течение учебного года и во время нашей летней исследовательской программы. Многие студенты продолжают представлять свои выводы на профессиональных конференциях и собственном симпозиуме Штейнмеца Союза.

Студенческие клубы

Студенты-математики делятся своей любовью к математике за пределами класса. Союзное отделение Ассоциации женщин-математиков проводит множество мероприятий, в том числе обеды с профессорами, программы с местными учащимися средних и старших классов, тематические дискуссии и многое другое. Активный математический клуб, возглавляемый студентами, регулярно собирается для вечеров просмотра фильмов и игр, дискуссий, волонтерской работы, сеансов решения проблем и, что является фаворитом кампуса, благотворительной распродажи выпечки в День числа Пи.

После Союза

• Актуарный аналитик, Watson Wyatt Worldwide
• Американское математическое общество/Американская ассоциация развития науки (AMS/AAAS) Научный и инженерный научный сотрудник Конгресса
• Заместитель вице-президента, Barclay’s Capital Inc.
• Адъюнкт-профессор математики в Saddleback College
• Координатор лаборатории CAMD, Brigham and Women’s Hospital
• Сотрудник по науке о данных, Fannie Mae
• Финансовый аналитик, Starr Companies
• Сотрудник по иностранным делам и научный сотрудник AAAS по политике в области науки и техники, Государственный департамент США
• Инженер по интеграции, Leidos Inc.

  No related posts.