Последовательность решения примеров по математике: Порядок действий в Математике

Содержание

Порядок действий в примерах по математике — «Семья и Школа»

Содержание

Порядок действий в примерах по математике

Опубликовано 30.04.202221.09.2022 от Admin — Оставить комментарий

В статье рассмотрим порядок действий в примерах по математике, которые содержат скобки, умножение, деление, сложение и вычитание. В статье также приведены примеры, начиная от простых и заканчивая сложными.

Правила выполнения действий для решения примеров:

Сначала вычислить то, что находится в скобках. Если скобок нет, то переходим к следующему пункту.
Читаем выражение слева направо. Если встретится умножение или деление, то сразу же выполняем эту операцию. Если нет умножения или деления, то переходим к следующему пункту.
Читаем выражение слева направо. Если встретится сложение или вычитание , то сразу же выполняем эту операцию.

Пример 1. 12 – 3 + 2 + 5

Читаем его слева направо:
1) 12 — 3 = 9. Запишем число 9 в главном выражении ➜ 9+2+5

2) 9 + 2 = 11. Запишем число 11 в главном выражении ➜ 11+5
3) 11 + 5 = 16.
Ответ: 12 — 3 + 2 + 5 = 16

Иногда удобно расставить порядок действий над самим выражением. Для этого над операцией, которую необходимо выполнить, указывают её очередь. К примеру, в выражении 10 − 1 + 2 + 3 все действия выполняются последовательно слева направо, поэтому для него можно определить следующий порядок:

1 2 3

12 – 3 + 2 + 5 = 16

Также, можно поставить знак равенства и сразу начать вычислять выражение в порядке приоритета действий:

1 2 3

12 – 3 + 2 + 5 = 9 + 2 + 5 = 11 + 5 = 16

Пример 2.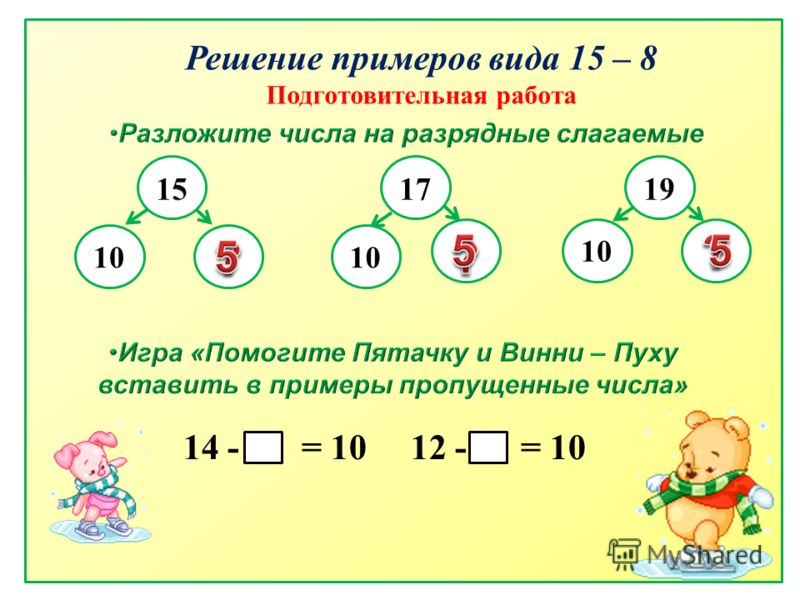 12 – (7 + 2) + 5 × 3

Применим правила порядка действий. Прочитаем правила в порядке их приоритета.
1) сначала вычислить то, что находится в скобках: 7+2=9. Запишем полученное число 9 в главном выражении вместо выражения в скобках ➜ 12-9+5×3

2) вычислить умножение и деление: 5×3=15. Запишем полученное число 15 в главном выражении ➜ 12-9+15
3) вычислить сложение и вычитание: 12-9+15.

3 1 4 2

12 – (7 + 2) + 5 × 3 = 12 – 9 + 5 × 3 = 12 – 9 + 15 = 3 + 15 = 18

Пример 3. 20 – 5 × 3 + 24 : (7 – 3) × 2 + (12 – 7)

Расставим порядок действий.

6 3 7 4 1 5 8 2

20 – 5 × 3 + 24 : (7 – 3) × 2 + (12 – 7)

1) Действие в скобках будет первым. Так как в примере скобки встречаются два раза, то выполняем действия в скобках по порядку 7-3=4 и 12-7=5
2) далее выполняется умножение и деление в порядке следования
3) и последним выполняется умножение и деление в порядке следования

6 3 7 4 1 5 8 2

1) 20 – 5 × 3 + 24 : (7 – 3) × 2 + (12 – 7) =

20 – 5 × 3 + 24 : 4 × 2 + 5 =

2) 20 – 5 × 3 + 24 : 4 × 2 + 5 = 20 – 15 + 6 × 2 + 5 = 20 – 15 + 12 + 5 =

3) 20 – 15 + 12 + 5 = 5 + 12 + 5 = 17 + 5 = 22

Таким образом, для правильного решения примеров по математике необходимо правильно определить порядок действий в примерах.

Для тренировки решения примеров по математике на порядок действий можно скачать программы:

Порядок действий в пределах 20 (сложение и вычитание)
Порядок действий в пределах 100 (все действия)
Порядок действий в пределах 1000 (все действия)
Сложные примеры на порядок действий

Для освоения темы вам также могут понадобится темы: раскрытие скобок и законы математики.

Рубрика: Для школьников

Метка Математика

Порядок действий в математике

Метки

Головоломки Досуг Задачи Логика Математика Смекалка

Порядок выполнения действий в математике нередко становится настоящим камнем преткновения. Мы изучали его в начальных классах школы и, по идее, должны помнить всю жизнь. Но теория, как говорил Мефистофель, суха. Да и кому, по правде говоря, интересны примеры, где порядок действий расписан заранее?

Другое дело — задания из нашей подборки. В них тебе дается лишь набор цифр и число, которое нужно получить. А какие действия и в каком порядке выполнять, решать только тебе. И тут уж ответ не вычислишь, а тем более не угадаешь. Ведь для решения необходимо мыслить и творчески, и аналитически. А это помогает нам успешно находить выход из самых сложных жизненных ситуаций.

Порядок действий в математике

Начнем с примеров попроще.
Поставь в записи 1 * 3 * 2 * 1 * 2 = 10 вместо звездочек знаки арифметических действий, чтобы получилось верное равенство. Попробуй найти как можно больше вариантов решения со скобками и без.
У тебя есть четыре цифры: 5, 5, 5 и 1. С помощью сложения, вычитания, умножения, деления и скобок получи из них число 24, используя каждую из этих цифр только 1 раз.
Используя цифры (1, 3, 4, 6), скобки и арифметические операции (сложение, вычитание, умножение, деление), получи число 24. Разрешается использовать только эти цифры и только эти операции. Каждую цифру можно использовать только один раз. Операции и скобки можно использовать любое число раз.© Depositphotos

Ответы

Как я уже говорил, тут открывается широкий простор для творчества. Мне сходу удалось найти только одно решение без скобок: 1 + 3 х 2 + 1 + 2 = 10. И одно со скобками:

1 х (3 + 2) х 1 х 2 = 10. Но решений, скорее всего, намного больше. Попробуй найти недостающие!
Я предложил эту задачку своим друзьям. И перед тем как назвать верный ответ, расскажу вам об ошибочных, а также весьма остроумных вариантах решения. Самый распространенный ответ: 5 х 5 – 1 = 24. Был еще такой вариант: 5 + 5 + 5 + 5 + 5 – 1 = 24. Да, ответ в обоих случаях, конечно, 24. Но как быть с условием? В нём четко сказано, что нужно использовать каждую из цифр и только 1 раз! © Depositphotos
Интересное решение за пределами математики предложила девушка бариста. По ее словам, достаточно выпить 5 чашек кофе, затем еще 5 чашек и еще 5 чашек за один день, чтобы получить 24 часа бодрствования. Мы не советуем даже пробовать это повторить. Ведь больше 300 миллилитров бодрящего напитка в день способны навредить твоему здоровью. Но попытка свести воедино математику, кулинарию и физиологию заслуживает всяческого уважения.
© Pexels
Возвращаясь к математике, признаюсь, что найти решение для этого примера было очень непросто. У меня оно получилось таким: (5 — (1 : 5)) х 5= 24.
Но, может, кто-нибудь из наших читателей найдет еще один вариант?
Мы уже решили два примера. Поэтому с последним проблем быть не должно. И опять нас выручает деление на дробь:
6 / ( 1 — ( 3 / 4 ) ) = 24.
© Pexels

Как видишь, наши забавные задачки помогают провести время с пользой. Ведь сообразительность помогает искать необычные, интересные и простые пути решения, достигая результата не только в игре, но и в реальной жизни кратчайшим путем.

Порядок операций | Brilliant Math & Science Wiki

Бывший блестящий член, Матин Насери, Сатвик Голечха, а также

способствовал

Содержимое

Общие мнемоники для порядка операций
Сложение и умножение
Экспоненты
Скобки
Смотрите также

Есть два распространенных мнемонических приема для запоминания правильного порядка операций. Однако при их использовании важно помнить, что истинный порядок операций определен выше, и, в частности, этот порядок операций не делает различий между умножением и делением (или сложением и вычитанием) при упорядочивании.

PEMDAS или «Пожалуйста, извините, моя дорогая тетя Салли»:

P арентесы
E компоненты
М умножение
D ivision
A дополнение
S
вычитание

БОДМАС:

B ракетки
O ряды (показатели и радикалы)
D ivision
M умножение
A дополнение
S вычитание

Обратите внимание, что наивное обращение с любым из них может привести к ошибкам, поскольку и сложение/вычитание, и умножение/деление должны группироваться и оцениваться слева направо. Более точной мнемоникой может быть PE(MD)(AS) и BO(DM)(AS).

Одним из требований является выполнение умножения перед сложением. Например, в выражении 2+3×4 2 + 3 х 4 2+3 х 4 мы получим ответ 5 х 4 = 20 5 х 4 = 20 5 х 4 = 20, если мы начнем с добавления 2 и 3, но мы получим 2 + 12 = 14 2 + 12 = 14 2 + 12 = 14, если сначала умножим. Поскольку важно, чтобы все интерпретировали выражение 2+3×4 2 + 3 \times 4 2+3×4 одинаково, мы просто

определите правильный порядок, в котором умножение выполняется первым. Таким образом, 2+3×4=2+(3×4)=2+12=14 2 + 3 х 4 = 2 + ( 3 х 4 ) = 2 + 12 = 14 2+3 х 4=2+ (3×4)=2+12=14.

Сколько будет 2×4+3×5 2×4+3×5 2×4+3×5?
Следуя правильному порядку операций, мы видим, что мы должны вычислить 2×4 2 \times 4 2×4 и 3×5 3 \times 5 3×5, прежде чем делать какое-либо сложение.
Таким образом, правильный ответ: 2×4+3×5=8+15=23 2 х 4 + 3 х 5 = 8 + 15 = 23 2 х 4 + 3 х 5 = 8 + 15 = 23. □_\квадрат□

Что такое 48÷2×12? 48 \дел 2 \умножить на 12 ? 48÷2×12?
Если бы мы небрежно следили за PEMDAS, ответом было бы сначала выполнить умножение, что дало бы нам 48÷24=2 48 \div 24 = 2 48÷24=2.
Однако это неверно.
Мы не делаем различий между умножением и делением, а выполняем их слева направо. Это дает
48÷2×12=24×12=288. □ 48 \дел 2 \умножить на 12 = 24 \умножить на 12 = 288. \ _\квадрат48÷2×12=24×12=288. □ 92 = 361. \_\квадрат(3+42)2=(3+16)2=192=361. □

Упрощение выражений
Рациональные показатели

Цитировать как: Порядок операций. Brilliant.org . Извлекаются из https://brilliant.org/wiki/order-of-operations/

1.3: Порядок операций

Последнее обновление
Сохранить как PDF

Идентификатор страницы: 41986

Самар ЭльХитти, Марианна Бонаноме, Холли Карли, Томас Тредлер и Лин Чжоу Технологический колледж Нью-Йорка Сити CUNY
NY via технологий в CUNY Academic Works

Что означает выражение «3 умножить на 4 плюс 5». Кто-то ответит 17, а кто-то 27. Почему? Чтобы устранить двусмысленность, мы можем написать

\[(3 х 4)+5=17 \нечисло\]

\[3 \cdot(4+5)=27, \номер\]

, где мы должны сначала оценить количество в скобках. Поскольку писать много круглых скобок может быть несколько громоздко, существует важное соглашение или соглашение, согласно которому, если мы просто пишем $3 \times 4+5$, мы имеем в виду $(3 \times 4)+5 .$ То есть при отсутствии скобок мы должны умножить, прежде чем складывать. Это часть так называемого Порядка Операций. Это нужно помнить.

Определение: 1.24: Порядок действий

При вычислении выражения, включающего сложение, вычитание, умножение и деление, которое не имеет круглых скобок или показателей степени, мы сначала выполняем слева направо все операции умножения и деления. Затем слева направо сложение и вычитание. Если есть части выражения, заключенные в круглые скобки, сначала нужно оценить то, что находится внутри круглых скобок.

Примечание 1. 25

Вычитание можно превратить в сложение, а затем сложение можно выполнять в любом порядке, не обязательно слева направо. Это объясняет, почему сложение и вычитание идут вместе в порядке операций. Будет аналогичное утверждение для умножения и деления, но оно будет отложено до обсуждения дробей.

‘PE(MD)(AS)’ — это простой способ запомнить порядок операций. Это означает, что порядок следующий: Скобки, Экспоненты (это будет включено позже), Умножение и Деление (взятые вместе слева направо) и, наконец, Сложение и Вычитание (взятые вместе слева направо).

Давайте попробуем решить несколько задач.

Пример 1.26

$3+2(3+5)=3+2(8)=3+16=19$
$3-2(-4+7)=3-2(3)=3-6=-3$
$-3-4-2(-2 \cdot 6-5)=-3-4-2(-12-5)=-3-4-2(-17)=-3-4-(- 34)=-3-4+34=27$
$-(3-(-6))-(1-4 \cdot(-5)+4)=-(3+6)-(1-(-20)+4)=-9-(1 +20+4)=-9-25=-9+(-25)=-34$
$-2(-14 \дел 7+7)=-2(-2+7)=-2(5)=-10$
$-3(-2 \cdot 7-(-5)(4) \div 2)=-3(-14-(-20) \div 2)=-3(-14-(-10)) =-3(-4)=12$
$6 \div 2 \times 3=3 \times 3=9$ Примечание: $6 \div 2 \times 36=6 \div 6=1$
$-2(3-1) 2-(8-22) \дел 4=-2(2) 2-(8-4) \дел 4=-2(4)-4 \дел 4=-8 -1=-9$

Выход Проблема

Вычислить: $\влево(3^{3}+5\вправо) \div 4-4(7-2)$

Эта страница под названием 1.

Выполнение арифметических операций. Решение разобранных примеров.

Альфашкола
Статьи
Порядок выполнения арифметических операций

Как правильно вычислить $\frac{48}{2}(9+3)$ ? Один получает в ответе $288$, второй $2$. В таких случаях стоит помнить, что первое действие выполняется в скобках, и здесь важно знать порядок арифметических операций.

Порядок арифметических операций — это порядок, в котором все алгебраические выражения должны быть выполнены. Зачастую значение выражения меняется в зависимости от порядка его вычисления. Порядок выполнения арифметических операций:

действия в скобках
радикалы, то есть корни
умножение и деление
сложение и вычитание

Круглые скобки — это изогнутые символы $()$, которые помещаются вокруг части выражения, чтобы показать, что выражения внутри них должны быть вычислены в первую очередь. В круглых скобках следует соблюдать тот же порядок операций. Сначала вычисляются выражения в скобках, затем корни, то есть радикалы, умножение и деление и в конце сложение и вычитание. Если есть несколько одинаковых арифметических операций, то действия выполняются в порядке слева направо.

Пример 1. Вычислить:

Сначала выполняем умножение в скобках $2*8=16$, потом деление $16:4=4$ и затем сложение $4+1,2=5,2$. В результате выражения получаем $5,2.$

Пример 2. Вычислить:

Сначала обратим внимание, что нет скобок и корней, поэтому мы сразу переходим к умножению и делению $3*3=9$, затем переходим к сложению и вычитанию, работая слева направо $9-5=4$ и $4+2=6$ . В результате выражения получаем $6.$

Логическое обоснование порядка арифметических операций, помимо скобок, которые, очевидно, являются первыми, заключается в том, что умножение — это повторное сложение, а возведение в степень — это повторное умножение. Кроме того, деление обратно умножению.

Например, выражение:

должно быть решено в следующем порядке: вычисляем выражение в скобках $6+7=13$, потом выполняем умножение $2*13=26$ и затем отнимаем от получившегося значения $82$ и получаем $-56$. Это и есть наш окончательный результат -56.

Если бы желаемый порядок решения выражения был бы другим, на основе исходной задачи, то скобки были бы расположены по-другому. Порядок операций очень важен, поэтому вы должны понимать порядок арифметических операций на хорошем уровне.

Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!

Запишитесь на бесплатное тестирование знаний!

Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности

Наши преподаватели

Жанна Александровна Бояркина

Репетитор по математике

Стаж (лет)

Образование:

Благовещенский государственный педагогический институт

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Татьяна Валентиновна Дмитриева

Репетитор по математике

Стаж (лет)

Образование:

Ивановский государственный университет

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Никита Сергеевич Анохин

Репетитор по математике

Стаж (лет)

Образование:

Керченский государственный морской технологический университет

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Предметы

Математика
Репетитор по физике
Репетитор по химии
Репетитор по русскому языку
Репетитор по английскому языку
Репетитор по обществознанию
Репетитор по истории России
Репетитор по биологии
Репетитор по географии
Репетитор по информатике

Специализации

Подготовка к ЕГЭ по математике (базовый уровень)
Репетитор по геометрии
Репетитор по химии для подготовки к ЕГЭ
Репетитор для подготовки к сочинению ЕГЭ по русскому
Репетитор для подготовки к ОГЭ по истории
ВПР по физике
Репетитор для подготовки к ВПР по обществознанию
Репетитор для подготовки к ЕГЭ по обществознанию
Репетитор по информатике для подготовки к ЕГЭ
Программирование Pascal

Последовательности и серии – рабочие примеры

Последовательность $\{ a_{n} \}$ — это бесконечный список чисел $$a_{1}, a_{2}, a_{3}, \ldots,$$ где у нас есть одно число $a_{n}$ для каждого положительного целого числа $n$.

Определение последовательностей.

Мы можем задать последовательность различными способами.

Выкройка. Мы можем указать его, перечислив некоторые элементы и подразумевая, что Показанная схема продолжается.

Пример.

Например $$2, 4, 6, 8, \ldots$$ будет последовательность, состоящая из четных положительных целых чисел.

Формула. Мы также можем указать последовательность, дав формулу для термина, который соответствует целому числу $n$.

Пример.

Например, последовательность $$2, 4, 6, 8, \ldots$$ можно также задать явной формулой $$a_{n} = 2n.$$ Рекурсивно. Наконец, мы также можем предоставить правило для получения следующего члена последовательности из предыдущих. Это называется рекурсивно определенной последовательностью.

Пример.

Например, последовательность $$2, 4, 6, 8, \ldots$$ можно указать по правилу $$a_{1} = 2 \quad \text{ и } \quad a_{n} = a_{n-1} +2 \text{ для } n\geq 2. $$ Это правило гласит, что мы получаем следующий член, беря предыдущий член и добавляя $2$. Поскольку мы начинаем с числа 2, мы получаем все четные положительные целые числа.

Давайте обсудим эти способы определения последовательностей более подробно и рассмотрим несколько примеров.

Часть 1. Арифметические последовательности
Последовательность, которую мы видели в предыдущем абзаце, является примером того, что называется арифметической последовательностью : каждый член получается добавление фиксированного числа к предыдущему термину.
Альтернативно, разница между последовательными сроками всегда равна одно и тоже.
Общая формула.
Если последовательность $a_{n}$ арифметическая, то существует фиксированное число $d$, такое что $a_{n+1} -a_{n} =d$ для любого $n.$ Число $d$ обычно называют 9.0009 шаг или разница . Попробуем найти формулу члена $a_{n}$ арифметической прогрессии через $d$ и $a_{1}$.
Начнем с $a_{n} = a_{n-1} + d$. Применяя это снова, мы видим, что поскольку $a_{n-1} = a_{n-2} + d$, мы получаем, что $a_{n} = a_{n-2} + d +d = a_{n- 2} + 2d$. Мы можем продолжить этот путь и получить: \начать{выравнивать*} а_{п} &= а_{п} = а_{п-1} + д \\ &= a_{n-2} + d +d = a_{n-2} + 2d \\ &= a_{n-3} + d + d = a_{n-3} + 3d \\ &\vточки\\ &= а_{2} + (n-2)d \\ &= а_{1} + (n-1)d \\ \конец{выравнивание*} Таким образом, мы получаем, что в арифметической последовательности $a_{n}$ с шагом размером $d$ формула для $a_{n}$ задается следующим образом: $$a_{n} = a_{1} + (n-1)d$$
Пример. Рассмотрим последовательность $3, 8, 13, 18, 23, 28, \ldots$. Это арифметика? Если это так, найдите формулу для $a_{n}$ и используйте ее, чтобы найти $a_{101}$, 101-й член последовательности.
Раствор. Эта последовательность является арифметической, так как разница между каждым членом составляет 5$
(8-3 = 13-8 = 18-13 = \cdots = 5$). с шагом $d=5$ и первым членом $a_{1} = 3$.
Наша формула выше дает $a_{n} = a_{1} + (n-1)d = 3 + (n-1)5$.
Для $a_{101}$ мы подставляем $n=101$ в эту формулу, чтобы получить $a_{101} = 3 + (100)5 = 503$.
Часть 2. Геометрические последовательности
Рассмотрим последовательность $2, 4, 8, 16, 32, 64, \ldots$. Эта последовательность не является арифметической, так как разница между терминами не всегда одинакова. Если мы посмотрим внимательно, то увидим, что мы получаем следующий член последовательности как , умножая предыдущий член на то же число . Соответственно, соотношение последовательных терминов всегда одинаково (а именно $2$).
Последовательность $a_{n}$, где существует фиксированное $r$, так что $\frac{a_{n}}{a_{n-1}} = r$ для всех $n$ называется геометрическим последовательность. Число $r$ обычно называют отношением .
Общая формула.
Попробуем найти формулу члена $a_{n}$ геометрической прогрессии через $r$ и первый член. {n-1} a_{1}$$ 9{n-1} a$ или правило, что $a_{n} = r a_{n-1}$.
Последнее правило является примером рекурсивного правила . Рекурсивно определенная последовательность представляет собой последовательность, в которой правило для создания следующего члена в последовательности записано явно в терминах предыдущих членов.
Рассмотрим следующий (довольно известный) пример.
Пример.
Определим последовательность $a_{n}$ следующим образом: Пусть $$a_{1} = 1 \quad , \quad a_{2} = 1 \quad \text{ и} \quad a_{n} = a_{n-1} + a_{n-2} \text{ для } n\geq 2.$$ Это правило гласит, что для получения следующего члена последовательности необходимо сложить два предыдущих члена. Поскольку это правило требует двух предыдущих членов, нам нужно указать первые два члена последовательности $a_{1}, a_{2}$, чтобы начать работу. Используя это, мы можем начать перечислять термины в последовательности и получить $1, 1, 2, 3, 5, 8, 13, 21, 34,\ldots$. (Это хорошо известное последовательность Фибоначчи .)
Пример.
Рассмотрим рекурсивно определенную последовательность $$a_{1} = 1 \quad , \quad a_{2} = 1 \quad , \quad a_{3} = 1 \quad \text{, и} \quad a_{n} = \frac{a_{n-3}}{a_{n-1} + a_{n-2}} \text{ for } n\geq 3.$$ Назовите первые 7 членов этой последовательности.
Раствор. \начать{выравнивать*} а_{1} &= 1 \\ а_{2} &= 1 \\ а_{3} &= 1 \\ a_{4} &= \frac{1}{1+1} = \frac{1}{2} \\ a_{5} &=\frac{1}{1+\frac{1}{2}} = \frac{1}{\frac{3}{2}} = \frac{2}{3} \\ a_{6} &= \frac{1}{\frac{1}{2} + \frac{2}{3}} = \frac{1}{\frac{7}{6}} = \frac{ 6}{7} \\ a_{7} &= \frac{ \frac{1}{2}}{\frac{2}{3} + \frac{6}{7}} = \frac{ \frac{1}{2}} {\ гидроразрыва {32} {21}} = \ гидроразрыва {21} {64} \конец{выравнивание*}
Часть 4: Последовательности через списки
Метод использования списка для указания последовательности, пожалуй, самый сложно, так как это требует от нас просмотра короткого фрагмента последовательности, и угадать шаблон или правило, которое используется для создания термины в последовательности.
Теперь, когда мы рассмотрели еще несколько примеров последовательностей, мы можем обсудить, как искать закономерности и вычислять по заданному списку, как найти рассматриваемую последовательность.
Пример.
Когда дается список, например, $1, 3, 9, 27, 81, \ldots$ мы можем попробовать ищите закономерность несколькими способами.
Теперь, когда мы увидели арифметические, геометрические и рекурсивные последовательности, одна вещь, которую мы можем сделать, это попытаться проверить, является ли данная последовательность является одним из этих типов.
Арифметика? Чтобы проверить, является ли последовательность арифметической, мы проверяем, является ли разница последовательных терминов всегда одинакова. В этом случае изменения разницы: $$a_2- a_1 = 3-1 =2 \neq 6 = 9-3 = a_3-a_2.$$ Геометрический? Чтобы проверить, является ли последовательность геометрической, мы проверяем, всегда ли соотношение последовательных членов одинаково. В случае, если это так, мы заключаем, что последовательность является геометрической: $$\frac{3}{1}= \frac{9{\text{th}}$ термин в последовательность.
Раствор. Мы быстро видим, что этот ряд не является геометрическим, поскольку $\frac{1}{-3} \neq \frac{-3}{-7}$.
Теперь мы можем проверить, является ли последовательность арифметической. Если мы посмотрим на различия последовательных членов, мы получим: $-3 — 1 = -4 = -7 — (-3) = -11 — (-7)$, поэтому мы видим, что это арифметическая последовательность с разностью $d=-4$. Итак, общий термин $$a_{n} = a_{1} + (n-1) d = 1 + (n-1) (-4) = — 4n + 5.$$
(Мы также можем попытаться найти рекурсивное определение этой последовательности.)
8.2: Решение задач с помощью арифметических последовательностей
Последнее обновление
Сохранить как PDF
Идентификатор страницы
83159
Дженнифер Фрейденрайх
Diablo Valley College
Арифметические последовательности, представленные в разделе 8. 1, имеют множество приложений в математике и повседневной жизни. В этом разделе рассматриваются эти приложения.
Пример 8.2.1
Бак для воды дает течь. Каждую неделю бак теряет $5$ галлонов воды из-за утечки. Изначально бак полный и содержит $1500$ галлонов.
Сколько галлонов осталось в баке $20$ недель спустя?
Сколько недель до заполнения бака наполовину?
Сколько недель до полного опустошения бака?
Решение
Эту задачу можно рассматривать либо как линейную функцию, либо как арифметическую последовательность. Таблица значений дает нам несколько подсказок к формуле.
Проблема позволяет нам начать последовательность с любого значения $n$-, которое мы пожелаем. Удобнее всего начать с $n = 0$ и установить $a_0 = 1500$.
Следовательно, $a_n = −5n + 1500$
Сколько галлонов осталось в баке $20$ недель спустя?
Поскольку утечка впервые была замечена на первой неделе, $20$ недель после первой недели соответствует $n = 20$. Используйте формулу где $\textcolor{red}{n = 20}$:
$a_{20} = −5(\textcolor{red}{20}) + 1500 = −100 + 1500 = 1400$
Таким образом, через $20$ недель бак содержит $1400$ галлонов воды.
Сколько недель до заполнения бака наполовину? Наполовину полный бак будет $750$ галлонов. Нам нужно найти $n$, когда $\textcolor{red}{a_n = 750}$.
$\begin{array} &750 &= −5n + 1500 &\text{Подставьте \(a_n = 750$ в общий термин.} \\ 750 − 1500 &= −5n + 1505 − 1500 &\text {Вычтите $1500$ из каждой части уравнения.} \\ −750 &= −5n &\text{Упростите каждую часть уравнения.} \\ \dfrac{−750}{−5} &= \ dfrac{−5n}{−5} &\text{Разделить обе части на $−5$.} \\ 150 &= n & \end{array}\)
Поскольку $n$ — это номер недели, этот ответ говорит нам, что на неделе $150$ бак наполовину полон. Однако большинство людей лучше поняли бы ответ, если бы он был сформулирован следующим образом: «Бак наполовину полон через 150 недель». Этот ответ звучит более естественно и предпочтительнее.
Сколько недель до того, как бак опустеет? Бак пуст, когда $a_n = 0$ галлонов. Найдите $n$ такое, что $\textcolor{red}{a_n = 0}$.
$\begin{array}& 0 &= −5n + 1500 &\text{Подставить \(a_n=0$ в общий термин.} \\ 0 − 1500 &= −5n + 1500 − 1500 &\ text{Вычтите $1500$ из каждой части уравнения.} \\ −1500 &= −5n &\text{Упростить.} \\ \dfrac{−1500}{−5} &= \dfrac{−5n }{−5} &\text{Разделить обе части на $−5$.} \\ 300 &= n & \end{массив}\)
Поскольку $n$ — это номер недели, этот ответ говорит нам, что на неделе $300$ резервуар пуст. Однако большинство людей лучше поняли бы ответ, если бы он был сформулирован следующим образом: « Резервуар пуст после 300 недель. ». Этот ответ звучит более естественно и предпочтительнее.
Пример 8.2.2
Ниже показаны три этапа узора с использованием спичек. Для каждого этапа требуется определенное количество спичек. Если мы будем продолжать в том же духе…
Сколько спичек нужно, чтобы сложить фигуру на этапе $34$?
Для какого этапа потребуется $220$ спичек?
Решение
Этап 1 Этап 2 Этап 3
Создадим таблицу значений. Пусть $n =$ номер этапа, и пусть $a_n =$ количество спичек, использованных на этом этапе. Затем обратите внимание на общую разницу.
Найти значение $a_0$:
$\begin{массив} &a_0 + 3 &= 4 \\ a_0 + 3 — 3 &= 4 — 3 \\ a_0 &= 1 \end{массив}$
Общий член последовательности:
$а_п = 3п + 1$
Вычислить $a_{34}$, чтобы найти количество спичек на этапе $34$:
$a_{34} = 3(\textcolor{red}{34}) + 1 = 103$.
На сцене $103$ спичек $34$.
Для какого этапа потребуется $220$ спичек? Ищем этап-номер по количеству спичек. Найдите $n$, если $a_n = 220$.
$\begin{массив} &220 &= 3n + 1 \\ 219 &= 3n \\ 73 &= n \end{массив}$
Ответ Этап $73$ потребует $220$ спичек.
Пример 8.2.3
Кори покупает $5$ товаров в продуктовом магазине по ценам $a_1$, $a_2$, $a_3$, $a_4$, $a_5$, что является арифметическим последовательность. Наименее дорогой товар стоит $$1,89$, а общая стоимость $5$ товаров — $$12,95$. Какова стоимость каждого предмета?
Раствор
Расположите $5$ предметов в порядке их расходования: от меньшего к большему и слева направо. Поскольку это арифметическая последовательность, каждый элемент стоит на $d$ больше долларов, чем предыдущий. Цена каждого товара может быть записана в виде цены самого дешевого товара, $a_1$ и $a_1 = $1,89$.
На приведенной выше диаграмме приведены $5$ выражения стоимости $5$ предметов в терминах $a_1$, а общая разница равна $d$.
$\begin{array} &a_1 + a_2 + a_3 + a_4 + a_5 &= 12,95 &\text{Общая стоимость \(5$ элементов равна $12,95$$.} \\ a_1 + (a_1 + d) + (a_1 + 2d) + (a_1 + 3d) + (a_1 + 4d) &= 12,95 &\text{Подстановки см. на схеме.} \\ 5s_1 + 10d &= 12,95 &\text{Соберите одинаковые термины.} \\ 5(1,89) + 10d &= 12,95 &a_1 = 1,89. \\ 9,45 + 10d &= 12,95 &\text{Упростить.} \\ 9,45 + 10d — 9,45 &= 12,95 — 9,45 &\text{Вычесть $9,45$ с каждой стороны уравнения.} \\ 10d &= 3,50 &\text{Упростите. Затем разделите обе части на $10$.} \\ d &= 0,35 &\text{Общая разница составляет $$0,35$ .} \end{массив}\)
Теперь, когда мы знаем общую разницу $d = $0,35$, мы можем ответить на вопрос.
Цена каждого предмета следующая: $1,89$, 2,24$, 2,59$, 2,94$, 3,29$$.
1. Кабельная компания ZKonnect требует от клиентов подписать $2$-летний контракт на использование их услуг. Ниже описывается штраф за нарушение контракта: Ваши услуги подпадают под действие соглашения о минимальном сроке действия $24$ месяцев. Если контракт расторгается до окончания $24$-месячного контракта, плата за досрочное расторжение оценивается следующим образом: $$230$ плата за расторжение оценивается, если контракт расторгается в первые $30\ ) дней службы. После этого плата за расторжение договора уменьшается на \($10$ за каждый месяц действия контракта.
Если Джек заключает договор с ZKonnect 1 апреля ^st $2021$, но прекращает предоставление услуг 10 января ^th $2022$, какова плата Джека за досрочное расторжение?
Общий термин $a_n$ описывает плату за расторжение указанного контракта. Опишите значение переменной $n$ в контексте этой задачи. Найдите общий термин $a_n$.
Плата за досрочное расторжение договора представляет собой конечную или бесконечную последовательность? Объяснять.
Найдите значение $a_{13}$ и интерпретируйте его значение словами.
2. На сегодняшний день фармацевтическая компания произвела $4$ миллионов доз вакцины. Они обещают дополнительное производство со скоростью $1,2$ миллиона доз в месяц в течение следующего года.
Сколько всего доз вакцины будет произведено через год?
Общий термин $a_n$ описывает общее количество произведенных доз вакцины. Опишите значение переменной $n$ в контексте этой задачи. Найдите общий термин$a_n$.
Найдите значение $a_8$ и интерпретируйте его значение словами.
3. Театр, показанный справа, имеет $22$ мест в первом ряду секции «A Center». Каждый ряд позади первого ряда получает два дополнительных места.
Пусть $a_n = 22 + 2n$, начиная с $n = 0$. Укажите первые $10$ значений этой последовательности.
Используя $a_n = 22 + 2n$, найдите значение $a_{10}$ и интерпретируйте его словесное значение в контексте этой задачи. Осторожный! Есть ли $n=$ номер строки?
Сколько мест всего в секции «А Центр», если в секции $12$ рядов?
4) Бревна укладываются в стопку с $48$ бревнами в нижнем ряду и $24$ в верхнем ряду. Каждый ряд уменьшается на три бревна.
Сколько рядов журналов в стеке, как описано?
Напишите общий термин $a_n$, чтобы описать количество журналов в строке двумя разными способами. Каждый общий терм должен давать одну и ту же последовательность, независимо от его начального $n$-значения. 92\)].
6) Ниже показаны три этапа узора с использованием спичек. Каждый этап добавляет еще один треугольник и требует определенного количества спичек. Если следовать схеме…
Сколько спичек нужно, чтобы сложить фигуру на этапе $34$?
Какой этап потребует $325$ спичек?
Этап 1 Этап 2 Этап 3
7) Ниже показаны три этапа узора с использованием спичек. Для каждого этапа требуется определенное количество спичек.
No related posts.