правила с доказательствами, определение, примеры
Признаки делимости чисел в математике — объяснение
ОпределениеПризнаки делимости чисел — это условия, правила, по которым можно определить, делится ли число на заданное нам значение, т.е. кратно ли число делителю.
Делителем является число, на которое делится заданное число без остатка — нацело.
Термин «кратно» — синоним слову «делится».
Правила с доказательствами, определение
- Признак делимости на 10.
Любое натуральное число, которое оканчивается цифрой 0, делится без остатка на 10. Чтобы получить частное, нужно отбросить нуль.
Правило 1Если запись натурального числа заканчивается нулем, то число делится на 10 нацело.
Если запись натурального числа заканчивается любой другой цифрой, то число не делится нацело на 10.
Доказательство.
Например, 370 делится нацело на 10, так как 370:10=37.
Но 378 не делится без остатка на 10, потому что получим неполное частное: 378:10=37 (остаток 8).
На конце числа 378 стоит цифра 8 — она и будет остатком при делении на 10. Значит, 378 не делится нацело на 10.
Применение признака позволяет не производить расчеты, а сразу отвечать на вопрос, делится ли заданное число на десять.
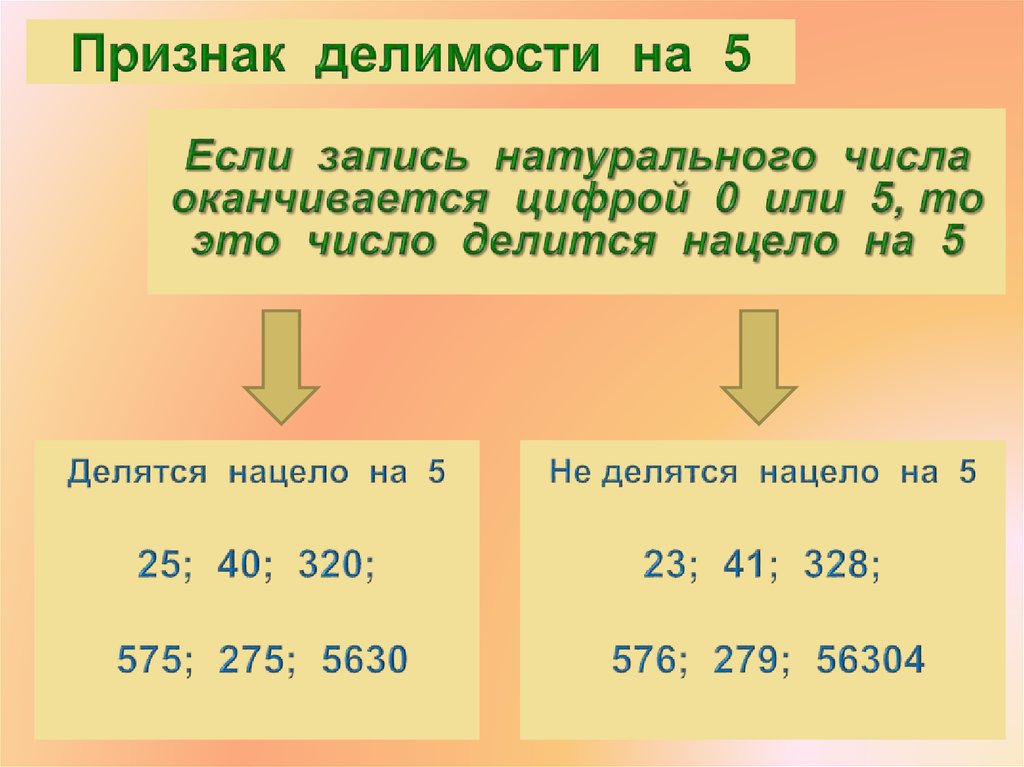
- Признак делимости на 5.
Число 20 можно представить в виде произведения: 20=4*5.
Тогда число 5 является делителем числа 20, т. е. 20 делится на пять нацело, без остатка.
Число 15 представляют в виде произведения двух множителей: 15=3*5 .
Тогда число 5 является делителем числа 15, т. е. 15 делится на 5 нацело.
В разрядах единиц 20 и 15 стоят 0 и 5 соответственно.
Разряд — это место цифры в числе.
Правило 2Если запись натурального числа заканчивается цифрами 0 или 5, то такое число делится нацело на 5.
Можно перефразировать признак:
Если в разряде единиц заданного числа стоит 0 или 5, то число делится на 5.
Если запись натурального числа заканчивается цифрой, отличной от нуля и пяти, то число на 5 нацело не делится.
Доказательство.
Числа 645 и 760 делятся на 5, так как они заканчиваются 5 и 0 соответственно.
Проверка:
645:5=129760:5=152.
344 не делится нацело на 5 по признаку делимости:
344:5=68 (остаток 4) .
- Признаки делимости на 2.
Если число делится нацело на 2, то его называют четным. Если число не делится нацело на 2, то его называют нечетным.
Цифры 0, 2, 4, 6, 8 — четные, а 1, 3, 5, 7, 9 — нечетные. Тогда любое число будет четным, если в разряде единиц у него стоит четная цифра, а нечетным — в разряде единиц стоит нечетная цифра.
Правило 3Если запись натурального числа оканчивается четной цифрой, то число делится на 2 нацело.
Если натуральное число оканчивается нечетной цифрой, то не делится нацело на 2.
Доказательство.
Числа 14 и 56 делятся нацело на 2, так как они заканчиваются четными цифрами — 4 и 6.
14:2=756:2=28.
Число 13 не делится нацело на 2, так как запись натурального числа заканчивается нечетной цифрой 3.
13:2=6 (остаток 1).
- Признак делимости на 9.
Если сумма цифр числа делится нацело на 9, то и само число делится нацело на 9.
Если сумма цифр числа не делится нацело на 9, то и само число не делится нацело на 9.
Доказательство.
Рассмотрим, делится ли 98 на 9.
Сумма цифр числа: 9+8=17.
17 не делится нацело на 9, тогда число 98 не делится нацело на 9.
Проверяем: 98:9=10 (остаток 8).
Возьмем число 468. Используя признак делимости на 9, считаем сумму цифр числа 468: 4+6+8=18 .
18 делится нацело на 9, значит, 468 делится нацело на 9:
468:9=52.
- Признак делимости на 3.
Если сумма цифр числа делится нацело на 3, то и само число делится нацело на 3.
Если сумма цифр числа не делится нацело на 3, то и само число не делится нацело на три.
Число 27 делится нацело на 3, так как сумма цифр делится на 3 нацело.
2+7=99:3=3.
И, соответственно, 27:3=9.
Число 261 делится на 3 по признаку делимости:
2+6+1=9.
Девять делится на 3 нацело, значит, число 261 делится на 3 нацело.
261:3=87 .
Дополнительные признаки делимости:
- Признак делимости на 4.
Натуральное число делится на 4 нацело в том случае, когда запись числа заканчивается двумя нулями или две последние цифры делятся на 4.
Например, по этому признаку число 144 делится на 4, так как 44 — две последние цифры — делится нацело на 4.
44:4=11 .
Проверка: 144:4=36 .
- Признак делимости на 6.
Натуральное число делится на 6 нацело тогда, когда число делится нацело и на 2, и на 3.
Значит, признак делимости на 6 включает в себя применения признака делимости на два и признака делимости на три.
Например, число 438 делится на 6 нацело.
Используя признак делимости на 6, поочередно применяем признаки делимости на 2 и 3.
Если число заканчивается четной цифрой, то оно делится на 2: число 438 заканчивается четной цифрой 8.
Если сумма цифр числа делится нацело на 3, то и само число делится нацело на 3:4+3+8=15 .
Значит, число делится и на 2, и на 3. Тогда 438 делится на 6 нацело.
Проверка: 438:6=73 .
- Признак делимости на 8.
Натуральное число делится на 8 нацело, если запись числа заканчивается тремя нулями либо если три последние цифры образуют число, которое делится на 8.
Например, 58000 делится на 8 по признаку делимости, так как число заканчивается тремя нулями.
Проверка: 58000:8=7250 .
Остальные признаки делимости можно вывести самостоятельно.
Где применяется в жизни
В жизни признаки делимости удобно применять тогда, когда под рукой нет гаджетов. И процесс определения делимости чисел значительно упрощается. При этом не нужно даже высчитывать результат непосредственного деления, если в задаче необходимо просто определить, делится ли одно число на другое.
Области применения признаков делимости:
- торговля — например, определение примерной стоимости покупки, когда ограничены денежные ресурсы;
- строительство — примерное распределение стройматериала;
- математические игры и головоломки;
- бизнес — определение капитала и т. д.
Примеры решения задач
Пример 1Назовите 3 числа, которые делятся на 2.
Решение.
Вспоминаем признак делимости на 2:
Если число заканчивается четной цифрой, то оно делится на 2.
Тогда искомыми числами могут быть, например: 456, 768, 800.
Цифры 6, 8, 0 — четные: значит, числа 456, 768, 800 делятся на 2.
Пример 2Какие из чисел 234, 450, 400, 3400, 35, 900, 235 000 делятся на 100?
Пояснение.
Мы знаем признак делимости на 10:
Если число заканчивается 0, то число делится на 10.
Когда нужно определить, делится ли число на 100, действуем аналогично признаку делимости на 10. Только в этом случае нужно искать те числа, которые заканчиваются двумя нулями.
Тогда в ответе будут числа: 400, 3400, 900, 235 000.
Аналогично действуем тогда, когда нужно найти числа, которые делятся на 1000, 1000 и так далее. Ищем числа по количеству нулей после единицы в делителе.
Пример 3Какие из чисел 100, 35, 450, 5680, 20 делятся и на 5, и на 10.
Решение.
Число делится на 5, если заканчивается 0 или 5.
Число делится на 10, если заканчивается 0.
Тогда, чтобы число делилось и на 5, и на 10, нужно найти в признаках что-то общее.
Общим будет окончание чисел на 0.
По признакам делимости на 5, и на 10 получаем в ответе числа: 100, 450, 5680 и 20.
Пример 4Найдите три числа, которые делятся на 2 и на 9.
Решение.
Чтобы число делилось и на 2, и на 9, должны выполняться условия обоих признаков.
Число делится на 2 тогда, когда оканчивается четной цифрой. Четные цифры — это 0, 2, 4, 6, 8.
Число делится на 9 тогда, когда сумма цифр числа делится на 9.
Тогда искомыми числами могут быть: 18, 396 и 468.
В разряде единиц в 18, 396 и 468 стоят 8, 6 и 8 соответственно — четные цифры, значит числа 18, 396 и 468 делятся на 2.
Осталось проверить, делятся ли они на 9. Считаем сумму цифр в числах.
18: 1+8=9 — 9 делится на 9;396: 3+9+6=18 — 18 делится на 9;468: 4+6+8=18 — 18 делится на 9..
Значит, числа 18, 396 и 468 делятся на 9.
Числа удовлетворяют условиям.
Ответ: 18, 396 и 468.
Пример 5Какие из чисел 456, 567, 3453, 768 и 34500 кратны 3?
Объяснение.
Слово «кратно» является синонимом «делится». Тогда нужно найти числа, которые делятся на 3.
По признаку делимости искомыми будут числа, сумма цифр которых делится на три нацело.
456: 4+5+6=15;567: 5+6+7=18;3453: 3+4+5+6=18;768: 7+6+8=21;34500: 2+4+5=11. .
Выбираем те числа, сумма которых делится на 3:
456, так как сумма цифр равна 15, а 15 делится на 3 нацело;
567, потому что сумма цифр равна 18, а 18 делится на 3 нацело;
3453 — сумма цифр равна 18, значит, число делится на 3;
768 — сумма цифр равна 21, значит, число делится на 3.
Ответ: 456, 567, 3453 и 768.
Признаки делимости натуральных чисел от 2 до 25 и на 50
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай».
Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
1. Признаки делимости натуральных чисел от 2 до 25 и на 50
2. Что такое признак делимости
Признак делимости натуральногочисла n на m — способ быстро определить,
делится ли n на m — быстрее, чем при
попытке выполнить деление и посмотреть,
какой остаток. Обычно признаки делимости
используются для ускорения ручных
расчётов, значительная их часть плохо
приспособлена для программирования.
3. Признаки делимости на 2, 5, 10.
• Признаки делимости на 2, 5, 10 — самые простые извсех: достаточно лишь посмотреть на последнюю
цифру числа. Признак делимости на 2: если число
оканчивается на 0, 2, 4, 6 или 8, то число делится на
два (то есть последняя цифра должна делиться на
2), иначе не делится.
Признак делимости на 5: еслипоследняя цифра числа — 0 или 5, то число делится
на 5, иначе не делится. Признак делимости на 10:
если число оканчивается на 0, оно делится на 10,
иначе не делится. Признак делимости на 100: число
должно оканчиваться на 00. Как определить,
делится ли число на 1000, 10000 и т.д., тут, видимо,
и так ясно.
4. Признаки делимости на 3, 6, 9, 18
• Признаки делимости на 3, 6, 9, 18• Признак делимости на 3: число делится на 3 тогда и только
тогда, когда сумма цифр его делится на 3.
• Признак делимости на 6: если число одновременно делится на
2 и на 3, то оно делится на 6. Такой признак можно применить
исходя из того, что числа 2 и 3 не имеют общих делителей,
кроме 1.
Признак делимости на 9: аналогично — если сумма цифр числа
делится на 9, то и число делится на 9, иначе не делится.
Поскольку 9 и 2 имеют в качестве общего делителя только 1,то:
• Признак делимости на 18: если число одновременно делится
на 2 и 9, то оно делится на 18.
5. Признаки делимости на 20, 25 и 50
• Если проверяемое число оканчивается на00, 20, 40, 60, 80, то оно делится на 20, если
на 00, 25, 50, 75, то оно делится на 25, если
на 00 или 50, то оно делится на 50.
Названные в этом абзаце признаки
делимости, использующие две последние
— делители числа 100.
• Один из признаков делимости на 7: утроенное
количество десятков, сложенное с количеством
единиц, делится на 7. Например, 231 делится на 7:
23 * 3 + 1 = 70 — делится на 7. 2009 делится на 7: 200
* 3 + 9 = 609; 60 * 3 + 9 = 189; 18 * 3 + 9 = 63 делится на 7.
Пусть s1 — сумма цифр, занимающих нечётные
позиции, s2 — сумма цифр, занимающих чётные
позиции. Если |s1-s2| делится на 11, то и число
делится на 11. Допустим, возьмём 7421 * 11 =
81631. s1 = 8 + 6 + 1 = 15; s2 = 3 + 1 = 4; |s1 — s2| = 11.
English Русский Правила
Делимость на 11 — пустышки
Двузначные числа, которые делятся на 11, трудно не заметить, потому что они просто повторяют одну и ту же цифру дважды.
Вот все числа меньше 100, которые делятся на 11:
11 22 33 44 55 66 77 88 99
Для чисел от 100 до 200 используйте следующее правило: каждое трехзначное число, первая и третья цифры которого в сумме составляют его вторую цифру, делится на 11. Например, предположим, что вы хотите определить, делится ли число 154 на 11. Просто сложите первую и третью цифры:
1 + 4 = 5
Поскольку в сумме эти два числа составляют вторую цифру 5, число 154 делится на 11. Если разделить, получится 154 ÷ 11 = 14, целое число.
Теперь предположим, что вы хотите выяснить, делится ли 136 на 11. Сложите первую и третью цифры:
1 + 6 = 7
Поскольку первая и третья цифры дают в сумме 7, а не 3, число 136 не делится на 11. Вы можете найти, что 136 ÷ 11 = 12r4.
Для чисел любой длины это правило несколько сложнее, но все же зачастую проще, чем деление в длинную сторону. Чтобы узнать, делится ли число на 11, поставьте попеременно знаки плюс и минус перед каждой цифрой, а затем вычислите результат.
Например, предположим, что вы хотите узнать, делится ли число 15 983 на 11. Для начала поставьте знаки плюс и минус перед альтернативными цифрами (каждая вторая цифра):
+1 — 5 + 9 — 8 + 3 = 0
Поскольку результат равен 0, число 15 983 делится на 11. Если вы проверите деление, 15 983 ÷ 11 = 1 453.
Теперь предположим, что вы хотите узнать, делится ли 9 181 909 на 11. Снова поставьте знаки плюс и минус перед чередующимися цифрами и вычислите результат:
+9 — 1 + 8 — 1 + 9 — 0 + 9 = 33
Поскольку 33 делится на 11, число 9 181 909 также делится на 11. Фактический ответ:
.9 181 909 ÷ 11 = 834 719
Эта статья из книги:
- Базовая математика и предварительная алгебра для чайников,
Об авторе книги:
и математика из Университета Рутгерса.
Он зарабатывал себе на жизнь в течение многих лет написанием огромного количества логических головоломок, большим количеством документации по программному обеспечению и редкими рецензиями на книги или фильмы. Попутно он также оплатил несколько счетов за уборку дома, декоративную роспись и (в течение десяти часов) розничные продажи. Хотя больше всего ему нравится писать.Эту статью можно найти в категории:
- Базовая математика,
тесты на делимость | IB Maths Resources от Intermathematics
Тесты на делимость позволяют вычислить, можно ли разделить одно число на другое число. Например, можно ли 354 разделить на 3? Можно ли разделить 247 742 на 11? Итак, каковы правила проверки делимости и, что более интересно, как мы можем их доказать?
Правило делимости на 3
Самое известное правило делимости — это правило деления на 3.
Все, что вам нужно сделать, это сложить цифры числа, и если вы получите число, которое само кратно 3, то исходное число делится на 3. . Например, 354 делится на 3, потому что 3+5+4 = 12, а 12 можно разделить на 3.
Мы можем доказать это с помощью функции по модулю. Это позволяет нам вычислить остаток при делении любого числа на другое. Например, 21 ≡ 3 (модуль 6). Это означает, что остаток от деления 21 на 6 равен 3.
Итак, сначала начнем с нашего числа, которое мы хотим разделить на 3:
n = a + 10b + 100c + 1000d + …….
Теперь деление на 3 аналогично работе в моде 3, поэтому мы можем переписать это n в терминах мода 3:
n = a + 1b + 1c + 1d + ……. (mod 3)
(это потому, что 10 ≡ 1 mod 3, 100 ≡ 1 mod 3, 1000 ≡ 1 mod 3 и т. д.)
Теперь, чтобы число делилось на 3, эту сумму нужно добавить к кратному 3. Следовательно, если a + b + c + d + …. ≡ 0 (mod 3), то исходное число также делится на 3.
Правило делимости для 11
Это правило гораздо менее известно, но весьма неплохо.
По сути, вы берете цифры любого числа и поочередно вычитаете и складываете их. Если ответ кратен 11 (или 0), то исходное число делится на 11. Например, 121 кратно 11, потому что 1-2+1 = 0. 247 742 — потому что 2-4+7-7+ 4-2 = 0.
Еще раз мы можем доказать это, используя оператор по модулю.
n = а + 10b + 100c + 1000d + …..
и на этот раз работаем по модулю 11:
n = a + -1b +1c + -1d + ….. (mod 11)
это потому что для простоты расчета мы можем записать 10 ≡ -1 (mod 11 ). Это потому, что -1 ≡ 10 ≡ 21 ≡ 32 ≡ 43 (mod 11). Все числа, кроме 11, одинаковы по модулю 11. При этом 100 ≡ 1 (мод 11). Этот чередующийся образец будет продолжаться.
Следовательно, если поочередно вычитать и прибавлять цифры, то если ответ делится на 11, то и исходное число будет кратно.
Палиндромные числа
Палиндромные числа — это числа, которые одинаково читаются как вперед, так и назад. Например, 247 742 — это палиндромное число, как и 123 321.
Любое палиндромное число, которое является четным числом цифр, также делится на 11. Мы можем убедиться в этом, рассмотрев (например) число:
n = a + 10b + 100c + 1000c + 10 000b + 100 000a mod 11 мы получим тот же шаблон, что и раньше:
n = a – b +c – c +b – a (mod 11)
, значит n = 0 (mod 11). Следовательно, n делится на 11. Это работает только для четных палиндромных чисел, поскольку, когда числа симметричны, они сокращаются.
Важные ресурсы для студентов IB:
1) Руководства по исследованию и ресурсы Paper 3
Я собрал четыре подробных руководства в формате pdf, чтобы помочь студентам подготовиться к исследовательской курсовой работе и исследованиям Paper 3. Руководители по исследованию рассказывают о критериях выставления оценок, распространенных ошибках учащихся, отличных идеях для исследований, технических советах, методах моделирования и различных статистических методах с подробными объяснениями. Я также составил 17 полных вопросов для исследования, которые также являются отличной отправной точкой для исследований.