Геометрические сложения и вычитания векторов
Толкование
- Геометрические сложения и вычитания векторов
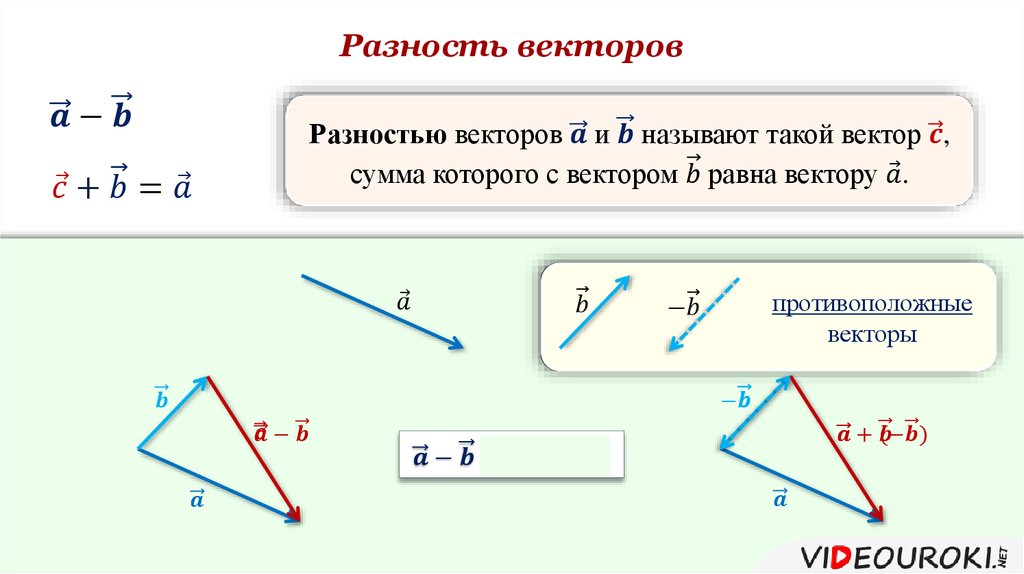
встречаются весьма часто в физике и механике; таковы, например, сложения сил, приложенных к одной точке, сложения скоростей, ускорений и проч. Геометрическое сложение двух векторов АА1 и BB1 имеет целью построение третьего вектора СС1, такого, проекция которого на какое бы то ни было направление равнялась бы сумме проекций на то же направление слагаемых векторов AA1 и ВВ1. Построение этого вектора CC1, называемого геометрической суммой слагаемых векторов, производится так: из какой-либо точки О (черт. 1) проводится длина Оα1, равная ипараллельная вектору АА1; из конца её α1

Черт. 1.
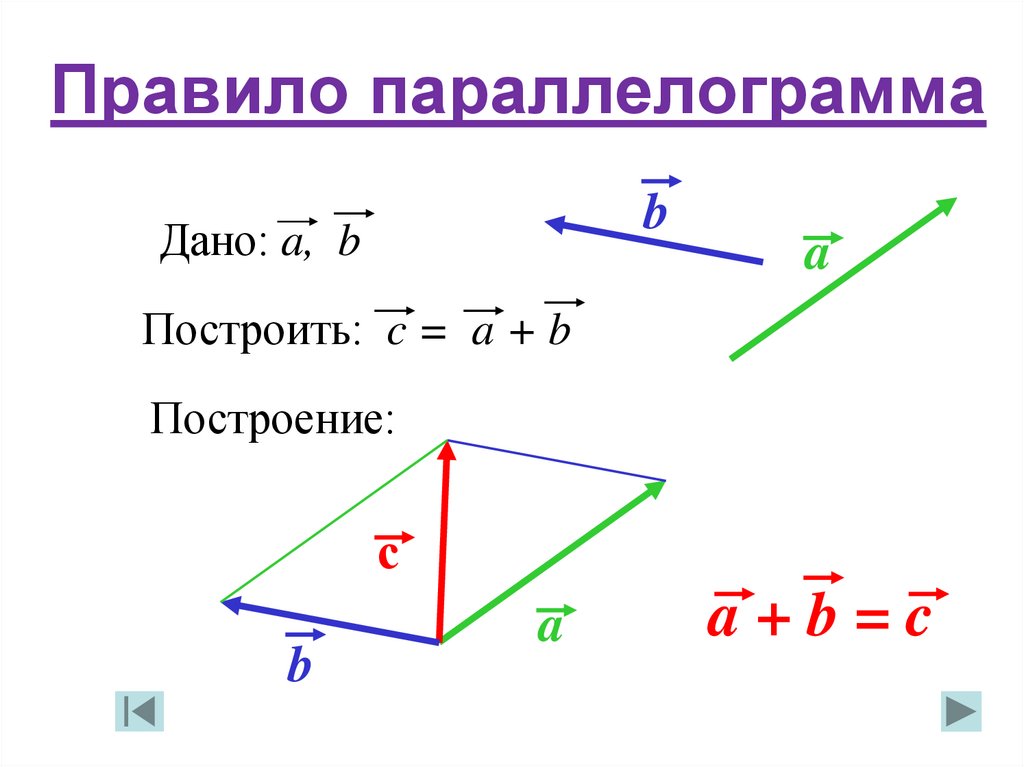
Можно сначала отложить Oβ‘, равную и параллельную ВВ1 и от точки β‘ отложить β‘β1, равную и параллельную AA1; — результат получится тот же самый. Можно еще сказать так: геометрическая сумма изображается диагональю параллелограмма, построенного на сторонах равных и параллельных геометрически слагаемым векторам, отложенных от какой-либо точки О, причем и диагональ надо провести из той же точки О. Геометрическое вычитание вектора ВВ1 из вектора АА1 имеет целью найти такой вектор DD1
проекция которого на какое-либо направление равнялась бы разности проекций векторов АА1 и ВВ1 на то же направление. Говоря иначе, геометрическая разность DD1 между геометрически уменьшаемым вектором АА1 и геометрически вычитаемым вектором ВВ1 равна геометрической сумме векторов AA1 и B1B, причем последний равен и противоположен ВВ1. Из этого следует, что построение геометрической разности между АА1 и ВВ1 должно быть произведено по правилу построения геометрической суммы векторов В1В и АА1, т. е. надо провести Oβ‘ (черт. 2), равную и параллельную В1В, из β‘ провести
Из этого следует, что построение геометрической разности между АА1 и ВВ1 должно быть произведено по правилу построения геометрической суммы векторов В1В и АА1, т. е. надо провести Oβ‘ (черт. 2), равную и параллельную В1В, из β‘ провести Черт. 2.
Если полученную геометрическую разность DD1 геометрически придать к ВВ1, то их геометрическая сумма будет равна АА1.
Д. Б.
Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона. — С.-Пб.: Брокгауз-Ефрон. 1890—1907.
Игры ⚽ Нужен реферат?
- Геометрическая изомерия
- Геометрия
Полезное
Тест на сложение и вычитание векторов за 9 класс – тренажер от Skills4u
Зарегистрируйся и получи 7 дней бесплатного доступа к тренажерам и персональный план прокачки знаний до 100%!
Вопросов в тесте: 13
Среднее время прохождения: ~10:00
Зарегистрируйся и получи персональный план прокачки знаний до 100%!
Как работает платформа Skills4u
Тестирование по предмету за класс
Платформа определит, какие темы сформированы слабо и составит индивидуальный план обучения
Персональный план обучения
План обучения и повторений поможет ученику в закреплении всех необходимых тем по предмету
Закрепление темы на 100%
Платформа напомнит и проконтролирует все повторения для закрепления каждой темы на 100%
Проработка слабых тем с предыдущих классов
Чтобы идеально овладеть предметом, рекомендуем закрепить пробелы, начиная с самых простых тем
Почему нужно пройти общее тестирование по геометрии за 9 класс, а не по отдельной теме «Сложение и вычитание векторов»
Пройдя тестирование за класс вы получите ПОЛНУЮ КАРТИНУ ЗНАНИЙ ПО ВСЕМ ТЕМАМ.
Такой подход позволит глубинно проанализировать знания, вывести успеваемость и понимание предмета на качественно новый уровень.
Пройдя тестирование по одной теме вы получите РЕЗУЛЬТАТ ЗНАНИЙ ТОЛЬКО ЭТОЙ ТЕМЫ, которая, возможно, плохо изучена. Такой метод не является комплексным и дает лишь точечное понимание знаний по предмету.
Зарегистрироваться и пройти тестирование
Вы хорошо усвоили тему «Сложение и вычитание векторов» за 9 класс? Тем, кто только что закончил изучение или находится в процессе, рекомендуем пройти несложный тест на тему «Сложение векторов» и оценить собственный уровень подготовки по геометрии.
Наш интерактивный тест на сложение векторов состоит всего из 13 вопросов, но в нем есть задания различного типа. Вам предстоит вычислить сумму или разность векторов, определить его длину и найти утверждение, которое соответствует истине. Писать ничего не придется. Нужно только выбрать верный ответ из 2-4-х, появляющихся на экране монитора.
После завершения тестирования система анализирует количество верных ответов, а также учитывает суммарное время, потраченное на выполнение заданий. Если результат вас удовлетворяет – поздравляем: вы хорошо выучили сложение векторов за 9 класс. Если же итог неутешительный, тема «Сложение векторов» дается вам с трудом, советуем позаниматься дополнительно, воспользовавшись возможностями, которые предоставляет образовательная платформа Skills4u. Для этого нужно зарегистрироваться на сайте и оформить подписку на месяц, полугодие или полный учебный год.
В первый раз каждый желающий может пройти тест на сложение и вычитание векторов для 9 класса абсолютно бесплатно. Большинство примеров можно решить в уме, а со временем вы научитесь замечать только правильные ответы.
Наши тренажеры на сложение векторов основаны на принципе осознанного повторения. Интеллектуальная образовательная платформа оценивает ваши знания и обнаруживает пробелы. Новые задания предлагаются с учетом индивидуальной подготовки ученика и могут повторяться до тех пор, пока вы не научитесь находить правильные ответы. Это достойная альтернатива занятиям с репетитором.
Как правило, для того чтобы хорошо изучить вычитание и сложение векторов по геометрии для 9 класса, достаточно вернуться к выполнению заданий в этот же день через несколько часов, а затем регулярно заниматься на тренажере в последующие 4-5 дней. Этого времени достаточно, чтобы выработать устойчивый учебный навык по данной теме и научиться без ошибок решать примеры. Система пришлет напоминание, когда нужно приступить к занятиям.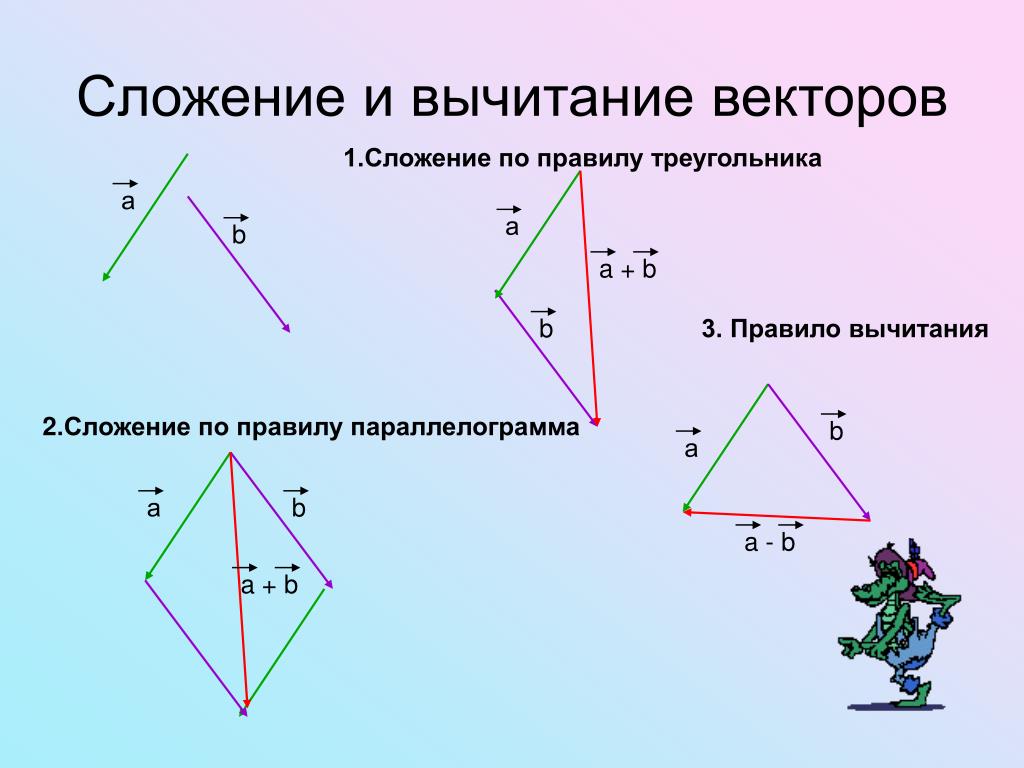
Тренажеры очень удобны, если вам предстоит самостоятельная работа по сложению и вычитанию векторов. Начните готовиться за несколько дней, и результат вас поразит и обрадует. Вы просто перестанете замечать неверные решения и будете уверенно оперировать формулами и определениями. Многочисленные положительные отзывы наших учеников подтверждают неоспоримую пользу занятий на тренажерах, размещенных на сайте образовательной платформы Skills4u. Более того, вы можете изучать не только сложение векторов, но и другие темы по геометрии, а также прокачивать учебные навыки по любым предметам школьной программы.
Как растут результаты учеников
после занятий на тренажерах Skills4u
Занятия
на Skills4u
Занятия
с учебником
Успеваемость
Мотивация
Внимательность
Скорость
Самостоятельность
Запоминание
Первичный Тест «Сложение и вычитание векторов» по геометрии за 9 класс онлайн и бесплатно предоставляется всем желающим.
Советуем пройти тестирование за весь 9 класс по геометрии, чтобы узнать пробелы в знаниях по всем темам и получить индивидуальный план обучения.
После регистрации вы получите 7 дней бесплатного доступа, чтобы увидеть первые результаты занятий и оценить эффективность тренажеров.
Зарегистрироваться и пройти тестирование
Присоединяйтесь к нам. У вас все получится!
А для комплексного результата пройдите общее тестирование за
класс! Узнайте пробелы в знаниях по всем темам
Занимайся 20 минут в день и прокачай знания по школьной программе за месяц!
Родитель
Наслаждайтесь прогрессом вашего ребенка в школе и на платформе
Учитель/
репетитор
Задавайте и проверяйте домашние задания прямо на платформе
Зарегистрироваться и пройти тестирование
59910
учеников уже занимаются с нами
4.
 3: Геометрический смысл сложения векторов
3: Геометрический смысл сложения векторов- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 14519
- Кен Каттлер
- Университет Бригама Янга via Lyryx 9{n}\) — это упорядоченный список чисел. В конкретном случае \(n=2,3\) это можно использовать для определения точки в двух- или трехмерном пространстве. Эта точка задается относительно некоторых осей координат.
Рассмотрим случай \(n=3\). Напомним, что перемещение вектора без изменения его длины или направления не меняет вектор. Это важно в геометрическом представлении сложения векторов.
Предположим, у нас есть два вектора, \(\vec{u}\) и \(\vec{v}\) в \(\mathbb{R}^{3}\).
 Каждый из них можно изобразить геометрически, поместив хвост каждого вектора в \(0\) и его точку в \(\left( u_{1}, u_{2}, u_{3}\right)\) и \ (\left(v_{1}, v_{2}, v_{3}\right)\) соответственно. Предположим, мы сдвинем вектор \(\vec{v}\) так, чтобы его хвост оказался в точке \(\vec{u}\). Мы знаем, что это не меняет вектор \(\vec{v}\). Теперь нарисуйте новый вектор от хвоста \(\vec{u}\) до точки \(\vec{v}\). Этот вектор равен \(\vec{u}+\vec{v}\). 9n\) для любого \(n\) дается в следующем определении.
Каждый из них можно изобразить геометрически, поместив хвост каждого вектора в \(0\) и его точку в \(\left( u_{1}, u_{2}, u_{3}\right)\) и \ (\left(v_{1}, v_{2}, v_{3}\right)\) соответственно. Предположим, мы сдвинем вектор \(\vec{v}\) так, чтобы его хвост оказался в точке \(\vec{u}\). Мы знаем, что это не меняет вектор \(\vec{v}\). Теперь нарисуйте новый вектор от хвоста \(\vec{u}\) до точки \(\vec{v}\). Этот вектор равен \(\vec{u}+\vec{v}\). 9n\) для любого \(n\) дается в следующем определении.Определение \(\PageIndex{1}\): геометрия сложения векторов
Пусть \(\vec{u}\) и \(\vec{v}\) — два вектора. Сдвиньте \(\vec{v}\) так, чтобы хвост \(\vec{v}\) оказался на точке \(\vec{u}\). Затем нарисуйте стрелку, которая идет от хвоста \(\vec{u}\) к точке \(\vec{v}\). Эта стрелка представляет собой вектор \(\vec{u}+\vec{v}\).
Рисунок \(\PageIndex{1}\)Это определение проиллюстрировано на следующем рисунке, на котором \(\vec{u}+\vec{v}\) показан для особого случая \(n=3\) .
Рисунок \(\PageIndex{2}\)
Обратите внимание на параллелограмм, созданный \(\vec{u}\) и \(\vec{v}\) на приведенной выше диаграмме. Тогда \(\vec{u} + \vec{v}\) — направленная диагональ параллелограмма, определяемая двумя векторами \(\vec{u}\) и \(\vec{v}\).
Если у вас есть вектор \(\vec{v}\), его аддитивным обратным \(-\vec{v}\) будет вектор, имеющий ту же величину, что и \(\vec{v}\), но противоположное направление. Когда кто-то пишет \(\vec{u}-\vec{v,}\), это означает \(\vec{u} + \left(-\vec{v}\right)\), как и в случае с действительными числами. Следующий пример иллюстрирует эти определения и соглашения.
Пример \(\PageIndex{1}\): графическое сложение векторов
Рассмотрим следующее изображение векторов \(\vec{u}\) и \(\vec{v}\).
Рисунок \(\PageIndex{3}\)Эскиз рисунка \(\vec{u}+\vec{v},\vec{u}-\vec{v}.\)
Решение
Мы Сначала нарисуйте \(\vec{u}+\vec{v}.\) Начните с рисования \(\vec{u}\), а затем в точке \(\vec{u}\) поместите хвост из \(\vec{v}\), как показано.
Рисунок \(\PageIndex{4}\) Тогда \(\vec{u}+\vec{v}\) — это вектор, полученный в результате рисования вектора от хвоста \(\vec{u}\) до кончика \(\vec{v}\ ).
Тогда \(\vec{u}+\vec{v}\) — это вектор, полученный в результате рисования вектора от хвоста \(\vec{u}\) до кончика \(\vec{v}\ ).Далее рассмотрим \(\vec{u}-\vec{v}.\) Это означает \(\vec{u}+\left( -\vec{v} \ вправо). Вот картинка.
Рисунок \(\PageIndex{5}\)Эта страница под названием 4.3: Геометрическое значение сложения векторов распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована Кеном Каттлером (Lyryx) через исходный контент это было отредактировано в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- Кен Каттлер
- Лицензия
- СС BY
- Версия лицензии
- 4,0
- Показать страницу TOC
- нет
- Теги
- source@https://lyryx.
 com/first-course-linear-алгебра
com/first-course-linear-алгебра - сложение векторов
- source@https://lyryx.
Сложение и вычитание векторов. Резюме – Гипертекст по физике
[закрыть]
- Физические величины бывают нескольких типов.
- Тип физической величины определяет тип используемой математики.
- В этой книге рассматриваются только два типа: скалярные величины и векторные величины — обычно сокращаются до скаляров и векторов .
Сравнение физических величин * Гравитационное поле — это векторное поле в классической физике и тензорное поле в общей теории относительности. Тензор — это математический объект, более сложный, чем вектор, вроде того, как вектор сложнее скаляра. внешний вид скаляров векторов определение количество, имеющее
величину толькоколичество, которое имеет
величину и направлениевверх, вниз, влево, вправо
вперед, назад
север, восток, запад, юг
параллельно, перпендикулярно
радиально, по касательной
положительно, отрицательно
пеленг
угол наклона, депрессии
угол относительно…
прямое восхождение, склонениепримеры расстояние
время
скоростьмасса
энергия
площадь поверхности
объем
плотностьперемещение скорость
ускорение
сила
вес
импульс
площадь проекцииполя Поле Хиггса гравитационное поле*, электрическое поле, магнитное поле, электромагнитное поле, электрослабые поля, глюонное поле математика обычная арифметика
сложение, вычитание
сумма (+), разность (-)
умножениегеометрия, тригонометрия, векторная арифметика
векторное сложение, векторное вычитание
результирующая (∑), изменение (∆)
скалярное произведение (·), векторное произведение (×)растворы диаграммы часто бывают полезны диаграммы по существу обязательны ответы число с единицей число с единицей и направлением угла
-или-
число с единицей вдоль каждой оси координат
-или-
стрелка, нарисованная в масштабе в определенном направлении- Добавление вектора
- Параллельные векторы ведут себя как числа на числовой прямой.

- Добавьте величины векторов в том же направлении.
- Вычесть величины векторов из напротив направления.
- Перпендикулярные векторы ведут себя как точки на координатной плоскости.
- Используйте теорему Пифагора для определения магнитуды .
- Используйте функцию касательной для определения направления .
- Векторы в стандартной позиции имеют общее происхождение и используются в правиле параллелограмма сложения векторов
- Построить параллелограмм, используя два вектора в стандартном положении.
- Равнодействующая есть диагональ параллелограмма, выходящая из общей вершины.
- Ваша диаграмма должна выглядеть как параллелограмм, составленный из векторов. (Примечание: когда два исходных вектора перпендикулярны, параллелограмм будет прямоугольником.)
- Векторы, расположенные голова к хвосту (с хвостом второго вектора, расположенным над головой первого), используются в правиле треугольника сложения векторов.

- Параллельные векторы ведут себя как числа на числовой прямой.


 Из этого следует, что построение геометрической разности между АА1 и ВВ1 должно быть произведено по правилу построения геометрической суммы векторов В1В и АА1, т. е. надо провести Oβ‘ (черт. 2), равную и параллельную В1В, из β‘ провести
Из этого следует, что построение геометрической разности между АА1 и ВВ1 должно быть произведено по правилу построения геометрической суммы векторов В1В и АА1, т. е. надо провести Oβ‘ (черт. 2), равную и параллельную В1В, из β‘ провести 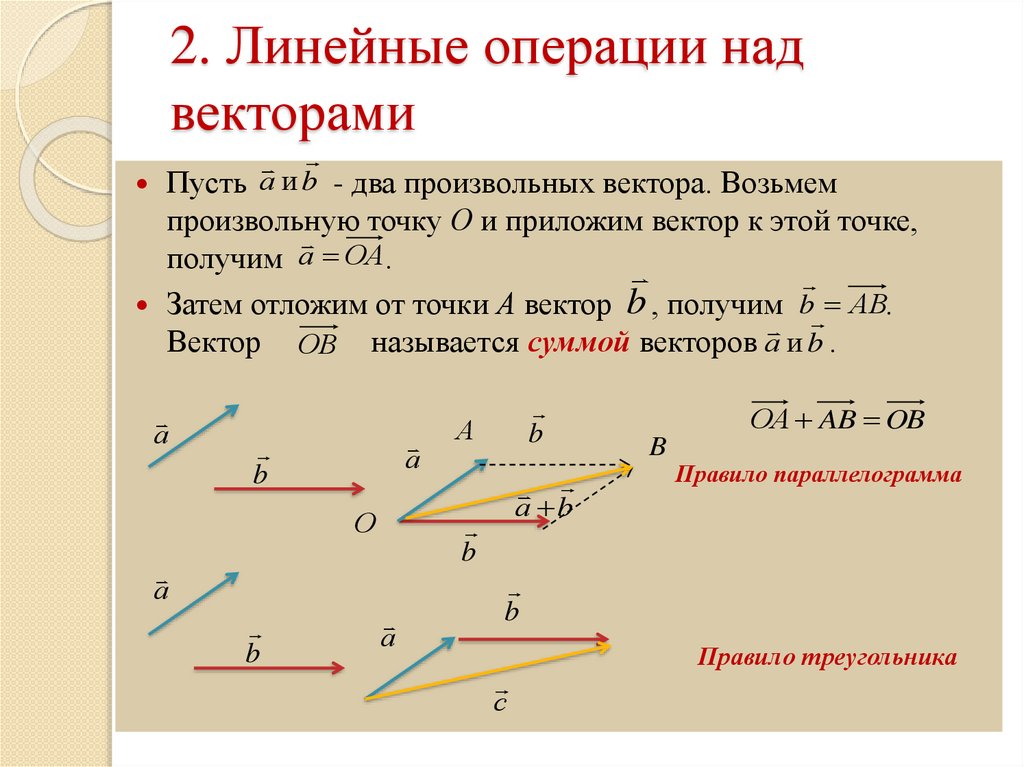 Каждый из них можно изобразить геометрически, поместив хвост каждого вектора в \(0\) и его точку в \(\left( u_{1}, u_{2}, u_{3}\right)\) и \ (\left(v_{1}, v_{2}, v_{3}\right)\) соответственно. Предположим, мы сдвинем вектор \(\vec{v}\) так, чтобы его хвост оказался в точке \(\vec{u}\). Мы знаем, что это не меняет вектор \(\vec{v}\). Теперь нарисуйте новый вектор от хвоста \(\vec{u}\) до точки \(\vec{v}\). Этот вектор равен \(\vec{u}+\vec{v}\). 9n\) для любого \(n\) дается в следующем определении.
Каждый из них можно изобразить геометрически, поместив хвост каждого вектора в \(0\) и его точку в \(\left( u_{1}, u_{2}, u_{3}\right)\) и \ (\left(v_{1}, v_{2}, v_{3}\right)\) соответственно. Предположим, мы сдвинем вектор \(\vec{v}\) так, чтобы его хвост оказался в точке \(\vec{u}\). Мы знаем, что это не меняет вектор \(\vec{v}\). Теперь нарисуйте новый вектор от хвоста \(\vec{u}\) до точки \(\vec{v}\). Этот вектор равен \(\vec{u}+\vec{v}\). 9n\) для любого \(n\) дается в следующем определении.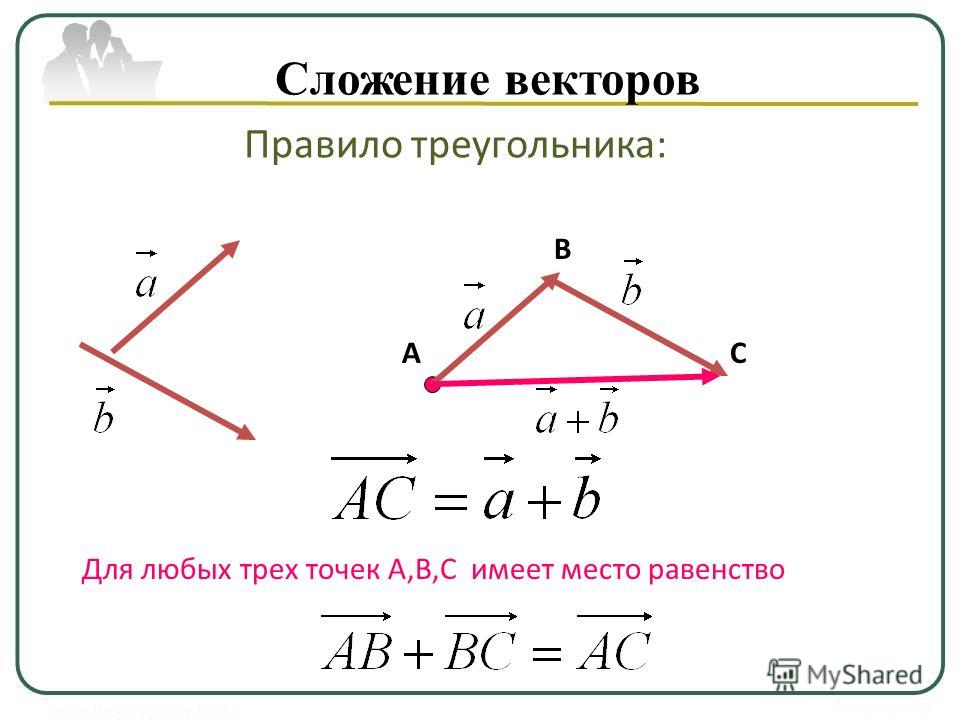
 Тогда \(\vec{u}+\vec{v}\) — это вектор, полученный в результате рисования вектора от хвоста \(\vec{u}\) до кончика \(\vec{v}\ ).
Тогда \(\vec{u}+\vec{v}\) — это вектор, полученный в результате рисования вектора от хвоста \(\vec{u}\) до кончика \(\vec{v}\ ).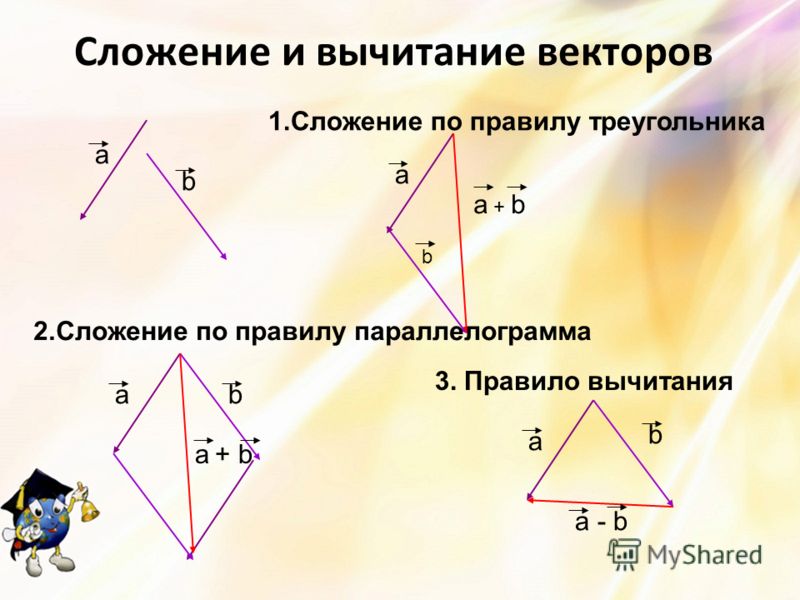 com/first-course-linear-алгебра
com/first-course-linear-алгебра