Решать примеры по математике 7 класс: Математика (ответы и решения)

Содержание

Решения задач

Тридцать третий Математический праздник (27 февраля 2022 года)
Решения в формате PDF
Рабочие критерии проверки:
— «классический» Математический праздник (6 класс и 7 класс)
— «Математический праздник в Математической вертикали» (6 класс и 7 класс)

Тридцать второй Математический праздник (18 апреля 2021 года)
Решения в формате PDF
Рабочие критерии проверки: 6 класс, 7 класс
«Математический праздник в Математической вертикали»: 6 класс, 7 класс
Рабочие критерии проверки: 6 класс, 7 класс

Тридцать первый Математический праздник (09 февраля 2020 года)
Решения в формате PDF
Рабочие критерии проверки: 6 класс, 7 класс
«Математический праздник в Математической вертикали»: 6 класс, 7 класс

Тридцатый Математический праздник (17 февраля 2019 года)
Решения в формате PDF
Рабочие критерии проверки: 6 класс, 7 класс

Двадцать девятый Математический праздник (18 февраля 2018 года)
Решения в формате PDF
Рабочие критерии проверки: 6 класс, 7 класс

Двадцать восьмой Математический праздник (19 февраля 2017 года)
Решения в формате PDF
Рабочие критерии проверки: 6 класс, 7 класс

Двадцать седьмой Математический праздник (21 февраля 2016 года)
Решения в формате PDF
Рабочие критерии проверки: 6 класс, 7 класс

Двадцать шестой Математический праздник (15 февраля 2015 года)
Решения в формате PDF
Рабочие критерии проверки: 6 класс, 7 класс

Двадцать пятый Математический праздник (16 февраля 2014 года)
Решения в формате PDF (555 К, 12 страниц)
Рабочие критерии проверки: 6 класс, 7 класс

Двадцать четвёртый Математический праздник (17 февраля 2013 года)

Решения в формате PDF (308 К, 12 страниц)
Рабочие критерии проверки: 6 класс, 7 класс

Двадцать третий Математический праздник (19 февраля 2012 года)
Решения в формате PDF (486 К, 12 страниц)
Рабочие критерии проверки: 6 класс, 7 класс

Двадцать второй Математический праздник (13 февраля 2011 года)
Решения в формате PDF (141 К, 16 страниц)
Рабочие критерии проверки: 6 класс, 7 класс

Двадцать первый Математический праздник (14 февраля 2010 года)
Решения в формате PDF (96 К, 12 страниц)

Двадцатый Математический праздник (15 февраля 2009 года)
Решения в формате PDF (102 К, 12 страниц)

Девятнадцатый Математический праздник (17 февраля 2008 года)
Решения в формате PDF (132 К, 8 страниц)

Восемнадцатый Математический праздник (11 февраля 2007 года)
6 класс
7 класс
Решения в формате PDF (98 Кб, 8 страниц)

Семнадцатый Математический праздник (12 февраля 2006 года)

6 класс
7 класс
Решения в формате PDF (551 Кб, 8 страниц)

Шестнадцатый Математический праздник (13 февраля 2005 года)
6 класс
7 класс
Решения в формате PDF (217 Кб, 8 страниц)

Пятнадцатый Математический праздник (15 февраля 2004 года)
6 класс
7 класс
Решения в формате PDF (214 Кб, 7 страниц)

Четырнадцатый Математический праздник (16 февраля 2003 года)
6 класс
7 класс
Решения в формате PDF (214 Кб, 8 страниц)

Тринадцатый Математический праздник (17 февраля 2002 года)
6 класс
7 класс
Решения в формате PDF (131 Кб, 8 страниц)

Двенадцатый Математический праздник (18 февраля 2001 года)
6 класс
7 класс
Решения в формате PDF (183 Кб, 4*2 страниц)

Одиннадцатый Математический праздник (13 февраля 2000 года)
6 класс
7 класс
Решения в формате PDF (88 Кб, 6 страниц)

Десятый Математический праздник (21 февраля 1999 года)
6 класс
7 класс

Дата последнего изменения: 11 марта 2022 года

Как репетитор по математике в 7 классе работает с системами — Колпаков Александр Николаевич

Изучение математики в 7 классе принципиально отличается от всего того, что предлагалось ранее в 5 — 6 классах. И дело не только в названиях тем и разделении предмета на алгебру и геометрию. Помимо введения новых понятий и правил меняется характер работы с числами и выражениями. Многое из того, что репетитор по математике показывает в 7 классе является обобщением ранее пройденного, но поднимающее использование математики на принципиально новый уровень. Такое продвижение предполагает прочное усвоение вычислительной базы, которое к 7 классу должно быть достигнуто. Должно, но не обязано.

Значительные пробелы отстающих школьников, обращающихся к репетитору по математике в тот или иной период учебы в школе, ставят неразрешимые проблемы перед использованием традиционных методик объяснений, а именно методик прямого изложения материала. Креативный репетитор по математике находится в постоянном поиске новых форм и способов подачи объяснений конкретному ученику. И это очень непросто сделать.

Как репетитор по математике работает с трудными темами?

Трудность каждой конкретной темы — весьма относительное понятие. Все зависит от того, с какой стороны к ней подойти и насколько ученик способен воспринимать ту или иную форму объяснений репетитора. Многие сложные понятия упрощаются, если репетитору по математике удается подобрать какое-нибудь простое и лаконичное описание математического процесса, сравнить его с чем-то обыденным и понятным, связать новое с ранее изученным. Это непростая задача, но репетитору нужно стремиться к ее выполнению. В алгебре, при объяснении нового материала, бывает достаточно точно подобрать соответствующие примеры работы правила на числах. У многих учеников 7 класса все еще преобладает тип мышления «от общего к частному», поэтому, стремление репетитора по математике к абсолютной стрости и полноте объяснений (доказательств), к использованию общих форм, рассмотрению всех случаев или педантичной проверке равносильности в переходах может перечеркнуть все усилия по обеспечению понимания.

Важно добиться первоначального понимания, пусть ученику не открывается вся картина происходящего в алгоритме, а лишь приоткрывается некая завеса нового.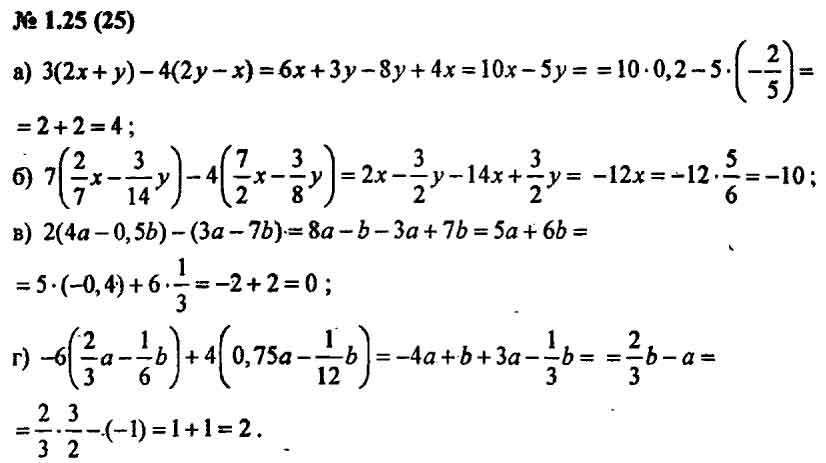 В некоторых случаях уже одно такое продвижение можно ставить в заслугу репетитору по математике, ибо ребенок начинает хоть что-то решать самостоятельно. Это крайне важно, ибо результаты практической работы помогает осмыслить многие моменты, которые оказались непонятыми.

Иногда репетиторы по математике, особенно начинающие, путают два состояния ученика: не понял и не запомнил. Если ребенок говорит «я не понимаю», — это не всегда означает, что слова репетитора по математике остались не осмысленными. Часто бывает наоборот: заявляет, что все понятно, но на проверку оказывается, что он просто заучил те или иные ходы в решении. Репетитору важно уметь отличать эти два состояния и правильно их использовать.

Как правило, решение систем методом подстановки вызывает у детей 7 класса дикое отвращение и неприязнь. Почему? Процесс, который описывает репетитор по математике на первом уроке по данной теме, очень трудно увязывается с привычным занятием в алгебре 7 класса. Дети настолько привыкают к однострочным одношаговым решениям (какими являются преобразования многочленов). Поэтому, когда репетитор по математике исписывает равносильными системами целую страницу в тетради, ученик почти всегда заявляет: «я не понимаю». «Стоп! Давай разберемся», — говорю я ему. Что именно из этого ты не понял, а что просто не успел запомнить? Если репетитор по математике поставит вопрос именно таким ребром, он переводит деятельность ученика из созерцательной в оценочную. Нужно дать время на то, чтобы привыкнуть к записям и запомнить ходы. Это облегчит оценку того, что именно не понятно. Главное не торопить ученика и дать ему возможность высказаться. Пусть это будут невнятные фразы, лишенные логики. Мастерство репетитора заключается в том, чтобы выявить проблему даже по «обрывкам мыслей» ученика.

Конечно, я описываю ситуацию, в которой репетитор не провел с учеником соответствующую подготовительную работу. А она обязательно нужна.

Подготовительная работа репетитора

Нужны задания на проверку конкретных пар чисел для конкретной системы.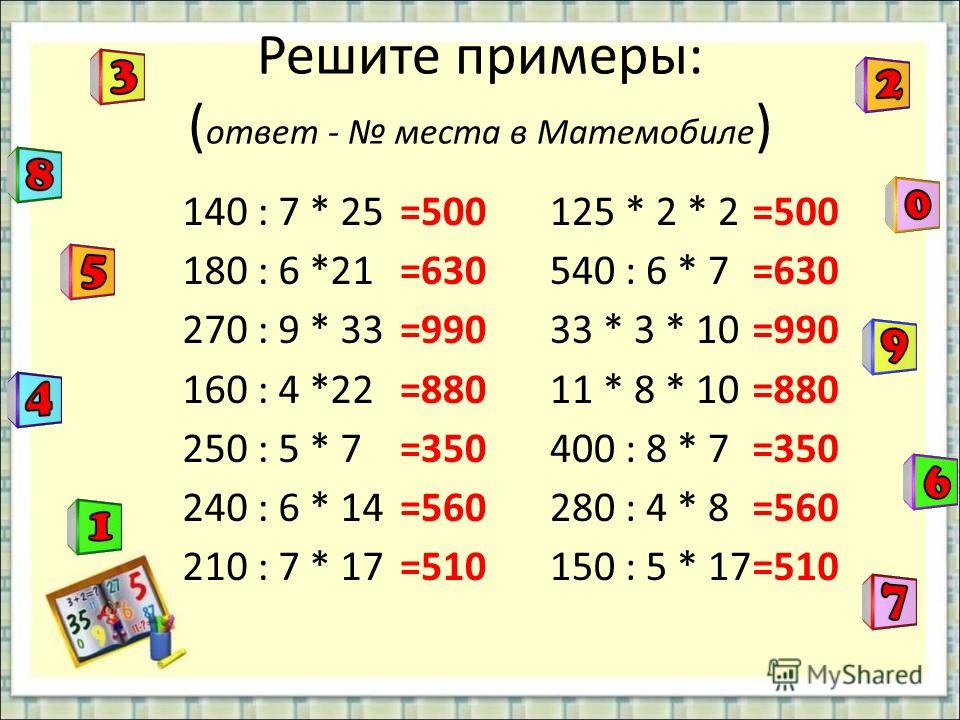 В процессе выполнения простейших заданий репетитор обкатывает новую терминологию: пара чисел, удовлетворяющая системе, решение системы, проверка пары. Я еще употребляю фразы «вставка чисел», «вставка пары»
Важно убедить ученика в том, что совсем не обязательно искать пару чисел, которая при вставке в начальную систему даст два верных равенства. Мы же ищем саму пару.

Самому слабому ученику достаточно сказать, что при замене одной системы на другую не меняется самое главное — ее ответ, поэтому не важно, какую именно систему решать. Пара, подходящая для одной из них — подойдет и для другой. Это можно просто проверить на конкретных числах. Надо чувствовать ученика и не ввязываться в объяснения равносильности переходов в 7 классе, какими бы точными они не были. Если все-таки репетитор по математике хочет донести до сознания ученика логику алгоритма, это нужно делать после того, как ученик его запомнит.

Если ученик более-менее толковый, репетитор по математике применяет числовую методику проверки равносильности.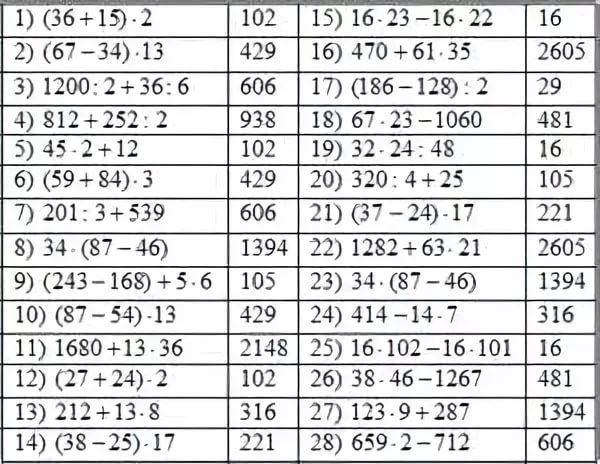 Покажу ее работу на примере

Пусть задана система линейных уравнений:

Как ее решить — все вы отлично знаете. Но как объяснить это решение слабому учащемуся? Вот она — головная боль для преподавателя. Дети в 7 классе не воспринимают общие математические методы доказательства равносильности, под лупой которых, конечно же, вся логика преобразований оказывается на поверхности.

Какие методики могут быть задействованы в принципе? Обычно репетитор по математике проводит равносильные преобразования по классической схеме:

Однако нельзя оставлять такую форму без каких-либо объяснений.

Что чаще всего не понятно ученику?

Как правило к моменту изучения темы «метод подстановки», учащиеся 7 класса уже имеют выражать переменную y через переменную x. Будем считать, что репетитор по математике решил эту проблему в теме «графический способ решения систем уравнений». Тогда самый непонятный ход — вставка выражения 3-x во второе уравнение системы на место x.

Как репетитор может объяснить замену игрека на 3-x ?
Я покажу как можно работать со средним учеником по методике числовой проверки ( если ученик сильный — для него вполне подойдут строгие математические обоснования «в обе стороны»). Итак, рассмотрим равносильный переход между системами:

Надо убедить ученика в том, что одна и та же пара чисел (она предоставляется в готовом виде) превращает каждое равенство в верное. Репетитор говорит: «Давай проверим пару (2;1), то есть х=2; y=1. Вставим их на места букв в систему (1).Получим: Эти равенства верные, поэтому пара чисел (2;1) — решение системы (1). Но 1=3-2 и поэтому можно вместо единицы в нижнем уравнении написать в скобках (3-2). От этого при подсчете не изменится результат». Далее репетитор по математике меняет 1 на разность 3 — 2
и спрашивает ученика: «Какая запись получится, если мы задумаем эту же пару (2;1) вставить во вторую систему? Будут ли ее равенства верными? Конечно, ведь мы только что их проверили (в этот момент репетитор по математике показывает на записанную систему №3). Вставка пары (2;1) приводит нас к повторению той же самой записи, к копии уже проверенного равенства. Поэтому пара (2;1) будет еще и решением системы №2. Значит у них одинаковые ответы (понимаю, что вывод не выдерживает никакой критики с точки зрения строгой математики и проверка проведена в одну сторону, но дети проглотят такой маневр репетитора). Поэтому вместо того, чтобы решать первую систему, мы можем решать вторую и через нее искать эту пару (если она неизвестна).

Остальные равносильные преобразования репетитору по математике не составит труда объяснить. В них нет ничего нового. Обычное решение уравнения с одной переменной. Понятно, что икс должен быть корнем уравнения (2). Ученики в 7 классе обычно понимают, что его надо найти.

Замечу, что ответ нужно записывать не в виде x=2; y=1, а в виде пары (2;1). Это будет способствовать скорейшему формированию у ученика представления об ответе, как о некоторой точке координатной плоскости.

Репетитор по математике 7 класс — Колпаков А.Н. Москва, Строгино.

Wolfram|Alpha Примеры: Common Core Math: 7 класс

О-о! Wolfram|Alpha не работает без JavaScript.

Пожалуйста, включите JavaScript. Если вы не знаете, как это сделать, вы можете найти инструкции здесь. Как только вы это сделаете, обновите эту страницу, чтобы начать использовать Wolfram|Alpha.

Примеры для

В седьмом классе учащиеся начинают свободно оперировать выражениями и решать уравнения, в том числе с отрицательными числами и числами, выраженными в виде дробей или десятичных дробей. Студенты вычисляют с процентами и отношениями и описывают пропорциональные отношения, используя числовые, графические, алгебраические и словесные представления. Учащиеся анализируют и сравнивают данные из случайных выборок и обобщают, чтобы сделать выводы о популяциях. Учащиеся также работают с вероятностью, проводя вероятностные эксперименты и вычисляя вероятности с помощью вероятностных моделей. Учащиеся вычисляют площади, объемы и площади поверхности правильных и неправильных форм и решают задачи, связанные с углами, в том числе рисуют фигуры, соответствующие заданным геометрическим условиям, и классифицируют типы треугольников.

Стандарты Common Core

Получить информацию об Стандартах Common Core.

Поиск определенного стандарта:

CCSS.

Math.Content.7.G.A.1Общий базовый стандарт седьмого класса EE.B.4

Поиск всех стандартов седьмого класса:

Общие базовые стандарты седьмого классаВыражения и уравнения

Работа с выражениями и решение уравнений и неравенства, в том числе с отрицательными числами.

Упрощение выражений (CCSS.Math.Content.7.EE.A.1):

расширенная форма 3.2 (x — 5) — 8x + 4 (2.7 + x) объединять одинаковые члены 1/2x + 2 — 3/4x + 3/2

Факторные выражения (CCSS.Math.Content.7.EE.A.1):

коэффициент 6x + 18

Решить уравнение (CCSS.Math.Content.7.EE.B.4a):

решить 0,5 (x + 3) = -15решить 46,4 = 4x + 11,2

Решить неравенство (CCSS.Math.Content.7.EE.B.4b):

решить 8 — x > 2,2Больше примеровГеометрия

Рисовать фигуры и вычислять геометрические измерения.

Нарисуйте треугольник с заданными длинами сторон, если это возможно (CCSS.Math.Content.7.G.A.2):

треугольник с длинами сторон 2, 6 и 7

Нарисуйте фигуры с заданными условиями (CCSS.Math.Content.

7 .Г.А.2): параллелограмм со всеми прямыми углами

Решение для измерения окружности (CCSS.Math.Content.7.G.B.4):

площадь круга с радиусом = 2

Решение для измерения трехмерных тел (CCSS.Math.Content.7 .G.B.6):

объем цилиндра с радиусом = 2 и высотой = 5Еще примерыСистема счисления

Выполнять арифметические действия с целыми, дробными и десятичными дробями, в том числе с несколькими операциями в одном выражении.

Сложение и вычитание рациональных чисел (CCSS.Math.Content.7.NS.A.1):

-4 + 9/2-5/8 — 1/4

Распознавать закономерности в умножении и делении (CCSS.Math.Content.7.NS.A.2):

отрицательное число * положительное число

Выполнять несколько операций с рациональным числом числа (CCSS.Math.Content.7.NS.A.2c):

(-5)(-2) — (4)(-3)(-1/2 + 3/8 + 1/4 + -3 /2) / 2

Преобразование рационального числа в десятичное (CCSS.Math.Content.7.NS.A.2d):

5/8 в виде десятичного числаБольше примеровRatios & Proportions

Вычисление с отношениями и процентами в различных контекстах.

Определение удельной скорости, связанной с коэффициентом (CCSS.Math.Content.7.RP.A.1):

0,75 фута за 0,25 часа5 миль на 1/8 галлона

Представлять изменения количества в процентах (CCSS.Math.Content.7.RP.A.3):

5 увеличить на 300%

Определить цены и чаевые, используя проценты (CCSS.Math.Content.7.RP.A.3):

Чаевые 20 % при 38,40 долл. США 80 долл. США со скидкой 30 %Больше примеров Бесплатные неограниченные практические задачи по алгебре

СВЯЗАННЫЕ ПРИМЕРЫ

Алгебра

Базовая математика: 6 класс

Математика: 8 класс

Элементарная математика

Статистика и вероятность

Анализ и сравнение наборов данных, в том числе полученных из вероятностных экспериментов.

Сравните центры двух наборов данных (CCSS.Math.Content.7.SP.B.4):

среднее {2, 1, 4, 8, 2, 1} и среднее {7, 8, 6, 8, 9, 4}медиана {187, 202, 112, 198, 155} и медиана {34, 78, 61, 42, 89}

Сравните изменчивость двух наборов данных (CCSS.

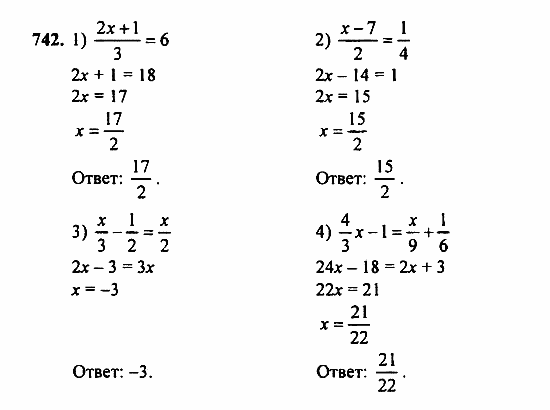Math.Content.7.SP.B.4 ): IQR {2, 4, 8, 2, 1} по сравнению с IQR {7, 8, 6, 9, 9}

Проведение вероятностных экспериментов (CCSS.Math.Content.7.SP.C.6):

20 подбрасываний монеты вероятность выпадения 7 на двух шестигранных костяхБольше примеров

Математика, 7 класс, Применение математики в работе, Уточнение задачи Навыки решения

CCSS.Math.Content.7.EE.B.4 7 класс, выражения и уравнения

Кластер: решение реальных и математических задач с использованием числовых и алгебраических выражений и уравнений

Стандарт: использование переменных для представления величин в реальной или математической задаче и построение простых уравнений и неравенств для решения проблемы, рассуждая о количествах.