Вычислительная математика лекции
САНКТПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
А. Н. Кирсяев, В. Е. Куприянов.
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА.
КОНСПЕКТ ЛЕКЦИЙ.
САНКТПЕТЕРБУРГ 2011
1.Введение.
Вычислительная математика занимается разработкой численных методов решения математических задач. Численное решение содержит набор чисел с ограниченным количеством десятичных цифр и уже по этой причине всегда является приближенным. Это в свою очередь обусловливает необходимость анализа адекватности решения. (Как это сделать?).
1.1.Источники погрешностей.
Вычислительная математика имеет дело с математическими моделями исследуемых процессов и явлений. Наличие погрешностей обусловлено рядом причин:
1.Погрешность модели.
2.Погрешность исходных данных.
3.Методическая погрешность.
4.Вычислительная погрешность (погрешность округления).
1.2.Погрешность округления.
Имеем дело с вещественными числами, которые, как правило,
представлены в форме с плавающей запятой: , где β –
основание системы исчисления; M- мантисса (0≤M<β), l- порядок числа.
Упрощенная структура машинного слова для хранения вещественных чисел имеет вид:
Sp | SM | P0P1…. Pk-1Pk | d1 d2 …… dt |
|
|
|
|
Sp – код знака порядка;
SM – код знака мантиссы;
9
k+1 – количество разрядов порядка; t – количество разрядов мантиссы.
Множество хранимых чисел:
fl(x) =
l
0 ≤ di ≤β-1;i= 1, …, t.
0 ≤ pj ≤β-1;j = 0,…,k.
Обычно предполагают d1 ≠ 0 (нормированные системы).
Здесь x R, а fl(x) F, F – множество чисел, хранимых в ЭВМ.
В отличие от R, F дискретно и содержит конечное число элементов,
то есть существуют fl(x1), fl(x2) F, между которыми нет элементов,
принадлежащих F. Возникает относительная погрешность .
Её максимальная величина носит название машинной точности
εM ≈β-t.При компьютерных вычислениях получается
(1+ εM)fl(x) = fl(x). Таким образом, уже в процессе ввода числа в ЭВМ возникает относительная погрешность εM.
Минимальное положительное число, представимое в ЭВМ,
называется машинным нулем
0M |
| ; | . Если | , то fl(x) = 0 |
|
(исчезновение порядка).
Максимальное по модулю число, представимое в ЭВМ,
называется машинной бесконечностью . Если ,
возникает переполнение разрядной сетки и вычисления аварийно останавливаются.
1.3.Особенности машинной арифметики
Пример 1. Пусть t = 8, тогда 108+1-108 = 0; 108 -108 + 1 = 1.
10
Программирование и математика / Habr
В последнее время на Хабре появилось несколько постов на тему важности математики для программистов, выскажу и я свое мнение.Не согласен с тем, что каждому программисту нужно фундаментальное математическое образование в объемах 5 университетских курсов. Оно не нужно в таком объеме большинству программистов, за исключением специалистов по вычислительным методам. Конечно же, изучение математики развивает мышление. Но есть и другие дисциплины, изучение которых развивает мышление и способствует формированию разносторонне развитой личности. Однако же, эти дисциплины не читают программистам в советских ВУЗах вообще, или читают только основы. Согласен, что математика в объемах первого курса университета (математического факультета) нужна как базис. Но учить программиста математике 5 лет именно как основной дисциплине — это неправильно.
В СССР, где были заложены принципы существующей по сей день программы обучения программистов на постсоветском пространстве, не понимали, что такое программирование и смотрели на него узко, как на специфический раздел математики. Отсюда и перекос в методике обучении программистов, когда 5 лет их учат именно математике, а собственно программированию уделяют мало внимания. Раньше программирование изучали вообще по остаточному принципу даже на программистских факультетах и специальностях (сужу по ПМПУ СПбГУ, как сейчас учат в ВУЗах я доподлинно не знаю, но вижу косвенно по уровню специалистов).
В Советском Союзе программирование сводили к вычислительным методам, видя для него применение в обсчете и моделировании физических процессов, типа полета ракеты или взрыва ядерной бомбы. Ну и еще советскую власть интересовала цифровая обработка сигналов, прежде всего для целей, описанных в «Круге первом» у Солженицына. Действительно, для специалиста по вычислительным методам или конкретно по цифровой обработке сигналов отличное знание математики играет ключевую роль в дальнейшей карьере. Поэтому программа обучения программистов являлась вариацией классического университетского курса математики.
Основная задача, с которой будут сталкиваться программисты с фундаментальным образованием в своей практике — это обработка информации. Соответственно учить нужно в первую очередь структурам данных и алгоритмам, моделям данных для СУБД, способам организации вычислений, принципам организации сетевых протоколов и так далее. Многие программисты так же будут заниматься разработкой инструментальных средств, «программированием для программирования» в чистом виде. И математику им следует давать в том объеме, в котором она нужна для этих основных областей деятельности будущих специалистов в computer science. Математика должна сопровождать курс программирования, а не наоборот.
Конечно, никто не пострадает от того, что прослушает 5-летний классический советский фундаментальный курс математики. Если сможет его осилить в полном объеме, а не просто кое-как сдать экзамены. Только эти знания в основном лягут мертвым грузом, а лет через 10 выветрятся из головы практически полностью (да, человек сможет их «подновить» при необходимости — но большинство этого никогда не сделают за ненадобностью). Конечно, изучение математики в таких объемах полезно для развития мозга. Но упущенное время никак не вернуть! А мозг можно развивать не только через глубокое, на уровне университета, изучение дифференциальной геометрии или топологии
Для развития разносторонней личности, чтобы раздвинуть рамки своего мышления, было бы полезно (гипотетически) изучить не только математику, но и физику, химию, биологию (особенно генетику), медицину, психологию, юриспруденцию, экономику, менеджмент, лингвистику, английский и иврит. 🙂 И еще десяток других направлений. Знания в ряде перечисленных областей скорее пригодятся в реальной жизни и принесут больше пользы, чем дифференциальное исчисление, например. Однако же если узкую выборку из этих дисциплин и читают программистам в университетах, то далеко не 5 лет, а урывками, на ознакомительном уровне. Ведь всем прекрасно понятно, что нельзя объять необъятное.
Так же я считаю и с математикой для программистов — не нужно перегружать ей мозг программиста настолько, что собственно изучение самого программирования становится какой-то побочной, сопутствующей веткой. Нужно читать математику по мере столкновения с проблемами при изучении самого программирования. Да оно и интересней. Например, программисту обычно не интересно в чистом виде слушать курс комбинаторики. Но прослушать его на фоне анализа быстродействия только что изученных алгоритмов обработки данных намного интересней! habr.com
Вычислительная математика
Министерство образования Российской Федерации
Государственное образовательное учреждение
высшего профессионального образования
«Хабаровский государственный технический университет»
Методические указания по выполнению лабораторных работ 1 8
для студентов 2-го курса специальностей
210100 «Управление и информатика в технических системах»
и 071900 «Информационные сети»
Хабаровск
Издательство ХГТУ
УДК
Вычислительная математика: Методические указания по выполнению лабораторных работ для студентов специальностей 210100 «Управление и информатика в технических системах» и 071900 «Информационные системы» / Сост. И. В. Епанешникова. Хабаровск: Изд-во Хабар. гос. техн. ун-та, 2004. -42 с.
Методические указания разработаны на кафедре «Автоматика и системотехника» и предназначены для оказания помощи студентам, выполняющим лабораторные работы по дисциплине «Вычислительная математика».
Содержат сведения по основным численным методам, варианты заданий и краткое описание хода выполнения лабораторных работ.
Печатается в соответствии с решениями кафедры «Автоматика и системотехника» и методического совета ИИТ.
Главный редактор Л. А. Суевалова Редактор Л. С. Бакаева Компьютерная верстка И. В. Епанешниковой
Подписано в печать . Формат 60 x 84 1/16. Бумага писчая. Гарнитура “Таймс”. Печать офсетная. Усл. печ. л. . Тираж 150 экз. Заказ .Издательство Хабаровского государственного технического университета.
680035, Хабаровск, ул. Тихоокеанская, 136.
Отдел оперативной полиграфии издательства
Хабаровского государственного технического университета.
680035, Хабаровск, ул. Тихоокеанская, 136.
Хабаровский государственный технический университет, 2004
Лабораторная работа 1
РЕШЕНИЕ СИСТЕМ
ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
Цель и задачи работы: изучение прямых и итерационных методов решения систем линейных алгебраических уравнений.
К решению систем линейных алгебраических уравнений (СЛАУ) сводятся многие задачи (идентификация, оптимальное управление), они являются основой решения других задач вычислительной математики (системы дифференциальных уравнений и т. д.).
Методы решения СЛАУ разделяются на две группы:
Точные, или прямые, методы. Они характеризуются тем, что погрешность, как правило, определяется только погрешностью округления. К этой группе относятся методы Крамера, Гаусса и его модификации, прогонки и т. д. Метод Крамера менее эффективен для использования при решении задач на ЭВМ, поскольку требует большого числа арифметических операций. Метод Гаусса эффективен до порядка системы
 .
.Итерационные. Основаны на получении и уточнении последовательных приближений к точному решению. Эффективны, когда много нулевых коэффициентов и высок порядок системы. Методы: простых итераций, Зейделя и т. д. Эффективны до порядка систем
 .
.
С помощью этих методов решаются системы вида
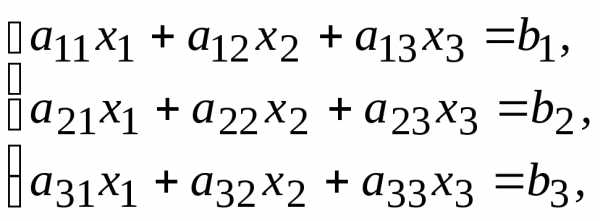 (1.1)
(1.1)
или,
иначе, векторно-матричных уравнений 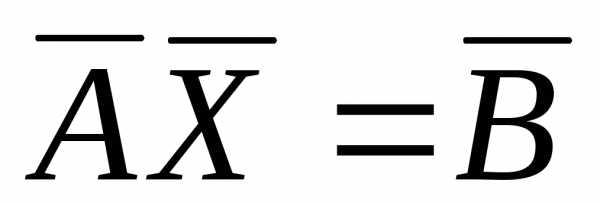 ,
где
,
где —
вещественная матрица коэффициентов
системы
—
вещественная матрица коэффициентов
системы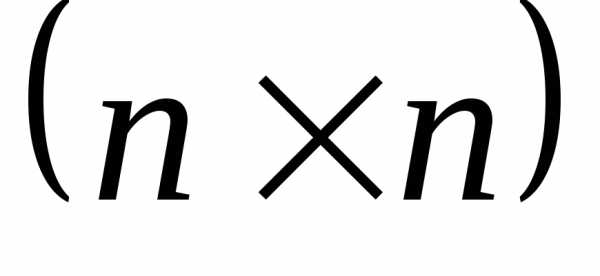 ;
; — вектор свободных членов;
— вектор свободных членов;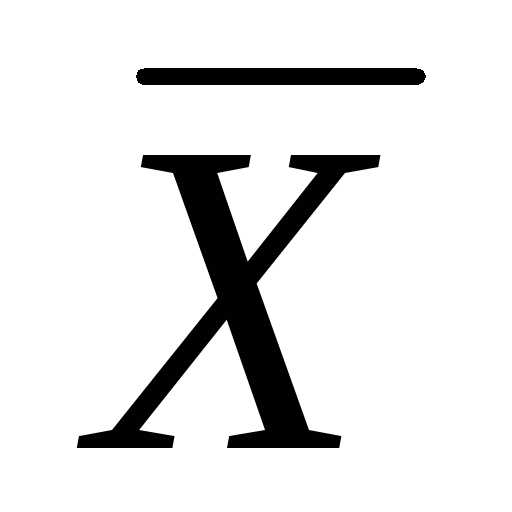 —
вектор неизвестных.
—
вектор неизвестных.
Решение существует и является единственным, если выполняется условие
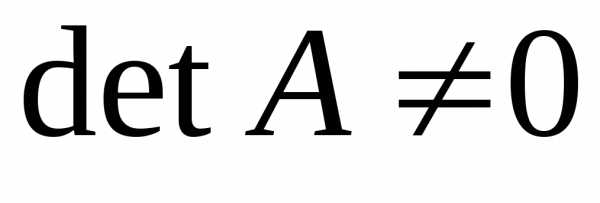 .
.
Прямые методы решения систем линейных алгебраических уравнений Метод Гаусса
Метод
Гаусса заключается в последовательном
исключении неизвестных. Предположим,
что 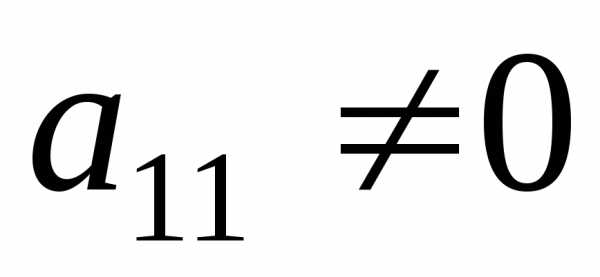 .
В противном случае можно поменять
местами первое уравнение с уравнением,
в котором коэффициент при
.
В противном случае можно поменять
местами первое уравнение с уравнением,
в котором коэффициент при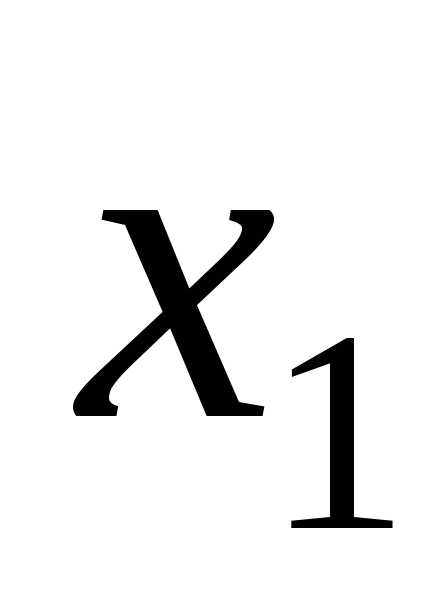 не равен 0.
не равен 0.
Разделим первое уравнение системы на
 .
Получим
.
Получим
, (1.2)
где 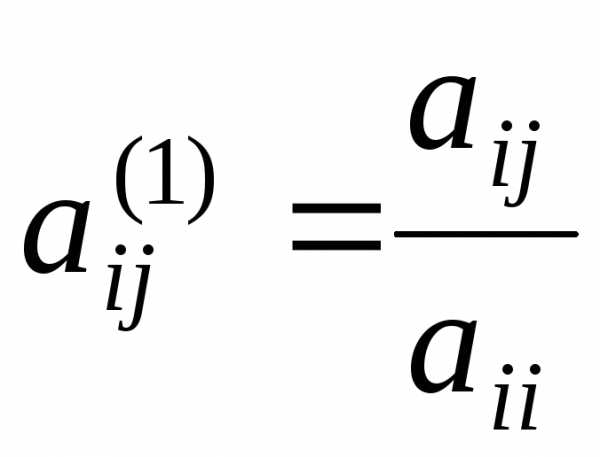 ;
;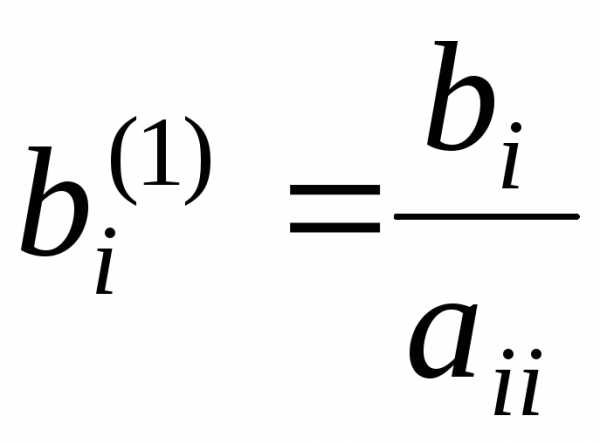 .
.
Умножим разрешающее уравнение (1.2) на
 и вычтем полученное уравнение из второго
уравнения системы (1.1). Аналогично
преобразуем остальные уравнения:
и вычтем полученное уравнение из второго
уравнения системы (1.1). Аналогично
преобразуем остальные уравнения:
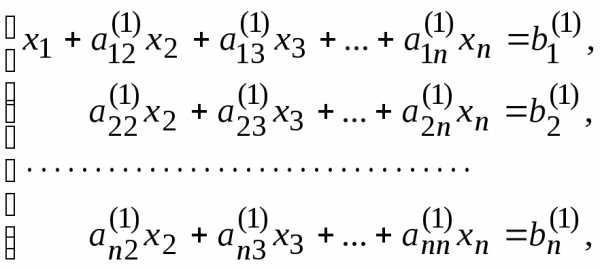 (1.3)
(1.3)
где ,,… ,
,(j=2, 3,…, n).
Если
коэффициент 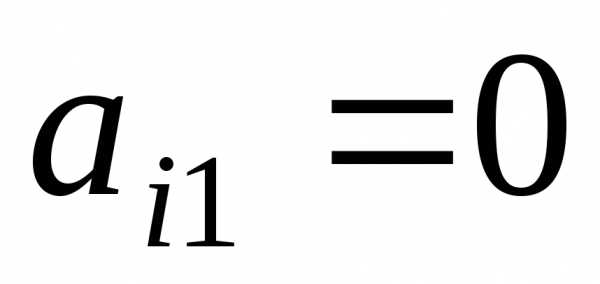 ,
тоi-е
уравнение системы (1.1) войдет в систему
(1.3) без изменений, т. е.
,
тоi-е
уравнение системы (1.1) войдет в систему
(1.3) без изменений, т. е. 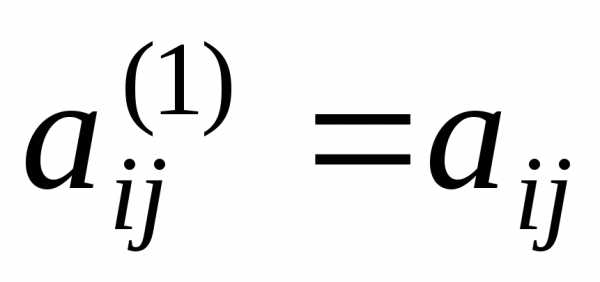 ,
,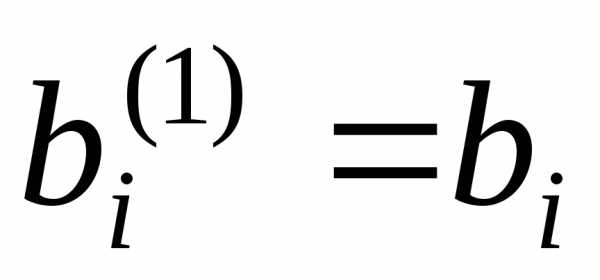 ,
(i
= 2, 3,…, n).
,
(i
= 2, 3,…, n).
Оставив без изменений первое уравнение, можно сделать второе уравнение разрешающим и применить описанную процедуру к системе из
 уравнений, исключив
уравнений, исключив из третьего и последующих уравнений
из третьего и последующих уравнений
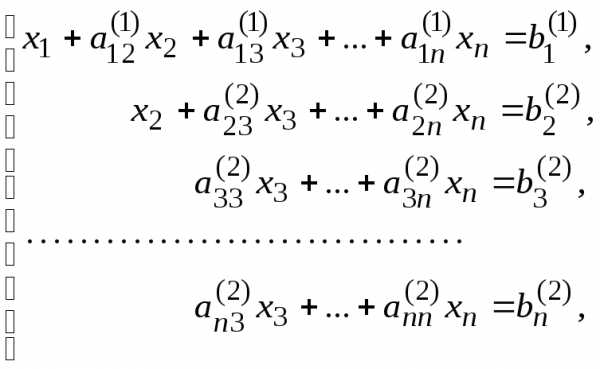
где 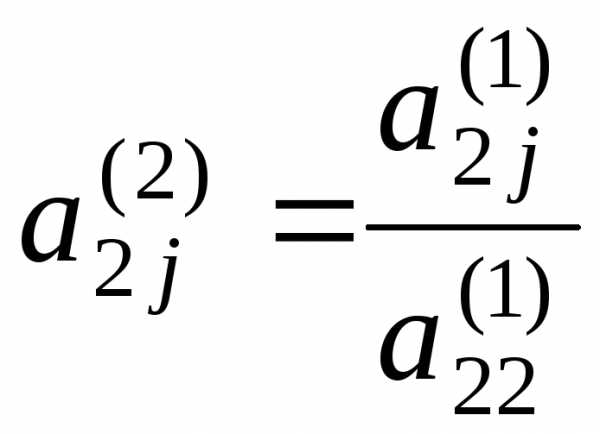 ,
,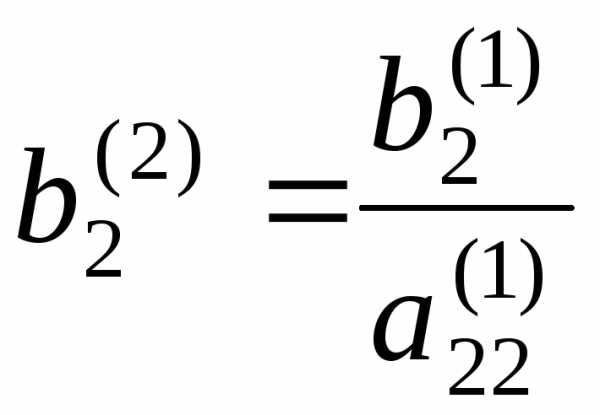 ,,…,,(j=3,
4,…, n).
,,…,,(j=3,
4,…, n).
Продолжая аналогичные вычисления, приведем систему (1.1) к эквивалентной системе
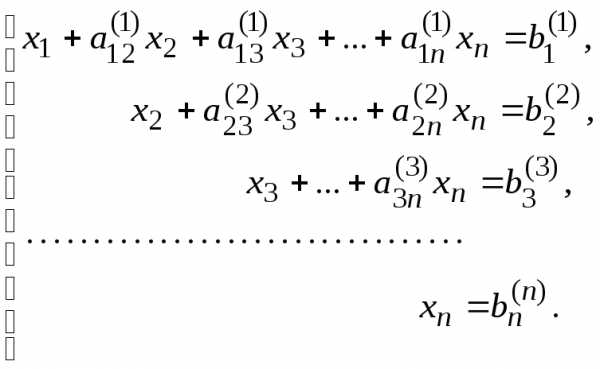 (1.4)
(1.4)
Приведение системы (1.1) к эквивалентной системе (1.4) — прямой ход метода Гаусса. При обратном ходе происходит вычисление неизвестных, начиная с последнего, по формуле
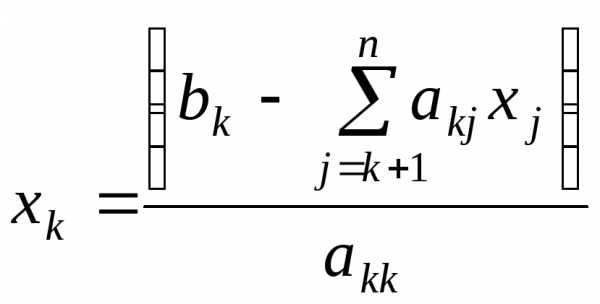 .
.
Алгоритм данного метода можно записать следующим образом.
Для ;
для ;
 ;
;;
для ;
;
Для ;
 .
.
Здесь пункты 1 6 представляют собой прямой ход, пункты 7 и 8 обратный ход метода Гаусса.
studfiles.net

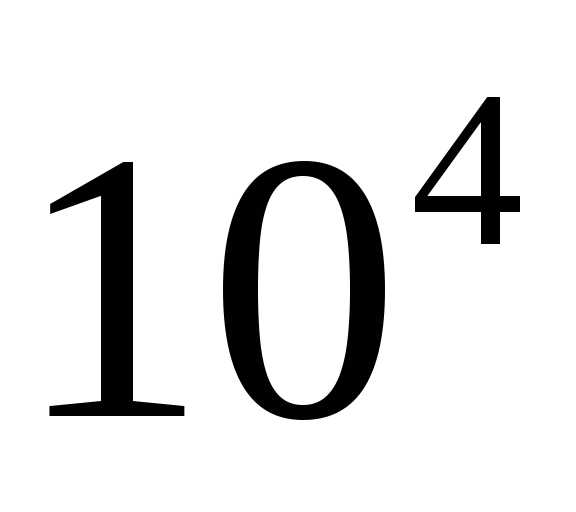 .
.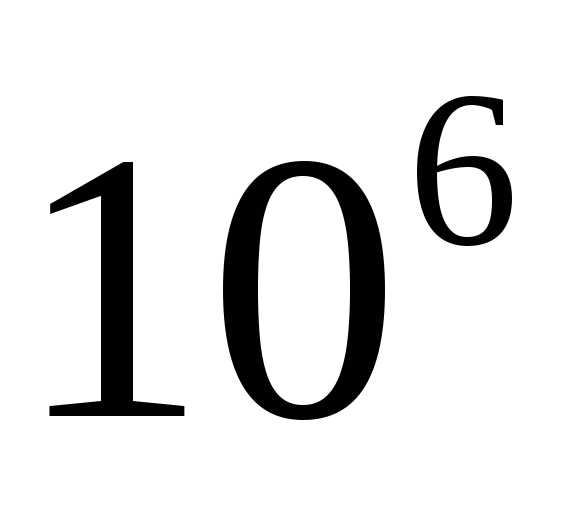 .
.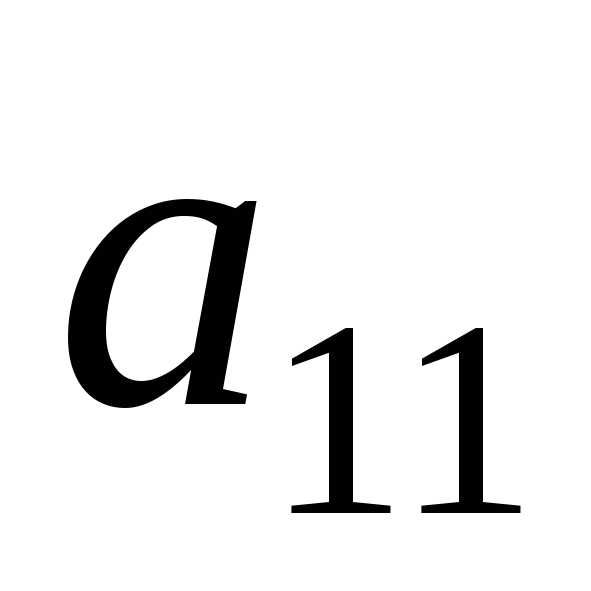 .
Получим
.
Получим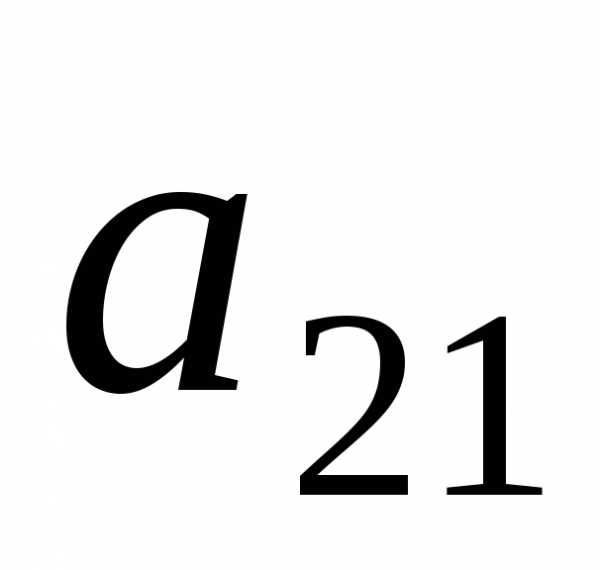 и вычтем полученное уравнение из второго
уравнения системы (1.1). Аналогично
преобразуем остальные уравнения:
и вычтем полученное уравнение из второго
уравнения системы (1.1). Аналогично
преобразуем остальные уравнения: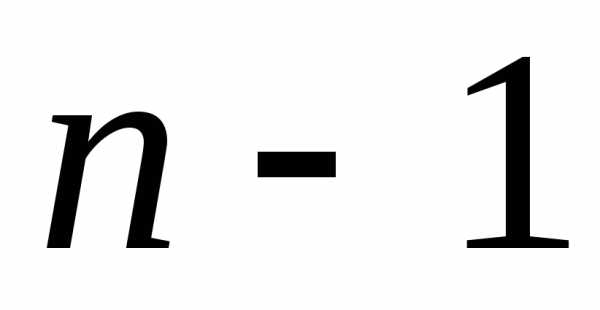 уравнений, исключив
уравнений, исключив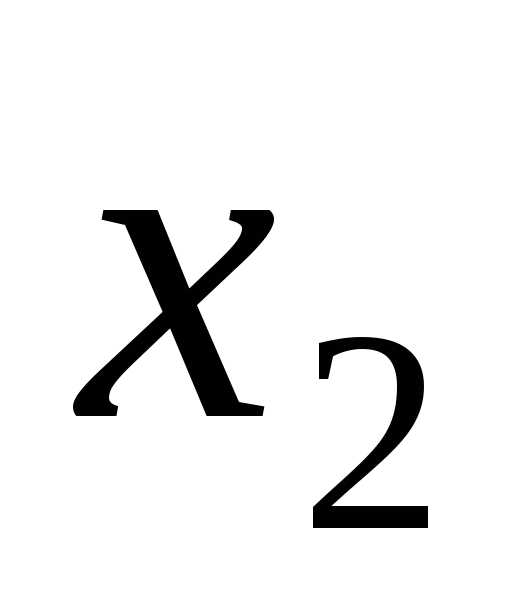 из третьего и последующих уравнений
из третьего и последующих уравнений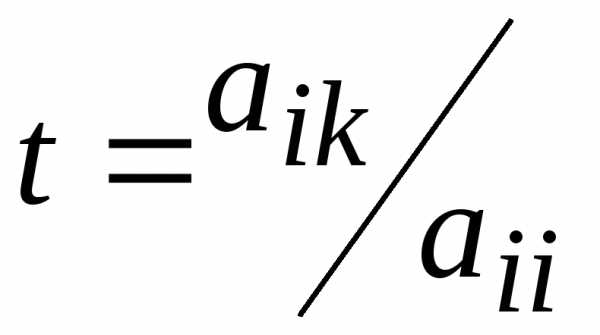 ;
;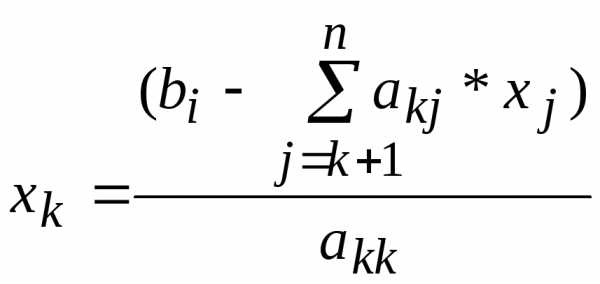 .
.