Гиперболические функции | Математика | FANDOM powered by Wikia
Гиперболи́ческие фу́нкции — семейство элементарных функций, выражающихся через экспоненту и тесно связанных с тригонометрическими функциями.
Определение
Файл:Hyperbola-hyperbolic functions.png Файл:Circle sincos.pngГиперболические функции задаются следующими формулами:
- гиперболический синус:
- $ \mathop{\mathrm{sh}}\,x=\frac{e^x-e^{-x}}{2} $ (в зарубежной литературе обозначается $ \sinh x $)
Существует сленговые названия: «шинус», «шимус»(?). Однако их использование не научно.
- гиперболический косинус:
- $ \mathop{\mathrm{ch}}\,x=\frac{e^x+e^{-x}}{2} $ (в зарубежной литературе обозначается $ \cosh x $)
Существует сленговые названия: «чосинус», «кошинус». Однако их использование не научно.
- гиперболический тангенс:
- $ \mathop{\mathrm{th}}\,x=\frac{\mathop{\mathrm{sh}}\,x}{\mathop{\mathrm{ch}}\,x} $ (в зарубежной литературе обозначается $ \tanh x $).
Существует сленговые названия: «щангенс», «тахинус». Однако их использование не научно.
Иногда также определяются
- гиперболический котангенс:
- $ \mathop{\mathrm{cth}}\,x=\frac{1}{\mathop{\mathrm{th}}\,x} $,
Существует сленговые названия: «кочангенс», «кохинус». Однако их использование не научно.
- гиперболические секанс и косеканс:
- $ \mathop{\mathrm{sch}}\,x=\frac{1}{\mathop{\mathrm{ch}}\,x} $,
- $ \mathop{\mathrm{csch}}\,x=\frac{1}{\mathop{\mathrm{sh}}\,x} $.
Геометрическое определение
Ввиду соотношения $ \mathop{\mathrm{ch}}^2t-\mathop{\mathrm{sh}}^2t=1 $ гиперболические функции дают параметрическое представление гиперболы $ x^2-y^2=1 $ ($ x=\mathop{\mathrm{ch}}\,t $, $ y=\mathop{\mathrm{sh}}\,t $). При этом аргумент $ t=2S $, где $ S $ — площадь криволинейного треугольника $ OQR $, взятая со знаком «+», если сектор лежит выше оси $ OX $, и «−» в противоположном случае. Это определение аналогично определению тригонометрических функций через единичную окружность, которое тоже можно построить подобным образом.
Свойства
Связь с тригонометрическими функциями
Гиперболические функции выражаются через тригонометрические функции от мнимого аргумента.
$ \mathop{\mathrm{sh}}\,x=-i\sin(ix),\quad\mathop{\mathrm{ch}}\,x=\cos(ix),\quad\mathop{\mathrm{th}}\,x=-i\mathop{\mathrm{tg}}\,(ix) $.
Важные тождества
- $ \mathop{\mathrm{sh}}\,x+\mathop{\mathrm{ch}}\,x=e^x $
- $ \mathop{\mathrm{ch}}^2x-\mathop{\mathrm{sh}}^2x=1 $
- Чётность:
- $ \mathop{\mathrm{sh}}(-x)=-\mathop{\mathrm{sh}}\,x $
- $ \mathop{\mathrm{ch}}(-x)=\mathop{\mathrm{ch}}\,x $
- $ \mathop{\mathrm{th}}(-x)=-\mathop{\mathrm{th}}\,x $
- Формулы сложения:
- $ \mathop{\mathrm{sh}}(x+y)=\mathop{\mathrm{sh}}\,x\,\mathop{\mathrm{ch}}\,y+\mathop{\mathrm{sh}}\,y\,\mathop{\mathrm{ch}}\,x $
- $ \mathop{\mathrm{ch}}(x+y)=\mathop{\mathrm{ch}}\,x\,\mathop{\mathrm{ch}}\,y+\mathop{\mathrm{sh}}\,y\,\mathop{\mathrm{sh}}\,x $
- Формулы двойного угла:
- $ \mathop{\mathrm{sh}}\,2x=2\mathop{\mathrm{ch}}\,x\,\mathop{\mathrm{sh}}\,x=\frac{2\mathop{\mathrm{th}}\,x}{1-\mathop{\mathrm{th}}^2x} $
- $ \mathop{\mathrm{ch}}\,2x=\mathop{\mathrm{ch}}^2x+\mathop{\mathrm{sh}}^2x=\frac{1+\mathop{\mathrm{th}}^2x}{1-\mathop{\mathrm{th}}^2x} $
- $ \mathop{\mathrm{th}}\,2x=\frac{2\mathop{\mathrm{th}}\,x}{1+\mathop{\mathrm{th}}^2x} $
- Производные:
- $ (\mathop{\mathrm{sh}}\,x)^\prime=\mathop{\mathrm{ch}}\,x $
- $ (\mathop{\mathrm{ch}}\,x)^\prime=\mathop{\mathrm{sh}}\,x $
- $ (\mathop{\mathrm{th}}\,x)^\prime=\frac{1}{\mathop{\mathrm{ch}}^2x} $
- $ \mathop{\mathrm{sh}}\,x=\int^x_0\mathop{\mathrm{ch}}tdt $
- $ \mathop{\mathrm{ch}}\,x=1+\int^x_0\mathop{\mathrm{sh}}tdt $
- $ \mathop{\mathrm{th}}\,x=\int^x_0\frac{dt}{\mathop{\mathrm{ch}}^2t} $
- Интегралы:
- $ \int\mathop{\mathrm{sh}}\,x\,dx=\mathop{\mathrm{ch}}\,x+C $
- $ \int\mathop{\mathrm{ch}}\,x\,dx=\mathop{\mathrm{sh}}\,x+C $
- $ \int\mathop{\mathrm{th}}\,x\,dx=\ln\mathop{\mathrm{ch}}\,x+C $
- $ \int\frac{1}{\mathop{\mathrm{ch}}^2x}\,dx=\mathop{\mathrm{th}}\,x+C $
- $ \int\frac{1}{\mathop{\mathrm{sh}}^2x}\,dx=-\mathop{\mathrm{cth}}\,x+C $
Разложение в степенные ряды
- $ \mathop{\mathrm{sh}}\,x=x+\frac{x^3}{3!}+\frac{x^5}{5!}+\frac{x^7}{7!}+\ldots=\sum_{n=0}^\infty\frac{x^{2n+1}}{(2n+1)!} $
- $ \mathop{\mathrm{ch}}\,x=1+\frac{x^2}{2!}+\frac{x^4}{4!}+\frac{x^6}{6!}+\ldots=\sum_{n=0}^\infty\frac{x^{2n}}{(2n)!} $
- $ \mathop{\mathrm{th}}\,x=x-\frac{x^3}{3}+\frac{2x^5}{15}-\frac{17x^7}{315}+\ldots=\sum_{n=1}^\infty\frac{(-1)^{n-1}2^{2n}(2^{2n}-1)B_nx^{2n-1}}{(2n)!},\quad|x|<\frac{\pi}{2} $
- $ \mathop{\mathrm{cth}}\,x=\frac{1}{x}+\frac{x}{3}-\frac{x^3}{45}+\frac{2x^5}{945}+\ldots=\frac{1}{x}+\sum_{n=1}^\infty\frac{(-1)^{n-1}2^{2n}B_nx^{2n-1}}{(2n)!},\quad0<|x|<\pi $ (Ряд Лорана)
Здесь $ B_n $ — числа Бернулли.
Графики
500px
Аналитические свойства
Гиперболический синус и гиперболический косинус аналитичны во всей комплексной плоскости, за исключением существенно особой точки на бесконечности. Гиперболический тангенс аналитичен везде, кроме полюсов в точках $ z=i\pi(n+1/2) $, где $ n $ — целое. Вычеты во всех этих полюсах равны единице. Гиперболический котангенс аналитичен везде, кроме точек $ z=i\pi n $, вычеты его в этих полюсах также равны единице.
Обратные гиперболические функции
Читаются ареа… (-синус и т. д.) — от лат. «area» — «площадь».
- $ \mathop{\mathrm{Arsh}}\,x=\ln(x+\sqrt{x^2+1}) $ — обратный гиперболический синус: $ \mathop{\mathrm{sh}}(\mathop{\mathrm{Arsh}}\,x)=x $
- $ \mathop{\mathrm{Arch}}\,x=\ln(x\pm\sqrt{x^2-1}) $ — обратный гиперболический косинус
- $ \mathop{\mathrm{Arth}}\,x=\ln\left(\frac{\sqrt{1-x^2}}{1-x}\right)=\frac{1}{2}\ln\left(\frac{1+x}{1-x}\right) $ — обратный гиперболический тангенс
math.wikia.org
Лекция 05. Гиперболические функции
Лекция 5. Гиперболические функции.
5.1. Гиперболические косинус и синус.
Гиперболический
косинус – это функция, зависящая от переменной х:  .
.
Обозначение ch – сокращение латинских слов соsinus hyperbolicus.
Cвязь с показательной функцией следующая:
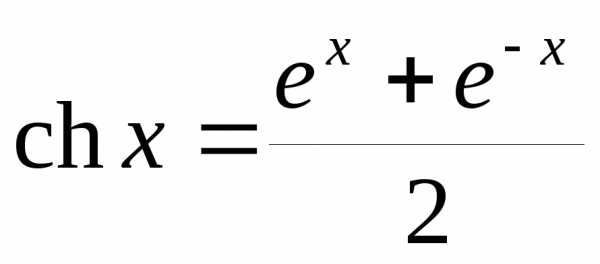
График функции 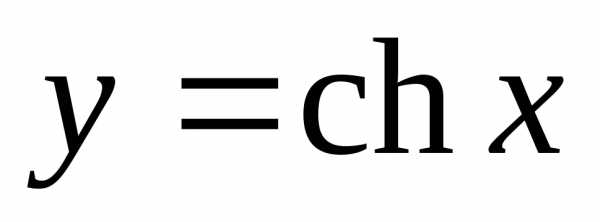 изображён на рис. 5.1.
изображён на рис. 5.1.
Функция 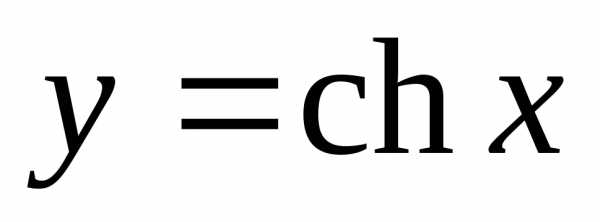 принимает значения, не меньшие единицы
(
принимает значения, не меньшие единицы
( ).
).
| Рис. 5.1. |
Гиперболический
синус – это функция, зависящая от переменной х: 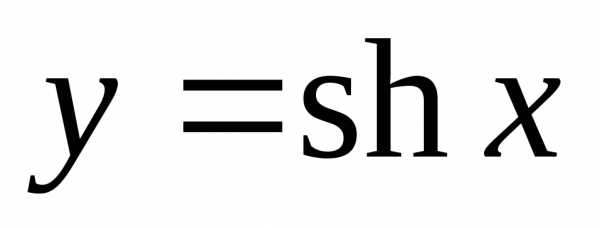 .
.
Обозначение sh – сокращение латинских слов sinus hyperbolicus.
Cвязь с показательной функцией следующая:
 .
(5.2)
.
(5.2)
График функции 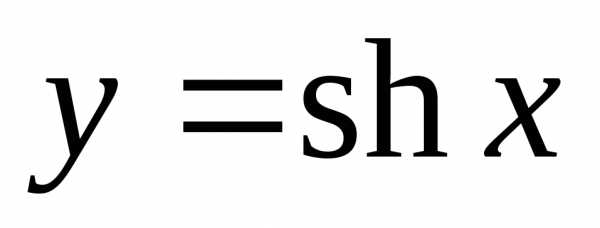 изображён на рис. 5.2.
изображён на рис. 5.2.
Функция  принимает все возможные значения.
принимает все возможные значения.
| Рис. 5.2. |
5.2. Гиперболические тангенс и котангенс.
Гиперболическим тангенсом и котангенсом называются соответственно функции
, (5.3)
. (5.4)
Значения функции 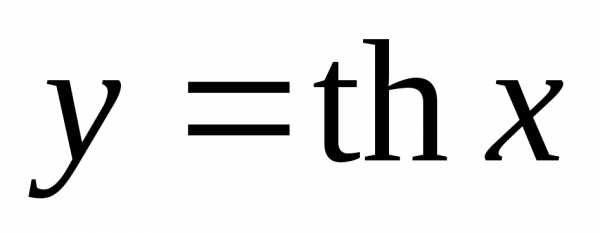
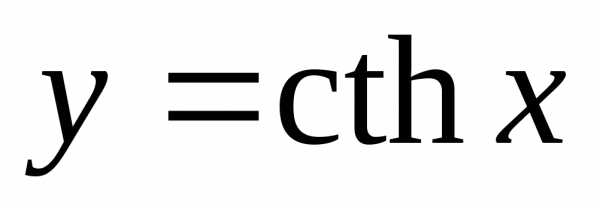 больше +1 при
больше +1 при 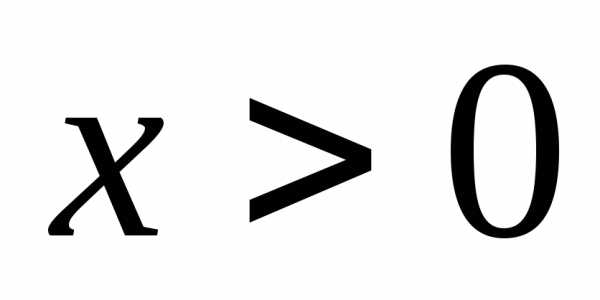 и меньше –1 при
и меньше –1 при 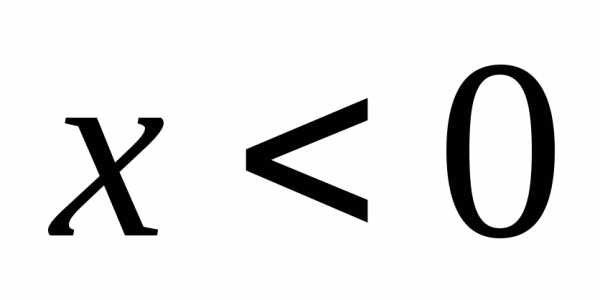 .
Прямые
.
Прямые  и
и 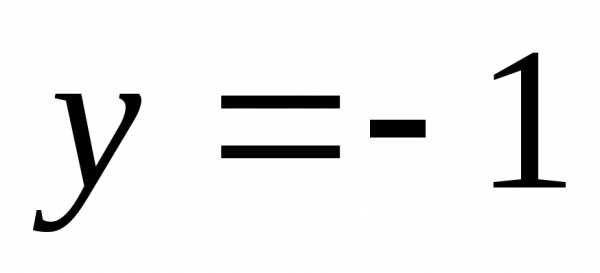 служат горизонтальными асимптотами
для обеих функций
служат горизонтальными асимптотами
для обеих функций  и
и 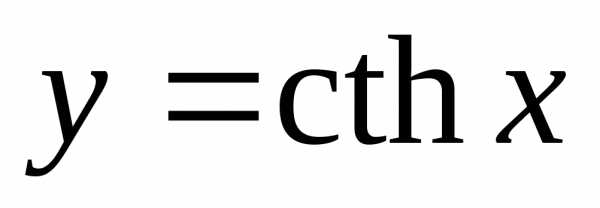 .
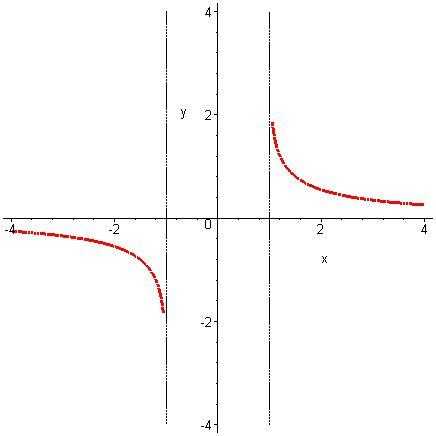
. График функции  изображён
на рис. 5.3,
изображён
на рис. 5.3,  – на рис. 5.4.
– на рис. 5.4.
|
|
Рис. 5.3. | Рис. 5.4. |
5.3. Формулы для гиперболических функций.
Гиперболические функции связаны отношениями
, , 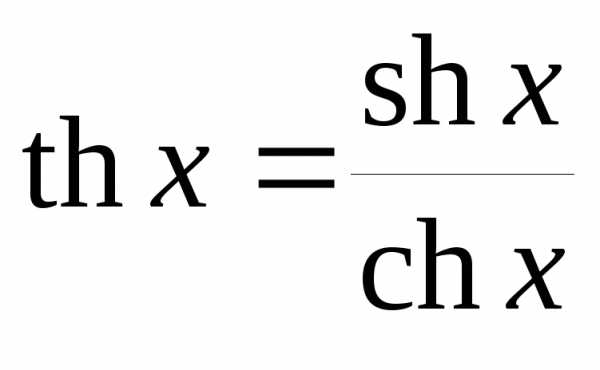 ,
, 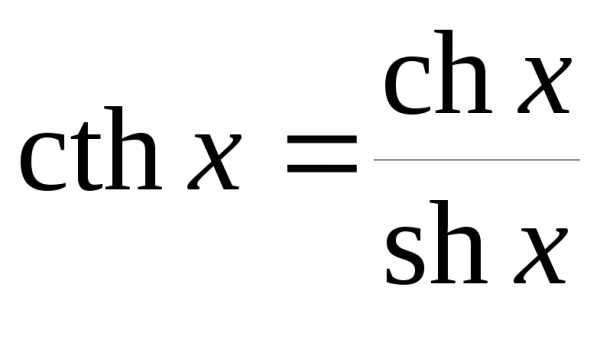 .
.
Для гиперболических функций доказываются формулы, аналогичные тригонометрическим. Так, например,
,
,
.
Эти формулы вытекают из формул (5.1)–(5.4).
Для каждой
тригонометрической формулы, не содержащей
постоянных величин под знаками
тригонометрических функций, есть
аналогичное соотношение между
гиперболическими функциями. Для получения
этих соотношений нужно в тригонометрических
формулах заменить всюду 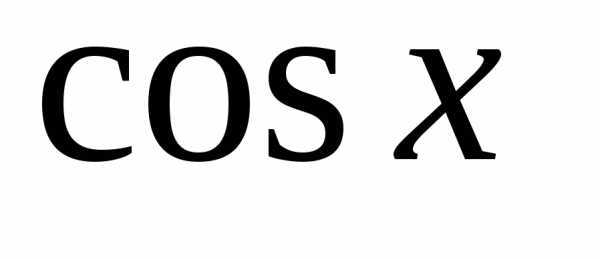 на
на  ,
а
,
а 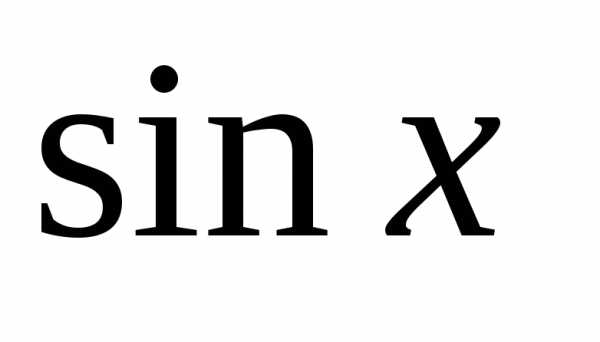 на
на  ,
мнимости устранятся сами собой.
,
мнимости устранятся сами собой.
Пример 5.1. Из тригонометрической формулы c помощью указанной замены получаем .
Разделив обе части равенства на i, получим .
Пример 5.2. Из формулы получаем .
Так как 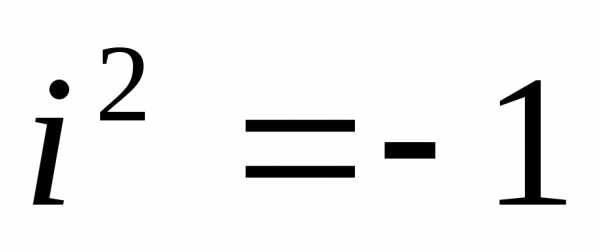
5.4. Обратные гиперболические функции.
Для гиперболических
функций  ,
, 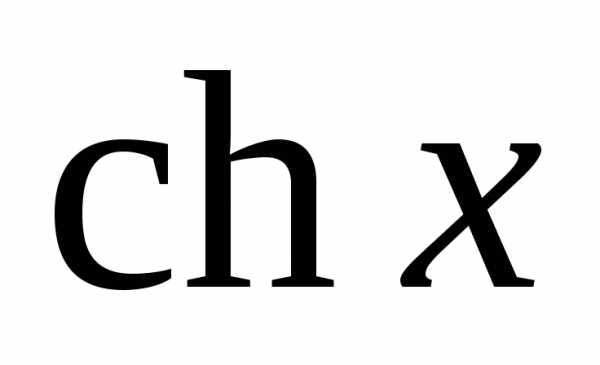 ,
, 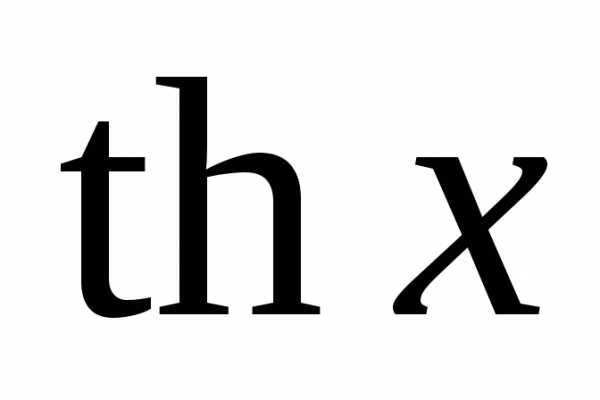 ,
, 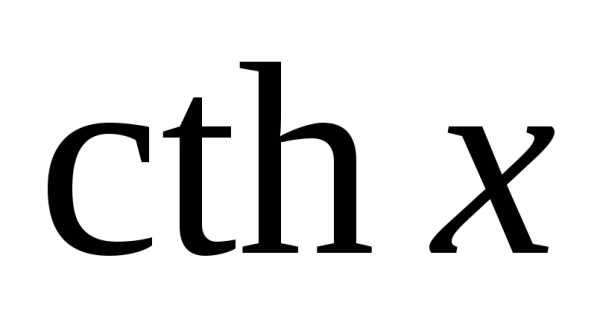 существуют обратные гиперболические
функции:
существуют обратные гиперболические
функции:
 – гиперболический
ареасинус (рис. 5.5),
– гиперболический
ареасинус (рис. 5.5),
 – гиперболический
ареакосинус (рис. 5.6),
– гиперболический
ареакосинус (рис. 5.6),
 – гиперболический
ареатангенс (рис. 5.5),
– гиперболический
ареатангенс (рис. 5.5),
 – гиперболический
ареакотангенс (рис. 5.7).
– гиперболический
ареакотангенс (рис. 5.7).Слово area в переводе с латинского означает площадь, что и объясняет приведённые названия.
Функция  однозначно определена на всей числовой
оси. Через элементарные функции она
выражается так:
.
однозначно определена на всей числовой
оси. Через элементарные функции она
выражается так:
.
Функция  однозначна, она определена в промежутке
однозначна, она определена в промежутке 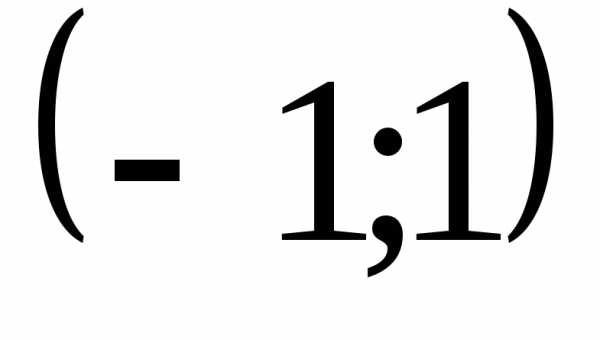 .
Через элементарные функции выражается
так:
,
где
.
Через элементарные функции выражается
так:
,
где 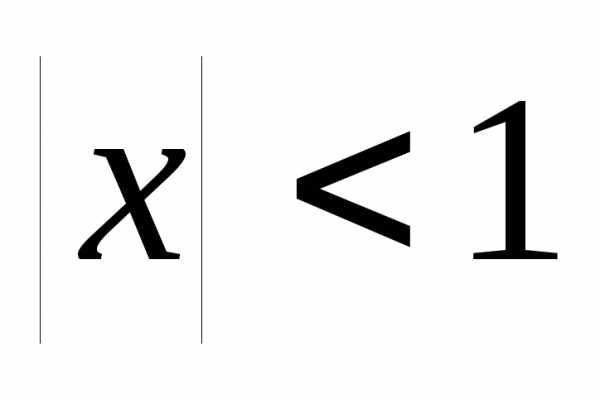 .
.
| Рис. 5.5. |
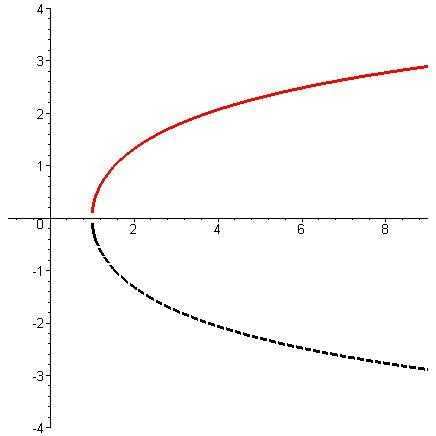
Функция 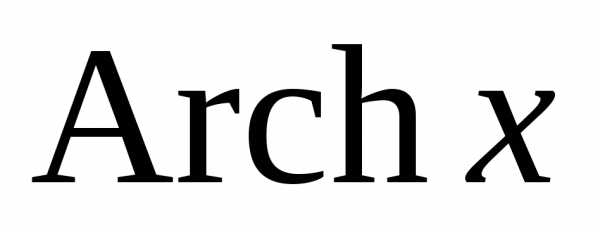 определена на интервале
определена на интервале  и двузначна, значения её равны по
абсолютной величине и отличаются знаком.
Обычно рассматриваются лишь положительные
значения; соответствующая ветвь графика
(главная ветвь) расположена выше оси Ох.
При этом условии функция
и двузначна, значения её равны по
абсолютной величине и отличаются знаком.
Обычно рассматриваются лишь положительные
значения; соответствующая ветвь графика
(главная ветвь) расположена выше оси Ох.
При этом условии функция 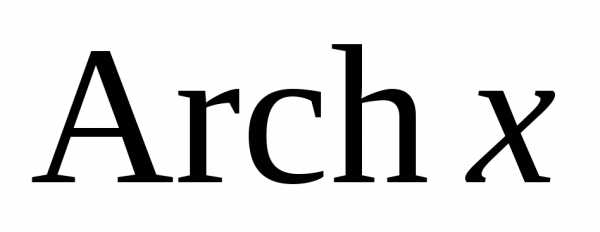 становится однозначной, через элементарные
функции выражается так:
,
становится однозначной, через элементарные
функции выражается так:
,  .
.
| Рис. 5.6. |
Функция  определена вне промежутка
определена вне промежутка 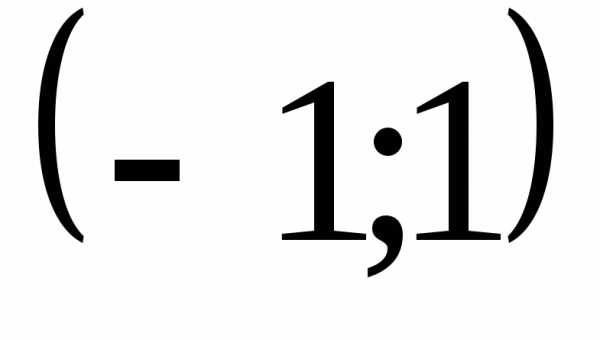 .
Прямые
.
Прямые 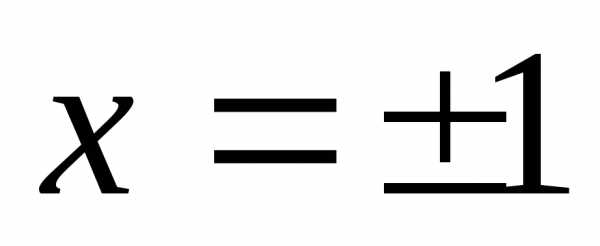 служат асимптотами для кривой
.
Выразим через элементарные функции:
служат асимптотами для кривой
.
Выразим через элементарные функции:
,
где 
| Рис. 5.7. |
25
studfiles.net
Графики гиперболических функций
Поиск ЛекцийОпределение гиперболических синусов, косинусов, тангенсов и котангенсов
Графики гиперболических функций
Свойства
Связь (сумма)
Чётность
Разность квадратов
Формулы суммы и разности аргументов
Формулы произведений гиперболического синуса и косинуса
Формулы суммы и разности гиперболических функций
Формулы производных
Формулы интегралов
Формулы неравенства
Появление названия «гиперболическая функция»
Применение гиперболических функций.
Введение
Гиперболи́ческие фу́нкции — семейство элементарных функций, выражающихся через экспоненту и тесно связанных с тригонометрическими функциями.
Гиперболические функции были введены Винченцо Риккати (Vincenzo Riccati) в 1757 году («Opusculorum», том I). Он получил их из рассмотрения единичной гиперболы. Винсент Риккати (итал. Vincenzo de Riccati; 11 января 1707, Кастель-Франко — 17 января 1775, Тревизо) — итальянский математик, иностранный почётный член Петербургской Академии Наук с 17 января 1760 года. Известен как создатель гиперболических функций. Отец Винсента Якопо Франческо Риккати (в честь которого названо уравнение Риккати) был одним из крупных итальянских математиков того времени. Винсент Риккати унаследовал интересы отца в области дифференциальных уравнений, которые естественно возникали при решении геометрических задач. Это привело его к изучению конических сечений в декартовых координатах и к заинтересованности в изучении гиперболы1.
Современная математика рассматривает гиперболические функции, как пары экспоненциальной функции, но Риккати исследовал их свойства, используя только геометрические свойства гиперболы х² — y² = 1 или 2xy = 1. Он использовал геометрические методы, хотя он был знаком с работами Эйлера, предшествовавших выходу книги Риккати.
Над гиперболическими функциями Риккати работал вместе с Джироламо Саладини. Риккати не только рассмотрел эти новые функции, но и на основе связанных с ними интегральных формул и с помощью геометрических методов получил интегральную формулу для тригонометрических функций. Его книга «Institutiones» признана как первый обширный трактат по интегральному исчислению. Работы Эйлера и Ламберта изданы позже. Саладини и Риккати также рассматривали другие геометрические проблемы, в том числе трактрису, строфоиду. Риккати применял для гиперболических функций обозначения и в дальнейшем в обозначениях гиперболических функций утвердился некоторый разнобой.
Цель данной работы – изучить гиперболические функции и их применение.
Определения гиперболических синусов, косинусов, тангенсов и котангенсов
Гиперболическим синусом называется функция:
Гиперболическим косинусом называется функция:
Гиперболическим тангенсом называется функция:
Гиперболическим котангенсом называется функция:
Гиперболическим секансом и косекансом называется функции:
,
.
Графики гиперболических функций
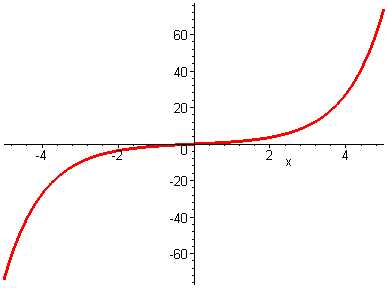
Рисунок 1- график гиперболического синуса y = sh x
Рисунок 2- график гиперболического косинуса y = ch x
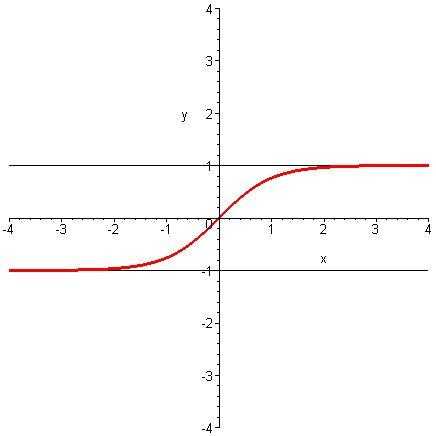
Рисунок 3- график гиперболической функции тангенсаy = th x
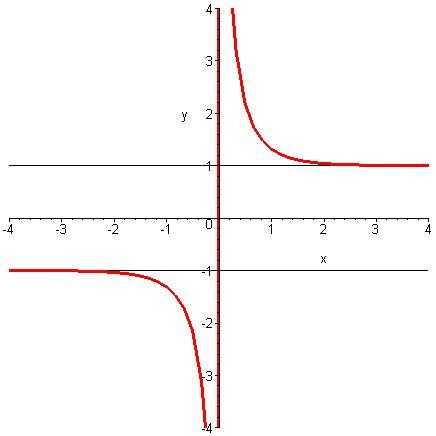
Рисунок 4- график гиперболической функции котангенса y = cth x
Свойства
Связь (сумма)
sin iz = i sh z ; cos iz = ch z
sh iz = i sin z ; ch iz = cos z
tg iz = i th z ; ctg iz = – i cth z
th iz = i tg z ; cth iz = – i ctg z
Здесь i – мнимая единица, i2 = –1.
Применяя эти формулы к тригонометрическим функциям, получаем формулы, связывающие гиперболические функции.
Чётность
sh(–x) = – sh x; ch(–x) = ch x.
th(–x) = – th x; cth(–x) = – cth x.
Функция ch(x) – четная. Функции sh(x), th(x), cth(x) – нечетные.
Разность квадратов
ch2 x – sh2 x = 1.
Рекомендуемые страницы:
Поиск по сайту
poisk-ru.ru
Гиперболические функции — Википедия
Гиперболи́ческие фу́нкции — семейство элементарных функций, выражающихся через экспоненту и тесно связанных с тригонометрическими функциями.
Содержание
- 1 Определение
- 1.1 Геометрическое определение
- 2 Свойства
- 2.1 Связь с тригонометрическими функциями
- 2.2 Важные соотношения
- 2.3 Неравенства
- 2.4 Разложение в степенные ряды
- 2.5 Графики
- 2.6 Аналитические свойства
- 3 Обратные гиперболические функции
- 3.1 Графики
- 4 История
- 5 Применение
- 6 Литература
- 7 Ссылки
Определение[ | ]
| shx{\displaystyle \operatorname {sh} x} | chx{\displaystyle \operatorname {ch} x} |
Гиперболические функции задаются следующими формулами:
- гиперболический синус:
- shx=ex−e−x2{\displaystyle \operatorname {sh} x={\frac {e^{x}-e^{-x}}{2}}}
(в англоязычной литературе обозначается sinhx{\displaystyle \sinh x})
- гиперболический косинус:
- chx=ex+e−x2{\displaystyle \operatorname {ch} x={\frac {e^{x}+e^{-x}}{2}}}
(в англоязычной литературе обозначается coshx{\displaystyle \cosh x})
- гиперболический тангенс:
- thx=shxchx=ex−e−xex+e−x=e2x−1e2x+1{\displaystyle \operatorname {th} x={\frac {\operatorname {sh} x}{\operatorname {ch} x}}={\frac {e^{x}-e^{-x}}{e^{x}+e^{-x}}}={\frac {e^{2x}-1}{e^{2x}+1}}}
(в англоязычной литературе обозначается tanhx{\displaystyle \tanh x})
- гиперболический котангенс:
- cthx
encyclopaedia.bid
ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ — GrandKid
ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ — Гиперболические синус (sh x) и косинус (сh x) определяются следующими равенствами:
Гиперболические тангенс и котангенс определяются по аналогии с тригонометрическими тангенсом и котангенсом:
Аналогично определяются гиперболические секанс и косеканс:
Имеют место формулы:
Свойства гиперболических функций во многом аналогичны свойствам тригонометрических функций (см.). Уравнения х=соs t, у=sin t определяют окружность х²+у² = 1; уравнения х=сh t, у=sh t определяют гиперболу х² — у²=1. Как тригонометрические функции определяются из окружности единичного радиуса, так и гиперболические функции определяются из равнобочной гиперболы х² — у²=1. Аргумент t есть двойная площадь заштрихованного криволинейного треугольника ОМЕ (рис. 48), аналогично тому как для круговых (тригонометрических) функций аргумент t численно равен удвоенной площади криволинейного треугольника ОКЕ (рис. 49):
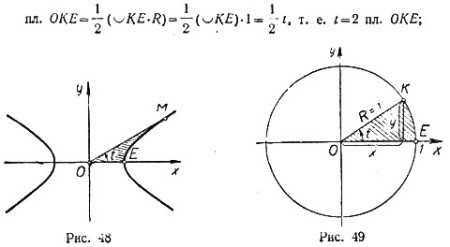 для круга
для круга
для гиперболы
Теоремы сложения для гиперболических функций аналогичны теоремам сложения для тригонометрических функций:
Эти аналогии легко усматриваются, если за аргумент х принять комплексное переменное г. Гиперболические функции связаны с тригонометрическими функциями следующими формулами: sh x = — i sin ix, ch x = cos ix,где i — одно из значений корня √-1 . Гиперболические функции sh х, а также и сh x: могут принимать сколько, угодно большие значения (отсюда, естественно, и большие единицы) в отличие от тригонометрических функций sin х, соs х, которые для действительных значений не могут быть по модулю больше единицы.
Гиперболические функции играют роль в геометрии Лобачевского (см. Лобачевского геометрия), используются при изучении сопротивления материалов, в электротехнике и других отраслях знаний. Встречаются в литературе также обозначения гиперболических функций такие sinh x; соsh х; tgh x.
grandkid.ru
ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ — это… Что такое ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ?
функции, определяемые формулами:
— гиперболический синус,
-г иперболический косинус.
Иногда рассматривается также гиперболический тангенс;
Другие обозначения: sinh x,Sh x,cosh x, Ch x,tgh x,tanh x,Th x. Графики см. на рис. 1.
Основные соотношения:
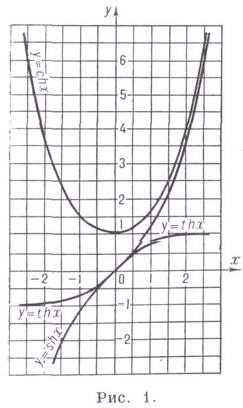
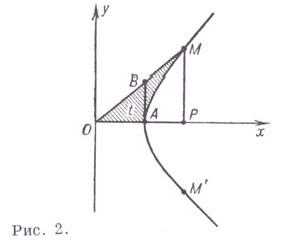
Геометрическая интерпретация Г. ф. аналогична интерпретации тригонометрических функций (рис. 2). Параметрич. уравнения гиперболы позволяют истолковать абсциссу и ординату точки Мравносторонней гиперболы как гиперболнч.
косинус и синус; гиперболич. тангенс-отрезок АВ. Параметр tравен удвоенной площади сектора ОАМ, где AM — дуга гиперболы. Для точки (при ) параметр tотрицателен. Обратные гиперболические функции определяются формулами:
Производные и основные интегралы от Г. ф.:
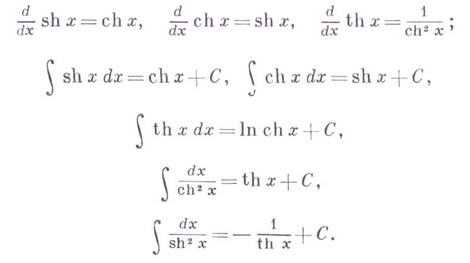
Во всей плоскости комплексного переменного z Г. ф. и могут быть определены рядами:
таким образом,
Имеются обширные таблицы для Г. ф. Значения Г. ф. можно получить также из таблиц для е х и е -х.
Лит.:[1] Янке Е., Эмде Ф., Леш Ф., Специальные функции. Формулы, графики, таблицы, 2 изд., пер. с нем., М., 1968; [2] Таблицы круговых и гиперболических синусов и косинусов в радиацией мере угла, М., 1958; [3] Таблицы е x и е -x, М., 1955. В. И. Битюцков.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
dic.academic.ru
Гиперболические функции Википедия
Гиперболи́ческие фу́нкции — семейство элементарных функций, выражающихся через экспоненту и тесно связанных с тригонометрическими функциями.
Содержание
- 1 Определение
- 1.1 Геометрическое определение
- 2 Свойства
- 2.1 Связь с тригонометрическими функциями
- 2.2 Важные соотношения
- 2.3 Неравенства
- 2.4 Разложение в степенные ряды
- 2.5 Графики
- 2.6 Аналитические свойства
- 3 Обратные гиперболические функции
- 3.1 Графики
- 4 История
- 5 Применение
- 6 Литература
- 7 Ссылки
Определение[ | ]
| shx{\displaystyle \operatorname {sh} x} | chx{\displaystyle \operatorname {ch} x} |
Гиперболические функции задаются следующими формулами:
- гиперболический синус:
- shx=ex−e−x2{\displaystyle \operatorname {sh} x={\frac {e^{x}-e^{-x}}{2}}}
(в англоязычной литературе обозначается sinhx{\displaystyle \sinh x})
- гиперболический косинус:
- chx=ex+e−x2{\displaystyle \operatorname {ch} x={\frac {e^{x}+e^{-x}}{2}}}
(в англоязычной литературе обозначается coshx{\displaystyle \cosh x})
- гиперболический тангенс:
- thx=shxchx=ex−e−xex+e−x=e2x
ru-wiki.ru