Составить задачу по математике: Простейшие задачи по математике

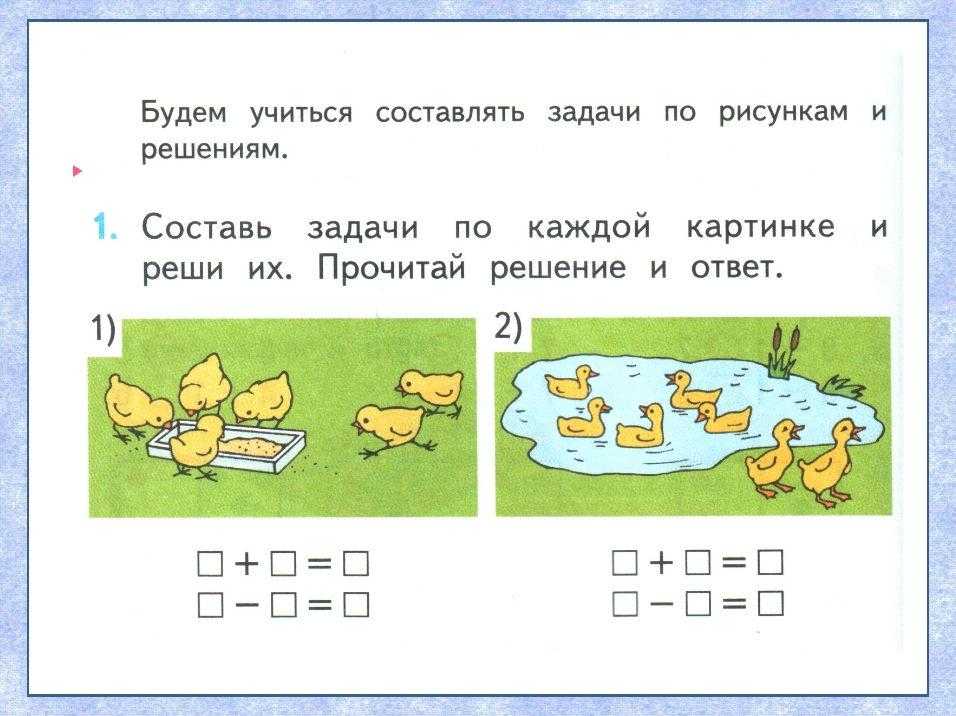
Примеры для 2 класса по математике

Занимательная математика

Дошкольнику | 1 класс | 2 класс | 3 класс | 4 класс

Детям наскучили обычные примеры из учебников. Предложите ребёнку красочные увлекательные задания на сложение и вычитание от ЛогикЛайк.

С занятиями  от LogicLike.com дети развивают математические способности, логическое мышление и смело решают олимпиадные задания.

Предлагаем 9 веселых арифметических заданий для второклассников, которые подойдут для дополнительных, факультативных занятий или олимпиад. Решать сейчас эти примеры в уме или в тетради необязательно.

На сайте ЛогикЛайк дети могут выполнять интерактивные задания в своем учебном профиле. В блоге мы приводим примеры заданий для родителей и учителей. Подборка поможет понять, какие задания точно увлекут детей математикой! 😉

Определи, сколько стоит сыр?

Чтобы решать, нажимайте Начать!

Смотреть ответ

Ответ:

7-3=4.

Магический квадрат

Чтобы решать, нажимайте Начать!

В магическом квадрате сумма чисел в любой горизонтали, вертикали и диагонали одинакова.

Определи недостающие числа.

Смотреть ответ

Ответ:

Сумма чисел в каждой горизонтали, вертикали и диагонали равна 12.

На платформе ЛогикЛайк более 2500 заданий для развития логики и математического мышления.

Монстрик Цифроежка

Чтобы решать, нажимайте Начать!

На торте было двузначное число. Монстрик съел цифру 9. Число уменьшилось на 36. Какое это было число: 36, 63 или 93?

Смотреть решение

Ответ:

39-3=36.

Арифметический ребус

Чтобы решать, нажимайте Начать!

Узнать ответ

Ответ:

6=3+3
11-3=8

Создать аккаунт

и решать задачи с любого устройства!

Заколдованные цифры

Чтобы решать, нажимайте Начать!

Волшебник превратил цифры в геометрические фигуры. Помоги расколдовать цифры и запиши примеры.

Смотреть решение

Ответ:

10-9=1
9+0=9

Чтобы набрать 22 очка, в какие шары нужно попасть?

Чтобы решать, нажимайте Начать!

Смотреть ответ

Ответ:

16+4+2.

Примеры и задачи ЛогикЛайк повышают интерес к учёбе и развивают навыки нестандартного мышления.

Найди недостающие числа

Чтобы решать, нажимайте Начать!

Каждое верхнее число равно сумме двух чисел под ним.

Узнать ответ

Ответ:

4, 1, 4, 0, 1.

Математический ребус

Чтобы решать, нажимайте Начать!

Верни цифры и знак в пример.

Узнать ответ

Ответ:

32-23=9.

Подключайтесь к ЛогикЛайк!

Более 2 000 000 ребят со всего мира уже занимаются математикой и логикой на LogicLike.com.

Начать обучение! Начать обучение

Задача (условие, вопрос, схема, выражение, ответ). 1-й класс

Цели:

1. Закрепление навыков устного счёта в пределах 10.
2. Повторить составление выражений по рисункам, соотношение между целым и его частями.
3. Уточнить термины, связанные с понятием «задача»: условие, вопрос, выражение, решение, ответ.
4. Научить делать краткую запись в виде схем, познакомить с записью решения в тетради.
5. Учить составлять задачи по схемам и числовым выражениям.
6. Развивать мышление, речь, творческие способности.

Оборудование:

• наглядность к устному счёту: ромашки, поезд, зайчик, Великий Математик;
• иллюстрация к задаче;
• плакаты: условие, вопрос, схема, выражение, решение, ответ;
• схемы к задачам;
• плакат (проверка № 5 с. 45).

Ход урока

I. Организационный момент.

II. Вводная беседа.

— Ребята, сегодня на уроке мы отправляемся с вами путешествовать в страну Математики и нас будет сопровождать Великий Математик. Математика – это точная наука, требующая хороших знаний, чёткого выполнения всех арифметических действий.

— Какие действия мы с вами уже знаем?

(Сложение и вычитание. )

— Во 2 классе мы познакомимся с умножением и делением.

— Сегодня на уроке мы будем заниматься наблюдениями, открывать математические закономерности, изучать новый материал.

III. Устный счёт.

1) Путешествовать мы с вами отправляемся на поезде, но прежде, чем наш поезд тронется, мы должны получить билеты. Для этого разделимся на команды и поиграем в игру «Кто быстрее?»

(Учащиеся выходят к доске и дописывают нужные числа.)

I ряд – 1 команда.

II ряд – 2 команда.

III ряд – 3 команда.

2) А теперь надо узнать № поезда. Для этого решим цепочку примеров:

Проверка (у каждого учащегося цифры, ответ показывает каждый с места).

(На доске картинка с зайчиком).

— Зайчик тоже хочет отправиться с нами путешествовать, но он не знает номер поезда, ему достался трудный пример. Он записан под цепочкой.

(Учащиеся записывают пример в тетради и решают. )

3 + 4 – 2 + 3 – 4 + 5 = ?

— Что вы заметили? (В примере выполнены те же действия, что и в цепочке. Значит ответ будет такой же 9.)

Значит Зайка едет в нашем поезде – берём его с собой.

Наш поезд отправился, давайте сосчитаем:

— Сколько пассажиров в каждом вагоне?

9-6	3	4+5	9	8-4	4
3+3	6	7-5	2	3+4	7

(Ответы в тетради.)

— Прочитаем ответы.

3

6

9

2

4

7

— Запишите их в порядке возрастания и вы отгадаете слово.

(На доске все картинки перемешаны, выходит ученик и располагает их в порядке возрастания.)

2	3	4	6	7	9
З	А	Д	А	Ч	А

— Какое слово получилось? (Дети отвечают хором.)

IV. Знакомство с новым материалом.

Тема сегодняшнего урока: Задача.

Наш поезд делает I остановку в лесу. Рассмотрите иллюстрацию. Составьте задачу про детей.

«Мальчик и девочка пошли в лес за грибами. Мальчик нашёл 2 гриба, а девочка 4.Сколько всего грибов нашли дети?»

— Правильно. Без чего нет задачи? (Без вопроса.)

— В задаче всегда о чём-то спрашивается, без вопроса нет задачи. Это нужно хорошо понять и запомнить.

— Задачу можно разбить на 2 части:

1. Условие – то, что известно.
2. Вопрос – то, что неизвестно.

(На доске постепенно открываются плакаты: условие, вопрос, схема, выражение, решение, ответ.)

— Давайте повторим условие нашей задачи, вопрос.

— А теперь запишем в тетради: Задача.

— Ниже запишите выражение: 4 + 2.

— Найдите его значение: 4 + 2 = 6(гр.)

— Полученное равенство называют решением задачи, а значение выражения 6 грибов – ответом задачи.

Ответ: 6 грибов. (На доске записан образец записи.)

— Разобраться в этом помогает рисунок, но если числа большие то делать рисунок неудобно – слишком много предметов надо рисовать. На помощь приходит схема-отрезок, разбитый на части. Разбивая отрезок на части, мы получаем те же самые соотношения между частью и целым, что и при разбиении совокупностей предметов.

(На доске схема.)

— Какой мы делаем вывод? (Наглядно представить содержание задачи можно сопоставив целое всему отрезку, а части – частям отрезка.)

— Что такое целое? (Отрезок.)

— Что обозначает весь отрезок? (Число грибов, собранных детьми.)

— Что такое части? (Части отрезка.)

— Что обозначают части отрезка? (Грибы, собранные мальчиком и девочкой.)

— Что показывает знак вопроса? (Находят целое.)

— Каким действием решаем задачу? (Сложением.)

— Почему? (Находим целое.)

V. Закрепление.

1) Следующая остановка нашего поезда «Поиграй-ка».

— А сейчас мы с вами немного поиграем.

— Великий Математик прислал конверты с задачами.

(Работа в группах).

— Каждой группе нужно определить, что относится к условию, вопросу, найти схему, записать выражение, решение, назвать ответ.

Проверка:

А) Условие. Во дворе играли 6 ребят. Двое ушли домой.

Вопрос. Сколько ребят осталось во дворе?

Схема:

На доске выражение: 6 – 2.

Решение: 6 – 2 = 4(р.)

Ответ: 4 ребят.

Б) Условие. В хоре пело 4 мальчика и 6 девочек.

Вопрос. Сколько детей пело в хоре?

Схема:

Выражение: 6 + 4.

Решение: 6 + 4 = 10(д.)

Ответ: 10 детей.

В) Условие. Из клетки улетело сначала 2 попугая, а потом ещё 3.

Вопрос. Сколько попугаев улетело из клетки?

Схема:

Выражение: 2 + 3.

Решение: 2 + 3 = 5(п.)

Ответ: 5 птиц.

Физкультурная минутка.

2) Наш поезд продолжает путешествие.

— Следующая остановка: «Объясни-ка».

— Откройте учебник с. 44 урок 23 № 2.

— Что нужно сделать? (Соотнести записи в рамках с соответствующими терминами.)

— Выполните самостоятельно.

— Назовите условие, вопрос, выражение, решение.

— Что обозначает весь отрезок? (Число конфет у девочки. )

— Его части? (Число конфет, которые она подарила и число конфет, которые у неё остались.)

— Почему задача решается вычитанием? (Ищем части.)

— Как найти часть? (Из целого вычитаем другую часть.)

3) Перейдём к №3. Составьте задачу по рисунку.

На столе лежали яблоки в 2-х вазах. В 1 вазе – 5 яблок, во 2 – 2 яблока.

— Сколько всего яблок лежало в двух вазах?

— Назовите условие, вопрос, выражение, решение.

— Что обозначает весь отрезок? (Все яблоки, лежащие на 1 и 2 вазе.)

— Его части? (1 ваза с яблоками, 2 – с яблоками.)

— Почему задача решается сложением? (Находим целое.)

4) Путешествие наше продолжается, но нам надо забрать багаж в камере хранения ( №5).

Расшифруем записи – код ячеек.

— Что нужно выполнить? (Составить выражение с заданным числовым значением и дорисовать картинки.) Выполните самостоятельно.

Проверка (плакат на доске).

№ 6

— Наше путешествие подходит к концу.

— И в последнем задании Великий Математик зашифровал слово.

— Если вы правильно выполните действие и сосчитаете, то узнаете слово (умница).

— Великий Математик считает, что вы все умницы, так как хорошо работали на уроке и правильно отвечали на все вопросы, и выполнили все задания.

VI. Итог урока.

— Что нового узнали, чем занимались на уроке?

— Где можно использовать эти знания?

Обучение студентов написанию математических задач

Почему учащиеся должны писать свои собственные задачи

Знание того, как лучше всего решать текстовые задачи, — это только одна сторона медали. Чтобы полностью понять математические концепции, учащиеся должны сами испытать процесс создания текстовых задач. Это может стать неожиданностью. Конечно, создать сценарий и придумать связанную с ним задачу проще, чем решить эту задачу, верно? Это зависит. Написать задачу со словами, требующую простого сложения, намного проще, чем задачу с более сложными процедурами и операциями. Первый подойдет для младших классов, которые только привыкают к решению текстовых задач.

Многим учащимся сложно создавать задачи для более сложных понятий. Например, многим учащимся трудно придумать ситуации, которые точно представляют умножение или деление дробей. Это довольно продвинутая концепция, которую трудно применить в реальной жизни. Большинство студентов, при достаточной практике, могут распознать, когда им нужно умножать и когда им нужно делить дроби в текстовой задаче. Однако на самом деле представить сценарий, представляющий операцию, гораздо сложнее. Когда учащиеся участвуют в продуктивной борьбе, которая помогает им разобраться в таких сложных понятиях, как эта, они начинают понимать гораздо больше, чем просто процедуры.

Как облегчить учащимся создание текстовых задач

Все учащиеся могут решать текстовые задачи. В зависимости от класса и готовности, сложность текстовых задач, которые мы просим наших учеников написать, будет варьироваться. Студенты должны иметь много опыта и практиковаться в решении текстовых задач, прежде чем они должны их написать. Вот несколько советов, о которых следует помнить, когда вы начнете отрабатывать этот навык у учащихся:

Дайте им модель

Студенты всегда лучше отрабатывают новые навыки, когда у них есть пример. Когда они впервые начнут писать свои собственные задачи, дайте им модель, на которой они будут основывать свои словесные задачи. По мере того, как они получают больше практики, они могут начать отклоняться от модели и проявлять творческий подход. Предоставление им модели для начала позволит им иметь фокус и отправную точку.

Начните с малого

Не ожидайте, что учащиеся смогут автоматически писать словесные задачи, столь же сложные, как и те, которые они решают. Это два очень разных процесса. Даже если у вас есть учащийся, который преуспевает в решении сложных задач, он все равно должен начать с более простых задач по написанию задач, например, с одной операцией, прежде чем пытаться писать более сложные текстовые задачи. По мере того, как она будет чувствовать себя более комфортно, вы можете постепенно увеличивать строгость и сложность.

Используйте их словесные задачи в своем обучении

Для учителя нет ничего более увлекательного, чем помогать учащимся приобретать ценные навыки с помощью действий, которые сокращают нагрузку на учителя! Это прекрасная возможность дать учащимся возможность работать вместе, почувствовать гордость за свою работу и облегчить свою работу: пусть учащиеся обмениваются словесными задачами и решают задачи друг друга. Вы захотите предварительно просмотреть текстовые задачи учащихся, но это отличный способ привлечь учащихся к ответственности. Предложите им решать словесные задачи друг друга — это отличный способ расширить их возможности и дать им некоторую ответственность за свое обучение! Вы можете сделать это анонимно для студентов, которые могут чувствовать себя неловко. Некоторые ученики испытывают беспокойство, когда дело доходит до того, чтобы поделиться своей работой с одноклассниками.

Письмо для объяснения мышления при решении математических задач

Слышали ли вы когда-нибудь, чтобы ваши ученики говорили: «Фу, почему я должен писать о том, как я решил математическую задачу?» Если учащиеся могут СКАЗАТЬ вам, что они сделали для решения проблемы, они могут НАПИСАТЬ об этом. Кажется сложной задачей заставить студентов писать, но шаг за шагом вы можете это сделать. Этот пост в блоге длинный, но его стоит прочитать, если вы серьезно относитесь к тому, чтобы помочь учащимся уверенно объяснить свои мысли.

Почему учащиеся должны писать о своих мыслях

Давайте задумаемся о том, почему мы просим учащихся делиться своими мыслями, когда они решают математические задачи. Перенесемся в трудовые годы. Когда предприятия нанимают сотрудников, сотруднику никогда не дадут решить математическую задачу. Им будет дана ПРОБЛЕМА, которую нужно решить.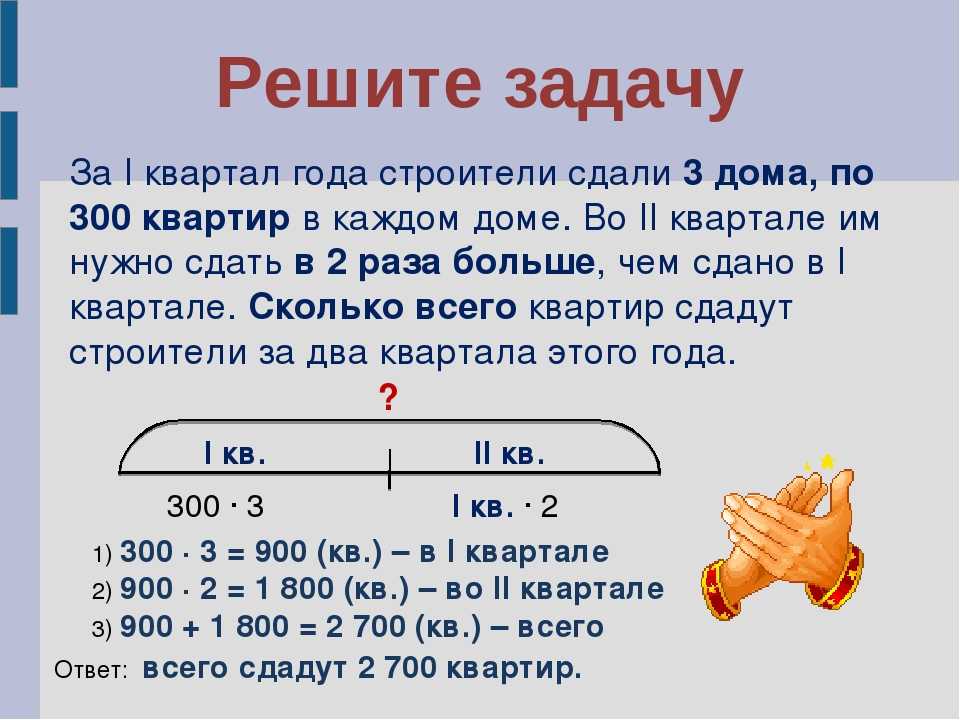 Им нужно будет отстаивать свое мнение перед своим начальником, чтобы убедить его/ее в своих выводах. Студенты готовятся к будущему.

Дайте учащимся структуру при решении задач.

Попросите учащихся переформулировать или сказать своими словами, в чем заключается задача. Учащиеся рассказывают, что они знают и что им нужно выяснить.

Затем попросите учащихся  нарисовать картинку, диаграмму, эскиз, Т-образную диаграмму, таблицу или что-то еще, что поможет продемонстрировать их мышление. Предложите учащимся рисовать стрелки и подчеркивать то, что помогает им объяснить, о чем они думают. Студенты должны показать, что они думают в этом пространстве.

Затем попросите учащихся  написать , используя слова, предложения, списки или что-то еще, что нужно, чтобы объяснить шаги, которые они предприняли для решения проблемы. Предложите учащимся сделать вид, что человек, читающий их объяснение, вообще ничего не понимает, поэтому они должны быть очень ясными в своем объяснении.

Учащиеся сформулируйте ответ и подчеркните его или обведите его рамкой. Напомните учащимся всегда маркировать единицы в своем ответе. Они также докажут свою правоту .

Соберите образцы работ учащихся и попрактикуйтесь в подсчете баллов. Примеры заданий

Когда вы решаете проблемы и интегрируете письмо в процесс, будьте терпеливы. Требуется время, чтобы помочь учащимся привыкнуть к объяснению и рисованию своих мыслей.

Ищите замечательные примеры учащихся, чтобы показать им, как выглядят замечательные картинки, рисунки и пояснения. Поговорите со своими партнерами по обучению и помогите друг другу найти примеры студенческих работ, которые вы можете использовать для практического оценивания. Соберите свою копилку замечательных примеров и пополняйте ее каждый год. Не забудьте заштриховать имена учащихся в целях конфиденциальности. Пометьте работы: Студент A, B, C и т. д. Использование фактической работы учащихся помогает учащимся понять, что от них требуется.

Научите учащихся читать Руководство по подсчету баллов

Научите разделы руководства по подсчету баллов вашего округа или штата. Объедините учащихся в группы по четыре человека. Дайте каждому учащемуся в группе выполненное задание по математике и руководство по подсчету баллов. После того, как вы нашли несколько примеров задач для учащихся, дайте учащимся задание оценить реальное задание по математике. Попросите учащихся использовать руководство по подсчету очков и оценить математическое задание. Предложите учащимся обсудить свое мнение по мере того, как они оценивают задание. Со временем учащиеся станут чувствовать себя более комфортно, защищая свое мышление. После того, как учащиеся оценят свою работу, покажите фактические баллы, полученные за задание. Обсудите и позвольте учащимся сравнить выставленные ими баллы с фактически полученными баллами. Если вы дадите учащимся три или четыре возможности оценить студенческую работу, вы увидите, как укрепится их уверенность в себе.

Демонстрация размышлений

Показывайте примеры, обучая учащихся не спеша рисовать наброски и маркировать их. Рисуйте и используйте T-диаграммы для организации данных. T-диаграммы очень удобны и помогают увидеть закономерности. Нарисуйте числовые линии и покажите прыжки, необходимые для получения ответа. Нарисуйте карту или рисунок. Поощряйте использование цвета, если это помогает визуальному объяснению.

Письмо для объяснения мышления

Предложите учащимся начать с использования порядковых слов, таких как «Сначала я…, затем я…, затем я…, в конце я…»  Поощряйте учащихся замедляться и объяснять так, как если бы они говорили.

Когда учащиеся ответят, попросите их обозначить единицы, а затем либо подчеркнуть свой окончательный ответ, либо обвести его рамкой. Я люблю шутить со студентами, когда они забывают обозначать единицы измерения. Я говорю: «Ваш ответ 14? 14 зубочисток? 14 копеек? 14 тысяч долларов? 14 огурцов?» Студенты смеются и понимают, что единицы измерения имеют значение.

Подтверждение правильности ответа

Важной частью математической задачи является подтверждение правильности ответа. Студенты могут начать со слов: «Я прав, потому что я прав». Со временем они будут становиться все лучше и лучше и, в конце концов, станут мастерами доказательства правильности своего ответа. Вы должны побудить их думать как адвокат защиты, чья работа состоит в том, чтобы убедиться, что их клиент невиновен, и применить этот метод к своим «доказательствам». Используйте аналогию с историей о Джеке и бобовом стебле, чтобы подготовить почву для доказательства невиновности или виновности Джека. По сюжету Джек несколько раз поднимается по бобовому стеблю и каждый раз возвращается домой с вещами, которые он взял у огра, включая гуся, золотые монеты и арфу. Попросите учащихся представить, что они адвокаты, обвиняющие Джека во взломе и проникновении в дом огра и краже его имущества. Как адвокат Джека, вы не можете сказать присяжным и судье: «Я прав, потому что я знаю, что я прав». Вы должны ДОКАЗАТЬ это фактами и другими доказательствами. То же самое верно и в решении математических задач. Откуда вы знаете, что вы правы? Вы можете доказать это? Какие факты и детали у вас есть? Соответствует ли ваша картинка написанному вами уравнению? Вы решили задачу по-другому и получили тот же ответ? Правильно ли помечен ваш эскиз, чтобы подтвердить ваши мысли? Попросите своих учеников выступить в роли жюри и дайте ответ «большой палец вверх/я убежден» или «большой палец вниз/я не убежден».

Будьте терпеливы! Продолжай практиковаться!

Делайте это один день за раз и знайте, что при постоянной последовательной практике ваши ученики будут все более и более комфортно писать, объясняя математическое мышление. Напомните своим ученикам, что их будущий босс поставит перед ними реальную проблему, которую нужно решить, и они должны быть опытными, чтобы обосновать свое мнение. С практикой у студентов появится уверенность в том, что они будут выполнять задание охотно и с удовольствием.