Зачем нашим детям нужны текстовые задачи по математике
«Ну зачем нам эта математика? Зачем решать задачи?» — ноют многие школьники и мечтают, чтобы задачки и уравнения исчезли из учебников алгебры. Наш блогер, учитель математики Александр Шевкин, объясняет, почему не стоит отказываться от текстовых задач на уроках.
Ещё до выхода в 1703 году известного учебника «Арифметика» Л. Ф. Магницкого в России существовала традиция обучать арифметике через решение задач практического содержания. Так же обучали детей азам математики и у других народов.
Многие типовые задачи решали «по правилам», сообщённым учителем. Ученики часто не понимали, почему применяемое правило приводит к верному результату. Тогда и не ставили задачи, чтобы ученик всё понимал. Он должен был выучить «правило» и применять его «по разумению». Вот пример задачи и её решения из математической рукописи:
Задача. Один человек выпьет кадь кваса в 14 дней, а с женою выпьет ту же кадь в 10 дней. Спрашивается, в сколько дней жена его отдельно выпьет ту же кадь.
Решение. Вынь 10 из 14 — останется 4. Молви: 4 даст 10. Что даст 14? Умножь 14 на 10, будет 140; дели 140 на 4, будет 35 дней. За 35 дней одна жена кадь квасу выпьет.
С той поры методика обучения существенно шагнула вперёд, но даже в середине XX века в обучении решению задач в советской школе сохранились следы обучения «по правилам». Более подробно об этом написано в книге «Обучение решению текстовых задач в 5–6-х классах» (раздел «Статьи» на сайте).
В заметке «Как эффективно обучать детей решению текстовых задач» я уже писал о последствиях отказа от арифметических способов решения текстовых задач и раннего применения уравнений для решения задач. Приведу ещё один аргумент сторонников такого отказа. «По мнению С. Л. Соболева, как правило, после овладения алгеброй тот же школьник уже не в состоянии решить прежнюю задачу арифметическими приёмами. Зачем же тогда обманывать детей, а не приучать их к абстрактному мышлению с самого младшего класса?» — Н. А. Менчинская, М.
И. Моро.
Так вот на самом деле всё обстоит совсем не так. Мои многолетние наблюдения показали, что если ученик в шестом классе обучен делить число в данном отношении арифметическим способом, то в девятом классе он именно этим способом вычисляет части, на которые биссектриса угла делит противолежащую сторону треугольника с заданными сторонами.
Вернёмся к традициям. В России, потом в СССР до середины 60-х годов XX века обучали решению типовых текстовых задач арифметическими способами, развивая мышление и речь школьников. Интересно, что это почти исключительно российский феномен. Приведу примеры из статей В. С. Доценко и А. Л. Тоома, сохранённых на упомянутом выше сайте.
Вот пример использования текстовых задач во Франции. Интересно отношение преподавателей университета к возможности включения такой задачи в контрольную работу: «В этом учебном году на семестровой контрольной одной из задач была такая:
Воздушный шар летит в одном направлении со скоростью 20 км/час в течение 1 ч.
и 45 мин. Затем направление движения меняется на заданный угол (60°), и воздушный шар летит ещё 1 ч. и 45 мин. с той же скоростью. Найти расстояние от точки старта до точки приземления.
Перед контрольной на протяжении двух недель среди преподавателей университета шла бурная дискуссия — не слишком ли сложна эта задача для наших студентов. В конце концов решили рискнуть выставить её на контрольную, но с условием, что те, кто её решит, получат дополнительно несколько премиальных очков. Затем в помощь преподавателям, которые будут проверять студенческие работы, автор этой задачи дал её решение. Решение занимало половину страницы и было неправильным. Когда я это заметил, коллеги тут же успокоили меня очень простым аргументом: «Чего ты нервничаешь? Всё равно эту задачу никто не решит…» И они оказались правы. Из полутора сотен студентов, писавших контрольную, её решили только два человека (и это были китайцы)». — В. С. Доценко.
В одной из своих статей А. Л. Тоом пишет: «Когда я приехал в США девять лет назад и начал преподавать, я обнаружил, что многие университетские студенты очень плохо справляются с решением текстовых задач.
Когда я стал читать некоторую американскую образовательную литературу, я обнаружил странный (для меня) подход к текстовым задачам, совершенно отличный от того, к какому я привык в России. Похоже, что многие считают, что задачи, решаемые на уроках математики, должны быть как можно ближе к повседневной жизни. Я полагаю, что этот подход берёт своё начало у известного американского психолога и преподавателя Э. Торндайка, в чьей авторитетной книге „Психология алгебры“ имеется глава, названная „Нереальные и бесполезные задачи“, начинающаяся так: „В предыдущей главе было показано, что около половины задач, дающихся в стандартных курсах, ненастоящие, поскольку в реальной жизни ответ никогда не понадобится. Очевидно, не стоит, разве что для объёма, таким образом соединять алгебраическую работу с никчёмностью“».
В той же статье А. Л. Тоом приводит задачу, которая «может использоваться чуть ли не повсюду на земном шаре без всяких ограничений, и „аргументы“, на основании которых эта задача должна быть отвергнута»:
Салли на пять лет старше своего брата Билла.
Через четыре года она будет в два раза старше, чем тогда будет Биллу. Сколько лет Салли сейчас?
Она объявляется негодной по следующей причине: «Прежде всего, кто бы мог задать подобный вопрос? Кому это может понадобиться? Если Билл и Салли сами не знают, это какая-то семья идиотов». Если бы обличитель «негодной» задачи не поленился её решить, то, возможно, он был бы справедливее к малым детям, ведь Биллу всего 1 год, а Салли 6 лет.
Вот ещё пример. В другой статье А. Л. Тоом приводит высказывание З. Усыскина о традиционных текстовых задачах, опубликованное в главном американском журнале для учителей математики в старших классах «Учитель математики» (Mathematics Teacher): «Алгебра имеет так много подлинных приложений, что фальшивые традиционные текстовые задачи больше не нужны». Почему З. Усыскин называет традиционные текстовые задачи фальшивыми? Он приводит задачу:
У одного человека в кошельке 20 монет, одни по 5 центов, другие по 10 центов, на общую сумму в доллар и 75 центов.
Сколько у него монет по 5 центов? Сколько по 10 центов?
Затем З. Усыскин пишет: «Поскольку монеты в кошельке посчитаны, то почему бы не сосчитать отдельно монеты в 5 центов и отдельно в 10 центов?» В России (и, я думаю, в огромном большинстве стран) этот странный аргумент был бы оставлен как неудачная шутка, но в Америке к нему относятся с большим почтением.
А. Л. Тоом писал: «Теперь посмотрим на следующую задачу:
Самолёт взлетает и направляется на восток со скоростью 350 миль в час. В то же время взлетает другой самолёт и направляется на запад со скоростью 400 миль в час. Когда расстояние между ними достигнет 2000 миль?
Я не вижу ничего порочного в этой лёгкой задаче. По-моему, она годится в классе и даже имеет некоторые достоинства. Например, её можно использовать для демонстрации идеи относительного движения, помогающей решить её без алгебры: в системе координат, связанной с одним самолётом, другой движется со скоростью 350 + 400 = 750 миль в час, поэтому время, необходимое, чтобы увеличить расстояние на 2000 миль, равно 2000/750 часов = 2 часа 40 минут.
Однако несколько лет назад эта задача была упомянута в «Учителе математики» со следующим уничижительным комментарием: «Всякий нормальный ученик должен спросить: «А кому это надо?» Никому нет дела, кроме учителя алгебры, задающего такие задачи, и ученика, которому нужна отметка. Наша программа и без того слишком перегружена, чтобы включать такие причуды»».
Рассмотрим последний пример. Ниже приведены «правила», автор которых неизвестен (перевод А. Л. Тоома). Они были посланы на один американский дискуссионный лист под названием math-teach. Все дискуссии на этом листе доступны в интернете. Эти «правила» можно посчитать шуткой, но мы помним, что в каждой шутке есть доля правды:
Правило 1. Насколько возможно, избегай читать условие задачи. Чтение условия только отнимает время и запутывает.
Правило 2. Выпиши все числа из условия в том порядке, в каком они там даны. Не забудь о числах, написанных словами.
Правило 3. Если правило 2 дало тебе три числа или больше, то лучше всего сложить их все.
Правило 4. Если чисел только два и они примерно одной величины, то лучше всего вычесть одно из другого.
Правило 5. Если чисел только два и одно много меньше другого, то попробуй разделить, а если не разделится, то перемножь.
Правило 6. Если у задачи такой вид, как будто надо применить формулу, выбери формулу с достаточным числом переменных, чтобы использовать все данные.
Правило 7. Если с правилами 1–6 ничего хорошего не получается, сделай последнюю отчаянную попытку. Возьми все числа, полученные с помощью правила 2, и заполни страницы две всевозможными операциями с ними. Затем обведи кружком пять-шесть полученных чисел на каждой странице на случай, если какое-нибудь из них окажется ответом. Может, и получишь что-нибудь за то, что старался.
Публикуя «правила 1–7», я выражаю надежду, что умение школьников (и учителей) России решать текстовые задачи ещё не доведено до такого отчаянного состояния, что нам не остаётся ничего другого, как поместить «правила 1–7» в виде плаката на классной стене и обращаться к ним при столкновении с мало-мальски сложной задачей.
Вы находитесь в разделе «Блоги». Мнение автора может не совпадать с позицией редакции.
Текстовые задачи в школьном курсе математики.
Примеры разбора арифметических текстовых задач.
Синтетически-аналитический и аналитико-синтетический методы.
Первый вопрос: «О каких величинах идет речь в задаче?»
Решение любой текстовой задачи начинается с разбора ее условия. Осмыслить зависимости между данными и искомыми величинами задачи учащиеся смогут через планомерное применение общих приемов умственных действий. В 5 классе применяются арифметические методы решения задач.
Методы:
1 Синтетический.
Заключается
в том, что разбор задачи начинается
исходя из известных данных в задаче.
Выделяют 2 известных данных и к ним
подбирают вопрос. Затем снова выделяют
2 известных данных и к ним подбирают
вопрос. И так до тех пор, пока не ответим
на вопрос задачи. С помощью синтетического
приема осуществляется разбиение задачи
на части, т.
е на простые задачи (задачи,
решаемые одним действием).
Пример. Расстояние между А и В 430 км. Из А в В выехала грузовая машина. Два часа спустя навстречу ей из В вышла легковая машина. Скорость грузовой машины 60 км/ч, а скорость легковой – в 1,5 раза больше. Через сколько часов после своего выхода легковая машина встретит грузовую.
Схема синтетического разбора
2 Аналитический метод
заключается в том, что разбор задачи начинается с вопроса в котором исходят от неизвестного. К неизвестному ставят вопрос и подбирают 2 данных, причем одно или оба данных могут быть неизвестными. Затем снова к неизвестному ставят вопрос и снова подбор двух данных. И так до тех пор, пока оба данных будут известны, т.е. разбор задачи заканчивается и выполняются действия от последнего к первому.
Схема аналитического разбора задачи.
3 Аналитико-синтетический метод
заключается
в том, что разбор задачи начинается с
помощью аналитического приема, т.
4 Метод вспомогательных задач
заключается в том, что сначала решается вспомогательная задача. В этом случае учащиеся осмысливают план рассуждения, а затем этот план применяют к более сложным задачам и т.о. получают обобщенный метод.
Пример. Имеющийся запас топлива составляет 80% от того, что требуется в текущем году. На сколько процентов надо увеличить имеющийся запас, чтобы полностью обеспечить потребности в топливе?
Вспомогательная задача. Школа получила 500 учебников вместо 800. На сколько процентов надо увеличить число учебников?
5 Обобщенные методы решения задач.
Традиционно текстовые задачи классифицируются следующим образом:
— задачи на движение; — на работу; — на проценты; — количество, стоимость и другие группы задач.
Однако
рассматривая функциональный анализ
задачи можно заметить, что самые
разнообразные по фабуле задачи имеют
одну и ту же модель, т.
к. в них идет речь
о процесе. Всякий процесс характеризуется
следующими величинами: скорость, время,
результат процесса (объема процесса),
которые связаны между собой зависимостью
(здесь школьный курс – равномерные
процессы):
Результат = Скорость * Время.
Поэтому общим приемом умственной деятельности решения текстовых задач на «процессы» относятся следующие:
Выяснить, о каком процессе идет речь в задаче (движение, работа и т.д.).
Выяснить, какими величинами характеризуется всякий процесс.
Выяснить, сколько процессов описано в задаче (2 человека идут навстречу – 3 процесса).
Выяснить, какие из величин, характеризующих процесс, известны, а какие – нет.
Обозначить неизвестные величины через переменные, а другие известные величины этого процесса, выразить через переменные и условие задачи.
Выяснить, какие данные в задаче использованы и использовать их для составления уравнений.
Решить полученные уравнения или системы уравнений.
Выполнить анализ полученных результатов.
Пример. Бассейн наполняется 2-мя трубами, действующими одновременно, за 2 часа. За сколько часов может наполнить бассейн 1-я труба, если она действует одна. Причем она наполняет бассейн на 3 часа быстрее, чем вторая.
3 процесса: 1 труба наполняет, 2 труба наполняет, обе (вместе) наполняют.
Решение:
Объяснение текстовых задач для начальной школы
Решение текстовых задач в начальной школе является неотъемлемой частью учебной программы по математике. Вот более 30 математических задач, которые можно практиковать с детьми, а также советы экспертов по их решению.
Этот блог является частью нашей серии блогов, предназначенных для учителей, школ и родителей, поддерживающих домашнее обучение.
Что такое словесная задача?
Словесная задачка по математике — это математический вопрос, написанный в виде одного или нескольких предложений, который требует от детей применить свои математические знания к «реальному» сценарию.
Это означает, что дети должны быть знакомы со словарным запасом, связанным с математическими символами, к которым они привыкли, чтобы понять смысл словесной задачи.
Например:
Разве недостаточно блестящей арифметики?
Короче говоря, нет. Ученики должны хорошо понимать прочитанное, даже по математике. Сверхурочные математические задачи становятся все более сложными и требуют от учащихся глубокого концептуального понимания и способности вспоминать и применять знания быстро и точно.
По мере прохождения математического образования учащиеся должны уметь применять математические рассуждения и разрабатывать математические аргументы и доказательства с использованием математического языка. Они также должны быть динамичными, применяя свои математические знания для решения множества все более сложных задач.
Чтобы поддержать это, школы принимают подход к математике, основанный на мастерстве
«Обучение для мастерства», определяется с помощью следующих компонентов: заниматься математикой».
(Суть преподавания математики для достижения мастерства, 2016 г.)
Мастерство помогает детям глубже изучать математику
Свободное владение арифметикой важно; однако с этим часто связано распространенное заблуждение, что после того, как ребенок освоил числовые навыки, соответствующие его классу/возрасту, его следует перевести на следующий класс/возраст числовых навыков.
Мастерский подход поощряет изучение широты и глубины этих математических понятий (если беглость речи обеспечена) посредством рассуждений и решения проблем.
Как научить детей решать текстовые задачи?
Вот две простые стратегии, которые можно применить ко многим текстовым задачам перед их решением.
- Что вы уже знаете?
- Как можно изобразить/отобразить эту задачу графически?
Давайте посмотрим, как это можно применить к текстовым задачам, чтобы получить ответ.
Решение простой задачи со словами
В классе 28 учеников.
У учителя есть 8 литров апельсинового сока.
Она наливает каждому ученику по 225 миллилитров апельсинового сока.
Сколько апельсинового сока осталось?
1. Что вы уже знаете?
- В 1 литре 1000 мл
- Налив = жидкость, выходящая из бутылки = вычитание
- Для каждого = умножить
- Осталось = требуется вычитание в какой-то момент
2. Как можно изобразить/изобразить эту проблему?
Гистограмма, также известная как ленточная диаграмма, всегда является отличным способом представления проблем.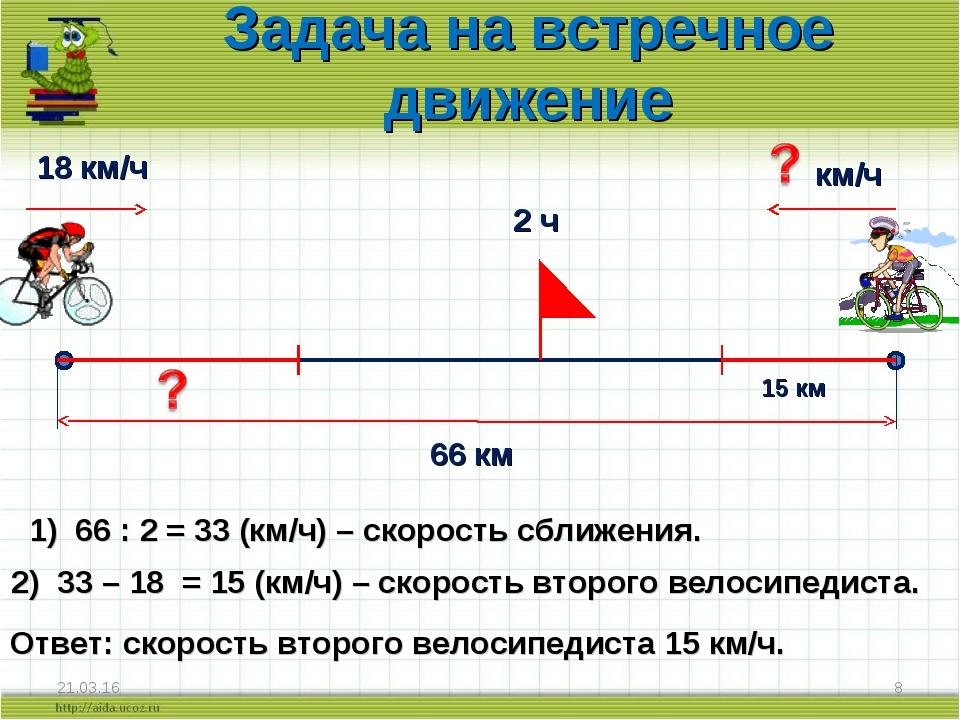
Однако, если вы не знакомы с этим, всегда есть другие способы нарисовать это.
Подробнее: Что такое барная модель
Например, для этого вопроса вы можете нарисовать 28 учеников (или палку x 28) с надписью «225 мл» над каждым, а затем полупустую бутылку с надписью « 8 литров отмечены вверху.
Теперь поработаем над математикой. Это многоступенчатая задача для 5-го класса, поэтому нам нужно использовать то, что мы уже знаем и нарисовали, чтобы разбить шаги.
Решение более сложной задачи со смешанными словамиМара в книжном магазине.
Она покупает одну книгу за 6,99 долларов и другую, которая стоит на 3,40 доллара больше, чем первая книга.
Она платит 20-долларовой купюрой.
Какие сдачи получает Мара? (Что осталось?)
1. Что вы уже знаете?
- Больше = добавить
- Использование десятичных знаков означает, что мне нужно будет правильно расставить десятичные точки в вычислениях
- Сдача из денег = вычесть
2.
Как эту проблему можно нарисовать/изобразить графически?
См. этот пример моделирования стержня для этого вопроса:
Теперь задействуем математику, используя то, что мы уже знаем, и то, что мы нарисовали, чтобы разбить шаги.
Мара в книжном магазине.
Она покупает одну книгу за 6,99 долларов и другую, которая стоит на 3,40 доллара больше, чем первая книга. 1) 6,99 долл. США + (6,99 долл. США + 3,40 долл. США) = 17,38 долл. США
Она платит 20-долларовой купюрой.
Какие сдачи получает Мара? 2) $20 – $17,38 = $2,62
Математические задачи для детей от детского сада до 5 классаЧем больше дети узнают о математике в начальной школе, тем сложнее будут задачи со словами, с которыми они будут сталкиваться.
Ниже вы найдете некоторую информацию о типах текстовых задач, с которыми ваш ребенок будет сталкиваться из года в год, и о том, как текстовые задачи применимы к каждому начальному классу.
На протяжении всего детского сада ребенок, скорее всего, знакомится со словесными задачами с помощью конкретных ресурсов (манипулятивных средств, таких как физические устройства, такие как монеты, карты, жетоны или числовые линии), чтобы помочь им. понять проблему.
Примером текстовой задачи для детского сада может быть
У Криса есть 3 красных и 2 зеленых мяча. Сколько всего прыгающих мячей у Криса?
Словесные задачи 1-й классПервый класс является продолжением детского сада, когда речь идет о словесных задачах, когда дети все еще используют конкретные ресурсы, чтобы помочь им понять и визуализировать задачи, над которыми они работают
Пример текстовой задачи для первого класса будет:
Класс из 10 детей, у каждого в пенале по 5 карандашей. Сколько всего карандашей?
Словесные задачи во 2-м классе Во втором классе дети перестанут использовать конкретные ресурсы при решении текстовых задач и перейдут к использованию письменных методов.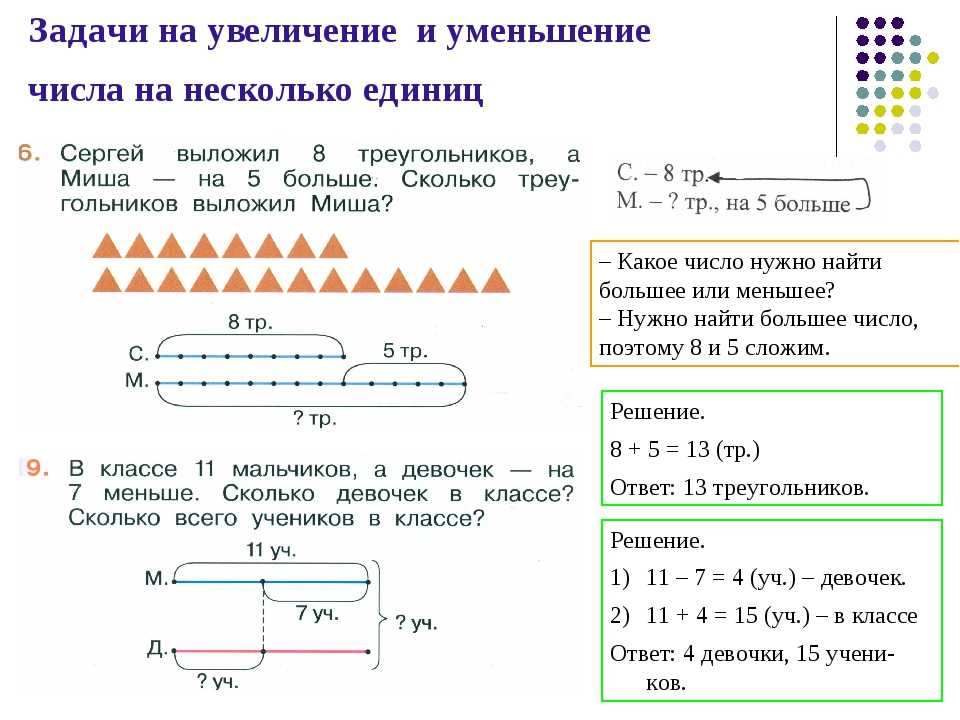
Учителя начнут демонстрировать сложение и вычитание в пределах 100, складывая до 4 двузначных чисел за раз.
В этом же году будут введены двухэтапные текстовые задачи. Это задача, требующая выполнения двух отдельных вычислений.
Задача для второго класса: геометрические свойства фигуры
Шон делает фигуры из пластиковых соломинок.
В вершинах, где встречаются соломинки, он скрепляет их кусочками пластилина
Вот некоторые из форм, которые он делает:
| Форма | 91914 Количество соломинок 4 комков глины для лепки||
| A | 4 | 4 |
| B | 3 | 3 |
| C | 6 | 6 |
One of Sean’s shapes is a triangle. Что он? Поясните свой ответ.
Ответ: фигура В в виде треугольника имеет 3 стороны (соломинка) и 3 вершины или угла (глина)
Словесная задача для 2 класса: Статистика 2 класс собирает камешки.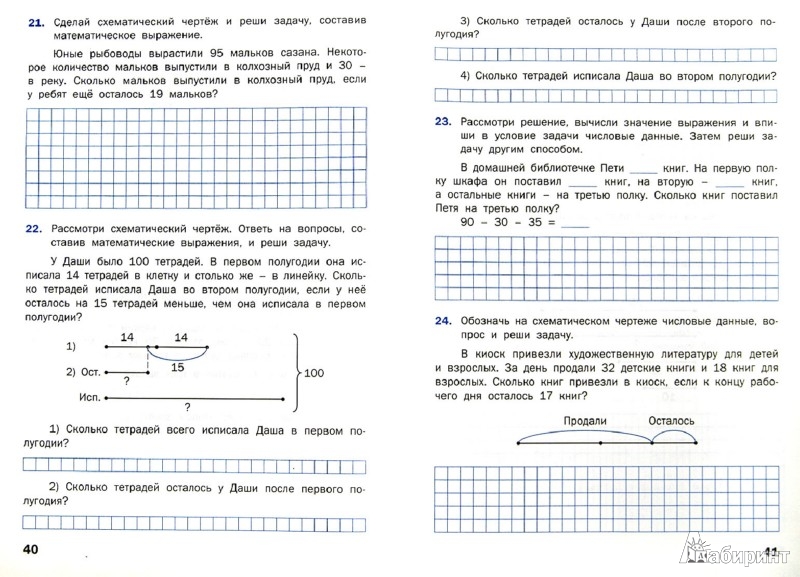
На этой пиктограмме показано разное количество камешков, которое находит каждая группа.
Речевые задачи в 3-м классе
На этом этапе обучения в начальной школе дети должны уверенно пользоваться письменными методами сложения и вычитания. Они начнут умножать и делить в пределах 100.
В этом году детям будут предложены различные задачи, в том числе двухэтапные, и они должны будут разработать соответствующий метод, необходимый для решения каждой из них.
Задача для 3-го класса: числа и разряды
Мое число состоит из четырех цифр и имеет 7 в разряде сотен.
Наибольшее значение в моем числе имеет цифра 2.
Наименьшее значение в моем числе — 6.
В моем числе на 3 десятка меньше, чем сотен.
Какой у меня номер?
Ответ: 2,746
Словесные задачи в 4-м классе
Одно- и двухшаговые словесные задачи продолжаются в четвертом классе, но в этом же году дети знакомятся со словесными задачами, содержащими десятичные дроби.
Словесная задача для четвертого класса: Дроби и десятичные дроби
Стэн, Фрэнк и Джон моют машины возле своих домов.
Стэн помыл 0,5 своей машины.
Фрэнк помыл 1/5 часть своей машины.
Норм помыл 2/5 своей машины.
Кто больше всех вымыл?
Объясните свой ответ.
Ответ: Стэн (он выстирал 0,5, тогда как Фрэнк выстирал только 0,2 и Норма 0,4)
Словесные задачи в 5-м классе
В пятом классе дети переходят от двухшаговых задачников к многошаговым задачам. К ним относятся дроби и десятичные дроби.
Вот несколько примеров задач по математике, которые предстоит решить в пятом классе.
Задача для 5-го класса. Соотношение и пропорция
Ангел Севера — большая статуя в Англии. Его высота 20 метров, а ширина 54 метра.
Элли делает масштабную модель Ангела Севера. Ее модель ростом 40 сантиметров. Насколько широка ее модель?
Ответ: 108см
Словесная задачка в пятом классе – Алгебра
Амина делает конструкции с двумя разными формами.
Каждой форме она присваивает значение.
Рассчитать значение каждой формы.
Ответ: 36 (шестиугольник) и 25.
Словесная задача для пятого класса: Измерение
В классе 28 учеников.
У учителя есть 8 литров апельсинового сока.
Она наливает каждому ученику по 225 миллилитров апельсинового сока.
Сколько апельсинового сока осталось?
Ответ: 1,7 литра или 1700 мл
Тематические задачи
Следующие примеры дают вам представление о том, с какими математическими задачами ваш ребенок столкнется в начальной школе
Задача со значением разряда для четвертого класса
Эта машина вычитает одну сотую каждый раз, когда нажимается кнопка. Стартовый номер 8,43. Какое число покажет машина, если кнопку нажать шесть раз? Ответ: 8.37
Скачать бесплатно словесные задачи с числами и разрядами для 2, 3, 4 и 5 классов
Словесные задачи на сложение и вычитание для 2 класса
У Сэма 64 конфеты.
Ему дают еще 12. Затем он отдает 22. Сколько конфет у него осталось? Ответ: 54
Скачать бесплатно задачи на сложение и вычитание для 2, 3, 4 и 5 классов
Задача на сложение для 2 класса
Сэмми загадывает число. Он вычитает 70. Его новое число — 12. Какое число придумал Сэмми? Ответ: 82
Задача на вычитание пятый класс
Температура в 7 часов вечера была 4oC. К полуночи похолодало на 9 градусов. Какая была температура в полночь? Ответ: -5oC
Задача на умножение третий класс
Яйца продаются в коробках по 12 штук. Яйца в коробки доставляются в магазины в ящиках. В каждом ящике по 9 коробок. Сколько яиц в ящике? Ответ: 108
Скачать бесплатно задачи на умножение для 2, 3, 4 и 5 классов.
Задача на деление для пятого класса
Каждый день фабрика производит 3572 кисти для рисования. Они упакованы в коробки по 19 штук. Сколько коробок производит фабрика каждый день? Ответ: 188
Загрузите бесплатные текстовые задачи на деление для 2, 3, 4 и 5 классов.
Бесплатный ресурс: Используйте эти четыре задачи со словами на сложение, вычитание, умножение и деление вместе.
Задача на дробь, четвертый класс
В конце каждого дня на шоколадной фабрике остается 1 и 2/6 коробок конфет. Сколько коробок конфет осталось к концу недели? Ответ: 9 и 2/6 или 9 и 1/3
Скачать бесплатно задачи на дроби и десятичные дроби для 2, 3, 4 и 5 классов.
Задача на деньги для второго класса
Люси и Нур нашли деньги на игровой площадке на перемене. Люси нашла 2 десятицентовика и 1 пенни, а Нур нашла 2 четвертака и 1 цент. Сколько центов нашли Люси и Нур? Ответ: Люси = 0,21 доллара, Нур = 0,60 доллара; 0,21 $ + 0,61 $ = 0,81 $
Задача на площадь 3-й класс
Размер прямоугольника 6 см на 5 см.
Какова его площадь? Ответ: 30 см2
Задача о периметре 3-й класс
Бассейн отеля Sunshine Inn имеет длину 20 м и ширину 7 м. Мэри дважды обплывает край бассейна.
Сколько метров она проплыла? Ответ: 108m
Словесная задача на пропорции 5 класс (кроссовер с измерением)
Местный совет провел день, рисуя двойные желтые линии. Они используют 1 банку желтой краски на каждые 100 м покрашенной дороги. Сколько банок краски понадобится им, чтобы покрасить участок дороги длиной 2 км? Ответ: 20 горшков
Словесная задача PEMDAS для пятого класса
Заключите пару скобок в один из этих вычислений так, чтобы они давали два разных ответа. Каковы ответы?
50 – 10 × 5 =
50 – 10 × 5 =
Словесная задача на объем, пятый класс
Этот большой прямоугольный параллелепипед был сделан путем штабелирования транспортных контейнеров на лодке. Каждый отдельный транспортный контейнер имеет длину 6 м, ширину 4 м и высоту 3 м. Каков объем большого куба? Ответ: 864m3
Помните: словесные задачи могут измениться, но математика не изменится
Дети могут легко растеряться, когда впервые столкнутся со словесными задачками, но важно напомнить им, что пока контекст проблемы может быть представлен по-разному, математика, стоящая за ним, остается прежней.
Словесные задачи — это хороший способ перенести математику в реальный мир и сделать математику более актуальной для вашего ребенка. Так что помогите им попрактиковаться или даже попросите их поменяться местами и составить для вас несколько словесных задач.
Есть ли у вас ученики, которым нужна дополнительная помощь по математике?
Предоставьте своим учащимся четвертого и пятого классов больше возможностей для закрепления навыков обучения и практики с помощью персонализированного обучения элементарной математике с их собственным онлайн-репетитором по математике.
Каждый учащийся получает дифференцированное обучение, предназначенное для устранения индивидуальных пробелов в обучении, а организованное обучение гарантирует, что каждый учащийся учится в нужном темпе. Уроки соответствуют стандартам и оценкам вашего штата, плюс вы будете получать регулярные отчеты о каждом шаге.
Программы доступны для четвертого и пятого классов, и вы можете попробовать 6 уроков абсолютно бесплатно.
Проблемы с задачами по математике
ByBob Cunningham, EdM
Краткие советы, которые помогут детям решить математические задачи
Совет 1
Разметьте задачу.
Разметьте задачу.
Попросите детей прочитать задачу один раз. Затем попросите их прочитать его еще раз, обведя кружком важные слова и фразы. Это может помочь детям сосредоточиться и не торопиться.
Исследуйте темы, выбранные нашими экспертами
Математика
Школьные трудности
Первопричины
Проблемы в Word Чтобы получить правильный ответ, дети должны уметь читать слова, выяснять, какую математическую операцию использовать, а затем правильно выполнять вычисления.
Нарушение любого из этих навыков может вызвать проблемы. Если кажется, что дети хорошо разбираются в математике, но у них возникают трудности с решением текстовых задач, вот возможные причины:
Проблемы с чтением: Чтобы решать текстовые задачи, дети должны хорошо читать. Таким образом, даже если они обычно хорошо справляются с математикой, трудности с чтением могут усложнить словесные задачи.
Проблемы с пониманием математических фраз и понятий: Даже если дети умеют читать, у них могут возникнуть проблемы с поиском подсказок в текстовых задачах. Эти подсказки представляют собой фразы, которые помогают детям понять, что им нужно сделать, чтобы решить задачу, например сложить или вычесть. Затем дети должны перевести эти фразы в числовое предложение, например, «два плюс три равно пяти».
Проблемы с концентрацией и самоконтролем: Дети могут отвлекаться на слова или теряться в голове. Другие дети борются с самоконтролем и торопятся решить проблему.